ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
|
|
|
- Ada Gigli
- 7 anni fa
- Visualizzazioni
Transcript
1 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due variabili e rappresentarli graficamente: 1. f(, y) = log( +y 15)+7 6 y 1. f(, y) = +4 y 1 y ( 3. f(, y) = log 4. f(, y) = y +y + y+ y 5. f(, y) = e +y+ y 6. f(, y) = + y 4 + y f(, y) = ( 8. f(, y) = log ) +y y 36 4 y 4 9y 36 ) Risultati degli esercizi sugli insiemi di definizione: (1) Parte di piano esterna all iperbole y = 1 ed alla circonferenza (compresa) + y = 16 - () Parte di piano interna alla circonferenza + y = 1 ed esterna alla parabola (compresa) y = (3) Parte di piano esterna alla parabola y = nel semipiano inferiore alla retta y = + e interna alla parabola nel semipiano superiore - (4) Tutto R - (5) Parte di piano nel primo e terzo quadrante compresa tra le due rette y = e y = (comprese) - (6) Parte di piano esterna alla circonferenza + y = 4 e all iperbole y = 1 (comprese) - (7) Parte di piano interna alla circonferenza +y = 4 (compresa) ed esterna all ellisse 4 + 9y = 36 - (8) Parte di piano compresa tra la circonferenza + y = 4 e l ellisse 4 + 9y = 36. ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 1
2 Limiti Calcolare i seguenti limiti: 3 3 (1) lim (,y) (0,0) y () lim (,y) (0,0) (3) lim (,y) (0,0) (4) lim (,y) (1,0) (5) lim (,y) (0,0) (6) lim (,y) (1,) (7) lim (,y) (0,1) 3 + y 3 3y 3 y 5y + y ( 1) 3 + y y + 1 ( 3 ) y 1 + y sin y ( 1) 3 + ( 1) + (y ) + y 4y + 5 (y 1) 3 [ + (y 1) ] 5 y (8) lim (,y) (0,0) + y 4 Risultati degli esercizi sui limiti: (1) - () 0 - (3) Il limite non esiste - (4) Il limite non esiste (anche solo lungo l asse ) - (5) 0 - (6) 1 - (7) Il limite non esiste - (8) Il limite non esiste. Continuità eterminare l insieme di continuità delle seguenti funzioni in due variabili: { log(1+ +y ) (, y) (0, 0) (1) f(, y) = +y 0 (, y) = (0, 0) { sin 1 y 0 () f(, y) = y 0 y = 0 { ( ) y (3) f(, y) = 1 arctan y 0 y 0 y = 0 (4) f(, y) = { log(1+ ) ( +y ) 4 5 (, y) (0, 0) 0 (, y) = (0, 0) ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z)
3 { + y 0 (5) f(, y) = 0 = 0 { + y 1 0 (6) f(, y) = 0 = 0 Risultati degli esercizi sulla continuità: (1) f continua in tutto R - () f continua in R \{(, 0), 0} - (3) f continua in tutto R - (4) f continua in tutto R - (5) f continua in R \{(0, y), y 0} - (6) f continua in R \{(0, y), y 1 }. EQUAZIONI IFFERENZIALI Equazioni lineari del primo ordine Risolvere le seguenti equazioni differenziali ordinarie lineari del primo ordine e i problemi di Cauchy, specificando l insieme su cui è definita la soluzione: 1. y () + y() = e. y () + tan y() = sin 3. 1 y () + y() = arcsin 4. y () + y() = 3 5. y () cos + y() = tan 6. { y () + y() = 3 e y(0) = 1 7. { y () + y() y(1) = = e Calcolare lim 0 + y() { y () 7y() = 8e 3 y(0) = 3 { y () + n y() = a n y(1) = 0 { y () + y() e = 0 y(a) = b Calcolare y (0) y(0) ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 3
4 Risultati ( degli ) esercizi sulle equazioni lineari del primo ordine: (1) y() = + c e in R - () y() = cos + c cos in R \ { π + kπ} k Z - (3) y() = c e arcsin +arcsin 1 in ( 1, 1) - (4) y() = c in R \ {0} - (5) y() = c e tan +tan 1 in R \ { kπ 4 } k Z - (6) y() = e (3+1) in R - (7) y() = ( 1 ) 1 e + in (0, + ). Il limite richiesto vale 1 - (8) y() = e3 +e 7 in R. y (0) y(0) vale 10 e si può ricavare derivando la soluzione oppure, più velocemente, direttamente dall equazione. - (9) y() = a( 1) in (0, + ). - (10) y() = e +ab e a in (0, + ) se a > 0 e in (, 0) se a < 0. Equazioni del primo ordine a variabili separabili Risolvere i seguenti problemi di Cauchy per equazioni differenziali ordinarie del primo ordine a variabili separabili, specificando l insieme su cui è definita la soluzione: y () = y () 1. y(0) = y () = y() y(0) = 1 y () = 3 cos sin y () y(0) = 1 y () = (e y() 1) y(0) = log 3 y () = e 3y() y(0) = 0 Risultati degli esercizi sulle equazioni a variabili separabili: (1) y() = 1 1 per ( 1, 1) - () y() = 1 + per R - (3) y() = 1 ( per ( π, π 3 ) - (4) y() = log( + e 3 ) per R - (5) y() = 1 3 log 3e 1 per ( log 3, + ). cos 3 ) ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 4
5 Equazioni di Bernoulli Risolvere le seguenti equazioni differenziali ordinarie di Bernoulli: 1. { y () = y() + y() y(1) = 1. y () + y() = y ln 3. y () y() tan + y cos = 0 4. y () + y() 5. y () = 4y() = y() cos + y() Risultati degli esercizi sulle equazioni di Bernoulli: (1) y() = (e 1 4 1) 1 per R - () y() = 1+ln +c con > 0, 1+ln +c 0 ( ) 1 - (3) y() = (+c) cos per π +kπ, +c 0 - (4) y() = c+ln cos + tan con 0 e π + kπ - (5) y() = 4 ( 1 ln + c) con 0. Equazioni lineari a coefficienti costanti - Omogenee Risolvere le seguenti equazioni differenziali ordinarie lineari a coefficienti costanti omogenee, e relativi problemi di Cauchy: 1. y () y () 3y() = 0. y () y () = 0 y () + 9y () = 0 3. y(0) = 1 y (0) = y () 4y () + 5y() = 0 y(0) = 0 y (0) = y () 6y () + 9y() = 0 y(0) = 1 y (0) = 1 y () y () y() = 0 y(0) = 0 y (0) = 1 ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 5
6 7. 8. y (IV ) () 16y() = 0 lim + e y() = 3 y (IV ) () + 8y () = 0 y(0) = 0 lim + y() = 1 - Non omogenee Risolvere le seguenti equazioni differenziali ordinarie lineari a coefficienti costanti non omogenee, e relativi problemi di Cauchy. Si ricorda che nel metodo di somiglianza il termine noto è del tipo speciale: f() = P (n) () e α cos β + Q (m) () e α sin β. 1. y () + y () + y() = 3 cos 4 sin. y () + 3y () + y() = e 3. y () 6y () + 8y() = y () + y() = cos 5. y () + y () + y() = e 6. y () y () = e 3 y () + y () = 7. y(0) = 1 y (0) = y () 8y () + 16y() = e 4 y(0) = 0 y (0) = 1 y () y () = (1 ) y(0) = 1 y (0) = 1 y () + 4y () = cos y(0) = y (0) = y (0) = y () y () + y() = e 1. y () + y() = cos + 1 cos ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 6
7 Risultati degli esercizi sulle EO lineari a coefficienti costanti: Omogenee: (1) y() = c 1 e 3 + c e - () y() = c 1 e + c - (3) y() = cos sin 3 - (4) y() = e sin - (5) y() = ( + 1)e 3 - (6) y() = 1 3 e 1 3 e - (7) Gli zeri del polinomio caratteristico sono,, i e i. La soluzione generica è y() = c 1 e + c e + c 3 cos + c 4 sin. Imponendo la condizione richiesta, lim + (c 1 e 4 + c + c 3 e cos + c 4 e sin ) = 3, deve essere c 1 = 0 perché e 4 ha limite infinito e c 3 = c 4 = 0 perché e cos e e sin non hanno limite. Risulta quindi c = 3 e la soluzione del problema è y() = 3e - (8) Gli zeri del polinomio caratteristico sono 0,, 1 + i 3 e 1 i 3. La soluzione generica è y() = c 1 + c e + c 3 e cos 3 + c 4 e sin 3. Imponendo la prima condizione si ha c 1 + c + c 3 = 0, e imponendo la seconda lim + (c 1 + c e + c 3 e cos 3 + c 4 e sin 3) = 1, deve essere c 3 = c 4 = 0 perché e cos 3 e e sin 3 non hanno limite e risulta quindi c 1 = 1. La soluzione del problema è y() = 1 e Non omogenee: (1) Con metodo di somiglianza, il termine noto è di tipo speciale con α = 0 e β =. α + iβ non è soluzione del polinomio caratteristico e quindi una soluzione particolare è del tipo y p () = A cos + B sin. La soluzione è y() = c 1 e + c e + cos - () Con metodo di somiglianza, il termine noto è di tipo speciale con α = 1 e β = 0. α + iβ è soluzione semplice del polinomio caratteristico e quindi una soluzione particolare è del tipo y p () = Ae. La soluzione è y() = c 1 e + c e + e - (3) Con metodo di somiglianza, il termine noto è di tipo speciale con α = 0 e β = 0. α + iβ non è soluzione del polinomio caratteristico e quindi una soluzione particolare è del tipo y p () = A + B + C. La soluzione è y() = c 1 e 4 + c e (4) Con metodo di somiglianza, il termine noto è di tipo speciale con Q() = 0, α = 0 e β = 1. α + iβ è soluzione del polinomio caratteristico e quindi una soluzione particolare è del tipo y p () = [A cos + B sin ]. La soluzione è y() = c 1 cos + c sin + sin - (5) Con metodo di somiglianza, il termine noto è di tipo speciale con P () =, α = 1 e β = 0. α + iβ non è soluzione del polinomio caratteristico e quindi una soluzione particolare è del tipo y p () = (A + B)e. La soluzione è y() = c 1 e cos +c e sin ( 4 5 )e - (6) Si applica il principio di sovrapposizione. Per f 1 () = si trova una soluzione particolare della forma y p1 () = (A + B) e per f () = e 3 si trova una soluzione particolare della forma y p () = Ae 3. La soluzione è y() = c 1 + c e e3 - (7) 0 è soluzione semplice del polinomio caratteristico, quindi una soluzione particolare è del tipo y p () = (A +B+C). La soluzione è y() = e (8) α+iβ = 4 è soluzione doppia del polinomio caratteristico, quindi una soluzione particolare è del tipo y p () = A e 4. La soluzione è y() = ( 1 + )e 4 - (9) 0 è soluzione semplice del polinomio caratteristico, quindi una soluzione particolare è del tipo y p () = (A + B). La soluzione è y() = e + - (10) α + iβ = i è soluzione del polinomio caratteristico, quindi una soluzione particolare è del tipo y p () = A cos + B sin. La soluzione è y() = 1 16 sin 1 8 cos - (11) ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 7
8 Il termine noto non è di tipo speciale. Si procede con metodo della variazione delle costanti. La soluzione è y() = c 1 e + c e e + e log - (1) Si applica il principio di sovrapposizione. Per f 1 () = cos si trova una soluzione particolare della forma y p1 () = (A cos + B sin ) e per f () = 1 cos si procede con metodo della variazione delle costanti. La soluzione è y() = c 1 cos +c sin + cos log cos + 3 sin. 3 FUNZIONI IN UE VARIABILI (II parte) Continuità, derivabilità parziale, differenziabilità Stabilire se le seguenti funzioni sono continue, derivabili parzialmente e differenziabili nell origine, eventualmente al variare dei parametri reali che vi compaiono: ( ) ( y 1 ) sin (, y) (0, 0) +y 1. f(, y) = 0 (, y) = (0, 0) y (, y) (0, 0) +y. f(, y) = 0 (, y) = (0, 0) 3. f(, y) = y + y (, y) (0, 0) 0 (, y) = (0, 0) 3 + y(y 1)+y y 3 (, y) (0, 0) +y 4. f(, y) = 0 (, y) = (0, 0) 5. f(, y) = 6. f(, y) = 7. f(, y) = { { (+3y) 3 +y + log(1 + y ) (, y) (0, 0) 0 (, y) = (0, 0) (e y 1) α +y (, y) (0, 0) 0 (, y) = (0, 0) 1+α+βy e +y +y (, y) (0, 0) 0 (, y) = (0, 0) ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 8
9 Risultati degli esercizi sulla regolarità: (1) La funzione risulta continua, derivabile parzialmente e differenziabile. Il limite per la differenziabilità si può fare con le maggiorazioni - () La funzione risulta continua e derivabile parzialmente ma non è differenziabile (si può vedere facendo il limite lungo le rette passanti per l origine) - (3) La funzione risulta continua, derivabile parzialmente e differenziabile - (4) La funzione risulta continua, derivabile parzialmente e differenziabile - (5) La funzione risulta continua, derivabile parzialmente e differenziabile - (6) La funzione è continua solo per α > 1 ed è derivabile con derivate parziali nulle per α > 0. Inoltre è differenziabile per α > 3 - (7) La funzione non è continua per nessuna scelta dei parametri (si può vedere facendo il limite lungo l asse che vale + o a seconda del segno di α con α 1 e di, e vale 1 per α = 1). Inoltre non essendo continua lungo gli assi non è neanche derivabile parzialmente (come funzione di una variabile lungo gli assi la non continuità implica la non derivabilità), e dunque non è neanche differenziabile nell origine. erivate direzionali 1. eterminare la derivata direzionale di f(, y) = e cos y nel punto (0, 0) in direzione v = (1, ).. eterminare la derivata direzionale di f(, y) = y nel punto (0, 0) in direzione v = (1, 1). 3. Sia f(, y) = 3 y. Stabilire se f è continua in R. Calcolare le derivate parziali e le derivate direzionali lungo una generica direzione ˆv nel punto (1, ). Stabilire se la funzione è differenziabile nell origine. 4. ata la funzione: log 3 (1+ 1 ) + e y (, y) (1, 0) ( 1) +y f(, y) = 1 (, y) = (1, 0) stabilire se la funzione è continua e differenziabile nel punto (1, 0). Calcolare inoltre la derivata direzionale di f nel punto (1, 0) lungo la direzione normale esterna nel punto (1, 0) al cerchio di centro (1, 1) e raggio 1. Risultati degli esercizi sulle derivate direzionali: (1) Il versore corrispondente a v è ˆv = ( 1 5, 5 ). Applicando la definizione oppure la formula del prodotto del gradiente per il versore, si trova fˆv (0, 0) = () Il ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 9
10 versore corrispondente a v è ˆv = ( 1 1, ). Poichè la funzione non è differenziabile nell origine, si può applicare solo la definizione e si trova fˆv (0, 0) = 0 - (3) La funzione è continua in tutto R e differenziabile (e quindi derivabile) in tutto il piano privato degli assi. f (1, ) = 3 3 e fy (1, ) = 1. Nel punto (1, ) la funzione è differenziabile e quindi le derivate direzionali lungo ˆv = (v 1, v ) sono fˆv (1, ) = 3 3 v v 4. Le derivate parziali nell origine esistono e sono nulle ma f non è differenziabile nell origine - (4) La funzione risulta continua nel punto (1, 0), ma non differenziabile (non esiste f (1, 0)). La direzione ˆv normale esterna nel punto (1, 0) al cerchio di centro (1, 1) e raggio 1 è quella in direzione ê = (0, 1) dell asse y ma in verso opposto, ovvero ˆv = (0, 1) = ê. Pertanto la derivata direzionale richiesta è fˆv (1, 0) = fê (1, 0) = f y (1, 0) = Piano tangente eterminare l equazione del piano tangente al grafico delle seguenti funzioni nel punto a fianco indicato: 1. f(, y) = 3 y + 5y + y 3 P (0, 1, 1). f(, y) = 1 ( +y ) P (1, 1, 1 4 ) Risultati degli esercizi sul piano tangente: (1) z(, y) = 5 + 3y - () z(, y) = 1 1 y INTEGRALI OPPI Aree di domini in R Calcolare l area dei seguenti domini in R : 1. = { (, y) R : y 9 ; 8 y 5 }. = {(, y) R R : y tan π3 ; + y R } R > 0 Risultati degli esercizi sulle aree dei domini in R : (1) Si divide il dominio in due domini normali rispetto ad, tra 0 e 1 e tra 1 e. Si trova che l area vale () Si può considerare il dominio normale rispetto ad y, oppure dividerlo in due domini normali rispetto ad, oppure usare le coordinate polari con θ [ π 4, π 3 ] e ρ [ R sin θ, R]. Si trova che l area vale π R. ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 10
11 Integrali doppi su domini normali Calcolare i seguenti integrali doppi su unioni di domini normali: 1. d dy 4 y = {(, y) R : 0 1 ; y min{ ; 1}}. + y e y d dy è il triangolo di vertici O(0, 0), A(1, 1), B(1, ) sin ( + y) d dy { = (, y) R : π 0 ; + y π } ( y ) d dy è il triangolo di vertici O(0, 0), A(1, 1), B(, 1) d dy 1 + = { (, y) R : 0 1 ; y } e y d dy = {(, y) R : 0 y ; y min{ y ; 1}} y 1 + d dy y = { (, y) R : 0 1 ; 1 y } y d dy = { (, y) R : 0 1 ; y 1 } y d dy = { (, y) R : + y 1 } d dy { = (, y) R : y + } + 3 ; y ; y + y d dy = { (, y) R : 4 + 9y 36 ; y 0 } ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 11
12 Risultati degli esercizi sugli integrali doppi su domini normali: (1) () e e (3) π (4) (5) 5 π log - (6) e e - (7) 1 + log( + ) - (8) (9) (10) 4 - (11) Con coordinate ellittiche = 3ρ cos θ, y = ρ sin θ con ρ [0, 1] e θ [0, π], si trova che l integrale vale 8. Integrali doppi con coordinate polari Calcolare i seguenti integrali doppi con coordinate polari: 1. d dy y = {(, y) R : 0 ; 1 + y 4}. y + y e +y d dy = {(, y) R : y 0 ; + y 1} y 1 d dy y = {(, y) R : y 0 ; + y 1} y 1 d dy y + y = {(, y) R : y 0 ; 1 + y 3} ye + y d dy e ye +y d dy + y = {(, y) R : y ; 0 ; 1 + y 4} {(, y) R : 3 y ; 0 ; 1 + y 4} d dy = {(, y) R : y ; 1 + y } y d dy = {(, y) R : + y 1} y + y d dy = {(, y) R : y 0 ; + y 0} y d dy è la metà superiore del cerchio di centro a (a>0) passante per (0,0) ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 1
13 Risultati degli esercizi sugli integrali doppi con coordinate polari: (1) [1 arctan + arctan 1] - () e+e 1 - (3) log 4 - (4) π 6 - (5) Il primo integrale vale e 1 + e e 1 ) e 1 e il secondo integrale vale 3 (e 1 e 1 - (6) 1 3 (4 ) - (7) 1 - (8) (9) a CURVE E INTEGRALI CURVILINEI Lunghezza di una curva Calcolare la lunghezza dei seguenti archi di curva: 1. γ(t) = (cos t; cos t sin t) t [ ] 0, π. γ(t) = (t 3 ; t ) t [0, 1] 3. γ(t) = (t; t 3 ) t [ ] 0, 1 4 Risultati degli esercizi sulla lunghezza di una curva: (1) La curva è un arco di curva regolare in quanto è derivabile con derivata continua γ (t) = ( cos t sin t; cos t sin t) (0, 0) per ogni t ( 0, π ). Inoltre γ (t) = 1 e si ha π 0 γ (t) dt = π - () La curva è un arco di curva regolare in quanto è derivabile con derivata continua γ (t) = (3t ; t) (0, 0) per ogni t (0, 1). Inoltre γ (t) = t 9t + 4 e si ha 1 0 γ (t) dt = (3) La curva è un arco di curva regolare in quanto è derivabile per t ( 0, 4] 1 con derivata continua γ (t) = (1; 3 ( t) (0, 0) per ogni t 0, 1 4). Inoltre γ (t) = γ (t) dt = Integrali curvilinei t e si ha opo aver verificato che il sostegno delle seguenti curve è contenuto nel dominio delle funzioni f(, y), calcolare i seguenti integrali curvilinei: 1. ds γ(t) = (t; t ) t [0, a], a 0 γ. 1 y ds γ(t) = (sin t; cos t) t [0, π] γ 3. [0, γ 1 + y ds γ(t) = (cos t; sin t) t π ] 4. y ds γ(t) = (t; e t ) t [0, log ] 5. γ γ y ds γ è l ellisse a + y = 1, a, b > 0;, y 0 b ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 13
14 Risultati degli esercizi sugli integrali curvilinei: (1) Il dominio di f è R. La curva è regolare in quanto è derivabile con derivata continua γ (t) = (1; t) (0, 0) per ogni t (0, a). Inoltre γ (t) = 1 + 4t [ (1 + 4a) 3 1 e si ha a 0 f(γ(t)) γ (t) dt = () Il sostegno di γ è contenuto nel dominio di f che è {(, y) R : y 1}. La curva è regolare in quanto è derivabile con derivata continua γ (t) = (cos t; sin t) (0, 0) per ogni t (0, π). Inoltre γ (t) = 1 e si ha π 0 f(γ(t)) γ (t) dt = - (3) Il dominio di f è R. La curva è regolare in quanto è derivabile con derivata continua γ (t) = ( sin t; cos t) (0, 0) per ogni t ( 0, π ). Inoltre γ (t) = 1 e si ha π 0 f(γ(t)) γ (t) dt = π 4 - (4) Il dominio di f è R. La curva è regolare in quanto è derivabile con derivata continua γ (t) = (1; e t ) (0, 0) per ogni t (0, log ). Inoltre γ (t) = 1 + e t e si ha log 0 f(γ(t)) γ (t) dt = (5) Il dominio di f è R. L ellisse γ(t) = (a cos t; b sin t) è regolare in quanto è derivabile con derivata continua γ (t) = ( a sin t; b cos t) (0, 0) per ogni t ( 0, π ). Inoltre γ (t) = a sin t + b cos t e si ha π 0 f(γ(t)) γ (t) dt = ab(a +ab+b ) 3(a+b). 6 FORME IFFERENZIALI E CAMPI VETTORIALI 1. ata la forma differenziale ω(, y) = e y d + (1 + e y ) dy, calcolare il suo integrale sulla curva di equazione y = + e cos fra i punti di ascissa = 0 e = 1.. eterminare ϕ C 1 (R) con ϕ(0) = 0 tale che la forma differenziale ω(, y) = [ + ϕ(y)] d + [(y ϕ(y))] dy sia esatta e calcolarne la primitiva che si annulla nell origine. 3. Trovare tutte le funzioni a, b C 1 (R) tali che la forma differenziale sia esatta e calcolarne le primitive. γ ω(, y) = a(y) d + b() dy 4. Sia γ l arco dell ellisse + y = 1 tra i punti A( 3, 0) e B(0, ) percorso 9 4 in verso antiorario. Calcolare ( ) 1 + ( + y) d ( + y) dy 5. Sia γ la curva definita da γ(t) = (1 t ; t 6 ) t [0, 1]. Calcolare + 4y d + 4y + 4y dy γ ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 14 ]
15 6. Stabilire quanto vale l integrale della forma differenziale ω = (y + 1) d + ( 5y 3 3y ) dy y 3 sulle curve congiungenti i punti P (0, 1) e Q(, 1). 7. Sia γ la frontiera del dominio T = {(, y) R : 1 ( 8) +y }. Calcolare f(log ( + y)) d + f(log ( + y)) dy +γ dove f è una funzione di classe C 1 ([0, )). 8. eterminare le regioni del piano su cui è esatta la forma ( ω = y 1 ) d + dy e determinare le primitive di ω su tali regioni. 9. Sia F : R R il campo vettoriale ( y F (, y) = (1 + ) ; 1 ) 1 + ire se F è conservativo e in caso affermativo determinare il potenziale. 10. Siano F : R R il campo vettoriale F (, y) = (e [sin( + y) + cos( + y)] ; e cos( + y)) e γ n : [0, π] R le curve definite da γ n (t) = (cos nt ; sin nt) con n N e n 1. ire se F è conservativo e in caso affermativo determinare il potenziale. Calcolare inoltre il lavoro di F lungo γ n. 11. Sia F : R R il campo vettoriale F (, y) = ( 3 + y ; + y ) ire se F è conservativo e in caso affermativo determinare il potenziale. 1. eterminare per quali valori di a R si annulla il lavoro del campo vettoriale F : R R F (, y) = ( + y ; ay) sulla curva γ(t) = (cos t, sin t) con t [0, π]. ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 15
16 Risultati degli esercizi su forme differenziali e campi vettoriali: Le costanti che compaiono vanno intese in R. (1) Il calcolo diretto dell integrale non è agevole, ma la forma è esatta. Calcolando la differenza dei valori di una primitiva agli estremi (1, 1+e cos 1) e (0, 1), l integrale vale e cos 1 + e 1+e cos 1 - () La condizione di chiusura dà ϕ (y) = y ϕ(y). Risolvendo questa equazione differenziale con ϕ(0) = 0, si ottiene ϕ(y) = e y + y 1. La primitiva di ω che si annulla nell origine è f(, y) = + (e y + y 1) - (3) La condizione di chiusura dà a y (y) = b () che è possibile solo se sono costanti a y (y) = b () = C. Si trova quindi a(y) = Cy + c 1 e b() = C + c. Le primitive di ω sono f(, y) = Cy + c 1 + c y + c - (4) L arco di ellisse è contenuto nel semipiano > 10 dove la forma è definita ed esatta. L integrale si può calcolare direttamente parametrizzando la curva oppure con la differenza dei valori di una primitiva agli estremi. L integrale risulta arctan + 10 arctan (5) La curva γ non passa per l origine, dove la forma non è definita. Si può calcolare l integrale direttamente oppure sfruttando il fatto che la forma è chiusa in R \{(0, 0)}. Questo dominio non è semplicemente connesso e dunque non si può concludere che la forma sia esatta in tutto R \{(0, 0)}, ma la forma è localmente esatta in domini semplicemente connessi lontano dall origine. Si può quindi trovare una primitiva e calcolarne la differenza agli estremi. L integrale vale log - (6) La forma è definita e chiusa nell insieme E = {(, y) R : y < 3 } che è semplicemente connesso. Le primitive sono f(, y) = (y + 1) y 3 + c e l integrale vale f(, 1) f(0, 1) = 3, ma solo lungo le curve congiungenti P e Q aventi il supporto contenuto in E - (7) La forma è definita e chiusa nell insieme E = {(, y) R : + y > 0} che è semplicemente connesso e quindi è esatta. Poiché T è una corona circolare tutta contenuta in E, l integrale della forma sulla sua frontiera è nullo - (8) La forma è esatta su Ω 1 = {(, y) R : < 0} e Ω = {(, y) R : > 0}. Le primitive sono f(, y) = y log( ) + c in Ω 1 e f(, y) = y log + c in Ω - (9) Il campo risulta irrotazionale in tutto R e quindi è conservativo. Il potenziale è U(, y) = y + c - (10) Il campo 1+ risulta conservativo in R e il potenziale è U(, y) = e sin( + y) + c. Le curve γ n sono chiuse per n pari e quindi il lavoro è nullo. Per n dispari il lavoro vale U( 1, 0) U(1, 0) = (e + e 1 ) sin 1 - (11) Il campo risulta irrotazionale in tutto R e quindi è conservativo. Il potenziale è U(, y) = 3 + y + y + c - (1) Calcolando l integrale di F lungo γ tramite la definizione, si trova che l integrale è nullo per ogni valore di a reale. ott.ssa Silvia Marconi - Analisi II, Ing. Civile - Trasporti (M-Z) 16
ESERCIZI DI ANALISI II Ingegneria per l Ambiente e il Territorio a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria per l Ambiente e il Territorio a.a. 006/007 FUNZIONI IN UE VARIABILI Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due variabili
ESERCIZI I ANALISI II Ingegneria per l Ambiente e il Territorio a.a. 006/007 FUNZIONI IN UE VARIABILI Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due variabili
Facoltà di Architettura Valle Giulia Corso di Laurea Specialistica Quinquennale U.E. 1 CALCOLO INTEGRALE PER LE FUNZIONI DI UNA VARIABILE
 Facoltà di Architettura Valle Giulia Corso di Laurea Specialistica Quinquennale U.E. Istituzioni di Matematica 2 a.a. 2007-2008 http://www.dmmm.uniroma.it/persone/capitanelli CALCOLO INTEGRALE PER LE FUNZIONI
Facoltà di Architettura Valle Giulia Corso di Laurea Specialistica Quinquennale U.E. Istituzioni di Matematica 2 a.a. 2007-2008 http://www.dmmm.uniroma.it/persone/capitanelli CALCOLO INTEGRALE PER LE FUNZIONI
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Limite. Se D non è limitato si può fare il limite di f(x) per x che tende
 Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Campi conservativi e forme esatte - Esercizi svolti
 Campi conservativi e forme esatte - Esercizi svolti 1) Dire se la forma differenziale è esatta. ω = 2 2 (1 + 2 2 ) 2 d + 2 2 (1 + 2 2 ) 2 d 2) Individuare in quali regioni sono esatte le seguenti forme
Campi conservativi e forme esatte - Esercizi svolti 1) Dire se la forma differenziale è esatta. ω = 2 2 (1 + 2 2 ) 2 d + 2 2 (1 + 2 2 ) 2 d 2) Individuare in quali regioni sono esatte le seguenti forme
Statistica Matematica e Trattamento Informatico dei Dati. Analisi Matematica 3. Esercizi svolti nelle lezioni. V. Del Prete
 Statistica Matematica e Trattamento Informatico dei Dati A.A.00-0 Analisi Matematica 3 Esercizi svolti nelle lezioni V. Del Prete Numeri complessi Argomenti ed esercizi svolti nelle lezioni 30.09.00 e
Statistica Matematica e Trattamento Informatico dei Dati A.A.00-0 Analisi Matematica 3 Esercizi svolti nelle lezioni V. Del Prete Numeri complessi Argomenti ed esercizi svolti nelle lezioni 30.09.00 e
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
ALCUNE SOLUZIONI DI ESERCIZI SU CAMPI VETTORIALI
 ALCUNE SOLUZIONI DI ESERCIZI SU CAMPI VETTORIALI Appello Febbraio 995 ( F (( + y i y (( + y j. ( Stabilire se F è conservativo e in caso affermativo trovarne un ( Calcolare il lavoro compiuto dal campo
ALCUNE SOLUZIONI DI ESERCIZI SU CAMPI VETTORIALI Appello Febbraio 995 ( F (( + y i y (( + y j. ( Stabilire se F è conservativo e in caso affermativo trovarne un ( Calcolare il lavoro compiuto dal campo
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Esercizi 17.XI.2017 1. Verificare che le curve definite dalle seguenti parametrizzazioni sono regolari, o regolari
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Esercizi 17.XI.2017 1. Verificare che le curve definite dalle seguenti parametrizzazioni sono regolari, o regolari
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
3 ) (5) Determinare la proiezione ortogonale del punto (2, 1, 2) sul piano x + 2y + 3z + 4 = 0.
 1 Calcolo vettoriale 1 Scrivere il vettore w =, 6 sotto forma di combinazione lineare dei vettori u = 1, e v = 3, 1 R w = v 4u Determinare la lunghezza o il modulo del vettore, 6, 3 R 7 3 Determinare la
1 Calcolo vettoriale 1 Scrivere il vettore w =, 6 sotto forma di combinazione lineare dei vettori u = 1, e v = 3, 1 R w = v 4u Determinare la lunghezza o il modulo del vettore, 6, 3 R 7 3 Determinare la
Analisi Matematica II - INGEGNERIA Gestionale - B 20 luglio 2017 Cognome: Nome: Matricola:
 Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Esercizi. f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 )
 Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Prima parte: DOMINIO E INSIEMI DI LIVELLO
 FUNZIONI DI DUE VARIABILI 1 Prima parte: DOMINIO E INSIEMI DI LIVELLO Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, limitati, convessi, connessi
FUNZIONI DI DUE VARIABILI 1 Prima parte: DOMINIO E INSIEMI DI LIVELLO Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, limitati, convessi, connessi
Forme differenziali e campi vettoriali: esercizi svolti
 Forme differenziali e campi vettoriali: esercizi svolti 1 Esercizi sul Teorema di Green......................... 2 2 Esercizi sul Teorema di Stokes......................... 4 3 Esercizi sul Teorema di
Forme differenziali e campi vettoriali: esercizi svolti 1 Esercizi sul Teorema di Green......................... 2 2 Esercizi sul Teorema di Stokes......................... 4 3 Esercizi sul Teorema di
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = tan(2x 2 + 3y 2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 7-9- - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 7-9- - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
y (b) f(x, y) = y log x sin x (c) f(x, y) = tan y (d) f(x, y) = e x y (f) f(x, y) = cos(x 2 + y 2 )
 FUNZIONI DI PIÙ VARIABILI. Siano date le seguenti funzioni: (a) f(x, y) = 3x + y (c) h(x, y) = x y (b) g(x, y) = xy (d) k(x, y) = x + y Determinare e disegnare nel piano cartesiano il dominio delle funzioni
FUNZIONI DI PIÙ VARIABILI. Siano date le seguenti funzioni: (a) f(x, y) = 3x + y (c) h(x, y) = x y (b) g(x, y) = xy (d) k(x, y) = x + y Determinare e disegnare nel piano cartesiano il dominio delle funzioni
Prof. R. Capone Esercitazioni di Matematica IV Corso di studi in Matematica
 Forme differenziali lineari Sia Ω R un insieme aperto e siano A, B, C: Ω R funzioni continue in Ω. Si definisce forma differenziale ω in Ω l espressione ω = A(, y, z)d + B(, y, z)dy + C(, y, z)dz Data
Forme differenziali lineari Sia Ω R un insieme aperto e siano A, B, C: Ω R funzioni continue in Ω. Si definisce forma differenziale ω in Ω l espressione ω = A(, y, z)d + B(, y, z)dy + C(, y, z)dz Data
Prove scritte dell esame di Analisi Matematica II a.a. 2011/2012
 Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
Argomento 6: Derivate Esercizi. I Parte - Derivate
 6: Derivate Esercizi I Parte - Derivate E. 6.1 Calcolare le derivate delle seguenti funzioni: 1) log 5 3 + cos ) + 3 + 4 + 3 3) 5 tan 4) ( + 3e ) sin 5) arctan( + 1) 6) log 7) 10) + + 3 8) 3 3 1 + 16 11)
6: Derivate Esercizi I Parte - Derivate E. 6.1 Calcolare le derivate delle seguenti funzioni: 1) log 5 3 + cos ) + 3 + 4 + 3 3) 5 tan 4) ( + 3e ) sin 5) arctan( + 1) 6) log 7) 10) + + 3 8) 3 3 1 + 16 11)
ESERCIZI PRECORSO DI MATEMATICA
 ESERCIZI PRECORSO DI MATEMATICA EQUAZIONI 1. cot( 10 ) 3. tan 3 3. cos( 45 ) +1 0 4. sin sin 5. tan( 180 ) tan( 3) 6. 5 cos 4sin cos 7. 3sin 3 cos 0 8. 3 cos + sin 3 0 9. sin3 sin( 45 + ) 10. 6sin 13sin
ESERCIZI PRECORSO DI MATEMATICA EQUAZIONI 1. cot( 10 ) 3. tan 3 3. cos( 45 ) +1 0 4. sin sin 5. tan( 180 ) tan( 3) 6. 5 cos 4sin cos 7. 3sin 3 cos 0 8. 3 cos + sin 3 0 9. sin3 sin( 45 + ) 10. 6sin 13sin
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013
 Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Derivate parziali, derivate direzionali, differenziabilità. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) =
 Derivate parziali, derivate direzionali, differenziabilità 1. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) = 3 x (y 1) + 1. b) Calcolare D v f(0, 1), dove v è il versore
Derivate parziali, derivate direzionali, differenziabilità 1. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) = 3 x (y 1) + 1. b) Calcolare D v f(0, 1), dove v è il versore
Università degli Studi di Salerno - Facoltà di Ingegneria Matematica II - Prova Scritta - 09/06/2006
 Matematica II - Prova Scritta - 09/06/2006 f(x, y) = (y x)e x2 y 2, 2. Risolvere le seguenti equazioni differenziali: y 2 = 1 1 (2x y) 2, y 2y + y 2y = e x (x 1). 3. Calcolare il seguente integrale curvilineo
Matematica II - Prova Scritta - 09/06/2006 f(x, y) = (y x)e x2 y 2, 2. Risolvere le seguenti equazioni differenziali: y 2 = 1 1 (2x y) 2, y 2y + y 2y = e x (x 1). 3. Calcolare il seguente integrale curvilineo
Ingegneria Tessile, Biella Analisi II
 Ingegneria Tessile, Biella Analisi II Esercizi svolti In questo file sono contenute le soluzioni degli esercizi sui campi vettoriali (cf foglio 5 di esercizi) Attenzione: in alcuni esercizi il calcolo
Ingegneria Tessile, Biella Analisi II Esercizi svolti In questo file sono contenute le soluzioni degli esercizi sui campi vettoriali (cf foglio 5 di esercizi) Attenzione: in alcuni esercizi il calcolo
Alcuni esercizi: funzioni di due variabili e superfici
 ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04/11/ 13
 Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04// 3 Esercizio. Si consideri la funzione ) se 0 f) e se 0. e si verifichi che non è continua in 0. Che tipo di discontinuità presenta in
Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04// 3 Esercizio. Si consideri la funzione ) se 0 f) e se 0. e si verifichi che non è continua in 0. Che tipo di discontinuità presenta in
1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi:
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Test di autovalutazione 1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi: (a) A = {z C : z, 0 arg z /} (b) B = {w
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Test di autovalutazione 1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi: (a) A = {z C : z, 0 arg z /} (b) B = {w
Politecnico di Bari - A.A. 2012/2013 Corso di Laurea in Ingegneria Elettrica Esame di ANALISI MATEMATICA - 3 Luglio 2013.
 Esame di ANALISI MATEMATICA - 3 Luglio 2013 (1) Studiare il carattere della serie numerica n 1( 1) n F 0 (n), dove F (x) = Z x 0 log(1 + e t2 ) dt (x 1). (6 punti) log(1 + e t2 ) (2) ata la funzione f(x,
Esame di ANALISI MATEMATICA - 3 Luglio 2013 (1) Studiare il carattere della serie numerica n 1( 1) n F 0 (n), dove F (x) = Z x 0 log(1 + e t2 ) dt (x 1). (6 punti) log(1 + e t2 ) (2) ata la funzione f(x,
2.9 Esercizi e prove d esame
 65 R. Tauraso - Analisi Matematica II.9 Esercizi e prove d esame Esercizio.. Calcolare la lunghezza dell arco di catenaria data dal grafico della funzione f e + e, con, ]. L arco si parametrizza ponendo
65 R. Tauraso - Analisi Matematica II.9 Esercizi e prove d esame Esercizio.. Calcolare la lunghezza dell arco di catenaria data dal grafico della funzione f e + e, con, ]. L arco si parametrizza ponendo
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 19/06/2010 A
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Corso di Laurea in Ingegneria Gestionale - Sede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame
 Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Esercizi di Analisi Matematica 3. Prima parte
 Esercizi di Analisi Matematica 3 per le Facoltà di Ingegneria Prima parte Corrado Lattanzio e Bruno Rubino Versione preliminare L Aquila, ottobre 5 Indice 1 Curve, superfici e campi vettoriali 3 1.1 Curve
Esercizi di Analisi Matematica 3 per le Facoltà di Ingegneria Prima parte Corrado Lattanzio e Bruno Rubino Versione preliminare L Aquila, ottobre 5 Indice 1 Curve, superfici e campi vettoriali 3 1.1 Curve
FUNZIONI 3. calcolare: a) lim f ( x)
 ) Data la funzione di equazione a) lim f ( ) b) lim f ( ) f FUNZIONI ), scriverne il dominio poi calcolare: 5 c) lim f ( ) d) lim f ( ) ( ± 5 ) Data la funzione di equazione f ( ) 5, scriverne il dominio
) Data la funzione di equazione a) lim f ( ) b) lim f ( ) f FUNZIONI ), scriverne il dominio poi calcolare: 5 c) lim f ( ) d) lim f ( ) ( ± 5 ) Data la funzione di equazione f ( ) 5, scriverne il dominio
f df(p 0 ) lim = 0 f(x, y) dxdy =
 CORSO I LAUREA IN INGEGNERIA EILE - UNIVERSIÀ LA SAPIENZA, ROMA CORSO I ANALISI MAEMAICA 2 (LEERE M - Z) - a. a. 2007/ 08 FORMULARIO SINEICO I ANALISI MAEMAICA 2 Coordinate polari x = ρ cos(θ) y = ρ sin(θ),
CORSO I LAUREA IN INGEGNERIA EILE - UNIVERSIÀ LA SAPIENZA, ROMA CORSO I ANALISI MAEMAICA 2 (LEERE M - Z) - a. a. 2007/ 08 FORMULARIO SINEICO I ANALISI MAEMAICA 2 Coordinate polari x = ρ cos(θ) y = ρ sin(θ),
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Analisi 4 - SOLUZIONI (compito del 29/09/2011)
 Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Esercizi sulle funzioni f : R 2 R. Soluzioni
 Esercizi sulle funzioni f : R R Soluzioni. Disegnare il grafico della funzione f : R R, nei casi: (a) f(, ) =. La funzione dipende solo dalla coordinata. In questo caso il grafico rappresenta un piano
Esercizi sulle funzioni f : R R Soluzioni. Disegnare il grafico della funzione f : R R, nei casi: (a) f(, ) =. La funzione dipende solo dalla coordinata. In questo caso il grafico rappresenta un piano
Analisi Matematica II. Esercizi per le vacanze pasquali
 Analisi Matematica II Esercizi per le vacanze pasquali Corso di laurea in Ingegneria Meccanica. A.A. 2008-2009. Esercizio 1. Stabilire se la funzione reale f di due variabili reali, definita come sin(
Analisi Matematica II Esercizi per le vacanze pasquali Corso di laurea in Ingegneria Meccanica. A.A. 2008-2009. Esercizio 1. Stabilire se la funzione reale f di due variabili reali, definita come sin(
1 Integrali curvilinei
 Integrali curvilinei Richiamo: + x dx x + x + x log ) + + x. Exercise Verificare la formula precedente. Exercise Calcolare a + b x dx, con a, b qualsiasi. Exercise 3 Calcolare la lunghezza dell arco di
Integrali curvilinei Richiamo: + x dx x + x + x log ) + + x. Exercise Verificare la formula precedente. Exercise Calcolare a + b x dx, con a, b qualsiasi. Exercise 3 Calcolare la lunghezza dell arco di
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017
 Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Curve e lunghezza di una curva
 Curve e lunghezza di una curva Definizione 1 Si chiama curva il luogo geometrico dello spazio di equazioni parametriche descritto da punto p, chiuso e limitato. Definizione 2 Si dice che il luogo C è una
Curve e lunghezza di una curva Definizione 1 Si chiama curva il luogo geometrico dello spazio di equazioni parametriche descritto da punto p, chiuso e limitato. Definizione 2 Si dice che il luogo C è una
0.1 Arco di curva regolare
 .1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
.1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
Università degli Studi di Roma - La Sapienza, Facoltà di Architettura Formulario di Matematica *
 Università degli Studi di Roma - La Sapienza, Facoltà di Architettura Formulario di Matematica *. Distanza tra due punti A ; ) e B ; ) del piano cartesiano: AB = ) + ) +. Punto medio M del segmento AB
Università degli Studi di Roma - La Sapienza, Facoltà di Architettura Formulario di Matematica *. Distanza tra due punti A ; ) e B ; ) del piano cartesiano: AB = ) + ) +. Punto medio M del segmento AB
ANALISI MATEMATICA 3
 ANALISI MATEMATICA 3 Corso di laurea triennale in Fisica, F480 Prova scritta del 8//003 prof. Marco Vignati ] Sia dato il problema di Cauchy xy + y = 0 i) Determinarne la soluzione locale. y () = 3 ii)
ANALISI MATEMATICA 3 Corso di laurea triennale in Fisica, F480 Prova scritta del 8//003 prof. Marco Vignati ] Sia dato il problema di Cauchy xy + y = 0 i) Determinarne la soluzione locale. y () = 3 ii)
Ricordiamo che l operatore divergenza agisce su un campo vettoriale F ed è definito come segue: div F (x) = x i. i=1. x 2 + y 2
 Capitolo 4 Campi vettoriali Ultimo aggiornamento: 3 maggio 2017 Ricordiamo che l operatore divergenza agisce su un campo vettoriale F ed è definito come segue: div F x = n F i x. x i i=1 Esercizio 4.1
Capitolo 4 Campi vettoriali Ultimo aggiornamento: 3 maggio 2017 Ricordiamo che l operatore divergenza agisce su un campo vettoriale F ed è definito come segue: div F x = n F i x. x i i=1 Esercizio 4.1
Analisi Matematica 2 (prof.g.cupini) A.A CdL Astronomia - Univ. Bologna REGISTRO DELLE LEZIONI
 Analisi Matematica 2 (prof.g.cupini) A.A.2016-2017 - CdL Astronomia - Univ. Bologna REGISTRO DELLE LEZIONI GLI ARGOMENTI IN GIALLO SARANNO OGGETTO DI VERIFICA SOLO NELL'ESAME DI TEORIA. Lu, 26 settembre
Analisi Matematica 2 (prof.g.cupini) A.A.2016-2017 - CdL Astronomia - Univ. Bologna REGISTRO DELLE LEZIONI GLI ARGOMENTI IN GIALLO SARANNO OGGETTO DI VERIFICA SOLO NELL'ESAME DI TEORIA. Lu, 26 settembre
Esercizi di Analisi 2. Nicola Fusco (Dipartimento di Matematica e Applicazioni, Università Federico II, Napoli) 1. Successioni e Serie di Funzioni
 Esercizi di Analisi 2 Nicola Fusco (Dipartimento di Matematica e Applicazioni, Università Federico II, Napoli) 1. Successioni e Serie di Funzioni 1.1 Al variare di α IR studiare la convergenza della serie
Esercizi di Analisi 2 Nicola Fusco (Dipartimento di Matematica e Applicazioni, Università Federico II, Napoli) 1. Successioni e Serie di Funzioni 1.1 Al variare di α IR studiare la convergenza della serie
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
DERIVATE E LORO APPLICAZIONE
 DERIVATE E LORO APPLICAZIONE SIMONE ALGHISI 1. Applicazione del calcolo differenziale 1 Abbiamo visto a lezione che esiste un importante legame tra la continuità di una funzione y = f(x) in un punto x
DERIVATE E LORO APPLICAZIONE SIMONE ALGHISI 1. Applicazione del calcolo differenziale 1 Abbiamo visto a lezione che esiste un importante legame tra la continuità di una funzione y = f(x) in un punto x
Compiti d Esame A.A. 2005/2006
 Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi:
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, itati, convessi, connessi per archi; punti di frontiera
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, itati, convessi, connessi per archi; punti di frontiera
Matematica classe 5 C a.s. 2012/2013
 Matematica classe 5 C a.s. 2012/2013 Asintoti e grafici 1) Una funzione y = f(x) gode delle seguenti caratteristiche: D / 4, y 0 se x 0 x 2, lim, 3. Rappresentare un grafico qualitativo della funzione.
Matematica classe 5 C a.s. 2012/2013 Asintoti e grafici 1) Una funzione y = f(x) gode delle seguenti caratteristiche: D / 4, y 0 se x 0 x 2, lim, 3. Rappresentare un grafico qualitativo della funzione.
quando il limite delle somme di Riemann esiste. In tal caso diciamo che la funzione è integrabile sul rettangolo.
 Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Curve e integrali curvilinei: esercizi svolti
 Curve e integrali curvilinei: esercizi svolti 1 Esercizi sulle curve parametriche....................... 1.1 Esercizi sulla parametrizzazione delle curve............. 1. Esercizi sulla lunghezza di una
Curve e integrali curvilinei: esercizi svolti 1 Esercizi sulle curve parametriche....................... 1.1 Esercizi sulla parametrizzazione delle curve............. 1. Esercizi sulla lunghezza di una
1) D0MINIO. x x 4x + 3 Determinare il dominio della funzione f (x) = x Deve essere
 ) DMINIO + 3 Determinare il dominio della funzione f ) + 3 Deve essere Ovviamente, inoltre: se > + 3 ) 3) quindi < o 3 se < + 3, + 3 quindi 7 Determinare il dominio della funzione f ) + 5 Deve essere +
) DMINIO + 3 Determinare il dominio della funzione f ) + 3 Deve essere Ovviamente, inoltre: se > + 3 ) 3) quindi < o 3 se < + 3, + 3 quindi 7 Determinare il dominio della funzione f ) + 5 Deve essere +
Breve formulario di matematica
 Luciano Battaia a 2 = a ; lim sin = 1, se 0; sin(α + β) = sin α cos β + cos α sin β; f() = e 2 f () = 2e 2 ; sin d = cos + k; 1,2 = b± ; a m a n = 2a a n+m ; log a 2 = ; = a 2 + b + c; 2 + 2 = r 2 ; e
Luciano Battaia a 2 = a ; lim sin = 1, se 0; sin(α + β) = sin α cos β + cos α sin β; f() = e 2 f () = 2e 2 ; sin d = cos + k; 1,2 = b± ; a m a n = 2a a n+m ; log a 2 = ; = a 2 + b + c; 2 + 2 = r 2 ; e
Esercizi proposti. x b) f(x) = 2. Determinare i punti di non derivabilità delle funzioni
 Esercizi proposti 1. Calcolare la derivata prima f () per le seguenti funzioni: a) f() = c) f() = ( 1 + 1 b) f() = 1 arctan ) d) f() = cos ( ( + ) 5) e) f() = 1 + sin 1 f) f() = arcsin 1. Determinare i
Esercizi proposti 1. Calcolare la derivata prima f () per le seguenti funzioni: a) f() = c) f() = ( 1 + 1 b) f() = 1 arctan ) d) f() = cos ( ( + ) 5) e) f() = 1 + sin 1 f) f() = arcsin 1. Determinare i
A Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica) Simulazione compito d esame
 COGNOME NOME Matr. A Analisi Matematica (Corso di Laurea in Informatica e Bioinformatica) Firma dello studente Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. A Analisi Matematica (Corso di Laurea in Informatica e Bioinformatica) Firma dello studente Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
5 Simulazione di prova d Esame di Stato
 5 Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario Tra le parabole di equazione k, individuare la parabola γ tangente alla
5 Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario Tra le parabole di equazione k, individuare la parabola γ tangente alla
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Esercizi su: insiemi, intervalli, intorni. 4. Per ognuna delle successive coppie A e B di sottoinsiemi di Z determinare A B, A B, a) A C d) C (A B)
 Esercizi su: insiemi, intervalli, intorni. Per ognuna delle successive coppie A e B di sottoinsiemi di N determinare A B, A B, A c e B c. a) A = { N + = 0}, B = { N = 6}, b) A = { N < 5}, B = { N < },
Esercizi su: insiemi, intervalli, intorni. Per ognuna delle successive coppie A e B di sottoinsiemi di N determinare A B, A B, A c e B c. a) A = { N + = 0}, B = { N = 6}, b) A = { N < 5}, B = { N < },
(a) Le derivate parziali f x. f y = x2 + 2xy + 3 si annullano contemporaneamente in (1, 2) e ( 1, 2). Le derivate seconde di f valgono.
 Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
variabili. se i limiti esistono e si chiamano rispettivamente derivata parziale rispetto ad x e rispetto ad y.
 Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare [cos x] x kπ/ al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare [cos x] x kπ/ al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Secondo compito in itinere 3 Febbraio 2014
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Febbraio 04 Cognome: Nome: Matricola: Compito A Es: 8 punti Es: 8 punti Es: 8 punti Es4: 8 punti Totale a) Determinare
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Febbraio 04 Cognome: Nome: Matricola: Compito A Es: 8 punti Es: 8 punti Es: 8 punti Es4: 8 punti Totale a) Determinare
Istituzioni di Matematiche Modulo B (SG)
 Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
Domande da 6 punti. Prima parte del programma
 Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Analisi Matematica II (Prof. Paolo Marcellini)
 Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazioni del 04/03/014 e 06/03/014 Michela Eleuteri 1 eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazioni del 04/03/014 e 06/03/014 Michela Eleuteri 1 eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;
![a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [; a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;](/thumbs/69/60588320.jpg) ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
testi e soluzioni delle prove di esonero di Analisi Matematica II
 testi e soluzioni delle prove di esonero di Analisi Matematica II A.R. Sambucini Dipartimento di Matematica e Informatica Via Vanvitelli - 63 Perugia - Italy copyright by the author(s) document created
testi e soluzioni delle prove di esonero di Analisi Matematica II A.R. Sambucini Dipartimento di Matematica e Informatica Via Vanvitelli - 63 Perugia - Italy copyright by the author(s) document created
ULTERIORI ESERCIZI SUL CALCOLO DIFFERENZIALE
 ULTERIORI ESERCIZI SUL CALCOLO DIFFERENZIALE 1 Scrivi l equazione della retta tangente al grafico di f(x) = (1 + 2x) 4 nel suo punto di intersezione con l asse y 2 Scrivi l equazione della retta tangente
ULTERIORI ESERCIZI SUL CALCOLO DIFFERENZIALE 1 Scrivi l equazione della retta tangente al grafico di f(x) = (1 + 2x) 4 nel suo punto di intersezione con l asse y 2 Scrivi l equazione della retta tangente
Corso di Geometria III - A.A. 2016/17 Esercizi
 Corso di Geometria III - A.A. 216/17 Esercizi (ultimo aggiornamento del file: 2 ottobre 215) Esercizio 1. Calcolare (1 + 2i) 3, ( ) 2 + i 2, (1 + i) n + (1 i) n. 3 2i Esercizio 2. Sia z = x + iy. Determinare
Corso di Geometria III - A.A. 216/17 Esercizi (ultimo aggiornamento del file: 2 ottobre 215) Esercizio 1. Calcolare (1 + 2i) 3, ( ) 2 + i 2, (1 + i) n + (1 i) n. 3 2i Esercizio 2. Sia z = x + iy. Determinare
{ x + 2y = 3 αx + 2y = 1 αx + y = 0. f(x) = e x 2 +3x+4 x 5. f(x) = x 3 e 7x.
 0 Gennaio 006 Teoria: Definizione di derivata puntuale e suo significato geometrico Esercizio Determinare l equazione del piano contenente i vettori u = (,, 3 e v = (,, e passante per P o = (,, Scrivere
0 Gennaio 006 Teoria: Definizione di derivata puntuale e suo significato geometrico Esercizio Determinare l equazione del piano contenente i vettori u = (,, 3 e v = (,, e passante per P o = (,, Scrivere
4. Calcolare il baricentro delle seguenti regioni del piano dotate di densità unitaria:
 INTEGRLI OPPI e TRIPLI Esercii risolti. Calcolare i seguenti integrali doppi: a b c d e f g h i j k y d dy,, y :, y }; d dy,, y :, y }; + y + y d dy,, y :, y }; y d dy,, y :, y }; y d dy,, y :, y + };
INTEGRLI OPPI e TRIPLI Esercii risolti. Calcolare i seguenti integrali doppi: a b c d e f g h i j k y d dy,, y :, y }; d dy,, y :, y }; + y + y d dy,, y :, y }; y d dy,, y :, y }; y d dy,, y :, y + };
Prima prova di verifica in itinere di ANALISI MATEMATICA II. 12 Marzo 2008 Compito A. 1 (punti 3)
 anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
SYLLABUS DI MATEMATICA Liceo Linguistico Classe III
 SYLLABUS DI MATEMATICA Liceo Linguistico Classe III LE EQUAZIONI DI SECONDO GRADO Le equazioni di secondo grado e la loro risoluzione. La formula ridotta. Equazioni pure, spurie e monomie. Le relazioni
SYLLABUS DI MATEMATICA Liceo Linguistico Classe III LE EQUAZIONI DI SECONDO GRADO Le equazioni di secondo grado e la loro risoluzione. La formula ridotta. Equazioni pure, spurie e monomie. Le relazioni
Dipartimento di Matematica Corso di laurea in Fisica Compito di Geometria assegnato il 1 Febbraio 2002
 Compito di Geometria assegnato il 1 Febbraio 2002 Trovare l equazione della conica irriducibile tangente all asse x nel punto A(2, 0), tangente all asse y e passante per i punti B(1, 1) e C(2, 2) Scrivere
Compito di Geometria assegnato il 1 Febbraio 2002 Trovare l equazione della conica irriducibile tangente all asse x nel punto A(2, 0), tangente all asse y e passante per i punti B(1, 1) e C(2, 2) Scrivere
Analisi Matematica II (Prof. Paolo Marcellini)
 Analisi Matematica II Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 5//14 Michela Eleuteri 1 eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Analisi Matematica II Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 5//14 Michela Eleuteri 1 eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
1 Rette e piani nello spazio
 1 Rette e piani nello spazio Esercizio 1.1 È assegnato un riferimento cartesiano 0xyz. Sono assegnati la retta x = t, r : y = t, z = t, il piano π : x + y + z = 0 ed il punto P = (1, 1, 1). Scrivere le
1 Rette e piani nello spazio Esercizio 1.1 È assegnato un riferimento cartesiano 0xyz. Sono assegnati la retta x = t, r : y = t, z = t, il piano π : x + y + z = 0 ed il punto P = (1, 1, 1). Scrivere le
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = e (x3 +x) y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Esempio di grafico di una funzione reale di due variabili reali
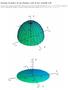 Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Esercizi di Analisi Matematica B. Massimo Cicognani
 Esercizi di Analisi Matematica B Massimo Cicognani ii Indice Testi. Serie numeriche e serie di potenze.................2 Funzioni di più variabili reali.................. 5.3 Equazioni differenziali......................
Esercizi di Analisi Matematica B Massimo Cicognani ii Indice Testi. Serie numeriche e serie di potenze.................2 Funzioni di più variabili reali.................. 5.3 Equazioni differenziali......................
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
ELIO CABIB. Esami di Analisi 2
 ELIO CABIB Esami di Analisi ELIO CABIB cabib@uniud.it professore di Analisi Matematica Università di Udine Esami di Analisi Indice Appelli 997-98 3//998..................................... 6//998.....................................
ELIO CABIB Esami di Analisi ELIO CABIB cabib@uniud.it professore di Analisi Matematica Università di Udine Esami di Analisi Indice Appelli 997-98 3//998..................................... 6//998.....................................
Verifica di matematica. Nel piano riferito a coordinate ortogonali monometriche (x; y) è assegnata la curva Γ di equazione: 2
 0 Marzo 00 Verifica di matematica roblema Si consideri l equazione ln( + ) 0. a) Si dimostri che ammette due soluzioni reali. Nel piano riferito a coordinate ortogonali monometriche (; ) è assegnata la
0 Marzo 00 Verifica di matematica roblema Si consideri l equazione ln( + ) 0. a) Si dimostri che ammette due soluzioni reali. Nel piano riferito a coordinate ortogonali monometriche (; ) è assegnata la
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = log(1 + x 2 y) lim x 2 x
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-14 Esercizio 1. (14 punti) Data la funzione = log(1 + x y) i) determinare il dominio e studiare l esistenza del ite (x,y) (,) x x ii)
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-14 Esercizio 1. (14 punti) Data la funzione = log(1 + x y) i) determinare il dominio e studiare l esistenza del ite (x,y) (,) x x ii)
determinare una soluzione y(t) dell equazione completa e, quindi dedurne tutte le y(t) soluzioni dell equazione.
 ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
Esame di maturità scientifica, corso di ordinamento a. s
 Problema 1 Esame di maturità scientifica, corso di ordinamento a. s. -4 Sia f la funzione definita da: f()=- Punto 1 Disegnate il grafico G di f()=-. La funzione f()=- è una funzione polinomiale (una cubica).
Problema 1 Esame di maturità scientifica, corso di ordinamento a. s. -4 Sia f la funzione definita da: f()=- Punto 1 Disegnate il grafico G di f()=-. La funzione f()=- è una funzione polinomiale (una cubica).
Nome Cognome. Classe 3D 25 Febbraio Verifica di matematica
 Nome Cognome. Classe D Febbraio Verifica di matematica ) Data l equazione: k 6 a) Scrivi per quali valori di k rappresenta un ellisse, precisando per quali valori è una circonferenza b) Scrivi per quali
Nome Cognome. Classe D Febbraio Verifica di matematica ) Data l equazione: k 6 a) Scrivi per quali valori di k rappresenta un ellisse, precisando per quali valori è una circonferenza b) Scrivi per quali
Teorema delle Funzioni Implicite
 Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane Lezione 1-04/10/2016 - Serie Numeriche (1): definizione e successione
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane Lezione 1-04/10/2016 - Serie Numeriche (1): definizione e successione
determinare le coordinate di P ricordando la relazione che permette di calcolare le coordinate del punto medio di un segmento si
 PROBLEMA Determinare il punto simmetrico di P( ;) rispetto alla retta x y =0 Soluzione Il simmetrico di P rispetto ad una retta r è il punto P che appartiene alla retta passante per P, perpendicolare ad
PROBLEMA Determinare il punto simmetrico di P( ;) rispetto alla retta x y =0 Soluzione Il simmetrico di P rispetto ad una retta r è il punto P che appartiene alla retta passante per P, perpendicolare ad
