Salvo avviso contrario V denota un k-spazio spazio vettoriale (di dimensione finita).
|
|
|
- Cesare Pastore
- 4 anni fa
- Visualizzazioni
Transcript
1 a.a FORME BILINEARI Salvo avviso contrario V denota un k-spazio spazio vettoriale (di dimensione finita). Data una base F = {f 1,..., f n } di V = v, w V si ha v = n x i f i, w = n y i f i con x i, y i k univocamente determinati. Definizione 0.1. Un applicazione b : V V k è una forma bilineare (in breve f.b.) se è lineare rispetto a ciascuno degli argomenti ossia: v, w, v, w V, λ k b(v + v, w) = b(v, w) + b(v, w) b(v, w + w ) = b(v, w) + b(v, w ) b(λv, w) = λb(v, w) = b(v, λw). È una f.b. simmetrica se b(v, w) = b(w, v), f.b. antisimmetrica se b(v, w) = b(w, v) 1. Esempio 0.. Data A M n (k), definendo b A : k n k n k via b A (x, y) = t xay, si ottiene una f.b. per le proprietà del prodotto righe per colonne di matrici. Se A = I n b In (x, y) = t xi n y, è t x y = n x i y i è detta f.b. standard di k n. Definizione 0.3. Data una base F di V, se b : V V k è una f.b., la matrice di b rispetto a F è A = (a ij ) M n (k) definita da b(f i, f j ) := a ij, 1 i, j n. Viceversa, se A = (a ij M n (k) la f.b. associata ad A rispetto a F è b F A (v, w) := t xay. Osservazione ) Essendo b F A (w, v) = t yax ed essendo b(v, w) k, ossia t b(v, w) = b(v, w) per ogni f.b. b, e t b F A (v, w) = t y t Ax si ha b F A (v, w) = bf A (w, v) se e solo se A è simmetrica. Analogamente per il caso antisimmetrico. ) Complessivamente, abbiamo visto che, fissata la base F, associando a una f.b. b la sua matrice rispetto a F si ottiene una c.b.u. (dipendente da F ) tra l insieme Bil(V ) delle f.b. su V ed M n (k) che associa matrici simmetriche a f.b. simmetriche e matrici antisimmetriche a f.b. antisimmetriche. Proposizione 0.5. Siano F = {f 1,..., f n }, G = {g 1,..., g n } due basi di V e b : V V k una f.b., con A = (a ij ) = (b(f i, f j )) M n (k) B = (b ij ) = (b(g i, g j )). Se v = n x i f i = n x i g i e w = n y i f i = n y i g i si ha b(v, w) = t xay = t x By, posto M = MG F, si ha anche x = Mx, y = My = t xay = t (Mx )AMy = t x t MAMy = B = t MAM 1 b è antisimmetrica b(v, v) = 0k infatti se è antisimmetrica risulta b(v, v) = b(v, v) = 0 k se invece b(v, v) = 0 k si ha 0 k = b(v + w, v + w) = b(v, v) + b(v, w) + b(w, v) + b(w, w) ossia b(v, w) = b(w, v). np P Essendo v = x i f i, w = n y i f i si ha b(v, w) = P n x i y j b(f i, f j ) = t xay. i,j=1 1
2 FORME BILINEARI e quindi A = ( t M) 1 BM 1. Definizione 0.6. Due matrici A, B M n (k) sono congruenti se esiste M Gl n (k) tale che B = t MAM. La congruenza è una relazione di equivalenza in M n (k). Due matrici A, B M n (k) rappresentano la stessa f.b. su V se e solo se sono congruenti. Pertanto la caratteristica di una matrice che rappresenta una f.b. b non dipende dalla base scelta ed è detta rango di b. Definizione ) Una f.b. b di rango n = dim k V è detta non degenere. ) Dati una f.b.s. b su V e un vettore v V, un vettore w V è ortogonale a v (rispetto a b) se b(v, w) = 0 k. Osservazione 0.8. Dati una f.b.s. b su V e un sottinsieme S V (in particolare un sottospazio) S b S b := {w V : b(v, w) = 0, v S} è un sottospazio di V infatti w, w Sb, λ k si ha: b(v, w + w ) = b(v, w) + b(v, w ) = 0 k + 0 k = 0 k b(λv, w) = λb(v, w) = 0 k. Definizione ) S è detto spazio ortogonale a S (rispetto a b), se S = {v} si scrive semplicemente v. ) Due sottospazi U, W V sono ortogonali se U W (o per simmetria W U ). 3) V è detto radicale di V. Osservazione ) V = (0 V ) se e solo se b è non degenere. Siano F = {f 1,..., f n } una base di V e A M n (k) la matrice di b rispetto a F se ρ(a) = n e x 0 k n è il vettore delle coordinate di 0 V v V rispetto a F si ha t xa (0,..., 0) = y k n tale che t xay 0 k = il vettore w V di coordinate y rispetto a F è tale che b(v, w) 0 k ; viceversa se 0 k n x y k n tale che t xay 0 k necessariamente A ha rango n. Ossia, b è non degenere se e solo se per ogni 0 V v V esiste w V tale che b(v, w) 0 k o, equivalentemente, se e solo se per ogni 0 V w V esiste v V tale che b(v, w) 0 k e quindi la tesi. Definizione Un vettore v V è isotropo rispetto a una f.b.s. b se v v ossia b(v, v) = 0 k. Osservazione ) 0 V è isotropo per ogni f.b.s. ) Se v V è isotropo e λ k, essendo b(λv, λv) = λ b(v, v) = λ 0 k = 0 k, il sottospazio L(v) è costituito da vettori tutti isotropi. Definizione Uno spazio vettoriale U con dim k U =, h f.b.s. non degenere e 0 U u U vettore isotropo è detto piano iperbolico (e. h è detta forma iperbolica). Osservazione Un piano iperbolico (U, h) possiede una base F = {f 1, f } formata da vettori isotropi tali che h(f 1, f ) = 1 k. Per ipotesi esiste 0 U u U vettore isotropo, quindi possiamo scegliere f 1 = u, essendo h non degenere
3 FORME BILINEARI 3 esiste v U tale che h(f 1, v) 0 k = {f 1, v} è libero 3 ed f = 1 h(f v soddisfa 1,v) h(f 1, f ) = 1 k. Il vettore f := f h(f,f )f1 soddisfa h(f, f ) = h(f, f ) h(f,f ) h(f 1, f ) h(f,f ) h(f 1, f ) + h(f,f ) 4 h(f 1, f 1 ) = 0 k e quindi insieme a f 1 fornisce la base richiesta. Definizione Una base di un piano iperbolico (U, h) come in Osservazione 0.14 ( è detta ) iperbolica e la matrice associata ad h rispetto a una base iperbolica è Esempio )h(x, y) = x 1 y + x y 1 è una forma iperbolica e la base canonica è iperbolica. ) k(x, y) = 1 x 1y 1 1 x y ( è una forma iperbolica e la matrice associata ad k 1 ) rispetto alla base canonica è Trovare una base iperbolica per k. Se v V è non-isotropo (anisotropo) rispetto a una f.b.s. b, posto w V, a v (w) := b(v, w) b(v, v) k, si ha b(v, w a v (w)v) = 0 k, ossia w a v (w)v v. Inoltre, siccome w = a v (w)v + (w a v (w)v) si ha V = L(v) v (infatti poiché v è anisotropo si ha L(v) v = (0 V ). Definizione ) Il coefficiente di Fourier di w V rispetto a un dato v V 4 è a v (w). ) Una base ortogonale (o dualizzante) per (V, b) è una base F = {f 1,..., f n } costituita da vettori a due a due. Osservazione F = {f 1,..., f n } è una base ortogonale (ossia b(f i, f j ) = 0 k i j) se e solo se la matrice A = (b(f i, f j )) è diagonale, nel qual caso se v = n x i f i, w = n y i f i = b(v, w) = n a ii x i y i. n.b. se F = {f 1,..., f n } è b.o. per (V, b) anche F = {λ 1 f 1,..., λ n f n } è tale λ 1,..., λ n k, ossia se esiste b.o. essa non è unica. Definizione Data una f.b.s. b : V V k, ponendo q b (v) := b(v, v) si definisce un applicazione q b : V k detta forma quadratica associata a b. Esempio 0.0. Se b è la f.b.s.s. su k n, b(x, y) = n x i y i la f.q. associata, detta f.q. standard (f.q.s.), è q(x) = n x i. Proposizione 0.1. Data una f.b.s. b : V V k, la f.q. associata q soddisfa: 1) q(λv) = λ q(v) ) b(v, w) = q(v + w) q(v) q(w). 3 Se fosse v = λf1 per qualche λ k si avrebbe h(f 1, v) = λh(f 1, f 1 ) = λ0 k = 0 k. 4 Definito solo se v è anisotropo.
4 4 FORME BILINEARI Prova. Per definizione q(λv) = b(λv, λv) = λ b(v, v) = λ q(v); q(b + w) q(v) q(w) = b(v + w, v + w) b(v, v) b(w, w) = b(v, v) + b(v, w) + b(w, v) + b(w, w) b(v, v) b(w, w) = b(v, w) (essendo b simmetrica). Inoltre se F = {f 1,..., f n } è una base di V, v = n x i f i e A = (a ij ) = (b(f i, f j ))= t A M n (k) è la matrice di b rispetto a F si ha q(v) = t xax = n a ij x i x j = q(v) = Q(x) con Q(X) = n a ij X i X j forma quadratica nelle i,j=1 i,j=1 indeterminate X 1,..., X n e Q(X) = t XAX con A = (a ij ) M n (k) matrice simmetrica. Teorema 0.. Data una f.b.s. b qualsiasi esiste una base diagonalizzanate per b (o, equivalentemente, una qualsiasi A = (a ij ) M n (k) matrice simmetrica è congruente a una matrice diagonale). Prova. Per induzione su n = dim k V, se n = 1 non c è niente da dimostrare. Supponiamo allora n e di avere dimostrato che ogni f.b.s. su uno spazio di dimensione n 1 ammette base diagonalizzante. Se b è la forma nulla, essendo la matrice nulla diagonale, non c è nulla da dimostrare. Supponiamo dunque b 0 ossia che v, w V tali che b(v, w) 0. Proviamo innanzi tutto che almeno uno fra v, w, v + w è anisotropo, infatti, se v, w sono entrambi isotropi si dimostra che 0 b(v + w, v + w) = b(v, v) + b(v, w) + b(w, w). Sia f 1 V un vettore anisotropo (ossia tale che b(f 1, f 1 ) 0), cosicché V = L(f 1 ) f1, in particolare dim k f1 = n 1 e vale l ipotesi induttiva per la f.b.s. b indotta da b su f1 che quindi possiede base diagonalizzante {f,..., f n }. Allora F = {f 1, f,..., f n } è base per V per ipotesi {f,..., f n } è libero e, essendo f 1 anisotropo, f 1 / L({f,..., f n }) = f1. Vale inoltre b(f i, f j ) = δ ij giacché b(f 1, f i ) = 0, i n essendo f i f1, i n e anche b(f i, f j ) = b (f i, f j ) = δ ij, i, j n, ossia F è base diagonalizzante per b. Teorema 0.3. Se il campo base k è algebricamente chiuso 5, data ( una f.b.s. ) b Ir O qualsiasi esiste una G tale che la matrice di b rispetto a G sia D = O O con r= rango di b, O M r,n r (k), O M n r,r (k), O M n r (k),(o, equivalentemente, una qualsiasi A = (a ij ) M n (k) matrice simmetrica è congruente a una matrice diagonale come D). Prova. Chiaramente le due affermazioni sono equivalenti. Dal Teorema 0. sappiamo che esiste base F = {f 1, f,..., f n } diagonalizzante per b, sia essa A = a a Salvo riordinare F, possiamo supporre r a ii 0, a nn r n e 0 = a r+1r+1 = = a nn. Siano α 1,..., α r k tali che αi = a ii, 1 i r (questi esistono essendo k algebricamente chiuso), ponendo g i := α 1 i f i, 1 i r e g r+j := f r+j, 1 j n r, si ottiene una b.o. G per cui vale: b(g i, g i ) = b(α 1 i f i, α 1 i f i ) = α i b(f i, f i ) = α i a ii = 1, 1 i r. 5 In particolare se k = C.
5 FORME BILINEARI 5 Teorema 0.4 (Sylvester). Se k = R esiste p N, p r = rango di b 6 e una base G = {g 1, g,..., g n } di V tale che la matrice di b rispetto a G sia I p ( ) D = 0 I r p (o, equivalentemente, una qualsiasi A = (a ij ) M n (R) matrice simmetrica è congruente a una matrice diagonale ( ) come sopra con r e p dipendenti solo da A). Prova. Chiaramente le due affermazioni sono equivalenti. Dal Teorema 0. sappiamo che esiste base F = {f 1, f,..., f n } tale che per ogni v = risulti q(v) = n a ii x i n x i f i V (n.b. il numero dei coefficienti a ii 0 è uguale al rango r di b e quindi dipende solo da b). Salvo riordinare F possiamo supporre e che a 11,..., a pp > 0 per qualche p r e quindi α 1,..., α r R tali che α i = a ii, 1 i p, (α p+j ) = a p+jp+j, 1 j r p. r a ii 0 Come nel Teorema 0.3 si verifica che, rispetto alla base G : g i := fi α i, 1 i r, g r+j := f r+j 1 i n r, la matrice di b è della forma voluta, pertanto risulta n ( ) q(v) = x x p x p+1 + x r, v = x i g i V. Proviamo infine che p dipende solo da b e non dalla base G, supponiamo che rispetto a un altra base H = {h 1, h,..., h n } risulti n ( ) q(v) = z1 + + zt zp+1 + zr, v = z i h i V. Se t p (supponiamo per esempio t < p) siano U := L({g 1,..., g p }), W := L({h t+1,..., h n }) essendo dim R U + dim R W = p + n t > n per il lemma di Grassmann risulta U W (0 V ), ossia, 0 V v U W per cui vale p n t v = x i g i = z t+j h j. Essendo 0 V v, risulterebbe quindi sia q(v) > 0 che q(v) < 0 dunque deve essere necessariamente t = p. Definizione ) La ( ) é detta forma canonica della forma quadratica q, p è detto indice di positività di q ed r p è detto indice di negatività di q, infine la coppia (p, r p) è detta segnatura di q. ) Una f.q. definita su un R-spazio vettoriale V è: - definita positiva se q(v) > 0 v V \ {0 V }, - definita negativa se q(v) < 0 v V \ {0 V }, - semidefinita positiva se q(v) 0 v V, - semidefinita negativa se q(v) 0 v V, -indefinita se non è né semidefinita positiva né semidefinita negativa. 6 n.b. p dipende solo da b e non dalla base scelta. j=1
6 6 FORME BILINEARI Osservazione ) La forma canonica (risp. la segnatura) di una f.q. reale è: - x x n (risp. (n, 0)) se q è definita positiva, - x 1 x n (risp. (0, n)) se q è definita negativa, - x x r, 0 r n (risp. (r, 0)) se q è semidefinita positiva, - x 1 x r, 0 r n (risp. (0, r)) se q è semidefinita negativa, - x x p x p+1 x r, 0 r n (risp. (p, r p)) se q è indefinita. Per le matrici simmetriche reali si ha un risultato analogo. ) Il teoreme di Sylvester dice che in ogni classe di congruenza di matrici simmetriche reali è contenuta un unica matrice diagonale del tipo ( ) e che le matrici di questo tipo costituiscono un insieme completo di rappresentanti delle classi di congruenza di matrici simmetriche reale di ordine dato. Le f.b.s. definite positive sugli spazi vettoriali reali sono importanti nella geometria euclidea (permettono di introdurre tutte le nozioni di natura metrica). Altri tipi di f.b.s. sono importanti in geometria e fisica. Esempio ) Lo spazio euclideo n-dimensionale è (R n, f.q.s.). )In R 4 la forma quadratica λ(x 1, x, x 3, x 4 ) = x 1 + x + x 3 x 4 è detta forma di Minkowski (è non degenere, indefinita, di segnatura (3, 1)). La coppia (R 4, λ) è detta spazio di di Minkowski e interviene nella relatività ristretta.
GEOMETRIA 1 ottava parte
 GEOMETRIA 1 ottava parte Cristina Turrini C. di L. in Fisica - 214/215 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA 1 1 / 15 index 1 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA
GEOMETRIA 1 ottava parte Cristina Turrini C. di L. in Fisica - 214/215 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA 1 1 / 15 index 1 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica. Corso di Geometria ed Algebra Docente F. Flamini
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Forme bilineari simmetriche
 Forme bilineari simmetriche Qui il campo dei coefficienti è sempre R Definizione 1 Sia V uno spazio vettoriale Una forma bilineare su V è una funzione b: V V R tale che v 1, v 2, v 3 V b(v 1 + v 2, v 3
Forme bilineari simmetriche Qui il campo dei coefficienti è sempre R Definizione 1 Sia V uno spazio vettoriale Una forma bilineare su V è una funzione b: V V R tale che v 1, v 2, v 3 V b(v 1 + v 2, v 3
Applicazioni lineari simmetriche e forme quadratiche reali.
 Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
GAAL: Capitolo dei prodotti scalari
 GAAL: Capitolo dei prodotti scalari Teorema di Rappresentazione rappresentabile Aggiunto Autoaggiunto Unitariamente diagonalizzabile Teorema spettrale reale Accoppiamento Canonico Forme bilineari Prodotti
GAAL: Capitolo dei prodotti scalari Teorema di Rappresentazione rappresentabile Aggiunto Autoaggiunto Unitariamente diagonalizzabile Teorema spettrale reale Accoppiamento Canonico Forme bilineari Prodotti
Similitudine (ortogonale) e congruenza (ortogonale) di matrici.
 Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
GE210 Geometria e algebra lineare 2 A.A. 2018/2019
 GE210, I Semestre, Crediti 9 GE210 Geometria e algebra lineare 2 A.A. 2018/2019 Prof. Angelo Felice Lopez 1. Forme bilineari e forme quadratiche Forme bilineari, simmetriche ed antisimmetriche. Esempi:
GE210, I Semestre, Crediti 9 GE210 Geometria e algebra lineare 2 A.A. 2018/2019 Prof. Angelo Felice Lopez 1. Forme bilineari e forme quadratiche Forme bilineari, simmetriche ed antisimmetriche. Esempi:
Forme bilineari e prodotti scalari
 Forme bilineari e prodotti scalari Il prodotto scalare standard di R n può anche essere scritto come un prodotto riga per colonna u, v R n = u t Iv dove I è la matrice identità. Possiamo generalizzare
Forme bilineari e prodotti scalari Il prodotto scalare standard di R n può anche essere scritto come un prodotto riga per colonna u, v R n = u t Iv dove I è la matrice identità. Possiamo generalizzare
GEOMETRIA 1 quarta parte
 GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 36 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 36 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
Corso di Laurea in Fisica. Geometria. a.a Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche
 Corso di Laurea in Fisica. Geometria. a.a. 2009-10. Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche Sia V uno spazio vettoriale reale. Sia 1. Osservazioni preliminari. : V V R un
Corso di Laurea in Fisica. Geometria. a.a. 2009-10. Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche Sia V uno spazio vettoriale reale. Sia 1. Osservazioni preliminari. : V V R un
GEOMETRIA 1 quarta parte
 GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2015/2016 Cristina Turrini (C. di L. in Fisica - 2015/2016) GEOMETRIA 1 1 / 76 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2015/2016 Cristina Turrini (C. di L. in Fisica - 2015/2016) GEOMETRIA 1 1 / 76 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
{Geometria per [Fisica e (Fisica e Astrofisica)]}
![{Geometria per [Fisica e (Fisica e Astrofisica)]} {Geometria per [Fisica e (Fisica e Astrofisica)]}](/thumbs/103/157763717.jpg) {Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
{Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
Capitolo IV SPAZI VETTORIALI EUCLIDEI
 Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Appendice: Forme quadratiche
 Appendice: Forme quadratiche A A 2006/2007 1 Prodotto Scalare Definizione 11 Si definisce Spazio Euclideo uno spazio vettoriale con assegnato un prodotto scalare Definizione 12 Sia V uno spazio vettoriale
Appendice: Forme quadratiche A A 2006/2007 1 Prodotto Scalare Definizione 11 Si definisce Spazio Euclideo uno spazio vettoriale con assegnato un prodotto scalare Definizione 12 Sia V uno spazio vettoriale
Corso di Laurea in Fisica. Geometria. a.a Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche
 Corso di Laurea in Fisica. Geometria. a.a. 2012-13. Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche Sia V uno spazio vettoriale reale. Sia 1. Osservazioni preliminari. : V V R un
Corso di Laurea in Fisica. Geometria. a.a. 2012-13. Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche Sia V uno spazio vettoriale reale. Sia 1. Osservazioni preliminari. : V V R un
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE210 - Geometria 2 a.a Prima prova di esonero TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 08-09 Prima prova di esonero TESTO E SOLUZIONI. Sia k 0 un numero reale. Sia V uno spazio vettoriale reale e sia e = {e,
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 08-09 Prima prova di esonero TESTO E SOLUZIONI. Sia k 0 un numero reale. Sia V uno spazio vettoriale reale e sia e = {e,
Anno Accademico 2015/2016
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I I Docente
25 - Funzioni di più Variabili Introduzione
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Applicazioni lineari e diagonalizzazione
 Autovalori e autovettori Matrici associate a applicazioni lineari Endomorfismi semplici e matrici diagonalizzabili Prodotti scalari e Teorema Spettrale nel caso generale 2 2006 Politecnico di Torino 1
Autovalori e autovettori Matrici associate a applicazioni lineari Endomorfismi semplici e matrici diagonalizzabili Prodotti scalari e Teorema Spettrale nel caso generale 2 2006 Politecnico di Torino 1
Spazi euclidei, endomorfismi simmetrici, forme quadratiche. R. Notari
 Spazi euclidei, endomorfismi simmetrici, forme quadratiche R. Notari 14 Aprile 2006 1 1. Proprietà del prodotto scalare. Sia V = R n lo spazio vettoriale delle n-uple su R. Il prodotto scalare euclideo
Spazi euclidei, endomorfismi simmetrici, forme quadratiche R. Notari 14 Aprile 2006 1 1. Proprietà del prodotto scalare. Sia V = R n lo spazio vettoriale delle n-uple su R. Il prodotto scalare euclideo
NORMA DI UN VETTORE. Una NORMA VETTORIALE su R n è una funzione. : R n R +
 NORMA DI UN VETTORE Una NORMA VETTORIALE su R n è una funzione. : R n R + {0}, che associa ad ogni vettore x R n di componenti x i, i = 1,..., n, uno scalare in modo che valgano le seguenti proprietà:
NORMA DI UN VETTORE Una NORMA VETTORIALE su R n è una funzione. : R n R + {0}, che associa ad ogni vettore x R n di componenti x i, i = 1,..., n, uno scalare in modo che valgano le seguenti proprietà:
22 Coniche proiettive
 Geometria e Topologia I (U1-4) 2006-giu-06 95 22 Coniche proiettive (22.1) Definizione. Sia K[x 0, x 1,..., x n ] l anello dei polinomi nelle indeterminate (variabili) x 0, x 1,..., x n. Un polinomio di
Geometria e Topologia I (U1-4) 2006-giu-06 95 22 Coniche proiettive (22.1) Definizione. Sia K[x 0, x 1,..., x n ] l anello dei polinomi nelle indeterminate (variabili) x 0, x 1,..., x n. Un polinomio di
Daniela Lera A.A
 Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2016-2017 Richiami Algebra Lineare Spazio normato Uno spazio lineare X si dice normato se esiste una funzione
Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2016-2017 Richiami Algebra Lineare Spazio normato Uno spazio lineare X si dice normato se esiste una funzione
Esercizi di Geometria - 1
 Esercizi di Geometria - Samuele Mongodi - smongodi@snsit Di seguito si trovano alcuni esercizi assai simili a quelli che vi troverete ad affrontare nei test e negli scritti dell esame Non è detto che vi
Esercizi di Geometria - Samuele Mongodi - smongodi@snsit Di seguito si trovano alcuni esercizi assai simili a quelli che vi troverete ad affrontare nei test e negli scritti dell esame Non è detto che vi
Esercitazioni di Geometria A: spazi euclidei
 Esercitazioni di Geometria A: spazi euclidei 9-10 marzo 2016 Esercizio 1 Sia V uno spazio vettoriale sul campo K = R e si consideri una base B = {e 1, e 2, e 3 }. Si consideri la matrice a coefficienti
Esercitazioni di Geometria A: spazi euclidei 9-10 marzo 2016 Esercizio 1 Sia V uno spazio vettoriale sul campo K = R e si consideri una base B = {e 1, e 2, e 3 }. Si consideri la matrice a coefficienti
Esercizi di Geometria - 2
 Esercizi di Geometria - 2 Samuele Mongodi - s.mongodi@sns.it La prima sezione contiene alcune domande aperte e alcune domande verofalso, come quelle che potrebbero capitare nel test. E consigliabile, nel
Esercizi di Geometria - 2 Samuele Mongodi - s.mongodi@sns.it La prima sezione contiene alcune domande aperte e alcune domande verofalso, come quelle che potrebbero capitare nel test. E consigliabile, nel
Geometria I. Soluzioni della prova scritta del 19 settembre 2016
 Geometria I Soluzioni della prova scritta del 9 settembre 6 Esercizio Consideriamo una forma bilineare simmetrica g : V V R su uno spazio vettoriale reale V di dimensione finita, una sua base B e la matrice
Geometria I Soluzioni della prova scritta del 9 settembre 6 Esercizio Consideriamo una forma bilineare simmetrica g : V V R su uno spazio vettoriale reale V di dimensione finita, una sua base B e la matrice
Autovalori e autovettori di una matrice quadrata
 Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5. Indice. 2. Esercizi 5
 ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Forme bilineari e prodotti scalari
 Forme bilineari e prodotti scalari Avvertenza: Gli argomenti che esponiamo brevemente in queste note sono tutti trattati in maggior dettaglio nel capitolo del libro di testo Abate De Fabritiis. Nel corso
Forme bilineari e prodotti scalari Avvertenza: Gli argomenti che esponiamo brevemente in queste note sono tutti trattati in maggior dettaglio nel capitolo del libro di testo Abate De Fabritiis. Nel corso
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura. Geometria Proiettiva Docente F.
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Geometria Proiettiva Docente F. Flamini CONICHE PROIETTIVE: Classificazione e forme canoniche proiettive Si
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Geometria Proiettiva Docente F. Flamini CONICHE PROIETTIVE: Classificazione e forme canoniche proiettive Si
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
Lezione Diagonalizzazione ortogonale per matrici simmetriche
 Lezione 22 22. Diagonalizzazione ortogonale per matrici simmetriche La Proposizione 2. afferma che ogni matrice simmetrica reale è diagonalizzabile su R: ilrisultatoprincipalediquestasezioneèchelamatricechediagonalizzapuò
Lezione 22 22. Diagonalizzazione ortogonale per matrici simmetriche La Proposizione 2. afferma che ogni matrice simmetrica reale è diagonalizzabile su R: ilrisultatoprincipalediquestasezioneèchelamatricechediagonalizzapuò
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
Geometria e Topologia I 18 maggio
 Geometria e Topologia I 18 maggio 2005 64 17 Mappe affini (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine o trasformazione
Geometria e Topologia I 18 maggio 2005 64 17 Mappe affini (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine o trasformazione
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Esercitazioni del Marzo di Geometria A
 Esercitazioni del -5 Marzo di Geometria A Università degli Studi di Trento Corso di laurea in Matematica AA 07/08 Matteo Bonini matteobonini@unitnit Esercizio Si consideri la matrice 0 A 0 0 0 0 (i Scrivere
Esercitazioni del -5 Marzo di Geometria A Università degli Studi di Trento Corso di laurea in Matematica AA 07/08 Matteo Bonini matteobonini@unitnit Esercizio Si consideri la matrice 0 A 0 0 0 0 (i Scrivere
Complementi di Algebra e Fondamenti di Geometria
 Complementi di Algebra e Fondamenti di Geometria Capitolo 5 Forme quadratiche inr n M. Ciampa Ingegneria Elettrica, a.a. 2009/2010 Capitolo 5 Forme quadratiche inr n In questo capitolo si definisce la
Complementi di Algebra e Fondamenti di Geometria Capitolo 5 Forme quadratiche inr n M. Ciampa Ingegneria Elettrica, a.a. 2009/2010 Capitolo 5 Forme quadratiche inr n In questo capitolo si definisce la
0.1 Coordinate in uno spazio vettoriale
 0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
Sapienza Università di Roma Corso di laurea in Ingegneria Energetica Geometria A.A ESERCIZI DA CONSEGNARE prof.
 Sapienza Università di Roma Corso di laurea in Ingegneria Energetica Geometria A.A. 2015-2016 ESERCIZI DA CONSEGNARE prof. Cigliola Consegna per Martedì 6 Ottobre Esercizio 1. Una matrice quadrata A si
Sapienza Università di Roma Corso di laurea in Ingegneria Energetica Geometria A.A. 2015-2016 ESERCIZI DA CONSEGNARE prof. Cigliola Consegna per Martedì 6 Ottobre Esercizio 1. Una matrice quadrata A si
Spazi Vettoriali ed Applicazioni Lineari
 Spazi Vettoriali ed Applicazioni Lineari 1. Sottospazi Definizione. Sia V uno spazio vettoriale sul corpo C. Un sottoinsieme non vuoto W di V è un sottospazio vettoriale di V se è chiuso rispetto alla
Spazi Vettoriali ed Applicazioni Lineari 1. Sottospazi Definizione. Sia V uno spazio vettoriale sul corpo C. Un sottoinsieme non vuoto W di V è un sottospazio vettoriale di V se è chiuso rispetto alla
ESERCIZI DI GEOMETRIA E ALGEBRA LINEARE (II PARTE) In ogni sezione gli esercizi sono tendenzialmente ordinati per difficoltà crescente.
 ESERCIZI DI GEOMETRIA E ALGEBRA LINEARE (II PARTE) versione: 24 maggio 27 In ogni sezione gli esercizi sono tendenzialmente ordinati per difficoltà crescente Autovettori e autovalori Esercizio Trova gli
ESERCIZI DI GEOMETRIA E ALGEBRA LINEARE (II PARTE) versione: 24 maggio 27 In ogni sezione gli esercizi sono tendenzialmente ordinati per difficoltà crescente Autovettori e autovalori Esercizio Trova gli
SPAZI VETTORIALI CON PRODOTTO SCALARE A =
 SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010
 Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010 In quetsa dispensa: V è uno spazio vettoriale di dimensione d sul campo complesso C generato dai vettori v 1,..., v d. Le variabili m,
Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010 In quetsa dispensa: V è uno spazio vettoriale di dimensione d sul campo complesso C generato dai vettori v 1,..., v d. Le variabili m,
Esempi. In R 2, le coppia (2, 5) è combinazione lineare dei vettori (0, 1) e (1, 1). Infatti:
 Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE210 - Geometria 2 a.a Prova scritta del TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 08-09 Prova scritta del 0--09 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Sia V uno spazio vettoriale reale di dimensione
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 08-09 Prova scritta del 0--09 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Sia V uno spazio vettoriale reale di dimensione
0.1 Forme quadratiche
 0.1. FORME QUADRATICHE 1 0.1 Forme quadratiche In questa sezione possiamo applicare il Teorema degli Assi Principali per giustificare alcune fatti che sono stati utilizzati nella riduzione a forma canonica
0.1. FORME QUADRATICHE 1 0.1 Forme quadratiche In questa sezione possiamo applicare il Teorema degli Assi Principali per giustificare alcune fatti che sono stati utilizzati nella riduzione a forma canonica
Dim. Usare la chiusura rispetto al prodotto esterno (vedi appunti lezione o libri di testo).
 ESERCIZI PER CASA di GEOMETRIA per il Corso di Laurea di Scienze dei Materiali, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 28 maggio 29 Sottospazi di uno spazio vettoriale, sistemi
ESERCIZI PER CASA di GEOMETRIA per il Corso di Laurea di Scienze dei Materiali, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 28 maggio 29 Sottospazi di uno spazio vettoriale, sistemi
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE210
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE A.A. - - Docente: Prof. A. Verra Tutori: Simona Dimase e Annamaria Iezzi Soluzioni tutorato numero 6 (6 Novembre ) Coniche.
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE A.A. - - Docente: Prof. A. Verra Tutori: Simona Dimase e Annamaria Iezzi Soluzioni tutorato numero 6 (6 Novembre ) Coniche.
Appunti del corso di Geometria II
 Università del Salento Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Matematica Appunti del corso di Geometria II Alessandro Montinaro ANNO ACCADEMICO 2015-2016 L obiettivo
Università del Salento Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Matematica Appunti del corso di Geometria II Alessandro Montinaro ANNO ACCADEMICO 2015-2016 L obiettivo
I VERIFICA DI GEOMETRIA 1 CORSO DI LAUREA IN MATEMATICA - 4 DICEMBRE 2007
 A I VERIFICA DI GEOMETRIA 1 CORSO DI LAUREA IN MATEMATICA - 4 DICEMBRE 2007 ESERCIZIO 1. Si consideri il seguente sistema di equazioni lineari x + y + 2z = 1 2x + ky + 4z = h 2x 2y + kz = 0 (a) Determinare,
A I VERIFICA DI GEOMETRIA 1 CORSO DI LAUREA IN MATEMATICA - 4 DICEMBRE 2007 ESERCIZIO 1. Si consideri il seguente sistema di equazioni lineari x + y + 2z = 1 2x + ky + 4z = h 2x 2y + kz = 0 (a) Determinare,
GEOMETRIA PER FISICI ELENCO DEGLI ARGOMENTI TRATTATI DURANTE LE LEZIONI
 GEOMETRIA PER FISICI 2016-17 ELENCO DEGLI ARGOMENTI TRATTATI DURANTE LE LEZIONI 1. MARTEDÌ 4 OTTOBRE 2016 Informazioni organizzative. Chiacchiere. Panoramica sul corso. Tre esempi di linearità. 2. GIOVEDÌ
GEOMETRIA PER FISICI 2016-17 ELENCO DEGLI ARGOMENTI TRATTATI DURANTE LE LEZIONI 1. MARTEDÌ 4 OTTOBRE 2016 Informazioni organizzative. Chiacchiere. Panoramica sul corso. Tre esempi di linearità. 2. GIOVEDÌ
Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE
 Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE 1. Matrici ortogonali Ricordiamo che, nel Cap. VII, abbiamo studiato le matrici di cambio di base in un R spazio vettoriale. In tale occasione, abbiamo
Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE 1. Matrici ortogonali Ricordiamo che, nel Cap. VII, abbiamo studiato le matrici di cambio di base in un R spazio vettoriale. In tale occasione, abbiamo
Geometria I 2009-mag
 Geometria I 2009-mag-06 124 17 Mappe affini Cfr: Nacinovich, Cap V, 3 [3]. (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine
Geometria I 2009-mag-06 124 17 Mappe affini Cfr: Nacinovich, Cap V, 3 [3]. (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Si dimostra che queste funzioni godono delle proprietà delle norme (ossia sono norme).
 Norma di un vettore I Una norma vettoriale su R n è una funzione : R n R + {}, che associa ad ogni vettore x R n, di componenti x i, i = 1,..., n, uno scalare, in modo che valgano le seguenti proprietà:
Norma di un vettore I Una norma vettoriale su R n è una funzione : R n R + {}, che associa ad ogni vettore x R n, di componenti x i, i = 1,..., n, uno scalare, in modo che valgano le seguenti proprietà:
Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. a m,1 x 1 + a m,2 x a m,n x n = b m
 1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
Geometria BAER Canale I Esercizi 9
 Geometria BAER Canale I Esercizi 9 Esercizio 1. Si trovi la matrice del prodotto standard di R 3 rispetto alle basi B = (2, 0, 1) t, (1, 0, 2) t, (1, 1, 1) t } e D = (2, 2, 1) t, ( 1, 2, 2) t, (2, 1, 2)
Geometria BAER Canale I Esercizi 9 Esercizio 1. Si trovi la matrice del prodotto standard di R 3 rispetto alle basi B = (2, 0, 1) t, (1, 0, 2) t, (1, 1, 1) t } e D = (2, 2, 1) t, ( 1, 2, 2) t, (2, 1, 2)
Geometria 2. Università degli Studi di Trento Corso di Laurea in matematica A.A. 2010/ luglio 2011
 Geometria 2 Università degli Studi di Trento Corso di Laurea in matematica A.A. 2010/2011 25 luglio 2011 Si svolgano i seguenti esercizi. Esercizio 1. Denotiamo con E 4 il 4 spazio euclideo numerico dotato
Geometria 2 Università degli Studi di Trento Corso di Laurea in matematica A.A. 2010/2011 25 luglio 2011 Si svolgano i seguenti esercizi. Esercizio 1. Denotiamo con E 4 il 4 spazio euclideo numerico dotato
GEOMETRIA 1 Autovalori e autovettori
 GEOMETRIA 1 Autovalori e autovettori Gilberto Bini - Anna Gori - Cristina Turrini 2018/2019 Gilberto Bini - Anna Gori - Cristina Turrini (2018/2019) GEOMETRIA 1 1 / 28 index Matrici rappresentative "semplici"
GEOMETRIA 1 Autovalori e autovettori Gilberto Bini - Anna Gori - Cristina Turrini 2018/2019 Gilberto Bini - Anna Gori - Cristina Turrini (2018/2019) GEOMETRIA 1 1 / 28 index Matrici rappresentative "semplici"
Geometria BAER A.A. Canale I Foglio esercizi 4
 Geometria BAER A.A. Canale I Foglio esercizi 4 Esercizio. Si trovino basi degli spazi delle soluzioni dei seguenti sistemi lineari Soluzione: Sol(S ) = L[ x + 3x x 3 + 5x 4 = S : x + 3x x 3 + x 4 = S x
Geometria BAER A.A. Canale I Foglio esercizi 4 Esercizio. Si trovino basi degli spazi delle soluzioni dei seguenti sistemi lineari Soluzione: Sol(S ) = L[ x + 3x x 3 + 5x 4 = S : x + 3x x 3 + x 4 = S x
0 1 k. k k k +4. b) Posto k = 0, si calcoli l inversa di A e l inversa di T.
 Esercizi per il Parziale 2, Prof. Fioresi, 2016 1. Cambi di base, determinante e inversa 1. Si trovino le coordinate del vettore v = (1, 1,2) espresso nella base canonica, rispetto alla base B = {(1, 4,3),(5,3,
Esercizi per il Parziale 2, Prof. Fioresi, 2016 1. Cambi di base, determinante e inversa 1. Si trovino le coordinate del vettore v = (1, 1,2) espresso nella base canonica, rispetto alla base B = {(1, 4,3),(5,3,
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
GEOMETRIA 1 terza parte
 GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
Quadriche Maurizio Cornalba 7/6/2016
 Quadriche Maurizio Cornalba 7/6/2016 Sia K un campo. Informalmente, una ipersuperficie (algebrica) nello spazio proiettivo P n K è il luogo dei punti [t 0 : t 1 : : t n ] tali che (t 0, t 1,..., t n )
Quadriche Maurizio Cornalba 7/6/2016 Sia K un campo. Informalmente, una ipersuperficie (algebrica) nello spazio proiettivo P n K è il luogo dei punti [t 0 : t 1 : : t n ] tali che (t 0, t 1,..., t n )
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
6. Spazi euclidei ed hermitiani
 6. Spazi euclidei ed hermitiani 6.1 In [GA] 5.4 abbiamo definito il prodotto scalare fra vettori di R n (che d ora in poi chiameremo prodotto scalare standard su R n ) e abbiamo considerato le seguenti
6. Spazi euclidei ed hermitiani 6.1 In [GA] 5.4 abbiamo definito il prodotto scalare fra vettori di R n (che d ora in poi chiameremo prodotto scalare standard su R n ) e abbiamo considerato le seguenti
Spazi vettoriali metrici.
 Spazi vettoriali metrici Prodotti scalari e hermitiani Spazi vettoriali metrici Definizione Sia V uno spazio vettoriale su R e sia g: V V R una funzione Se per ogni v, v, v, w, w, w V e λ R si ha g(v +
Spazi vettoriali metrici Prodotti scalari e hermitiani Spazi vettoriali metrici Definizione Sia V uno spazio vettoriale su R e sia g: V V R una funzione Se per ogni v, v, v, w, w, w V e λ R si ha g(v +
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3
 Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
0 1 k. k k k +4. b) Posto k = 0, si calcoli l inversa di A e l inversa di T.
 Esercizi per il Parziale 2, Prof. Fioresi, 2018 1. Cambi di base, determinante e inversa 1. Si trovino le coordinate del vettore v = (1, 1,2) espresso nella base canonica, rispetto alla base B = {(1, 4,3),(5,3,
Esercizi per il Parziale 2, Prof. Fioresi, 2018 1. Cambi di base, determinante e inversa 1. Si trovino le coordinate del vettore v = (1, 1,2) espresso nella base canonica, rispetto alla base B = {(1, 4,3),(5,3,
2. Fra tutti i rettangoli inscritti in una circonferenza, determinare quello di area massima.
 2. Fra tutti i rettangoli inscritti in una circonferenza, determinare quello di area massima. 3. Fra tutti i cilindri a base rotonda inscritti in una sfera, determinare quello di volume massimo. 4. Dimostrare
2. Fra tutti i rettangoli inscritti in una circonferenza, determinare quello di area massima. 3. Fra tutti i cilindri a base rotonda inscritti in una sfera, determinare quello di volume massimo. 4. Dimostrare
Autovettori e autovalori
 Autovettori e autovalori Definizione 1 Sia A Mat(n, n), matrice a coefficienti reali. Si dice autovalore di A un numero λ R tale che v 0 R n Av = λv. Ogni vettore non nullo v che soddisfa questa relazione
Autovettori e autovalori Definizione 1 Sia A Mat(n, n), matrice a coefficienti reali. Si dice autovalore di A un numero λ R tale che v 0 R n Av = λv. Ogni vettore non nullo v che soddisfa questa relazione
Geometria BAER Canale A-K Esercizi 8
 Geometria BAER 6-7 Canale A-K Esercizi 8 Esercizio Si consideri il sottospazio (a) Si trovi una base ortonormale di U (b) Si trovi una base ortonormale di U U = L v =, v, v 3 = (c) Si scriva la matrice
Geometria BAER 6-7 Canale A-K Esercizi 8 Esercizio Si consideri il sottospazio (a) Si trovi una base ortonormale di U (b) Si trovi una base ortonormale di U U = L v =, v, v 3 = (c) Si scriva la matrice
Prodotti scalari e matrici
 Prodotti scalari e matrici 1 Forme bilineari e matrici In questa sezione vogliamo studiare la corrispondenza biunivoca che esiste tra l insieme delle forme bilineari su di un certo spazio vettoriale V
Prodotti scalari e matrici 1 Forme bilineari e matrici In questa sezione vogliamo studiare la corrispondenza biunivoca che esiste tra l insieme delle forme bilineari su di un certo spazio vettoriale V
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE210 - Geometria 2 a.a Prova scritta del TESTO E SOLUZIONI.
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 08-09 Prova scritta del --09 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Sia k R tale che k > 0, k 4 e sia b k : R
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 08-09 Prova scritta del --09 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Sia k R tale che k > 0, k 4 e sia b k : R
Soluzioni della prova scritta di Geometria 1 del 27 giugno 2019 (versione I)
 Soluzioni della prova scritta di Geometria 1 del 7 giugno 019 (versione I) Esercizio 1. Sia R 4 lo spazio quadridimensionale standard munito del prodotto scalare standard con coordinate canoniche (x 1,
Soluzioni della prova scritta di Geometria 1 del 7 giugno 019 (versione I) Esercizio 1. Sia R 4 lo spazio quadridimensionale standard munito del prodotto scalare standard con coordinate canoniche (x 1,
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
FORME BILINEARI E QUADRATICHE
 FORME BILINEARI E QUADRATICHE CORSO DI GEOMETRIA ANALITICA 2007-08, UNIVERSITÀ DI ROMA 1 1. Forme bilineari e quadratiche Definizione 1.1. Sia V uno spazio di dimensione finita su di un campo K; un applicazione
FORME BILINEARI E QUADRATICHE CORSO DI GEOMETRIA ANALITICA 2007-08, UNIVERSITÀ DI ROMA 1 1. Forme bilineari e quadratiche Definizione 1.1. Sia V uno spazio di dimensione finita su di un campo K; un applicazione
ENDOMORFISMI. NOTE DI ALGEBRA LINEARE
 ENDOMORFISMI. NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 15 GENNAIO 2011 1. Endomorfismi e sottospazi invarianti Definizione 1.1. Sia V uno spazio vettoriale su K. Un endomorfismo di V è una qualsiasi
ENDOMORFISMI. NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 15 GENNAIO 2011 1. Endomorfismi e sottospazi invarianti Definizione 1.1. Sia V uno spazio vettoriale su K. Un endomorfismo di V è una qualsiasi
4 Autovettori e autovalori
 4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
Corso di Laurea in Matematica - Esame di Geometria 1. Prova scritta del 7 settembre 2015
 Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
(P x) (P y) = x P t (P y) = x (P t P )y = x y.
 Matrici ortogonali Se P è una matrice reale n n, allora (P x) y x (P t y) per ogni x,y R n (colonne) Dim (P x) y (P x) t y (x t P t )y x t (P t y) x (P t y), CVD Ulteriori caratterizzazioni delle matrici
Matrici ortogonali Se P è una matrice reale n n, allora (P x) y x (P t y) per ogni x,y R n (colonne) Dim (P x) y (P x) t y (x t P t )y x t (P t y) x (P t y), CVD Ulteriori caratterizzazioni delle matrici
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
Definizione 1. Una matrice n m a coefficienti in K é una tabella del tipo. ... K m, detto vettore riga i-esimo, ed a im
 APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
GE110 - Geometria 1. Prova in Itinere 2 27 Maggio 2010
 GE110 - Geometria 1 Prova in Itinere 2 27 Maggio 2010 COGNOME e NOME : Problema 1: Problema 2: Problema 3: 1 2 Problema 1. Nello spazio affine reale A 5 R si fissi il riferimento affine canonico, e siano
GE110 - Geometria 1 Prova in Itinere 2 27 Maggio 2010 COGNOME e NOME : Problema 1: Problema 2: Problema 3: 1 2 Problema 1. Nello spazio affine reale A 5 R si fissi il riferimento affine canonico, e siano
ESAME DI GEOMETRIA. 6 febbraio 2002 CORREZIONE QUIZ
 ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
Esercizi su applicazioni lineari. Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K.
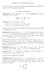 Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
ESERCIZI DI ALGEBRA LINEARE (II PARTE) In ogni sezione gli esercizi sono tendenzialmente ordinati per difficoltà crescente.
 ESERCIZI DI ALGEBRA LINEARE (II PARTE) versione: 4 maggio 26 In ogni sezione gli esercizi sono tendenzialmente ordinati per difficoltà crescente Autovettori e autovalori Esercizio Trova gli autovalori
ESERCIZI DI ALGEBRA LINEARE (II PARTE) versione: 4 maggio 26 In ogni sezione gli esercizi sono tendenzialmente ordinati per difficoltà crescente Autovettori e autovalori Esercizio Trova gli autovalori
Corso di Laurea in Matematica - Esame di Geometria UNO. Prova scritta del 22 gennaio 2015
 Corso di Laurea in Matematica - Esame di Geometria UNO Prova scritta del 22 gennaio 2015 Cognome Nome Numero di matricola Corso (A o B) Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi.
Corso di Laurea in Matematica - Esame di Geometria UNO Prova scritta del 22 gennaio 2015 Cognome Nome Numero di matricola Corso (A o B) Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi.
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
Elementi di Algebra Lineare
 Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
3. Determinare dimensione a basi per l annullatore ker(f) e per il complemento. Esercizio 2. Sia V uno spazio vettoriale reale di dimensione finita d.
 Esercizi --- 5-- Esercizio. Sia f =: L A : R 4 R 4, ove A = 3 e sia B =:.. Dimostrare che B è una base di R 4.. Determinare la matrice di L A nella base B. 3. Determinare dimensione a basi per l annullatore
Esercizi --- 5-- Esercizio. Sia f =: L A : R 4 R 4, ove A = 3 e sia B =:.. Dimostrare che B è una base di R 4.. Determinare la matrice di L A nella base B. 3. Determinare dimensione a basi per l annullatore
