Modelli Concettuali. Dal problema alla soluzione
|
|
|
- Leonardo Fedele
- 9 anni fa
- Visualizzazioni
Transcript
1 Modelli Concettuali Dal problema alla soluzione Il processo di soluzione di un problema può sembrare semplice: c'è un problema reale, concreto, che provoca certi inconvenienti. Si studia il problema concreto e si costruisce una soluzione altrettanto concreta che risolve il problema eliminando gli inconvenienti. Problema concreto Soluzione concreta Una riflessione più attenta rivela che il percorso dal problema concreto alla soluzione concreta passa per il mondo dell'astrazione e dei ragionamenti, dei concetti, dei modelli (un modello è un insieme di concetti tra loro correlati). Mondo dell'astrazione Modello del problema 2. progettazione Modello della soluzione 1. analisi 3. realizzazione Mondo della concretezza Problema concreto 4. collaudo Soluzione concreta 1. Analisi del problema. Lo studio del problema conduce a comprenderne gli elementi essenziali, e a costruire un modello del problema. Il processo introduce elementi di astrazione e quindi di generalità: generalmente un unico modello si adatta a molti problemi particolari simili a quello di partenza. Si passa dal mondo della concretezza al mondo dell'astrazione. 2. Progettazione. Dal modello del problema si passa al modello della soluzione, utilizzando concetti il più possibile indipendenti da tecnologie particolari. Infatti uno stesso modello di soluzione potrà avere realizzazioni diverse con diverse tecnologie. 3. Realizzazione. Il modello della soluzione viene calato su certe tecnologie concretamente disponibili, e viene realizzata una soluzione concreta. In questa fase si torna dal mondo dell'astrazione al mondo della concretezza. 4. Collaudo. Si verifica che la soluzione concreta risolva effettivamente il problema. Se si è lavorato bene, la soluzione è in grado di risolvere non soltanto il problema di partenza, ma tutta una gamma di problemi simili. Giuseppe D'Amico dicembre pag. 1 di 5
2 Modello concettuale del problema L'attività di analisi è finalizzata alla comprensione profonda del problema, e alla costruzione del suo modello concettuale. Modello: si considera del problema solo ciò che è essenziale (il nocciolo del problema), e si trascura ciò che è episodico o accidentale. Concettuale: espresso in termini di concetti. Quali? I concetti propri del problema, che vanno definiti con il massimo di chiarezza e precisione. Esempi di modelli concettuali Creare modelli concettuali è difficile e faticoso. Il risultato può rivelarsi di grandissima utilità. Alcuni modelli concettuali hanno richiesto secoli per la loro formulazione; ma essi hanno cambiato il corso della storia, e sono entrati a far parte della cultura generale dell'umanità. Ne citiamo due, di livello altissimo, solo per chiarire che cosa significa "afferrare il nocciolo del problema" e "rappresentarlo con precisione": modello della gravitazione universale modello della partita doppia. 1. Gravitazione universale Un modello che spiega il movimento dei corpi celesti. Pochi concetti fondamentali: Punto Materiale: una astrazione di un corpo materiale in cui tutta la massa del corpo è concentrata in un punto. Nel modello tutti i corpi celesti (stelle, pianeti, ) come punti materiali. Forza di Gravitazione: due punti materiali di massa m1 e m2 si attraggono con forza m1 m2 F = k 2 d dove d è la distanza tra i due punti materiali. Che cosa c'è di più semplice, di più preciso, di più generale? Molto spesso un modello concettuale è rappresentato mediante un diagramma entità/relazioni. Le entità sono i concetti fondamentali, e si rappresentano mediante rettangoli. Le relazioni tra i concetti si rappresentano mediante frecce o linee che collegano i concetti. Punto Materiale Forza di Attrazione Spiegazione del diagramma: Esistono punti materiali, dotati di massa e posizione. Ogni punto materiale è soggetto a molte forze di attrazione. Ogni forza di attrazione è relativa a due punti materiali. Essa è direttamente proporzionale al prodotto delle due masse e inversamente proporzionale al quadrato della distanza dei due punti. 2. Partita doppia Il modello concettuale della partita doppia è alla base di tutti i modelli contabili utilizzati nella realtà. Un documento introduttivo sui concetti della partita doppia è presente in questo sito (PartitaDoppia.pdf). Concetti fondamentali: Nel modello della partita doppia ogni fatto è rappresentato da una transazione. Ogni transazione è uno spostamento di risorse da un conto di origine a un conto di destinazione. Ogni conto può essere origine per certe tranzazioni, e destinazione per altre. L'ammontare delle risorse spostate è misurata mediante unità di denaro. Un diagramma entità/relazioni per la partita doppia: Giuseppe D'Amico dicembre pag. 2 di 5
3 Conto Transazione 3. Proprietà immobiliari Adesso torniamo alla nostra piccolezza. Un piccolo esempio riguardante una comunità di soggetti che posseggono immobili. Esistono degli immobili (case, terreni). Esistono dei soggetti (persone, società, enti,...). Ogni soggetto può essere proprietario di uno o più immobili da solo o insieme ad altri soggetti. Quota di proprietà: il fatto che il soggetto X è proprietario di una quota Q dell'immobile I. Regola: per ogni immobile la somma delle quote di proprietà relative ai vari soggetti deve essere 100%. Soggetto Immobile Quota di Proprietà Modello dinamico La definizione delle entità e delle relazioni definisce la struttura del modello: di quali concetti fondamentali (entità) esso è composto, e come questi concetti siano interrelati. Ciò spesso non è sufficiente: infatti, se si tratta di una realtà capace di evolvere, dobbiamo studiare (e modellare) anche le modalità e le leggi del cambiamento. Modalità di evoluzione: accadimenti L'evoluzione di una realtà si può modellare mediante accadimenti discreti che provocano cambiamenti. Quali sono questi accadimenti? Per il problema delle proprietà immobiliari essi sono: Costruzione o demolizione di un immobile; Compravendita di un immobile. Quale metodo? Produrre un modello concettuale non è facile. Si impara facendo (e sbagliando). Alcuni consigli: Leggere e assimilare tutto ciò che si trova sull'argomento. Partire dalla pagina bianca. Aggiungere solo ciò di cui si è sicuri. Togliere ciò che è incerto, confuso, ambiguo. Diffidare delle eccezioni. Procedere dal semplice al complesso. Far diventare semplice il complesso. Verificare continuamente. Le regole fondamentali mi sembrano essere sempre quelle formulate da Cartesio (Discorso sul metodo, 1637). Le riporto tali e quali. La prima regola era di non accettare mai nulla per vero, senza conoscerlo evidentemente come tale: cioè di evitare scrupolosamente la precipitazione e la prevenzione; e di non comprendere nei miei giudizi niente più di quanto si Giuseppe D'Amico dicembre pag. 3 di 5
4 fosse presentato alla mia ragione tanto chiaramente e distintamente da non lasciarmi nessuna occasione di dubitarne. La seconda, di dividere ogni problema preso in esame in tante parti quanto fosse possibile e richiesto per risolverlo più agevolmente. La terza, di condurre ordinatamente i miei pensieri cominciando dalle cose più semplici e più facili a conoscersi, per salire a poco a poco, come per gradi, sino alla conoscenza delle più complesse; supponendo altresì un ordine tra quelle che non si precedono naturalmente l'un l'altra. E l'ultima, di fare in tutti i casi enumerazioni tanto perfette e rassegne tanto complete, da essere sicuro di non omettere nulla. Modello della soluzione: applicazione informatica Immaginiamo ora di volere risolvere un problema (di cui abbiamo un modello concettuale) mediante un'applicazione informatica. Il mondo dell'informatica è vasto e complicato, perchè esistono svariate tecnologie all'interno delle quali scegliere: linguaggi di programmazione basi di dati interfacce con l'utente locali o via web. Tuttavia è possibile produrre un modello di applicazione che trascura tutte le particolarità tecnologiche, e si concentra invece sul nucleo concettuale, cioè su quelle caratteristiche fondamentali che qualsiasi realizzazione deve possedere per risolvere il problema. Modello astratto di una applicazione informatica Utenti Applicazione Op Base informativa Una qualsiasi applicazione informatica offre servizi applicativi ai suoi utenti. Essa possiede una base informativa dove è memorizzato un modello del suo mondo (entità e relazioni); esegue operazioni su richiesta dei suoi utenti. Una applicazione è completamente determinata quando sono determinate la sua base informativa le sue operazioni. Un esempio di applicazione Per fissare le idee, pensiamo ad una applicazione per il problema delle proprietà immobiliari. Base Informativa Lo schema della base informativa deriva direttamente dallo schema entità/relazioni. Soggetto Immobile Quota di Proprietà Operazioni di aggiornamento Sono quelle che realizzano gli accadimenti individuati nello studio del problema. Soggetto: creazione, variazione, eliminazione. Immobile: creazione, variazione, eliminazione. Quota di proprietà: creazione, variazione, eliminazione. Giuseppe D'Amico dicembre pag. 4 di 5
5 Operazioni di consultazione Ricerca dei soggetti con determinate caratteristiche Consultazione di un determinato soggetto con tutte le sue quote di proprietà Ricerca degli immobili con particolari caratteristiche Consultazione di un determinato immobile con tutte le sue quote di proprietà Situazioni irregolari Ricordiamo che nel modello delle proprietà immobiliari c'e una regola: Per ogni immobile la somma delle quote di proprietà relative ai vari soggetti deve essere 100%. Una interpretazione pienamente rigorosa di questa regola impedirebbe - la nascita di un immobile, se non immediatamente dotato di tutte le sue quote di proprietà; - la eliminazione di un soggetto dotato di qualche quota di proprietà - la variazione di una quota di proprietà. Questa interpretazione potrebbe risultare troppo rigida. Possiamo allora interpretare la regola in modo più flessibile: è possibile che il modello si trovi in uno stato provvisorio di irregolarità, purchè esso proceda verso uno stato di regolarità. In questo caso, dobbiamo aggiungere un'operazione che ci consente di conoscere se siamo, per qualche immobile, in una situazione di irregolarità: Ricerca degli immobili irregolari Il risultato di questa informazione fornisce la lista degli immobili per cui il totale delle quote di possesso è diverso da 100% Conclusione Modello concettuale del problema Accadimenti Entità Relazioni Modello concettuale della soluzione Base Informativa Entità Relazioni Operazioni Aggiornamento Consultazione Regole Giuseppe D'Amico dicembre pag. 5 di 5
Diagrammi di Gantt & reticolare
 Diagrammi di Gantt & reticolare Henry Laurence Gantt (1861-1919) era un ingegnere meccanico e consulente di management statunitense. Nel 1917 ideò il diagramma di Gantt che è divenuto uno dei principali
Diagrammi di Gantt & reticolare Henry Laurence Gantt (1861-1919) era un ingegnere meccanico e consulente di management statunitense. Nel 1917 ideò il diagramma di Gantt che è divenuto uno dei principali
Le leggi di Keplero e la gravitazione universale. Enrico Degiuli Classe Terza
 Le leggi di Keplero e la gravitazione universale Enrico Degiuli Classe Terza Giovanni Keplero Keplero è stato un astronomo tedesco vissuto a cavallo tra il 1500 e il 1600. Ha condotto lunghi studi sul
Le leggi di Keplero e la gravitazione universale Enrico Degiuli Classe Terza Giovanni Keplero Keplero è stato un astronomo tedesco vissuto a cavallo tra il 1500 e il 1600. Ha condotto lunghi studi sul
Estratto da: Yona Friedman, L'ordine complicato. Come costruire un'immagine, traduzione di Paolo Tramannoni, con una nota di Manuel Orazi,
 Estratto da: Yona Friedman, L'ordine complicato. Come costruire un'immagine, traduzione di Paolo Tramannoni, con una nota di Manuel Orazi, Quodlibet-Abitare, Macerata 2011. Ulteriori informazioni: http://www.quodlibet.it/schedap.php?id=1963
Estratto da: Yona Friedman, L'ordine complicato. Come costruire un'immagine, traduzione di Paolo Tramannoni, con una nota di Manuel Orazi, Quodlibet-Abitare, Macerata 2011. Ulteriori informazioni: http://www.quodlibet.it/schedap.php?id=1963
Fasi di creazione di un programma
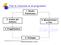 Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
INFORMATICA. Scienza dei calcolatori elettronici (computer science) Scienza dell informazione (information science)
 INFORMATICA Cosa è l informatica Scienza dei calcolatori elettronici (computer science) Scienza dell informazione (information science) E una scienza E una tecnologia Cosa può essere automatizzato nell
INFORMATICA Cosa è l informatica Scienza dei calcolatori elettronici (computer science) Scienza dell informazione (information science) E una scienza E una tecnologia Cosa può essere automatizzato nell
MICROSOFT ACCESS IL MODELLO E/R
 MICROSOFT ACCESS IL MODELLO E/R LE ENTITA Le entità di un database sono le singole tabelle che comporranno la struttura del nostro database. Le tabelle sono formate da attributi (o campi) che ne definiscono
MICROSOFT ACCESS IL MODELLO E/R LE ENTITA Le entità di un database sono le singole tabelle che comporranno la struttura del nostro database. Le tabelle sono formate da attributi (o campi) che ne definiscono
INSIEME N. L'insieme dei numeri naturali (N) è l'insieme dei numeri interi e positivi.
 INSIEME N L'insieme dei numeri naturali (N) è l'insieme dei numeri interi e positivi. N = {0;1;2;3... Su tale insieme sono definite le 4 operazioni di base: l'addizione (o somma), la sottrazione, la moltiplicazione
INSIEME N L'insieme dei numeri naturali (N) è l'insieme dei numeri interi e positivi. N = {0;1;2;3... Su tale insieme sono definite le 4 operazioni di base: l'addizione (o somma), la sottrazione, la moltiplicazione
CONCETTI E ARCHITETTURA DI UN SISTEMA DI BASI DI DATI
 CONCETTI E ARCHITETTURA DI UN SISTEMA DI BASI DI DATI Introduzione alle basi di dati (2) 2 Modelli dei dati, schemi e istanze (1) Nell approccio con basi di dati è fondamentale avere un certo livello di
CONCETTI E ARCHITETTURA DI UN SISTEMA DI BASI DI DATI Introduzione alle basi di dati (2) 2 Modelli dei dati, schemi e istanze (1) Nell approccio con basi di dati è fondamentale avere un certo livello di
Sviluppo di programmi
 Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
I.I.S MASCALUCIA PROGRAMMAZIONE DI FISICA LICEO CLASSICO A.S. 2009-2010
 IIS MASCALUCIA PROGRAMMAZIONE DI FISICA LICEO CLASSICO AS 2009-2010 Modulo A Grandezze fisiche e misure Le basi dell algebra e dei numeri relativi Proporzionalità tra grandezze Calcolo di equivalenze tra
IIS MASCALUCIA PROGRAMMAZIONE DI FISICA LICEO CLASSICO AS 2009-2010 Modulo A Grandezze fisiche e misure Le basi dell algebra e dei numeri relativi Proporzionalità tra grandezze Calcolo di equivalenze tra
Lezione 6. Forze attive e passive. L interazione gravitazionale. L interazione elettromagnetica. WWW.SLIDETUBE.IT
 Lezione 6 Forze attive e passive. L interazione gravitazionale. L interazione elettromagnetica. Classificazione delle Forze Distinguiamo tra: Forze attive Forze passive Forze attive Le 4 forze fondamentali:
Lezione 6 Forze attive e passive. L interazione gravitazionale. L interazione elettromagnetica. Classificazione delle Forze Distinguiamo tra: Forze attive Forze passive Forze attive Le 4 forze fondamentali:
Matematica con il foglio di calcolo
 Matematica con il foglio di calcolo Sottotitolo: Classe: V primaria Argomento: Numeri e operazioni Autore: Guido Gottardi, Alberto Battaini Introduzione: l uso del foglio di calcolo offre l opportunità
Matematica con il foglio di calcolo Sottotitolo: Classe: V primaria Argomento: Numeri e operazioni Autore: Guido Gottardi, Alberto Battaini Introduzione: l uso del foglio di calcolo offre l opportunità
Legge di gravitazione universale
 Legge di gravitazione universale Famosissima è la legge che fu ispirata, come i libri sono soliti raccontare, dalla caduta di una mela sulla testa di Isaac Newton (1642-1727). Questa nota relazione, che
Legge di gravitazione universale Famosissima è la legge che fu ispirata, come i libri sono soliti raccontare, dalla caduta di una mela sulla testa di Isaac Newton (1642-1727). Questa nota relazione, che
GRIGLIA DI CORREZIONE Matematica Classe I Scuola secondaria di I grado
 GRIGLIA DI CORREZIONE Matematica Classe I Scuola secondaria di I grado LEGENDA AMBITI: NU (Numeri), SF (Spazio e figure), DP (Dati e previsioni), RF (Relazioni e funzioni) LEGENDA PROCESSI: 1. Conoscere
GRIGLIA DI CORREZIONE Matematica Classe I Scuola secondaria di I grado LEGENDA AMBITI: NU (Numeri), SF (Spazio e figure), DP (Dati e previsioni), RF (Relazioni e funzioni) LEGENDA PROCESSI: 1. Conoscere
PROGRAMMAZIONE DI FISICA NEL TRIENNIO DEL LICEO CLASSICO
 PROGRAMMAZIONE DI FISICA NEL TRIENNIO DEL LICEO CLASSICO 1. OBIETTIVI GENERALI Utilizzare correttamente e consapevolmente le procedure di calcolo Cogliere analogie e differenze strutturali tra argomenti
PROGRAMMAZIONE DI FISICA NEL TRIENNIO DEL LICEO CLASSICO 1. OBIETTIVI GENERALI Utilizzare correttamente e consapevolmente le procedure di calcolo Cogliere analogie e differenze strutturali tra argomenti
7 Cenni di ottica per la fotografia
 7 Cenni di ottica per la fotografia 7.1 Schematizzazione di un obiettivo fotografico Gli obiettivi fotografici sono generalmente composti da un numero elevato di lenti. Tuttavia per semplicità possiamo
7 Cenni di ottica per la fotografia 7.1 Schematizzazione di un obiettivo fotografico Gli obiettivi fotografici sono generalmente composti da un numero elevato di lenti. Tuttavia per semplicità possiamo
Cosa è l Informatica?
 Cosa è l Informatica? Scienza degli elaboratori elettronici (Computer Science) Scienza dell informazione Scienza della rappresentazione, memorizzazione, elaborazione e trasmissione dell informazione Elaboratore
Cosa è l Informatica? Scienza degli elaboratori elettronici (Computer Science) Scienza dell informazione Scienza della rappresentazione, memorizzazione, elaborazione e trasmissione dell informazione Elaboratore
LA LEGGE DI COULOMB PER I MAGNETI
 1 LA LEGGE DI COULOMB PER I MAGNETI Lo scopo di questo esperimento è quello di riprodurre quello storico e importante ormai scomparso dai testi scolastici perché ritenuto non attinente alla realtà. È noto,
1 LA LEGGE DI COULOMB PER I MAGNETI Lo scopo di questo esperimento è quello di riprodurre quello storico e importante ormai scomparso dai testi scolastici perché ritenuto non attinente alla realtà. È noto,
Il concetto di calcolatore e di algoritmo
 Il concetto di calcolatore e di algoritmo Elementi di Informatica e Programmazione Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Informatica
Il concetto di calcolatore e di algoritmo Elementi di Informatica e Programmazione Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Informatica
3.Dinamica e forze. La dinamica è quella parte della meccanica che studia il moto di un corpo facendo riferimento alle cause esterne che lo generano.
 3.Dinamica e forze La dinamica è quella parte della meccanica che studia il moto di un corpo facendo riferimento alle cause esterne che lo generano. Le due grandezze fondamentali che prendiamo in considerazione
3.Dinamica e forze La dinamica è quella parte della meccanica che studia il moto di un corpo facendo riferimento alle cause esterne che lo generano. Le due grandezze fondamentali che prendiamo in considerazione
SCHEDA PER IL DOCENTE DESCRIZIONE DELL ITINERARIO DI LABORATORIO
 SCHEDA PER IL DOCENTE DESCRIZIONE DELL ITINERARIO DI LABORATORIO I Titolo della scheda Un itinerario di Laboratorio: LA DENSITÀ Esperienze di laboratorio per la misura della densità di una sostanza solida
SCHEDA PER IL DOCENTE DESCRIZIONE DELL ITINERARIO DI LABORATORIO I Titolo della scheda Un itinerario di Laboratorio: LA DENSITÀ Esperienze di laboratorio per la misura della densità di una sostanza solida
FOCUS IL MERCATO IMMOBILIARE: DIVERSIFICARE PER SPECIALIZZARE. Mercoledì 2 dicembre 2015 NAPOLI Tiempo Business Center
 FOCUS IL MERCATO IMMOBILIARE: DIVERSIFICARE PER SPECIALIZZARE Mercoledì 2 dicembre 2015 NAPOLI Tiempo Business Center Parliamo di MLS Il Multiple Listing Service (MLS) è un metodo operativo attivo fra
FOCUS IL MERCATO IMMOBILIARE: DIVERSIFICARE PER SPECIALIZZARE Mercoledì 2 dicembre 2015 NAPOLI Tiempo Business Center Parliamo di MLS Il Multiple Listing Service (MLS) è un metodo operativo attivo fra
Matematica - Classe Prima
 Matematica - Classe Prima NUCLEI FONDANTI COMPETENZE DA SVILUPPARE CONTENUTI NUMERI e QUANTITÁ Saper riconoscere ed utilizzare i numeri naturali in diversi contesti. Saper comprendere ed utilizzare addizioni
Matematica - Classe Prima NUCLEI FONDANTI COMPETENZE DA SVILUPPARE CONTENUTI NUMERI e QUANTITÁ Saper riconoscere ed utilizzare i numeri naturali in diversi contesti. Saper comprendere ed utilizzare addizioni
La rivoluzione scientifica. Copernico, Galileo, Newton
 La rivoluzione scientifica Copernico, Galileo, Newton La rivoluzione scientifica è quel movimento di idee che nel corso del XVI e XVII secolo portò all abbandono della precedente immagine della realtà,
La rivoluzione scientifica Copernico, Galileo, Newton La rivoluzione scientifica è quel movimento di idee che nel corso del XVI e XVII secolo portò all abbandono della precedente immagine della realtà,
Sintesi degli argomenti di fisica trattati (parte uno)
 Sintesi degli argomenti di fisica trattati (parte uno) La grandezza fisica è una proprietà dello spazio o della materia che può essere misurata. Fare una misura vuol dire confrontare la grandezza fisica
Sintesi degli argomenti di fisica trattati (parte uno) La grandezza fisica è una proprietà dello spazio o della materia che può essere misurata. Fare una misura vuol dire confrontare la grandezza fisica
INGLESE SCUOLA DELL INFANZIA
 INGLESE SCUOLA DELL INFANZIA CAMPO D ESPERIENZA: I DISCORSI E LE PAROLE (comunicazione, lingua, cultura) È lo specifico campo delle capacità comunicative riferite al linguaggio orale e al primo contatto
INGLESE SCUOLA DELL INFANZIA CAMPO D ESPERIENZA: I DISCORSI E LE PAROLE (comunicazione, lingua, cultura) È lo specifico campo delle capacità comunicative riferite al linguaggio orale e al primo contatto
ELEMENTI FONDANTI L IDENTITA DEI SERVIZI o-6 - PRINCIPI QUALITATIVI DEL PROGETTO EDUCATIVO -
 AMBIENTAMENTO PROGETTO EDUCATIVO COLLEGIALITA FORMAZIONE DOCUMENTAZIONE SPAZI- AMBIENTE PARTECIPAZIONE DELLE FAMIGLIE ELEMENTI FONDANTI L IDENTITA DEI SERVIZI o-6 - PRINCIPI QUALITATIVI DEL PROGETTO EDUCATIVO
AMBIENTAMENTO PROGETTO EDUCATIVO COLLEGIALITA FORMAZIONE DOCUMENTAZIONE SPAZI- AMBIENTE PARTECIPAZIONE DELLE FAMIGLIE ELEMENTI FONDANTI L IDENTITA DEI SERVIZI o-6 - PRINCIPI QUALITATIVI DEL PROGETTO EDUCATIVO
QUANTITA DI MOTO Corso di Fisica per Farmacia, Facoltà di Farmacia, Università G. D Annunzio, Cosimo Del Gratta 2006
 QUANTITA DI MOTO DEFINIZIONE(1) m v Si chiama quantità di moto di un punto materiale il prodotto della sua massa per la sua velocità p = m v La quantità di moto è una grandezza vettoriale La dimensione
QUANTITA DI MOTO DEFINIZIONE(1) m v Si chiama quantità di moto di un punto materiale il prodotto della sua massa per la sua velocità p = m v La quantità di moto è una grandezza vettoriale La dimensione
Sceneggiare un unità di lavoro per la LIM (modello 1)
 Sceneggiare un unità di lavoro per la LIM (modello 1) Nel format proposto, si richiede al corsista di descrivere la fase di ideazione e progettazione dell'unità, le risorse utilizzate ed il contesto in
Sceneggiare un unità di lavoro per la LIM (modello 1) Nel format proposto, si richiede al corsista di descrivere la fase di ideazione e progettazione dell'unità, le risorse utilizzate ed il contesto in
I numeri irrazionali nella geometria e nella storia. Daniela Valenti, Treccani scuola
 I numeri irrazionali nella geometria e nella storia 1 Costruzioni geometriche di!a Con la geometria possiamo costruire un segmento che sia lungo esattamente!a Una costruzione semplice e versatile è basata
I numeri irrazionali nella geometria e nella storia 1 Costruzioni geometriche di!a Con la geometria possiamo costruire un segmento che sia lungo esattamente!a Una costruzione semplice e versatile è basata
CAPITOLO 9: LA GRAVITAZIONE. 9.1 Introduzione.
 CAPITOLO 9: LA GRAVITAZIONE 9.1 Introduzione. Un altro tipo di forza piuttosto importante è la forza gravitazionale. Innanzitutto, è risaputo che nel nostro sistema di pianeti chiamato sistema solare il
CAPITOLO 9: LA GRAVITAZIONE 9.1 Introduzione. Un altro tipo di forza piuttosto importante è la forza gravitazionale. Innanzitutto, è risaputo che nel nostro sistema di pianeti chiamato sistema solare il
I database. Introduzione alla teoria delle basi di dati
 I database Introduzione alla teoria delle basi di dati 1 Cosa sono e a cosa servono i Database Un database (o base di dati) e' una raccolta organizzata di dati correlati. Il principale scopo di un database
I database Introduzione alla teoria delle basi di dati 1 Cosa sono e a cosa servono i Database Un database (o base di dati) e' una raccolta organizzata di dati correlati. Il principale scopo di un database
Anno 2. Circonferenza e retta: definizioni e proprietà
 Anno 2 Circonferenza e retta: definizioni e proprietà 1 Introduzione I Sumeri furono tra i primi popoli ad occuparsi di matematica, e in particolare di problemi relativi alla. La è una figura geometrica
Anno 2 Circonferenza e retta: definizioni e proprietà 1 Introduzione I Sumeri furono tra i primi popoli ad occuparsi di matematica, e in particolare di problemi relativi alla. La è una figura geometrica
PROGRAMMAZIONE DIDATTICA DI MATEMATICA
 ISTITUTO COMPRENSIVO F. D'ASSISI TEZZE SUL BRENTA (VI) PROGRAMMAZIONE DIDATTICA DI MATEMATICA CLASSE 3^ OBIETTIVI FORMATIVI: I NUMERI CONOSCENZE ABILITA COMPETENZE Leggere, rappresentare e utilizzare i
ISTITUTO COMPRENSIVO F. D'ASSISI TEZZE SUL BRENTA (VI) PROGRAMMAZIONE DIDATTICA DI MATEMATICA CLASSE 3^ OBIETTIVI FORMATIVI: I NUMERI CONOSCENZE ABILITA COMPETENZE Leggere, rappresentare e utilizzare i
MODELLO e RAPPRESENTAZIONE
 MODELLO e RAPPRESENTAZIONE I calcolatori elaborano informazione e restituiscono nuova informazione: questa deve essere rappresentata in forma simbolica Esempio : Per poter gestire una biblioteca dobbiamo
MODELLO e RAPPRESENTAZIONE I calcolatori elaborano informazione e restituiscono nuova informazione: questa deve essere rappresentata in forma simbolica Esempio : Per poter gestire una biblioteca dobbiamo
ARTE E IMMAGINE NUCLEI FONDANTI DELLA DISCIPLINA. riconoscere ed usare i linguaggi visivi. Produzione e rielaborazione dei messaggi visivi.
 ARTE E IMMAGINE NUCLEI FONDANTI DELLA DISCIPLINA Capacità di vedere osservare e comprendere riconoscere ed usare i linguaggi visivi. Conoscenza ed uso delle tecniche espressive. Produzione e rielaborazione
ARTE E IMMAGINE NUCLEI FONDANTI DELLA DISCIPLINA Capacità di vedere osservare e comprendere riconoscere ed usare i linguaggi visivi. Conoscenza ed uso delle tecniche espressive. Produzione e rielaborazione
DIPARTIMENTO DI MATEMATICA CRITERI DI VALUTAZIONE
 DIPARTIMENTO DI MATEMATICA CRITERI DI VALUTAZIONE 1. SCUOLA DELL INFANZIA Nella scuola dell Infanzia vengono adottati alcuni descrittori generali riguardanti i seguenti campi: a. Autonomia b. Socializzazione
DIPARTIMENTO DI MATEMATICA CRITERI DI VALUTAZIONE 1. SCUOLA DELL INFANZIA Nella scuola dell Infanzia vengono adottati alcuni descrittori generali riguardanti i seguenti campi: a. Autonomia b. Socializzazione
SISTEMI INFORMATIVI E DATABASE
 SISTEMI INFORMATIVI E DATABASE SISTEMA INFORMATIVO AZIENDALE (S.I.) In una realtà aziendale si distingue: DATO elemento di conoscenza privo di qualsiasi elaborazione; insieme di simboli e caratteri. (274,
SISTEMI INFORMATIVI E DATABASE SISTEMA INFORMATIVO AZIENDALE (S.I.) In una realtà aziendale si distingue: DATO elemento di conoscenza privo di qualsiasi elaborazione; insieme di simboli e caratteri. (274,
Capitolo 6. Il processo decisionale delle imprese: la massimizzazione del profitto
 Capitolo 6 Il processo decisionale delle imprese: la massimizzazione del profitto Per raggiungere l'obiettivo del massimo profitto, le imprese devono risolvere una serie di problemi. Dove produrre? Quanti
Capitolo 6 Il processo decisionale delle imprese: la massimizzazione del profitto Per raggiungere l'obiettivo del massimo profitto, le imprese devono risolvere una serie di problemi. Dove produrre? Quanti
Algoritmo. La programmazione. Algoritmo. Programmare. Procedimento di risoluzione di un problema
 Algoritmo 2 Procedimento di risoluzione di un problema La programmazione Ver. 2.4 Permette di ottenere un risultato eseguendo una sequenza finita di operazioni elementari Esempi: Una ricetta di cucina
Algoritmo 2 Procedimento di risoluzione di un problema La programmazione Ver. 2.4 Permette di ottenere un risultato eseguendo una sequenza finita di operazioni elementari Esempi: Una ricetta di cucina
CURRICOLO VERTICALE MATEMATICA RELAZIONI/ DATI E PREVISIONI/ MISURA
 CURRICOLO VERTICALE MATEMATICA / DATI E PREVISIONI/ MISURA SCUOLA PRIMARIA CONOSCENZE (Concetti) ABILITA Classe 1^ - Classificazione - in situazioni concrete, classificare persone, oggetti, figure, numeri
CURRICOLO VERTICALE MATEMATICA / DATI E PREVISIONI/ MISURA SCUOLA PRIMARIA CONOSCENZE (Concetti) ABILITA Classe 1^ - Classificazione - in situazioni concrete, classificare persone, oggetti, figure, numeri
RAPPORTI E PROPORZIONI
 RAPPORTI E PROPORZIONI RAPPORTI E PROPORZIONI Definizione: Dicesi rapporto fra due numeri, preso in un certo ordine, il quoziente della divisione fra il primo di essi e il secondo. Il rapporto tra i numeri
RAPPORTI E PROPORZIONI RAPPORTI E PROPORZIONI Definizione: Dicesi rapporto fra due numeri, preso in un certo ordine, il quoziente della divisione fra il primo di essi e il secondo. Il rapporto tra i numeri
La Struttura. Schema di scarico di un viadotto con travate semplicemente appoggiate. Schema di scarico di un ponte strallato
 La Struttura Obiettivo del Corso è quello di fornire un approccio metodologico per la trattazione analitica dei modelli meccanici della parte resistente della Costruzione. La trattazione è fondata su un
La Struttura Obiettivo del Corso è quello di fornire un approccio metodologico per la trattazione analitica dei modelli meccanici della parte resistente della Costruzione. La trattazione è fondata su un
Critiche alla teoria di Piaget. Critiche alla teoria di Piaget. Critiche alla teoria di Piaget. Critiche alla teoria di Piaget 16/10/2014
 Carenza nella progettazione sperimentale e nell analisi dei dati Eccesso di teorizzazione rispetto ai dati a disposizione Difficoltà di interpretazione dei suoi scritti Interesse per il soggetto ideale
Carenza nella progettazione sperimentale e nell analisi dei dati Eccesso di teorizzazione rispetto ai dati a disposizione Difficoltà di interpretazione dei suoi scritti Interesse per il soggetto ideale
La storia della scienza e la nascita del metodo scientifico
 La storia della scienza e la nascita del metodo scientifico Breve storia della scienza La nascita del pensiero scientifico e del metodo sperimentale: Cartesio e Galilei Scienza e tecnica Tecnica e società
La storia della scienza e la nascita del metodo scientifico Breve storia della scienza La nascita del pensiero scientifico e del metodo sperimentale: Cartesio e Galilei Scienza e tecnica Tecnica e società
Le basi di dati. Definizione 1. Lezione 2. Bisogna garantire. Definizione 2 DBMS. Differenza
 Definizione 1 Lezione 2 Le basi di dati Gli archivi di dati Organizzato in modo integrato attraverso tecniche di modellazione di dati Gestiti su memorie di massa Con l obiettivo Efficienza trattamento
Definizione 1 Lezione 2 Le basi di dati Gli archivi di dati Organizzato in modo integrato attraverso tecniche di modellazione di dati Gestiti su memorie di massa Con l obiettivo Efficienza trattamento
Unità di apprendimento 6. Dal problema al programma
 Unità di apprendimento 6 Dal problema al programma Unità di apprendimento 6 Lezione 1 Conosciamo gli algoritmi e i linguaggi In questa lezione impareremo: cos è un problema come affrontarlo come descrivere
Unità di apprendimento 6 Dal problema al programma Unità di apprendimento 6 Lezione 1 Conosciamo gli algoritmi e i linguaggi In questa lezione impareremo: cos è un problema come affrontarlo come descrivere
Corso di Laurea Ingegneria Informatica
 Corso di Laurea Ingegneria Informatica Presentazione del corso di Fondamenti di Informatica 2 C. Limongelli - A. Miola Febbraio 2007 http://www.dia.uniroma3.it/~java/fondinf2/ Presentazione Corso 1 Contenuti
Corso di Laurea Ingegneria Informatica Presentazione del corso di Fondamenti di Informatica 2 C. Limongelli - A. Miola Febbraio 2007 http://www.dia.uniroma3.it/~java/fondinf2/ Presentazione Corso 1 Contenuti
Introduzione alle basi di dati: Il modello concettuale
 Introduzione alle basi di dati: Il modello concettuale A cura del Prof. Claudio Traini algoritmi + strutture dati = programmi Niklaus Wirth 1 L approccio 2 L approccio alle basi di dati Fasi del processo
Introduzione alle basi di dati: Il modello concettuale A cura del Prof. Claudio Traini algoritmi + strutture dati = programmi Niklaus Wirth 1 L approccio 2 L approccio alle basi di dati Fasi del processo
RIASSUNTI DI CHIMICA
 Tecla Spelgatti RIASSUNTI DI CHIMICA per il liceo scientifico 2 - LA TAVOLA PERIODICA Questo testo è distribuito con licenza Common Creative: http://creativecommons.org/licenses/ CC BY-NC-ND Attribuzione
Tecla Spelgatti RIASSUNTI DI CHIMICA per il liceo scientifico 2 - LA TAVOLA PERIODICA Questo testo è distribuito con licenza Common Creative: http://creativecommons.org/licenses/ CC BY-NC-ND Attribuzione
LA GRAVITAZIONE. Legge di Gravitazione Universale 08/04/2015 =6, /
 LA GRAVITAZIONE Definizione (forza di attrazione gravitazionale) Due corpi puntiformi di massa e si attraggono vicendevolmente con una forza (forza che il corpo A esercita sul corpo B), o (forza che il
LA GRAVITAZIONE Definizione (forza di attrazione gravitazionale) Due corpi puntiformi di massa e si attraggono vicendevolmente con una forza (forza che il corpo A esercita sul corpo B), o (forza che il
(4 π 2 /kt) m t / r 2 = (4 π 2 /ks) m s / r 2
 Le leggi di Keplero Lo studio del moto dei pianeti, tramite accurate misure, permise a Keplero tra il 1600 ed il 1620 di formulare le sue tre leggi: I legge: I pianeti percorrono orbite ellittiche intorno
Le leggi di Keplero Lo studio del moto dei pianeti, tramite accurate misure, permise a Keplero tra il 1600 ed il 1620 di formulare le sue tre leggi: I legge: I pianeti percorrono orbite ellittiche intorno
Algoritmi e Programmi
 Algoritmi e Programmi Algoritmi e Programmi Le azioni che si compiono ogni giorno sono finalizzate alla risoluzione di problemi. Problema di elaborazione Insieme dati di partenza Risultato ricerca Algoritmi
Algoritmi e Programmi Algoritmi e Programmi Le azioni che si compiono ogni giorno sono finalizzate alla risoluzione di problemi. Problema di elaborazione Insieme dati di partenza Risultato ricerca Algoritmi
VERIFICA FILOSOFIA. ESERCIZIO 1 (quesiti a risposta multipla) (valutazione max 30 punti)
 nome ------------------------------ cognome ------------------------------ classe 4C VERIFICA FILOSOFIA ESERCIZIO 1 (quesiti a risposta multipla) (valutazione max 30 punti) A) Aristotele spiega il divenire
nome ------------------------------ cognome ------------------------------ classe 4C VERIFICA FILOSOFIA ESERCIZIO 1 (quesiti a risposta multipla) (valutazione max 30 punti) A) Aristotele spiega il divenire
Esercitazioni di Statistica
 Esercitazioni di Statistica Rappresentazioni grafiche Prof. Livia De Giovanni [email protected] Esercizio 1 Si consideri la seguente distribuzione delle industrie tessili secondo il fatturato
Esercitazioni di Statistica Rappresentazioni grafiche Prof. Livia De Giovanni [email protected] Esercizio 1 Si consideri la seguente distribuzione delle industrie tessili secondo il fatturato
Le forze. Cos è una forza? in quiete. in moto
 Le forze Ricorda che quando parli di: - corpo: ti stai riferendo all oggetto che stai studiando; - deformazione. significa che il corpo che stai studiando cambia forma (come quando pesti una scatola di
Le forze Ricorda che quando parli di: - corpo: ti stai riferendo all oggetto che stai studiando; - deformazione. significa che il corpo che stai studiando cambia forma (come quando pesti una scatola di
4. LE FORZE E LA LORO MISURA
 4. LE FORZE E LA LORO MISURA 4.1 - Le forze e i loro effetti Tante azioni che facciamo o vediamo non sono altro che il risultato di una o più forze. Le forze non si vedono e ci accorgiamo della loro presenza
4. LE FORZE E LA LORO MISURA 4.1 - Le forze e i loro effetti Tante azioni che facciamo o vediamo non sono altro che il risultato di una o più forze. Le forze non si vedono e ci accorgiamo della loro presenza
CORSO BASE PER ARREDATORE PeS
 CORSO BASE PER ARREDATORE PeS 1) CONCETTO DI DISEGNO IN SCALA (Pag. 2-4) 2) UTILIZZO DI SCALIMETRO E FOGLIO QUADRETTATO (Pag. 5) 3) MODALITA DI DISEGNO IN PIANTA : SIMBOLOGIA, INGOMBRI, ESEMPI TIPO DI
CORSO BASE PER ARREDATORE PeS 1) CONCETTO DI DISEGNO IN SCALA (Pag. 2-4) 2) UTILIZZO DI SCALIMETRO E FOGLIO QUADRETTATO (Pag. 5) 3) MODALITA DI DISEGNO IN PIANTA : SIMBOLOGIA, INGOMBRI, ESEMPI TIPO DI
MATEMATICA PER LO STUDIO DELLE INTERAZIONI STRATEGICHE: TEORIA DEI GIOCHI. Anna TORRE
 MATEMATICA PER LO STUDIO DELLE INTERAZIONI STRATEGICHE: TEORIA DEI GIOCHI Anna TORRE Dipartimento di Matematica, Università di Pavia, Via Ferrata 1, 27100, Pavia, Italy. E-mail: [email protected] 1 GIOCHI
MATEMATICA PER LO STUDIO DELLE INTERAZIONI STRATEGICHE: TEORIA DEI GIOCHI Anna TORRE Dipartimento di Matematica, Università di Pavia, Via Ferrata 1, 27100, Pavia, Italy. E-mail: [email protected] 1 GIOCHI
Cosa vuol dire misurare l'area di una figura piana a contorno curvilineo?
 Cosa vuol dire misurare l'area di una figura piana a contorno curvilineo? Idea elementare: 1. fissare un quadratino come unità di misura 2. contare quante volte questo può essere riportato nella figura
Cosa vuol dire misurare l'area di una figura piana a contorno curvilineo? Idea elementare: 1. fissare un quadratino come unità di misura 2. contare quante volte questo può essere riportato nella figura
 1 anno fisica -potenze di 10, equivalenze e notazione scientifica -misure ed incertezze -grandezze scalari e vettoriali e relative operazioni -esprimere il risultato di una misura e saper rappresentare
1 anno fisica -potenze di 10, equivalenze e notazione scientifica -misure ed incertezze -grandezze scalari e vettoriali e relative operazioni -esprimere il risultato di una misura e saper rappresentare
Il linguaggio di programmazione Python
 Università Roma Tre Dipartimento di Matematica e Fisica Percorso Abilitante Speciale Classe A048 Matematica Applicata Corso di Informatica Il linguaggio di programmazione Python Marco Liverani ([email protected])
Università Roma Tre Dipartimento di Matematica e Fisica Percorso Abilitante Speciale Classe A048 Matematica Applicata Corso di Informatica Il linguaggio di programmazione Python Marco Liverani ([email protected])
Forze Legge di Gravitazione Universale
 Forze Legge di Gravitazione Universale Una forza di attrazione *gravitazionale* agisce tra due corpi rispettivamente di massa M 1 ed M 2, separati da una distanza R tra i loro centri. Questa forza è direttamente
Forze Legge di Gravitazione Universale Una forza di attrazione *gravitazionale* agisce tra due corpi rispettivamente di massa M 1 ed M 2, separati da una distanza R tra i loro centri. Questa forza è direttamente
per lo sviluppo di curricoli per competenze al triennio,
 Prima Bozza di lavoro creata da Silvia Faggioli IIs Aldini Valeriani Bologna per lo sviluppo di curricoli per competenze al triennio, asse scientifico tecnologico Asse scientifico tecnologico Triennio
Prima Bozza di lavoro creata da Silvia Faggioli IIs Aldini Valeriani Bologna per lo sviluppo di curricoli per competenze al triennio, asse scientifico tecnologico Asse scientifico tecnologico Triennio
PROGRAMMA PREVENTIVO
 Settore Servizi Scolastici e Educativi PAGINA: 1 PROGRAMMA PREVENTIVO A.S. 2015/16 SCUOLA LICEO LINGUISTICO A. MANZONI DOCENTE: C. FRESCURA MATERIA: FISICA Classe 3 Sezione B FINALITÀ DELLA DISCIPLINA
Settore Servizi Scolastici e Educativi PAGINA: 1 PROGRAMMA PREVENTIVO A.S. 2015/16 SCUOLA LICEO LINGUISTICO A. MANZONI DOCENTE: C. FRESCURA MATERIA: FISICA Classe 3 Sezione B FINALITÀ DELLA DISCIPLINA
Come ragiona il computer. Problemi e algoritmi
 Come ragiona il computer Problemi e algoritmi Il problema Abbiamo un problema quando ci poniamo un obiettivo da raggiungere e per raggiungerlo dobbiamo mettere a punto una strategia Per risolvere il problema
Come ragiona il computer Problemi e algoritmi Il problema Abbiamo un problema quando ci poniamo un obiettivo da raggiungere e per raggiungerlo dobbiamo mettere a punto una strategia Per risolvere il problema
Problema: dati i voti di tutti gli studenti di una classe determinare il voto medio della classe.
 Problema: dati i voti di tutti gli studenti di una classe determinare il voto medio della classe. 1) Comprendere il problema 2) Stabilire quali sono le azioni da eseguire per risolverlo 3) Stabilire la
Problema: dati i voti di tutti gli studenti di una classe determinare il voto medio della classe. 1) Comprendere il problema 2) Stabilire quali sono le azioni da eseguire per risolverlo 3) Stabilire la
Materiale per gli alunni
 Testi semplificati di storia Materiale per gli alunni LIVELLO DI COMPETENZA LINGUISTICA RICHIESTA: A2- B1 SI RIVOLGE A: studenti della scuola secondaria di I grado al 3 anno Prerequisiti: Gli alunni sanno
Testi semplificati di storia Materiale per gli alunni LIVELLO DI COMPETENZA LINGUISTICA RICHIESTA: A2- B1 SI RIVOLGE A: studenti della scuola secondaria di I grado al 3 anno Prerequisiti: Gli alunni sanno
