SEZIONI. Introduzione
|
|
|
- Michele Pagano
- 10 anni fa
- Просмотров:
Транскрипт
1 SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è rappresentato da un piano. La superficie che risulta dall intersezione del solido con la superficie secante è detta sezione. La parte del solido che viene effettivamente attraversata dalla superficie secante viene rappresentata con apposito tratteggio (campitura). Le sezioni sono oggetto di normativa specifica; in particolare si fa riferimento alla norma ISO Appunti di Disegno Tecnico Industriale 129 1
2 Sezione di un prisma Per determinare la sezione piana di un prisma, semplicemente si proiettano i punti di intersezione tra il piano di sezione e gli spigoli del prisma. Si tracciano innanzitutto tre viste: una vista principale (Vp), una vista dall alto Vp () ed una vista da sinistra (). Si disegna quindi la traccia del piano di sezione (-). In questo caso si è preso un piano ortogonale al piano corrispondente alla vista principale. Si determinano, sulla vista principale, le intersezioni degli spigoli con il piano di sezione. La sezione in vista da sinistra si ottiene quindi tracciando le orizzontali dai punti di intersezione ed intersecando gli spigoli corrispondenti. La sezione in vista dall alto si sovrappone alla vista stessa. Appunti di Disegno Tecnico Industriale 130 Sezione di un tronco di piramide Per determinare la sezione piana di un tronco di piramide (o di una piramide) si procede analogamente al caso precedente. Si tracciano innanzitutto tre viste: una vista principale (Vp), una vista dall alto Vp () ed una vista da sinistra (). Si disegna quindi la traccia del piano di sezione (-). In questo caso si è preso un piano ortogonale al piano corrispondente alla vista principale. Si determinano, sulla vista principale, le intersezioni degli spigoli con il piano di sezione. La sezione in vista da sinistra si ottiene quindi tracciando le orizzontali dai punti di intersezione ed intersecando gli spigoli corrispondenti. La sezione in vista dall alto si ottiene analogamente. Appunti di Disegno Tecnico Industriale 131 2
3 Sezione di un cilindro La curva risultante dalla sezione di un cilindro con un piano può essere una circonferenza (se il piano è ortogonale all asse), un rettangolo (se il piano è parallelo all asse) o (se il piano è inclinato rispetto all asse). La costruzione, nei primi due casi, è immediata, e non Vp viene qui trattata. Si consideri quindi un cilindro con le sue proiezioni su tre piani e la traccia del piano di sezione (-). Si determinano, sulla vista principale, le intersezioni degli spigoli con il piano di sezione. La sezione in vista da sinistra si ottiene quindi tracciando le orizzontali dai punti di intersezione ed intersecando con queste le generatrici corrispondenti. La sezione in vista dall alto si sovrappone alla vista stessa. Appunti di Disegno Tecnico Industriale 132 Sezione di una sfera (1) La curva risultante dall intersezione di un piano con una sfera è una circonferenza. In proiezione quindi, quando il piano di proiezione non è parallelo al piano di sezione, la curva risultante sarà un ellisse. Si tracciano tre viste della Vp sfera (tre circonferenze) e nella vista principale si disegna la traccia del piano di sezione (-). Sulla vista principale si traccia un numero arbitrario di circonferenze, e si determinano le loro intersezioni con la traccia del piano di sezione. Sulla vista dall alto si trovano le tracce dei piani di sezione corrispondenti alle circonferenze tracciate. Dall intersezione di tali tracce con le verticali abbassate dai punti di intersezione trovati nella Vp si trovano, per Appunti di Disegno Tecnico Industriale 133 3
4 Sezione di una sfera (2) intersezione, i punti dell ellisse che rappresentano la sezione della sfera sulla vista dall alto Vp In maniera analoga si determina la proiezione della sezione sulla vista da sinistra: si riportano su di essa le tracce dei piani di sezione ausiliari, queste, per intersezione con le orizzontali tracciate dai punti di intersezione trovati nella vista principale froniscono i punti della sezione. Appunti di Disegno Tecnico Industriale 134 Sezione di un cono: ellisse (1) La curva risultante dalla sezione piana di un cono può essere: una circonferenza (il piano è ortogonale all asse); una parabola (il piano è parallelo ad una generatrice); un iperbole (il piano è parallelo all asse); un ellisse in tutti gli altri casi. Nel caso dell ellisse si inizia tracciando tre viste del cono e Vp la traccia del piano di sezione (-). Si tracciano quindi delle generatrici ausiliarie sulla vista principale e si determinano le loro corrispondenti sulla vista dall alto. Si determinano, sulla vista principale, le intersezioni delle generatrici con il piano di sezione. Si abbassano le verticali dai punti così ottenuti e per intersezione con le proiezioni delle generatrici sulla si trovano i punti della proiezione della sezione. Appunti di Disegno Tecnico Industriale 135 4
5 Sezione di un cono: ellisse (2) Si determinano quindi le proiezioni delle generatrici ausiliarie sulla vista da sinistra. Vp Si tracciano, dai punti di intersezione sulla vista principale, le orizzontali che per intersezione con le generatrici determinano i punti della sezione nella vista da sinistra. Appunti di Disegno Tecnico Industriale 136 Sezione di un cono: iperbole Nel caso dell iperbole (piano sezionatore parallelo all asse del cono) si procede utilizzando una tecnica analoga a quella vista per la sfera. Nella vista dall alto si traccia un numero arbitrario di circonferenze che Vp rappresentano sezioni del cono su piani ausiliari. Sempre nella stessa vista si determinano le intersezioni delle circonferenze con la traccia del piano di sezione. Nella vista principale si determinano le tracce dei piani ausiliari e le si prolungano nella vista da sinistra. I punti di intersezione trovati nella vista dall alto si riportano nella vista da sinistra. L intersezione delle proiettanti con le tracce dei piani ausiliari determinano i punti della sezione. Appunti di Disegno Tecnico Industriale 137 5
6 Sezione di un cono: parabola Se il piano di sezione è parallelo ad una generatrice (angolo di inclinazione del piano rispetto all asse del cono uguale all angolo di semiapertura del cono stesso) la curva risultante dalla sezione è una parabola. Anche in questo caso si inizia tracciando sulla le Vp circonferenze sezione sui piani ausiliari e disegnando sulla Vp le tracce dei piani di sezione ausiliari. Si determinano quindi sulla Vp le intersezioni tra le tracce dei piani ausiliari con la traccia del piano di sezione. Le verticali dai punti trovati determinano, per intersezione con le circonferenze i punti della sezione sulla. Per determinare la sezione sulla si procede in modo analogo al caso precedente. Appunti di Disegno Tecnico Industriale 138 Normativa principi generali Nelle trasparenze successive vengono presentati i principi base per la rappresentazione di viste in sezione secondo la norma ISO Piano di sezione: piano immaginario che taglia l oggetto rappresentato Traccia del piano di sezione: linea che indica la posizione del piano o dei piani di sezione Taglio: sezione che mostra in aggiunta in contorni disposti posteriormente al piano di sezione Sezione: rappresentazione che mostra solo i contorni dell oggetto che giacciono su uno o più piani di sezione ATTENIONE: nella pratica si tende ad utilizzare il termine sezione per indicare quanto sopra definito come taglio. Le sezioni devono essere eseguite solamente quando necessarie, per consentire chiarezza e sintesi di espressione. La traccia dei piani di sezione deve essere rappresentata con linea mista fine ingrossata alle estremità, con due frecce agli estremi indicanti il verso di proiezione. Ciascuna freccia deve (tranne casi particolari) essere contrassegnata da una stessa lettera maiuscola. Appunti di Disegno Tecnico Industriale 139 6
7 Sezioni con un solo piano Nelle sezioni con un solo piano l elemento sezionatore è unico. È il tipo di sezione più semplice, ed è molto utilizzato. La parte dell oggetto effettivamente attraversata dal piano di sezione è contraddistinta dal tratteggio (campitura). Parte posteriore al piano di sezione Vista in sezione Parte attraversata dal piano di sezione Indicazione della sezione Sezione A-A Traccia del piano di sezione A Frecce A Lettere Appunti di Disegno Tecnico Industriale 140 Sezioni con piani paralleli (I) In molti casi è conveniente rappresentare in un unica vista in sezione il risultato del taglio eseguito su più piani paralleli. Traccia del 2 piano di sezione La linea della traccia va ingrossata in corrispondenza del cambio del piano di sezione Traccia del 1 piano di sezione Appunti di Disegno Tecnico Industriale 141 7
8 Sezioni con piani paralleli (II) Nelle viste in sezione eseguite con piani paralleli può essere utile eseguire uno sfalsamento del tratteggio in corrispondenza del cambio del piano di sezione. Il cambio del piano di sezione può essere messo in ulteriore evidenza con linee miste fini. Appunti di Disegno Tecnico Industriale 142 Sezioni con piani incidenti. Ribaltamenti (1/3) In alcuni casi, specialmente con oggetti di rotazione, è utile rappresentare in un unica vista in sezione il risultato del taglio eseguito su più piani incidenti. ERRATO CORRETTO Il piano di proiezione deve essere parallelo ad uno dei due piani di sezione. La parte del pezzo che risulterebbe di scorcio in proiezione ortografica deve essere rappresentata ribaltata sul piano di proiezione. Traccia del 2 piano di sezione Sezione A-A Traccia del 1 piano di sezione Appunti di Disegno Tecnico Industriale 143 A Direzione di proiezione A 8
9 Sezioni con piani incidenti. Ribaltamenti (2/3) tri esempi di sezioni con piani incidenti. ERRATO CORRETTO CORRETTO ERRATO Appunti di Disegno Tecnico Industriale 144 Sezioni con piani incidenti. Ribaltamenti (3/3) tri esempi di sezioni con piani incidenti. CORRETTO CORRETTO Appunti di Disegno Tecnico Industriale 145 9
10 Semisezioni Gli oggetti simmetrici possono essere rappresentati con una semivista ed una semisezione. Semivista Semisezione A-A A A Appunti di Disegno Tecnico Industriale 146 Sezioni parziali (strappi) Le sezioni parziali, dette anche strappi, si utilizzano in pezzi in cui bisogna mettere in evidenza zone interne di limitata estensione. Le sezioni parziali sono delimitate dai contorni dell oggetto e da una linea continua fine irregolare. Non si indica la traccia del piano di sezione. Appunti di Disegno Tecnico Industriale
11 Sezioni ribaltate in luogo Per la rappresentazione di oggetti la cui sezione trasversale ha almeno un asse di simmetria si possono utilizzare le sezioni ribaltate in luogo. La sezione è disegnatasopra l elemento sezionato. I contorni della sezione sono tracciati con linea fine. Il piano di sezione è individuato dall asse di simmetria. Appunti di Disegno Tecnico Industriale 148 Sezioni in vicinanza Le sezioni in vicinanza possono essere disposte o sul prolungamento della traccia del piano di sezione, ovvero in una posizione laterale diversa, anche ruotata. In questo caso vanno indicate le frecce e le relative lettere di richiamo. Sezione in vicinanza posta sul prolungamento della traccia del piano di sezione. Sezione in vicinanza posta in posizione diversa, con indicazione delle lettere. Appunti di Disegno Tecnico Industriale
12 Sezioni successive Le sezioni successive si possono considerare come una successione di sezioni poste in vicinanza, ovvero come allineamento di sezioni trasversali. Notare che le parti in vista non sezionate non vengono rappresentate. Successione di sezioni poste in vicinanza lineamento di sezioni trasversali Appunti di Disegno Tecnico Industriale 150 Il tratteggio nelle sezioni La parte di un oggetto effettivamente attraversata dal piano di sezione è rappresentata con opportuno tratteggio (campitura). Il tratteggio è normato dalla UNI Tratteggi generali Tratteggi specifici per materiali solidi Solidi Materiale predominante volgimenti elettrici Aeriformi Materiale in evidenza Materiale isolante Liquidi Materiale ausiliario Materiale trasparente Terreno Materiale legnoso Conglomerato cementizio Appunti di Disegno Tecnico Industriale
13 Esecuzione ed impiego dei tratteggi (UNI EN ISO ) L esecuzione del tratteggio è soggetta a diverse regole di rappresentazione che sono qui riassunte. Oggetti diversi adiacenti devono essere campiti con diverso tratteggio Oggetti di spessore sottile possono essere anneriti completamente Superfici grandi possono essere campite solo lungo i bordi Nelle sezioni di edifici il tratteggio può essere omesso Appunti di Disegno Tecnico Industriale 152 Elementi che non si sezionano (1) Per motivi di chiarezza alcuni elementi, anche se attraversati dal piano di sezione, si rappresentano come non sezionati. Questo per evitare che l interpretazione del disegno venga complicata quando gli oggetti non contengono elementi tali da rendere significativa una rappresentazione in sezione. Non si sezionano i denti delle ruote dentate Non si sezionano le chiavette e le linguette, quando tagliate da un piano longitudinale Non si sezionano le razze di ruote e di pulegge Non si sezionano gli alberi, quando tagliati da un piano longitudinale Non si sezionano le spine ed i perni, quando tagliati da un piano longitudinale Appunti di Disegno Tecnico Industriale
14 Elementi che non si sezionano (2) Segue dalla trasparenza precedente. Non si sezionano le rosette Non si sezionano i dadi Non si sezionano gli elementi volventi (sfere o rulli) di cuscinetti Non si sezionano le viti quando tagliate da un piano longitudinale Appunti di Disegno Tecnico Industriale 154 Elementi che non si sezionano (3) Segue dalla trasparenza precedente. Non si sezionano le nervature, quando tagliate da un piano longitudinale Nervature Appunti di Disegno Tecnico Industriale
 6 Generalità Quando un pezzo presenta fori o cavità, il disegno può risultare di difficile comprensione a causa della presenza di numerose linee tratteggiate. 7 Generalità Sezionando ( tagliando ) con
6 Generalità Quando un pezzo presenta fori o cavità, il disegno può risultare di difficile comprensione a causa della presenza di numerose linee tratteggiate. 7 Generalità Sezionando ( tagliando ) con
Sezioni e Norme di rappresentazione
 Knowledge ided Engineering Manufacturing and Related Technologies DISEGNO TECNICO INDUSTRILE Sezioni e Norme di rappresentazione Ing. Daniele Regazzoni Dipartimento di Ingegneria 1... nella lezione precedente
Knowledge ided Engineering Manufacturing and Related Technologies DISEGNO TECNICO INDUSTRILE Sezioni e Norme di rappresentazione Ing. Daniele Regazzoni Dipartimento di Ingegneria 1... nella lezione precedente
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
PROIEZIONI ORTOGONALI
 PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI
 DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI Lezione 3: Proiezioni Ortogonali con il metodo europeo Francesca Campana Le proiezioni ortogonali Le proiezioni ortogonali descrivono bi-dimensionalmente un oggetto
DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI Lezione 3: Proiezioni Ortogonali con il metodo europeo Francesca Campana Le proiezioni ortogonali Le proiezioni ortogonali descrivono bi-dimensionalmente un oggetto
Unificazione nel disegno. Enti di unificazione
 Unificazione nel disegno Norme per l esecuzione e la lettura dei disegni finalizzate ad una interpretazione univoca conforme alla volontà del progettista. Enti di unificazione ISO: International standard
Unificazione nel disegno Norme per l esecuzione e la lettura dei disegni finalizzate ad una interpretazione univoca conforme alla volontà del progettista. Enti di unificazione ISO: International standard
La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico
 La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico 1 La quotatura è ottenuta con i seguenti elementi La linea
La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico 1 La quotatura è ottenuta con i seguenti elementi La linea
CORSO DI FONDAMENTI DI DISEGNO TECNICO LEZIONE 2 PROIEZIONI ORTOGONALI
 PERCORSI ABILITANTI SPECIALI (PAS) - A.A. 2013-2014 UNIVERSITÀ DI PISA DIPARTIMENTO DI INGEGNERIA CIVILE E INDUSTRIALE (DICI) CORSO DI FONDAMENTI DI DISEGNO TECNICO LEZIONE 2 PROIEZIONI ORTOGONALI 1 CENNI
PERCORSI ABILITANTI SPECIALI (PAS) - A.A. 2013-2014 UNIVERSITÀ DI PISA DIPARTIMENTO DI INGEGNERIA CIVILE E INDUSTRIALE (DICI) CORSO DI FONDAMENTI DI DISEGNO TECNICO LEZIONE 2 PROIEZIONI ORTOGONALI 1 CENNI
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
Principi generali di normativa per il Disegno Tecnico e introduzione alle Proiezioni Ortogonali
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10 Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Docente: Gianmaria
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10 Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Docente: Gianmaria
QUOTATURA. Introduzione
 QUOTATURA 182 Introduzione Per quotatura si intende l insieme delle norme che permettono l indicazione esplicita delle dimensioni(lineari ed angolari) dell oggetto rappresentato. Poiché a ciascun disegno
QUOTATURA 182 Introduzione Per quotatura si intende l insieme delle norme che permettono l indicazione esplicita delle dimensioni(lineari ed angolari) dell oggetto rappresentato. Poiché a ciascun disegno
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
CONI, CILINDRI, SUPERFICI DI ROTAZIONE
 CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
RUOTE DENTATE. Introduzione
 RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
Ruote Dentate. Ing. Alessandro Carandina A.A. 2014/2015. Disegno Tecnico Industriale per Ingegneria Meccanica
 Ruote Dentate Ing. Alessandro Carandina A.A. 2014/2015 Disegno Tecnico Industriale per Ingegneria Meccanica Introduzione TRASMISSIONE DEL MOTO DA UN ASSE AD UN ALTRO 2 CINGHIA SINCRONA Assi paralleli Alberi
Ruote Dentate Ing. Alessandro Carandina A.A. 2014/2015 Disegno Tecnico Industriale per Ingegneria Meccanica Introduzione TRASMISSIONE DEL MOTO DA UN ASSE AD UN ALTRO 2 CINGHIA SINCRONA Assi paralleli Alberi
 Proiezioni Ortogonali Scopo del Disegno e del Disegno Tecnico Disegno: Rappresentare su un piano bidimensionale (ad esempio un foglio di carta) un oggetto nella realtà tridimensionale. Non è richiesta
Proiezioni Ortogonali Scopo del Disegno e del Disegno Tecnico Disegno: Rappresentare su un piano bidimensionale (ad esempio un foglio di carta) un oggetto nella realtà tridimensionale. Non è richiesta
Disegno di Macchine. corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana
 Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 4 Componentistica di base: alberi, trasmissione per cinghie e catene, giunti Alberi Appunti
Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 4 Componentistica di base: alberi, trasmissione per cinghie e catene, giunti Alberi Appunti
100 DOMANDE PER L'ESAME ORALE DI DISEGNO DI MACCHINE
 100 DOMANDE PER L'ESAME ORALE DI DISEGNO DI MACCHINE Queste domande sono state tratte dai registri delle sessioni d'esame orale degli scorsi anni. L'esame orale, di regola, viene svolto ponendo tre domande:
100 DOMANDE PER L'ESAME ORALE DI DISEGNO DI MACCHINE Queste domande sono state tratte dai registri delle sessioni d'esame orale degli scorsi anni. L'esame orale, di regola, viene svolto ponendo tre domande:
la restituzione prospettica da singolo fotogramma
 la restituzione prospettica da singolo fotogramma arch. francesco guerini [email protected] politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
la restituzione prospettica da singolo fotogramma arch. francesco guerini [email protected] politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
Introduzione al 3D con Autocad
 2 Introduzione al 3D con Autocad Coso di CAD B condotto da Daniela Sidari a.a. 2012/2013 19.02.2013 Modellazione geometrica 3D wireframe superfici solidi Si distinguono tre tecniche principali di modellazione:
2 Introduzione al 3D con Autocad Coso di CAD B condotto da Daniela Sidari a.a. 2012/2013 19.02.2013 Modellazione geometrica 3D wireframe superfici solidi Si distinguono tre tecniche principali di modellazione:
Disegno Tecnico Aerospaziale L (A-L) Disegno Tecnico Industriale L (A-L) Anno Accademico 2007/2008
 Alma Mater Studiorum Università di Bologna Seconda Facoltà di Ingegneria con Sede a Cesena Disegno Tecnico Aerospaziale L (A-L) Disegno Tecnico Industriale L (A-L) Anno Accademico 2007/2008 Docente: Tutor:
Alma Mater Studiorum Università di Bologna Seconda Facoltà di Ingegneria con Sede a Cesena Disegno Tecnico Aerospaziale L (A-L) Disegno Tecnico Industriale L (A-L) Anno Accademico 2007/2008 Docente: Tutor:
DISEGNO TECNICO INDUSTRIALE
 DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
Esercizi complementari al corso di DISEGNO TECNICO INDUSTRIALE (MECL, AUTL, MATL), a.a. 2005/06.
 UNIVERSITÀ DI BRESCIA - FACOLTA DI INGEGNERIA DIPARTIMENTO DI INGEGNERIA MECCANICA Gabriele Baronio, Valerio Villa. Esercizi complementari al corso di (MECL, AUTL, MATL), a.a. 2005/06. La presente raccolta
UNIVERSITÀ DI BRESCIA - FACOLTA DI INGEGNERIA DIPARTIMENTO DI INGEGNERIA MECCANICA Gabriele Baronio, Valerio Villa. Esercizi complementari al corso di (MECL, AUTL, MATL), a.a. 2005/06. La presente raccolta
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Università degli Studi della Calabria. Collegamenti smontabili non filettati
 Collegamenti smontabili non filettati Collegamenti albero-mozzo ELEMENTI ESIGENZE Anelli Scanalati Chiavette Linguette Spine elastici a Impedimento alla rotazione si si si si Impedimento alla traslazione
Collegamenti smontabili non filettati Collegamenti albero-mozzo ELEMENTI ESIGENZE Anelli Scanalati Chiavette Linguette Spine elastici a Impedimento alla rotazione si si si si Impedimento alla traslazione
La spirale iperbolica: Fu descritta per la prima volta da Pierre Varignon (1654-1722). L equazione, espressa in coordinate polari, è del tipo:
 Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
QUOTATURA DISEGNO TECNICO
 QUOTATURA DISEGNO TECNICO La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico. La quotatura deve quindi definire
QUOTATURA DISEGNO TECNICO La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico. La quotatura deve quindi definire
Fig. 2. Proiezioni ortogonali di un parallelepipedo su piani esterni alla figura
 3. LE PROIEZIONI ORTOGONALI Le proiezioni ortogonali sono originate dallo scopo di proiettare su un piano (il foglio della rappresentazione) un oggetto posto nello spazio, che conservi le stesse caratteristiche
3. LE PROIEZIONI ORTOGONALI Le proiezioni ortogonali sono originate dallo scopo di proiettare su un piano (il foglio della rappresentazione) un oggetto posto nello spazio, che conservi le stesse caratteristiche
Creare primitive solide
 Creare primitive solide I solidi sono caratterizzati dal fatto di avere una massa oltre alle superfici e agli spigoli. Rappresentano l intero volume dell oggetto. Caratteristiche Il solido viene creato:
Creare primitive solide I solidi sono caratterizzati dal fatto di avere una massa oltre alle superfici e agli spigoli. Rappresentano l intero volume dell oggetto. Caratteristiche Il solido viene creato:
CURVE DI LIVELLO. Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello.
 CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
Perchè le sezioni? Alternative alle linee nascoste per: Chiarezza Unicità (evitare equivoci) Dimensionamento (Quotatura)
 Le Sezioni Perchè le sezioni? Alternative alle linee nascoste per: Chiarezza Unicità (evitare equivoci) Dimensionamento (Quotatura) Definizione di Sezione La Sezione è la rappresentazione, secondo il metodo
Le Sezioni Perchè le sezioni? Alternative alle linee nascoste per: Chiarezza Unicità (evitare equivoci) Dimensionamento (Quotatura) Definizione di Sezione La Sezione è la rappresentazione, secondo il metodo
PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON
 PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON La muratura armata rappresenta un sistema costruttivo relativamente nuovo ed ancora non molto conosciuto e le richieste di chiarimenti sulle modalità di
PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON La muratura armata rappresenta un sistema costruttivo relativamente nuovo ed ancora non molto conosciuto e le richieste di chiarimenti sulle modalità di
LEZIONI N 24 E 25 UNIONI SALDATE
 LEZIONI N 24 E 25 UNIONI SALDATE Le saldature si realizzano prevalentemente con il metodo dell arco elettrico, utilizzando elettrodi rivestiti, che forniscono il materiale di apporto. Il collegamento è
LEZIONI N 24 E 25 UNIONI SALDATE Le saldature si realizzano prevalentemente con il metodo dell arco elettrico, utilizzando elettrodi rivestiti, che forniscono il materiale di apporto. Il collegamento è
LE SEZIONI TRASVERSALI
 LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
Scheda. Descrizione della macchina
 Scheda 1 Lavorazione: Macchina: TORNITURA TORNIO PARALLELO Descrizione della macchina I torni sono macchine che eseguono l asportazione di truciolo: lo scopo è ottenere superfici esterne e interne variamente
Scheda 1 Lavorazione: Macchina: TORNITURA TORNIO PARALLELO Descrizione della macchina I torni sono macchine che eseguono l asportazione di truciolo: lo scopo è ottenere superfici esterne e interne variamente
Norme. Norme. Università degli Studi di Brescia DIMI
 - UNI Disegno Tecnico 1 Normazione e unificazione Norma: Regola che fissa le condizioni di esecuzione di un oggetto o di elaborazione di un prodotto di cui si vogliano UNIFICARE l impiego od assicurarne
- UNI Disegno Tecnico 1 Normazione e unificazione Norma: Regola che fissa le condizioni di esecuzione di un oggetto o di elaborazione di un prodotto di cui si vogliano UNIFICARE l impiego od assicurarne
FUNZIONE. Si scrive: A B f: A B x y=f(x) (si legge: f funzione da A in B) x f y= f(x)
 1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
Il programma CONFELMOD CAD creazione e modifica
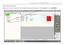 CREAZIONE DEI PEZZI DEL MODELLO Dopo aver fatto la lista di tutti i componenti nella scheda modello si passa alla creazione dei pezzi. Si seleziona il modello e si clicca su Apri Modello 1 Con questa operazione
CREAZIONE DEI PEZZI DEL MODELLO Dopo aver fatto la lista di tutti i componenti nella scheda modello si passa alla creazione dei pezzi. Si seleziona il modello e si clicca su Apri Modello 1 Con questa operazione
LE SCALE DI RAPPRESENTAZIONE
 IL SUPPORTO La CARTA DA DISEGNO è raggruppabile in due tipi fondamentali: - carta opaca o bianca - carta trasparente o da lucido, usata per disegni a china. GLI STRUMENTI Il gruppo di linee da usare per
IL SUPPORTO La CARTA DA DISEGNO è raggruppabile in due tipi fondamentali: - carta opaca o bianca - carta trasparente o da lucido, usata per disegni a china. GLI STRUMENTI Il gruppo di linee da usare per
Laboratorio di Rappresentazione e Modellazione dell Architettura
 Laboratorio di Rappresentazione e Modellazione dell Architettura Seconda Università di Napoli Facoltà di Architettura Corso di Laurea in Architettura Laboratorio di Rappresentazione e Modellazione dell
Laboratorio di Rappresentazione e Modellazione dell Architettura Seconda Università di Napoli Facoltà di Architettura Corso di Laurea in Architettura Laboratorio di Rappresentazione e Modellazione dell
DALLE CARTE ALLE SEZIONI GEOLOGICHE
 DALLE CARTE ALLE SEZIONI GEOLOGICHE PROFILO TOPOGRAFICO Il profilo topografico, detto anche profilo altimetrico, è l intersezione di un piano verticale con la superficie topografica. Si tratta quindi di
DALLE CARTE ALLE SEZIONI GEOLOGICHE PROFILO TOPOGRAFICO Il profilo topografico, detto anche profilo altimetrico, è l intersezione di un piano verticale con la superficie topografica. Si tratta quindi di
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
esercitazioni di Disegno di Macchine Anno Accademico 2013-2014 Prof. Alessandro Tasora [email protected] tel. 051 90 5895
 esercitazioni di Disegno di Macchine Anno Accademico 2013-2014 Prof. Alessandro Tasora [email protected] tel. 051 90 5895 NOTE: Svolgere le esercitazioni su fogli A3 lisci, preferibilmente tipo cartoncino.
esercitazioni di Disegno di Macchine Anno Accademico 2013-2014 Prof. Alessandro Tasora [email protected] tel. 051 90 5895 NOTE: Svolgere le esercitazioni su fogli A3 lisci, preferibilmente tipo cartoncino.
ISTRUZIONI PER LA DETERMINAZIONE DELL OMBREGGIAMENTO DI SUPERFICI TRASPARENTI SU PARETE VERTICALE
 ISTRUZIONI PER LA DETERMINAZIONE DELL OMBREGGIAMENTO DI SUPERFICI TRASPARENTI SU PARETE VERTICALE Per ogni superficie trasparente presente sulle facciate degli edifici è possibile costruire una maschera
ISTRUZIONI PER LA DETERMINAZIONE DELL OMBREGGIAMENTO DI SUPERFICI TRASPARENTI SU PARETE VERTICALE Per ogni superficie trasparente presente sulle facciate degli edifici è possibile costruire una maschera
Parte Seconda. Geometria
 Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Il controllo della visualizzazione
 Capitolo 3 Il controllo della visualizzazione Per disegnare in modo preciso è necessario regolare continuamente l inquadratura in modo da vedere la parte di disegno che interessa. Saper utilizzare gli
Capitolo 3 Il controllo della visualizzazione Per disegnare in modo preciso è necessario regolare continuamente l inquadratura in modo da vedere la parte di disegno che interessa. Saper utilizzare gli
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
Corso di Disegno di Macchine + Abilità Informatiche. Test di autovalutazione 14 marzo 2012 / A
 Test di autovalutazione 14 marzo 2012 / A 1) Quali, tra le seguenti coppie, è composta da forme duali? a. Il piano punteggiato e la stella di piani; b. la retta punteggiata e lo spazio punteggiato; c.
Test di autovalutazione 14 marzo 2012 / A 1) Quali, tra le seguenti coppie, è composta da forme duali? a. Il piano punteggiato e la stella di piani; b. la retta punteggiata e lo spazio punteggiato; c.
Unità Didattica 3 ESERCITAZIONE IL PLASTICO. Unità Didattica 1 CURVE DI LIVELLO. Unità Didattica 2 PROFILO ALTIMETRICO
 ARGOMENTO INTERDISCIPLINARE: TECNOLOGIA-SCIENZE-GEOGRAFIA Unità Didattica 1 CURVE DI LIVELLO Unità Didattica 2 PROFILO ALTIMETRICO................................. Unità Didattica 3 ESERCITAZIONE IL PLASTICO
ARGOMENTO INTERDISCIPLINARE: TECNOLOGIA-SCIENZE-GEOGRAFIA Unità Didattica 1 CURVE DI LIVELLO Unità Didattica 2 PROFILO ALTIMETRICO................................. Unità Didattica 3 ESERCITAZIONE IL PLASTICO
Modellare una poltrona
 7 Modellare una poltrona Sfruttando i comandi di costruzione delle superfici, modelleremo un arredo di media complessità, la poltrona, alla ricerca di una geometria organica che rispetti la continuità
7 Modellare una poltrona Sfruttando i comandi di costruzione delle superfici, modelleremo un arredo di media complessità, la poltrona, alla ricerca di una geometria organica che rispetti la continuità
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
r.berardi NOTE E SCHEDE OPERATIVE PER APPRENDERE LE PROIEZIONI ORTOGONALI
 r.berardi NOTE E SCHEDE OPERATIVE PER APPRENDERE LE PROIEZIONI ORTOGONALI 1. Proiezioni Assonometriche e ortogonali 2. Teoria delle proiezioni ortogonali Pag. 1 Pag. 2. 3. SCHEDE OPERATIVE SULLE PROIEZIONI
r.berardi NOTE E SCHEDE OPERATIVE PER APPRENDERE LE PROIEZIONI ORTOGONALI 1. Proiezioni Assonometriche e ortogonali 2. Teoria delle proiezioni ortogonali Pag. 1 Pag. 2. 3. SCHEDE OPERATIVE SULLE PROIEZIONI
Introduzione al Disegno Tecnico Metodi di Rappresentazione
 Knowledge Aided Engineering Manufacturing and Related Technologies DISEGNO TECNICO INDUSTRIALE Introduzione al Disegno Tecnico Metodi di Rappresentazione Prof. Caterina Rizzi Dipartimento di Ingegneria
Knowledge Aided Engineering Manufacturing and Related Technologies DISEGNO TECNICO INDUSTRIALE Introduzione al Disegno Tecnico Metodi di Rappresentazione Prof. Caterina Rizzi Dipartimento di Ingegneria
RUGOSITÀ. Introduzione
 RUGOSITÀ 299 Introduzione Le superfici degli oggetti reali sono di solito affette da irregolarità microgeometriche. Tali irregolarità possono essere casuali (tipico nei pezzi prodotti per fusione), ovvero
RUGOSITÀ 299 Introduzione Le superfici degli oggetti reali sono di solito affette da irregolarità microgeometriche. Tali irregolarità possono essere casuali (tipico nei pezzi prodotti per fusione), ovvero
DISEGNO E LABORATORIO CAD
 CORSO DI DISEGNO E LABORATORIO CAD CIVILI C.D.L. INGEGNERIA CIVILE, AMBIENTALE E EDILE A.A. 2014 2015 P R O G R A M M A DISEGNO E LABORATORIO CAD Docente: Ing. Marco NOCERA [email protected] Codocente:
CORSO DI DISEGNO E LABORATORIO CAD CIVILI C.D.L. INGEGNERIA CIVILE, AMBIENTALE E EDILE A.A. 2014 2015 P R O G R A M M A DISEGNO E LABORATORIO CAD Docente: Ing. Marco NOCERA [email protected] Codocente:
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
VERIFICA DI MATEMATICA. CLASSI TERZE (3AS, 3BS, 3CS, 3DS, 3ES) 2 settembre 2013 COGNOME E NOME.. CLASSE.
 VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
ALLEGATO II Dispositivi di attacco
 ALLEGATO II Dispositivi di attacco. : il testo compreso fra i precedenti simboli si riferisce all aggiornamento di Maggio 2011 Nel presente allegato sono riportate le possibili conformazioni dei dispositivi
ALLEGATO II Dispositivi di attacco. : il testo compreso fra i precedenti simboli si riferisce all aggiornamento di Maggio 2011 Nel presente allegato sono riportate le possibili conformazioni dei dispositivi
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 2006/2007 SIMULAZIONE DI II PROVA - A
 LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
Rappresentazione delle saldature
 TIPI DI GIUNTI SALDATI (UNI 1307-2a parte) Si definisce giunto saldato la zona in cui avviene il collegamento dei pezzi mediante saldatura. Le superfici minori dei pezzi, vicine e interessate alla saldatura,
TIPI DI GIUNTI SALDATI (UNI 1307-2a parte) Si definisce giunto saldato la zona in cui avviene il collegamento dei pezzi mediante saldatura. Le superfici minori dei pezzi, vicine e interessate alla saldatura,
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
ESTRATTO ATTUATORE CON VITE SENZA FINE PER TRAIETTORIE NON LINEARI E ALZACRISTALLI REALIZZATO CON IL MEDESIMO
 ESTRATTO ATTUATORE CON VITE SENZA FINE PER TRAIETTORIE NON LINEARI E ALZACRISTALLI REALIZZATO CON IL MEDESIMO [email protected] Attuatore per traiettorie non lineari dotato di
ESTRATTO ATTUATORE CON VITE SENZA FINE PER TRAIETTORIE NON LINEARI E ALZACRISTALLI REALIZZATO CON IL MEDESIMO [email protected] Attuatore per traiettorie non lineari dotato di
Tecniche grafiche per il disegno a mano libera il segno espressivo
 Tecniche grafiche per il disegno a mano libera il segno espressivo Tecnica a tratto o di solo contorno textures e trattamenti di campo chiaroscuro acquerello Alcuni suggerimenti utili.. Una corretta postura
Tecniche grafiche per il disegno a mano libera il segno espressivo Tecnica a tratto o di solo contorno textures e trattamenti di campo chiaroscuro acquerello Alcuni suggerimenti utili.. Una corretta postura
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Inserimento di distanze e di angoli nella carta di Gauss
 Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
FRESATRICI CLASSIFICAZIONE DELLE FRESATRICI
 FRESATRC CLASSFCAZONE DELLE FRESATRC Le fresatrici si distinguono principalmente per la disposizione dell albero portafresa e per le possibilità di movimento della tavola portapezzo. Si classificano in
FRESATRC CLASSFCAZONE DELLE FRESATRC Le fresatrici si distinguono principalmente per la disposizione dell albero portafresa e per le possibilità di movimento della tavola portapezzo. Si classificano in
Lenti sottili/1. Menisco convergente. Menisco divergente. Piano convessa. Piano concava. Biconcava. Biconvessa. G. Costabile
 Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Gli oggetti 3D di base
 Gli oggetti 3D di base 04 Attraverso gli oggetti 3D di base, AutoCAD dispiega la sua capacità di modellazione per volumi e per superfici per quei modelli che si possono pensare come composizioni di oggetti
Gli oggetti 3D di base 04 Attraverso gli oggetti 3D di base, AutoCAD dispiega la sua capacità di modellazione per volumi e per superfici per quei modelli che si possono pensare come composizioni di oggetti
STUDIO DI UNA FUNZIONE
 STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
1 INTRODUZIONE E-2 DISEGNO TECNICO
 E-2 DISEGNO TECNICO 1 INTRODUZIONE 1.1 La normativa e gli enti preposti al disegno tecnico La descrizione di un oggetto può essere fatta mediante una esposizione verbale con parole che saranno necessariamente
E-2 DISEGNO TECNICO 1 INTRODUZIONE 1.1 La normativa e gli enti preposti al disegno tecnico La descrizione di un oggetto può essere fatta mediante una esposizione verbale con parole che saranno necessariamente
G6. Studio di funzione
 G6 Studio di funzione G6 Come tracciare il grafico di una funzione data Nei capitoli precedenti si sono svolti tutti gli argomenti necessari per tracciare il grafico di una funzione In questo capitolo
G6 Studio di funzione G6 Come tracciare il grafico di una funzione data Nei capitoli precedenti si sono svolti tutti gli argomenti necessari per tracciare il grafico di una funzione In questo capitolo
Anno 4 Grafico di funzione
 Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
METODO PER LA DESCRIZIONE DEL CAMPO MAGNETICO ROTANTE
 Ing. ENRICO BIAGI Docente di Tecnologie elettrice, Disegno, Progettazione ITIS A. Volta - Perugia ETODO PER LA DESCRIZIONE DEL CAPO AGNETICO ROTANTE Viene illustrato un metodo analitico-grafico per descrivere
Ing. ENRICO BIAGI Docente di Tecnologie elettrice, Disegno, Progettazione ITIS A. Volta - Perugia ETODO PER LA DESCRIZIONE DEL CAPO AGNETICO ROTANTE Viene illustrato un metodo analitico-grafico per descrivere
24 - Strutture simmetriche ed antisimmetriche
 24 - Strutture simmetriche ed antisimmetriche ü [.a. 2011-2012 : ultima revisione 1 maggio 2012] In questo capitolo si studiano strutture piane che presentano proprieta' di simmetria ed antisimmetria sia
24 - Strutture simmetriche ed antisimmetriche ü [.a. 2011-2012 : ultima revisione 1 maggio 2012] In questo capitolo si studiano strutture piane che presentano proprieta' di simmetria ed antisimmetria sia
INTRODUZIONE AI SISTEMI CAD
 INTRODUZIONE AI SISTEMI CAD 407 Introduzione Il termine CAD sta per Computer-aided Design. L interpretazione corretta del termine è quella di progettazione assistita dal calcolatore (e non di disegno assistito
INTRODUZIONE AI SISTEMI CAD 407 Introduzione Il termine CAD sta per Computer-aided Design. L interpretazione corretta del termine è quella di progettazione assistita dal calcolatore (e non di disegno assistito
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Corso di Automazione industriale
 Corso di Automazione industriale Lezione 11 Macchine utensili e controllo numerico Programmazione CNC Università degli Studi di Bergamo, Automazione Industriale, A.A. 2015/2016, A. L. Cologni 1 Introduzione
Corso di Automazione industriale Lezione 11 Macchine utensili e controllo numerico Programmazione CNC Università degli Studi di Bergamo, Automazione Industriale, A.A. 2015/2016, A. L. Cologni 1 Introduzione
 Elementi di macchine 9 Elementi di macchine Generalità La costruzione di una macchina si basa anche sull utilizzo di componenti commerciali normalizzati; tali componenti possono essere impiegati come reperiti
Elementi di macchine 9 Elementi di macchine Generalità La costruzione di una macchina si basa anche sull utilizzo di componenti commerciali normalizzati; tali componenti possono essere impiegati come reperiti
Le applicazioni degli integrali al calcolo di aree e volumi nelle prove di maturità
 Le applicazioni degli integrali al calcolo di aree e volumi nelle prove di maturità Angelo Ambrisi Ne plus ultra. Non si va oltre! Gli integrali costituiscono le colonne d Ercole dell insegnamento della
Le applicazioni degli integrali al calcolo di aree e volumi nelle prove di maturità Angelo Ambrisi Ne plus ultra. Non si va oltre! Gli integrali costituiscono le colonne d Ercole dell insegnamento della
Studio di funzioni ( )
 Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
TRASFORMAZIONI GEOMETRICHE NEL PIANO. Parte 1
 TRASFORMAZIONI GEOMETRICHE NEL PIANO Parte 1 La geometria è la scienza che studia la forma e l estensione dei corpi e le trasformazioni che questi possono subire. In generale per trasformazione geometrica
TRASFORMAZIONI GEOMETRICHE NEL PIANO Parte 1 La geometria è la scienza che studia la forma e l estensione dei corpi e le trasformazioni che questi possono subire. In generale per trasformazione geometrica
COLLEGAMENTI ALBERO-MOZZO
 COLLEGAMENTI ALBERO-MOZZO 342 Introduzione I collegamenti albero-mozzo sono collegamenti smontabili che consentono di rendere solidali, rispetto alla rotazione attorno ad un asse comune, una parte piena
COLLEGAMENTI ALBERO-MOZZO 342 Introduzione I collegamenti albero-mozzo sono collegamenti smontabili che consentono di rendere solidali, rispetto alla rotazione attorno ad un asse comune, una parte piena
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Prodotti Siderurgici. 12. SISTEMI DI GIUNZIONE Unioni saldate, unioni bullonate
 Prodotti Siderurgici 12. SISTEMI DI GIUNZIONE Unioni saldate, unioni bullonate Premessa Il presente documento vuole fornire indicazioni semplici e concrete per i collegamenti nelle costruzioni metalliche,
Prodotti Siderurgici 12. SISTEMI DI GIUNZIONE Unioni saldate, unioni bullonate Premessa Il presente documento vuole fornire indicazioni semplici e concrete per i collegamenti nelle costruzioni metalliche,
Minicorso Regole di Disegno Meccanico
 Parte 3 Minicorso Regole di Disegno Meccanico di Andrea Saviano Tolleranze dimensionali di lavorazione Accoppiamenti mobili, stabili e incerti Giochi e interferenze Posizione della zona di tolleranza e
Parte 3 Minicorso Regole di Disegno Meccanico di Andrea Saviano Tolleranze dimensionali di lavorazione Accoppiamenti mobili, stabili e incerti Giochi e interferenze Posizione della zona di tolleranza e
SEZIONI E NORME DI RAPPRESENTAZIONE. Ing. Davide Russo Dipartimento IGIP
 SEZIONI E NORME DI RAPPRESENTAZIONE Ing. Davide Russo Dipartimento IGIP ... NELLA LEZIONE PRECEDENTE Le viste ausiliarie I ribaltamenti Raccordi e tangenze Spigoli convenzionali... altre particolarità
SEZIONI E NORME DI RAPPRESENTAZIONE Ing. Davide Russo Dipartimento IGIP ... NELLA LEZIONE PRECEDENTE Le viste ausiliarie I ribaltamenti Raccordi e tangenze Spigoli convenzionali... altre particolarità
SymCAD/C.A.T.S. modulo Antincendio
 SymCAD/C.A.T.S. modulo Antincendio Potente ed aggiornato strumento di progettazione di reti idranti e sprinkler secondo le norme UNI EN 12845, UNI 10779 e NFPA 13 - - - - - - - - - - - - - - - - - - -
SymCAD/C.A.T.S. modulo Antincendio Potente ed aggiornato strumento di progettazione di reti idranti e sprinkler secondo le norme UNI EN 12845, UNI 10779 e NFPA 13 - - - - - - - - - - - - - - - - - - -
Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione:
 Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
