Dati e Algoritmi 1: A. Pietracaprina. Alberi Generali
|
|
|
- Carlotta Lombardo
- 6 anni fa
- Visualizzazioni
Transcript
1 Dati e Algoritmi 1: A. Pietracaprina Alberi Generali 1
2 Alexander Calder, Arc of Petals, Peggy Guggenheim Collection, Venice. 2
3 Cos è un albero? root$ Albero Informalmente: collezione di nodi; collegamenti: minimali (che garantiscano la connessione); di tipo padre-figlio struttura gerarchica (lista = caso estremo di albero) 3
4 Campi Applicativi 1 strutture dati: dizionari; code con priorità 2 esplorazione risorse: filesystem; siti di e-commerce; 3 sistemi distribuiti e reti di comunicazione: sincronizzazione, broadcast, gathering 4 analisi di algoritmi: albero della ricorsione 5 classificazione: alberi di decisione 6 compressione di dati (codici di Huffman) 7 biologia computazionale: alberi filogenetici 4
5 Alberi (Tree) (Capitolo 8 [GTG14]) Definizione di Albero radicato (rooted tree) Un albero radicato T è una collezione di nodi che, se non è vuota, soddisfa le seguenti proprietà: un nodo speciale r T (r. = radice) v T, v r :!u T : u è padre di v (v è figlio di u) v T, v r : risalendo di padre in padre si arriva a r (= ogni nodo è discendente dalla radice.) r" u" v" 5
6 Nota Nel libro la terza condizione: v T, v r : risalendo di padre in padre si arriva a r manca. Senza di questa, la seguente collezione r" u" v" con u padre di v e v padre di u sarebbe un albero... che ha poco senso. Questa collezione piuttosto è una foresta di alberi. 6
7 Alberi: altre definizioni r" u" v" w" z" Antenati x è antenato di y se x = y oppure x è antenato del padre di y (es: u è antenato di w Discendenti x è discendente di y se y è antenato di x Nodi interni Nodi con 1 figli 7
8 Alberi: altre definizioni (continua) r" u" v" w" z" Nodi esterni (= foglie) Nodi senza figli. Sottoalbero con radice v T v = albero formato da tutti i discendenti di v Albero ordinato T è un albero ordinato se per ogni nodo interno v T è definito un ordinamento lineare tra i figli u 1, u 2,..., u k di v. 8
9 Definizione Ricorsiva Definizione ricorsiva di albero radicato Un albero radicato T è una collezione di nodi che, se non è vuota, risulta partizionata in questo modo: per un qualche k 0, dove: r è radice T = {r} T 1 T 3 T k, i, 1 i k: T i è un albero non vuoto la cui radice (chiamiamola u i ) è figlia di r r" u 1" u 2" u k" " T 1" T 2" T k" 9
10 Alberi: ancora definizioni 10 Profondità (depth) di un nodo v in un albero T Definizioni alternative: 1 profondità depth T (v) di v = antenati(v) - 1; 2 se v = r radice depth(v) = 0 altrimenti depth(v) = 1 + depth(padre(v)) Livello i Insieme dei nodi a profondità i ( i 0) Altezza (height) di un nodo v in un albero T se v è foglia height(v) = 0 altrimenti height(v) = 1 + max w:w figlio di v (height(w))
11 Alberi: ancora definizioni... e una proposizione 11 Altezza di un albero T Altezza height(t ) di T = height(r), r è radice di T Proposizione (Proposition 8.3 [GTG14]) Dato un abero T, height(t ) = max v T :v foglia (depth(v))
12 Esempio 12 DEPTH& 0& 1& h=2& h=2& h=4& h=3& LIVELLO& 0& 1& 2& h=0& h=1& h=1& h=0& h=2& h=0& 2& 3& h=0& h=0& h=1& h=0& h=0& 3& 4& h=0& altezza& 4&
13 13 Proposizione (Proposition 8.3 [GTG14]) Dato un albero T, height(t ) = max v T :v foglia (depth(v)) Dimostrazione (Esercizio R-8.2 [GTG14]) Induzione su n = numero di nodi di T base: n=1 OK passo induttivo: fisso n 1. Come hp. induttiva assumiamo che la proprietà valga per qualsiasi albero con m nodi, per 1 m n. Consideriamo un albero T con n + 1 nodi. Dato che n + 1 > 1, si ha che T è del tipo: r" u 1" u 2" " u k" k 1 " T 1" T 2" T k"
14 14 Dimostrazione (continua) r" u 1" u 2" " u k" k 1 " T 1" T 2" T k" height(t ) (def ) = 1 + max 1 i k (height(u i)) (hp.ind.) = 1 + max ( max (depth Ti (v))) 1 i k v T i v foglia = max ( max (1 + depth Ti (v))) 1 i k v T i v foglia = max max 1 i k v T i v foglia = max depth T (v) v T v foglia depth T (v)
15 15 Implementazione di un albero generale Nodo (Position<E>) (Struttura linkata) parent& element& children& Albero (Tree<E>) numelements$ root$
16 16 Complessità Nell analisi degli algoritmi che usano i metodi dell interfaccia, assumeremo che gli iteratori abbiano complessità lineare nel numero di oggetti scansionati, e che gli altri metodi abbiano complessità costante. È facile sviluppare implementazioni che soddisfino questi requisiti.
17 Calcolo della profondità di un nodo (Algoritmo ricorsivo) 17 Algoritmo: depth(t,v) Input: v T Output: profondità di v in T if (T.isRoot(v)) then return 0; else return 1+depth(T,T.parent(v)); Osservazione [GTG14] definisce il metodo depth dentro una classe astratta che implementa l interfaccia Tree
18 18 Complessità di depth La complessità di depth è espressa dalla seguente relazione di ricorrenza in funzione della profondità d del nodo { c 1 d = 0 t(d) = t(d 1) + c 2 d > 0 c 1, c 2 > 0 costanti Esercizio: Dimostrare per induzione su d che t(d) = c 2 d + c 1, per ogni d 0 t(d) = Θ (d + 1) N.B.: [GTG14] è meno formale e non usa una relazione di ricorrenza
19 Calcolo della profondità di un nodo (Algoritmo iterativo) 19 Algoritmo: iter-depth(t,v) Input: v T Output: profondità di v in T d 0 ; while!(t.isroot(v)) do v T.parent(v); d d + 1 return d Complessità Θ (d + 1)
20 Calcolo dell altezza di un nodo 20 Algoritmo: height(t,v) Input: v T Output: altezza di v in T h 0; foreach w T.children(v) do h max{h, 1+height(T,w)} ; return h Osservazione La complessità dell algoritmo può essere espressa tramite una relazione di ricorrenza, in funzione della taglia (= numero di nodi) del sottoalbero T v. Tuttavia l utilizzo della relazione di ricorrenza risulta complicato dal fatto che il numero di chiamate ricorsive e la taglia dei sottoproblemi risolti da queste chiamate sono variabili che dipendono dalla istanza. In questo caso, per l analisi facciamo un argomento ad hoc (pag. 287 [GTG14]).
21 21 Complessità di height Analizziamo la complessità di height(t, v) per step successivi: 1 Come per qualsiasi algoritmo ricorsivo, la complessità può essere determinata sommando il numero di operazioni eseguite da ciascuna chiamata dell algoritmo, escludendo quelle dalle chiamate ricorsive al suo interno. 2 L algoritmo viene invocato esattamente una volta su ogni nodo u T v. (La dimostrazione per induzione sull altezza di T v è lasciata come esercizio.) 3 Per ogni u T v, il costo attribuito alla chiamata height(t, u) è Θ (c u + 1), dove c u è il numero di figli di u. 4 (Proposizione 8.4 [GTG14]) Se T v contiene n nodi (n = T v ), si ha che u T v c u = n 1. Si dimostra osservando che ogni nodo di T v tranne la radice ha un padre (unico) in T v e contribuisce 1 alla sommatoria.
22 22 Complessità di height (continua) Dai punti 1-4 deduciamo che la complessità di height(t, v) è Θ (c u + 1) = Θ (2n 1) = Θ (n), u T v dove n = T v. Osservazione È facile verificare che le complessità determinate per depth e height sono tight (da qui l uso di Θ ( )). Inoltre, tutte le istanze della stessa taglia (profondità d del nodo v per depth e numero di nodi n in T v per height) hanno la stessa complessità.
23 Visite di Alberi 23 Visita Accedere a tutti i nodi dell albero eseguendo una qualche operazione ad ogni nodo ( visita ). Preorder Prima il padre e poi (ricorsivamente) i sottoalberi radicati nei figli. Postorder Prima (ricorsivamente) i sottoalberi radicati nei figli, poi il padre.
24 24 Algoritmo preorder(t,v) Input: nodo v T Output: visita di tutti i nodi di T v visita v; foreach w T.children(v) do preorder(t,w) Chiamata iniziale preorder(t,t.root()) Visita in Preorder Nota Se l albero è ordinato la visita tocca i figli di un nodo A nell ordine dato. B B A C C D E F G E F G D A(B(E(F(C(D(G( A(B(E(F(C(D(G(
25 25 Algoritmo postorder(t,v) Input: nodo v T Output: visita di tutti i nodi di T v foreach w T.children(v) do postorder(t,w) visita v; Chiamata iniziale postorder(t,t.root()) Visita in Postorder Nota Se l albero è ordinato la visita tocca i figli di un nodo A nell ordine dato. B B A C C D D Osservazione L algoritmo height è un esempio di visita in postorder, in cui la visita di un nodo è il calcolo della sua altezza date quelle dei suoi figli. E F G E F G E(F(B(C(G(D(A( E(F(B(C(G(D(A(
26 26 Complessità delle visite Determiniamo la complessità di preorder(t,t.root()) e postorder(t,t.root()), in funzione del numero di nodi n di T. L analisi è simile a quella dell algoritmo height Ciascuna chiamata su un nodo u T esegue un numero di operazioni (escluse quelle fatte dalle chiamate riscorsive al suo interno) che è Θ (c u t u ), dove c u è il numero di figli di u e t u è il costo della visita di u Dato che l algoritmo viene invocato esattamente una volta per ogni nodo u T, la complessità totale è ( ) ( Θ (c u t u ) = Θ n + t u ). u T u T Nel caso in cui t u = O (1) per ogni u, la complessità della visita in preorder o postorder risulta essere Θ (n).
27 Esempio di visita in preorder 27 Albero: struttura di un libro in sezioni (capitoli, paragrafi, ecc.) Visita di un nodo: stampa nome sezione. La visita dell albero produce quindi l indice del libro: Book: Chapter1, Section 1.1., Section 1.2, Section 1.2.1, Section 1.2.2, Chapter 2, Section 2.1, Section 2.2, Section 2.2.1, Section Altro esempio: modo in cui spesso i file system presentano la sequenza di cartelle e file.
28 28 Esercizio Progettare un algoritmo che dato un albero T, per ciascun nodo v T memorizzi la sua profondità in un campo v.depth, e analizzarne la complessità in funzione del numero di nodi n dell albero. (Suggerimento: modificare la visita in preorder.)
29 29 Svolgimento Idea: se il nodo è la radice, la sua profondità viene impostata a 0, altrimenti si imposta la profondità a 1+la profondità del padre, che si assume già impostata. Lo pseudocodice è il seguente (prima invocazione con v = T.root()): Algoritmo alldepths(t,v) Input: nodo v T (il padre, se esiste, ha depth impostato) Output: tutti i nodi di T v con campo depth impostato if (T.isRoot(v)) then v.depth 0; else v.depth 1+T.parent(v).depth; foreach w T.children(v) do alldepths(t,w); Complessità: Θ (n), dato che l algoritmo ha la stessa struttura della visita in preorder e la visita di un nodo (impostazione del campo depth) richiede O (1) operazioni.
30 Esempio di visita in postorder 30 Albero: struttura del file system Nodi: directory (nodi interni) o file (nodi foglia). Inizialmente ogni nodo v ha un campo v.size che rappresenta lo spazio occupato dal nodo. Tuttavia, se il nodo è una directory tale spazio non include quello dei file o directory in esso contenuti. Visita di un nodo: memorizzazione nel campo size dello spazio complessivo associato al nodo (che include anche quello dei file e directory in esso contenuti). La visita dell albero determina quindi lo spazio occupato da tutti i file e directory.
31 31 Esempio 1K# 1K# 3K# 1K# 10K# 5K# 4K# 8K# 3K# 1K# 36K# 1K# 3K# 1K# 20K# 3K# 12K# 10K# 5K# 4K# 8K# 3K# 10K# 5K# 4K# 8K# 3K#
32 32 Lo pseudocodice dell algoritmo è il seguente (prima invocazione con v = T.root()): Algoritmo diskspace(t,v) Input: nodo v T Output: spazio aggregato di T v + aggiornamento di u.size u T v con lo spazio aggregato di T u s 0; foreach w T.children(v) do s s+diskspace(t,w); v.size v.size +s; return v.size; Complessità: Θ (n) (dove n è il numero di nodi dell albero), dato che l algoritmo ha la stessa struttura della visita in postorder e la visita di un nodo (impostazione del campo size) richiede O (1) operazioni.
33 33 Definizione Sia T albero ordinato e siano u, v T due nodi allo stesso livello. Diciamo che u è a sinistra di v ( v è a destra di u) se u viene prima di v nella visita in preorder. NB: si assume che nella visita in preorder i figli di un nodo siano visitati secondo l ordine a loro assegnato Osservazione La definizione è coerente con il modo di disegnare gli alberi.
34 Esercizi 34 Esercizio (simile a R-8.19 di [GTG14]) Si supponga che la visita in preorder di un albero ordinato di 6 nodi incontri i nodi nell ordine ABCDEF. 1 Dire quali delle seguenti sequenze può rappresentare la visita in postorder dello stesso albero (motivando la risposta): BAFECD, CDBFEA, CDAEFB. 2 Disegnare l albero compatibile con le due sequenze di preorder e postorder.
35 35 Svolgimento 1 Dall ordine preorder si deduce che A è radice e quindi deve essere visitato per ultimo in postorder. Quindi l unica sequenza compatibile è CDBFEA 2 Osservazioni: B deve essere il primo figlio di A (da preorder); C e D devono essere figli di B (da preorder e postorder); E deve essere il secondo figlio di A (da preorder); ed F deve essere il figlio di E (da postorder). Il disegno è lasciato come esercizio.
36 Esercizio Si supponga di calcolare l altezza di un albero T di n nodi invocando l algoritmo depth(t, v) da ciascuna foglia v di T e restituendo come altezza la massima profondità ottenuta. Dimostrare che tale strategia ha una complessità al caso pessimo Ω ( n 2). (È l algoritmo heightbad decritto in [GTG14]. Si veda anche l esercizio C-8.27 del testo.) Svolgimento Dato che il calcolo della profondità d v di un nodo v richiede Θ (d v + 1) operazioni, la complessità della strategia indicata è Ω (1 + d v ) v:v foglia Gli esempi nel prossimo lucido mostrano che per ogni n esiste un albero di n nodi in cui v:v foglia (1 + d v ) Ω ( n 2). 36
37 37
38 38 Esercizio 4 (C-8.50 [GTG14]) Sia T un albero. Dati due nodi v, w T si definisce il Lowest Common Ancestor di v e w (LCA(v, w)) come l antenato comune più profondo. Progettare un algoritmo efficiente per trovare LCA(v, w), analizzandone la complessità. Svolgimento L idea dell algoritmo è di risalire dal più profondo dei due nodi passati in input sino all antenato che sta alla stessa profondità dell altro, e da qui risalire da entrambi sino a trovare il primo antenato comune. (Si osservi che un antenato in comune esiste sicuramente ed è la radice.) Per determinare la profondità di un nodo si utilizza l algoritmo depth visto a lezione.
39 39 Lo pseudocodice dell algoritmo è il seguente: Algoritmo LCA(v, w) input v, w T output LCA(v, w) d v depth(v); d w depth(w) if (d v > d w ) then for i 1 to d v d w do v T.parent(v) else for i 1 to d w d v do w T.parent(w) while (v w) do { v T.parent(v) w T.parent(w) } return v
40 40 Complessità: Le invocazioni di depth hanno complessità proporzionale alle profondità di v e w. I cicli for e il ciclo while eseguono, ciascuno, un numero di iterazioni limitato superiormente dalla massima profondità dei due nodi, e in ciascuna iterazione eseguono un numero costante di operazioni. Dato che la profondità di un nodo è limitata superiormente dall altezza dell albero, concludiamo che la complessità dell algoritmo è O (h), con h altezza di T. Esercizio: Dimostrare che la complessità è Θ ( ). Osservazione Le complessità di algoritmi su alberi si esprimono spesso in funzione del numero di nodi n o dell altezza h. Si noti che una complessità espressa in funzione di h può essere anche espressa in funzione di n usando il fatto che 0 h < n.
41 41 Esercizio Progettare un algoritmo che dato un albero T, per ciascun nodo v T memorizzi la sua altezza in un campo v.height, e analizzarne la complessità in funzione del numero di nodi n dell albero.
42 Errata 42 Cambiamenti rispetto alla prima versione dei lucidi: Lucido 16: aggiunta osservazione
Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree
 Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Si definisca Interval Tree un albero binario di ricerca le
Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Si definisca Interval Tree un albero binario di ricerca le
Alberi ( GT. 7 ) In informatica, un albero è un modello astratto con cui viene rappresentata una struttura gerarchica
 Alberi ( GT. 7 ) Albero definizioni Albero ADT (Abstract Data Type) Algoritmi di base su alberi Alberi binari Strutture dati per rappresentare alberi Implementazione AlberoBinario 1 Alberi (GT. 7) In informatica,
Alberi ( GT. 7 ) Albero definizioni Albero ADT (Abstract Data Type) Algoritmi di base su alberi Alberi binari Strutture dati per rappresentare alberi Implementazione AlberoBinario 1 Alberi (GT. 7) In informatica,
Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi
 Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Dimostrare che un albero non vuoto con n nodi interni, dove ogni nodo interno ha almeno
Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Dimostrare che un albero non vuoto con n nodi interni, dove ogni nodo interno ha almeno
Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base
 Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1. Sia T una stringa arbitraria di lunghezza n 1 su un alfabeto Σ. È sempre possibile
Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1. Sia T una stringa arbitraria di lunghezza n 1 su un alfabeto Σ. È sempre possibile
Dati e Algoritmi I (Pietracaprina) Esercizi svolti sui Grafi
 Dati e Algoritmi I (Pietracaprina) Esercizi svolti sui Grafi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 (Esercizio C-14.34 del testo [GTG14]) Sia G = (V, E) un grafo non diretto con n =
Dati e Algoritmi I (Pietracaprina) Esercizi svolti sui Grafi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 (Esercizio C-14.34 del testo [GTG14]) Sia G = (V, E) un grafo non diretto con n =
Divide et impera su alberi
 Divide et impera su alberi Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli di u. Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u):
Divide et impera su alberi Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli di u. Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u):
Alberi. Definizioni principali
 Definizioni principali Un albero è una struttura dati che contiene oggetti organizzati gerarchicamente (a differenza della lista di nodi, dell'array list, i cui elementi sono organizzati linearmente) radice
Definizioni principali Un albero è una struttura dati che contiene oggetti organizzati gerarchicamente (a differenza della lista di nodi, dell'array list, i cui elementi sono organizzati linearmente) radice
Dati e Algoritmi 1: A. Pietracaprina. Grafi (II parte)
 Dati e Algoritmi 1: A. Pietracaprina Grafi (II parte) 1 Breath-First Search (algoritmo iterativo) Si assume una rappresentazione tramite liste di adiacenza. L ordine con cui si visitano i vicini di un
Dati e Algoritmi 1: A. Pietracaprina Grafi (II parte) 1 Breath-First Search (algoritmo iterativo) Si assume una rappresentazione tramite liste di adiacenza. L ordine con cui si visitano i vicini di un
Alberi binari (radicati e ordinati) della radice Il padre del nodo 5 e del nodo 3
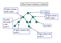 Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
Problemi di ordinamento
 Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti
 Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Note per la Lezione 4 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
Algoritmi e Strutture Dati
 Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
Alberi binari e alberi binari di ricerca
 Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
Alberi. Alberi: definizioni. Alberi Binari. Esercizi su alberi binari: metodi ricorsivi. Struttura dati per alberi generici. ASD-L - Luca Tesei
 Alberi Alberi: definizioni Alberi Binari Esercizi su alberi binari: metodi ricorsivi Struttura dati per alberi generici 1 Alberi Gli alberi sono strutture dati naturalmente ricorsive Un albero è un particolare
Alberi Alberi: definizioni Alberi Binari Esercizi su alberi binari: metodi ricorsivi Struttura dati per alberi generici 1 Alberi Gli alberi sono strutture dati naturalmente ricorsive Un albero è un particolare
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti
 Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 27 marzo 2012 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 27 marzo 2012 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Esercizio 1. E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1. livello 0 FB = -1. livello 1 FB = -1.
 Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
Algoritmi e Strutture Dati
 Heap Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Heap Heap binari: definizione Un heap binario è una struttura dati composta
Heap Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Heap Heap binari: definizione Un heap binario è una struttura dati composta
23/10/2016. gli alberi. alcune definizioni. un esempio. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica.
 gli alberi Un albero è una struttura dati NON LINEARE organizzata gerarchicamente. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica È costituito da un insieme di nodi collegati tra di loro:
gli alberi Un albero è una struttura dati NON LINEARE organizzata gerarchicamente. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica È costituito da un insieme di nodi collegati tra di loro:
Esercizi su alberi binari
 Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Algoritmi Greedy. Tecniche Algoritmiche: tecnica greedy (o golosa) Un esempio
 Algoritmi Greedy Tecniche Algoritmiche: tecnica greedy (o golosa) Idea: per trovare una soluzione globalmente ottima, scegli ripetutamente soluzioni ottime localmente Un esempio Input: lista di interi
Algoritmi Greedy Tecniche Algoritmiche: tecnica greedy (o golosa) Idea: per trovare una soluzione globalmente ottima, scegli ripetutamente soluzioni ottime localmente Un esempio Input: lista di interi
Alberi. Strutture dati: Alberi. Alberi: Alcuni concetti. Alberi: definizione ricorsiva. Alberi: Una prima realizzazione. Alberi: prima Realizzazione
 Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
LE STRUTTURE DATI DINAMICHE: GLI ALBERI. Cosimo Laneve
 LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
Espressioni aritmetiche
 Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
In questa lezione. Heapsort. ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 114
![In questa lezione. Heapsort. ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 114 In questa lezione. Heapsort. ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 114](/thumbs/65/52995013.jpg) In questa lezione Heapsort ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 11 1 Paternità L heapsort è stato pubblicato da J. W. J. Williams nel 106. Pochi mesi
In questa lezione Heapsort ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 11 1 Paternità L heapsort è stato pubblicato da J. W. J. Williams nel 106. Pochi mesi
Algoritmi e Strutture Dati. HeapSort
 Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Introduzione alla gestione delle collezioni di oggetti
 Introduzione alla gestione delle collezioni di oggetti Alcune tecniche di base Un esempio: l ADT Dizionario (mutabile) Un esempio: l ADT Pila (mutabile) Un esempio: l ADT Coda (mutabile) Tecniche di rappresentazione
Introduzione alla gestione delle collezioni di oggetti Alcune tecniche di base Un esempio: l ADT Dizionario (mutabile) Un esempio: l ADT Pila (mutabile) Un esempio: l ADT Coda (mutabile) Tecniche di rappresentazione
Alberi ed Alberi Binari
 Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità
 Albero binario di ricerca Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità Proprietà: sia x un nodo di un (sotto)albero binario di ricerca Se y è un nodo del sottoalbero
Albero binario di ricerca Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità Proprietà: sia x un nodo di un (sotto)albero binario di ricerca Se y è un nodo del sottoalbero
Alberi Binari di Ricerca
 Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Esercizi di Algoritmi e Strutture Dati
 Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 3 novembre 2010 1 Trova la somma/1 Scrivere un algoritmo che dati in input un array A[1... n] di n interi
Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 3 novembre 2010 1 Trova la somma/1 Scrivere un algoritmo che dati in input un array A[1... n] di n interi
Alberi binari di ricerca
 Alberi binari di ricerca Ilaria Castelli castelli@dii.unisi.it Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/20010 I. Castelli Alberi binari di ricerca, A.A. 2009/20010
Alberi binari di ricerca Ilaria Castelli castelli@dii.unisi.it Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/20010 I. Castelli Alberi binari di ricerca, A.A. 2009/20010
Alberi. In informatica, un albero è un modello astratto di una struttura dati gerarchica
 Il TDA Tree Alberi In informatica, un albero è un modello astratto di una struttura dati gerarchica Struttura dati non lineare Si pensi al file system di un sistema operativo Le relazioni in un albero
Il TDA Tree Alberi In informatica, un albero è un modello astratto di una struttura dati gerarchica Struttura dati non lineare Si pensi al file system di un sistema operativo Le relazioni in un albero
GLI ALBERI BINARI DI RICERCA. Cosimo Laneve
 GLI ALBERI BINARI DI RICERCA Cosimo Laneve argomenti 1. alberi binari di ricerca 2. la ricerca di elementi e la complessità computazionale 3. operazione di cancellazione di elementi 4. esempi/esercizi
GLI ALBERI BINARI DI RICERCA Cosimo Laneve argomenti 1. alberi binari di ricerca 2. la ricerca di elementi e la complessità computazionale 3. operazione di cancellazione di elementi 4. esempi/esercizi
Algoritmi e strutture dati
 Algoritmi e strutture dati Roberto Cordone A. A. 2015-16 Capitolo 3 Implementazioni dei dizionari ordinati Nota: queste dispense sono un rapido riassunto delle lezioni svolte nel dicembre 2015 e gennaio
Algoritmi e strutture dati Roberto Cordone A. A. 2015-16 Capitolo 3 Implementazioni dei dizionari ordinati Nota: queste dispense sono un rapido riassunto delle lezioni svolte nel dicembre 2015 e gennaio
Tempo e spazio di calcolo (continua)
 Tempo e spazio di calcolo (continua) I numeri di Fibonacci come case study (applichiamo ad un esempio completo le tecniche illustrate nei lucidi precedenti) Abbiamo introdotto tecniche per la correttezza
Tempo e spazio di calcolo (continua) I numeri di Fibonacci come case study (applichiamo ad un esempio completo le tecniche illustrate nei lucidi precedenti) Abbiamo introdotto tecniche per la correttezza
ADT Coda con priorità
 Code con priorità ADT Coda con priorità Una coda con priorità è una struttura dati dinamica che permette di gestire una collezione di dati con chiave numerica. Una coda con priorità offre le operazioni
Code con priorità ADT Coda con priorità Una coda con priorità è una struttura dati dinamica che permette di gestire una collezione di dati con chiave numerica. Una coda con priorità offre le operazioni
Esercizi Capitolo 6 - Alberi binari di ricerca
 Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Implementazione ADT: Alberi
 Implementazione ADT: Alberi Livelli di astrazione 2001/2002 1 Esercitazione 5 (E6): alberi (tree) albero struttura dati fondamentale, soprattutto per le operazioni di ricerca tipi di albero con radice
Implementazione ADT: Alberi Livelli di astrazione 2001/2002 1 Esercitazione 5 (E6): alberi (tree) albero struttura dati fondamentale, soprattutto per le operazioni di ricerca tipi di albero con radice
Strutture dati per insiemi disgiunti
 Strutture dati per insiemi disgiunti Servono a mantenere una collezione S = {S 1, S 2,..., S k } di insiemi disgiunti. Ogni insieme S i è individuato da un rappresentante che è un particolare elemento
Strutture dati per insiemi disgiunti Servono a mantenere una collezione S = {S 1, S 2,..., S k } di insiemi disgiunti. Ogni insieme S i è individuato da un rappresentante che è un particolare elemento
Problemi, istanze, soluzioni
 lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
Elezione di un leader in una rete ad anello
 Elezione di un leader in una rete ad anello Corso di Algoritmi Distribuiti Prof. Roberto De Prisco Lezione n a cura di Rosanna Cassino e Sergio Di Martino Introduzione In questa lezione viene presentato
Elezione di un leader in una rete ad anello Corso di Algoritmi Distribuiti Prof. Roberto De Prisco Lezione n a cura di Rosanna Cassino e Sergio Di Martino Introduzione In questa lezione viene presentato
Tempo e spazio di calcolo (continua)
 Tempo e spazio di calcolo (continua) I numeri di Fibonacci come case study (applichiamo ad un esempio completo le tecniche illustrate nei lucidi precedenti) Abbiamo introdotto tecniche per la correttezza
Tempo e spazio di calcolo (continua) I numeri di Fibonacci come case study (applichiamo ad un esempio completo le tecniche illustrate nei lucidi precedenti) Abbiamo introdotto tecniche per la correttezza
Alberi Binari di Ricerca e Alberi Rosso-Neri
 Alberi Binari di Ricerca e Alberi Rosso-Neri Obiettivi Studiare strutture dati che consentano di effettuare in modo efficiente le operazioni di Minimo e massimo Successore Inserimento e cancellazione Ricerca
Alberi Binari di Ricerca e Alberi Rosso-Neri Obiettivi Studiare strutture dati che consentano di effettuare in modo efficiente le operazioni di Minimo e massimo Successore Inserimento e cancellazione Ricerca
ADT Dizionario. Ordered search table. Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D:
 Ordered search table Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D: possiamo memorizzare le entrate di D in un array list S in ordine non decrescente di chiavi:
Ordered search table Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D: possiamo memorizzare le entrate di D in un array list S in ordine non decrescente di chiavi:
Laboratorio di Algoritmi e Strutture Dati. Aniello Murano. people.na.infn.it/~murano/ Murano Aniello - Lab. di ASD Terza Lezione
 Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ Heap e Heapsort Algoritmi di ordinamento Insertion Sort Quicksort Heapsort Insertion Sort L
Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ Heap e Heapsort Algoritmi di ordinamento Insertion Sort Quicksort Heapsort Insertion Sort L
Algoritmi e strutture dati
 Algoritmi e Strutture Dati Capitolo 4 Ordinamento Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Esempi: ordinare alfabeticamente lista di nomi, o insieme
Algoritmi e Strutture Dati Capitolo 4 Ordinamento Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Esempi: ordinare alfabeticamente lista di nomi, o insieme
ALBERI : introduzione SOMMARIO ALBERI ALBERI. ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI
 SOMMARIO ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI Dimensione e Altezza ALBERI BINARI DI RICERCA (BST) Introduzione Ricerca, inserimento e cancellazione Implementazione
SOMMARIO ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI Dimensione e Altezza ALBERI BINARI DI RICERCA (BST) Introduzione Ricerca, inserimento e cancellazione Implementazione
Appunti Senza Pretese di Programmazione II: Costruzione di un Albero Bilanciato
 Appunti Senza Pretese di Programmazione II: Costruzione di un Albero Bilanciato Alessandro Panconesi DSI, La Sapienza via Salaria 113, 00198, Roma Consideriamo un problema che ci consentirá di vedere un
Appunti Senza Pretese di Programmazione II: Costruzione di un Albero Bilanciato Alessandro Panconesi DSI, La Sapienza via Salaria 113, 00198, Roma Consideriamo un problema che ci consentirá di vedere un
Università degli Studi di L Aquila Facoltà di Scienze M.F.N. Corso di Laurea in Informatica. Modulo di Laboratorio di Algoritmi e Strutture Dati
 Università degli Studi di L Aquila Facoltà di Scienze M.F.N. Corso di Laurea in Informatica Modulo di Laboratorio di Algoritmi e Strutture Dati Alberi binari Giovanna Melideo melideo@di.univaq.it 1 Alberi
Università degli Studi di L Aquila Facoltà di Scienze M.F.N. Corso di Laurea in Informatica Modulo di Laboratorio di Algoritmi e Strutture Dati Alberi binari Giovanna Melideo melideo@di.univaq.it 1 Alberi
Algoritmi e Strutture Dati
 Algoritmi Ricorsivi e Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 I conigli di Fibonacci Ricerca Binaria L isola dei conigli
Algoritmi Ricorsivi e Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 I conigli di Fibonacci Ricerca Binaria L isola dei conigli
Tipi di dato e Strutture dati elementari
 Tipi di dato e Strutture dati elementari Ing. Paolo Craca Anno accademico 2007/2008 Tipi di dato e Strutture dati elementari 1 / 40 Cosa vedremo in questo seminario 1 Introduzione 2 Pile 3 Code 4 5 Bibliografia
Tipi di dato e Strutture dati elementari Ing. Paolo Craca Anno accademico 2007/2008 Tipi di dato e Strutture dati elementari 1 / 40 Cosa vedremo in questo seminario 1 Introduzione 2 Pile 3 Code 4 5 Bibliografia
Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari.
 Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari. Algoritmi e Strutture Dati + Lab A.A. / Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro ALBERO
Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari. Algoritmi e Strutture Dati + Lab A.A. / Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro ALBERO
Tecniche Algoritmiche: divide et impera
 Tecniche Algoritmiche: divide et impera Una breve presentazione F. Damiani - Alg. & Lab. 04/05 Divide et impera (o Divide and conquer) Per regnare occorre tenere divisi i nemici e trarne vantaggio F. Damiani
Tecniche Algoritmiche: divide et impera Una breve presentazione F. Damiani - Alg. & Lab. 04/05 Divide et impera (o Divide and conquer) Per regnare occorre tenere divisi i nemici e trarne vantaggio F. Damiani
Dati e Algoritmi 1: A. Pietracaprina. Mappa/Dizionario (I parte)
 Dati e Algoritmi 1: A. Pietracaprina Mappa/Dizionario (I parte) 1 Mappa/Dizionario Definizione generale Collezione di entry che supporta, come metodi principali: ricerca, inserimento, rimozione Vari ADT:
Dati e Algoritmi 1: A. Pietracaprina Mappa/Dizionario (I parte) 1 Mappa/Dizionario Definizione generale Collezione di entry che supporta, come metodi principali: ricerca, inserimento, rimozione Vari ADT:
Dizionari Liste invertite e Trie
 Dizionari Liste invertite e Trie Lucidi tratti da Crescenzi Gambosi Grossi, Strutture di dati e algoritmi Progettazione, analisi e visualizzazione Addison-Wesley, 2006 Dizionari Universo U delle chiavi
Dizionari Liste invertite e Trie Lucidi tratti da Crescenzi Gambosi Grossi, Strutture di dati e algoritmi Progettazione, analisi e visualizzazione Addison-Wesley, 2006 Dizionari Universo U delle chiavi
Alberi e alberi binari I Un albero è un caso particolare di grafo
 Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Alberi. Se x è il genitore di y, allora y è un figlio di x. Un albero binario è un albero in cui ogni nodo ha al massimo due figli.
 Alberi Un albero è un insieme di oggetti, chiamati nodi, su cui è definita una relazione binaria G(x, y) che leggiamo x è genitore di y tale che: 1. esiste un unico nodo, chiamato radice, che non ha genitori;
Alberi Un albero è un insieme di oggetti, chiamati nodi, su cui è definita una relazione binaria G(x, y) che leggiamo x è genitore di y tale che: 1. esiste un unico nodo, chiamato radice, che non ha genitori;
Informatica 3. Informatica 3. LEZIONE 14: Alberi binari: introduzione. Lezione 14 - Modulo 1. Definizioni. Introduzione. Definizioni e proprietà
 Informatica 3 Informatica 3 LEZIONE 14: Alberi binari: introduzione Lezione 14 - Modulo 1 Modulo 1: Definizioni e proprietà Modulo 2: Attraversamento degli alberi binari Definizioni e proprietà Politecnico
Informatica 3 Informatica 3 LEZIONE 14: Alberi binari: introduzione Lezione 14 - Modulo 1 Modulo 1: Definizioni e proprietà Modulo 2: Attraversamento degli alberi binari Definizioni e proprietà Politecnico
Organigramma Gerarchia. (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre
 Alberi Struttura dati Albero Organigramma Gerarchia (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre Esempio di un organigramma di un azienda Tree terminology
Alberi Struttura dati Albero Organigramma Gerarchia (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre Esempio di un organigramma di un azienda Tree terminology
Alberi binari ( 7.3)
 Alberi binari ( 7.3) + a 3 b Albero Binario ( 7.3) DEFINIZIONE Albero Binario è un albero ordinato in cui ogni nodo ha al più due figli. Un albero binario si dice proprio se ogni nodo ha o zero o figli
Alberi binari ( 7.3) + a 3 b Albero Binario ( 7.3) DEFINIZIONE Albero Binario è un albero ordinato in cui ogni nodo ha al più due figli. Un albero binario si dice proprio se ogni nodo ha o zero o figli
Alberi di ricerca binari
 Fulvio Corno, Matteo Sonza Reorda Dip. Automatica e Informatica Politecnico di Torino Introduzione Gli alberi di ricerca binari (Binary Search Tree, o BST) sono una struttura di dati che supporta in modo
Fulvio Corno, Matteo Sonza Reorda Dip. Automatica e Informatica Politecnico di Torino Introduzione Gli alberi di ricerca binari (Binary Search Tree, o BST) sono una struttura di dati che supporta in modo
Lezione 7 Alberi binari: visite e alberi di ricerca
 Lezione 7 Alberi binari: visite e alberi di ricerca Informatica 6 Maggio 2015 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per
Lezione 7 Alberi binari: visite e alberi di ricerca Informatica 6 Maggio 2015 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per
Ordinamento per inserzione e per fusione
 Ordinamento per inserzione e per fusione Alessio Orlandi 15 marzo 2010 Fusione: problema Problema Siano A e B due array di n A e n B interi rispettivamente. Si supponga che A e B siano ordinati in modo
Ordinamento per inserzione e per fusione Alessio Orlandi 15 marzo 2010 Fusione: problema Problema Siano A e B due array di n A e n B interi rispettivamente. Si supponga che A e B siano ordinati in modo
Esercitazione. Ricorsione. May 31, Esercizi presi dal libro di Rosen
 Esercitazione Ricorsione May 31, 2016 Esercizi presi dal libro di Rosen Problema 2 a) sezione 5.3 Data la seguente funzione definita ricorsivamente come: f(n+1) = 2f(n) f(0) = 3 Determinare il valore di
Esercitazione Ricorsione May 31, 2016 Esercizi presi dal libro di Rosen Problema 2 a) sezione 5.3 Data la seguente funzione definita ricorsivamente come: f(n+1) = 2f(n) f(0) = 3 Determinare il valore di
Albero binario. Alberi binari (introduzione) Terminologia. Alberi di ricerca binaria (BST)
 Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
Algoritmi e Strutture Dati Laboratorio 15/12/2008. Daniele Loiacono
 Algoritmi e Strutture Dati Laboratorio 15/12/2008 Problema della compressione Rappresentare i dati in modo efficiente Impiegare il numero minore di bit per la rappresentazione Goal: risparmio spazio su
Algoritmi e Strutture Dati Laboratorio 15/12/2008 Problema della compressione Rappresentare i dati in modo efficiente Impiegare il numero minore di bit per la rappresentazione Goal: risparmio spazio su
Algoritmi e Strutture Dati. Capitolo 4 Ordinamento: Selection e Insertion Sort
 Algoritmi e Strutture Dati Capitolo 4 Ordinamento: Selection e Insertion Sort Ordinamento Dato un insieme S di n elementi presi da un dominio totalmente ordinato, ordinare S in ordine non crescente o non
Algoritmi e Strutture Dati Capitolo 4 Ordinamento: Selection e Insertion Sort Ordinamento Dato un insieme S di n elementi presi da un dominio totalmente ordinato, ordinare S in ordine non crescente o non
 Da libro di testo Cormen et al. CAP 21: par 21.1, 21.2, 21.3 pagg. 468-477 Strutture dati per insiemi disgiunti Una struttura dati per insiemi disgiunti mantiene una collezione S={S 1,S 2,,S k } di insiemi
Da libro di testo Cormen et al. CAP 21: par 21.1, 21.2, 21.3 pagg. 468-477 Strutture dati per insiemi disgiunti Una struttura dati per insiemi disgiunti mantiene una collezione S={S 1,S 2,,S k } di insiemi
Esercitazione 6. Alberi binari di ricerca
 Esercitazione 6 Alberi binari di ricerca Struttura base Rappresentabile attraverso una struttura dati concatenata in cui ogni nodo è un oggetto di tipo struttura Ogni nodo contiene: campo chiave (key)
Esercitazione 6 Alberi binari di ricerca Struttura base Rappresentabile attraverso una struttura dati concatenata in cui ogni nodo è un oggetto di tipo struttura Ogni nodo contiene: campo chiave (key)
Il Branch & Bound. Definizione 1. Sia S R n. La famiglia S = {S 1, S 2,..., S k S} tale che S 1 S 2 S k = S viene detta suddivisione di S.
 Il Branch & Bound Il metodo Branch & Bound è una tecnica che permette di risolvere all ottimo un generico problema di Programmazione Lineare Intera. Tale metodo si basa su due concetti cardine: quello
Il Branch & Bound Il metodo Branch & Bound è una tecnica che permette di risolvere all ottimo un generico problema di Programmazione Lineare Intera. Tale metodo si basa su due concetti cardine: quello
Algoritmi (9 CFU) (A.A ) Heap e Algoritmo HeapSort. Prof. V. Cutello Algoritmi 1
 Algoritmi (9 CFU) (A.A. 2009-10) Heap e Algoritmo HeapSort. Prof. V. Cutello Algoritmi 1 Overview Definiamo la struttura dati heap Operazioni di costruzione e gestione di un heap Algoritmo Heapsort Code
Algoritmi (9 CFU) (A.A. 2009-10) Heap e Algoritmo HeapSort. Prof. V. Cutello Algoritmi 1 Overview Definiamo la struttura dati heap Operazioni di costruzione e gestione di un heap Algoritmo Heapsort Code
In questa lezione Alberi binari di ricerca: la cancellazione
 In questa leione Alberi binari di ricerca: la cancellaione 1 L algoritmo di Hibbard per cancellare (1962) Sia il nodo da cancellare: 1) è una foglia: si rimuove 2) ha un solo figlio x: si rende x figlio
In questa leione Alberi binari di ricerca: la cancellaione 1 L algoritmo di Hibbard per cancellare (1962) Sia il nodo da cancellare: 1) è una foglia: si rimuove 2) ha un solo figlio x: si rende x figlio
PROVETTE D ESAME. Algoritmi e Strutture Dati
 PROVETTE D ESAME Algoritmi e Strutture Dati ESERCIZIO 1 Si ottengano limiti superiori e inferiori per la seguente ricorrenza ESERCIZIO 1 ESERCIZIO 2 Dato un albero binario T, il grado di sbilanciamento
PROVETTE D ESAME Algoritmi e Strutture Dati ESERCIZIO 1 Si ottengano limiti superiori e inferiori per la seguente ricorrenza ESERCIZIO 1 ESERCIZIO 2 Dato un albero binario T, il grado di sbilanciamento
alberi tipo astratto, implementazione, algoritmi
 alberi tipo astratto, implementazione, algoritmi argomenti tipo astratto albero definizione implementazione in Java algoritmi di visita alberi binari implementazione di alberi binari in Java ASD - Alberi
alberi tipo astratto, implementazione, algoritmi argomenti tipo astratto albero definizione implementazione in Java algoritmi di visita alberi binari implementazione di alberi binari in Java ASD - Alberi
Algoritmi e Strutture Dati. Alberi
 Algoritmi e Strutture Dati Alberi Alberto Montresor Università di Trento 2017/10/19 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1 Introduzione
Algoritmi e Strutture Dati Alberi Alberto Montresor Università di Trento 2017/10/19 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1 Introduzione
Esercizi di Algoritmi e Strutture Dati
 Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 29 novembre 2010 1 Rotazioni semplici in ABR Si consideri l operazione di rotazione semplice applicata
Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 29 novembre 2010 1 Rotazioni semplici in ABR Si consideri l operazione di rotazione semplice applicata
Algoritmi e strutture di dati 2
 Algoritmi e strutture di dati 2 Paola Vocca Lezione 1: Divide et Impera 1 Paradigma del divide et impera Strutturato in tre fasi. Sia Π() istanza di dimensione di un problema computazionale Π (dove è immediato
Algoritmi e strutture di dati 2 Paola Vocca Lezione 1: Divide et Impera 1 Paradigma del divide et impera Strutturato in tre fasi. Sia Π() istanza di dimensione di un problema computazionale Π (dove è immediato
Heap e code di priorità
 Heap e code di priorità Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica AA 2009/2010
Heap e code di priorità Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica AA 2009/2010
Laboratorio di Python
 Laboratorio di Python Alberi binari Lab15 12 Maggio 2017 Outline Correzione esercizi per oggi Alberi binari Teoria Esercizi Esercizi per casa Saluti Esercizio 1 per casa Scrivere una funzione palindroma(s)
Laboratorio di Python Alberi binari Lab15 12 Maggio 2017 Outline Correzione esercizi per oggi Alberi binari Teoria Esercizi Esercizi per casa Saluti Esercizio 1 per casa Scrivere una funzione palindroma(s)
Il TDA Tree. Alberi. Esempio. Alberi. Applicazioni. Definizione di albero
 Il T Tree lberi In informatica, un albero è un modello astratto di una struttura dati gerarchica Struttura dati non lineare Si pensi al file system di un sistema operativo Le relazioni in un albero sono
Il T Tree lberi In informatica, un albero è un modello astratto di una struttura dati gerarchica Struttura dati non lineare Si pensi al file system di un sistema operativo Le relazioni in un albero sono
Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi
 Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore
Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore
Algoritmi greedy. Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione
 Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione Gli algoritmi greedy sono algoritmi basati sull idea
Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione Gli algoritmi greedy sono algoritmi basati sull idea
Visite di alberi binari. Laboratorio di Algoritmi e Strutture Dati
 Visite di alberi binari Laboratorio di Algoritmi e Strutture Dati Visita di Alberi Gli alberi possono essere visitati (o attraversati) in diversi modi: Visita in Preordine: prima si visita il nodo e poi
Visite di alberi binari Laboratorio di Algoritmi e Strutture Dati Visita di Alberi Gli alberi possono essere visitati (o attraversati) in diversi modi: Visita in Preordine: prima si visita il nodo e poi
Informatica 3. Informatica 3. LEZIONE 17: Alberi generici. Lezione 17 - Modulo 1. Introduzione. ADT dell albero generico.
 Informatica 3 Informatica 3 LEZIONE 17: lberi generici Lezione 17 - Modulo 1 Modulo 1: Definizione e DT Modulo 2: Implementazione Modulo 3: lberi e classi di equivalenza Definizione e DT Politecnico di
Informatica 3 Informatica 3 LEZIONE 17: lberi generici Lezione 17 - Modulo 1 Modulo 1: Definizione e DT Modulo 2: Implementazione Modulo 3: lberi e classi di equivalenza Definizione e DT Politecnico di
Un esempio: l ADT Dizionario (mutabile) Definizione. Alberi binari di ricerca (BST = binary search tree) search(chiave k) -> elem
 Un esempio: l ADT Dizionario (mutabile) Algoritmi e Laboratorio a.a. 2006-07 Lezioni Gli alberi di ricerca sono usati per realizzare in modo efficiente il tipo di dato astratto dizionario Parte 19-D Alberi
Un esempio: l ADT Dizionario (mutabile) Algoritmi e Laboratorio a.a. 2006-07 Lezioni Gli alberi di ricerca sono usati per realizzare in modo efficiente il tipo di dato astratto dizionario Parte 19-D Alberi
Laboratorio di Programmazione II Corso di Laurea in Bioinformatica Dipartimento di Informatica - Università di Verona
 Laboratorio di Programmazione II Corso di Laurea in Bioinformatica Dipartimento di Informatica - Università di Verona Sommario Implementazione con Vettori Implementazione con Strutture Collegate Concetti
Laboratorio di Programmazione II Corso di Laurea in Bioinformatica Dipartimento di Informatica - Università di Verona Sommario Implementazione con Vettori Implementazione con Strutture Collegate Concetti
Analisi algoritmi ricorsivi e relazioni di ricorrenza
 Analisi algoritmi ricorsivi e relazioni di ricorrenza Punto della situazione Finora abbiamo affrontato: il tempo di esecuzione di un algoritmo, l analisi asintotica con le notazioni asintotiche e la tecnica
Analisi algoritmi ricorsivi e relazioni di ricorrenza Punto della situazione Finora abbiamo affrontato: il tempo di esecuzione di un algoritmo, l analisi asintotica con le notazioni asintotiche e la tecnica
Introduzione agli algoritmi Prova di esame del 30/6/2016 Prof.sse E. Fachini - R. Petreschi
 B Introduzione agli algoritmi Prova di esame del 30/6/2016 Prof.sse E. Fachini - R. Petreschi Si consideri l operazione di inserimento in un AVL. Si supponga di trovarsi nel caso in cui una rotazione a
B Introduzione agli algoritmi Prova di esame del 30/6/2016 Prof.sse E. Fachini - R. Petreschi Si consideri l operazione di inserimento in un AVL. Si supponga di trovarsi nel caso in cui una rotazione a
Alberi Binari di Ricerca
 Alberi Binari di Ricerca Prof. G. M. Farinella gfarinella@dmi.unict.it www.dmi.unict.it/farinella Riferimenti Bibliografici Cormen T.H., Leiserson C.E., Rivest R.L Introduction to Algorithms, Third Edition,
Alberi Binari di Ricerca Prof. G. M. Farinella gfarinella@dmi.unict.it www.dmi.unict.it/farinella Riferimenti Bibliografici Cormen T.H., Leiserson C.E., Rivest R.L Introduction to Algorithms, Third Edition,
Union-find. Insiemi disgiunti. F. Damiani - Alg. & Lab. 04/05 (da C. Demetrescu et al - McGraw-Hill)
 Union-find Insiemi disgiunti Il problema Union-find Mantenere una collezione di insiemi disgiunti di elementi distinti (interi in 1 n) durante una sequenza delle seguenti operazioni: union(a,b) = unisce
Union-find Insiemi disgiunti Il problema Union-find Mantenere una collezione di insiemi disgiunti di elementi distinti (interi in 1 n) durante una sequenza delle seguenti operazioni: union(a,b) = unisce
ricerca di un elemento, verifica dell appartenenza di un elemento
 Alberi Binari di Ricerca Gli alberi binari di ricerca (o, alberi di ricerca binaria) sono strutture dati che consentono, su un insieme di elementi con un ordine totale le operazioni di: ricerca di un elemento,
Alberi Binari di Ricerca Gli alberi binari di ricerca (o, alberi di ricerca binaria) sono strutture dati che consentono, su un insieme di elementi con un ordine totale le operazioni di: ricerca di un elemento,
In questa lezione Strutture dati elementari: Pila Coda
 In questa lezione Strutture dati elementari: Pila Coda 1 strutture dati (astratte) Una struttura dati astratti consiste di uno o più insiemi con delle operazioni che li modificano (insiemi dinamici). Le
In questa lezione Strutture dati elementari: Pila Coda 1 strutture dati (astratte) Una struttura dati astratti consiste di uno o più insiemi con delle operazioni che li modificano (insiemi dinamici). Le
3.4 Metodo di Branch and Bound
 3.4 Metodo di Branch and Bound Consideriamo un generico problema di Ottimizzazione Discreta dove X è la regione ammissibile. (P ) z = max{c(x) : x X} Metodologia generale di enumerazione implicita (Land
3.4 Metodo di Branch and Bound Consideriamo un generico problema di Ottimizzazione Discreta dove X è la regione ammissibile. (P ) z = max{c(x) : x X} Metodologia generale di enumerazione implicita (Land
ALGORITMI CORSO DI STUDIO IN INFORMATICA (laurea triennale) UNIVERSITÀ DEGLI STUDI DI CATANIA ANNO ACCADEMICO 2014/15
 ANNO ACCADEMICO 2014/15 1 a prova in itinere 13 gennaio 2015 ESERCIZIO 1 Si risolva l equazione di ricorrenza al variare del parametro reale a>1. T (n) = 27 n a T + n 2 log n a ESERCIZIO 2 Si ordinino
ANNO ACCADEMICO 2014/15 1 a prova in itinere 13 gennaio 2015 ESERCIZIO 1 Si risolva l equazione di ricorrenza al variare del parametro reale a>1. T (n) = 27 n a T + n 2 log n a ESERCIZIO 2 Si ordinino
Alberi. Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo. Fosco.
 Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Un algoritmo realizza una relazione funzionale tra i valori di input e quelli di output
 Un algoritmo realizza una relazione funzionale tra i valori di input e quelli di output F = { (s, s ) } per ogni s esiste una e una sola coppia (s, s ). Esempio: un algoritmo che calcola il quadrato di
Un algoritmo realizza una relazione funzionale tra i valori di input e quelli di output F = { (s, s ) } per ogni s esiste una e una sola coppia (s, s ). Esempio: un algoritmo che calcola il quadrato di
TRIE (albero digitale di ricerca)
 TRIE (albero digitale di ricerca) Struttura dati impiegata per memorizzare un insieme S di n stringhe (il vocabolario V). Tabelle hash le operazioni di dizionario hanno costo O(m) al caso medio per una
TRIE (albero digitale di ricerca) Struttura dati impiegata per memorizzare un insieme S di n stringhe (il vocabolario V). Tabelle hash le operazioni di dizionario hanno costo O(m) al caso medio per una
Il tipo astratto coda con priorità: specifiche sintattiche e semantiche. Realizzazioni.
 Il tipo astratto coda con priorità: specifiche sintattiche e semantiche. Realizzazioni. Algoritmi e Strutture Dati + Lab A.A. 14/15 Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro
Il tipo astratto coda con priorità: specifiche sintattiche e semantiche. Realizzazioni. Algoritmi e Strutture Dati + Lab A.A. 14/15 Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 1 Un introduzione informale agli algoritmi Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Definizione informale di algoritmo Insieme di istruzioni, definite
Algoritmi e Strutture Dati Capitolo 1 Un introduzione informale agli algoritmi Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Definizione informale di algoritmo Insieme di istruzioni, definite
