TESTI E SOLUZIONI DEI PROBLEMI
|
|
|
- Abele Cornelio Bassi
- 6 anni fa
- Visualizzazioni
Transcript
1 Univerità degli Studi di Udine, Coro di Laurea in Ingegneria Meccanica A.A. 217/218, Seione di Giugno/Luglio 218, Secondo Appello Eame di FISICA I, Prova critta del 2 Luglio 218 TESTI E SOLUZIONI DEI PROBLEMI PROBLEMA A1 Un veicolo i maa M = 5 kg che i muove in un tratto di trada orizzontale e rettilineo riente, oltre alla pinta F del motore, di una forza reitente (riultante dell attrito con l afalto e della reitenza dell aria) di ampiezza R = R +kv 2, dove v è la velocità itantanea dell auto, R = 15 N e k = 1.5 N 2 /m 2. Nel cao in cui il veicolo i muova di moto uniforme con velocità V = 1 km/h: a) determinare la potenza viluppata dal motore. Invece, nel cao in cui il veicolo, partendo da fermo, i muova di moto uniformemente accelerato con a = 5. m/ 2 per un intervallo di tempo t = 1., calcolare: b) la velocità finale raggiunta dal veicolo; c) l energia W pea dal motore durante tutta l accelerazione. Soluzione Quando il veicolo i muove a velocità cotante, eendo l accelerazione nulla, dovrà eere nulla anche riultante delle forze che agice u di eo. Quindi la pinta del motore F bilancerà la forza reitente e i avrà F = R +kv 2 La potenza viluppata dal motore corriponde alla potenza meccanica aociata alla forza F pari a P = FV = (R +kv 2 )V = W = 36.3 kw. Nel cao di moto uniformemente accelerato con accelerazione a, la velocità varia econdo la legge v(t) = at e quindi nell intervallo di tempo indicato la velocità raggiunta dal veicolo è Dalla 2 a legge della dinamica egue che v f = a t = 5. m/ = 18 km/h. Ma = F R = F R kv 2 F = F(t) = Ma+R +kv 2 = Ma+R +ka 2 t 2, e queto dimotra che in tal cao la pinta del motore non è cotante. Anche la potenza itantanea viluppata dal motore dipende dal tempo ed è pari a P(t) = F(t) v(t) = (Ma+R +ka 2 t 2 )at = (Ma+R )at+ka 3 t 3. Dalla definizione della potenza meccanica egue che l energia pea dal motore dell intervallo di tempo dt è pari a dw = P(t)dt e coneguentemente, l energia pea dal motore nell intera accelerazione i ottiene come egue W = t P(t)dt = (Ma+R )a t tdt+ka 3 t t 3 dt = (Ma+R )a t2 2 +ka3 t4 4 = J. PROBLEMA A2Uncorpodimaam = 1.kgèagganciato tramiteunacordaideale(inetenibile edi maatracurabile) all ae di uncilindroomogeneo di maam = 15. kg eraggio R (vedi figura); entrambi poggiano u dei piani orizzontali. Intorno al cilindro è avvolta una econda corda ideale il cui capo detro (vedi figura) è tirato con una forza F F F. Il corpo di maa m riente di attrito con il piano di appoggio caratterizzato dai coefficienti µ =.8 e µ k =.5. Sapendo che la corda avvolta intorno al cilindro non litta mai e che anche il cilindro non litta mai ripetto al piano di appoggio, determinare: a) il modulo di F F F, Fmin, al di opra del quale il itema non è più in equilibrio tatico;
2 b) l accelerazione del corpo di maa m nel cao in cui il modulo di F F F è pari a 3Fmin ; c) il minimo valore del coefficiente di attrito tra cilindro e piano di appoggio, µ,min, neceario affinché il cilindro poa (effettivamente) non littare. m M R F F F Soluzione Il itema arà in equilibrio tatico fino a quando ogni ingolo corpo lo arà. A tale copo coniderando un ae x orizzontale vero initra e applicando la 2 a legge della dinamica nelle forme lineare (per il corpo di maa m) e angolare (per il cilindro ripetto all ae paante per il punto di contatto con il piano di appoggio) dovranno valere le eguenti { = T f = 2RF RT, dove f è la forza di attrito tatico che agice ul corpo di maa m e T è la tenione della corda di initra. 1 Eliminando T tra le due relazioni abbiamo Ma per la forza di attrito tatico vale la eguente 2RF Rf = F = f 2. f f,max con f,max = µ N m = µ mg, e pertanto, dovrà eere F F min = 1 2 µ mg = 39.2 N. Quando il modulo dif upera Fmin il itema non arà più in equilibrio e l applicazione della 2 a legge della dinamica nelle forme lineare e angolare porterà alle eguenti ma = T f k = T µ k mg, I P α = 2RF RT dove ora a e α ono è l accelerazione lineare di m e l accelerazione angolare del cilindro. D altra parte, f k = µ k mg è la forza di attrito dinamico agente u m e I P è il momento d inerzia del cilindro ripetto all ae paante per il punto di itantaneo contatto. Oervando che il cilindro egue un moto di puro rotolamento vero detra e e indichiamo con a cm l accelerazione del uo centro di maa, poiamo crivere le eguenti { α = acm /R a = a cm α = a R. Quindi, eliminando T tra le due precedenti equazioni (dalla prima i ha T = ma+µ k mg e i otituice nella econda), i ottiene I P a R = 2RF Rma µ krmg, dalla quale i ricava a = R2 (2F µ k mg) I P +mr 2. 1 Si noti che eendo le corde ideali e prive di maa, la tenione della corda di detra arà empre, indipendentemente dal uo moto, pari al modulo di F F F.
3 Notando che per il momento d inerzia I P abbiamo (dal teorema degli ai paralleli) I P = I cm +MR 2 = 1 2 MR2 +MR 2 = 3 2 MR2, e ponendo F = 3F min = 3 2 µ mg, l accelerazione del corpo di maa m diventa a = 2(3µ µ k )mg 3M +2m = 5.73 m/2. Per valutare il coefficiente di attrito tatico relativo al contatto tra cilindro e relativo piano di appoggio dobbiamo calcolare la corripondente forza di attrito tatico f (cil). Avendo già calcolato a, i può procedere in vari modi: ad eempio, upponendo f (cil) diretta vero detra e applicando la 2 a legge in forma lineare al moto del cilindro teo, i ottiene Ma cm = F T +f,cil f (cil) = Ma cm F +T = Ma F +ma+µ k mg = (M +m)a F +µ k mg. Sotituendo F = 3F min = 3 2 µ mg e facendo il calcolo utilizzando il valore numerico di a, i ottiene ( ) 3 f (cil) = (M +m)a 2 µ µ k mg = 74.6 N Quindi, dovendo eere f (cil) f,max (cil) = µ (cil) N M = µ (cil) Mg, i ha µ (cil),min = f(cil) µ (cil) Mg =.57. PROBLEMA A3 Ad un ga ideale biatomico viene fatto eguire il ciclo reveribile chematizzato in figura cotituito da un epanione iobara (1 2), un epanione adiabatica (2 3) e una compreione ioterma (3 1). Preione e volume dello tato 1 ono p 1 = 3. atm e = 3. dm 3 ; nello tato 3 il volume del ga è V 3 = 4. Sapendo che il numero di moli di ga è n = 3. mol, determinare: a) la temperatura T 2 e il volume V 2 dello tato 2; b) il lavoro L prodotto dal ga nell intero ciclo; c) il rendimento η del ciclo. Il lavoro L prodotto dal ciclo (quello calcolato al punto b)) viene p 1 2 utilizzato per comprimere un numero di moli n (identico a quello menzionato in precedenza) di un econdo ga ideale lungo unatraformazione politropica (pv k = cot.) con k = 3. Sapendola preione e il volume dello tato iniziale di tale ga ono identici a quello dello tato 1 del primoga, determinare: d) la ua temperatura T f alla fine della compreione. Soluzione Prima di tutto i noti che è T 1 = p 1 = 365 K. Dato lo tato 2 appartiene ia all iobara 1 2 che all adiabatica 2 3 devono valere le eguenti 3 V V 2 T 2 = T 1 ; T 2 V γ 1 2 = T 3 V γ 1 3. Combinandoquete duerelazioni e notandoche T 3 = T 1 (dato che gli tati 1 e 3 giacciono ull ioterma 3 1) e V 3 = 4, i ha V 2 = γ ; T 2 = p 1V 2 = 1 41 γ T 1,
4 dove γ è l eponente delle adiabatiche che, eendo il ga biatomico, è pari a 7/5. otituendo abbiamo V 2 = 4 2/7 = 44.6 dm 3 ; T 2 = 4 2/7 T 1 = 543 K. Il lavoro L compiuto dal ga e il calore Q cambiato dallo teo nell intero ciclo ono uguali. Pertanto potremo crivere L = Q 12 +Q 31, dove i è già tenuto conto del fatto che nella traformazione 2 3 il calore cambiato è nullo. Quindi, tenendo preente la natura iobara e ioterma delle traformazioni 1 2 e 3 1, i ha e Q 31 = L 31 = 1 Pertanto il lavoro totale è 3 Q 12 = nc p (T 2 T 1 ) = n 7 ) (4 2 R 2/7 1 T 1 = J, pdv = T 1 V1 V 3 dv V = T 1ln ( V1 [ 7 ( ) ] L = 4 2/7 1 ln4 T 1 = J. 2 V 3 ) = T 1 ln4 = J. Nel ciclo, il calore viene aorbito olo nella traformazione iobara 1 2. Pertanto il rendimento del ciclo è η = L = Q 12 +Q 31 = 1+ Q 31 2ln4 = 1 Q a Q 12 Q 12 7 ( 4 2/7 1 ) =.185. Se il lavoro L viene utilizzato per comprimere il econdo ga lungo una politropica con eponente k = 3 allora il lavoro compiuto da tale ga dovrà eere pari a L. In altre parole, eendo lo tato iniziale di tale ga identico a quello del primo, indicando con p f, V f e T f la preione, il volume e la temperatura di tale ga alla fine della compreione, dovremo avere Per la politropica l integrale è pari a Vf Vf pdv = L. pdv = 1 1 k (p fv f p 1 ) = 1 k (T f T 1 ), dove, nell ultimo paaggio, i è fatto uo della legge dei ga ideali. Perciò, dall ugualianza precedente i ottiene 1 k (T f T 1 ) = L T f = T 1 + (k 1)L = 594 K. PROBLEMA B1 Un veicolo i maa M = 8 kg che i muove in un tratto di trada orizzontale e rettilineo riente, oltre alla pinta F del motore, di una forza reitente (riultante dell attrito con l afalto e della reitenza dell aria) di ampiezza R = R +kv 2, dove v è la velocità itantanea dell auto, R = 25 N e k = 2. N 2 /m 2. Nel cao in cui il veicolo i muova di moto uniforme con velocità V = 13 km/h: a) determinare la potenza viluppata dal motore. Invece, nel cao in cui il veicolo, partendo da fermo, i muova di moto uniformemente accelerato con a = 3. m/ 2 per un intervallo di tempo t = 15., calcolare: b) la velocità finale raggiunta dal veicolo; c) l energia W pea dal motore durante tutta l accelerazione.
5 Soluzione Quando il veicolo i muove a velocità cotante, eendo l accelerazione nulla, dovrà eere nulla anche riultante delle forze che agice u di eo. Quindi la pinta del motore F bilancerà la forza reitente e i avrà F = R +kv 2 La potenza viluppata dal motore corriponde alla potenza meccanica aociata alla forza F pari a P = FV = (R +kv 2 )V = W = 13 kw. Nel cao di moto uniformemente accelerato con accelerazione a, la velocità varia econdo la legge v(t) = at e quindi nell intervallo di tempo indicato la velocità raggiunta dal veicolo è Dalla 2 a legge della dinamica egue che v f = a t = 45. m/ = 162 km/h. Ma = F R = F R kv 2 F = F(t) = Ma+R +kv 2 = Ma+R +ka 2 t 2, e queto dimotra che in tal cao la pinta del motore non è cotante. Anche la potenza itantanea viluppata dal motore dipende dal tempo ed è pari a P(t) = F(t) v(t) = (Ma+R +ka 2 t 2 )at = (Ma+R )at+ka 3 t 3. Dalla definizione della potenza meccanica egue che l energia pea dal motore dell intervallo di tempo dt è pari a dw = P(t)dt e coneguentemente, l energia pea dal motore nell intera accelerazione i ottiene come egue W = t P(t)dt = (Ma+R )a t tdt+ka 3 t t 3 dt = (Ma+R )a t2 2 +ka3 t4 4 = J. PROBLEMA B2 Intorno ad un cilindro omogeneo di maa M = 2. kg e raggio R è avvolta una corda ideale (inetenibile e di maa tracurabile) e al capo libero della tea è agganciato un corpo di maa m = 15. kg (vedi figura); entrambi poggiano u dei piani orizzontali. All ae del cilindro è agganciata una econda corda ideale il cui capo detro (vedi figura) è tirato con una forza F F F. Il corpo di maa m riente di attrito con il piano di appoggio caratterizzato dai coefficienti µ =.7 e µ k =.4. Sapendo che la corda avvolta intorno al cilindro non litta mai e che anche il cilindro non litta mai ripetto al piano di appoggio, determinare: a) il modulo di F F F, Fmin, al di opra del quale il itema non è più in equilibrio tatico; b) l accelerazione del centro di maa del cilindro, a cm, nel cao in cui il modulo di F F F è pari a 2Fmin ; c) il minimo valore del coefficiente di attrito tra cilindro e piano di appoggio, µ,min, neceario affinché il cilindro poa (effettivamente) non littare. m M R F Soluzione Il itema arà in equilibrio tatico fino a quando ogni ingolo corpo lo arà. A tale copo coniderando un ae x orizzontale vero initra e applicando la 2 a legge della dinamica nelle forme lineare (per il corpo di maa m) e angolare (per il cilindro ripetto all ae paante per il punto di contatto con il piano di appoggio) dovranno valere le eguenti { = T f = RF 2RT,
6 dove f è la forza di attrito tatico che agice ul corpo di maa m e T è la tenione della corda di initra. 2 Eliminando T tra le due equazioni abbiamo Ma per la forza di attrito tatico vale la eguente e pertanto, dovrà eere RF 2Rf = F = 2f. f f,max con f,max = µ N m = µ mg, F F min = 2µ mg = 26 N. Quando il modulo dif upera Fmin il itema non arà più in equilibrio e l applicazione della 2 a legge della dinamica nelle forme lineare e angolare porterà alle eguenti ma = T f k = T µ k mg, I P α = RF 2RT dove ora a e α ono l accelerazione lineare di m e l accelerazione angolare del cilindro, ripettivamente. D altra parte, f k = µ k mg è la forza di attrito dinamico agente u m e I P è il momento d inerzia del cilindro ripetto all ae paante per il punto di itantaneo contatto. Oervando che il cilindro egue un moto di puro rotolamento vero detra e e indichiamo con a cm l accelerazione del uo centro di maa, poiamo crivere le eguenti { α = acm /R a = 2a cm α = a 2R. Quindi, eliminando T tra le due precedenti equazioni (dalla prima i ha T = ma+µ k mg e i otituice nella econda) e facendo la otituzione a = 2a cm, i ottiene dalla quale i ricava I P a cm R = RF 4Rma cm 2µ k Rmg, a cm = R2 (F 2µ k mg) I P +4mR 2. Notando che per il momento d inerzia I P abbiamo (dal teorema degli ai paralleli) I P = I cm +MR 2 = 1 2 MR2 +MR 2 = 3 2 MR2, e ponendo F = 2F min = 4µ mg, l accelerazione del centro di maa del cilindro diventa a cm = 4(2µ µ k )mg 3M +8m = 3.27 m/2. Per valutare il coefficiente di attrito tatico relativo al contatto tra cilindro e relativo piano di appoggio dobbiamo calcolare la corripondente forza di attrito tatico f (cil). Avendo già calcolato a cm, i può procedere in vari modi: ad eempio, upponendo f (cil) diretta vero detra e applicando la 2 a legge in forma lineare al moto del cilindro teo, i ottiene Ma cm = F T +f,cil f (cil) = Ma cm F +T = Ma cm F +2ma cm +µ k mg = (M +2m)a cm F +µ k mg. 2 Si noti che eendo le corde ideali e prive di maa, la tenione della corda di detra arà empre, indipendentemente dal moto, pari al modulo di F F F.
7 Sotituendo F = 2F min = 4µ mg e facendo il calcolo utilizzando il valore numerico di a cm, i ottiene f (cil) = (M +2m)a cm (4µ µ k )mg = 19 N, dove il egno negativo ci egnala che f (cil) è diretta in vero oppoto a quanto coniderato (è diretta vero initra. Quindi, dovendo eere f (cil) f,max (cil) = µ (cil) N m = µ (cil) Mg, i ha µ (cil),min = f(cil) µ (cil) Mg =.967. PROBLEMA B3 Ad un ga ideale poliatomico viene fatto eguire il ciclo reveribile p chematizzato in figura cotituito da un epanione ioterma (1 2), 1 unaiocora(2 3)eunacompreioneadiabatica(3 1). Preione e volume dello tato 1ono p 1 = 4. atm e = 5. dm 3 ; nello tato 2 la preione del ga è p 2 = p 1 /2. Sapendo che il numero di moli di ga è n = 6. mol, determinare: 2 a) la temperatura T 3 e la preione p 3 dello tato 3; 3 b) il lavoro L prodotto dal ga nell intero ciclo; c) il rendimento η del ciclo. V Il lavoro L prodotto dal ciclo (quello calcolato al punto b)) viene utilizzato per comprimere un numero di moli n (identico a quello menzionato in precedenza) di un econdo ga ideale lungo unatraformazione politropica (pv k = cot.) con k = 2. Sapendola preione e il volume dello tato iniziale di tale ga ono identici a quello dello tato 1 del primo ga, determinare d) la ua temperatura T f alla fine della compreione. Soluzione Prima di tutto i noti che è T 1 = p 1 Dato che lo tato 2 giace ulla ioterma 1 2 allora è = 46 K. p 2 V 2 = p 1 V 2 V 3 = p 1 p 2 = 2 = 1 dm 3. Quindi, dato che gli tati 3 e 1 giacciono ull adiabatica 3 1 ( ) γ p 3 V γ 3 = p 1V γ V1 1 p 3 = p 1 = 2 γ p 1, e T 3 V γ 1 3 = T 1 V γ 1 1 T 3 = V 3 ( V1 V 3 ) γ 1 T 1 = 2 1 γ T 1, dove γ è l eponente delle adiabatiche che, eendo il ga poliatomico, è pari a 4/3. Sotituendo abbiamo p 3 = 2 4/3 p 1 = 1.58 atm; T 3 = 2 1/3 T 1 = 322 K. Il lavoro L compiuto dal ga e il calore Q cambiato dallo teo nell intero ciclo ono uguali. Pertanto potremo crivere L = Q 12 +Q 23, dove i è già tenuto conto del fatto che nella traformazione 3 1 il calore cambiato è nullo. Quindi, tenendo preente la natura ioterma e iocora delle traformazioni 1 2 e 2 3, i ha 2 V2 ( ) dv Q 12 = L 12 = pdv = T 1 V = T V2 1ln = T 1 ln2 = J. 1
8 e ( Q 23 = nc V (T 3 T 2 ) nc V (T 3 T 1 ) = n3r 1 2 1/3) T 1 = J, Pertanto il lavoro totale è [ ( L = ln /3)] T 1 = J. Nel ciclo, il calore viene aorbito olo nella traformazione ioterma 1 2. Pertanto il rendimento del ciclo è η = L = Q 12 +Q 23 = 1+ Q 23 = 1 3 ( 1 2 1/3 ) =.17. Q a Q 12 Q 12 ln2 Se il lavoro L viene utilizzato per comprimere il econdo ga lungo una politropica con eponente k = 2 allora il lavoro compiuto da tale ga dovrà eere pari a L. In altre parole, eendo lo tato iniziale di tale ga identico a quello del primo, indicando con p f, V f e T f la preione, il volume e la temperatura di tale ga alla fine della compreione, dovremo avere Per la politropica l integrale è pari a Vf Vf pdv = L. pdv = 1 1 k (p fv f p 1 ) = 1 k (T f T 1 ), dove, nell ultimo paaggio, i è fatto uo della legge dei ga ideali. Perciò, dall ugualianza precedente i ottiene 1 k (T f T 1 ) = L T f = T 1 + (k 1)L = 436 K.
Traiettoria La traiettoria è la linea che unisce le posizioni successive occupate dal punto materiale in movimento. Sistema di riferimento
 Punto materiale Quando l oggetto in movimento è molto piccolo ripetto alla ditanza che percorre, può eere tudiato come e foe un punto (non ha dimenioni, non ha un orientamento). Traiettoria La traiettoria
Punto materiale Quando l oggetto in movimento è molto piccolo ripetto alla ditanza che percorre, può eere tudiato come e foe un punto (non ha dimenioni, non ha un orientamento). Traiettoria La traiettoria
RACCOLTA DI ESERCIZI TRATTI DA TEMI D ESAME - parte 1^
 A.A. 2005/2006 Sitemi energetici (CINDK) RACCOLA DI ESERCIZI RAI DA EMI D ESAME - parte ^. Acqua viene caldata in una pentola ben chiua pota u un fornello mentre viene frullata con un frullatore. Durante
A.A. 2005/2006 Sitemi energetici (CINDK) RACCOLA DI ESERCIZI RAI DA EMI D ESAME - parte ^. Acqua viene caldata in una pentola ben chiua pota u un fornello mentre viene frullata con un frullatore. Durante
F = 150 N F 1 =? = 3,1 s. 3,2
 ESERCIZI SVOLTI : Principi di Newton Lavoro Energia Prof.. Marletta ITC Zanon - Udine ESERCIZIO (): Una caa di 30 kg viene tirata con una corda che forma un angolo di 50 col pavimento u una uperficie licia.
ESERCIZI SVOLTI : Principi di Newton Lavoro Energia Prof.. Marletta ITC Zanon - Udine ESERCIZIO (): Una caa di 30 kg viene tirata con una corda che forma un angolo di 50 col pavimento u una uperficie licia.
TESTI E SOLUZIONI DEI PROBLEMI
 Università degli Studi di Udine Corso di Laurea in Ingegneria Gestionale A.A. 05/06 Sessione di Giugno/Luglio 06 Esame di FISICA GENERALE CFU) Primo Appello PROVA SCRITTA 3 Giugno 06 TESTI E SOLUZIONI
Università degli Studi di Udine Corso di Laurea in Ingegneria Gestionale A.A. 05/06 Sessione di Giugno/Luglio 06 Esame di FISICA GENERALE CFU) Primo Appello PROVA SCRITTA 3 Giugno 06 TESTI E SOLUZIONI
Esercitazione n 8 FISICA SPERIMENTALE (C.L. Ing. Edi.) (Prof. Gabriele Fava) A.A. 2010/2011
 Eercitazione n 8 FISICA SPERIMENALE (C.L. Ing. Edi.) (Prof. abriele Fava) A.A. 00/0 Dinamica dei itemi rigidi. Un corpo rigido omogeneo è fermo u un piano inclinato di un angolo = 0 ripetto all orizzontale.
Eercitazione n 8 FISICA SPERIMENALE (C.L. Ing. Edi.) (Prof. abriele Fava) A.A. 00/0 Dinamica dei itemi rigidi. Un corpo rigido omogeneo è fermo u un piano inclinato di un angolo = 0 ripetto all orizzontale.
Postulato delle reazioni vincolari
 Potulato delle reazioni vincolari Ad ogni vincolo agente u un punto materiale P può eere otituita una forza, chiamata reazione vincolare, che realizza lo teo effetto dinamico del vincolo. reazione vincolare
Potulato delle reazioni vincolari Ad ogni vincolo agente u un punto materiale P può eere otituita una forza, chiamata reazione vincolare, che realizza lo teo effetto dinamico del vincolo. reazione vincolare
LAVORO ED ENERGIA. 1J = 1N 1m
 ppunti di fiica LVORO ED ENERGI LVORO Nel linguaggio cientifico il termine lavoro ha un ignificato ben precio e talvolta divero da quello che queto termine aume nel linguaggio quotidiano. In fiica il concetto
ppunti di fiica LVORO ED ENERGI LVORO Nel linguaggio cientifico il termine lavoro ha un ignificato ben precio e talvolta divero da quello che queto termine aume nel linguaggio quotidiano. In fiica il concetto
TESTI E SOLUZIONI DEI PROBLEMI
 Università degli Studi di Udine, Corso di Laurea in Ingegneria Meccanica Esami di FISICA I 9 CFU e Fisica Generale CFU A.A. 07/08, Sessione di Settembre 08, Prova scritta del 3 Settembre 08 TESTI E SOLUZIONI
Università degli Studi di Udine, Corso di Laurea in Ingegneria Meccanica Esami di FISICA I 9 CFU e Fisica Generale CFU A.A. 07/08, Sessione di Settembre 08, Prova scritta del 3 Settembre 08 TESTI E SOLUZIONI
Meccanica Applicata alle Macchine Appello del 12/01/2012
 Meccanica Applicata alle Macchine Appello del 12/01/2012 1. Eeguire l analii tatica del meccanimo in figura 2 (cala 1:1). Si calcoli l azione reitente ul membro 5 quando F m =1N. 2. In figura 1 è rappreentato
Meccanica Applicata alle Macchine Appello del 12/01/2012 1. Eeguire l analii tatica del meccanimo in figura 2 (cala 1:1). Si calcoli l azione reitente ul membro 5 quando F m =1N. 2. In figura 1 è rappreentato
TESTI E SOLUZIONI DEI PROBLEMI
 Università degli Studi di Udine, Corso di Laurea in Ingegneria Gestionale A.A. 06/07, Sessione di Giugno/Luglio 07, Esame di FISICA GENERALE CFU Primo Appello, PROVA SCRITTA, 6 Giugno 07 TESTI E SOLUZIONI
Università degli Studi di Udine, Corso di Laurea in Ingegneria Gestionale A.A. 06/07, Sessione di Giugno/Luglio 07, Esame di FISICA GENERALE CFU Primo Appello, PROVA SCRITTA, 6 Giugno 07 TESTI E SOLUZIONI
Calcolo della tensione ammissibile Dovendo essere il grado di sicurezza non inferiore a 3 si ricava che il coefficiente di sicurezza γ è 3 per cui:
 Il recipiente diegnato in figura ha una configurazione cilindrica avente diametro interno D = 000 mm è chiuo con fondi emiferici, eo è itemato u due elle A e B pote ad una ditanza L AB = 7000 mm e fuoriece
Il recipiente diegnato in figura ha una configurazione cilindrica avente diametro interno D = 000 mm è chiuo con fondi emiferici, eo è itemato u due elle A e B pote ad una ditanza L AB = 7000 mm e fuoriece
Compito 19 Luglio 2016
 Compito 19 Luglio 016 Roberto onciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 015-016 Compito di Fisica Generale I per matematici 19 Luglio 016
Compito 19 Luglio 016 Roberto onciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 015-016 Compito di Fisica Generale I per matematici 19 Luglio 016
Fisica Generale I (primo e secondo modulo) A.A , 1 Febbraio 2010
 Fisica Generale I (primo e secondo modulo) A.A. 2009-0, Febbraio 200 Esercizi di meccanica relativi al primo modulo del corso di Fisica Generale I, anche equivalente ai corsi di Fisica Generale e 2 per
Fisica Generale I (primo e secondo modulo) A.A. 2009-0, Febbraio 200 Esercizi di meccanica relativi al primo modulo del corso di Fisica Generale I, anche equivalente ai corsi di Fisica Generale e 2 per
Esercitazione 7. Soluzione. Il sistema è isolato, quindi l energia totale si conserva. Applicando il primo principio della termodinamica si ottiene:
 Esercitazione 7 Esercizio 1 Una massa m g = 20 g di ghiaccio a 0 C è contenuta in un recipiente termicamente isolato. Successivamente viene aggiunta una massa m a = 80 di acqua a 80 C. Quale sarà, all
Esercitazione 7 Esercizio 1 Una massa m g = 20 g di ghiaccio a 0 C è contenuta in un recipiente termicamente isolato. Successivamente viene aggiunta una massa m a = 80 di acqua a 80 C. Quale sarà, all
PROBLEMI RISOLTI DI DINAMICA
 PROBLEMI RISOLTI DI DINAMICA 1 Un autoobile di aa 100 Kg auenta in odo unifore la ua velocità di 30 / in 0 a) Quale forza agice durante i 0? b) Quale forza arebbe necearia per ipriere un accelerazione
PROBLEMI RISOLTI DI DINAMICA 1 Un autoobile di aa 100 Kg auenta in odo unifore la ua velocità di 30 / in 0 a) Quale forza agice durante i 0? b) Quale forza arebbe necearia per ipriere un accelerazione
v 2 0 = GM R R = GMm R 2 2π (1 giorno) = 2π R = rad/s. ω terra = = rad/s; ω s = v 0
 Università degli Studi di Udine, Corsi di Laurea in Ingegneria Gestionale ed Ingegneria Elettronica A.A. 202/203, Sessione di Gennaio/Febbraio 204, Primo Appello FISICA GENERALE I 2 CFU), Prova scritta
Università degli Studi di Udine, Corsi di Laurea in Ingegneria Gestionale ed Ingegneria Elettronica A.A. 202/203, Sessione di Gennaio/Febbraio 204, Primo Appello FISICA GENERALE I 2 CFU), Prova scritta
Esercizi svolti di geometria delle aree Alibrandi U., Fuschi P., Pisano A., Sofi A. ESERCIZIO n.7
 ESERCZO n.7 Data la ezione cava riportata in Figura, determinare: a) gli ai principali centrali di inerzia; b) l ellie principale centrale di inerzia; c) il nocciolo centrale di inerzia. cm cm A#7 . Determinazione
ESERCZO n.7 Data la ezione cava riportata in Figura, determinare: a) gli ai principali centrali di inerzia; b) l ellie principale centrale di inerzia; c) il nocciolo centrale di inerzia. cm cm A#7 . Determinazione
Esercitazioni del 09/06/2010
 Esercitazioni del 09/06/2010 Problema 1) Un anello di massa m e di raggio r rotola, senza strisciare, partendo da fermo, lungo un piano inclinato di un angolo α=30 0. a) Determinare la legge del moto.
Esercitazioni del 09/06/2010 Problema 1) Un anello di massa m e di raggio r rotola, senza strisciare, partendo da fermo, lungo un piano inclinato di un angolo α=30 0. a) Determinare la legge del moto.
Esame di Fisica per Ingegneria Elettronica e delle Telecomunicazioni (Parte I):
 Esame di Fisica per Ingegneria Elettronica e delle Telecomunicazioni Parte I: 06-07-06 Problema. Un punto si muove nel piano xy con equazioni xt = t 4t, yt = t 3t +. si calcolino le leggi orarie per le
Esame di Fisica per Ingegneria Elettronica e delle Telecomunicazioni Parte I: 06-07-06 Problema. Un punto si muove nel piano xy con equazioni xt = t 4t, yt = t 3t +. si calcolino le leggi orarie per le
POLITECNICO DI MILANO Fondamenti di Fisica Sperimentale, a. a I appello, 12 luglio 2016
 POLITECNICO DI MILANO Fondamenti di Fisica Sperimentale, a. a. 015-16 I appello, 1 luglio 016 Giustificare le risposte e scrivere in modo chiaro e leggibile. Scrivere in stampatello nome, cognome, matricola
POLITECNICO DI MILANO Fondamenti di Fisica Sperimentale, a. a. 015-16 I appello, 1 luglio 016 Giustificare le risposte e scrivere in modo chiaro e leggibile. Scrivere in stampatello nome, cognome, matricola
Liceo Scientifico Cassini Esercizi di fisica, classe 3G, foglio7
 Liceo Scientifico Caini Eercizi di fiica, clae 3G, foglio7 Problema1 In una gara ui 200m un corridore percorre i primi 40m con un accelerazione di 1.5 m ed il reto della gara di moto rettilineo uniforme.
Liceo Scientifico Caini Eercizi di fiica, clae 3G, foglio7 Problema1 In una gara ui 200m un corridore percorre i primi 40m con un accelerazione di 1.5 m ed il reto della gara di moto rettilineo uniforme.
TERMODINAMICA E TERMOFLUIDODINAMICA. Cap. 6 CICLI TERMODINAMICI DIRETTI ED INVERSI
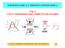 ERMODINAMICA E ERMOFLUIDODINAMICA Cap. 6 CICLI ERMODINAMICI DIREI ED INVERSI max min Sorgente termica (Bruciatore) Q H = Q in a 2 Caldaia 2 L - = L in L + = L urbina out Pompa Condenatore = 2 = Q C = Q
ERMODINAMICA E ERMOFLUIDODINAMICA Cap. 6 CICLI ERMODINAMICI DIREI ED INVERSI max min Sorgente termica (Bruciatore) Q H = Q in a 2 Caldaia 2 L - = L in L + = L urbina out Pompa Condenatore = 2 = Q C = Q
Meccanica 15Aprile 2016
 Meccanica 15Aprile 2016 Problema 1 (1 punto) Una pallottola di massa m= 20 g arriva con velocità V= 300 m/s, inclinata verso il basso di un anglo = 15 rispetto al piano orizzontale, su un blocco di massa
Meccanica 15Aprile 2016 Problema 1 (1 punto) Una pallottola di massa m= 20 g arriva con velocità V= 300 m/s, inclinata verso il basso di un anglo = 15 rispetto al piano orizzontale, su un blocco di massa
Esempi Calcolo Antitrasformate
 Eempi Calcolo Antitraformate Note per il Coro di FdA - Info April, 05 Il punto focale del coiddetto metodo di Heaviide per l antitraformazione di un egnale regolare a traformata razionale conite nel riconocere
Eempi Calcolo Antitraformate Note per il Coro di FdA - Info April, 05 Il punto focale del coiddetto metodo di Heaviide per l antitraformazione di un egnale regolare a traformata razionale conite nel riconocere
Appunti ed esercitazioni di Microonde 2
 Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
Esercitazione di Controlli Automatici 1 n 6
 4 maggio 007 Eercitazione di Controlli Automatici n 6 a.a. 006/07 Si conideri il itema della eercitazione n 5 cotituito da un braccio robotico in rotazione, utilizzato per la movimentazione di oggetti.
4 maggio 007 Eercitazione di Controlli Automatici n 6 a.a. 006/07 Si conideri il itema della eercitazione n 5 cotituito da un braccio robotico in rotazione, utilizzato per la movimentazione di oggetti.
19.12. Impianti motori con turbine a gas
 19.12. Impianti motori con turbine a ga Approfondimenti 19.12.1. Generalità. Il ciclo di Brayton (o ciclo di oule) Il rendimento (h) di un ciclo termodinamico può eere epreo dalla relazione: h q up q inf
19.12. Impianti motori con turbine a ga Approfondimenti 19.12.1. Generalità. Il ciclo di Brayton (o ciclo di oule) Il rendimento (h) di un ciclo termodinamico può eere epreo dalla relazione: h q up q inf
Dimensionamento dell impianto pneumatico di trasporto semola
 Dimenionamento dell impianto pneumatico di traporto emola Il dimenionamento viene condotto con riferimento all impianto di traporto pneumatico della emola alla linea di produzione della pata lunga Dati
Dimenionamento dell impianto pneumatico di traporto emola Il dimenionamento viene condotto con riferimento all impianto di traporto pneumatico della emola alla linea di produzione della pata lunga Dati
= 20 m/s in una guida verticale circolare. v A A
 Eercizio (tratto dal Problema 4.39 del Mazzoldi Un corpo di maa m = 00 Kg entra con elocità A licia di raggio = 5 m. Calcolare: = 0 m/ in una guida erticale circolare. la elocità nei punti B e C;. la reazione
Eercizio (tratto dal Problema 4.39 del Mazzoldi Un corpo di maa m = 00 Kg entra con elocità A licia di raggio = 5 m. Calcolare: = 0 m/ in una guida erticale circolare. la elocità nei punti B e C;. la reazione
FISICA per SCIENZE BIOLOGICHE A.A. 2013/2014 1) FLUIDI V= 5 dm3 a= 2 m/s2 aria = g / cm 3 Spinta Archimedea Tensione della fune
 FISICA per SCIENZE BIOLOGICHE A.A. 2013/2014 II Compitino 26 Giugno 2014 1) FLUIDI Un bambino trattiene un palloncino, tramite una sottile fune. Il palloncino ha volume V= 5 dm 3. La sua massa, senza il
FISICA per SCIENZE BIOLOGICHE A.A. 2013/2014 II Compitino 26 Giugno 2014 1) FLUIDI Un bambino trattiene un palloncino, tramite una sottile fune. Il palloncino ha volume V= 5 dm 3. La sua massa, senza il
A: L = 2.5 m; M = 0.1 kg; v 0 = 15 m/s; n = 2 B: L = 2 m; M = 0.5 kg; v 0 = 9 m/s ; n = 1
 Esercizio 1 Un asta di lunghezza L e massa trascurabile, ai cui estremi sono fissati due corpi uguali di massa M (si veda la figura) giace ferma su un piano orizzontale privo di attrito. Un corpo di dimensioni
Esercizio 1 Un asta di lunghezza L e massa trascurabile, ai cui estremi sono fissati due corpi uguali di massa M (si veda la figura) giace ferma su un piano orizzontale privo di attrito. Un corpo di dimensioni
Soluzioni Compito di Fisica I I Sessione I Appello Anno Accademico
 catcode`"active Soluzioni Compito di Fisica I I Sessione I Appello Anno Accademico 014-015 Esercizio n.1: Un blocco M è inizialmente fermo nel tratto orizzontale di una guida priva di attrito (figura 1).
catcode`"active Soluzioni Compito di Fisica I I Sessione I Appello Anno Accademico 014-015 Esercizio n.1: Un blocco M è inizialmente fermo nel tratto orizzontale di una guida priva di attrito (figura 1).
2. METODO DEGLI SPOSTAMENTI O EQUAZIONE DELLA LINEA ELASTICA, PER LA SOLUZIONE DI TRAVI IPERSTATICHE
 METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
ESEMPI DI ANALISI DI CIRCUITI DINAMICI LINEARI. corso: Teoria dei Circuiti. docente: Stefano PASTORE. 1 Esempio di tableau dinamico (tempo e Laplace)
 ESEMPI DI ANALISI DI CIRCUITI DINAMICI LINEARI coro: Teoria dei Circuiti docente: Stefano PASTORE 1 Eempio di tableau dinamico (tempo e Laplace) 1.1 Dominio del tempo Conideriamo il eguente circuito dinamico
ESEMPI DI ANALISI DI CIRCUITI DINAMICI LINEARI coro: Teoria dei Circuiti docente: Stefano PASTORE 1 Eempio di tableau dinamico (tempo e Laplace) 1.1 Dominio del tempo Conideriamo il eguente circuito dinamico
D. MR (*) 2. Il modulo dell accelerazione angolare α della carrucola vale rad A s rad B s rad C s rad D. 55.
 acoltà di Ingegneria a prova intracoro di iica I 30.0.0 Copito A (*) Eercizio n. Una carrucola, aiilabile ad un dico di aa 3.7 kg e raggio 70 c, è libera di ruotare intorno ad un ae orizzontale paante
acoltà di Ingegneria a prova intracoro di iica I 30.0.0 Copito A (*) Eercizio n. Una carrucola, aiilabile ad un dico di aa 3.7 kg e raggio 70 c, è libera di ruotare intorno ad un ae orizzontale paante
Esperienza n 6: Pendolo di Kater
 Eperienza n 6: Pendolo di Kater Sperimentatori: Marco Erculiani (N maricola 4549 v.o.) Ivan Noro (N matricola 458656 v.o.) Materiale a dipoizione: I materiali utilizzati per queta eperienza ono: Un pendolo
Eperienza n 6: Pendolo di Kater Sperimentatori: Marco Erculiani (N maricola 4549 v.o.) Ivan Noro (N matricola 458656 v.o.) Materiale a dipoizione: I materiali utilizzati per queta eperienza ono: Un pendolo
Fisica Generale I (primo modulo) A.A , 9 febbraio 2009
 Fisica Generale I (primo modulo) A.A. 2008-09, 9 febbraio 2009 Esercizio 1. Due corpi di massa M 1 = 10kg e M 2 = 5Kg sono collegati da un filo ideale passante per due carrucole prive di massa, come in
Fisica Generale I (primo modulo) A.A. 2008-09, 9 febbraio 2009 Esercizio 1. Due corpi di massa M 1 = 10kg e M 2 = 5Kg sono collegati da un filo ideale passante per due carrucole prive di massa, come in
Esercitazione 16 Novembre 2012 Circuiti dinamici del secondo ordine. t come riportato in figura.
 Eercitazione Noembre ircuiti dinamici del econdo ordine ircuito L- erie Per quanto riguarda queto circuito, l eercizio egue la traccia della oluzione del compito d eame numero, reperibile in rete al olito
Eercitazione Noembre ircuiti dinamici del econdo ordine ircuito L- erie Per quanto riguarda queto circuito, l eercizio egue la traccia della oluzione del compito d eame numero, reperibile in rete al olito
VII ESERCITAZIONE - 29 Novembre 2013
 VII ESERCITAZIONE - 9 Novembre 013 I. MOMENTO DI INERZIA DEL CONO Calcolare il momento di inerzia di un cono omogeneo massiccio, di altezza H, angolo al vertice α e massa M, rispetto al suo asse di simmetria.
VII ESERCITAZIONE - 9 Novembre 013 I. MOMENTO DI INERZIA DEL CONO Calcolare il momento di inerzia di un cono omogeneo massiccio, di altezza H, angolo al vertice α e massa M, rispetto al suo asse di simmetria.
Esercitazione 8. Soluzione Il rendimento di una macchina di Carnot in funzione delle temperature è: η = 1 T 2 T 1 = = 60%
 Esercitazione 8 Esercizio 1 - Macchina di arnot Una macchina di arnot assorbe una certa quantità di calore Q 1 da una sorgente a temperatura T 1 e cede calore Q 2 ad una seconda sorgente a temperatura
Esercitazione 8 Esercizio 1 - Macchina di arnot Una macchina di arnot assorbe una certa quantità di calore Q 1 da una sorgente a temperatura T 1 e cede calore Q 2 ad una seconda sorgente a temperatura
Compito di Fondamenti di Automatica settembre 2006
 Compito di Fondamenti di Automatica ettembre 2006 Eercizio 1. Si conideri lo chema di figura (operazionale ideale, eccetto per il guadagno che puó eere definito da una G(), reitenze uguali, condenatori
Compito di Fondamenti di Automatica ettembre 2006 Eercizio 1. Si conideri lo chema di figura (operazionale ideale, eccetto per il guadagno che puó eere definito da una G(), reitenze uguali, condenatori
Con riferimento ad uno schema di trave semplicemente appoggiata di lunghezza L = 6 m il momento flettente massimo in mezzeria è pari a:
 Eempio Verifica dell apertura delle feure Si conidera la ezione rettangolare caratterizzata dalle eguenti proprietà: - bae b = 00 mm, - altezza totale h = 00 mm, - copriferro c =0 mm, - altezza utile d
Eempio Verifica dell apertura delle feure Si conidera la ezione rettangolare caratterizzata dalle eguenti proprietà: - bae b = 00 mm, - altezza totale h = 00 mm, - copriferro c =0 mm, - altezza utile d
VII ESERCITAZIONE. Soluzione
 VII ESERCITAZIONE 1. MOMENTO DI INERZIA DEL CONO Calcolare il momento di inerzia di un cono omogeneo massiccio, di altezza H, angolo al vertice α e massa M, rispetto al suo asse di simmetria. Calcoliamo
VII ESERCITAZIONE 1. MOMENTO DI INERZIA DEL CONO Calcolare il momento di inerzia di un cono omogeneo massiccio, di altezza H, angolo al vertice α e massa M, rispetto al suo asse di simmetria. Calcoliamo
E i = mgh 0 = mg2r mv2 = mg2r mrg = E f. da cui si ricava h 0 = 5 2 R
 Esercizio 1 Un corpo puntiforme di massa m scivola lungo una pista liscia di raggio R partendo da fermo da un altezza h rispetto al fondo della pista come rappresentato in figura. a) Determinare il valore
Esercizio 1 Un corpo puntiforme di massa m scivola lungo una pista liscia di raggio R partendo da fermo da un altezza h rispetto al fondo della pista come rappresentato in figura. a) Determinare il valore
Esame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A
 Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c 2 ; P 1 1( ( + 4 ; P 2 ( ( + 1 (
Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c 2 ; P 1 1( ( + 4 ; P 2 ( ( + 1 (
CORSO DI LAUREA IN SCIENZE BIOLOGICHE II compitino di FISICA, 17 Giugno 2010
 CORSO DI LAUREA IN SCIENZE BIOLOGICHE II compitino di FISICA, 17 Giugno 2010 1) Due cariche +2q e q sono fissate lungo l asse x, rispettivamente nei punti O = (0,0) ed A=(d,0), con d = 2 m. Determinare:
CORSO DI LAUREA IN SCIENZE BIOLOGICHE II compitino di FISICA, 17 Giugno 2010 1) Due cariche +2q e q sono fissate lungo l asse x, rispettivamente nei punti O = (0,0) ed A=(d,0), con d = 2 m. Determinare:
FISICA per SCIENZE BIOLOGICHE A.A. 2012/2013 APPELLO 18 Luglio 2013
 FISICA per SCIENZE BIOLOGICHE A.A. 2012/2013 APPELLO 18 Luglio 2013 1) Un corpo di massa m = 500 g scende lungo un piano scabro, inclinato di un angolo θ = 45. Prosegue poi lungo un tratto orizzontale
FISICA per SCIENZE BIOLOGICHE A.A. 2012/2013 APPELLO 18 Luglio 2013 1) Un corpo di massa m = 500 g scende lungo un piano scabro, inclinato di un angolo θ = 45. Prosegue poi lungo un tratto orizzontale
