Minimi quadrati: introduzione alla compensazione
|
|
|
- Rosalia Lombardi
- 7 anni fa
- Visualizzazioni
Transcript
1 Minimi quadrati: introduzione alla compensazione Osservazioni ripetute di massima precisione della stessa quantità forniscono risultati differenti quindi esse non sono fenomeni deterministici ma stocastici: possono essere modellizzate mediante variabili casuali Un modello appropriato per la loro descrizione è la distribuzione gaussiana, completamente definita dalla media e dalla covarianza ( µ e C ) xx
2 f ( x)= 1 ( 2π ) n/2 ( detc ) xx n/2 e 1 2 x µ x ( ) T C 1 xx ( x µ x ) normalmente distribuite. Osservazioni topografiche e geodetiche sono acquisite per stimare posizioni di punti in un sistema di riferimento assegnato. Osservazioni topografiche e geodetiche sono sempre di alta precisione e possono essere descritte come variabili casuali
3 Assegnato X0Y (SR 2D), mediante misure di distanze e angoli, possono essere determinate le coordinate di punti. Da un punto di vista geometrico, il numero minimo necessario di osservazioni per determinare posizioni è univocamente definito.
4 Sorgono due problemi Le stime delle posizioni dipendono dagli errori di osservazione Gli errori non possono essere controllati Soluzione le posizioni dei punti sono modellate come variabili casuali (normalmente distribuite): le accuratezze devono essere determinate insieme alle posizioni Sono necessarie osservazioni ridondanti per effettuare le crossvalidazioni Osservazioni ridondanti permettono la valutazione degli errori e delle accuratezze
5 L'effetto di osservazioni ridondanti Data l'altezza H del punto 1, devono 1 essere determinate le altezze H, 2 H. 3 Da un punto di vista puramente geometrico, due osservazioni sono necessarie e sufficienti, per esempio ΔH 12, ΔH 0 23 : 0 H =H +ΔH H =H +ΔH + ΔH Il pedice o indica il valore dell'osservazione che, rispetto all'osservabile, contiene il relativo errore.
6 Ogni errore ε nelle osservazioni ΔH 12 e ΔH 0 23 si propaga 0 direttamente nelle stime H e 2 H : 3 Ĥ 2=H 1+ΔH 12+ε 12 Ĥ =H +ΔH + ε + ΔH + ε Introduciamo l'osservazione ridondante ΔH 31
7 Condizioni geometriche ΔH 12 + ΔH 23 + ΔH 31 = 0 Gli errori di osservazione ΔH + ΔH + ΔH = ε ε è l'errore di chiusura e fornisce una stima empirica dell'errore di misura ε= ε + ε + ε Nota che ε può essere calcolato, mentre gli errori individuali restano incogniti.
8 Secondo problema Le quote stimate dipendono dal percorso * ΔH 12 = ΔH 12 0, ** Δ H12 = ΔH31 Δ H , * ** ΔH ΔH Una possibile soluzione L'errore di chiusura ε viene distribuito fra tutte le osservazioni in modo che le loro stime a posteriori soddisfino le condizioni geometriche ΔĤ12 + ΔĤ23 + ΔĤ31 = 0 e che le stime delle quote siano univoche
9 Posizione algebrica del problema 2 incognite H, 2 H in 3 osservazioni 3 ΔH 12 0, ΔH 23 0, ΔH equazioni di osservazione H2 H 1 = ΔH12 s = H3 H 2 = ΔH23 H1 H 3 = ΔH31 che sono completamente equivalenti a un'equazione di condizione (la somma delle tre) ΔH + ΔH + ΔH = che non è soddisfatta dalle tre osservazioni Il sistema di 3 equazioni in 2 incognite è algebricamente impossibile quando vengono inserite le osservazioni
10 H H = ΔH s = H H = ΔH H H = ΔH Infatti ogni equazione dipende linearmente dalle altre due a sinistra, ma non a destra per la presenza degli errori
11 Quindi vengono introdotte 3 incognite, ε 12, ε 23, ε 31, che rappresentano le correzioni da applicare alle osservazioni per ottenere i loro valori calcolati a posteriori ΔH ˆ ˆ ˆ 12, ΔH23, Δ H31 che soddisfano il precedente sistema. Il nuovo sistema è algebricamente sottodeterminato H 2 H 1 = ΔH 12 ε 0 12 ŝ = H 3 H 2 = ΔH 230 ε 23 H 1 H 3 = ΔH 310 ε 31 5 incognite H, 2 H, 3 ε 12, ε 23, ε e solo 3 equazioni 31
12 Quindi si devono aggiungere 2 ulteriori equazioni per costruire un sistema con soluzione algebrica univoca. Le 2 equazioni sono ottenute imponendo una condizione (arbitraria) sulle incognite la condizione fornisce un criterio per distribuire l'errore di chiusura e pone un principio di stima
13 Un esempio di principio di stima Ripartizione uguale dell'errore di chiusura ε ε 12 =ε 23 =ε 31 = 3 Osservazioni ricalcolate: stime delle osservabili Δ Ĥ =ΔH ε Δ Ĥ =ΔH ε Δ Ĥ =ΔH ε Quote calcolate: stime dei parametri H ˆ 2=H ˆ 1+ΔH 12 H ˆ =H +ΔH ˆ
14 Note Lo scopo della compensazione di rete: la stima dei parametri (posizioni) a partire da osservazioni ridondanti mediante applicazione di un principio di stima Inoltre, stima dell'accuratezza dei parametri Minimi quadrati: principio di stima usualmente adottato nella compensazione di reti.
15 Principio dei minimi quadrati Proprietà generali Non dipende dalla distribuzione di probabilità delle osservazioni Stime di minima varianza nella classe degli stimatori lineari e corretti I parametri e le loro accuratezze vengono calcolati in forma chiusa Mediante simulazione, possono essere predette le accuratezze finali dei parametri a partire dalle precisioni delle osservazioni I minimi quadrati non forniscono stime robuste
16 Minimi quadrati: dati y : vettore delle osservazioni (dimensione m), estratto dalla 0 variabile casuale y(osservabili), definito nello spazio m R n y deve appartenere a un sottospazio lineare V ( y V m dimensione n m in R (modello funzionale lineare) n ) con la covarianza di y è nota a meno di un fattore di proporzionalità 2 σ (chiamata anche varianza a priori) 2 C = σ Q (modello stocastico) yy
17 Minimi quadrati: obiettivi La stima ŷ di y tale che y V n La stima Cyy = σˆ 2 Q C yy ˆˆ di Principio di stima 2 C yy, ovvero la stima di σ dato Q ( y y) Q ( y y ) = min T 1 0 0
18 Interpretazione geometrica: il triangolo di livellazione y ΔH = ΔH Δ H Modello funzionale (lineare) n ΔH 12 + ΔH 23 + ΔH 31 = 0 y V (equazione di un piano nello spazio tridimensionale)
19 Modello stocastico 2 Q= I Cyy = σ I Stimatore ai minimi quadrati T 1 ( y0 y) Q ( y0 y) = min n y V ŷ è il punto y n V a minima distanza da 0
20 Interpretazione geometrica delle equazioni di condizione e di osservazione Equazione di condizione: ΔH 12 + ΔH 23 + ΔH 31 = 0 Equazioni di osservazione: ΔH 12 = H2 H1 ΔH 23 = H3 H1 ΔH = H H Entrambe rappresentano un piano in R3
21 Applicazione dei MQ nella compensazione di rete Quale modello (condizione o osservazioni)? Tipicamente, si è interessati alla stima di parametri che sono incogniti ma sono legati alle osservazioni da equazioni di osservazione Nella livellazione osservazioni: differenze di quota parametri: quote equazioni di osservazione: H j H i= ΔHij
22 Generalmente, l'implementazione delle equazioni di condizione è più complessa. Al contrario, le equazioni di osservazione possono facilmente essere implementate: una equazione per ogni osservazione Nel seguito, si adotterà e discuterà quest'ultimo modello
23 I Minimi Quadrati: formalizzazione mediante equazioni sulle osservazioni Siano date m osservazioni y o y1 o y 2o =... ym o per ogni osservazione i-esima valga y y ε i i i o = +, ε E[ ε ] i 0; = 0 i
24 Si ha y y, [ y ] 0 = + ε E = o y y: vettore delle osservabili, incognite; y : vettore delle osservazioni, note; o ε : vettore degli errori di osservazione, incogniti. Sia noto il modello stocastico delle osservazioni, ovvero la loro matrice di covarianza: C = C = Q 2 yy εε σ 0 2 σ 0 è la varianza a priori, Q è la matrice dei cofattori:
25 Sia x il vettore contenente n (n m ) parametri incogniti: x x x 1 2 =... x n Sia noto il modello deterministico del problema, ovvero la relazione funzionale fra parametri x e osservabiliy y = Ax + b A è la matrice disegno, b è un vettore m-dimensionale noto.
26 Minimi quadrati: principio e stimatori Si cercano ˆx e ŷ tali che yˆ = Axˆ+ b T 1 ( yo y) Q ( yo y ) = min Nel seguito vengono riportate senza dimostrazione le stime fornite dai MQ.
27 Dalle equazioni di condizione si ricava il cosiddetto sistema normale T 1 ˆ = ( o ) Nx A Q y b, ove N = T 1 A Q A è detta matrice normale Si hanno due casi: A è di rango pieno, ovvero le sue colonne sono linearmente indipendenti: Ax = 0 x = 0 il problema non presenta deficienza di rango.
28 A non è di rango pieno, ovvero alcune sue colonne sono linearmente dipendenti dalle altre: Ax = 0 per qualche x 0 in questo caso il problema presenta deficienza di rango. Le reti geodetiche, semplicemente poste, presentano deficienza di rango: si osservano differenze di posizione, si vogliono stimare posizioni.
29 Esempio di analisi di deficienza di rango Siano A, B e C tre punti di livellazione Siano stati misurati i dislivelli da A a B ( DH ), ABo da B a C ( DH ) BCo e da C a A ( DH ). CAo Siamo in presenza di tre osservazioni: sono sufficienti per stimare le quote dei tre punti A, B, C?
30 Pensando al problema dal punto di vista fisico, è evidente che i valori delle osservazioni di dislivello del triangolo non vengono modificati aggiungendo un valore H comune alle 3 quote supposte incognite: DH = H H = ( H + H ) ( H + H ) AB B A B A DH = H H = ( H + H ) ( H + H ) BC C B C B DH = H H = ( H + H ) ( H + H ) CA A C A C ovvero le quote dei punti (parametri incogniti), presentano 1 grado di libertà, rispetto ai dislivelli (osservabili); la situazione non cambia aggiungendo una o più osservazioni di dislivello.
31
32 Verifica algebrica In forma matriciale, scriviamo il sistema deterministico H H = DH H H = DH H H = DH B A AB A C CA C B BC DH AB O H A DH BC H O = B + ε DHCA H O C y O = y + ε = Ax + ε
33 Nel presente esempio si considerano le misure di uguale 2 2 precisione (che indichiamo con σ ) e scorrelate: C = σ I yy A non è di rango pieno: infatti = 0 Si provi a calcolare N: avrà la stessa deficienza di rango e risulterà quindi non invertibile A titolo di esercizio lo si verifichi anche aggiungendo una nuova osservazione di dislivello, ad esempio DH AC
34 Importante su deficienza di rango e ridondanza La ridondanza e la deficienza di rango riguardano aspetti completamente disgiunti in un sistema di equazioni sulle osservazioni La ridondanza è collegata al controllo reciproco delle osservazioni La deficienza di rango è collegata alla stimabilità di un certo insieme di parametri rispetto a un certo insieme di osservazioni
35 La deficienza di rango e i sistemi di riferimento Per rimuovere la deficienza di rango si devono identificare e fissare preventivamente i parametri non stimabili minimali (gradi di libertà intrinseci) del problema: Nel caso di reti topografiche e geodetiche, questo significa fissare un sistema di riferimento Ad esempio, nella rete di livellazione, sono stimabili le quote di tutti i punti della rete meno uno (un grado di libertà). La deficienza di rango può essere eliminata includendo nella rete un punto di quota nota e fissando tale quota.
36 Verifica Supponiamo la quota di A nota. Il nuovo sistema diviene DH ABO DH BCO DH CAO = H B H C + H A 0 H A ε y O = y + ε = Ax + b + ε Ponendo nuovamente C yy = σ 2 I, è immediato verificare che la nuova matrice disegno ha rango pieno e che il seguente sistema normale è risolvibile.
37 Ultime note Per eliminare la deficienza di rango si può fissare il numero minimo di gradi di libertà non stimabili In tal caso la soluzione è detta a minimi vincoli Nella compensazione di reti topografiche e geodetiche locali, anche per considerazioni di opportunità statistica, si introducono più punti noti, ovvero precedentemente misurati, appartenenti a reti di ordine superiore. In tal caso la soluzione è sovravincolata e si parla di inquadramento della rete locale nella rete di ordine superiore.
38 Soluzione del problema normale e stima delle incognite Siano risolti i problemi di deficienza di rango: si hanno le seguenti stime. Stima dei parametri incogniti: ˆx = N 1 A T Q 1 (y o b); stima delle osservabili e degli scarti: ŷ = Aˆx + b ˆε = ŷ o ŷ
39 La ridondanza e le stime di covarianza Ridondanza: differenza fra numero di osservazioni e numero di parametri incogniti, detta anche numero di gradi di libertà: R= m n stima della varianza a posteriori: ˆ σ 2 = ˆε T Q 1 ˆε m n
40 stima della matrice di covarianza dei parametri: C ˆxˆx = ˆ σ 2 N 1 ; stima della matrice di covarianza delle osservabili: T C = ˆ σ AN A ; 2 1 yy ˆˆ 0 stima della matrice di covarianza degli scarti T C = ˆ σ ( Q AN A ) 2 1 εε ˆˆ 0
41 La linearizzazione di un problema non lineare Non esiste una formulazione dei MQ applicabile al problema non lineare y = f( x ) ove fx ( ) = f ( x, x,..., x ) f ( x, x,..., x ) f ( x, x,..., x ) m 1 2 n n n
42 Per risolvere un sistema non lineare è prima necessario linearizzarlo Si devono conoscere valori approssimati per i parametri incogniti:!x =!x 1,...,!x n T :!x 1 x 1,...,!x n x n ;
43 E' allora possibile linearizzare la relazione y= f( x ) mediante uno sviluppo di Taylor arrestato al primo ordine nell intorno di!x y 1 f 1 (!x) + f 1 x 1 (!x) (x 1!x 1 ) f 1 x n (!x) (x n!x n ) y 2 f 2 (!x) + f 2 x 1 (!x) (x 1!x 1 ) f 2 x n (!x) (x n!x n ) y m f m (!x) + f m x 1 (!x) (x 1!x 1 ) f m x n (!x) (x n!x n ) ovvero
44 y = f(!x) + J(!x)(x!x) o anche η = Aξ ove η 1 = y 1 f 1 (!x),...,η 1 = y m f m (!x) ξ = x!x A ij = f i x j Si ottiene dunque il problema lineare η O = η + ε, E η O = η = Aξ
45 Mediante MQ si risolve il problema lineare rispetto al vettore dei parametri incogniti ξ; si calcolano i parametri finali mediante la ˆx =!x + ˆξ ŷ =!y + ˆη Nota il metodo da adottarsi per ricavare i valori approssimati dipende da caso a caso
46 Un esempio di linearizzazione Sia P un punto di posizione incognita in R 3 : P P P X P Y Z = siano invece P 1, P 2, P 3 e P 4 quattro punti di posizione nota: = Z Y X P X P Y Z = X P Y Z =
47 Da P sono state misurate le distanze ai quattro punti, ottenendo i valori ρp ; ρp ; ρp ; ρ O O O P ; si indichi con O ρ O il vettore delle osservazioni di distanza. E noto un valore approssimato della posizione di P!P =!X P!Y P!Z P si vuole stimare la posizione di P.
48 Procedimento La generica equazione di osservazione da P a P i è ρ = ( X X ) + ( Y Y ) + ( Z Z ) i i 2 i 2 i 2 P P P P ρ = ρ + ε i i i PO P la relazione che lega le distanze (osservate a meno degli errori) alle incognite (la posizione di P) è non lineare; il sistema è ridondante: 4 osservazioni per 3 incognite; è possibile risolverlo mediante MQ ma deve prima essere linearizzato.
49 Linearizzazione della generica distanza da P a P i : ρ P i = ( X P X i ) 2 + (Y P Y i ) 2 + (Z P Z i ) 2 (! X P X i ) 2 + (! Y P Y i ) 2 + (!Z P Z i ) (!X P X i ) (! X P X i ) 2 + (! Y P Y i ) 2 + (! Z P Z i ) 2 ( X P!X P ) + (! Y P Y i ) (!X P X i ) 2 + (!Y P Y i ) 2 + (!Z P Z i ) 2 (Y P!Y P ) + (! Z P Z i ) (!X P X i ) 2 + (!Y P Y i ) 2 + (!Z P Z i ) 2 (Z P!Z P )
50 ρ i P!ρ P i +!e P i ξ ove!ρ P i = (!X P X i ) 2 + (!Y P Y i ) 2 + (!Z P Z i ) 2 (distanza calcolata nei valori approssimati)!x i!e P = 1 P X i!y i!ρ P Y i P!Z P Z i (versore approssimato da P i a P)
51 X P!X P ξ = Y P!Y P Z P Z! P (correzioni da apportare alle coordinate approssimate) Il problema assume dunque la forma 1 ρ PO 2 ρ PO 3 ρ PO 4 ρ PO =!ρ P 1!ρ P 2!ρ P 3!ρ P 4 +!e X 1!e X 2!e X 3!e X 4!e Y 1!e Y 2!e Y 3!e Y 4!e Z 1!e Z 2!e Z 3!e Z 4 ξ X ξ Y ξ Z
52 Ovvero η O = y O!y = y!y + ε = η + ε η = Aξ ora risolvibile mediante MQ.
53 Gli errori di modello (outliers) Possono essere su tutto il modello ma tipicamente sono su singole osservazioni: comportano stime errate dei parametri incogniti. Esistono algoritmi per: verificare a posteriori la correttezza globale dei modelli adottati (test del modello globale); identificare eventuali errori di modello su singole osservazioni (identificazione degli outlier e data snooping); identificare l affidabilità dei risultati di una compensazione.
54 La verifica di ipotesi per i dati e le reti geodetiche Nell elaborazione dei dati grezzi (ad esempio le osservazioni GPS) e nella compensazione di reti geodetiche tipicamente vi sono outlier dovuti: 1. all approssimata conoscenza del modello stocastico delle osservazioni (vengono ipotizzate più accurate e meno correlate di quanto non siano in realtà); 2. alla presenza di isolati e grossolani errori di modello deterministico (termini di disturbo di entità significativa e non modellizzabili multipath per il GPS, errori grossolani di stazionamento, ).
55 La verifica statistica di ipotesi E' un operazione che consente di stabilire se, statisticamente, ovvero con una certa probabilità di errore, valga una certa ipotesi H. 0 Si costruisce una statistica campionaria ( F exp ) che, sotto l ipotesi H 0, debba seguire una distribuzione nota; che viceversa, qualora H 0 sia sbagliata, vada ad assumere valori grandi, ovvero non accettabili statisticamente; si confronta quindi la statistica campionaria con i valori limite ammessi dalla sua distribuzione teorica.
56 Esecuzione di un test su una statistica F Scelgo la significatività α del test; fisso F lim tale che, se vale H 0 P{ F exp > F lim H } 0 < α Se F exp > F lim rigetto H 0 La significatività del test è la probabilità di sbagliare rigettando H0.
57 Prima si verifica la correttezza del modello globale, poi si individuano eventuali outlier, infine si corregge il modello stocastico.
58 Il test del χ 2 o test globale sul modello Ipotesi fondamentale: il modello adottato è corretto H y= Ax. 0 : Ipotesi alternativa: il modello adottato è sbagliato x H a : y = [ A δ A] δ x m R { A δ A } = R con [ ] Se H 0 è vera ε T Q 1 ε σ 2 0 (m n) ~ χ (m n) m n 2
59 Statistica di test: 2 ˆ σ 0 2 ( m n) = χ 2 sp σ 0 sia α il livello di significatività del test; 2 2 sia χlim = χm n( α) il valore teorico tale che P(0 χ χ ) = 1 α 2 2 m n lim se se χ χ χ H 0 viene accettata; 2 2 sp lim > χ H 0 viene rigettata: sono presenti errori di modello. 2 2 sp lim
60 Esempio Sia stata effettuata una compensazione di 10 osservazioni in 2 incognite; a fronte di un σ = dichiarato a priori si sia ottenuto un ˆ σ = 2.375cm cm Sia fissato α = 5% : 1 α = 95% = 0.95; dai dati precedenti si ricava ( m n) = 8; il χ = χ (0.05) = lim 8 ˆ χ sp = ( m n) σ = 8 = 19> σ 0
61 Il test non è superato: quindi vi è, a un livello di probabilità del 95%, un errore di modello. Se si fosse fissato α = 1%, si sarebbe ottenuto χlim = χ8 (0.01) = 20.1 > χsp ovvero vi sono errori di modello a livello di significatività 5%, ma non a livello di significatività 1%.
62 Il test locale sulla singola osservazione Serve per identificare errori di modello deterministico su una singola osservazione y : i O Ipotesi fondamentale H : y= 0 Ax. Ipotesi alternativa: H a : y = A e i x δ i, e = i T ovvero un singolo errore sulla singola osservazione i-esima. Se vale H0 (con alcune semplificazioni) la statistica di test è semplicemente
63 ˆε i = z sp ~ N(0,1) = Z σ εi Test sui residui normalizzati: si confronta z sp con i valori limite della normale standardizzata; definito z lim il valore teorico tale che P(0 z z ) 1 α lim =, lim P( z > z ) = α se z zlim H0 viene accettata; se z zlim > H 0 viene rigettata.
64 In effetti, per la non robustezza dei MQ, un outlier modifica anche gli scarti delle altre osservazioni, fatto che spesso complica la sua identificazione mediante il test rigoroso. E tipicamente adottato un procedimento iterativo (data snooping). 1. Innanzitutto si verifica l esistenza di osservazioni isolate cui corrispondano scarti inaccettabili rispetto all accuratezza strumentale. 2. Se ve ne sono, vengono eliminate una per una, partendo dalla più grande, ricompensando ogni volta i dati e verificando la convergenza del test sul modello globale. 3. Se la precedente analisi non evidenzia casi di evidenti outlier
65 si costruiscono i residui (pseudo) normalizzati ˆε i σ εi 4. Anziché confrontare i residui normalizzati con un valore limite, si effettua un confronto relativo fra residui (pseudo) normalizzati; se ve ne è uno significativamente più grande degli altri, si elimina l osservazione corrispondente, ricompensando i dati. 5. Si procede iterativamente; verificando la convergenza del test sul modello globale. 6. Si devono poi controllare le osservazioni eliminate (calcolando i loro scarti) per eliminarle definitivamente o reintrodurle.
66 Ultime note Qualora il test sul modello globale non venga superato ma non vi siano sospetti outlier (ovvero una situazione con scarti normalizzati omogenei) vi è tipicamente un problema di sottostima generale degli elementi della matrice di covarianza delle osservazioni (sovrastima delle precisioni). Questo può essere ovviato mediante la Correzione del modello stocastico, qui non discussa.
67 Accuratezza dei parametri stimati Sono stati eseguiti il test globale sul modello e il data snooping con esiti positivi. Si considera ora la stima dei parametri, ˆx e della relativa matrice di 2 1 covarianza C = N. xx ˆˆ σˆ 0 Ci si chiede quale sia la regione di confidenza per il valore vero dei parametri incogniti, ovvero la regione dello spazio n-dimensionale alla quale il vettore x appartiene con livello di probabilità assegnata.
68 La regione di confidenza per il vettore dei parametri incogniti ad un certo livello di probabilità 1-α è data dalla T ( x xˆ) C ( x x ˆ) F ( α) 1 xx ˆˆ n,( m n) ove Fn,( m n)( α) è il valore della distribuzione di Fisher a n,( m n) gradi di libertà, corrispondente alla probabilità 1 α ; α : in genere si scelgono i valori 0.01, 0.05, 0.10, ovvero ( 1 α : 0.99, 0.95, 0.90.
69 Per analizzare la regione di confidenza di ξ: si estrae dal vettore ˆx il sottovettore ˆξ corrispondente ai parametri ξ di interesse; quindi si estrae dalla matrice di covarianza totale C xx ˆˆ la matrice di covarianza del vettore ˆξ, C ˆˆ; ξξ sia 2 x1 σ1 σ12... σ 1n 2 x 2 σ21 σ2... σ2n x=, C xx ˆˆ = xn σn1 σn2... σn se ad esempio xi ξ = x si ha j C σ σ = 2 i ij ˆˆ ξξ 2 σ ji σ j
70 la regione di confidenza con probabilità 1 α per il vettore ξ è data dalla ˆ T ( ξ ξ) ( C ) ( ξ ξ ˆ) F ( α) 1 ξξ ˆˆ r,( m n) Ellissi di errore in planimetria In genere, nell analisi dei risultati di compensazione di reti geodetiche e topografiche, per ogni punto si scinde il problema in analisi planimetrica e analisi altimetrica: ellissi di errore in planimetria (x i ˆx i ) T C ˆxi ˆx i 1 (x i ˆx i ) F 2,( M N ) (α )
71 Ellissi di errore standard Si sceglie F 2,( M N ) (α ) = 1 corrispondente a α 0.61 per ( M N ) > 10 Data la matrice di covarianza delle coordinate planimetriche (X, Y) del punto C xx ˆˆ = σˆ σˆ 2 X XY σˆ XY 2 Y σˆ si vogliono calcolare i parametri (semiasse maggiore e minore, angolo fra semiasse maggiore e asse X) dell ellissi di errore standard.
72 Il calcolo dei semiassi I valori σ max,min sono le radici degli autovalori λ della matrice C ˆxˆx, ovvero le soluzioni del sistema det(c ˆxˆx λi) = det ˆ σ X 2 λ ˆ σ XY ˆ σ XY ˆ σ Y 2 λ = 0 si ha dunque λ 2 ( σˆ 2 X + σˆ 2 Y )λ + σˆ X2 σˆ 2 2 Y σˆ XY = 0 ovvero
73 λ = σ ˆ 2 2 X + σˆ Y max,min 2 ± 1 2 ( σˆ 2 X σˆ 2 Y ) σˆ XY corrispondenti a σ STD max,σ STDmin = σˆ 2 2 X + σˆ Y 2 ± 1 2 ( σˆ 2 X σˆ 2 Y ) σˆ XY Il calcolo di θ Indichiamo con θ l angolo antiorario fra X e il semiasse maggiore dell ellissi d errore; il versore nel sistema [X,Y] v = cosθ sinθ
74 coincide con l autovettore v max corrispondente a λ max, ovvero con il vettore soluzione del sistema C ˆxˆx v max = λ max v max ; (C ˆxˆx λ max I)v max = 0 ovvero ( ˆ σ X 2 λ max )v 1max + ˆ σ XY v 2max = 0 σˆ XY v 1max + ( σˆ 2 Y λ max )v 2max = 0 Si ha dunque
75 σ X 2 tanθ = v 2 = λ ˆ max v 1 ˆ σ XY e, dalla relazione trigonometrica tan2θ = 2tanθ / (1 tan 2 θ), si ha σ tan2θ = ˆ 2 2 X σˆ Y 2σˆ XY ovvero θ = 1 2 arctg ˆ σ X 2 ˆ σ Y 2 2 ˆ σ XY
76 I parametri di qualunque altra ellissi, con F 2,(m n) (α ) 1, sono dati dalla σ max = σ min = F 2,(m n) (α ) σ STDmax F 2,(m n) (α ) σ STDmin
77 Regione di confidenza 3D La regione tridimensionale di confidenza delle coordinate [X P,Y P,Z P ] di un punto stimato in 3D è data da un ellissoide centrato in [ ˆX,ŶP,ẐP P ], i cui parametri (semiassi e relative direzioni) dipendono dalla matrice di covarianza delle stime delle coordinate del punto. Le regole di calcolo (qui non riportate) sono più complesse di quelle del caso 2D.
78 Anche in questo caso si può definire Ellissoide di errore standard Si sceglie F 3,( M N ) (α ) = 1 corrispondente a α 0.81 per ( M N ) > 10 In questo caso l'ellissoide è caratterizzato da 3 semiassi: minimo, medio e massimo i loro 3 angoli di orientamento rispetto agli assi del SR
I minimi quadrati e loro applicazione alla compensazione geodetica. Ludovico Biagi Politecnico di Milano, DIIAR
 I minimi quadrati e loro applicazione alla compensazione geodetica Ludovico Biagi Politecnico di Milano, DIIAR ludovico.biagi@polimi.it Premesse definizione euristica di distribuzione, formalizzazione
I minimi quadrati e loro applicazione alla compensazione geodetica Ludovico Biagi Politecnico di Milano, DIIAR ludovico.biagi@polimi.it Premesse definizione euristica di distribuzione, formalizzazione
Richiami di statistica e loro applicazione al trattamento di osservazioni topografiche e geodetiche
 Richiami di statistica e loro applicazione al trattamento di osservazioni topografiche e geodetiche Ludovico Biagi Politecnico di Milano, DIIAR ludovico.biagi@polimi.it (materiale didattico preparato in
Richiami di statistica e loro applicazione al trattamento di osservazioni topografiche e geodetiche Ludovico Biagi Politecnico di Milano, DIIAR ludovico.biagi@polimi.it (materiale didattico preparato in
Una nota sulle sessioni con più ricevitori
 Una nota sulle sessioni con più ricevitori L elaborazione di una sessione GPS su ricevitori fornisce la stima della base congiungente i punti; una sessione con n ricevitori permette la costruzione (e la
Una nota sulle sessioni con più ricevitori L elaborazione di una sessione GPS su ricevitori fornisce la stima della base congiungente i punti; una sessione con n ricevitori permette la costruzione (e la
RETI TOPOGRAFICHE. 1. Premessa
 RETI TOPOGRAFICHE 1. Premessa Una rete topografica è costituita da un insieme di punti, detti vertici della rete, connessi fra di loro da un insieme di misure di distanze e di angoli azimutali e zenitali;
RETI TOPOGRAFICHE 1. Premessa Una rete topografica è costituita da un insieme di punti, detti vertici della rete, connessi fra di loro da un insieme di misure di distanze e di angoli azimutali e zenitali;
Il metodo delle osservazioni indirette
 Il metodo delle osservazioni indirette Teoria della stima ai minimi quadrati Il criterio di massima verosimiglianza Sia data una grandezza η e si abbiano n osservazioni indipendenti l i (i=1,...,n) di
Il metodo delle osservazioni indirette Teoria della stima ai minimi quadrati Il criterio di massima verosimiglianza Sia data una grandezza η e si abbiano n osservazioni indipendenti l i (i=1,...,n) di
Topografia e cartografia digitale
 Prof. Fausto Sacerdote Topografia e cartografia digitale Capitolo 4. Reti topografiche dispense del corso Modulo Professionalizzante Corso per Tecnico in Cartografia Tematica per i Sistemi Informativi
Prof. Fausto Sacerdote Topografia e cartografia digitale Capitolo 4. Reti topografiche dispense del corso Modulo Professionalizzante Corso per Tecnico in Cartografia Tematica per i Sistemi Informativi
Tecniche di sondaggio
 SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA
 Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
CONFRONTO TRA LA MEDIE DI DUE CAMPIONI INDIPENDENTI
 CONFRONTO TRA LA MEDIE DI DUE CAMPIONI INDIPENDENTI ipotesi sul confronto tra le medie di due campioni indipendenti Obiettivo: decidere, attraverso il confronto tra le medie dei due campioni indipendenti,
CONFRONTO TRA LA MEDIE DI DUE CAMPIONI INDIPENDENTI ipotesi sul confronto tra le medie di due campioni indipendenti Obiettivo: decidere, attraverso il confronto tra le medie dei due campioni indipendenti,
TOPOGRAFIA 2013/2014. Prof. Francesco-Gaspare Caputo
 TOPOGRAFIA 2013/2014 L operazione di misura di una grandezza produce un numero reale che esprime il rapporto della grandezza stessa rispetto a un altra, a essa omogenea, assunta come unità di misura. L
TOPOGRAFIA 2013/2014 L operazione di misura di una grandezza produce un numero reale che esprime il rapporto della grandezza stessa rispetto a un altra, a essa omogenea, assunta come unità di misura. L
Statistica Applicata all edilizia: Stime e stimatori
 Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
Stima dei parametri. La v.c. multipla (X 1, X 2,.., X n ) ha probabilità (o densità): Le f( ) sono uguali per tutte le v.c.
 Stima dei parametri Sia il carattere X rappresentato da una variabile casuale (v.c.) che si distribuisce secondo la funzione di probabilità f(x). Per investigare su tale carattere si estrae un campione
Stima dei parametri Sia il carattere X rappresentato da una variabile casuale (v.c.) che si distribuisce secondo la funzione di probabilità f(x). Per investigare su tale carattere si estrae un campione
Contenuto del capitolo
 Capitolo 8 Stima 1 Contenuto del capitolo Proprietà degli stimatori Correttezza: E(Stimatore) = parametro da stimare Efficienza Consistenza Intervalli di confidenza Per la media - per una proporzione Come
Capitolo 8 Stima 1 Contenuto del capitolo Proprietà degli stimatori Correttezza: E(Stimatore) = parametro da stimare Efficienza Consistenza Intervalli di confidenza Per la media - per una proporzione Come
Identificazione dei Modelli e Analisi dei Dati 6/5/1993
 Identificazione dei Modelli e Analisi dei Dati 6/5/1993 3. Siano date due V.C. X e Y, di cui è supposta nota la ddp congiunta. Sia Xˆ (Y) uno stimatore di X basato sull'osservazione di Y. Ci si prefigge
Identificazione dei Modelli e Analisi dei Dati 6/5/1993 3. Siano date due V.C. X e Y, di cui è supposta nota la ddp congiunta. Sia Xˆ (Y) uno stimatore di X basato sull'osservazione di Y. Ci si prefigge
Contenuti: Capitolo 14 del libro di testo
 Test d Ipotesi / TIPICI PROBLEMI DI VERIFICA DI IPOTESI SONO Test per la media Test per una proporzione Test per la varianza Test per due campioni indipendenti Test di indipendenza Contenuti Capitolo 4
Test d Ipotesi / TIPICI PROBLEMI DI VERIFICA DI IPOTESI SONO Test per la media Test per una proporzione Test per la varianza Test per due campioni indipendenti Test di indipendenza Contenuti Capitolo 4
Analisi della disponibilità d acqua. Valutazione dell impianto attraverso il calcolo di un indice economico (criterio)
 Analisi della disponibilità d acqua Valutazione dell impianto attraverso il calcolo di un indice economico (criterio) Approccio diverso a seconda del criterio di valutazione Nel caso di criterio statistico
Analisi della disponibilità d acqua Valutazione dell impianto attraverso il calcolo di un indice economico (criterio) Approccio diverso a seconda del criterio di valutazione Nel caso di criterio statistico
Università di Siena. Teoria della Stima. Lucidi del corso di. Identificazione e Analisi dei Dati A.A
 Università di Siena Teoria della Stima Lucidi del corso di A.A. 2002-2003 Università di Siena 1 Indice Approcci al problema della stima Stima parametrica Stima bayesiana Proprietà degli stimatori Stime
Università di Siena Teoria della Stima Lucidi del corso di A.A. 2002-2003 Università di Siena 1 Indice Approcci al problema della stima Stima parametrica Stima bayesiana Proprietà degli stimatori Stime
Test delle Ipotesi Parte I
 Test delle Ipotesi Parte I Test delle Ipotesi sulla media Introduzione Definizioni basilari Teoria per il caso di varianza nota Rischi nel test delle ipotesi Teoria per il caso di varianza non nota Test
Test delle Ipotesi Parte I Test delle Ipotesi sulla media Introduzione Definizioni basilari Teoria per il caso di varianza nota Rischi nel test delle ipotesi Teoria per il caso di varianza non nota Test
Calcolo delle Probabilità e Statistica Matematica: definizioni prima parte. Cap.1: Probabilità
 Calcolo delle Probabilità e Statistica Matematica: definizioni prima parte Cap.1: Probabilità 1. Esperimento aleatorio (definizione informale): è un esperimento che a priori può avere diversi esiti possibili
Calcolo delle Probabilità e Statistica Matematica: definizioni prima parte Cap.1: Probabilità 1. Esperimento aleatorio (definizione informale): è un esperimento che a priori può avere diversi esiti possibili
CHEMIOMETRIA. CONFRONTO CON VALORE ATTESO (test d ipotesi) CONFRONTO DI VALORI MISURATI (test d ipotesi) CONFRONTO DI RIPRODUCIBILITA (test d ipotesi)
 CHEMIOMETRIA Applicazione di metodi matematici e statistici per estrarre (massima) informazione chimica (affidabile) da dati chimici INCERTEZZA DI MISURA (intervallo di confidenza/fiducia) CONFRONTO CON
CHEMIOMETRIA Applicazione di metodi matematici e statistici per estrarre (massima) informazione chimica (affidabile) da dati chimici INCERTEZZA DI MISURA (intervallo di confidenza/fiducia) CONFRONTO CON
Corso Integrato di Statistica Informatica e Analisi dei Dati Sperimentali. Esercitazione E
 Corso Integrato di Statistica Informatica e Analisi dei Dati Sperimentali A.A 2009-2010 Esercitazione E Scopo dell esercitazione Applicazioni del teorema del limite centrale. Rappresentazione delle incertezze
Corso Integrato di Statistica Informatica e Analisi dei Dati Sperimentali A.A 2009-2010 Esercitazione E Scopo dell esercitazione Applicazioni del teorema del limite centrale. Rappresentazione delle incertezze
Analisi di Regressione Multipla
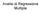 Analisi di Regressione Multipla Stima OLS della relazione Test Score/STR : TestScore! = 698.9.8 STR, R =.05, SER = 18.6 (10.4) (0.5) E una stima credibile dell effetto causale sul rendimento nei test di
Analisi di Regressione Multipla Stima OLS della relazione Test Score/STR : TestScore! = 698.9.8 STR, R =.05, SER = 18.6 (10.4) (0.5) E una stima credibile dell effetto causale sul rendimento nei test di
Statistica Applicata all edilizia: il modello di regressione
 Statistica Applicata all edilizia: il modello di regressione E-mail: orietta.nicolis@unibg.it 27 aprile 2009 Indice Il modello di Regressione Lineare 1 Il modello di Regressione Lineare Analisi di regressione
Statistica Applicata all edilizia: il modello di regressione E-mail: orietta.nicolis@unibg.it 27 aprile 2009 Indice Il modello di Regressione Lineare 1 Il modello di Regressione Lineare Analisi di regressione
Vettore (o matrice) casuale (o aleatorio): vettore (o matrice) i cui elementi sono variabili aleatorie
 Variabili (vettori e matrici) casuali Variabile casuale (o aleatoria): Variabile che può assumere un insieme di valori ognuno con una certa probabilità La variabile aleatoria rappresenta la popolazione
Variabili (vettori e matrici) casuali Variabile casuale (o aleatoria): Variabile che può assumere un insieme di valori ognuno con una certa probabilità La variabile aleatoria rappresenta la popolazione
GEOMETRIA svolgimento di uno scritto del 11 Gennaio 2012
 GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
PAROLE CHIAVE Accuratezza, Accuracy, Esattezza, PRECISIONE, Precision, Ripetibilità, Affidabilità, Reliability, Scarto quadratico medio (sqm), Errore
 PAROLE CHIAVE Accuratezza, Accuracy, Esattezza, PRECISIONE, Precision, Ripetibilità, Affidabilità, Reliability, Scarto quadratico medio (sqm), Errore medio, Errore quadratico medio (eqm), Deviazione standard,
PAROLE CHIAVE Accuratezza, Accuracy, Esattezza, PRECISIONE, Precision, Ripetibilità, Affidabilità, Reliability, Scarto quadratico medio (sqm), Errore medio, Errore quadratico medio (eqm), Deviazione standard,
Intervalli di confidenza
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Intervalli di confidenza Ines Campa Probabilità e Statistica - Esercitazioni
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Intervalli di confidenza Ines Campa Probabilità e Statistica - Esercitazioni
1. variabili dicotomiche: 2 sole categorie A e B
 Variabile X su scala qualitativa (due categorie) modello di regressione: variabili quantitative misurate almeno su scala intervallo (meglio se Y è di questo tipo e preferibilmente anche le X i ) variabili
Variabile X su scala qualitativa (due categorie) modello di regressione: variabili quantitative misurate almeno su scala intervallo (meglio se Y è di questo tipo e preferibilmente anche le X i ) variabili
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di:
 Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Esperimentazioni di Fisica 1. Prova d esame del 20 febbraio 2018 SOLUZIONI
 Esperimentazioni di Fisica 1 Prova d esame del 20 febbraio 2018 SOLUZIONI Esp-1-Soluzioni - - Page 2 of 6 01/02/2018 1. (12 Punti) Quesito. In un esperimento è stata misurata la grandezza Y in funzione
Esperimentazioni di Fisica 1 Prova d esame del 20 febbraio 2018 SOLUZIONI Esp-1-Soluzioni - - Page 2 of 6 01/02/2018 1. (12 Punti) Quesito. In un esperimento è stata misurata la grandezza Y in funzione
Calcolo Numerico con elementi di programmazione
 Calcolo Numerico con elementi di programmazione (A.A. 2014-2015) Appunti delle lezioni sui metodi numerici per la soluzione di sistemi lineari Metodi Iterativi la soluzione si ottiene tramite approssimazioni
Calcolo Numerico con elementi di programmazione (A.A. 2014-2015) Appunti delle lezioni sui metodi numerici per la soluzione di sistemi lineari Metodi Iterativi la soluzione si ottiene tramite approssimazioni
Università di Pavia Econometria. Richiami di Statistica. Eduardo Rossi
 Università di Pavia Econometria Richiami di Statistica Eduardo Rossi Università di Pavia Campione casuale Siano (Y 1, Y 2,..., Y N ) variabili casuali tali che le y i siano realizzazioni mutuamente indipendenti
Università di Pavia Econometria Richiami di Statistica Eduardo Rossi Università di Pavia Campione casuale Siano (Y 1, Y 2,..., Y N ) variabili casuali tali che le y i siano realizzazioni mutuamente indipendenti
Note sulla probabilità
 Note sulla probabilità Maurizio Loreti Dipartimento di Fisica Università degli Studi di Padova Anno Accademico 2002 03 1 La distribuzione del χ 2 0.6 0.5 N=1 N=2 N=3 N=5 N=10 0.4 0.3 0.2 0.1 0 0 5 10 15
Note sulla probabilità Maurizio Loreti Dipartimento di Fisica Università degli Studi di Padova Anno Accademico 2002 03 1 La distribuzione del χ 2 0.6 0.5 N=1 N=2 N=3 N=5 N=10 0.4 0.3 0.2 0.1 0 0 5 10 15
Analisi della varianza
 Analisi della varianza Prof. Giuseppe Verlato Sezione di Epidemiologia e Statistica Medica, Università di Verona ANALISI DELLA VARIANZA - 1 Abbiamo k gruppi, con un numero variabile di unità statistiche.
Analisi della varianza Prof. Giuseppe Verlato Sezione di Epidemiologia e Statistica Medica, Università di Verona ANALISI DELLA VARIANZA - 1 Abbiamo k gruppi, con un numero variabile di unità statistiche.
Esperimentazioni di Fisica 1. Prova in itinere del 12 giugno 2018
 Esperimentazioni di Fisica 1 Prova in itinere del 1 giugno 018 Esp-1 Prova in Itinere n. - - Page of 6 1/06/018 1. (1 Punti) Quesito L incertezza da associare alle misurazioni eseguite con un certo strumento
Esperimentazioni di Fisica 1 Prova in itinere del 1 giugno 018 Esp-1 Prova in Itinere n. - - Page of 6 1/06/018 1. (1 Punti) Quesito L incertezza da associare alle misurazioni eseguite con un certo strumento
La curva di regressione è il luogo dei punti aventi come ordinate le medie condizionate
 Correlazione e regressione Correlazione: le due variabili casuali sono considerate in modo per così dire simmetrico. Regressione: una delle due variabili dipende dall'altra, che per così dire la precede
Correlazione e regressione Correlazione: le due variabili casuali sono considerate in modo per così dire simmetrico. Regressione: una delle due variabili dipende dall'altra, che per così dire la precede
Corso di Statistica - Prof. Fabio Zucca IV Appello - 5 febbraio Esercizio 1
 Corso di Statistica - Prof. Fabio Zucca IV Appello - 5 febbraio 2015 Nome e cognome: Matricola: c I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. 8994
Corso di Statistica - Prof. Fabio Zucca IV Appello - 5 febbraio 2015 Nome e cognome: Matricola: c I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. 8994
LEZIONI DI STATISTICA MEDICA
 LEZIONI DI STATISTICA MEDICA Lezione n.11 - Principi dell inferenza statistica - Campionamento - Distribuzione campionaria di una media e di una proporzione - Intervallo di confidenza di una media e di
LEZIONI DI STATISTICA MEDICA Lezione n.11 - Principi dell inferenza statistica - Campionamento - Distribuzione campionaria di una media e di una proporzione - Intervallo di confidenza di una media e di
LA DISTRIBUZIONE NORMALE o DI GAUSS
 p. 1/2 LA DISTRIBUZIONE NORMALE o DI GAUSS Osservando gli istogrammi delle misure e degli scarti, nel caso di osservazioni ripetute in identiche condizioni Gli istogrammi sono campanulari e simmetrici,
p. 1/2 LA DISTRIBUZIONE NORMALE o DI GAUSS Osservando gli istogrammi delle misure e degli scarti, nel caso di osservazioni ripetute in identiche condizioni Gli istogrammi sono campanulari e simmetrici,
ESTRAZIONE DI DATI 3D DA IMMAGINI DIGITALI. (Visione 3D)
 ESTRAZIONE DI DATI 3D DA IMMAGINI DIGITALI () Calibrazione intrinseca Spesso risulta utile calibrare la sola componente intrinseca di un sistema di visione (matrice K), e non si dispone di oggetti di forma
ESTRAZIONE DI DATI 3D DA IMMAGINI DIGITALI () Calibrazione intrinseca Spesso risulta utile calibrare la sola componente intrinseca di un sistema di visione (matrice K), e non si dispone di oggetti di forma
05. Errore campionario e numerosità campionaria
 Statistica per le ricerche di mercato A.A. 01/13 05. Errore campionario e numerosità campionaria Gli schemi di campionamento condividono lo stesso principio di fondo: rappresentare il più fedelmente possibile,
Statistica per le ricerche di mercato A.A. 01/13 05. Errore campionario e numerosità campionaria Gli schemi di campionamento condividono lo stesso principio di fondo: rappresentare il più fedelmente possibile,
Analisi multivariata per osservazioni appaiate. Analisi multivariata per osservazioni appaiate
 Introduzione Notazione Modello additivo Verifica d ipotesi Sia X una variabile q-dimensionale, a valori reali, non degenere, osservata in k tempi diversi (τ 1, τ 2,..., τ k ), sulle stesse n unità statistiche
Introduzione Notazione Modello additivo Verifica d ipotesi Sia X una variabile q-dimensionale, a valori reali, non degenere, osservata in k tempi diversi (τ 1, τ 2,..., τ k ), sulle stesse n unità statistiche
Elaborazione statistica di dati
 Elaborazione statistica di dati CONCETTI DI BASE DI STATISTICA ELEMENTARE Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Collaudo sistemi di produzione IPOTESI:
Elaborazione statistica di dati CONCETTI DI BASE DI STATISTICA ELEMENTARE Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Collaudo sistemi di produzione IPOTESI:
Laboratorio di Didattica di elaborazione dati 5 STIMA PUNTUALE DEI PARAMETRI. x i. SE = n.
 5 STIMA PUNTUALE DEI PARAMETRI [Adattato dal libro Excel per la statistica di Enzo Belluco] Sia θ un parametro incognito della distribuzione di un carattere in una determinata popolazione. Il problema
5 STIMA PUNTUALE DEI PARAMETRI [Adattato dal libro Excel per la statistica di Enzo Belluco] Sia θ un parametro incognito della distribuzione di un carattere in una determinata popolazione. Il problema
Ulteriori Conoscenze di Informatica e Statistica
 Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it Indici di forma Descrivono le
Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it Indici di forma Descrivono le
Analisi delle componenti principali
 Analisi delle componenti principali Serve a rappresentare un fenomeno k-dimensionale tramite un numero inferiore o uguale a k di variabili incorrelate, ottenute trasformando le variabili osservate Consiste
Analisi delle componenti principali Serve a rappresentare un fenomeno k-dimensionale tramite un numero inferiore o uguale a k di variabili incorrelate, ottenute trasformando le variabili osservate Consiste
Università di Siena. Corso di STATISTICA. Parte seconda: Teoria della stima. Andrea Garulli, Antonello Giannitrapani, Simone Paoletti
 Università di Siena Corso di STATISTICA Parte seconda: Teoria della stima Andrea Garulli, Antonello Giannitrapani, Simone Paoletti Master E 2 C Centro per lo Studio dei Sistemi Complessi Università di
Università di Siena Corso di STATISTICA Parte seconda: Teoria della stima Andrea Garulli, Antonello Giannitrapani, Simone Paoletti Master E 2 C Centro per lo Studio dei Sistemi Complessi Università di
Intervalli di confidenza
 Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Esercizi di statistica
 Esercizi di statistica Test a scelta multipla (la risposta corretta è la prima) [1] Il seguente campione è stato estratto da una popolazione distribuita normalmente: -.4, 5.5,, -.5, 1.1, 7.4, -1.8, -..
Esercizi di statistica Test a scelta multipla (la risposta corretta è la prima) [1] Il seguente campione è stato estratto da una popolazione distribuita normalmente: -.4, 5.5,, -.5, 1.1, 7.4, -1.8, -..
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Maria Prandini Dipartimento di Elettronica e Informazione Politecnico di Milano
 Note relative a test di bianchezza rimozione delle componenti deterministiche da una serie temporale a supporto del Progetto di Identificazione dei Modelli e Analisi dei Dati Maria Prandini Dipartimento
Note relative a test di bianchezza rimozione delle componenti deterministiche da una serie temporale a supporto del Progetto di Identificazione dei Modelli e Analisi dei Dati Maria Prandini Dipartimento
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
11 luglio Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
LEZIONE 16 A = Verifichiamo se qualcuna fra le entrate a di A è suo autovalore. determinare per quale entrata a di A risulta rk(a ai 2 ) 1.
 LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
Ulteriori Conoscenze di Informatica e Statistica. Popolazione. Campione. I risultati di un esperimento sono variabili aleatorie.
 Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it I risultati di un esperimento
Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it I risultati di un esperimento
Corso in Statistica Medica
 Corso in Statistica Medica Introduzione alle tecniche statistiche di elaborazione dati Intervalli di confidenza Dott. Angelo Menna Università degli Studi di Chieti G. d Annunziod Annunzio Anno Accademico
Corso in Statistica Medica Introduzione alle tecniche statistiche di elaborazione dati Intervalli di confidenza Dott. Angelo Menna Università degli Studi di Chieti G. d Annunziod Annunzio Anno Accademico
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A PROVA SCRITTA DI GEOMETRIA DEL Compito A Corso del Prof.
 CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. 202-203 PROVA SCRITTA DI GEOMETRIA DEL 8-02-3 Compito A Corso del Prof. Manlio BORDONI Esercizio. Sia W il sottospazio vettoriale di R 4 generato dai vettori
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. 202-203 PROVA SCRITTA DI GEOMETRIA DEL 8-02-3 Compito A Corso del Prof. Manlio BORDONI Esercizio. Sia W il sottospazio vettoriale di R 4 generato dai vettori
I numeri complessi. Andrea Corli 31 agosto Motivazione 1. 2 Definizioni 1. 3 Forma trigonometrica di un numero complesso 3
 I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE
 S.S.I.S TOSCANA F.I.M. -II anno STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE PROBLEMA 1 Vogliamo valutare la percentuale p di donne fumatrici tra le donne in età fertile. Procediamo all estrazione
S.S.I.S TOSCANA F.I.M. -II anno STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE PROBLEMA 1 Vogliamo valutare la percentuale p di donne fumatrici tra le donne in età fertile. Procediamo all estrazione
Laboratorio di Chimica Fisica. Analisi Statistica
 Università degli Studi di Bari Dipartimento di Chimica 9 giugno F.Mavelli- Laboratorio Chimica Fisica - a.a. 3-4 F.Mavelli Laboratorio di Chimica Fisica a.a. 3-4 Analisi Statistica dei Dati Analisi Statistica
Università degli Studi di Bari Dipartimento di Chimica 9 giugno F.Mavelli- Laboratorio Chimica Fisica - a.a. 3-4 F.Mavelli Laboratorio di Chimica Fisica a.a. 3-4 Analisi Statistica dei Dati Analisi Statistica
Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio Esercizio 1
 Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio 2012 Esercizio 1 (a) Si calcola il polinomio caratteristico λ 2 1 p(λ) = det k 1 2k λ k 1 2 2 λ usando lo sviluppo di Laplace secondo
Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio 2012 Esercizio 1 (a) Si calcola il polinomio caratteristico λ 2 1 p(λ) = det k 1 2k λ k 1 2 2 λ usando lo sviluppo di Laplace secondo
Università della Calabria
 Università della Calabria FACOLTA DI INGEGNERIA Corso di Laurea in Ingegneria Civile CORSO DI IDROLOGIA N.O. Prof. Pasquale Versace SCHEDA DIDATTICA N 3 CURVE DI PROBABILITÀ PLUVIOMETRICA A.A. 00- CURVE
Università della Calabria FACOLTA DI INGEGNERIA Corso di Laurea in Ingegneria Civile CORSO DI IDROLOGIA N.O. Prof. Pasquale Versace SCHEDA DIDATTICA N 3 CURVE DI PROBABILITÀ PLUVIOMETRICA A.A. 00- CURVE
IL METODO DELLE OSSERVAZIONI INDIRETTE
 Metodo delle osservazioni indirette.nb CORSO DI TOPOGRAFIA A - A.A. 2005-2006 LEZIONE - 25.05.06 IL METODO DELLE OSSERVAZIONI INDIRETTE IL CRITERIO DI MASSIMA VEROSIMIGLIANZA Sia data una grandezza h e
Metodo delle osservazioni indirette.nb CORSO DI TOPOGRAFIA A - A.A. 2005-2006 LEZIONE - 25.05.06 IL METODO DELLE OSSERVAZIONI INDIRETTE IL CRITERIO DI MASSIMA VEROSIMIGLIANZA Sia data una grandezza h e
Argomenti della lezione: Campionamento Stima Distribuzione campionaria Campione Popolazione Sottoinsieme degli elementi (o universo) dell '
 Lezione 2 Argomenti della lezione: La statistica inferenziale: concetti di base Campionamento Stima Distribuzione campionaria Popolazione (o universo) Insieme di tutti gli elementi cui si rivolge il ricercatore
Lezione 2 Argomenti della lezione: La statistica inferenziale: concetti di base Campionamento Stima Distribuzione campionaria Popolazione (o universo) Insieme di tutti gli elementi cui si rivolge il ricercatore
Modelli descrittivi, statistica e simulazione
 Modelli descrittivi, statistica e simulazione Master per Smart Logistics specialist Roberto Cordone (roberto.cordone@unimi.it) Statistica inferenziale Cernusco S.N., giovedì 25 febbraio 2016 (9.00/13.00)
Modelli descrittivi, statistica e simulazione Master per Smart Logistics specialist Roberto Cordone (roberto.cordone@unimi.it) Statistica inferenziale Cernusco S.N., giovedì 25 febbraio 2016 (9.00/13.00)
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di:
 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza di Variabili Aleatorie Sistema di Variabili
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza di Variabili Aleatorie Sistema di Variabili
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi
 La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
Statistica. Capitolo 12. Regressione Lineare Semplice. Cap. 12-1
 Statistica Capitolo 1 Regressione Lineare Semplice Cap. 1-1 Obiettivi del Capitolo Dopo aver completato il capitolo, sarete in grado di: Spiegare il significato del coefficiente di correlazione lineare
Statistica Capitolo 1 Regressione Lineare Semplice Cap. 1-1 Obiettivi del Capitolo Dopo aver completato il capitolo, sarete in grado di: Spiegare il significato del coefficiente di correlazione lineare
MODELLO DI REGRESSIONE LINEARE. le ipotesi del modello di regressione classico, stima con i metodi dei minimi quadrati e di massima verosimiglianza,
 MODELLO DI REGRESSIONE LINEARE le ipotesi del modello di regressione classico, stima con i metodi dei minimi quadrati e di massima verosimiglianza, teorema di Gauss-Markov, verifica di ipotesi e test di
MODELLO DI REGRESSIONE LINEARE le ipotesi del modello di regressione classico, stima con i metodi dei minimi quadrati e di massima verosimiglianza, teorema di Gauss-Markov, verifica di ipotesi e test di
Ulteriori conoscenze di informatica Elementi di statistica Esercitazione3
 Ulteriori conoscenze di informatica Elementi di statistica Esercitazione3 Sui PC a disposizione sono istallati diversi sistemi operativi. All accensione scegliere Windows. Immettere Nome utente b## (##
Ulteriori conoscenze di informatica Elementi di statistica Esercitazione3 Sui PC a disposizione sono istallati diversi sistemi operativi. All accensione scegliere Windows. Immettere Nome utente b## (##
PROVA SCRITTA DEL 10 LUGLIO 2008 e SOLUZIONI. Per ognuno dei seguenti quiz indicare l unica risposta corretta tra le quattro proposte.
 Geometria B1-02efe Geometria - 13bcg PROVA SCRITTA DEL 10 LUGLIO 2008 e SOLUZIONI Per ognuno dei seguenti quiz indicare l unica risposta corretta tra le quattro proposte. Esercizio 1. Sia u, v, w vettori
Geometria B1-02efe Geometria - 13bcg PROVA SCRITTA DEL 10 LUGLIO 2008 e SOLUZIONI Per ognuno dei seguenti quiz indicare l unica risposta corretta tra le quattro proposte. Esercizio 1. Sia u, v, w vettori
Esercitazione del
 Esercizi sulla regressione lineare. Esercitazione del 21.05.2013 Esercizio dal tema d esame del 13.06.2011. Si consideri il seguente campione di n = 9 osservazioni relative ai caratteri ed Y: 7 17 8 36
Esercizi sulla regressione lineare. Esercitazione del 21.05.2013 Esercizio dal tema d esame del 13.06.2011. Si consideri il seguente campione di n = 9 osservazioni relative ai caratteri ed Y: 7 17 8 36
Analisi statistica e matematico-finanziaria II. Alfonso Iodice D Enza Università degli studi di Cassino e del Lazio Meridionale
 delle sui delle Analisi statistica e matematico-finanziaria II Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino e del Lazio Meridionale sulle particolari ali dei dati Outline
delle sui delle Analisi statistica e matematico-finanziaria II Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino e del Lazio Meridionale sulle particolari ali dei dati Outline
Analisi della varianza: I contrasti e il metodo di Bonferroni
 Analisi della varianza: I contrasti e il metodo di Bonferroni 1 Contrasti In molti problemi risulta importante stabilire, nel caso venga rifiutata l ipotesi nulla, di uguaglianza delle medie µ j delle
Analisi della varianza: I contrasti e il metodo di Bonferroni 1 Contrasti In molti problemi risulta importante stabilire, nel caso venga rifiutata l ipotesi nulla, di uguaglianza delle medie µ j delle
Tutorato di Complementi di Analisi Matematica e Statistica 30 maggio 2016
 Tutorato di Complementi di Analisi Matematica e Statistica 30 maggio 2016 Esercizi possibili di probabilità e statistica Notazioni: U(a, b) è la distribuzione di probabilità uniforma nell intervallo (a,
Tutorato di Complementi di Analisi Matematica e Statistica 30 maggio 2016 Esercizi possibili di probabilità e statistica Notazioni: U(a, b) è la distribuzione di probabilità uniforma nell intervallo (a,
Sviluppando ancora per colonna sulla prima colonna della prima matrice e sulla seconda della seconda matrice si ottiene:
 M. CARAMIA, S. GIORDANI, F. GUERRIERO, R. MUSMANNO, D. PACCIARELLI RICERCA OPERATIVA Isedi Esercizi proposti nel Cap. 5 - Soluzioni Esercizio 5. - La norma Euclidea di è 9 6 5 - Il versore corrispondente
M. CARAMIA, S. GIORDANI, F. GUERRIERO, R. MUSMANNO, D. PACCIARELLI RICERCA OPERATIVA Isedi Esercizi proposti nel Cap. 5 - Soluzioni Esercizio 5. - La norma Euclidea di è 9 6 5 - Il versore corrispondente
= q q1
 COMPENSAZIONE CON IL METODO DEI MINIMI QUADRATI. Introduzione Le misure geodetiche e topografiche, che in molti casi non riguardano solo distanze e angoli, ma anche quantità non puramente geometriche,
COMPENSAZIONE CON IL METODO DEI MINIMI QUADRATI. Introduzione Le misure geodetiche e topografiche, che in molti casi non riguardano solo distanze e angoli, ma anche quantità non puramente geometriche,
GEOMETRIA 1 Autovalori e autovettori
 GEOMETRIA 1 Autovalori e autovettori Gilberto Bini - Anna Gori - Cristina Turrini 2018/2019 Gilberto Bini - Anna Gori - Cristina Turrini (2018/2019) GEOMETRIA 1 1 / 28 index Matrici rappresentative "semplici"
GEOMETRIA 1 Autovalori e autovettori Gilberto Bini - Anna Gori - Cristina Turrini 2018/2019 Gilberto Bini - Anna Gori - Cristina Turrini (2018/2019) GEOMETRIA 1 1 / 28 index Matrici rappresentative "semplici"
Concetti di teoria dei campioni ad uso degli studenti di Statistica Economica e Finanziaria, A.A. 2017/2018. Giovanni Lafratta
 Concetti di teoria dei campioni ad uso degli studenti di Statistica Economica e Finanziaria, A.A. 2017/2018 Giovanni Lafratta ii Indice 1 Spazi, Disegni e Strategie Campionarie 1 2 Campionamento casuale
Concetti di teoria dei campioni ad uso degli studenti di Statistica Economica e Finanziaria, A.A. 2017/2018 Giovanni Lafratta ii Indice 1 Spazi, Disegni e Strategie Campionarie 1 2 Campionamento casuale
L analisi dei dati. Primi elementi. EEE- Cosmic Box proff.: M.Cottino, P.Porta
 L analisi dei dati Primi elementi Metodo dei minimi quadrati Negli esperimenti spesso si misurano parecchie volte due diverse variabili fisiche per investigare la relazione matematica tra le due variabili.
L analisi dei dati Primi elementi Metodo dei minimi quadrati Negli esperimenti spesso si misurano parecchie volte due diverse variabili fisiche per investigare la relazione matematica tra le due variabili.
I appello di calcolo delle probabilità e statistica
 I appello di calcolo delle probabilità e statistica A.Barchielli, L. Ladelli, G. Posta 8 Febbraio 13 Nome: Cognome: Matricola: Docente: I diritti d autore sono riservati. Ogni sfruttamento commerciale
I appello di calcolo delle probabilità e statistica A.Barchielli, L. Ladelli, G. Posta 8 Febbraio 13 Nome: Cognome: Matricola: Docente: I diritti d autore sono riservati. Ogni sfruttamento commerciale
STATISTICA A K (60 ore)
 STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it Richiami sulla regressione Marco Riani, Univ. di Parma 1 MODELLO DI REGRESSIONE y i = a + bx i + e i dove: i = 1,, n a + bx i rappresenta
STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it Richiami sulla regressione Marco Riani, Univ. di Parma 1 MODELLO DI REGRESSIONE y i = a + bx i + e i dove: i = 1,, n a + bx i rappresenta
DISTRIBUZIONI DI CAMPIONAMENTO
 DISTRIBUZIONI DI CAMPIONAMENTO 12 DISTRIBUZIONE DI CAMPIONAMENTO DELLA MEDIA Situazione reale Della popolazione di tutti i laureati in odontoiatria negli ultimi 10 anni, in tutte le Università d Italia,
DISTRIBUZIONI DI CAMPIONAMENTO 12 DISTRIBUZIONE DI CAMPIONAMENTO DELLA MEDIA Situazione reale Della popolazione di tutti i laureati in odontoiatria negli ultimi 10 anni, in tutte le Università d Italia,
x ;x Soluzione Gli intervalli di confidenza possono essere ottenuti a partire dalla seguente identità: da cui si ricava: IC x ;x = +
 ESERCIZIO 6.1 Si considerino i 0 campioni di ampiezza n = estratti da una popolazione X di N = 5 elementi distribuiti normalmente, con media µ = 13,6 e σ = 8,33. A partire dalle 0 determinazioni della
ESERCIZIO 6.1 Si considerino i 0 campioni di ampiezza n = estratti da una popolazione X di N = 5 elementi distribuiti normalmente, con media µ = 13,6 e σ = 8,33. A partire dalle 0 determinazioni della
Nel modello omoschedastico la varianza dell errore non dipende da i ed è quindi pari a σ 0.
 Regressione [] el modello di regressione lineare si assume una relazione di tipo lineare tra il valore medio della variabile dipendente Y e quello della variabile indipendente X per cui Il modello si scrive
Regressione [] el modello di regressione lineare si assume una relazione di tipo lineare tra il valore medio della variabile dipendente Y e quello della variabile indipendente X per cui Il modello si scrive
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Minimi quadrati ordinari Interpretazione geometrica. Eduardo Rossi
 Minimi quadrati ordinari Interpretazione geometrica Eduardo Rossi Il MRLM Il modello di regressione lineare multipla è usato per studiare le relazioni tra la variabile dipendente e diverse variabili indipendenti
Minimi quadrati ordinari Interpretazione geometrica Eduardo Rossi Il MRLM Il modello di regressione lineare multipla è usato per studiare le relazioni tra la variabile dipendente e diverse variabili indipendenti
Probabilità e Statistica
 Probabilità e Statistica Intervalli di confidenza Marco Pietro Longhi C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica a.s. 2018/2019 Marco Pietro Longhi Prob. e Stat. 1
Probabilità e Statistica Intervalli di confidenza Marco Pietro Longhi C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica a.s. 2018/2019 Marco Pietro Longhi Prob. e Stat. 1
Analisi e scelta dei dati di input
 Analisi e scelta dei dati di input Corso di Tecniche di Simulazione, a.a. 2005/2006 Francesca Mazzia Dipartimento di Matematica Università di Bari 24 Aprile 2006 Francesca Mazzia (Univ. Bari) Analisi e
Analisi e scelta dei dati di input Corso di Tecniche di Simulazione, a.a. 2005/2006 Francesca Mazzia Dipartimento di Matematica Università di Bari 24 Aprile 2006 Francesca Mazzia (Univ. Bari) Analisi e
Analisi della Regressione Lineare
 Analisi della Regressione Lineare Master in Tecnologie Bioinformatiche 29/09/06 Adriano Decarli 1 29/09/06 Adriano Decarli 2 29/09/06 Adriano Decarli 3 29/09/06 Adriano Decarli 4 29/09/06 Adriano Decarli
Analisi della Regressione Lineare Master in Tecnologie Bioinformatiche 29/09/06 Adriano Decarli 1 29/09/06 Adriano Decarli 2 29/09/06 Adriano Decarli 3 29/09/06 Adriano Decarli 4 29/09/06 Adriano Decarli
Errata corrige. p. 10 riga 5 del secondo paragrafo: misurare
 Errata corrige p. 9 esercizio 5. Modificare testo dell esercizio come segue: Dati una retta r e un punto P, esistono infiniti piani per P paralleli a r: si tratta dei piani che contengono la retta s per
Errata corrige p. 9 esercizio 5. Modificare testo dell esercizio come segue: Dati una retta r e un punto P, esistono infiniti piani per P paralleli a r: si tratta dei piani che contengono la retta s per
Soluzioni dello scritto di Geometria del 28 Maggio 2009
 Soluzioni dello scritto di Geometria del 8 Maggio 9 1) Trovare le equazioni del sottospazio V(w, x, y, z) R 4 generato dalle quaterne c 1 = (,,, 1) e c = (, 1, 1, ). ) Trovare una base per OGNI autospazio
Soluzioni dello scritto di Geometria del 8 Maggio 9 1) Trovare le equazioni del sottospazio V(w, x, y, z) R 4 generato dalle quaterne c 1 = (,,, 1) e c = (, 1, 1, ). ) Trovare una base per OGNI autospazio
Σ (x i - x) 2 = Σ x i 2 - (Σ x i ) 2 / n Σ (y i - y) 2 = Σ y i 2 - (Σ y i ) 2 / n. 13. Regressione lineare parametrica
 13. Regressione lineare parametrica Esistono numerose occasioni nelle quali quello che interessa è ricostruire la relazione di funzione che lega due variabili, la variabile y (variabile dipendente, in
13. Regressione lineare parametrica Esistono numerose occasioni nelle quali quello che interessa è ricostruire la relazione di funzione che lega due variabili, la variabile y (variabile dipendente, in
Cognome e Nome:... Matricola e corso di laurea:...
 Statistica - corso base Prof. B. Liseo Prova di esame dell 8 gennaio 2014 Cognome e Nome:................................................................... Matricola e corso di laurea:...................................................
Statistica - corso base Prof. B. Liseo Prova di esame dell 8 gennaio 2014 Cognome e Nome:................................................................... Matricola e corso di laurea:...................................................
Dispensa di Statistica
 Dispensa di Statistica 1 parziale 2012/2013 Diagrammi... 2 Indici di posizione... 4 Media... 4 Moda... 5 Mediana... 5 Indici di dispersione... 7 Varianza... 7 Scarto Quadratico Medio (SQM)... 7 La disuguaglianza
Dispensa di Statistica 1 parziale 2012/2013 Diagrammi... 2 Indici di posizione... 4 Media... 4 Moda... 5 Mediana... 5 Indici di dispersione... 7 Varianza... 7 Scarto Quadratico Medio (SQM)... 7 La disuguaglianza
Variabili indipendenti qualitative. In molte applicazioni si rende necessario l introduzione di un fattore a due o più livelli.
 Variabili indipendenti qualitative Di solito le variabili nella regressione sono variabili continue In molte applicazioni si rende necessario l introduzione di un fattore a due o più livelli Ad esempio:
Variabili indipendenti qualitative Di solito le variabili nella regressione sono variabili continue In molte applicazioni si rende necessario l introduzione di un fattore a due o più livelli Ad esempio:
Ulteriori Conoscenze di Informatica e Statistica
 ndici di forma Ulteriori Conoscenze di nformatica e Statistica Descrivono le asimmetrie della distribuzione Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 ( piano) tel.: 06 55 17 72 17
ndici di forma Ulteriori Conoscenze di nformatica e Statistica Descrivono le asimmetrie della distribuzione Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 ( piano) tel.: 06 55 17 72 17
- ciascun autovalore di T ha molteplicità geometrica uguale alla moltplicitaà algebrica.
 Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e

 8(+#.%09:;
8(+#.%09:;