MECCANICA ANALITICA E RELATIVISTICA - I ESONERO - 14/12/2016
|
|
|
- Rebecca Ricci
- 4 anni fa
- Visualizzazioni
Transcript
1 MECCANICA ANALITICA E RELATIVISTICA - I ESONERO - 14/1/016 In un piano verticale è scelto un sistema di riferimento di assi cartesiani ortogonali Oz di origine O e con l asse z orientato verso il basso. In tale piano si muove un asta rigida omogenea di estremi A e B, massa M e lunghezza L (vd figura). Il punto D di tale asta dista L/4 dall estremo A ed è obbligato a scorrere senza attrito su di una guida parallela all asse e passante per il punto P di coordinate (0, d). Oltre alla forza peso l asta è soggetta a due forze attive F 1 = KP D e F = KHB, dove K > 0 e H è la proiezione ortogonale di B sull asse. Scegliamo come coordinate lagrangiane per descrivere il sistema l ascissa del punto D e l angolo θ che l asta forma con la guida parallela all asse. 1. Scrivere la lagrangiana del sistema e le equazioni del moto.. Trovare le posizioni di equilibrio e discuterne il numero e la stabilità in funzione del parametro λ = 4d 3L 4Mg 9LK. 3. Si ponga in queste domande K = M = g = L = 1 e d = 10/9. Scelta, quindi, una posizione di equilibrio stabile si determinino le frequenze delle piccole oscillazioni. O H B G P D θ A z
2 II Esonero di Meccanica Analitica e Relativistica - 5/01/017 Proff. S. Caprara, M. Grilli, L. Gualtieri 1. Si risolva il seguente problema nell ambito della relatività ristretta. Due astronavi si muovono lungo l asse. Ambedue partono contemporaneamente dall origine. La prima si muove con velocità c/ per un tempo T, poi inverte il moto e torna con velocità c/4 nell origine, dove si ferma. La seconda si muove con velocità c/3 per un tempo 3 T, poi inverte il moto e torna con velocità c/3 nell origine, dove si ferma. I due astronauti avevano portato a bordo un orologio ciascuno. Una volta ambedue nell origine li confrontano: chi ha segnato meno tempo e di quanto?. Si risolva il seguente problema nell ambito della relatività ristretta. Un corpo di massa a riposo m si muove lungo l asse ed è soggetto ad un energia potenziale U() = A 5 (con A > 0). Sapendo che transita per l origine con velocità v 0, si determini la massima distanza d dall origine raggiunta. 3. Sia data la trasformazione Q = 16p 4 q P = 1 3 qβ p 3 Si dica per quali valori reali di β la trasformazione è canonica e si ricavi la funzione generatrice F 1 (q, Q). 4. Si risolva il seguente problema nell ambito della relatività ristretta. Sia dato, in un sistema di riferimento inerziale, un sistema di coordinate spazio-temporale (ct,, y, z). Indicare se esiste un sistema di riferimento nel quale i due eventi E 1 = (1, cos α, sin α, 1), E = (4, 0, 0, 1) (α = π/3) avvengono nella stessa posizione, e, in tal caso, determinare la trasformazione di coordinate tra tale riferimento e il riferimento di partenza. 5. Si risolva il seguente problema nell ambito della relatività ristretta. Una particella di massa a riposo m, ferma nell origine delle coordinate, viene urtata da una particella di massa a riposo 4 5m che si muove nel verso positivo dell asse con velocità v = 3 5c. A seguito dell urto, si produce un unica particella di massa a riposo M che si muove con velocità V. Determinare M e V, assumendo assegnata m.
3 Scritto di Meccanica Analitica e Relativistica - 7 febbraio 017 Proff. S. Caprara, M. Grilli, L. Gualtieri ESERCIZIO 1 La sbarra rigida e omogenea AB, di massa M e lunghezza L, è vincolata a ruotare senza attrito attorno al suo centro di massa, restando sempre sul piano z, sul quale è adottato un sistema di riferimento cartesiano ortogonale la cui origine O coincide con il centro di massa immobile della sbarra. Il punto materiale P, di massa m, è vincolato a muoversi senza attrito lungo l asse w, giacente sul piano z, perpendicolare ad AB e passante per O. Il punto P è collegato ad O da una molla di costante elastica K e lunghezza a riposo nulla. Sul sistema agisce anche la forza di gravità, la cui accelerazione g è diretta nel verso positivo dell asse z. Si indichi con g > 0 il modulo dell accelerazione di gravità. Si adottino come coordinate lagrangiane l angolo θ che la sbarra AB forma con il verso positivo dell asse z e l ascissa ρ di P lungo l asse w, come indicato in Fig. 1. Si scrivano la lagrangiana del sistema e le equazioni del moto. Si individuino le posizioni di equilibrio del sistema e se ne determini la stabilità. Siano ora M = 6, m = 1, L = 4, K = 1, g = 1. Scelta una posizione di equilibrio stabile, si determinino le frequenze delle piccole oscillazioni attorno a tale posizione. A O θ z M,L K ρ P B m w g Fig. 1 ESERCIZIO Data la trasformazione Q = p 1/α q 1/ ; P = (pq) 1/ ln q si dica per quali valori di α la trasformazione è canonica e si ricavi la funzione generatrice F 1 (q, Q).
4 Scritto di Meccanica Analitica e Relativistica del 8 giugno 017 Proff. S. Caprara, M. Grilli, L. Gualtieri ESERCIZIO 1 Una guida circolare rigida, di massa M e raggio R, è vincolata a ruotare attorno al suo punto fisso O sul piano orizzontale y, sul quale è fissato un sistema di riferimento cartesiano ortogonale con origine in O. Un punto materiale P di massa m può scorrere senza attrito lungo la guida circolare. Il punto P è collegato da una molla di lunghezza a riposo nulla e costante elastica K al punto H, proiezione ortogonale di P sulla retta = a, con a > R. Sia C il centro della guida circolare. Si adottino come variabili lagrangiane l angolo θ che il diametro OA della guida circolare forma con il verso positivo dell asse e l angolo φ che il segmento CP forma con il verso positivo dell asse ξ, parallelo all asse e passante per il punto C (si veda la Fig. 1). Si scrivano la lagrangiana del sistema e le equazioni del moto. Si individuino le posizioni di equilibrio del sistema e se ne determini la stabilità. Siano ora a = 3R, M = m, K/m = 1. Scelta una posizione di equilibrio stabile, si determinino le frequenze delle piccole oscillazioni attorno a tale posizione. y O C R θ A φ P K ξ H =a Fig. 1 ESERCIZIO Si determini per quale valore del parametro reale α la trasformazione ( ) α p Q = q ( q ) α p P = 3 è canonica e, in corrispondenza di tale valore, si trovi la funzione generatrice F 1 (q, Q). ESERCIZIO 3 Due particelle relativistiche di massa m e velocità v 1 = 1 13 c e v = 5 13c si muovono nel verso positivo dell asse di un opportuno sistema di riferimento cartesiano, con la particella più veloce che segue la più lenta, di modo che ad un certo istante esse si urtano. A seguito dell urto tra le due particelle, si forma un unica particella di massa M e velocità u. Si determini u. Si determini il valore del rapporto M/m.
5 Scritto di Meccanica Analitica e Relativistica - 14 luglio 017 Proff. S. Caprara, M. Grilli, L. Gualtieri ESERCIZIO 1 In un piano verticale sia posto un sistema di assi cartesiani Oz, con z verticale discendente. In tale piano si muove una asta omogenea pesante AB di massa M e lunghezza L. Sia S il punto dell asta che si trova a distanza 3d dal punto A, con L = 4d. Il punto S dell asta è obbligato a scorrere senza attrito lungo una guida rettilinea coincidente con l asse delle z, ed è soggetto ad una forza elastica che lo attrae verso l origine: F 1 = kos, k > 0. L estremo A è soggetto ad una forza elastica che lo attrae verso l asse delle : F = kha, k > 0, ove H è la proiezione del punto A sull asse delle (vedi figura). Si indichi con g l accelerazione di gravità. Si assumano come variabili lagrangiane la coordinata z di S e l angolo φ che SA forma con l asse z. 1. Scrivere la funzione di Lagrange del sistema. (Per ragioni di tempo non si chiede di scrivere le equazioni del moto).. Trovare le posizioni di equilibrio e discuterne il numero al variare di k. 3. Posto in questa domanda M = 3, d = 1, k =, g = 3, studiare la stabilità delle posizioni di equilibrio e, scelta una posizione di equilibrio stabile, trovare la frequenza delle piccole oscillazioni attorno ad essa. N.B. I G = ML 1 (G= baricentro). Ricordiamo che la forza peso è presente. B O z S φ H A Fig. 1 ESERCIZIO Si risolva il seguente problema nell ambito della relatività ristretta. Due astronavi si muovono lungo l asse. Ambedue partono contemporaneamente dall origine. La prima si muove con velocità c/4 per un tempo T, poi si ferma. La seconda si muove, nello stesso verso della prima, con velocità c/ per un tempo T, poi inverte il moto e si dirige verso la prima astronave con velocità c/ fino a quando la incontra, e lì si ferma. 1. I due astronauti avevano portato a bordo un orologio ciascuno. Quando si incontrano li confrontano: chi ha segnato meno tempo e di quanto?. In ognuna delle due astronavi c è una telecamera che mostra il quadrante di un orologio e ne invia l immagine a terra mediante un segnale elettromagnetico. Al tempo T (misurato a terra) dopo la partenza delle astronavi, queste immagini vengono osservate e confrontate. Quanto tempo segnano gli orologi mostrati nelle immagini?
6 Scritto di Meccanica Analitica e Relativistica - 1 settembre 017 Proff. S. Caprara, M. Grilli, L. Gualtieri ESERCIZIO 1 In un piano verticale sia posto un sistema di assi cartesiani Oz, con z verticale discendente. In tale piano si muove un asta rigida, omogenea e pesante AB, di massa m e lunghezza l. L estremo A dell asta può scivolare senza attrito lungo una guida coincidente con l asse w, che forma angoli di 45 con gli assi e z (si veda la Fig. 1), ed è soggetto ad una forza elastica che lo attrae verso l origine, F 1 = k OA, k > 0. L estremo B è soggetto ad una forza elastica F = k HB, k > 0, dove H è la proiezione di B sull asse delle (si veda la Fig. 1). Si indichi con g > 0 il modulo dell accelerazione di gravità. Si assumano come variabili lagrangiane l ascissa ξ di A lungo l asse w e l angolo θ che l asta AB forma con la direzione verticale discendente (si veda la Fig. 1). g O k ξ A H k z θ m l B w Fig Si scriva la funzione di Lagrange del sistema. (Per ragioni di tempo non si chiede di scrivere le equazioni del moto).. Si trovino le posizioni di equilibrio del sistema e se ne discuta il numero e la stabilità al variare di k. 3. Ponendo ora m =, l = 1, k =, g = 8, si scelga una posizione di equilibrio stabile e si trovino le frequenze delle piccole oscillazioni attorno ad essa. N.B.: Il momento d inerzia dell asta rispetto al suo centro di massa è I G = ml 1 (G= centro di massa di AB). Si ricordi che la forza peso è presente. ESERCIZIO Sono assegnati nello spazio-tempo di Minkovski (, y, z, ct) i due eventi E 1 = (1, 5, 3, ) e E = (3, 5, 3, α), con α parametro reale. 1. Per quali valori di α esiste un sistema di riferimento inerziale in cui i due eventi sono simultanei?. Trovare, in funzione dei valori di α ammissibili, la velocità v = (v, v y, v z ) di tale sistema di riferimento.
7 Prova in itinere di Meccanica Analitica e Relativistica - novembre 017 In un piano orizzontale è fissato un sistema di assi cartesiani Oy. In tale piano si muove una guida circolare rigida, omogenea, di centro C, massa M e raggio R. Il punto A della guida circolare è vincolato a scivolare senza attrito lungo una guida coincidente con l asse (si veda la Fig. 1), ed è soggetto ad una forza elastica che lo attrae verso l origine, F 1 = k OA, k > 0. Il punto B della guida circolare, diametralmente opposto rispetto ad A, è soggetto ad una forza elastica F = k HB, k > 0, dove H è la proiezione di B sulla retta = a (si veda la Fig. 1). La guida circolare è libera di ruotare attorno ad un asse passante per A e perpendicolare al piano assegnato. Si assumano come variabili lagrangiane l ascissa di A e l angolo θ che il diametro AB forma con l asse (si veda la Fig. 1). 1. Si scrivano la funzione di Lagrange del sistema e le equazioni del moto.. Si trovino le posizioni di equilibrio del sistema e se ne discuta il numero e la stabilità al variare di a (, + ). 3. Ponendo ora M = 1, k =, a = R = 1, si scelga una posizione di equilibrio stabile e si trovino le frequenze delle piccole oscillazioni attorno ad essa. N.B.: Il momento d inerzia della guida circolare rispetto al suo centro di massa, coincidente con il centro C, è I C = MR. y M B k H C O k A θ R =a Fig. 1
8 Esonero di Meccanica Analitica e Relativistica del 17 gennaio 018 Si risolvano gli esercizi 1,,3 e un esercizio a scelta tra 4a e 4b. 1. Trasformazioni canoniche. Data la trasformazione Q = q α log p P = q p β dalle variabili canoniche q, p alle variabili Q, P, dire per quali valori dei parametri reali α, β la trasformazione è canonica. In corrispondenza di tali valori, determinare la funzione generatrice della trasformazione canonica, F (q, Q).. Trasformazioni di Lorentz. Si risolva il seguente problema nell?ambito della relatività ristretta. Sia dato, in un sistema di riferimento inerziale, un sistema di coordinate (ct,, y, z). Siano dati due eventi E 1, E di coordinate, nel riferimento dato, E 1 = (1, 1, 0, 0) E = (4, 1, 1, 0). 1. Indicare se esiste un riferimento in cui gli eventi E 1, E avvengono nella stessa posizione e, in tal caso, determinare la trasformazione di coordinate tra tale riferimento e il riferimento di partenza.. Determinare la separazione temporale cδt tra gli eventi E 1, E nel nuovo riferimento. 3. Cinematica relativistica. Dopo aver sincronizzato gli orologi, due astronauti (A e B) partono all istante t = 0 dall origine O di un sistema di coordinate cartesiane fissato sul piano Oy. L astronauta A percorre un tratto di lunghezza L nel verso positivo dell asse, con velocità c, un tratto di lunghezza L nel verso positivo dell asse y, con velocità c, un tratto di lunghezza L nel verso negativo dell asse, con velocità c 4, e ritorna in O percorrendo un tratto di lunghezza L nel verso negativo dell asse y, con velocità c 4. La traiettoria dell astronauta A è dunque un quadrato. L astronauta B percorre in andata e ritorno la diagonale dello stesso quadrato, con velocità c 6. Verificare che i due astronauti impiegano lo stesso tempo T (misurato da un orologio rimasto in quiete in O) per completare i rispettivi tragitti e determinare T. Quando i due astronauti si incontrano nuovamente in O, confrontano i loro orologi, che segnano, rispettivamente, τ A e τ B. Determinare τ A e τ B e indicare quale dei due tempi è il più piccolo. 4a. Dinamica relativistica. Una particella relativistica di massa propria m è vincolata a muoversi lungo l asse sotto l azione di una forza conservativa la cui energia potenziale è V () = γ 4, dove γ > 0 è un parametro dimensionale. La massima distanza dall origine raggiunta dalla particella è d. Determinare la velocità v 0 con la quale la particella transita per l origine. Sotto quale condizione su d si recupera il risultato classico per v 0? 4b. Urti. Si risolva il seguente problema nell ambito della relatività ristretta. Una particella di massa a riposo m si muove lungo l asse con velocità v 1 = 3 5 c e collide con una particella di massa a riposo 3 4m che viaggia sempre lungo l asse con velocità v = 4 5c. In seguito all urto, si produce un unica particella di massa a riposo M che si muove con velocità V. Determinare M e V assumendo assegnata m.
9 Compito di Meccanica Analitica e Relativistica - 6 febbraio 018 ESERCIZIO 1: MECCANICA LAGRANGIANA In un piano verticale, in cui è fissato un sistema di assi cartesiani Oz, con l asse z verticale discendente, si muove un asta rigida e omogenea AB, di massa M e lunghezza L, il cui estremo A è vincolato a scorrere senza attrito lungo la guida circolare γ, di centro O e raggio R = L. L estremo B dell asta è soggetto alla forza F e = K HB, K > 0, con H proiezione ortogonale di B sull asse. Si adottino come coordinate lagrangiane l angolo θ che OA forma con l asse z e l angolo φ che AB forma con la verticale discendente (si veda la Fig. 1). Sia g > 0 l intensità dell accelerazione di gravità. Nello svolgimento, per comodità, si ponga Mg = fkl, f > Si scriva la funzione di Lagrange del sistema (per mancanza di tempo, non sono richieste le equazioni del moto).. Si trovino le otto posizioni di equilibrio del sistema e si discuta, al variare di f > 0, la stabilità di quelle con θ, φ [0, π], le altre essendo equivalenti a queste per simmetria. 3. Ponendo ora M = 1, K = 1, L = R = 1, g = 6 (ovvero f = 6), si scelga una posizione di equilibrio stabile e si trovino le frequenze delle piccole oscillazioni attorno ad essa. N.B.: Il momento d inerzia dell asta rispetto al suo centro di massa G è I G = 1 1 ML. γ O θ H R=L A g K z φ M,L B Fig. 1 ESERCIZIO : TRASFORMAZIONI CANONICHE Data la trasformazione Q = 1 3 q 1/ p α P = q 3/ p β dalle variabili canoniche q, p alle variabili Q, P, dire per quali valori dei parametri reali α, β la trasformazione è canonica. In corrispondenza di tali valori, determinare la funzione generatrice F 3 (p, Q) della trasformazione canonica. ESERCIZIO 3: RELATIVITÀ RISTRETTA Si risolva il seguente problema nell ambito della relatività ristretta. Sono assegnati nello spazio-tempo di Minkovski (ct,, y, z) i due eventi E 1 = (1, 0, 0, 0) e E = (4, α, α, 0). 1. Determinare per quali valori di α esistono sistemi di riferimento inerziali in cui i due eventi sono simultanei.. Trovare la velocità v = (v, v y, v z ) di uno di questi sistemi di riferimento in funzione di α. 3. Posto α = 5, determinare la distanza spaziale tra i due eventi nel sistema di riferimento in cui sono simultanei.
10 Compito di Meccanica Analitica e Relativistica - 0 Febbraio 018 ESERCIZIO 1: MECCANICA LAGRANGIANA E HAMILTONIANA In un piano orizzontale è fissato un sistema di assi cartesiani Oy. In tale piano si muove un asta rigida e omogenea AB, di massa M e lunghezza L. Il centro di massa G dell asta è vincolato a scorrere senza attrito lungo una guida coincidente con l asse (si veda la Fig. 1), ed è soggetto ad una forza elastica che lo attrae verso l origine O, F 1 = K OG, K > 0. L estremo B dell asta è soggetto ad una forza elastica F = K PB, K > 0, dove P è il punto di coordinate (a, 0), con a R. Si adottino come coordinate lagrangiane l ascissa di G e l angolo θ che l asta AB forma con l asse (si veda la Fig. 1). 1. Si scrivano la funzione di Lagrange L del sistema e le equazioni del moto.. Si ricavi l espressione dei momenti coniugati, p e p θ, e della Hamiltoniana H. 3. Si trovino le posizioni di equilibrio del sistema e se ne discuta il numero e la stabilità al variare di a (, + ). 4. Ponendo ora M = 1, K = 1, L = a = 1, si scelga una posizione di equilibrio stabile e si trovino le frequenze delle piccole oscillazioni attorno ad essa. N.B.: Il momento d inerzia dell asta rispetto al suo centro di massa G è è I G = 1 1 ML. y O K A M,L G θ B K P=( a,0) Fig. 1 Data la trasformazione ESERCIZIO : TRASFORMAZIONI CANONICHE. Q = e q p α P = β p e q dalle variabili canoniche q, p alle variabili Q, P, dire per quali valori dei parametri reali α, β la trasformazione è canonica. In corrispondenza di tali valori, determinare la funzione generatrice F (q, P ) della trasformazione canonica. ESERCIZIO 3: RELATIVITÀ RISTRETTA Si risolva il seguente problema nell ambito della relatività ristretta. Un astronave parte dalla Terra muovendosi lungo l asse con una velocità pari a c/. Dopo un intervallo tempo T 0 = 1 anno, dalla Terra viene inviato un messaggio radio con il quale si richiede che l astronave torni indietro. Appena ricevuto il messaggio, l astronave inverte la direzione del moto e si dirige verso la Terra con una velocità pari a c/3. 1. Determinare, nel sistema di riferimento della Terra, quanto tempo è trascorso dalla partenza quando l astronave riceve il messaggio, e che distanza essa ha percorso in quell istante.. Quando l astronave torna sulla Terra, gli astronauti confrontano il loro orologio con un orologio rimasto sulla Terra. Quale orologio ha segnato meno tempo, e di quanto?
11 Compito di Meccanica Analitica e Relativistica del 6 luglio 018 Esercizio 1: Meccanica Lagrangiana. In un piano orizzontale, sul quale è fissato un sistema di assi cartesiani ortogonali Oy, si muove un disco rigido e omogeneo, di raggio R e massa M. Il punto A sul bordo del disco è vincolato a scorrere senza attrito lungo una guida coincidente con l asse Oy. Il disco è libero di ruotare attorno ad un asse perpendicolare al piano Oy e passante per A. Il punto B del disco, diametralmente opposto ad A, è attratto verso il punto fisso P= (a, 0) da una forza elastica F = K PB, con K > 0. Si adottino come coordinate lagrangiane l ordinata y di A e l angolo θ che il diametro AB del disco forma con il verso positivo dell asse Oy (si veda la Fig. 1). 1. Si scrivano la funzione di Lagrange L del sistema e le equazioni del moto.. Si trovino le posizioni di equilibrio del sistema e se ne discuta il numero e la stabilità al variare del parametro a/r (, + ). 3. Ponendo ora a = R = 1, K = 1, M = 1, si scelga una posizione di equilibrio stabile e si determinino le frequenze delle piccole oscillazioni attorno ad essa. N.B.: Il momento d inerzia del disco rispetto al suo centro di massa G è I G = 1 MR. y B M A y θ G R K O P =( a,0 ) Fig. 1 Esercizio : Trasformazioni canoniche. Data la trasformazione ( ) 1 Q 6 q = p 9 α µ+3 ( P = 3 p 9 ) ( ) µ Q 6 α dalle variabili canoniche Q, p alle variabili q, P, dire per quali valori dei parametri reali α, µ la trasformazione è canonica. In corrispondenza di tali valori, determinare la funzione generatrice F (q, P ) della trasformazione canonica. Esercizio 3: Relatività ristretta. Si risolva il seguente problema nell ambito della relatività ristretta. Un astronave parte dalla Terra muovendosi lungo l asse con velocità v 1 = 3 5 c. Quando a bordo è trascorso un tempo 4T 0 (con T 0 = 1 anno), l astronave inverte il verso del moto e torna a Terra, muovendosi con velocità v = c. Determinare, al ritorno a Terra dell astronave, quanto tempo è trascorso dalla sua partenza nel sistema di riferimento solidale con la Terra, e nel sistema di riferimento solidale con l astronave.
12 Soluzione del Compito di Meccanica Analitica e Relativistica del 6 luglio 018 Esercizio 1: Meccanica Lagrangiana. 1. Si ha G = R sin θ, y G = y + R cos θ, B = R sin θ, y B = y + R cos θ. Quindi l energia cinetica è T = 1 M ( ẋ G + ẏg ) 1 + I θ G = 1 ( M ẏ + 3 ) R θ R sin θ ẏ θ. L energia potenziale è U = 1 K [ ( B P ) + (y B y P ) ] = 1 K ( y + 4Ry cos θ 4Ra sin θ ) + 4R + a. La funzione di Lagrange è L = T U e le equazioni del moto sono M ( ÿ R sin θ θ R cos θ θ ) = K (y + R cos θ),. Le derivate dell energia potenziale sono M ( ) 3 R θ R sin θ ÿ U = K(y + R cos θ), θ U = KR (y sin θ + a cos θ). Annullando le derivate dell energia potenziale si determinano le posizioni di equilibrio. Si ha y = R cos θ, (R sin θ a) cos θ = 0 = KR (y sin θ + a cos θ). La prima posizione di equilibrio è cos θ 1 = 0, θ 1 = π e y 1 = 0. La seconda posizione di equilibrio è cos θ = 0, θ = π e y = 0. Si hanno poi due posizioni equivalenti con cos θ 0, sin θ 3,4 = a R, cos θ 3 > 0 e cos θ 4 < 0, cioè y 3 = 4R a e y 4 = 4R a. Queste due posizioni esistono solo se 1 < Le derivate seconde dell energia potenziale sono a R < 1 < a R <. yyu = K, θθu = KR (a sin θ y cos θ), yθu = θyu = KR sin θ. L hessiano nella prima posizione vale K R(a R) e poiché U > 0 la condizione necessaria e sufficiente di equilibrio è che l hessiano sia positivo. Si ha quindi che la posizione di equilibrio (y 1, θ 1 ) è stabile per a R >. L hessiano nella seconda posizione vale K R(a + R) e poiché U > 0 la condizione necessaria e sufficiente di equilibrio è che l hessiano sia positivo. Si ha quindi che la posizione di equilibrio (, θ ) è stabile per a R <. Nelle posizioni 3, 4 l hessiano 4K R cos θ è sempre positivo, quindi queste posizioni di equilibrio sono stabili quando esistono, cioè per < a R <. Riassumendo, per a R < si hanno due posizioni di equilibrio, la prima instabile e la seconda stabile; per < a R < si hanno quattro posizioni di equilibrio, la prima e la seconda instabili, la terza e la quarta (equivalenti) stabili; per a R > si hanno due posizioni di equilibrio, la prima stabile, la seconda instabile. 3. Per i valori assegnati dalla traccia le posizioni stabili sono la 3 e la 4. La matrice dell energia cinetica è Tẏẏ = M, T θ θ = 3 MR, Tẏ θ = T θẏ = MR sin θ = 1 Ma. La matrice dell energia potenziale nelle posizioni di equilibrio stabile è L equazione secolare det U ij ω T ij = 0 dà U = K, U θθ = 4KR, U θ = U θ = Ka. R ( K Mω ) ( 4K 3 Mω ) a (K 1 Mω ) = 0,
13 Sostituendo i valori si trova l equazione biquadratica che ammette evidentemente due soluzioni positive, 5 ω 4 18 ω + 1 = 0, ω ± = 9 ± 1 5 ω + =.717, ω = Quindi le frequenze dei due modi normali sono ω + = e ω = Esercizio : Trasformazioni canoniche. Esprimendo Q e P come funzioni di q e p otteniamo: Q = α q 6 p 4/3, P = 3 q µ p 1/3. Imponendo che la parentesi di Poisson [Q, P ] qp sia uguale ad 1 si ottiene µ = 5 e α = Sappiamo che df (q, P ) = p dq + Q dp. Per ottenere F (q, P ) bisogna quindi esprimere p e Q come funzioni di q e P. Ottrniamo: ed integrando p dq o, alternativamente, Q dp otteniamo p = 7 q 15 P 3, Q = p 4 q 14, F (q, P ) = 7 14 q 14 p 3. Esercizio 3: Relatività ristretta. Prendendo come origine del tempo coordinato t e del tempo proprio dell astronave τ l istante in cui l astronave parte, siano t 1, τ 1 il tempo coordinato e il tempo proprio nel momento in cui questa inverte il suo senso di marcia, e siano t, τ il tempo coordinato e il tempo proprio al ritorno a terra. Sarà, essendo v 1 = 3 5 c e v = c, τ 1 = 1 v 1 c t 1 = la posizione dell astronave quando inverte il senso di marcia sarà t 1 = 4 5 t 1 = 4T 0 t 1 = 5T 0, = v 1 t 1 = 3cT 0. Nel viaggio di ritorno l astronave impiega un tempo coordinato t t 1 = v = 6T 0 e un tempo proprio τ τ 1 = 1 v c (t t 1 ) = T 0 = 3 3T 0, quindi t = 6T 0 + 5T 0 = 11T 0, τ = ( )T 0.
14 Compito di Meccanica Analitica e Relativistica del 3 settembre 018 Esercizio 1: Meccanica Lagrangiana. In un piano orizzontale, sul quale è fissato un sistema di assi cartesiani ortogonali Oy, si muove una lamina quadrata rigida e omogenea, ABCD, di lato L e massa M. Il vertice A della lamina è vincolato a scorrere senza attrito lungo una guida coincidente con l asse O. La lamina è libera di ruotare attorno ad un asse perpendicolare al piano Oy e passante per A. Il vertice C della lamina è attratto verso il punto fisso P= (0, a) da una forza elastica F = K PC, con K > 0. Si adottino come coordinate lagrangiane l ascissa di A e l angolo θ che la diagonale AC della lamina forma con il verso positivo dell asse O (si veda la Fig. 1). 1. Si scrivano la funzione di Lagrange L del sistema e le equazioni del moto.. Si trovino le posizioni di equilibrio del sistema e se ne discuta il numero e la stabilità al variare del parametro a L [0, + ). 3. Ponendo ora a L = 1, K M = 1, si scelga una posizione di equilibrio stabile e si determinino le frequenze delle piccole oscillazioni attorno ad essa. N.B.: Il momento d inerzia della lamina quadrata rispetto al suo centro di massa G è I G = 1 6 ML. y C B L P=(0, a) K M G θ D O A Fig. 1 Esercizio : Trasformazioni canoniche. Data la trasformazione Q = (36) γ P γ e (α βγ) q p = 36 P e β q dalle variabili canoniche P, q alle variabili Q, p, dire per quali valori dei parametri reali α, β, γ la trasformazione è canonica. In corrispondenza di tali valori, determinare la funzione generatrice F (q, P ) della trasformazione canonica. Esercizio 3: Relatività ristretta. Si risolva il seguente problema nell ambito della relatività ristretta. Sia dato, in un sistema di riferimento inerziale, un sistema di coordinate spazio-temporale (ct,, y, z). Siano dati i due eventi E 1 = (α, 1, α, 3), E = (α, 1, 1, 3) 1. Indicare per quali valori del parametro reale α esiste un sistema di riferimento nel quale gli eventi E 1, E sono contemporanei, e, per questi valori di α, determinare una trasformazione di coordinate tra tale riferimento e il riferimento di partenza.. Indicare per quali valori del parametro reale α esiste un sistema di riferimento nel quale gli eventi E 1, E avvengono nella stessa posizione e, per questi valori di α, determinare una trasformazione di coordinate tra tale riferimento e il riferimento di partenza. 3. Nel caso α =, determinare la separazione temporale tra gli eventi nel sistema di riferimento in cui questi avvengono nella stessa posizione.
15 Soluzione del Compito di Meccanica Analitica e Relativistica del 3 settembre 018 Esercizio 1: Meccanica Lagrangiana. 1. Si ha G = + L cos θ, y G = L sin θ, C = + L cos θ, y C = L sin θ. Quindi l energia cinetica è T = 1 M ( ẋ G + ẏg ) 1 + I θ G = 1 ( M ẋ + 3 L θ ) L sin θ ẋ θ. L energia potenziale è U = 1 K [ ( C P ) + (y C y P ) ] = 1 ( K + L cos θ ) La sin θ + 1 K ( L + a ). La funzione di Lagrange è L = T U e le equazioni del moto sono ( ) M ẍ L sin θ θ ( L cos θ θ = K + ) L cos θ, M ( ) 3 L θ L sin θ ẍ = KL ( sin θ + a cos θ).. Le derivate dell energia potenziale sono ( U = K + ) L cos θ, θ U = KL ( sin θ + a cos θ). Annullando le derivate dell energia potenziale si determinano le posizioni di equilibrio. Si ha = ( ) L cos θ, L sin θ a cos θ = 0 La prima posizione di equilibrio è cos θ 1 = 0, θ 1 = π e 1 = 0. La seconda posizione di equilibrio è cos θ = 0, θ = π e = 0. Si hanno poi due posizioni equivalenti con cos θ 0, sin θ 3,4 = a L, cos θ 3 > 0 e cos θ 4 < 0, cioè 3 = L a e 4 = L a. Poiché la traccia assegna a 0, aueste due posizioni esistono solo se a 0 L < 1 0 a L <. Le derivate seconde dell energia potenziale sono U = K, θθu = KL (a sin θ cos θ), θu = θu = KL sin θ. L hessiano nella prima posizione vale K L(a L) e poiché U > 0 la condizione necessaria e sufficiente di equilibrio è che l hessiano sia positivo. Si ha quindi che la posizione di equilibrio ( 1, θ 1 ) è stabile per a L >. L hessiano nella seconda posizione vale K L(a + L) e poiché U > 0 la condizione necessaria e sufficiente di equilibrio è che l hessiano sia positivo. Si ha quindi che la posizione di equilibrio (, θ ) non è stabile per nessun valore di a L 0. Nelle posizioni 3, 4 l hessiano K L cos θ è sempre positivo, quindi queste posizioni di equilibrio sono stabili quando esistono, cioè per 0 a L <. Riassumendo, per 0 a L < si hanno quattro posizioni di equilibrio, la prima e la seconda instabili, la terza e la quarta (equivalenti) stabili; per a L > si hanno due posizioni di equilibrio, la prima stabile, la seconda instabile. 3. Per i valori assegnati dalla traccia le posizioni stabili sono la 3 e la 4. La matrice dell energia cinetica è Tẋẋ = M, T θ θ = 3 ML, Tẋ θ = T θẋ = ML sin θ = 1 Ma. La matrice dell energia potenziale nelle posizioni di equilibrio stabile è U = K, U θθ = KL, U θ = U θ = Ka.
16 L equazione secolare det U ij ω T ij = 0 dà ( ) ( K K M ω M 1 ) 3 ω Sostituendo i valori si trova l equazione biquadratica che ammette evidentemente due soluzioni positive, ( ) 10 ω± = 1 ± 5 ( a ) ( K L M 1 ) ω = 0, 5 ω 4 0 ω + 1 = 0, ω + = 3.65, ω = Quindi le frequenze dei due modi normali sono ω + = e ω = Esercizio : Trasformazioni canoniche. Esprimendo Q e P come funzioni di q e p otteniamo: Q = e αq p γ, P = 1 6 eβq p 1/. Imponendo che la parentesi di Poisson [Q, P ] qp sia uguale ad 1 si ottiene α = β = 3 e γ = 1. Sappiamo che df (q, P ) = p dq + Q dp. Per ottenere F (q, P ) bisogna quindi esprimere p e Q come funzioni di q e P. Otteniamo: ed integrando p dq o, alternativamente, Q dp otteniamo p = 36 e 6q P, Q = 1 P e 6q, F (q, P ) = 6 e 6q P. Esercizio 3: Relatività ristretta. La separazione tra i due eventi è L intervallo spazio-temporale è E = (α, 0, α 1, 0). E = α (α 1) = α Esiste un sistema di riferimento in cui i due eventi sono contemporanei se E < 0 ovvero α < 1. La trasformazione di coordinate tra questo riferimento e quello di partenza è la trasformazione di Lorentz speciale con v = (0, βc, 0), tale che E 0 = γ( E 0 β E ) = γ(α β(α 1)) = 0 ovvero β = α α 1.. Esiste un sistema di riferimento in cui i due eventi avvengono nella stessa posizione se E > 0 ovvero α > 1. La trasformazione di coordinate tra questo riferimento e quello di partenza è la trasformazione di Lorentz speciale con v = (0, βc, 0), tale che E = γ( E β E 0 ) = γ(α 1 βα) = 0 ovvero β = α 1 α.
17 3. Se α =, per β = α 1 α = 1 gli eventi avvengono nella stessa posizione, con separazione temporale Essendo γ = (1 β ) 1/ = / 3, E 0 = E 0 = γ( E 0 β E ) = γ(α β(α 1)) = 0. che nel riferimento in cui E = 0, E 0 = E = α 1 = 3. 3 ( 1/) = 3. A questo risultato si arrivava anche osservando
18 Prova in itinere di Meccanica Analitica e Relativistica del 7 novembre 018 In un piano orizzontale, sul quale è fissato un sistema di assi cartesiani ortogonali Oy, si muove una guida circolare, rigida e omogenea, di centro G, massa M e raggio R. Lungo un diametro della guida è saldata una barra AB, rigida e omogenea, di massa m e lunghezza L = R. Il punto C della barra, che dista d = R dall estremo A, è vincolato a scorrere senza attrito lungo una guida coincidente con l asse O. Il sistema è libero di ruotare rigidamente attorno ad un asse perpendicolare al piano Oy, passante per C, ed è soggetto alle due forze attive F a = K H a A e F b = K H b B, con K > 0, dove H a è la proiezione ortogonale di A sulla retta = γ e H b è la proiezione ortogonale di B sulla retta = γ, con γ > 0. Si adottino come coordinate lagrangiane l ascissa di C e l angolo θ che la barra AB forma con il verso positivo dell asse O (si veda la Fig. 1). 1. Si scrivano la funzione di Lagrange L del sistema e le equazioni del moto.. Si trovino le posizioni di equilibrio del sistema e se ne discuta il numero e la stabilità al variare del parametro (0, + ). γ R 3. Ponendo ora γ = 3, R = 1, M = 3, m = 1, K = 1, si scelga una posizione di equilibrio stabile e si determinino le frequenze delle piccole oscillazioni attorno ad essa. N.B.: Il momento d inerzia del sistema rispetto al suo centro di massa G è I G = ( M + m 3 ) R. y H a M B m G θ R K O C K A = γ = γ H b Fig. 1
19 Soluzione della prova in itinere di Meccanica Analitica e Relativistica del 11 novembre Si ha G = + R cos θ, y G = R sin θ, A = R cos θ, B = + 3R cos θ. Quindi l energia cinetica è T = 1 (M + m) ( ẋ G + ẏg ) 1 + I θ G = 1 [ ( 5 (M + m) ẋ + 4 M + 7 ) ] 1 m R θ (M + m)r sin θ ẋ θ. L energia potenziale è U = 1 K [ ( A Ha ) + ( B Hb ) ] = 1 K ( R cos θ + γ ) + 1 K ( + 3R cos θ γ ). La funzione di Lagrange è L = T U e le equazioni del moto sono (M + m) (ẍ R sin θ θ R ) cos θ θ = K ( + R cos θ),. Le derivate dell energia potenziale sono ( 5 4 M + 7 ) 1 m R M + m θ R sin θ ẍ = KR sin θ ( + 5R cos θ 4γ). U = K ( + R cos θ), θ U = KR sin θ (4γ 5R cos θ). Annullando le derivate dell energia potenziale si determinano le posizioni di equilibrio. Si ha = R cos θ, ( + 5R cos θ 4γ) sin θ = 0 La prima posizione di equilibrio è sin θ 1 = 0, θ 1 = 0 e 1 = R. La seconda posizione di equilibrio è sin θ = 0, θ = π e = R. Si hanno poi due posizioni equivalenti con sin θ 0, cos θ 3,4 = γ R, sin θ 3 > 0 e sin θ 4 < 0, e 3,4 = γ. Poiché la traccia assegna γ > 0, queste due posizioni esistono solo se Le derivate seconde dell energia potenziale sono U = K, θθu = KR 0 < γ R 1. [ (4γ 5R cos θ) cos θ + 5R sin θ ], θu = θu = KR sin θ. L hessiano nella prima posizione vale 4K R(γ R) e poiché U > 0 la condizione necessaria e sufficiente di equilibrio stabile è che l hessiano sia positivo. Si ha quindi che la posizione di equilibrio ( 1, θ 1 ) è stabile per γ R > 1. L hessiano nella seconda posizione vale 4K R(γ + R) e poiché U > 0 si ha che la posizione di equilibrio (, θ ) non è stabile per nessun valore di γ R 0. Nelle posizioni 3, 4 l hessiano 4K R sin θ è sempre positivo, quindi queste posizioni di equilibrio sono stabili quando esistono, cioè per 0 < γ R 1. Riassumendo, per 0 γ R 1 si hanno quattro posizioni di equilibrio, la prima e la seconda instabili, la terza e la quarta (equivalenti) stabili; per γ R > 1 si hanno due posizioni di equilibrio, la prima stabile, la seconda instabile. 3. Per i valori assegnati dalla traccia le posizioni stabili sono la 3 e la 4. La matrice dell energia cinetica è ( 5 Tẋẋ = M + m = 4, T θ θ = 4 M + 7 ) 1 m R = 13 3, T ẋ θ = T θẋ = R (M + m) sin θ = sin θ.
20 La matrice dell energia potenziale nelle posizioni di equilibrio stabile è U = K =, U θθ = 5 KR sin θ = 5 sin θ, U θ = U θ = KR sin θ = sin θ. L equazione secolare det U ij ω T ij = 0 dà ( 4 ω ) ( 5 sin θ 13 ) 3 ω ( 1 ω ) sin θ = 0, dove sin θ = 1 cos θ = 1 γ biquadratica R = 5 9 nelle posizioni di equilibrio 3,4. Sostituendo i valori si trova l equazione che ammette evidentemente due soluzioni positive, ω ± = 7 ± 7 68 Quindi le frequenze dei due modi normali sono ω + = 34 ω 4 7 ω + 5 = 0, ω + = 1, ω = e ω =
21 Prova in itinere di Meccanica Analitica e Relativistica del 16 gennaio 019 Si risolvano gli esercizi 1,,3 e un esercizio a scelta tra 4a e 4b. 1. Trasformazioni canoniche. Data la trasformazione Q = 1 γ qβ ln p P = q p α dalle variabili canoniche q, p alle variabili Q, P, dire per quali valori dei parametri reali α, β, γ la trasformazione è canonica. In corrispondenza di tali valori, determinare la funzione generatrice della trasformazione canonica, F 4 (p, P ).. Trasformazioni di Lorentz. Si risolva il seguente problema nell ambito della relatività ristretta. Sia dato, in un sistema di riferimento inerziale, un sistema di coordinate (ct,, y, z). Siano dati due eventi E 1, E di coordinate, nel riferimento dato, E 1 = ( 1, 1, 1, 3) E = (4, 1, 1, 1). 1. Indicare se esiste un riferimento in cui gli eventi E 1, E avvengono nella stessa posizione e, in tal caso, determinare la trasformazione di coordinate tra tale riferimento e il riferimento di partenza.. Determinare la separazione temporale c t tra gli eventi E 1, E nel nuovo riferimento. 3. Cinematica relativistica. Dopo aver sincronizzato gli orologi, due astronauti (A e B) partono da terra, muovendosi lungo l asse in versi opposti; l astronave di A ha una velocità di modulo c/, l astronave di B ha una velocità di modulo c/3. Ognuno dei due astronauti, quando il proprio orologio indica che è trascorso un tempo τ 0 = 1 anno dalla partenza, inverte istantaneamente il verso del proprio moto, tornando a terra. Qual è la differenza tra i tempi di arrivo T A e T B dei due astronauti, misurata da un orologio rimasto in quiete a terra? 4a. Dinamica relativistica. Una particella relativistica di massa propria m è vincolata a muoversi lungo l asse sotto l azione di una forza conservativa la cui energia potenziale è V () = A, con A > 0. Ad un certo istante, la particella transita per l origine con velocità v 0 > 0. Si determini l ascissa massima M raggiunta dalla particella in funzione di v 0 ; si determini quindi v 0, sapendo che A M = 1 4 mc. 4b. Urti. Si risolva il seguente problema nell ambito della relatività ristretta. Una particella di massa a riposo m 1 = 7 0 m si muove lungo l asse con velocità v 1 = 4 5 c ed urta una particella di massa m = 3 4m a riposo nell origine del sistema di coordinate. Nell urto viene prodotta un unica particella di massa M e velocità V. Determinare M e V assumendo assegnata m.
22 Soluzioni della prova in itinere di MAR del 16 gennaio Trasformazioni canoniche. Per fissare i parametri α, β, γ imponiamo la condizione: [Q, P ] q,p = 1 = βα γ qβ p α 1 ln p 1 γ pα 1 q β dalla quale segue che α = 1, β = 0, γ = 1. la trasformazione canonica risulta quindi essere: Q = ln p P = q p Il differenziale df 4 (p, P ) = q dp + Q dp ci dice che F 4 si ottiene integrando q dp a P fissato o Q dp a p fissato, considerando q = q(p, P ) e Q = Q(p, P ). Si ottiene: P F 4 (p, P ) = dp = P ln p p F 4 (p, P ) = ln p dp = P ln p. Trasformazioni di Lorentz. La separazione tra gli eventi E 1, E è il quadrivettore L intervallo spazio-temporale tra gli eventi è la norma E 1 E = (5, 0, 0, 4). E 1 E = 5 16 = 9 > 0 quindi la separazione è di tipo tempo, ed esiste un riferimento inerziale in cui gli eventi avvengono nella stessa posizione. Nel riferimento di partenza c t = 5, z = 4, mentre = y = 0, quindi il riferimento cercato è in moto lungo l asse z rispetto a quello di partenza, e le sue coordinate si ottengono con una trasformazione di Lorentz speciale t = γ (t v ) c z = y = y z = γ(z vt) con v = (0, 0, v) velocità del nuovo riferimento rispetto al vecchio, e γ = ( 1 v /c ) 1/. Nel nuovo riferimento i due eventi E 1, E avvengono nella stessa posizione, quindi z = γ ( z v ) c c t = 0 z v c c t = 4 v c 5 = 0 quindi v = 4 ( 5 c γ = 1 16 ) 1/ = La separazione temporale nel nuovo riferimento è c t = γ (c t v ) c z = 5 [5 ( 4/5)( 4)] = 3. 3
23 3. Cinematica Relativistica. Prendiamo come origine dei tempi propri e coordinati l evento O di partenza degli astronauti da terra. Quando l astronauta A inverte il proprio moto, il suo tempo proprio è τ 0 mentre il tempo coordinato è t A = τ 0 1 v A c 1 = τ = τ 0. 3 Quando l astronauta B inverte il proprio moto, il suo tempo proprio è τ 0 mentre il tempo coordinato è t B = τ 0 1 v B c 1 = τ = 3τ 0. Il ritorno a terra dell astronauta A avviene al tempo coordinato (che è anche il tempo misurato da un orologio rimasto a terra) T A = t A, mentre il ritorno a terra dell astronauta B avviene al tempo coordinato T B = t B. La differenza tra questi due tempi è ( 4 T A T B = 3 3 ) τ 0 = τ 0 = anni. 4a. Dinamica relativistica. L ascissa in questione è quella del punto di inversione del moto. Per la conservazione dell energia meccanica si ha mc = A M + mc M = mc 1 1. A 1 v 0 c 1 v 0 c Per la condizione posta dal problema 1 5 = 4 1 v 0 c v 0 = 3 5 c. 1 4b. Urti. Il fattore γ 1 della particella 1 risulta essere γ 1 = p = ( 3 mc, 0, 0, 0) 4 e per la legge di conservazione del quadrimpulso: p 1 = ( mc, mc, 0, 0) = (9 4 mc, 9 mc, 0, 0) 5 p 1 + p = (3 mc, 9 mc, 0, 0) = (ΓMc, ΓMV, 0, 0) 5 = 5 3. I due quadrimpulsi risultano quindi: dalla quale si ottiene: e di conseguenza: ΓM = 3m ΓM V c = 9 5 m V c = 3 5, Γ = 5 4, M = 1 5 m.
24 Compito di Meccanica Analitica e Relativistica del 9 gennaio 019 Esercizio 1: Meccanica Lagrangiana. In un piano verticale, sul quale è fissato un sistema di assi cartesiani ortogonali Oz, con asse z verticale discendente, si muove il sistema rigido formato da una guida circolare omogenea, di raggio R e massa m, e da una barra omogenea, di lunghezza R e massa m, saldata sul diametro AB della guida circolare (si veda la Fig. 1). Il punto A del sistema è vincolato a scorrere senza attrito lungo l asse Oz. Sul sistema agiscono le forze attive F 1 = k OA, con k > 0, F = k HG, dove G è il centro di massa del sistema e H è la proiezione ortogonale di G sull asse O, e la forza peso, diretta nel verso positivo dell asse Oz. Si indichi con g > 0 il valore dell accelerazione di gravità. Si adottino come coordinate lagrangiane la coordinata z di A e l angolo θ che AB forma con il verso positivo dell asse Oz. 1. Si scrivano la funzione di Lagrange L del sistema e le equazioni del moto.. Si trovino le posizioni di equilibrio del sistema e se ne discuta il numero e la stabilità al variare del parametro λ = mg kr [0, + ). 3. Ponendo ora g = 1, m = 1, R = 1, k = 4, si scelga una posizione di equilibrio stabile e si determinino le frequenze delle piccole oscillazioni attorno ad essa. N.B.: Il momento d inerzia sistema rigido guida+barra rispetto al suo centro di massa G è I G = 4 3 mr. O z A k θ H k R G m m B g z Fig. 1 Esercizio : Trasformazioni canoniche. Data la trasformazione p = 1 α ln( Q q 3/ ) P = 1 3 ( Q)6/α q β (9/α) dalle variabili q, Q alle variabili p, P, dire per quali valori dei parametri reali α, β la trasformazione è canonica. In corrispondenza di tali valori, determinare la funzione generatrice F (q, P ) della trasformazione canonica. Esercizio 3: Relatività ristretta. Si risolva il seguente problema nell ambito della relatività ristretta. Una astronave parte da terra muovendosi lungo l asse con velocità c/4. Dopo un tempo T = 1 anno, da terra viene inviato un segnale elettromagnetico verso l astronave. Quando l astronave riceve il segnale, essa inverte il verso del moto, tornando verso terra con velocità c/. Nel momento in cui inverte il senso di marcia, l astronave manda un segnale elettromagnetico verso terra. 1. Determinare l intervallo di tempo, misurato da un orologio a terra, tra il ricevimento del segnale emesso dall astronave, e l arrivo dell astronave stessa.. Determinare il ritardo tra l orologio a terra e quello sull astronave, misurato nell istante in cui l astronave è tornata a terra.
25 Soluzione del Compito di Meccanica Analitica e Relativistica del 9 gennaio 019 Esercizio 1: Meccanica Lagrangiana. 1. Si ha G = R sin θ, z G = z + R cos θ. Quindi l energia cinetica è L energia potenziale è T = 1 (m) ( ẋ G + żg ) 1 + I θ G = 1 m ( ż R θ 4R sin θ ż θ U = 1 kz + 1 k(z + R cos θ) mg(z + R cos θ). La funzione di Lagrange è L = T U e le equazioni del moto sono. Le derivate dell energia potenziale sono z R sin θ θ R cos θ θ = g k m (z + R cos θ ), [ ] 10 k 3 R θ R sin θ z = (z + R cos θ) g R sin θ. m z U = k (z + R cos θ) mg, θ U = R sin θ [mg k(z + R cos θ)]. Annullando le derivate dell energia potenziale si determinano le posizioni di equilibrio. Si ha z + R mg cos θ = k, ( ) z + R cos θ mg sin θ = 0. La prima posizione di equilibrio è sin θ 1 = 0, θ 1 = 0 e z 1 = mg k R. La seconda posizione di equilibrio è sin θ = 0, θ = π e z = mg k + R. Si hanno poi due posizioni equivalenti con sin θ 3,4 0, z 3,4 = 0, cos θ 3,4 = mg kr, sin θ 3 > 0 e sin θ 4 < 0. Queste due posizioni esistono solo se Le derivate seconde dell energia potenziale sono 0 mg kr 1 0 λ 1. zzu = k, θθu = R cos θ [mg k(z + R cos θ)] + kr sin θ, zθu = θzu = kr sin θ. L hessiano nella prima posizione vale k R ( mg kr ) 1 e poiché zz U > 0 la condizione necessaria e sufficiente di equilibrio stabile è che l hessiano sia positivo. Si ha quindi che la posizione di equilibrio (z 1, θ 1 ) è stabile per λ > 1. L hessiano nella seconda posizione vale k R ( mg kr + ) 1 e poiché zz U > 0 la condizione necessaria e sufficiente di equilibrio stabile è che l hessiano sia positivo. Si ha quindi che la posizione di equilibrio (z, θ ) non è stabile per nessun valore di λ 0. Nelle posizioni 3, 4 l hessiano K R sin θ è sempre positivo, quindi queste posizioni di equilibrio sono stabili quando esistono, cioè per 0 λ 1. Riassumendo, per 0 λ < 1 si hanno quattro posizioni di equilibrio, la prima e la seconda instabili, la terza e la quarta (equivalenti) stabili; per λ > 1 si hanno due posizioni di equilibrio, la prima stabile, la seconda instabile. 3. Per i valori assegnati dalla traccia le posizioni stabili sono la 3 e la 4. Si ha cos θ 3,4 = 1 e sin θ 3,4 = ± 3. La matrice dell energia cinetica è Tżż = m T θ θ = 10 3 mr, Tż θ = T θż = mr sin θ. La matrice dell energia potenziale nelle posizioni di equilibrio stabile è U zz = k, U θθ = kr sin θ, U zθ = U θz = kr sin θ. k ).
26 L equazione secolare det U ij ω T ij = 0 dà Sostituendo i valori si trova l equazione biquadratica che ammette evidentemente due soluzioni positive, ( ) ( k 3k m ω 4m 10 ) 3 ω 3 ( ) k 4 m ω = 0, ω ± = 31 ± ω 4 6 ω + 36 = 0, ω + = 4.98, ω = Quindi le frequenze dei due modi normali sono ω + =.3 e ω = Esercizio : Trasformazioni canoniche. Esprimendo Q in funzione di p e q otteniamo: Q = 1 q3/ e αp Imponendo che la parentesi di Poisson [Q, P ] qp sia uguale ad 1 si ottiene P = 1 3 qβ e 6p (1) [Q, P ] = q β+3/ 1 e (α+6)p 1 (9 αβ) = 1. 6 che implica α = 6, β = 1. La trasformazione è quindi canonica se Q = 1 q3/ e 6p Per ottenere F (q, P ) bisogna ricavare p e Q in funzione di q e P : P = 1 3 q 1/ e 6p. () p = 1 6 ln(3 q1/ P ) Q = 1 6 Sappiamo che df (q, P ) = p dq + Q dp e quindi: 1 q F (q, P ) = 6 P 1 F (q, P ) = ln P dq + 6 f(q) = 1 1 ln q dq q ln 3 q P. (3) dp + f(q) F (q, P ) = q ln P + 1 ln q dq + 1 q ln ln q dq + 1 q ln 3 (4) 6 Esercizio 3: Relatività ristretta. Fissiamo l origine degli orologi a terra e sull astronave al momento della partenza, e sia = 0 la posizione della terra. Sia A l evento in cui l astronave è raggiunta dal segnale elettromagnetico. Il tempo t A e la posizione A di questo evento si ottengono risolvendo il sistema di equazioni A = c(t A T ) A = c 4 t A,
27 che ha come soluzione t A = 4 3 T, A = c 3 T. 1. Siano B l evento del ricevimento a terra del segnale dall astronave, e C l evento del ritorno a terra dell astronave. Poichè il segnale viene emesso in A, quindi t B = t A + A c = 4 3 T T = 5 3 T t C = t A + A c/ = 4 3 T + 3 T = T t C t B = 1 3 T.. Sia v 1 = c/4 la velocità nel tratto OA, v = c/ la velocità nel tratto AC. L orologio sull astronave, nell evento A, misura il tempo proporio τ A = 1 v 1 c t A = T = 3 T. L intervallo di tempo proprio sull astronave tra A e C è τ C τ A = 1 v c (t C t A ) = 1 1 (T 43 ) 3 4 T = quindi 3 T = 3 3 T, e il ritardo è τ C = T 1.87T 3 t C τ C = T 1.87T = 0.13T.
28 Compito di Meccanica Analitica e Relativistica del 19 febbraio 019 Esercizio 1: Meccanica Lagrangiana. In un piano orizzontale, sul quale è fissato un sistema di assi cartesiani ortogonali Oy, si muove una guida quadrata omogenea ABCD, di lato a e massa m. Il punto medio M del lato AB della guida quadrata è vincolato a scorrere senza attrito lungo l asse O, e la guida quadrata è libera di ruotare attorno ad un asse perpendicolare al piano Oy e passante per M (si veda la Fig. 1). Sul sistema agiscono le forze attive F 1 = k OM, con k > 0, e F = k HB, con H proiezione ortogonale di B sulla retta y = d (con d > 0). Si adottino come coordinate lagrangiane l ascissa di M e l angolo θ che il lato AB della guida quadrata forma con il verso positivo dell asse O. 1. Si scrivano la funzione di Lagrange L del sistema e le equazioni del moto.. Si trovino le posizioni di equilibrio del sistema e se ne discuta il numero e la stabilità al variare del parametro λ = a d > Ponendo ora k = 1, m = 1, a = 4, d = 1, si scelga una posizione di equilibrio stabile e si determinino le frequenze delle piccole oscillazioni attorno ad essa. N.B.: Il momento d inerzia della guida quadrata rispetto al suo centro di massa G è I G = 4 3 ma. y H y=d k O k A B M θ G a m C D Fig. 1 Esercizio : Trasformazioni canoniche. Data la trasformazione Q = 1 ( 3 qα 1 γ p ) P = γ q β p dalle variabili q, p alle variabili Q, P. Dire per quali valori dei parametri reali α, β, γ la trasformazione è canonica. In corrispondenza di tali valori, determinare la funzione generatrice F (q, P ) della trasformazione canonica. (Si F suggerisce, nel calcolo della funzione generatrice, di integrare le espressioni di q e F P, trovandone le soluzioni generali, e imporre che siano la stessa funzione; in alternativa, eseguire il calcolo dell integrale di linea lungo una linea scelta in modo tale da rendere semplice il calcolo). Esercizio 3: Relatività ristretta. Si risolva il seguente problema nell ambito della relatività ristretta. Una particella di massa a riposo m 1 si muove lungo l asse con velocità v 1 ed urta una particella di massa m a riposo nell origine del sistema di coordinate. Nell urto viene prodotta un unica particella di massa M e velocità V. Sapendo che v 1 = 3 c e m1 M = 3 4, determinare V e m M.
Meccanica Analitica e Relativistica - I Esonero - 14/12/2016
 Meccanica nalitica e Relativistica - I Esonero - 14/12/2016 In un piano verticale è scelto un sistema di riferimento di assi cartesiani ortogonali z di origine e con l asse z orientato verso il basso.
Meccanica nalitica e Relativistica - I Esonero - 14/12/2016 In un piano verticale è scelto un sistema di riferimento di assi cartesiani ortogonali z di origine e con l asse z orientato verso il basso.
Meccanica Analitica e Relativistica - I Esonero - 14/12/2016
 Meccanica Analitica e Relativistica - I Esonero - 14/12/2016 In un piano verticale è scelto un sistema di riferimento di assi cartesiani ortogonali Oz di origine O e con l asse z orientato verso il basso.
Meccanica Analitica e Relativistica - I Esonero - 14/12/2016 In un piano verticale è scelto un sistema di riferimento di assi cartesiani ortogonali Oz di origine O e con l asse z orientato verso il basso.
Primo compito di esonero Meccanica Razionale
 Primo compito di esonero 9 aprile 20 Un punto materiale P di massa m è vincolato a muoversi senza attrito su un profilo descritto dall equazione y = 4 x 2 in un piano verticale soggetto al peso e ad una
Primo compito di esonero 9 aprile 20 Un punto materiale P di massa m è vincolato a muoversi senza attrito su un profilo descritto dall equazione y = 4 x 2 in un piano verticale soggetto al peso e ad una
Primo compito di esonero. Meccanica Razionale - Canale A - La. 23 aprile Docente C. Cammarota
 Primo compito di esonero Meccanica Razionale - Canale A - La 23 aprile 2014 Docente C. Cammarota Un punto materiale P di massa m è vincolato a muoversi senza attrito su un profilo descritto dall equazione
Primo compito di esonero Meccanica Razionale - Canale A - La 23 aprile 2014 Docente C. Cammarota Un punto materiale P di massa m è vincolato a muoversi senza attrito su un profilo descritto dall equazione
Corso di meccanica analitica. Compito Scritto del 11 febbraio 2013.
 Corso di meccanica analitica. Compito Scritto del 11 febbraio 2013. In un piano orizzontale π un disco omogeneo di massa M e raggio R e libero di ruotare senza attrito attorno al suo centro O. Sul disco
Corso di meccanica analitica. Compito Scritto del 11 febbraio 2013. In un piano orizzontale π un disco omogeneo di massa M e raggio R e libero di ruotare senza attrito attorno al suo centro O. Sul disco
Primo compito di esonero. Meccanica Razionale - Canale A - La. 22 aprile Docente C. Cammarota
 Primo compito di esonero Meccanica Razionale - Canale A - La 22 aprile 203 Docente C. Cammarota Un punto materiale P di massa m è vincolato a muoversi senza attrito su un profilo descritto dall equazione
Primo compito di esonero Meccanica Razionale - Canale A - La 22 aprile 203 Docente C. Cammarota Un punto materiale P di massa m è vincolato a muoversi senza attrito su un profilo descritto dall equazione
Tutorato 8 - MA/FM210-12/5/2017
 Tutorato 8 - MA/FM - /5/7 Esercizio. Si calcolino i momenti principali di inerzia dei seguenti corpi rigidi rispetto al loro centro di massa:. Disco sottile omogeneo di massa M e raggio R [Risposta: I
Tutorato 8 - MA/FM - /5/7 Esercizio. Si calcolino i momenti principali di inerzia dei seguenti corpi rigidi rispetto al loro centro di massa:. Disco sottile omogeneo di massa M e raggio R [Risposta: I
FM210 - Fisica Matematica 1 Tutorato 11 ( )
 Corso di laurea in atematica - Anno Accademico 3/4 F - Fisica atematica Tutorato (--) Esercizio. Si calcolino i momenti principali di inerzia dei seguenti corpi rigidi rispetto al loro centro di massa:.
Corso di laurea in atematica - Anno Accademico 3/4 F - Fisica atematica Tutorato (--) Esercizio. Si calcolino i momenti principali di inerzia dei seguenti corpi rigidi rispetto al loro centro di massa:.
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Dinamica dei sistemi materiali Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Dinamica dei sistemi materiali Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Foglio di Esercizi 7 Meccanica Razionale a.a. 2018/19 Canale A-L (P. Buttà)
 Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Foglio di Esercizi 5 Meccanica Razionale a.a. 2017/18 Canale A-L (P. Buttà)
 Foglio di Esercizi 5 Meccanica Razionale a.a. 017/18 Canale A-L (P. Buttà) Esercizio 1. Su un piano orizzontale sono poste due guide immateriali circolari di centri fissi O 1 e O e uguale raggio r; sia
Foglio di Esercizi 5 Meccanica Razionale a.a. 017/18 Canale A-L (P. Buttà) Esercizio 1. Su un piano orizzontale sono poste due guide immateriali circolari di centri fissi O 1 e O e uguale raggio r; sia
PROVA SCRITTA DI MECCANICA RAZIONALE (21 gennaio 2011)
 PRV SRITT DI MENI RZINLE (21 gennaio 2011) Il sistema in figura, posto in un piano verticale, è costituito di un asta rigida omogenea (massa m, lunghezza 2l) i cui estremi sono vincolati a scorrere, senza
PRV SRITT DI MENI RZINLE (21 gennaio 2011) Il sistema in figura, posto in un piano verticale, è costituito di un asta rigida omogenea (massa m, lunghezza 2l) i cui estremi sono vincolati a scorrere, senza
FM210 / MA - Seconda prova pre-esonero ( ) R cos u. dove h è una costante positiva. Oltre alla forza peso, l asta è soggetta ad una forza
 FM10 / MA - Seconda prova pre-esonero (6-5-017) Esercizio 1. Un asta rigida omogenea AB di lunghezza R e massa M è vincolata ad avere l estremo A sull asse fisso x, orientato verticalmente verso l alto,
FM10 / MA - Seconda prova pre-esonero (6-5-017) Esercizio 1. Un asta rigida omogenea AB di lunghezza R e massa M è vincolata ad avere l estremo A sull asse fisso x, orientato verticalmente verso l alto,
FM210 / MA - Secondo scritto ( )
 FM10 / MA - Secondo scritto (6-7-017) Esercizio 1. Un asta rigida omogenea di lunghezza l e massa M è vincolata a muoversi su un piano verticale di coordinate x-y (con l asse x orizzontale e l asse y verticale,
FM10 / MA - Secondo scritto (6-7-017) Esercizio 1. Un asta rigida omogenea di lunghezza l e massa M è vincolata a muoversi su un piano verticale di coordinate x-y (con l asse x orizzontale e l asse y verticale,
FM210 / MA - Soluzioni della seconda prova di esonero ( )
 FM10 / MA - Soluzioni della seconda prova di esonero (31-5-017) Esercizio 1. Un asta rigida omogenea AB di lunghezza l e massa M è vincolata a muoversi su un piano verticale Π, con estremo A fissato nel
FM10 / MA - Soluzioni della seconda prova di esonero (31-5-017) Esercizio 1. Un asta rigida omogenea AB di lunghezza l e massa M è vincolata a muoversi su un piano verticale Π, con estremo A fissato nel
ESERCIZI 121. P 1 z 1 y x. a) P 2. Figura 12.25: Sistema discusso nell esercizio 41.
 ESERCIZI 121 Esercizio 41 Un sistema meccanico è costituito da 3 punti 0, 1 e 2 di massa m vincolati a muoversi sulla superficie di un cilindro circolare retto di raggio r = 1. Si scelga un sistema di
ESERCIZI 121 Esercizio 41 Un sistema meccanico è costituito da 3 punti 0, 1 e 2 di massa m vincolati a muoversi sulla superficie di un cilindro circolare retto di raggio r = 1. Si scelga un sistema di
Mediterranea Metodi e Modelli Matematici per le Applicazioni
 Facoltà d Ingegneria A.A. 2006/2007 Appello del 28/06/2007 Un sistema materiale è costituito da un asta AB, omogenea di massa 2m e lunghezza 2R, e da un punto materiale P di massa m. L asta è incernierata
Facoltà d Ingegneria A.A. 2006/2007 Appello del 28/06/2007 Un sistema materiale è costituito da un asta AB, omogenea di massa 2m e lunghezza 2R, e da un punto materiale P di massa m. L asta è incernierata
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 30 Gennaio 207 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi in un piano un sistema di riferimento Oxy. In
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 30 Gennaio 207 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi in un piano un sistema di riferimento Oxy. In
Compito di gennaio 2001
 Compito di gennaio 001 Un asta omogenea A di massa m e lunghezza l è libera di ruotare attorno al proprio estremo mantenendosi in un piano verticale All estremità A dell asta è saldato il baricentro di
Compito di gennaio 001 Un asta omogenea A di massa m e lunghezza l è libera di ruotare attorno al proprio estremo mantenendosi in un piano verticale All estremità A dell asta è saldato il baricentro di
Prova Scritta di di Meccanica Analitica. 28 Giugno Problema 1. Si consideri un punto materiale di massa unitaria soggetto ad un potenziale
 Prova Scritta di di Meccanica Analitica 8 Giugno 018 Problema 1 Si consideri un punto materiale di massa unitaria soggetto ad un potenziale V (x) = 1 x + x x > 0 determinare le frequenze delle piccole
Prova Scritta di di Meccanica Analitica 8 Giugno 018 Problema 1 Si consideri un punto materiale di massa unitaria soggetto ad un potenziale V (x) = 1 x + x x > 0 determinare le frequenze delle piccole
Università degli Studi Mediterranea di Reggio Calabria Facoltà d Ingegneria Meccanica Razionale A.A. 2005/ Appello del 04/07/2006
 Facoltà d Ingegneria Meccanica Razionale A.A. 2005/2006 - Appello del 04/07/2006 In un piano verticale Oxy, un sistema materiale è costituito da un disco omogeneo, di centro Q, raggio R e massa 2m, e da
Facoltà d Ingegneria Meccanica Razionale A.A. 2005/2006 - Appello del 04/07/2006 In un piano verticale Oxy, un sistema materiale è costituito da un disco omogeneo, di centro Q, raggio R e massa 2m, e da
Corsi di laurea in Matematica e Fisica - Anno Accademico 2017/18 FM210 / MA
 Corsi di laurea in Matematica e Fisica - Anno Accademico 07/8 FM0 / MA Seconda Prova di Esonero [8-5-08]. Un sistema meccanico è costituito da due sbarre uguali, rettilinee, omogenee, pesanti, di massa
Corsi di laurea in Matematica e Fisica - Anno Accademico 07/8 FM0 / MA Seconda Prova di Esonero [8-5-08]. Un sistema meccanico è costituito da due sbarre uguali, rettilinee, omogenee, pesanti, di massa
Compito del 14 giugno 2004
 Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
ESERCIZI 53. i=1. i=1
 ESERCIZI 53 Esercizio 47 Si dimostri la 57.10). [Suggerimento. Derivando la seconda delle 57.4) e utilizzando l identità di Jacobi per il prodotto vettoriale cfr. l esercizio 46), si ottiene d N m i ξ
ESERCIZI 53 Esercizio 47 Si dimostri la 57.10). [Suggerimento. Derivando la seconda delle 57.4) e utilizzando l identità di Jacobi per il prodotto vettoriale cfr. l esercizio 46), si ottiene d N m i ξ
2) Si consideri il seguente sistema d equazioni differenziali di due equazioni nelle due incognite u (x,y) e v (x,y): "x + x "u.
 Anno Accademico 008/009 Appello del 17/0/009 1) In un piano Oxy un punto materiale P di massa m scorre lungo l asse verticale Oy, mentre un altro punto materiale Q di massa m scorre lungo una retta s disposta
Anno Accademico 008/009 Appello del 17/0/009 1) In un piano Oxy un punto materiale P di massa m scorre lungo l asse verticale Oy, mentre un altro punto materiale Q di massa m scorre lungo una retta s disposta
Φ D 2 L. k > 0. M O=A s. sistema (che è rappresentato in figura ). Infine, vogliamo calcolare le reazioni vincolari sul sistema.
 Esercizio 1. Un sistema materiale è costituito da una lamina piana omogenea di massa M e lato L e da un asta AB di lunghezza l e massa m. La lamina scorre con un lato sull asse x ed è soggetta a una forza
Esercizio 1. Un sistema materiale è costituito da una lamina piana omogenea di massa M e lato L e da un asta AB di lunghezza l e massa m. La lamina scorre con un lato sull asse x ed è soggetta a una forza
II compito di esonero di Meccanica Razionale per fisici del 2 maggio 1989 Università dell Aquila
 II compito di esonero di Meccanica Razionale per fisici del 2 maggio 1989 Università dell Aquila Agli estremi di una sbarretta di lunghezza 2l e massa trascurabile sono saldate due particelle puntiformi
II compito di esonero di Meccanica Razionale per fisici del 2 maggio 1989 Università dell Aquila Agli estremi di una sbarretta di lunghezza 2l e massa trascurabile sono saldate due particelle puntiformi
Compito di Istituzioni di Fisica Matematica 8 Luglio 2013
 Compito di Istituzioni di Fisica Matematica 8 Luglio 203 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi un sistema di riferimento Oxyz, con asse Oz verticale ascendente. Un asta omogenea
Compito di Istituzioni di Fisica Matematica 8 Luglio 203 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi un sistema di riferimento Oxyz, con asse Oz verticale ascendente. Un asta omogenea
Sistemi Dinamici e Meccanica Classica A/A Alcuni Esercizi
 Sistemi Dinamici e Meccanica Classica A/A 2008 2009. Alcuni Esercizi G.Falqui, P. Lorenzoni, Dipartimento di Matematica e Applicazioni, Università di Milano Bicocca. Versione del 23 Dicembre 2008 con esercizi
Sistemi Dinamici e Meccanica Classica A/A 2008 2009. Alcuni Esercizi G.Falqui, P. Lorenzoni, Dipartimento di Matematica e Applicazioni, Università di Milano Bicocca. Versione del 23 Dicembre 2008 con esercizi
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Meccanica analitica III parte Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Meccanica analitica III parte Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Prova Scritta di di Meccanica Analitica. 3 giugno Un punto di massa unitaria si muove soggetto al potenziale ) V (x) = x exp.
 Prova Scritta di di Meccanica Analitica 3 giugno 015 Problema 1 Un punto di massa unitaria si muove soggetto al potenziale V x = x exp x a Determinare le posizioni di equilibrio e la loro stabilitá b Tracciare
Prova Scritta di di Meccanica Analitica 3 giugno 015 Problema 1 Un punto di massa unitaria si muove soggetto al potenziale V x = x exp x a Determinare le posizioni di equilibrio e la loro stabilitá b Tracciare
Esercizi da fare a casa
 apitolo 1 Esercizi da fare a casa 1.1 Premesse I seguenti esercizi sono risolubili nella seconda settimana di corso. Per quelli del primo gruppo le soluzioni si possono estrarre dal mio libro di Esercizi
apitolo 1 Esercizi da fare a casa 1.1 Premesse I seguenti esercizi sono risolubili nella seconda settimana di corso. Per quelli del primo gruppo le soluzioni si possono estrarre dal mio libro di Esercizi
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Meccanica analitica II parte Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Meccanica analitica II parte Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Soluzione degli esercizi dello scritto di Meccanica del 08/07/2019
 Soluzione degli esercizi dello scritto di Meccanica del 08/07/2019 Esercizio 1 Un asta rigida di lunghezza L = 0.8 m e massa M è vincolata nell estremo A ad un perno liscio ed è appesa all altro estremo
Soluzione degli esercizi dello scritto di Meccanica del 08/07/2019 Esercizio 1 Un asta rigida di lunghezza L = 0.8 m e massa M è vincolata nell estremo A ad un perno liscio ed è appesa all altro estremo
Compito del 21 giugno 2004
 Compito del 1 giugno 00 Una lamina omogenea di massa m è costituita da un quadrato ABCD di lato a da cui è stato asportato il quadrato HKLM avente i vertici nei punti medi dei lati di ABCD. La lamina è
Compito del 1 giugno 00 Una lamina omogenea di massa m è costituita da un quadrato ABCD di lato a da cui è stato asportato il quadrato HKLM avente i vertici nei punti medi dei lati di ABCD. La lamina è
Prova Scritta di di Meccanica Analitica. 4 Luglio ) Si consideri un punto materiale di massa m soggetto al potenziale.
 Prova Scritta di di Meccanica Analitica 4 Luglio 7 Problema ) Si consideri un punto materiale di massa m soggetto al potenziale V x) ax 4 determinare la dipendenza del periodo dall energia. ) Si scriva
Prova Scritta di di Meccanica Analitica 4 Luglio 7 Problema ) Si consideri un punto materiale di massa m soggetto al potenziale V x) ax 4 determinare la dipendenza del periodo dall energia. ) Si scriva
Prova Scritta di di Meccanica Analitica
 Prova Scritta di di Meccanica Analitica 7 gennaio 015 Problema 1 Un punto di massa unitaria si muove sull asse x soggetto al potenziale V (x) = x e x a) Determinare le posizioni di equilibrio e la loro
Prova Scritta di di Meccanica Analitica 7 gennaio 015 Problema 1 Un punto di massa unitaria si muove sull asse x soggetto al potenziale V (x) = x e x a) Determinare le posizioni di equilibrio e la loro
FM210 / MA - Seconda prova pre-esonero ( )
 FM10 / MA - Seconda prova pre-esonero (3-5-018) 1. Un sistema meccanico è costituito da due sbarre uguali AB e BC, rettilinee, omogenee, di massa M e lunghezza l, incernierate tra loro in B. Le due sbarre
FM10 / MA - Seconda prova pre-esonero (3-5-018) 1. Un sistema meccanico è costituito da due sbarre uguali AB e BC, rettilinee, omogenee, di massa M e lunghezza l, incernierate tra loro in B. Le due sbarre
FISICA MATEMATICA (Ingegneria Civile) V APPELLO ( ) A.A.2017/18
 FISICA ATEATICA Ingegneria Civile V APPELLO 05.09.208 A.A.207/8 COGNOE E NOE.............................. N.Ro ATR.................................................. LUOGO E DATA DI NASCITA....................................................................................
FISICA ATEATICA Ingegneria Civile V APPELLO 05.09.208 A.A.207/8 COGNOE E NOE.............................. N.Ro ATR.................................................. LUOGO E DATA DI NASCITA....................................................................................
Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 2014/ Prova Scritta del 08/02/2016
 Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 014/015 - Prova Scritta del 08/0/016 ISTRUZIONI: LEGGERE ATTENTAMENTE Può essere svolta la prima parte (A1 e A) oppure la seconda
Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 014/015 - Prova Scritta del 08/0/016 ISTRUZIONI: LEGGERE ATTENTAMENTE Può essere svolta la prima parte (A1 e A) oppure la seconda
Introduzione alla Fisica Moderna - a.a
 Introduzione alla Fisica Moderna - a.a. 015-16 7/9/016 Nome Cognome Matricola: 1) Si consideri il sistema di equazioni del primo ordine ẋ = y, ẏ = η y sin x, determinando i punti di equilibrio, il loro
Introduzione alla Fisica Moderna - a.a. 015-16 7/9/016 Nome Cognome Matricola: 1) Si consideri il sistema di equazioni del primo ordine ẋ = y, ẏ = η y sin x, determinando i punti di equilibrio, il loro
Corso di Laurea in Ingegneria Meccanica Anno Accademico 2010/2011 Meccanica Razionale
 Corso di Laurea in Ingegneria Meccanica Anno Accademico 2010/2011 Meccanica Razionale Nome... N. Matricola... Ancona, 21 gennaio 2011 1. Un disco materiale pesante di massa m e raggio R si muove nel piano
Corso di Laurea in Ingegneria Meccanica Anno Accademico 2010/2011 Meccanica Razionale Nome... N. Matricola... Ancona, 21 gennaio 2011 1. Un disco materiale pesante di massa m e raggio R si muove nel piano
MA - Soluzioni della seconda prova pre-esonero ( )
 M - Soluzioni della seconda prova pre-esonero (5-5-15) 1. Una lamina sottile pesante, omogenea, di massa M, ha la forma di un triangolo rettangolo isoscele, i cui cateti B e C hanno lunghezza l. La lamina
M - Soluzioni della seconda prova pre-esonero (5-5-15) 1. Una lamina sottile pesante, omogenea, di massa M, ha la forma di un triangolo rettangolo isoscele, i cui cateti B e C hanno lunghezza l. La lamina
Prova Scritta di di Meccanica Analitica. 7 Giugno 2017
 Prova Scritta di di Meccanica Analitica 7 Giugno 217 Problema 1 1) Si consideri un pendolo di massa m e lunghezza l il cui punto di aggancio si muove di moto uniformente accelerato lungo l asse orizzontale
Prova Scritta di di Meccanica Analitica 7 Giugno 217 Problema 1 1) Si consideri un pendolo di massa m e lunghezza l il cui punto di aggancio si muove di moto uniformente accelerato lungo l asse orizzontale
x = λ y = λ z = λ. di libertà del sistema ed individuare un opportuno sistema di coordinate lagrangiane.
 1 Università di Pavia Facoltà di Ingegneria Corso di Laurea in Ingegneria Industriale Correzione prova scritta Esame di Fisica Matematica 22 febbraio 2012 1. Determinare, per il seguente sistema di vettori
1 Università di Pavia Facoltà di Ingegneria Corso di Laurea in Ingegneria Industriale Correzione prova scritta Esame di Fisica Matematica 22 febbraio 2012 1. Determinare, per il seguente sistema di vettori
Sistemi Dinamici e Meccanica Classica A/A Alcuni Esercizi
 Sistemi Dinamici e Meccanica Classica A/A 2008 2009. Alcuni Esercizi G.Falqui, P. Lorenzoni, Dipartimento di Matematica e Applicazioni,Università di Milano Bicocca. Seconda versione preliminare, 15 Dicembre
Sistemi Dinamici e Meccanica Classica A/A 2008 2009. Alcuni Esercizi G.Falqui, P. Lorenzoni, Dipartimento di Matematica e Applicazioni,Università di Milano Bicocca. Seconda versione preliminare, 15 Dicembre
Esercizi di Meccanica Razionale - Parte III. 1. Un sistema rigido e costituito da due aste AB e BC, di lunghezza rispettivamente
 Universita' degli Studi di ncona Esercizi di Meccanica Razionale - Parte III 1. Un sistema rigido e costituito da due aste e, di lunghezza rispettivamente L ed l e di massem ed m, saldate ad angolo retto
Universita' degli Studi di ncona Esercizi di Meccanica Razionale - Parte III 1. Un sistema rigido e costituito da due aste e, di lunghezza rispettivamente L ed l e di massem ed m, saldate ad angolo retto
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 18 Settembre 27 usare fogli diversi per esercizi diversi) Primo Esercizio In un piano si fissi un sistema di riferimento Oxy. Un
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 18 Settembre 27 usare fogli diversi per esercizi diversi) Primo Esercizio In un piano si fissi un sistema di riferimento Oxy. Un
Esercitazione 2. Soluzione
 Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
MA - Soluzioni dell esame scritto del
 MA - Soluzioni dell esame scritto del 7-9-015 1. Si consideri un punto materiale di massa m vincolato a muoversi su una superficie ellissoidale di equazione (x + y ) + z = R, sottoposto all azione della
MA - Soluzioni dell esame scritto del 7-9-015 1. Si consideri un punto materiale di massa m vincolato a muoversi su una superficie ellissoidale di equazione (x + y ) + z = R, sottoposto all azione della
Esercitazione 2. Soluzione
 Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
FM210 - Fisica Matematica I
 Corso di laurea in Matematica - Anno Accademico 11/1 FM1 - Fisica Matematica I Soluzioni al tutorato del 9-1-1 1. Due particelle di massa m e coordinate x, y R si muovono sotto l effetto di una forza centrale
Corso di laurea in Matematica - Anno Accademico 11/1 FM1 - Fisica Matematica I Soluzioni al tutorato del 9-1-1 1. Due particelle di massa m e coordinate x, y R si muovono sotto l effetto di una forza centrale
Corsi di laurea in Matematica e Fisica - Anno Accademico 2017/18 FM210 / MA. Primo Scritto [ ]
![Corsi di laurea in Matematica e Fisica - Anno Accademico 2017/18 FM210 / MA. Primo Scritto [ ] Corsi di laurea in Matematica e Fisica - Anno Accademico 2017/18 FM210 / MA. Primo Scritto [ ]](/thumbs/93/112641904.jpg) Corsi di laurea in Matematica e Fisica - Anno Accademico 017/18 FM10 / MA Primo Scritto [1-6-018] 1. Si consideri il sistema meccanico bidimensionale per x R. ẍ = ( x 4 1)x, (a) Si identifichino due integrali
Corsi di laurea in Matematica e Fisica - Anno Accademico 017/18 FM10 / MA Primo Scritto [1-6-018] 1. Si consideri il sistema meccanico bidimensionale per x R. ẍ = ( x 4 1)x, (a) Si identifichino due integrali
Esercizio: pendolo sferico. Soluzione
 Esercizio: pendolo sferico Si consideri un punto materiale di massa m vincolato a muoversi senza attrito sulla superficie di una sfera di raggio R e soggetto alla forza di gravita. Ridurre il moto alle
Esercizio: pendolo sferico Si consideri un punto materiale di massa m vincolato a muoversi senza attrito sulla superficie di una sfera di raggio R e soggetto alla forza di gravita. Ridurre il moto alle
Corso di Laurea in Ingegneria Meccanica Anno Accademico 2017/2018 Meccanica Razionale - Prova teorica del 5/4/2018.
 Corso di Laurea in Ingegneria Meccanica Anno Accademico 2017/2018 Meccanica Razionale - Prova teorica del 5/4/2018 Prova teorica - A Nome... N. Matricola... Ancona, 5 aprile 2018 1. Gradi di libertà di
Corso di Laurea in Ingegneria Meccanica Anno Accademico 2017/2018 Meccanica Razionale - Prova teorica del 5/4/2018 Prova teorica - A Nome... N. Matricola... Ancona, 5 aprile 2018 1. Gradi di libertà di
Esercizi di statica e dinamica I parte
 Esercizi di statica e dinamica I parte EQ1) Una lamina CD di forma quadrata (lato 2L e densità in un suo generico punto P, µ(p) = 3m 8L 4 GP 2, con G punto d incontro delle diagonali del quadrato) è vincolata
Esercizi di statica e dinamica I parte EQ1) Una lamina CD di forma quadrata (lato 2L e densità in un suo generico punto P, µ(p) = 3m 8L 4 GP 2, con G punto d incontro delle diagonali del quadrato) è vincolata
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA
 DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 16 Febbraio 27 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi un sistema di riferimento Oxy in un piano e
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 16 Febbraio 27 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi un sistema di riferimento Oxy in un piano e
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Svincolamento statico Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica Razionale
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Svincolamento statico Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica Razionale
Soluzioni Prova Scritta di di Meccanica Analitica. 17 aprile Un punto di massa unitaria si muove lungo una retta soggetto al potenziale
 Soluzioni Prova Scritta di di Meccanica Analitica 17 aprile 15 Problema 1 Un punto di massa unitaria si muove lungo una retta soggetto al potenziale V x = exp x / a Tracciare il grafico del potenziale
Soluzioni Prova Scritta di di Meccanica Analitica 17 aprile 15 Problema 1 Un punto di massa unitaria si muove lungo una retta soggetto al potenziale V x = exp x / a Tracciare il grafico del potenziale
EQUAZIONI DI LAGRANGE E STAZIONARIETÀ DEL POTENZIALE
 EQUAZIONI DI LAGRANGE E STAZIONARIETÀ DEL POTENZIALE Equazioni di Lagrange in forma non conservativa Riprendiamo l equazione simbolica della dinamica per un sistema olonomo a vincoli perfetti nella forma
EQUAZIONI DI LAGRANGE E STAZIONARIETÀ DEL POTENZIALE Equazioni di Lagrange in forma non conservativa Riprendiamo l equazione simbolica della dinamica per un sistema olonomo a vincoli perfetti nella forma
PROVA SCRITTA DI MECCANICA RAZIONALE (11 giugno 2005) (C.d.L. Ing. Edile - Architettura. Prof. A. Muracchini)
 RV SRITT DI MENI RZINLE (11 giugno 2005) (.d.l. Ing. Edile - rchitettura. rof.. Muracchini) Il sistema rappresentato in figura, mobile in un piano verticale z, è costituito di un disco circolare pesante
RV SRITT DI MENI RZINLE (11 giugno 2005) (.d.l. Ing. Edile - rchitettura. rof.. Muracchini) Il sistema rappresentato in figura, mobile in un piano verticale z, è costituito di un disco circolare pesante
LAUREA DI PRIMO LIVELLO IN FISICA ISTITUZIONI DI FISICA MATEMATICA ESAME 20 Settembre 2005 PARTE A P O
 LAUREA DI PRIMO LIVELLO IN FISICA ISTITUZIONI DI FISICA MATEMATICA ESAME 0 Settembre 005 PARTE A Esercizio 1. Nel piano cartesiano Oxy con asse y verticale ascendente, un punto materiale P di massa m è
LAUREA DI PRIMO LIVELLO IN FISICA ISTITUZIONI DI FISICA MATEMATICA ESAME 0 Settembre 005 PARTE A Esercizio 1. Nel piano cartesiano Oxy con asse y verticale ascendente, un punto materiale P di massa m è
Compito di gennaio 2005
 Compito di gennaio 2005 In un piano verticale, si consideri il vincolo mobile costituito da una semicirconferenza di raggio R e centro C, i cui estremi A e B possono strisciare lungo l asse delle ascisse:
Compito di gennaio 2005 In un piano verticale, si consideri il vincolo mobile costituito da una semicirconferenza di raggio R e centro C, i cui estremi A e B possono strisciare lungo l asse delle ascisse:
, con x =, y. 3. Si disegni il grafico delle curve di livello sul piano delle fasi (x, ẋ) al variare di E e si discuta la natura qualitativa del moto.
 7 o tutorato - MA - Prova Pre-Esonero - 8/4/5 Esercizio Una massa puntiforme m è vincolata a muoversi nel piano verticale xy (con x l asse orizzontale e y l asse verticale orientato verso l alto), su una
7 o tutorato - MA - Prova Pre-Esonero - 8/4/5 Esercizio Una massa puntiforme m è vincolata a muoversi nel piano verticale xy (con x l asse orizzontale e y l asse verticale orientato verso l alto), su una
Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 2013/ Prova Scritta del 01/07/2014
 Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 013/014 - Prova Scritta del 01/07/014 ISTRUZIONI: LEGGERE ATTENTAMENTE Gli studenti che hanno seguito il corso di Meccanica Classica
Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 013/014 - Prova Scritta del 01/07/014 ISTRUZIONI: LEGGERE ATTENTAMENTE Gli studenti che hanno seguito il corso di Meccanica Classica
1. Siano A e B due punti di un atto di moto rigido piano. Dire quale delle seguenti affermazioni è errata:
 Università del Salento Facoltà di Ingegneria Corsi di Laurea in Ingegneria Industriale e Civile Prova scritta di Meccanica Razionale 20 giugno 2016 Soluzioni Parte 1: Domande a risposta multipla. 1. Siano
Università del Salento Facoltà di Ingegneria Corsi di Laurea in Ingegneria Industriale e Civile Prova scritta di Meccanica Razionale 20 giugno 2016 Soluzioni Parte 1: Domande a risposta multipla. 1. Siano
Soluzione degli esercizi dello scritto di Meccanica del 17/06/2019
 Soluzione degli esercizi dello scritto di Meccanica del 17/06/2019 Esercizio 1 Un corpo rigido è formato da un asta di lunghezza L = 2 m e massa trascurabile, ai cui estremi sono fissati due corpi puntiformi,
Soluzione degli esercizi dello scritto di Meccanica del 17/06/2019 Esercizio 1 Un corpo rigido è formato da un asta di lunghezza L = 2 m e massa trascurabile, ai cui estremi sono fissati due corpi puntiformi,
Prova Scritta di di Meccanica Analitica. 11 febbraio Problema 1
 Prova Scritta di di Meccanica Analitica 11 febbraio 019 Problema 1 Si consideri un punto materiale P di massa m vincolato a muoversi su una retta orizzontale e connesso mediante una molla di costante elastica
Prova Scritta di di Meccanica Analitica 11 febbraio 019 Problema 1 Si consideri un punto materiale P di massa m vincolato a muoversi su una retta orizzontale e connesso mediante una molla di costante elastica
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 6 Giugno 2017 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi in un piano un sistema di riferimento Oxy. Si
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 6 Giugno 2017 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi in un piano un sistema di riferimento Oxy. Si
Corso di Laurea in Ingegneria Meccanica Anno Accademico 2017/2018 Meccanica Razionale - Prova teorica del 10/2/2018.
 Corso di Laurea in Ingegneria Meccanica Anno Accademico 2017/2018 Meccanica Razionale - Prova teorica del 10/2/2018 Prova teorica - A Nome... N. Matricola... Ancona, 10 febbraio 2018 1. Un asta AB di lunghezza
Corso di Laurea in Ingegneria Meccanica Anno Accademico 2017/2018 Meccanica Razionale - Prova teorica del 10/2/2018 Prova teorica - A Nome... N. Matricola... Ancona, 10 febbraio 2018 1. Un asta AB di lunghezza
Meccanica 15Aprile 2016
 Meccanica 15Aprile 2016 Problema 1 (1 punto) Una pallottola di massa m= 20 g arriva con velocità V= 300 m/s, inclinata verso il basso di un anglo = 15 rispetto al piano orizzontale, su un blocco di massa
Meccanica 15Aprile 2016 Problema 1 (1 punto) Una pallottola di massa m= 20 g arriva con velocità V= 300 m/s, inclinata verso il basso di un anglo = 15 rispetto al piano orizzontale, su un blocco di massa
Università degli Studi Mediterranea di Reggio Calabria Facoltà d Ingegneria Meccanica Razionale A.A. 2005/ Appello del 04/07/2006
 Facoltà d Ingegneria Meccanica Razionale A.A. 2005/2006 - Appello del 04/07/2006 In un piano verticale Oxy, un sistema materiale è costituito da un disco omogeneo, di centro Q, raggio R e massa 2m, e da
Facoltà d Ingegneria Meccanica Razionale A.A. 2005/2006 - Appello del 04/07/2006 In un piano verticale Oxy, un sistema materiale è costituito da un disco omogeneo, di centro Q, raggio R e massa 2m, e da
Prova Scritta di di Meccanica Analitica. 10 Febbraio 2017
 Prova Scritta di di Meccanica Analitica 10 Febbraio 017 Problema 1 Si consideri un punto materiale di massa m soggetto alla forza peso e vincolato ad una curva in un piano verticale y x x Schematizzare
Prova Scritta di di Meccanica Analitica 10 Febbraio 017 Problema 1 Si consideri un punto materiale di massa m soggetto alla forza peso e vincolato ad una curva in un piano verticale y x x Schematizzare
PROVA SCRITTA DI MECCANICA RAZIONALE (12 gennaio 2018) (Prof. A. Muracchini)
 PRV SRITT DI MENI RZINLE (12 gennaio 2018) Il sistema in figura, mobile in un piano verticale, è costituito di un disco rigido D, omogeneo (massa M, raggio R) vincolato in modo che il punto del suo bordo
PRV SRITT DI MENI RZINLE (12 gennaio 2018) Il sistema in figura, mobile in un piano verticale, è costituito di un disco rigido D, omogeneo (massa M, raggio R) vincolato in modo che il punto del suo bordo
Compito 19 Luglio 2016
 Compito 19 Luglio 016 Roberto onciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 015-016 Compito di Fisica Generale I per matematici 19 Luglio 016
Compito 19 Luglio 016 Roberto onciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 015-016 Compito di Fisica Generale I per matematici 19 Luglio 016
Tutorato 6 - FM210. avendo usato la condizione di puro rotolamento r φ = ẏ e. 2) I punti di equilibrio sono i punti critici del potenziale:
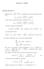 Tutorato 6 - FM10 Soluzione Esercizio 1 R l = l, applicando il teorema di Koenig abbi- 1 Abbiamo OC = amo T disco = 1 mẏ + 1 mr φ = 1 mẏ avendo usato la condizione di puro rotolamento r φ = ẏ e T asta
Tutorato 6 - FM10 Soluzione Esercizio 1 R l = l, applicando il teorema di Koenig abbi- 1 Abbiamo OC = amo T disco = 1 mẏ + 1 mr φ = 1 mẏ avendo usato la condizione di puro rotolamento r φ = ẏ e T asta
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 6 Giugno 08 (usare fogli diversi per esercizi diversi) Primo Esercizio i) Assumiamo che Q sia un punto di un corpo rigido piano
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 6 Giugno 08 (usare fogli diversi per esercizi diversi) Primo Esercizio i) Assumiamo che Q sia un punto di un corpo rigido piano
Corso di Laurea in Ingegneria Meccanica Anno Accademico 2018/2019 Meccanica Razionale - Appello del 13/4/2019
 orso di Laurea in Ingegneria Meccanica Anno Accademico 2018/2019 Meccanica Razionale - Appello del 1/4/2019 Nome... N. Matricola... Ancona, 1 aprile 2019 1. Un asta OA di massa M e lunghezza L si muove
orso di Laurea in Ingegneria Meccanica Anno Accademico 2018/2019 Meccanica Razionale - Appello del 1/4/2019 Nome... N. Matricola... Ancona, 1 aprile 2019 1. Un asta OA di massa M e lunghezza L si muove
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 30 Gennaio 2018 (usare fogli diversi per esercizi diversi) Primo Esercizio In un piano verticale si fissi un sistema di riferimento
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 30 Gennaio 2018 (usare fogli diversi per esercizi diversi) Primo Esercizio In un piano verticale si fissi un sistema di riferimento
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 18 Luglio 7 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi in un piano un sistema di riferimento Oxy. L estremo
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 18 Luglio 7 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi in un piano un sistema di riferimento Oxy. L estremo
Soluzione del Secondo Esonero A.A , del 28/05/2013
 Soluzione del Secondo Esonero A.A. 01-013, del 8/05/013 Primo esercizio a) Sia v la velocità del secondo punto materiale subito dopo l urto, all inizio del tratto orizzontale con attrito. Tra il punto
Soluzione del Secondo Esonero A.A. 01-013, del 8/05/013 Primo esercizio a) Sia v la velocità del secondo punto materiale subito dopo l urto, all inizio del tratto orizzontale con attrito. Tra il punto
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 30 Gennaio 27 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi in un piano un sistema di riferimento Oxy. In
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 30 Gennaio 27 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi in un piano un sistema di riferimento Oxy. In
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Meccanica analitica I parte Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Meccanica analitica I parte Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Compito di Fisica 1 Ingegneria elettrica e gestionale Soluzioni fila B
 Compito di Fisica 1 Ingegneria elettrica e gestionale Soluzioni fila B Massimo Vassalli 26 Marzo 2008 NB: dal momento che i dati numerici degli esercizi non sono comuni a tutti i compiti, i risultati sono
Compito di Fisica 1 Ingegneria elettrica e gestionale Soluzioni fila B Massimo Vassalli 26 Marzo 2008 NB: dal momento che i dati numerici degli esercizi non sono comuni a tutti i compiti, i risultati sono
Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 2013/ Prova Scritta del 17/01/2014
 Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 13/14 - Prova Scritta del 17/1/14 ISTRUZIONI: LEGGERE ATTENTAMENTE Gli studenti che seguono il corso di Meccanica Classica dell a.a.
Università di Pisa - Corso di Laurea in Fisica Meccanica Classica a.a. 13/14 - Prova Scritta del 17/1/14 ISTRUZIONI: LEGGERE ATTENTAMENTE Gli studenti che seguono il corso di Meccanica Classica dell a.a.
Esercizio: pendoli accoppiati. Soluzione
 Esercizio: pendoli accoppiati Si consideri un sistema di due pendoli identici, con punti di sospensione posti alla stessa quota in un piano verticale. I due pendoli sono collegati da una molla di costante
Esercizio: pendoli accoppiati Si consideri un sistema di due pendoli identici, con punti di sospensione posti alla stessa quota in un piano verticale. I due pendoli sono collegati da una molla di costante
Soluzione della prova scritta del 18 Aprile 2011
 Soluzione della prova scritta del 18 Aprile 011 1. Nel sistema di figura, posto in un piano verticale, i due dischi, di peso, sono omogenei e hanno raggio, mentrelalaminaquadratahalato epeso. La lamina
Soluzione della prova scritta del 18 Aprile 011 1. Nel sistema di figura, posto in un piano verticale, i due dischi, di peso, sono omogenei e hanno raggio, mentrelalaminaquadratahalato epeso. La lamina
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 10 Gennaio 2017 (usare fogli diversi per esercizi diversi) Primo Esercizio Si consideri il sistema di riferimento Oxy. L estremo
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 10 Gennaio 2017 (usare fogli diversi per esercizi diversi) Primo Esercizio Si consideri il sistema di riferimento Oxy. L estremo
SOLUZIONE Il diagramma delle forze che agiscono sul corpo è mostrata in figura:
 Esercizio 1 Un blocco di massa M inizialmente fermo è lasciato libero di muoversi al tempo t = 0 su un piano inclinato scabro (µ S e µ D ). a) Determinare il valore limite di θ (θ 0 ) per cui il blocco
Esercizio 1 Un blocco di massa M inizialmente fermo è lasciato libero di muoversi al tempo t = 0 su un piano inclinato scabro (µ S e µ D ). a) Determinare il valore limite di θ (θ 0 ) per cui il blocco
Compito 21 Giugno 2016
 Compito 21 Giugno 2016 Roberto Bonciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 2015-2016 Compito di Fisica Generale I per matematici 21 Giugno
Compito 21 Giugno 2016 Roberto Bonciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 2015-2016 Compito di Fisica Generale I per matematici 21 Giugno
Esercitazione 5. Esercizio 1. Equilibrio e stabilità ( )
 Esercitazione 5 (12.11.2012) Esercizio 1 In un piano verticale π, un disco omogeneo di massa m e raggio R è vincolato in modo tale che il punto del suo bordo scorre senza attrito sull asse x di un riferimento
Esercitazione 5 (12.11.2012) Esercizio 1 In un piano verticale π, un disco omogeneo di massa m e raggio R è vincolato in modo tale che il punto del suo bordo scorre senza attrito sull asse x di un riferimento
Esame 12/02/2004 Soluzione
 Teoria dei Sistemi Dinamici 1GTG/2GTG Esame 12/2/24 Prego segnalare errori o inesattezze a basilio.bona@polito.it 1 Sistemi di riferimento, rototraslazioni (6 punti) Esercizio 1.1 Costruire la matrice
Teoria dei Sistemi Dinamici 1GTG/2GTG Esame 12/2/24 Prego segnalare errori o inesattezze a basilio.bona@polito.it 1 Sistemi di riferimento, rototraslazioni (6 punti) Esercizio 1.1 Costruire la matrice
E i = mgh 0 = mg2r mv2 = mg2r mrg = E f. da cui si ricava h 0 = 5 2 R
 Esercizio 1 Un corpo puntiforme di massa m scivola lungo una pista liscia di raggio R partendo da fermo da un altezza h rispetto al fondo della pista come rappresentato in figura. a) Determinare il valore
Esercizio 1 Un corpo puntiforme di massa m scivola lungo una pista liscia di raggio R partendo da fermo da un altezza h rispetto al fondo della pista come rappresentato in figura. a) Determinare il valore
FM210 - Fisica Matematica I
 Corso di laurea in Matematica - Anno Accademico 01/14 FM10 - Fisica Matematica I Seconda Prova di Esonero [1-10-014] 1. (1 punti. Una massa puntiforme m si muove su una guida liscia di equazione y = de
Corso di laurea in Matematica - Anno Accademico 01/14 FM10 - Fisica Matematica I Seconda Prova di Esonero [1-10-014] 1. (1 punti. Una massa puntiforme m si muove su una guida liscia di equazione y = de
FM210 - Fisica Matematica I
 Corso di laurea in Matematica - Anno Accademico 212/13 FM21 - Fisica Matematica I Soluzioni della Seconda Prova Pre-esonero [9-1-213] Esercizio 2 (a) Osserviamo che il sistema è conservativo e il potenziale
Corso di laurea in Matematica - Anno Accademico 212/13 FM21 - Fisica Matematica I Soluzioni della Seconda Prova Pre-esonero [9-1-213] Esercizio 2 (a) Osserviamo che il sistema è conservativo e il potenziale
p i = 0 = m v + m A v A = p f da cui v A = m m A
 Esercizio 1 Un carrello di massa m A di dimensioni trascurabili è inizialmente fermo nell origine O di un sistema di coordinate cartesiane xyz disposto come in figura. Il carrello può muoversi con attrito
Esercizio 1 Un carrello di massa m A di dimensioni trascurabili è inizialmente fermo nell origine O di un sistema di coordinate cartesiane xyz disposto come in figura. Il carrello può muoversi con attrito
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 7 Luglio 8 (usare fogli diversi per esercizi diversi) Primo Esercizio Si consideri il corpo rigido piano descritto in figura, formato
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 7 Luglio 8 (usare fogli diversi per esercizi diversi) Primo Esercizio Si consideri il corpo rigido piano descritto in figura, formato
