3. Le coordinate geografiche: latitudine e longitudine
|
|
|
- Camillo Verde
- 7 anni fa
- Visualizzazioni
Transcript
1 Introduzione 3. Le coordinate geografiche: latitudine e longitudine Ogni volta che vogliamo individuare un punto sulla superficie terrestre gli associamo due numeri, le coordinate geografiche: la latitudine e la longitudine. Se assimiliamo la Terra ad un oggetto sferico, possiamo immaginare di tracciare sulla sua superficie dei cerchi, detti meridiani e paralleli. I meridiani sono cerchi tutti uguali che si intersecano ai Poli, a differenza dei paralleli che sono cerchi di lunghezza differente. Di questi, il cerchio massimo è l Equatore, gli altri cerchi hanno dimensioni sempre più piccole man mano che dall Equatore ci si sposta verso i Poli. Naturalmente si identifica un parallelo di riferimento, l Equatore, che è il cerchio massimo. La scelta di un meridiano di riferimento è invece una scelta del tutto arbitraria. Attualmente si prende il meridiano passante per l Osservatorio Astronomico di Greenwich, nei pressi di Londra, detto primo meridiano o meridiano fondamentale o meridiano di Greenwich. Tale convenzione è in atto dall ottobre del La latitudine è la distanza angolare di un punto (P) dall Equatore, misurata lungo il meridiano che passa per quel punto (Figura 2, angolo PCP ). La latitudine è misurata in gradi, il suo valore può variare da +90 (latitudine del Polo Nord) a -90 (latitudine del Polo Sud) e vale 0 per tutti i punti lungo l Equatore. La longitudine di un punto (P) è l angolo compreso tra il meridiano per quel punto e il meridiano fondamentale (di Greenwich) (Figura 2, angolo OAP). Figura 2 15
2 In conclusione possiamo considerare i paralleli come quei cerchi, sulla superficie terrestre formati da tutti e soli i punti che hanno la stessa latitudine e i meridiani come i cerchi formati dai punti che hanno la stessa longitudine e quindi la stessa ora. Nelle nostre visite scopriremo che esistono luoghi particolari a Roma in cui queste linee immaginarie sono state concretizzate e rese visibili (in particolare la linea Meridiana di Piazza San Pietro e quella di Santa Maria degli Angeli). 4. Differenze di longitudine e differenze di tempo Una rotazione completa del nostro pianeta avviene in 24h. Un meridiano ruota dunque intorno all asse terrestre di 360 in 24h. Con una proporzione otteniamo le seguenti corrispondenze: 24h 360 1h 15 4m 1 Le misure di angoli, fatte a partire dal meridiano di riferimento di Greenwich, sono misure di longitudine, quindi queste relazioni ci indicano che, se si è verificato il momento del mezzogiorno solare vero in una certa località, dopo un ora di tempo si verificherà il mezzogiorno solare vero in un altra località che dalla prima dista 15 di longitudine, dopo due ore si verificherà il mezzogiorno solare vero in un altra località ancora, che dalla prima dista 30 di longitudine e così via. Ovvero, come mostrato dalla figura successiva, se in una località definita sono le ore 12h, nello stesso istante, in una qualsiasi altra località che si trovi a 15 di longitudine più ad ovest di questa, sono ancora le ore 11h (Figura 3). Figura 3 Quindi c è una corrispondenza tra differenze di longitudine e differenze di tempo tra coppie di luoghi che si trovano su diversi meridiani. Cioè se conosciamo la longitudine di due luoghi diversi, e determiniamo l ora in uno dei due, possiamo calcolare e sapere che ore sono nell altro.. 16
3 Introduzione Quindi la differenza tra due orari solari presi simultaneamente in due diverse località, se espressa in misura angolare, corrisponde alla differenza di longitudine tra le due località. Le conversioni delle misure angolari in misure di tempo e viceversa si ottiene tenendo conto che un angolo giro (360 ) corrisponde ad un intervallo di 24 ore, da cui risulta: 5. L ora solare vera, l ora media del fuso e l Equazione del tempo Spesso sulla meridiana e sull orologio meccanico leggiamo due orari differenti. Perché accade questo? In realtà la meridiana e l orologio meccanico stanno indicando due cose diverse. L una indica l ora locale vera, l altro indica l ora media del fuso. L ora locale vera è direttamente collegata al passaggio del Sole sul meridiano locale, nel nostro caso sul meridiano di Roma. Ma abbiamo detto che è possibile costruire una ideale griglia di meridiani e paralleli, cioè che per ogni punto sulla superficie terrestre è possibile tracciare il meridiano che lo attraversa. Questo significa che, per ogni punto sulla Terra, anche se si prendono in considerazione due punti molto vicini, l ora solare vera, che è quella direttamente collegata al passaggio del Sole al meridiano, risulta diversa. Prendiamo in considerazione due città non molto distanti: Roma, con longitudine geografica Est, e Bari Est. Il Sole passerà prima sul meridiano di Bari e poi su quello di Roma. Per capire quanto tempo intercorre tra i due passaggi al meridiano, calcoliamo la distanza in longitudine tra queste due città che risulta di Con le conversioni da unità angolari ad unità di tempo si ottiene che una differenza di longitudine di 4 20 corrisponde ad una distanza in tempo di 17m 20s. Quindi il Sole passa sul meridiano di Bari ad un certo istante e solo 17 minuti e 20 secondi dopo sul meridiano di Roma. Allo stesso modo se consideriamo una città più ad ovest di Roma, per esempio Torino, longitudine geografica 7 40 Est, avremo Quindi, dal momento in cui il Sole passa sul meridiano di Roma, dovranno passare 19 minuti e 20 secondi prima del passaggio al meridiano sulla città di Torino. Scandire i ritmi della nostra vita civile sull ora solare vera sarebbe oggi impossibile, per questo l intera superficie terrestre è stata suddivisa in 24 fusi orari, cioè in 24 zone ognuna delle quali è compresa tra due meridiani che distano tra loro 15 (1h, in unità di tempo). Convenzionalmente in tutto il territorio appartenente al fuso si ha la stessa ora che è quella del Meridiano Centrale del Fuso. Il fuso orario dell Italia 17
4 è quello che fa riferimento al meridiano di longitudine 15 Est da Greenwich e che passa per l Etna. La differenza di longitudine però non è l unico elemento che determina la differenza tra l ora letta su un orologio solare e quella letta su un orologio meccanico. Esiste una complicazione ulteriore dovuta al fatto che, poiché la velocità osservata del nostro astro non è uniforme, ma varia durante l anno, l intervallo di tempo tra due successivi transiti del Sole al meridiano in un dato luogo, detto giorno solare vero, non ha sempre la stessa durata. Quindi si rende necessaria l introduzione del concetto di Sole Medio o di Sole fittizio (Figura 4). Figura 4 Il Sole Medio è quell astro fittizio che, partendo dall equinozio di primavera insieme al Sole vero, percorre l Equatore Celeste con velocità costante in modo da ritornare al successivo equinozio di primavera insieme al Sole vero, che nello stesso arco di tempo si sarà mosso sull Eclittica, ma con una velocità variabile. Si definisce quindi il tempo solare medio (ora solare media) l angolo orario del Sole Medio e di conseguenza il giorno solare medio l intervallo di tempo necessario affinché l angolo orario del Sole Medio aumenti di 24h. La differenza tra tempo solare vero e tempo solare medio è detta Equazione del Tempo. L Equazione del Tempo varia di giorno in giorno, rimanendo quasi uguale da un anno all altro e assumendo valori positivi e negativi (±16 min. circa) a seconda che il Sole vero sia rispettivamente in ritardo o in anticipo rispetto al Sole medio (Tabella 1). 18
5 Introduzione TABELLA 1 DELL EQUAZIONE DEL TEMPO Se tali valori si riportano su un grafico con i 12 mesi si disegna una sorta di sinusoide; se si riportano su un grafico con i giorni di pari declinazione del Sole si ottiene invece un 8 allungato da una parte (curva detta analemma). Come si vede nel grafico e nella tabella, l Equazione del tempo si annulla quattro volte all anno (il 15 aprile, il 15 giugno, il primo di settembre e il 25 dicembre). Assume valori assoluti massimi quattro volte l anno: - verso il 12 febbraio (-14m, 4) - verso il 15 maggio (+3m, 8) - verso il 27 luglio (-6m, 3) - verso il 3 novembre (+16m, 4) 19
6 Figura 5 La longitudine di Roma è Est e la correzione rispetto al meridiano medio del fuso, risulta 2 30 ovvero 10m 0s. Quindi, per esempio, effettuando delle osservazioni sull orologio solare il 1 gennaio a Roma, ci accorgeremo che il mezzogiorno locale vero avviene quando l orologio meccanico segna le ore: 12h + 3m 16s s = 12h 13m 16s perché alle 12 abbiamo aggiunto la correzione per l Equazione del Tempo del 1 Gennaio e la differenza per la longitudine di Roma. Tutte le volte che parleremo del mezzogiorno ci riferiremo quindi al mezzogiorno solare vero. Per questo motivo, per rendere il più efficaci possibile le visite, consigliamo di tenere conto di tutte le correzioni al mezzogiorno e di controllare l Equazione del Tempo per il giorno prescelto per la visita. 20
PREREQUISITI ASPETTI TEORICI
 .- 1 - PREREQUISITI ASPETTI TEORICI LA SFERA CELESTE ED I SUOI ELEMENTI VOLTA E SFERA CELESTE LE PRINCIPALI COORDINATE ASTRONOMICHE COORDINATE ORIZZONTALI E COORDINATE EQUATORIALI pag. 2 pag. 3 CORRISPONDENZA
.- 1 - PREREQUISITI ASPETTI TEORICI LA SFERA CELESTE ED I SUOI ELEMENTI VOLTA E SFERA CELESTE LE PRINCIPALI COORDINATE ASTRONOMICHE COORDINATE ORIZZONTALI E COORDINATE EQUATORIALI pag. 2 pag. 3 CORRISPONDENZA
Misure di longitudine con le lune di Giove di Lucia Corbo
 Misure di longitudine con le lune di Giove di Lucia Corbo Nel 1610 Galilei scoprì col suo cannocchiale che intorno al Pianeta Giove ruotavano quattro satelliti, scomparendo e ricomparendo continuamente.
Misure di longitudine con le lune di Giove di Lucia Corbo Nel 1610 Galilei scoprì col suo cannocchiale che intorno al Pianeta Giove ruotavano quattro satelliti, scomparendo e ricomparendo continuamente.
Il tempo. Appunti di Geografia a cura di A. Pulvirenti
 Il tempo Appunti di Geografia a cura di A. Pulvirenti Le immagini presenti in questo file sono state reperite in rete o modificate da testi cartacei e vengono utilizzate solo per l elevato contenuto didattico.
Il tempo Appunti di Geografia a cura di A. Pulvirenti Le immagini presenti in questo file sono state reperite in rete o modificate da testi cartacei e vengono utilizzate solo per l elevato contenuto didattico.
La sfera celeste. Coordinate locali altazimutali Coordinate universali equatoriali
 La sfera celeste Coordinate locali altazimutali Coordinate universali equatoriali Volta celeste Volta parte della sfera visibile al di sopra dell orizzonte celeste (intersezione del piano tangente all
La sfera celeste Coordinate locali altazimutali Coordinate universali equatoriali Volta celeste Volta parte della sfera visibile al di sopra dell orizzonte celeste (intersezione del piano tangente all
Le Coordinate Astronomiche
 Le Stelle vanno a scuola Le Coordinate Astronomiche Valentina Alberti Novembre 2003 1 2 INDICE Indice 1 Coordinate astronomiche 3 1.1 Sistema dell orizzonte o sistema altazimutale.......... 3 1.2 Sistema
Le Stelle vanno a scuola Le Coordinate Astronomiche Valentina Alberti Novembre 2003 1 2 INDICE Indice 1 Coordinate astronomiche 3 1.1 Sistema dell orizzonte o sistema altazimutale.......... 3 1.2 Sistema
Il giorno. stella fissa. stella fissa. Meridiano del luogo. Meridiano del luogo
 Il giorno Intervallo di tempo necessario per una rotazione completa della Terra intorno al suo asse. 1) Giorno siderale (o sidereo) 23 h 56 m 2) Giorno solare vero (o apparente) ~24 h 3) Giorno solare
Il giorno Intervallo di tempo necessario per una rotazione completa della Terra intorno al suo asse. 1) Giorno siderale (o sidereo) 23 h 56 m 2) Giorno solare vero (o apparente) ~24 h 3) Giorno solare
Le coordinate geografiche
 Le coordinate geografiche La Terra non ha la forma di una sfera perfetta: per descriverla e rappresentarla la si approssima a una forma ellissoidale leggermente schiacciata ai poli, detta geoide. Per identificare
Le coordinate geografiche La Terra non ha la forma di una sfera perfetta: per descriverla e rappresentarla la si approssima a una forma ellissoidale leggermente schiacciata ai poli, detta geoide. Per identificare
SISTEMI DI COORDINATE SULLA SUPERFICIE SFERICA (di mortola carlo)
 SISTEMI DI COORDINATE SULLA SUPERFICIE SFERICA (di mortola carlo) Per individuare univocamente un punto di una superficie sferica si possono utilizzare due sistemi di coordinate sferiche, e precisamente:
SISTEMI DI COORDINATE SULLA SUPERFICIE SFERICA (di mortola carlo) Per individuare univocamente un punto di una superficie sferica si possono utilizzare due sistemi di coordinate sferiche, e precisamente:
LA TERRA. La Terra studiata come copro celeste, risulta essere un PIANETA un copro celeste di forma sferica che ruota attorno ad una stella il SOLE
 IL PIANETA TERRA LA TERRA La Terra studiata come copro celeste, risulta essere un PIANETA un copro celeste di forma sferica che ruota attorno ad una stella il SOLE FORMA E DIMENSIONI DELLA TERRA Agli
IL PIANETA TERRA LA TERRA La Terra studiata come copro celeste, risulta essere un PIANETA un copro celeste di forma sferica che ruota attorno ad una stella il SOLE FORMA E DIMENSIONI DELLA TERRA Agli
UNITÀ DIDATTICA 11 LE COORDINATE GEOGRAFICHE
 UNITÀ DIDATTICA 11 LE COORDINATE GEOGRAFICHE 11.1 Il reticolato geografico La forma della Terra si discosta poco da quella di una sfera. Sulla superficie terrestre, considerata come sferica, è possibile
UNITÀ DIDATTICA 11 LE COORDINATE GEOGRAFICHE 11.1 Il reticolato geografico La forma della Terra si discosta poco da quella di una sfera. Sulla superficie terrestre, considerata come sferica, è possibile
IL MOTO di ROTAZIONE. CONSEGUENZE del MOTO di ROTAZIONE
 IL MOTO di ROTAZIONE moto di rotazione: il moto di rotazione è il movimento che la Terra compie attorno al proprio asse, da ovest verso est, in senso antiorario per un osservatore posto al polo nord celeste;
IL MOTO di ROTAZIONE moto di rotazione: il moto di rotazione è il movimento che la Terra compie attorno al proprio asse, da ovest verso est, in senso antiorario per un osservatore posto al polo nord celeste;
SHUO DQQR $QQR,QWHUQD]LRQDOH GHOO $VWURQRPLD,<$
![SHUO DQQR $QQR,QWHUQD]LRQDOH GHOO $VWURQRPLD,<$ SHUO DQQR $QQR,QWHUQD]LRQDOH GHOO $VWURQRPLD,<$](/thumbs/54/35044472.jpg) &$/(1'$5,2 $6752120,&2 SHUO DQQR $QQR,QWHUQD]LRQDOH GHOO $VWURQRPLD,
&$/(1'$5,2 $6752120,&2 SHUO DQQR $QQR,QWHUQD]LRQDOH GHOO $VWURQRPLD,
TOPOGRAFIA e CARTOGRAFIA
 1. Un ettometro corrisponde a : a. 100 m ; b. 1.000 m ; c. 10.000 m ; 2. Un chilometro corrisponde a : a. 100 m ; b. 1.000 m ; c. 10.000 m ; 3. Un decametro corrisponde a : a. 0,1 m ; b. 0,01 m ; c. 10
1. Un ettometro corrisponde a : a. 100 m ; b. 1.000 m ; c. 10.000 m ; 2. Un chilometro corrisponde a : a. 100 m ; b. 1.000 m ; c. 10.000 m ; 3. Un decametro corrisponde a : a. 0,1 m ; b. 0,01 m ; c. 10
Società alpina delle Giulie Sezione di Trieste del Club Alpino Italiano. Topografia e orientamento
 Società alpina delle Giulie Sezione di Trieste del Club Alpino Italiano Topografia e orientamento Introduzione Per un alpinista sapersi orientare in montagna è altrettanto importante che saper arrampicare
Società alpina delle Giulie Sezione di Trieste del Club Alpino Italiano Topografia e orientamento Introduzione Per un alpinista sapersi orientare in montagna è altrettanto importante che saper arrampicare
LA LATITUDINE E LA LONGITUDINE
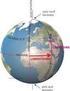 LC.06.02.06 LA LATITUDINE E LA LONGITUDINE Prerequisiti: nozioni scientifiche e matematiche acquisite durante la scuola secondaria di primo grado Obiettivi: studio della latitudine e della longitudine
LC.06.02.06 LA LATITUDINE E LA LONGITUDINE Prerequisiti: nozioni scientifiche e matematiche acquisite durante la scuola secondaria di primo grado Obiettivi: studio della latitudine e della longitudine
Topografia e orientamento
 CAI - ALPINISMO GIOVANILE Secondo Corso Di Avvicinamento Alla Montagna 2012 Topografia e orientamento C A I B o r g o m a n e r o A l p i n i s m o G i o v a n i l e 2 0 1 2 Pagina 1 Introduzione Per un
CAI - ALPINISMO GIOVANILE Secondo Corso Di Avvicinamento Alla Montagna 2012 Topografia e orientamento C A I B o r g o m a n e r o A l p i n i s m o G i o v a n i l e 2 0 1 2 Pagina 1 Introduzione Per un
NAVIGAZIONE ASTRONOMICA. Circolo Astrofili di Mestre Guido Ruggieri
 3 Novembre 2008, ore 21:00 Introduzione. Orientamento sulla Terra. Coordinate orizzontali degli astri, azimuth e altezza. Coordinate equatoriali degli astri, Ascensione Retta e Declinazione. 17 Novembre
3 Novembre 2008, ore 21:00 Introduzione. Orientamento sulla Terra. Coordinate orizzontali degli astri, azimuth e altezza. Coordinate equatoriali degli astri, Ascensione Retta e Declinazione. 17 Novembre
GLI STRUMENTI DELLA GEOGRAFIA
 GLI STRUMENTI DELLA GEOGRAFIA Che cos è la geografia La geografia (dal greco géo, Terra, e graphìa, scrittura, disegno) è la disciplina che studia e descrive la Terra e il rapporto che esiste fra l uomo
GLI STRUMENTI DELLA GEOGRAFIA Che cos è la geografia La geografia (dal greco géo, Terra, e graphìa, scrittura, disegno) è la disciplina che studia e descrive la Terra e il rapporto che esiste fra l uomo
pianeta Terra caratteristiche generali
 pianeta Terra caratteristiche generali Eratostene 275 195 ac http://www.youtube.com/watch?v=-o99ih9kbpw pianeta Terra alcune delle caratteristiche principali Massa: 5,9 x 10 24 kg Raggio medio: 6.371
pianeta Terra caratteristiche generali Eratostene 275 195 ac http://www.youtube.com/watch?v=-o99ih9kbpw pianeta Terra alcune delle caratteristiche principali Massa: 5,9 x 10 24 kg Raggio medio: 6.371
Come costruire una meridiana equatoriale
 Pagina 1 di 5 Come costruire una meridiana equatoriale La meridiana equatoriale è l'orologio solare più semplice da costruire. Per capire come funziona, supponiamo che la Terra sia disposta in modo che
Pagina 1 di 5 Come costruire una meridiana equatoriale La meridiana equatoriale è l'orologio solare più semplice da costruire. Per capire come funziona, supponiamo che la Terra sia disposta in modo che
Il reticolato geografico. Meridiani e paralleli.
 Il reticolato geografico. Meridiani e paralleli. Per localizzare un punto qualsiasi sulla superficie terrestre, cioè per individuarne la posizione esatta, i geografi hanno tracciato sul globo terrestre
Il reticolato geografico. Meridiani e paralleli. Per localizzare un punto qualsiasi sulla superficie terrestre, cioè per individuarne la posizione esatta, i geografi hanno tracciato sul globo terrestre
sfera celeste e coordinate astronomiche
 sfera celeste e coordinate astronomiche sfera celeste La sfera celeste appare come una grande sfera che ruota su se stessa, al cui centro sta la Terra immobile, e sulla cui superficie stanno le stelle
sfera celeste e coordinate astronomiche sfera celeste La sfera celeste appare come una grande sfera che ruota su se stessa, al cui centro sta la Terra immobile, e sulla cui superficie stanno le stelle
Moti della Terra: Rotazione, Rivoluzione, Moti millenari
 Moti della Terra: Rotazione, Rivoluzione, Moti millenari moto di rotazione giorno sidereo: 23h 56m 4s velocità di rotazione moto di rotazione: conseguenze Alternarsi del dì e della notte Moto apparente
Moti della Terra: Rotazione, Rivoluzione, Moti millenari moto di rotazione giorno sidereo: 23h 56m 4s velocità di rotazione moto di rotazione: conseguenze Alternarsi del dì e della notte Moto apparente
STRUMENTI DI CONTROLLO. Lucia Ceccherini Nelli
 STRUMENTI DI CONTROLLO Lucia Ceccherini Nelli 2 6.1 Alcune nozioni fondamentali di geografia astronomica 6.1 Inclinazione dell asse terrestre 6.1.1. Equinozi e Solstizi Durante il movimento di rivoluzione,
STRUMENTI DI CONTROLLO Lucia Ceccherini Nelli 2 6.1 Alcune nozioni fondamentali di geografia astronomica 6.1 Inclinazione dell asse terrestre 6.1.1. Equinozi e Solstizi Durante il movimento di rivoluzione,
1. Sistemi di coordinate nello spazio
 1. Sistemi di coordinate nello spazio La longitudine e la latitudine vengono comunemente impiegate per la localizzazione dei punti sulla superficie terrestre, l ascensione retta e la declinazione per la
1. Sistemi di coordinate nello spazio La longitudine e la latitudine vengono comunemente impiegate per la localizzazione dei punti sulla superficie terrestre, l ascensione retta e la declinazione per la
Progetto Laboratori Lauree Scientifiche
 Progetto Laboratori Lauree Scientifiche Laboratorio sulle funzioni trigonometriche Le ore di insolazione giornaliera in funzione della latitudine Bozza di progetto Nel seguito verrà presentata la descrizione
Progetto Laboratori Lauree Scientifiche Laboratorio sulle funzioni trigonometriche Le ore di insolazione giornaliera in funzione della latitudine Bozza di progetto Nel seguito verrà presentata la descrizione
How to compute the sun vector for path planning
 How to compute the sun vector for path planning 1 Calcolo dell illuminazione delle celle solari Si consideri la Fig. 1. Il rover si sposta sulla mappa, variando nel tempo la sua posizione p = ( x y z )
How to compute the sun vector for path planning 1 Calcolo dell illuminazione delle celle solari Si consideri la Fig. 1. Il rover si sposta sulla mappa, variando nel tempo la sua posizione p = ( x y z )
Scuola Primaria Classi 4 A e 4 B Is5tuto Comprensivo Castelverde Roma
 Scuola Primaria Classi 4 A e 4 B Is5tuto Comprensivo Castelverde Roma Orientamento topologico Ø cerchiamo punti di riferimento Ø chiediamo indicazioni Ø consultiamo la cartina Cerchiamo dei pun5 di riferimento.
Scuola Primaria Classi 4 A e 4 B Is5tuto Comprensivo Castelverde Roma Orientamento topologico Ø cerchiamo punti di riferimento Ø chiediamo indicazioni Ø consultiamo la cartina Cerchiamo dei pun5 di riferimento.
Moti della Terra: Rotazione, Rivoluzione, Moti millenari
 Moti della Terra: Rotazione, Rivoluzione, Moti millenari moto di rotazione giorno sidereo: 23h 56m 4s velocità di rotazione moto di rotazione: conseguenze Alternarsi del dì e della notte Moto apparente
Moti della Terra: Rotazione, Rivoluzione, Moti millenari moto di rotazione giorno sidereo: 23h 56m 4s velocità di rotazione moto di rotazione: conseguenze Alternarsi del dì e della notte Moto apparente
LEZIONI DI CARTOGRAFIA
 LEZIONI DI CARTOGRAFIA by Andrea ErDuca Palladino PART. 2 LA CARTA TOPOGRAFICA IMPORTANTE: QUESTA GUIDA E STATA REDATTA ESCLUSIVAMENTE PER UN USO INTERNO DELL ASSOCIAZIONE E PERTANTO VIETATA LA DIVULGAZIONE
LEZIONI DI CARTOGRAFIA by Andrea ErDuca Palladino PART. 2 LA CARTA TOPOGRAFICA IMPORTANTE: QUESTA GUIDA E STATA REDATTA ESCLUSIVAMENTE PER UN USO INTERNO DELL ASSOCIAZIONE E PERTANTO VIETATA LA DIVULGAZIONE
OLIMPIADI ITALIANE DI ASTRONOMIA 2014 FINALE NAZIONALE Prova Teorica - Categoria Junior
 OLIMPIADI ITALIANE DI ASTRONOMIA 2014 FINALE NAZIONALE Prova Teorica - Categoria Junior 1. Le quattro stagioni Si scrivano gli intervalli entro cui variano l ascensione retta ( ) e la declinazione ( )
OLIMPIADI ITALIANE DI ASTRONOMIA 2014 FINALE NAZIONALE Prova Teorica - Categoria Junior 1. Le quattro stagioni Si scrivano gli intervalli entro cui variano l ascensione retta ( ) e la declinazione ( )
Elementi di Astronomia di posizione. Sabina Sabatini INAF Istituto di Astrofisica e Planetologia Spaziale
 Elementi di Astronomia di posizione Sabina Sabatini INAF Istituto di Astrofisica e Planetologia Spaziale sabina.sabatini@iaps.inaf.it 5 Febbraio 2016 Le coordinate astronomiche Definiscono le posizioni
Elementi di Astronomia di posizione Sabina Sabatini INAF Istituto di Astrofisica e Planetologia Spaziale sabina.sabatini@iaps.inaf.it 5 Febbraio 2016 Le coordinate astronomiche Definiscono le posizioni
Ma cosa si pensava della forma della terra prima delle fotografie?
 Ma cosa si pensava della forma della terra prima delle fotografie? Anassimandro (IV sec. a.c.) Omero (VIII sec. a.c.?) Aristotele (384-322 a.c.) riportava due osservazioni a riprova della sfericità della
Ma cosa si pensava della forma della terra prima delle fotografie? Anassimandro (IV sec. a.c.) Omero (VIII sec. a.c.?) Aristotele (384-322 a.c.) riportava due osservazioni a riprova della sfericità della
unità 5. L orientamento e la misura del tempo
 giorno Sole osservazione del cielo notte Stella Polare/Croce del sud longitudine in base all ora locale Orientamento coordinate geografiche latitudine altezza della stella Polare altezza del Sole bussola
giorno Sole osservazione del cielo notte Stella Polare/Croce del sud longitudine in base all ora locale Orientamento coordinate geografiche latitudine altezza della stella Polare altezza del Sole bussola
L Astrolabio. di Alberto Nicelli. GAE Gruppo Astrofili Eporediesi
 L Astrolabio di Alberto Nicelli GAE Gruppo Astrofili Eporediesi L Astrolabio (vedi kit allegato) è così costituito: Il Piatto, che riproduce in proiezione stereografica: o l Orizzonte Locale, relativo
L Astrolabio di Alberto Nicelli GAE Gruppo Astrofili Eporediesi L Astrolabio (vedi kit allegato) è così costituito: Il Piatto, che riproduce in proiezione stereografica: o l Orizzonte Locale, relativo
OLIMPIADI ITALIANE DI ASTRONOMIA. Angoli e Coordinate
 Corso di preparazione alle Olimpiadi INAF Osservatorio Astronomico di Teramo Scuola Secondaria di I Grado «F. Savini» Teramo OLIMPIADI ITALIANE DI ASTRONOMIA Angoli e Coordinate Mauro Dolci INAF - Osservatorio
Corso di preparazione alle Olimpiadi INAF Osservatorio Astronomico di Teramo Scuola Secondaria di I Grado «F. Savini» Teramo OLIMPIADI ITALIANE DI ASTRONOMIA Angoli e Coordinate Mauro Dolci INAF - Osservatorio
Moti della Terra. Rotazione Rivoluzione Precessione e nutazioni Moti millenari
 Moti della Terra Rotazione Rivoluzione Precessione e nutazioni Moti millenari Asse terrestre 23 27 asse equatore Piano eclittica L asse terrestre -passante per il centro, emergente ai Poli, punti della
Moti della Terra Rotazione Rivoluzione Precessione e nutazioni Moti millenari Asse terrestre 23 27 asse equatore Piano eclittica L asse terrestre -passante per il centro, emergente ai Poli, punti della
1. Il pianeta blu 2. La longitudine e la latitudine 3. I moti della Terra nello spazio 4. Luce e buio sulla Terra 5. La Luna, il nostro satellite 6.
 1. Il pianeta blu 2. La longitudine e la latitudine 3. I moti della Terra nello spazio 4. Luce e buio sulla Terra 5. La Luna, il nostro satellite 6. Le eclissi 7. Le maree Il pianeta blu Ecco come appare
1. Il pianeta blu 2. La longitudine e la latitudine 3. I moti della Terra nello spazio 4. Luce e buio sulla Terra 5. La Luna, il nostro satellite 6. Le eclissi 7. Le maree Il pianeta blu Ecco come appare
In prima approssimazione, guardandoci intorno. Note su Nord-Sud-Est-Ovest Enrica Giordano e Nicoletta Lanciano febbraio 2008
 Note su Nord-Sud-Est-Ovest Enrica Giordano e Nicoletta Lanciano febbraio 2008 Le cose devono essere apprese solo per essere nuovamente disimparate, oppure, cosa più probabile, per essere corrette R. Feynman
Note su Nord-Sud-Est-Ovest Enrica Giordano e Nicoletta Lanciano febbraio 2008 Le cose devono essere apprese solo per essere nuovamente disimparate, oppure, cosa più probabile, per essere corrette R. Feynman
L illuminazione della Terra
 L illuminazione della Terra I moti della Terra nello spazio Sole Mercurio Venere Terra La Terra e gli altri pianeti orbitano intorno al Sole, che è una stella con un raggio di circa 700 000 km e dista
L illuminazione della Terra I moti della Terra nello spazio Sole Mercurio Venere Terra La Terra e gli altri pianeti orbitano intorno al Sole, che è una stella con un raggio di circa 700 000 km e dista
Scientifico Tecnologico
 Scientifico Tecnologico Compiti vacanze estive giugno 2016 La Terra nel sistema solare S.L.Murialdo Pinerolo Materiale didattico co-finanziato dal POR FSE 2014-2020 PERIODO DI RIFERIMENTO OBIETTIVO VALUTATO
Scientifico Tecnologico Compiti vacanze estive giugno 2016 La Terra nel sistema solare S.L.Murialdo Pinerolo Materiale didattico co-finanziato dal POR FSE 2014-2020 PERIODO DI RIFERIMENTO OBIETTIVO VALUTATO
Latitudine e longitudine: come misurarle nel cortile di casa di Diego Alberto
 Latitudine e longitudine: come misurarle nel cortile di casa di Diego Alberto Questo articolo illustra come misurare la latitudine e la longitudine di un luogo: nel caso specifico, il Comune di Foglizzo,
Latitudine e longitudine: come misurarle nel cortile di casa di Diego Alberto Questo articolo illustra come misurare la latitudine e la longitudine di un luogo: nel caso specifico, il Comune di Foglizzo,
Sfera Celeste e Coordinate Astronomiche. A. Stabile Dipartimento di Ingegneria Università degli Studi del Sannio Benevento Atripalda, 9 Maggio 2011
 Astronomiche A. Stabile Dipartimento di Ingegneria Università degli Studi del Sannio Benevento Atripalda, 9 Maggio 2011 Unità di lunghezza e distanze tipiche 1. Sistema Solare: 1 UA = 149,5 milioni di
Astronomiche A. Stabile Dipartimento di Ingegneria Università degli Studi del Sannio Benevento Atripalda, 9 Maggio 2011 Unità di lunghezza e distanze tipiche 1. Sistema Solare: 1 UA = 149,5 milioni di
Piano cartesiano e retta
 Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
208. Declinazione e inclinazione gnomonica di un piano verticale di Michele T. Mazzucato
 Numero Maggio 014 08. Declinazione e inclinazione gnomonica di un piano verticale di Michele T. Mazzucato Siccome il ferro s arrugginisce sanza l esercizio e l acqua si putrefa o nel freddo s addiaccia,
Numero Maggio 014 08. Declinazione e inclinazione gnomonica di un piano verticale di Michele T. Mazzucato Siccome il ferro s arrugginisce sanza l esercizio e l acqua si putrefa o nel freddo s addiaccia,
LABORATORIO DI MATEMATICA: COORDINATE POLARI ESTENSIONE DELLE FUNZIONI TRIGONOMETRICHE
 LABORATORIO DI MATEMATICA: COORDINATE POLARI ESTENSIONE DELLE FUNZIONI TRIGONOMETRICHE Uno strumento, che ci suggerisce come ampliare le nostre conoscenze, è il radar, strumento fondamentale nella navigazione
LABORATORIO DI MATEMATICA: COORDINATE POLARI ESTENSIONE DELLE FUNZIONI TRIGONOMETRICHE Uno strumento, che ci suggerisce come ampliare le nostre conoscenze, è il radar, strumento fondamentale nella navigazione
LA STELLA DELLA NOSTRA VITA
 LA STELLA DELLA NOSTRA VITA (di mortola carlo) Il Sole (vero) non è affidabile per la misurazione del tempo perché non percorre, apparentemente, l'equatore celeste, dove si misurano i tempi degli astri,
LA STELLA DELLA NOSTRA VITA (di mortola carlo) Il Sole (vero) non è affidabile per la misurazione del tempo perché non percorre, apparentemente, l'equatore celeste, dove si misurano i tempi degli astri,
MATEMATICA E MISURA DEL TEMPO
 MATEMATICA E MISURA DEL TEMPO La percezione del tempo è diversa rispetto alla percezione dello spazio fisico La natura del tempo e l importanza del tempo nelle più varie attività umane (società, economia,
MATEMATICA E MISURA DEL TEMPO La percezione del tempo è diversa rispetto alla percezione dello spazio fisico La natura del tempo e l importanza del tempo nelle più varie attività umane (società, economia,
Problema 1. Sirio ( 2000 = 6h 45m;
 Problema 1. Sirio ( 2000 = 6 h 45 m ; 2000 = -16 43', m = -1,46) è la stella più luminosa visibile nel cielo è un affermazione sicuramente vera per un osservatore posto a Stilo. Sapreste dire in quali
Problema 1. Sirio ( 2000 = 6 h 45 m ; 2000 = -16 43', m = -1,46) è la stella più luminosa visibile nel cielo è un affermazione sicuramente vera per un osservatore posto a Stilo. Sapreste dire in quali
Stefania Ferrari a.s. 2003/2004. Stefania Ferrari, Scuola Media di Bomporto,
 Stefania Ferrari a.s. 2003/2004 1 1 - GLI ELEMENTI NATURALI La geografia studia gli elementi naturali, cioè le cose della natura. I fiumi, i mari, le montagne e le pianure sono elementi naturali. Anche
Stefania Ferrari a.s. 2003/2004 1 1 - GLI ELEMENTI NATURALI La geografia studia gli elementi naturali, cioè le cose della natura. I fiumi, i mari, le montagne e le pianure sono elementi naturali. Anche
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Unità 4 Paragrafo 1 La forma e le dimensioni della Terra
 Unità 4 Paragrafo 1 La forma e le dimensioni della Terra forma ellissoide di rotazione più precisamente geoide sfera schiacciata ai poli solido più gonio dove ci sono i continenti e un po depresso nelle
Unità 4 Paragrafo 1 La forma e le dimensioni della Terra forma ellissoide di rotazione più precisamente geoide sfera schiacciata ai poli solido più gonio dove ci sono i continenti e un po depresso nelle
AERONAUTICA MILITARE CENTRO OPERATIVO PER LA METEOROLOGIA EFFEMERIDI AERONAUTICHE
 AERONAUTICA MILITARE CENTRO OPERATIVO PER LA METEOROLOGIA EFFEMERIDI AERONAUTICHE 2 0 1 6 AERONAUTICA MILITARE CENTRO OPERATIVO PER LA METEOROLOGIA EFFEMERIDI AERONAUTICHE 2 0 1 6 INDICE Pag. Descrizione
AERONAUTICA MILITARE CENTRO OPERATIVO PER LA METEOROLOGIA EFFEMERIDI AERONAUTICHE 2 0 1 6 AERONAUTICA MILITARE CENTRO OPERATIVO PER LA METEOROLOGIA EFFEMERIDI AERONAUTICHE 2 0 1 6 INDICE Pag. Descrizione
Riferire una posizione sulla superficie terrestre
 Geodesia Riferire una posizione sulla superficie terrestre Coordinate geografiche Sistema di riferimento latitudine e longitudine Equatore Primo Meridiano Paralleli di latitudine Meridiani di longitudine
Geodesia Riferire una posizione sulla superficie terrestre Coordinate geografiche Sistema di riferimento latitudine e longitudine Equatore Primo Meridiano Paralleli di latitudine Meridiani di longitudine
LA TERRA. La TERRA ha la forma di una grande sfera un po schiacciata alle estremità, chiamate POLI.
 LA TERRA La TERRA ha la forma di una grande sfera un po schiacciata alle estremità, chiamate POLI. Per poterla studiare possiamo rappresentare la TERRA per mezzo di un mappamondo (globo). Su di esso possiamo
LA TERRA La TERRA ha la forma di una grande sfera un po schiacciata alle estremità, chiamate POLI. Per poterla studiare possiamo rappresentare la TERRA per mezzo di un mappamondo (globo). Su di esso possiamo
La corrente alternata
 La corrente alternata Corrente continua e corrente alternata Le correnti continue sono dovute ad un generatore i cui poli hanno sempre lo stesso segno e pertanto esse percorrono un circuito sempre nello
La corrente alternata Corrente continua e corrente alternata Le correnti continue sono dovute ad un generatore i cui poli hanno sempre lo stesso segno e pertanto esse percorrono un circuito sempre nello
162. Determinazione approssimata delle coordinate geografiche terrestri Michele T. Mazzucato
 162. Determinazione approssimata delle coordinate geografiche terrestri Michele T. Mazzucato cercherò stanotte di precisare la nostra latitudine e domani a mezzogiorno la nostra longitudine. Cyrus Smith
162. Determinazione approssimata delle coordinate geografiche terrestri Michele T. Mazzucato cercherò stanotte di precisare la nostra latitudine e domani a mezzogiorno la nostra longitudine. Cyrus Smith
Cenni di geografia astronomica. Giorno solare e giorno siderale.
 Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
1 Nozioni utili sul piano cartesiano
 Nozioni utili sul piano cartesiano Nozioni utili sul piano cartesiano Il piano cartesiano è un sistema di riferimento costituito da due rette perpendicolari (una orizzontale detta asse delle ascisse x
Nozioni utili sul piano cartesiano Nozioni utili sul piano cartesiano Il piano cartesiano è un sistema di riferimento costituito da due rette perpendicolari (una orizzontale detta asse delle ascisse x
Anno 4 Archi e angoli
 Anno 4 Archi e angoli 1 Introduzione In questa lezione illustreremo gli angoli e gli archi. In particolare, parleremo di: angoli e archi orientati metodi di misurazione degli angoli in funzione dell unità
Anno 4 Archi e angoli 1 Introduzione In questa lezione illustreremo gli angoli e gli archi. In particolare, parleremo di: angoli e archi orientati metodi di misurazione degli angoli in funzione dell unità
Esercizio 6. Calcolo di Δh (h c h s ) Calcolo trigonometrico del punto determinativo
 Esercizio 6 Ripetere l esercizio 4 (dalla formula di Eulero in poi) considerando un punto stimato di 24 00,0 N 115 00,0 W e verificare graficamente che le rette di altezza coincidono, anche se i punti
Esercizio 6 Ripetere l esercizio 4 (dalla formula di Eulero in poi) considerando un punto stimato di 24 00,0 N 115 00,0 W e verificare graficamente che le rette di altezza coincidono, anche se i punti
LATITUDINE E LONGITUDINE
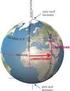 LATITUDINE E LONGITUDINE La posizione di un punto sul globo terrestre si misura per mezzo dei meridiani e dei paralleli. I meridiani, linee idealmente tracciate intorno alla Terra passando per i poli,
LATITUDINE E LONGITUDINE La posizione di un punto sul globo terrestre si misura per mezzo dei meridiani e dei paralleli. I meridiani, linee idealmente tracciate intorno alla Terra passando per i poli,
pianeta Terra caratteristiche generali
 pianeta Terra caratteristiche generali Eratostene 275 195 ac http://www.youtube.com/watch?v=-o99ih9kbpw pianeta Terra, alcune delle caratteristiche principali Massa: 5,9 x 10 24 kg Raggio medio: 6.371
pianeta Terra caratteristiche generali Eratostene 275 195 ac http://www.youtube.com/watch?v=-o99ih9kbpw pianeta Terra, alcune delle caratteristiche principali Massa: 5,9 x 10 24 kg Raggio medio: 6.371
Lezione 5 MOTO CIRCOLARE UNIFORME
 Corsi di Laurea in Scienze motorie - Classe L-22 (D.M. 270/04) Dr. Andrea Malizia 1 MOTO CIRCOLARE UNIFORME 2 Per descrivere un moto curvilineo occorrono due assi cartesiani ortogonali ed un orologio.
Corsi di Laurea in Scienze motorie - Classe L-22 (D.M. 270/04) Dr. Andrea Malizia 1 MOTO CIRCOLARE UNIFORME 2 Per descrivere un moto curvilineo occorrono due assi cartesiani ortogonali ed un orologio.
Est Greenwich 5
 La terra La Terra, per gli scopi pratici della navigazione, può essere considerata, senza apprezzabili errori, come perfettamente sferica, costituita da una superficie liscia ed omogenea. La terra ruota
La terra La Terra, per gli scopi pratici della navigazione, può essere considerata, senza apprezzabili errori, come perfettamente sferica, costituita da una superficie liscia ed omogenea. La terra ruota
LA SPIEGAZIONE DI QUESTI FENOMENI SEMBRA ESSEREE CHE IL SOLE E LE STELLE GIRINO INTORNO A NOI E COSI SI E PENSATO MILLENNI.
 I MOTI DELLA TERRA POLARE. OGNI GIORNO VEDIAMO IL SOLE SORGERE AD EST, DESCRIVERE UN ARCO NEL CIELO E TRAMONTARE A OVEST. INOLTRE SE OSSERVIAMO IL CIELO STELLATO IN UNA NOTTE SERENA, DOPO QUALCHE ORA CI
I MOTI DELLA TERRA POLARE. OGNI GIORNO VEDIAMO IL SOLE SORGERE AD EST, DESCRIVERE UN ARCO NEL CIELO E TRAMONTARE A OVEST. INOLTRE SE OSSERVIAMO IL CIELO STELLATO IN UNA NOTTE SERENA, DOPO QUALCHE ORA CI
I moti della terra 1
 I moti della terra 1 La Terra ruota su se stessa 2 2. Il moto di rotazione della Terra La rotazione terrestre si compie da Ovest verso Est in verso antiorario. A causa della forma della Terra, la velocità
I moti della terra 1 La Terra ruota su se stessa 2 2. Il moto di rotazione della Terra La rotazione terrestre si compie da Ovest verso Est in verso antiorario. A causa della forma della Terra, la velocità
( ρ, θ + π ) sono le coordinate dello stesso punto. Pertanto un punto P può essere descritto come
 Coordinate polari Il sistema delle coordinate cartesiane è uno dei possibili sistemi per individuare la posizione di un punto del piano, relativamente ad un punto fisso O, mediante una coppia ordinata
Coordinate polari Il sistema delle coordinate cartesiane è uno dei possibili sistemi per individuare la posizione di un punto del piano, relativamente ad un punto fisso O, mediante una coppia ordinata
MOTO DI ROTAZIONE da ovest verso est asse terrestre
 I moti della Terra La Terra compie numerosi movimenti poiché gira: intorno a se stessa a 0,4 Km/s; attorno al Sole a 30 Km/s; insieme a tutto il sistema solare a 220 Km/s quindi è come se si muovesse
I moti della Terra La Terra compie numerosi movimenti poiché gira: intorno a se stessa a 0,4 Km/s; attorno al Sole a 30 Km/s; insieme a tutto il sistema solare a 220 Km/s quindi è come se si muovesse
Piano cartesiano e Retta
 Piano cartesiano e Retta 1 Piano cartesiano e Retta 1. Richiami sul piano cartesiano 2. Richiami sulla distanza tra due punti 3. Richiami punto medio di un segmento 4. La Retta (funzione lineare) 5. L
Piano cartesiano e Retta 1 Piano cartesiano e Retta 1. Richiami sul piano cartesiano 2. Richiami sulla distanza tra due punti 3. Richiami punto medio di un segmento 4. La Retta (funzione lineare) 5. L
Un punto del piano può essere individuato dalle sue coordinate cartesiane o anche dalle sue coordinate polari:
 Un punto del piano può essere individuato dalle sue coordinate cartesiane o anche dalle sue coordinate polari: Figura 1 Per passare da coordinate polari a quelle cartesiane usiamo { x = r cos θ y = r sin
Un punto del piano può essere individuato dalle sue coordinate cartesiane o anche dalle sue coordinate polari: Figura 1 Per passare da coordinate polari a quelle cartesiane usiamo { x = r cos θ y = r sin
22 gennaio 2014 TOPOGRAFIA e ORIENTAMENTO
 22 gennaio 2014 TOPOGRAFIA e ORIENTAMENTO Per chi non sa dove andare qualunque strada é quella giusta! Topografia: Scienza della rappresentazione del territorio al fine di consentire l esatta individuazione
22 gennaio 2014 TOPOGRAFIA e ORIENTAMENTO Per chi non sa dove andare qualunque strada é quella giusta! Topografia: Scienza della rappresentazione del territorio al fine di consentire l esatta individuazione
Cartografia, topografia e orientamento
 Cartografia, topografia e orientamento Soluzioni delle esercitazioni Mi sono portato la carta UTM, il goniometro, la bussola, l altimetro, lo scalimetro, il righello, il coordinatometro, la matita, ed
Cartografia, topografia e orientamento Soluzioni delle esercitazioni Mi sono portato la carta UTM, il goniometro, la bussola, l altimetro, lo scalimetro, il righello, il coordinatometro, la matita, ed
Cartografia, topografia e orientamento
 Cartografia, topografia e orientamento Esercitazioni Mi sono portato la carta UTM, il goniometro, la bussola, l altimetro, lo scalimetro, il righello, il coordinatometro, la matita, ed ho pure l alpestoc,
Cartografia, topografia e orientamento Esercitazioni Mi sono portato la carta UTM, il goniometro, la bussola, l altimetro, lo scalimetro, il righello, il coordinatometro, la matita, ed ho pure l alpestoc,
ALCUNE CONSIDERAZIONI SULLA DIFFERENZA TRA CAMMINO LOSSODROMICO ED ORTODROMICOINVIATE AD UN COLLEGA DI NAVIGAZIONE
 ALCUNE CONSIDERAZIONI SULLA DIFFERENZA TRA CAMMINO LOSSODROMICO ED ORTODROMICOINVIATE AD UN COLLEGA DI NAVIGAZIONE(di mortolacarlo) La riduzione di un dato angolo al primo quadrante, significa trovare
ALCUNE CONSIDERAZIONI SULLA DIFFERENZA TRA CAMMINO LOSSODROMICO ED ORTODROMICOINVIATE AD UN COLLEGA DI NAVIGAZIONE(di mortolacarlo) La riduzione di un dato angolo al primo quadrante, significa trovare
Risolviamo un esercizio per illustrare il fenomeno in modo dettagliato anche se,in alcuni punti, semplificato.
 PARADOSSO DEI GEMELLI Il cosiddetto paradosso dei gemelli è forse una delle conseguenze più popolari della teoria della relatività di Einstein. In realtà non si tratta di un vero e proprio paradosso, bensì
PARADOSSO DEI GEMELLI Il cosiddetto paradosso dei gemelli è forse una delle conseguenze più popolari della teoria della relatività di Einstein. In realtà non si tratta di un vero e proprio paradosso, bensì
Anno Accademico 2007/2008. Astronomia. Corso di Laurea in Scienze Naturali. Alessandro Marconi
 Anno Accademico 2007/2008 Astronomia Corso di Laurea in Scienze Naturali Alessandro Marconi Dipartimento di Astronomia e Scienza dello Spazio, Università di Firenze Bibliografia Il testo su cui sono basate
Anno Accademico 2007/2008 Astronomia Corso di Laurea in Scienze Naturali Alessandro Marconi Dipartimento di Astronomia e Scienza dello Spazio, Università di Firenze Bibliografia Il testo su cui sono basate
Lezione 3: come si descrive il moto dei corpi
 Lezione 3 - pag.1 Lezione 3: come si descrive il moto dei corpi 3.1. Correlare posizione e tempo Quando diciamo che un corpo si muove intendiamo dire che la sua posizione, misurata rispetto al sistema
Lezione 3 - pag.1 Lezione 3: come si descrive il moto dei corpi 3.1. Correlare posizione e tempo Quando diciamo che un corpo si muove intendiamo dire che la sua posizione, misurata rispetto al sistema
EQUAZIONE DELLA RETTA
 EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
Programma Didattico Annuale
 LICEO SCIENTIFICO STATALE GALILEO GALILEI PdQ - 7.06 Ediz.: 1 Rev.: 0 Data 02/09/05 Alleg.: D01 PROG. M2 PROCEDURA della QUALITA' Programma Didattico Annuale Anno Scolastico 2011/2012 MATERIA : Scienze
LICEO SCIENTIFICO STATALE GALILEO GALILEI PdQ - 7.06 Ediz.: 1 Rev.: 0 Data 02/09/05 Alleg.: D01 PROG. M2 PROCEDURA della QUALITA' Programma Didattico Annuale Anno Scolastico 2011/2012 MATERIA : Scienze
CARTOGRAFIA 2 V 1 LA CARTA TRADIZIONALE. È la rappresentazione sul piano della superficie terrestre secondo determinate norme e segni convenzionali
 CARTOGRAFIA 2 V 2 P V 3 V 1 π LA CARTA TRADIZIONALE È la rappresentazione sul piano della superficie terrestre secondo determinate norme e segni convenzionali È costituita da un disegno che rappresenta
CARTOGRAFIA 2 V 2 P V 3 V 1 π LA CARTA TRADIZIONALE È la rappresentazione sul piano della superficie terrestre secondo determinate norme e segni convenzionali È costituita da un disegno che rappresenta
1.4 Geometria analitica
 1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
Funzioni implicite - Esercizi svolti
 Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
OLIMPIADI ITALIANE DI ASTRONOMIA 2015 FINALE NAZIONALE 19 Aprile Prova Teorica - Categoria Senior
 OLIMPIADI ITALIANE DI ASTRONOMIA 2015 FINALE NAZIONALE 19 Aprile Prova Teorica - Categoria Senior 1. Vero o falso? Quale delle seguenti affermazioni può essere vera? Giustificate in dettaglio la vostra
OLIMPIADI ITALIANE DI ASTRONOMIA 2015 FINALE NAZIONALE 19 Aprile Prova Teorica - Categoria Senior 1. Vero o falso? Quale delle seguenti affermazioni può essere vera? Giustificate in dettaglio la vostra
Geometria solare. Università IUAV - Venezia
 Corso di Fisica Tecnica Ambientale Architettura-energia-ambiente: introduzione alla sostenibilità Laboratorio Integrato 1 anno CLASARCH indirizzo sostenibilità Geometria solare Università IUAV - Venezia
Corso di Fisica Tecnica Ambientale Architettura-energia-ambiente: introduzione alla sostenibilità Laboratorio Integrato 1 anno CLASARCH indirizzo sostenibilità Geometria solare Università IUAV - Venezia
Calcolo dell altezza di un rilievo lunare: l esempio di Arzachel
 Calcolo dell altezza di un rilievo lunare: l esempio di Arzachel Lo scopo della suddetta esperienza è il calcolo dell altezza di un particolare rilievo lunare, scelto appositamente per la conformazione
Calcolo dell altezza di un rilievo lunare: l esempio di Arzachel Lo scopo della suddetta esperienza è il calcolo dell altezza di un particolare rilievo lunare, scelto appositamente per la conformazione
Relazione. Esperienza didattica all'osservatorio astronomico (POF 2011)
 1 Esperienza didattica all'osservatorio astronomico (POF 2011) Relazione Gruppo: Camilla Chiappetta, Anna D Errico, Caterina Filippini, Sara Giorgini, Giulia Laura Montani Procedura calcolo Moretus Il
1 Esperienza didattica all'osservatorio astronomico (POF 2011) Relazione Gruppo: Camilla Chiappetta, Anna D Errico, Caterina Filippini, Sara Giorgini, Giulia Laura Montani Procedura calcolo Moretus Il
IL PLANETARIO DEL LICEO SCACCHI
 IL PLANETARIO DEL LICEO SCACCHI Prof. Luciana Carrieri (responsabile del planetario) Il Planetario del Liceo Scacchi di Bari è uno strumento ottico che proietta su una cupola di 5 metri di diametro l immagine
IL PLANETARIO DEL LICEO SCACCHI Prof. Luciana Carrieri (responsabile del planetario) Il Planetario del Liceo Scacchi di Bari è uno strumento ottico che proietta su una cupola di 5 metri di diametro l immagine
Rilevamenti Veri. 10 Est Greenwich 5
 Rilevamenti Veri Da ogni posizione geografica (detta anche punto o punto nave )si può indicare la posizione di un altro oggetto indicandone il rilevamento e la distanza. Il rilevamento (o azimuth) è l'angolo
Rilevamenti Veri Da ogni posizione geografica (detta anche punto o punto nave )si può indicare la posizione di un altro oggetto indicandone il rilevamento e la distanza. Il rilevamento (o azimuth) è l'angolo
5. Massimi, minimi e flessi
 1 5. Massimi, minimi e flessi Funzioni crescenti e decrescenti A questo punto dovremmo avere imparato come si calcolano le derivate di una funzione razionale fratta, ma dobbiamo capire in che modo queste
1 5. Massimi, minimi e flessi Funzioni crescenti e decrescenti A questo punto dovremmo avere imparato come si calcolano le derivate di una funzione razionale fratta, ma dobbiamo capire in che modo queste
GEOMETRIA ANALITICA
 GEOMETRIA ANALITICA matematica@blogscuola.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un
GEOMETRIA ANALITICA matematica@blogscuola.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un
Risolviamo un esercizio per illustrare il fenomeno in modo dettagliato anche se,in alcuni punti, semplificato.
 PARADOSSO DEI GEMELLI Il cosiddetto paradosso dei gemelli è forse una delle conseguenze più popolari della teoria della relatività di Einstein. In realtà non si tratta di un vero e proprio paradosso, bensì
PARADOSSO DEI GEMELLI Il cosiddetto paradosso dei gemelli è forse una delle conseguenze più popolari della teoria della relatività di Einstein. In realtà non si tratta di un vero e proprio paradosso, bensì
Geoportale in Comune. Censimento, Catalogazione e condivisione dei dati territoriali Interoperabilità tra le PA Locali e il Geoportale Nazionale
 Geoportale in Comune Censimento, Catalogazione e condivisione dei dati territoriali Interoperabilità tra le PA Locali e il Geoportale Nazionale Educazione ambientale nella scuola La Terra Il reticolo geografico
Geoportale in Comune Censimento, Catalogazione e condivisione dei dati territoriali Interoperabilità tra le PA Locali e il Geoportale Nazionale Educazione ambientale nella scuola La Terra Il reticolo geografico
LA RETTA NEL PIANO CARTESIANO
 LA RETTA NEL PIANO CARTESIANO LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un verso di percorrenza;
LA RETTA NEL PIANO CARTESIANO LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un verso di percorrenza;
Impiego luoghi di posizione isolati rilevamento di sicurezza
 PAS A056 C180 LEZIONE 4 Impiego luoghi di posizione isolati rilevamento di sicurezza Impiego luoghi di posizione isolati rlv / allineam. guida dist. sicurezza Punto con rilevamenti successivi stesso oggetto
PAS A056 C180 LEZIONE 4 Impiego luoghi di posizione isolati rilevamento di sicurezza Impiego luoghi di posizione isolati rlv / allineam. guida dist. sicurezza Punto con rilevamenti successivi stesso oggetto
Derivate. Rette per uno e per due punti. Rette per uno e per due punti
 Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
La prima apertura dell Osservatorio Astronomico Galileo Galilei risale al Nel 2004 il Comune di Peccioli affida la gestione alla AAAV (Associazi
 La prima apertura dell Osservatorio Astronomico Galileo Galilei risale al 1997. Nel 2004 il Comune di Peccioli affida la gestione alla AAAV (Associazione Astrofili Alta Valdera) appositamente costituita.
La prima apertura dell Osservatorio Astronomico Galileo Galilei risale al 1997. Nel 2004 il Comune di Peccioli affida la gestione alla AAAV (Associazione Astrofili Alta Valdera) appositamente costituita.
FUNZIONI GONIOMETRICHE
 FUNZIONI GONIOMETRICHE ANGOLI Col termine angolo indichiamo la parte di piano limitata da due semirette aventi la stessa origine, chiamata vertice. Possiamo definire anche l angolo come la parte di piano
FUNZIONI GONIOMETRICHE ANGOLI Col termine angolo indichiamo la parte di piano limitata da due semirette aventi la stessa origine, chiamata vertice. Possiamo definire anche l angolo come la parte di piano
Le carte geografiche
 Le carte geografiche Definizione delle carte geografiche Le carte sono rappresentazioni approssimate,simboliche e ridotte della terra oppure di una parte della terra. Esse concentrano in un foglio di dimensioni
Le carte geografiche Definizione delle carte geografiche Le carte sono rappresentazioni approssimate,simboliche e ridotte della terra oppure di una parte della terra. Esse concentrano in un foglio di dimensioni
