APPENDICE 4. sono determinati imponendo che la (2) sia verificata p W M
|
|
|
- Giovanni Romeo
- 5 anni fa
- Visualizzazioni
Transcript
1 APPENDICE 4 PROBLEA DI DIRICHLET PER L EQUAZIONE DI POISSON 2D SOLUZIONE COL ETODO DEGLI ELEENTI FINITI EDIANTE ATLAB assmlano d Aquno Fomulazone del poblema Consdeamo l seguente poblema d valo al contono: 2 u = u = g f n su, () 2 dove u C ( ), f C ( ), g C ( ). In tal potes la soluzone u del poblema esste ed è unca nello spazo delle funzon contnue, devabl due volte e con devate lmtate. Tale soluzone vene detta soluzone fote del poblema (). S è vsto dalla tattazone potata nella nota 4 ce esste una fomulazone debole del poblema (), desctta dalla seguente equazone: p uˆ dv = p f dv + p u dv p C ( ), (2) dove p è la geneca funzone peso appatenente allo spazo delle funzon contnue ce s annullano sulla fontea d, la funzone û è tale ce u = uˆ + u spett la condzone al contono u = g, con u polungamento d g nell nteno d (esste sempe se g è suffcentemente egolae). In questo modo è facle vefcae ce l ncognta û è soluzone d un poblema d Dclet omogeneo. E mpotante ossevae ce spetto alla fomulazone fote () stavolta è cesta mnoe egolatà alla funzone ncognta, n quanto è suffcente ce essa sa devable una sola volta. etodo d Galen Questo metodo consste nel cecae un appossmazone û della soluzone û n uno spazo a dmensone fnta. A tale scopo s consdea un sottospazo W d C ( ) d dmensone fnta e una base d quest ultmo B { w K, } funzon d base s ottene: = w =,. Espmo la funzone ncognta û medante le uˆ = a w, (3) dove coeffcent a sono detemnat mpono ce la (2) sa vefcata p W. In ealtà, l fatto ce le funzon w sono lneamente ndpent mplca ce è suffcente mpoe la (2) pe le sole funzon d base w. Dunque, appae cao ce così faco la (2) s taduce n un sstema d equazon n altettante ncognte :
2 = ( w w dv) a = w f dv + w u dv =, K,, (4) ce s può scvee nella foma usuale: L a = b, (5) dove la matce d stffness L, smmetca e defnta postva, è caattezzata da l, = w w dv (6) e l temne noto da b = w f dv + w u dv. (7) etodo degl element fnt C feamo adesso alla soluzone della (4) n un domno bdmensonale. Assumamo ce sa stata Τ =, K, del domno n tangol (ad. Es. quella d fgua ). effettuata una patzone { } Nt Fg.. Tangolazone del domno E necessao a questo punto effettuae la scelta delle funzon d base. La scelta pù comune consste nello sceglee funzon lnea dette a ta tal ce: w ( P ) δ, =, (8) dove δ, è l smbolo d Konece. E mpotante sottolneae ce questa scelta mplca un ulteoe popetà della matce L ce consste nella spastà. Opeae con matc spase puttosto ce pene è molto pù convenente n quanto la soluzone del conseguente sstema lneae può essee ottenuta con metod teatv ce n queste condzon offono pestazon molto elevate. Con questa scelta delle funzon d base, esta oa da patcolazzae le espesson degl ntegal (6)-(7), teno oppotunamente n conto l fatto ce l domno è stato suddvso n tangol. Consdeamo l tangolo d vetc P, P, P (tena supposta antoaa) avent coodnate catesane spettvamente x, y ),( x, y ),( x, y ). L espessone analtca della geneca funzone w stetta all -mo tangolo ( è: w ( x, y) = a x + b y + c, (9) ( ) ( ) ( ) ( )
3 a ( ) A = 2 A = 2 ( ) ( y y ), b ( x x ) = 2 A [( x y x y ) + ( x y x y ) + ( x y x y )] ( ), c = ( x y x y ) 2 A è l aea del tangolo., () e l gadente d ( ) w è dato dalla semplce espessone: ( ) ( ) ( ) w ( x, y) = a xˆ + b yˆ. () D conseguenza coeffcent dat dalla (6) dventano: Nt w w dv = w w dv = = = Nt ( ) ( ) ( ) ( ) ( a a + b b ) l, = A. (2) () () () Pocé pe la natua delle funzon a ta coeffcent a, b, a, soltanto nel tangolo -mo, s vede caamente ce contbuscono al coeffcente tangol ce anno n comune entamb vetc P, P (fg. 2). () b sono dves da zeo l, solo Fg.2. Contbut a coeffcent Cò suggesce ce al momento dell mplementazone, come vedemo successvamente, un modo effcente pe calcolae quest coeffcent è effettuae un cclo su tangol della mes e sommae contbut d cascun tangolo a coeffcent elatv a nod ad esso appatenent. Resta oa da affontae l assemblaggo del temne noto (7). Pe quanto guada l pmo ntegale, esstono fomule d dvesa accuatezza: una comunemente usata ed accuata al pmo odne nell aea del tangolo è: ( b) A w f dv f ( P ), (3) 3 ( b) dove P ( P + P + P )/ 3 l, = è l bacento del tangolo. Pe quanto guada l secondo temne, è necessao specfcae la foma della funzone u. S supponga d odnae nod della mes nel seguente modo come:, K, N 4 K, N +,, N Ne. Così faco sceglamo la funzone u 3 nod nten nod d fontea
4 u N + = Ne s= N + g( P s ) w s. (4) In questo modo la u è nulla ne nod nten, dunque s a ce ne nod nten la funzone ncognta û concde con l ncognta u del poblema nzale (). Sosttuo le (3)-(4) nella (7) s ottene: b = N t = w f dv + N t = w u dv N t = N + Ne ( b) A f ( P ) + g( Ps ) l, s. (5) 3 s= N + A questo punto ossevamo ce è suffcente consdeae soltanto le N equazon sctte pe nod nten della mes, dato ce la funzone ncognta è nota sulla fontea. Cò consente un spamo d memoa e d costo computazonale nella soluzone d un sstema lneae d odne nfeoe, sopattutto nel caso usuale d applcazon n cu la soluzone del poblema d valo al contono deve essee effettuata petutamente (ad es. pe ogn passo tempoale d una ntegazone numeca). Implementazone con atlab Poblema d Dclet nel ceco untao Nella dscussone pecedente s è supposto ce fosse dsponble una tangolazone del domno ; d seguto vedamo come geneae questa mes tangolae con atlab. Il modo pù mmedato consste nell utlzzo del toolbox PDE (patal dffeental equatons) ce pemette tamte una comoda ntefacca utente d dsegnae l domno 2D e geneae n manea automatca la mes tangolae. Dal pompt d atlab, dgtando l comando pdetool s apà la fnesta pncpale del toolbox (fg.3) fg.3. Fnesta pncpale d pdetool Clccando su pulsant della baa degl stument è possble taccae domn d dvese fome, ance combnandone pù d uno. E convenente dsegnae pma l domno gossolanamente e po modfcane paamet faco doppo clc su d esso (fg. 4).
5 Fg. 4. odfca delle caattestce geometce del domno Una volta ceato l domno è possble geneae la mes ago sul pulsante con l tangolo ed eventualmente affnala con l pulsante a fanco a seconda delle esgenze d accuatezza. Una volta geneata la mes è possble espotala medante l comando Expot mes nel menu es (fg. 5). Fg. 5. Espotazone della mes n atlab La mes vene espotata pe default nelle matc p, e, t ce descvamo bevemente d seguto: atce p: matce de nod della mes [ 2 N p ] ( N p è l numeo d nod della mes). La pma ga contene le ascsse de nod, la seconda contene le odnate. La numeazone de nod è data dall ndce d colonna n questa matce (la colonna -ma cosponde a nodo ). 7 N e ( N e è l numeo d nod del contono). La pma e la seconda ga contengono gl ndc de nod nzal e fnal de segment elementa d fontea, la teza e la quata ga contengono valo nzal e fnal del paameto (non levante a fn della nosta tattazone), la qunta ga contene l numeo del segmento d fontea, la sesta e la settma contengono nume de sottodomn a desta e a snsta del segmento. Le ge mpotant sono le pme due ce ne cas d domn semplc c fonscono l elenco de nod d fontea, cosa ce seve a fn del tattamento delle condzon al contono. atce e: matce del contono della mes [ ]
6 atce t: matce de tangol della mes [ ] 4 N t ( N t è l numeo d tangol). E fose la pù mpotante n quanto fonsce la elazone d appatenenza ta nod e tangol. La geneca colonna -ma cosponde al -mo tangolo e contene la tena antoaa degl ndc de nod,, appatenent ad esso. Il valoe nella quata ga è l numeo d sottodomno al quale appatene l tangolo ed è utle pe poblem d valo al contono n cu paamet dell equazone sono dves a seconda delle zone del domno (ad es. delettc con dvese pemttvtà, ecc.). Vedamo oa come costue un codce semplce con atlab pe solvee l poblema fomulato pecedentemente. Innanztutto saà necessao ceae ed espotae la mes come appena desctto. Nel seguto s suppone ce la stuttua dat espotata sa quella d default delle matc p, e, t. Nella fase d nzalzzazone s defnscono paamet, le matc e vetto ce s utlzzano pe solvee l sstema lneae. S not ce la matce d stffness K è esplctamente defnta spasa pe tae vantaggo delle potenzaltà d atlab nell opeae su matc spase. Inolte qu vene ance fssato l valoe della funzone ncognta ne nod d fontea attaveso la functon g_fun.m Nt=sze(t,2); Np=sze(p,2); Ne=sze(e,2); K=spase(Np,Np); F=zeos(Np,); U=zeos(Np,); F=e(,:); U(F)=g_fun(p(,F),p(2,F)); % numeo d tangol della mes % numeo d nod % numeo d nod d fontea % matce d stffness % temne noto % vettoe delle ncognte nodal % ndc de nod d fontea % mpongo U=g sulla fontea del domno Successvamente s passa all assemblaggo della matce d stffness e del temne noto (pe cu vene utlzzata la funzone f_fun.m), effettuato medante un cclo su tangol come accennato n pecedenza: fo n=:nt n=t(,n); n=t(2,n); n=t(3,n); x=p(,n); y=p(2,n); x=p(,n); y=p(2,n); x=p(,n); y=p(2,n); % ASSEBLAGGIO della matce d stffness % ndc de nod del tangolo n-mo % coodnate de vetc del tangolo n-mo a=y-y; b=x-x; a=y-y; b=x-x; a=y-y; b=x-x; D=[ x y; x y; x y]; A=det(D)/2; % aea del tangolo n-mo A=det(D)/2 px=/2/a*a; py=/2/a*b; px=/2/a*a; py=/2/a*b; px=/2/a*a; % component x,y de gadent d w, w, w
7 py=/2/a*b; K(n,n) = K(n,n) + A*(px*px+py*py); stffness K(n,n) = K(n,n) + A*(px*px+py*py); K(n,n) = K(n,n) + A*(px*px+py*py); K(n,n) = K(n,n) + A*(px*px+py*py); K(n,n) = K(n,n); K(n,n) = K(n,n) + A*(px*px+py*py); K(n,n) = K(n,n); K(n,n) = K(n,n) + A*(px*px+py*py); K(n,n) = K(n,n); % contbut alla matce d xc=(x+x+x)/3; yc=(y+y+y)/3; % coodnate del bacento del tangolo n-mo F([n n n])=f([n n n])+f_fun(xc,yc)*a/3; % assemblaggo temne noto Successvamente esta da mplementae le condzon al contono. Una manea semplce ma non ottmale consste nell mpoe dettamente ne nod d fontea le equazon u = g( P ) = N, K, N + N (6) e avo qu supposto ce nod sano odnat n modo da avee pma quell nten e po quell d fontea, cosa ce non accade automatcamente all atto della geneazone d mes. In ealtà l odnamento non è mpotante e nella patca le (6) possono essee mplementate potandole nel temne noto come segue: K(F,:Np)=; % mplementazone delle condzon al contono tpo Dclet fo =:Ne % Nel nodo -mo d fontea l'equazone è U()=g() K(F(),F())=; F(F)=U(F); Il passo fnale consste nella soluzone del sstema lneae assemblato pecedentemente e nella vsualzzazone della soluzone: U=K\-F; % Soluzone del sstema lneae pdeplot(p,e,t,'xydata',u,'contou','on'); % plot della soluzone Questo codce d esempo è dsponble nel fle DemoPosson.m. Infne, s pota a ttolo llustatvo una pocedua pe costue l sstema dotto alle equazon ne nod nten, ottenuto sommando un ulteoe contbuto al temne noto (ved eq.(5)) elmnando po nella matce d stffness ge e colonne elatve a nod d fontea. Così faco s duce l odne del sstema lneae e se ne veloczza la soluzone. fo =:Np f any(==e(,:ne)) K(,:Np)=zeos(,Np); F=F-U()*K(:Np,); K(:Np,)=zeos(Np,); K=spase(Np-Ne,Np); K2=spase(Np-Ne,Np-Ne); F=zeos(Np-Ne,); % cclo su nod % se l nodo "" è d fontea alloa % azzeo ga -ma d K % completo l'assemblaggo del temne noto % azzeo la colonna -ma d K % matce d stffness auslaa dotta % matce d stffness dotta % temne noto dotto a sol punt nten
8 w=; fo =:Np f K(,)~= K(w,:Np)=K(,:Np); F(w)=F(); w=w+; w=; fo =:Np f K(,)~= K2(:Np-Ne,w)=K(:Np-Ne,); w=w+; U=K2\-F; w=; fo =:Np f not(any(==e(,:ne))) U()=U(w); w=w+; % cclo d elmnazone ge nod d fontea % cclo d elmnazone colonne nod d fontea % soluzone del poblema dotto % costuzone dell'ncognta su tutt nod pdeplot(p,e,t,'xydata',u,'contou','on'); % plot della soluzone Questo stalco d codce è ncluso nello scpt DemoPosson2.m Bencma Testng del codce E buona noma, una volta pepaato un codce numeco, effettuae un test su un caso dotato d soluzone analtca allo scopo d vefcae ce non v sano eo gossolan. A ttolo d esempo, nel nosto caso del poblema (), un caso semplce è l seguente: 2 u = n u = su, dove è l dsco d cento l ogne e d aggo untao. E facle vefcae ce la soluzone analtca è la 2 2 x y funzone u( x, y) =. 4 Nella fgua a fanco s pota un dagamma della soluzone ottenuta con l codce pesentato. Lo scpt PDEtool pe costue la mes è contenuto nel fle esuntds.m Rfement []. G. ano, Appunt del Coso d odell Numec pe Camp, 25 [2]. Patal Dffeental Equatons Toolbox use s gude, Te atwos 22.
ESERCITAZIONE DEL 10 MARZO 2005
 ESERCITAZIONE DEL 10 MARZO 005 Poblema pano n.5 Dato l sstema composto da un asta gda vncolata con una cenea n O e un dsco gdo d aggo R vncolato all asta da un contatto blateo con puo otolamento, detemnae
ESERCITAZIONE DEL 10 MARZO 005 Poblema pano n.5 Dato l sstema composto da un asta gda vncolata con una cenea n O e un dsco gdo d aggo R vncolato all asta da un contatto blateo con puo otolamento, detemnae
Algebra vettoriale: un breve formulario. E r
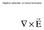 slde# Geoge Stokes Ilanda 1819 1903 Olve Heavsde Inghltea 1850 195 G. Stokes dede mpotant contbut alla teoa della popagaone ondulatoa con patcolae femento a flud (equaon d Nave-Stokes) all'ottca e all
slde# Geoge Stokes Ilanda 1819 1903 Olve Heavsde Inghltea 1850 195 G. Stokes dede mpotant contbut alla teoa della popagaone ondulatoa con patcolae femento a flud (equaon d Nave-Stokes) all'ottca e all
ESPERIMENTO CASUALE. P(X) è la funzione di probabilità secondo la quale ad ogni numero reale di X si assegna una misura di probabilità.
 ESPERIMENTO CASUALE S Spazo camponao : è l nseme d event necessa e ncompatbl che s pesentano come sultat dell ESPERIMENTO CASUALE. X è l nseme de nume eal assocato ad S, n modo che ad ogn elemento (evento)
ESPERIMENTO CASUALE S Spazo camponao : è l nseme d event necessa e ncompatbl che s pesentano come sultat dell ESPERIMENTO CASUALE. X è l nseme de nume eal assocato ad S, n modo che ad ogn elemento (evento)
Operatori differenziali (1)
 Opeato dffeenal Gadente opea s no scalae; a come sltato n vettoe gad Φ Φ Φ Φ Φ Dvegena opea s n vettoe; a come sltato no scalae dv Rotaonale o otoe opea s n vettoe; a come sltato n vettoe ot Esectaon d
Opeato dffeenal Gadente opea s no scalae; a come sltato n vettoe gad Φ Φ Φ Φ Φ Dvegena opea s n vettoe; a come sltato no scalae dv Rotaonale o otoe opea s n vettoe; a come sltato n vettoe ot Esectaon d
Risultati esame scritto Fisica 2-29/09/2014 orali: alle ore presso aula O
 sultat esame sctto Fsca - 9/9/ oal: -- alle oe. pesso aula O gl student nteessat a vsonae lo sctto sono pegat d pesentas l gono dell'oale Nuovo odnamento matcola voto 66 9 6 ammesso 9 nc 5 9 5 56 nc 5
sultat esame sctto Fsca - 9/9/ oal: -- alle oe. pesso aula O gl student nteessat a vsonae lo sctto sono pegat d pesentas l gono dell'oale Nuovo odnamento matcola voto 66 9 6 ammesso 9 nc 5 9 5 56 nc 5
Approcci algoritmici. Capitolo Approccio sequenziale. y = y (che collegano il modello di trasporto a quello di
 Captolo 3 Appocc algotmc In questo captolo descveemo alcun appocc algotmc mat alla soluone del poblema pesentato nel pmo captolo. C sono dves mod d pos spetto ad un poblema con un numeo così elevato d
Captolo 3 Appocc algotmc In questo captolo descveemo alcun appocc algotmc mat alla soluone del poblema pesentato nel pmo captolo. C sono dves mod d pos spetto ad un poblema con un numeo così elevato d
Esempio 1 Determinazione modi propri e forme modali per sistema a 2 gdl 7.1
 Esempo Detemnazone mod pop e fome modal pe sstema a gdl 7. Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca Coso d Pogettazone Assstta delle Stuttue
Esempo Detemnazone mod pop e fome modal pe sstema a gdl 7. Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca Coso d Pogettazone Assstta delle Stuttue
CONDUZIONE NON STAZIONARIA
 CONDUZIONE NON AZIONARIA Caso geneale de sstem a tempeatua unfome ebbene l pocesso d conduzone non stazonaa n un soldo sa comunemente dovuto allo sco temco convettvo dal fludo ccostante, alt pocess d sco
CONDUZIONE NON AZIONARIA Caso geneale de sstem a tempeatua unfome ebbene l pocesso d conduzone non stazonaa n un soldo sa comunemente dovuto allo sco temco convettvo dal fludo ccostante, alt pocess d sco
Leggi di Biot-Savart e di Ampère. Fisica II - CdL Chimica
 Legg d Bot-Savat e d Ampèe d P R dl Ossevazon spemental Legge d Bot-Savat db ds espemento: X db... assumendo n fomula Legge d Bot-Savat db ds pemeabltà magnetca X db Il campo magnetco è dstbuto ntono al
Legg d Bot-Savat e d Ampèe d P R dl Ossevazon spemental Legge d Bot-Savat db ds espemento: X db... assumendo n fomula Legge d Bot-Savat db ds pemeabltà magnetca X db Il campo magnetco è dstbuto ntono al
ESERCITAZIONE 8. Esercitazioni del corso FONDAMENTI DI PROCESSI CHIMICI Prof. Gianpiero Groppi
 Dpatmento d Enega oltecnco d Mlano azza eonado da nc - 01 MINO Esectazon del coso FONDMENI DI ROESSI HIMII of. Ganpeo Gopp ESERIIONE 8 alcolo della tempeatua d bolla e d ugada d una mscela n-butano/n-esano
Dpatmento d Enega oltecnco d Mlano azza eonado da nc - 01 MINO Esectazon del coso FONDMENI DI ROESSI HIMII of. Ganpeo Gopp ESERIIONE 8 alcolo della tempeatua d bolla e d ugada d una mscela n-butano/n-esano
Algoritmi e Strutture di Dati
 Algotm e Stuttue d Dat Quck-sot m.patgnan Nota d copyght queste sldes sono potette dalle legg sul copyght l ttolo ed l copyght elatv alle sldes (nclus, ma non lmtatamente, mmagn, foto, anmazon, vdeo, audo,
Algotm e Stuttue d Dat Quck-sot m.patgnan Nota d copyght queste sldes sono potette dalle legg sul copyght l ttolo ed l copyght elatv alle sldes (nclus, ma non lmtatamente, mmagn, foto, anmazon, vdeo, audo,
Ottimizzazione Combinatoria
 Ottmzzazone Combnatoa Clusteng de dat Lezone Lezon a cua d Sla Canale contatto e-mal: canale@ds.unoma.t Unestà d Roma La Sapenza Dpatmento d Infomatca e Sstemstca Coso d Lauea n Ingegnea Gestonale Defnzone
Ottmzzazone Combnatoa Clusteng de dat Lezone Lezon a cua d Sla Canale contatto e-mal: canale@ds.unoma.t Unestà d Roma La Sapenza Dpatmento d Infomatca e Sstemstca Coso d Lauea n Ingegnea Gestonale Defnzone
Leggi di Biot-Savart e di Ampère. Fisica II - CdL Chimica
 Legg d ot-savat e d Ampèe q d q P R dl Ossevazon spemental d Legge d ot-savat ds q espemento: X d d d d d d d ds 1 ds 2 sen q... assumendo n fomula I ds ˆ d k m 2 d Legge d ot-savat ds q X d d k c m pemeabltà
Legg d ot-savat e d Ampèe q d q P R dl Ossevazon spemental d Legge d ot-savat ds q espemento: X d d d d d d d ds 1 ds 2 sen q... assumendo n fomula I ds ˆ d k m 2 d Legge d ot-savat ds q X d d k c m pemeabltà
Figura 1 Geometria attuale. Figura 2 Sezione trapezia
 ESERCITAZIONE N. 4 (20 aple 2005) Dmensonamento daulco d un canale apeto PROBLEMA Nel pogetto d ecupeo d un aea s ntende potae alla luce un canale che n passato è stato tombnato con tubazon pefabbcate
ESERCITAZIONE N. 4 (20 aple 2005) Dmensonamento daulco d un canale apeto PROBLEMA Nel pogetto d ecupeo d un aea s ntende potae alla luce un canale che n passato è stato tombnato con tubazon pefabbcate
Economia del turismo
 Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2013-2014 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 8 I MODELLI
Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2013-2014 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 8 I MODELLI
ESERCITAZIONE DEL 3 MARZO 2005
 ESERCITAZIONE DEL 3 MARZO 2005 Ela lnda (on passo p ostante) Equazon dell ela: x = R os θ y = R sn θ z = p 2π θ 5 La uva appatene al lndo olae, on geneat paallele all asse z, d equazone: x 2 + y 2 = R
ESERCITAZIONE DEL 3 MARZO 2005 Ela lnda (on passo p ostante) Equazon dell ela: x = R os θ y = R sn θ z = p 2π θ 5 La uva appatene al lndo olae, on geneat paallele all asse z, d equazone: x 2 + y 2 = R
Lezione 9. N-poli. N-poli passivi. Pilotato in tensione
 Lezone 9 N-pol 4 Fn oa c samo lmtat a bpol. Esstono peò anche dspostv che non sono conducbl a bpol, nel senso che non nteagscono con l esteno attaveso due sol pol. In fgua è appesentato un quadpolo, ma
Lezone 9 N-pol 4 Fn oa c samo lmtat a bpol. Esstono peò anche dspostv che non sono conducbl a bpol, nel senso che non nteagscono con l esteno attaveso due sol pol. In fgua è appesentato un quadpolo, ma
Esercizi sulle reti elettriche in corrente continua (parte 2)
 Esecz sulle et elettche n coente contnua (pate ) Eseczo 3: etemnae gl equalent d Theenn e d Noton del bpolo complementae al esstoe R 5 nel ccuto n fgua e calcolae la coente che ccola attaeso l esstoe R
Esecz sulle et elettche n coente contnua (pate ) Eseczo 3: etemnae gl equalent d Theenn e d Noton del bpolo complementae al esstoe R 5 nel ccuto n fgua e calcolae la coente che ccola attaeso l esstoe R
Calcolo del lavoro compiuto dalle forze elementari
 Calcolo del lavoo computo dalle foze elementa avoo computo da una foza costante In base alla defnzone, l lavoo computo da una foza costante, l cu punto d applcazone s sposta da a, vale: F s F s F s S not
Calcolo del lavoo computo dalle foze elementa avoo computo da una foza costante In base alla defnzone, l lavoo computo da una foza costante, l cu punto d applcazone s sposta da a, vale: F s F s F s S not
Sommario. Facoltà di Economia E E2 E 5 E 4. S x1. Le Variabili Casuali o Variabili Aleatorie. francesco mola. Lezione n 13.
 Coso d Statstca Facoltà d conoma a.a. - fancesco mola Sommao Le Vaabl Casual o Vaabl Aleatoe Lezone n Lez._a.a. 9- statstca-fancesco mola Vaabl Casual Vaabl Casual (cont. Una Vaable Casuale è una egola
Coso d Statstca Facoltà d conoma a.a. - fancesco mola Sommao Le Vaabl Casual o Vaabl Aleatoe Lezone n Lez._a.a. 9- statstca-fancesco mola Vaabl Casual Vaabl Casual (cont. Una Vaable Casuale è una egola
Sommario. Corso di Statistica Facoltà di Economia. Le Variabili Casuali o Variabili Aleatorie. Lezione n 16. Francesco Mola. Variabili Casuali (cont
 Coso d Statstca Facoltà d conoma Lezone n 6 z Sommao Le Vaabl Casual o Vaabl Aleatoe a.a. - Fancesco Mola a.a. - statstca-fancesco mola Vaabl Casual Vaabl Casual (cont cont.) Una Vaable Casuale è una egola
Coso d Statstca Facoltà d conoma Lezone n 6 z Sommao Le Vaabl Casual o Vaabl Aleatoe a.a. - Fancesco Mola a.a. - statstca-fancesco mola Vaabl Casual Vaabl Casual (cont cont.) Una Vaable Casuale è una egola
I vettori. A cura di dott. Francesca Fattori Speranza dott. Francesca Paolucci
 I vetto cua d dott. Fancesca Fatto Speana (speana@fs.unoma3.t) dott. Fancesca Paolucc GRNDEZZE SLRI E VETTORILI S defnscono gandee SLRI quelle gandee caatteate solo da un valoe numeco o modulo come: tempo,
I vetto cua d dott. Fancesca Fatto Speana (speana@fs.unoma3.t) dott. Fancesca Paolucc GRNDEZZE SLRI E VETTORILI S defnscono gandee SLRI quelle gandee caatteate solo da un valoe numeco o modulo come: tempo,
Sessione live #1 Settimana #2 dal 10 al 16 marzo. Statistica descrittiva: Indici di posizione, dispersione e forma Istogramma frequenze, box plot
 Sessone lve #1 Settmana # dal 10 al 16 mazo Statstca descttva: Indc d poszone, dspesone e foma Istogamma fequenze, box plot Lezon CD: 1 - - 3 Eseczo 1 S consde la seguente dstbuzone delle nduste tessl
Sessone lve #1 Settmana # dal 10 al 16 mazo Statstca descttva: Indc d poszone, dspesone e foma Istogamma fequenze, box plot Lezon CD: 1 - - 3 Eseczo 1 S consde la seguente dstbuzone delle nduste tessl
IL Potenziale elettrostatico
 Ve.. d 27/5/9 IL Potenzale ettostatco ) La oza ettca è consevatva Patamo col vecae che la oza ettca è consevatva, lmtandoc nzalmente al caso d cache ettche puntom. Posta una caca +Q ema n un punto ogne,
Ve.. d 27/5/9 IL Potenzale ettostatco ) La oza ettca è consevatva Patamo col vecae che la oza ettca è consevatva, lmtandoc nzalmente al caso d cache ettche puntom. Posta una caca +Q ema n un punto ogne,
Prova scritta del corso di Fisica con soluzioni
 Pova sctta del coso d Fsca con soluzon Pof. F. cc-tesengh 13/02/2013 Quest 1. State ossevando una gosta d quelle con seggoln volant che ga a veloctà angolae costante. Su uno de seggoln è seduto un bambno
Pova sctta del coso d Fsca con soluzon Pof. F. cc-tesengh 13/02/2013 Quest 1. State ossevando una gosta d quelle con seggoln volant che ga a veloctà angolae costante. Su uno de seggoln è seduto un bambno
= E! Se E ha proprietà di simmetria Enorme semplificazione
 pplcazon del teoema d Gauss a dstbuzon d caca smmetche Il teoema d Gauss è utle pe detemnae l campo elettco geneato da dstbuzon d caca che pesentano una qualche smmeta spazale. qn Φ ˆ E E Se E ha popetà
pplcazon del teoema d Gauss a dstbuzon d caca smmetche Il teoema d Gauss è utle pe detemnae l campo elettco geneato da dstbuzon d caca che pesentano una qualche smmeta spazale. qn Φ ˆ E E Se E ha popetà
Campo elettrico e campo magnetico statici
 1 Campo elettco e campo magnetco statc Flusso d un campo vettoale Consdeamo una zona d spazo n cu sa pesente un ceto campo vettoale v e, n uesto spazo, una ceta supefce (apeta o chusa) Dvdamo l'ntea supefce
1 Campo elettco e campo magnetco statc Flusso d un campo vettoale Consdeamo una zona d spazo n cu sa pesente un ceto campo vettoale v e, n uesto spazo, una ceta supefce (apeta o chusa) Dvdamo l'ntea supefce
Laboratorio: Metodi quantitativi per il calcolo del VaR. Aldo Nassigh Financial Risk Management A.A. 2011/12 Lezione 4
 Laboatoo: Metod quanttatv pe l calcolo del VaR Aldo Nassgh Fnancal Rsk Management A.A. 011/1 Lezone 4 METODO PARAMETRICO Sngolo fattoe d scho e poszone lneae Poszone l cu valoe attuale è soggetto ad un
Laboatoo: Metod quanttatv pe l calcolo del VaR Aldo Nassgh Fnancal Rsk Management A.A. 011/1 Lezone 4 METODO PARAMETRICO Sngolo fattoe d scho e poszone lneae Poszone l cu valoe attuale è soggetto ad un
Fluidodinamica Applicata Esempi (1-5) di Flusso Irrotazionale
 Poltecnco d Tono Fldodnamca Applcata 3. Esemp -5 d Flsso Iotaonale Flsso bdmensonale La none d coente Nel caso bdmensonale c è n lteoe popetà: Fg.3 Integamo n A ed samo Gass. dd nds n n A A A ma se è desctta
Poltecnco d Tono Fldodnamca Applcata 3. Esemp -5 d Flsso Iotaonale Flsso bdmensonale La none d coente Nel caso bdmensonale c è n lteoe popetà: Fg.3 Integamo n A ed samo Gass. dd nds n n A A A ma se è desctta
Flusso attraverso una superficie chiusa
 Flusso attaveso una supefce chusa D solto uello che s chede d calcolae è l flusso del campo attaveso una supefce chusa (coè una supefce che dvde lo spazo n due egon una ntena ed una estena alla supefce)
Flusso attaveso una supefce chusa D solto uello che s chede d calcolae è l flusso del campo attaveso una supefce chusa (coè una supefce che dvde lo spazo n due egon una ntena ed una estena alla supefce)
Sviluppo dell algoritmo per l allineamento dello spettrometro magnetico di PAMELA
 Svluppo dell algotmo pe l allneamento dello spettometo magnetco d PAMELA Fancesca Gamb Unvestà degl Stud d Fenze Congesso Nazonale SIF 19 Settembe 003 Lo spettometo magnetco d PAMELA Lo spettometo magnetco
Svluppo dell algotmo pe l allneamento dello spettometo magnetco d PAMELA Fancesca Gamb Unvestà degl Stud d Fenze Congesso Nazonale SIF 19 Settembe 003 Lo spettometo magnetco d PAMELA Lo spettometo magnetco
N X Y SVOLGIMENTO.
 RELAZIONE. La cenea dell pesostentatoe d un aeeo leggeo è collegata alla centna d estemtà tamte chodatua secondo le ndcazon potate n fgua. Lo sfozo d taglo massmo agente sul peno della cenea è pa a 00
RELAZIONE. La cenea dell pesostentatoe d un aeeo leggeo è collegata alla centna d estemtà tamte chodatua secondo le ndcazon potate n fgua. Lo sfozo d taglo massmo agente sul peno della cenea è pa a 00
Condizioni di equilibrio TD nelle reazioni chimiche
 Condzon d equlbo TD nelle eazon chmche Voglamo studae l metodo geneale pe la detemnazone delle condzon d equlbo d un sstema fomato da N spece chmche dvese n pesenza d una eazone chmca. S utlzza una funzone
Condzon d equlbo TD nelle eazon chmche Voglamo studae l metodo geneale pe la detemnazone delle condzon d equlbo d un sstema fomato da N spece chmche dvese n pesenza d una eazone chmca. S utlzza una funzone
3 Il teorema di Gauss
 3 Il teoema d Gauss 3. Il flusso d un vettoe attaveso una supefce Pe una pozone d supefce che sa pana, dsposta nello spazo, c è una dezone che sulta ndvduata n modo unvoco ed è quella della pependcolae
3 Il teoema d Gauss 3. Il flusso d un vettoe attaveso una supefce Pe una pozone d supefce che sa pana, dsposta nello spazo, c è una dezone che sulta ndvduata n modo unvoco ed è quella della pependcolae
MACCHINA ELEMENTARE CON UN SOLO AVVOLGIMENTO
 MAHINA ELEMENTARE ON UN SOLO AVVOLGIMENTO S consde una macchna elementae avente le seguent caattestche: statoe a pol salent otoe clndco un avvolgmento sul otoe pol pp = 1 θ = θ m ω = ω m 1 La macchna può
MAHINA ELEMENTARE ON UN SOLO AVVOLGIMENTO S consde una macchna elementae avente le seguent caattestche: statoe a pol salent otoe clndco un avvolgmento sul otoe pol pp = 1 θ = θ m ω = ω m 1 La macchna può
Corrente elettrica. Conduttore in equilibrio. Condutture in cui è mantenuta una differenza di potenziale (ddp) E=0 V=cost
 Coente elettca Conduttoe n equlbo B E 0 E0 cost B Conduttue n cu è mantenuta una dffeenza d potenzale (ddp) > B E 0 _ B Un campo elettco all nteno d un conduttoe appesenta una stuazone d non equlbo. Un
Coente elettca Conduttoe n equlbo B E 0 E0 cost B Conduttue n cu è mantenuta una dffeenza d potenzale (ddp) > B E 0 _ B Un campo elettco all nteno d un conduttoe appesenta una stuazone d non equlbo. Un
Matematica Computazionale(6cfu) Ottimizzazione(8cfu)
 Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
r v i i P = m i i dt (M r cm ) = Mv r r i = d avendo definito il concetto di centro di massa (CM) del sistema ( M = m i r r r cm
 6. Sstem d patcelle Legge della dnamca d taslazone pe un sstema d patcelle È possble scvee una legge pe l moto collettvo d un nseme d patcelle nteagent fa loo e con l esteno. Questo modo d fae pemette
6. Sstem d patcelle Legge della dnamca d taslazone pe un sstema d patcelle È possble scvee una legge pe l moto collettvo d un nseme d patcelle nteagent fa loo e con l esteno. Questo modo d fae pemette
Approfondimento 7.4 - Altri tipi di test di significatività del coefficiente di correlazione di Pearson
 Appofondmento 7.4 - Alt tp d test d sgnfcatvtà del coeffcente d coelazone d Peason Una delle cause pncpal della cattva ntepetazone del test d sgnfcatvtà d è che s fonda su un potes nulla pe cu ρ 0. In
Appofondmento 7.4 - Alt tp d test d sgnfcatvtà del coeffcente d coelazone d Peason Una delle cause pncpal della cattva ntepetazone del test d sgnfcatvtà d è che s fonda su un potes nulla pe cu ρ 0. In
Meccanica dei sistemi
 Meccanca de sste 1. 1. Moento angolae 2. Moento d una foza 3. Foze cental 4. Sste d punt ateal 5. Foze estene e Foze ntene 6. Cento d assa d un sstea 7. Consevazone della quantta d oto 8. Teoea del oento
Meccanca de sste 1. 1. Moento angolae 2. Moento d una foza 3. Foze cental 4. Sste d punt ateal 5. Foze estene e Foze ntene 6. Cento d assa d un sstea 7. Consevazone della quantta d oto 8. Teoea del oento
Fisica 1 Elettrostatica. Preliminari matematici
 Fsca 1 Elettostatca Pelmna matematc Pogamma della leone Camp scala e vettoal Opeato deenal su camp Vettoe aea Opeaon ntegal su camp Teoem ntegal Camp Matematcamente sono unon eal (o complesse) che appesentano
Fsca 1 Elettostatca Pelmna matematc Pogamma della leone Camp scala e vettoal Opeato deenal su camp Vettoe aea Opeaon ntegal su camp Teoem ntegal Camp Matematcamente sono unon eal (o complesse) che appesentano
Esercizi sulle reti elettriche in corrente continua (parte 2)
 Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
g r =-g k r campo vettoriale distribuzione delle masse T n (x,y,z,t) campo tensoriale forze agenti sul corpo
 Campo Con l temne campo ntendamo ndcae una funzone che fonsce l valoe assunto n ogn punto d uno spazo da una detemnata quanttà fsca che può tovae desczone n fome matematche dvese: Esempo: campo fsco desczone
Campo Con l temne campo ntendamo ndcae una funzone che fonsce l valoe assunto n ogn punto d uno spazo da una detemnata quanttà fsca che può tovae desczone n fome matematche dvese: Esempo: campo fsco desczone
posizione, velocità, quantità di moto, energia cinetica, momento angolare, ecc.
 Unvestà a Sapena FONDAMENTI DEA MECCANICA QUANTISTICA Pma delle legg ( Postulat vedamo concett Vaabl dnamce Funone d onda o d stato 3 Opeato Vaable Dnamca S tatta d una qualsas vaable ce defnsce l moto
Unvestà a Sapena FONDAMENTI DEA MECCANICA QUANTISTICA Pma delle legg ( Postulat vedamo concett Vaabl dnamce Funone d onda o d stato 3 Opeato Vaable Dnamca S tatta d una qualsas vaable ce defnsce l moto
B - ESERCIZI: IP e TCP:
 Unverstà d Bergamo Dpartmento d Ingegnera dell Informazone e Metod Matematc B - ESERCIZI: IP e TCP: F. Martgnon Archtetture e Protocoll per Internet Eserczo b. S consder l collegamento n fgura A C =8 kbt/s
Unverstà d Bergamo Dpartmento d Ingegnera dell Informazone e Metod Matematc B - ESERCIZI: IP e TCP: F. Martgnon Archtetture e Protocoll per Internet Eserczo b. S consder l collegamento n fgura A C =8 kbt/s
Intorduzione alla teoria delle Catene di Markov
 Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Teorema del momento angolare. Momento angolare totale rispetto al polo P che può essere mobile F31 F13 F32. r r r r r F23. r r P1 F21.
 Teoea del oento angolae F F3 3 Moento angolae totale spetto al polo che può essee oble F3 F3 F3 L ( v ) F O d v + dv + [( ) + ( )] (E) (I) v v v F F Teoea del oento angolae (E) v + + v v v F v v p M (
Teoea del oento angolae F F3 3 Moento angolae totale spetto al polo che può essee oble F3 F3 F3 L ( v ) F O d v + dv + [( ) + ( )] (E) (I) v v v F F Teoea del oento angolae (E) v + + v v v F v v p M (
Metodi variazionali. ed agiscono sulla FORMA DEBOLE DEL PROBLEMA
 Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Predimensionamento reti chiuse
 Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. La
Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. La
Predimensionamento reti chiuse
 Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. a dfferenza
Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. a dfferenza
Elementi di Calcolo delle Probabilità
 Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2011/2012 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Facoltà d Economa UnCal Calendao - Lezon: dal
Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2011/2012 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Facoltà d Economa UnCal Calendao - Lezon: dal
PROPRIETÀ DEL CAMPO ELETTROSTATICO (PARTE 2) G. Pugliese 1
 PROPRIETÀ DEL CMPO ELETTROSTTICO (PRTE 2) G. Puglese Campo elettostatco & elettco F 0 E S pala d foza elettostatca uando sa le cache che geneano l campo (elettostatco) che 0 sono fsse e costant Quando
PROPRIETÀ DEL CMPO ELETTROSTTICO (PRTE 2) G. Puglese Campo elettostatco & elettco F 0 E S pala d foza elettostatca uando sa le cache che geneano l campo (elettostatco) che 0 sono fsse e costant Quando
Metodi variazionali. ed agiscono sulla FORMA DEBOLE DEL PROBLEMA
 Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Definizione di mutua induzione
 Mutua nduzone Defnzone d mutua nduzone Una nduttanza poduce un campo magnetco popozonale alla coente che v scoe. Se le lnee d foza d questo campo magnetco ntesecano una seconda nduttanza, n questo d poduce
Mutua nduzone Defnzone d mutua nduzone Una nduttanza poduce un campo magnetco popozonale alla coente che v scoe. Se le lnee d foza d questo campo magnetco ntesecano una seconda nduttanza, n questo d poduce
Soluzione del compito del 5 settembre 2012
 del compto del 5 settembe Ottca geometca Un aggo d luce banca ncde su un psma d veto d angolo d apetua φ 6 con un angolo d ncdena 45. A causa della dspesone della luce, l aggo s sepaa n un pennello d agg
del compto del 5 settembe Ottca geometca Un aggo d luce banca ncde su un psma d veto d angolo d apetua φ 6 con un angolo d ncdena 45. A causa della dspesone della luce, l aggo s sepaa n un pennello d agg
Economia del turismo
 Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2014-2015 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 4 LA DOMANDA
Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2014-2015 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 4 LA DOMANDA
Analisi agli elementi finiti di campi vettoriali
 Anals agl element fnt d camp vettoral Carlo Forestere December, 04 Formulazone n forma debole d equazon d campo vettorale Sa R un domno bdmensonale Fg. rempto da un materale lneare, sotropo, tempo nvarante,
Anals agl element fnt d camp vettoral Carlo Forestere December, 04 Formulazone n forma debole d equazon d campo vettorale Sa R un domno bdmensonale Fg. rempto da un materale lneare, sotropo, tempo nvarante,
Corso di. Gasdinamica II Tommaso Astarita
 Corso d Gasdnamca II Tommaso Astarta astarta@unna.t www.docent.unna.t Gasdnamca II Tommaso Astarta 5.0.008 Metodo d Eulero S supponga d avere una equazone dfferenzale del prmo ordne: f ( x, ) x xo o Defnendo
Corso d Gasdnamca II Tommaso Astarta astarta@unna.t www.docent.unna.t Gasdnamca II Tommaso Astarta 5.0.008 Metodo d Eulero S supponga d avere una equazone dfferenzale del prmo ordne: f ( x, ) x xo o Defnendo
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 2: 21 febbraio 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 2: 21 febbrao 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Defnzone. f : R R s dce addtva se per ogn
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 2: 21 febbrao 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Defnzone. f : R R s dce addtva se per ogn
INTERPOLAZIONE MEDIANTE CURVE SPLINE. '' ( b ) = 0
 INTERPOLAZIONE EDIANTE CURVE SPLINE Defnzone del problema Sovente, nelle applcazon grafche (CAD Computer Aed Desgn), s ha la necesstà d traccare, dat alcun punt, una lnea che l raccord e che sa suffcentemente
INTERPOLAZIONE EDIANTE CURVE SPLINE Defnzone del problema Sovente, nelle applcazon grafche (CAD Computer Aed Desgn), s ha la necesstà d traccare, dat alcun punt, una lnea che l raccord e che sa suffcentemente
La soluzione delle equazioni differenziali con il metodo di Galerkin
 Il metodo de resdu pesat per gl element fnt a soluzone delle equazon dfferenzal con l metodo d Galerkn Tra le procedure generalmente adottate per formulare e rsolvere le equazon dfferenzal con un metodo
Il metodo de resdu pesat per gl element fnt a soluzone delle equazon dfferenzal con l metodo d Galerkn Tra le procedure generalmente adottate per formulare e rsolvere le equazon dfferenzal con un metodo
Magnetostatica e magnetoquasistatica nel vuoto
 Unvestà degl tud d Cassno Magnetostatca e magnetoquasstatca nel vuoto Antono Maffucc, Fabo Vllone Ve. - aple 004 . Le equazon della magnetostatca. Le equazon della magnetostatca sono: H tˆ dl () nˆ d 0
Unvestà degl tud d Cassno Magnetostatca e magnetoquasstatca nel vuoto Antono Maffucc, Fabo Vllone Ve. - aple 004 . Le equazon della magnetostatca. Le equazon della magnetostatca sono: H tˆ dl () nˆ d 0
Integrazione numerica dell equazione del moto per un sistema lineare viscoso a un grado di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
= 4. L unita di misura della carica elettrica nel S.I. è il coulomb (C).
 LGG DI COULOMB (3) L unta d msua della caca elettca nel.i. è l coulomb (C). F π o La caca elettca d C è uella caca che posta nel vuoto ad m d dstanza da una caca elettca uguale la espnge con la foza d
LGG DI COULOMB (3) L unta d msua della caca elettca nel.i. è l coulomb (C). F π o La caca elettca d C è uella caca che posta nel vuoto ad m d dstanza da una caca elettca uguale la espnge con la foza d
Campo magnetico N S N S
 Foze fa calamte. Campo magnetco Alcun fenomen S S S S S S S S S S Ago magnetco: tende ad allneas con l campo magnetco. Momento delle foze le calamte tendono ad allneas... Ago magnetco Magnete d foma sfeca
Foze fa calamte. Campo magnetco Alcun fenomen S S S S S S S S S S Ago magnetco: tende ad allneas con l campo magnetco. Momento delle foze le calamte tendono ad allneas... Ago magnetco Magnete d foma sfeca
Sistemi Intelligenti Reinforcement Learning: Evaluative Feedback
 Sstem Intellgent Renfocement Leanng: Evaluatve Feedbac Albeto Boghese Unvestà degl Stud d Mlano Laboatoo d Sstem Intellgent Applcat (AIS-Lab Dpatmento d Scenze dell Infomazone boghese@ds.unm.t /9 http:\\homes.ds.unm.t\
Sstem Intellgent Renfocement Leanng: Evaluatve Feedbac Albeto Boghese Unvestà degl Stud d Mlano Laboatoo d Sstem Intellgent Applcat (AIS-Lab Dpatmento d Scenze dell Infomazone boghese@ds.unm.t /9 http:\\homes.ds.unm.t\
Momento angolare. Considero il moto di una particella di massa m lungo la traiettoria indicata e calcolo la variazione del suo momento angolare
 Noe fle d:\scuola\cos\coso fsca\eccanca\oento angolae\oento angolae, d'neza e cento d assa.doc eato l 0//00 9.46 Densone fle: 48640 byte laboato l 7//00 alle oe 0.44, salvato l 5//0 7. stapato l 7//00
Noe fle d:\scuola\cos\coso fsca\eccanca\oento angolae\oento angolae, d'neza e cento d assa.doc eato l 0//00 9.46 Densone fle: 48640 byte laboato l 7//00 alle oe 0.44, salvato l 5//0 7. stapato l 7//00
Realizzazione di FSM sincrone. Sommario. Introduzione. Sommario. M. Favalli
 Realzzazone d FSM sncrone M. Favall Engneerng Department n Ferrara Realzzazone d FSM Anals e sntes de sstem dgtal / Introduzone Realzzazone d FSM Anals e sntes de sstem dgtal 2 / Una volta ottenuto l automa
Realzzazone d FSM sncrone M. Favall Engneerng Department n Ferrara Realzzazone d FSM Anals e sntes de sstem dgtal / Introduzone Realzzazone d FSM Anals e sntes de sstem dgtal 2 / Una volta ottenuto l automa
Il Campo Elettrico. = u. Asimmetria fra le cariche: origina un entità presente in tutti i punti dello spazio sperimenta la forza
 ezone : l campo elettco ed l potenzale elettostatco Il Campo lettco F 4πε 4πε u u F esecta su una foza popozonale a: caca esploatce temne vettoale che dpende da e dalla poszone, detto campo elettco podotto
ezone : l campo elettco ed l potenzale elettostatco Il Campo lettco F 4πε 4πε u u F esecta su una foza popozonale a: caca esploatce temne vettoale che dpende da e dalla poszone, detto campo elettco podotto
{ 1, 2,..., n} Elementi di teoria dei giochi. Giovanni Di Bartolomeo Università degli Studi di Teramo
 Element d teora de goch Govann D Bartolomeo Unverstà degl Stud d Teramo 1. Descrzone d un goco Un generco goco, Γ, che s svolge n un unco perodo, può essere descrtto da una Γ= NSP,,. Ess sono: trpla d
Element d teora de goch Govann D Bartolomeo Unverstà degl Stud d Teramo 1. Descrzone d un goco Un generco goco, Γ, che s svolge n un unco perodo, può essere descrtto da una Γ= NSP,,. Ess sono: trpla d
Il campo B è uscente. Fisica Generale per Architettura - G. Cantatore 1
 Lezone 18 - Foza magnetca su fl pecos da coent Abbamo vsto che un campo magnetco esecta una foza sulle cache n movmento: quando queste cache n moto sono confnate all nteno d un conduttoe flfome c aspettamo
Lezone 18 - Foza magnetca su fl pecos da coent Abbamo vsto che un campo magnetco esecta una foza sulle cache n movmento: quando queste cache n moto sono confnate all nteno d un conduttoe flfome c aspettamo
Flussi potenziali, moti irrotazionali
 Captolo 4 Fluss potenzal, mot otazonal Una stuazone asntotca che s vefca fequentemente n poblem fludodnamc, n aeeonautca e meccanca è quella pe Re che dà luogo a fluss Eulean. In tale stuazone s possono
Captolo 4 Fluss potenzal, mot otazonal Una stuazone asntotca che s vefca fequentemente n poblem fludodnamc, n aeeonautca e meccanca è quella pe Re che dà luogo a fluss Eulean. In tale stuazone s possono
Calcolo della derivata nel punto iniziale. Estrapolazione al primo ordine in t/2 e calcolo della derivata. Estrapolazione al secondo ordine in t
 Il meodo d Runge-Kua Rassumendo possamo de che l meodo d Runge- Kua d odne due consse nell esegue una esapolazone del pmo odne da a x(/ nel aluae la deaa x (/ e nell ulzzala pe oenee una sma d x( esaa
Il meodo d Runge-Kua Rassumendo possamo de che l meodo d Runge- Kua d odne due consse nell esegue una esapolazone del pmo odne da a x(/ nel aluae la deaa x (/ e nell ulzzala pe oenee una sma d x( esaa
Le equazionidimaxwell 1873: Trattato sull elettricità e sul magnetismo
 Lezone : quazon d Maxwell, enega e quanttà d moto del campo eletto-magnetco Le equazondmaxwell 873: Tattato sull elettctà e sul magnetsmo álegge d Gauss pe elettctà ρ ε álegge d Gauss pe l magnetsmo álegge
Lezone : quazon d Maxwell, enega e quanttà d moto del campo eletto-magnetco Le equazondmaxwell 873: Tattato sull elettctà e sul magnetsmo álegge d Gauss pe elettctà ρ ε álegge d Gauss pe l magnetsmo álegge
Fig d (2.2.1) MR
 4 CAPITOLO RICHIAMI SUI PRINCIPI FONDAMENTALI DELLA FLUIDODINAMICA ED ACCENNI AI PRINCIPALI METODI DI SOLUIONE IN AMBIENTE NAVALE/OFFSHORE PER IL CALCOLO DEI CARICHI D ONDA IN REGIME DI RADIAIONE/DIFFRAIONE
4 CAPITOLO RICHIAMI SUI PRINCIPI FONDAMENTALI DELLA FLUIDODINAMICA ED ACCENNI AI PRINCIPALI METODI DI SOLUIONE IN AMBIENTE NAVALE/OFFSHORE PER IL CALCOLO DEI CARICHI D ONDA IN REGIME DI RADIAIONE/DIFFRAIONE
Una semplice applicazione del metodo delle caratteristiche: la propagazione di un onda di marea all interno di un canale a sezione rettangolare.
 Una semplce applcazone del metodo delle caratterstche: la propagazone d un onda d marea all nterno d un canale a sezone rettangolare. In generale la propagazone d un onda monodmensonale n una corrente
Una semplce applcazone del metodo delle caratterstche: la propagazone d un onda d marea all nterno d un canale a sezone rettangolare. In generale la propagazone d un onda monodmensonale n una corrente
Metodi di integrazione numerica
 Metod d ntegazone numeca Con patcolae emento agl element sopaametc ove compae anche l Jacobano, non è possble espmee analtcamente temn che compaono nell ntegale d volume dell elemento Occoe qund coee all
Metod d ntegazone numeca Con patcolae emento agl element sopaametc ove compae anche l Jacobano, non è possble espmee analtcamente temn che compaono nell ntegale d volume dell elemento Occoe qund coee all
Università degli Studi di Milano. Facoltà di Scienze Matematiche Fisiche e Naturali
 Unvestà degl Stud d Mlano Facoltà d Scenze Matematche Fsche e Natual Cos d Lauea n: Infomatca ed Infomatca pe le Telecomuncazon Anno accademco /, Lauea Tennale, Edzone duna FISICA Lezone n. 7 ( oe) Ganluca
Unvestà degl Stud d Mlano Facoltà d Scenze Matematche Fsche e Natual Cos d Lauea n: Infomatca ed Infomatca pe le Telecomuncazon Anno accademco /, Lauea Tennale, Edzone duna FISICA Lezone n. 7 ( oe) Ganluca
Sistemi di coordinate curvilinee (1)
 Sstem d coodnate clnee ( Un sstema d coodnate clnee ( nello spao R è defnto con femento ad n sstema catesano da fnon del tpo: con femento ad n sstema catesano da fnon del tpo: ( ( : La fnone ettoale: (
Sstem d coodnate clnee ( Un sstema d coodnate clnee ( nello spao R è defnto con femento ad n sstema catesano da fnon del tpo: con femento ad n sstema catesano da fnon del tpo: ( ( : La fnone ettoale: (
SOLUZIONI PER IL CONTROLLO DEL RISCALDAMENTO GLOBALE
 Confeenza Nazonale su Cambament Clmatc Roma / settembe 7, Palazzo FAO SOLUZIONI PER IL CONROLLO DEL RISCALDAMENO GLOBALE F. Cotana, F. Ross, M. Flppon () () CIRIAF - Cento Inteunvestao d Rceca sull Inqunamento
Confeenza Nazonale su Cambament Clmatc Roma / settembe 7, Palazzo FAO SOLUZIONI PER IL CONROLLO DEL RISCALDAMENO GLOBALE F. Cotana, F. Ross, M. Flppon () () CIRIAF - Cento Inteunvestao d Rceca sull Inqunamento
PROCEDURA INFORMATIZZATA PER LA COMPENSAZIONE DELLE RETI DI LIVELLAZIONE. (Metodo delle Osservazioni Indirette) - 1 -
 PROCEDURA INFORMATIZZATA PER LA COMPENSAZIONE DELLE RETI DI LIVELLAZIONE (Metodo delle Osservazon Indrette) - - SPECIFICHE DI CALCOLO Procedura software per la compensazone d una rete d lvellazone collegata
PROCEDURA INFORMATIZZATA PER LA COMPENSAZIONE DELLE RETI DI LIVELLAZIONE (Metodo delle Osservazon Indrette) - - SPECIFICHE DI CALCOLO Procedura software per la compensazone d una rete d lvellazone collegata
TERMODINAMICA E TERMOFLUIDODINAMICA TRASMISSIONE DEL CALORE PER CONDUZIONE
 EMODINAMICA E EMOFUIDODINAMICA ASMISSIONE DE CAOE PE CONDUZIONE 1 (t) A H ( t ) (x,t) (t) 0 x x e s se w 1 ( x, t ) x ( x, t ) asmssone del caloe pe conduzone Indce 1) Il postulato d Foue pe la conduzone
EMODINAMICA E EMOFUIDODINAMICA ASMISSIONE DE CAOE PE CONDUZIONE 1 (t) A H ( t ) (x,t) (t) 0 x x e s se w 1 ( x, t ) x ( x, t ) asmssone del caloe pe conduzone Indce 1) Il postulato d Foue pe la conduzone
Elementi di Calcolo delle Probabilità
 Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2013/2014 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Dpatmento d Economa, Statstca e Fnanza Unvestà
Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2013/2014 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Dpatmento d Economa, Statstca e Fnanza Unvestà
di una delle versioni del compito di Geometria analitica e algebra lineare del 12 luglio 2013 distanza tra r ed r'. (punti 2 + 3)
 Esempo d soluzone d una delle verson del compto d Geometra analtca e algebra lneare del luglo 3 Stablre se la retta r, d equazon parametrche x =, y = + t, z = t (nel parametro reale t), è + y + z = sghemba
Esempo d soluzone d una delle verson del compto d Geometra analtca e algebra lneare del luglo 3 Stablre se la retta r, d equazon parametrche x =, y = + t, z = t (nel parametro reale t), è + y + z = sghemba
Elementi di Calcolo delle Probabilità
 Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2015/2016 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Dpatmento d Economa, Statstca e Fnanza Unvestà
Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2015/2016 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Dpatmento d Economa, Statstca e Fnanza Unvestà
CAPITOLO I CAMPI ELETTROMAGNETICI RICHIAMI ED APPROFONDIMENTI
 G. Lupò Modellstca elettomagnetca de Mateal 7/8 APITOLO I AMPI ELETTROMAGNETII RIHIAMI ED APPROFONDIMENTI I. Modello geneale dell elettomagnetsmo [ 4] Questo oso s colloca a valle delle fomazone base devante
G. Lupò Modellstca elettomagnetca de Mateal 7/8 APITOLO I AMPI ELETTROMAGNETII RIHIAMI ED APPROFONDIMENTI I. Modello geneale dell elettomagnetsmo [ 4] Questo oso s colloca a valle delle fomazone base devante
COMPARATORI. Comparatore invertente
 COMPAATOI Un cmpaate è un ccut ce a due pssbl val d uscta, medante qual gnala l sultat del cnfnt delle tensn su due ngess amplfcate peaznale ad anell apet csttusce un cmpaate mplce, ce cnfnta un gnale
COMPAATOI Un cmpaate è un ccut ce a due pssbl val d uscta, medante qual gnala l sultat del cnfnt delle tensn su due ngess amplfcate peaznale ad anell apet csttusce un cmpaate mplce, ce cnfnta un gnale
TEORIA ASSIOMATICA DELLA RADIAZIONE
 TEORA AOMATCA DELLA RADAZONE ntoduzone alle antenne ed alla adazone elettomagnetca L appocco assomatco-deduttvo allo studo della popagazone elettomagnetca s basa sulla possbltà d pote ndagae ed analzzae
TEORA AOMATCA DELLA RADAZONE ntoduzone alle antenne ed alla adazone elettomagnetca L appocco assomatco-deduttvo allo studo della popagazone elettomagnetca s basa sulla possbltà d pote ndagae ed analzzae
Verifica reti con più serbatoi (II)
 Verfca ret con pù serbato (I) Condzon al contorno per gl N nod della rete e corrspondent ncognte: Condzone mposta Incognta A) carco pezometrco portata concentrata B) portata concentrata carco pezometrco
Verfca ret con pù serbato (I) Condzon al contorno per gl N nod della rete e corrspondent ncognte: Condzone mposta Incognta A) carco pezometrco portata concentrata B) portata concentrata carco pezometrco
Economia del turismo. Prof.ssa Carla Massidda
 Economa del tusmo Pof.ssa Cala Massdda Pate 2 Agoment Defnzone d domanda tustca Detemnant della domanda tustca L elastctà della domanda tustca La stma della domanda tustca Defnzone d domanda tustca Dato
Economa del tusmo Pof.ssa Cala Massdda Pate 2 Agoment Defnzone d domanda tustca Detemnant della domanda tustca L elastctà della domanda tustca La stma della domanda tustca Defnzone d domanda tustca Dato
Descrizione del modello matematico
 Captolo 2 escone del modello matematco n questo captolo svluppeemo un modello matematco pe l poblema d mnmaone de cost d taspoto. Quest cost appesentano un fattoe mpotante nelle opeaon foestal n quanto,
Captolo 2 escone del modello matematco n questo captolo svluppeemo un modello matematco pe l poblema d mnmaone de cost d taspoto. Quest cost appesentano un fattoe mpotante nelle opeaon foestal n quanto,
6. Catene di Markov a tempo continuo (CMTC)
 6. Catene d Markov a tempo contnuo (CMTC) Carla Seatzu, 8 Marzo 28 Defnzone Una CMTC è un processo stocastco defnto come segue: lo spazo d stato è dscreto: X{x,x 2, }. L nseme X può essere sa fnto sa nfnto
6. Catene d Markov a tempo contnuo (CMTC) Carla Seatzu, 8 Marzo 28 Defnzone Una CMTC è un processo stocastco defnto come segue: lo spazo d stato è dscreto: X{x,x 2, }. L nseme X può essere sa fnto sa nfnto
Robotica industriale. Quantità meccaniche. Prof. Paolo Rocco
 Robotca ndustale Quanttà eccanche Pof. Paolo Rocco (aolo.occo@ol.t) Cento d assa Consdeao un sstea d unt ateal, cascuno de qual abba assa e la cu osone sa desctta dal vettoe setto ad una tena. Defnao cento
Robotca ndustale Quanttà eccanche Pof. Paolo Rocco (aolo.occo@ol.t) Cento d assa Consdeao un sstea d unt ateal, cascuno de qual abba assa e la cu osone sa desctta dal vettoe setto ad una tena. Defnao cento
7. Proprietà dei circuiti lineari adinamici
 A. Moand, Unestà d Bolona Elettotecnca T-A, A.A. 6/7 7. Popetà de ccut lnea adnamc Foma matcale del sstema solente d un ccuto lneae. Ccuto nete. Coeffcent d ete. ecpoctà de ccut lnea. Popetà d soapposzone.
A. Moand, Unestà d Bolona Elettotecnca T-A, A.A. 6/7 7. Popetà de ccut lnea adnamc Foma matcale del sstema solente d un ccuto lneae. Ccuto nete. Coeffcent d ete. ecpoctà de ccut lnea. Popetà d soapposzone.
Elementi di Geometria delle Masse
 Eleent eoeta elle Masse BCENTO S conse un sstea costtuto a N punt ateal,... N otat assa,... N, soggett alla foa peso F, F,... F N. Cascun punto è soggetto a una foa etta veso l basso e con popoonale alla
Eleent eoeta elle Masse BCENTO S conse un sstea costtuto a N punt ateal,... N otat assa,... N, soggett alla foa peso F, F,... F N. Cascun punto è soggetto a una foa etta veso l basso e con popoonale alla
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa lezione 16: 2 maggio 2012
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 16: 2 maggo 2012 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? CCT/CCTEu S tratta d un ttolo a cedola varable:
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 16: 2 maggo 2012 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? CCT/CCTEu S tratta d un ttolo a cedola varable:
Il campo magnetico prodotto da correnti continue
 Leone 6: l campo magnetco podotto da coent contnue l potenale vettoe l campo magnetco podotto da coent contnue Ossevaon spemental: á Osted: coent elettche danno luogo a camp magnetc; á Legge d ot-savat:
Leone 6: l campo magnetco podotto da coent contnue l potenale vettoe l campo magnetco podotto da coent contnue Ossevaon spemental: á Osted: coent elettche danno luogo a camp magnetc; á Legge d ot-savat:
Una rendita è una somma di capitali pagabili (o esigibili) a determinate scadenze, fissate secondo intervalli regolari di tempo.
 14. Le endte 14.1 Nozon geneal Una endta è una somma d captal pagabl (o esgbl) a detemnate scadenze, fssate secondo ntevall egola d tempo. Ognuno d quest captal è detto ata; gl ntevall sono dett peod e
14. Le endte 14.1 Nozon geneal Una endta è una somma d captal pagabl (o esgbl) a detemnate scadenze, fssate secondo ntevall egola d tempo. Ognuno d quest captal è detto ata; gl ntevall sono dett peod e
Analisi Modale. Le evoluzioni libere dei due sistemi a partire dalla condizione iniziale x(0) = x 0 sono
 Captolo 1 INTRODUZIONE 21 Anals Modale S facca rfermento al sstema tempo-dscreto e al sstema tempo-contnuo x(k +1)=Ax(k) ẋ(t) =Ax(t) Le evoluzon lbere de due sstem a partre dalla condzone nzale x() = x
Captolo 1 INTRODUZIONE 21 Anals Modale S facca rfermento al sstema tempo-dscreto e al sstema tempo-contnuo x(k +1)=Ax(k) ẋ(t) =Ax(t) Le evoluzon lbere de due sstem a partre dalla condzone nzale x() = x
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 2: 18 febbraio 2014
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 2: 18 febbrao 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? Defnzone. f : R R s dce moltplcatva se per
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 2: 18 febbrao 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? Defnzone. f : R R s dce moltplcatva se per
