METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 7 FEBBRAIO 2017
|
|
|
- Ottavio Lombardi
- 5 anni fa
- Visualizzazioni
Transcript
1 METODI MATEMATICI PER LA FIICA PROVA CRITTA - 7 FEBBRAIO 7 i risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 6/3) i calcoli l integrale V = L z dz L = {z : z ( )} {z : Re(z) = Im(z) ( )} z + ovvero L è l unione dei semiassi reale e immaginario positivi entrambi percorsi dall origine all infinito OLUZIONE DEL PRIMO PROBLEMA L integrale può scritto come la somma dei due contributi V = x x + d x + i y (i y) + id y L + L con z = x + i y I due integrali sono proporzionali infatti con i = e iπ/ si ha i y y L = id y = (i y) e3iπ/4 + y + d y = e3iπ/4 L quindi per l integrale completo si ottiene l espressione V = + e 3iπ/4 L D altro canto l integrale L può essere calcolato sfruttando il teorema de residui sul percorso chiuso Γ R rappresentato dalla frontiera del quarto di cerchio centrato nell origine di raggio R e appartenente al primo quadrante ovvero Γ R = {z : z ( R)} {z : z = R arg(z) ( π/)} ( {z : Re(z) = Im(z) ( R)}) u tale percorso nel limite R si ha lim R Γ R z z + dz = L L = e 3iπ/4 L = arg(z ) (π/) z Res z + z da cui si ottiene L in termini della somma dei residui dei poli che l integranda ha nel primo quadrante z L = Res e 3iπ/4 z + z L integranda ha poli semplici nei punti arg(z ) (π/) z = e iπ(+)/ = 7 All interno di Γ R R > cadono i primi due: z = e iπ/ e z = e 3iπ/ i residui corrispondenti sono Ne consegue che R = Res L = e 3iπ/4 z z + z Res = z/ z 7 z z + z = z 3/ = z + Res z + z e 3iπ/6 e 39iπ/6 = z = z z = z e 3iπ/6 + e 39iπ/6 e 3iπ/4 = e3iπ/6 + e 3iπ/6 iπ cos(3π/6) e 3iπ/4 e 6iπ/6 = e 3iπ/ e3iπ/4 7 febbraio 7 page of 7
2 Usando questa espressione per L si ottiene l integrale cercato V = + e 3iπ/4 L = iπe 3iπ/ infine riassorbendo il segno meno nell esponenziale + e 3iπ/4 πe 3iπ/ cos(3π/6) = cot(3π/) cos(3π/6) e3iπ/4 V = πe 5iπ/ cot(3π/) cos(3π/6) ECONDO PROBLEMA (PUNTEGGIO 6/3) i calcoli l integrale T = Re(z) z 3 dz dove è il percorso chiuso mostrato in figura Im(z) 3 4 Re(z) OLUZIONE DEL ECONDO PROBLEMA Il percorso di integrazione è l unione di quattro archi A e quattro tratti rettilinei L = 3 4 con A = {z : z = e iθ θ [ 3π/]} L = {z : z [ 4]} A = {z : z = e iθ θ [π/ 3π/]} L = {z : Re(z) = Im(z) [ ]} A 3 = {z : z = 3e iθ θ [π/ 3π/]} L 3 = {z : Re(z) = Im(z) [ 3]} A 4 = {z : z = 4e iθ θ [ 3π/]} L 4 = {z : Re(z) = Im(z) [ 4 3]} in particolare si ha = 4 =( ) A 4 = L dove il segno variabile ( ) indica che gli archi sono percorsi alternativamente in senso orario e antiorario mentre dei tratti rettilinei solo L 3 è percorso in senso inverso e il corrispondente segno meno è incluso nella definizione L integrale può essere scritto come segue T = z + z z 3 dz = z z 3 dz = 4 ( ) = A z dz + 3 z dz L 3 la seconda identità di ha in quanto l integranda ha una sola singolarità polare nell origine che non è contenuta nel percorso chiuso Calcoliamo gli integrali sugli archi facendo la sostituzione z = r e iθ con i raggi r = 7 febbraio 7 page of 7
3 = 3 4 A θ z dz = 3 θ L ( + i)/3 = r i/3 = idθ = e3iθ i/9 = 3 ( + i)/ = 4 r 3 Gli integrali sui tratti rettilinei si calcolano usando invece la rappresentazione cartesiana z = x + i y 4 z dz = d x 3 x = 3 4 L L 3 L 4 z 3 dz = dz = i z3 z 3 dz = i i y i y 3 id y = i d y y = i 6 d y y = i d y y = i L integrale cercato è quindi la somma degli contributi e vale T = + i 3 + i 3 i i i i 6 + i = i TERZO PROBLEMA (PUNTEGGIO 6/3) La funzione meromorfa f (z) che ha solo poli semplici ammette lo sviluppo di Mittag-Leffler A () f (z) = f + z z dove f è una costante e {z } è l insieme dei poli semplici i dimostri che la funzione g(z) = f (z) ha sviluppo di Mittag-Leffler con g = f R() = A () OLUZIONE DEL TERZO PROBLEMA () R g(z) = g + (z z ) + R () z z R () = A() f + m = A (m) z z m I poli della funzione f (z) e quindi della funzione g(z) sono isolati ne consegue che in un opportuno intorno U del generico z si ha f (z) = φ (z) z z dove la funzione φ (z) è analitica e non nulla z U Il -esimo residuo coincide con il valore della funzione φ (z) in z = z ovvero A () = φ (z ) Per la funzione g(z) avremo g(z) = φ (z) (z z ) quindi g(z) ha solo poli doppi nei punti in cui la f (z) ha i poli semplici Lo sviluppo di Mittag-Leffler ha la forma () R g(z) = g + (z z ) + R () z z 7 febbraio 7 page 3 of 7
4 Il valore costante g si ottiene considerando il limite g = lim g(p j ) = lim f (p j ) = lim f + A () p j z = f + f A () lim + lim p j z A () p j z = f dove la successione {p j } j= si accumula all infinito p j e ha intersezione vuota con l insieme dei poli {p j } j= {z } = I valori dei coefficienti di Laurent delle parti principali si ottengono con la formula integrale R () j = γ g(z) dz j = (z z ) j+ dove γ è una circonferenza che avvolge solo il -esimo polo z Con j = si ha R () = g(z)(z z )dz γ = A (m) f + (z z )dz z z γ m m = f + f A (m) A (m) A (n) + (z z )dz z z m m (z z mn m )(z z n ) γ gli unici integrali diversi da zero sono quelli che contengono il polo semplice /(z z ) tutti gli altri poli non contribuiscono non essendo inclusi in γ Il primo termine in f è nullo così come la prima somma infatti il polo /(z z ) per m = è cancellato dal fattore (z z ) Dalla seconda (doppia) somma si ha un solo contributo non nullo quello contenente il polo doppio /(z z ) per m = n = che diventa singolo a causa del fattore (z z ) In definitiva per R () si ha il valore cercato R () = A (m) A (n) (z z γ mn m )(z z n ) (z z )dz = A () Il coefficiente R () ovvero il residuo è R () = g(z)dz γ = = γ γ f + m f + f A (m) z z m m dz A (m) A (m) A (n) + dz z z m (z z mn m )(z z n ) con le stesse considerazioni del caso precedente si ha contributo non nullo dal termine con m = della prima somma e da quelli con m = o n = della seconda Il termine con m = n = dà invece contributo nullo Ne consegue che anche per R () si ottiene il valore cercato R () = A () f + A () A (m) dz = A () A (m) f + z z γ (z z m = m )(z z ) (z m = z m ) 7 febbraio 7 page 4 of 7
5 QUARTO PROBLEMA (PUNTEGGIO 6/3) Dopo aver verificato che la matrice A = non è diagonalizzabile si ottengano gli autovalori e gli autovettori Infine si calcoli la matrice B = sen (A) OLUZIONE DEL QUARTO PROBLEMA Gli autovalori sono le soluzione dell equazione secolare in a a det a = a ( a) 3 = si ha quindi massima degenerazione: a = a = a 3 = Gli autovettori sono x x x y = y = y z y + z z da cui si ha la sola condizione y = cegliamo la terna u = u = u 3 = La matrice non è diagonalizzabile poiché non ammette un insieme di autovettori linearmente indipendenti come diretta conseguenza dell annullamento della seconda componente Infatti la molteplicità geometrica ovvero la dimensione dello spazio vettoriale generato dagli autovettori è pari a ed è strettamente minore della molteplicità algebrica che è invece pari a 3 (il grado dell equazione secolare) Per calcolare la funzione seno della matrice A non possiamo usare il teorema spettrale non essendo A diagonalizzabile usiamo direttamente lo sviluppo in serie di Taylor Le potenze dispari di A sono: A 3 = A 5 = A 3 A = A 7 = A 5 A = = A + = 3 5 sen(x) = ( ) x + ( + )! = = = = = = 3 7 febbraio 7 page 5 of 7
6 Ne consegue che B = sen(a) = ( ) A + ( + )! = = B = = ( ) (+)! ( ) sen() sen() cos() sen() = (+)! ( ) = ()! = ( ) (+)! QUINTO PROBLEMA (PUNTEGGIO 6/3) i determini la matrice C che verifica l identità OLUZIONE DEL QUINTO PROBLEMA ln(c) = Diagonalizziamo la matrice hermitiana ln(c) Gli autovalori si ottengono come soluzioni dell equazione secolare c det c = ( c) 3 + c = c e sono c = c = c 3 = c(c )(c ) = Gli autovettori u = u = u 3 = sono ortogonali poiché gli autovalori sono diversi non c è degenerazione e la matrice è hermitiana Usando la matrice unitaria diagonalizzante diagonalizziamo l equazione iniziale come U = / / / / diag(c c c 3 ) = U ln(c)u = ln(c d ) = diag(ln(l ) ln(l ) ln(l 3 )) dove C d è la rappresentazione diagonale di C ovvero C d = diag(l l l 3 ) = U CU Ne consegue che l = e c = 3 e quindi C d = e e 7 febbraio 7 page 6 of 7
7 La rappresentazione della matrice C rispetto alla base canonica si ottiene invertendo la trasformazione unitaria / / / / C = UC d U = / / e e / / da cui C = ( + e )/ ( e )/ e ( e )/ ( + e )/ ETO PROBLEMA (PUNTEGGIO 6/3) i risolva l equazione differenziale usando il metodo della trasformata di Fourier OLUZIONE DEL ETO PROBLEMA u (x) α u(x) = δ (x + β) α β > Facendo la trasformata di Fourier di ambo i membri si ottiene α ũ() = π δ (x + β)e ix d x = da cui si ricava la trasformata di Fourier della soluzione δ(x + β)e ix π ũ() = i e iβ π + α + i δ(x + β)e ix d x = i e iβ π π La soluzione è l anti-trasformata di Fourier di ũ() u(x) = i π π e iβ + α eix d = e i(x+β) + α d = e α(x+β) eα(x+β) x + β > x + β < È Facile verificare che per x + β = la funzione trovata è soluzione dell equazione (omogenea) infatti d d x α u(x) = La verifica completa può essere fatta considerando la rappresentazione integrale di Fourier della soluzione ovvero u(x) = e i(x+β) + α d Applicando l operatore differenziale d d x α in definitiva u(x) = d d x α si ottiene l identità cercata infatti ( α )e i(x+β) d = e i(x+β) d = d e i(x+β) d = d δ(x + β) + α d x π d x d d x α u(x) = δ (x + β) 7 febbraio 7 page 7 of 7
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - SETTEMBRE 6 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: 6/3) Si calcoli l integrale in valore principale P = Pr x sen(x) x
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - SETTEMBRE 6 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: 6/3) Si calcoli l integrale in valore principale P = Pr x sen(x) x
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 4 LUGLIO 7 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati:. la correttezza del risultato ottenuto e della procedura utilizzata;.
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 4 LUGLIO 7 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati:. la correttezza del risultato ottenuto e della procedura utilizzata;.
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 19 SETTEMBRE 2018
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 9 SETTEMBRE 8 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati:. la correttezza del risultato ottenuto e della procedura utilizzata;.
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 9 SETTEMBRE 8 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati:. la correttezza del risultato ottenuto e della procedura utilizzata;.
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 4 DICEMBRE 2018
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 4 DICEMBRE 18 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: 1 la correttezza del risultato ottenuto e della procedura utilizzata;
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 4 DICEMBRE 18 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: 1 la correttezza del risultato ottenuto e della procedura utilizzata;
METODI MATEMATICI PER LA FISICA
 Si svolgano cortesemente i seguenti esercizi. ESERCIZIO (6 PUNTI) Si calcoli l integrale con m, n ed L {z : Im(z) l > 0}. SOLUZIONE METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 26 FEBBRAIO 204 J L (z
Si svolgano cortesemente i seguenti esercizi. ESERCIZIO (6 PUNTI) Si calcoli l integrale con m, n ed L {z : Im(z) l > 0}. SOLUZIONE METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 26 FEBBRAIO 204 J L (z
Metodi Matematici per la Fisica
 Si svolgano cortesemente i seguenti esercizi Esercizio (6 punti) Si calcoli l integrale Metodi Matematici per la Fisica Prova scritta - dicembre 03 I = sen (x) cosh 3 (x) Possiamo riscrivere l integrale
Si svolgano cortesemente i seguenti esercizi Esercizio (6 punti) Si calcoli l integrale Metodi Matematici per la Fisica Prova scritta - dicembre 03 I = sen (x) cosh 3 (x) Possiamo riscrivere l integrale
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 7 DICEMBRE 6 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 6/3) Si stabilisca per quali valori di α l integrale M(α) = converge
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 7 DICEMBRE 6 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 6/3) Si stabilisca per quali valori di α l integrale M(α) = converge
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 24 FEBBRAIO 215 Si svolgano cortesemente i seguenti esercizi. ESERCIZIO 1 (PUNTEGGIO: 6/3) Si calcoli l integrale Im(z) K= cos(x) x d x. Suggerimento: Si
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 24 FEBBRAIO 215 Si svolgano cortesemente i seguenti esercizi. ESERCIZIO 1 (PUNTEGGIO: 6/3) Si calcoli l integrale Im(z) K= cos(x) x d x. Suggerimento: Si
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 6 GIUGNO 7 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 3/3) Facendo uso delle proprietà della matrici di Pauli, si calcoli
METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 6 GIUGNO 7 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 3/3) Facendo uso delle proprietà della matrici di Pauli, si calcoli
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 20 FEBBRAIO 2018
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - FEBBRAIO 8 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati:. la correttezza del risultato ottenuto e della procedura utilizzata;.
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - FEBBRAIO 8 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati:. la correttezza del risultato ottenuto e della procedura utilizzata;.
METODI MATEMATICI PER LA FISICA
 MEODI MAEMAICI PER LA FISICA PROVA SCRIA - 6 SEEMBRE 6 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNEGGIO: 6/3) Si calcoli l integrale S arccos() + 3 Suggerimento È utile iniziare con
MEODI MAEMAICI PER LA FISICA PROVA SCRIA - 6 SEEMBRE 6 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNEGGIO: 6/3) Si calcoli l integrale S arccos() + 3 Suggerimento È utile iniziare con
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 FEBBRAIO 6 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: 6/3) Si calcoli l integrale SOLUZIONE DEL PRIMO PROBLEMA M=. (+ x
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 FEBBRAIO 6 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: 6/3) Si calcoli l integrale SOLUZIONE DEL PRIMO PROBLEMA M=. (+ x
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 5 GIUGNO 6 Si svolgano cortesemente i seguenti Problemi. PRIMO PROBLEMA (PUNTEGGIO: 3/3) Dati due operatori hermitiani  and ˆB in uno spazio di Hilbert
METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 5 GIUGNO 6 Si svolgano cortesemente i seguenti Problemi. PRIMO PROBLEMA (PUNTEGGIO: 3/3) Dati due operatori hermitiani  and ˆB in uno spazio di Hilbert
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 LUGLIO 08 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: la correttezza del risultato ottenuto e della procedura utilizzata;
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 LUGLIO 08 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: la correttezza del risultato ottenuto e della procedura utilizzata;
Metodi Matematici per la Fisica
 Si svolgano cortesemente i seguenti esercizi Esercizio (6 punti) Calcolare l integrale in valore principale I Pr Metodi Matematici per la Fisica Prova scritta - 6 gennaio 03 γ dz ( + z ) sen (z), con γ
Si svolgano cortesemente i seguenti esercizi Esercizio (6 punti) Calcolare l integrale in valore principale I Pr Metodi Matematici per la Fisica Prova scritta - 6 gennaio 03 γ dz ( + z ) sen (z), con γ
METODI MATEMATICI PER LA FISICA
 Si svolgano cortesemente i seguenti esercizi. ESERCIZIO (5 PUNTI) METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 LUGLIO 4 Sia f (z) una funzione analitica nel dominio D = {z : z (, ), > }, con f (z),
Si svolgano cortesemente i seguenti esercizi. ESERCIZIO (5 PUNTI) METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 LUGLIO 4 Sia f (z) una funzione analitica nel dominio D = {z : z (, ), > }, con f (z),
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 20 FEBBRAIO 2019
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - FEBBRAIO 9 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: la correttezza del risultato ottenuto e della procedura utilizzata;
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - FEBBRAIO 9 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: la correttezza del risultato ottenuto e della procedura utilizzata;
Metodi Matematici per la Fisica
 Metodi Matematici per la Fisica Prova scritta - giugno 0 Esercizio 8 punti) Si consideri la funzione fz) = z sinz) sin[sinz)], si studino e classifichino le singolarità e, di conseguenza, si stabilisca
Metodi Matematici per la Fisica Prova scritta - giugno 0 Esercizio 8 punti) Si consideri la funzione fz) = z sinz) sin[sinz)], si studino e classifichino le singolarità e, di conseguenza, si stabilisca
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PRIMO ESONERO - 26 FEBBRAIO 206 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: /0) Si ottenga il valore dell integrale N= z = z 2 + senh(/z) dz.
METODI MATEMATICI PER LA FISICA PRIMO ESONERO - 26 FEBBRAIO 206 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: /0) Si ottenga il valore dell integrale N= z = z 2 + senh(/z) dz.
Metodi Matematici per la Fisica
 Metodi Matematici per la Fisica Prova scritta - 6 settembre Esercizio 6 punti Calcolare l integrale π dx I π + 4 cos x. Con la sostituzione z e ix quindi: x i lnz e dx idz/z l integrale diventa dz/z I
Metodi Matematici per la Fisica Prova scritta - 6 settembre Esercizio 6 punti Calcolare l integrale π dx I π + 4 cos x. Con la sostituzione z e ix quindi: x i lnz e dx idz/z l integrale diventa dz/z I
METODI MATEMATICI PER LA FISICA
 Si svolgano cortesemente i seguenti esercii. METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 30 APRILE 05 ESERCIZIO (PUNTEGGIO: 4/30) Si studi il comportamento dell integrale in valore principale al variare
Si svolgano cortesemente i seguenti esercii. METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 30 APRILE 05 ESERCIZIO (PUNTEGGIO: 4/30) Si studi il comportamento dell integrale in valore principale al variare
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - LUGLIO 9 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: la correttea del risultato ottenuto e della procedura utiliata; la
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - LUGLIO 9 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: la correttea del risultato ottenuto e della procedura utiliata; la
METODI MATEMATICI PER LA FISICA
 Si svolgano cortesemente i seguenti esercizi ESERCIZIO (6 PUNTI) METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 4 SETTEMBRE 4 Si calcoli l integrale S = Γ Re(z) z 4 + z, con Γ = {z : z = Re iθ, θ [, π]}
Si svolgano cortesemente i seguenti esercizi ESERCIZIO (6 PUNTI) METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 4 SETTEMBRE 4 Si calcoli l integrale S = Γ Re(z) z 4 + z, con Γ = {z : z = Re iθ, θ [, π]}
Metodi Matematici per la Fisica
 Si svolgano cortesemente i seguenti esercizi. Metodi Matematici per la Fisica Prova scritta - 6 febbraio 3 Esercizio 6 punti Si calcoli l integrale con a e b reali e < a < b. I a x b x + dx, Riscriviamo
Si svolgano cortesemente i seguenti esercizi. Metodi Matematici per la Fisica Prova scritta - 6 febbraio 3 Esercizio 6 punti Si calcoli l integrale con a e b reali e < a < b. I a x b x + dx, Riscriviamo
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 9 APRILE 7 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: la correttezza del risultato ottenuto e della procedura utilizzata;
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 9 APRILE 7 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: la correttezza del risultato ottenuto e della procedura utilizzata;
METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2
![METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2 METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2](/thumbs/96/130608003.jpg) METODI MATEMATICI PER L INGEGNERIA - A.A. 29- Primo appello del 9/6/2 Risolvere i seguenti esercizi, spiegando il procedimento usato. Calcolare la proiezione in L 2 π 2, π 2 di xt = t sul sottospazio generato
METODI MATEMATICI PER L INGEGNERIA - A.A. 29- Primo appello del 9/6/2 Risolvere i seguenti esercizi, spiegando il procedimento usato. Calcolare la proiezione in L 2 π 2, π 2 di xt = t sul sottospazio generato
Metodi Matematici per la Fisica
 Metodi Matematici per la Fisica Prova scritta - 6 ottobre 0 Esercizio (6 punti Si usi il metodo dei residui per calcolare l integrale J (z + sin 3 (/z, z con il cammino d integrazione percorso in senso
Metodi Matematici per la Fisica Prova scritta - 6 ottobre 0 Esercizio (6 punti Si usi il metodo dei residui per calcolare l integrale J (z + sin 3 (/z, z con il cammino d integrazione percorso in senso
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - GENNAIO 7 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 7/) Si calcoli l integrale J Suggerimento: Si faccia attenzione al residuo
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - GENNAIO 7 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 7/) Si calcoli l integrale J Suggerimento: Si faccia attenzione al residuo
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 18 GENNAIO 2019
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 8 GENNAIO 09 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: la correttea del risultato ottenuto e della procedura utiliata;
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 8 GENNAIO 09 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: la correttea del risultato ottenuto e della procedura utiliata;
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - FEBBRAIO 06 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: 6/0) Si calcoli l integrale SOLUZIONE DEL PRIMO PROBLEMA Q = cosh (ln
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - FEBBRAIO 06 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: 6/0) Si calcoli l integrale SOLUZIONE DEL PRIMO PROBLEMA Q = cosh (ln
Metodi Matematici per la Fisica
 Metodi Matematici per la Fisica Prova scritta - 7 febbraio Eserciio (6 punti) Calcolare il valore principale di Cauchy dell integrale con a e b reali e a, b >. J = P.V. Soluione L integrale può essere
Metodi Matematici per la Fisica Prova scritta - 7 febbraio Eserciio (6 punti) Calcolare il valore principale di Cauchy dell integrale con a e b reali e a, b >. J = P.V. Soluione L integrale può essere
METODI MATEMATICI DELLA FISICA A.A. 2006/2007 Prof. C. Presilla. Prova finale 29 marzo 2007
 METODI MATEMATICI DELLA FISICA A.A. 006/007 Prof. C. Presilla Prova finale 9 marzo 007 Cognome Nome in sostituzione delle prove in itinere segnare penalità esercizio voto 3 4 5 6 Esercizio Siano a, b,
METODI MATEMATICI DELLA FISICA A.A. 006/007 Prof. C. Presilla Prova finale 9 marzo 007 Cognome Nome in sostituzione delle prove in itinere segnare penalità esercizio voto 3 4 5 6 Esercizio Siano a, b,
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - LUGLIO 7 Si risolvano cortesemente i seguenti problemi sapendo che verranno valutati:. la correttezza del risultato ottenuto e della procedura utilizzata;.
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - LUGLIO 7 Si risolvano cortesemente i seguenti problemi sapendo che verranno valutati:. la correttezza del risultato ottenuto e della procedura utilizzata;.
Soluzione. (a) L insieme F 1 e linearmente indipendente; gli insiemi F 2 ed F 3 sono linearmente
 1. Insiemi di generatori, lineare indipendenza, basi, dimensione. Consideriamo nello spazio vettoriale R 3 i seguenti vettori: v 1 = (0, 1, ), v = (1, 1, 1), v 3 = (, 1, 0), v 4 = (3, 3, ). Siano poi F
1. Insiemi di generatori, lineare indipendenza, basi, dimensione. Consideriamo nello spazio vettoriale R 3 i seguenti vettori: v 1 = (0, 1, ), v = (1, 1, 1), v 3 = (, 1, 0), v 4 = (3, 3, ). Siano poi F
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Teorema dei residui: applicazioni
 Teorema dei residui: applicazioni Docente:Alessandra Cutrì ichiamo: Teorema dei residui Teorema dei esidui:sia f H(A \ {z, z 2,... z N }), z, z 2,... z N singolarità isolate per f e sia γ una curva chiusa,
Teorema dei residui: applicazioni Docente:Alessandra Cutrì ichiamo: Teorema dei residui Teorema dei esidui:sia f H(A \ {z, z 2,... z N }), z, z 2,... z N singolarità isolate per f e sia γ una curva chiusa,
Modelli e Metodi Matematici della Fisica. S1/AC
 Modelli e Metodi Matematici della Fisica. S/AC Filippo Cesi 2 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 2 CFU (AA 2-) 6 CFU (solo anal. funzionale) 6 CFU (solo anal. complessa)
Modelli e Metodi Matematici della Fisica. S/AC Filippo Cesi 2 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 2 CFU (AA 2-) 6 CFU (solo anal. funzionale) 6 CFU (solo anal. complessa)
Corso di Laurea in Matematica, A.A. 2013/2014 Analisi Reale e Complessa, Esame del y 2 x2 + y 2 2 R 2 ; 1 }
 NOME:................. MATRICOLA:................. Corso di Laurea in Matematica, A.A. 3/ Analisi Reale e Complessa, Esame del 8..5 Si stabilisca se la formula x + y α se f(x, y x + y x + y, x + y se x
NOME:................. MATRICOLA:................. Corso di Laurea in Matematica, A.A. 3/ Analisi Reale e Complessa, Esame del 8..5 Si stabilisca se la formula x + y α se f(x, y x + y x + y, x + y se x
MODELLI e METODI MATEMATICI della FISICA. Esercizi - A.A
 MODELLI e METODI MATEMATICI della FISICA Esercizi - A.A. 08-9 settimana Esercizi:. Risolvere il problema di Cauchy y (x) = αy (x) + y (x) y (x) = αy (x) + y 3 (x) y 3(x) = αy 3 (x) con condizioni iniziali
MODELLI e METODI MATEMATICI della FISICA Esercizi - A.A. 08-9 settimana Esercizi:. Risolvere il problema di Cauchy y (x) = αy (x) + y (x) y (x) = αy (x) + y 3 (x) y 3(x) = αy 3 (x) con condizioni iniziali
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 2016/2017 Prof. C. Presilla. Prova A1 27 aprile 2017
 MODELLI E METODI MATEMATICI DELLA FISICA A.A. 206/207 Prof. C. Presilla Prova A 27 aprile 207 Cognome Nome Matricola iscritto al secondo anno iscritto al terzo anno fuoricorso o con più di 55 CFU penalità
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 206/207 Prof. C. Presilla Prova A 27 aprile 207 Cognome Nome Matricola iscritto al secondo anno iscritto al terzo anno fuoricorso o con più di 55 CFU penalità
NOME:... MATRICOLA:... Corso di Laurea in Matematica, A.A. 2012/2013 Analisi Reale e Complessa, Test del dx x 1/3 (x 4 + 5x 2 + 4).
 NOME:... MATRICOLA:.... Corso di Laurea in Matematica, A.A. 202/203 Analisi Reale e Complessa, Test del 4.0.203 ) Calcolare l integrale improprio x /3 (x 4 + 5x 2 + 4). 0 Suggerimento: estendere la funzione
NOME:... MATRICOLA:.... Corso di Laurea in Matematica, A.A. 202/203 Analisi Reale e Complessa, Test del 4.0.203 ) Calcolare l integrale improprio x /3 (x 4 + 5x 2 + 4). 0 Suggerimento: estendere la funzione
Appello Straordinario AC
 Appello Straordinario AC 2016-2017 Esercizio I Si consideri la seguente funzione f(z) f(z) = 1 (e z 1) sin(z). 1. Si determini la natura della singolarità di f in z = 0. 2. Nel caso si tratti di una singolarità
Appello Straordinario AC 2016-2017 Esercizio I Si consideri la seguente funzione f(z) f(z) = 1 (e z 1) sin(z). 1. Si determini la natura della singolarità di f in z = 0. 2. Nel caso si tratti di una singolarità
ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 22 gennaio Soluzioni compito 1
 ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del gennaio 6 - Soluzioni compito E Determinare l insieme di definizione e di olomorfia della funzione ( ) f(z)
ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del gennaio 6 - Soluzioni compito E Determinare l insieme di definizione e di olomorfia della funzione ( ) f(z)
MODELLI e METODI MATEMATICI della FISICA. Programma dettagliato del corso - A.A
 MODELLI e METODI MATEMATICI della FISICA Programma dettagliato del corso - A.A. 2017-18 Lezione 1, 28 febbraio 2018: Introduzione ai numeri complessi. Rappresentazione cartesiana e polare. Radice n-esima
MODELLI e METODI MATEMATICI della FISICA Programma dettagliato del corso - A.A. 2017-18 Lezione 1, 28 febbraio 2018: Introduzione ai numeri complessi. Rappresentazione cartesiana e polare. Radice n-esima
METODI MATEMATICI DELLA FISICA A.A. 2004/2005 Prof. C. Presilla. Prova di recupero 14 settembre 2005
 METODI MATEMATICI DELLA FISICA A.A. 2004/2005 Prof. C. Presilla Prova di recupero 4 settembre 2005 Cognome Nome Corso di Laurea in sostituzione delle prove in itinere segnare) 2 3 penalità esercizio voto
METODI MATEMATICI DELLA FISICA A.A. 2004/2005 Prof. C. Presilla Prova di recupero 4 settembre 2005 Cognome Nome Corso di Laurea in sostituzione delle prove in itinere segnare) 2 3 penalità esercizio voto
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 2008/2009 Prof. F. Cesi e C. Presilla. Prova Finale 2 Febbraio 2010
 MODELLI E METODI MATEMATICI DELLA FISICA A.A. 8/9 Prof. F. Cesi e C. Presilla Prova Finale Febbraio 1 Cognome Nome Canale Cesi (Astrofisica) Presilla (Fisica) intendo MANTENEE il voto degli esoneri 1 penalità
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 8/9 Prof. F. Cesi e C. Presilla Prova Finale Febbraio 1 Cognome Nome Canale Cesi (Astrofisica) Presilla (Fisica) intendo MANTENEE il voto degli esoneri 1 penalità
MATEMATICA II (Durante) Aversa, Marzo 2001., B = , e D = Si calcoli il rango delle matrici A, B, C, D.
 MATEMATICA II (Durante) Aversa, Marzo 2001. COGNOME........................ NOME............... MATRICOLA............ 1. Dati i tre vettori u, v e w di R 3, si dica se essi sono linearmente dipendenti
MATEMATICA II (Durante) Aversa, Marzo 2001. COGNOME........................ NOME............... MATRICOLA............ 1. Dati i tre vettori u, v e w di R 3, si dica se essi sono linearmente dipendenti
MODELLI e METODI MATEMATICI della FISICA. Programma dettagliato del corso - A.A
 MODELLI e METODI MATEMATICI della FISICA Programma dettagliato del corso - A.A. 2018-19 Lezione 1, 25 febbraio 2019: Organizzazione del corso. Introduzione ai numeri complessi. Rappresentazione cartesiana
MODELLI e METODI MATEMATICI della FISICA Programma dettagliato del corso - A.A. 2018-19 Lezione 1, 25 febbraio 2019: Organizzazione del corso. Introduzione ai numeri complessi. Rappresentazione cartesiana
CM86sett.tex COMPLEMENTI DI MATEMATICA a.a Laurea magistrale in Ingegneria Elettrotecnica
 CM86sett.tex COMPLEMENTI DI MATEMATICA a.a. 2008-2009 Laurea magistrale in Ingegneria Elettrotecnica Settima settimana 0..2008 - lunedì (2 ore) 0.0. Teorema. (di Picard) - Data una f olomorfa, in un intorno
CM86sett.tex COMPLEMENTI DI MATEMATICA a.a. 2008-2009 Laurea magistrale in Ingegneria Elettrotecnica Settima settimana 0..2008 - lunedì (2 ore) 0.0. Teorema. (di Picard) - Data una f olomorfa, in un intorno
Corso di Geometria Ing. Informatica e Automatica Test 1: soluzioni
 Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
1 Esercizio A Soluzione
 Prova scritta di: Studio di Funzioni di Interesse Fisico del 07/04/200. Firmare e riconsegnare il testo d esame 2. Spegnere e non utilizzare i cellulari 3. Indicare, contrassegnando l opzione scelta, se
Prova scritta di: Studio di Funzioni di Interesse Fisico del 07/04/200. Firmare e riconsegnare il testo d esame 2. Spegnere e non utilizzare i cellulari 3. Indicare, contrassegnando l opzione scelta, se
Compito di Analisi Matematica, Seconda parte, COGNOME: NOME: MATR.:
 Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
Esercizi di Analisi Complessa. Corso di Laurea in Matematica
 Esercizi di Analisi Complessa Corso di Laurea in Matematica Terminologia, notazioni. In uno spazio metrico (X, d indicheremo con U r (x o la palla aperta con centro x o X e raggio r > 0 : U r (x o := {
Esercizi di Analisi Complessa Corso di Laurea in Matematica Terminologia, notazioni. In uno spazio metrico (X, d indicheremo con U r (x o la palla aperta con centro x o X e raggio r > 0 : U r (x o := {
Modelli e Metodi Matematici della Fisica. S1
 Modelli e Metodi Matematici della Fisica S Filippo Cesi 0 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 6 CFU 8 CFU 4 + 6 CFU altro: problema 4 5 6 7 8 9 0 test totale voto in trentesimi
Modelli e Metodi Matematici della Fisica S Filippo Cesi 0 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 6 CFU 8 CFU 4 + 6 CFU altro: problema 4 5 6 7 8 9 0 test totale voto in trentesimi
Numeri complessi. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) I numeri complessi Analisi A 1 / 37
 Numeri complessi Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) I numeri complessi Analisi A 1 / 37 Introduzione I numeri complessi vengono introdotti perché tutte
Numeri complessi Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) I numeri complessi Analisi A 1 / 37 Introduzione I numeri complessi vengono introdotti perché tutte
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
5 Un applicazione: le matrici di rotazione
 5 Un applicazione: le matrici di rotazione 51 Rotazioni nel piano di un angolo ϑ Si vuole considerare il caso della rotazione nel piano di un vettore di R di un angolo ϑ assegnato Chiaramente si tratta
5 Un applicazione: le matrici di rotazione 51 Rotazioni nel piano di un angolo ϑ Si vuole considerare il caso della rotazione nel piano di un vettore di R di un angolo ϑ assegnato Chiaramente si tratta
Compito di Analisi Matematica II del 28 giugno 2006 ore 11
 Compito di Analisi Matematica II del 28 giugno 26 ore Esercizio. ( punti) Calcolare il flusso del campo vettoriale F (,, z) = (z, z 2, z 2 ) } uscente dalla frontiera di D = (,, z) R 3 : 2 + z 2, z,. Svolgimento
Compito di Analisi Matematica II del 28 giugno 26 ore Esercizio. ( punti) Calcolare il flusso del campo vettoriale F (,, z) = (z, z 2, z 2 ) } uscente dalla frontiera di D = (,, z) R 3 : 2 + z 2, z,. Svolgimento
Esercitazione 05: Trasformata di Laplace e funzione di trasferimento
 Esercitazione 05: Trasformata di Laplace e funzione di trasferimento 28 marzo 208 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state
Esercitazione 05: Trasformata di Laplace e funzione di trasferimento 28 marzo 208 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state
NUMERI COMPLESSI ED EQUAZIONI ALGEBRICHE
 NUMERI COMPLESSI ED EQUAZIONI ALGEBRICHE. Esercizi Esercizio. Scrivere la forma algebrica, la forma trigonometrica e quella esponenziale dei seguenti numeri complessi: z = + i, z = (cos( π ) + i sin(π
NUMERI COMPLESSI ED EQUAZIONI ALGEBRICHE. Esercizi Esercizio. Scrivere la forma algebrica, la forma trigonometrica e quella esponenziale dei seguenti numeri complessi: z = + i, z = (cos( π ) + i sin(π
Algebra lineare Geometria 1 15 luglio 2009
 Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
x = v y = v Per x = r cos θ e y = r sin θ, si ha x r + v y r = v x Applichiamo CauchyRiemann alla prime due Per confronto otteniamo = +r
 Soluzioni Esercitazione.. La funzione w = f(z) = R(r, θ)e iφ(r,θ), dove z = + i = re iθ à data in coordinate polari nello spazio su cui è definita (il piano z) e lo spazio in cui assume valori. Per risolvere
Soluzioni Esercitazione.. La funzione w = f(z) = R(r, θ)e iφ(r,θ), dove z = + i = re iθ à data in coordinate polari nello spazio su cui è definita (il piano z) e lo spazio in cui assume valori. Per risolvere
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Algebra Lineare Corso di Ingegneria Biomedica Compito del
 Algebra Lineare Corso di Ingegneria Biomedica Compito del -- - È obbligatorio consegnare tutti i fogli, anche il testo del compito e i fogli di brutta. - Le risposte senza giustificazione sono considerate
Algebra Lineare Corso di Ingegneria Biomedica Compito del -- - È obbligatorio consegnare tutti i fogli, anche il testo del compito e i fogli di brutta. - Le risposte senza giustificazione sono considerate
Numeri complessi. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Numeri complessi Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) I numeri complessi Analisi Matematica 1 1 / 34 Introduzione L introduzione dei numeri complessi
Numeri complessi Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) I numeri complessi Analisi Matematica 1 1 / 34 Introduzione L introduzione dei numeri complessi
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
Facoltà di Architettura Valle Giulia Corso di Laurea Specialistica Quinquennale U.E. 1 CALCOLO INTEGRALE PER LE FUNZIONI DI UNA VARIABILE
 Facoltà di Architettura Valle Giulia Corso di Laurea Specialistica Quinquennale U.E. Istituzioni di Matematica 2 a.a. 2007-2008 http://www.dmmm.uniroma.it/persone/capitanelli CALCOLO INTEGRALE PER LE FUNZIONI
Facoltà di Architettura Valle Giulia Corso di Laurea Specialistica Quinquennale U.E. Istituzioni di Matematica 2 a.a. 2007-2008 http://www.dmmm.uniroma.it/persone/capitanelli CALCOLO INTEGRALE PER LE FUNZIONI
Matematica Applicata Tutoraggio 3. in serie di Laurent nella corona circolare 0 < z 1 < 2.
 Serie di Laurent Esercizio Sviluppare z 2 in serie di Laurent nella corona circolare 0 < z < 2. Soluzione con il calcolo dei coefficienti. Scomponendo f(z) in frazioni semplici, si ha ( 2 z ) z + il primo
Serie di Laurent Esercizio Sviluppare z 2 in serie di Laurent nella corona circolare 0 < z < 2. Soluzione con il calcolo dei coefficienti. Scomponendo f(z) in frazioni semplici, si ha ( 2 z ) z + il primo
NUMERI COMPLESSI Esercizi svolti. d) (1 i) 3. b) (1 + i)(1 i)(1 + 3 i) c) 1 i 1
 Calcolare le seguenti potenze di i: NUMERI COMPLESSI Esercizi svolti a) i b) i 7 c) i d) i e) i f) i 9 Semplificare le seguenti espressioni: a) i) i i) b) + i) i) + ) 0 i c) i) i) i) d) i) Verificare che
Calcolare le seguenti potenze di i: NUMERI COMPLESSI Esercizi svolti a) i b) i 7 c) i d) i e) i f) i 9 Semplificare le seguenti espressioni: a) i) i i) b) + i) i) + ) 0 i c) i) i) i) d) i) Verificare che
Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio Esercizio 1
 Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio 2012 Esercizio 1 (a) Si calcola il polinomio caratteristico λ 2 1 p(λ) = det k 1 2k λ k 1 2 2 λ usando lo sviluppo di Laplace secondo
Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio 2012 Esercizio 1 (a) Si calcola il polinomio caratteristico λ 2 1 p(λ) = det k 1 2k λ k 1 2 2 λ usando lo sviluppo di Laplace secondo
Metodi Matematici della Fisica. S3
 Metodi Matematici della Fisica. S Filippo Cesi 0 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 6 CFU 8 CFU 4 + 6 CFU altro: problema 4 5 6 7 8 9 0 test totale voto in trentesimi voto
Metodi Matematici della Fisica. S Filippo Cesi 0 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 6 CFU 8 CFU 4 + 6 CFU altro: problema 4 5 6 7 8 9 0 test totale voto in trentesimi voto
Modelli e Metodi Matematici della Fisica. S2/AC
 Modelli e Metodi Matematici della Fisica. S/AC Filippo Cesi 010 11 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 1 CFU (AA 010-11) 6 CFU (solo anal. funzionale) 6 CFU (solo anal. complessa)
Modelli e Metodi Matematici della Fisica. S/AC Filippo Cesi 010 11 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 1 CFU (AA 010-11) 6 CFU (solo anal. funzionale) 6 CFU (solo anal. complessa)
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA
 Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Esempi di esercizi d esame A.A. 2006/07 Analisi Matematica 2 Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli
 Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 2017/2018 Canali A C, e L Pa
 Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
Geometria BAER Canale A-K Esercizi 8
 Geometria BAER Canale A-K Esercizi 8 Esercizio. Si consideri il sottospazio U = L v =, v, v 3 =. (a) Si trovino le equazioni cartesiane ed una base ortonormale di U. (b) Si trovi una base ortonormale di
Geometria BAER Canale A-K Esercizi 8 Esercizio. Si consideri il sottospazio U = L v =, v, v 3 =. (a) Si trovino le equazioni cartesiane ed una base ortonormale di U. (b) Si trovi una base ortonormale di
Soluzioni 7.2. dx (1 + x 2 ) 3. f(z) = (1 + z 2 ) 3. 2 (z + i) 5 = 3i 16. y K. R R x. dx (1 + x 2 ) 3 = 3π 8. e ax dx 1 + e x, 0 < a < 1
 () Polo triplo in i Soluzioni 7.2 f(z) = ( + 2 ) 3 ( + z 2 ) 3 Res (f, i) = 2 2 (z + i) 5 = 3i 6 i R f(z)dz = R ( + 2 ) 3 + dz ( + z 2 ) 3 = 2πi Res (f, i) = 3π 8 Nel limite R l integrale lungo dà contributo
() Polo triplo in i Soluzioni 7.2 f(z) = ( + 2 ) 3 ( + z 2 ) 3 Res (f, i) = 2 2 (z + i) 5 = 3i 6 i R f(z)dz = R ( + 2 ) 3 + dz ( + z 2 ) 3 = 2πi Res (f, i) = 3π 8 Nel limite R l integrale lungo dà contributo
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI
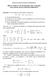 Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Esame di Analisi Matematica 2 24/7/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Analisi Matematica III (Fisica) 07 Gennaio 2016
 Analisi Matematica III (Fisica 7 Gennaio 16 1. (1 punti Calcolare l area della sezione del cilindro x + y 4 determinata dal piano di equazione z x + y. (Possibilmente in due modi differenti Ci sono vari
Analisi Matematica III (Fisica 7 Gennaio 16 1. (1 punti Calcolare l area della sezione del cilindro x + y 4 determinata dal piano di equazione z x + y. (Possibilmente in due modi differenti Ci sono vari
NUMERI COMPLESSI - ESERCIZI
 NUMERI COMPLESSI - ESERCIZI Ecco una raccolta di esercizi apparsi nei compiti scritti di Analisi Matematica 1 degli anni passati con problemi ed equazioni in campo 1. Proprietà algebriche e geometriche
NUMERI COMPLESSI - ESERCIZI Ecco una raccolta di esercizi apparsi nei compiti scritti di Analisi Matematica 1 degli anni passati con problemi ed equazioni in campo 1. Proprietà algebriche e geometriche
Esercizio III Calcolare la trasformata di Fourier della funzione. Esercizio IV Sviluppare la funzione. Tema d esame. Giugno 2004
 Tema d esame. Giugno 24 Esercizio I Calcolare il seguente integrale col metodo dei residui 2π dφ < a < () + a 2 2a cos φ Esercizio II Trovare la soluzione dell equazione di Laplace nella regione del piano
Tema d esame. Giugno 24 Esercizio I Calcolare il seguente integrale col metodo dei residui 2π dφ < a < () + a 2 2a cos φ Esercizio II Trovare la soluzione dell equazione di Laplace nella regione del piano
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 2011/2012 Prof. C. Presilla. Prova A1 3 Maggio 2012
 MODELLI E METODI MATEMATICI DELLA FISICA A.A. 211/212 Prof. C. Presilla Prova A1 3 Maggio 212 Cognome Nome II anno III anno o successivi penalità esercizio voto 1 2 3 4 5 6 Esercizio 1 Determinare tutte
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 211/212 Prof. C. Presilla Prova A1 3 Maggio 212 Cognome Nome II anno III anno o successivi penalità esercizio voto 1 2 3 4 5 6 Esercizio 1 Determinare tutte
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
Corso di Geometria III - A.A. 2016/17 Esercizi
 Corso di Geometria III - A.A. 216/17 Esercizi (ultimo aggiornamento del file: 2 ottobre 215) Esercizio 1. Calcolare (1 + 2i) 3, ( ) 2 + i 2, (1 + i) n + (1 i) n. 3 2i Esercizio 2. Sia z = x + iy. Determinare
Corso di Geometria III - A.A. 216/17 Esercizi (ultimo aggiornamento del file: 2 ottobre 215) Esercizio 1. Calcolare (1 + 2i) 3, ( ) 2 + i 2, (1 + i) n + (1 i) n. 3 2i Esercizio 2. Sia z = x + iy. Determinare
Esercizi sulle funzioni polidrome (non svolti a lezione per mancanza di tempo)
 Esercizi sulle funzioni polidrome non svolti a lezione per mancanza di tempo) ACHTUNG: Questi appunti sono pieni di errori... Okkio... Esercizio 1 Calcolare in campo complesso, l integrale π dθ + cos θ)
Esercizi sulle funzioni polidrome non svolti a lezione per mancanza di tempo) ACHTUNG: Questi appunti sono pieni di errori... Okkio... Esercizio 1 Calcolare in campo complesso, l integrale π dθ + cos θ)
Esercizio 1. Calcolare per n Z z 2. Soluzione: Per n 0 si ha che l integrale é nullo per il teorema integrale di Cauchy. Per n = 1 si ha che 2
 Sapienza - Università di Roma Facoltà di Ingegneria - A.A. -4 Esercitazione per il corso di Metodi Matematici per l Ingegneria (Docente Daniela Giachetti) a cura di Ida de Bonis Esercizio. Calcolare per
Sapienza - Università di Roma Facoltà di Ingegneria - A.A. -4 Esercitazione per il corso di Metodi Matematici per l Ingegneria (Docente Daniela Giachetti) a cura di Ida de Bonis Esercizio. Calcolare per
14 febbraio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Esercizio 1. (i) Si dia la definizione di successione delle somme parziali per una serie di funzioni. (ii) Data la serie n + 1.
 Sapienza - Università di Roma Facoltà di Ingegneria - A.A. 0-04 Esercitazione per il corso di Metodi Matematici per l Ingegneria a cura di Daniela Giachetti Esercizio. (i) Si dia la definizione di successione
Sapienza - Università di Roma Facoltà di Ingegneria - A.A. 0-04 Esercitazione per il corso di Metodi Matematici per l Ingegneria a cura di Daniela Giachetti Esercizio. (i) Si dia la definizione di successione
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA PRIMO APPELLO, 15 GIUGNO 2010 VERSIONE A. 1 a 1. 0 a a 2
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA PRIMO APPELLO, 5 GIUGNO 2 VERSIONE A Esercizio Al variare del parametro reale a, si consideri l endomorfismo : R R definito dalle condizioni: a a a 2 a a 2 =,
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA PRIMO APPELLO, 5 GIUGNO 2 VERSIONE A Esercizio Al variare del parametro reale a, si consideri l endomorfismo : R R definito dalle condizioni: a a a 2 a a 2 =,
NOME:... MATRICOLA:... Corso di Laurea in Matematica, A.A. 2011/2012 Analisi Reale e Complessa, Test del
 NOME:... MATRICOLA:.... Corso di Laurea in Matematica, A.A. 011/01 Analisi Reale e Complessa, Test del 7.01.01 1) Si dia un esempio di i) un dominio semplicemente connesso D di C non contenente l origine,
NOME:... MATRICOLA:.... Corso di Laurea in Matematica, A.A. 011/01 Analisi Reale e Complessa, Test del 7.01.01 1) Si dia un esempio di i) un dominio semplicemente connesso D di C non contenente l origine,
1 Parziale di Studio di Funzioni di Interesse Fisico, 26/02/2009
 Parziale di Studio di Funzioni di Interesse Fisico, 6/0/009. Riconsegnare il testo degli esercizi, firmato, congiuntamente all elaborato scritto.. Firmare e consegnare solo il materiale che si desidera
Parziale di Studio di Funzioni di Interesse Fisico, 6/0/009. Riconsegnare il testo degli esercizi, firmato, congiuntamente all elaborato scritto.. Firmare e consegnare solo il materiale che si desidera
Compiti di geometria & algebra lineare. Anno: 2004
 Compiti di geometria & algebra lineare Anno: 24 Anno: 24 2 Primo compitino di Geometria e Algebra 7 novembre 23 totale tempo a disposizione : 3 minuti Esercizio. [8pt.] Si risolva nel campo complesso l
Compiti di geometria & algebra lineare Anno: 24 Anno: 24 2 Primo compitino di Geometria e Algebra 7 novembre 23 totale tempo a disposizione : 3 minuti Esercizio. [8pt.] Si risolva nel campo complesso l
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 7 febbraio Soluzioni compito 1
 ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 7 febbraio 7 - Soluzioni compito E Calcolare, usando i metodi della variabile complessa, cos(z ) dz dove é
ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 7 febbraio 7 - Soluzioni compito E Calcolare, usando i metodi della variabile complessa, cos(z ) dz dove é
Capitolo 1 ANALISI COMPLESSA
 Capitolo ANALISI COMPLESSA .6 Calcolo di integrali definiti mediante il teorema dei residui Il teorema dei residui (.33) è di grande utilità perché permette non solo di calcolare integrali naturalmente
Capitolo ANALISI COMPLESSA .6 Calcolo di integrali definiti mediante il teorema dei residui Il teorema dei residui (.33) è di grande utilità perché permette non solo di calcolare integrali naturalmente
Algebra lineare Geometria 1 11 luglio 2008
 Algebra lineare Geometria 1 11 luglio 2008 Esercizio 1. Si considerino la funzione: { R f : 3 R 3 (α, β, γ) ( 2β α γ, (k 1)β + (1 k)γ α, 3β + (k 2)γ ) dove k è un parametro reale, e il sottospazio U =
Algebra lineare Geometria 1 11 luglio 2008 Esercizio 1. Si considerino la funzione: { R f : 3 R 3 (α, β, γ) ( 2β α γ, (k 1)β + (1 k)γ α, 3β + (k 2)γ ) dove k è un parametro reale, e il sottospazio U =
