Esercizi proposti. 1 Numeri complessi. 1.1 Forma cartesiana. Esercizio 1.1 Dato il numero complesso. z = 7 3 7i,
|
|
|
- Rosa Salvatori
- 4 anni fa
- Visualizzazioni
Transcript
1 Numeri complessi Esercizi proposti 1 Numeri complessi 1.1 Forma cartesiana Esercizio 1.1 Dato il numero complesso z = 7 3 7i, a) determinare la parte reale x di z: x = Re z, b) determinare la parte immaginaria y di z: y = Im z, c) determinare il modulo r di z: r = z, d) determinare l argomento ϑ di z: ϑ = arg z, e) scrivere z in forma polare trigonometrica e in forma esponenziale, f) determinare il complesso coniugato z di z. (Risultato: Rez = 7 3, Imz = 7, z = 14, arg z = π/6, z = 14(cos( π/6) + i sin( π/6), z = 14(cos(π/6) + i sin(π/6).) Esercizio 1.2 Dato il numero complesso z = i, a) determinare la parte reale x di z: x = Re z, b) determinare la parte immaginaria y di z: y = Im z, c) determinare il modulo r di z: r = z, d) determinare l argomento ϑ di z: ϑ = arg z, e) scrivere z in forma polare trigonometrica e in forma esponenziale, f) determinare il complesso coniugato z di z. (Risultato: Rez = 13, Imz = 13 3, z = 26, arg z = 2π/3, z = 26(cos(2π/3) + i sin(2π/3), z = 26(cos( 2π/3) + i sin( 2π/3).) Esercizio 1.3 Dati il numero complesso z = i e w = i c 2007 Politecnico di Torino 1
2 Forma cartesiana a) Scivere in forma cartesiana la somma di z e di w, b) Scivere in forma cartesiana il prodotto di z e di w, c) Scivere in forma cartesiana z diviso w, d) Calcolare modulo e argomento di z w, e) Calcolare modulo e argomento di z/w. (Risultato: z + w = ( ) + i( ), z w = i, z/w = ( 22/10)i, z w = 220, arg(z w) = π/6, z/w = 22/10, arg(z/w) = π/2.) Esercizio 1.4 Risolvere in campo complesso l equazione: ( z) 2 + 6z + 8 = 0. (Risultato: z 1 = 2, z 2 = 4, z 3 = 3 + i 35, z 4 = 3 i 35.) Esercizio 1.5 Risolvere in campo complesso l equazione: z (Im z) 2 8 = 2i. (Risultato: z 1 = 3 + (1/ 3)i, z 2 = 3 (1/ 3)i, z 3 = 5 + (1/ 5)i, z 4 = 5 (1/ 5)i.) Esercizio 1.6 Risolvere in campo complesso l equazione: z = 0, e scrivere il polinomio z come prodotto di due polinomi di secondo grado a coefficienti reali. (Risultato: z 1 = 2/2+( 2/2)i, z 2 = 2/2 ( 2/2)i, z 3 = 2/2+( 2/2)i, z 4 = 2/2 ( 2/2)i, z = (z 2 z 2 + 1)(z 2 + z 2 + 1).) Esercizio 1.7 Risolvere in campo complesso l equazione: z 2 + i z = 0. (Risultato: z 1 = 0, z 2 = i, z 3 = 3/2 + ( 1/2)i, z 4 = 3/2 + ( 1/2)i.) c 2007 Politecnico di Torino 2
3 Forma polare trigonometrica 1.2 Forma polare trigonometrica Esercizio 1.8 Dato il numero complesso z = i, d) scrivere, in forma polare trigonometrica, il complesso coniugato z di z, e) calcolare z 5, f) calcolare 3 z. (Risultato: z = 24, arg z = 3π/4, z = 24(cos(3π/4)+i sin(3π/4)), z = 24(cos( 3π/4)+ i sin( 3π/4)), z 5 = 24 5 (cos(15π/4) + i sin(15π/4)), 3 z = 3 24(cos(π/4 + k 2π/3) + i sin(π/4 + k 2π/3)), k = 0, 1, 2.) Esercizio 1.9 Dato il numero complesso z = 64i, d) calcolare le radici seste complesse di z: 6 z. (Risultato: z = 64, arg z = 3π/2, z = 64(cos(3π/2)+i sin(3π/2)), 6 z = 2(cos(π/4+ k 2π/6) + i sin(π/4 + k 2π/6)), k = 0, 1, 2, 3, 4, 5.) Esercizio 1.10 Dato il numero complesso z = 243, d) calcolare le radici quarte complesse di z: 5 z. c 2007 Politecnico di Torino 3
4 Forma polare trigonometrica (Risultato: z = 243, arg z = 0, z = 243(cos(0) + i sin(0)), 5 z = 3(cos(k 2π/5) + i sin(k 2π/5)), k = 0, 1, 2, 3, 4.) Esercizio 1.11 Calcolare modulo e aromento del seguente numero complesso: z = i (17 (cos(π/12) + i sin(π/12))) 3 i e scriverlo in forma polare trigonometrica. (Risultato: z = 3, arg z = 2π/3, z = 3(cos(2π/3) + i sin(2π/3)).) Esercizio 1.12 Calcolare modulo e aromento del seguente numero complesso: 2 2 i z = ( 3) i e scriverlo in forma polare trigonometrica e in forma cartesiana. (Risultato: z = 3, arg z = π/2, z = 3(cos(π/2) + i sin(π/2)), z = 3i.) Esercizio 1.13 Calcolare modulo e aromento del seguente numero complesso: z = 7(cos(π/3) + i sin(π/3)) (8(cos(π/9) + i sin(π/9))) 28(cos(π/6) + i sin(π/6)) e scriverlo in forma polare trigonometrica. (Risultato: z = 2, arg z = 5π/18, z = 2(cos(5π/18) + i sin(5π/18)).) Esercizio 1.14 Calcolare le radici quarte del seguente numero complesso: z = 256 (cos(π/3) + i sin(π/3)). ( Risultato: z = 4(cos(π/12) + i sin(π/12)) 4(cos(π/12 + π/2) + i sin(π/12 + π/2)) 4(cos(π/12 + π) + i sin(π/12 + π)) 4(cos(π/ π/2) + i sin(π/ π/2)).) c 2007 Politecnico di Torino 4
5 Forma esponenziale 1.3 Forma esponenziale Esercizio 1.15 Dato il seguente numero complesso: z = i calcolare modulo e argomento di z e scrivere z in forma esponenziale. (Risultato: z = , arg z = π/4, z = e iπ/4.) Esercizio 1.16 Dato il seguente numero complesso: z = 7 + 7i la settima potenza di z. (Risultato: z = 7 2, arg z = 3π/4, z = 7 2 e 3iπ/4, z 7 = (7 2) 7 e 5iπ/4.) Esercizio 1.17 Dato il seguente numero complesso: z = i la radice ottava di z. (Risultato: z = 58, arg z = 11π/6, z = 58 e 11iπ/6, 8 z = 8 58 e 11iπ/48 + k 2iπ/8, k = 0, 1,..., 7.) Esercizio 1.18 Dato il seguente numero complesso: z = π 2 π 2i la radice quarta di z. (Risultato: z = 2π, arg z = 3π/4, z = 2π e 3iπ/4, 4 z = 4 2π e 3iπ/16 + k 2iπ/4, k = 0, 1, 2, 3.) Esercizio 1.19 Dato il seguente numero complesso: z = e 5 3 /2 i e 5 /2 il logaritmo complesso di z. (Risultato: z = e 5, arg z = 7π/6, z = e 5+7iπ/6, log z = 5 + 7iπ/6 + 2kπi, k Z.) c 2007 Politecnico di Torino 5
Esercizi svolti. 1 Numeri complessi. 1.1 Forma cartesiana. Esercizio 1.1 Dato il numero complesso. z = 4 3 4i,
 Numeri complessi Esercizi svolti 1 Numeri complessi 1.1 Forma cartesiana Esercizio 1.1 Dato il numero complesso z = 4 3 4i, a) determinare la parte reale x di z: x = Re z, b) determinare la parte immaginaria
Numeri complessi Esercizi svolti 1 Numeri complessi 1.1 Forma cartesiana Esercizio 1.1 Dato il numero complesso z = 4 3 4i, a) determinare la parte reale x di z: x = Re z, b) determinare la parte immaginaria
Esercizi 1. Numeri complessi e polinomi
 Esercizi 1 08\0\016 Numeri complessi e polinomi David Barbato Esercizio 1. Scrivere in forma algebrica i seguenti numeri complessi: a) z = 1 + i)1 i) b) z = 1 +i c) z = 6 i d) z = +i i e) z = 1+i 1 i)i
Esercizi 1 08\0\016 Numeri complessi e polinomi David Barbato Esercizio 1. Scrivere in forma algebrica i seguenti numeri complessi: a) z = 1 + i)1 i) b) z = 1 +i c) z = 6 i d) z = +i i e) z = 1+i 1 i)i
Numeri complessi. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Numeri complessi Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) I numeri complessi Analisi Matematica 1 1 / 34 Introduzione L introduzione dei numeri complessi
Numeri complessi Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) I numeri complessi Analisi Matematica 1 1 / 34 Introduzione L introduzione dei numeri complessi
Numeri Complessi. Sono numeri del tipo z = a + ib, dove a e b R, e i = 1 è detta unità immaginaria i R e i 2 = 1
 Numeri Complessi Sono numeri del tipo z = a + ib, dove a e b R, e i = 1 è detta unità immaginaria i R e i 2 = 1 L insieme dei numeri complessi è indicato con C. a è detta parte reale del numero complesso
Numeri Complessi Sono numeri del tipo z = a + ib, dove a e b R, e i = 1 è detta unità immaginaria i R e i 2 = 1 L insieme dei numeri complessi è indicato con C. a è detta parte reale del numero complesso
Numeri Complessi R 2. P = (x P,y P ) x P. z = (x,y) y P (0,0)
 Numeri Complessi Un numero complesso z può essere definito come una coppia ordinata (x,y) di numeri reali x e y. L insieme dei numeri complessi è denotato con C e può essere identificato con il piano cartesiano
Numeri Complessi Un numero complesso z può essere definito come una coppia ordinata (x,y) di numeri reali x e y. L insieme dei numeri complessi è denotato con C e può essere identificato con il piano cartesiano
Numeri Complessi. Sono numeri del tipo z = a + ib, dove a e b, e i = 1 è detta unità immaginaria i e i 2 = 1
 Numeri Complessi Sono numeri del tipo z = a + ib, dove a e b, e i = 1 è detta unità immaginaria i e i 2 = 1 L insieme dei numeri complessi è indicato con. a è detta parte reale del numero complesso b è
Numeri Complessi Sono numeri del tipo z = a + ib, dove a e b, e i = 1 è detta unità immaginaria i e i 2 = 1 L insieme dei numeri complessi è indicato con. a è detta parte reale del numero complesso b è
I Numeri complessi - Motivazioni
 I Numeri complessi - Motivazioni In Telecomunicazioni Elettronica Informatica Teoria dei segnali... si studiano i segnali, cioè delle grandezze fisiche dipendenti dal tempo, matematicamente esprimibili
I Numeri complessi - Motivazioni In Telecomunicazioni Elettronica Informatica Teoria dei segnali... si studiano i segnali, cioè delle grandezze fisiche dipendenti dal tempo, matematicamente esprimibili
Numeri complessi. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) I numeri complessi Analisi A 1 / 37
 Numeri complessi Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) I numeri complessi Analisi A 1 / 37 Introduzione I numeri complessi vengono introdotti perché tutte
Numeri complessi Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) I numeri complessi Analisi A 1 / 37 Introduzione I numeri complessi vengono introdotti perché tutte
Numeri Complessi R 2. P = (x P,y P ) x P. z = (x,y) y P (0,0)
 Numeri Complessi Un numero complesso z può essere definito come una coppia ordinata (x,y) di numeri reali x e y. L insieme dei numeri complessi è denotato con C e può essere identificato con il piano cartesiano
Numeri Complessi Un numero complesso z può essere definito come una coppia ordinata (x,y) di numeri reali x e y. L insieme dei numeri complessi è denotato con C e può essere identificato con il piano cartesiano
NUMERI COMPLESSI ED EQUAZIONI ALGEBRICHE
 NUMERI COMPLESSI ED EQUAZIONI ALGEBRICHE. Esercizi Esercizio. Scrivere la forma algebrica, la forma trigonometrica e quella esponenziale dei seguenti numeri complessi: z = + i, z = (cos( π ) + i sin(π
NUMERI COMPLESSI ED EQUAZIONI ALGEBRICHE. Esercizi Esercizio. Scrivere la forma algebrica, la forma trigonometrica e quella esponenziale dei seguenti numeri complessi: z = + i, z = (cos( π ) + i sin(π
ESERCITAZIONE 4: I NUMERI COMPLESSI
 ESERCITAZIONE 4: I NUMERI COMPLESSI Tiziana Raparelli 19/0/008 1 DEFINIZIONI E PROPRIETÀ Vogliamo risolvere l equazione x + 1 = 0, estendiamo dunque l insieme dei numeri reali, introducendo l unità immaginaria
ESERCITAZIONE 4: I NUMERI COMPLESSI Tiziana Raparelli 19/0/008 1 DEFINIZIONI E PROPRIETÀ Vogliamo risolvere l equazione x + 1 = 0, estendiamo dunque l insieme dei numeri reali, introducendo l unità immaginaria
NUMERI COMPLESSI. = 2 + 5i A3) Calcolare in forma trigonometrica le soluzioni complesse dell equazione iz 4 9 = 0
 NUMERI COMPLESSI A) Calcolare in forma cartesiana ( + i) 3 = A) ( + 5i) (3 + 4i) Calcolare in forma cartesiana = + 5i A3) Calcolare in forma trigonometrica le soluzioni complesse dell equazione iz 4 9
NUMERI COMPLESSI A) Calcolare in forma cartesiana ( + i) 3 = A) ( + 5i) (3 + 4i) Calcolare in forma cartesiana = + 5i A3) Calcolare in forma trigonometrica le soluzioni complesse dell equazione iz 4 9
Politecnico di Milano. Scuola di Ingegneria Industriale. Corso di Analisi e Geometria 1 (Docente: Federico Lastaria) Ottobre 2012 Esercizi
 Politecnico di Milano. Scuola di Ingegneria Industriale. Corso di Analisi e Geometria (Docente: Federico Lastaria) Ottobre 0 Esercizi Indice Esercizi e complementi. Numeri complessi...................................
Politecnico di Milano. Scuola di Ingegneria Industriale. Corso di Analisi e Geometria (Docente: Federico Lastaria) Ottobre 0 Esercizi Indice Esercizi e complementi. Numeri complessi...................................
I numeri complessi. Richiami di teoria. AMA Ing.Edile - Prof. Colombo 1. Esercitazioni: Francesco Di Plinio -
 AMA Ing.Edile - Prof. Colombo 1 Esercitazioni: Francesco Di Plinio - francesco.diplinio@libero.it I numeri complessi. Richiami di teoria. 1.1 Numeri complessi. Un numero complesso è un espressione della
AMA Ing.Edile - Prof. Colombo 1 Esercitazioni: Francesco Di Plinio - francesco.diplinio@libero.it I numeri complessi. Richiami di teoria. 1.1 Numeri complessi. Un numero complesso è un espressione della
z = i 4 2i 3. a)z = (1 + i) 6 e b)w = i 17. 4) Scrivere in forma trigonometrica i seguenti numeri complessi: a)8 b)6i c)( cos( π 3 ) i sin(π 3 ))7.
 NUMERI COMPLESSI Esercizi svolti. 1 Calcolare la parte reale e la parte immaginaria di z = i i. Determinare il valore assoluto e il coniugato di az = 1 + i 6 e bw = i 17. Scrivere in forma cartesiana i
NUMERI COMPLESSI Esercizi svolti. 1 Calcolare la parte reale e la parte immaginaria di z = i i. Determinare il valore assoluto e il coniugato di az = 1 + i 6 e bw = i 17. Scrivere in forma cartesiana i
Radici quadrate di numeri negativi. Perchè?
 Numeri Complessi Radici quadrate di numeri negativi Perchè? Problema: Cardano, Ars Magna cap.xxxvii, (1545) Dividi 10 in due parti il cui prodotto è 40 Girolamo Cardano (Pavia, 24 settembre 1501 Roma,
Numeri Complessi Radici quadrate di numeri negativi Perchè? Problema: Cardano, Ars Magna cap.xxxvii, (1545) Dividi 10 in due parti il cui prodotto è 40 Girolamo Cardano (Pavia, 24 settembre 1501 Roma,
Ripasso delle matematiche elementari: esercizi proposti
 Ripasso delle matematiche elementari: esercizi proposti I Equazioni e disequazioni algebriche Esercizi sui polimoni.............................. Esercizi sulle equazioni di grado superiore al secondo............
Ripasso delle matematiche elementari: esercizi proposti I Equazioni e disequazioni algebriche Esercizi sui polimoni.............................. Esercizi sulle equazioni di grado superiore al secondo............
DOCENTE: Vincenzo Pappalardo MATERIA: Matematica I NUMERI COMPLESSI
 DOCENTE: Vincenzo Pappalardo MATERIA: Matematica I NUMERI COMPLESSI INTRODUZIONE Problema: Esiste la radice quadrata di un numero reale x negativo? ( 4) =? Nell insieme dei numeri reali R il problema non
DOCENTE: Vincenzo Pappalardo MATERIA: Matematica I NUMERI COMPLESSI INTRODUZIONE Problema: Esiste la radice quadrata di un numero reale x negativo? ( 4) =? Nell insieme dei numeri reali R il problema non
NUMERI COMPLESSI Esercizi svolti. d) (1 i) 3. b) (1 + i)(1 i)(1 + 3 i) c) 1 i 1
 Calcolare le seguenti potenze di i: NUMERI COMPLESSI Esercizi svolti a) i b) i 7 c) i d) i e) i f) i 9 Semplificare le seguenti espressioni: a) i) i i) b) + i) i) + ) 0 i c) i) i) i) d) i) Verificare che
Calcolare le seguenti potenze di i: NUMERI COMPLESSI Esercizi svolti a) i b) i 7 c) i d) i e) i f) i 9 Semplificare le seguenti espressioni: a) i) i i) b) + i) i) + ) 0 i c) i) i) i) d) i) Verificare che
Note sui numeri complessi
 Note sui numeri complessi Andrea Damiani 2 marzo 2015 Numero complesso Definiamo, senza ulteriori considerazioni, unità immaginaria la quantità i = 1 Definiamo poi il numero immaginario z = a + i b in
Note sui numeri complessi Andrea Damiani 2 marzo 2015 Numero complesso Definiamo, senza ulteriori considerazioni, unità immaginaria la quantità i = 1 Definiamo poi il numero immaginario z = a + i b in
29. Numeri complessi
 ANALISI Argomenti della Lezione 9. Numeri complessi 11 gennaio 01 9.1. L insieme C. L insieme C dei numeri complessi é l insieme delle coppie ordinate di numeri reali C = R R La tradizione vuole che la
ANALISI Argomenti della Lezione 9. Numeri complessi 11 gennaio 01 9.1. L insieme C. L insieme C dei numeri complessi é l insieme delle coppie ordinate di numeri reali C = R R La tradizione vuole che la
NUMERI COMPLESSI - ESERCIZI
 NUMERI COMPLESSI - ESERCIZI Ecco una raccolta di esercizi apparsi nei compiti scritti di Analisi Matematica 1 degli anni passati con problemi ed equazioni in campo 1. Proprietà algebriche e geometriche
NUMERI COMPLESSI - ESERCIZI Ecco una raccolta di esercizi apparsi nei compiti scritti di Analisi Matematica 1 degli anni passati con problemi ed equazioni in campo 1. Proprietà algebriche e geometriche
Alessio Del Padrone Esercizi di Geometria: Numeri Complessi e Polinomi (Ingegneria A.A. 10/11)
 Alessio Del Padrone Esercizi di Geometria: Numeri Complessi e Polinomi (Ingegneria A.A. 10/11) 1. Disegnare sul piano di Argand-Gauss e porre in forma trigonometrica-esponenziale (i.e. determinarne modulo
Alessio Del Padrone Esercizi di Geometria: Numeri Complessi e Polinomi (Ingegneria A.A. 10/11) 1. Disegnare sul piano di Argand-Gauss e porre in forma trigonometrica-esponenziale (i.e. determinarne modulo
Esercizi sui numeri complessi. Corso di Laurea in Informatica A.A. Docente: Andrea Loi. 1. Trovare parte reale e immaginaria dei numeri complessi:
 Esercizi sui numeri complessi Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1 Esercitazione 1. Trovare parte reale e immaginaria dei numeri complessi: 3 + i 5 4i e Soluzione: 3 + i
Esercizi sui numeri complessi Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1 Esercitazione 1. Trovare parte reale e immaginaria dei numeri complessi: 3 + i 5 4i e Soluzione: 3 + i
Soluzioni. 1. Calcolare la parte reale e immaginaria del numero complesso. z = i i. 3 (2 + i) = i i = i.
 20 Roberto Tauraso - Analisi 2 Soluzioni 1. Calcolare la parte reale e immaginaria del numero complesso R. z = i + 3 2 i. z = i + 3 2 i 2 i = 6 5 + ( 1 + 3 5 3 (2 + i) = i + 2 4 + 1 ) i = 6 5 + 8 5 i.
20 Roberto Tauraso - Analisi 2 Soluzioni 1. Calcolare la parte reale e immaginaria del numero complesso R. z = i + 3 2 i. z = i + 3 2 i 2 i = 6 5 + ( 1 + 3 5 3 (2 + i) = i + 2 4 + 1 ) i = 6 5 + 8 5 i.
Numeri Complessi. Perché i numeri complessi? PSfrag replacements
 Numeri Complessi Sono numeri del tipo = a + ib, dove a e b R, e i = 1 è detta unità immaginaria i R e i = 1 3 + 3i i i L insieme dei numeri complessi è indicato con C. a è detta parte reale del numero
Numeri Complessi Sono numeri del tipo = a + ib, dove a e b R, e i = 1 è detta unità immaginaria i R e i = 1 3 + 3i i i L insieme dei numeri complessi è indicato con C. a è detta parte reale del numero
Argomento 14 Soluzioni degli esercizi
 Argomento Soluzioni degli esercizi SUGGERIMENTI ESERCIZIO 0 Porre x + = z ESERCIZIO Le equazioni di secondo grado in z si risolvono sostanzialmente come si suole fare nel campo reale, senza restrizioni
Argomento Soluzioni degli esercizi SUGGERIMENTI ESERCIZIO 0 Porre x + = z ESERCIZIO Le equazioni di secondo grado in z si risolvono sostanzialmente come si suole fare nel campo reale, senza restrizioni
Soluzioni del tutorato di AC310
 Universitá degli Studi Roma Tre - Corso di Laurea in Matematica Soluzioni del tutorato di AC310 A.A. 01-013 - Docente: Prof. Pierpaolo Esposito Tutori: Dario Giannini e Giulia Salustri Tutorato 1 9 Ottobre
Universitá degli Studi Roma Tre - Corso di Laurea in Matematica Soluzioni del tutorato di AC310 A.A. 01-013 - Docente: Prof. Pierpaolo Esposito Tutori: Dario Giannini e Giulia Salustri Tutorato 1 9 Ottobre
L esigenza di introdurre i numeri complessi è dovuta al fatto che diverse operazioni sui numeri reali R non sempre sono possibili.
 1 I Numeri Complessi L esigenza di introdurre i numeri complessi è dovuta al fatto che diverse operazioni sui numeri reali R non sempre sono possibili. x 2 + 1 = 0? log( 10)? log 2 3? 1? Allo scopo di
1 I Numeri Complessi L esigenza di introdurre i numeri complessi è dovuta al fatto che diverse operazioni sui numeri reali R non sempre sono possibili. x 2 + 1 = 0? log( 10)? log 2 3? 1? Allo scopo di
Prerequisiti. A(x) B(x).
 Prerequisiti 4 Equazioni e disequazioni irrazionali Proprietà: la casistica delle equazioni e disequazioni irrazionali è ilitata, potendosi presentare un qualsivoglia numero di radici in ogni membro Noi
Prerequisiti 4 Equazioni e disequazioni irrazionali Proprietà: la casistica delle equazioni e disequazioni irrazionali è ilitata, potendosi presentare un qualsivoglia numero di radici in ogni membro Noi
Introduzione ai numeri complessi. Federico Lastaria. Analisi e Geometria 1. Numeri Complessi 1/16
 Introduzione ai numeri complessi Federico Lastaria. Analisi e Geometria 1. Numeri Complessi 1/16 Definizione (Campo complesso C. Prima definizione.) Il campo complesso C è costituito da tutte le espressioni
Introduzione ai numeri complessi Federico Lastaria. Analisi e Geometria 1. Numeri Complessi 1/16 Definizione (Campo complesso C. Prima definizione.) Il campo complesso C è costituito da tutte le espressioni
Numeri complessi. Esercizi
 Numeri complessi. Esercizi Mauro Saita e-mail: maurosaita@tiscalinet.it Indice Esercizi isposte e suggerimenti. 7 Esercizi Esercizio.. Scrivere in forma algebrica (x + iy) i seguenti numeri complessi:
Numeri complessi. Esercizi Mauro Saita e-mail: maurosaita@tiscalinet.it Indice Esercizi isposte e suggerimenti. 7 Esercizi Esercizio.. Scrivere in forma algebrica (x + iy) i seguenti numeri complessi:
Numeri complessi. Esercizi.
 Numeri complessi. Esercizi. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria. Marzo 014. Indice 1 Numeri complessi 1.1 Test di autovalutazione............................... 1. Test di
Numeri complessi. Esercizi. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria. Marzo 014. Indice 1 Numeri complessi 1.1 Test di autovalutazione............................... 1. Test di
sin 3 x x x cos x lim Verificare se la funzione: (x 2)2 f(x) = ln (x 2) sia dotata di minimo assoluto nell intervallo aperto (3, + )
 Esercizio 1 Verificare che il numero complesso z = ( 1 3 i)/2 algebrica: 2z 4 + 3z 3 2z 3 è radice dell equazione Esercizio 2 x 0 sin 3 x x x cos x Esercizio 3 Verificare se la funzione: (x 2)2 f(x) =
Esercizio 1 Verificare che il numero complesso z = ( 1 3 i)/2 algebrica: 2z 4 + 3z 3 2z 3 è radice dell equazione Esercizio 2 x 0 sin 3 x x x cos x Esercizio 3 Verificare se la funzione: (x 2)2 f(x) =
Numeri Complessi R 2. P = (x P,y P ) x P. z = (x,y) y P (0,0)
 Numeri Complessi Un numero complesso z può essere definito come una coppia ordinata (x,y) di numeri reali x e y. L insieme dei numeri complessi è denotato con C e può essere identificato con il piano cartesiano
Numeri Complessi Un numero complesso z può essere definito come una coppia ordinata (x,y) di numeri reali x e y. L insieme dei numeri complessi è denotato con C e può essere identificato con il piano cartesiano
Definizione 1 L insieme C dei numeri complessi è costituito dalle coppie (u,v) di numeri reali con le operazioni di somma e prodotto definite da:
 1 Numeri complessi L equazione x 2 + 1 = 0 (1) non ha soluzioni tra i numeri reali, ma ammettiamo che essa abbia una soluzione i in un qualche insieme di numeri C. Se in C valgono le usuali proprietà del
1 Numeri complessi L equazione x 2 + 1 = 0 (1) non ha soluzioni tra i numeri reali, ma ammettiamo che essa abbia una soluzione i in un qualche insieme di numeri C. Se in C valgono le usuali proprietà del
Compito di Analisi Matematica, Seconda parte, COGNOME: NOME: MATR.:
 Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
Fondamenti di ALGEBRA LINEARE E GEOMETRIA
 Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 7 Capitolo
Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 7 Capitolo
Facoltà di Architettura Valle Giulia Corso di Laurea Specialistica Quinquennale U.E. 1 CALCOLO INTEGRALE PER LE FUNZIONI DI UNA VARIABILE
 Facoltà di Architettura Valle Giulia Corso di Laurea Specialistica Quinquennale U.E. Istituzioni di Matematica 2 a.a. 2007-2008 http://www.dmmm.uniroma.it/persone/capitanelli CALCOLO INTEGRALE PER LE FUNZIONI
Facoltà di Architettura Valle Giulia Corso di Laurea Specialistica Quinquennale U.E. Istituzioni di Matematica 2 a.a. 2007-2008 http://www.dmmm.uniroma.it/persone/capitanelli CALCOLO INTEGRALE PER LE FUNZIONI
Insiemi numerici: i numeri complessi
 Insiemi numerici: i numeri complessi Riccarda Rossi Università di Brescia Analisi I Introduzione Storicamente: I si è passati da N a Z perché la sottrazione di due numeri naturali non è operazione interna
Insiemi numerici: i numeri complessi Riccarda Rossi Università di Brescia Analisi I Introduzione Storicamente: I si è passati da N a Z perché la sottrazione di due numeri naturali non è operazione interna
Sistemi e Tecnologie della Comunicazione
 Sistemi e Tecnologie della Comunicazione Complementi 1: numeri complessi I numeri complessi La definizione dei numeri complessi nasce dalla esigenza di trovare una soluzione alla equazione: x 1 che non
Sistemi e Tecnologie della Comunicazione Complementi 1: numeri complessi I numeri complessi La definizione dei numeri complessi nasce dalla esigenza di trovare una soluzione alla equazione: x 1 che non
0.1 Numeri complessi C
 0.1. NUMERI COMPLESSI C 1 0.1 Numeri complessi C Abbiamo visto sopra come l introduzione dei numeri irrazionali può essere motivata dalla necessità di trovare soluzione all equazione x = 0 che non ha soluzioni
0.1. NUMERI COMPLESSI C 1 0.1 Numeri complessi C Abbiamo visto sopra come l introduzione dei numeri irrazionali può essere motivata dalla necessità di trovare soluzione all equazione x = 0 che non ha soluzioni
Esercitazioni di Matematica Generale
 Esercitazioni di Matematica Generale Corso di laurea in Economia e Management Numeri Complessi - Funzioni Reali di Variabile Reale 05 Ottobre 017 Esercizio 1 Scrivere in forma algebrica (z = a + ib, a,
Esercitazioni di Matematica Generale Corso di laurea in Economia e Management Numeri Complessi - Funzioni Reali di Variabile Reale 05 Ottobre 017 Esercizio 1 Scrivere in forma algebrica (z = a + ib, a,
Appunti di Algebra Lineare - 1
 Appunti di Algebra Lineare - 1 Mongodi Samuele - s.mongodi@sns.it 10/11/2009 Le note che seguono non vogliono, né possono, essere il sostituto delle lezioni frontali di teoria e di esercitazione; anzi,
Appunti di Algebra Lineare - 1 Mongodi Samuele - s.mongodi@sns.it 10/11/2009 Le note che seguono non vogliono, né possono, essere il sostituto delle lezioni frontali di teoria e di esercitazione; anzi,
04 - Numeri Complessi
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA I Corso di laurea in Ingegneria Elettrotecnica A.A: 2018/2019 Codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA I Corso di laurea in Ingegneria Elettrotecnica A.A: 2018/2019 Codocente: Dott. Salvatore Fragapane Lezione 1-28/09/2018, dalle 10.00 alle 12.00 in aula 7 - Numeri
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA I Corso di laurea in Ingegneria Elettrotecnica A.A: 2018/2019 Codocente: Dott. Salvatore Fragapane Lezione 1-28/09/2018, dalle 10.00 alle 12.00 in aula 7 - Numeri
Analisi e Geometria 1
 Analisi e Geometria Politecnico di Milano Ingegneria Esercizi Numeri complessi. Scrivere in forma algebrica i seguenti numeri complessi. a) z + i) i) + i) i) b) z + i) i) + i) + + i) i) + i) + i) c) z
Analisi e Geometria Politecnico di Milano Ingegneria Esercizi Numeri complessi. Scrivere in forma algebrica i seguenti numeri complessi. a) z + i) i) + i) i) b) z + i) i) + i) + + i) i) + i) + i) c) z
Esercizio 1 Calcolare i limiti delle seguenti successioni per n + :
 Esercizio 1 Calcolare i limiti delle seguenti successioni per n + : 1. n = (n 2 + sin n) sin 2 n 2. n = n cos( π ) sin( 2π ) n 3n 2 3. n = n e sin 1 n n 4. n = log a (n n 2 1) + log a n 5. n = n + 5 n
Esercizio 1 Calcolare i limiti delle seguenti successioni per n + : 1. n = (n 2 + sin n) sin 2 n 2. n = n cos( π ) sin( 2π ) n 3n 2 3. n = n e sin 1 n n 4. n = log a (n n 2 1) + log a n 5. n = n + 5 n
Geometria e Algebra Lineare
 Università di Bergamo Primo anno di Ingegneria Anno accademico 20182019 Geometria e Algebra Lineare Domande su: Numeri complessi e Risoluzione di sistemi con il metodo di Gauss 1 Numeri complessi Esercizio
Università di Bergamo Primo anno di Ingegneria Anno accademico 20182019 Geometria e Algebra Lineare Domande su: Numeri complessi e Risoluzione di sistemi con il metodo di Gauss 1 Numeri complessi Esercizio
Esercitazione sui numeri complessi
 . Esponeniali e logaritmi. Sviluppi in serie di potene 3. Singolarità e residui 4. Integrali su circuiti semplici. Esponeniali e logaritmi Esercitaione sui numeri complessi February 7, 03 Eserciio. Calcolare
. Esponeniali e logaritmi. Sviluppi in serie di potene 3. Singolarità e residui 4. Integrali su circuiti semplici. Esponeniali e logaritmi Esercitaione sui numeri complessi February 7, 03 Eserciio. Calcolare
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
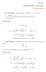 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
Foglio N.1 Numeri Complessi. Ricordiamo che l insieme delle coppie reali
 Foglio N.1 Numeri Complessi Ricordiamo che l insieme delle coppie reali f( ) : 2 Rg che indichiamo con R 2, con le seguenti operazioni: Addizione: ( )+( ) =( + + ) Prodotto per uno scalare: ( ) =( ) 2
Foglio N.1 Numeri Complessi Ricordiamo che l insieme delle coppie reali f( ) : 2 Rg che indichiamo con R 2, con le seguenti operazioni: Addizione: ( )+( ) =( + + ) Prodotto per uno scalare: ( ) =( ) 2
Esponenziale complesso
 Esponenziale complesso Paola Rubbioni Analisi Matematica II - CdL in Ingegneria Informatica ed Elettronica a.a. 2016/2017 1 Serie nel campo complesso Per fornire il concetto di serie nel campo complesso
Esponenziale complesso Paola Rubbioni Analisi Matematica II - CdL in Ingegneria Informatica ed Elettronica a.a. 2016/2017 1 Serie nel campo complesso Per fornire il concetto di serie nel campo complesso
1. Scrivere in forma algebrica il seguente numero complesso:
 TERZA LEZIONE (8/10/009) Argomenti trattati: NUMERI COMPLESSI - rappresentazione algebrica e trigonometrica, soluzioni di disequazioni, Formule di De Moivre, radici n esime, equazioni. 1 Esercizi svolti
TERZA LEZIONE (8/10/009) Argomenti trattati: NUMERI COMPLESSI - rappresentazione algebrica e trigonometrica, soluzioni di disequazioni, Formule di De Moivre, radici n esime, equazioni. 1 Esercizi svolti
Note sui numeri complessi
 Note sui numeri complessi 1 Introduzione Queste note raccolgono alcune nozioni fondamentali sui numeri complessi. La trattazione non ha alcuna pretesa di completezza e si limita a richiamare gli elementi
Note sui numeri complessi 1 Introduzione Queste note raccolgono alcune nozioni fondamentali sui numeri complessi. La trattazione non ha alcuna pretesa di completezza e si limita a richiamare gli elementi
Esercitazione sui numeri complessi
 Esercitazione sui numeri complessi Davide Boscaini Queste sono le note da cui ho tratto le esercitazioni del giorno Ottobre 0. Come tali sono ben lungi dall essere esenti da errori, invito quindi chi ne
Esercitazione sui numeri complessi Davide Boscaini Queste sono le note da cui ho tratto le esercitazioni del giorno Ottobre 0. Come tali sono ben lungi dall essere esenti da errori, invito quindi chi ne
Esercizi di Analisi Matematica 1, utili per la preparazione all esame scritto - Seconda parte SOLUZIONI
 Esercizi di Analisi Matematica Esercizi di Analisi Matematica, utili per la preparazione all esame scritto - Seconda parte SOLUZIONI Es. Per ognuna delle seguenti figure, dire se la curva nel piano cartesiano
Esercizi di Analisi Matematica Esercizi di Analisi Matematica, utili per la preparazione all esame scritto - Seconda parte SOLUZIONI Es. Per ognuna delle seguenti figure, dire se la curva nel piano cartesiano
Note sui numeri complessi
 Note sui numeri complessi 1 Introduzione Queste note raccolgono alcune nozioni fondamentali sui numeri complessi. La trattazione non ha alcuna pretesa di completezza e si limita a richiamare gli elementi
Note sui numeri complessi 1 Introduzione Queste note raccolgono alcune nozioni fondamentali sui numeri complessi. La trattazione non ha alcuna pretesa di completezza e si limita a richiamare gli elementi
Modelli e Metodi Matematici della Fisica. S1/AC
 Modelli e Metodi Matematici della Fisica. S/AC Filippo Cesi 2 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 2 CFU (AA 2-) 6 CFU (solo anal. funzionale) 6 CFU (solo anal. complessa)
Modelli e Metodi Matematici della Fisica. S/AC Filippo Cesi 2 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 2 CFU (AA 2-) 6 CFU (solo anal. funzionale) 6 CFU (solo anal. complessa)
(a, b) + (c, d) = (a + c, b + d) (1) (a, b) + (0, 0) = (a + 0, b + 0) = (a, b) (a, b) + ( a, b) = (a a, b b) = (0, 0)
 Numeri Complessi I numeri complessi sono un'estensione dei numeri reali, vengono introdotti anchè tutte le equazioni algebriche ammettano soluzioni. Dato l'insieme R = R R = { (a, b) R R } deniamo per
Numeri Complessi I numeri complessi sono un'estensione dei numeri reali, vengono introdotti anchè tutte le equazioni algebriche ammettano soluzioni. Dato l'insieme R = R R = { (a, b) R R } deniamo per
Esercizi. Alberto Saracco. December 11, Esercizio 1.1 Calcola il prodotto tra z = 1 + 2i e il suo coniugato z.
 1 Esercizi Alberto Saracco December 11, 2009 1 Numeri complessi 1.1 Esercizi Esercizio 1.1 Calcola il prodotto tra z = 1 + 2i e il suo coniugato z. Esercizio 1.2 Calcola il prodotto tra z = 1 i e il suo
1 Esercizi Alberto Saracco December 11, 2009 1 Numeri complessi 1.1 Esercizi Esercizio 1.1 Calcola il prodotto tra z = 1 + 2i e il suo coniugato z. Esercizio 1.2 Calcola il prodotto tra z = 1 i e il suo
Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 2007 Tema A
 Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 7 Tema A Cognome e Nome Matr... Disegnare un grafico approssimativo della funzione f() log( ). Indicare sul grafico
Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 7 Tema A Cognome e Nome Matr... Disegnare un grafico approssimativo della funzione f() log( ). Indicare sul grafico
Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 14 gennaio 2019 Parte B Tema B1
 Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 14 gennaio 2019 Parte B Tema B1 Tempo a disposizione: due ore. Calcolatrici, libri e appunti non sono
Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 14 gennaio 2019 Parte B Tema B1 Tempo a disposizione: due ore. Calcolatrici, libri e appunti non sono
CAPITOLO 1. I numeri complessi
 CAPITOLO 1 I numeri complessi È noto che l equazione x 2 + 1 = 0 non ha soluzioni reali. Costruiamo un ampliamento dell insieme dei numeri reali in modo che anche questa equazione possa avere soluzione.
CAPITOLO 1 I numeri complessi È noto che l equazione x 2 + 1 = 0 non ha soluzioni reali. Costruiamo un ampliamento dell insieme dei numeri reali in modo che anche questa equazione possa avere soluzione.
I numeri complessi. Andrea Corli 31 agosto Motivazione 1. 2 Definizioni 1. 3 Forma trigonometrica di un numero complesso 3
 I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
ISTITUZIONI DI MATEMATICA I. (prof. M.P.Cavaliere) NUMERI COMPLESSI E EQUAZIONI
 ISTITUZIONI DI MATEMATICA I (prof. M.P.Cavaliere) NUMERI COMPLESSI E EQUAZIONI I numeri complessi Anche se il campo reale è sufficientemente ricco per la maggior parte delle applicazioni, tuttavia le equazioni
ISTITUZIONI DI MATEMATICA I (prof. M.P.Cavaliere) NUMERI COMPLESSI E EQUAZIONI I numeri complessi Anche se il campo reale è sufficientemente ricco per la maggior parte delle applicazioni, tuttavia le equazioni
Algebra Lineare Ingegneria Chimica Anno Accademico 2018/19
 Algebra Lineare Ingegneria Chimica Anno Accademico 2018/19 Caboara Lezione 1 ottobre 2018 Esercizio 1 Disegnare nel piano di Gauss z C z < 2} L interno della circonfernza di centro l origine e raggio 2,
Algebra Lineare Ingegneria Chimica Anno Accademico 2018/19 Caboara Lezione 1 ottobre 2018 Esercizio 1 Disegnare nel piano di Gauss z C z < 2} L interno della circonfernza di centro l origine e raggio 2,
Scomposizione in fratti semplici
 0.0.. Scomposizione in fratti semplici La determinazione dell evoluzione libera e dell evoluzione forzata di un sistema lineare stazionario richiedono l antitrasformazione di una funzione razionale fratta
0.0.. Scomposizione in fratti semplici La determinazione dell evoluzione libera e dell evoluzione forzata di un sistema lineare stazionario richiedono l antitrasformazione di una funzione razionale fratta
Compiti di geometria & algebra lineare. Anno: 2004
 Compiti di geometria & algebra lineare Anno: 24 Anno: 24 2 Primo compitino di Geometria e Algebra 7 novembre 23 totale tempo a disposizione : 3 minuti Esercizio. [8pt.] Si risolva nel campo complesso l
Compiti di geometria & algebra lineare Anno: 24 Anno: 24 2 Primo compitino di Geometria e Algebra 7 novembre 23 totale tempo a disposizione : 3 minuti Esercizio. [8pt.] Si risolva nel campo complesso l
NUMERI COMPLESSI. I numeri complessi
 NATURALI INTERI RAZIONALI REALI IRRAZIONALI COMPLESSI NUMERI COMPLESSI Definiione Rappresentaione Forma trig. ed esp. Operaioni Addiione Coniugio Moltiplicaione Potena n-esima Reciproco Diisione Radice
NATURALI INTERI RAZIONALI REALI IRRAZIONALI COMPLESSI NUMERI COMPLESSI Definiione Rappresentaione Forma trig. ed esp. Operaioni Addiione Coniugio Moltiplicaione Potena n-esima Reciproco Diisione Radice
1. La serie esponenziale. z n n! é una serie di potenze convergente in tutto il piano: infatti la serie dei moduli
 Ahlfors, pag.42,..,47 Bozza da rivedere La serie (1) 1. La serie esponenziale é una serie di potenze convergente in tutto il piano: infatti la serie dei moduli z n é una serie a termini reali non negativi
Ahlfors, pag.42,..,47 Bozza da rivedere La serie (1) 1. La serie esponenziale é una serie di potenze convergente in tutto il piano: infatti la serie dei moduli z n é una serie a termini reali non negativi
[FE] Funzioni elementari
![[FE] Funzioni elementari [FE] Funzioni elementari](/thumbs/94/118385503.jpg) [FE] Funzioni elementari 1 Problema. Trovare tutte le soluzioni dell equazione sin z =. Disegnare accuratamente sul piano complesso le soluzioni che si trovano all interno del rettangolo di vertici: (
[FE] Funzioni elementari 1 Problema. Trovare tutte le soluzioni dell equazione sin z =. Disegnare accuratamente sul piano complesso le soluzioni che si trovano all interno del rettangolo di vertici: (
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulle funzioni di variabile complessa (1)
 Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulle funzioni di variabile complessa 1) Marco Bramanti Politecnico di Milano November 7, 2016 1 Funzioni olomorfe e campi di
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulle funzioni di variabile complessa 1) Marco Bramanti Politecnico di Milano November 7, 2016 1 Funzioni olomorfe e campi di
Corso di Geometria III - A.A. 2016/17 Esercizi
 Corso di Geometria III - A.A. 216/17 Esercizi (ultimo aggiornamento del file: 2 ottobre 215) Esercizio 1. Calcolare (1 + 2i) 3, ( ) 2 + i 2, (1 + i) n + (1 i) n. 3 2i Esercizio 2. Sia z = x + iy. Determinare
Corso di Geometria III - A.A. 216/17 Esercizi (ultimo aggiornamento del file: 2 ottobre 215) Esercizio 1. Calcolare (1 + 2i) 3, ( ) 2 + i 2, (1 + i) n + (1 i) n. 3 2i Esercizio 2. Sia z = x + iy. Determinare
Matematica con esercitazioni, Modulo 2. Analisi matematica. Diario delle lezioni.
 Matematica con esercitazioni, Modulo. Analisi matematica. Diario delle lezioni. Laurea triennale Chimica e tecnologie per l ambiente e per i materiali. Rimini Avvertenza per gli studenti: il libro di testo
Matematica con esercitazioni, Modulo. Analisi matematica. Diario delle lezioni. Laurea triennale Chimica e tecnologie per l ambiente e per i materiali. Rimini Avvertenza per gli studenti: il libro di testo
I numeri reali x e y sono detti parte reale e parte immaginaria del numero complesso x + iy esiscrive Re (x + iy) =x e Im (x + iy) =y.
 Numeri complessi Chiamiamo numero complesso ogni scrittura del tipo x + iy con x, y R,dove i è un simbolo, detto unità immaginaria. Il loro insieme si denota con C. I numeri reali x e y sono detti parte
Numeri complessi Chiamiamo numero complesso ogni scrittura del tipo x + iy con x, y R,dove i è un simbolo, detto unità immaginaria. Il loro insieme si denota con C. I numeri reali x e y sono detti parte
Matematica del Continuo Informatica per la Comunicazione Digitale Anno accademico Modelli di esercizi per la Parte 1
 Matematica del Continuo Informatica per la Comunicazione Digitale Anno accademico 018-019 Modelli di esercizi per la Parte 1 La Parte 1 del compito scritto, o delle prove intermedie, potrebbe includere
Matematica del Continuo Informatica per la Comunicazione Digitale Anno accademico 018-019 Modelli di esercizi per la Parte 1 La Parte 1 del compito scritto, o delle prove intermedie, potrebbe includere
NUMERI COMPLESSI. Test di autovalutazione
 NUMERI COMPLESSI Test di autovalutazione 1. Se due numeri complessi z 1 e z 2 sono rappresentati nel piano di Gauss da due punti simmetrici rispetto all origine: (a) sono le radici quadrate di uno stesso
NUMERI COMPLESSI Test di autovalutazione 1. Se due numeri complessi z 1 e z 2 sono rappresentati nel piano di Gauss da due punti simmetrici rispetto all origine: (a) sono le radici quadrate di uno stesso
Facoltà di Ingegneria, Test di recupero del debito 01/09/2011 tempo assegnato: 45 m codice prova: A
 Facoltà di Ingegneria, Test di recupero del debito 01/09/2011 tempo assegnato: 45 m codice prova: A ATTENZIONE! Il test è composto da 15 domande, ognuna con quattro risposte di cui una sola corretta. Il
Facoltà di Ingegneria, Test di recupero del debito 01/09/2011 tempo assegnato: 45 m codice prova: A ATTENZIONE! Il test è composto da 15 domande, ognuna con quattro risposte di cui una sola corretta. Il
CENNI DI TRIGONOMETRIA E CENNI SUI NUMERI COMPLESSI PER L ELETTROTECNICA
 CENNI DI TRIGONOMETRIA E CENNI SUI NUMERI COMPLESSI PER L ELETTROTECNICA (per classi elettrotecnica e automazione) Autore Nunzio Siciliano rev. Nov.2014 Quest'opera è distribuita con Licenza Creative Commons
CENNI DI TRIGONOMETRIA E CENNI SUI NUMERI COMPLESSI PER L ELETTROTECNICA (per classi elettrotecnica e automazione) Autore Nunzio Siciliano rev. Nov.2014 Quest'opera è distribuita con Licenza Creative Commons
NUMERI COMPLESSI. Esercizi svolti., e) i 34, f) i 7. 10 i
 NUMERI COMPLESSI Esercizi svolti 1. Calcolare le seguenti potenze di i: a) i, b) i, c) i 4, d) 1 i, e) i 4, f) i 7. Semplificare le seguenti espressioni: a) ( i) i(1 ( 1 i), b) ( + i)( i) 5 + 1 ) 10 i,
NUMERI COMPLESSI Esercizi svolti 1. Calcolare le seguenti potenze di i: a) i, b) i, c) i 4, d) 1 i, e) i 4, f) i 7. Semplificare le seguenti espressioni: a) ( i) i(1 ( 1 i), b) ( + i)( i) 5 + 1 ) 10 i,
OPERAZIONI FONDAMENTALI CON I NUMERI COMPLESSI
 I Numeri Complessi L'esigenza di introdurre i numeri complessi è dovuta al fatto che diverse operazioni sui numeri reali IR non sempre sono possibili. x 2 + 1 = 0? log (-10)? log -2 3? (-1) ½? Allo scopo
I Numeri Complessi L'esigenza di introdurre i numeri complessi è dovuta al fatto che diverse operazioni sui numeri reali IR non sempre sono possibili. x 2 + 1 = 0? log (-10)? log -2 3? (-1) ½? Allo scopo
Risoluzione di ax 2 +bx+c = 0 quando a, b, c sono numeri complessi.
 LeLing14: Ancora numeri complessi e polinomi Ārgomenti svolti: Risoluzione di ax + bx + c = 0 quando a, b, c sono numeri complessi La equazione di Eulero: e i θ = cos(θ) + i sin(θ) La equazione x n = a,
LeLing14: Ancora numeri complessi e polinomi Ārgomenti svolti: Risoluzione di ax + bx + c = 0 quando a, b, c sono numeri complessi La equazione di Eulero: e i θ = cos(θ) + i sin(θ) La equazione x n = a,
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 7 FEBBRAIO 2017
 METODI MATEMATICI PER LA FIICA PROVA CRITTA - 7 FEBBRAIO 7 i risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 6/3) i calcoli l integrale V = L z dz L = {z : z ( )} {z : Re(z) = Im(z)
METODI MATEMATICI PER LA FIICA PROVA CRITTA - 7 FEBBRAIO 7 i risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 6/3) i calcoli l integrale V = L z dz L = {z : z ( )} {z : Re(z) = Im(z)
Funzioni Complesse di variabile complessa
 Funzioni Complesse di variabile complessa Docente:Alessandra Cutrì Richiami sui numeri complessi Indichiamo con C il campo dei Numeri complessi z = x + iy C, ses x, y R i := 1 (Rappresentazione cartesiana
Funzioni Complesse di variabile complessa Docente:Alessandra Cutrì Richiami sui numeri complessi Indichiamo con C il campo dei Numeri complessi z = x + iy C, ses x, y R i := 1 (Rappresentazione cartesiana
2 + 4i 3. = i. = 1 z 2 1 i (iii) Rez + Imz = 2. = i z = i.
 Esercizio 1 Esprimete in forma algebrica i seguenti numeri complessi : (i) (5 i)( i) (ii) + i (iii) i (iv) 1 + i i. (i) (5 i)( i) = (15 ) + i( 5 6) = 1 11i; (ii) + i = = + i; (iii) i = i + i + i = 6 +
Esercizio 1 Esprimete in forma algebrica i seguenti numeri complessi : (i) (5 i)( i) (ii) + i (iii) i (iv) 1 + i i. (i) (5 i)( i) = (15 ) + i( 5 6) = 1 11i; (ii) + i = = + i; (iii) i = i + i + i = 6 +
Disequazioni in una variabile. Disequazioni in due variabili
 Disequazioni in una variabile Disequazioni in due variabili 2 () 2 3 > (2) 2 + + > (3) 2 3 + 2 < (4) 2 > + (5) 2 < 3 (6) 3 8 > 5 + 3 + + 5 (7) + < 2 < 2 (8) 2 α (α parametro reale) (9) 3 log /2 ( ) < 2
Disequazioni in una variabile Disequazioni in due variabili 2 () 2 3 > (2) 2 + + > (3) 2 3 + 2 < (4) 2 > + (5) 2 < 3 (6) 3 8 > 5 + 3 + + 5 (7) + < 2 < 2 (8) 2 α (α parametro reale) (9) 3 log /2 ( ) < 2
Esonero di Analisi Matematica I (A)
 Esonero di Analisi Matematica I (A) Ingegneria Edile, 19 dicembre 2000 () 1. Studiare il seguente ite: x 0 log 2 (cos x) ( 3 1 x 1 ) e (x3 ) 1. 2. Dire per quali numeri complessi entrambe le radici quadrate
Esonero di Analisi Matematica I (A) Ingegneria Edile, 19 dicembre 2000 () 1. Studiare il seguente ite: x 0 log 2 (cos x) ( 3 1 x 1 ) e (x3 ) 1. 2. Dire per quali numeri complessi entrambe le radici quadrate
Le funzioni trigonometriche e l esponenziale complesso
 Le funzioni trigonometriche e l esponenziale complesso 1 r1 Sia xoy un sistema di riferimento cartesiano ortonormale Una circonferenza che: 1. ha centro l origine O degli assi y. ha raggio r1 O x E una
Le funzioni trigonometriche e l esponenziale complesso 1 r1 Sia xoy un sistema di riferimento cartesiano ortonormale Una circonferenza che: 1. ha centro l origine O degli assi y. ha raggio r1 O x E una
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (E) Dire il comportamento della serie n=0 n+2n n 3 +n! motivando la risposta. [2]. (E) Dire il comportamento della serie n=0 n+2n n 3 +3 n motivando la risposta.
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (E) Dire il comportamento della serie n=0 n+2n n 3 +n! motivando la risposta. [2]. (E) Dire il comportamento della serie n=0 n+2n n 3 +3 n motivando la risposta.
Svolgimento degli esercizi del Capitolo 1
 Analisi Matematica a edizione Svolgimento degli esercizi del Capitolo a) Si ha perciò si distinguono due casi: I) se x < 7,siha x 7 se x 7 x 7 7 x se x < 7, x 7 7 x x x 5 x 5, e poiché 5 > 7 la disequazione
Analisi Matematica a edizione Svolgimento degli esercizi del Capitolo a) Si ha perciò si distinguono due casi: I) se x < 7,siha x 7 se x 7 x 7 7 x se x < 7, x 7 7 x x x 5 x 5, e poiché 5 > 7 la disequazione
e non ci possono chiaramente essere minori di ordine più grande per cui il rango per minori è 2. Rango per pivot: Svolgiamo la riduzione
 18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
II Esonero di Matematica Discreta - a.a. 06/07. Versione B
 II Esonero di Matematica Discreta - a.a. 06/07 1. Nell anello dei numeri interi Z: Versione B a. Determinare la scrittura posizionale in base 9 del numero che in base 10 si scrive) 5293 e la scrittura
II Esonero di Matematica Discreta - a.a. 06/07 1. Nell anello dei numeri interi Z: Versione B a. Determinare la scrittura posizionale in base 9 del numero che in base 10 si scrive) 5293 e la scrittura
b+ 1 x b+1 log x x e x sin x tan x log cos x cot x log sin x 1 cos 2 x tan x 1 sin 2 x 1 1 x 2 arcsin x 1 arctan x tanh x 1 sinh 2 x coth x 1
 Capitolo Integrali b Funzione (b \{ }) e Primitiva b+ b+ log e sin cos cos sin tan log cos cot log sin cos tan sin cot arcsin + arctan sinh cosh cosh sinh tanh log(cosh ) coth log(sinh ) cosh tanh sinh
Capitolo Integrali b Funzione (b \{ }) e Primitiva b+ b+ log e sin cos cos sin tan log cos cot log sin cos tan sin cot arcsin + arctan sinh cosh cosh sinh tanh log(cosh ) coth log(sinh ) cosh tanh sinh
ANALISI MATEMATICA III (ELM+TEM) A.A Prerequisiti
 ANALISI MATEMATICA III (ELM+TEM) A.A. 2012-2013 Prerequisiti March 20, 2013 1 Richiami sui numeri complessi 1.1 Forma algebrica. Un numero complesso z in forma algebrica è un numero del tipo z = a + jb
ANALISI MATEMATICA III (ELM+TEM) A.A. 2012-2013 Prerequisiti March 20, 2013 1 Richiami sui numeri complessi 1.1 Forma algebrica. Un numero complesso z in forma algebrica è un numero del tipo z = a + jb
I NUMERI COMPLESSI Nell insieme dei numeri reali R non è possibile risolvere l'equazione di secondo grado
 COME NASCONO I NUMERI COMPLESSI Lo spunto per la nascita dei numeri complessi derivò dal tentativo di soluzione di un problema chiaramente impossibile. Dividere 10 in due parti il cui prodotto dia 40.
COME NASCONO I NUMERI COMPLESSI Lo spunto per la nascita dei numeri complessi derivò dal tentativo di soluzione di un problema chiaramente impossibile. Dividere 10 in due parti il cui prodotto dia 40.
Numeri complessi. x 2 = 1.
 1 Numeri complessi Nel corso dello studio della matematica si assiste ad una progressiva estensione del concetto di numero. Dall insieme degli interi naturali N si passa a quello degli interi relativi
1 Numeri complessi Nel corso dello studio della matematica si assiste ad una progressiva estensione del concetto di numero. Dall insieme degli interi naturali N si passa a quello degli interi relativi
II Esonero di Matematica Discreta - a.a. 06/07. Versione C
 II Esonero di Matematica Discreta - a.a. 06/07 1. Nell anello dei numeri interi Z: Versione C a. Determinare la scrittura posizionale in base 9 del numero che in base 10 si scrive) 5612 e la scrittura
II Esonero di Matematica Discreta - a.a. 06/07 1. Nell anello dei numeri interi Z: Versione C a. Determinare la scrittura posizionale in base 9 del numero che in base 10 si scrive) 5612 e la scrittura
Esercizi svolti sugli integrali
 Esercizio. Calcolare il seguente integrale indefinito x dx. Soluzione. Poniamo da cui x = t derivando rispetto a t abbiamo t = x x = t dx dt = quindi ( t x dx = ) poiché t = t, abbiamo t dt = = in definitiva:
Esercizio. Calcolare il seguente integrale indefinito x dx. Soluzione. Poniamo da cui x = t derivando rispetto a t abbiamo t = x x = t dx dt = quindi ( t x dx = ) poiché t = t, abbiamo t dt = = in definitiva:
