Esercizio Determinare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (i) y = 3y cos(x);
|
|
|
- Albana Cavallaro
- 4 anni fa
- Visualizzazioni
Transcript
1 134 Capitolo 4. Equazioni differenziali ordinarie del problema di Cauchy (4.28) bisogna risolvere il sistema lineare (nelle incognite c 1,..., c n )) c 1 y 1 (x 0 ) c n y n (x 0 ) = y 0, c 1 y 1 (x 0) c n y n (x 0) = y 1,.. c 1 y (n 1) 1 (x 0 ) c n y n (n 1) = y n 1, che può essere riscritto in forma matriciale come W(x 0 )C = Y 0 dove W(x 0 ) è la matrice wronskiana (valutata in x 0 ) costruita a partire dalle funzioni y 1,...,y n e C = (c 1,..., c n ). Nel caso in cui si utilizzi il metodo di variazione delle costanti per risolvere l equazione differenziale in (4.28), la soluzione del problema di Cauchy è data da n ( x ) y(x) = y s (x) ĉ s + (W 1 (t)b(t)) s dt, per ogni x I, x 0 s=1 dove il vettore ĉ = (ĉ 1,..., ĉ n ) è dato da c = W 1 (x 0 )Y 0 e Y 0 = (y 0,..., y n 1 ). 4.5 Esercizi Esercizio Determinare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (i) y = 3y cos(x); (ii) y = y 2x + log(x); (iii) x 2 y = 2y 3; (iv) y = e 2x y x ; (v) y = y log(x) + x x ; (vi) y = y cos(x) + sin(x)cos(x). Esercizio (i) Determinare tutte le soluzioni dell equazione differenziale del primo ordine y (x) = (x + y(x)) 2 x y(x) 1. (ii) Determinare tutte le soluzioni dell equazione differenziale del primo ordine y = y ( y ) x log. x Suggerimento: porre z(x) = y(x)/x.
2 4.5. Esercizi 135 Esercizio Determinare le soluzioni dei seguenti problemi di Cauchy: (i) (ii) y = 3x 2 y + x 2 x 5, y(0) = 0; y = (1 + y 2 )sin(x), y(0) = 1. Esercizio Determinare le soluzioni dei seguenti problemi di Cauchy: (i) (ii) (iii) (iv) (v) y = 2xy + 3x 3 y 2/3, y(0) = 8; y = y + sin(x)y 1/3, y( π 2 ) = 1; y y(x xy) = 0, y(0) = 1 2 ; y = ( ) 3 y + y 1/3, y(1) = 1; y + y 4x + 3x 2 3x = sin(x) 3x y 2, y(1) = 2. Esercizio Determinare l integrale generale delle seguenti equazioni differenziali lineari omogenee a coefficienti costanti: (i) y y = 0; (ii) y + 4y = 0; (iii) y + 4y + 2y = 0; (iv) y = 0; (v) y = 0; (vi) y 4y + 6y 4y = 0; (vii) y + 4y = 0; (viii) y + 4y = 0; (ix) y iv + 2y + y = 0. Esercizio Determinare l integrale generale delle seguenti equazioni differenziali lineari a coefficienti costanti: (i) y + y = x;
3 136 Capitolo 4. Equazioni differenziali ordinarie (ii) y + y = xe x ; (iii) y 2y = x 2 + e 2x ; (iv) y + y = cos(x); (v) y 5y + 9y 5y = x + e 2x. Esercizio Data un equazione differenziale di ordine tre lineare omogenea a coefficienti costanti, quale tra i seguenti può essere il suo integrale generale? (i) c 1 + c 2 x + c 3 e 3x per ogni x R, al variare di c 1, c 2, c 3 R; (ii) c 1 + c 2 x + c 3 cos(x) per ogni x R, al variare di c 1, c 2, c 3 R; (iii) c 1 + c 2 x + c 3 e 3x + x 2 per ogni x R, al variare di c 1, c 2, c 3 R; (iv) c 1 + c 2 x + x 2 per ogni x R, al variare di c 1, c 2 R. Esercizio Di quale delle seguenti equazioni, la famiglia di funzioni x c 1 e x + c 2 e 2x + x 2 (c 1, c 2 R), è l integrale generale? (i) y y 2y = 0; (ii) y y y = x 2 ; (iii) y iv y 2y = 4; (iv) y y 2y = 2 2x 2x 2. Esercizio Un equazione differenziale lineare con integrale generale ce 3x + e 2x, al variare di c R, è (i) omogenea a coefficienti costanti del secondo ordine; (ii) non omogenea a coefficienti costanti del primo ordine; (iii) non omogenea a coefficienti costanti del primo ordine; (iv) omogenea a coefficienti costanti del primo ordine. Esercizio La funzione y(x) = 3e 2x 2xe 3x può essere l integrale particolare di un equazione differenziale del primo ordine lineare ed omogenea a coefficienti costanti? Esercizio La funzione y(x) = c 1 e 2x + c 2 xe 3x può essere l integrale generale di un equazione differenziale del secondo ordine lineare ed omogenea a coefficienti costanti? Esercizio Data un equazione differenziale del secondo ordine lineare ed omogenea a coefficienti costanti tale che una sua qualsiasi soluzione tende a 0 quando x + assumendo infinite volte il valore 0, cosa si può dire delle soluzioni del polinomio caratteristico?
4 4.6. Soluzioni 137 Esercizio Data un equazione differenziale del secondo ordine lineare ed omogenea a coefficienti costanti tale che una sua qualsiasi soluzione non ha limite quando x + essendo però limitata, cosa si può dire delle soluzioni del polinomio caratteristico? Esercizio Si consideri l equazione differenziale lineare del secondo ordine a coefficienti costanti y + a 0 y + a 1 y = e 3x. Stabilire quali condizioni devono verificare i coefficienti a 0 e a 1 affinché tutte le soluzioni di tale equazione tendano a + quando x +? Suggerimento: analizzare la forma delle soluzioni dell equazione al variare delle radici del polinomio caratteristico. Esercizio Determinare l integrale generale della seguente equazione differenziale lineare a coefficienti costanti y y = 1 + e x. Suggerimento: si usi il metodo di variazione delle costanti. 4.6 Soluzioni (i) L integrale generale è dato da y(x) = ce 3x cos(x) 1 10 sin(x) per ogni x R, al variare di c R. (ii) Ha senso studiare l equazione differenziale in I + = ]0, + [ e in I = ], 0[. In entrambi gli insiemi l integrale generale è dato da y(x) = c ± x 2 xlog(x) x per ogni x I ±, al variare di c ± R. (iii) Dividendo per x 0, l equazione si trasforma nell equazione equivalente y = 2 x 2 y 3 x 2, le cui soluzioni in I + = ]0, + [ e in I = ], 0[ sono le funzioni y ± (x) = c ± e 2 x 3 2, definite per x I ±, al variare di c ± R. (iv) Le soluzioni in I + = ]0, + [ e in I = ], 0[ sono le funzioni y ± (x) = c± x 1 2 e 2x 1 4x e 2x, definite per x I ±, al variare di c ± R. (v) L integrale generale dell equazione è dato dalle funzioni y(x) = ce x x x + x x, definite per x > 0, al variare di c R. (vi) L integrale generale dell equazione è dato dalle funzioni y(x) = ce sin(x) +sin(x) 1, definite per x R, al variare di c R (i) Questa è un equazione differenziale del tipo y = f(ax + by + c), essendo f(x, y) = (x+y) 2 x y 1, e si risolve con la sostituzione z = ax+by+c, in questo caso z = x + y. Si ha dunque dz d(y + x) = = y + 1 = ((x + y) 2 x y 1) + 1 = z 2 z, dx dx
5 138 Capitolo 4. Equazioni differenziali ordinarie e l equazione z = z 2 z è a variabili separabili, ed ha come integrale generale le funzioni z(x) = (1 + ce x ) 1, al variare di c R, più la soluzione z 0. L integrale generale cercato è dunque y(x) = x + (1 + ce x ) 1, al variare di c R, più la soluzione y(x) = x. (ii) In questo caso abbiamo f(x, y) = g( y x ). Operando la sostituzione z = y x si ottiene dz dx = d(y/x) = y y/x (y/x)log(y/x) y/x = dx x x z log z z = z log z z, x e l equazione z = x è a variabili separabili con integrale generale z(x) = e 1+c x per ogni x R, al variare di c R. Quindi l integrale generale dell equazione di partenza è y(x) = xe 1+c x, al variare di c R (i) È il problema di Cauchy associato ad un equazione lineare di ordine 1. L integrale generale è ce x + x 3 /3, e la soluzione del problema di Cauchy è la funzione y : R R data da y(x) = x 3 /3 per ogni x R. (ii) È il problema di Cauchy associato ad un equazione a variabili separabili. La soluzione è la funzione y : I R definita da ( π ) y(x) = tan cos(x), per ogni x I, dove I = x R : cos(x) > 1 π 4 } Sono tutti problemi di Cauchy associati ad equazioni di Bernoulli. (i) Una soluzione (non l unica: si veda l osservazione alla fine dell Esempio 4.3.5) è la 3 funzione y(x) = (2e x x2 2) 9 definita in R. (ii) Una soluzione è data da y(x) = ( ) e π 2 3 e 3 x cos(x) 4 } 3/2 13 sin(x), definita nell insieme I = x R : ( ) 4 e π 3 e 2 3 x 6 13 cos(x) 4 13 sin(x) > 0}. ) 1 (iii) L unica soluzione del problema è la funzione y(x) = (e x definita in R. Osserviamo che l equazione, si può trattare come equazione a variabili separabili in quanto y = xy(1 y). ( (iv) L unica soluzione del problema è la funzione y(x) = definita in ) 3 e 1 x x ]0, + [. (v) L unica soluzione del problema è la funzione y(x) = x 1/3 (8+cos(1) cos(x)) 1/3 definita in ]0, + [ (i) Il polinomio caratteristico è λ 2 1, le cui soluzioni sono λ = 1 e λ = 1. Quindi y(x) = c 1 e x + c 2 e x per ogni x R, al variare di c 1 e c 2 in R.
6 4.6. Soluzioni 139 (ii) Il polinomio caratteristico è λ 2 +4, le cui soluzioni sono λ = 2 ı e λ = 2 ı. Quindi y(x) = c 1 cos(2x) + c 2 sin(2x) per ogni x R, al variare di c 1 e c 2 in R. (iii) Il polinomio caratteristico è λ 2 + 4λ + 2, le cui soluzioni sono λ = e λ = 2 2. Quindi y(x) = c 1 e ( 2+ 2)x + c 2 e (2+ 2)x per ogni x R, al variare di c 1 e c 2 in R. (iv) Il polinomio caratteristico è λ 2, la cui soluzione è λ = 0 con molteplicità 2. Quindi y(x) = c 1 + c 2 x per ogni x R, al variare di c 1 e c 2 in R. (v) Il polinomio caratteristico è λ 3, la cui soluzione è λ = 0 con molteplicità 3. Quindi y(x) = c 1 + c 2 x + c 3 x 2 per ogni x R, al variare di c 1, c 2 e c 3 in R. (vi) Il polinomio caratteristico è λ 3 4λ 2 +6λ 4, le cui soluzioni sono λ = 2, λ = 1+ ı e λ = 1 ı. Quindi y(x) = c 1 e 2x + c 2 e x cos(x) + c 3 e x sin(x) per ogni x R, al variare di c 1, c 2 e c 3 in R. (vii) Il polinomio caratteristico è λ 3 + 4λ 2 = λ 2 (λ + 4), le cui soluzioni sono λ = 0 (con molteplicità 2) e λ = 4. Quindi y(x) = c 1 + c 2 x + c 3 e 4x per ogni x R, al variare di c 1, c 2 e c 3 in R. (viii) Il polinomio caratteristico è λ 3 + 4λ = λ(λ 2 + 4), le cui soluzioni sono λ = 0, λ = 2 ı e λ = 2 ı. Quindi y(x) = c 1 +c 2 cos(2x)+c 3 sin(2x) per ogni x R, al variare di c 1, c 2 e c 3 in R. (ix) Il polinomio caratteristico è λ 4 +2λ 2 +1 = (λ 2 +1) 2, le cui soluzioni sono λ = ı (con molteplicità 2) e λ = ı (con molteplicità 2). Quindi y(x) = c 1 cos(x)+c 2 sin(x)+ c 3 xcos(x) + c 4 xsin(x) per ogni x R, al variare di c 1, c 2, c 3 e c 4 in R (i) L integrale generale dell equazione omogenea associata è y(x) = c 1 + c 2 e x, per ogni x R, al variare di c 1 e c 2 in R. Una soluzione particolare è del tipo v(x) = (ax + b)x (infatti il secondo membro è un polinomio di primo grado, e λ = 0 è radice del polinomio caratteristico, quindi bisogna cercare una soluzione come v). Una soluzione particolare dell equazione non omogenea è y p (x) = x2 2 x. (ii) L integrale generale dell equazione omogenea associata è y(x) = c 1 + c 2 e x, per ogni x R, al variare di c 1 e c 2 in R. Una soluzione particolare è del tipo v(x) = (ax + b)xe x (infatti il secondo membro è un polinomio di primo grado moltiplicato per e x, e e x è soluzione dell equazione omogenea. Quindi bisogna cercare una soluzione come v). Una soluzione particolare dell equazione non omogenea è y p (x) = x2 2 e x xe x. (iii) L integrale generale dell equazione omogenea associata è y(x) = c 1 + c 2 x + c 3 e 2x, per ogni x R, al variare di c 1 e c 2 in R. Una soluzione particolare è del tipo v(x) = (ax 2 +bx+c)x 2 +dxe 2x (infatti il secondo
7 140 Capitolo 4. Equazioni differenziali ordinarie membro è un polinomio di secondo grado, ma 1 è soluzione doppia, inoltre e 2x è soluzione dell equazione omogenea e quindi bisogna cercare una soluzione come v). Una soluzione particolare dell equazione non omogenea è y p (x) = x4 24 x3 12 x2 8 + x 4 xe2x, per ogni x R, (iv) L integrale generale dell equazione omogenea associata è y(x) = c 1 cos(x) + c 2 sin(x), per ogni x R, al variare di c 1 e c 2 in R. Una soluzione particolare è del tipo v(x) = (a cos(x) + b sin(x))x (infatti il secondo membro è una combinazione lineare delle funzioni seno e coseno e λ = ı è radice del polinomio caratteristico). Una soluzione particolare dell equazione non omogenea è y p (x) = x 2 sin(x) per ogni x R. (v) L integrale generale dell equazione omogenea associata è y(x) = c 1 e x + c 2 e 2x sin(x) + c 3 e 2x cos(x), al variare di c 1, c 2 e c 3 in R. Una soluzione particolare è del tipo v(x) = Ae 2x + ax + b (infatti il secondo membro è un polinomio di grado 1 in x sommato ad un esponenziale e 2x, e quindi bisogna cercare una soluzione come v). Una soluzione particolare dell equazione non omogenea è y p (x) = e 2x x La risposta corretta è la (i) La risposta corretta è la (iv). Attenzione: le funzioni date sono soluzioni anche dell equazione (iii) ma non rappresentano tutte le soluzioni di tale equazione La risposta corretta è la (ii) Non può essere soluzione di un equazione differenziale del primo ordine lineare ed omogenea a coefficienti costanti, in quanto le soluzioni di tale equazione devono essere tutte della forma y(x) = ce λx Non può essere soluzione in quanto, se lo fosse 2 sarebbe radice del polinomio caratteristico. Allora tutte le soluzioni dovrebbero essere della forma (il polinomio caratteristico ha grado 2) y(x) = c 1 e 2x +c 2 e λ0x, al variare di c 1, c 2 in R se λ 0 (l altra radice del polinomio caratteristico) è diversa da 2; y(x) = c 1 e 2x + c 2 xe 2x, al variare di c 1, c 2 in R se λ 0 se λ = 2 è radice doppia del polinomio caratteristico.
8 4.6. Soluzioni Le soluzioni del polinomio caratteristico sono complesse e coniugate con parte reale negativa Le soluzioni del polinomio caratteristico sono complesse e coniugate con parte reale nulla Consideriamo per primo il caso in cui λ = 3 non sia radice del polinomio caratteristico P(λ) = λ 2 + a 0 λ + a 1. In questo caso la funzione ŷ(x) = 1 P(3) e3x è soluzione particolare dell equazione differenziale. Denotiamo con λ 1 e λ 2 le radici di P(λ). Allora (i) se λ 1, λ 2 R e λ 1 < λ 2, l integrale generale dell equazione differenziale è al variare di c 1, c 2 R; y(x) = c 1 e λ1x + c 2 e λ2x + 1 P(3) e3x, per ogni x R, (ii) se λ 1 = λ 2, l integrale generale dell equazione differenziale è al variare di c 1, c 2 R; y(x) = c 1 e λ1x + c 2 xe λ1x + 1 P(3) e3x, per ogni x R, (iii) se λ 1 = α + ıβ, l integrale generale dell equazione differenziale è y(x) = e αx c 1 cos(βx) + c 2 sin(βx)} + 1 P(3) e3x, per ogni x R, al variare di c 1, c 2 R. Nel caso (i) tutte le soluzioni tendono a + per x + se, e solo se, λ 1, λ 2 < 3 e P(3) > 0. Infatti se λ 1, λ 2 < 3, il termine a principale, per x tendente a +, è 1 P(3) e3x, comunque si scelgano le costanti c 1 e c 2. Se λ 2 > 3, il termine principale, per x +, è c 2 e λ2x (ovviamente nel caso c 2 0) e tale funzione tende a se c 2 < 0. Nel caso (ii) tutte le soluzioni tendono a + per x + se, e solo se, (λ 1 < 3 e P(3) > 0) se, e solo se, (a 0 > 6). Infine nel caso (iii) tutte le soluzioni tendono a + per x + se, e solo se, (α < 3 e P(3) > 0) se, e solo se, (a 0 > 6). Consideriamo ora il caso in cui λ = 3 sia radice del polinomio caratteristico. Se P(λ) (λ 3) 2, allora tutte le soluzioni dell equazione differenziale sono date da y(x) = c 1 e 3x + c 2 e λ1x + xe3x 6 + a 0, per ogni x R, al variare di c 1, c 2 R. Quindi tutte le soluzioni tendono a + per x + se, e solo se, (λ 1 < 3 e a 0 > 6) se, e solo se, (a 0 > 6).
9 142 Capitolo 4. Equazioni differenziali ordinarie Se P(λ) = (λ 3) 2, allora tutte le soluzioni dell equazione differenziale sono date da ( ) x 2 y(x) = 2 + c 1x + c 2 e 3x, per ogni x R, al variare di c 1, c 2 R e tutte queste funzioni tendono a + per x +. In termini dei coefficienti a 0 e a 1, tutte le soluzioni dell equazione differenziale tendono a + per x + se, e solo se, vale una delle seguenti condizioni: a 2 0 4a 1 > 0, (i) a 0 + a 2 0 4a 1 < 6, 9 + 3a 0 + a 1 > 0; a 2 0 4a 1 > 0, (ii) a 0 + a 2 0 4a 1 = 6, a 0 > 6; (iii) (iv) (v) a 2 0 4a 1 = 0, a 0 > 6; a0 = 6, a 1 = 9; a 2 0 4a 1 < 0, a 0 > L integrale generale è dato da c 1 e x + c 2 e x 1 3 (1 + e x ) 1 + e x ex log( 1 + e x 1) 1 4 xex ex, per ogni x R, al variare di c 1, c 2 R.
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti:
 Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti: 1. y 5y + 6y = 0 y(0) = 0 y (0) = 1 2. y 6y + 9y = 0
Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti: 1. y 5y + 6y = 0 y(0) = 0 y (0) = 1 2. y 6y + 9y = 0
Analisi Vettoriale - A.A Foglio di Esercizi n Esercizio. y [17] + y [15] = 0. z + z = 0
![Analisi Vettoriale - A.A Foglio di Esercizi n Esercizio. y [17] + y [15] = 0. z + z = 0 Analisi Vettoriale - A.A Foglio di Esercizi n Esercizio. y [17] + y [15] = 0. z + z = 0](/thumbs/98/136376494.jpg) Analisi Vettoriale - A.A. 23-24 Foglio di Esercizi n. 5 Determinare l integrale generale di 1. Esercizio y [17] + y [15] = Posto y [15] = z l equazione proposta diventa Il cui integrale generale é z +
Analisi Vettoriale - A.A. 23-24 Foglio di Esercizi n. 5 Determinare l integrale generale di 1. Esercizio y [17] + y [15] = Posto y [15] = z l equazione proposta diventa Il cui integrale generale é z +
6.3 Equazioni lineari del secondo ordine
 si supponga di conoscerne una soluzione ψ(x). Si verifichi che con la sostituzione y(x) = ψ(x) + 1, l equazione diventa lineare nell incognita v(x) v(x). Utilizzando questo metodo, si risolva l equazione
si supponga di conoscerne una soluzione ψ(x). Si verifichi che con la sostituzione y(x) = ψ(x) + 1, l equazione diventa lineare nell incognita v(x) v(x). Utilizzando questo metodo, si risolva l equazione
Equazioni differenziali
 Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
Soluzioni. 152 Roberto Tauraso - Analisi Risolvere il problema di Cauchy. { y (x) + 2y(x) = 3e 2x y(0) = 1
 5 Roberto Tauraso - Analisi Soluzioni. Risolvere il problema di Cauchy y (x) + y(x) = 3e x y() = R. Troviamo la soluzione generale in I = R. Una primitiva di a(x) = è A(x) = a(x) dx = dx = x e il fattore
5 Roberto Tauraso - Analisi Soluzioni. Risolvere il problema di Cauchy y (x) + y(x) = 3e x y() = R. Troviamo la soluzione generale in I = R. Una primitiva di a(x) = è A(x) = a(x) dx = dx = x e il fattore
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A Prof. G.Cupini
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI
 ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
Per determinare una soluzione particolare descriveremo un metodo che vale solo nel caso in cui la funzione f(x) abbia una forma particolare:
 42 Roberto Tauraso - Analisi 2 Ora imponiamo condizione richiesta: ( lim c e 4x + c 2 + c 3 e 2x cos(2x) + c 4 e 2x sin(2x) ) = 3. x + Il limite esiste se e solo c 3 = c 4 = perché le funzioni e 2x cos(2x)
42 Roberto Tauraso - Analisi 2 Ora imponiamo condizione richiesta: ( lim c e 4x + c 2 + c 3 e 2x cos(2x) + c 4 e 2x sin(2x) ) = 3. x + Il limite esiste se e solo c 3 = c 4 = perché le funzioni e 2x cos(2x)
EQUAZIONI DIFFERENZIALI
 EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
Sistemi differenziali 2 2: esercizi svolti. 1 Sistemi lineari Stabilità nei sistemi lineari
 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Un equazione differenziale ordinaria di ordine n è una relazione tra: 1. una variabile indipendente x R, 2. una funzione incognita y = y(x) a valori reali 3. le derivate
Equazioni differenziali ordinarie Un equazione differenziale ordinaria di ordine n è una relazione tra: 1. una variabile indipendente x R, 2. una funzione incognita y = y(x) a valori reali 3. le derivate
Matematica II. Risolvere o integrare una e.d. significa trovarne tutte le soluzione, che costituiscono il cosidetto integrale generale.
 Definizione Si dice equazione differenziale di ordine n nella funzione incognita y = y (x) una relazione fra y, le sue derivate y,..., y (n), e la variabila indipendente x Risolvere o integrare una e.d.
Definizione Si dice equazione differenziale di ordine n nella funzione incognita y = y (x) una relazione fra y, le sue derivate y,..., y (n), e la variabila indipendente x Risolvere o integrare una e.d.
Corso di Analisi Matematica 1 - professore Alberto Valli
 Università di Trento - Corso di Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio - 8/9 Corso di Analisi Matematica - professore Alberto Valli foglio di esercizi - dicembre 8 Integrali
Università di Trento - Corso di Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio - 8/9 Corso di Analisi Matematica - professore Alberto Valli foglio di esercizi - dicembre 8 Integrali
Equazioni differenziali del 2 ordine Prof. Ettore Limoli. Sommario. Equazione differenziale omogenea a coefficienti costanti
 Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Equazioni differenziali del secondo ordine a coefficienti costanti Un equazioni differenziale del secondo ordine a coefficienti costanti è del tipo
 9 Lezione Equazioni differenziali del secondo ordine a coefficienti costanti Def. (C) Un equazioni differenziale del secondo ordine a coefficienti costanti è del tipo u + au + bu = f(t), dove a e b sono
9 Lezione Equazioni differenziali del secondo ordine a coefficienti costanti Def. (C) Un equazioni differenziale del secondo ordine a coefficienti costanti è del tipo u + au + bu = f(t), dove a e b sono
4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159
 4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159 Una volta stabilito che per ogni funzione continua f l equazione (4.23) è risolubile, ci interessa determinarne l integrale generale.
4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159 Una volta stabilito che per ogni funzione continua f l equazione (4.23) è risolubile, ci interessa determinarne l integrale generale.
Alcuni esercizi sulle equazioni di erenziali
 Alcuni esercizi sulle equazioni di erenziali Calcolo dell integrale generale Per ciascuna delle seguenti equazioni di erenziali calcolare l insieme di tutte le possibili soluzioni. SUGGERIMENTO: Ricordatevi
Alcuni esercizi sulle equazioni di erenziali Calcolo dell integrale generale Per ciascuna delle seguenti equazioni di erenziali calcolare l insieme di tutte le possibili soluzioni. SUGGERIMENTO: Ricordatevi
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione
![Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione](/thumbs/88/116749009.jpg) Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Analisi Vettoriale - A.A Foglio di Esercizi n. 6 Soluzioni. 1. Esercizio Determinare l integrale generale dell equazione autonoma.
 Analisi Vettoriale - A.A. 23-24 Foglio di Esercizi n. 6 Soluzioni. Esercizio Determinare l integrale generale dell equazione autonoma.. Soluzione. y = y(y )(y 2) y(y )(y 2) dy = Tenuto conto che y(y )(y
Analisi Vettoriale - A.A. 23-24 Foglio di Esercizi n. 6 Soluzioni. Esercizio Determinare l integrale generale dell equazione autonoma.. Soluzione. y = y(y )(y 2) y(y )(y 2) dy = Tenuto conto che y(y )(y
EQUAZIONI DIFFERENZIALI Esercizi con soluzione
 EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
Equazioni differenziali
 Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 1 1 / 30 Formulazione del problema In generale
Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 1 1 / 30 Formulazione del problema In generale
Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008. Dott.ssa G. Bellomonte
 Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008 Dott.ssa G. Bellomonte Indice 1 Introduzione 2 2 Equazioni differenziali lineari del primo ordine
Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008 Dott.ssa G. Bellomonte Indice 1 Introduzione 2 2 Equazioni differenziali lineari del primo ordine
y = cos x y = (y ) 2 + c : giustifichino le due affermazioni. y = y y = y 2 y = y(1 y) y = xy Applicazioni Equazioni delle cinetica chimica:
 Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI
 ESERCIZI SULLE EQUAZIONI DIFFERENZIALI a cura di Michele Scaglia ESERCIZI SULLE EQUAZIONI DIFFERENZIALI LINEARI DEL PRIMO OR- DINE A VARIABILI SEPARABILI TRATTI DA TEMI D ESAME 3) [TE /0/00] Determinare
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI a cura di Michele Scaglia ESERCIZI SULLE EQUAZIONI DIFFERENZIALI LINEARI DEL PRIMO OR- DINE A VARIABILI SEPARABILI TRATTI DA TEMI D ESAME 3) [TE /0/00] Determinare
Analisi Vettoriale A.A Soluzioni del foglio 5. y = y 2, dy y 2 = x
 Analisi Vettoriale A.A. 2006-2007 - Soluzioni del foglio 5 5. Esercizio Assegnato il problema di Cauchy y = y 2, y(0) = k determinare per ogni k la soluzione y(x), determinare il suo insieme di esistenza,
Analisi Vettoriale A.A. 2006-2007 - Soluzioni del foglio 5 5. Esercizio Assegnato il problema di Cauchy y = y 2, y(0) = k determinare per ogni k la soluzione y(x), determinare il suo insieme di esistenza,
LEZIONI DI ANALISI MATEMATICA I. Equazioni Differenziali Ordinarie. Sergio Lancelotti
 LEZIONI DI ANALISI MATEMATICA I Equazioni Differenziali Ordinarie Sergio Lancelotti Anno Accademico 2006-2007 2 Equazioni differenziali ordinarie 1 Equazioni differenziali ordinarie di ordine n.................
LEZIONI DI ANALISI MATEMATICA I Equazioni Differenziali Ordinarie Sergio Lancelotti Anno Accademico 2006-2007 2 Equazioni differenziali ordinarie 1 Equazioni differenziali ordinarie di ordine n.................
Corso di laurea in ingegneria gestionale a.a. 2015/2016 Tutor: Andrea Bendinelli
 Corso di analisi matematica I 12 c.f.u. Facoltà di ingegneria dell'informazione, informatica e statistica Corso di laurea in ingegneria gestionale a.a. 2015/2016 Tutor: Andrea Bendinelli 1 Indice I Esercitazione
Corso di analisi matematica I 12 c.f.u. Facoltà di ingegneria dell'informazione, informatica e statistica Corso di laurea in ingegneria gestionale a.a. 2015/2016 Tutor: Andrea Bendinelli 1 Indice I Esercitazione
Matematica - Prova d esame (25/06/2004)
 Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014
 Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014 MATRICOLA:...NOME e COGNOME:............................................. Desidero sostenere la prova orale al prossimo appello
Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014 MATRICOLA:...NOME e COGNOME:............................................. Desidero sostenere la prova orale al prossimo appello
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Un equazione differenziale è un equazione in cui l incognita è una funzione, anziché un semplice numero, e tale funzione può apparire con diversi ordini di derivazione.
Equazioni differenziali ordinarie Un equazione differenziale è un equazione in cui l incognita è una funzione, anziché un semplice numero, e tale funzione può apparire con diversi ordini di derivazione.
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del sesto appello, 16 luglio 2018 Testi 1
 Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
Argomento 14 Esercizi: suggerimenti
 Argomento 4 Esercizi: suggerimenti Ex.. Equazione differenziale lineare del primo ordine, cioè del tipo: y + a(x) y = f(x) il cui integrale generale è dato dalla formula: ] y(x, C) = e [C A(x) + f(x)e
Argomento 4 Esercizi: suggerimenti Ex.. Equazione differenziale lineare del primo ordine, cioè del tipo: y + a(x) y = f(x) il cui integrale generale è dato dalla formula: ] y(x, C) = e [C A(x) + f(x)e
Soluzioni degli esercizi
 Equazioni differenziali Soluzioni degli esercizi Premessa: in tutti gli esercizi x denota la variabile indipendente, y la funzione (di x) incognita dell equazione differenziale. Un equazione differenziale
Equazioni differenziali Soluzioni degli esercizi Premessa: in tutti gli esercizi x denota la variabile indipendente, y la funzione (di x) incognita dell equazione differenziale. Un equazione differenziale
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
7.1. Esercizio. Assegnata l equazione differenziale lineare di primo
 ANALISI MATEMATICA I Soluzioni Foglio 7 14 maggio 2009 7.1. Esercizio. Assegnata l equazione differenziale lineare di primo ordine y + y = 1 determinarne tutte le soluzioni, determinare la soluzione y(x)
ANALISI MATEMATICA I Soluzioni Foglio 7 14 maggio 2009 7.1. Esercizio. Assegnata l equazione differenziale lineare di primo ordine y + y = 1 determinarne tutte le soluzioni, determinare la soluzione y(x)
Compito di Analisi Matematica, Seconda parte, COGNOME: NOME: MATR.:
 Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
Matematica e Statistica
 Matematica e Statistica Prova d Esame (26/07/2010) Università di Verona - Laurea in Biotecnologie - A.A. 2009/10 1 Matematica e Statistica Prova d Esame di MATEMATICA (26/07/2010) Università di Verona
Matematica e Statistica Prova d Esame (26/07/2010) Università di Verona - Laurea in Biotecnologie - A.A. 2009/10 1 Matematica e Statistica Prova d Esame di MATEMATICA (26/07/2010) Università di Verona
Correzione del quarto compitino di Analisi 1 e 2 A.A. 2014/2015
 Correzione del quarto compitino di Analisi e A.A. 04/05 Luca Ghidelli, Giovanni Paolini, Leonardo Tolomeo 4 maggio 05 Esercizio Testo. Risolvere il seguente problema di Cauchy: y = 3x e 8y y( ) = 0. Prima
Correzione del quarto compitino di Analisi e A.A. 04/05 Luca Ghidelli, Giovanni Paolini, Leonardo Tolomeo 4 maggio 05 Esercizio Testo. Risolvere il seguente problema di Cauchy: y = 3x e 8y y( ) = 0. Prima
Ricordo: per le equazioni di primo grado del tipo y + ay = f (dove a e f sono noti) una soluzione è data da. e A(t) f(t)dt + c
 Capitolo 5 Equazioni differenziali Equazioni lineari di primo grado Ultimo aggiornamento: 18 febbraio 2017 Ricordo: per le equazioni di primo grado del tipo y + ay = f (dove a e f sono noti) una soluzione
Capitolo 5 Equazioni differenziali Equazioni lineari di primo grado Ultimo aggiornamento: 18 febbraio 2017 Ricordo: per le equazioni di primo grado del tipo y + ay = f (dove a e f sono noti) una soluzione
Provetta scritta di Calcolo I Corsi di laurea in Fisica - Scienza e Tecnologia dei Materiali Prova scritta del 7/12/2005 Fila A
 Provetta scritta di Calcolo I Prova scritta del 7/2/25 Fila A ) Calcolare i limiti 3 x 3 x 4 ; b) lim sin(2x) + x2 x( cos(3x)) c) lim + 5 x 7 x 4 x 2 + x. 2) Determinare il massimo di x 3 (2 + x 4 ) 3/2,
Provetta scritta di Calcolo I Prova scritta del 7/2/25 Fila A ) Calcolare i limiti 3 x 3 x 4 ; b) lim sin(2x) + x2 x( cos(3x)) c) lim + 5 x 7 x 4 x 2 + x. 2) Determinare il massimo di x 3 (2 + x 4 ) 3/2,
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 3 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 3 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 3 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
ANALISI MATEMATICA 2 ING. GESTIONALE prof. Daniele Andreucci Prova tecnica del 17/01/2017
 I.1 ANALISI MATEMATICA 2 ING. GESTIONALE prof. Daniele Andreucci Prova tecnica del 17/01/2017 1. Trovare il minimo e il massimo assoluti, e i punti di estremo a essi relativi, della funzione nell insieme
I.1 ANALISI MATEMATICA 2 ING. GESTIONALE prof. Daniele Andreucci Prova tecnica del 17/01/2017 1. Trovare il minimo e il massimo assoluti, e i punti di estremo a essi relativi, della funzione nell insieme
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2
 Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2 ESERCIZI CON SOLUZIONE 1. Risolvere il seguente problema di Cauchy: 1 2 1 2 L equazione differenziale
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2 ESERCIZI CON SOLUZIONE 1. Risolvere il seguente problema di Cauchy: 1 2 1 2 L equazione differenziale
Registro dell insegnamento. Scienze Matematiche Fisiche e Naturali Analisi Matematica IV modulo Settore:... Corsi di studio:...
 UNIVERSITÀ DEGLI STUDI DI FIRENZE Registro dell insegnamento Anno Accademico 2007/2008 Facoltà: Insegnamento: Scienze Matematiche Fisiche e Naturali Analisi Matematica IV modulo Settore:..........................
UNIVERSITÀ DEGLI STUDI DI FIRENZE Registro dell insegnamento Anno Accademico 2007/2008 Facoltà: Insegnamento: Scienze Matematiche Fisiche e Naturali Analisi Matematica IV modulo Settore:..........................
a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;
![a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [; a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;](/thumbs/69/60588320.jpg) ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
Analisi Vettoriale - A.A Foglio di Esercizi n. 4 Soluzioni
 Analisi Vettoriale - A.A. 2003-2004 Foglio di Esercizi n. 4 Soluzioni. Esercizio Assegnata l equazione differenziale y = y sin(y) disegnare, in modo qualitativo, i grafici delle soluzioni. Si tratta di
Analisi Vettoriale - A.A. 2003-2004 Foglio di Esercizi n. 4 Soluzioni. Esercizio Assegnata l equazione differenziale y = y sin(y) disegnare, in modo qualitativo, i grafici delle soluzioni. Si tratta di
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica A. Pisa, 3 settembre 2018
 Università di Pisa - orso di Laurea in Informatica nalisi Matematica Pisa, settembre 208 ( cos x sin se x 0 Domanda Sia f : R R definita da f(x = x 0 se x = 0. non esiste la derivata di f in x = 0 f (0
Università di Pisa - orso di Laurea in Informatica nalisi Matematica Pisa, settembre 208 ( cos x sin se x 0 Domanda Sia f : R R definita da f(x = x 0 se x = 0. non esiste la derivata di f in x = 0 f (0
ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.
 ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.Patrizia Pera Parte 2 Funzioni reali di più variabili 1. Stabilire se i
ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.Patrizia Pera Parte 2 Funzioni reali di più variabili 1. Stabilire se i
ANALISI MATEMATICA I, Compito scritto del 5/07/2016 Corso di Laurea in Matematica. COGNOME e NOME... MATR T
 ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
SOLUZIONI COMPITO del 10/02/2015 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A. 4! x6. 6! + o(x6 ), con x = 1 n
 SOLUZIONI COMPITO del 0/02/205 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio Ricordando che per x 0 a n ( sin x x x3 3! (x3, con x cos n, cosx x2 2 + x4 4! x! (x, con x n, [ ( [ ( ] cos cos
SOLUZIONI COMPITO del 0/02/205 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio Ricordando che per x 0 a n ( sin x x x3 3! (x3, con x cos n, cosx x2 2 + x4 4! x! (x, con x n, [ ( [ ( ] cos cos
Compitino di Analisi Matematica 1 Prima parte, Tema A Ingegneria Civile, Ambientale e Edile COGNOME: NOME: MATR.: RISPOSTE:
 Compitino di Analisi Matematica 1 Prima parte, Tema A Ingegneria Civile, Ambientale e Edile 20 maggio 2014 COGNOME: NOME: MATR.: RISPOSTE: A B C D E 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 1 Prima parte,
Compitino di Analisi Matematica 1 Prima parte, Tema A Ingegneria Civile, Ambientale e Edile 20 maggio 2014 COGNOME: NOME: MATR.: RISPOSTE: A B C D E 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 1 Prima parte,
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 5 Giugno 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 5 Giugno 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Note sulle equazioni differenziali
 Note sulle equazioni differenziali 6 gennaio 009 Queste note (molto) informali per il corso di Matematica raccolgono alcuni tra i risultati più importanti relativi alle equazioni differenziali ordinarie
Note sulle equazioni differenziali 6 gennaio 009 Queste note (molto) informali per il corso di Matematica raccolgono alcuni tra i risultati più importanti relativi alle equazioni differenziali ordinarie
Scritto d esame di Analisi Matematica II
 Capitolo 2: Scritti d esame 145 Pisa, 1 Gennaio 2005 e gli insiemi f(x, y) = x 2 x 2 y + y, A = {(x, y) R 2 : x 2 + y 2 6, x 0, y 0}, B = {(x, y) R 2 : x 0, y 0}. (a) massimo e minimo di f(x, y) in A,
Capitolo 2: Scritti d esame 145 Pisa, 1 Gennaio 2005 e gli insiemi f(x, y) = x 2 x 2 y + y, A = {(x, y) R 2 : x 2 + y 2 6, x 0, y 0}, B = {(x, y) R 2 : x 0, y 0}. (a) massimo e minimo di f(x, y) in A,
Gruppo esercizi 1: Vettori e matrici [E.1] Date le due matrici e il vettore
![Gruppo esercizi 1: Vettori e matrici [E.1] Date le due matrici e il vettore Gruppo esercizi 1: Vettori e matrici [E.1] Date le due matrici e il vettore](/thumbs/74/70227812.jpg) Gruppo esercizi 1: Vettori e matrici [E.1] Date le due matrici e il vettore A = 1 2 0 0 2 1 B = 2 1 0 1 0 2 u = (1, 2, 1), 3 2 1 1 1 1 [E.2] Date le due matrici e il vettore A = 1 2 0 0 1 0 0 1 3 B = 1
Gruppo esercizi 1: Vettori e matrici [E.1] Date le due matrici e il vettore A = 1 2 0 0 2 1 B = 2 1 0 1 0 2 u = (1, 2, 1), 3 2 1 1 1 1 [E.2] Date le due matrici e il vettore A = 1 2 0 0 1 0 0 1 3 B = 1
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Scritto d esame di Matematica I
 Capitolo 2: Scritti d esame 139 Pisa, 19 Gennaio 2005 x 1 + (x + 1) log x (x 1)(2x 2). 2. Studiare la convergenza dei seguenti integrali impropri 1 dx e 2x 1, 0 dx e 2x 1, e, nel caso in cui convergano,
Capitolo 2: Scritti d esame 139 Pisa, 19 Gennaio 2005 x 1 + (x + 1) log x (x 1)(2x 2). 2. Studiare la convergenza dei seguenti integrali impropri 1 dx e 2x 1, 0 dx e 2x 1, e, nel caso in cui convergano,
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 18 luglio 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 18 luglio 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica A. Pisa, 13 luglio 2017
 omanda Sia A = {x R : x > 0}. Allora infa = A 0 omanda La funzione fx = x sin x x 4 A non ha nessun tipo di asintoto ha un asintoto orizzontale e nessun altro tipo di asintoto ha un asintoto verticale
omanda Sia A = {x R : x > 0}. Allora infa = A 0 omanda La funzione fx = x sin x x 4 A non ha nessun tipo di asintoto ha un asintoto orizzontale e nessun altro tipo di asintoto ha un asintoto verticale
Appunti sulle equazioni differenziali lineari del secondo ordine
 Appunti sulle equazioni differenziali lineari del secondo ordine 10 maggio 2009 Dopo aver trattato delle equazioni differenziali lineari del primo ordine (cioè quelle in cui interviene la sola derivata
Appunti sulle equazioni differenziali lineari del secondo ordine 10 maggio 2009 Dopo aver trattato delle equazioni differenziali lineari del primo ordine (cioè quelle in cui interviene la sola derivata
Università di Roma Tor Vergata - Corso di Laurea in Ingegneria Analisi Matematica I - Prova scritta del 10 Luglio 2019
 Università di Roma Tor Vergata - Corso di Laurea in Ingegneria nalisi Matematica I - Prova scritta del 0 Luglio 09 Esercizio. [5 punti] Calcolare lo sviluppo di Taylor dell ordine n = 5 con centro x 0
Università di Roma Tor Vergata - Corso di Laurea in Ingegneria nalisi Matematica I - Prova scritta del 0 Luglio 09 Esercizio. [5 punti] Calcolare lo sviluppo di Taylor dell ordine n = 5 con centro x 0
Analisi Matematica A e B Soluzioni prova scritta parziale n. 4
 Analisi Matematica A e B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 08-09 7 aprile 09. Determinare le soluzioni u(x) dell equazione differenziale u + u u = sin x + ex + e x. Soluzione.
Analisi Matematica A e B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 08-09 7 aprile 09. Determinare le soluzioni u(x) dell equazione differenziale u + u u = sin x + ex + e x. Soluzione.
- ciascun autovalore di T ha molteplicità geometrica uguale alla moltplicitaà algebrica.
 Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Esercizi con soluzioni dell esercitazione del 31/10/17
 Esercizi con soluzioni dell esercitazione del 3/0/7 Esercizi. Risolvere graficamente la disequazione 2 x 2 2 cos(πx). 2. Determinare l insieme di definizione della funzione arcsin(exp( x 2 )). 3. Trovare
Esercizi con soluzioni dell esercitazione del 3/0/7 Esercizi. Risolvere graficamente la disequazione 2 x 2 2 cos(πx). 2. Determinare l insieme di definizione della funzione arcsin(exp( x 2 )). 3. Trovare
x = t y = t z = t 3 1 A = B = 1 2
 11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
Calcolo Scientifico e Matematica Applicata Primo Parziale,
 Calcolo Scientifico e Matematica Applicata Primo Parziale, 19.11.2018 Risolvere gli esercizi 2,, 4 oppure, in alternativa, gli esercizi 1, 2,, 5. Valutazione degli esercizi: 1 4, 2 14, 8, 4 8, 5 4. 1.
Calcolo Scientifico e Matematica Applicata Primo Parziale, 19.11.2018 Risolvere gli esercizi 2,, 4 oppure, in alternativa, gli esercizi 1, 2,, 5. Valutazione degli esercizi: 1 4, 2 14, 8, 4 8, 5 4. 1.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 9 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 9 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
1) D0MINIO FUNZIONE. Determinare il dominio della funzione f (x) = 4 x 2 4x + 3 x 2 6x + 8 Deve essere. x 2 6x + 5 (x 1) (x 5)
 ) DMINIO FUNZIONE Determinare il dominio della funzione f (x) = x x + x x + 8 x x + (x ) (x ) Deve essere = quindi x (, ] (, ] (, + ). x x + 8 (x ) (x ) Determinare il dominio della funzione f (x) = x
) DMINIO FUNZIONE Determinare il dominio della funzione f (x) = x x + x x + 8 x x + (x ) (x ) Deve essere = quindi x (, ] (, ] (, + ). x x + 8 (x ) (x ) Determinare il dominio della funzione f (x) = x
Equazioni differenziali del II ordine. y 5y + 6y = 0 y(0) = 0 y (0) = 1
 Equazioni differenziali del II ordine 1. Risolvere il seguente problema di Cauchy: y 5y + 6y = 0 y (0) = 1. Determinare l integrale generale della seguente equazione differenziale: y 5y + 6y = f(x), con
Equazioni differenziali del II ordine 1. Risolvere il seguente problema di Cauchy: y 5y + 6y = 0 y (0) = 1. Determinare l integrale generale della seguente equazione differenziale: y 5y + 6y = f(x), con
Matematica per Scienze Biologiche e Biotecnologie. Docente Lucio Damascelli. Università di Tor Vergata. Alcuni recenti compiti di esame
 Matematica per Scienze Biologiche e Biotecnologie Docente Lucio Damascelli Università di Tor Vergata Alcuni recenti compiti di esame Nota Nei compiti di esame si chiedono 6 esercizi da svolgere in (al
Matematica per Scienze Biologiche e Biotecnologie Docente Lucio Damascelli Università di Tor Vergata Alcuni recenti compiti di esame Nota Nei compiti di esame si chiedono 6 esercizi da svolgere in (al
SOLUZIONI COMPITO del 10/01/2019 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A
 SOLUZIONI COMPITO del 0/0/209 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio Osserviamo che Pertanto, i = 2e iπ/, + i = 2e iπ/. e 7iπ/8, 2e iπ/ z = = e 2e 7iπ/2 = e 7iπ/8, iπ/ 2 8 2 e iπ/8, e
SOLUZIONI COMPITO del 0/0/209 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio Osserviamo che Pertanto, i = 2e iπ/, + i = 2e iπ/. e 7iπ/8, 2e iπ/ z = = e 2e 7iπ/2 = e 7iπ/8, iπ/ 2 8 2 e iπ/8, e
Equazioni di erenziali
 Equazioni di erenziali 1. Risolvere la seguente equazione y 0 = 2x cos 2 y. Risoluzione E un equazione di erenziale a variabili searabili. Sono integrali singolari y = 2 + k con k 2. Seariamo le variabili
Equazioni di erenziali 1. Risolvere la seguente equazione y 0 = 2x cos 2 y. Risoluzione E un equazione di erenziale a variabili searabili. Sono integrali singolari y = 2 + k con k 2. Seariamo le variabili
2 Equazioni Differenziali Ordinarie
 2 Equazioni Differenziali Ordinarie Un equazione differenziale ordinaria di ordine n è un equazione della forma ( F x, y, y,...,y (n)) = 0 (10) con F funzione di n + 2 variabili, continua in un insieme
2 Equazioni Differenziali Ordinarie Un equazione differenziale ordinaria di ordine n è un equazione della forma ( F x, y, y,...,y (n)) = 0 (10) con F funzione di n + 2 variabili, continua in un insieme
CODICE= Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A , Appelli 1, 2, 3 e 4
 Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
y 3y + 2y = 1 + x x 2.
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 03-04 (dott.ssa Vita Leonessa) Esercizi svolti: Equazioni differenziali ordinarie. Risolvere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 03-04 (dott.ssa Vita Leonessa) Esercizi svolti: Equazioni differenziali ordinarie. Risolvere
Equazioni differenziali
 Equazioni differenziali 1.1 Equazioni differenziali In analisi matematica un'equazione differenziale è una relazione tra una funzione u(x) non nota ed alcune sue derivate. Nel caso in cui u sia una funzione
Equazioni differenziali 1.1 Equazioni differenziali In analisi matematica un'equazione differenziale è una relazione tra una funzione u(x) non nota ed alcune sue derivate. Nel caso in cui u sia una funzione
Campo di Esistenza. Il campo di esistenza di una funzione f è il dominio più grande su cui ha significato la legge f.
 Campo di Esistenza Il campo di esistenza di una funzione f è il dominio più grande su cui ha significato la legge f. ESERCIZIO. Determinare il campo di esistenza della funzione f(x) = 9+2x. Soluzione:
Campo di Esistenza Il campo di esistenza di una funzione f è il dominio più grande su cui ha significato la legge f. ESERCIZIO. Determinare il campo di esistenza della funzione f(x) = 9+2x. Soluzione:
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 6 giugno 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 6 giugno 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x).
![x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x). x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x).](/thumbs/102/153351382.jpg) Funzioni Esercizio Siano f, g due funzioni definite da fx) = x x 2, gx) = ln x Trovare l insieme di definizione di f e g 2 Determinare le funzioni composte f g e g f, precisandone insieme di definizione
Funzioni Esercizio Siano f, g due funzioni definite da fx) = x x 2, gx) = ln x Trovare l insieme di definizione di f e g 2 Determinare le funzioni composte f g e g f, precisandone insieme di definizione
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Equazioni differenziali
 Capitolo 1 Equazioni differenziali Esercizio 1.1 Dopo averne discussa esistenza ed unicità, si risolva il seguente Problema di Cauchy, { ty (t)+y(t) = 0 y(1) = 2. Si dica inoltre su quale intervallo I
Capitolo 1 Equazioni differenziali Esercizio 1.1 Dopo averne discussa esistenza ed unicità, si risolva il seguente Problema di Cauchy, { ty (t)+y(t) = 0 y(1) = 2. Si dica inoltre su quale intervallo I
Test in Itinere di Analisi Matematica
 4 Prove d Esame di Analisi Matematica Versione 2006 Pisa, 5 Novembre 2002 La funzione f(x) = x da R in R è surgettiva Per ogni x 0 si ha che x 1 = x 1 La funzione f(x) = x da [0, + [ in [0, + [ è iniettiva
4 Prove d Esame di Analisi Matematica Versione 2006 Pisa, 5 Novembre 2002 La funzione f(x) = x da R in R è surgettiva Per ogni x 0 si ha che x 1 = x 1 La funzione f(x) = x da [0, + [ in [0, + [ è iniettiva
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 30 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 30 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Prova in itinere di Matematica Pisa, 26 novembre 2005
 Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
EQUAZIONI DIFFERENZIALI / ESERCIZI SVOLTI
 ANALISI MATEMATICA I - A.A. 011/01 EQUAZIONI DIFFERENZIALI / ESERCIZI SVOLTI L asterisco contrassegna gli esercizi più difficili. Determinare l integrale generale dell equazione differenziale y = e x y
ANALISI MATEMATICA I - A.A. 011/01 EQUAZIONI DIFFERENZIALI / ESERCIZI SVOLTI L asterisco contrassegna gli esercizi più difficili. Determinare l integrale generale dell equazione differenziale y = e x y
Istituzioni di Analisi 2 (programma, domande ed esercizi)
 Istituzioni di Analisi programma, domande ed esercizi) nona settimana Argomenti trattati Dal libro di testo: 3. punti critici vincolati), 3.3. estremi assoluti), 0.3. e 0.3. solo la definizione di compatto
Istituzioni di Analisi programma, domande ed esercizi) nona settimana Argomenti trattati Dal libro di testo: 3. punti critici vincolati), 3.3. estremi assoluti), 0.3. e 0.3. solo la definizione di compatto
Prova in itinere di Matematica Pisa, 26 novembre 2005
 Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
Analisi Matematica B Soluzioni prova scritta parziale n. 4
 Analisi Matematica B Soluzioni prova scritta parziale n. 4 Corso di laurea in Fisica, 017-018 4 maggio 018 1. Risolvere il problema di Cauchy { u u sin x = sin(x), u(0) = 1. Svolgimento. Si tratta di una
Analisi Matematica B Soluzioni prova scritta parziale n. 4 Corso di laurea in Fisica, 017-018 4 maggio 018 1. Risolvere il problema di Cauchy { u u sin x = sin(x), u(0) = 1. Svolgimento. Si tratta di una
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
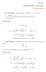 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
1. (4 punti) Calcolare i seguenti limiti: (a) lim. n arctan( n (log n)2 n. Assegnata la funzione f(x) = (3x + 1) e 1
 Matematica, 2 CFU Corso di laurea in Scienze Biologiche- A.A. 2009-200 Laurea Triennale-Corsi A e C 9 Febbraio 200- COMPITO - Totale punti 40, punteggio minimo 24 Nome Cognome. (4 punti) Calcolare i seguenti
Matematica, 2 CFU Corso di laurea in Scienze Biologiche- A.A. 2009-200 Laurea Triennale-Corsi A e C 9 Febbraio 200- COMPITO - Totale punti 40, punteggio minimo 24 Nome Cognome. (4 punti) Calcolare i seguenti
TEMA 1. F (x, y) = e xy + x + y.
 FONDAMENTI DI ANALII MATEMATICA 2 Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 23 gennaio 217 Primo appello Avvertenza: Nella prima
FONDAMENTI DI ANALII MATEMATICA 2 Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 23 gennaio 217 Primo appello Avvertenza: Nella prima
1. Riconoscere la natura delle coniche rappresentate dalle seguenti equazioni e disegnarle:
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
9.2 Il problema di Cauchy per le equazioni differenziali del primo ordine
 9.2 Il problema di Cauchy per le equazioni differenziali del primo ordine 349 y = f(y, x), (9.23) allora la sostituzione z = y conduce all equazione del primo ordine z = f(z, x) nell incognita z = z(x).
9.2 Il problema di Cauchy per le equazioni differenziali del primo ordine 349 y = f(y, x), (9.23) allora la sostituzione z = y conduce all equazione del primo ordine z = f(z, x) nell incognita z = z(x).
Matematica e Statistica
 Matematica e Statistica Prova d Esame (04/0/00) Università di Verona - Laurea in Biotecnologie - A.A. 009/0 Matematica e Statistica Prova d Esame di MATEMATICA (04/0/00) Università di Verona - Laurea in
Matematica e Statistica Prova d Esame (04/0/00) Università di Verona - Laurea in Biotecnologie - A.A. 009/0 Matematica e Statistica Prova d Esame di MATEMATICA (04/0/00) Università di Verona - Laurea in
Analisi - 10 settembre 2008 Corso di Laurea in Fisica - Fisica ed Astrofisica
 Analisi - 1 settembre 28 Corso di Laurea in Fisica - Fisica ed Astrofisica Chi deve fare lo scritto di Derivate e Integrali (vecchio ordinamento) deve svolgere gli esercizi: 1, 2, 3, 4, 5 Esercizio 1 Data
Analisi - 1 settembre 28 Corso di Laurea in Fisica - Fisica ed Astrofisica Chi deve fare lo scritto di Derivate e Integrali (vecchio ordinamento) deve svolgere gli esercizi: 1, 2, 3, 4, 5 Esercizio 1 Data
