Costruire una derivazione (note )
|
|
|
- Renzo Parente
- 7 anni fa
- Visualizzazioni
Transcript
1 Costruire una derivazione (note ) C. Faggian 1 Laboratorio 1 Scopo: sperimentare l uso delle regole di inferenza per costruire derivazioni, familiarizzarsi col metodo di ricerca dal basso verso l alto. In queste note andiamo anche un po oltre il contenuto del primo laboratorio, suggerendo alcune strategie, che saranno riprese nel prossimo laboratorio. 1.1 Lab1: esercizi Le regole di inferenza, ed un po di terminologia, sono dati in appendice. Chiedere alla macchina di usare le regole di inferenza date in appendice A per derivare questi sequenti: 1. A&B (A B)&B 2. A B A 3. A B A&B (!!) 4. A C (C B) (A B) 5. A B, C D A&C B&D 6. B C (A B) (A C) 7. (**) (A B)&(B C) (A B C) 8. (**) (A C)&(B C) (A&B) C Gli esercizi (**) sono da farsi dopo gli esercizi in sezione 1.5. Se siete riusciti a costruire una derivazione per (3.), qualcosa non torna. Forse le regole non sono applicate correttamente? 1.2 Ok, ma... in pratica? Scopo del gioco Costruire dal basso verso l alto un albero di derivazione che ha come radice (conclusione) il sequente da dimostrare, e come foglie delle identita (cioe sequenti Aiutaci a migliorare il corso, i laboratori, e queste note! Suggerimenti, correzioni, problemi e dubbi: cfaggian@studenti.math.unipd.it 1
2 della forma X X). L albero e costruito impilando regole di inferenza. Da dove inizio? Regola d oro: lavoriamo dal basso verso l alto Scrivo il sequente da derivare (lasciando abbastanza spazio bianco sopra!) cerco di costruire una derivazione, scegliendo ogni volta l ultima regola. Ogni volta, la domanda e e questo sequente, puo essere conclusione di che regola? Per rispondere, guardo che formule ci sono, e quindi quale connettivo puo essere stato introdotto per ultimo. Esempio. Consideriamo il sequente C, C D D. Che connettivi ho? Solo, che si trova a sinistra. C e un unica regola che introduce a sinistra, ed ha la forma:... X Y, X Y Se facciamo corrispondere il nostro sequente alla conclusione della regola, abbiamo X Y := C D, := D, e possiamo subito scrivere C D D C, C D D Per concludere, dobbiamo solo decidere come distibuire il contesto di C D, che e C. Ci conviene metterlo nella premessa di destra o in quella di sinistra? Come finisco? In alto, vogliamo avere solo identita (sono le foglie del nostro albero di derivazione). Quindi cerchiamo di trovarci con un identica formula a destra e a sinistra del comporta:...x X. Segretamente miriamo ad avere in alto sequenti della forma Γ, A A, che possiamo poi indebolire in A A. Esempio: fare esercizio 2. Come procedere: Usiamo le regole dei connettivi, indebolimento e contrazione... avendo in mente : a. A, A B B b. A A B e B A B c. A&B A e A&B B d. L esercizio in sezione 1.5 (molto, molto importante) 2
3 Gli assiomi [a.,b.,c.] forniscono una guid aimportante; ci segnalano che siamo vicini alla meta (le identita ): quando li riconosciamo, sappiamo ottenere le identita in un passo. Esempi: esercizi 1,4,5. Li svolgiamo piu avanti. Per trattare la contrazione, abbiamo bisogno degli esercizi in sezione Trucchi del mestiere Quando costruiamo una derivazione, abbiamo molte scelte possibili. Dal punto di vista di un informatico, una proprieta fondamentale del calcolo dei sequenti (su cui si basano algoritmi di proof-construction, di verifica e specifica dei programmi, ed anche il Prolog) e che e possibile arrangiare le regole in modo da minimizzare l indeterminismo. Questo garantisce che la ricerca di una derivazione per il sequente Γ termina o con una derivazione o con la sicurezza che una derivazione non esiste A questo scopo si possono dimostrare una serie di risultati del tipo: Se esiste una derivazione del sequente Γ, allore ne esiste una che ha la forma bla bla (per esempio: non usa la regola di cut) La conseguenza e che: possiamo limitarci a cercare derivazioni della forma bla bla (se una derivazione esiste, ce ne e una di quella forma) se non troviamo una derivazione della forma bla bla, allora inutile cercare oltre: non esistono derivazioni di Γ. Risultato 1. Se un sequente Γ ha una derivazione, allora ha anche una derivazione che non usa cut Morale: possiamo limitarci a cercare una derivazione senza cut. Risultato 2. le regole di formazione ( a destra, & a destra, a sinistra) possono essere applicate in qualunque momento, senza cambiare la dimostrabilita. Altre regole comportano una scelta che puo pregiudicare il seguito. In particolare: 3
4 La regola di a destra ci fa scegliere A oppure B. Lo stesso e vero per & a sinistra (ma vedremo in sezione 1.5 che la contrazione ci aiuta ad aggirare questo problema) La regola di a sinistra ci obbliga a scegliere un modo di spezzare il contesto in Γ 1 e Γ 2. Esempio. Pensate ad A, A B B. Possiamo leggere A B come se mi dai venti euro (A) di do un libro (B) oppure ho un programma che prende un intero (A) e restituisce un booleano (B).E necessaria la presenza di entrambe A e A B per liberare B. Questo non sarebbe possibile se in un passo precendente avessimo separato queste due formule. Morale: se nel sequente abbiamo diversi connettivi, e quindi diverse possibilita, conviene cominciare (dal basso) con le regole di formazione. 1.4 In pratica (riassumendo) Ecco alcune indicazioni. Abbiamo detto che lavoriamo dal basso verso l alto. In realta, lavoriamo dal basso (conclusione), guidati nelle scelte da cosa cerchiamo in alto (identita, anzi sequenti della forma Γ, X X). Aiuta avere in mente gli assiomi (a.),(b.),(c.). Alcuni (molti) passi sono automatici, alcuni punti richiedono un po di creativita. Conviene semplificare (in modo automatico) il sequente da dimostrare quanto possibile, e rimandiamo le vere scelte (non determinismo) alla fine, sperando a quel punto di avere un idea di come terminare. Fino a che e possibile, conviene usare (dal basso verso l alto) regole di formazione (funzionano sempre, non ipotechiamo il seguito, ed intanto semplifichiamo il sequente). Facciamo per prime le regole ad applicazione automatica: a destra, & a destra, a sinistra. Metteremo in questo gruppo anche la regola derivata dell esercizio Riserviamo la creativita al momento di fare delle scelte. A questo punto aiuta enormemente avere in mente (a.),(b.),(c.) (vedi gli esercizi svolti sotto), che ci forniscono un aiuto alla navigazione verso le identita. In particolare, avere in mente che Avere A B a sinistra ci permette di liberare B se forniamo A. una formula A B a destra la possiamo trasformare in A oppure in B, a seconda del bisogno (cercare di fare questa scelta solo quando sappiamo di cosa abbiamo bisogno!). lo stesso vale per A&B a sinistra (ma in questo caso il problema si puo risolvere senza fare scelte, vedi esercizio ) 4
5 Esempio, esercizio 4. A, A C, C B B 1 A C, C B (A B) A C (C B) (A B) Arrivati al punto [1], abbiamo applicato tutti i passi automatici, e siamo obbligati a fare delle scelte. Se esaminiamo la situazione, ci rendiamo conto di aver gia finito... Osserviamo che a destra abbiamo B. A sinistra, per liberare B ci serve C. Per liberare C, ci basta fornire A ad A C. Ora sappiamo come finire! Decompongo le due implicazioni a sinistra, distribuendo il contesto in modo appropriato. Per esempio: A A C C A, A C C B B A, A C, C B B 1 Esempio, esercizio 5. A&C, A B, C D B 1 A&C, A B, C D D 2 A&C, A B, C D B&D A B, C D A&C B&D Fin qui, abbiamo applicato tutte semplificazioni automatiche. Per terminare, decidiamo cosa fare sopra il punto [1]. Notiamo che: abbiamo bisogno di un B a sinistra. A B ci libera un B se gli forniamo un A. A&C lo possiamo trasformare in un A... Per concludere, possiamo iniziare a decomporre A&C, oppure A B (e indifferente), invece C D non serve (possiamo indebolirlo). Per esempio: Cosa facciamo sopra [2]? A A A&C A B B A&C, A B, C D B 1 Esempio, esercizio 6 A, B C A C 1 B, B C A C 2 A B, B C A C B C (A B) (A C) Ora devo fare delle scelte. Per terminare: 5
6 sopra [1] osservo che A appare sia a sinistra che a destra: mi basta trasformare A C in A. Come finisco? sopra [2], noto che a destra posso trasformare A C in A oppure in C. Osservo che a sin., se fornisco B a B C si libera C. Quindi posso finire con: Indebolimento C C B B C A C B, B C A C 2 La regola di indebolimento, conviene farla alla fine, o almeno quando sappiamo di cosa abbiamo bisogno. Avere delle formule in piu (il famoso contesto Γ a sinistra) non impedisce mai l applicazione di una regola, ma il materiale che ci portiamo avanti puo tornare utile. In pratica. Non preoccuparsi dell indebolimento. Basta pensarci alla fine. Abbiamo gia visto che, segretamente, cerchiamo Γ, A A. 1.5 Contrazione: il nostro joker! Il solo punto delicato e l uso della contrazione. Cosa la rende delicata? Che tendiamo a dimenticarla... In realta, la contrazione e un alleato prezioso. Se siamo una macchina, possiamo agevolmente creare una copia di ogni formula in cui serve una scelta prima di decomporla (dal basso verso l alto, contrazione = creare una copia). Alla macchina non disturba portare avanti sequenti con un gran numero di formule, anche se e poco pratico per un essere umano. All essere umano conviene comunque ricordare che, se abbiamo contrazione a sinistra, allora tutte le formula a sinistra su cui ho fatto una scelta sono riutilizzabili. Per esempio, se nel sequente ho la formula A&B, e la uso per ottenere A, moralmente ho ancora una copia di A&B. Infatti, posso modificare la derivazione come segue: Γ, A Γ, A&B puo diventare Γ, A&B, A Γ, A&B, A&B, Γ, A&B In pratica se ci si trova ad un punto morto, chiedersi se aiuterebbe avere ancora presente una delle formule che stanno sotto, e modificare la derivazione scritta di conseguenza. Esempio: gli esercizi sotto, e poi esercizio (8). Ancora piu conveniente, e incorporare la contrazione nella regola, come facciamo sotto. 6
7 1.5.1 Esercizio (molto molto importante) Dimostrare che la seguente regola e derivabile (cioe mostrare che possiamo riempire lo spazio tra premesse e conclusione con regole di inferenza ufficiali.) Γ, A, B Γ, A&B & bis Come fare. So che da A&B posso ottenere (dal basso verso l alto) A. So che da A&B posso ottenere (dal basso verso l alto) B. Poiche mi servono sia A sia B, duplico A&B con una contrazione: Γ, A, B Γ, A&B, A&B Γ, A&B In pratica (importante!) Quando non sappiamo fare una scelta, possiamo sempre usare le regole derivata vista sopra. Esempio. Provare a fare l esercizio 8. Osservazione. Due difficolta (fare una scelta e gestire la contrazione) si annullano: usando la regole & bis, non facciamo scelte quando abbiamo a sinistra il connettivo &. Tutta la nostra creativita si puo concentrare sul connettivo a destra ed a sinistra (in quest ultimo caso la situazione puo essere migliorata, ma non del tutto). Su questi ultimi punti faremo pratica nel prossimo laboratorio. Intanto, immaginate un sistema meraviglioso in cui avete contrazione sia a destra sia a sinistra... possiamo fare in modo che qualunque scelta facciamo vada bene? Esempio, esercizio 8. A, B (A&B) C Completare... A, C (A&B) C A, (B C) (A&B) C C C C, B C C C, (B C) (A&B) C (A C), (B C) (A&B) C (A C)&(B C) (A&B) C 7
8 2 Esercizi: LJ Per capire la ricerca di derivazioni, leggere in particolare le sezioni 1.4 ed 1.5, e poi provare a svolgere alcuni degli esercizi sotto, a scelta. Il calcolo per LJ e dato in appendice B. 1. Dimostrare che la seguenti due regola sono derivabili in LJ. Γ A Γ, B Γ, A B Γ, A B A Γ, A B, B Γ, A B 2. Costruire una derivazione in LJ per i seguenti sequenti. Gli esercizi con asterisco sono particolarmente raccomandati. 1. p (p&q) p 2. * p q, r s p r q s 3. * (b c)&(a b) d (a c) 4. (a b) (a c) a (b c) 5. * (p (q p))&q p 6. p q&r (p q)&(p r) 7. (p r) (q r) p&q r 8. ** p (p q), p q 3. Costruire una derivazione in LJ per questi sequenti (se possibile): 1. p p q 2. p q, q p 3. p q (p&q) 4. (p&q) p q 5. p&q ( p q) 6. p q (p q) 7. (p q) q p 4. Potrebbe essere comodo derivare direttamente regole per la negazione, anziche tradurre ogni volta in A = A Che regole potremmo dare alla macchina per A (a destra e a sinistra)? 8
9 A Le regole di inferenza per lab1 Queste regole sono un frammento di LJ. Le estenderemo nel prossimo laboratorio. Identitá: A A Γ, A Γ, A&B oppure Γ, B Γ, A&B Connettivi: Γ A Γ B Γ A&B Γ, A Γ, B Γ, A B Γ A Γ A B oppure Γ B Γ A B Γ 1 A Γ 2, B Γ 1, Γ 2, A B Γ, A B Γ A B Indebolimento: Γ Γ, Σ Contrazione: Γ, A Γ, A, A Precedenze. I connettivi e & hanno la precedenza su. Quindi scrivendo A B C si intende (A B) C. Invece A B&C e ambiguo, e deve essere parentizzato in modo esplicito. Anatomia di una regola Consideriamo come esempio questa regola: Γ, A Γ, B Γ, A B Il sequente Γ, A B e la conclusione della regola, i due sequenti Γ, A e Γ, B sono le premesse. Questa regola introduce a sinistra la formula A B, che chiamiamo formula principale della regola. Γ sta per una lista di formule: tutte le formule che troviamo accanto a A B. Chiamiamo Γ il contesto di A B. La lista Γ puo anche essere vuota. 9
10 B Regole di LJ Identitá: A A Falso: Γ, Connettivi: Γ, A Γ, A&B Γ, B Γ, A&B Γ A Γ B Γ A&B Γ, A Γ, B Γ, A B Γ 1 A Γ 2, B Γ 1, Γ 2, A B Γ A Γ A B Γ, A B Γ A B Γ B Γ A B Indebolimento: Γ Γ, Σ Contrazione: Γ, A Γ, A, A Come abbiamo discusso (vedi note del laboratorio 1), le regole sui connettivi distinte da asterisco richiedono una scelta non determinista, mentre le altre possono essere applicate in modo automatico qualunque momento. Per rendere piu efficiente la ricerca di prove, grazie alla contrazione possiamo sostitire le due regole indicate da (**) con la seguente regola derivata Γ, A, B Γ, A&B &bis 10
Calcolo dei Sequenti Proposizionale: Note ed Esercizi
 Calcolo dei Sequenti Proposizionale: Note ed Esercizi mace@dsiuniveit 11 ottobre 2007 1 Costruire una derivazione Definizione 1 (Derivazione) Una derivazione in LJ (rispettivamente LK) è un albero finito
Calcolo dei Sequenti Proposizionale: Note ed Esercizi mace@dsiuniveit 11 ottobre 2007 1 Costruire una derivazione Definizione 1 (Derivazione) Una derivazione in LJ (rispettivamente LK) è un albero finito
9 Calcolo dei sequenti LC p
 9 Calcolo dei sequenti LC p In questa sezione mostriamo un metodo più elegante, semplice e soprattutto AUTOMATICO per mostrare se una proposizione è valida o meno e soddisfacibile o meno. Tale metodo è
9 Calcolo dei sequenti LC p In questa sezione mostriamo un metodo più elegante, semplice e soprattutto AUTOMATICO per mostrare se una proposizione è valida o meno e soddisfacibile o meno. Tale metodo è
Corso di Logica I. Modulo sul Calcolo dei Sequenti. Dispensa Lezione III.
 Corso di Logica I. Modulo sul Calcolo dei Sequenti. Dispensa Lezione III. Giovanni Casini Teorema di corrispondenza fra il calcolo sui sequenti SND c e il calcolo dei sequenti SC c. In queste pagine andiamo
Corso di Logica I. Modulo sul Calcolo dei Sequenti. Dispensa Lezione III. Giovanni Casini Teorema di corrispondenza fra il calcolo sui sequenti SND c e il calcolo dei sequenti SC c. In queste pagine andiamo
Semantica e prammatica. Gianluigi Bellin
 Semantica e prammatica Gianluigi Bellin November 16, 2010 Promesse. Consideriamo il problema di formalizzare il seguente enunciato Se tu non aiuti me quando io ho bisogno di te, io non aiuto te quando
Semantica e prammatica Gianluigi Bellin November 16, 2010 Promesse. Consideriamo il problema di formalizzare il seguente enunciato Se tu non aiuti me quando io ho bisogno di te, io non aiuto te quando
1 Esercizi: il calcolo proposizionale (LJ)
 Laboratorio 2, esercizi e note 1 Scopo: 1. Saper costruire derivazioni in logica proposizionale (LJ), usando anche la negazione; sfruttare la contrazione a sinistra. Vedi Sezione 4 2. Familiarizzarsi con
Laboratorio 2, esercizi e note 1 Scopo: 1. Saper costruire derivazioni in logica proposizionale (LJ), usando anche la negazione; sfruttare la contrazione a sinistra. Vedi Sezione 4 2. Familiarizzarsi con
7. A che serve il calcolo dei sequenti? Dà procedura di decisione
 7. A che serve il calcolo dei sequenti? Dà procedura di decisione Il calcolo dei sequenti serve a costruire alberi di derivazione come ad esempio ax-id P, Q Q P&Q Q & S ax-id P, Q P P&Q P P&Q Q&P & S &
7. A che serve il calcolo dei sequenti? Dà procedura di decisione Il calcolo dei sequenti serve a costruire alberi di derivazione come ad esempio ax-id P, Q Q P&Q Q & S ax-id P, Q P P&Q P P&Q Q&P & S &
1. equivalenze e implicazioni logiche. Esercizio 1.2. Trovare le implicazioni che legano i seguenti enunciati (x, y R):
 . equivalenze e implicazioni logiche Esercizio.. Trovare le implicazioni che legano i seguenti enunciati (x, y R): () x < y, () x = y, () x y, () x y, () (x y) > 0. Osserviamo subito che (x y) > 0 equivale
. equivalenze e implicazioni logiche Esercizio.. Trovare le implicazioni che legano i seguenti enunciati (x, y R): () x < y, () x = y, () x y, () x y, () (x y) > 0. Osserviamo subito che (x y) > 0 equivale
Esercizi sulle radici
 Esercizi sulle radici Semplificazione Per semplificare una radice utilizzando, quando necessario, i valori assoluti, dobbiamo ricordare che se una radice ha indice pari, il suo radicando (il numero che
Esercizi sulle radici Semplificazione Per semplificare una radice utilizzando, quando necessario, i valori assoluti, dobbiamo ricordare che se una radice ha indice pari, il suo radicando (il numero che
Logica per la Programmazione
 Logica per la Programmazione Lezione 2 Dimostrazione di tautologie Proof System pag. 1 Un Problema di Deduzione Logica [da un test di ingresso] Tre amici, Antonio, Bruno e Corrado, sono incerti se andare
Logica per la Programmazione Lezione 2 Dimostrazione di tautologie Proof System pag. 1 Un Problema di Deduzione Logica [da un test di ingresso] Tre amici, Antonio, Bruno e Corrado, sono incerti se andare
Analisi Sintattica. Maria Rita Di Berardini. Universitá di Camerino Ruolo del parser
 Ruolo del parser Analisi 1 1 Dipartimento di Matematica e Informatica Universitá di Camerino mariarita.diberardini@unicam.it Ruolo del parser Ruolo dell analisi sintattica Ruolo del parser Metodologie
Ruolo del parser Analisi 1 1 Dipartimento di Matematica e Informatica Universitá di Camerino mariarita.diberardini@unicam.it Ruolo del parser Ruolo dell analisi sintattica Ruolo del parser Metodologie
Logica Computazionale Sequenti e Deduzione Naturale
 Logica Computazionale 2009 - Sequenti e Deduzione Naturale Gianluigi ellin November 24, 2009 Complementi per la soluzione dell esercizio 3, Compito 4. 1 Nozioni Preliminari Consideriamo il calcolo dei
Logica Computazionale 2009 - Sequenti e Deduzione Naturale Gianluigi ellin November 24, 2009 Complementi per la soluzione dell esercizio 3, Compito 4. 1 Nozioni Preliminari Consideriamo il calcolo dei
15. Nozione di modello e verità di un predicato
 15. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
15. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
Compito di logica 28 giugno 2007 SOLUZIONI Fornire una derivazione in LJ dei sequenti: A A A B, B A A A B B A A A
 Es. 1. Compito di logica 28 giugno 2007 SOLUZIONI Fornire una derivazione in LJ dei sequenti: a. A (B C) (A B) (A C) B B C C A A B C, B C A (B C), (A B), A C A (B C), (A B) (A C) A (B C) (A B) (A C) b.
Es. 1. Compito di logica 28 giugno 2007 SOLUZIONI Fornire una derivazione in LJ dei sequenti: a. A (B C) (A B) (A C) B B C C A A B C, B C A (B C), (A B), A C A (B C), (A B) (A C) A (B C) (A B) (A C) b.
Ragionamento Automatico Calcolo dei Sequenti. Lezione 5 Ragionamento Automatico Carlucci Aiello, 2004/05 Lezione 5 0. Il calcolo dei sequenti
 Il calcolo dei sequenti Ragionamento Automatico Calcolo dei Sequenti Materiale cartaceo distribuito in aula Il calcolo dei sequenti nella logica proposizionale Il calcolo dei sequenti nella logica predicativa
Il calcolo dei sequenti Ragionamento Automatico Calcolo dei Sequenti Materiale cartaceo distribuito in aula Il calcolo dei sequenti nella logica proposizionale Il calcolo dei sequenti nella logica predicativa
Progetto Informatica. Primo esempio Gruppo 1. Laura Tarsitano
 Progetto Informatica Primo esempio Gruppo 1 Laura Tarsitano laura.tarsitano@criadcoding.it Come costruire un micromondo Quando si costruisce un micromondo su Snap! bisogna immaginare di costruire uno spettacolo
Progetto Informatica Primo esempio Gruppo 1 Laura Tarsitano laura.tarsitano@criadcoding.it Come costruire un micromondo Quando si costruisce un micromondo su Snap! bisogna immaginare di costruire uno spettacolo
Scomposizione in fattori dei polinomi
 Scomposizione in fattori dei polinomi Scomporre in fattori un polinomio significa esprimere quel polinomio come prodotto di altri polinomi di grado inferiore ad esso. Questo procedimento può essere visto
Scomposizione in fattori dei polinomi Scomporre in fattori un polinomio significa esprimere quel polinomio come prodotto di altri polinomi di grado inferiore ad esso. Questo procedimento può essere visto
Linguaggi formali e compilazione
 Linguaggi formali e compilazione Corso di Laurea in Informatica A.A. 2014/2015 Linguaggi formali e compilazione Generalità delle ǫ-transizioni Gli automi non deterministici, come abbiamo visto, possono
Linguaggi formali e compilazione Corso di Laurea in Informatica A.A. 2014/2015 Linguaggi formali e compilazione Generalità delle ǫ-transizioni Gli automi non deterministici, come abbiamo visto, possono
15. Nozione di modello e verità di un predicato
 15. Nozione di modello e verità di un predicato Def. (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è dato
15. Nozione di modello e verità di un predicato Def. (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è dato
Fasi di creazione di un programma
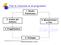 Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
Agenti Basati su Logica
 Agenti Basati su Logica Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 09/04/2018 Agenti basati sulla logica Generico agente logico Il mondo del Wumpus Logica proposizionale Inferenza
Agenti Basati su Logica Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 09/04/2018 Agenti basati sulla logica Generico agente logico Il mondo del Wumpus Logica proposizionale Inferenza
Equazioni di primo grado
 Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
T4T-aggiornamento insegnanti Secondo incontro febbraio 2017
 T4T-aggiornamento insegnanti Secondo incontro febbraio G. Barbara Demo Dipartimento di Informatica Università di Torino barbara@di.unito.it 2/9/ 1 Cosa è T4T? Perchè questo progetto? T4T sta per Teachers
T4T-aggiornamento insegnanti Secondo incontro febbraio G. Barbara Demo Dipartimento di Informatica Università di Torino barbara@di.unito.it 2/9/ 1 Cosa è T4T? Perchè questo progetto? T4T sta per Teachers
usare le funzioni aritmetiche e logiche di base come. Volgiamo costruire un foglio elettronico in cui registriamo i voti presi
 4.3 Funzioni e formule 4.3.1 Funzioni aritmetiche e logiche 4.3.1.1. usare le funzioni aritmetiche e logiche di base come addizione, sottrazione, moltiplicazione, divisione Volgiamo costruire un foglio
4.3 Funzioni e formule 4.3.1 Funzioni aritmetiche e logiche 4.3.1.1. usare le funzioni aritmetiche e logiche di base come addizione, sottrazione, moltiplicazione, divisione Volgiamo costruire un foglio
T2C Training to Code. Algoritmo e Ripeti. Laura Tarsitano
 T2C Training to Code Algoritmo e Ripeti Laura Tarsitano 1 Algoritmo/Sequenza Una lista di passi da seguire per risolvere un problema o svolgere un certo compito 2 Primo esempio 1 - Disegno Costruiamo un
T2C Training to Code Algoritmo e Ripeti Laura Tarsitano 1 Algoritmo/Sequenza Una lista di passi da seguire per risolvere un problema o svolgere un certo compito 2 Primo esempio 1 - Disegno Costruiamo un
ESAME di LOGICA PER INFORMATICA 24 giugno 2003
 ESAME di LOGICA PER INFORMATICA 24 giugno 2003 Compito 1 Esercizio 1. Siano Φ e Ψ due insiemi consistenti di formule. Dire, giustificando la risposta, se Φ Ψ e Φ Ψ sono consistenti. Soluzione. Se fosse
ESAME di LOGICA PER INFORMATICA 24 giugno 2003 Compito 1 Esercizio 1. Siano Φ e Ψ due insiemi consistenti di formule. Dire, giustificando la risposta, se Φ Ψ e Φ Ψ sono consistenti. Soluzione. Se fosse
Sistemi di inferenza Consentono di derivare formule da altre formule: formalizzazione del ragionamento. Un sistema di inferenza è costituito da: un
 Sistemi di inferenza Consentono di derivare formule da altre formule: formalizzazione del ragionamento. Un sistema di inferenza è costituito da: un insieme di assiomi un insieme di regole di inferenza,
Sistemi di inferenza Consentono di derivare formule da altre formule: formalizzazione del ragionamento. Un sistema di inferenza è costituito da: un insieme di assiomi un insieme di regole di inferenza,
per l Innovazione Didattica
 Pensiero Computazionale e Coding per l Innovazione Didattica Algoritmo e Ripeti Laura Tarsitano PENSIERO COMPUTAZIONALE PER L'INNOVAZIONE DIDATTICA 1 Algoritmo/Sequenza Una lista di passi da seguire per
Pensiero Computazionale e Coding per l Innovazione Didattica Algoritmo e Ripeti Laura Tarsitano PENSIERO COMPUTAZIONALE PER L'INNOVAZIONE DIDATTICA 1 Algoritmo/Sequenza Una lista di passi da seguire per
Ragionamento Automatico Richiami di tableaux proposizionali
 Richiami di logica e deduzione proposizionale Ragionamento Automatico Richiami di tableaux proposizionali (L. Carlucci Aiello & F. Pirri: SLL, Cap. 5) La logica proposizionale I tableau proposizionali
Richiami di logica e deduzione proposizionale Ragionamento Automatico Richiami di tableaux proposizionali (L. Carlucci Aiello & F. Pirri: SLL, Cap. 5) La logica proposizionale I tableau proposizionali
Sviluppo di programmi
 Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
Semantica di Kripke per LJ
 Semantica di Kripke per LJ mace@dsi.unive.it Consideriamo il linguaggio proposizionale Prop, delle proposizioni A, B, C,... generate induttivamente. Innanzitutto, ammettiamo una proposizione costante e
Semantica di Kripke per LJ mace@dsi.unive.it Consideriamo il linguaggio proposizionale Prop, delle proposizioni A, B, C,... generate induttivamente. Innanzitutto, ammettiamo una proposizione costante e
Logica proposizionale
 Definire un linguaggio formale Logica proposizionale Sandro Zucchi 2013-14 Definiamo un linguaggio formale LP (che appartiene a una classe di linguaggi detti linguaggi della logica proposizionale) Per
Definire un linguaggio formale Logica proposizionale Sandro Zucchi 2013-14 Definiamo un linguaggio formale LP (che appartiene a una classe di linguaggi detti linguaggi della logica proposizionale) Per
RISOLUZIONE IN LOGICA PROPOSIZIONALE. Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine
 RISOLUZIONE IN LOGICA PROPOSIZIONALE Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine 1. Risoluzione Definitione 1.1. Un letterale l è una variabile proposizionale (letterale
RISOLUZIONE IN LOGICA PROPOSIZIONALE Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine 1. Risoluzione Definitione 1.1. Un letterale l è una variabile proposizionale (letterale
Due tipi di logica. Gianluigi Bellin
 Due tipi di logica Gianluigi Bellin 15 Novembre 2012 Calcolo dei sequenti LK, logica classica. axiom Γ, A A, A, Γ Γ, A R Γ, A L A, Γ R Γ, A Γ, B Γ, A B A, B, Γ L A B, Γ A, Γ B, Γ, A B, Γ R Γ A B, L Γ,
Due tipi di logica Gianluigi Bellin 15 Novembre 2012 Calcolo dei sequenti LK, logica classica. axiom Γ, A A, A, Γ Γ, A R Γ, A L A, Γ R Γ, A Γ, B Γ, A B A, B, Γ L A B, Γ A, Γ B, Γ, A B, Γ R Γ A B, L Γ,
Calcoli dei sequenti classici e lineare
 Calcoli dei sequenti classici e lineare Gianluigi Bellin November 5, 2009 Scheda per il compito 2, scadenza rinviata al marteedì 10 novembre 2009 1 Calcolo dei sequenti classico 1.1 Linguaggio ed interpretazione
Calcoli dei sequenti classici e lineare Gianluigi Bellin November 5, 2009 Scheda per il compito 2, scadenza rinviata al marteedì 10 novembre 2009 1 Calcolo dei sequenti classico 1.1 Linguaggio ed interpretazione
Dal male il bene? L errore secondo alcuni concorrenti delle Olimpiadi della Matematica
 Dal male il bene? L errore secondo alcuni concorrenti delle Olimpiadi della Matematica Ludovico Pernazza Livorno, 16 ottobre 2014 Lo scopo dell indagine Una delle caratteristiche della matematica che rende
Dal male il bene? L errore secondo alcuni concorrenti delle Olimpiadi della Matematica Ludovico Pernazza Livorno, 16 ottobre 2014 Lo scopo dell indagine Una delle caratteristiche della matematica che rende
Logica per la Programmazione
 Logica per la Programmazione Lezione 3 Dimostrazione di Tautologie e Sintassi del Calcolo osizionale Antonio, Corrado e Bruno... formalmente Tautologie: dimostrazioni e controesempi Sintassi del Calcolo
Logica per la Programmazione Lezione 3 Dimostrazione di Tautologie e Sintassi del Calcolo osizionale Antonio, Corrado e Bruno... formalmente Tautologie: dimostrazioni e controesempi Sintassi del Calcolo
Integrale indefinito
 Integrale indefinito 1 Primitive di funzioni Definizione 1.1 Se f: [a, b] R è una funzione, una sua primitiva è una funzione derivabile g: [a, b] R tale che g () = f(). Ovviamente la primitiva di una funzione,
Integrale indefinito 1 Primitive di funzioni Definizione 1.1 Se f: [a, b] R è una funzione, una sua primitiva è una funzione derivabile g: [a, b] R tale che g () = f(). Ovviamente la primitiva di una funzione,
Argomento 8 Integrali indefiniti
 8. Integrale indefinito Argomento 8 Integrali indefiniti Definizione 8. Assegnata la funzione f definita nell intervallo I, diciamo che una funzione F con F : I R è una primitiva di f in I se i) F è derivabile
8. Integrale indefinito Argomento 8 Integrali indefiniti Definizione 8. Assegnata la funzione f definita nell intervallo I, diciamo che una funzione F con F : I R è una primitiva di f in I se i) F è derivabile
Derivazione numerica. Introduzione al calcolo numerico. Derivazione numerica (II) Derivazione numerica (III)
 Derivazione numerica Introduzione al calcolo numerico Il calcolo della derivata di una funzione in un punto implica un processo al limite che può solo essere approssimato da un calcolatore. Supponiamo
Derivazione numerica Introduzione al calcolo numerico Il calcolo della derivata di una funzione in un punto implica un processo al limite che può solo essere approssimato da un calcolatore. Supponiamo
Sviluppo di programmi
 Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
T2C2 Training to Code 2
 T2C2 Training to Code 2 Primo Esempio Laura Tarsitano laura.tarsitano@criadcoding.it Come costruire un micromondo Quando si costruisce un micromondo su Snap! bisogna immaginare di costruire uno spettacolo
T2C2 Training to Code 2 Primo Esempio Laura Tarsitano laura.tarsitano@criadcoding.it Come costruire un micromondo Quando si costruisce un micromondo su Snap! bisogna immaginare di costruire uno spettacolo
Stabilire se il punto di coordinate (1,1) appartiene alla circonferenza centrata nell origine e di raggio 1.
 Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Scelte ed alternative
 Scelte ed alternative Condizioni complesse Operatori booleani Operatori booleani in C Esercizio proposto Verifica della soluzione 2 Condizioni complesse Logica Booleana Le condizioni semplici (es. confronti)
Scelte ed alternative Condizioni complesse Operatori booleani Operatori booleani in C Esercizio proposto Verifica della soluzione 2 Condizioni complesse Logica Booleana Le condizioni semplici (es. confronti)
CALCOLO PROPOSIZIONALE
 CALCOLO PROPOSIZIONALE UN PROBLEMA DI DEDUZIONE LOGICA (da un test d ingresso) Tre amici, Antonio, Bruno e Corrado, sono incerti se andare al cinema. Si sa che: Se Corrado va al cinema, allora ci va anche
CALCOLO PROPOSIZIONALE UN PROBLEMA DI DEDUZIONE LOGICA (da un test d ingresso) Tre amici, Antonio, Bruno e Corrado, sono incerti se andare al cinema. Si sa che: Se Corrado va al cinema, allora ci va anche
Logica per la Programmazione
 Logica per la Programmazione Lezione 2 Dimostrazione di Tautologie Tabelle di Verità Dimostrazioni per sostituzione Leggi del Calcolo Proposizionale A. Corradini e F.Levi Dip.to Informatica Logica per
Logica per la Programmazione Lezione 2 Dimostrazione di Tautologie Tabelle di Verità Dimostrazioni per sostituzione Leggi del Calcolo Proposizionale A. Corradini e F.Levi Dip.to Informatica Logica per
MATRICI E OPERAZIONI
 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
Esercizi con i tableaux in logica del primo ordine
 Esercizi con i tableaux in logica del primo ordine Sandro Zucchi 2013-14 Regole per Q(TAB) Il sistema di tableaux che abbiamo adottato per LQ consiste nelle regole di LP(TAB) + le regole seguenti: dove
Esercizi con i tableaux in logica del primo ordine Sandro Zucchi 2013-14 Regole per Q(TAB) Il sistema di tableaux che abbiamo adottato per LQ consiste nelle regole di LP(TAB) + le regole seguenti: dove
(ED IMPARARE LE REGOLE DELLE OPERAZIONI)
 COME CALCOLARE IL PERIMETRO DI UN RETTANGOLO (ED IMPARARE LE REGOLE DELLE OPERAZIONI) Mettiamo che io abbia 8 panini, per calcolare la loro somma posso fare panino+panino+panino+panino+panino+panino+panino+panino=
COME CALCOLARE IL PERIMETRO DI UN RETTANGOLO (ED IMPARARE LE REGOLE DELLE OPERAZIONI) Mettiamo che io abbia 8 panini, per calcolare la loro somma posso fare panino+panino+panino+panino+panino+panino+panino+panino=
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE
 NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
Funzioni Esponenziale e Logaritmica. Prof. Simone Sbaraglia
 Funzioni Esponenziale e Logaritmica Prof. Simone Sbaraglia Funzione Esponenziale Vogliamo definire propriamente le funzioni esponenziali e logaritmiche che abbiamo introdotto in precedenza. Qual e` il
Funzioni Esponenziale e Logaritmica Prof. Simone Sbaraglia Funzione Esponenziale Vogliamo definire propriamente le funzioni esponenziali e logaritmiche che abbiamo introdotto in precedenza. Qual e` il
Ottimizzazione vincolata
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Soluzioni delle Esercitazioni V 15-19/10/ x 1 = = /x + = 0. 1+e x = 1. lnx 1+1/x = = = +.
 Soluzioni delle Esercitazioni V 5-9/0/208 A. Limiti I iti che seguono si possono calcolare con l algebra dei iti. 2 3 4 5 6 7 8 9 0 +2 3 = +2 3 = 3 2. e = ) e = e. / + = 0 + = 0 + = 0. +e = +0 = = 0. +/
Soluzioni delle Esercitazioni V 5-9/0/208 A. Limiti I iti che seguono si possono calcolare con l algebra dei iti. 2 3 4 5 6 7 8 9 0 +2 3 = +2 3 = 3 2. e = ) e = e. / + = 0 + = 0 + = 0. +e = +0 = = 0. +/
6. Perchè costruire alberi di derivazione?
 6. Perchè costruire alberi di derivazione? pr è radice di una derivazione in LC p pr è TAUTOLOGIA e più in generale Γ è radice di una derivazione in LC p Γ & è TAUTOLOGIA ovvero Γ è VALIDO posto Γ & (pr
6. Perchè costruire alberi di derivazione? pr è radice di una derivazione in LC p pr è TAUTOLOGIA e più in generale Γ è radice di una derivazione in LC p Γ & è TAUTOLOGIA ovvero Γ è VALIDO posto Γ & (pr
Grammatiche libere da contesto. Grammatiche libere da contesto
 rammatiche e Linguaggi Liberi da Contesto Abbiamo visto che molti linguaggi non sono regolari. Consideriamo allora classi piu grandi di linguaggi. Linguaggi Liberi da Contesto (CFL) sono stati usati nello
rammatiche e Linguaggi Liberi da Contesto Abbiamo visto che molti linguaggi non sono regolari. Consideriamo allora classi piu grandi di linguaggi. Linguaggi Liberi da Contesto (CFL) sono stati usati nello
METODI MATEMATICI PER L INFORMATICA
 METODI MATEMATICI PER L INFORMATICA Tutorato Lezione 5 05/05/2016 Corso per matricole congrue a 1 Docente: Margherita Napoli Tutor: Amedeo Leo Dimostrazioni e prove Esercizio 7 pagina 91 Utilizzare una
METODI MATEMATICI PER L INFORMATICA Tutorato Lezione 5 05/05/2016 Corso per matricole congrue a 1 Docente: Margherita Napoli Tutor: Amedeo Leo Dimostrazioni e prove Esercizio 7 pagina 91 Utilizzare una
Grammatiche libere da contesto. Grammatiche libere da contesto
 rammatiche e Linguaggi Liberi da Contesto Abbiamo visto che molti linguaggi non sono regolari. Consideriamo allora classi piu grandi di linguaggi. Linguaggi Liberi da Contesto (CFL) sono stati usati nello
rammatiche e Linguaggi Liberi da Contesto Abbiamo visto che molti linguaggi non sono regolari. Consideriamo allora classi piu grandi di linguaggi. Linguaggi Liberi da Contesto (CFL) sono stati usati nello
LE EQUAZIONI LINEARI LE IDENTITA ( )( ) 5. a Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a
 LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Dispensa di Informatica Teorica (Elementi) - Teorema di Cook
 Teorema di ook (Idea generale) Dato L NP, costruire una trasformazione polinomiale f da L a L (sodd, e), cioè il linguaggio composto dalle stringhe che corrispondono ad istanze del problema sodd. La trasformazione
Teorema di ook (Idea generale) Dato L NP, costruire una trasformazione polinomiale f da L a L (sodd, e), cioè il linguaggio composto dalle stringhe che corrispondono ad istanze del problema sodd. La trasformazione
Intelligenza Artificiale I
 Intelligenza Artificiale I Logica formale Calcolo simbolico Marco Piastra Logica formale - Calcolo simbolico - 1 Calcolo simbolico? Una fbf è conseguenza logica di un insieme di fbf sse qualsiasi modello
Intelligenza Artificiale I Logica formale Calcolo simbolico Marco Piastra Logica formale - Calcolo simbolico - 1 Calcolo simbolico? Una fbf è conseguenza logica di un insieme di fbf sse qualsiasi modello
Intelligenza Artificiale I
 Intelligenza Artificiale I Logica formale Calcolo simbolico Marco Piastra Logica formale - Calcolo simbolico - 1 Conseguenza, decidibilità Una fbf è conseguenza logica di un insieme di fbf sse qualsiasi
Intelligenza Artificiale I Logica formale Calcolo simbolico Marco Piastra Logica formale - Calcolo simbolico - 1 Conseguenza, decidibilità Una fbf è conseguenza logica di un insieme di fbf sse qualsiasi
Lezione 4. Da questa definizione si ha dunque che le similitudini sono particolari trasformazioni affini.
 Lezione 4 Trasformazioni affini tra piani Una affinità f tra due piani P e Q è una trasformazione biunivoca di P in Q che conserva l allineamento. Ciò significa che comunque si scelgano tre punti allineati
Lezione 4 Trasformazioni affini tra piani Una affinità f tra due piani P e Q è una trasformazione biunivoca di P in Q che conserva l allineamento. Ciò significa che comunque si scelgano tre punti allineati
DIMOSTRAZIONI E TAUTOLOGIE, IPOTESI NON TAUTOLOGICHE. Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini
 DIMOSTRAZIONI E TAUTOLOGIE, IPOTESI NON TAUTOLOGICHE Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini INFERENZE CORRETTE E TAUTOLOGIE Il Calcolo Proposizionale permette di formalizzare
DIMOSTRAZIONI E TAUTOLOGIE, IPOTESI NON TAUTOLOGICHE Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini INFERENZE CORRETTE E TAUTOLOGIE Il Calcolo Proposizionale permette di formalizzare
Somma diretta di sottospazi vettoriali
 Capitolo 8 Somma diretta di sottospazi vettoriali 8.1 Introduzione Introduciamo un caso particolare di somma di due sottospazi vettoriali: la somma diretta. Anche questo argomento è stato visto nel corso
Capitolo 8 Somma diretta di sottospazi vettoriali 8.1 Introduzione Introduciamo un caso particolare di somma di due sottospazi vettoriali: la somma diretta. Anche questo argomento è stato visto nel corso
Geometria BAER Canale I Esercizi 10
 Geometria BAER Canale I Esercizi 10 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Geometria BAER Canale I Esercizi 10 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
DIMOSTRAZIONE DI IMPLICAZIONI TAUTOLOGICHE. Corso di Logica per la Programmazione A.A. 2010/11 Andrea Corradini
 DIMOSTRAZIONE DI IMPLICAZIONI TAUTOLOGICHE Corso di Logica per la Programmazione A.A. 2010/11 Andrea Corradini DIGRESSIONE: SULLA SINTASSI DEL CALCOLO PROPOSIZIONALE Abbiamo già presentato la grammatica
DIMOSTRAZIONE DI IMPLICAZIONI TAUTOLOGICHE Corso di Logica per la Programmazione A.A. 2010/11 Andrea Corradini DIGRESSIONE: SULLA SINTASSI DEL CALCOLO PROPOSIZIONALE Abbiamo già presentato la grammatica
Programmazione dinamica
 5 Programmazione dinamica 5.1 Stringhe Palindrome Una stringa si dice palindroma se è uguale alla sua trasposta, ossia se è la stessa letta da sinistra a destra, o da destra a sinistra (es: anna, osso,
5 Programmazione dinamica 5.1 Stringhe Palindrome Una stringa si dice palindroma se è uguale alla sua trasposta, ossia se è la stessa letta da sinistra a destra, o da destra a sinistra (es: anna, osso,
Logica per la Programmazione
 Logica per la Programmazione Lezione 3 Dimostrazione di Tautologie e Sintassi del Calcolo osizionale Antonio, Corrado e Bruno... formalmente Tautologie: dimostrazioni e controesempi Sintassi del Calcolo
Logica per la Programmazione Lezione 3 Dimostrazione di Tautologie e Sintassi del Calcolo osizionale Antonio, Corrado e Bruno... formalmente Tautologie: dimostrazioni e controesempi Sintassi del Calcolo
Intelligenza Artificiale. Logica proposizionale: calcolo simbolico
 Intelligenza Artificiale Logica proposizionale: calcolo simbolico Marco Piastra Logica formale (Parte 2) - 1 Parte 2 Calcolo logico Assiomi Derivazioni Derivazioni e conseguenza logica Completezza Logica
Intelligenza Artificiale Logica proposizionale: calcolo simbolico Marco Piastra Logica formale (Parte 2) - 1 Parte 2 Calcolo logico Assiomi Derivazioni Derivazioni e conseguenza logica Completezza Logica
Qualche informazione su gruppi e anelli
 Qualche informazione su gruppi e anelli 1. Gruppi e sottogruppi: prime proprietà Cominciamo subito scrivendo la definizione formale di gruppo. Definizione 0.1. Un gruppo G è un insieme non vuoto dotato
Qualche informazione su gruppi e anelli 1. Gruppi e sottogruppi: prime proprietà Cominciamo subito scrivendo la definizione formale di gruppo. Definizione 0.1. Un gruppo G è un insieme non vuoto dotato
Patente Europea del Computer ECDL - MODULO 3
 Patente Europea del Computer ECDL - MODULO 3 Lezione 3 di 3 Aiuto Controllo ortografico Opzioni di Word Stampa unione Per richiamare la Guida in linea di Word, possiamo utilizzare il pulsante azzurro a
Patente Europea del Computer ECDL - MODULO 3 Lezione 3 di 3 Aiuto Controllo ortografico Opzioni di Word Stampa unione Per richiamare la Guida in linea di Word, possiamo utilizzare il pulsante azzurro a
Sistemi Deduttivi. Marco Piastra. Intelligenza Artificiale I. Intelligenza Artificiale I - A.A Sistemi Deduttivi[1]
![Sistemi Deduttivi. Marco Piastra. Intelligenza Artificiale I. Intelligenza Artificiale I - A.A Sistemi Deduttivi[1] Sistemi Deduttivi. Marco Piastra. Intelligenza Artificiale I. Intelligenza Artificiale I - A.A Sistemi Deduttivi[1]](/thumbs/88/115134024.jpg) Intelligenza Artificiale I Sistemi Deduttivi Marco Piastra Intelligenza Artificiale I - A.A. 2010- Sistemi Deduttivi[1] Calcolo simbolico? Una fbf è conseguenza logica di un insieme di fbf sse qualsiasi
Intelligenza Artificiale I Sistemi Deduttivi Marco Piastra Intelligenza Artificiale I - A.A. 2010- Sistemi Deduttivi[1] Calcolo simbolico? Una fbf è conseguenza logica di un insieme di fbf sse qualsiasi
A m n B n p = P m p. 0 1 a b c d. a b. 0 a 0 c Il risultato e lo stesso solo nel caso in cui c = 0 e a = d.
 Matematica II, 220404 Il prodotto di matrici e un operazione parziale che prende in entrata una matrice A ed una matrice B, tali che il numero delle colonne di A sia uguale al numero delle righe di B,
Matematica II, 220404 Il prodotto di matrici e un operazione parziale che prende in entrata una matrice A ed una matrice B, tali che il numero delle colonne di A sia uguale al numero delle righe di B,
3 Omotetie del piano. 4 Omotetie del piano. Fondamenti e didattica della matematica B. Geometria delle similitudini. k = 3.
 1 2 Fondamenti e didattica della matematica B 5 marzo 2007 Geometria delle similitudini Marina Bertolini (marina.bertolini@mat.unimi.it) Dipartimento di Matematica F.Enriques Università degli Studi di
1 2 Fondamenti e didattica della matematica B 5 marzo 2007 Geometria delle similitudini Marina Bertolini (marina.bertolini@mat.unimi.it) Dipartimento di Matematica F.Enriques Università degli Studi di
Lo STUDIO, questo sconosciuto!
 Lo STUDIO, questo sconosciuto! 1.A. che cosa penso della GEOGRAFIA Evidenzia due risposte fra le seguenti, poi scrivi la tua motivazione. Geografia è interessante è noiosa aiuta a capire il mondo è difficile
Lo STUDIO, questo sconosciuto! 1.A. che cosa penso della GEOGRAFIA Evidenzia due risposte fra le seguenti, poi scrivi la tua motivazione. Geografia è interessante è noiosa aiuta a capire il mondo è difficile
Errata corrige del libro Introduzione alla logica e al linguaggio matematico
 Errata corrige del libro Introduzione alla logica e al linguaggio matematico 28 gennaio 2009 Capitolo 1 Pag. 7, Definizione 6. Il complemento di un sottoinsieme A di I è il sottoinsieme A = {x I : x /
Errata corrige del libro Introduzione alla logica e al linguaggio matematico 28 gennaio 2009 Capitolo 1 Pag. 7, Definizione 6. Il complemento di un sottoinsieme A di I è il sottoinsieme A = {x I : x /
14. Nozione di modello e verità di un predicato
 14. Nozione di modello e verità di un predicato Per definire la validità di un predicato facciamo uso della nozione di modello. Intuitivamente un modello definisce in modo primitivo l interpretazione delle
14. Nozione di modello e verità di un predicato Per definire la validità di un predicato facciamo uso della nozione di modello. Intuitivamente un modello definisce in modo primitivo l interpretazione delle
Un pilinomio di grado n può essere scritto nella forma:
 ESAME DI MATURITA 2010 - QUESITI DELLA SECONDA PROVA DI MATEMATICA - LICEO SCIENTIFICO TRADIZIONALE A cura di Alberto Bellato Soluzioni a cura di Studentville.it e Votailprof.it Attenzione: il contenuto
ESAME DI MATURITA 2010 - QUESITI DELLA SECONDA PROVA DI MATEMATICA - LICEO SCIENTIFICO TRADIZIONALE A cura di Alberto Bellato Soluzioni a cura di Studentville.it e Votailprof.it Attenzione: il contenuto
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13)
 LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 4 Sommario. Dimostriamo il Teorema di Completezza per il Calcolo dei Predicati del I ordine. 1. Teorema di Completezza Dimostriamo il Teorema
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 4 Sommario. Dimostriamo il Teorema di Completezza per il Calcolo dei Predicati del I ordine. 1. Teorema di Completezza Dimostriamo il Teorema
13. Nozione di modello e verità di un predicato
 13. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
13. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
Anno Scolastico 2014/15 - Classe 1D Verifica di matematica dell 11 Maggio Soluzioni degli esercizi. 2(x 2) 2(x 1) + 2 = 3x
 Anno Scolastico 2014/15 - Classe 1D Verifica di matematica dell 11 Maggio 2015 - Soluzioni degli esercizi Risolvere le seguenti equazioni. Dove è necessario, scrivere le condizioni di accettabilità e usarle
Anno Scolastico 2014/15 - Classe 1D Verifica di matematica dell 11 Maggio 2015 - Soluzioni degli esercizi Risolvere le seguenti equazioni. Dove è necessario, scrivere le condizioni di accettabilità e usarle
Linguaggi. Claudio Sacerdoti Coen 15/04/ : Deduzione naturale per la logica del prim ordine. Universitá di Bologna
 Linguaggi 19: Universitá di Bologna 15/04/2011 Outline 1 Semantica Wikipedia: Deduzione naturaler per la logica del prim ordine Abbiamo già dato le regole per la deduzione naturale
Linguaggi 19: Universitá di Bologna 15/04/2011 Outline 1 Semantica Wikipedia: Deduzione naturaler per la logica del prim ordine Abbiamo già dato le regole per la deduzione naturale
Corso di Laurea in Fisica. Geometria 1. a.a Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 17/11/06 B =
 Corso di Laurea in Fisica. Geometria. a.a. 26-7. Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 7//6 Soluzione esercizio. Sia B {e, e 2 } e sia B {v, v 2 }. La matrice B del cambiamento di base
Corso di Laurea in Fisica. Geometria. a.a. 26-7. Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 7//6 Soluzione esercizio. Sia B {e, e 2 } e sia B {v, v 2 }. La matrice B del cambiamento di base
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8/11/2013
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
4 La Logica come base di ogni scienza. 5 Alla ricerca della forma logica. logica
 4 La Logica come base di ogni scienza La Logica è alla base di ogni scienza (o teoria) in quanto è fondamento di ogni scienza non tanto per i contenuti specifici ma per la loro articolazione deduttiva.
4 La Logica come base di ogni scienza La Logica è alla base di ogni scienza (o teoria) in quanto è fondamento di ogni scienza non tanto per i contenuti specifici ma per la loro articolazione deduttiva.
Se con e indichiamo l elemento neutro di in G, e deve appartenere ad H.
 Abbiamo visto a lezione che una sottoalgebra B di un algebra A è identificabile con l immagine di un omomorfismo iniettivo a valori in A. Una sottoalgebra B di A è in particolare un sottoinsieme non vuoto
Abbiamo visto a lezione che una sottoalgebra B di un algebra A è identificabile con l immagine di un omomorfismo iniettivo a valori in A. Una sottoalgebra B di A è in particolare un sottoinsieme non vuoto
1. Esistono numeri della forma , ottenuti cioè ripetendo le cifre 2006 un certo numero di volte, che siano quadrati perfetti?
 1 Congruenze 1. Esistono numeri della forma 200620062006...2006, ottenuti cioè ripetendo le cifre 2006 un certo numero di volte, che siano quadrati perfetti? No, in quanto tutti questi numeri sono congrui
1 Congruenze 1. Esistono numeri della forma 200620062006...2006, ottenuti cioè ripetendo le cifre 2006 un certo numero di volte, che siano quadrati perfetti? No, in quanto tutti questi numeri sono congrui
Corso di Analisi Matematica 1 - professore Alberto Valli
 Università di Trento - Corso di Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio - 06/7 Corso di Analisi Matematica - professore Alberto Valli foglio di esercizi - ottobre 06 iti.
Università di Trento - Corso di Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio - 06/7 Corso di Analisi Matematica - professore Alberto Valli foglio di esercizi - ottobre 06 iti.
Esercizi per il corso Matematica clea
 Esercizi per il corso Matematica clea Daniele Ritelli anno accademico 008/009 Lezione : Numeri naturali e principio di induzione Esercizi svolti. Provare che + + + n. Provare che + + + n n(n + ) n(n +
Esercizi per il corso Matematica clea Daniele Ritelli anno accademico 008/009 Lezione : Numeri naturali e principio di induzione Esercizi svolti. Provare che + + + n. Provare che + + + n n(n + ) n(n +
Esercitazioni per il corso di Logica Matematica
 Esercitazioni per il corso di Logica Matematica Luca Motto Ros 27 febbraio 2005 Nota importante. Queste pagine contengono appunti personali dell esercitatore e sono messe a disposizione nel caso possano
Esercitazioni per il corso di Logica Matematica Luca Motto Ros 27 febbraio 2005 Nota importante. Queste pagine contengono appunti personali dell esercitatore e sono messe a disposizione nel caso possano
LOGICA PER LA PROGRAMMAZIONE a.a. 2017/18 Prima esercitazione 28/9/2017 Soluzioni Proposte
 LOGICA PER LA PROGRAMMAZIONE a.a. 2017/18 Prima esercitazione 28/9/2017 Soluzioni Proposte Attenzione: Le soluzioni che seguono sono considerate corrette dai docenti. possono esistere altre soluzioni corrette,
LOGICA PER LA PROGRAMMAZIONE a.a. 2017/18 Prima esercitazione 28/9/2017 Soluzioni Proposte Attenzione: Le soluzioni che seguono sono considerate corrette dai docenti. possono esistere altre soluzioni corrette,
Esercizi di Matematica per la prova di ammissione alla Scuola Galileiana /16
 Esercizi di Matematica per la prova di ammissione alla Scuola Galileiana - 015/16 Esercizio 1 Per quali valori n Z \ {0} l espressione è un numero intero positivo? (n + 5)(n + 6) 6n Soluzione. Il problema
Esercizi di Matematica per la prova di ammissione alla Scuola Galileiana - 015/16 Esercizio 1 Per quali valori n Z \ {0} l espressione è un numero intero positivo? (n + 5)(n + 6) 6n Soluzione. Il problema
Aritmetica sui numeri interi
 CHAPTER 1 Aritmetica sui numeri interi L insieme dei numeri naturali N è certamente l insieme numerico più familiare. Non consideriamo lo zero 0 come elemento dell insieme N; non è stata infatti naturale
CHAPTER 1 Aritmetica sui numeri interi L insieme dei numeri naturali N è certamente l insieme numerico più familiare. Non consideriamo lo zero 0 come elemento dell insieme N; non è stata infatti naturale
La matematica non è un opinione, lo è oppure...?
 La matematica non è un opinione, lo è oppure...? Giulio Giusteri Dipartimento di Matematica e Fisica Università Cattolica del Sacro Cuore Brescia 26 Febbraio 2010 Vecchie conoscenze Dedurre... dedurre...
La matematica non è un opinione, lo è oppure...? Giulio Giusteri Dipartimento di Matematica e Fisica Università Cattolica del Sacro Cuore Brescia 26 Febbraio 2010 Vecchie conoscenze Dedurre... dedurre...
