Corso di Reti Logiche
|
|
|
- Bernarda Nicoletta Ferrante
- 9 anni fa
- Просмотров:
Транскрипт
1 Corso di Reti Logiche Minimizzazione degli Stati nelle Macchine Sequenziali Dipartimento di Informatica e Sistemistica Università Degli Studi di Napoli Federico II 1
2 Le Macchine o Automi E necessario individuare il comportamento del sistema che stiamo realizzando indipendentemente da come questo viene fisicamente costruito Gli Automi sono un buono strumento per rappresentare questo comportamento
3 Il Modello Matematico Macchina di Mealy Una macchina sequenziale (a stati finiti) è una quintupla ordinata di enti M(Q,I,U,t,w), dove: Q è un insieme finito di Stati Interni I è un insieme finito di Stati di Ingresso U è un insieme finito di Stati di Uscita t è una funzione D Q I Q w è una funzione D Q I U
4 Il Modello Matematico Macchina di Moore Una macchina sequenziale (a stati finiti) è una quintupla ordinata di enti M(Q,I,U,t,w), dove: Q è un insieme finito di Stati Interni I è un insieme finito di Stati di Ingresso U è un insieme finito di Stati di Uscita t è una funzione D Q I Q w è una funzione D Q U
5 Descrizione della macchina Il comportamento della macchina può essere descritto come una tabella o come un grafo: Tabella Stato/Ingresso prossimo stato Grafo Passaggi di stato Mealy: uscita associata all arco Moore: uscita associata al nodo
6 Esempio Automa in grado di riconoscere la sequenza 101 0/0 S 0 1/1 1/0 0/0 S S 1 0/0 1/0 0 1 S 0 S 0 /0 S 1 /0 S 1 S /0 S 1 /0 S S 0 /0 S 0 /1 6
7 Modello generale Una Macchina Sequenziale può essere realizzata con: Una macchina Combinatoria Un elemento di ritardo Stato Ingresso d Macchina Combinatoria Stato Prossimo Uscita 7
8 Le Parti della Macchina L ingresso della macchina combinatoria è l ingresso della macchina sequenziale più l uscita del ritardo (lo stato precedente). L uscita della macchina combinatoria è l uscita della macchina sequenziale più il prossimo stato della macchina. 8
9 Funzioni uscita e stato prossimo L uscita e lo stato prossimi possono considerarsi funzioni della sequenza di ingressi applicata a partire da un certo stato iniziale, e dallo stato iniziale stesso: u k = λ(q 0, J k ) q k+1 = δ(q 0, J k ) Se λ è definita ovunque, la macchina si dice non completa Un uscita potrebbe essere definita per J k e non per un J j con k>j Sequenza J j non applicabile in q 0 9
10 Equivalenza Occorre formalizzare il fatto che due macchine possano avere lo stesso funzionamento reagire nello stesso modo (con le stesse uscite) alle stesse sequenze di ingressi Definizione di stati equivalenti in macchine complete: Producono la stessa sequenza di uscite per qualsiasi sequenza di ingressi 10
11 Equivalenza Un modo per riconoscere stati equivalenti (fondamentale negli algoritmi che vedremo) è usare la proprietà ricorsiva degli stati equivalenti: Due stati sono equivalenti se lo sono tutte le possibili coppie di stati successivi, e sono uguali tutte le possibili uscite successive 11
12 Equivalenza I due stati possono appartenere anche alla stessa macchina Due macchine complete M e M' sono equivalenti se per ciascuno stato q di M esiste almeno uno stato q di M ad esso equivalente e, viceversa 1
13 Equivalenza e macchine incompete La definizione precedente non può essere applicata così com è non tutte le possibili sequenze sono applicabili a tutti gli stati Si introducono i concetti di Compatibilità tra stati Inclusione tra macchine 1
14 Stati compatibili Due stati sono compatibili se per ogni sequenza di ingressi applicabili ad entrambi le uscite prodotte sono identiche A differenza della relazione vista prima per macchine complete, la compatibilità NON è una relazione di equivalenza: Gode delle proprietà Riflessiva Simmetrica Ma NON di quella transitiva Ciò complica la ricerca di macchine equivalenti minime 1
15 Compatibilità Così come l equivalenza, anche la compatibilità può essere definita ricorsivamente Due stati sono compatibili se tutti i possibili stati prossimi sono compatibili, e tutte le possibili uscite prossime sono uguali Non essendo una relazione di equivalenza, non è possibile utilizzare le proprietà delle classi di equivalenza. Si generalizza con il concetto di famiglia di insiemi di stati compatibili massimi 1
16 Compatibilità Per le macchine incomplete, non si parla quindi di equivalenza, ma di inclusione: Una macchina M ne include una M in una coppia di stati q e q se tutte le sequenze di ingressi applicabili ad M a partire da q lo sono anche per M a partire da q producendo la stessa uscita Se è possibile trovare per ciascuno stato di M uno q che soddisfa la precedente definizione, allora M include M è possibile usare M in luogo della M M ed M possono includersi l un l altra diremo in questo caso che le due macchine sono equivalenti 16
17 Compatibilità ed equivalenza Nel caso di macchine complete le due definizioni di equivalenza coincidono Tra due macchine equivalenti, conviene scegliere quella con meno stati problema di minimizzazione individuare la macchina con il minor numero di stati tra tutte le possibili macchine equivalenti 17
18 Problema della Minimizzazione Partendo da una macchina M(Q,I,U,τ,ω), ne vogliamo trovare a macchina M (Q,I,U,τ,ω ) equivalente ad M e con il minor numero di stati Partiamo dalla famiglia di insiemi di stati compatibili massimi F=(S 1,S,...,S n ) 18
19 Problema della Minimizzazione La F gode delle seguenti proprietà, essenziali nei metodi di minimizzazione: Gli elementi S di F sono disgiunti Gli elementi S di F coprono l insieme degli stati Q Tutti gli stati di un elemento S di F portano alla stessa uscita (eventualmente non definita) F è chiusa: da due stati di uno stesso elemento S di F si arriva a due stati che appartengono ad una stessa S Ricerchiamo la M'(F,I,U,τ,ω') ha un numero di stati non superiore a M 19
20 Ricerca della famiglia F Algoritmo del partizionamento Metodo tabellare di Paull-Unger Procedono per eliminazione Partono da una presunta F (inizialmente coincidente con Q) e cercano di individuare incompatibilità fin quando è possibile 0
21 Algoritmo del partizionamento Si individuano gli stati incompatibili rispetto alle uscite per ciascun ingresso Le partizioni individuate si esaminano rispetto allo stato prossimo Si itera fintantoché tutte le partizioni non verificano la definizione di compatibilità 1
22 Algoritmo del partizionamento
23 Metodo di Paull-Unger Riorganizza il procedimento visto prima in forma di griglia diagonale incompatibilità stati Possibili coppie di stati prossimi
24 Metodo di Paull-Unger Si marcano come incompatibili le coppie di stati che portano ad uscite differenti per almeno un ingresso Si indicano le coppie di possibili stati prossimi in ogni casella Si continua iterativamente il procedimento partizionando rispetto agli stati
25 Metodo di Paull-Unger 1 i 1 /A /B /A i /B /A /B Ogni stato è confrontato con tutti gli altri, ma solo una volta: 1 è confrontato con 6 è confrontato con 6 etc etc. 6 /B /B /A /B /A /B 6 1
26 Metodo di Paull-Unger i 1 i Confrontiamo lo stato 1 con : Per entrambi gli ingressi, le uscite sono diverse 1 e sono non-equivalenti 1 /A /B /B /A /A /B /B /B 6 /B /A /A /B 6 1 6
27 Metodo di Paull-Unger i 1 i Confrontiamo lo stato 1 con : Le uscite sono uguali per entrambi gli ingessi 1 e potrebbero essere equivalenti 1 6 /A /B /A /B /B /A /B /A /B /B /A /B 6 - Per la proprietà ricorsiva dell equivalenza, 1 e sono effettivamente equivalenti se lo sono tutte le possibili coppie di stati prossimi: e (per i 1 ) e e (per i ), che è sempre vera 1 7
28 Metodo di Paull-Unger 1 6 Confrontiamo lo stato 1 con : C è almeno un ingresso per cui le uscite i 1 i sono diverse 1 e sono non-equivalenti /A /B /B /A /A /B /B /B /B /A /A /B 6-1 8
29 Metodo di Paull-Unger 1 6 i 1 /A /B /A /B /B /A i /B /A /B /B /A /B Al termine del primo passo, abbiamo individuato tutte le coppie che sono sicuramente non-equivalenti in base alle uscite (considerate per tutti i possibili ingressi). Le caselle non barrate sono coppie di possibili stati equivalenti. Bisogna adesso ripercorre la tabella per verificare l equivalenza degli stati prossimi
30 Metodo di Paull-Unger Scorriamo come prima la tabella L equivalenza 1- dipende dall equivalenza -, che al momento non è nota
31 Metodo di Paull-Unger Gli stati 1 e 6 sono sicuramente non-equivalenti poiché non lo sono e Il procedimento si itera fino quando non è più possibile individuare coppie non equivalenti. In questo caso si vede continuando che non sono presenti stati equivalenti 1 1
32 Row-merging 1 I 1 6/A 6/A i /B /B Nel caso che per due stati (ad ed. 1 e ) siano uguali tutte le possibili uscite e tutti i possibili stati prossimi, l equivalenza è sempre garantita I due stati sono di fatto un unico stato e possono subito essere accorpati. Nella tabella può essere effettuato un rowmerging 6 1
33 Row-merging 1 I 1 6/A i /B 6/A /B Si elimina uno dei due (ad esempio lo stato ) Nella tabella, dovunque compaia come stato prossimo, si sostituisce 1
34 Paull-Unger: esempio Riconosciamo immediatamente le equivalenze tra 10-1: sostituiti con 10 (row-merging) 8 16 (essendo 10 1): sostituiti con 8 1 (essendo 8 16): sostituiti con 7 (essendo 10 1): sostituiti con : sostituiti con 11 i 1 i q q / u 1 q q q q q 6 q 7 / u 1 q q 8 q 9 q 0 1 q 6 q 1 q 7 q 1 q 8 /u q 1 q 9 q 9 0 q 1 q 6 q 9 q q q 6 /u 0
35 Paull-Unger: esempio Riconosciamo immediatamente le equivalenze tra 10-1: sostituiti con 10 (row-merging) 8 16 (essendo 10 1): sostituiti con 8 1 (essendo 8 16): sostituiti con 7 (essendo 10 1): sostituiti con : sostituiti con 11 i 1 i q q / u 1 q q q q q 6 q 7 / u 1 q q 8 q 9 q 0 1 q 6 q 1 q 7 q 1 q 8 /u q 1 q 9 q 9 0 q 1 q 6 q 9 q q q 6 /u 0
36 Paull-Unger: esempio i 1 i q q / u 1 q q q q q 6 q / u 1 q q 8 q 9 q 0 1 q 6 q 1 q 8 /u q 0 1 q 9 q 9 0 q 1 q In questo caso, gli stati hanno tutti insiemi di uscite uguali, tranne 8, che quindi sicuramente è non-equivalente rispetto a tutti gli altri. Procediamo quindi con il metodo di Paull-Unger cercando equivalenze tra gli stati rimanenti: 1,,,,,6,9,10,11 6
37 Paull-Unger: esempio i 1 i q q / u 1 q q q q q 6 q / u 1 q q 8 q 9 q 0 1 q 6 q 1 q 9 q 9 0 q 1 q
38 Paull-Unger: esempio Essendo 8 non equivalente con nessun altro stato, possono essere barrate tutte le caselle che contengono
39 Paull-Unger: esempio Si procede cercando ulteriori nonequivalenze
40 Paull-Unger: esempio Si itera il procedimento fin quando non è possibile trovare ulteriori condizioni di nonequivalenza. La situazione stabile così trovata corrisponde al fatto che la partizione degli stati così trovata è chiusa
41 Paull-Unger: esempio Osservando la griglia, si nota che: - gli stati 1,,,11 sono tra loro equivalenti -,6,10 sono tra loro equivalenti - non è equivalente a nessun altro - 9 non è equivalente a nessun altro
42 Paull-Unger: esempio i 1 i q q / u 1 q q q q q 6 q / u 1 q q 8 q 9 q 0 1 q 6 q 1 q 8 /u q 0 1 q 9 q 9 0 q 1 q - gli stati 1,,,11 sono equivalenti -,6,10 sono equivalenti - non è equivalente a nessun altro - 9 non è equivalente a nessun altro - 8 non è equivalente a nessun altro Possiamo quindi creare i nuovi stati da usare nella macchina ridotta: S 0 = (1,,,11) S 1 = (,6,10) S = () S = (9) S = (8)
43 Paull-Unger: esempio i 1 i q q / u 1 q q q q q 6 q / u 1 q q 8 q 9 q 0 1 q 6 q 1 q 8 /u q 0 1 q 9 q 9 0 q 1 q i 1 i S 0 S 1 S 0 / u 1 S 1 S S 0 S S S / u 1 S S 0 S S S 0 /u S 1 S 0 = (1,,,11) S 1 = (,6,10) S = () S = (9) S = (8)
44 Minimizzazione per macchine incomplete Come osservato in precedenza, nel caso di macchine incomplete non è possibile ottenere una partizione degli stati I differenti insiemi di stati compatibili possono sovrapporsi non è detto che il numero di insiemi non possa essere superiore al numero di singoli stati Procediamo innanzitutto per ricerca degli insiemi compatibili massimi Risolviamo poi un problema di copertura minima con gli insiemi così individuati
45 Minimizzazione per macchine incomplete L algoritmo procede creando tutti i possibili insiemi compatibili eventualmente scorporando un insieme in due separando SOLTANTO eventuali stati incompatibili Es: (1,,,) (1,,) (1,,) se Essendo interessati ad insiemi massimi, elimineremo di volta in volta insiemi contenuti in altri
46 Esempio i 1 i i i q /- -/- q 6 /- q /- q /u q /- -/- q q q /- -/- q 6 /- q /- q /u q /- -/- q -/- q 7 /- q /u q 6 /- q 6 q /- -/- q /- q 6 / u q 7 q /- q 7 /u q /- -/- 6
47 Esempio i 1 i i i q /- -/- q 6 /- q /- q /u q /- -/- q q q /- -/- q 6 /- q /- q /u q /- -/- q -/- q 7 /- q /u q 6 /- Consideriamo inizialmente come famiglia di insiemi di compatibilità massimi quella costituita da un unico insieme che include tutti gli stati q 6 q /- -/- q /- q 6 / u q 7 q /- q 7 /u q /- -/- 7
48 Esempio i 1 i i i q /- -/- q 6 /- q /- q /u q /- -/- q q q /- -/- q 6 /- q /- q /u q /- -/- q -/- q 7 /- q /u q 6 /- q 6 q /- -/- q /- q 6 / u q 7 q /- q 7 /u q /- -/- Gli stati e 7 sono sicuramente incompatibili poiché per i producono uscite diverse (risp. u e u ) Scorporiamo l insieme iniziale (1,,,,,6,7) (1,,,,,6) (1,,,,6,7) 8
49 Esempio i 1 i i i q /- -/- q 6 /- q /- q /u q /- -/- q q q /- -/- q 6 /- q /- q /u q /- -/- q -/- q 7 /- q /u q 6 /- q 6 q /- -/- q /- q 6 / u q 7 q /- q 7 /u q /- -/- Gli stati e 7 sono sicuramente incompatibili poiché per i producono uscite diverse (risp. u e u ). Scorporiamo l unico dei due insiemi precedenti che contiene entrambi e 7 (1,,,,6,7) (1,,,6,7) (1,,,,6) 9
50 Esempio i 1 i i i q /- -/- q 6 /- q /- q /u q /- -/- q q q /- -/- q 6 /- q /- q /u q /- -/- q -/- q 7 /- q /u q 6 /- q 6 q /- -/- q /- q 6 / u q 7 q /- q 7 /u q /- -/- Osserviamo che tra i tre insiemi che abbiamo ottenuto è presente uno incluso in uno degli altri due. Essendo interessati ad insiemi massimi, possiamo eliminarlo Rimangono i due insiemi (1,,,,,6) e (1,,,6,7) 0
51 Esempio i 1 i i i q /- -/- q 6 /- q /- q /u q /- -/- q q q /- -/- q 6 /- q /- q /u q /- -/- q -/- q 7 /- q /u q 6 /- q 6 q /- -/- q /- q 6 / u q 7 q /- q 7 /u q /- -/- A questo punto, dobbiamo cominciare a verificare la proprietà di chiusura sulla famiglia di insiemi correntemente definita. Per ciascuno insieme della famiglia, e per ciascuno degli ingessi dobbiamo verificare che l insieme degli stati successivi sia incluso in un unico insieme della famiglia Applicando l ingresso i 1 Applicando gli stati (1,,,,,6) generano rispettivamente gli stati (1,1,,1,-,). Questi Partiamo dall ingresso i 1 sono TUTTI inclusi in un unico insieme tra quelli correntemente definiti 1
52 Esempio i 1 i i i q /- -/- q 6 /- q /- q /u q /- -/- q q q /- -/- q 6 /- q /- q /u q /- -/- q -/- q 7 /- q /u q 6 /- q 6 q /- -/- q /- q 6 / u q 7 q /- q 7 /u q /- -/- Applicando l ingresso i all insieme (1,,,,,6) otteniamo l insieme di stati prossimi (,,,,7,-). Questi NON appartengono tutti ad uno stesso insieme della famiglia. In particolare, 7 è incompatibile con e. Dato che è lo stato a generare 7, scorporiamo insieme a tutti gli stati non incompatibili con esso (ovvero soltanto 6) Consideriamo l ingresso i
53 Esempio Riconosciamo delle inclusioni in altri sottoinsiemi della famiglia (ovviamente non consideriamo quello che abbiamo diviso!) (1,,,,6) (-,,-,,-) (1,,,,6) (6,-,6,-,6) Iteriamo in maniera simile con gli altri ingressi ed i nuovi insiemi
54 Esempio i 1 i i i q /- -/- q 6 /- q /- q /u q /- -/- q q q /- -/- q 6 /- q /- q /u q /- -/- q -/- q 7 /- q /u q 6 /- Trovati gli insiemi, è possibile costruire le nuove funzioni uscita e stato prossimo q 6 q /- -/- q /- q 6 / u q 7 q /- q 7 /u q /- -/- -
55 Esempio i 1 i i i q /- -/- q 6 /- q /- q /u q /- -/- q q q /- -/- q 6 /- q /- q /u q /- -/- q -/- q 7 /- q /u q 6 /- Trovati gli insiemi, è possibile costruire le nuove funzioni uscita e stato prossimo q 6 q /- -/- q /- q 6 / u q 7 q /- q 7 /u q /- -/- In alcuni casi, la scelta NON è univoca!! -
56 Esempio - i 1 i i i q /- -/- q 6 /- q /- q /u q /- -/- q q q /- -/- q 6 /- q /- q /u q /- -/- q -/- q 7 /- q /u q 6 /- q 6 q /- -/- q /- q 6 / u q 7 q /- q 7 /u q /- -/- (1,,,,6) S 1 (,6,7) S i 1 i i i S S 1 S 1 S 1 /u S /- 1 o S /u S S 1 /- S /u S /u S 1 o S /u 6
57 Esempio i 1 i i i q /- -/- q 6 /- q /- q /u q /- -/- q q q /- -/- q 6 /- q /- q /u q /- -/- q -/- q 7 /- q /u q 6 /- q 6 q /- -/- q /- q 6 / u q 7 q /- q 7 /u q /- -/- (1,,,,6) S 1 (,6,7) S Apparentemente controintuitivo i 1 i i i S 1 S 1 S 1 /u S /- S 1 o S /u S S 1 /- S /u S /u S 1 o S /u Cosa succede applicando le sequenze di ingressi i, i, i 1 partendo dallo stato per ciascuna delle quattro possibili scelte? Non sembra che sia indifferente scegliere S 1 o S come stato prossimo per la coppia S 1 /i! In realtà, questa sequenza corrisponde ad una condizione di don t care 7
58 Metodo di Paull Unger per macchine incomplete Il metodo di Paull Unger può ancora essere applicato converge ad uno schema nel quale è possibile identificare tutte le coppie di stati compatibili Costruire la famiglia di insiemi di compatibilità massimi è tuttavia meno ovvio che nel caso di macchine complete 8
59 Paull Unger: esempio Partiamo dal confrontare lo stato 6 con tutti i precedenti, poi con tutti i precendenti, etc: (,6) 6, => (,,6) 6 => (,) => (,6) (,,6) (,,,6) (1,,,6) (1,,,6) 9
Macchine sequenziali. Automa a Stati Finiti (ASF)
 Corso di Calcolatori Elettronici I Macchine sequenziali Prof. Roberto Canonico Università degli Studi di Napoli Federico II Dipartimento di Ingegneria Elettrica e delle Tecnologie dell Informazione Corso
Corso di Calcolatori Elettronici I Macchine sequenziali Prof. Roberto Canonico Università degli Studi di Napoli Federico II Dipartimento di Ingegneria Elettrica e delle Tecnologie dell Informazione Corso
Automa a Stati Finiti (ASF)
 Automa a Stati Finiti (ASF) E una prima astrazione di macchina dotata di memoria che esegue algoritmi Introduce il concetto fondamentale di STATO che informalmente può essere definito come una particolare
Automa a Stati Finiti (ASF) E una prima astrazione di macchina dotata di memoria che esegue algoritmi Introduce il concetto fondamentale di STATO che informalmente può essere definito come una particolare
Minimizzazione degli stati di reti sequenziali asincrone (RSA) / sincrone (RSS)
 Minimizzazione degli stati di reti sequenziali asincrone (RSA) / sincrone (RSS) Problema: Data una tabella di flusso (TdF) contraddistinta da un numero arbitrario N di stati s 1, s 2,, s N, individuare
Minimizzazione degli stati di reti sequenziali asincrone (RSA) / sincrone (RSS) Problema: Data una tabella di flusso (TdF) contraddistinta da un numero arbitrario N di stati s 1, s 2,, s N, individuare
Precorsi di matematica
 Precorsi di matematica Francesco Dinuzzo 12 settembre 2005 1 Insiemi Il concetto di base nella matematica moderna è l insieme. Un insieme è una collezione di elementi. Gli elementi di un insieme vengono
Precorsi di matematica Francesco Dinuzzo 12 settembre 2005 1 Insiemi Il concetto di base nella matematica moderna è l insieme. Un insieme è una collezione di elementi. Gli elementi di un insieme vengono
AUTOMA A STATI FINITI
 Gli Automi Un Automa è un dispositivo, o un suo modello in forma di macchina sequenziale, creato per eseguire un particolare compito, che può trovarsi in diverse configurazioni più o meno complesse caratterizzate
Gli Automi Un Automa è un dispositivo, o un suo modello in forma di macchina sequenziale, creato per eseguire un particolare compito, che può trovarsi in diverse configurazioni più o meno complesse caratterizzate
1. equivalenze e implicazioni logiche. Esercizio 1.2. Trovare le implicazioni che legano i seguenti enunciati (x, y R):
 . equivalenze e implicazioni logiche Esercizio.. Trovare le implicazioni che legano i seguenti enunciati (x, y R): () x < y, () x = y, () x y, () x y, () (x y) > 0. Osserviamo subito che (x y) > 0 equivale
. equivalenze e implicazioni logiche Esercizio.. Trovare le implicazioni che legano i seguenti enunciati (x, y R): () x < y, () x = y, () x y, () x y, () (x y) > 0. Osserviamo subito che (x y) > 0 equivale
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo. Paolo Baiti 1 Lorenzo Freddi 1
 Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università di Udine, via delle Scienze
Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università di Udine, via delle Scienze
Reti Logiche 1. Prof. B. Buttarazzi A.A. 2009/2010. Reti Sequenziali
 Reti Logiche Prof. B. Buttarazzi A.A. 29/2 Reti Sequenziali Sommario Analisi di Reti Sequenziali Sintesi di Reti Sequenziali Esercizi 3/6/2 Corso di Reti Logiche 29/ 2 Analisi di Reti Sequenziali Passare
Reti Logiche Prof. B. Buttarazzi A.A. 29/2 Reti Sequenziali Sommario Analisi di Reti Sequenziali Sintesi di Reti Sequenziali Esercizi 3/6/2 Corso di Reti Logiche 29/ 2 Analisi di Reti Sequenziali Passare
Sintesi di Reti Sequenziali Sincrone
 Sintesi di Reti Sequenziali Sincrone Maurizio Palesi Maurizio Palesi 1 Macchina Sequenziale Una macchina sequenziale è definita dalla quintupla (I,U,S,δ,λ ) dove: I è l insieme finito dei simboli d ingresso
Sintesi di Reti Sequenziali Sincrone Maurizio Palesi Maurizio Palesi 1 Macchina Sequenziale Una macchina sequenziale è definita dalla quintupla (I,U,S,δ,λ ) dove: I è l insieme finito dei simboli d ingresso
RIDUZIONE DEL NUMERO DI STATI DI UN AUTOMA
 RIDUZIONE DEL NUMERO DI STATI DI UN AUTOMA Il numero degli stati di un automa può risultare elevato, perché l insieme stesso degli stati può essere ridondante, in quanto vi possono essere più stati che
RIDUZIONE DEL NUMERO DI STATI DI UN AUTOMA Il numero degli stati di un automa può risultare elevato, perché l insieme stesso degli stati può essere ridondante, in quanto vi possono essere più stati che
Reti sequenziali asincrone
 Reti sequenziali asincrone Esercizio Una rete sequenziale asincrona è caratterizzata da due segnali di ingresso (E, X) e da un segnale di uscita (Z). I segnali di ingresso non variano mai contemporaneamente,
Reti sequenziali asincrone Esercizio Una rete sequenziale asincrona è caratterizzata da due segnali di ingresso (E, X) e da un segnale di uscita (Z). I segnali di ingresso non variano mai contemporaneamente,
FSM: Macchine a Stati Finiti
 FSM: Macchine a Stati Finiti Introduzione Automi di Mealy Automi di Moore Esempi Sommario Introduzione Automi di Mealy Automi di Moore Esempi Sommario Introduzione Metodo per descrivere macchine di tipo
FSM: Macchine a Stati Finiti Introduzione Automi di Mealy Automi di Moore Esempi Sommario Introduzione Automi di Mealy Automi di Moore Esempi Sommario Introduzione Metodo per descrivere macchine di tipo
Sintesi di Reti sequenziali Sincrone
 Sintesi di Reti sequenziali Sincrone alcolatori ElettroniciIngegneria Telematica Sintesi di Reti Sequenziali Sincrone na macchina sequenziale è definita dalla quintupla δ, λ) dove: I è l insieme finito
Sintesi di Reti sequenziali Sincrone alcolatori ElettroniciIngegneria Telematica Sintesi di Reti Sequenziali Sincrone na macchina sequenziale è definita dalla quintupla δ, λ) dove: I è l insieme finito
Capitolo 1. Gli strumenti. 1.1 Relazioni
 Capitolo 1 Gli strumenti Consideriamo un insieme X. In geometria siamo abituati a considerare insiemi i cui elementi sono punti ad esempio, la retta reale, il piano cartesiano. Più in generale i matematici
Capitolo 1 Gli strumenti Consideriamo un insieme X. In geometria siamo abituati a considerare insiemi i cui elementi sono punti ad esempio, la retta reale, il piano cartesiano. Più in generale i matematici
ESAME DI ARCHITETTURA I COMPITO A
 ESAME DI ARCHITETTURA I COMPITO A Esercizio (6 punti) Si consideri l automa di Mealy specificato dalla seguente tabella: S S/ S S S2/ S3/ S2 S2/ S3/ S3 S/ S/ S4 S/ S S5 S2/ S3/ ) Disegnare l automa. 2)
ESAME DI ARCHITETTURA I COMPITO A Esercizio (6 punti) Si consideri l automa di Mealy specificato dalla seguente tabella: S S/ S S S2/ S3/ S2 S2/ S3/ S3 S/ S/ S4 S/ S S5 S2/ S3/ ) Disegnare l automa. 2)
Appunti sui Codici di Reed Muller. Giovanni Barbarino
 Appunti sui Codici di Reed Muller Giovanni Barbarino Capitolo 1 Codici di Reed-Muller I codici di Reed-Muller sono codici lineari su F q legati alle valutazioni dei polinomi sullo spazio affine. Per semplicità
Appunti sui Codici di Reed Muller Giovanni Barbarino Capitolo 1 Codici di Reed-Muller I codici di Reed-Muller sono codici lineari su F q legati alle valutazioni dei polinomi sullo spazio affine. Per semplicità
Luca Costabile Esercizi di Logica Matematica Dispensa Calcolo Proposizionale 1
 Luca Costabile Esercizi di Logica Matematica Dispensa Calcolo Proposizionale 1 Esercizio 1.12 Per dimostrare che per ogni funzione esiste una formula in cui compaiono le variabili tale che la corrispondente
Luca Costabile Esercizi di Logica Matematica Dispensa Calcolo Proposizionale 1 Esercizio 1.12 Per dimostrare che per ogni funzione esiste una formula in cui compaiono le variabili tale che la corrispondente
01 - Elementi di Teoria degli Insiemi
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 01 - Elementi di Teoria degli Insiemi Anno Accademico 2013/2014
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 01 - Elementi di Teoria degli Insiemi Anno Accademico 2013/2014
Possibile applicazione
 p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
LOGICA SEQUENZIALE. Un blocco di logica puramente combinatoria è un. blocco con N variabili di ingresso e M variabili di uscita
 LOGICA SEQUENZIALE Logica combinatoria Un blocco di logica puramente combinatoria è un blocco con N variabili di ingresso e M variabili di uscita che sono funzione (booleana) degli ingressi in un certo
LOGICA SEQUENZIALE Logica combinatoria Un blocco di logica puramente combinatoria è un blocco con N variabili di ingresso e M variabili di uscita che sono funzione (booleana) degli ingressi in un certo
Geometria e Topologia I (U1-4) 2006-mag-10 61
 Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
Luigi Piroddi
 Automazione industriale dispense del corso (a.a. 2008/2009) 10. Reti di Petri: analisi strutturale Luigi Piroddi [email protected] Analisi strutturale Un alternativa all analisi esaustiva basata sul
Automazione industriale dispense del corso (a.a. 2008/2009) 10. Reti di Petri: analisi strutturale Luigi Piroddi [email protected] Analisi strutturale Un alternativa all analisi esaustiva basata sul
Introduzione ai grafi. Introduzione ai grafi p. 1/2
 Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
Appunti di informatica. Lezione 7 anno accademico Mario Verdicchio
 Appunti di informatica Lezione 7 anno accademico 2016-2017 Mario Verdicchio L algoritmo di Euclide per l MCD Dati due numeri A e B, per trovare il loro MCD procedere nel seguente modo: 1. dividere il maggiore
Appunti di informatica Lezione 7 anno accademico 2016-2017 Mario Verdicchio L algoritmo di Euclide per l MCD Dati due numeri A e B, per trovare il loro MCD procedere nel seguente modo: 1. dividere il maggiore
Definizione. Il valore assoluto lascia inalterato ciò che è già positivo e rende positivo ciò che positivo non è.
 VALORE ASSOLUTO Definizione a a, a, se a se a 0 0 Esempi.. 7 7. 9 9 4. x x, x, se x se x Il valore assoluto lascia inalterato ciò che è già positivo e rende positivo ciò che positivo non è. Utilizzando
VALORE ASSOLUTO Definizione a a, a, se a se a 0 0 Esempi.. 7 7. 9 9 4. x x, x, se x se x Il valore assoluto lascia inalterato ciò che è già positivo e rende positivo ciò che positivo non è. Utilizzando
0.1 Esercizi calcolo combinatorio
 0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
Corso di elettrotecnica Materiale didattico: i grafi
 Corso di elettrotecnica Materiale didattico: i grafi A. Laudani 12 ottobre 2005 I grafi costituiscono uno strumento matematico che permette di descrivere e schematizzare una grande varietà di problemi
Corso di elettrotecnica Materiale didattico: i grafi A. Laudani 12 ottobre 2005 I grafi costituiscono uno strumento matematico che permette di descrivere e schematizzare una grande varietà di problemi
Corso di Reti Logiche. Macchine Sequenziali. Dipartimento di Informatica e Sistemistica Università degli Studi di Napoli Federico II
 Corso di Reti Logiche Macchine Sequenziali Dipartimento di Informatica e Sistemistica Università degli Studi di Napoli Federico II 1 Macchine sequenziali Š Includono il fattore tempo nel funzionamento
Corso di Reti Logiche Macchine Sequenziali Dipartimento di Informatica e Sistemistica Università degli Studi di Napoli Federico II 1 Macchine sequenziali Š Includono il fattore tempo nel funzionamento
Indice. 1 Cenni di logica. 2 Elementi di teoria degli insiemi. 3 Relazioni e funzioni. 4 Strutture algebriche
 Indice 1 Cenni di logica 2 Elementi di teoria degli insiemi 3 Relazioni e funzioni 4 Strutture algebriche Silvia Pianta - Laura Montagnoli Geometria I - Prerequisiti - UCSC A.A. 2015/2016 1 / 36 1. Cenni
Indice 1 Cenni di logica 2 Elementi di teoria degli insiemi 3 Relazioni e funzioni 4 Strutture algebriche Silvia Pianta - Laura Montagnoli Geometria I - Prerequisiti - UCSC A.A. 2015/2016 1 / 36 1. Cenni
ESEMPIO Un esempio di insieme vuoto è l insieme dei numeri reali di quadrato 4. B A
 TEORI DEGLI INSIEMI GENERLIT Un insieme è un ente costituito da oggetti. Il concetto di insieme e di oggetto si assumono come primitivi. Se un oggetto a fa parte di un insieme si dice che esso è un suo
TEORI DEGLI INSIEMI GENERLIT Un insieme è un ente costituito da oggetti. Il concetto di insieme e di oggetto si assumono come primitivi. Se un oggetto a fa parte di un insieme si dice che esso è un suo
LA RETTA. La retta è un insieme illimitato di punti che non ha inizio, né fine.
 LA RETTA La retta è un insieme illimitato di punti che non ha inizio, né fine. Proprietà: Per due punti del piano passa una ed una sola retta. Nel precedente modulo abbiamo visto che ad ogni punto del
LA RETTA La retta è un insieme illimitato di punti che non ha inizio, né fine. Proprietà: Per due punti del piano passa una ed una sola retta. Nel precedente modulo abbiamo visto che ad ogni punto del
Insiemi: Rappresentazione
 Insiemi: Rappresentazione Elencazione Per rappresentare un insieme per elencazione si indicheranno i suoi elementi tra parentesi graffe. Caratteristica Un insieme è rappresentato per caratteristica quando
Insiemi: Rappresentazione Elencazione Per rappresentare un insieme per elencazione si indicheranno i suoi elementi tra parentesi graffe. Caratteristica Un insieme è rappresentato per caratteristica quando
Stabilire se il punto di coordinate (1,1) appartiene alla circonferenza centrata nell origine e di raggio 1.
 Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
RISOLUZIONE IN LOGICA PROPOSIZIONALE. Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine
 RISOLUZIONE IN LOGICA PROPOSIZIONALE Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine 1. Risoluzione Definitione 1.1. Un letterale l è una variabile proposizionale (letterale
RISOLUZIONE IN LOGICA PROPOSIZIONALE Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine 1. Risoluzione Definitione 1.1. Un letterale l è una variabile proposizionale (letterale
Metodo di Quine e MC-Cluskey 2/2 Prof. Mario Cannataro Università degli Studi Magna Graecia di Catanzaro
 Fondamenti di Informatica II Ingegneria Informatica e Biomedica I anno, II semestre A.A. 2005/2006 Metodo di Quine e MC-Cluskey 2/2 Prof. Mario Cannataro Università degli Studi Magna Graecia di Catanzaro
Fondamenti di Informatica II Ingegneria Informatica e Biomedica I anno, II semestre A.A. 2005/2006 Metodo di Quine e MC-Cluskey 2/2 Prof. Mario Cannataro Università degli Studi Magna Graecia di Catanzaro
nota 1. Aritmetica sui numeri interi.
 nota 1. Aritmetica sui numeri interi. Numeri interi. Numeri primi. L algoritmo di Euclide per il calcolo del mcd. Equazioni diofantee di primo grado. Congruenze. Il Teorema Cinese del Resto. 1 0. Numeri
nota 1. Aritmetica sui numeri interi. Numeri interi. Numeri primi. L algoritmo di Euclide per il calcolo del mcd. Equazioni diofantee di primo grado. Congruenze. Il Teorema Cinese del Resto. 1 0. Numeri
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
ELEMENTI di TEORIA degli INSIEMI
 ELEMENTI di TEORI degli INSIEMI & 1. Nozioni fondamentali. ssumeremo come primitivi il concetto di insieme e di elementi di un insieme. Nel seguito gli insiemi saranno indicati con lettere maiuscole (,,C,...)
ELEMENTI di TEORI degli INSIEMI & 1. Nozioni fondamentali. ssumeremo come primitivi il concetto di insieme e di elementi di un insieme. Nel seguito gli insiemi saranno indicati con lettere maiuscole (,,C,...)
Misura. Istituzioni di matematiche 2. Come facciamo a misurare? Come facciamo a misurare? Diego Noja
 Istituzioni di matematiche 2 Diego Noja ([email protected]) 10 marzo 2009 Misura CDL Scienze della Formazione Primaria Istituzioni di matematiche 2 pagina 1 CDL Scienze della Formazione Primaria Istituzioni
Istituzioni di matematiche 2 Diego Noja ([email protected]) 10 marzo 2009 Misura CDL Scienze della Formazione Primaria Istituzioni di matematiche 2 pagina 1 CDL Scienze della Formazione Primaria Istituzioni
4. METODI DUALI DEL SIMPLESSO
 4. MEODI DUALI DEL SIMPLESSO R. adei 1 Una piccola introduzione R. adei 2 MEODI DUALI DEL SIMPLESSO L obiettivo del capitolo è illustrare e giustificare i metodi duali del simplesso. Entrambi i metodi
4. MEODI DUALI DEL SIMPLESSO R. adei 1 Una piccola introduzione R. adei 2 MEODI DUALI DEL SIMPLESSO L obiettivo del capitolo è illustrare e giustificare i metodi duali del simplesso. Entrambi i metodi
RETI LINEARI R 3 I 3 R 2 I 4
 RETI LINERI 1 Leggi di Kirchoff. Metodo delle correnti di maglia R 1 R 3 I 1 I 3 E 1 J 1 J 2 J 3 I 2 I 4 R 4 I 5 R 5 I 6 R 6 J 4 R 7 Il calcolo delle correnti e delle differenze di potenziale in un circuito
RETI LINERI 1 Leggi di Kirchoff. Metodo delle correnti di maglia R 1 R 3 I 1 I 3 E 1 J 1 J 2 J 3 I 2 I 4 R 4 I 5 R 5 I 6 R 6 J 4 R 7 Il calcolo delle correnti e delle differenze di potenziale in un circuito
01 - Elementi di Teoria degli Insiemi
 Università degli Studi di Palermo Scuola Politecnica Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 01 - Elementi di Teoria degli Insiemi Anno Accademico 2015/2016
Università degli Studi di Palermo Scuola Politecnica Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 01 - Elementi di Teoria degli Insiemi Anno Accademico 2015/2016
Insiemi di numeri reali
 Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Sintesi Sequenziale Sincrona Sintesi Comportamentale di reti Sequenziali Sincrone
 Sintesi Sequenziale Sincrona Sintesi Comportamentale di reti Sequenziali Sincrone Il problema dell assegnamento degli stati versione del 9/1/03 Sintesi: Assegnamento degli stati La riduzione del numero
Sintesi Sequenziale Sincrona Sintesi Comportamentale di reti Sequenziali Sincrone Il problema dell assegnamento degli stati versione del 9/1/03 Sintesi: Assegnamento degli stati La riduzione del numero
8. Completamento di uno spazio di misura.
 8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
Equazioni di primo grado
 Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
Macchine di Turing: somma di due numeri
 Informatica Teorica 2/2 M.Di Ianni Macchine di Turing: somma di due numeri Vogliamo definire una macchina di Turing che, presi in input due numeri n e m espressi in notazione binaria, calcola il valore
Informatica Teorica 2/2 M.Di Ianni Macchine di Turing: somma di due numeri Vogliamo definire una macchina di Turing che, presi in input due numeri n e m espressi in notazione binaria, calcola il valore
Cammini minimi fra tutte le coppie
 Capitolo 12 Cammini minimi fra tutte le coppie Consideriamo il problema dei cammini minimi fra tutte le coppie in un grafo G = (V, E, w) orientato, pesato, dove possono essere presenti archi (ma non cicli)
Capitolo 12 Cammini minimi fra tutte le coppie Consideriamo il problema dei cammini minimi fra tutte le coppie in un grafo G = (V, E, w) orientato, pesato, dove possono essere presenti archi (ma non cicli)
Elementi di Analisi Combinatoria
 Elementi di Analisi Combinatoria Angelica Malaspina Dipartimento di Matematica, Informatica ed Economia Università degli Studi della Basilicata, Italy [email protected] Lo studio dei vari raggruppamenti
Elementi di Analisi Combinatoria Angelica Malaspina Dipartimento di Matematica, Informatica ed Economia Università degli Studi della Basilicata, Italy [email protected] Lo studio dei vari raggruppamenti
nota 1. Aritmetica sui numeri interi.
 nota 1. Aritmetica sui numeri interi. Numeri interi. Numeri primi. L algoritmo di Euclide per il calcolo del mcd. Equazioni diofantee di primo grado. Congruenze. Il Teorema Cinese del Resto. 1 0. Numeri
nota 1. Aritmetica sui numeri interi. Numeri interi. Numeri primi. L algoritmo di Euclide per il calcolo del mcd. Equazioni diofantee di primo grado. Congruenze. Il Teorema Cinese del Resto. 1 0. Numeri
Corso di Laurea in Matematica Geometria 2. Foglio di esercizi n. 1 a.a Soluzioni
 Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 1 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.1, 3.2,
Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 1 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.1, 3.2,
Metodo di Quine-McCluskey. Algoritmo. Sommario. Sommario. M. Favalli
 Sommario Metodo di Quine-McCluskey M. Favalli Engineering Department in Ferrara 2 3 Sommario Analisi e sintesi dei sistemi digitali / Algoritmo Analisi e sintesi dei sistemi digitali 2 / 2 3 Metodo esatto
Sommario Metodo di Quine-McCluskey M. Favalli Engineering Department in Ferrara 2 3 Sommario Analisi e sintesi dei sistemi digitali / Algoritmo Analisi e sintesi dei sistemi digitali 2 / 2 3 Metodo esatto
Esercitazioni di Reti Logiche
 Esercitazioni di Reti Logiche Sintesi di Reti Sequenziali Zeynep KIZILTAN Dipartimento di Scienze dell Informazione Universita degli Studi di Bologna Anno Academico 2007/2008 Sintesi dei circuiti sequenziali
Esercitazioni di Reti Logiche Sintesi di Reti Sequenziali Zeynep KIZILTAN Dipartimento di Scienze dell Informazione Universita degli Studi di Bologna Anno Academico 2007/2008 Sintesi dei circuiti sequenziali
Sistemi di 1 grado in due incognite
 Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
RELAZIONI, FUNZIONI, INSIEMI NUMERICI. 1. Relazioni. Siano X e Y due insiemi non vuoti. Si definisce il prodotto cartesiano
 RELAZIONI, FUNZIONI, INSIEMI NUMERICI C. FRANCHI 1. Relazioni Siano X e Y due insiemi non vuoti. Si definisce il prodotto cartesiano X Y := {(x, y) x X, y Y } dove con (x, y) si intende la coppia ordinata
RELAZIONI, FUNZIONI, INSIEMI NUMERICI C. FRANCHI 1. Relazioni Siano X e Y due insiemi non vuoti. Si definisce il prodotto cartesiano X Y := {(x, y) x X, y Y } dove con (x, y) si intende la coppia ordinata
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Successioni, massimo e minimo limite e compattezza in R
 Università di Roma Tor Vergata Corso di Laurea in Scienze e Tecnologie per i Media Successioni, massimo e minimo limite e compattezza in R Massimo A. Picardello BOZZA 10.11.2011 21:24 i CAPITOLO 1 Successioni
Università di Roma Tor Vergata Corso di Laurea in Scienze e Tecnologie per i Media Successioni, massimo e minimo limite e compattezza in R Massimo A. Picardello BOZZA 10.11.2011 21:24 i CAPITOLO 1 Successioni
1 Relazioni. Definizione Una relazione R su un insieme A si dice relazione d ordine se gode delle proprietà 1), 3), 4).
 1 Relazioni 1. definizione di relazione; 2. definizione di relazione di equivalenza; 3. definizione di relazione d ordine Definizione Una corrispondenza tra due insiemi A e B è un sottoinsieme R del prodotto
1 Relazioni 1. definizione di relazione; 2. definizione di relazione di equivalenza; 3. definizione di relazione d ordine Definizione Una corrispondenza tra due insiemi A e B è un sottoinsieme R del prodotto
Esercitazioni per il corso di Logica Matematica
 Esercitazioni per il corso di Logica Matematica Luca Motto Ros 02 marzo 2005 Nota importante. Queste pagine contengono appunti personali dell esercitatore e sono messe a disposizione nel caso possano risultare
Esercitazioni per il corso di Logica Matematica Luca Motto Ros 02 marzo 2005 Nota importante. Queste pagine contengono appunti personali dell esercitatore e sono messe a disposizione nel caso possano risultare
1 Soluzione degli esercizi del capitolo 4
 "Introduzione alla matematica discreta /ed" - M. G. Bianchi, A. Gillio degli esercizi del capitolo 4 Esercizio 4. (pag. 47) Sia X =,,3,4} e sia R la relazione su X così definita: R = (,),(,),(,),(,),(,4),(3,3),(4,)}.
"Introduzione alla matematica discreta /ed" - M. G. Bianchi, A. Gillio degli esercizi del capitolo 4 Esercizio 4. (pag. 47) Sia X =,,3,4} e sia R la relazione su X così definita: R = (,),(,),(,),(,),(,4),(3,3),(4,)}.
Equazioni goniometriche risolvibili per confronto di argomenti
 Equazioni goniometriche risolvibili per confronto di argomenti In questa dispensa si esaminano le equazioni goniometriche costituite dall uguaglianza di due funzioni goniometriche, nei cui argomenti compare
Equazioni goniometriche risolvibili per confronto di argomenti In questa dispensa si esaminano le equazioni goniometriche costituite dall uguaglianza di due funzioni goniometriche, nei cui argomenti compare
La codifica digitale
 La codifica digitale Codifica digitale Il computer e il sistema binario Il computer elabora esclusivamente numeri. Ogni immagine, ogni suono, ogni informazione per essere compresa e rielaborata dal calcolatore
La codifica digitale Codifica digitale Il computer e il sistema binario Il computer elabora esclusivamente numeri. Ogni immagine, ogni suono, ogni informazione per essere compresa e rielaborata dal calcolatore
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Algoritmo di Branch & Bound
 Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Algoritmo di Branch & Bound Docente: Renato Bruni [email protected] Corso di: Ottimizzazione Combinatoria
Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Algoritmo di Branch & Bound Docente: Renato Bruni [email protected] Corso di: Ottimizzazione Combinatoria
LE EQUAZIONI DI SECONDO GRADO
 LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Il Metodo di Newton, o delle Tangenti Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria [email protected] Il Metodo di Newton, o delle Tangenti 6 Novembre 2016 Indice 1 Metodo di Newton, o delle tangenti 2 1.1
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria [email protected] Il Metodo di Newton, o delle Tangenti 6 Novembre 2016 Indice 1 Metodo di Newton, o delle tangenti 2 1.1
Raggiungibilità, Controllabilità, Osservabilità e Determinabilità
 Raggiungibilità, Controllabilità, Osservabilità e Determinabilità Si determini se i sistemi lineari tempo invarianti ẋ(t) = Ax(t) + Bu(t), Σ c : y(t) = Cx(t) + Du(t). x(k + ) = Ax(k) + Bu(k), Σ d : y(k)
Raggiungibilità, Controllabilità, Osservabilità e Determinabilità Si determini se i sistemi lineari tempo invarianti ẋ(t) = Ax(t) + Bu(t), Σ c : y(t) = Cx(t) + Du(t). x(k + ) = Ax(k) + Bu(k), Σ d : y(k)
1 Relazione di congruenza in Z
 1 Relazione di congruenza in Z Diamo ora un esempio importante di relazione di equivalenza: la relazione di congruenza modn in Z. Definizione 1 Sia X = Z, a,b Z ed n un intero n > 1. Si dice a congruo
1 Relazione di congruenza in Z Diamo ora un esempio importante di relazione di equivalenza: la relazione di congruenza modn in Z. Definizione 1 Sia X = Z, a,b Z ed n un intero n > 1. Si dice a congruo
Fondamenti di informatica II 1. Sintesi di reti logiche sequenziali
 Titolo lezione Fondamenti di informatica II 1 Sintesi di reti logiche sequenziali Reti combinatorie e sequenziali Fondamenti di informatica II 2 Due sono le tipologie di reti logiche che studiamo Reti
Titolo lezione Fondamenti di informatica II 1 Sintesi di reti logiche sequenziali Reti combinatorie e sequenziali Fondamenti di informatica II 2 Due sono le tipologie di reti logiche che studiamo Reti
Reti logiche: analisi, sintesi e minimizzazione Esercitazione. Venerdì 9 ottobre 2015
 Reti logiche: analisi, sintesi e minimizzazione Esercitazione Venerdì 9 ottobre 05 Punto della situazione Stiamo studiando le reti logiche costruite a partire dalle porte logiche AND, OR, NOT per progettare
Reti logiche: analisi, sintesi e minimizzazione Esercitazione Venerdì 9 ottobre 05 Punto della situazione Stiamo studiando le reti logiche costruite a partire dalle porte logiche AND, OR, NOT per progettare
Funzioni elementari: funzioni potenza
 Funzioni elementari: funzioni potenza Lezione per Studenti di Agraria Università di Bologna (Università di Bologna) Funzioni elementari: funzioni potenza 1 / 36 Funzioni lineari Come abbiamo già visto,
Funzioni elementari: funzioni potenza Lezione per Studenti di Agraria Università di Bologna (Università di Bologna) Funzioni elementari: funzioni potenza 1 / 36 Funzioni lineari Come abbiamo già visto,
COME CALCOLARE LA COMBINAZIONE DI MINIMO COSTO DEI FATTORI
 COME CALCOLARE LA COMBINAZIONE DI MINIMO COSTO DEI FATTORI In questa Appendice, mostreremo come un impresa possa individuare la sua combinazione di minimo costo dei fattori produttivi attraverso il calcolo
COME CALCOLARE LA COMBINAZIONE DI MINIMO COSTO DEI FATTORI In questa Appendice, mostreremo come un impresa possa individuare la sua combinazione di minimo costo dei fattori produttivi attraverso il calcolo
Ingegneria Meccanica; Algebra lineare e Geometria 2008/2009
 Capitolo Ingegneria Meccanica; Algebra lineare e Geometria 8/9. Esercii svolti su rette e piani Eserciio. Stabilire se le due rette r e s sono coincidenti oppure no: ( ( ( ( ( ( 7 r : = + t ; s : = + t
Capitolo Ingegneria Meccanica; Algebra lineare e Geometria 8/9. Esercii svolti su rette e piani Eserciio. Stabilire se le due rette r e s sono coincidenti oppure no: ( ( ( ( ( ( 7 r : = + t ; s : = + t
Introduciamo ora un altro campo, formato da un numero finito di elementi; il campo delle classi resto modulo n, con n numero primo.
 Capitolo 3 Il campo Z n 31 Introduzione Introduciamo ora un altro campo, formato da un numero finito di elementi; il campo delle classi resto modulo n, con n numero primo 32 Le classi resto Definizione
Capitolo 3 Il campo Z n 31 Introduzione Introduciamo ora un altro campo, formato da un numero finito di elementi; il campo delle classi resto modulo n, con n numero primo 32 Le classi resto Definizione
ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI A. MARTINI Castelfranco Veneto (TV) Docente: Daniele De Pieri.
 6 settembre 008 Giochi Matematici. Il gioco dei grattacieli (puoi trovare una versione online all indirizzo: http://gamescene.com/skyscrapers_game.html) In una città ci sono solo grattacieli da, 0, 0 o
6 settembre 008 Giochi Matematici. Il gioco dei grattacieli (puoi trovare una versione online all indirizzo: http://gamescene.com/skyscrapers_game.html) In una città ci sono solo grattacieli da, 0, 0 o
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Sommario. 1 Realizzazione del STG. Introduzione. 1 traduzione delle specifiche informali in specifiche formali (STG o
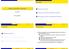 Sommario Sintesi di macchine a stati finiti 1 Realizzazione del ST M. avalli 2 utoma minimo di SM completamente specificate 6th June 2007 3 Ottimizzazione di SM non completamente specificate Sommario ()
Sommario Sintesi di macchine a stati finiti 1 Realizzazione del ST M. avalli 2 utoma minimo di SM completamente specificate 6th June 2007 3 Ottimizzazione di SM non completamente specificate Sommario ()
