Introduzione. Esempio di costruzione one del contorno delle radici. Esempio... 4
|
|
|
- Evangelista Bernardi
- 7 anni fa
- Visualizzazioni
Transcript
1 Appunti di Controlli Automatici 1 Capitolo 5 parte II Il contorno delle radici Introduzione... 1 Eempio di cotruzione del contorno delle radici... 1 Eempio... 4 Introduzione Il procedimento per la cotruzione del luogo delle radici i può applicare anche quando, invece di variare la cotante di guadagno, i varia qualche altro parametro della funzione di traferimento del itema, come ad eempio la cotante di tempo relativa ad un polo oppure quella relativa ad uno zero reale. Il tracciato decritto nel piano compleo dalle radici dell equazione caratteritica al variare del parametro i dice contorno delle radici. Queta denominazione trae origine dal fatto che, come vedremo, e oltre alla cotante di guadagno i fa variare un altro parametro, in più o in meno ripetto al valore nominale, i ottiene una famiglia di curve che contorna il luogo delle radici appoggiandoi ad eo. In generale, è poibile far variare un qualiai altro parametro del itema divero dal guadagno, a patto però che uno o più coefficienti dell equazione caratteritica riultino funzioni lineari di tale parametro: in particolare, i deve poter porre l equazione caratteritica nella forma a () = p() + 1q() + r() = dove 1 e ono due parametri ripetto ai quali i intende determinare il contorno delle radici. Nei cai più claici, 1 è la cotante di guadagno, mentre è un qualiai altro parametro del itema coniderato. La cotruzione del contorno delle radici è utile per la determinazione dei valori ottimi dei più importanti parametri delle reti correttrici. Eempio di cotruzione one del contorno delle radici Al fine di comprendere come i cotruice il contorno delle radici di un itema, facciamo riferimento ad un eempio concreto. Conideriamo perciò un itema avente la eguente funzione di traferimento in anello aperto: G() = a> ( + a)
2 Appunti di Controlli Automatici Capitolo 5 (parte II) L equazione caratteritica del itema è ( + a) + = + a + = Se tudiamo come variano le radici di queta equazione al variare di, otteniamo il luogo delle radici del itema. Se, invece, tudiamo come variano le uddette radici al variare del polo =-a, allora otteniamo il contorno delle radici del itema ripetto a tale polo. Al fine di cotruire queto contorno, i parte determinando il luogo delle radici del itema ottenuto da quello di partenza ponendo a=. Sotto queta ipotei, la funzione di traferimento in anello aperto del itema è, per cui i tratta di un itema privo di zeri e con un polo doppio nell origine. Il luogo delle radici di un iffatto itema è quello riportato nella figura eguente: A queto punto, fiiamo arbitrariamente un valore del guadagno, che indichiamo con. In corripondenza di queto valore di, il itema preenta due poli il cui valore è facilmente ricavabile dall equazione caratteritica del itema, da riolvere ponendo appunto =: = p + = p 1 = j = j p 1 p Riconideriamo ora l equazione caratteritica + a + = del itema di partenza: e fiiamo =, le radici di queta equazione variano al variare di a. Scriviamo allora l equazione nella forma
3 Il contorno delle radici 1+ a = + A ben vedere, queta equazione è nella claica formula 1+ G()=, per cui poiamo coniderarla come l equazione caratteritica di un itema avente funzione di traferimento in anello aperto ag () = a a> + Ciò ignifica che poiamo determinare il luogo delle radici di tale itema, oia il modo con cui le radici dell equazione 1+ a = variano al variare del + parametro a (ovviamente per = fiato). Dobbiamo dunque determinare il luogo delle radici del itema avente funzione di traferimento in anello aperto ag(). I poli di queto itema ono evidentemente gli tei riportati nell ultima figura e ad ei i aggiunge uno zero nell origine: p 1 p Il luogo delle radici corripondente a queta mappa i individua abbatanza facilmente e riulta eere il eguente: Queto è dunque il luogo delle radici per = ed al variare del polo =-a (con a>). A queto punto, cegliamo un altro valore di in corripondenza del quale determinare nuovamente il uddetto luogo. Per eempio, e prendiamo =>, è facile accorgeri che il nuovo luogo è fatto nel modo eguente:
4 Appunti di Controlli Automatici Capitolo 5 (parte II) Mentre il ramo ituato ull ae reale rimane invariato, la emicirconferenza che decrive il movimento dei poli complei coniugati è adeo a raggio maggiore. In modo del tutto analogo, e prendiamo un valore di inferiore a, otteniamo una emicirconferenza di raggio inferiore a quella ottenuta per : In definitiva, quindi, abbiamo tracciato il contorno delle radici per il itema G() = in eame, ripetto al polo =-a. Tale contorno può eere fruttato ( + a) nel modo eguente: fiato un qualiai punto u tale contorno, poiamo immediatamente determinare il corripondente valore di e il corripondente valore di a: il valore di lo otteniamo in quanto le curve del contorno ono parametrizzate, oia ciacuna di ee è aociata ad un precio valore di ; una volta individuato queto, mediante una emplice operazione di taratura del luogo, iamo in grado di determinare il valore di a> corripondente ad. Eempio Partendo dallo teo itema coniderato nel paragrafo precedente, introduciamo un nuovo polo nella funzione di traferimento: L equazione caratteritica del itema è G() = ( + a)( + 1) a>, > 4
5 Il contorno delle radici ( + a)( + 1) + = + (a + 1) + a + = Per tracciare il contorno delle radici ripetto al parametro a, dobbiamo prima aicurarci che uno o più coefficienti di queta equazione caratteritica iano funzioni lineari del parametro teo: dobbiamo cioè poter porre l equazione in una forma del tipo a () = p() + 1q() + r() =. Nel notro cao, poiamo ricrivere l equazione nella forma ( + 1) + a( + 1) + = e quindi deduciamo che poiamo tracciare il contorno. Coì come abbiamo fatto nell eempio precedente, cominciamo determinando il luogo delle radici del itema ottenuto da quello di partenza ponendo a=. La funzione di traferimento in anello aperto di queto itema è dunque ( + 1) Si tratta di un itema privo di zeri e con tre poli (di cui uno in 1 ed uno doppio nell origine): -1 Dobbiamo determinare il luogo delle radici di queto itema. A parte l ormai nota immetria ripetto all ae reale, poiamo immediatamente tracciare il ramo che parte da =-1 e termina all infinito poggiato ull ae reale negativo. Dobbiamo poi determinare gli altri due rami, tendenti anch ei all infinito: il centroide riulta eere nel punto σ C= 1/, mentre i due aintoti formano con l ae reale angoli, ripettivamente, di π/ e 5π/: 5
6 Appunti di Controlli Automatici Capitolo 5 (parte II) A queto punto, per tracciare i due rami, dobbiamo olo capire e ei entrano nel emipiano initro oppure no. Per decidere queto, poiamo utilizzare il criterio di Routh, al fine di verificare e eite qualche valore di tale che tutti e tre i poli del itema riultino a parte reale negativa: l equazione caratteritica (ottenuta da quella del itema di partenza ponendo a=) è + + =, per cui la tabella di Routh riulta eere Si oerva, allora, che, per qualiai valore di >, c è una ola permanenza di egno, dal che deduciamo che non ci ono mai tre radici nel emipiano initro, per cui il luogo arà enz altro del tipo eguente: Queto è dunque il luogo delle radici del itema ottenuto da quello di partenza per a=. A queto punto, fiiamo arbitrariamente un valore del guadagno : upponiamo ad eempio di prendere =1. Dobbiamo determinare i poli che il itema preenta in corripondenza di queto. Per determinare tali poli, ci ono due poibilità: il primo modo è quello di otituire =1 nell equazione caratteritica e di determinare le corripondenti radici: tuttavia, l equazione caratteritica + (a + 1) + a + = non è facilmente riolvibile per via analitica, per cui il metodo non è applicabile (coì come lo era tato, invece, nell eempio precedente). Il econdo modo è quello di procedere, per tentativi, nel modo eguente: fiiamo un punto di prova ul luogo determinato poco fa (conviene fiarlo ull ae reale) e procediamo ad una emplice taratura del luogo (mediante la relazione ui moduli) al fine di individuare il corripondente : avremo = + 1 Se queto valore di riulta maggiore di =1, andiamo a cegliere un punto più vicino, mentre, e riulta inferiore a =1, andiamo a cegliere un punto più lontano. Procedendo in queto modo, batano pochi tentativi per individuare il punto corretto. 6
7 Il contorno delle radici Supponiamo allora di aver portato a termine il procedimento appena decritto e di aver quindi individuato i tre poli p 1, p, p corripondenti a =1. Siano, ad eempio, quelli indicati nella figura eguente: p 1 p p A queto punto, riconideriamo l equazione caratteritica + (a + 1) + a + = del itema di partenza: fiando =1, poiamo porre l equazione nella forma ( + 1) 1+ a = ( + 1) + 1 Queta equazione è ancora una volta nella forma 1+ G()=, per cui poiamo coniderarla come l equazione caratteritica di un itema avente funzione di traferimento in anello aperto ( + 1) ag () = a a> ( + 1) + 1 Poiamo allora determinare il luogo delle radici di tale itema, oia il modo ( + 1) con cui le radici dell equazione 1+ a = variano al variare del parametro ( + 1) + 1 a (e per =1). I poli del nuovo itema in eame ono, ovviamente, quelli indicati nell ultima figura riportata e ad ei i aggiungono uno zero nell origine ed uno zero in =-1: p 1 p -1 p 7
8 Appunti di Controlli Automatici Capitolo 5 (parte II) Il luogo delle radici corripondente a queta mappa i traccia abbatanza facilmente e riulta eere il eguente: Queto è dunque il luogo delle radici per =1 ed al variare del polo =-a (con a>). Scegliamo adeo un altro valore di in corripondenza del quale determinare nuovamente il uddetto luogo. Per eempio, e prendiamo >1, il nuovo luogo corriponde emplicemente ad un allontanamento dei tre poli ripetto all origine (mentre rimane invariata la poizione degli zeri): In modo del tutto analogo i cotruice il luogo ottenuto per <1. andry@iol.it ito peronale: 8
Il Luogo delle Radici
 Il Luogo delle Radici Il luogo delle radici è un procedimento, otanzialmente grafico, che permette di analizzare come varia il poizionamento dei poli di un itema di controllo in retroazione al variare
Il Luogo delle Radici Il luogo delle radici è un procedimento, otanzialmente grafico, che permette di analizzare come varia il poizionamento dei poli di un itema di controllo in retroazione al variare
Esame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A
 Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c ; P 1 1( ( + 4 ; P ( ( + ( + 3 ;
Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c ; P 1 1( ( + 4 ; P ( ( + ( + 3 ;
Esercizi svolti di geometria delle aree Alibrandi U., Fuschi P., Pisano A., Sofi A. ESERCIZIO n.7
 ESERCZO n.7 Data la ezione cava riportata in Figura, determinare: a) gli ai principali centrali di inerzia; b) l ellie principale centrale di inerzia; c) il nocciolo centrale di inerzia. cm cm A#7 . Determinazione
ESERCZO n.7 Data la ezione cava riportata in Figura, determinare: a) gli ai principali centrali di inerzia; b) l ellie principale centrale di inerzia; c) il nocciolo centrale di inerzia. cm cm A#7 . Determinazione
Compito di Fondamenti di Automatica settembre 2006
 Compito di Fondamenti di Automatica ettembre 2006 Eercizio 1. Si conideri lo chema di figura (operazionale ideale, eccetto per il guadagno che puó eere definito da una G(), reitenze uguali, condenatori
Compito di Fondamenti di Automatica ettembre 2006 Eercizio 1. Si conideri lo chema di figura (operazionale ideale, eccetto per il guadagno che puó eere definito da una G(), reitenze uguali, condenatori
1 = (parabola unitaria) si determini l errore di regolazione a regime:
 A - Tet d ingreo alla Prova Scritta di Controlli Automatici A del Ottobre 00 ( + ) ( ) + ) Dato un itema dinamico Σ con funzione di traferimento T() crivere i modi di Σ : ( + ) + 9 t { modi di Σ } {, tt,,
A - Tet d ingreo alla Prova Scritta di Controlli Automatici A del Ottobre 00 ( + ) ( ) + ) Dato un itema dinamico Σ con funzione di traferimento T() crivere i modi di Σ : ( + ) + 9 t { modi di Σ } {, tt,,
Esame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A
 Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c 2 ; P 1 1( ( + 4 ; P 2 ( ( + 1 (
Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c 2 ; P 1 1( ( + 4 ; P 2 ( ( + 1 (
Corso di Fondamenti di Automatica A.A. 2015/16. Diagrammi di Bode
 1 Coro di Fondamenti di Automatica A.A. 015/16 Diagrammi di Bode Prof. Carlo Coentino Dipartimento di Medicina Sperimentale e Clinica Univerità degli Studi Magna Graecia di Catanzaro tel: 0961-3694051
1 Coro di Fondamenti di Automatica A.A. 015/16 Diagrammi di Bode Prof. Carlo Coentino Dipartimento di Medicina Sperimentale e Clinica Univerità degli Studi Magna Graecia di Catanzaro tel: 0961-3694051
SEGNALI E SISTEMI 31 agosto 2017
 SEGNALI E SISTEMI 31 agoto 2017 Eercizio 1. [3+3+3+4 punti] Si conideri il modello ingreo/ucita LTI e cauale decritto dalla eguente equazione differenziale: dove a è un parametro reale. d 2 v(t) 2 +(1
SEGNALI E SISTEMI 31 agoto 2017 Eercizio 1. [3+3+3+4 punti] Si conideri il modello ingreo/ucita LTI e cauale decritto dalla eguente equazione differenziale: dove a è un parametro reale. d 2 v(t) 2 +(1
Esercitazione di Controlli Automatici 1 n 6
 4 maggio 007 Eercitazione di Controlli Automatici n 6 a.a. 006/07 Si conideri il itema della eercitazione n 5 cotituito da un braccio robotico in rotazione, utilizzato per la movimentazione di oggetti.
4 maggio 007 Eercitazione di Controlli Automatici n 6 a.a. 006/07 Si conideri il itema della eercitazione n 5 cotituito da un braccio robotico in rotazione, utilizzato per la movimentazione di oggetti.
K c s h. P(s) 1/K d. U(s) + Y(s)
 Eame di Fondamenti di Automatica Coro di Laurea Vecchio Ordinamento in Ingegneria Elettronica febbraio 3 Compito A Cognome: Nome Matricola: Email:. Ricavare la funzione di traferimento tra u ed y nel eguente
Eame di Fondamenti di Automatica Coro di Laurea Vecchio Ordinamento in Ingegneria Elettronica febbraio 3 Compito A Cognome: Nome Matricola: Email:. Ricavare la funzione di traferimento tra u ed y nel eguente
Esercitazione di Controlli Automatici 1 n 2. a.a. 2006/07
 6 marzo 007 Eercitazione di Controlli Automatici n a.a. 006/07 Riferendoi al itema di controllo della temperatura in un locale di piccole dimenioni dicuo nella eercitazione precedente, e di eguito riportato:.
6 marzo 007 Eercitazione di Controlli Automatici n a.a. 006/07 Riferendoi al itema di controllo della temperatura in un locale di piccole dimenioni dicuo nella eercitazione precedente, e di eguito riportato:.
ESERCIZIO 1 L/2 C.R. D
 SRIZIO Il itema di corpi rigidi in figura è oggetto ad uno potamento impreo (cedimento), in direzione verticale e vero il bao, in corripondenza del vincolo in. Si vuole determinare la nuova configurazione
SRIZIO Il itema di corpi rigidi in figura è oggetto ad uno potamento impreo (cedimento), in direzione verticale e vero il bao, in corripondenza del vincolo in. Si vuole determinare la nuova configurazione
dove x 0 R n è fissato.
 AMMISSIONE AL QUARTO ANNO: prova di ANALISI MATEMATICA (matematici e fiici) 26 Sia α (, ) (a) Provare che eite c α >, indipendente da t e, tale che (b) Calcolare c /2 (t σ) α (σ ) α dσ = c α, t, () (c)
AMMISSIONE AL QUARTO ANNO: prova di ANALISI MATEMATICA (matematici e fiici) 26 Sia α (, ) (a) Provare che eite c α >, indipendente da t e, tale che (b) Calcolare c /2 (t σ) α (σ ) α dσ = c α, t, () (c)
Bode Diagram. 1.2 Determinare il valore del guadagno del sistema. Disegnare gli zeri ed i poli nel piano complesso.
 5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
ANALISI DI SISTEMI IN RETROAZIONE TEOREMA DI NYQUIST
 ANALISI DI SISTEMI IN RETROAZIONE TEOREMA DI NYQUIST PROPRIETÀ DEI SISTEMI IN RETROAZIONE U E G () H () Si fa riferimento ad un generico itema in retroazione con funzione di traferimento a ciclo chiuo.
ANALISI DI SISTEMI IN RETROAZIONE TEOREMA DI NYQUIST PROPRIETÀ DEI SISTEMI IN RETROAZIONE U E G () H () Si fa riferimento ad un generico itema in retroazione con funzione di traferimento a ciclo chiuo.
Criterio di stabilità di Bode. tramite la risposta in frequenza viene indicata come condizione di innesco dell instabilità la
 Criterio di tabilità di Bode Sia dato un itema retroazionato con f.d.t. eprea F( H ( tramite la ripota in frequenza viene indicata come condizione di inneco dell intabilità la G ( j H ( j 0 cioè G ( j
Criterio di tabilità di Bode Sia dato un itema retroazionato con f.d.t. eprea F( H ( tramite la ripota in frequenza viene indicata come condizione di inneco dell intabilità la G ( j H ( j 0 cioè G ( j
Corso di Progetto di Strutture. POTENZA, a.a Serbatoi e tubi
 Coro di Progetto di Strutture POTENZA, a.a. 0 03 Serbatoi e tubi Dott. arco VONA Scuola di Ingegneria, Univerità di Bailicata marco.vona@uniba.it http://.uniba.it/utenti/vona/ CONSIDERAZIONI INTRODUTTIVE
Coro di Progetto di Strutture POTENZA, a.a. 0 03 Serbatoi e tubi Dott. arco VONA Scuola di Ingegneria, Univerità di Bailicata marco.vona@uniba.it http://.uniba.it/utenti/vona/ CONSIDERAZIONI INTRODUTTIVE
Esercitazioni di Controlli Automatici L-A
 Eercitazioni di Controlli Automatici L-A Progetto di un regolatore Data le eguente funzione di traferimento G(): G() = + 0 3 + 7. 2 + 0.7 + () i richiede di progettare un regolatore R() che poto in cacata
Eercitazioni di Controlli Automatici L-A Progetto di un regolatore Data le eguente funzione di traferimento G(): G() = + 0 3 + 7. 2 + 0.7 + () i richiede di progettare un regolatore R() che poto in cacata
2. METODO DEGLI SPOSTAMENTI O EQUAZIONE DELLA LINEA ELASTICA, PER LA SOLUZIONE DI TRAVI IPERSTATICHE
 METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
Modellistica e controllo PID di un pendolo inverso
 Modellitica e controllo PID di un pendolo invero Note per le lezioni del coro di Controlli Automatici - A.A. 2009/0 Prof.a Maria Elena Valcher Modellitica Un ata di maa m è incernierata ad un carrello
Modellitica e controllo PID di un pendolo invero Note per le lezioni del coro di Controlli Automatici - A.A. 2009/0 Prof.a Maria Elena Valcher Modellitica Un ata di maa m è incernierata ad un carrello
ESEMPI DI ANALISI DI CIRCUITI DINAMICI LINEARI. corso: Teoria dei Circuiti. docente: Stefano PASTORE. 1 Esempio di tableau dinamico (tempo e Laplace)
 ESEMPI DI ANALISI DI CIRCUITI DINAMICI LINEARI coro: Teoria dei Circuiti docente: Stefano PASTORE 1 Eempio di tableau dinamico (tempo e Laplace) 1.1 Dominio del tempo Conideriamo il eguente circuito dinamico
ESEMPI DI ANALISI DI CIRCUITI DINAMICI LINEARI coro: Teoria dei Circuiti docente: Stefano PASTORE 1 Eempio di tableau dinamico (tempo e Laplace) 1.1 Dominio del tempo Conideriamo il eguente circuito dinamico
Progetto di reti correttrici e controllori PID e traduzione nel discreto con il metodo di emulazione
 Progetto di reti correttrici e controllori PID e traduione nel dicreto con il metodo di emulaione Eerciio. Si conideri lo chema di controllo rappreentato in figura dove P () = con a = 40. a + r(t) + S
Progetto di reti correttrici e controllori PID e traduione nel dicreto con il metodo di emulaione Eerciio. Si conideri lo chema di controllo rappreentato in figura dove P () = con a = 40. a + r(t) + S
Lezione 18. Stabilità di sistemi retroazionati. F. Previdi - Fondamenti di Automatica - Lez. 18 1
 Lezione 18. Stabilità di itemi retroazionati F. Previdi - Fondamenti di Automatica - Lez. 18 1 Schema 1. Stabilità di itemi retroazionati 2. Diagramma di Nyquit 3. Criterio di Nyquit 4. Etenioni del Criterio
Lezione 18. Stabilità di itemi retroazionati F. Previdi - Fondamenti di Automatica - Lez. 18 1 Schema 1. Stabilità di itemi retroazionati 2. Diagramma di Nyquit 3. Criterio di Nyquit 4. Etenioni del Criterio
Postulato delle reazioni vincolari
 Potulato delle reazioni vincolari Ad ogni vincolo agente u un punto materiale P può eere otituita una forza, chiamata reazione vincolare, che realizza lo teo effetto dinamico del vincolo. reazione vincolare
Potulato delle reazioni vincolari Ad ogni vincolo agente u un punto materiale P può eere otituita una forza, chiamata reazione vincolare, che realizza lo teo effetto dinamico del vincolo. reazione vincolare
Esercizio. Il circuito di figura rappresenta un filtro passa-banda. Dopo aver ricavato la funzione di trasferimento, sapendo che
 Eercizio Clae 5ª Elettronici Materia Sitemi Argomento Funzioni di traferimento Il circuito di figura rappreenta un filtro paa-banda. Dopo aver ricavato la funzione di traferimento, apendo che R = 2k Ω
Eercizio Clae 5ª Elettronici Materia Sitemi Argomento Funzioni di traferimento Il circuito di figura rappreenta un filtro paa-banda. Dopo aver ricavato la funzione di traferimento, apendo che R = 2k Ω
Trasmissione di Simboli Isolati
 Coro di COMUNICAZIONI ELETTRICHE Docente : Prof. Roberto Gaudino Tutore : Prof. Vito De Feo Eercitazione n 6 Tramiione di Simboli Iolati Anno Accademico 007-008 Eercizio Quale delle forme d'onda h(t) in
Coro di COMUNICAZIONI ELETTRICHE Docente : Prof. Roberto Gaudino Tutore : Prof. Vito De Feo Eercitazione n 6 Tramiione di Simboli Iolati Anno Accademico 007-008 Eercizio Quale delle forme d'onda h(t) in
Stati limite nel cemento armato Stato limite ultimo per tensioni normali: applicazioni BOZZA
 Lezione n. 1 Stati limite nel cemento armato Stato limite ultimo per tenioni normali: applicazioni Nel eguito i riportano alcuni eempi di applicazione delle procedure decritte nel paragrao precedente.
Lezione n. 1 Stati limite nel cemento armato Stato limite ultimo per tenioni normali: applicazioni Nel eguito i riportano alcuni eempi di applicazione delle procedure decritte nel paragrao precedente.
Corso Tecnologie dei Sistemi di Controllo. Controllo PID
 Coro Controllo PID Ing. Valerio Scordamaglia Univerità Mediterranea di Reggio Calabria, Loc. Feo di Vito, 896, RC, Italia D.I.M.E.T. : Dipartimento di Informatica, Matematica, Elettronica e Traporti Struttura
Coro Controllo PID Ing. Valerio Scordamaglia Univerità Mediterranea di Reggio Calabria, Loc. Feo di Vito, 896, RC, Italia D.I.M.E.T. : Dipartimento di Informatica, Matematica, Elettronica e Traporti Struttura
Esercizi di Controlli Automatici - 9 A.A. 2009/2010
 Eercizi di Controlli Automatici - 9 A.A. 2009/200 Eercizio. Dato il eguente chema, in cui gli amplificatori operazionali ono uppoti ideali, i calcoli la funzione di traferimento G() tra v in (t) e v out
Eercizi di Controlli Automatici - 9 A.A. 2009/200 Eercizio. Dato il eguente chema, in cui gli amplificatori operazionali ono uppoti ideali, i calcoli la funzione di traferimento G() tra v in (t) e v out
DINAMICHE COMPLESSE NEL FERRO DI CAVALLO
 DINAMICHE COMPLEE NEL FERRO DI CAVALLO La mappa a erro di cavallo L inieme invariante Dinamica imbolica Dinamiche nell inieme invariante Ferro di cavallo e cao C. Piccardi e F. Dercole Politecnico di Milano
DINAMICHE COMPLEE NEL FERRO DI CAVALLO La mappa a erro di cavallo L inieme invariante Dinamica imbolica Dinamiche nell inieme invariante Ferro di cavallo e cao C. Piccardi e F. Dercole Politecnico di Milano
Lezione 12 - I cerchi di Mohr
 Lezione 1 - I cerchi di Mohr [Ultimareviione: reviione:15 15dicembre dicembre008] In queta lezione i decrive un claico metodo di viualizzazione dello tato tenionale nell'intorno di un punto generico P
Lezione 1 - I cerchi di Mohr [Ultimareviione: reviione:15 15dicembre dicembre008] In queta lezione i decrive un claico metodo di viualizzazione dello tato tenionale nell'intorno di un punto generico P
1. Introduzione Il convertitore a semplice semionda Il sistema di controllo... 5
 . Introduzione... 2 2. Il convertitore a emplice emionda... 3 2. Il itema di controllo... 5 3. Il convertitore monofae nella configurazione a ponte... 7 4. Il fenomeno della commutazione... . Introduzione
. Introduzione... 2 2. Il convertitore a emplice emionda... 3 2. Il itema di controllo... 5 3. Il convertitore monofae nella configurazione a ponte... 7 4. Il fenomeno della commutazione... . Introduzione
Appunti ed esercitazioni di Microonde 2
 Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
a) Caso di rottura duttile con armatura compressa minore di quella tesa
 LEZIONI N 39 E 40 FLESSIONE SEMPLICE: LA DOPPIA ARMATURA E LA SEZIONE A T LA VERIFICA DELLA SEZIONE INFLESSA CON DOPPIA ARMATURA a) Cao di rottura duttile con armatura comprea minore di quella tea Si può
LEZIONI N 39 E 40 FLESSIONE SEMPLICE: LA DOPPIA ARMATURA E LA SEZIONE A T LA VERIFICA DELLA SEZIONE INFLESSA CON DOPPIA ARMATURA a) Cao di rottura duttile con armatura comprea minore di quella tea Si può
CONTROLLO DIGITALE LAUREA TRIENNALE IN ING. INFORMATICA E DELL AUTOMAZIONE A.A. 2017/2018 LAUREA MAGISTRALE IN ING. ELETTRICA A.A.
 LAUREA TRIENNALE IN ING. INFORMATICA E DELL AUTOMAZIONE A.A. 7/8 LAUREA MAGISTRALE IN ING. ELETTRICA A.A. 7/8 APPELLO 9//8 Sia aegnata la eguente equazione alle differenze: y(k).3679y(k ) +.3679y(k ) =.3679u(k
LAUREA TRIENNALE IN ING. INFORMATICA E DELL AUTOMAZIONE A.A. 7/8 LAUREA MAGISTRALE IN ING. ELETTRICA A.A. 7/8 APPELLO 9//8 Sia aegnata la eguente equazione alle differenze: y(k).3679y(k ) +.3679y(k ) =.3679u(k
Regolazione e Controllo dei Sistemi Meccanici Figura 1: Schema di un montacarichi.
 Regolazione e Controllo dei Sitemi Meccanici 7-7-28 Figura : Schema di un montacarichi. Il itema in figura, cotituito da un motore elettrico azionante un verricello dove è avvolto un cavo di materiale
Regolazione e Controllo dei Sitemi Meccanici 7-7-28 Figura : Schema di un montacarichi. Il itema in figura, cotituito da un motore elettrico azionante un verricello dove è avvolto un cavo di materiale
Controllo di Azionamenti Elettrici. Lezione n 3. Caratteristiche e predisposizione dei regolatori PID
 Controllo di Azionamenti Elettrici Lezione n 3 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di alermo Caratteritiche e predipoizione dei regolatori ID 1 Introduzione
Controllo di Azionamenti Elettrici Lezione n 3 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di alermo Caratteritiche e predipoizione dei regolatori ID 1 Introduzione
= 20 m/s in una guida verticale circolare. v A A
 Eercizio (tratto dal Problema 4.39 del Mazzoldi Un corpo di maa m = 00 Kg entra con elocità A licia di raggio = 5 m. Calcolare: = 0 m/ in una guida erticale circolare. la elocità nei punti B e C;. la reazione
Eercizio (tratto dal Problema 4.39 del Mazzoldi Un corpo di maa m = 00 Kg entra con elocità A licia di raggio = 5 m. Calcolare: = 0 m/ in una guida erticale circolare. la elocità nei punti B e C;. la reazione
Trasformazione di Laplace
 Traformazione di Laplace Gabriele Sicuro. Definizioni fondamentali Sia data una funzione f : C; ea i dice originale e ono oddifatte le eguenti condizioni: () f (t) per t
Traformazione di Laplace Gabriele Sicuro. Definizioni fondamentali Sia data una funzione f : C; ea i dice originale e ono oddifatte le eguenti condizioni: () f (t) per t
Controlli Automatici LA Risposte dei sistemi
 //8 Controlli Automatici LA Analii dei itemi dinamici lineari Ripote al gradino di itemi tipici Relazioni Funzione di Traferimento/Ripote Prof. Carlo Roi DEIS-Univerità di Bologna Tel. 5 93 Email: croi@dei.unibo.it
//8 Controlli Automatici LA Analii dei itemi dinamici lineari Ripote al gradino di itemi tipici Relazioni Funzione di Traferimento/Ripote Prof. Carlo Roi DEIS-Univerità di Bologna Tel. 5 93 Email: croi@dei.unibo.it
LEZIONI N 35 E 36 ANALISI ALLO STATO LIMITE ULTIMO DELLA SEZIONE INFLESSA
 LEZIONI N 35 E 36 ANALISI ALLO STATO LIMITE ULTIMO DELLA SEZIONE INFLESSA Nel cao delle ezioni inflee di cemento armato, la verifica di icurezza allo tato limite ultimo di reitenza conite nel controllare
LEZIONI N 35 E 36 ANALISI ALLO STATO LIMITE ULTIMO DELLA SEZIONE INFLESSA Nel cao delle ezioni inflee di cemento armato, la verifica di icurezza allo tato limite ultimo di reitenza conite nel controllare
Esercizi di Segnali e Sistemi. GLI ESERCIZI 1,2,3,4,11 COSTITUISCONO UN TEMA D ESAME TIPICO
 Eercizi di Segnali e Sitemi. GLI ESERCIZI,2,3,4, COSTITUISCONO UN TEMA D ESAME TIPICO Eempio Conideriamo la funzione di traferimento G() = + Si calcoli la forma di Smith Mc-Millan. Soluzione: G() = N(),
Eercizi di Segnali e Sitemi. GLI ESERCIZI,2,3,4, COSTITUISCONO UN TEMA D ESAME TIPICO Eempio Conideriamo la funzione di traferimento G() = + Si calcoli la forma di Smith Mc-Millan. Soluzione: G() = N(),
Sistemi a segnali campionati
 Capitolo. INRODUZIONE 6. Sitemi a egnali campionati Si conideri il eguente itema lineare tempo continuo: G() : ẋ(t) Ax(t)+Bu(t) y(t) Cx(t) U() G() Y() Se i inerice un ricotruttore di ordine zero H () e
Capitolo. INRODUZIONE 6. Sitemi a egnali campionati Si conideri il eguente itema lineare tempo continuo: G() : ẋ(t) Ax(t)+Bu(t) y(t) Cx(t) U() G() Y() Se i inerice un ricotruttore di ordine zero H () e
L equazione che descrive il moto del corpo è la seconda legge della dinamica
 Eercizio ul piano inclinato La forza peo è data dalla formula p mg Allora e grandezze geometriche: poono eere critte utilizzando l angolo di inclinazione del piano oppure le Angolo di inclinazione orza
Eercizio ul piano inclinato La forza peo è data dalla formula p mg Allora e grandezze geometriche: poono eere critte utilizzando l angolo di inclinazione del piano oppure le Angolo di inclinazione orza
Esercitazione 16 Novembre 2012 Circuiti dinamici del secondo ordine. t come riportato in figura.
 Eercitazione Noembre ircuiti dinamici del econdo ordine ircuito L- erie Per quanto riguarda queto circuito, l eercizio egue la traccia della oluzione del compito d eame numero, reperibile in rete al olito
Eercitazione Noembre ircuiti dinamici del econdo ordine ircuito L- erie Per quanto riguarda queto circuito, l eercizio egue la traccia della oluzione del compito d eame numero, reperibile in rete al olito
Lezione 2 - Algebra. x + 1 x 2 a b + b a 2. Problema 2 Siano a, b, c R, provare che
 Lezione - Algebra Problema 1 Siano a, b R +, dimotrare che a b + b a Soluzione: Poniamo x = a, oerviamo che b (x 1) 0 x x + 1 0 x + 1 x dato che x > 0, poiamo dividere ambo i membri per x, otteniamo: Problema
Lezione - Algebra Problema 1 Siano a, b R +, dimotrare che a b + b a Soluzione: Poniamo x = a, oerviamo che b (x 1) 0 x x + 1 0 x + 1 x dato che x > 0, poiamo dividere ambo i membri per x, otteniamo: Problema
COSTRUZIONE GRAFICA ASINTOTICA DEI FATTORI 1/(1+T) E T/(1+T) T T. non compensata compensata H V
 COSTRUZIONE GRAFICA ASINTOTICA DEI FATTORI /(+T) E T/(+T) vˆ = = G G vg c vg vˆ + T vˆ g + G g c vref T + vˆ H + T vˆ ref Z ref c out iˆ Z load out + T iˆ load T non compenata compenata H ( ) Gvd ( ) V
COSTRUZIONE GRAFICA ASINTOTICA DEI FATTORI /(+T) E T/(+T) vˆ = = G G vg c vg vˆ + T vˆ g + G g c vref T + vˆ H + T vˆ ref Z ref c out iˆ Z load out + T iˆ load T non compenata compenata H ( ) Gvd ( ) V
Le ipotesi di base che si utilizzano sono le stesse quattro già viste con riferimento al caso della flessione semplice e cioè:
 LEZIONI N 44 E 45 CALCOLO A ROTTURA DELLA SEZIONE PRESSOINFLESSA PROBLEMI DI VERIFICA La procedura di verifica dei pilatri di c.a., ottopoti a forzo normale e momento flettente, è baata ulla cotruzione
LEZIONI N 44 E 45 CALCOLO A ROTTURA DELLA SEZIONE PRESSOINFLESSA PROBLEMI DI VERIFICA La procedura di verifica dei pilatri di c.a., ottopoti a forzo normale e momento flettente, è baata ulla cotruzione
Risonanza. Tracciare gli andamenti del modulo e della fase dell impedenza in funzione della frequenza f per il seguente bipolo: A R 1 R 2
 6 Eercitazioni aggiuntive Eercizio 6. Tracciare gli andamenti del modulo e della fae dell impedenza in funzione della frequenza f per il eguente bipolo: A B [W]; [W]; [mf] Si calcoli l impedenza del bipolo
6 Eercitazioni aggiuntive Eercizio 6. Tracciare gli andamenti del modulo e della fae dell impedenza in funzione della frequenza f per il eguente bipolo: A B [W]; [W]; [mf] Si calcoli l impedenza del bipolo
Definizioni e relazioni fondamentali
 Capitolo 1 Definizioni e relazioni fondamentali 1.1 Definizioni di E e B Il campo elettrico E (m 1 ) e l induzione magnetica B (T) ono definiti in riferimento alla forza che agice u una carica in movimento
Capitolo 1 Definizioni e relazioni fondamentali 1.1 Definizioni di E e B Il campo elettrico E (m 1 ) e l induzione magnetica B (T) ono definiti in riferimento alla forza che agice u una carica in movimento
16. Onde elastiche. m s
 1 Catena di ocillatori 16. Onde elatiche Vogliamo dicutere il fenomeno della propagazione ondulatoria in un mezzo elatico. A tale copo conideriamo un inieme di punti materiali dipoti lungo una retta, ad
1 Catena di ocillatori 16. Onde elatiche Vogliamo dicutere il fenomeno della propagazione ondulatoria in un mezzo elatico. A tale copo conideriamo un inieme di punti materiali dipoti lungo una retta, ad
Asse neutro che taglia la soletta. Influenza delle modalità costruttive
 Univerità degli Studi di Roma Tre Coro di Tecnica dll delle Cotruzioni i I Modulo A/A 27-88 LEZIONE N 15 CLS TRAVE COMPOSTE ACCIAIO-CLS CLS SEMPLICEMENTE APPOGGIATA Analii allo tato limite ultimo della
Univerità degli Studi di Roma Tre Coro di Tecnica dll delle Cotruzioni i I Modulo A/A 27-88 LEZIONE N 15 CLS TRAVE COMPOSTE ACCIAIO-CLS CLS SEMPLICEMENTE APPOGGIATA Analii allo tato limite ultimo della
Scambio termico per convezione
 Scambio termico per convezione La convezione forzata Equazione di Newton w > Equazione di Newton q c q q& ( T ) = h A T c ( T ) = h T Fluo Fluo pecifico 1 Fenomenologia w > q& Il meccanimo di cambio termico
Scambio termico per convezione La convezione forzata Equazione di Newton w > Equazione di Newton q c q q& ( T ) = h A T c ( T ) = h T Fluo Fluo pecifico 1 Fenomenologia w > q& Il meccanimo di cambio termico
SIST DI CONTROLLO IN RETROAZ. NEGATIVA Proprietà generali dei sistemi in retroazione
 SIST DI CONTROLLO IN RETROAZ. NEGATIVA Proprietà generali dei itemi in retroazione R E C G + - Y H G rappreenta il regolatore, l'amplificatore di potenza, l'attuatore ed il itema controllato e prende il
SIST DI CONTROLLO IN RETROAZ. NEGATIVA Proprietà generali dei itemi in retroazione R E C G + - Y H G rappreenta il regolatore, l'amplificatore di potenza, l'attuatore ed il itema controllato e prende il
Uso della trasformata di Laplace per il calcolo della risposta
 Uo della traformata di Laplace per il calcolo della ripota Conigli generali (Aggiornato 7//) ) Si vuole qui richiamare l attenzione ul fatto che la preenza di zeri o di una truttura triangolare a blocchi
Uo della traformata di Laplace per il calcolo della ripota Conigli generali (Aggiornato 7//) ) Si vuole qui richiamare l attenzione ul fatto che la preenza di zeri o di una truttura triangolare a blocchi
A tal fine consideriamo un esempio come punto di partenza per le nostre considerazioni.
 Moto Parabolico Sino ad ora abbiamo ito due tipi di moto: moto rettilineo uniforme moto uniformemente accelerato lo tudio che è tato condotto fino a queto punto ha preo in coniderazione un moto alla olta,
Moto Parabolico Sino ad ora abbiamo ito due tipi di moto: moto rettilineo uniforme moto uniformemente accelerato lo tudio che è tato condotto fino a queto punto ha preo in coniderazione un moto alla olta,
Esame di FONDAMENTI di AUTOMATICA Compito B (Nuovo ordinamento) 16 Giugno 2008 (Bozza di soluzione)
 Eame di FONDAMENTI di AUTOMATICA Compito B (Nuovo ordinamento 6 Giugno 28 (Bozza di oluzione NB. Si coniglia vivamente di ripaare anche argomenti non trettamente inerenti la materia oggetto della prova
Eame di FONDAMENTI di AUTOMATICA Compito B (Nuovo ordinamento 6 Giugno 28 (Bozza di oluzione NB. Si coniglia vivamente di ripaare anche argomenti non trettamente inerenti la materia oggetto della prova
Modello monodimensionale per le correnti in moto turbolento vario. Fig. 1
 Modello monodimenionale per le correnti in moto turbolento vario 1. Decompoizione dei campi di moto turbolento vario Prima di affrontare la definizione del modello per le correnti in moto turbolento vario,
Modello monodimenionale per le correnti in moto turbolento vario 1. Decompoizione dei campi di moto turbolento vario Prima di affrontare la definizione del modello per le correnti in moto turbolento vario,
1. Teorema di reciprocità
 1. Teorema di reciprocità Conideriamo un mezzo in cui ono preenti le orgenti (J 1, M 1 ) che producono un campo (E 1, H 1 ) e le orgenti (J 2, M 2 ) che producono un campo (E 2, H 2 ). Determineremo una
1. Teorema di reciprocità Conideriamo un mezzo in cui ono preenti le orgenti (J 1, M 1 ) che producono un campo (E 1, H 1 ) e le orgenti (J 2, M 2 ) che producono un campo (E 2, H 2 ). Determineremo una
Funzioni razionali proprie
 Funzioni razionali proprie Riga 5: P n P αk αkt n e = R α k k k e = = Q Q' α k α t k P e Q ono polinomi di Il grado di P è inferiore a quello di Q α k k=,..n ono gli zeri tutti emplici di Q R α = P α α
Funzioni razionali proprie Riga 5: P n P αk αkt n e = R α k k k e = = Q Q' α k α t k P e Q ono polinomi di Il grado di P è inferiore a quello di Q α k k=,..n ono gli zeri tutti emplici di Q R α = P α α
MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 3) 28 Novembre 2008
 MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 3) 28 Novembre 2008 Soluzioni 1.(4 punti) L indice di maa corporea (IMC) è ottenuto dal rapporto tra maa, eprea in Kg, e l altezza al quadrato, eprea in
MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 3) 28 Novembre 2008 Soluzioni 1.(4 punti) L indice di maa corporea (IMC) è ottenuto dal rapporto tra maa, eprea in Kg, e l altezza al quadrato, eprea in
Interazioni Elettrodeboli. Lezione n. 9. Campo di Dirac Invarianza di Gauge Globale Campi interagenti
 Interazioni Elettrodeboli prof. Franceco Ragua Univerità di Milano Lezione n. 9 27.1.214 Campo di Dirac Invarianza di Gauge Globale Campi interagenti anno accademico 214-215 Quantizzazione del Campo di
Interazioni Elettrodeboli prof. Franceco Ragua Univerità di Milano Lezione n. 9 27.1.214 Campo di Dirac Invarianza di Gauge Globale Campi interagenti anno accademico 214-215 Quantizzazione del Campo di
MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008
 MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008 SOLUZIONI 1. (4 punti) L indice di maa corporea (IMC) è ottenuto dal rapporto tra maa, eprea in Kg, e l altezza, eprea in m, al quadrato.
MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008 SOLUZIONI 1. (4 punti) L indice di maa corporea (IMC) è ottenuto dal rapporto tra maa, eprea in Kg, e l altezza, eprea in m, al quadrato.
Note sulle vibrazioni molecolari
 Note ulle vibrazioni molecolari Daniele Toffoli May 5, 016 La teoria dei gruppi trova una importante applicazione nella claificazione della immetria dei modi normali di vibrazione in accordo alle rappreentazioni
Note ulle vibrazioni molecolari Daniele Toffoli May 5, 016 La teoria dei gruppi trova una importante applicazione nella claificazione della immetria dei modi normali di vibrazione in accordo alle rappreentazioni
1_ Filtro passa-basso Con A(jw) si indica la funzione di trasferimento del filtro, il cui modulo A assume un valore costante
 PPUNTI DI ELETTNIC FILTI TTII 6 Campi di applicazione I filtri nel ettore dell elettronica ono utilizzati per : attenuare i diturbi, il rumore e le ditorioni applicati al egnale utile; eparare due egnale
PPUNTI DI ELETTNIC FILTI TTII 6 Campi di applicazione I filtri nel ettore dell elettronica ono utilizzati per : attenuare i diturbi, il rumore e le ditorioni applicati al egnale utile; eparare due egnale
I sistemi retroazionati. Per lo studio si può utilizzarne uno a reazione unitaria per rendere standard i risultati:
 I itemi retroazionati Facciamo riferimento allo chema a blocchi: Per lo tudio i può utilizzarne uno a reazione unitaria per rendere tandard i riultati: i due ono equivalenti: infatti il primo ha una f.d.t.
I itemi retroazionati Facciamo riferimento allo chema a blocchi: Per lo tudio i può utilizzarne uno a reazione unitaria per rendere tandard i riultati: i due ono equivalenti: infatti il primo ha una f.d.t.
FONDAMENTI DI SISTEMI DINAMICI (prof. Vincenzo LIPPIELLO A.A ) Corso di Laurea in Ingegneria Elettronica e delle Telecomunicazioni - II anno
 Voto Cognome/Nome & No. Matricola FONDAMENTI DI SISTEMI DINAMICI (prof. Vincenzo LIPPIELLO A.A. 5 6) Coro di Laurea in Ingegneria Elettronica e delle Telecomunicazioni - II anno PROVA DEL 6 GENNAIO 7 Ripondere
Voto Cognome/Nome & No. Matricola FONDAMENTI DI SISTEMI DINAMICI (prof. Vincenzo LIPPIELLO A.A. 5 6) Coro di Laurea in Ingegneria Elettronica e delle Telecomunicazioni - II anno PROVA DEL 6 GENNAIO 7 Ripondere
CONTROLLI AUTOMATICI L-B ESERCIZI SUL CONTROLLO IN RETROAZIONE
 CONTROLLI AUTOMATICI L-B ESERCIZI SUL CONTROLLO IN RETROAZIONE Ing. Nicola Diolaiti DEIS-Univerità di Bologna Tel. 5 29379 / 68 e-mail: ndiolaiti@dei.unibo.it http://www-lar.dei.unibo.it/people/ndiolaiti
CONTROLLI AUTOMATICI L-B ESERCIZI SUL CONTROLLO IN RETROAZIONE Ing. Nicola Diolaiti DEIS-Univerità di Bologna Tel. 5 29379 / 68 e-mail: ndiolaiti@dei.unibo.it http://www-lar.dei.unibo.it/people/ndiolaiti
Lezione 19 ALCUNI PROBLEMI RELATIVI A CONDOTTE A SEZIONE CIRCOLARE
 Appunti dei cori di Idraulica e Idrodinamica ezione 9 ACNI PROBEMI REATIVI A CONOTTE A SEZIONE CIRCOARE Come accennato nella EZIONE 8, e conideriamo il moto tazionario di un fluido incomprimibile all interno
Appunti dei cori di Idraulica e Idrodinamica ezione 9 ACNI PROBEMI REATIVI A CONOTTE A SEZIONE CIRCOARE Come accennato nella EZIONE 8, e conideriamo il moto tazionario di un fluido incomprimibile all interno
LA VERIFICA E IL PROGETTO CONDIZIONATO DELLA SEZIONE INFLESSA CON ARMATURA SEMPLICE
 LEZIONI N 37 E 38 LA VERIFICA E IL PROGETTO CONDIZIONATO DELLA SEZIONE INFLESSA CON ARMATURA SEMPLICE VERIFICA DELLA SEZIONE INFLESSA DUTTILE Dopo il cao particolare della rottura bilanciata, conideriamo
LEZIONI N 37 E 38 LA VERIFICA E IL PROGETTO CONDIZIONATO DELLA SEZIONE INFLESSA CON ARMATURA SEMPLICE VERIFICA DELLA SEZIONE INFLESSA DUTTILE Dopo il cao particolare della rottura bilanciata, conideriamo
Resistenza a sforzo normale e flessione (elementi monodimensionali) [ ]
![Resistenza a sforzo normale e flessione (elementi monodimensionali) [ ] Resistenza a sforzo normale e flessione (elementi monodimensionali) [ ]](/thumbs/59/42756809.jpg) 41 1. Calcolo dell armatura longitudinale delle travi in funzione delle azioni riultanti dall analii; 2. Calcolo dell armatura a taglio delle travi in funzione del taglio dovuto ai momenti reitenti delle
41 1. Calcolo dell armatura longitudinale delle travi in funzione delle azioni riultanti dall analii; 2. Calcolo dell armatura a taglio delle travi in funzione del taglio dovuto ai momenti reitenti delle
UNITA' 21 SOMMARIO U.21 LE MODALITÀ DI TRASMISSIONE DEL CALORE ATTENZIONE
 U.21/0 UNITA' 21 SOMMARIO U.21 LE MODALITÀ DI TRASMISSIONE DEL CALORE 21.1. Introduzione 21.2. Conduzione 21.3. Convezione 21.4. Irraggiamento 21.5. Modalità imultanee di tramiione del calore ATTENZIONE
U.21/0 UNITA' 21 SOMMARIO U.21 LE MODALITÀ DI TRASMISSIONE DEL CALORE 21.1. Introduzione 21.2. Conduzione 21.3. Convezione 21.4. Irraggiamento 21.5. Modalità imultanee di tramiione del calore ATTENZIONE
Tecnologie dei Sistemi di Automazione
 Facoltà di Ingegneria Tecnologie dei Sitemi di Automazione rof. Gianmaria De Tommai Lezione 4 Regolatori ID indutriali: Leggi di controllo e utilizzo Coro di Laurea Codice inegnamento Email docente Anno
Facoltà di Ingegneria Tecnologie dei Sitemi di Automazione rof. Gianmaria De Tommai Lezione 4 Regolatori ID indutriali: Leggi di controllo e utilizzo Coro di Laurea Codice inegnamento Email docente Anno
La trasformata di Fourier in Ottica
 Edoardo Milotti 5/11/2007 La traformata di Fourier in Ottica Queta nota contiene una breviima introduzione alle traformate di Fourier in Ottica 1. Il principio di Huygen Il principio di Huygen afferma
Edoardo Milotti 5/11/2007 La traformata di Fourier in Ottica Queta nota contiene una breviima introduzione alle traformate di Fourier in Ottica 1. Il principio di Huygen Il principio di Huygen afferma
1) Progettazione di codici ciclici. 2) Esercizi sui codici ciclici. Mauro De Sanctis corso di Informazione e Codifica Università di Roma Tor Vergata
 Argomenti della Lezione Progettazione di codici ciclici Eercizi ui codici ciclici Codici ciclici Oervazione: Se g divide ia m che n con m
Argomenti della Lezione Progettazione di codici ciclici Eercizi ui codici ciclici Codici ciclici Oervazione: Se g divide ia m che n con m
Fondamenti di Automatica Figura 1: Schema di centrifuga industriale: a) vista in assonometria b) vista frontale.
 Fondamenti di Automatica 6-9-26 Figura : Schema di centrifuga indutriale: a) vita in aonometria b) vita frontale. A In Fig..a è riportato lo chema emplificato di una centrifuga orizzontale indutriale di
Fondamenti di Automatica 6-9-26 Figura : Schema di centrifuga indutriale: a) vita in aonometria b) vita frontale. A In Fig..a è riportato lo chema emplificato di una centrifuga orizzontale indutriale di
Controlli Automatici (AUT) - 09AKSBL. Progetto dinamico. Funzioni compensatrici elementari. Struttura di controllo con compensazione in cascata d a
 Controlli Automatici (AUT) - 9AKSBL Funzioni compenatrici elementari Progetto di controllori in cacata Struttura di controllo con compenazione in cacata d a r + + e + C () + u + G() y - d y + dt + L obiettivo
Controlli Automatici (AUT) - 9AKSBL Funzioni compenatrici elementari Progetto di controllori in cacata Struttura di controllo con compenazione in cacata d a r + + e + C () + u + G() y - d y + dt + L obiettivo
Tecnologie Informatiche per l Automazione Industriale
 Tecnologie Informatiche per l Automazione Indutriale Prof. Gianmaria De Tommai Regolatori PID indutriali: Leggi di controllo e utilizzo Coro di Laurea Codice inegnamento Email docente Anno accademico N46
Tecnologie Informatiche per l Automazione Indutriale Prof. Gianmaria De Tommai Regolatori PID indutriali: Leggi di controllo e utilizzo Coro di Laurea Codice inegnamento Email docente Anno accademico N46
Lezione 9. Schemi di controllo avanzati parte prima. F. Previdi - Controlli Automatici - Lez. 9 1
 Lezione 9. Schemi di controllo avanzati parte prima F. Previdi - Controlli Automatici - Lez. 9 Schema. Regolatori in anello aperto Controllo multivariabile:. Regolatori di diaccoppiamento 3. Controllo
Lezione 9. Schemi di controllo avanzati parte prima F. Previdi - Controlli Automatici - Lez. 9 Schema. Regolatori in anello aperto Controllo multivariabile:. Regolatori di diaccoppiamento 3. Controllo
Ing. Mariagrazia Dotoli Controlli Automatici NO (9 CFU) Antitrasformata di Laplace PROCEDIMENTI DI ANTITRASFORMAZIONE
 PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
Grandezze fisiche, vettori:
 Grandezze fiice, vettori: Generalità: oluzioni Problema di: Generalità - I0001 Sceda 3 Ripetizioni Cagliari di Manuele Atzeni - 3497702002 - info@ripetizionicagliari.it Eeguire le converioni di unità di
Grandezze fiice, vettori: Generalità: oluzioni Problema di: Generalità - I0001 Sceda 3 Ripetizioni Cagliari di Manuele Atzeni - 3497702002 - info@ripetizionicagliari.it Eeguire le converioni di unità di
DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA
 DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA Quando i oerva un atro nell'itante del uo paaggio al idiano dell'oervatore i parla di oervazioni idiane. Un atro, in
DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA Quando i oerva un atro nell'itante del uo paaggio al idiano dell'oervatore i parla di oervazioni idiane. Un atro, in
Esperienza n 6: Pendolo di Kater
 Eperienza n 6: Pendolo di Kater Sperimentatori: Marco Erculiani (N maricola 4549 v.o.) Ivan Noro (N matricola 458656 v.o.) Materiale a dipoizione: I materiali utilizzati per queta eperienza ono: Un pendolo
Eperienza n 6: Pendolo di Kater Sperimentatori: Marco Erculiani (N maricola 4549 v.o.) Ivan Noro (N matricola 458656 v.o.) Materiale a dipoizione: I materiali utilizzati per queta eperienza ono: Un pendolo
Ø Le funi sono dispositivi che permettono di trasmettere l azione di una forza applicata in un dato punto ad un punto diverso.
 Tenione Ø Le funi ono dipoitivi che permettono di tramettere l azione di una forza applicata in un dato punto ad un punto divero. Ø La fune viene coniderata inetenibile e priva di maa ed il modulo della
Tenione Ø Le funi ono dipoitivi che permettono di tramettere l azione di una forza applicata in un dato punto ad un punto divero. Ø La fune viene coniderata inetenibile e priva di maa ed il modulo della
Diffusione e membrane
 Eercizi di fiica per Medicina C.Patrignani, Univ. Genova (rev: 9 Ottobre 2003) 1 Diffuione e membrane 1) Calcolare il fluo avvettivo di oluto in un tubicino di ezione 0.1 mm 2 in cui corrono 0.2 ml al
Eercizi di fiica per Medicina C.Patrignani, Univ. Genova (rev: 9 Ottobre 2003) 1 Diffuione e membrane 1) Calcolare il fluo avvettivo di oluto in un tubicino di ezione 0.1 mm 2 in cui corrono 0.2 ml al
Lezione. Tecnica delle Costruzioni
 Lezione Tecnica delle otruzioni La fleione compota Verifica di ezioni oggette a fleione compota Fleione compota 1 tadio (Formule di Scienza delle otruzioni) on riferimento alla ezione omogeneizzata vale
Lezione Tecnica delle otruzioni La fleione compota Verifica di ezioni oggette a fleione compota Fleione compota 1 tadio (Formule di Scienza delle otruzioni) on riferimento alla ezione omogeneizzata vale
F = 150 N F 1 =? = 3,1 s. 3,2
 ESERCIZI SVOLTI : Principi di Newton Lavoro Energia Prof.. Marletta ITC Zanon - Udine ESERCIZIO (): Una caa di 30 kg viene tirata con una corda che forma un angolo di 50 col pavimento u una uperficie licia.
ESERCIZI SVOLTI : Principi di Newton Lavoro Energia Prof.. Marletta ITC Zanon - Udine ESERCIZIO (): Una caa di 30 kg viene tirata con una corda che forma un angolo di 50 col pavimento u una uperficie licia.
Capitolo. Semplificazioni di schemi a blocchi. 4.1 Blocchi in cascata. 4.2 Blocchi in parallelo. 4.3 Blocchi in catena chiusa (reazione negativa)
 Capitolo 4 Semplificazioni di chemi a blocchi 4. Blocchi in cacata 4. Blocchi in parallelo 4.3 Blocchi in catena chiua (reazione negativa) 4.4 Blocchi in catena chiua (reazione poitiva) 4.5 Spotamento
Capitolo 4 Semplificazioni di chemi a blocchi 4. Blocchi in cacata 4. Blocchi in parallelo 4.3 Blocchi in catena chiua (reazione negativa) 4.4 Blocchi in catena chiua (reazione poitiva) 4.5 Spotamento
Liceo Scientifico Cassini Esercizi di fisica, classe 3G, foglio7
 Liceo Scientifico Caini Eercizi di fiica, clae 3G, foglio7 Problema1 In una gara ui 200m un corridore percorre i primi 40m con un accelerazione di 1.5 m ed il reto della gara di moto rettilineo uniforme.
Liceo Scientifico Caini Eercizi di fiica, clae 3G, foglio7 Problema1 In una gara ui 200m un corridore percorre i primi 40m con un accelerazione di 1.5 m ed il reto della gara di moto rettilineo uniforme.
Politecnico di Milano
 Politecnico di Milano FONDAMENTI DI AUTOMATICA Coro di laurea in Ingegneria Getionale ez. A-D Prof. C. Piccardi prova parziale, 3//7 COGNOME: NOME: MATRICOLA: FIRMA: Vito del docente: PARTE A Voto totale
Politecnico di Milano FONDAMENTI DI AUTOMATICA Coro di laurea in Ingegneria Getionale ez. A-D Prof. C. Piccardi prova parziale, 3//7 COGNOME: NOME: MATRICOLA: FIRMA: Vito del docente: PARTE A Voto totale
Controlli automatici. Luogo delle radici. Ing. Alessandro Pisano
 Controlli autoatici uogo delle radici Ing. Aleandro iano iano@diee.unica.it Il luogo delle radici nace er riolvere il eguente roblea: Dati due olinoi () e (), deterinare coe variano, al variare del nuero
Controlli autoatici uogo delle radici Ing. Aleandro iano iano@diee.unica.it Il luogo delle radici nace er riolvere il eguente roblea: Dati due olinoi () e (), deterinare coe variano, al variare del nuero
Un sistema reazionato può essere schematizzato come combinazione di due blocchi lineari e di un circuito sommatore, così come mostrato in Fig.
 STILITÀ DEI CIRCUITI REIONTI Introduzione Un itema reazionato può eere chematizzato come combinazione di due blocchi lineari e di un circuito ommatore, coì come motrato in Fig.: E U Σ Fig.: chema a blocchi
STILITÀ DEI CIRCUITI REIONTI Introduzione Un itema reazionato può eere chematizzato come combinazione di due blocchi lineari e di un circuito ommatore, coì come motrato in Fig.: E U Σ Fig.: chema a blocchi
Dimensionamento dell impianto pneumatico di trasporto semola
 Dimenionamento dell impianto pneumatico di traporto emola Il dimenionamento viene condotto con riferimento all impianto di traporto pneumatico della emola alla linea di produzione della pata lunga Dati
Dimenionamento dell impianto pneumatico di traporto emola Il dimenionamento viene condotto con riferimento all impianto di traporto pneumatico della emola alla linea di produzione della pata lunga Dati
09. Luogo delle Radici
 Controlli Automatici 09. Luogo delle Radici Prof. Cesare Fantuzzi Ing. Cristian Secchi Ing. Federica Ferraguti ARSControl - DISMI - Università di Modena e ggio Emilia E-mail: {nome.cognome}@unimore.it
Controlli Automatici 09. Luogo delle Radici Prof. Cesare Fantuzzi Ing. Cristian Secchi Ing. Federica Ferraguti ARSControl - DISMI - Università di Modena e ggio Emilia E-mail: {nome.cognome}@unimore.it
7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo
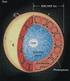 7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo Si è vito opra il trattamento generale dello cattering neutronico in mezzi infiniti. Ora conidereremo il cao della ditribuzione
7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo Si è vito opra il trattamento generale dello cattering neutronico in mezzi infiniti. Ora conidereremo il cao della ditribuzione
Un problema di dadi. Michele Impedovo
 Un problema di dadi Michele Impedovo Riaunto Quante volte, in media, occorre lanciare un dado a facce perché tutte le facce ecano almeno una volta? Per riolvere queto problema non è neceario calcolare
Un problema di dadi Michele Impedovo Riaunto Quante volte, in media, occorre lanciare un dado a facce perché tutte le facce ecano almeno una volta? Per riolvere queto problema non è neceario calcolare
