Risposte ai quesiti posti negli appelli della prima sessione LOGICA E COMUNICAZIONE, A.A , 12 CFU
|
|
|
- Violetta Scognamiglio
- 7 anni fa
- Visualizzazioni
Transcript
1 Risposte ai quesiti posti negli appelli della prima sessione LOGICA E COMUNICAZIONE, A.A , 12 CFU A) I appello (prova ridotta), 21 gennaio, primo gruppo Le risposte ai quesiti 1,2,4 sono contenute nel libro di testo. 3. Quale numero (scritto in base 10) è rappresentato dalla successione finita di bit ? Come si rappresenta in base 2 il numero 37 (in base 10)? a) La successione finita di bit in base 2 rappresenta il numero che in base 10 si scrive 36. b) Il numero che in base 10 si scrive 37 è rappresentato in base 2 dalla successione finita di bit Sia X={a,b,c} e Y={a,b,d}. Scrivi gli elementi degli insiemi X Y, X Y, X Y, (X). X Y={a,b}, X Y={a,b,c,d}, X Y={<a,a>,<a,b>,<a,c>,<b,a>,<b,b>,<b,d>, <c,a>,<c,b>,<c,d>}, (X)= {, {a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}} 6. Sia M una Macchina di Turing con queste istruzioni: <s 0,1,1,R,s 0 >, <s 0,0,1,L,s 2 >, <s 2,0,0,R,s 1 >, <s 2,1,1,L,s 2 >. Sia dato a questa macchina un nastro che abbia solo due caselle consecutive piene: (caselle vuote) (caselle vuote). Sia s 0 lo stato in cui si trova la macchina e sia la prima casella piena da sinistra a destra quella su cui è posizionato il puntatore della macchina M. c) Qual è il numero rappresentato sul nastro? d) Come è fatto il nastro e qual è lo stato della macchina dopo un passo di computazione, dopo due passi di computazione, dopo tre passi di computazione? e) Qual è il numero rappresentato sul nastro dopo tre passi di computazione? Risposta: a) Il numero rappresentato sul nastro è 1. b) Dopo un passo di computazione il nastro è (caselle vuote) (caselle vuote) e lo stato della macchina è s 0 (il puntatore è posizionato sulla casella sottolineata), dopo due passi di computazione il nastro è (caselle vuote) (caselle vuote) e lo stato della macchina è s 0 (il puntatore è posizionato sulla casella sottolineata), dopo tre passi di computazione il nastro è (caselle vuote) (caselle vuote) e lo stato della macchina è s 2 (il puntatore è posizionato sulla casella sottolineata) c) dopo tre passi di computazione sul nastro è rappresentato il numero 2. 1
2 B) I appello (prova ridotta), 21 gennaio, secondo gruppo Le risposte ai quesiti 1,2,4 sono contenute nel libro di testo. 3. Quale numero (scritto in base 10) è rappresentato dalla successione finita di bit ? Come si rappresenta in base 2 il numero 39 (in base 10)? a) La successione finita di bit in base 2 rappresenta il numero che in base 10 si scrive 38. b) Il numero che in base 10 si scrive 39 è rappresentato in base 2 dalla successione finita di bit Sia X={0,1,2} e Y={0,3,4}. Scrivi gli elementi degli insiemi X Y, X Y, X Y, (X). X Y={0}, X Y={0,1,2,3,4}, X Y={<0,0>,<0,3>,<0,4>,<1,0>,<1,3>,<1,4>, <2,0>,<2,3>,<2,4>}, (X)= {, {0},{1},{2},{0,1},{0,2},{1,2},{0,1,2}} 6. Sia M una Macchina di Turing con queste istruzioni: <s 0,1,1,R,s 0 >, <s 0,0,1,L,s 2 >, <s 2,0,0,R,s 1 >, <s 2,1,1,L,s 2 >. Sia dato a questa macchina un nastro che abbia solo due caselle consecutive piene: (caselle vuote) (caselle vuote). Sia s 0 lo stato in cui si trova la macchina e sia la seconda casella piena da sinistra a destra quella su cui è posizionato il puntatore della macchina M. b. Come è fatto il nastro e qual è lo stato della macchina dopo un passo di computazione, dopo due passi di computazione, dopo tre passi di computazione? c. Qual è il numero rappresentato sul nastro dopo tre passi di computazione? Risposta: a) il numero rappresentato sul nastro è 1 b) dopo un passo di computazione il nastro è (caselle vuote) (caselle vuote) e lo stato della macchina è s 0 (il puntatore è posizionato sulla casella sottolineata), dopo due passi di computazione il nastro è (caselle vuote) (caselle vuote) e lo stato della macchina è s 2 (il puntatore è posizionato sulla casella sottolineata), dopo tre passi di computazione il nastro è (caselle vuote) (caselle vuote) e lo stato della macchina è s 2 (il puntatore è posizionato sulla casella sottolineata) c) dopo tre passi di computazione sul nastro è rappresentato il numero 2. 2
3 C) II appello (prova intera), 22 gennaio Le risposte alle domande 1,2,3,6,7,8,9 sono contenute nel libro di testo. 4. Scrivere usando la seconda lettura odierna la seguente proposizione categorica Nessun politico trascura l opinione pubblica, fare la negazione della proposizione così ottenuta e riscrivere tale negazione in lingua italiana. a) La proposizione si scrive x:t (P(x)? Q(x)) ossia x:t ( P(x) Q(x)) dove T è il tipo di cui si parla, P sta per la proprietà essere politico, Q sta per la proprietà trascurare l opinione pubblica. b) La negazione di quella proposizione è x:t (P(x) Q(x)) c) In lingua italiana la negazione di quella proposizione si scrive Qualche politico trascura l opinione pubblica. 5. Sia A la seguente proposizione: Se Giovanni partecipa a questa prova e riceve un risultato positivo, allora consegue 12 CFU e viene valutato con un voto maggiore di 18. Analizzare A usando i connettivi classici; poi, analizzare A usando soltanto la congiunzione, la disgiunzione e la negazione classiche; infine, fare la negazione della proposizione così ottenuta e riscrivere tale negazione in lingua italiana. a) Analisi di A usando i connettivi classici: B C? D E dove B è Giovanni partecipa a questa prova, C è Giovanni riceve un risultato positivo, D è Giovanni consegue 12 CFU, D è Giovanni viene valutato con un voto maggiore di 18 b) Analisi di A usando soltanto la congiunzione, la disgiunzione e la negazione classica: ( B C) (D E ). c) Negazione della proposizione A : (B C) ( D E). d) La negazione della proposizione A in lingua italiana: Giovanni partecipa a questa prova e riceve un risultato positivo, ma non consegue 12 CFU o non viene valutato con un voto maggiore di Sia X={2,3,5,7} e Y={2,4,6}. Scrivi gli elementi degli insiemi X Y, X Y, X Y, (X). Risposta: X Y = {2}, X Y={2,3,4,5,6,7}, X Y = {<2,2>,<2,4>,<2,6>,<3,2>,<3,4>,<3,6>, <5,2>,<5,4>,<5,6>,<7,2>,<7,4>,<7,6>}, (X) = {,{2},{3},{5},{7},{2,3},{2,5},{2,7},{3,5},{3,7},{5,7},{2,3,5},{2,3,7},{2,5,7}, {3,5,7},{2,3,5,7}} 11. Sia M una Macchina di Turing con queste istruzioni: <s 0,1,1,R,s 0 >, <s 0,0,1,L,s 2 >, <s 2,0,0,R,s 1 >, <s 2,1,1,L,s 2 >. Sia dato a questa macchina un nastro che abbia solo tre caselle consecutive piene: (caselle vuote) (caselle vuote). Sia s 0 lo stato in cui si trova M e il puntatore di M sia posizionato sulla prima (da sinistra a destra) casella piena. b. Come è fatto il nastro, qual è lo stato di M e dove è posizionato il puntatore di M dopo un passo di computazione, dopo due passi di computazione, dopo tre passi di computazione, dopo quattro passi di computazione? c. Qual è il numero rappresentato sul nastro dopo quattro passi di computazione? 3
4 Risposta: a) Il numero rappresentato sul nastro è 2. b) Dopo un passo di computazione il nastro è (caselle vuote) (caselle vuote) e lo stato della macchina è s 0 (il puntatore è posizionato sulla casella sottolineata), dopo due passi di computazione il nastro è (caselle vuote) (caselle vuote) e lo stato della macchina è s 0 (il puntatore è posizionato sulla casella sottolineata), dopo tre passi di computazione il nastro è (caselle vuote) (caselle vuote) e lo stato della macchina è s 0 (il puntatore è posizionato sulla casella sottolineata), dopo quattro passi di computazione il nastro è (caselle vuote) (caselle vuote) e lo stato della macchina è s 2 (il puntatore è posizionato sulla casella sottolineata) c) dopo quattro passi di computazione sul nastro è rappresentato il numero 3. 4
5 D) III appello (prova ridotta), 19 febbraio Le risposte ai quesiti 1,2,4 sono contenute nel libro di testo. 3. Scrivi in base 10 il numero rappresentato dalla successione finita di bit ? Come si rappresenta in base 2 il numero che in base 10 è scritto 48? a) La successione finita di bit in base 2 rappresenta il numero che in base 10 si scrive 51. b) Il numero che in base 10 si scrive 48 è rappresentato in base 2 dalla successione finita di bit Sia X={3,9,7} e Y={2,7,8}. Scrivi gli elementi degli insiemi X Y, X Y, X Y, (X). X Y={7}, X Y={2,3,7,8,9}, X Y={<3,2>,<2,7>,<3,8>,<9,2>,<9,7>,<9,8>, <7,2>,<7,7>,<7,8>}, (X)= {, {3},{9},{7},{3,9},{3,7},{9,7},{2,9,7}} 6. Sia M una Macchina di Turing con queste istruzioni: <s 0,1,0,R,s 0 >, <s 0,0,0,L,s 2 >, <s 2,0,1,R,s 1 >, <s 2,1,1,L,s 2 >. Sia dato a questa macchina un nastro che abbia solo tre caselle consecutive piene: (caselle vuote) (caselle vuote). Sia s 0 lo stato in cui si trova la macchina e sia la prima casella piena da sinistra a destra quella su cui è posizionato il puntatore della macchina M. b. Dopo quanti passi di computazione la macchina raggiunge lo stato s 1? c. Qual è il numero rappresentato sul nastro quando la macchina si ferma? a. Sul nastro è rappresentato il numero 2. b. La macchina raggiunge lo stato s 1 dopo 5 passi di computazione. Dopo un passo resta nello stato s 0, il nastro è (caselle vuote) (caselle vuote), e il puntatore è sulla casella sottolineata; dopo due passi resta nello stato s 0, il nastro è (caselle vuote) (caselle vuote), e il puntatore è sulla casella sottolineata; dopo tre passi resta nello stato s 0, il nastro è (caselle vuote) (caselle vuote), e il puntatore è sulla casella sottolineata; dopo quattro passi va nello stato s 2, il nastro è (caselle vuote) (caselle vuote), e il puntatore è sulla casella sottolineata; dopo cinque passi raggiunge lo stato s 1, il nastro è (caselle vuote) (caselle vuote), e il puntatore è sulla casella sottolineata. c. Quando la macchina si ferma (ossia raggiunge lo stato s 1 ), sul nastro è rappresentato il numero 0. 5
6 E) IV appello (prova intera), 20 febbraio Le risposte alle domande 1,2,3,6,7,8,9 sono contenute nel libro di testo. 4. Scrivere usando la seconda lettura odierna la seguente proposizione categorica Qualche politico presenta le sue dimissioni, fare la negazione della proposizione così ottenuta e riscrivere tale negazione in lingua italiana. a) La proposizione si scrive x:t (P(x) Q(x)) dove T è il tipo di cui si parla, P sta per la proprietà essere politico, Q sta per la proprietà presentare le sue dimissioni. b) La negazione di quella proposizione è x:t ( P(x) Q(x)), ossia x:t(p(x)? Q(x)) c) In lingua italiana la negazione di quella proposizione si scrive Nessun politico presenta le sue dimissioni. 5. Sia A la seguente proposizione: Se Giovanni non partecipa a questa prova o non riceve un risultato positivo, e vuole conseguire 12 CFU in questo insegnamento, allora deve partecipare alla prova di giugno. Analizzare A usando i connettivi classici; poi, analizzare A usando soltanto la congiunzione, la disgiunzione e la negazione classiche; infine, fare la negazione della proposizione così ottenuta e riscrivere tale negazione in lingua italiana. 1. Analisi di A usando i connettivi classici: ( B C) D? E dove B è Giovanni partecipa a questa prova, C è Giovanni riceve un risultato positivo, D è Giovanni vuole conseguire 12 CFU, D è Giovanni deve partecipare alla prova di giugno 2. Analisi di A usando soltanto la congiunzione, la disgiunzione e la negazione classica: ((B C) D) E. 3. Negazione della proposizione A : (( B C) D) E 4. Negazione della proposizione A in lingua italiana: Giovanni non partecipa a questa prova o riceve un risultato positivo, e vuole conseguire 12 CFU in questo insegnamento, ma non deve partecipare alla prova di giugno 10. Sia X={a,b,c,d} e Y={e,f,g}. Scrivi gli elementi degli insiemi X Y, X Y, X Y, (X). X Y=, X Y={a,b,c,d,e,f,g}, X Y={<a,e>,<a,f>,<a,g>,<b,e>,<b,f>,<b,g>, <c,e>,<c,f>,<c,g>, <d,e>,<d,f>,<d,g>}, (X)= {, {a},{b},{c},{d},{a,b}, {a,c}, {a,d},{b,c},{b,d},{c,d}, {a,b,c},{a,c,d}, {a,b,d}, {b,c,d}, {a,b,c,d}} 11. Sia M una Macchina di Turing con queste istruzioni: <s 0,1,0,R,s 0 >, <s 0,0,0,L,s 2 >, <s 2,0,1,R,s 1 >, <s 2,1,1,L,s 2 >. Sia dato a questa macchina un nastro che abbia solo quattro caselle consecutive piene: (caselle vuote) (caselle vuote). Sia s 0 lo stato in cui si trova la macchina e sia la prima casella piena da sinistra a destra quella su cui è posizionato il puntatore della macchina M. b. Dopo quanti passi di computazione la macchina raggiunge lo stato s 1? c. Qual è il numero rappresentato sul nastro quando la macchina si ferma? 6
7 a. Sul nastro è rappresentato il numero 2. b. La macchina raggiunge lo stato s 1 dopo 6 passi di computazione. Dopo un passo resta nello stato s 0, il nastro è (caselle vuote) (caselle vuote), e il puntatore è sulla casella sottolineata; dopo due passi resta nello stato s 0, il nastro è (caselle vuote) (caselle vuote), e il puntatore è sulla casella sottolineata; dopo tre passi resta nello stato s 0, il nastro è (caselle vuote) (caselle vuote), e il puntatore è sulla casella sottolineata; dopo quattro passi resta nello stato s 0, il nastro è (caselle vuote) (caselle vuote), e il puntatore è sulla casella sottolineata; dopo cinque passi va nello stato s 2, il nastro è (caselle vuote) (caselle vuote), e il puntatore è sulla casella sottolineata; dopo sei passi raggiunge lo stato s 1, il nastro è (caselle vuote) (caselle vuote), e il puntatore è sulla casella sottolineata. c. Quando la macchina si ferma (ossia raggiunge lo stato s 1 ), sul nastro è rappresentato il numero 0. 7
La nozione di algoritmo
 La nozione di algoritmo Agostino Dovier Dip. di Matematica e Informatica, Univ. Udine UDINE, Aprile 2015 Agostino Dovier (DIMI) La nozione di algoritmo UDINE 1 / 17 Un algoritmo viene descritto in un certo
La nozione di algoritmo Agostino Dovier Dip. di Matematica e Informatica, Univ. Udine UDINE, Aprile 2015 Agostino Dovier (DIMI) La nozione di algoritmo UDINE 1 / 17 Un algoritmo viene descritto in un certo
Fondamenti d Informatica: Le Macchine di Turing. Barbara Re, Phd
 Fondamenti d Informatica: Le Macchine di Turing Barbara Re, Phd Esercizio 1 } Consideriamo una MdT che modifica una sequenza di A rimpiazzando ogni A in posizione dispari con una B (la prima A ha posizione
Fondamenti d Informatica: Le Macchine di Turing Barbara Re, Phd Esercizio 1 } Consideriamo una MdT che modifica una sequenza di A rimpiazzando ogni A in posizione dispari con una B (la prima A ha posizione
Logica Algoritmi Cognizione
 Logica Algoritmi Cognizione Le nozioni di DECIDIBILITÀ e COMPUTABILITÀ e i loro limiti Formulazione della logica in termini di teorie formalizzate e di dimostrazioni (all interno di teorie formalizzate)
Logica Algoritmi Cognizione Le nozioni di DECIDIBILITÀ e COMPUTABILITÀ e i loro limiti Formulazione della logica in termini di teorie formalizzate e di dimostrazioni (all interno di teorie formalizzate)
Macchine di Turing. Francesco Paoli. Istituzioni di logica, Francesco Paoli (Istituzioni di logica, ) Macchine di Turing 1 / 29
 Macchine di Turing Francesco Paoli Istituzioni di logica, 2016-17 Francesco Paoli (Istituzioni di logica, 2016-17) Macchine di Turing 1 / 29 Alan M. Turing (1912-1954) Francesco Paoli (Istituzioni di logica,
Macchine di Turing Francesco Paoli Istituzioni di logica, 2016-17 Francesco Paoli (Istituzioni di logica, 2016-17) Macchine di Turing 1 / 29 Alan M. Turing (1912-1954) Francesco Paoli (Istituzioni di logica,
Informatica teorica Lez. n 7 Macchine di Turing. Macchine di Turing. Prof. Giorgio Ausiello Università di Roma La Sapienza
 Macchine di Turing Argomenti della lezione Definizione della macchina di Turing Riconoscimento e accettazione di linguaggi Macchine a più nastri La macchina di Turing èun è automa che può leggere e scrivere
Macchine di Turing Argomenti della lezione Definizione della macchina di Turing Riconoscimento e accettazione di linguaggi Macchine a più nastri La macchina di Turing èun è automa che può leggere e scrivere
INSIEMI. DEF. Un INSIEME è una qualsiasi collezione di oggetti.
 INSIEMI DEF. Un INSIEME è una qualsiasi collezione di oggetti. Esso è ben definito quando è chiaro se un oggetto appartiene o non appartiene all insieme stesso. Esempio. E possibile definire l insieme
INSIEMI DEF. Un INSIEME è una qualsiasi collezione di oggetti. Esso è ben definito quando è chiaro se un oggetto appartiene o non appartiene all insieme stesso. Esempio. E possibile definire l insieme
Sesto modulo: Logica Obiettivi 1. individuare dei "calcoli logici" che consentano di meccanizzare l attività deduttiva
 Sesto modulo: Logica Obiettivi 1. individuare dei "calcoli logici" che consentano di meccanizzare l attività deduttiva 2. stabilire quali ragionamenti sono corretti e quali no 3. distinguere tra condizione
Sesto modulo: Logica Obiettivi 1. individuare dei "calcoli logici" che consentano di meccanizzare l attività deduttiva 2. stabilire quali ragionamenti sono corretti e quali no 3. distinguere tra condizione
Macchina di Turing ... !!... !!! a b b! b a! Nastro di Input. testina. s t q i. s r. Unità di Controllo q j S / D / F
 Macchina di Turing Nastro di Input...!!! a b b! b a! testina!!... s r s t q i Unità di Controllo q j Q S / D / F P Definizione Formale Una macchina di Turing deterministica è una sestupla
Macchina di Turing Nastro di Input...!!! a b b! b a! testina!!... s r s t q i Unità di Controllo q j Q S / D / F P Definizione Formale Una macchina di Turing deterministica è una sestupla
Prerequisiti Matematici
 Prerequisiti Matematici Richiami di teoria degli insiemi Relazioni d ordine, d equivalenza Richiami di logica Logica proposizionale, tabelle di verità, calcolo dei predicati Importante: Principio di Induzione
Prerequisiti Matematici Richiami di teoria degli insiemi Relazioni d ordine, d equivalenza Richiami di logica Logica proposizionale, tabelle di verità, calcolo dei predicati Importante: Principio di Induzione
MODULO 1. Prof. Onofrio Greco. Prof. Greco Onofrio
 ECDL MODULO 1 Prof. Onofrio Greco Modulo 1 Concetti di base dell ICT Modulo 2 Uso del Computer e Gestione dei File Modulo 3 - Elaborazione testi Modulo 4 Foglio Elettronico Modulo 5 Uso delle Basi di Dati
ECDL MODULO 1 Prof. Onofrio Greco Modulo 1 Concetti di base dell ICT Modulo 2 Uso del Computer e Gestione dei File Modulo 3 - Elaborazione testi Modulo 4 Foglio Elettronico Modulo 5 Uso delle Basi di Dati
Testi di esame precedenti a.a. e soluzioni
 Fondamenti di Informatica mod. 2 2018/2019 M.Di Ianni Testi di esame precedenti a.a. e soluzioni 1 Problemi Problema 6.1: Dimostrare che, per ogni costante intera positiva k, 2 nk è una funzione time-constructible.
Fondamenti di Informatica mod. 2 2018/2019 M.Di Ianni Testi di esame precedenti a.a. e soluzioni 1 Problemi Problema 6.1: Dimostrare che, per ogni costante intera positiva k, 2 nk è una funzione time-constructible.
Logica degli enunciati; Operazioni con le proposizioni; Proprietà delle operazioni logiche; Tautologie; Regole di deduzione; Logica dei predicati;
 Logica degli enunciati; Operazioni con le proposizioni; Proprietà delle operazioni logiche; Tautologie; Regole di deduzione; Logica dei predicati; Implicazione logica. Equivalenza logica; Condizione necessaria,
Logica degli enunciati; Operazioni con le proposizioni; Proprietà delle operazioni logiche; Tautologie; Regole di deduzione; Logica dei predicati; Implicazione logica. Equivalenza logica; Condizione necessaria,
Due tipi di logica. Gianluigi Bellin
 Due tipi di logica Gianluigi Bellin 15 Novembre 2012 Calcolo dei sequenti LK, logica classica. axiom Γ, A A, A, Γ Γ, A R Γ, A L A, Γ R Γ, A Γ, B Γ, A B A, B, Γ L A B, Γ A, Γ B, Γ, A B, Γ R Γ A B, L Γ,
Due tipi di logica Gianluigi Bellin 15 Novembre 2012 Calcolo dei sequenti LK, logica classica. axiom Γ, A A, A, Γ Γ, A R Γ, A L A, Γ R Γ, A Γ, B Γ, A B A, B, Γ L A B, Γ A, Γ B, Γ, A B, Γ R Γ A B, L Γ,
Capitolo 5: Macchine di Turing e calcolabilitá secondo Turing
 Capitolo 5: Macchine di Turing e calcolabilitá secondo Turing 1 Macchina di Turing (MDT ) Un dispositivo che accede a un nastro (potenzialmente) illimitato diviso in celle contenenti ciascuna un simbolo
Capitolo 5: Macchine di Turing e calcolabilitá secondo Turing 1 Macchina di Turing (MDT ) Un dispositivo che accede a un nastro (potenzialmente) illimitato diviso in celle contenenti ciascuna un simbolo
Informatica e Laboratorio di Programmazione Automi Alberto Ferrari. Alberto Ferrari Informatica e Laboratorio di Programmazione
 Informatica e Laboratorio di Programmazione Automi Alberto Ferrari Alberto Ferrari Informatica e Laboratorio di Programmazione automa o automa: macchina astratta o realizza un certo algoritmo, secondo
Informatica e Laboratorio di Programmazione Automi Alberto Ferrari Alberto Ferrari Informatica e Laboratorio di Programmazione automa o automa: macchina astratta o realizza un certo algoritmo, secondo
Corso di Elementi di Informatica Anno accademico 2015/16
 Corso di Laurea triennale in Ingegneria Navale in condivisione con Corso di Laurea triennale in Ingegneria Chimica (matr. P-Z) Corso di Elementi di Informatica Anno accademico 2015/16 Docente: Ing. Alessandra
Corso di Laurea triennale in Ingegneria Navale in condivisione con Corso di Laurea triennale in Ingegneria Chimica (matr. P-Z) Corso di Elementi di Informatica Anno accademico 2015/16 Docente: Ing. Alessandra
Turing cercò di fornire una risposta matematica al problema CHE COSA SIGNIFICA CALCOLARE?
 STORIA DELLE CONOSCENZE SCIENTIFICHE SULL UOMO E SULLA NATURA a.a. 2016 2017 Prof. Roberto Giuntini, PhD. Introduzione alla storia dell intelligenza artificiale e della robotica Modulo II: Le macchine
STORIA DELLE CONOSCENZE SCIENTIFICHE SULL UOMO E SULLA NATURA a.a. 2016 2017 Prof. Roberto Giuntini, PhD. Introduzione alla storia dell intelligenza artificiale e della robotica Modulo II: Le macchine
ALGORITMI E COMPLESSITA COMPUTAZIONALI LA MACCHINA DI TURING.
 ALGORITMI E COMPLESSITA COMPUTAZIONALI LA MACCHINA I TURING francesca.piersigilli@unicam.it MACCHINA I TURING (MdT) Nel 936 il matematico inglese Alan Turing propose l'idea di una macchina immaginaria
ALGORITMI E COMPLESSITA COMPUTAZIONALI LA MACCHINA I TURING francesca.piersigilli@unicam.it MACCHINA I TURING (MdT) Nel 936 il matematico inglese Alan Turing propose l'idea di una macchina immaginaria
Metodo alternativo per il calcolo delle divisioni.
 Metodo alternativo per il calcolo delle divisioni. A cura di Eugenio Amitrano Contenuto dell articolo: 1. Introduzione........ 2 2. Descrizione......... 2 3. Conclusioni......... 1. Introduzione Il presente
Metodo alternativo per il calcolo delle divisioni. A cura di Eugenio Amitrano Contenuto dell articolo: 1. Introduzione........ 2 2. Descrizione......... 2 3. Conclusioni......... 1. Introduzione Il presente
VALORE MINIMO DEL RENDIMENTO DI COMBUSTIONE DEI GENERATORI DI CALORE RILEVABILE NEL CORSO DEI CONTROLLI DI EFFICIENZA ENERGETICA
 compresa fra lo 01.01.1998 e il 15 84,4 86,4 86,4 89,3 92,2 91,4 89,4 15,5 84,4 86,4 86,4 89,3 92,2 91,4 89,4 16 84,4 86,4 86,4 89,3 92,2 91,4 89,4 16,5 84,4 86,4 86,4 89,3 92,2 91,4 89,4 17 84,5 86,5
compresa fra lo 01.01.1998 e il 15 84,4 86,4 86,4 89,3 92,2 91,4 89,4 15,5 84,4 86,4 86,4 89,3 92,2 91,4 89,4 16 84,4 86,4 86,4 89,3 92,2 91,4 89,4 16,5 84,4 86,4 86,4 89,3 92,2 91,4 89,4 17 84,5 86,5
Cenni di Logica. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Cenni di Logica Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Cenni di Logica Analisi Matematica 1 1 / 15 Scopo: introdurre nozioni di logica & terminologia
Cenni di Logica Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Cenni di Logica Analisi Matematica 1 1 / 15 Scopo: introdurre nozioni di logica & terminologia
LIBRO ADOTTATO. A. FACCHINI: ALGEBRA E MATEMATICA DISCRETA, ed. ZANICHELLI LIBRI CONSIGLIATI
 LIBRO ADOTTATO A. FACCHINI: ALGEBRA E MATEMATICA DISCRETA, ed. ZANICHELLI LIBRI CONSIGLIATI G.M. PIACENTINI CATTANEO: MATEMATICA DISCRETA, ed. ZANICHELLI C. COSTANTINO, P. LONGOBARDI, M. MAJ, C. NICOTERA:
LIBRO ADOTTATO A. FACCHINI: ALGEBRA E MATEMATICA DISCRETA, ed. ZANICHELLI LIBRI CONSIGLIATI G.M. PIACENTINI CATTANEO: MATEMATICA DISCRETA, ed. ZANICHELLI C. COSTANTINO, P. LONGOBARDI, M. MAJ, C. NICOTERA:
Circuiti digitali combinatori
 Circuiti digitali combinatori Parte 1 Definizioni George Boole George Boole (Lincoln, 2 novembre 1815 Ballintemple, 8 dicembre 1864) Matematico e logico britannico Considerato il fondatore della logica
Circuiti digitali combinatori Parte 1 Definizioni George Boole George Boole (Lincoln, 2 novembre 1815 Ballintemple, 8 dicembre 1864) Matematico e logico britannico Considerato il fondatore della logica
La logica (dal greco logos=ragione/parola) è la scienza del ragionamento. Nasce come branca della filosofia e dall'ottocento in poi diviene campo di
 La logica (dal greco logos=ragione/parola) è la scienza del ragionamento. Nasce come branca della filosofia e dall'ottocento in poi diviene campo di studio da parte anche dei matematici. LE PROPOSIZIONI
La logica (dal greco logos=ragione/parola) è la scienza del ragionamento. Nasce come branca della filosofia e dall'ottocento in poi diviene campo di studio da parte anche dei matematici. LE PROPOSIZIONI
LOGICA PER LA PROGRAMMAZIONE a.a. 2016/17 Seconda esercitazione - 11/10/16 - Soluzioni Proposte
 LOGICA ER LA ROGRAMMAZIONE a.a. 2016/17 Seconda esercitazione - 11/10/16 - Soluzioni roposte 1. Nei seguenti passi di dimostrazione, indicare il connettivo logico corretto da sostituire a? applicando il
LOGICA ER LA ROGRAMMAZIONE a.a. 2016/17 Seconda esercitazione - 11/10/16 - Soluzioni roposte 1. Nei seguenti passi di dimostrazione, indicare il connettivo logico corretto da sostituire a? applicando il
Curriculum AMMINISTRAZIONE E CONTROLLO STRATEGICO I anno (63 CFU)
 CORSO DI LAUREA MAGISTRALE IN STRATEGIA E CONSULENZA AZIENDALE CLASSE LM-77 PIANO DEGLI STUDI per gli studenti che si iscrivono al I anno nell a.a.2019/2020 Il Corso di laurea magistrale in Strategia e
CORSO DI LAUREA MAGISTRALE IN STRATEGIA E CONSULENZA AZIENDALE CLASSE LM-77 PIANO DEGLI STUDI per gli studenti che si iscrivono al I anno nell a.a.2019/2020 Il Corso di laurea magistrale in Strategia e
Macchine di TURING. Alan Mathison Turing ( )
 Macchine di TURING Alan Mathison Turing (1912 1954) Macchine di TURING Alan Mathison Turing (1912 1954) matematico, logico e crittanalista britannico, considerato uno dei padri dell informatica e uno dei
Macchine di TURING Alan Mathison Turing (1912 1954) Macchine di TURING Alan Mathison Turing (1912 1954) matematico, logico e crittanalista britannico, considerato uno dei padri dell informatica e uno dei
INSEGNAMENTI OPZIONALI GRUPPO 1
 CORSO DI LAUREA MAGISTRALE IN STRATEGIA E CONSULENZA AZIENDALE CLASSE LM-77 PIANO DEGLI STUDI per gli studenti che si iscrivono al I anno nell a.a.2018/19 Il Corso di laurea magistrale in Strategia e Consulenza
CORSO DI LAUREA MAGISTRALE IN STRATEGIA E CONSULENZA AZIENDALE CLASSE LM-77 PIANO DEGLI STUDI per gli studenti che si iscrivono al I anno nell a.a.2018/19 Il Corso di laurea magistrale in Strategia e Consulenza
Fondamenti di Informatica. Ipotesi fondamentale. Irrisolubilità. Prof. V.L. Plantamura Informatica e Comunicazione Digitale a.a.
 Fondamenti di Informatica Prof. V.L. Plantamura Informatica e Comunicazione Digitale a.a. 2006-2007 Ipotesi fondamentale Tesi di Church Qualunque algoritmo può essere espresso sotto forma di matrice funzionale
Fondamenti di Informatica Prof. V.L. Plantamura Informatica e Comunicazione Digitale a.a. 2006-2007 Ipotesi fondamentale Tesi di Church Qualunque algoritmo può essere espresso sotto forma di matrice funzionale
Macchina di Turing. La macchina di Turing e la realizzazione di una automa ed è costituita da:
 Macchina di Turing La macchina di Turing e la realizzazione di una automa ed è costituita da: a) un nastro illimitato suddiviso in caselle; b) una testina di lettura/scrittura; c) un organo di controllo
Macchina di Turing La macchina di Turing e la realizzazione di una automa ed è costituita da: a) un nastro illimitato suddiviso in caselle; b) una testina di lettura/scrittura; c) un organo di controllo
Sommario Codifica dei dati Macchina Astratta Definizioni Esempi
 Sommario Codifica dei dati Macchina Astratta Definizioni Esempi 1 2 Codifica dei dati È possibile introdurre la teoria della computabilità facendo riferimento ad algoritmi che elaborano numeri naturali
Sommario Codifica dei dati Macchina Astratta Definizioni Esempi 1 2 Codifica dei dati È possibile introdurre la teoria della computabilità facendo riferimento ad algoritmi che elaborano numeri naturali
Analizzatori sintattici a discesa ricorsiva
 Analizzatori sintattici a discesa ricorsiva E uno schema di analizzatore che sfrutta la descrizione grammaticale in EBNF adatto a grammatiche LL(1). Si basa sulla scrittura di procedure ricorsive ricavate
Analizzatori sintattici a discesa ricorsiva E uno schema di analizzatore che sfrutta la descrizione grammaticale in EBNF adatto a grammatiche LL(1). Si basa sulla scrittura di procedure ricorsive ricavate
Il metodo di eliminazione di Fermat.
 Il metodo di eliminazione di Fermat. Un passo essenziale del metodo delle tangenti di Descartes consiste nell eliminazione della variabile tra due equazioni: quella della curva di cui si vuole trovare
Il metodo di eliminazione di Fermat. Un passo essenziale del metodo delle tangenti di Descartes consiste nell eliminazione della variabile tra due equazioni: quella della curva di cui si vuole trovare
Esercizi con catene di Markov Pietro Caputo 12 dicembre 2006
 Esercizi con catene di Markov Pietro Caputo dicembre 006 Esercizio. Si considerino i lanci di un dado (6 facce equiprobabili). Sia X n il minimo tra i risultati ottenuti nei lanci,,..., n. Si calcoli la
Esercizi con catene di Markov Pietro Caputo dicembre 006 Esercizio. Si considerino i lanci di un dado (6 facce equiprobabili). Sia X n il minimo tra i risultati ottenuti nei lanci,,..., n. Si calcoli la
LA LOGICA ESERCIZI. Indica quali, fra le seguenti frasi, sono proposizioni logiche e attribuisci a queste ultime il relativo valore di verità.
 LA LOGICA 1. Le proposizioni logiche ESERCIZI Indica quali, fra le seguenti frasi, sono proposizioni logiche e attribuisci a queste ultime il relativo valore di verità. 1 A «1 1 è uguale a 5»; «Non si
LA LOGICA 1. Le proposizioni logiche ESERCIZI Indica quali, fra le seguenti frasi, sono proposizioni logiche e attribuisci a queste ultime il relativo valore di verità. 1 A «1 1 è uguale a 5»; «Non si
Linguaggio della Matematica
 Linguaggio della Matematica concetti primitivi: elementi fondamentali di natura intuitiva (punto, retta, insieme, elemento di un insieme,...). assiomi: enunciati, proposizioni vere a priori (gli assiomi
Linguaggio della Matematica concetti primitivi: elementi fondamentali di natura intuitiva (punto, retta, insieme, elemento di un insieme,...). assiomi: enunciati, proposizioni vere a priori (gli assiomi
Operatori di relazione
 Condizioni Negli algoritmi compaiono passi decisionali che contengono una proposizione (o predicato) dal cui valore di verità dipende la sequenza dinamica Chiamiamo condizioni tali proposizioni Nei casi
Condizioni Negli algoritmi compaiono passi decisionali che contengono una proposizione (o predicato) dal cui valore di verità dipende la sequenza dinamica Chiamiamo condizioni tali proposizioni Nei casi
LOGICA e INSIEMISTICA
 LOGICA e INSIEMISTICA Prof. Enrico Terrone A. S: 2008/09 Definizioni La logica è una parte speciale della matematica che si occupa, anziché dei numeri, delle proposizioni. Una proposizione è una frase
LOGICA e INSIEMISTICA Prof. Enrico Terrone A. S: 2008/09 Definizioni La logica è una parte speciale della matematica che si occupa, anziché dei numeri, delle proposizioni. Una proposizione è una frase
Automi e Macchine. Computabilità. Progetto Nazionale Lauree Scientifiche Licei Fracastoro e Messedaglia Verona, novembre/dicembre 2012.
 Automi e Macchine Computabilità Progetto Nazionale Lauree Scientifiche Licei Fracastoro e Messedaglia Verona, novembre/dicembre 2012 Computabilità AA 2012/13 Ugo Solitro Sommario Introduzione Automi a
Automi e Macchine Computabilità Progetto Nazionale Lauree Scientifiche Licei Fracastoro e Messedaglia Verona, novembre/dicembre 2012 Computabilità AA 2012/13 Ugo Solitro Sommario Introduzione Automi a
Algoritmi e Complessità
 Algoritmi e Complessità Università di Camerino Corso di Laurea in Informatica (tecnologie informatiche) III periodo didattico Docente: Emanuela Merelli Email:emanuela.merelli@unicam.it a.a. 2002-03 e.merelli
Algoritmi e Complessità Università di Camerino Corso di Laurea in Informatica (tecnologie informatiche) III periodo didattico Docente: Emanuela Merelli Email:emanuela.merelli@unicam.it a.a. 2002-03 e.merelli
7. A che serve il calcolo dei sequenti? Dà procedura di decisione
 7. A che serve il calcolo dei sequenti? Dà procedura di decisione Il calcolo dei sequenti serve a costruire alberi di derivazione come ad esempio ax-id P, Q Q P&Q Q & S ax-id P, Q P P&Q P P&Q Q&P & S &
7. A che serve il calcolo dei sequenti? Dà procedura di decisione Il calcolo dei sequenti serve a costruire alberi di derivazione come ad esempio ax-id P, Q Q P&Q Q & S ax-id P, Q P P&Q P P&Q Q&P & S &
Nome: Cognome: Matr.: Fila: Posto:
 Nome: Cognome: Matr.: Fila: Posto: Parte C C/Esercizio 1 (4 punti) Scrivere una funzione match con due puntatori a stringa come parametri. Il primo è il testo che si vuole riconoscere, il secondo è il
Nome: Cognome: Matr.: Fila: Posto: Parte C C/Esercizio 1 (4 punti) Scrivere una funzione match con due puntatori a stringa come parametri. Il primo è il testo che si vuole riconoscere, il secondo è il
NOZIONI DI LOGICA. Premessa
 NOZIONI DI LOGICA Premessa Il compito principale della logica è quello di studiare il nesso di conseguenza logica tra proposizioni, predisponendo delle tecniche per determinare quando la verità di una
NOZIONI DI LOGICA Premessa Il compito principale della logica è quello di studiare il nesso di conseguenza logica tra proposizioni, predisponendo delle tecniche per determinare quando la verità di una
Linguaggio della Matematica
 Linguaggio della Matematica concetti primitivi: elementi fondamentali di natura intuitiva (punto, retta, insieme, elemento di un insieme,...). assiomi: enunciati, proposizioni vere a priori (gli assiomi
Linguaggio della Matematica concetti primitivi: elementi fondamentali di natura intuitiva (punto, retta, insieme, elemento di un insieme,...). assiomi: enunciati, proposizioni vere a priori (gli assiomi
Scelte ed alternative
 Scelte ed alternative Condizioni complesse Operatori booleani Operatori booleani in C Esercizio proposto Verifica della soluzione 2 Condizioni complesse Logica Booleana Le condizioni semplici (es. confronti)
Scelte ed alternative Condizioni complesse Operatori booleani Operatori booleani in C Esercizio proposto Verifica della soluzione 2 Condizioni complesse Logica Booleana Le condizioni semplici (es. confronti)
Sviluppo di programmi
 Sviluppo di programmi FASE 1: Dare un nome al problema partendo dall analisi del problema FASE 2: Scrivere la specifica funzionale FASE 3: Scrittura dell algoritmo FASE 3.1: Introduzione delle variabili
Sviluppo di programmi FASE 1: Dare un nome al problema partendo dall analisi del problema FASE 2: Scrivere la specifica funzionale FASE 3: Scrittura dell algoritmo FASE 3.1: Introduzione delle variabili
Logica e filosofia della scienza (P) 6 CFU
 Logica e filosofia della scienza (P) 6 CFU Anno Accademico 2010-2011 Corso di laurea in Scienze della comunicazione Ivan Valbusa ivan.valbusa@univr.it Dipartimento di Filosofia, Pedagogia e Psicologia
Logica e filosofia della scienza (P) 6 CFU Anno Accademico 2010-2011 Corso di laurea in Scienze della comunicazione Ivan Valbusa ivan.valbusa@univr.it Dipartimento di Filosofia, Pedagogia e Psicologia
Introduzione alla logica matematica
 Introduzione alla logica matematica, Paolo Bison, A.A. 2004-05, 2004-10-26 p.1/29 Introduzione alla logica matematica Silvana Badaloni Paolo Bison Fondamenti di Informatica 1 A.A. 2004/05 Università di
Introduzione alla logica matematica, Paolo Bison, A.A. 2004-05, 2004-10-26 p.1/29 Introduzione alla logica matematica Silvana Badaloni Paolo Bison Fondamenti di Informatica 1 A.A. 2004/05 Università di
1 IL LINGUAGGIO MATEMATICO
 1 IL LINGUAGGIO MATEMATICO Il linguaggio matematico moderno è basato su due concetti fondamentali: la teoria degli insiemi e la logica delle proposizioni. La teoria degli insiemi ci assicura che gli oggetti
1 IL LINGUAGGIO MATEMATICO Il linguaggio matematico moderno è basato su due concetti fondamentali: la teoria degli insiemi e la logica delle proposizioni. La teoria degli insiemi ci assicura che gli oggetti
si vuole verificare: P5: pioverà
 Logica matematica ntroduzione alla logica matematica ilvana adaloni Paolo ison Fondamenti di nformatica AA 20004 niversità di Padova formalizzazione dei meccanismi di ragionamento la logica studia proposizioni
Logica matematica ntroduzione alla logica matematica ilvana adaloni Paolo ison Fondamenti di nformatica AA 20004 niversità di Padova formalizzazione dei meccanismi di ragionamento la logica studia proposizioni
Cenni di logica e calcolo proposizionale
 Cenni di logica e calcolo proposizionale Corso di Laurea in Informatica Università degli Studi di Bari (sede Brindisi) Analisi Matematica S.Milella (sabina.milella@uniba.it) Cenni di logica 1 / 10 Proposizioni
Cenni di logica e calcolo proposizionale Corso di Laurea in Informatica Università degli Studi di Bari (sede Brindisi) Analisi Matematica S.Milella (sabina.milella@uniba.it) Cenni di logica 1 / 10 Proposizioni
Elementi di Informatica A. A. 2016/2017
 Elementi di Informatica A. A. 2016/2017 Ing. Nicola Amatucci Università degli studi di Napoli Federico II Scuola Politecnica e Delle Scienze di Base nicola.amatucci@unina.it Algebra di Boole Elementi di
Elementi di Informatica A. A. 2016/2017 Ing. Nicola Amatucci Università degli studi di Napoli Federico II Scuola Politecnica e Delle Scienze di Base nicola.amatucci@unina.it Algebra di Boole Elementi di
ELEMENTI DI LOGICA. Siano p e q le due proposizioni: p: 3 è un numero primo q: 20 è divisibile per 5 Enunciare le proposizioni p q, p q.
 ELEMENTI DI LOGICA Proposizioni e operazioni 2 3 4 Stabilire quali di queste frasi sono proposizioni logiche e stabilirne il valore di verità: a) 5 è un numero dispari b) Napoli è il capoluogo della Campania
ELEMENTI DI LOGICA Proposizioni e operazioni 2 3 4 Stabilire quali di queste frasi sono proposizioni logiche e stabilirne il valore di verità: a) 5 è un numero dispari b) Napoli è il capoluogo della Campania
SIMULAZIONE I appello 20 dicembre 2018
 SIMULAZIONE I appello 20 dicembre 2018 nome: cognome: - Scrivere in modo CHIARO. Elaborati illegibili non saranno considerati. - NON si contano le BRUTTE copie. - Si ricorda di ESPLICITARE l uso della
SIMULAZIONE I appello 20 dicembre 2018 nome: cognome: - Scrivere in modo CHIARO. Elaborati illegibili non saranno considerati. - NON si contano le BRUTTE copie. - Si ricorda di ESPLICITARE l uso della
3.Consigli su come formalizzare in linguaggio formale
 3.Consigli su come formalizzare in linguaggio formale Riportiamo qui brevemente alcuni suggerimenti dell uso dei segni formali di congiunzione e implicazione e come tradurre alcuni enunciati in forma negativa.
3.Consigli su come formalizzare in linguaggio formale Riportiamo qui brevemente alcuni suggerimenti dell uso dei segni formali di congiunzione e implicazione e come tradurre alcuni enunciati in forma negativa.
Elementi di Algebra e Logica Determinare la tavola della verità di ciascuna delle seguenti forme proposizionali:
 Elementi di Algebra e Logica 2008. 8. Logica. 1. Determinare la tavola della verità di ciascuna delle seguenti forme proposizionali: (a) p ( q r); (b) p (q r); (c) (p q) ( p r); (d) (p q) ( p r); (e) (p
Elementi di Algebra e Logica 2008. 8. Logica. 1. Determinare la tavola della verità di ciascuna delle seguenti forme proposizionali: (a) p ( q r); (b) p (q r); (c) (p q) ( p r); (d) (p q) ( p r); (e) (p
Elementi di Logica Teoria degli insiemi
 Precorso di Analisi Matematica Facoltà d'ingegneria Università del Salento Elementi di Logica Teoria degli insiemi Proff. A. Albanese E. Mangino Dipartimento di Matematica e Fisica E. De Giorgi - Università
Precorso di Analisi Matematica Facoltà d'ingegneria Università del Salento Elementi di Logica Teoria degli insiemi Proff. A. Albanese E. Mangino Dipartimento di Matematica e Fisica E. De Giorgi - Università
Informatica/ Ing. Meccanica/ Edile/ Prof. Verdicchio/ 25/02/2016/ Foglio delle domande / VERSIONE 1
 Informatica/ Ing. Meccanica/ Edile/ Prof. Verdicchio/ 25/02/2016/ Foglio delle domande/ VERSIONE 1 1) In Python, se scrivo v = [ ] in un programma, vuol dire che a) v è un quadrato b) v è una list c) v
Informatica/ Ing. Meccanica/ Edile/ Prof. Verdicchio/ 25/02/2016/ Foglio delle domande/ VERSIONE 1 1) In Python, se scrivo v = [ ] in un programma, vuol dire che a) v è un quadrato b) v è una list c) v
Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica
 Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica Soluzione del compito di Matematica Discreta 1 del 25 luglio 200 1. Qual è il numero di applicazioni f : A = {1,..., 5} B
Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica Soluzione del compito di Matematica Discreta 1 del 25 luglio 200 1. Qual è il numero di applicazioni f : A = {1,..., 5} B
Macchina di Turing. Dipartimento di Elettronica e Informazione Politecnico di Milano. 17 marzo 2017
 Macchina di Turing Dipartimento di Elettronica e Informazione Politecnico di Milano 17 marzo 2017 Un modello di calcolo universale Macchina di Turing Gli AP sono più potenti degli FSA (= maggiori capacità
Macchina di Turing Dipartimento di Elettronica e Informazione Politecnico di Milano 17 marzo 2017 Un modello di calcolo universale Macchina di Turing Gli AP sono più potenti degli FSA (= maggiori capacità
Economia aziendale: presentazione del corso a.a Prof. Guido Modugno
 1 Economia aziendale: presentazione del corso a.a. 2018-19 Prof. Guido Modugno guido.modugno@deams.units.it 2 Mettere in grado lo studente di capire e analizzare il bilancio di una società OBIETTIVI DEL
1 Economia aziendale: presentazione del corso a.a. 2018-19 Prof. Guido Modugno guido.modugno@deams.units.it 2 Mettere in grado lo studente di capire e analizzare il bilancio di una società OBIETTIVI DEL
Algebra di Boole. Modulo 2. Università di Cagliari Dipartimento di Ingegneria Elettrica ed Elettronica Laboratorio di Elettronica (EOLAB)
 Algebra di Boole Modulo 2 Università di Cagliari Dipartimento di Ingegneria Elettrica ed Elettronica Laboratorio di Elettronica (EOLAB) Algebra di Boole L algebra di Boole o della commutazione è lo strumento
Algebra di Boole Modulo 2 Università di Cagliari Dipartimento di Ingegneria Elettrica ed Elettronica Laboratorio di Elettronica (EOLAB) Algebra di Boole L algebra di Boole o della commutazione è lo strumento
Anno 1. Definizione di Logica e operazioni logiche
 Anno 1 Definizione di Logica e operazioni logiche 1 Introduzione In questa lezione ci occuperemo di descrivere la definizione di logica matematica e di operazioni logiche. Che cos è la logica matematica?
Anno 1 Definizione di Logica e operazioni logiche 1 Introduzione In questa lezione ci occuperemo di descrivere la definizione di logica matematica e di operazioni logiche. Che cos è la logica matematica?
Logica e fondamenti di matematica
 Logica e fondamenti di matematica Docente: Prof. Roberto Giuntini (giuntini@unica.it) Logica proposizionale Logica e teoria dell argomantazione. Cap. 1: Enunciati. Enunciato: Non ogni discorso è dichiarativo
Logica e fondamenti di matematica Docente: Prof. Roberto Giuntini (giuntini@unica.it) Logica proposizionale Logica e teoria dell argomantazione. Cap. 1: Enunciati. Enunciato: Non ogni discorso è dichiarativo
SIMULAZIONE I appello 11 gennaio 2018
 SIMULAZIONE I appello 11 gennaio 2018 nome: cognome: - Scrivere in modo CHIARO. Elaborati illegibili non saranno considerati. - NON si contano le BRUTTE copie. - Si ricorda di ESPLICITARE l uso della regola
SIMULAZIONE I appello 11 gennaio 2018 nome: cognome: - Scrivere in modo CHIARO. Elaborati illegibili non saranno considerati. - NON si contano le BRUTTE copie. - Si ricorda di ESPLICITARE l uso della regola
Macchine di Turing: somma di due numeri
 Informatica Teorica 2/2 M.Di Ianni Macchine di Turing: somma di due numeri Vogliamo definire una macchina di Turing che, presi in input due numeri n e m espressi in notazione binaria, calcola il valore
Informatica Teorica 2/2 M.Di Ianni Macchine di Turing: somma di due numeri Vogliamo definire una macchina di Turing che, presi in input due numeri n e m espressi in notazione binaria, calcola il valore
Fondamenti di informatica Esercizi Svolti Macchine di Turing. Realizzati da: Roberto Quaranta Matr
 Fondamenti di informatica Esercizi Svolti Macchine di Turing Realizzati da: Roberto Quaranta Matr. 449028 Macchina di Turing che calcola la funzione Max(x, y) Q= {q 0, q 1, q 2, q 3, q 4, q 5, q 6,q F
Fondamenti di informatica Esercizi Svolti Macchine di Turing Realizzati da: Roberto Quaranta Matr. 449028 Macchina di Turing che calcola la funzione Max(x, y) Q= {q 0, q 1, q 2, q 3, q 4, q 5, q 6,q F
Introduzione alla logica matematica. Logica matematica. Paolo Bison
 Introduzione alla logica matematica Paolo Bison Fondamenti di Informatica Ingegneria Meccanica Università di Padova A.A. 2008/09 Logica matematica formalizzazione dei meccanismi di ragionamento la logica
Introduzione alla logica matematica Paolo Bison Fondamenti di Informatica Ingegneria Meccanica Università di Padova A.A. 2008/09 Logica matematica formalizzazione dei meccanismi di ragionamento la logica
Sviluppo di programmi
 Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
a cura di Luca Cabibbo e Walter Didimo
 a cura di Luca Caio e Walter Didimo Esercizi di Informatica teorica - Luca Caio e Walter Didimo macchine di Turing a nastro singolo macchine di Turing multinastro macchine di Turing trasduttrici macchine
a cura di Luca Caio e Walter Didimo Esercizi di Informatica teorica - Luca Caio e Walter Didimo macchine di Turing a nastro singolo macchine di Turing multinastro macchine di Turing trasduttrici macchine
Elementi di logica. SCOPO: introdurre nozioni di logica & vocabolario per una corretta interpretazione delle dimostrazioni.
 Elementi di logica SCOPO: introdurre nozioni di logica & vocabolario per una corretta interpretazione delle dimostrazioni. Quantificatori: elementi fondamentali del linguaggio matematico. quantificatore
Elementi di logica SCOPO: introdurre nozioni di logica & vocabolario per una corretta interpretazione delle dimostrazioni. Quantificatori: elementi fondamentali del linguaggio matematico. quantificatore
DIMOSTRAZIONI DI EQUIVALENZE, SUI CONNETTIVI E SULL'AMBIGUITA' DELLA SINTASSI. Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini
 DIMOSTRAZIONI DI EQUIVALENZE, SUI CONNETTIVI E SULL'AMBIGUITA' DELLA SINTASSI Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini SULLE LEGGI DEL CALCOLO PROPOSIZIONALE Abbiamo visto le
DIMOSTRAZIONI DI EQUIVALENZE, SUI CONNETTIVI E SULL'AMBIGUITA' DELLA SINTASSI Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini SULLE LEGGI DEL CALCOLO PROPOSIZIONALE Abbiamo visto le
Sviluppo di programmi
 Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
Informatica/ Ing. Meccanica/ Edile/ Prof. Verdicchio/ 30/06/2016/ Foglio delle domande / VERSIONE 1
 Informatica/ Ing. Meccanica/ Edile/ Prof. Verdicchio/ 30/06/2016/ Foglio delle domande/ VERSIONE 1 1) In Python, se scrivo v = [ ] in un programma, vuol dire che a) v è un quadrato b) v è un insieme vuoto
Informatica/ Ing. Meccanica/ Edile/ Prof. Verdicchio/ 30/06/2016/ Foglio delle domande/ VERSIONE 1 1) In Python, se scrivo v = [ ] in un programma, vuol dire che a) v è un quadrato b) v è un insieme vuoto
Descrizione di un algoritmo
 Descrizione di un algoritmo Si descrive un algoritmo cercando di sintetizzare il più possibile la sua sequenza di passi; Non si utilizza un linguaggio di programmazione specifico, ma è meglio utilizzare
Descrizione di un algoritmo Si descrive un algoritmo cercando di sintetizzare il più possibile la sua sequenza di passi; Non si utilizza un linguaggio di programmazione specifico, ma è meglio utilizzare
Turing, i nastri e le macchine
 Turing, i nastri e le macchine Giochiamo con i nastri Avete a disposizione un nastro diviso in sezioni rettangolari, che chiameremo caselle, ognuna delle quali può essere vuota oppure contenere la lettera
Turing, i nastri e le macchine Giochiamo con i nastri Avete a disposizione un nastro diviso in sezioni rettangolari, che chiameremo caselle, ognuna delle quali può essere vuota oppure contenere la lettera
Analisi Matematica A CONTENUTI DEL CORSO. MODALITÀ D ESAME: Prova Scritta + Prova orale. Ingegneria Civile Ingegneria per l Ambiente e il Territorio
 Analisi Matematica A Ingegneria Civile Ingegneria per l Ambiente e il Territorio Paola Gervasio orario di ricevimento: GIO. 9:30-11:30 Edificio di via Valotti, piano terra, tel. 030-3715734 e-mail: gervasio@ing.unibs.it
Analisi Matematica A Ingegneria Civile Ingegneria per l Ambiente e il Territorio Paola Gervasio orario di ricevimento: GIO. 9:30-11:30 Edificio di via Valotti, piano terra, tel. 030-3715734 e-mail: gervasio@ing.unibs.it
15. Nozione di modello e verità di un predicato
 15. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
15. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
10 Logica classica predicativa
 10 Logica classica predicativa Dopo aver studiato la logica classica proposizionale, ovvero la logica delle proposizioni classiche, passiamo a studiare la logica classica predicativa, ovvero quella dei
10 Logica classica predicativa Dopo aver studiato la logica classica proposizionale, ovvero la logica delle proposizioni classiche, passiamo a studiare la logica classica predicativa, ovvero quella dei
Analisi Matematica A
 Analisi Matematica A Ingegneria Civile Ingegneria per l Ambiente e il Territorio Paola Gervasio orario di ricevimento: GIO. 9:30-11:30 Edificio di via Valotti, piano terra, tel. 030-3715734 e-mail: gervasio@ing.unibs.it
Analisi Matematica A Ingegneria Civile Ingegneria per l Ambiente e il Territorio Paola Gervasio orario di ricevimento: GIO. 9:30-11:30 Edificio di via Valotti, piano terra, tel. 030-3715734 e-mail: gervasio@ing.unibs.it
Cenni di logica matematica e di teoria degli insiemi. CORSI INTRODUTTIVI Dipartimento di Ingegneria di Perugia a.a. 2016/2017 Paola Rubbioni
 Cenni di logica matematica e di teoria degli insiemi CORSI INTRODUTTIVI Dipartimento di Ingegneria di Perugia a.a. 2016/2017 Paola Rubbioni 1 1 Logica matematica Corsi Introduttivi - a.a. 2016/2017 2 Serve
Cenni di logica matematica e di teoria degli insiemi CORSI INTRODUTTIVI Dipartimento di Ingegneria di Perugia a.a. 2016/2017 Paola Rubbioni 1 1 Logica matematica Corsi Introduttivi - a.a. 2016/2017 2 Serve
Cenni di logica. Hynek Kovarik. Università di Brescia. Analisi Matematica A
 Cenni di logica Hynek Kovarik Università di Brescia Analisi Matematica A Hynek Kovarik (Università di Brescia) Cenni di logica Analisi Matematica A 1 / 21 Scopo: introdurre nozioni di logica & terminologia
Cenni di logica Hynek Kovarik Università di Brescia Analisi Matematica A Hynek Kovarik (Università di Brescia) Cenni di logica Analisi Matematica A 1 / 21 Scopo: introdurre nozioni di logica & terminologia
Calcolo I, a.a Primo esonero 11 novembre k + 2 k
 Calcolo I, a.a. 015 016 Primo esonero 11 novembre 015 1) 6 punti Dimostrare per induzione che 5 n +, n 1. Se n = 1 la disuguaglianza si riduce a 5 + che è vera. Supponiamo ora che la disuguaglianza sia
Calcolo I, a.a. 015 016 Primo esonero 11 novembre 015 1) 6 punti Dimostrare per induzione che 5 n +, n 1. Se n = 1 la disuguaglianza si riduce a 5 + che è vera. Supponiamo ora che la disuguaglianza sia
4 La Logica come base di ogni scienza. 5 Alla ricerca della forma logica. logica
 4 La Logica come base di ogni scienza La Logica è alla base di ogni scienza (o teoria) in quanto è fondamento di ogni scienza non tanto per i contenuti specifici ma per la loro articolazione deduttiva.
4 La Logica come base di ogni scienza La Logica è alla base di ogni scienza (o teoria) in quanto è fondamento di ogni scienza non tanto per i contenuti specifici ma per la loro articolazione deduttiva.
Somma di numeri floating point. Algoritmi di moltiplicazione e divisione per numeri interi
 Somma di numeri floating point Algoritmi di moltiplicazione e divisione per numeri interi Standard IEEE754 " Standard IEEE754: Singola precisione (32 bit) si riescono a rappresentare numeri 2.0 10 2-38
Somma di numeri floating point Algoritmi di moltiplicazione e divisione per numeri interi Standard IEEE754 " Standard IEEE754: Singola precisione (32 bit) si riescono a rappresentare numeri 2.0 10 2-38
Fasi di creazione di un programma
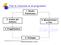 Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
Programma Annuale. Prof. Meomartino Michele
 Programma Annuale Disciplina: Tecnologie Informatiche Classe: 1F Anno Scolastico: 2017/2018 Prof. Meomartino Michele Prof. Garinetti Fabrizio Concetti dell informatica di base Terminologia generale Richiami
Programma Annuale Disciplina: Tecnologie Informatiche Classe: 1F Anno Scolastico: 2017/2018 Prof. Meomartino Michele Prof. Garinetti Fabrizio Concetti dell informatica di base Terminologia generale Richiami
9 Calcolo dei sequenti LC p
 9 Calcolo dei sequenti LC p In questa sezione mostriamo un metodo più elegante, semplice e soprattutto AUTOMATICO per mostrare se una proposizione è valida o meno e soddisfacibile o meno. Tale metodo è
9 Calcolo dei sequenti LC p In questa sezione mostriamo un metodo più elegante, semplice e soprattutto AUTOMATICO per mostrare se una proposizione è valida o meno e soddisfacibile o meno. Tale metodo è
Logica proposizionale
 Fondamenti di Informatica per la Sicurezza a.a. 2008/09 Logica proposizionale Stefano Ferrari UNIVERSITÀ DEGLI STUDI DI MILANO DIPARTIMENTO DI TECNOLOGIE DELL INFORMAZIONE Stefano Ferrari Università degli
Fondamenti di Informatica per la Sicurezza a.a. 2008/09 Logica proposizionale Stefano Ferrari UNIVERSITÀ DEGLI STUDI DI MILANO DIPARTIMENTO DI TECNOLOGIE DELL INFORMAZIONE Stefano Ferrari Università degli
Fondamenti d Informatica: Le Macchine di Turing. Barbara Re, Phd
 Fondamenti d Informatica: Le Macchine di Turing Barbara Re, Phd Agenda } Introdurremo } il formalismo delle Macchine di Turing nelle varie versioni } la nozione di calcolabilità e di decidibilità 2 La
Fondamenti d Informatica: Le Macchine di Turing Barbara Re, Phd Agenda } Introdurremo } il formalismo delle Macchine di Turing nelle varie versioni } la nozione di calcolabilità e di decidibilità 2 La
Dalla precedente lezione: LABORATORIO DI PROGRAMMAZIONE Corso di laurea in matematica 3 LA RAPPRESENTAZIONE DEI DATI (1) 28/02/2016
 LABORATORIO DI PROGRAMMAZIONE Corso di laurea in matematica 3 LA RAPPRESENTAZIONE DEI DATI (1) Marco Lapegna Dipartimento di Matematica e Applicazioni Universita degli Studi di Napoli Federico II wpage.unina.it/lapegna
LABORATORIO DI PROGRAMMAZIONE Corso di laurea in matematica 3 LA RAPPRESENTAZIONE DEI DATI (1) Marco Lapegna Dipartimento di Matematica e Applicazioni Universita degli Studi di Napoli Federico II wpage.unina.it/lapegna
15. Nozione di modello e verità di un predicato
 15. Nozione di modello e verità di un predicato Def. (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è dato
15. Nozione di modello e verità di un predicato Def. (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è dato
Cenni di logica matematica e di teoria degli insiemi Paola Rubbioni
 Cenni di logica matematica e di teoria degli insiemi Paola Rubbioni CORSI INTRODUTTIVI Dipartimento di Ingegneria di Perugia a.a. 2017/2018 1 Corsi Introduttivi - a.a. 2017/2018 2 1 Logica matematica Serve
Cenni di logica matematica e di teoria degli insiemi Paola Rubbioni CORSI INTRODUTTIVI Dipartimento di Ingegneria di Perugia a.a. 2017/2018 1 Corsi Introduttivi - a.a. 2017/2018 2 1 Logica matematica Serve
Macchina di Turing Universale
 Informatica Teorica 2010/2011 M.Di Ianni Macchina di Turing Universale Vogliamo definire una macchina di Turing U che, presi in input la descrizione di una macchina di Turing ad un nastro T ed un input
Informatica Teorica 2010/2011 M.Di Ianni Macchina di Turing Universale Vogliamo definire una macchina di Turing U che, presi in input la descrizione di una macchina di Turing ad un nastro T ed un input
Chiarificazione sulla forma delle regole del calcolo LC p
 Chiarificazione sulla forma delle regole del calcolo LC p Proviamo a spiegare un pò come mai le regole di LC p sono accettabili avvalendosi di tautologie classiche che riconosciamo grazie all utilizzo
Chiarificazione sulla forma delle regole del calcolo LC p Proviamo a spiegare un pò come mai le regole di LC p sono accettabili avvalendosi di tautologie classiche che riconosciamo grazie all utilizzo
Cenni di logica matematica e di teoria degli insiemi Paola Rubbioni
 Cenni di logica matematica e di teoria degli insiemi Paola Rubbioni CORSI INTRODUTTIVI Dipartimento di Ingegneria di Perugia a.a. 2018/2019 1 Corsi Introduttivi - a.a. 2017/2018 2 1 Logica matematica Serve
Cenni di logica matematica e di teoria degli insiemi Paola Rubbioni CORSI INTRODUTTIVI Dipartimento di Ingegneria di Perugia a.a. 2018/2019 1 Corsi Introduttivi - a.a. 2017/2018 2 1 Logica matematica Serve
Calcoli dei sequenti classici e lineare
 Calcoli dei sequenti classici e lineare Gianluigi Bellin November 5, 2009 Scheda per il compito 2, scadenza rinviata al marteedì 10 novembre 2009 1 Calcolo dei sequenti classico 1.1 Linguaggio ed interpretazione
Calcoli dei sequenti classici e lineare Gianluigi Bellin November 5, 2009 Scheda per il compito 2, scadenza rinviata al marteedì 10 novembre 2009 1 Calcolo dei sequenti classico 1.1 Linguaggio ed interpretazione
Algoritmi e Principi dell'informatica Seconda Prova in Itinere - 14 Febbraio 2014
 Algoritmi e Principi dell'informatica Seconda Prova in Itinere - 14 Febbraio 2014 Nome..Cognome.Matr. Laureando Avvisi importanti Il tempo a disposizione è di 1 ora e 30 minuti. Se non verranno risolti
Algoritmi e Principi dell'informatica Seconda Prova in Itinere - 14 Febbraio 2014 Nome..Cognome.Matr. Laureando Avvisi importanti Il tempo a disposizione è di 1 ora e 30 minuti. Se non verranno risolti
L AUTOMA ESECUTORE L AUTOMA ESECUTORE
 L AUTOMA ESECUTORE Metodo Risolutivo (algoritmo) Un automa capace di ricevere dall esterno una descrizione dello algoritmo richiesto DATI Esecutore RISULTATI cioè capace di interpretare un linguaggio (linguaggio
L AUTOMA ESECUTORE Metodo Risolutivo (algoritmo) Un automa capace di ricevere dall esterno una descrizione dello algoritmo richiesto DATI Esecutore RISULTATI cioè capace di interpretare un linguaggio (linguaggio
