Sistemi di Numerazione Binaria
|
|
|
- Antonina Giannini
- 7 anni fa
- Visualizzazioni
Transcript
1 Sistemi di Numerazione Binaria BIN.1
2 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato da numerali diversi in diversi sistemi ES 156 nel sistema decimale CLVI in numeri romani Il numero di caratteri nel numerale determina l intervallo di numeri rappresentabili ES interi a 3 cifre con segno in notazione decimale: [-999,+999] BIN.2
3 Numeri a precisione finita Numero finito di cifre Si perdono alcune proprietà: chiusura operatori ( +,, ) prop. associativa, distributiva,.. ES 2 cifre decimali e segno [-99,+99] 78+36=114 (Chiusura) 60+(50-40) (60+50)-40 (Associatività) Errori di arrotondamento Buchi nella rappresentazione dei reali ES usando numerali decimali con due sole cifre frazionarie: 0? BIN.3
4 Sistemi posizionali Ciascuna cifra rappresenta il coefficiente di una potenza della base L esponente è dato dalla posizione della cifra a m a m-1... a 0. a -1 a a -k m N=Σ a i b i i=-k 0 a i b-1 b = base Se la base è b occorrono b simboli: b = 10 {0,9} b = 2 {0,1} b = 8 {0,1,... 7} b = 16 {0,1,... 9,A,B,C,D,E,F} BIN.4
5 Conversione decimale-binario Si effettuano divisioni ripetute per 2 Il resto delle divisioni fornisce le cifre del numerale binario (a partire dalla meno significativa) ES (26) 10 =(11010) cifra meno significativa cifra più significativa Altrimenti si determina ad occhio quali potenze di 2 sono contenute nel numero ES (26) 10 = BIN.5
6 Intervalli rappresentati Rappresentando gli interi positivi e lo zero in notazione binaria con n cifre (bit) si copre l intervallo [0, 2 n -1] Si sfruttano tutte le 2 n disposizioni ES n=3 [0,7] NB Anche gli 0 non significativi devono essere rappresentati BIN.6
7 Ordini di grandezza Le potenze di = 1, 2, 4, 8, 16, 32, 64, 128, 256, = 1024 ~ K 2 20 = = ~ M 2 30 = = ~ G 2 40 =... = ~ T ES 2 26 = = 64 M Il numero di bit di un indirizzo binario determina le dimensioni della memoria: CPU bit indirizzo Memoria bit 64 K bit 1 Mega bit 16 Mega bit 64 Tera Pentium 46 bit 64 Tera BIN.7
8 Interi positivi e negativi Per rappresentare gli interi relativi, a parità di cifre si dimezza l intervallo dei valori assoluti Si utilizzano varie rappresentazioni Modulo e segno un bit per il segno 0: + 1: - n-1 bit per il modulo - intervallo [-2 n-1 +1, +2 n-1-1] ES n=4 bit intervallo [-7,+7] 5 = = 1101 NB intervallo simmetrico doppia rappresentazione dello zero BIN.8
9 Complemento a 1 Si aggiunge uno 0 a sinistra alla rappresentazione dei numeri positivi Per cambiare di segno si complementa il numerale bit a bit I numerali positivi iniziano per 0, i negativi per 1 Con n bit: [-2 n-1 +1, +2 n-1-1] È una notazione posizionale: Pesi: (-2 n-1 +1) 2 n ES n=4 bit intervallo [-7, +7] 5 = = 1010 (-7+2) Complementare = cambiare segno Doppia rappresentazione dello 0 BIN.9
10 Complemento a 2 I positivi hanno la stessa rappresentazione che in complemento a 1 I negativi si ottengono sommando 1 alla loro rappresentazione in complemento a 1 Intervallo con n bit: [-2 n-1, +2 n-1-1] Peso delle cifre: -2 n-1 2 n Regola pratica per complementare: Partendo da destra si lasciano invariati tutti i bit fino al primo 1 compreso, e poi si complementa bit a bit ES n=4 bit intervallo [-8, +7] 5 = = 1011 (-8+2+1) Intervallo più esteso Una sola rappresentazione dello 0 BIN.10
11 Eccesso 2 n-1 I numeri vengono rappresentati come somma fra il numero dato e una potenza di 2. Con n bit si rappresenta l eccesso 2 n-1 Intervallo come CP2: [-2 n-1,+2 n-1-1] Regola pratica: ES I numerali si ottengono da quelli in CP2 complementando il bit più significativo n=4 bit: eccesso 8, intervallo [-8,+7] =5 : =12 : 1100 Intervallo asimmetrico Rappresentazione unica dello 0 BIN.11
12 Rappresentazioni in eccesso È possibile definire rappresentazioni in eccesso un numero qualsiasi k L eccesso una potenza di 2 è solo un caso particolare, anche se molto interessante Rappresentando un intero m in eccesso k con n bit, si rappresenta in realtà il numero positivo k+m Deve comunque essere k 2 n L intervallo dei numeri rappresentabili dipende sia da k che da n: ES [-k, 2 n -k-1] n=8, k=127 [-127,+128] n=8, k=100 [-100,+155] n=8, k=50 [-50,+205] BIN.12
13 Rappresentazioni a confronto Decimale M&S CP1 CP2 Ecc BIN.13
14 Notazione in base 16 Per i numerali esadecimali occorrono 16 cifre { 0,1,... 9,A,B,C,D,E,F } Conversione esadecimale-binario: Si fa corrispondere a ciascuna cifra esadecimale il gruppo di 4 bit che ne rappresenta il valore ES F 5 7 A Conversione binario-esadecimale: Partendo da destra si fa corrispondere a ciascun gruppo di 4 o meno cifre binarie la cifra esadecimale che ne rappresenta il valore Si usano spesso stringhe esadecimali per rappresentare stringhe binarie BIN.14
15 Numerali e numeri Un numerale è solo una stringa di cifre Un numerale rappresenta un numero solo se si specifica un sistema di numerazione Lo stesso numerale rappresenta diversi numeri in diverse notazioni ES la stringa rappresenta: Centodiecimilacento in base 10 (+52) 10 in binario naturale (-11) 10 in complemento a 1 (-12) 10 in complemento a 2 (+20) 10 in eccesso 16 In esadecimale un numero dell ordine di vari milioni BIN.15
16 Addizioni binarie Le addizioni fra numerali si effettuano cifra a cifra (come in decimale) portando il riporto alla cifra successiva = = = = 0 con il riporto di 1 ES = = 0101 Se il numero di cifre non permette di rappresentare il risultato si ha un trabocco nella propagazione del riporto BIN.16
17 Addizioni in complemento In CP2 somme e sottrazioni tra numerali sono gestite nello stesso modo, ma si deve ignorare il trabocco: = 0010 = Se i due operandi hanno segno diverso il risultato è sempre corretto: = 1111 = Se i due operandi hanno lo stesso segno e il risultato segno diverso c è errore = 0011 = ( 9 non è compreso nell intervallo ) BIN.17
18 Conversioni in eccesso 2 n-1 Dato un numero m determinare il numero minimo di cifre n min necessarie Determinare la prima potenza di 2 superiore al modulo di m e confrontarla con gli estremi dell intervallo ES convertire (-347) 10 in eccesso 2 n = 256 < 347 < 512 = 2 9 intervallo con n bit: [-2 n-1,+2 n-1-1] pertanto n min = = = (-347) 10 in eccesso 2 9 è: BIN.18
19 Conversioni in CP1 e CP2 Se il numero è negativo: a) determinare il numero di bit n b) convertire il numero positivo corrispondente in notazione a n bit c) complementare il numerale così ottenuto ES convertire (-347) 10 in CP2 2 8 = 256 < 347 < 512 = 2 9 intervallo con n bit: [-2 n-1,+2 n-1-1] pertanto n min = in notazione a 10 bit: complementando a 2: BIN.19
20 Rapresentazione di numeri reali Con un numero finito di cifre è solo possibile rappresentare un numero razionale che approssima con un certo errore il numero reale dato Vengono usate due notazioni: A) Notazione in virgola fissa Dedica parte delle cifre alla parte intera e le altre alla parte frazionaria + XXX.YY B) Notazione in virgola mobile Dedica alcune cifre a rappresentare un esponente della base che indica l ordine di grandezza del numero rappresentato BIN.20
21 Notazione in virgola mobile Estende l intervallo di numeri rappresentati a parità di cifre, rispetto alla notazione in virgola fissa Numeri reali rappresentati tramite una coppia di numeri <m,e> n = m b m : mantissa normalizzata tra due potenze successive della base b i -1 m < b i e : esponente intero con segno Sia m che e hanno un numero fissato di cifre: Intervalli limitati Errori di arrotondamento e BIN.21
22 Esempio in base 10 Numerali a 5 cifre +.XXX + EE Mantissa : 3 cifre con segno 0.1 m < 1 Esponente: 2 cifre con segno -99 e Overflow negativo { Underflow Overflow positivo Notare che con lo stesso numero di cifre in notazione a punto fisso + XXX.YY : - L intervallo scende [ , ] - Ma si hanno 5 cifre significative invece di 3 BIN.22
23 Standard IEEE 754 (1985) Formato non proprietario cioè non dipendente dall architettura Semplice precisione a 32 bit: 1 +/ 8 23 esp mantissa Doppia precisione a 64 bit 1 +/ esp mantissa Notazioni in modulo e segno Alcune configurazioni dell esponente sono riservate BIN.23
24 IEEE 754 a 32 bit 1 +/ 8 23 esp mantissa Esponente: - Rappresentato in eccesso L intervallo è [-127, +128] - Le due configurazioni estreme non si usano, quindi: -126 e 127 Mantissa: - È sempre normalizzata - Se ne rappresenta solo la parte frazionaria Due rappresentazioni, a seconda del valore dell esponente: A) Numeri normalizzati e B) Numeri denormalizzati e= BIN.24
25 Numeri Normalizzati Un numerale si intende in questa rappresentazione quando: e In questa rappresentazione la mantissa è normalizzata tra 1 e 2: 1 < m 2 Quindi è sempre nella forma: 1.XXXXXXXXX Si usano tutti i 23 bit per rappresentare la sola parte frazionaria Gli intervalli di numeri rappresentati sono pertanto: (-2 128, ] [2-126,2 128 ) Gli estremi sono esclusi perché il massimo valore assoluto di m è molto vicino a 2 ma comunque inferiore L intervallo (-2-126, ) è intervallo di underflow BIN.25
26 Numeri Denormalizzati Un numerale si intende in questa rappresentazione quando: e= L esponente assume il valore convenzionale e=2-126 La mantissa è normalizzata tra 0 e 1: 0 < m 1 Quindi è sempre nella forma: 0.XXXXXXXXX Si usano tutti i 23 bit per rappresentare la sola parte frazionaria La più piccola mantissa vale 2-23 Gli intervalli rappresentati sono: (-2 126, ] [2-149,2 126 ) NB Più piccola è la mantissa minore è il numero di cifre significative BIN.26
27 Altre Configurazioni Lo Standard IEEE 754 attribuisce valori convenzionali a particolari configurazioni di e ed m A) e ed m tutti 0 rappresentano il valore 0 (altrimenti non rappresentabile) B) m tutti 0 ed e tutti 1 rappresentano l overflow C) m 0 ed e tutti 1 indicano la situazione Not A Number (NAN), cioè un valore indefinito (ad es. il risultato di una divisione per 0) NB Queste convezioni sono una caratteristica peculiare della notazione IEEE 754; non valgono, se non esplicitamente definite, per altre notazioni BIN.27
28 Standard IEEE 754 a 32 bit (estremi degli intervalli) Più grande normalizzato ~2 128 : X ~2 Più piccolo normalizzato : X Più grande denormalizzato ~2-126 : X ( ) 2 1 Più piccolo denormalizzato : X ( ) 2 = 2-23 BIN.28
29 Addizioni in virgola mobile Per addizionare e sottrarre occorre scalare le mantisse per eguagliare gli esponenti ES (Notazione IEEE 754) n 1 + n 2 n 1 : n 2 : e 1 = (26 ) 10, e 2 = (43 ) 10 : occorre scalare m 1 di 17 posti n' 1 : n 2 : Notare che l addendo più piccolo perde cifre significative BIN.29
30 Moltiplicazioni fra interi La tabellina delle moltiplicazioni è molto semplice: L operazione fra numerali si effettua come in decimale: si incolonnano e si sommano i prodotti parziali scalandoli opportunamente (11) x (5 ) = (55) Notare che ciascun prodotto parziale è pari a zero oppure al moltiplicando BIN.30
31 Moltiplicazioni in virgola fissa Si opera come in decimale, tenendo conto del numero di cifre frazionarie e riposizionando il punto frazionario: (2.75) x (1.25) = (3.4375) Notare che: Moltiplicare per 2 n equivale a spostare il punto di n posti a destra Moltiplicare per 2 -n equivale a spostare il punto di n posti a sinistra BIN.31
32 Moltiplicazioni in virgola mobile Si moltiplicano le mantisse e si sommano algebricamente gli esponenti Se necessario si scala la mantissa per normalizzarla e si riaggiusta l esponente ES n 3 = n 1 x n 2 n 1 : n 2 : e 1 = (26 ) 10, e 2 = (43 ) 10 - e 1 + e 2 = (69) 10 = m 1 x m 2 = si scala la mantissa di un posto - si aumenta di 1 l esponente n 3 : BIN.32
33 Errore assoluto e relativo Rappresentando un numero reale n in una notazione floating-point si commette un errore di approssimazione In realtà viene rappresentato un numero razionale n con un numero limitato di cifre significative Errore assoluto: e A = n-n Errore relativo: e R =e A /n = (n-n )/n Se la mantissa è normalizzata l errore relativo massimo è costante su tutto l intervallo rappresentato, ed è pari ad un unità sull ultima cifra rappresenta ES: 10 cifre frazionarie e R = 2-10 Nelle notazioni non normalizzate l errore relativo massimo non è costante BIN.33
34 Esempio 1: virgola mobile Rappresentazione binaria in virgola mobile a 16 bit: 1 bit per il segno (0=positivo) 8 bit per l'esponente, in eccesso bit per la parte frazionaria della mantissa normalizzata tra 1 e 2 Calcolare gli estremi degli intervalli rappresentati, i numerali corrispondenti, e l ordine di grandezza decimale. Rappresentare in tale notazione il numero n rappresentato in compl. a 2 dai tre byte FF5AB9. Calcolare l errore relativo ed assoluto che si commette rappresentando il n nella notazione data. BIN.34
35 Esempio 2: virgola mobile Rappresentazione binaria in virgola mobile a 16 bit: 1 bit per il segno (0=positivo) 8 bit per l'esponente, in eccesso bit per la parte frazionaria della mantissa normalizzata tra 1 e 2 Dato il numero razionale m rappresentato in tale notazione dai due byte 43A5, calcolare l intero n che approssima m per difetto, e rappresentarlo in complemento a 2 con 16 bit. BIN.35
36 Esempio 3: virgola mobile Rappresentazione binaria in virgola mobile a 16 bit: 1 bit per il segno (0=positivo) e bit per l'esponente, in eccesso 2 e e bit per la parte frazionaria della mantissa normalizzata tra 1 e 2 Calcolare il valore minimo e min di bit per l esponente che consenta di rappresentare il numero n rappresentato in compl. a 2 dai tre byte FF5AB9 BIN.36
37 Esempio 4: virgola mobile Rappresentazione binaria in virgola mobile a 16 bit: 1 bit per il segno (0=positivo) 7 bit per l'esponente, in eccesso 64 8 bit per la parte frazionaria della mantissa normalizzata tra 1 e 2 Dati m e n rappresentati in tale notazione dalle stringhe esadecimali FA53 e E8F2: Calcolare la somma di m e n e fornire la stringa esadecimale che la rappresenta nella notazione suddetta. BIN.37
Calcolatori Elettronici Parte III: Sistemi di Numerazione Binaria
 Anno Accademico 2001/2002 Calcolatori Elettronici Parte III: Sistemi di Numerazione Binaria Prof. Riccardo Torlone Università di Roma Tre Numeri e numerali! Numero: entità astratta! Numerale: stringa di
Anno Accademico 2001/2002 Calcolatori Elettronici Parte III: Sistemi di Numerazione Binaria Prof. Riccardo Torlone Università di Roma Tre Numeri e numerali! Numero: entità astratta! Numerale: stringa di
N= a i b i. Numeri e numerali. Sistemi di Numerazione Binaria. Sistemi posizionali. Numeri a precisione finita
 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Sistemi di Numerazione Binaria Lo stesso numero è rappresentato da
Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Sistemi di Numerazione Binaria Lo stesso numero è rappresentato da
Sistemi di Numerazione Binaria
 Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Sistemi di Numerazione Binaria
 Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Calcolatori Elettronici Parte II: Sistemi di Numerazione Binaria. Prof. Riccardo Torlone Università di Roma Tre
 Calcolatori Elettronici Parte II: Sistemi di Numerazione Binaria Prof. Riccardo Torlone Università di Roma Tre Unità di misura Attenzione però, se stiamo parlando di memoria: 1Byte = 8 bit 1K (KiB: KibiByte)
Calcolatori Elettronici Parte II: Sistemi di Numerazione Binaria Prof. Riccardo Torlone Università di Roma Tre Unità di misura Attenzione però, se stiamo parlando di memoria: 1Byte = 8 bit 1K (KiB: KibiByte)
Calcolatori Elettronici Parte II: Sistemi di Numerazione Binaria. Prof. Riccardo Torlone Università di Roma Tre
 Calcolatori Elettronici Parte II: Sistemi di Numerazione Binaria Prof. Riccardo Torlone Università di Roma Tre Unità di misura Attenzione però, se stiamo parlando di memoria: n 1Byte = 8 bit n 1K (KiB:
Calcolatori Elettronici Parte II: Sistemi di Numerazione Binaria Prof. Riccardo Torlone Università di Roma Tre Unità di misura Attenzione però, se stiamo parlando di memoria: n 1Byte = 8 bit n 1K (KiB:
Rappresentazione dei Numeri in Virgola Mobile Valeria Cardellini
 Rappresentazione dei Numeri in Virgola Mobile Valeria Cardellini Corso di Calcolatori Elettronici A.A. 2018/19 Università degli Studi di Roma Tor Vergata Dipartimento di Ingegneria Civile e Ingegneria
Rappresentazione dei Numeri in Virgola Mobile Valeria Cardellini Corso di Calcolatori Elettronici A.A. 2018/19 Università degli Studi di Roma Tor Vergata Dipartimento di Ingegneria Civile e Ingegneria
Calcolatori Elettronici
 Calcolatori Elettronici Rappresentazione in Virgola Mobile Francesco Lo Presti Rielaborate da Salvatore Tucci Rappresentazione di numeri reali q Con un numero finito di cifre è possibile rappresentare
Calcolatori Elettronici Rappresentazione in Virgola Mobile Francesco Lo Presti Rielaborate da Salvatore Tucci Rappresentazione di numeri reali q Con un numero finito di cifre è possibile rappresentare
Architetture dei Calcolatori (Lettere
 Architetture dei Calcolatori (Lettere J-K) Rappresentazione in Virgola Mobile Ing.. Davide D Amico Rappresentazione di numeri reali Con un numero finito di cifre Å possibile rappresentare solo un numero
Architetture dei Calcolatori (Lettere J-K) Rappresentazione in Virgola Mobile Ing.. Davide D Amico Rappresentazione di numeri reali Con un numero finito di cifre Å possibile rappresentare solo un numero
Rappresentazione di numeri reali. Rappresentazione in virgola mobile. Perché la rappresentazione in virgola mobile. Rappresentazione in virgola mobile
 Rappresentazione di numeri reali Rappresentazione in virgola mobile Architetture dei Calcolatori (lettere A-I) Con un numero finito di cifre è possibile rappresentare solo un numero razionale che approssima
Rappresentazione di numeri reali Rappresentazione in virgola mobile Architetture dei Calcolatori (lettere A-I) Con un numero finito di cifre è possibile rappresentare solo un numero razionale che approssima
Codifica dell Informazione per il Calcolo Scientifico
 Alfredo Cuzzocrea per il Calcolo Scientifico CODIFICA BINARIA Codifica binaria: usa un alfabeto di 2 simboli Utilizzata nei sistemi informatici Si utilizza una grandezza fisica (luminosità, tensione elettrica,
Alfredo Cuzzocrea per il Calcolo Scientifico CODIFICA BINARIA Codifica binaria: usa un alfabeto di 2 simboli Utilizzata nei sistemi informatici Si utilizza una grandezza fisica (luminosità, tensione elettrica,
Rappresentazione di numeri reali. Architetture dei Calcolatori (Lettere. Perché la rappresentazione in virgola mobile
 Rappresentazione di numeri reali Architetture dei Calcolatori (Lettere A-I) Rappresentazione in Virgola Mobile Ing.. Francesco Lo Presti Con un numero finito di cifre è possibile rappresentare solo un
Rappresentazione di numeri reali Architetture dei Calcolatori (Lettere A-I) Rappresentazione in Virgola Mobile Ing.. Francesco Lo Presti Con un numero finito di cifre è possibile rappresentare solo un
Rappresentazione di numeri reali. Architetture dei Calcolatori (Lettere. Perché la rappresentazione in virgola mobile
 Rappresentazione di numeri reali Architetture dei Calcolatori (Lettere A-I) Rappresentazione in Virgola Mobile Prof. Francesco Lo Presti Con un numero finito di cifre è possibile rappresentare solo un
Rappresentazione di numeri reali Architetture dei Calcolatori (Lettere A-I) Rappresentazione in Virgola Mobile Prof. Francesco Lo Presti Con un numero finito di cifre è possibile rappresentare solo un
Sistemi di Numerazione Binaria NB.1
 Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Rappresentazione in virgola mobile
 Rappresentazione in virgola mobile Architetture dei Calcolatori (lettere A-I) Rappresentazione di numeri reali Con un numero finito di cifre è possibile rappresentare solo un numero razionale che approssima
Rappresentazione in virgola mobile Architetture dei Calcolatori (lettere A-I) Rappresentazione di numeri reali Con un numero finito di cifre è possibile rappresentare solo un numero razionale che approssima
Rappresentazione dei numeri reali
 Rappresentazione dei numeri reali Rappresentazione di numeri reali Con un numero finito di cifre è solo possibile rappresentare un numero razionale che approssima con un certo errore il numero reale dato
Rappresentazione dei numeri reali Rappresentazione di numeri reali Con un numero finito di cifre è solo possibile rappresentare un numero razionale che approssima con un certo errore il numero reale dato
Conversione di base. Conversione decimale binario. Si calcolano i resti delle divisioni per due
 Conversione di base Dato N>0 intero convertirlo in base b dividiamo N per b, otteniamo un quoto Q 0 ed un resto R 0 dividiamo Q 0 per b, otteniamo un quoto Q 1 ed un resto R 1 ripetiamo finché Q n < b
Conversione di base Dato N>0 intero convertirlo in base b dividiamo N per b, otteniamo un quoto Q 0 ed un resto R 0 dividiamo Q 0 per b, otteniamo un quoto Q 1 ed un resto R 1 ripetiamo finché Q n < b
Interi positivi e negativi
 Definizioni: numerali e numeri Un numerale è solo una stringa di cifre Un numerale rappresenta un numero solo se si specifica un sistema di numerazione Lo stesso numerale rappresenta diversi numeri in
Definizioni: numerali e numeri Un numerale è solo una stringa di cifre Un numerale rappresenta un numero solo se si specifica un sistema di numerazione Lo stesso numerale rappresenta diversi numeri in
Sistemi di Numerazione Binaria (a.a )
 Sistemi di Numerazione Binaria (a.a. 2008-2009) NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero
Sistemi di Numerazione Binaria (a.a. 2008-2009) NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero
Algoritmi Istruzioni che operano su dati. Per scrivere un programma è necessario. che l esecutore automatico sia in grado di.
 Codifica di Dati e Istruzioni Fondamenti di Informatica Codifica dell Informazione Prof. Francesco Lo Presti Algoritmi Istruzioni che operano su dati Per scrivere un programma è necessario rappresentare
Codifica di Dati e Istruzioni Fondamenti di Informatica Codifica dell Informazione Prof. Francesco Lo Presti Algoritmi Istruzioni che operano su dati Per scrivere un programma è necessario rappresentare
Rappresentazione dei numeri reali in un calcolatore
 Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri reali in un calcolatore Lezione 3 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione di numeri
Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri reali in un calcolatore Lezione 3 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione di numeri
Esempio 1: virgola mobile
 Esempio 1: virgola mobile Rappresentazione binaria in virgola mobile a 16 bit: 1 bit per il (0=positivo) 8 bit per l'esponente, in eccesso 128 7 bit per la parte frazionaria della mantissa normalizzata
Esempio 1: virgola mobile Rappresentazione binaria in virgola mobile a 16 bit: 1 bit per il (0=positivo) 8 bit per l'esponente, in eccesso 128 7 bit per la parte frazionaria della mantissa normalizzata
Rappresentazione di numeri reali
 Rappresentazione di numeri reali Con un numero finito di cifre è solo possibile rappresentare un numero razionale che approssima con un certo errore il numero reale dato Vengono usate due notazioni: A)
Rappresentazione di numeri reali Con un numero finito di cifre è solo possibile rappresentare un numero razionale che approssima con un certo errore il numero reale dato Vengono usate due notazioni: A)
Definizione operativa di informazione. Codifica dell informazione. Alfabeto, sintassi e semantica. Codifica binaria dell informazione
 Definizione operativa di informazione Codifica dell informazione Architetture dei Calcolatori (lettere A-I) E necessario rappresentare istruzioni e dati in un formato che il calcolatore sia in grado di
Definizione operativa di informazione Codifica dell informazione Architetture dei Calcolatori (lettere A-I) E necessario rappresentare istruzioni e dati in un formato che il calcolatore sia in grado di
Codifica dell informazione
 Codifica dell informazione Architetture dei Calcolatori (lettere A-I) Definizione operativa di informazione E necessario rappresentare istruzioni e dati in un formato che il calcolatore sia in grado di
Codifica dell informazione Architetture dei Calcolatori (lettere A-I) Definizione operativa di informazione E necessario rappresentare istruzioni e dati in un formato che il calcolatore sia in grado di
Esercizi su Sistemi di Numerazione Binaria. Prof. Riccardo Torlone Università di Roma Tre
 Esercizi su Sistemi di Numerazione Binaria Prof. Riccardo Torlone Università di Roma Tre Esercizio 1 Si consideri una rappresentazione binaria in virgola mobile a 16 bit, di cui (nell'ordine da sinistra
Esercizi su Sistemi di Numerazione Binaria Prof. Riccardo Torlone Università di Roma Tre Esercizio 1 Si consideri una rappresentazione binaria in virgola mobile a 16 bit, di cui (nell'ordine da sinistra
Codifica di informazioni numeriche
 Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica Codifica di informazioni numeriche Fondamenti di Informatica - Ingegneria Elettronica Leonardo Querzoni querzoni@dis.uniroma1.it
Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica Codifica di informazioni numeriche Fondamenti di Informatica - Ingegneria Elettronica Leonardo Querzoni querzoni@dis.uniroma1.it
Conversione binario-ottale/esadecimale. Conversione binario-ottale/esadecimale. Rappresentazione di Numeri Interi Positivi (numeri naturali)
 Conversione binario-ottale/esadecimale Conversione binario-ottale/esadecimale Nella rappresentazione ottale (B=8) si usano gli 8 simboli,, 2, 3, 4, 5, 6, 7 In quella esadecimale (B=6) i 6 simboli,, 2,
Conversione binario-ottale/esadecimale Conversione binario-ottale/esadecimale Nella rappresentazione ottale (B=8) si usano gli 8 simboli,, 2, 3, 4, 5, 6, 7 In quella esadecimale (B=6) i 6 simboli,, 2,
Sistemi di Numerazione Binaria
 Sistemi di Numerazione Binaria ES.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Sistemi di Numerazione Binaria ES.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Fondamenti di Informatica - 1. Prof. B.Buttarazzi A.A. 2011/2012
 Fondamenti di Informatica - 1 Prof. B.Buttarazzi A.A. 2011/2012 I numeri reali Sommario Conversione dei numeri reali da base 10 a base B Rappresentazione dei numeri reali Virgola fissa Virgola mobile (mantissa
Fondamenti di Informatica - 1 Prof. B.Buttarazzi A.A. 2011/2012 I numeri reali Sommario Conversione dei numeri reali da base 10 a base B Rappresentazione dei numeri reali Virgola fissa Virgola mobile (mantissa
Informatica Generale 02 - Rappresentazione numeri razionali
 Informatica Generale 02 - Rappresentazione numeri razionali Cosa vedremo: Rappresentazione binaria dei numeri razionali Rappresentazione in virgola fissa Rappresentazione in virgola mobile La rappresentazione
Informatica Generale 02 - Rappresentazione numeri razionali Cosa vedremo: Rappresentazione binaria dei numeri razionali Rappresentazione in virgola fissa Rappresentazione in virgola mobile La rappresentazione
FONDAMENTI DI INFORMATICA. Prof. Alfredo Accattatis Slide (rielaborate) del prof. Emiliano Casalicchio
 FONDAMENTI DI INFORMATICA Prof. Alfredo Accattatis Slide (rielaborate) del prof. Emiliano Casalicchio 2 Caratteri e codifica Un carattere in MATLAB è rappresentato usando le virgolette singole 'a', 'x',
FONDAMENTI DI INFORMATICA Prof. Alfredo Accattatis Slide (rielaborate) del prof. Emiliano Casalicchio 2 Caratteri e codifica Un carattere in MATLAB è rappresentato usando le virgolette singole 'a', 'x',
Rappresentazione binaria
 Rappresentazione binaria Per informazione intendiamo tutto quello che viene manipolato da un calcolatore: numeri (naturali, interi, reali,... ) caratteri immagini suoni programmi... La più piccola unità
Rappresentazione binaria Per informazione intendiamo tutto quello che viene manipolato da un calcolatore: numeri (naturali, interi, reali,... ) caratteri immagini suoni programmi... La più piccola unità
Sistemi di Numerazione Binaria
 Sistemi di Numerazione Binaria 12/02/2011 Fondamenti di Informatica - Prof. Gregorio Cosentino 1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un
Sistemi di Numerazione Binaria 12/02/2011 Fondamenti di Informatica - Prof. Gregorio Cosentino 1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un
Rappresentazione binaria
 Rappresentazione binaria Per informazione intendiamo tutto quello che viene manipolato da un calcolatore: numeri (naturali, interi, reali,... ) caratteri immagini suoni programmi... La più piccola unità
Rappresentazione binaria Per informazione intendiamo tutto quello che viene manipolato da un calcolatore: numeri (naturali, interi, reali,... ) caratteri immagini suoni programmi... La più piccola unità
Algebra di Boole e porte logiche
 Algebra di Boole e porte logiche Dott.ssa Isabella D'Alba Corso PENTEST MIND PROJECT 2016 Algebra di Boole e porte logiche (I parte) Algebra di Boole I Sistemi di Numerazione (Posizionali, Non posizionali)
Algebra di Boole e porte logiche Dott.ssa Isabella D'Alba Corso PENTEST MIND PROJECT 2016 Algebra di Boole e porte logiche (I parte) Algebra di Boole I Sistemi di Numerazione (Posizionali, Non posizionali)
Codifica dell informazione numerica. Matteo Re, Nicola Basilico,
 Codifica dell informazione numerica Matteo Re, matteo.re@unimi.it Nicola Basilico, nicola.basilico@unimi.it Informazioni (edizione 2017-2018) Turno A (cognomi A - F) Nicola Basilico, dip. via Comelico,
Codifica dell informazione numerica Matteo Re, matteo.re@unimi.it Nicola Basilico, nicola.basilico@unimi.it Informazioni (edizione 2017-2018) Turno A (cognomi A - F) Nicola Basilico, dip. via Comelico,
Sistemi di Numerazione
 Sistemi di Numerazione Corso Università Numeri e Numerali Il numero cinque 5 V _ Π Arabo Romano Maya Greco Cinese Il sistema decimale Sistemi Posizionali 1 10 3 + 4 10 2 + 9 10 1 + 2 10 0 Sistemi Posizionali
Sistemi di Numerazione Corso Università Numeri e Numerali Il numero cinque 5 V _ Π Arabo Romano Maya Greco Cinese Il sistema decimale Sistemi Posizionali 1 10 3 + 4 10 2 + 9 10 1 + 2 10 0 Sistemi Posizionali
Rappresentazione in virgola mobile Barbara Masucci
 Architettura degli Elaboratori Rappresentazione in virgola mobile Barbara Masucci Punto della situazione Abbiamo visto le rappresentazioni dei numeri: Ø Sistema posizionale pesato per Ø Ø Interi positivi
Architettura degli Elaboratori Rappresentazione in virgola mobile Barbara Masucci Punto della situazione Abbiamo visto le rappresentazioni dei numeri: Ø Sistema posizionale pesato per Ø Ø Interi positivi
Rappresentazione numeri reali
 Rappresentazione numeri reali I numeri reali rappresentabili in un calcolatore sono in realtà numeri razionali che approssimano i numeri reali con un certo grado di precisione Per rappresentare un numero
Rappresentazione numeri reali I numeri reali rappresentabili in un calcolatore sono in realtà numeri razionali che approssimano i numeri reali con un certo grado di precisione Per rappresentare un numero
Fondamenti di Programmazione. Sistemi di rappresentazione
 Fondamenti di Programmazione Sistemi di rappresentazione Numeri e numerali Il numero cinque 5 V _ Π 五 Arabo Romano Maya Greco Cinese Il sistema decimale Sistemi posizionali 1 10 3 + 4 10 2 + 9 10 1 + 2
Fondamenti di Programmazione Sistemi di rappresentazione Numeri e numerali Il numero cinque 5 V _ Π 五 Arabo Romano Maya Greco Cinese Il sistema decimale Sistemi posizionali 1 10 3 + 4 10 2 + 9 10 1 + 2
Fondamenti di Programmazione. Sistemi di rappresentazione
 Fondamenti di Programmazione Sistemi di rappresentazione Numeri e numerali Il numero cinque 5 V _ Π 五 Arabo Romano Maya Greco Cinese Sistemi posizionali 1 10 3 + 4 10 2 + 9 10 1 + 2 10 0 Sistemi posizionali
Fondamenti di Programmazione Sistemi di rappresentazione Numeri e numerali Il numero cinque 5 V _ Π 五 Arabo Romano Maya Greco Cinese Sistemi posizionali 1 10 3 + 4 10 2 + 9 10 1 + 2 10 0 Sistemi posizionali
ARCHITETTUREDIELABORAZIONE,a.a Esercizi d esame NUMERI BINARI
 RHITETTUREDIELORZIONE,a.a. 2002-2003 Esercizi d esame NUMERI INRI 1) Si consideri una rappresentazione binaria in virgola mobile a 16 bit, di cui (nell ordine da sinistra a destra) 1 bit per il segno (0=positivo),
RHITETTUREDIELORZIONE,a.a. 2002-2003 Esercizi d esame NUMERI INRI 1) Si consideri una rappresentazione binaria in virgola mobile a 16 bit, di cui (nell ordine da sinistra a destra) 1 bit per il segno (0=positivo),
Informatica e Laboratorio di Programmazione Sistema Binario Alberto Ferrari. Alberto Ferrari Informatica e Laboratorio di Programmazione
 Informatica e Laboratorio di Programmazione Sistema Binario Alberto Ferrari Alberto Ferrari Informatica e Laboratorio di Programmazione analogico e digitale una grandezza (fisica o astratta) può essere
Informatica e Laboratorio di Programmazione Sistema Binario Alberto Ferrari Alberto Ferrari Informatica e Laboratorio di Programmazione analogico e digitale una grandezza (fisica o astratta) può essere
Codifica di Dati e Istruzioni. Architetture dei Calcolatori (Lettere. Sistema di Codifica: Numeri Interi (Decimali) Sistemi di Codifica.
 Codifica di Dati e Istruzioni Architetture dei Calcolatori (Lettere A-I) Codifica dell Informazione e Aritmetica Binaria Prof. Francesco Lo Presti Algoritmi Istruzioni che operano su dati Per scrivere
Codifica di Dati e Istruzioni Architetture dei Calcolatori (Lettere A-I) Codifica dell Informazione e Aritmetica Binaria Prof. Francesco Lo Presti Algoritmi Istruzioni che operano su dati Per scrivere
Operazioni artimetiche
 Operazioni artimetiche Per effettuare operazioni è necessario conoscere la definizione del comportamento per ogni coppia di simboli Per ogni operazione esiste una tabella Fondamenti di Informatica 1 Somma
Operazioni artimetiche Per effettuare operazioni è necessario conoscere la definizione del comportamento per ogni coppia di simboli Per ogni operazione esiste una tabella Fondamenti di Informatica 1 Somma
Rappresentazione dei dati
 Rappresentazione dei dati Rappresentazione dei dati Rappresentazione in base 2 e base 6 Aritmetica dei registri Come rappresentiamo i numeri? Base di numerazione: dieci Cifre: 2 3 4 5 6 7 8 9 Rappresentazione
Rappresentazione dei dati Rappresentazione dei dati Rappresentazione in base 2 e base 6 Aritmetica dei registri Come rappresentiamo i numeri? Base di numerazione: dieci Cifre: 2 3 4 5 6 7 8 9 Rappresentazione
Codifica. Rappresentazione di numeri in memoria
 Codifica Rappresentazione di numeri in memoria Rappresentazione polinomiale dei numeri Un numero decimale si rappresenta in notazione polinomiale moltiplicando ciascuna cifra a sinistra della virgola per
Codifica Rappresentazione di numeri in memoria Rappresentazione polinomiale dei numeri Un numero decimale si rappresenta in notazione polinomiale moltiplicando ciascuna cifra a sinistra della virgola per
Esercitazioni su rappresentazione dei numeri e aritmetica. Interi unsigned in base 2
 Esercitazioni su rappresentazione dei numeri e aritmetica Salvatore Orlando & Marta Simeoni Interi unsigned in base 2 Si utilizza un alfabeto binario A = {0,1}, dove 0 corrisponde al numero zero, e 1 corrisponde
Esercitazioni su rappresentazione dei numeri e aritmetica Salvatore Orlando & Marta Simeoni Interi unsigned in base 2 Si utilizza un alfabeto binario A = {0,1}, dove 0 corrisponde al numero zero, e 1 corrisponde
Lezione 3. I numeri relativi
 Lezione 3 L artimetcia binaria: i numeri relativi i numeri frazionari I numeri relativi Si possono rappresentare i numeri negativi in due modi con modulo e segno in complemento a 2 1 Modulo e segno Si
Lezione 3 L artimetcia binaria: i numeri relativi i numeri frazionari I numeri relativi Si possono rappresentare i numeri negativi in due modi con modulo e segno in complemento a 2 1 Modulo e segno Si
Rappresentazione numeri relativi e reali
 Rappresentazione numeri relativi e reali Lezione 2 Rappresentazione numeri relativi Rappresentazione numeri reali Rappresentazione in Modulo e Segno Rappresentare separatamente il segno (mediante un bit
Rappresentazione numeri relativi e reali Lezione 2 Rappresentazione numeri relativi Rappresentazione numeri reali Rappresentazione in Modulo e Segno Rappresentare separatamente il segno (mediante un bit
1-Rappresentazione dell informazione
 1-Rappresentazione dell informazione Informazioni: testi, numeri, immagini, suoni, etc.; Come viene rappresentata l informazione in un calcolatore? Uso di tecnologia digitale: tutto ciò che viene rappresentato
1-Rappresentazione dell informazione Informazioni: testi, numeri, immagini, suoni, etc.; Come viene rappresentata l informazione in un calcolatore? Uso di tecnologia digitale: tutto ciò che viene rappresentato
Rappresentazione dei Numeri
 Rappresentazione dei Numeri Rappresentazione dei Numeri Il sistema numerico binario è quello che meglio si adatta alle caratteristiche del calcolatore Il problema della rappresentazione consiste nel trovare
Rappresentazione dei Numeri Rappresentazione dei Numeri Il sistema numerico binario è quello che meglio si adatta alle caratteristiche del calcolatore Il problema della rappresentazione consiste nel trovare
Corso di Fondamenti di Informatica Rappresentazione dei dati numerici Aritmetica dei registri Anno Accademico 2011/2012 Francesco Tortorella
 Corso di Informatica Rappresentazione dei dati numerici Aritmetica dei registri Anno Accademico 2011/2012 Francesco Tortorella Numero e rappresentazione Spesso si confonde il numero con la sua rappresentazione
Corso di Informatica Rappresentazione dei dati numerici Aritmetica dei registri Anno Accademico 2011/2012 Francesco Tortorella Numero e rappresentazione Spesso si confonde il numero con la sua rappresentazione
Codifica dell informazione numerica
 Codifica dell informazione numerica Nicola Basilico, nicola.basilico@unimi.it Architetture degli Elaboratori I, Laboratorio - Corso di Laurea in Informatica, A.A. 201-2018 Informazioni (edizione 2017-2018)
Codifica dell informazione numerica Nicola Basilico, nicola.basilico@unimi.it Architetture degli Elaboratori I, Laboratorio - Corso di Laurea in Informatica, A.A. 201-2018 Informazioni (edizione 2017-2018)
Rappresentazione di dati: numerazione binaria. Appunti per la cl. 3 Di A cura del prof. Ing. Mario Catalano
 Rappresentazione di dati: numerazione binaria Appunti per la cl. 3 Di A cura del prof. Ing. Mario Catalano Rappresentazione binaria Tutta l informazione interna ad un computer è codificata con sequenze
Rappresentazione di dati: numerazione binaria Appunti per la cl. 3 Di A cura del prof. Ing. Mario Catalano Rappresentazione binaria Tutta l informazione interna ad un computer è codificata con sequenze
La codifica. dell informazione
 00010010101001110101010100010110101000011100010111 00010010101001110101010100010110101000011100010111 La codifica 00010010101001110101010100010110101000011100010111 dell informazione 00010010101001110101010100010110101000011100010111
00010010101001110101010100010110101000011100010111 00010010101001110101010100010110101000011100010111 La codifica 00010010101001110101010100010110101000011100010111 dell informazione 00010010101001110101010100010110101000011100010111
Unità aritmetica e logica
 Aritmetica del calcolatore Capitolo 9 Unità aritmetica e logica n Esegue le operazioni aritmetiche e logiche n Ogni altra componente nel calcolatore serve questa unità n Gestisce gli interi n Può gestire
Aritmetica del calcolatore Capitolo 9 Unità aritmetica e logica n Esegue le operazioni aritmetiche e logiche n Ogni altra componente nel calcolatore serve questa unità n Gestisce gli interi n Può gestire
Rappresentazione dell informazione
 Rappresentazione dell informazione La codifica delle informazioni codifica forma adatta per essere trattata dall elaboratore INFORMAZIONI DATI interpretazione 2 Informazioni Numeri Immagini fisse Interi
Rappresentazione dell informazione La codifica delle informazioni codifica forma adatta per essere trattata dall elaboratore INFORMAZIONI DATI interpretazione 2 Informazioni Numeri Immagini fisse Interi
Informazione binaria: - rappresentazione dei numeri razionali -
 Informazione binaria: - rappresentazione dei numeri razionali - Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Nel seguito vedremo tipologie
Informazione binaria: - rappresentazione dei numeri razionali - Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Nel seguito vedremo tipologie
UD 1.2e: La codifica Digitale dei Numeri CODIFICA DIGITALE DEI NUMERI
 Modulo 1: Le I.C.T. : La codifica Digitale dei Numeri CODIFICA DIGITALE DEI NUMERI Prof. Alberto Postiglione Corso di Informatica Generale (AA 07-08) Corso di Laurea in Scienze della Comunicazione Università
Modulo 1: Le I.C.T. : La codifica Digitale dei Numeri CODIFICA DIGITALE DEI NUMERI Prof. Alberto Postiglione Corso di Informatica Generale (AA 07-08) Corso di Laurea in Scienze della Comunicazione Università
Modulo 1: Le I.C.T. UD 1.2e: La codifica Digitale dei Numeri
 Modulo 1: Le I.C.T. : La codifica Digitale dei Numeri Prof. Alberto Postiglione Corso di Informatica Generale (AA 07-08) Corso di Laurea in Scienze della Comunicazione Università degli Studi di Salerno
Modulo 1: Le I.C.T. : La codifica Digitale dei Numeri Prof. Alberto Postiglione Corso di Informatica Generale (AA 07-08) Corso di Laurea in Scienze della Comunicazione Università degli Studi di Salerno
Lezione 2. Rappresentazione dell informazione
 Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Informatica (DI) Università degli Studi di Milano 1 Rappresentazione dell informazione
Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Informatica (DI) Università degli Studi di Milano 1 Rappresentazione dell informazione
Numeri frazionari nel sistema binario
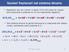 Numeri frazionari nel sistema binario Sappiamo che nei numeri in base 10 le cifre dopo la virgola sono associate a potenze di 10 con esponente negativo: 675,93 (10) = 6 10 2 +7 10 1 +5 10 0 +9 10-1 +3
Numeri frazionari nel sistema binario Sappiamo che nei numeri in base 10 le cifre dopo la virgola sono associate a potenze di 10 con esponente negativo: 675,93 (10) = 6 10 2 +7 10 1 +5 10 0 +9 10-1 +3
Architetture dei Calcolatori (Lettere
 Architetture dei Calcolatori (Lettere J-Z) Codifica dell Informazione e Aritmetica Binaria Ing.. Davide D AmicoD Codifica di Dati e Istruzioni Algoritmi Istruzioni che operano su dati Per scrivere un programma
Architetture dei Calcolatori (Lettere J-Z) Codifica dell Informazione e Aritmetica Binaria Ing.. Davide D AmicoD Codifica di Dati e Istruzioni Algoritmi Istruzioni che operano su dati Per scrivere un programma
Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri Roberto Navigli
 Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri Roberto Navigli 1 Da base 2 a base 10 I seguenti esercizi richiedono di convertire in base 10 la medesima stringa binaria
Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri Roberto Navigli 1 Da base 2 a base 10 I seguenti esercizi richiedono di convertire in base 10 la medesima stringa binaria
Fondamenti di Informatica - 1. Esercizi A.A. 2011/2012
 Fondamenti di Informatica - 1 Esercizi A.A. 2011/2012 Esercizio Esercizio Esercizio Esercizio Esercizio Dato ilnumero 11000000111100000000000000000000 rappresentato secondo lo standard floating point IEEE
Fondamenti di Informatica - 1 Esercizi A.A. 2011/2012 Esercizio Esercizio Esercizio Esercizio Esercizio Dato ilnumero 11000000111100000000000000000000 rappresentato secondo lo standard floating point IEEE
Rappresentazione di Numeri Reali. Rappresentazione in virgola fissa (fixed-point) Rappresentazione in virgola fissa (fixed-point)
 Rappresentazione di Numeri Reali Un numero reale è una grandezza continua Può assumere infiniti valori In una rappresentazione di lunghezza limitata, deve di solito essere approssimato. Esistono due forme
Rappresentazione di Numeri Reali Un numero reale è una grandezza continua Può assumere infiniti valori In una rappresentazione di lunghezza limitata, deve di solito essere approssimato. Esistono due forme
Calcolatori Elettronici
 Calcolatori Elettronici Codifica dell Informazione e Aritmetica Binaria Francesco Lo Presti Rielaborate da Salvatore Tucci Informazione Calcolatore : Sistema per elaborazione informazione Necessità della
Calcolatori Elettronici Codifica dell Informazione e Aritmetica Binaria Francesco Lo Presti Rielaborate da Salvatore Tucci Informazione Calcolatore : Sistema per elaborazione informazione Necessità della
Conversione binario-decimale. Interi unsigned in base 2. Esercitazioni su rappresentazione. dei numeri e aritmetica
 Esercitazioni su rappresentazione dei numeri e aritmetica Salvatore Orlando & Marta Simeoni Interi unsigned in base 2 I seguenti numeri naturali sono rappresentabili usando il numero di bit specificato?
Esercitazioni su rappresentazione dei numeri e aritmetica Salvatore Orlando & Marta Simeoni Interi unsigned in base 2 I seguenti numeri naturali sono rappresentabili usando il numero di bit specificato?
Rappresentazione e Codifica dell Informazione
 Rappresentazione e Codifica dell Informazione Capitolo 1 Chianese, Moscato, Picariello, Alla scoperta dei fondamenti dell informatica un viaggio nel mondo dei BIT, Liguori editore. Sistema di numerazione
Rappresentazione e Codifica dell Informazione Capitolo 1 Chianese, Moscato, Picariello, Alla scoperta dei fondamenti dell informatica un viaggio nel mondo dei BIT, Liguori editore. Sistema di numerazione
DIPARTIMENTO DI ELETTRONICA E INFORMAZIONE. Numeri in virgola. Marco D. Santambrogio Ver. aggiornata al 10 Novembre 2015
 Numeri in virgola Marco D. Santambrogio marco.santambrogio@polimi.it Ver. aggiornata al 10 Novembre 2015 Numeri in virgola fissa Fino a questo punto abbiamo assunto che Un vettore di bit rappresentasse
Numeri in virgola Marco D. Santambrogio marco.santambrogio@polimi.it Ver. aggiornata al 10 Novembre 2015 Numeri in virgola fissa Fino a questo punto abbiamo assunto che Un vettore di bit rappresentasse
Notazione posizionale. Codifica binaria. Rappresentazioni medianti basi diverse. Multipli del byte
 Codifica binaria Rappresentazione di numeri Notazione di tipo posizionale (come la notazione decimale). Ogni numero è rappresentato da una sequenza di simboli Il valore del numero dipende non solo dalla
Codifica binaria Rappresentazione di numeri Notazione di tipo posizionale (come la notazione decimale). Ogni numero è rappresentato da una sequenza di simboli Il valore del numero dipende non solo dalla
Lezione 1. Rappresentazione dei numeri. Aritmetica dei calcolatori. Rappresentazione dei numeri naturali in base 2
 Lezione 1 Rappresentazione dei numeri Aritmetica dei calcolatori Rappresentazione dei numeri naturali in base 2 Si utilizza un alfabeto binario A = {0,1} dove 0 corrisponde al numero zero e 1 corrisponde
Lezione 1 Rappresentazione dei numeri Aritmetica dei calcolatori Rappresentazione dei numeri naturali in base 2 Si utilizza un alfabeto binario A = {0,1} dove 0 corrisponde al numero zero e 1 corrisponde
Operazioni sui binari
 Operazioni sui binari Elementi di Informatica CdL Ingegneria Civile (A-Z) Università degli Studi di Napoli Federico II 15 marzo 2017 Ing. Giovanni Ponti ENEA C.R. Portici giovanni.ponti@enea.it 2 Operazioni
Operazioni sui binari Elementi di Informatica CdL Ingegneria Civile (A-Z) Università degli Studi di Napoli Federico II 15 marzo 2017 Ing. Giovanni Ponti ENEA C.R. Portici giovanni.ponti@enea.it 2 Operazioni
Interi unsigned in base 2. Esercitazioni su rappresentazione dei numeri e aritmetica. Conversione binario-decimale
 Arch. Elab. A M. Simeoni 1 Interi unsigned in base 2 Si utilizza un alfabeto binario A = {0,1}, dove 0 corrisponde al numero zero, e 1 corrisponde al numero uno d n1...d 1 d 0 con di d i {0,1} Esercitazioni
Arch. Elab. A M. Simeoni 1 Interi unsigned in base 2 Si utilizza un alfabeto binario A = {0,1}, dove 0 corrisponde al numero zero, e 1 corrisponde al numero uno d n1...d 1 d 0 con di d i {0,1} Esercitazioni
Numeri con segno ed in virgola
 Numeri con segno ed in virgola Marco D. Santambrogio marco.santambrogio@polimi.it Ver. aggiornata al 20 Marzo 2016 Obiettivi Complemento a due Numeri in virgola 2 Rappresentazione dei numeri In realtà,
Numeri con segno ed in virgola Marco D. Santambrogio marco.santambrogio@polimi.it Ver. aggiornata al 20 Marzo 2016 Obiettivi Complemento a due Numeri in virgola 2 Rappresentazione dei numeri In realtà,
DIPARTIMENTO DI ELETTRONICA E INFORMAZIONE. Numeri in virgola. Marco D. Santambrogio Ver. aggiornata al 14 Novembre 2014
 Numeri in virgola Marco D. Santambrogio marco.santambrogio@polimi.it Ver. aggiornata al 14 Novembre 2014 Ogni promessa è debito 2 Ogni promessa è debito 3 Ogni promessa è debito Dove sei? 4 Ogni promessa
Numeri in virgola Marco D. Santambrogio marco.santambrogio@polimi.it Ver. aggiornata al 14 Novembre 2014 Ogni promessa è debito 2 Ogni promessa è debito 3 Ogni promessa è debito Dove sei? 4 Ogni promessa
Abilità Informatiche e Telematiche
 Abilità Informatiche e Telematiche (Laurea Triennale + Laurea Magistrale) Marco Pedicini mailto:marco.pedicini@uniroma3.it Corso di Laurea Magistrale in Informazione, Editoria e Giornalismo, Università
Abilità Informatiche e Telematiche (Laurea Triennale + Laurea Magistrale) Marco Pedicini mailto:marco.pedicini@uniroma3.it Corso di Laurea Magistrale in Informazione, Editoria e Giornalismo, Università
Analogico vs. Digitale. LEZIONE II La codifica binaria. Analogico vs digitale. Analogico. Digitale
 Analogico vs. Digitale LEZIONE II La codifica binaria Analogico Segnale che può assumere infiniti valori con continuità Digitale Segnale che può assumere solo valori discreti Analogico vs digitale Il computer
Analogico vs. Digitale LEZIONE II La codifica binaria Analogico Segnale che può assumere infiniti valori con continuità Digitale Segnale che può assumere solo valori discreti Analogico vs digitale Il computer
Rappresentazione delle informazioni
 Testo di rif.to: [Congiu] - 1.1 (pg. 1 17) Rappresentazione delle informazioni -1.g Informazioni numeriche Cosa vedremo 1. I sistemi di numerazione Decimale, binario, esadecimale Conversioni di base 1
Testo di rif.to: [Congiu] - 1.1 (pg. 1 17) Rappresentazione delle informazioni -1.g Informazioni numeriche Cosa vedremo 1. I sistemi di numerazione Decimale, binario, esadecimale Conversioni di base 1
Numeri reali. Notazione scientifica (decimale) Floating Point. Normalizzazione. Esempi. Aritmetica del calcolatore (virgola mobile)
 Numeri reali Aritmetica del calcolatore (virgola mobile) Capitolo 9 1 Numeri con frazioni Posso essere rappresentati anche in binario Es.: 1001.1010 = 2 4 + 2 0 +2-1 + 2-3 =9.625 Quante cifre dopo la virgola?
Numeri reali Aritmetica del calcolatore (virgola mobile) Capitolo 9 1 Numeri con frazioni Posso essere rappresentati anche in binario Es.: 1001.1010 = 2 4 + 2 0 +2-1 + 2-3 =9.625 Quante cifre dopo la virgola?
Politecnico di Bari Sede di Foggia. docente: Prof. Ing. Michele Salvemini
 Corso di Laurea in Ingegneria Civile Politecnico di Bari Sede di Foggia Fondamenti di Informatica Anno Accademico 2011/2012 docente: Prof. Ing. Michele Salvemini Sommario I Codici I Sistemi di numerazione
Corso di Laurea in Ingegneria Civile Politecnico di Bari Sede di Foggia Fondamenti di Informatica Anno Accademico 2011/2012 docente: Prof. Ing. Michele Salvemini Sommario I Codici I Sistemi di numerazione
Sommario. Sistema binario. I Sistemi di numerazione. Codifica ASCII. Valori Numerici Negativi. Valori Numerici Reali. Posizionali e non posizionali
 Corso di Laurea in Ingegneria Civile Politecnico di Bari Sede di Foggia Fondamenti di Informatica Anno Accademico 2011/2012 docente: Prof. Ing. Michele Salvemini Sommario I Codici I Sistemi di numerazione
Corso di Laurea in Ingegneria Civile Politecnico di Bari Sede di Foggia Fondamenti di Informatica Anno Accademico 2011/2012 docente: Prof. Ing. Michele Salvemini Sommario I Codici I Sistemi di numerazione
Sommario. I Sistemi di numerazione Posizionale e non Posizionale (1/2) I Codici. I Codici I Sistemi di numerazione Posizionali e non posizionali
 Corso di Laurea in Ingegneria Civile Politecnico di Bari Sede di Foggia Fondamenti di Informatica Anno Accademico 2011/2012 docente: Prof. Ing. Michele Salvemini Sommario I Codici I Sistemi di numerazione
Corso di Laurea in Ingegneria Civile Politecnico di Bari Sede di Foggia Fondamenti di Informatica Anno Accademico 2011/2012 docente: Prof. Ing. Michele Salvemini Sommario I Codici I Sistemi di numerazione
Fondamenti di Informatica - 1. Prof. B.Buttarazzi A.A. 2011/2012
 Fondamenti di Informatica - 1 Prof. B.Buttarazzi A.A. 2011/2012 Sommario Operazioni aritmetiche tra numeri in virgola mobile Algoritmi Esempi Errore di rappresentazione (assoluto e relativo) Approssimazione
Fondamenti di Informatica - 1 Prof. B.Buttarazzi A.A. 2011/2012 Sommario Operazioni aritmetiche tra numeri in virgola mobile Algoritmi Esempi Errore di rappresentazione (assoluto e relativo) Approssimazione
Rappresentazione dei numeri reali
 Rappresentazione dei numeri reali La rappresentazione dei numeri reali in base 2 è completamente analoga a quella in base : Parte intera + parte frazionaria, separate da un punto La parte frazionaria è
Rappresentazione dei numeri reali La rappresentazione dei numeri reali in base 2 è completamente analoga a quella in base : Parte intera + parte frazionaria, separate da un punto La parte frazionaria è
Corso di Sistemi di Elaborazione delle informazioni
 Corso di Sistemi di Elaborazione delle informazioni Sistemi di Numerazione Francesco Fontanella I sistemi di numerazione Sono stati inventati i SISTEMI DI NUMERAZIONE: Forme di rappresentazione dei numeri
Corso di Sistemi di Elaborazione delle informazioni Sistemi di Numerazione Francesco Fontanella I sistemi di numerazione Sono stati inventati i SISTEMI DI NUMERAZIONE: Forme di rappresentazione dei numeri
Aritmetica dei Calcolatori
 Aritmetica dei Calcolatori Luca Abeni e Luigi Palopoli February 18, 2016 Informazione nei Computer Un computer è un insieme di circuiti elettronici......in ogni circuito, la corrente può passare o non
Aritmetica dei Calcolatori Luca Abeni e Luigi Palopoli February 18, 2016 Informazione nei Computer Un computer è un insieme di circuiti elettronici......in ogni circuito, la corrente può passare o non
Parte III Indice. Rappresentazione dei valori frazionari. Esercizi. in virgola fissa in virgola mobile III.1. Fondamenti di Informatica
 Parte III Indice Rappresentazione dei valori frazionari in virgola fissa in virgola mobile Esercizi III.1 Rappresentazione dei valori frazionari I valori frazionari sono del tipo: xxxxxxx xxxx,yyyyy yyyy
Parte III Indice Rappresentazione dei valori frazionari in virgola fissa in virgola mobile Esercizi III.1 Rappresentazione dei valori frazionari I valori frazionari sono del tipo: xxxxxxx xxxx,yyyyy yyyy
