Teorema 8.1. Siano (f 1, B 1 ), (g 1, G 1 ) due elementi analitici di centro z 1 (f 0, B 0 ) lungo γ: riesce (f 1, B 1 ) = (g 1, G 1 )
|
|
|
- Valentina Martino
- 5 anni fa
- Visualizzazioni
Transcript
1 8. Unicitá del prolungamento Sia γ un arco di curva regolare da z 0 a z 1 z = γ(t), t [0, 1], z 0 = γ(0), z 1 = γ(1) (f 0, B 0 ) sia un elemento analitico di centro z 0 e supponiamo che esso sia prolungabile lungo γ Teorema 8.1. Siano (f 1, B 1 ), (g 1, G 1 ) due elementi analitici di centro z 1 (f 0, B 0 ) lungo γ: riesce (f 1, B 1 ) = (g 1, G 1 ) ottenuti come prolungamento di Dimostrazione. Siano (f t, B t ), e (g t, G t ) gli elementi analitici che realizzano i due prolungamenti. Indichiamo con Ω [0, 1] l insieme dei t per i quali riesce Ne segue (f t, B t ) = (g t, G t ) 0 Ω Ω Ω é aperto: sia t 0 Ω f t0 (z) = g t0 (z) z B t0 G t0 esiste inoltre δ > 0 tale che t t 0 < δ γ(t) B t0 G t0 e quindi (f t, B t ) = (f t0, B t0 ), (g t, G t ) = (g t0, G t0 ) z γ(t) f t (z) = g t (z) Ω é chiuso: siano t n Ω, t n t 0 ne segue γ(t n ) γ(t 0 ) e quindi, da un certo n in poi, { ftn (z) = f γ(t n ) B t0 G t0 t0 (z) g tn (z) = g t0 (z) tenuto conto che t n Ω f tn (z) = g tn (z) z B tn G tn ne segue anche f t0 (z) = g t0 (z) in un intorno di γ(t 0 ), ovvero t 0 Ω. {Ω [0, 1], Ω, Ω aperto, Ω chiuso } Ω = [0, 1] 1
2 2 Osservazione 8.2. Sia A l aperto unione dei cerchi di convergenza B t degli elementi analitici (f t, B t ) che realizzano il prolungamento lungo γ, se z 0 A allora z 0 appartiene a qualche cerchio B t, forse a piú d uno! Supponiamo z 0 B t1, z 0 B t2 non é detto che riesca f t1 (z 0 ) = f t2 (z 0 ) Si pensi, ad esempio al prolungamento di log(z) lungo una curva γ che parta da 1 ed esegua un certo numero di giri intorno all origine: il prolungamento di (f 0, B 0 ) con f 0 la serie di potenze di log(z) e B 0 : z 1 < 1 conduce ad un elemento analitico finale unico. Tuttavia i punti z appartenenti all unione A dei vari cerchi B t appartengono a piú d un cerchio B tk : ciascuno dei corrispondenti valori f tk (z) é diverso e corrisponde a diverse determinazioni del logaritmo Prolungamento su curve vicine. Proposizione 8.3. Siano z(t) = γ(t), z (t) = λ(t) t [0, 1] due curve regolari da z 0 a z 1 entrambe. Esista il prolungamento di (f 0, B 0 ) lungo γ e sia ε > 0 il minimo ε = min ρ(t) t [0,1] essendo ρ(t) il raggio dei cerchi B t relativi agli elementi del prolungamento lungo γ: allora se γ(t) λ(t) 1 3 ε l elemento (f 0, B 0 ) é prolungabile anche lungo λ e l elemento cui si perviene é uguale a quello cui si perviene prolungando (f 0, B 0 ) lungo γ. Dimostrazione. Definiamo il prolungamento lungo λ al modo seguente: per ogni t 0 [0, 1] consideriamo il cerchio J t0 di centro λ(t 0 ) e raggio ε/3. J t0 B t0 essendo B t0 il cerchio di centro γ(t 0 ) e raggio ρ(t 0 ) relativo al prolungamento lungo γ. Consideriamo gli elementi analitici (f t0, J t0 ) costruiti servendosi delle serie di potenze f t0 convergenti in J t0 B t0. La famiglia di elementi analitici (f t0, J t0 ), t 0 [0, 1]
3 9. IL TEOREMA DI MONODROMIA 3 costituisce un prolungamento di (f 0, B 0 ) lungo λ. occorre verificare perció che se λ(t) J t0 t [t 0, t 0 + δ] riesca ma questo é ovvio perché (f t, J t ) = (f t0, J t0 ) γ(t) γ(t 0 ) γ(t) λ(t) + λ(t) λ(t 0 ) + λ(t ) γ(t 0 ) < < 1 3 ε ε ε = ε e quindi (f t, B t ) = (f t0, B t0 ) da cui ovviamente (f t, J t ) = (f t0, J t0 ) L elemento cui si perviene a prolungamento lungo λ completato é (f 1, J 1 ) ovviamente continuo, cioé equivalente a (f 1, B 1 ) Infatti 9. Il teorema di monodromia Siano z(t) = γ(t), z (t) = λ(t) t [0, 1] due curve regolari contenute in Ω, da z 0 a z 1 entrambe. Figura 1. Curve omotopiche in z 0 Esse si dicono omotopiche tra loro nell aperto Ω se esiste un applicazione z(t, τ) del quadrato chiuso Q = [0, 1] [0, 1] in Ω tale che sia continua in Q,
4 4 z(0, τ) = z 0, z(1, τ) = z 1 τ [0, 1] z(t, 0) = γ(t), z(t, 1) = λ(t) Esempio 9.1. Le curve γ : x = t, y = 1 2 (1 t2 ) e λ : X0t, y = 5 2 (1 t2 ), vedi Figura 1, sono omotopiche nell aperto z 0 L applicazione z(t, τ) in questo caso é { u(t, τ) = t z(t, τ)u(t, τ) + iv(t, tau) v(t, τ) = 1 2 (1 + 2τ)(1 t2 ) Teorema 9.2. Se Ω é semplicemente connesso allora curve regolari aventi gli stessi estremi sono sempre omotopiche Il Teorema di monodromia. Teorema 9.3. Sia F analitica secondo Weierstrass, sia Ω il suo dominio: se Ω é semplicemente connesso, F non ha punti critici, allora é monodroma. Osservazione 9.4. La condizione é naturalmente sufficiente ma é molto lontana dall essere necessaria: tutte le funzioni razionali, ad esempio, hanno dominio non semplicemente connesso, hanno punti critici e, tuttavia, sono monodrome. Dimostrazione. Sia z(t, τ) la funzione che esprime l omotopia tra le due curve da z 0 a z 1 : indichiamo con γ τ le curve parametrizzate da z(t, τ) per ogni τ [0, 1]. L ipotesi che F sia priva di punti critici assicura che é possibile eseguire il prolungamento di un qualsiasi elemento analitico (f 0, B 0 ) F lungo γ τ. La possibilitá del prolungamento lungo ogni γ τ equivale a riconoscere che una corrispondenza (t, τ) (f t,τ, B t,τ ) Proviamo che ε = inf ρ(t, τ) > 0 (t,τ) Q avendo indicato al solito con ρ(t, τ) il raggio del cerchio B t,τ. Se per assurdo fosse ε = 0 allora esisterebbe una successione (t n, τ n ) tale che lim ρ(t n, τ n ) = 0, n lim τ n = τ n
5 Consideriamo la curve intermedia 9. IL TEOREMA DI MONODROMIA 5 γ τ : z(t, τ ) su di essa é, come sulle altre possibile il prolungamento: indichiamo con ε τ = inf t [0,1] ρ(t, τ ), ε τ > 0 il minimo dei raggi dei cerchi B t,τ relativi a tale prolungamento. Per l uniforme continuitá della funzione z(t, τ) del resto riesce, da un certo n in poi z(t, τ n ) z(t, τ ) < 1 3 ε τ quindi, per la Proposizione 8.3, su tali curve γ τn esistono prolungamenti on cerchi di raggi almeno 1 3 ε τ. Affermazione che nega l ipotesi accolta per assurdo che riesca lim ρ(t n, τ n ) = 0 n Riconosciuto pertanto che ε > 0 si passa dal prolungamento lungo la ai prolungamenti lungo curve γ 0 : z(t, 0) z(t, τ 1 ), z(t, τ 2 ),... ciascuna vicina alla precedente nel senso della Proposizione 8.3. Si riconosce quindi che il prolungamento da un punto z 0 ad un altro z 1 é unico, qualunque sia la curva che si segua. La monodromia deriva quindi dal seguente semplice ragionamento: assegnato un punto z 0 Ω esso apparterrá al cerchio di convergenza di un elemento analitico (f 1, B 1 ) F : f 1 (z 0 ) sará uno dei valori di F, gli altri (eventuali) valori derivano dagli altri elementi analitici f 2, B 2 ), (f 3, B 3 ),... F tali che z 0 B k k = 2, 3,... ma (f k, B k ) F sono W-equivalenti a (f 1, B 1 ), quindi sono ottenuti da esso per prolungamento il teorema di monodromia dice che il risultato del prolungamento non dipende dalla curva: ma allora (f k, B k ) = (f 1, B 1 ), k = 2, 3,... f k (z 0 ) = f 1 (z 0 ) ovvero F 8z 0 ) é costituito da un solo valore.
6 Le funzioni monodrome. Sono le ordinarie funzioni analitiche o funzioni olomorfe. Tenuto conto del teorema di monodromia si puó del resto parlare di rami olomorfi o determinazioni olomorfe, di funzioni analitiche polidrome tutte le volte che ci si restringe ad un aperto semplicemente connesso. Non esiste una funzione olomorfa logaritmo in z 0 ma esistono logaritmi olomorfi in ogni aperto semplicemente connesso. Figura 2. Regioni di olomorfia per il logaritmo: sí a sinistra, no a destra. Non esiste una funzione olomorfa arcsin(z) = i log(iz + 1 z 2 ) definita in tutto il piano ma esistono rami olomorfi in ogni aperto semplicemente connesso che non contenga né z = 1 né z = 1, punti critici di arcsin(z).
Funzioni analitiche secondo Weierstrass
 CAPITOLO 5 Funzioni analitiche secondo Weierstrass La maggior parte dei risultati illustrati in questo capitolo non saranno dimostrati.. Introduzione Consideriamo le due seguenti funzioni: ϕ(z) = k=0 z
CAPITOLO 5 Funzioni analitiche secondo Weierstrass La maggior parte dei risultati illustrati in questo capitolo non saranno dimostrati.. Introduzione Consideriamo le due seguenti funzioni: ϕ(z) = k=0 z
Le funzioni continue
 Le funzioni continue Sia 1. Limiti di funzioni f : E X Y con X e Y spazi metrici. Indichiamo con d X e rispettivamente d Y rispettive espressioni della distanza. Se p D(E) allora ha senso parlare del (eventuale)
Le funzioni continue Sia 1. Limiti di funzioni f : E X Y con X e Y spazi metrici. Indichiamo con d X e rispettivamente d Y rispettive espressioni della distanza. Se p D(E) allora ha senso parlare del (eventuale)
Il teorema di Goursat
 CAPITOLO 8 Il teorema di Goursat. Premessa Sia f una funzione assegnata in un disco B: per rappresentarla con il Teorema di Rappresentazione di Cauchy é stato sfruttato che, R B risultato conseguito sotto
CAPITOLO 8 Il teorema di Goursat. Premessa Sia f una funzione assegnata in un disco B: per rappresentarla con il Teorema di Rappresentazione di Cauchy é stato sfruttato che, R B risultato conseguito sotto
Il teorema di rappresentazione
 APITOLO 6 Il teorema di rappresentazione. Introduzione Lemma.. Sia una circonferenza e sia A il cerchio racchiuso: riesce 2π i Dimostrazione. Primo caso: z / A = 0 se z / A se z A La funzione = é analitica
APITOLO 6 Il teorema di rappresentazione. Introduzione Lemma.. Sia una circonferenza e sia A il cerchio racchiuso: riesce 2π i Dimostrazione. Primo caso: z / A = 0 se z / A se z A La funzione = é analitica
Alcuni Teoremi sulle funzioni continue e uniforme continuità
 Alcuni Teoremi sulle funzioni continue e uniforme continuità Teorema 0. Una funzione f(x) è continua in x 0 se e solo se per ogni sucessione {x n } dom(f) con x n x 0 dom(f), risulta f(x n ) f(x 0 ). (Non
Alcuni Teoremi sulle funzioni continue e uniforme continuità Teorema 0. Una funzione f(x) è continua in x 0 se e solo se per ogni sucessione {x n } dom(f) con x n x 0 dom(f), risulta f(x n ) f(x 0 ). (Non
Serie prodotto. b k = B. a k = A,
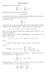 Assegnate due serie convergenti a k = A, Serie prodotto b k = B vogliamo occuparci di dare senso alla frase serie prodotto con la pretesa che tale serie prodotto converga e abbia somma il prodotto A B
Assegnate due serie convergenti a k = A, Serie prodotto b k = B vogliamo occuparci di dare senso alla frase serie prodotto con la pretesa che tale serie prodotto converga e abbia somma il prodotto A B
La convergenza uniforme
 La convergenza uniforme 1. Il tubo Sia {f n (x)} una successione convergente a f(x) per x E: disegniamo il grafico della funzione limite f(x) assegnato ε > 0 disegniamo la striscia - il tubo - intorno
La convergenza uniforme 1. Il tubo Sia {f n (x)} una successione convergente a f(x) per x E: disegniamo il grafico della funzione limite f(x) assegnato ε > 0 disegniamo la striscia - il tubo - intorno
Analisi vettoriale - A.A. 2003/04
 Soluzioni Analisi vettoriale - A.A. 2003/04 Foglio di esercizi n.7 1. Esercizio Studiare la convergenza delle seguenti serie di potenze: 2 n (n + 3)! x n 3(x 2) n, (2n)! log (n + 1). (1) 1.1. Soluzione.
Soluzioni Analisi vettoriale - A.A. 2003/04 Foglio di esercizi n.7 1. Esercizio Studiare la convergenza delle seguenti serie di potenze: 2 n (n + 3)! x n 3(x 2) n, (2n)! log (n + 1). (1) 1.1. Soluzione.
Argomenti della Lezione
 ANALISI Argomenti della Lezione 10 novembre 2011 16. Funzioni continue La definizione di funzione continua tramite la definizione di limite: f : (a, b) R é continua nel punto x 0 (a, b) se esiste l = f(x
ANALISI Argomenti della Lezione 10 novembre 2011 16. Funzioni continue La definizione di funzione continua tramite la definizione di limite: f : (a, b) R é continua nel punto x 0 (a, b) se esiste l = f(x
Spazi di Banach classici
 Spazi di Banach classici 1. Gli spazi L p ([, 1]) Le funzioni misurabili su [, 1] costituiscono uno spazio vettoriale V. Definizione 1.1. Due funzioni f, g V si dicono uguali quasi ovunque se esiste N
Spazi di Banach classici 1. Gli spazi L p ([, 1]) Le funzioni misurabili su [, 1] costituiscono uno spazio vettoriale V. Definizione 1.1. Due funzioni f, g V si dicono uguali quasi ovunque se esiste N
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
Rappresentazione conforme
 CAPITOLO 13 Rappresentazione conforme Ahlfors, pag.73,...,99 concetto ed esempi elementari, il gruppo lineare, enunciato del teorema di Riemann, problema di Dirichlet per il 2 nel cerchio, formula di Poisson.
CAPITOLO 13 Rappresentazione conforme Ahlfors, pag.73,...,99 concetto ed esempi elementari, il gruppo lineare, enunciato del teorema di Riemann, problema di Dirichlet per il 2 nel cerchio, formula di Poisson.
CAPITOLO 9. Le serie di potenze
 CAPITOLO 9 Le serie di potenze Ahlfors, pag. 33,..,45 Bozza da rivedere Le funzioni analitiche sono piú o meno polinomi in z, o i loro limiti, somme di serie di potenze in z. Prerequisiti fondamentali
CAPITOLO 9 Le serie di potenze Ahlfors, pag. 33,..,45 Bozza da rivedere Le funzioni analitiche sono piú o meno polinomi in z, o i loro limiti, somme di serie di potenze in z. Prerequisiti fondamentali
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria. Curve nello spazio Gennaio Lunghezza d arco
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria Curve nello spazio Gennaio 013 Indice 1 Lunghezza d arco 1 1.1 Parametrizzazione alla lunghezza d arco..................... 1. Ogni
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria Curve nello spazio Gennaio 013 Indice 1 Lunghezza d arco 1 1.1 Parametrizzazione alla lunghezza d arco..................... 1. Ogni
 Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
22 gennaio Esercizio. Disegnare i sottoinsiemi del piano determinati dalle seguenti disuguaglianze:
 ANALISI Soluzioni del Foglio 13 22 gennaio 2010 13.1. Esercizio. Disegnare i sottoinsiemi del piano determinati dalle seguenti disuguaglianze: x + y < 2, x 1 < 0, y < 3, max( x, y ) 4 x + y < 2 Se un punto
ANALISI Soluzioni del Foglio 13 22 gennaio 2010 13.1. Esercizio. Disegnare i sottoinsiemi del piano determinati dalle seguenti disuguaglianze: x + y < 2, x 1 < 0, y < 3, max( x, y ) 4 x + y < 2 Se un punto
SPAZI COMPATTI. Proposizione 2 Sia (X, d) uno spazio metrico. Se esso è sequenzialmente compatto allora è completo.
 SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
12. Funzioni numeriche misurabili.
 12. Funzioni numeriche misurabili. 12.1. Funzioni numeriche misurabili. D ora in avanti, nel corso di questi appunti, adotteremo la seguente terminologia: per far riferimento ad una funzione f : Ω R, per
12. Funzioni numeriche misurabili. 12.1. Funzioni numeriche misurabili. D ora in avanti, nel corso di questi appunti, adotteremo la seguente terminologia: per far riferimento ad una funzione f : Ω R, per
Soluzioni del Foglio 7
 7.1. Esercizio. Assegnate le funzioni ANALISI Soluzioni del Foglio 7 18 novembre 2009 e e sin(), dire quali possono essere prolungate per continuitá in = 0, studiare, per le funzioni che risultino prolungabili
7.1. Esercizio. Assegnate le funzioni ANALISI Soluzioni del Foglio 7 18 novembre 2009 e e sin(), dire quali possono essere prolungate per continuitá in = 0, studiare, per le funzioni che risultino prolungabili
si ha La lunghezza L si calcola per ciascun tratto L = (2t)2 + (3t 2 ) dt+ 2 (3t2 ) 2 + (2t) 2 dt = 4t2 + 9t 4 dt = t
 ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
Successioni di funzioni
 Successioni di funzioni 1. Primi esempi 1, x, x 2, x 3,..., x n,..., x [0, 2] e x, e 2x, e 3x,..., e nx,..., x [ 1, 1] f n (x) = 1, n = 1, 2, 3,..., x R (n + 1) 2 + x2 f n (x) = sin(x), n = 1, 2, 3,...,
Successioni di funzioni 1. Primi esempi 1, x, x 2, x 3,..., x n,..., x [0, 2] e x, e 2x, e 3x,..., e nx,..., x [ 1, 1] f n (x) = 1, n = 1, 2, 3,..., x R (n + 1) 2 + x2 f n (x) = sin(x), n = 1, 2, 3,...,
Definizione 1.1. Sia A un sottoinsieme dei numeri reali. Diciamo che A è un insieme induttivo se
 1 Numeri naturali, interi e razionali Definizione 1.1. Sia A un sottoinsieme dei numeri reali. Diciamo che A è un insieme induttivo se 1. 1 A. per ogni x A, si ha x + 1 A Definizione 1.. Chiamo insieme
1 Numeri naturali, interi e razionali Definizione 1.1. Sia A un sottoinsieme dei numeri reali. Diciamo che A è un insieme induttivo se 1. 1 A. per ogni x A, si ha x + 1 A Definizione 1.. Chiamo insieme
Geometria iperbolica - Primo foglio Andrea Petracci
 Geometria iperbolica - Primo foglio Andrea Petracci Esercizio 1. Teorema (Hopf-Rinow). Se M è una varietà riemanniana connessa, allora le seguenti affermazioni sono equivalenti: (1) M è completa con la
Geometria iperbolica - Primo foglio Andrea Petracci Esercizio 1. Teorema (Hopf-Rinow). Se M è una varietà riemanniana connessa, allora le seguenti affermazioni sono equivalenti: (1) M è completa con la
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Funzioni reali continue
 E-school di Arrigo Amadori Analisi I Funzioni reali continue 01 Introduzione. Fra tutte le funzioni numeriche reali, le funzioni continue assumono una importanza particolare. Le funzioni continue rappresentano
E-school di Arrigo Amadori Analisi I Funzioni reali continue 01 Introduzione. Fra tutte le funzioni numeriche reali, le funzioni continue assumono una importanza particolare. Le funzioni continue rappresentano
Primi elementi di topologia dell asse reale. Intorni
 Primi elementi di topologia dell asse reale. Intorni R è uno spazio metrico: La distanza d(x, y) tra due numeri reali x, y è il valore assoluto della loro differenza: d(x, y) = x y Definizione (Intorno
Primi elementi di topologia dell asse reale. Intorni R è uno spazio metrico: La distanza d(x, y) tra due numeri reali x, y è il valore assoluto della loro differenza: d(x, y) = x y Definizione (Intorno
Funzioni di più variabli: dominio, limiti, continuità
 Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità
 Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Massimo e minimo limite di successioni
 Massimo e minimo limite di successioni 1 Premesse Definizione 1.1. Definiamo R esteso l insieme R = R { } {+ }. In R si estende l ordinamento tra numeri reali ponendo < a < +, a R. In base a tale definizione,
Massimo e minimo limite di successioni 1 Premesse Definizione 1.1. Definiamo R esteso l insieme R = R { } {+ }. In R si estende l ordinamento tra numeri reali ponendo < a < +, a R. In base a tale definizione,
L espressione generale
 espressione generale Consideriamo equazioni differenziali di primo ordine di forma generale: in luogo della espressione lineare y = a(t)y + b(t) consideriamo, a secondo membro, un espressione y = f(t,
espressione generale Consideriamo equazioni differenziali di primo ordine di forma generale: in luogo della espressione lineare y = a(t)y + b(t) consideriamo, a secondo membro, un espressione y = f(t,
Esistenza ed unicità per equazioni differenziali
 Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
Federico Lastaria. Analisi e Geometria 1. Numeri reali 1/25
 Massimi e minimi Definizione (Massimo) Sia X R un sottoinsieme non vuoto. Si dice che M R è il massimo di X (e si scrive M = max X ) se: M X ; x X, x M. Definizione (Minimo) Sia X R un sottoinsieme non
Massimi e minimi Definizione (Massimo) Sia X R un sottoinsieme non vuoto. Si dice che M R è il massimo di X (e si scrive M = max X ) se: M X ; x X, x M. Definizione (Minimo) Sia X R un sottoinsieme non
11. Misure con segno.
 11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
Insiemi numerici. Definizioni
 1 Insiemi numerici Gli insiemi numerici sono insiemi i cui elementi sono numeri, cioè appartengono all'insieme N dei naturali, degli interi Z, dei razionali Q, dei reali R o dei complessi C ( es.: A =
1 Insiemi numerici Gli insiemi numerici sono insiemi i cui elementi sono numeri, cioè appartengono all'insieme N dei naturali, degli interi Z, dei razionali Q, dei reali R o dei complessi C ( es.: A =
2x 2. Soluzione: Il valore del limite l non puó che essere 1: infatti. Per determinare δ basta studiare la disuguaglianza. x 1. x 1 x 1.
 4.. Esercizio. Calcolare il ite { l = x x }, x e determinare δ tale che < δ implichi { x x } l < 0.5 ANALISI Soluzioni del Foglio 4 30 ottobre 009 Il valore del ite l non puó che essere : infatti { x x
4.. Esercizio. Calcolare il ite { l = x x }, x e determinare δ tale che < δ implichi { x x } l < 0.5 ANALISI Soluzioni del Foglio 4 30 ottobre 009 Il valore del ite l non puó che essere : infatti { x x
Successioni numeriche
 Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
NOTE SU EQUAZIONI DIFFERENZIALI ORDINARIE
 NOTE SU EQUAZIONI DIFFERENZIALI ORDINARIE ROBERTO GIAMBÒ INDICE 1. Spazi metrici e spazi normati 1 1.1. Contrazioni 2 2. Lo spazio delle curve continue 4 2.1. Spazi di Banach 4 3. Esistenza e unicità locale
NOTE SU EQUAZIONI DIFFERENZIALI ORDINARIE ROBERTO GIAMBÒ INDICE 1. Spazi metrici e spazi normati 1 1.1. Contrazioni 2 2. Lo spazio delle curve continue 4 2.1. Spazi di Banach 4 3. Esistenza e unicità locale
Esercitazioni di Geometria II
 Esercitazioni di Geometria II Letizia Pernigotti - pernigotti@science.unitn.it 8 maggio 202 Esercizio. [Metrica del riccio] Si considieri R 2 munito della metrica del riccio, la quale è definita da y x
Esercitazioni di Geometria II Letizia Pernigotti - pernigotti@science.unitn.it 8 maggio 202 Esercizio. [Metrica del riccio] Si considieri R 2 munito della metrica del riccio, la quale è definita da y x
Alcune nozioni di calcolo differenziale
 Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Figura 1. F = {y 2, x 2 }
 ANALISI VETTORIALE Soluzione esercizi 14 gennaio 211 7.1. Esercizio. Assegnato il campo vettoriale F = y 2, x 2 calcolare la circuitazione τ ds ovvero ( y 2 dx + x 2 dy ) essendo Ω il quadrato di vertici
ANALISI VETTORIALE Soluzione esercizi 14 gennaio 211 7.1. Esercizio. Assegnato il campo vettoriale F = y 2, x 2 calcolare la circuitazione τ ds ovvero ( y 2 dx + x 2 dy ) essendo Ω il quadrato di vertici
Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che
 1 Spazi metrici Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che 1) d(x, y) 0, x, y X; d(x, y) = 0 x = y, ) d(x, y) = d(y, x), x, y X, 3) d(x, z) d(x, y) +
1 Spazi metrici Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che 1) d(x, y) 0, x, y X; d(x, y) = 0 x = y, ) d(x, y) = d(y, x), x, y X, 3) d(x, z) d(x, y) +
Capitolo 5. Serie di Laurent. 5.1 Sviluppo in una corona circolare
 Capitolo 5 Serie di Laurent Mentre la serie di Taylor è lo strumento più idoneo per lo studio di una funzione olomorfa nell'intorno di un suo punto di regolarità, per il suo studio in un punto singolare
Capitolo 5 Serie di Laurent Mentre la serie di Taylor è lo strumento più idoneo per lo studio di una funzione olomorfa nell'intorno di un suo punto di regolarità, per il suo studio in un punto singolare
c i χ Ai (x) f(x) = f(x)dx = c i m(a i ) R
 1. Integrale di Lebesgue in La differenza fondamentale tra integrale di Lebesgue e integrale di iemann consiste nella diversa scelta delle decomposizioni su cui sostanzialmente si basa ogni integrale:
1. Integrale di Lebesgue in La differenza fondamentale tra integrale di Lebesgue e integrale di iemann consiste nella diversa scelta delle decomposizioni su cui sostanzialmente si basa ogni integrale:
[A-E] IST. DI MATEMATICA I. 3. Lezione. giovedì 6 ottobre Massimo e minimo.
![[A-E] IST. DI MATEMATICA I. 3. Lezione. giovedì 6 ottobre Massimo e minimo. [A-E] IST. DI MATEMATICA I. 3. Lezione. giovedì 6 ottobre Massimo e minimo.](/thumbs/72/67665235.jpg) IST. DI MATEMATICA I [A-E] giovedì 6 ottobre 2016 3. Lezione 3.1. Massimo e minimo. Definizioni di minimo e/o massimo per un insieme E di numeri reali: il numero min si dice minimo dell insieme E se min
IST. DI MATEMATICA I [A-E] giovedì 6 ottobre 2016 3. Lezione 3.1. Massimo e minimo. Definizioni di minimo e/o massimo per un insieme E di numeri reali: il numero min si dice minimo dell insieme E se min
Le funzioni con+nue (1)
 Le funzioni con+nue (1) Definizioni: - Sia I un intervallo, x 0 I. Una funzione f : I R è con$nua in x 0 se lim x x0 f(x) = f(x 0 ). La funzione f è con$nua nell'intervallo I se è con+nua in ogni punto
Le funzioni con+nue (1) Definizioni: - Sia I un intervallo, x 0 I. Una funzione f : I R è con$nua in x 0 se lim x x0 f(x) = f(x 0 ). La funzione f è con$nua nell'intervallo I se è con+nua in ogni punto
determinare una soluzione y(t) dell equazione completa e, quindi dedurne tutte le y(t) soluzioni dell equazione.
 ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
8. Completamento di uno spazio di misura.
 8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
Limiti e continuità. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68
 Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Matematica per le Scienze Sociali
 atematica per le Scienze Sociali Limite Passaggio al ite Continuità della unzione 5//05 Clelia Cascella Deinizione intuitiva di ite Se () è una unzione reale, se c ed l sono dei numeri reali, dire che
atematica per le Scienze Sociali Limite Passaggio al ite Continuità della unzione 5//05 Clelia Cascella Deinizione intuitiva di ite Se () è una unzione reale, se c ed l sono dei numeri reali, dire che
Studio qualitativo del grafico di una funzione
 Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
Le funzioni razionali
 CAPITOLO 3 Le funzioni razionali vedi Ahlfors, pag. 30, 3, 32 Definizione... Introduzione R(z) = P (z) Q(z) con P (z) e Q(z) due polinomi privi di zeri comuni. Siano β, β 2,..., β q gli zeri del polinomio
CAPITOLO 3 Le funzioni razionali vedi Ahlfors, pag. 30, 3, 32 Definizione... Introduzione R(z) = P (z) Q(z) con P (z) e Q(z) due polinomi privi di zeri comuni. Siano β, β 2,..., β q gli zeri del polinomio
Consideriamo un sistema dinamico tempo-invariante descritto da:
 IL PROBLEMA DELLA STABILITA Il problema della stabilità può essere affrontato in vari modi. Quella adottata qui, per la sua riconosciuta generalità ed efficacia, è l impostazione classica dovuta a M. A.
IL PROBLEMA DELLA STABILITA Il problema della stabilità può essere affrontato in vari modi. Quella adottata qui, per la sua riconosciuta generalità ed efficacia, è l impostazione classica dovuta a M. A.
Definizione DEFINIZIONE. Funzione reale di due variabili reali Indichiamo con R 2 l insieme di tutti i vettori bidimensionali.
 Definizione DEFINIZIONE Funzione reale di due variabili reali Indichiamo con R 2 l insieme di tutti i vettori bidimensionali. Dato un sottoinsiemed R 2, una funzione f: D R è una legge che assegna a ogni
Definizione DEFINIZIONE Funzione reale di due variabili reali Indichiamo con R 2 l insieme di tutti i vettori bidimensionali. Dato un sottoinsiemed R 2, una funzione f: D R è una legge che assegna a ogni
Funzioni continue. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Funzioni continue Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 1 / 44 Funzioni continue Definizione Siano f : A
Funzioni continue Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 1 / 44 Funzioni continue Definizione Siano f : A
Complementi di Analisi Matematica Ia. Carlo Bardaro
 Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Argomenti della Lezione
 13.1. Limiti all infinito. Sia ANALISI Argomenti della Lezione 13. Limiti di funzioni f : (a, + ) R ha senso cercare f(x) x + Esso, se esiste, é un numero l R ha la proprietá di ite 3 novembre 2011 ε >
13.1. Limiti all infinito. Sia ANALISI Argomenti della Lezione 13. Limiti di funzioni f : (a, + ) R ha senso cercare f(x) x + Esso, se esiste, é un numero l R ha la proprietá di ite 3 novembre 2011 ε >
Equazioni differenziali
 Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
Studio qualitativo. Emanuele Paolini 2 luglio 2002
 Studio qualitativo Emanuele Paolini 2 luglio 2002 Non sempre è possibile determinare esplicitamente le soluzione di una equazione differenziale. Ci proponiamo quindi di trovare dei metodi per determinare
Studio qualitativo Emanuele Paolini 2 luglio 2002 Non sempre è possibile determinare esplicitamente le soluzione di una equazione differenziale. Ci proponiamo quindi di trovare dei metodi per determinare
ANALISI MATEMATICA A SECONDO MODULO SOLUZIONI DEGLI ESERCIZI DELLA SETTIMANA 15. x 2 i
 ANALISI MATEMATICA A SECONDO MODULO SOLUZIONI DEGLI ESERCIZI DELLA SETTIMANA 15 (1) (Es 9 pag 117) Se per ogni x R n ( x := x 2 i ) 1/2 verificate che per ogni x, y R n vale la seguente legge del parallelogramma:
ANALISI MATEMATICA A SECONDO MODULO SOLUZIONI DEGLI ESERCIZI DELLA SETTIMANA 15 (1) (Es 9 pag 117) Se per ogni x R n ( x := x 2 i ) 1/2 verificate che per ogni x, y R n vale la seguente legge del parallelogramma:
p 1 : x + y + z = 0, p 2 : x y 2z = 1 Soluzione: Punto-retta
 ANALISI VETTORIALE Soluzione esercizi 12 novembre 2010 3.1. Esercizio. Determinare la distanza del punto Q = (3, 4) dalla retta r : x + y = 3, ovvero determinare il minimo della funzione f(x, y) = (x 3)
ANALISI VETTORIALE Soluzione esercizi 12 novembre 2010 3.1. Esercizio. Determinare la distanza del punto Q = (3, 4) dalla retta r : x + y = 3, ovvero determinare il minimo della funzione f(x, y) = (x 3)
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Successioni numeriche
 Successioni numeriche Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni Analisi A 1 / 35 Definizione Una successione a valori reali è una funzione f : N R
Successioni numeriche Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni Analisi A 1 / 35 Definizione Una successione a valori reali è una funzione f : N R
Campi conservativi. Riccarda Rossi. Università di Brescia. Analisi Matematica B
 Campi conservativi Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Campi conservativi Analisi Matematica B 1 / 99 Premessa Riccarda Rossi (Università di
Campi conservativi Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Campi conservativi Analisi Matematica B 1 / 99 Premessa Riccarda Rossi (Università di
Equazione di Laplace
 Equazione di Laplace. Introduzione Si da il nome di operatore di Laplace o laplaciano all operatore differenziale u = u xx + u yy + u zz in tre dimensioni, o agli analoghi in dimensioni diverse. L operatore
Equazione di Laplace. Introduzione Si da il nome di operatore di Laplace o laplaciano all operatore differenziale u = u xx + u yy + u zz in tre dimensioni, o agli analoghi in dimensioni diverse. L operatore
Curve parametrizzate. Esercizi. 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione
 Curve parametrizzate. Esercizi Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 014. 1 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione Qui di seguito si riporta
Curve parametrizzate. Esercizi Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 014. 1 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione Qui di seguito si riporta
Esercizi su curvatura e torsione.
 Esercizi su curvatura e torsione. e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 016. 1 Indice 1 Curvatura e torsione 1.1 Curve parametrizzate alla lunghezza d arco................... 1.
Esercizi su curvatura e torsione. e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 016. 1 Indice 1 Curvatura e torsione 1.1 Curve parametrizzate alla lunghezza d arco................... 1.
Massimo limite e minimo limite di una funzione
 Massimo limite e minimo limite di una funzione Sia f : A R una funzione, e sia p DA). Per ogni r > 0, l insieme ) E f p r) = { fx) x A I r p) \ {p} } è non vuoto; inoltre E f p r ) E f p r ) se 0 < r r.
Massimo limite e minimo limite di una funzione Sia f : A R una funzione, e sia p DA). Per ogni r > 0, l insieme ) E f p r) = { fx) x A I r p) \ {p} } è non vuoto; inoltre E f p r ) E f p r ) se 0 < r r.
7 Il Teorema di Bolzano - Weierstrass
 dimostrazione di (3.6). Supponiamo per esempio che f sia crescente e che x 0 < b Poniamo l + := inf f(x) x I,x 0
dimostrazione di (3.6). Supponiamo per esempio che f sia crescente e che x 0 < b Poniamo l + := inf f(x) x I,x 0
1-Forme Differenziali
 1-Forme Differenziali 30 novembre 2011 1 Definizioni di base Siano n N e A R n un insieme aperto. Con (R n ) denotiamo il duale topologico di R n, cioè l insieme (R n ) = {p : R n R : R-lineari e continue}.
1-Forme Differenziali 30 novembre 2011 1 Definizioni di base Siano n N e A R n un insieme aperto. Con (R n ) denotiamo il duale topologico di R n, cioè l insieme (R n ) = {p : R n R : R-lineari e continue}.
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2 Padova, 6.7.208 Si svolgano i seguenti esercizi facendo attenzione a giustificare le risposte. Delle affermazioni non motivate
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2 Padova, 6.7.208 Si svolgano i seguenti esercizi facendo attenzione a giustificare le risposte. Delle affermazioni non motivate
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Matematica I. Francesco Bonsante e Giuseppe Da Prato
 Matematica I Francesco Bonsante e Giuseppe Da Prato 31 Maggio 2008 Contents 1 Numeri reali 1 1.1 Sottoinsiemi di Q......................... 1 1.1.1 Estremo superiore e estremo inferiore.......... 2 1.2
Matematica I Francesco Bonsante e Giuseppe Da Prato 31 Maggio 2008 Contents 1 Numeri reali 1 1.1 Sottoinsiemi di Q......................... 1 1.1.1 Estremo superiore e estremo inferiore.......... 2 1.2
FAM. Un PM si muove nel piano xy e la sua traiettoria è un arco di cerchio di raggio R.
 Serie 9: Meccanica II FAM C. Ferrari Esercizio 1 Moto circolare uniforme (bis) Un PM si muove nel piano xy e la sua traiettoria è un arco di cerchio di raggio R. 1. Parametrizza la traiettoria con l ascissa
Serie 9: Meccanica II FAM C. Ferrari Esercizio 1 Moto circolare uniforme (bis) Un PM si muove nel piano xy e la sua traiettoria è un arco di cerchio di raggio R. 1. Parametrizza la traiettoria con l ascissa
Principali differenze tra la ristampa 2014 e l edizione 2008
 Principali differenze tra la ristampa 214 e l edizione 28 Di seguito sono riportate le principali modifiche apportate al testo dell edizione 28 con la ristampa riveduta e corretta del 214. Si avverte il
Principali differenze tra la ristampa 214 e l edizione 28 Di seguito sono riportate le principali modifiche apportate al testo dell edizione 28 con la ristampa riveduta e corretta del 214. Si avverte il
FUNZIONI CONTINUE E SEMICONTINUE
 Capitolo 5 FUNZIONI CONTINUE E SEMICONTINUE 5. DEFINIZIONI E PRIME PROPRIET Siano E ed F due spazi metrici con metriche d e δ; sia f una applicazione di E in F. Definizione 5... Si dice che f è continua
Capitolo 5 FUNZIONI CONTINUE E SEMICONTINUE 5. DEFINIZIONI E PRIME PROPRIET Siano E ed F due spazi metrici con metriche d e δ; sia f una applicazione di E in F. Definizione 5... Si dice che f è continua
Topologia, continuità, limiti in R n
 Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 2008/2009 Prof. C. Presilla. Prova in itinere 17 Aprile 2009
 MODELLI E METODI MATEMATICI DELLA FISICA A.A. 2008/2009 Prof. C. Presilla Prova in itinere 17 Aprile 2009 Cognome Nome penalità esercizio voto 1 2 3 4 5 6 Esercizio 1 Determinare per quali z C è convergente
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 2008/2009 Prof. C. Presilla Prova in itinere 17 Aprile 2009 Cognome Nome penalità esercizio voto 1 2 3 4 5 6 Esercizio 1 Determinare per quali z C è convergente
Teoria di Lebesgue. P n E = n=1
 Teoria di Lebesgue 1. La misura di Peano-Jordan La misura di Peano Jordan di un insieme é quasi sempre proposta per sottoinsiemi limitati E R 2 : si tratta di quanto suggerito dalla carta quadrettata,
Teoria di Lebesgue 1. La misura di Peano-Jordan La misura di Peano Jordan di un insieme é quasi sempre proposta per sottoinsiemi limitati E R 2 : si tratta di quanto suggerito dalla carta quadrettata,
Registro dell insegnamento. Emanuele Paolini
 UNIVERSITÀ DEGLI STUDI DI FIRENZE Registro dell insegnamento Anno Accademico 2009/2010 Facoltà: Insegnamento: Ingegneria (Università di Pisa) Analisi Matematica II e Complementi di Analisi Matematica Settore:..........................
UNIVERSITÀ DEGLI STUDI DI FIRENZE Registro dell insegnamento Anno Accademico 2009/2010 Facoltà: Insegnamento: Ingegneria (Università di Pisa) Analisi Matematica II e Complementi di Analisi Matematica Settore:..........................
Equazioni differenziali lineari
 CAPITOLO 15 Equazioni differenziali lineari 1. Il problema Assegnata l equazione differenziale lineare a 0 (z)w [n] + a 1 (z)w [n 1] +... + a n (z)w = b(z) dove le funzioni a 0 (z),..., a n (z), b(z) sono
CAPITOLO 15 Equazioni differenziali lineari 1. Il problema Assegnata l equazione differenziale lineare a 0 (z)w [n] + a 1 (z)w [n 1] +... + a n (z)w = b(z) dove le funzioni a 0 (z),..., a n (z), b(z) sono
3 La curva di Peano. insieme di misura nulla in R m. Definiamo, ora,
 Versione del 5/0/04 3 La curva di Peano Proposizione (a) Sia f : A R n R m con n < m. Se f è una funzione lipschitziana, allora f(a) è un insieme di misura nulla in R m. (b) Esiste una funzione ϕ C ( [0,
Versione del 5/0/04 3 La curva di Peano Proposizione (a) Sia f : A R n R m con n < m. Se f è una funzione lipschitziana, allora f(a) è un insieme di misura nulla in R m. (b) Esiste una funzione ϕ C ( [0,
Analisi Vettoriale - A.A Foglio di Esercizi n Esercizio
 Analisi Vettoriale - A.A. 3-4 Foglio di Esercizi n. 8 Soluzioni Dire se le funzioni. Esercizio sin (x) (x + )x, e x x, x x sono integrabili in senso classico o improprio negli intervalli [, ] e (, + ).
Analisi Vettoriale - A.A. 3-4 Foglio di Esercizi n. 8 Soluzioni Dire se le funzioni. Esercizio sin (x) (x + )x, e x x, x x sono integrabili in senso classico o improprio negli intervalli [, ] e (, + ).
Generalizzazioni del Teorema di Weierstrass
 Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
Modulo 5 Funzioni di piú variabili. A. Scanu
 Modulo 5 Funzioni di piú variabili A. Scanu 1 1 Generalitá In questo modulo studieremo funzioni di piú di una variabile cioé del tipo f : R n R m con n, m 1. In particolare prenderemo in considerazione
Modulo 5 Funzioni di piú variabili A. Scanu 1 1 Generalitá In questo modulo studieremo funzioni di piú di una variabile cioé del tipo f : R n R m con n, m 1. In particolare prenderemo in considerazione
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 17 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 17/10/2008 1 / 9 Definizione. Dati due numeri reali a e b,
Lezioni di Matematica 1 - I modulo Luciano Battaia 17 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 17/10/2008 1 / 9 Definizione. Dati due numeri reali a e b,
ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio. A. Figà Talamanca
 ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio A. Figà Talamanca 14 ottobre 2010 2 0.1 Ancora limiti di funzioni di variabile reale Esercizio 1 Sia f(x) = [sin x] definita nell insieme [0,
ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio A. Figà Talamanca 14 ottobre 2010 2 0.1 Ancora limiti di funzioni di variabile reale Esercizio 1 Sia f(x) = [sin x] definita nell insieme [0,
Se la serie converge in C, il limite a cui tende si chiama somma della serie.
 E-school di Arrigo Amadori Analisi I Serie di potenze 01 Introduzione. Le serie di potenze sono molto importanti perché costituiscono il punto di partenza per approssimare una funzione qualunque. Sono
E-school di Arrigo Amadori Analisi I Serie di potenze 01 Introduzione. Le serie di potenze sono molto importanti perché costituiscono il punto di partenza per approssimare una funzione qualunque. Sono
Esercizi. Soluzione: 1. Indicando con P il peso iniziale del materiale, si deve avere. . Il tempo richiesto è 800 log
 Esercizi Esercizio 4. Un materiale radioattivo è caratterizzato da un tempo di dimezzamento pari a 800 anni. Dopo quanto tempo un campione di tale materiale si sarà ridotto del 15%? Qual è il tempo di
Esercizi Esercizio 4. Un materiale radioattivo è caratterizzato da un tempo di dimezzamento pari a 800 anni. Dopo quanto tempo un campione di tale materiale si sarà ridotto del 15%? Qual è il tempo di
COMPLETEZZA DELL INSIEME DEI NUMERI REALI R.
 COMPLETEZZA DELL INSIEME DEI NUMERI REALI R. FABIO CIPRIANI 1. Completezza dell insieme dei numeri reali R. Nell insieme dei numeri reali R la condizione di Cauchy e necessaria e sufficiente per la convergenza
COMPLETEZZA DELL INSIEME DEI NUMERI REALI R. FABIO CIPRIANI 1. Completezza dell insieme dei numeri reali R. Nell insieme dei numeri reali R la condizione di Cauchy e necessaria e sufficiente per la convergenza
Corso di Analisi Matematica Successioni e loro limiti
 Corso di Analisi Matematica Successioni e loro limiti Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 30 1 Definizione di successione
Corso di Analisi Matematica Successioni e loro limiti Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 30 1 Definizione di successione
11.3 Teorema di esistenza e unicità della soluzione
 11. PROBLEMA DI CAUCHY: ESISTENZA E UNICITÀ DELLA SOLUZIONE 121 11.3 Teorema di esistenza e unicità della soluzione Ricordiamo (cfr. l esercizio 6 del capitolo 2) che, dati uno spazio vettoriale normato
11. PROBLEMA DI CAUCHY: ESISTENZA E UNICITÀ DELLA SOLUZIONE 121 11.3 Teorema di esistenza e unicità della soluzione Ricordiamo (cfr. l esercizio 6 del capitolo 2) che, dati uno spazio vettoriale normato
COMPATTEZZA. i) X è compatto, cioè ogni ricoprimento aperto ammette un sottoricoprimento finito.
 1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
Analisi Vettoriale A.A Soluzioni del Foglio 2
 Analisi Vettoriale A.A. 2006-2007 - Soluzioni del Foglio 2 2.1 Esercizio Assegnato il sistema e y + z + x 2 = 0 x 2 + y 2 + z 2 + y 1 = 0 dimostrare che in un intorno del punto (0,0,1) il sistema definisce
Analisi Vettoriale A.A. 2006-2007 - Soluzioni del Foglio 2 2.1 Esercizio Assegnato il sistema e y + z + x 2 = 0 x 2 + y 2 + z 2 + y 1 = 0 dimostrare che in un intorno del punto (0,0,1) il sistema definisce
6. FUNZIONI ANALITICHE. 6.1 Serie di Funzioni Olomorfe.
 6. FUNZIONI ANALITICHE. 6. Serie di Funzioni Olomorfe. 6.. Convergenza Uniforme. Sia Ω un insieme arbitrario e per ogni intero n sia f n : Ω C una funzione a valori complessi definita su E. Si dice che
6. FUNZIONI ANALITICHE. 6. Serie di Funzioni Olomorfe. 6.. Convergenza Uniforme. Sia Ω un insieme arbitrario e per ogni intero n sia f n : Ω C una funzione a valori complessi definita su E. Si dice che
Alcuni complementi sulla misura di Lebesgue in R N
 Alcuni complementi sulla misura di Lebesgue in R N Notazioni m Misura di Lebesgue in R N m e Misura esterna di Lebesgue in R N ; m e (E) = inf m(v ) V aperti V E m i Misura interna di Lebesgue in R N ;
Alcuni complementi sulla misura di Lebesgue in R N Notazioni m Misura di Lebesgue in R N m e Misura esterna di Lebesgue in R N ; m e (E) = inf m(v ) V aperti V E m i Misura interna di Lebesgue in R N ;
Successioni, massimo e minimo limite e compattezza in R
 Università di Roma Tor Vergata Corso di Laurea in Scienze e Tecnologie per i Media Successioni, massimo e minimo limite e compattezza in R Massimo A. Picardello BOZZA 10.11.2011 21:24 i CAPITOLO 1 Successioni
Università di Roma Tor Vergata Corso di Laurea in Scienze e Tecnologie per i Media Successioni, massimo e minimo limite e compattezza in R Massimo A. Picardello BOZZA 10.11.2011 21:24 i CAPITOLO 1 Successioni
Il teorema di Dini Le funzioni algebriche Funzioni analitiche secondo Weierstrass Polidromia e monodromia. 10, gennaio 2013
 10, gennaio 2013 Funzioni implicite nel campo reale e complesso: questioni di monodromia e polidromia L.Lamberti Indice Il teorema di Dini 1 Il teorema di Dini 2 3 4 Introduzione Il titolo funzioni implicite
10, gennaio 2013 Funzioni implicite nel campo reale e complesso: questioni di monodromia e polidromia L.Lamberti Indice Il teorema di Dini 1 Il teorema di Dini 2 3 4 Introduzione Il titolo funzioni implicite
Funzioni vettoriali di variabile scalare
 Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
7. Serie di Fourier Assegnata la funzione f(x) integrabile in [0, 2π] si possono determinare i suoi coefficienti di Fourier.
![7. Serie di Fourier Assegnata la funzione f(x) integrabile in [0, 2π] si possono determinare i suoi coefficienti di Fourier. 7. Serie di Fourier Assegnata la funzione f(x) integrabile in [0, 2π] si possono determinare i suoi coefficienti di Fourier.](/thumbs/98/137574113.jpg) (seguito dalla lezione precedente) 7. Serie di Fourier Assegnata la funzione f(x) tegrabile [, ] si possono determare i suoi coefficienti di Fourier f(n) = 1 si puó considerare la serie f(x)e x dx, n =,
(seguito dalla lezione precedente) 7. Serie di Fourier Assegnata la funzione f(x) tegrabile [, ] si possono determare i suoi coefficienti di Fourier f(n) = 1 si puó considerare la serie f(x)e x dx, n =,
