Appunti del Corso di Analisi Matematica I
|
|
|
- Domenica Serafini
- 5 anni fa
- Visualizzazioni
Transcript
1 Universitá La Sapienza a. a Appunti del Corso di Analisi Matematica I L.Lamberti Ultima revisione 14 giugno 21
2 Indice Capitolo 1. I numeri reali 3 1. Introduzione 3 2. Definizione assiomatica 3 3. Importanza dell estremo superiore 5 Capitolo 2. La costruzione di R 7 1. Le successioni di Cauchy 7 2. Lo spazio quoziente 8 3. Struttura algebrica su C 8 4. Struttura d ordine 1 5. Densitá dei razionali 1 6. La continuitá 11 Capitolo 3. Spazi metrici Insiemi numerabili La metrica 16 Capitolo 4. La compattezza I punti di accumulazione Insiemi connessi Insiemi compatti 19 Capitolo 5. Successioni Introduzione Proprietá algebriche La convergenza in R Sottosuccessioni Successioni di Cauchy Successioni monotone Limiti inferiore e superiore 27 Capitolo 6. Serie numeriche Introduzione Alcuni esempi I criteri di convergenza assoluta Il numero e di Nepero 36 1
3 2 INDICE 5. Sommatoria per parti 37 Capitolo 7. Serie prodotto 41 Capitolo 8. Riordinamenti Introduzione Il caso assolutamente convergente Il teorema di Riemann Dini 51 Capitolo 9. Funzioni continue Funzioni continue su compatti Funzioni inverse La continuitá uniforme Il teorema di continuitá uniforme Applicazioni 6 6. Il teorema di esistenza degli zeri Funzioni monotone 64 Capitolo 1. Integrali impropri di funzioni di una variabile Le funzioni continue Integrali impropri Integrali su intervalli limitati Integrali impropri di funzioni positive L indipendenza dalla successione Intervalli illimitati 73 Capitolo 11. Successioni di funzioni Primi esempi Convergenza puntuale 8 Capitolo 12. La convergenza uniforme Il tubo Test di convergenza uniforme per le serie 9 Capitolo 13. Importanza della convergenza uniforme Convergenza uniforme e continuitá Convergenza uniforme e integrabilitá Convergenza uniforme e derivabilitá 96 Capitolo 14. Serie di potenze Introduzione Serie derivata Conosciamo altre serie Le serie di Taylor Moltiplicazione di serie di potenze 18
4 INDICE 3 6. Divisione fra due serie di potenze 19 Capitolo 15. Equazioni lineari di primo ordine Il caso omogeneo Il caso non omogeneo Il problema di Cauchy generale Il caso dei coefficienti costanti La linearitá Riassumendo Alcuni problemi 116 Capitolo 16. Equazioni lineari di secondo ordine Costruzione di soluzioni Il problema di Cauchy Il teorema di unicitá L integrale generale Un interpretazione delle soluzioni Il caso non omogeneo La struttura delle soluzioni Costruzione di una soluzione Casi particolari 124 Capitolo 17. Equazioni generale di primo ordine Un equivalenza Generalitá e utilitá Due problemi di Cauchy La stima di Gronwall Il teorema d unicitá 134 Capitolo 18. Il teorema d esistenza per il problema di Cauchy Il Teorema d esistenza La successione La convergenza La funzione limite 142 Capitolo 19. Le equazioni autonome Introduzione Un approccio formale La teoria qualitativa Equazioni a variabili separabili Cambiare variabile Equazioni in forma omogenea Primitive di ordine superiore 149
5 4 INDICE Capitolo 2. A cosa servono le serie di potenze? Introduzione Un equazione differenziale semplicissima Un equazione lineare del second ordine La serie binomiale 156 Capitolo 21. Serie di Fourier Introduzione L approssimazione in media quadratica La forma complessa Risultati di approssimazione Il teorema fondamentale Serie di Fourier Applicazioni Completezza 169
6 CAPITOLO 1 I numeri reali 1. Introduzione La convivenza, la familiaritá, la fiducia nei numeri reali risale molto addietro, all inizio di ogni insegnamento matematico o piú in generale scientifico. La certezza di poter lavorare con tali numeri, il nome reali li classifica quasi come realtá metafisica, é molto piú solida di quella riposta, ad esempio, nei numeri razionali. Le cose stanno invece diversamente: i numeri reali corrispondono piú a esigenze legittimamente avvertite da molti che a oggetti reali, cioé, piú o meno razionalmente certi. Le esigenze avvertite, oltre quelle ovvie dell aritmetica e dell ordinamento maggiore-minore, sono sostanzialmente riconducibili a due (equivalenti): La risposta una coppia di classi contigue di numeri razionali deve ammettere elementi separatori un insieme di numeri razionali superiormente limitato deve ammettere estremo superiore. viene costruita per due strade: i numeri reali soddisfano tali esigenze una prima assiomatica, una seconda costruttiva. 2. Definizione assiomatica Definizione 2.1. I numeri reali sono un (l unico) campo ordinato archimedeo completo. 5
7 6 1. I NUMERI REALI Cosa sia un campo é spiegato in algebra (somma, prodotto, distributivitá del prodotto sulla somma, tutto come avviene nel campo Q dei numeri razionali). Le classi resto modulo p con p numero primo offrono esempi di campi, cioé insiemi su cui le operazioni di somma e di prodotto operano con relazioni analoghe a quelle incontrate sui numeri razionali. Cosa voglia dire ordinato corrisponde al significato naturale riconosciuto ad esempio sui numeri interi x < y z : x + z < y + z,... Cosa voglia dire archimedeo 1 corrisponde all idea che Cosa vuol dire completo: < x < y n : nx > y intersezione non vuota per intervalli incapsulati, esistenza dell estremo superiore per insiemi limitati. Osservazione 2.2. Esempio di campo ordinato non archimedeo: L insieme delle funzioni razionali r(x) = P (x) Q(x) dotato dell ordinaria somma e prodotto, costituisce un campo. Cambiando segno a numeratore e denominatore possiamo sempre ridurci ad avere il coefficiente del monomio di grado maggiore a denominatore positivo. Dichiariamo r(x) = p mx m p q n x n q > positivo se p m >. Diremo quindi che f(x) > g(x) f(x) g(x) > 1 Un ordinamento archimedeo é, sostanzialmente un ordinamento democratico: non é archimedea ad esempio la stratificazione in caste di parte della popolazione indiana nella quale la volontá di un numero comunque grande di paria non prevale sulla volontá di un elemento di una casta superiore
8 3. IMPORTANZA DELL ESTREMO SUPERIORE 7 Rispetto a questo ordinamento riesce ma infatti < 1 x < 1, n N : n x < 1 1 n x = x n > x in quanto il coefficiente del monomio piú alto x a numeratore é 1, positivo. Il campo delle funzioni razionali con l ordinamento scelto é un campo ordinato, non archimedeo. 3. Importanza dell estremo superiore L assioma d esistenza dell estremo superiore per ogni insieme superiormente limitato produce risultati molto importanti la illimitatezza superiore dei naturali, il valere di conseguenza della proprietá archimedea, la densitá dei razionali. Proposizione 3.1. L assioma dell estremo superiore implica che l insieme dei numeri naturali non é limitato superiormente. Dimostrazione. Sia y > supponiamo per assurdo che n N : n < y allora l insieme N avrebbe un estremo superiore Λ. Tenuto conto che dovrebbe esistere n N tale che Λ 1 < Λ Λ 1 < n Λ < 1 + n N L ultima proprietá contraddice il fatto che n N n Λ Corollario 3.2. L insieme dei naturali illimitato superiormente implica la proprietá archimedea. Dimostrazione. Siano < x < y: se per assurdo riuscisse n N : nx < y n < y x ovvero i naturali riuscirebbero limitati superiormente.
9 8 1. I NUMERI REALI Proposizione 3.3. La proprietá dell estremo superiore implica la densitá dei razionali. Dimostrazione. Siano x < y allora esistono n, m N tali che Ne segue n(y x) > 1, m 1 < nx < m nx < m < nx + 1 < ny nx < m < ny x < m n < y
10 CAPITOLO 2 La costruzione di R 1. Le successioni di Cauchy Definizione 1.1. Una successione {a n } di numeri razionali si dice di Cauchy, C, se per ogni razionale positivo ε esiste una soglia intera n ε tale che n, m n ε : a n a m ε Esempio 1.2. La successione {1, 2, 3, 4, 5,...} non é di Cauchy. La successione {17, 13, 25, 2, 2, 2, 2, 2, 2,...} é di Cauchy. Tutte le successioni convergenti sono di Cauchy. La successione {1., 1.4, 1.41, 1.414, , , , , , ,...} delle approssimazioni decimali di 2 é di Cauchy ma non é convergente (naturalmente nell ambito dei numeri razionali). Ad ogni numero razionale si possono associare tutte le successioni di Cauchy che convergono ad esso: ad esempio al numero r = 7 si possono associare le successioni di Cauchy {7, 7, 7, 7, 7,...}, {6.9, 6.99, 6.999, ,...}, ecc. Proposizione 1.3. Le successioni di Cauchy C sono tutte necessariamente limitate. Dimostrazione. Scelto ε = 1 sia n 1 la soglia corrispondente: allora n n 1 : a n a n1 1 a n 1 + a n1 di conseguenza, posto riesce M = max{ a 1, a 2,..., a n1 + 1} n : a n M 9
11 1 2. LA COSTRUZIONE DI R 1.1. Sottosuccessioni. Proposizione 1.4. Sia {a n } C: se una sottosuccessione {a nk } {a n } converge a l allora anche {a n } converge a l. Osservazione 1.5. Si noti che questo risultato non é affatto vero per successioni che non siano di Cauchy: nella successione {1, 1, 1, 1, 1,...} sono contenute le due sottosuccessioni {1, 1, 1,...} e { 1, 1, 1,...} convergenti una a 1 e l altra a 1, senza che l intera successione (che non é di Cauchy) converga. 2. Lo spazio quoziente Indicato con I C l insieme delle successioni di Cauchy che hanno limite zero la relazione {a n } {b n } {a n bn} I costituisce una relazione d equivalenza su C. Definizione 2.1. Lo spazio quoziente di C rispetto alla relazione determinata da I si dice insieme R dei numeri reali. La classe d equivalenza determinata dalla successione di Cauchy {a n } si indica con [{a n }] come pure con {a n } + I 3. Struttura algebrica su C Corollario 3.1. Somma, differenza, prodotto di due successioni di C é ancora una successione di C. Proposizione 3.2. Somma, differenza, prodotto di due classi d equivalenza [{a n }] e [{b n }] sono definite da [{a n ± b n }] e [{a n.b n }]. É naturale riconoscere alla classe [{1}] il ruolo di 1 cioé di unitá, elemento neutro relativo alla moltiplicazione, alla classe [{}] = I il ruolo di cioé di zero, elemento neutro relativo alla somma. Definizione 3.3. Gli elementi [{r}] si dicono numeri reali razionali o, semplicemente razionali.
12 3. STRUTTURA ALGEBRICA SU C 11 Osservazione 3.4. C é differenza tra il numero razionale r, la successione di Cauchy costante {r, r, r,...} e il numero reale razionale [{r}]: quest ultimo infatti é una classe d equivalenza. il numero reale razionale [{7}] é infatti la successione {7, 7, 7,...} la successione { 5, 3, 1, 7, 7, 7, 7,...} la successione {6, 6.9, 7.1, 6.99, 7.1,...} ecc. Proposizione 3.5. Se {a n } é una successione di C che non converge a, cioé se {a n } / I allora esiste δ > tale che m > M δ a m > δ oppure a m < δ Dimostrazione. Deve riuscire inf a n = δ > infatti se il loro estremo inferiore fosse dovrebbe esistere una sottosuccessione {a nk } infinitesima. Ma allora tutta la successione {a n } dovrebbe essere infinitesima contrariamente all ipotesi {a n } / I. Quindi i termini a n della successione devono cadere nelle due semirette (, δ) (δ, + ): dovendo stringersi fra loro finiranno per dover appartenere, dopo un certo indice n tutti ad una sola delle due semirette. Proposizione 3.6. Se [{a n }] [{}] allora esiste [{b n }] tale che [{a n }]. [{b n }] = [{1}] Dimostrazione. Possiamo supporre, eventualmente riferendosi ad una successione di Cauchy equivalente a quella assegnata, che riesca n : a n > δ: allora si possono considerare i reciproci b n = 1 a n essi, dal momento che {a n } é una successione di Cauchy, costituiscono anch essi una successione di Cauchy b n b m = a m a n a n a m 1 δ 2 a m a n ovviamente [{a n }]. [{b n }] = [{1}].
13 12 2. LA COSTRUZIONE DI R 4. Struttura d ordine Definizione 4.1. Due numeri reali [{a n }], [{b n }] si dicono l uno minore dell altro [{a n }] < [{b n }] se e solo se esistono δ Q positivo ed n N tali che n n : a n + δ b n É naturalmente possibile modificare i primi n termini delle due successioni di Cauchy {a n }, {b n } approdando a due nuove successioni {a n}, {b n} equivalenti alle precedenti per le quali valga la disuguaglianza n : a n + δ b n Osservazione 4.2. L ordinamento indicato é totale, nel senso che comunque si prendano due elementi [{a n }], [{b n }] R succede sempre una, e una sola delle tre possibilitá: [{a n }] = [{b n }] oppure [{a n }] < [{b n }] oppure [{a n }] > [{b n }] Infatti la successione di Cauchy {a n b n } puó appartenere ad I, e allora [{a n }], = [{b n }] oppure non appartenere ad I. Nella seconda possibilitá la precedente Proposizione 3.6 implica l esistenza di δ > e di n tale che n n : a n b n > δ oppure a n b n < δ ovvero [{a n }] > [{b n }] oppure [{a n }] < [{b n }] Corollario 4.3. Siano u e v due razionali con u < v, allora lo stesso ordinamento [{u}] < [{v}] si ritrova tra i rispettivi numeri reali razionali. 5. Densitá dei razionali Lemma 5.1. Siano [{a n }] < [{b n }] allora esiste un numero razionale r tale che il numero reale razionale [{r}] verifichi le condizioni [{a n }] < [{r}] < [{b n }]
14 6. LA CONTINUITÁ 13 Dimostrazione. Scegliamo rappresentanti delle due classi {a n } < {b n } in modo che n : b n a n > δ > e scegliamo la soglia N tale che dopo di essa riesca m a m a N δ 4, b m b N δ 4 Posto r = a N + δ 2 riesce n > N : a n < r < b n Infatti (occorre provare le due disuguaglianze) e analogamente a n < r : a N + δ 2 a n δ 2 a n a N δ 4 r < b n : b n a N δ 2 = b n a n + a n a N δ 2 δ δ 4 δ 2 = δ 4 A questo punto é evidente che il numero reale razionale [{a N + δ 2 }] é compreso tra i due numeri reali assegnati. 6. La continuitá Teorema 6.1. R soddisfa la proprietá dell estremo superiore. Dimostrazione. Sia A R un insieme non vuoto e limitato superiormente: sia [{M}] un maggiorante razionale. Sia r Q tale che il numero reale razionale verifichi [{r }] < α per qualche α A. Consideriamo i razionali r, r + 1, r + 2,... essi prima o poi raggiungono e superano M, quindi prima o poi diventano maggioranti di A. Indichiamo con r 1 = r + k il primo (il piú basso) di tali numeri che sia un maggiorante di A. Consideriamo a questo punto i razionali r 1 1, r , r ,..., r , r 1 Indichiamo con r 2 r 1 il primo (il piú basso) di tali numeri che sia un maggiorante di A.
15 14 2. LA COSTRUZIONE DI R Iterando il procedimento ci troviamo a considerare la successione razionale {r k }: proveremo che 1: {r k } é una successione di Cauchy (quindi la classe [{r k }] ad essa associata rappresenta un numero reale) 2: se α A riesce α [{r k }] 3: se β < [{r k }] allora β non é un maggiorante di A. Prima questione É la piú semplice: tutti gli r k con k cadono tra r 1 ed r, quindi distano fra loro meno di 1, tutti gli r k con k 1 cadono tra r 1.1 ed r 1, quindi distano fra loro meno di.1, tutti gli r k con k 2 cadono tra r 2.1 ed r 2, quindi distano fra loro meno di.1, ecc. Quindi la successione {r k } é una successione di Cauchy, quindi la sua classe λ = [{r k }] rappresenta un numero reale. Seconda questione Da come sono scelti i singoli numeri razionali r k tutte i numeri reali razionali λ k = [{r k }] da essi determinati sono maggioranti di A. Se, per assurdo, esistesse α = [{a n }] A, tale che riuscirebbe da cui k : λ < α λ < α λ k k : α λ < λ k λ = [{ 1 1 k }] fenomeno che impedisce che Terza questione α λ >
16 6. LA CONTINUITÁ 15 Per come sono costruiti gli r k i numeri reali razionali [{r k 1 1 }] k non sono maggioranti di A. Se β < λ esiste certamente k tale che β < [{r k 1 1 }] < λ k A questo punto se [{r k 1 }] non é un maggiorante di A non lo puó 1 k a maggior ragione esserlo neanche β Il numero reale λ precedentemente costruito rappresenta il sup A: risulta cioé provato che il campo ordinato R soddisfa l assioma dell estremo superiore.
17
18 CAPITOLO 3 Spazi metrici 1. Insiemi numerabili 1.1. I numeri cardinali. L equivalenza tra insiemi che si possono porre in corrispondenza biunivoca: la cardinalitá. Definizione 1.1. Un insieme E si dice numerabile se é in corrispondenza biunivoca con N insieme dei numeri naturali o con un sottoinsieme di esso. Gli elementi di un insieme numerabile si esauriscono in un insieme finito o una successione. Proposizione 1.2. (corollario pag.28) I numeri razionali costituiscono un insieme numerabile La notazione decimale. Per ogni x > sia n = max{n < x} n N Per ogni k sia n k il massimo { n k = max n + n 1 n N n } 1 < x k Si riconosce facilmente che Indicati con riesce x k = k i= k : n k 9 n i 1 i = n, n 1 n 2...n k x = sup x k Osservazione 1.3. La stessa costruzione precedente riferita alla base 1 puó essere fatta riferendosi ad altre basi, ad esempio alla base 2. In tal caso invece di successioni decimali di cifre, 1, 2,..., 9 si incontrano successioni di cifre, 1 solamente. Proposizione 1.4. (2.14, pag.28) I numeri reali costituiscono un insieme non numerabile. 17
19 18 3. SPAZI METRICI 2. La metrica Definizione 2.1. (definizione 2.15, pag. 29) Una funzione si dice una distanza se d(x, y) = x = y d(x, y) = d(y, x) d(x, z) d(x, y) + d(y, z) d : S S R + Esempio 2.2. (esempio 2.16, pag. 29) Sia S = R 2, indichiamo i suoi punti con le coordinate cartesiane P = (x 1, y 1 ), Q = (x 2, y 2 ) d(p, Q) = (x 2 x 1 ) 2 + (y 2 y 1 ) Piccolo GLOSSARIO. (def. 2.18, pag.3) Intorno di un punto. Punto di accumulazione Punto isolato Insieme chiuso Punto interno Insieme aperto Complementare Insieme perfetto Insieme limitato Insieme denso. Teorema 2.3. (2.2, pag.31) Se P é un punto di accumulazione allora in ogni suo intorno cadono infiniti punti di E. Teorema 2.4. (2.24, pag.32) unione di infiniti aperti intersezione di infiniti chiusi intersezione di un numero finito di aperti unione di un numero finito di chiusi.
20 CAPITOLO 4 La compattezza 1. I punti di accumulazione Teorema 1.1. Se E R 2 é chiuso e limitato allora ogni insieme infinito contenuto in E ammette punti di accumulazione appartenenti a E Teorema 1.2. (2.2, pag.31) Se P é un punto di accumulazione allora in ogni suo intorno cadono infiniti punti di E. Definizione 1.3. Assegnato un insieme A e indicato con D(A) l insieme dei suoi punti di accumulazione, l insieme si dice chiusura di A. A = A D(A) 1.1. La metrica discreta. Sia { 1 se P Q d(p, Q) = se P = Q quali insiemi sono aperti? quali sono chiusi? quali sono limitati? dato A chi é A? Teorema 1.4 (Bolzano - Weierstrass). (2.42, pag. 38) Ogni sottoinsieme E infinito e limitato di R ammette punti di accumulazione. Osservazione 1.5. É facile dimostrare come la tesi del Teorema di Bolzano Weierstrass cada se l insieme E non é limitato (Esempio E = 1, 2, 3,... i naturali) l insieme E non é infinito (Gli insiemi finiti non hanno punti di accumulazione) si lavorasse su sottoinsiemi dei soli razionali (la successione degli approssimanti {1, 1.4, 1.41,...} di 2 non ha punti di accumulazione in Q). Proposizione 1.6 (Bolzano - Weierstrass). Ogni sottoinsieme E infinito e limitato di R 2 ammette punti di accumulazione. 19
21 2 4. LA COMPATTEZZA Dimostrazione. Riesca E [a, b ] [c, d ] Indichiamo con E x [a, b ] l insieme delle ascisse dei punti di E e indichiamo con E y [c, d ] l insieme delle ordinate dei punti di E 1. Applicando il precedente Teorema di Bolzano Weierstrass a E x riconosciamo che D(E x ) : sia λ un punto di accumulazione di E x e sia {x n } E x una successione tale che lim x n = λ n Sia {y 1, y 2,,...} E y la successione delle ordinate dei punti di E le cui ascisse formavano la precedente successione convergente {x n }. Per il precedente Teorema di Bolzano Weierstrass l insieme {y 1, y 2,,...} ha punti di accumulazione: sia µ uno di essi e sia {y n1, y n2,...} {y 1, y 2,,...} una successione tale che lim y n k = µ k La successione {(x nk, y nk )} E é convergente a (λ, µ) che, pertanto riesce punto di accumulazione di E e pertanto prova che D(E). Teorema 1.7. Ogni successione {P n } E, insieme chiuso e limitato di R n ammette una sottosuccessione {P nk } convergente ad un punto di E. Dimostrazione. Supponiamo che E sia un insieme chiuso e limitato e supponiamo che {x n } sia una successione di punti di E. Se {x n } assume solo un numero finito di valori, almeno un valore sarà assunto infinite volte. Questo significa che esiste una successione estratta {x nk } che risulta costante e quindi convergente al valore costante. Se i valori assunti da {x n } sono infiniti, tenuto conto che E é limitato anche l insieme dei valori assunti da {x n } e limitato. Il teorema di Bolzano e Weierstrass ci dice allora che esiste un punto x che e punto di accumulazione dell insieme dei valori {x n }. Questo significa che ogni intorno di x contiene almeno un valore assunto da {x n }. Per ogni intero positivo k consideriamo l intorno di x di raggio 1/k: tale intorno contiene almeno un valore x nk con n k > n k 1. 1 É facile riconoscere che almeno uno dei due insiemi E x ed E y ha infiniti elementi: nel seguito, per semplicitá supponiamo che siano infiniti entrambi.
22 6. INSIEMI COMPATTI 21 Pertanto la successione estratta {x nk } converge a x. Tenuto conto che E e un insieme chiuso riesce lim x n k = x E k Viceversa se E e compatto fosse non limitato, per ogni intero positivo n, esisterebbe una successione {x n } E che soddisfa x n > n. e che quindi non pu o avere alcuna sottosuccessione convergente. Infine se E non fosse chiuso, esisterebbe una successione {x n } di elementi di E che converge ad un elemento x / E Ogni sottosuccessione di questa successione convergerebbe allo stesso elemento che non appartiene ad E e pertanto E non sarebbe compatto. Teorema 1.8. Se E R 2 é chiuso e limitato allora ogni insieme infinito contenuto in E ammette punti di accumulazione appartenenti a E Definizione 1.9. Un sottinsieme E di uno spazio metrico si dice compatto se ogni successione {P n } di punti di E ammette una successione estratta {P nk } convergente ad un punto di E. 2. Insiemi connessi Definizione 2.1. Due insieme A e B si dicono separati se A B = A B = Definizione 2.2. Un insieme si dice connesso se non é unione di due insiemi separati e non vuoti. Osservazione 2.3. Due insiemi A e B possono essere disgiunti A B = senza essere separati... La disgiunzione é un fatto insiemistico: la separazione coinvolge anche i punti di accumulazione, cioé coinvolge la metrica. Teorema 2.4. Gli insiemi connessi di R sono tutti e soli gli intervalli. 6. Insiemi compatti Definizione 6.1. Un insieme E contenuto in uno spazio metrico S si dice compatto se e solo se ogni successione {P n } E possiede sottosuccessioni convergenti a punti di E. Dal teorema di Bolzano-Weierstrass discende Proposizione 6.2. Ogni sottoinsieme limitato e chiuso di R n é compatto.
23 22 4. LA COMPATTEZZA Si riconosce anche Proposizione 6.3. Ogni compatto E di R n é chiuso e limitato. Dimostrazione. Supponiamo di riferirci al caso R 2. La tesi si riconosce per assurdo: α): limitatezza se E non fosse limitato allora, per ogni n si potrebbe trovare almeno un punto P n / I(O, n), avendo indicato con I(O, n) il cerchio di centro l origine e raggio n, i punti di tale successione, come pure quelli di ogni sottosuccessione, costituiscono un insieme illimitato, quindi non possono rappresentare una successione convergente. β): chiusura se E non fosse chiuso allora ci sarebbe almeno un punto Q di accumulazione per E che non appartiene ad E, presa quindi una successione {P n } E convergente a Q, riuscirebbe, contrariamente all ipotesi di compattezza, che anche ogni sottosuccessione la {P nk } dovendo convergere a Q / E non é convergente in E. Le due precedenti Proposizioni 6.2 e 6.3 implicano il seguente Teorema 6.4. I compatti di R n sono tutti e soli gli insiemi chiusi e limitati I ricoprimenti. Teorema 6.5. Sia E S compatto e sia {A n } una famiglia di insiemi aperti tali che E n= A n allora esiste un numero (finito) n tale che E n n= Dimostrazione. La dimostrazione si conduce anche in questo caso per assurdo: indichiamo con m B 1 = A 1, B 2 = A 1 A 2, B 3 = A 1 A 2 A 3,...B m = A n n= A n
24 Se 6. INSIEMI COMPATTI 23 m : E B m allora potremmo costruire una successione {P m } E prendendo m : P m / B m Tale successione non potrebbe avere sottosuccessioni convergenti: se infatti esistesse lim k P n k = Q E allora dovrebbe esistere n tale che Q A n B n e, tenuto conto che gli A n sono per ipotesi aperti dovrebbe esistere un intorno circolare di Q I(Q, ρ) A n B n ma allora i punti P nk dovrebbero definitivamente cadere dentro B n, contrariamente alla loro costruzione. Pertanto non deve essere possibile costruire una successione che verifichi la m : P m B m impossibilitá che equivale a dire che da un certo n non ci sono piú punti di E fuori di B n. L ultima affermazione equivale a dire che E B n che é esattamente la tesi del teorema. Teorema 6.6. Sia E un compatto di R n e siano {C n } E insiemi chiusi tali che m m : C n allora riesce anche n=1 C n n=1 Dimostrazione. Si tengano presenti i due seguenti risultati: F chiuso equivale a C(F ) aperto. C( F n ) = C(F n ) n=1 n=1
25 24 4. LA COMPATTEZZA Pertanto se, per assurdo, riuscisse C n = allora riuscirebbe ovvero cioé gli aperti n=1 ( ) C C n = R n n=1 R n = C(C n ) n=1 C(C n ) costituirebbero un ricoprimento di R n e quindi anche di E. Tenuto conto che E é compatto il precedente teorema garantirebbe che E n n=1 C(C n ) ma allora, passando di nuovo al complementare, ( n ) n C(E) C C(C n ) = C n = da cui n=1 n n=1 C n = contrariamente all ipotesi che tutte le intersezioni finite siano non vuote. n= La proprietá degli intervalli incapsulati. Proposizione 6.7. Siano I n = [a n, b n ] R una successione di intervalli incapsulati e non vuoti tali che allora l intersezione I 1 I 2 I 3... I n n=1 Dimostrazione. Basta ricordare che il primo intervallo I 1 = [a 1, b 1 ] in quanto insieme chiuso e limitato é compatto,
26 6. INSIEMI COMPATTI 25 allora basta applicare alla successione di chiusi {I 2, I 3,...} I 1 il teorema sull intersezione di chiusi per ottenere la tesi.
27
28 CAPITOLO 5 Successioni 1. Introduzione Definizione 1.1. Una successione {p n } X é una funzione p : N X L uso corrente indica i valori p(n) con la grafia p n. Teorema 1.2. Sia {p n } una successione di uno spazio metrico X convergenza: la notazione lim n p n = q significa ε > n : n n d(p n, q) ε avendo indicato con d la distanza assegnata sullo spazio X, unicitá del limite, limitatezza delle successioni convergenti, se q é punto di accumulazione di E allora esistono successioni {p n } E convergenti a q. Dimostrazione. I vari punti elencati sono ben noti per le successioni di numeri reali, sono anche noti per le successioni di numeri complessi. É interessante riconoscere che si tratta di proprietá definibili e riscontrabili in ogni spazio metrico. L unicitá del limite in particolare dipende dalla proprietá p q ρ > I(p, ρ) I(q, ρ) = 2. Proprietá algebriche Teorema 2.1. Siano {s n } e {t n } due successioni di numeri reali o complessi, convergenti rispettivamente a s e a t allora lim (s n + t n ) = lim s n + lim t n n n n lim (s n. t n ) = lim s n. lim t n n n n lim (s n /t n ) = lim s n / lim t n con l ovvia esclusione delle divisioni per n n n. 27
29 28 5. SUCCESSIONI 3. La convergenza in R 2 Lo spazio R 2 é spesso indicato anche come R R, notazione che ricorda il seguente risultato Teorema 3.1. La successione {p n } = {(x n, y n )} R 2 q = (ξ, η) se e solo se lim x n = ξ, n lim y n = η n 4. Sottosuccessioni converge a Teorema 4.1. Ogni successione limitata in R o in R 2 possiede infinite sottosuccessioni convergenti. Proposizione 4.2. Tutte le sottosuccessioni di una successione convergente a q sono convergenti a q. Definizione 4.3. Ciascun punto q che sia limite di una sottosuccessione {x nk } {x n } si dice punto limite della successione {x n }. 5. Successioni di Cauchy Una successione {p n } X con X spazio metrico, si dice di Cauchy se ε > n ε : n, m n ε d(p n, p m ) ε Teorema 5.1. Le successioni di Cauchy sono limitate. Teorema 5.2. Le successioni convergenti in uno spazio metrico sono (necessariamente) successioni di Cauchy. Proposizione 5.3. Se una sottosuccessione {p nk } {p n } di una successione di Cauchy converge a q allora tutta la successione {p n } converge a q. Teorema 5.4. Una successione di Cauchy di numeri reali é convergente. Dimostrazione. Sia {p nk } {p n } una sottosuccessione convergente (applicazione del teorema di Bolzano-Weierstrass) lim p n k = q k allora, per la precedente Proposizione 5.3, riesce anche lim p n = q k Proposizione 5.5. Una successione di Cauchy {p n } R k é convergente.
30 7. LIMITI INFERIORE E SUPERIORE 29 Proposizione 5.6. Una successione di Cauchy {p n } di numeri complessi é convergente. 6. Successioni monotone Per le successioni di numeri reali, e solo per esse, si puó avere il requisito della monotónia cioé il fenomeno che tutti i termini della successione verifichino la proprietá x n x n+1 oppure tutti i termini della successione verifichino la opposta proprietá x n x n+1 Nel primo caso, x n x n+1, si parla di successioni crescenti, nel secondo x n x n+1, di successioni decrescenti. Osservazione 6.1. Esistono sottili raffinatezze (raramente utili) che distinguono tra x n x n+1 e x n < x n+1 dichiarando le prime successioni crescenti o crescenti in senso lato o debole e dichiarando le altre, quelle con il <, crescenti in senso stretto. Analoghe raffinatezze distinguono tra successioni decrescenti e decrescenti in senso stretto. La non proponibilitá di successioni monotone di punti del piano o di numeri complessi deriva naturalmente dalla mancanza di ordinamento nel piano, nei complessi e in generale in ogni R n. Teorema 6.2. Una successione monotona {x n } converge se e solo se é limitata: in particolare riesce { lim n x n = sup x n lim n x n = inf x n crescenti decrescenti 7. Limiti inferiore e superiore I termini x n di una successione di numeri reali convergente al limite l hanno la proprietá di appartenere definitivamente, cioé per n sufficientemente alto, all intervallo [l ε, l + ε] Questo fenomeno naturalmente non accade per successioni non convergenti.
31 3 5. SUCCESSIONI In alternativa per una successione non convergente si possono cercare intervalli [a, b] che abbiano proprietá analoghe, cioé tale che i termini della successione finiscano definitivamente dentro di essi. Una risposta molto semplice, almeno per una successione limitata é la seguente: posto λ = inf.x n, Λ = sup.x n riesce n x n [λ, Λ] A questo punto il problema puó essere raffinato chiedendo quale sia l intervallo... piú piccolo nel quale finiscano definitivamente i termini della successione. É chiaro che posto riesce riesce come pure, posto riesce ecc. Tenuto conto che λ 1 = inf x n, Λ 1 = sup n>1 x n n>1 n > 1 x n [λ 1, Λ 1 ] λ 2 = inf x n, Λ 2 = sup n>2 x n n>2 n > 2 x n [λ 2, Λ 2 ] λ λ 1 λ 2... Λ 2 Λ 1 Λ posto l = lim λ n = sup λ n, l = lim Λ n = inf Λ n n n l intervallo [l, l ] sembra interessante ai fini del problema posto. Scelto ε > esiste certamente un n ε tale che Tenuto conto che l ε < λ nε Λ nε < l + ε si riconosce che n n ε : x n [λ nε, Λ nε ]
32 7. LIMITI INFERIORE E SUPERIORE 31 ε > n ε : n > n ε x n [l ε, l + ε] Definizione 7.1. Sia {x n } una successione reale e limitata, indicati con λ n = inf x k, Λ n = sup x k k n k n i numeri l = lim λ n = sup λ n, l = lim Λ n = inf Λ n n n si dicono rispettivamente limite inferiore e limite superiore della successione {x n }. Osservazione 7.2. I numeri λ n e Λ n precedentemente introdotti nel caso di una successione limitata si considerano anche relativamente a successioni non limitate: se {x n } é illimitata inferiormente tutti i λ n saranno, se {x n } é illimitata superiormente tutti i Λ n saranno +, Il limite inferiore di una successione illimitata inferiormente é pertanto, mentre il limite superiore di una successione illimitata superiormente é +. Le proprietá dei due limiti inferiore e superiore possono riassumersi nel seguente Teorema 7.3. Indicati con l ed l il limite inferiore e il limite superiore della successione {x n } ε > n ε tale che n n ε l ε x n l + ε σ > n σ : n n σ x n [l + σ, l σ] Corollario 7.4. La successione {x n } é convergente se e solo se il limite inferiore coincide con il limite superiore.
33
34 CAPITOLO 6 Serie numeriche 1. Introduzione Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica k=1 a k la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3 = a 1 + a 2 + a 3,... s n = che prende il nome di successione delle somme parziali o delle ridotte della serie assegnata. Definizione 1.1. Si dice che la serie a k é convergente se e solo se la successione {s n } ad essa associata é convergente. Se lim s n = S n allora si pone a k = S k=1 k=1 Il criterio di convergenza di Cauchy applicato alla {s n } ε > n ε : n, m n ε s n s m ε implica, tenuto conto che s n s m = il seguente m k=n+1 a k Teorema 1.2. La serie a k é convergente se e solo se k=1 ε > n ε : n, m n ε m 33 k=n+1 a k ε n k=1 a k
35 34 6. SERIE NUMERICHE Corollario 1.3. Condizione necessaria a che la serie a k converga é che riesca lim n a n = k=1 Dimostrazione. Basta applicare il precedente teorema alla scelta m = n + 1 Esempio 1.4. La serie 1/k non é convergente e fornisce un importante esempio di una serie i cui termini siano infinitesimi senza che questo basti alla convergenza della serie (Ovvero la non sufficienza della condizione espressa nel precedente Corollario) 1.1. La convergenza assoluta. Definizione 1.5. Una serie a termini complessi a k tale che la serie dei valori assoluti k=1 k=1 a k sia convergente prende il nome di serie k=1 assolutamente convergente. Teorema 1.6. Se la serie a k converge allora converge anche la serie a k. k=1 k=1 Dimostrazione. Perché la serie a k converga occorre e basta che sia soddisfatta la condizione del precedente Teorema 1.2. Tenuto conto che per la proprietá triangolare a n+1 + a n a m a n+1 + a n a m si riconosce che dall ipotesi di convergenza della a k si ricavi che la a k soddisfa la condizione di convergenza del Teorema 1.2. k= Le serie a termini reali positivi. Le serie a termini reali positivi producono successioni di somme parziali monotone crescenti s n = k=1 n n+1 a k a k = s n+1 k=1 Poiché le successioni monotone crescenti limitate superiormente sono convergenti le serie a termini positivi vengono naturalmente studiate k=1 k=1
36 1. INTRODUZIONE 35 per confronto Teorema 1.7. Siano a k e b k due serie a termini reali positivi i k=1 k=1 cui termini verifichino la relazione k a k b k allora se la serie maggiorante, minorante a k, k=1 se la serie minorante maggiorante, b k. k=1 b k, converge, converge anche la k=1 a k k=1 diverge, diverge anche la serie Dimostrazione. Il risultato deriva semplicemente dal fatto che indicate con {A n } e con {B n } le ridotte delle due serie k a k b k n A n B n per cui se converge, e quindi si mantiene limitata, la {B n } si mantiene limitata, e di conseguenza converge, anche la {A n }. Analogamente se non converge, e quindi non é limitata, la {A n } allora non é limitata, e quindi non converge, neanche la {B n }. Proposizione 1.8. I termini della serie a k soddisfino le disuguaglianze k a k d k Se la serie a termini reali positivi d k é convergente allora é conver- gente anche la a k. k=1 k=1 Dimostrazione. Il risultato deriva dal precedente Teorema 1.7 dal quale si deduce intanto che la serie a k é convergente. k=1 k=1 La convergenza allora della serie a termini complessi sua assoluta convergenza, Teorema 1.6. a k deriva dalla k=1
37 36 6. SERIE NUMERICHE 2. Alcuni esempi 2.1. Le serie geometriche. Si dicono serie geometriche quelle i cui addendi sono le successive potenze di una stessa base ρ 1: ρ k s n = 1 ρn+1 1 ρ É facile riconoscere che le serie geometriche con 1 < ρ < 1 convergono S = 1 1 ρ ρ 1 non convergono 2.2. Le serie armoniche generalizzate. Si dicono serie armoniche generalizzate quelle i cui addendi sono le potenze dei reciproci degli interi: 1 k p É facile riconoscere che le serie armoniche generalizzate con p non sono convergenti (i termini non costituiscono una successione infinitesima). I casi p > si valutano servendosi della seguente proposizione: Proposizione 2.1. Siano a 1 a 2 a 3... le due serie a k, 2 k a 2 k k=1 k=1 convergono o non convergono entrambe insieme. Dimostrazione. Si tratta di serie a termini positivi: quindi la loro convergenza o meno equivale alla limitatezza delle rispettive somme parziali. Dette s n e t n rispettivamente le due successioni delle somme parziali si ha, s 2 n = a 1 + (a 2 + a 3 ) + (a 4 + a 5 + a 6 + a 7 )... a 1 + 2a 2 + 4a = t n 1 s 2 n = a 1 +a 2 +(a 3 +a 4 )+(a 5 +a 6 +a 7 +a 8 ) a 1+a 2 +2a = 1 2 t n 1 Le due disuguaglianze riconoscono che i termini delle due successioni di somme parziali si maggiorano una con l altra: quindi se é limitata una é limitata anche l altra.
38 3. I CRITERI DI CONVERGENZA ASSOLUTA 37 La precedente proposizione puó essere applicata allo studio delle serie armoniche generalizzate 1 2 k 1 k p 2 = ( ) k 1 kp 2 p 1 riconoscendo quindi che convergono se p > 1 che non convergono se p 1 3. I criteri di convergenza assoluta Teorema 3.1. Assegnata la serie a k a termini complessi, posto k=1 l = lim sup n a n se l < 1 la serie converge, se l > 1 la serie non converge, se l = 1 il test non decide, nel senso che la serie puó essere convergente come essere non convergente. Dimostrazione. Sia, primo caso, l < 1: allora scelto l < ρ < 1 esiste un indice n ρ tale che n n n ρ : an ρ a n ρ n da cui, per confronto con la serie convergente ρ k, si riconosce che la k=1 a k é assolutamente convergente, quindi convergente. k=1 Sia, secondo caso, l > 1: allora scelto 1 < ρ < l esistono infiniti a nk ρ n k 1 quindi la successione {an } non é infinitesima, quindi la serie non puó convergere. Sia, terzo caso, l = 1: per rispondere basta fornire due esempi, uno di una serie convergente e uno di una non convergente. 1 convergente k 2 In entrambi i casi riesce k=1 k=1 lim n 1 k non convergente n 1 n = lim 2 n n 1 n = 1
39 38 6. SERIE NUMERICHE Teorema 3.2. Assegnata la serie a k a termini complessi, posto k=1 l = lim sup a n+1 a n se l < 1 la serie converge, se l > 1 la serie non converge, se l = 1 il test non decide, nel senso che la serie puó essere convergente come essere non convergente. Dimostrazione. La dimostrazione é analoga al precedente. 4. Il numero e di Nepero e 2, Ai modesti o vanitosi, ai violenti o timorosi do, cantando gaio ritmo, logaritmo... Giorgio Rabbeno É facile riconoscere, per confronto, che la serie a termini positivi, 1 k! é convergente: la sua somma rappresenta il celebre numero e = di Nepero. Esempio 4.1. ( 1 k! = lim ) n n n Proposizione 4.2. Il numero di Nepero é irrazionale. Dimostrazione. { 1 < e s n = k! < ( ) 2 1 (n + 1)! n } n + 1 k=n+1 da cui, valutando la serie geometrica comparsa a secondo membro ( ) 2 1 n = n = n + 1 n n + 1
40 5. SOMMATORIA PER PARTI 39 si ottiene n : < e s n < 1 n n! Se ora, per assurdo, fosse avremmo, scelto n = q Tenuto presente che < p q s q < 1 q q! e = p q, q > 1 ( ) p q! q s q < 1 q ( ) p q! q s q é un numero intero (il fattore q! annulla tutti i denominatori...) troveremmo un numero intero positivo minore di 1, cosa impossibile. Quindi e non puó essere razionale. 5. Sommatoria per parti La convergenza, o meno, di una serie a k b k k=1 i cui termini siano i prodotti di due successioni {a k } e {b k } puó essere, ragionevolmente ricavata da proprietá possedute dalle due successioni. Esempio 5.1. Ad esempio se k : a k = allora la serie a k b k converge qualunque siano i {b k }! Ad esempio se k : a k = c allora la serie a k b k converge se e solo se la serie ecc. ecc. k=1 b k é convergente! Teorema 5.2 (Abel). Consideriamo la serie a k b k e supponiamo che b 1 b 2 b 3..., allora la serie é convergente. lim b n =, A n = n k=1 k=1 n a k, A n M k=1 k=1
41 4 6. SERIE NUMERICHE Dimostrazione. Posto n A n = a k a n = A n A n 1 e quindi k=1 q a k b k = k=p q (A k A k 1 ) b k = k=p q A k b k k=p q 1 k=p 1 A k b k+1 = q 1 q 1 A k b k + A q b q A k b k+1 A p 1 b p = k=p k=p q 1 A k (b k b k+1 ) + A q b q A p 1 b p k=p pertanto, tenuto conto che b k b k+1, q q 1 a k b k A k (b k b k+1 ) + ( A q + A p 1 ) b p k=p k=p M ( q 1 ) (b k b k+1 ) + 2b p = M ((b p b q ) + 2b p ) 3Mb p k=p Tenuto conto delle ipotesi b 1 b 2 b 3..., scelto comunque ε > sia n ε tale che allora p, q n ε : 3Mb nε ε lim b n = n q a k b k ε che é la nota condizione di convergenza per la serie a k b k. k=p k=1
42 5. SOMMATORIA PER PARTI Applicazioni. Il caso di applicazione piú frequente del precedente Teorema 5.2 si incontra nelle cosiddette k=1 Infatti in questo caso si ha serie a termini di segno alterno ( 1) k b k, b 1 b 2 b 3..., lim n b n = a k = ( 1)k, A n = Esempio 5.3. La serie n a k, A n M = 1 k=1 ( 1) k k=1 é convergente. É importante osservare che la serie precedente non é assolutamente convergente: infatti la serie dei moduli diviene esattamente la serie armonica generalizzata relativa a p = 1 che é noto essere non convergente Le somme delle serie a termini di segno alterno. In altri termini S 2n+1 = S 2n 1 b 2n + b 2n+1 S 2n 1 S 2n+2 = S 2n + b 2n+1 b 2n+2 S 2n k S 2n+1 S 2n = b 2n+1 la sottosuccessione delle somme parziali dispari é decrescente, la sottosuccessione delle somme parziali pari é crescente, detta S la somma della serie riesce S 2n S S 2n+1 Ne segue quindi che S S k b k Il risultato indicato é particolarmente pregiato dal punto di vista numerico: infatti calcolata una somma parziale S k si puó riconoscere l intervallo al quale appartiene certamente la somma S della serie S [S k b k, S k + b k ] intervallo che, tenuto conto che lim k b k =, ha ampiezza via via piú piccola...!
43 42 6. SERIE NUMERICHE Esempio 5.4. Si voglia conoscere con la precisione di.1 la somma della serie ( 1) k 1. k k=1 Si tratta di decidere l attendibilitá ai fini della domanda posta delle varie somme parziali S n che possiamo calcolare. Tenuto presente che l errore che intercorre tra una S n e la somma S della serie é inferiore al termine b n si capisce che la somma S 1 fornisce l approssimazione richiesta. Infatti S S 1 b 1 = 1 1 =.1
44 CAPITOLO 7 Serie prodotto Assegnate due serie convergenti a k = A, b k = B vogliamo occuparci di dare senso alla frase serie prodotto con la pretesa che tale serie prodotto converga e abbia somma il prodotto A B delle somme delle due serie fattori. L idea che la serie a k b k semplicemente costruita dai prodotti dei termini corrispondenti soddisfi le pretese cade immediatamente: infatti neanche per somme finite (a + a 1 + a 2 ) (b + b 1 + b 2 ) a b + a 1 b 1 + a 2 b 2 esiste infatti un discreto numero di prodotti misti a b 1, a b 2,... che verrebbero trascurati. L idea suggerita invece dalla moltiplicazione di due polinomi é piú adatta: siano infatti riesce ovvero P (x) = a + a 1 x + a 2 x 2, Q(x) = b + b 1 x + b 2 x 2 P (x)q(x) = a b + (a b 1 + a 1 b )x + (a b 2 + a 1 b 1 + a 2 b )x 2 P (x)q(x) = c + c 1 x + c 2 x 2 c = a b c 1 = a b 1 + a 1 b c 2 = a b 2 + a 1 b 1 + a 2 b Definizione 1.5. Assegnate due serie a k, b k si dice loro serie prodotto la serie c k con k c k = a j b k j, K =, 1, 2,... j= 43
45 44 7. SERIE PRODOTTO Corollario 1.6. Nel caso di somme finite, cioé serie i cui termini sono tutti nulli da un certo posto in poi, riesce b k = Teorema 1.7. Siano a k a k = A, c k b k = B due serie convergenti, la prima a k sia assolutamente convergente. Allora la serie prodotto c k é convergente e la sua somma é il prodotto A B delle somme delle due serie fattori. Dimostrazione. Indichiamo con n C n = le somme parziali della serie prodotto C n = a b +(a b 1 +a 1 b )+(a b 2 +a 1 b 1 +a 2 b )+...+(a b n +a 1 b n a n b ) Riordinando i termini si ha anche C n = a (b + b b n ) + a 1 (b + b b n a n b Indicate con B n = c k n b k, A n = le somme parziali della b k si ha quindi n C n = a B n + a 1 B n 1 + a 2 B n a n B Indicate inoltre con β n = B B n le differenze tra le ridotte B n e il loro limite B riesce anche a k C n = a (B β n ) + a 1 (B β n 1 ) + a 2 (B β n 2 ) a n (B β ) = = B(a + a a n ) γ n = B A n γ n avendo indicato con γ n = a β n + a 1 β n a n β
46 7. SERIE PRODOTTO 45 Per ottenere che lim n C n = A B occorre quindi riconoscere che riesca lim n γ n =. Tenuto presente che lim β n =, n e quindi scelto ε > N tale che n N : β n ε, a k = M si ha, spezzando il gruppo di addendi che costituiscono γ n i due gruppi si ha quelli relativi ai β h con indici h [, N], quelli relativi ai β h con indici h [N + 1, n] N n n N : γ n a n h β h + β h a n h h= h=n+1 N N a n h β h + ε a h a n h β h + ε M h= Tenuto presente che h= la successione {a m } che produce una serie convergente é necessariamente infinitesima, che l addendo N h= a n hβ h é una combinazione lineare di un numero finito N + 1 di infinitesimi h= riesce e pertanto Pertanto a n, a n 1,..., a n N con N dipendente solo da ε lim n N a n h β h = h= lim sup γ n M ε lim C n = A B n 1.3. La funzione esponenziale. Consideriamo la serie prodotto delle due serie (uguali e assolutamente convergenti) 1 k!, 1 k!
47 46 7. SERIE PRODOTTO Riesce, per definizione, c = 1.1 = 1 c 1 = = 2 c 2 = 1 1 2! ! = 4 2! e, in generale, c n = j= c 3 = 1 1 3! ! + 1 2! ! = 8 3! n 1 1 j! (n j)! = 1 n! j= n j= n! j!(n j)! = 1 n! da cui tenuto conto che n ( ) n = (1 + 1) n = 2 n j n j= ( ) n j si ha c n = 2n n! In base al teorema dimostrato sulle serie prodotto riesce quindi n= 2 n n! = e2 Quanto riconosciuto sopra puó estendersi fino a riconoscere proprietá caratteristiche delle funzioni esponenziali. Consideriamo, per ogni a R la serie a n n! n= É facile riconoscere, servendosi ad esempio del criterio del rapporto, che si tratta di serie assolutamente convergente, quindi convergente. Indichiamo con a n S(a) = n! la somma. Scelti due qualsiasi valori a, b R consideriamo la serie prodotto delle due n= i termini della serie prodotto sono n= a n n!, n= b n n!
48 7. SERIE PRODOTTO 47 Pertanto c n = n a j j!b n j (n j)! = 1 n! j= = 1 n! n j= ( n )a j b n j = j (a + b) n n= n! n j= n! a j b n j j!(n j)! = (a + b)n n! é convergente ed ha come somma il prodotto delle somme delle due serie fattori, quindi S(a + b) = S(a). S(b) 1.4. Alcune proprietá. S(1) = e S(2) = e 2 S(a + b) = S(a)S(b) a : S(a) a : S( a) = 1 S(a) La somma S(a) precedentemente introdotta si chiama funzione esponenziale 1.5. Il caso complesso. Le serie a n n! n= possono essere considerate anche in relazione a valori a complessi: esse infatti sono assolutamente convergenti a n n! = a n n! e quindi convergenti. n= Osservazione 1.8. La funzione S(a) precedentemente introdotta ha il nome classico di funzione esponenziale ed é indicata con i simboli e a, n= Exp(a)
49
50 CAPITOLO 8 Riordinamenti La serie a termini di segno alterno 1. Introduzione (1) é convergente: la sua somma é nota, vale log(2). Essa fornisce l esempio fondamentale concernente la perdita, nell ambito delle serie, della proprietá commutativa della somma. É infatti possibile riconoscere, abbastanza facilmente, che ordinamenti diversi degli addendi della serie (1) producano serie convergenti a somme diverse. Indicati con a n = ( 1)n+1, n = 1, 2, 3,... n gli addendi della (1) indichiamo con {b k } la successione E chiaro che posto riesce A m = { b 2n = 1 2 a n, b 2n 1 = m a n, B 2m = n=1 B 2m = 1 2 A m 2m b n n=1 quindi dette A e B le somme delle due serie si ha B = 1 2 A Posto c n = a n + b n riesce C = c n = 3 2 A n=1 49
51 5 8. RIORDINAMENTI Ma c 2n 1 = a 2n 1 c 2n = a 2n + 1 { 2 a an se n pari n = se n dispari ovvero gli unici c k sono quelli di indice dispari e quelli pari con indice multiplo di 4: c 2n 1 = c 4n = 1 2n 1 2n 1 Si riconosce quindi come, al variare di n, gli addendi c n producano gli stessi addendi che producevano gli a n : tutt al più con un riordinamento Infatti se indichiamo i primi 2 termini a k si ha { 1, 1 2, 1 3, 1 4, 1 5, 1 6, 1 7, 1 8, 1 9, 1 1, 1 11, 1 12, 1 13, 1 14, 1 15, 1 16, 1 17, 1 18, 1 19, 1 } 2 mentre i primi 2 termini c k sono { 1,, 1 3, 1 2, 1 5,, 1 7, 1 4, 1 9,, 1 11, 1 6, 1 13,, 1 15, 1 8, 1 17,, 1 19, 1 } 1 Quindi, se il riordinamento non incidesse, in altri termini se per le serie convergenti valesse la proprietà commutativa della somma, allora dovrebbe riuscire c n = A n=1 invece... dalla c n = a n + b n si ha c n = (a n + b n ) = A A = 3 2 A A n=1 n=1 Esempio 1.1. Assegnato il numero dispari p riordiniamo la successione dei naturali allineando pacchetti ordinati di p 1 numeri pari seguiti ogni volta da un numero dispari. Indichiamo con {a n } la nuova successione: { 2[n/p] 1, se n mod p a n = 2 n 2 [n/p]] se n mod p avendo indicato con [n/p] la parte intera del quoziente. La costruzione della {a n } puó essere ottenuta con Mathematica al modo seguente
52 2. IL CASO ASSOLUTAMENTE CONVERGENTE 51 a[n_]:= If[Mod[n,p]==, 2 Floor[n/p] - 1, 2n - 2 Floor[n/p]] Ad esempio, scelto p = 5 il comando produce la seguente sequenza Table[a[n],{n,1,4}] 2, 4, 6, 8, 1, 1, 12, 14, 16, 3, 18, 2, 22, 24, 5, 26, 28, 3, 32, 7, 34, 36, 38, 4, 9, 42, 44, 46, 48, 11, 5, 52, 54, 56, 13, 58, 6, 62, 64, 15 Riordinando con questo procedimento la serie 1 produce, ad esempio una nuova serie i cui primi 3 termini sono i seguenti 1 2, 1 4, 1 6, 1 8, 1, 1 1, 1 12, 1 14, 1 16, 1 3, 1 18, 1 2, 1 22, 1 24, 1 5, 1 26, 1 28, 1 3, 1 32, 1 7, 1 34, 1 36, 1 38, 1 4, 1 9, 1 42, 1 44, 1 46, 1 48, Il caso assolutamente convergente Lemma 2.1. Per una serie a termini positivi vale la proprietà commutativa: se {a nk } è un riordinamento della successione {a n } allora a n = n=1 intendendo con ciò che se la serie n=1 a n converge allora converge anche la k=1 a n k e ha la stessa somma. Se non converge la prima, non converge neanche la seconda. Dimostrazione. Indicate con {A m } e con {B m } rispettivamente le successioni crescenti delle somme parziali della prima e della seconda serie riesce lim A m = sup{a m }, m m n : A m B n n m : B m A n Ne segue pertanto che k=1 a nk lim B m = sup{b m } m sup{a m } = sup{b n } lim m A m = lim m B m
53 52 8. RIORDINAMENTI Proposizione 2.2. Per una serie a k assolutamente convergente vale la proprietà commutativa: se {a nk } è un riordinamento della successione {a n } allora a n = n=1 Dimostrazione. Introdotte le funzioni parte positiva e parte negativa [x] + = x + x, [x] = x x 2 2 riesce [x] + x k=1 a nk [x] x pertanto, se la serie a k è assolutamente convergente allora le due serie a termini positivi [a k ] +, [a k ] sono entrambe assolutamente convergenti. Posto m m A m = a k, P m = [a k ] +, Q m = riesce A m = P m Q m E quindi dette A, P, Q m [a k ] rispettivamente le somme delle tre serie si ha A = P Q Qualunque sia il riordinamento che si applichi alla serie continuerà a valere per esso la corrispondente relazione a nk A m = P m Q m E quindi dette A, P, Q rispettivamente le somme delle tre serie si ha A = P Q ne deriva che A = A
54 3. IL TEOREMA DI RIEMANN DINI Il teorema di Riemann Dini 3.1. La favola dell onesto commerciante, della bilancia e dei tanti pesetti. Un onesto commerciante possiede una bilancia a due piatti corredata di una fila molto lunga di pesi, via via piú piccoli, rossi e blu, da usare con lo strano criterio di caricare i rossi sempre e solo sul piatto di sinistra e i blu su quello di destra. L onesto commerciante si fa un obbligo di pesare la merce in vendita con assoluta precisione, pesandola con grande attenzione sulla sua bilancia a due piatti. Posta la merce da pesare sul piatto di destra la bilancia si squilibra: piatto destro giú, piatto sinistro sú! Per eseguire la pesata, cioé per riequilibrare i piatti, l onesto commerciante pone sul piatto di sinistra uno dopo l altro i pesi rossi della fila che possiede: ne mette fino a che il piatto destro va sú e quello di sinistra giú. A questo punto comincia a caricare il piatto di sinistra con i pesi blu della fila: ne mette fino a che il piatto sinistro va sú e quello di destra giú. Di questo passo prosegue, caricando ogni volta il piatto piú in alto fino a farlo diventare il piú basso. Ogni volta la differenza dei pesi di un piatto rispetto a quelli dell altro approssima il peso della merce: l errore é, ogni volta minore dell ultimo pesetto aggiunto per invertire la reciproca posizione dei due piatti. Se la lunga fila di pesi disponibili contiene pesi via via piú piccoli si capisce che le approssimazioni del peso della merce ottenute saranno sempre migliori, e l onesto commerciante si sentirá giustamente con la coscienza a posto Le serie convergenti semplicemente. Sia a k una serie convergente semplicemente, cioé non convergente assolutamente, a k = + allora dall uguaglianza si riconosce che k=1 a k = k=1 [a k ] + k=1 [a k ] k=1 lim a k = k lim n n k=1 [a k] + = + n k=1 [a k] = + lim n Se infatti una delle due somme parziali a secondo membro, P n o Q n convergesse allora, dalla relazione A n = P n Q n si dedurrebbe che converge anche l altra e, quindi, che la serie sarebbe, contrariamente all ipotesi, convergente assolutamente. k=1 a k k=1
55 54 8. RIORDINAMENTI 3.3. Il teorema. Teorema 3.1. Sia k=1 a k una serie convergente ma non convergente assolutamente, allora comunque si scelga un numero reale S esiste un riordinamento {a nk } della successione {a n } tale che riesca a nk = S k=1 Dimostrazione. Supponiamo di aver scelto S : il caso S < si tratta ugualmente riferendosi al caso della serie ( a k ) e alla scelta del valore S. Indichiamo con {p k } e con {q k } le due successioni dei soli termini a k positivi e dei soli termini a h negativi, ordinati con lo stesso ordine con cui comparivano originalmente: tenuto conto che m m P m = p k, Q m = k=1 divergono entrambe esisterà un primo m 1 rispetto al quale riesce k=1 q k k=1 Valutiamo la differenza S P m1 P m1 S P m1 P m1 1 p m1 Prepariamo pertanto il riordinamento della {a k } ponendo ai primi m 1 posti i primi m 1 termini positivi p 1, p 2,..., p m1 Consideriamo ora il primo m 2 tale che Valutiamo la differenza P m1 Q m2 S S (P m1 Q m2 ) q m2 Proseguiamo pertanto il riordinamento della {a k } ponendo ai successivi m 2 posti i termini, negativi, che compongono Q m2 Consideriamo ora le somme p 1, p 2,..., p m1 q 1, q 2,... q m2 P 1 m = m k=m 1 +1 p k
56 3. IL TEOREMA DI RIEMANN DINI 55 esse differiscono dalle precedenti P m perchè non includono i primi m 1 addendi: tuttavia se divergevano le P m non possono che divergere anche queste P 1 m. Sia pertanto m 3 il primo indice tale che Valutiamo la differenza P m1 Q m2 + P 1 m 3 S P m1 Q m2 + P 1 m 3 S p m3 Proseguiamo pertanto il riordinamento della {a k } ponendo ai successivi m 3 posti i termini, positivi, che compongono P 1 m 3 p 1, p 2,..., p m1 q 1, q 2,... q m2, p m1 +1, p m1 +2,..., p m3 Di blocchetto positivo in blocchetto negativo e viceversa si riordinano tutti i termini {a k }: tale riordinamento produce una serie k=1 a nk della quale conosciamo alcune somme parziali S m1, S m1 +m 2, S m1 +m 2 +m 3,... Esse verificano le seguenti disuguaglianze Inoltre per ogni k esistono S S m1 S m1 +m 2 S S m1 +m 2 +m 3 S m1 +m 2 +m 3 S S m1 +m 2 +m 3 +m ν = n n+1 m j, µ = j=1 tali che la somma parziale S k sia compresa tra S ν ed S µ tenuto presente che anche S si trova tra S ν ed S µ riesce j=1 m j S S k S ν S + S S µ max{ a µ, a ν } Tenuto conto che la successione {a µ }, sottosuccessione della successione infinitesima {a n } è necessariamente infinitesima anch essa risulta provato che lim S k = S k
57 56 8. RIORDINAMENTI ovvero che il riordinamento realizzato determina una nuova serie convergente e con somma il numero S per altro arbitrario scelto inizialmente.
58 CAPITOLO 9 Funzioni continue Teorema 1.1. Sia 1. Funzioni continue su compatti f : X Y continua, sia K X compatto in X, allora l immagine f(k) é un compatto di Y. Dimostrazione. Per riconoscere che f(k) é un compatto occorre riconoscere che ogni successione {y n } f(k) ammette sottosuccessioni convergenti in f(k). Dire che y n f(k) vuol dire y n = f(x n ), Consideriamo pertanto la successione {x n } K x n K Per l ipotesi che K sia compatto in X la successione {x n } ammette sottosuccessioni {x nk } convergenti in K lim x n k = ξ K k Ma allora per l ipotesi che f sia continua riesce lim f(x n k ) = lim y nk = f(ξ) f(k) k k Si é pertanto trovata una sottosuccessione convergente in f(k). Proposizione 1.2. Sia {y nk } {y n } f : X R n continua, sia K X compatto in X, allora l immagine f(k) é un insieme chiuso e limitato in R n. 57
59 58 9. FUNZIONI CONTINUE Proposizione 1.3. Sia f : X R continua, sia K X compatto in X, allora l immagine f(k) ammette massimo e minimo. Domande: Esiste una funzione continua e biunivoca da [, 1] R a tutto R? Esiste una funzione continua e biunivoca da (, 1) R a tutto R? Esiste una funzione continua e biunivoca da tutto R a (, 1)? Per rispondere alla prima domanda si tenga conto del Teorema 1.1, per rispondere alle altre due si tengano presenti le due funzioni tan(x), arctan(x) 2. Funzioni inverse Teorema 2.1. Sia f : X Y continua, sia K X compatto in X, e sia biunivoca: allora la funzione inversa é continua anch essa. Dimostrazione. Indichiamo con f 1 la funzione inversa f 1 : Y X Naturalmente l inversa di f 1 é la f stessa. Per riconoscere che f 1 é continua occorre provare che per ogni aperto V X la sua contrimmagine rispetto a f 1 sia un aperto in Y : tenuto conto che l inversa di f 1 é la f stessa occorre pertanto provare che V X, aperto f(v ) sia aperto in Y Consideriamo il complementare di V in X C(V ) esso é, in quanto sottoinsieme chiuso di un compatto, compatto anch esso. Allora, tenuto conto del teorema precedente f (C(V )) é compatto in Y, quindi é chiuso in Y. Tenuto conto che in virtú della biunivocitá f (C(V )) = C (f(v ))
60 3. LA CONTINUITÁ UNIFORME 59 si riconosce che C (f(v )) é chiuso e, quindi, é aperto. C (C (f(v ))) = f(v ) Esempio 2.2. Sia E = [ 1, ] (1, 2] e sia f : E R R definita come segue { x + 1 se x [ 1, ] f(x) = x se x (1, 2] si tratta di una funzione continua, crescente, quindi biunivoca. L inversa f 1 : [ 1, 2] R R é definita { y 1 se y [, 1] f 1 (y) = y se y (1, 2] non é continua nel punto y = 1. Si noti che la funzione f assegnata non era definita su un compatto, cioé su un insieme chiuso e limitato: E infatti non é chiuso, manca il punto x = 1, estremo dell intervallo (1, 2] Continuitá dell inversa. Nel caso di f : [a, b] R [m, M] R continua e invertibile é facile riconoscere la continuitá dell inversa: sia y = f(x ) ovvero x = f 1 (y ) e sia ε > assegnato, consideriamo il compatto K = [a, b] C ((x ε, x + ε)) l immagine f(k) é un compatto, y o / f(k) esiste pertanto δ > tale che Pertanto (y δ, y + δ) f(k) = y (y δ, y + δ) [m, M] f 1 (y) (x ε, x + ε) che é la relazione di continuitá di f 1 nel punto y. 3. La continuitá uniforme Sia f : X Y continua: questo significa che scelto ε > una tantum, in corrispondenza ad ogni punto p X esiste una distanza di sicurezza δ P tale che x I(p, δ P ) f(x) I(f(p), ε) La dipendenza della distanza di sicurezza δ P dal punto P é del tutto evidente pensando al caso di funzioni f : R R, e al loro grafico nei tratti in cui il grafico é molto pendente la distanza di sicurezza δ P dovrá essere particolarmente piccola,
61 6 9. FUNZIONI CONTINUE Il titolo nei tratti in cui il grafico é quasi orizzontale la distanza di sicurezza δ P sará assai piú generosa... continuitá uniforme si riferisce all esistenza, o meno, di una distanza di sicurezza δ valida per tutti i punti di X 1. Esempio 3.1. La funzione f : R R, f(x) = x 2 non é uniformemente continua: infatti presi due punti x 1 e x 2 riesce f(x 1 ) f(x 2 ) = x 2 1 x 2 2 = x 1 + x 2. x 1 x 2 relazione che mette in evidenza come per ottenere che f(x 1 ) f(x 2 ) ε occorre che ε x 1 x 2 x 1 + x 2 e pertanto piú ci si riferisce a punti x 1 e x 2 grandi piú per ottenere che f(x 1 ) f(x 2 ) ε occorrerá prenderli vicini. In altri termini manca una distanza di sicurezza δ P buona ovunque. f(x) = sin(x) é uniforme- Esempio 3.2. La funzione f : R R, mente continua: 4. Il teorema di continuitá uniforme Teorema 4.1. Sia X compatto: ogni f : X Y continua é (anche, di conseguenza, necessariamente, ecc. ) uniformemente continua. Dimostrazione. Il risultato puó essere dimostrato per assurdo ammettendo cioé che esista un ε > in relazione al quale non esista alcun δ ε positivo che garantisca l implicazione d X (x 1, x 2 ) δ ε d Y (f(x 1 ), f(x 2 )) ε 1 La favoletta del cardiopatico e del suo medico. Un signore sofferente di cuore non deve esporsi a eccessive variazioni di altitudine: egli, che giustamente non vuole rinunciare a fare belle passeggiate, chiede al suo medico quanti chilometri possa fare ogni giorno. La risposta, giusta, del medico é: Dipende da dove lei abita: se risiede a Reggio Emilia puó camminare quanto le pare, se invece abita a Bolzano non deve allontanarsi da casa di piú di 5 metri, se abita a Cortina... beh le suggerirei di non uscire di casa!
62 4. IL TEOREMA DI CONTINUITÁ UNIFORME 61 Negare l esistenza di un tale δ ε > equivale ad ammettere che d X (ξ n, η n ) 1 n N ξ n, η n X : n d Y (f(ξ n ), f(η n )) ε A questo punto la compattezza di X e la continuitá di f conducono a una contraddizione: infatti essendo X compatto la successione {ξ n } ammette una sottosuccessione {ξ nk } convergente lim ξ n k = l X k essendo d X (ξ n, η n ) 1 n allora anche la sottosuccessione {η n k } é convergente allo stesso limite l essendo f continua riesce quindi lim f(ξ n k ) = f(l), lim f(η nk ) = f(l) k k e quindi lim d Y (f(ξ nk ), f(η nk )) = k L ultimo risultato contraddice la condizione d Y (f(ξ n ), f(η n )) ε ammessa per tutti i punti delle due successioni {ξ n } e {η n }. Quindi l ammissione fatta per assurdo conduce a una contraddizione: pertanto non é vera! Quindi é vero che ε > esiste un δ ε positivo che garantisce l implicazione d X (x 1, x 2 ) δ ε d Y (f(x 1 ), f(x 2 )) ε Proposizione 4.2. Sia f : X Y uniformemente continua: se {x n } X é una successione di Cauchy allora la successione trasformata y n = {f(x n )} é una successione di Cauchy in Y. Dimostrazione. Essendo f uniformemente continua ε > δ ε tale che d X (a, b) δ ε d Y (f(a), f(b)) ε ma allora d X (x p, x q ) δ ε d Y (y p, y q ) = d Y (f(x p ), f(x q )) ε Tenuto presente che la {x n } X é, per ipotesi, una successione di Cauchy esisterá ν ε tale che p, q ν ε d X (x p, x q ) δ ε
63 62 9. FUNZIONI CONTINUE e quindi p, q ν ε d Y (f(x p ), f(x q )) ε Osservazione 4.3. Al di fuori del caso di funzioni uniformemente continue non é piú vero che l immagine di una successione di Cauchy tramite una funzione continua sia ancora una successione di Cauchy: basta pensare alla funzione continua f : (, 1) R f(x) = 1 x Si consideri ad esempio la successione di Cauchy { x n = 1 } f(x n ) = n n 5. Applicazioni 5.1. Il limite sulla frontiera. Sia f : (a, b) R R, continua all interno di (a, b): un problema importante é riconoscere se esistano, o meno i limiti agli estremi Tenuto conto che lim f(x) x a + lim f(x) x b lim x x f(x) = l {ξ n } x lim n f(ξ n ) = l e tenuto conto che una successione a valori reali é convergente se e solo se é di Cauchy si riconosce il seguente Lemma 5.1. Sia f : E R R, sia x D(E), x / E: esiste se e solo se tale che se riesca Ne segue pertanto la lim x x f(x) = l ε > δ ε > x 1, x 2 E, x 1 x δ ε, x 2 x δ ε f(x 1 ) f(x 2 ) ε Proposizione 5.2. Sia f : (a, b) R R, uniformemente continua, allora esistono i due limiti agli estremi.
64 Indicati con A e B i due limiti lim f(x) = A x a + 5. APPLICAZIONI 63 lim f(x) = B x b chiamiamo F (x) la funzione A se x = a, F (x) = f(x) se a < x < b B se x = b, La funzione F (x) ora definita é continua sull intervallo chiuso [a, b] e coincide all interno con la f(x): essa si dice pertanto prolungamento per continuitá della f a [a, b] chiuso. Tenuto conto del precedente teorema 4.1 si puó riconoscere la seguente Proposizione 5.3. Una f : (a, b) R R é prolungabile in una funzione continua sulla chiusura [a, b] se e solo se é uniformemente continua in (a, b). Risultato che puó essere espresso in forma piú generale al modo seguente Teorema 5.4. Una f : E R R é prolungabile in una funzione continua sulla chiusura E se e solo se é uniformemente continua in E La funzione esponenziale. Scelta una base a > 1 é correttamente definita la funzione m f : Q R, n a m n il suo prolungamento nella celebrata funzione esponenziale di base a a x é null altro che l applicazione piú importante del precedente Teorema 5.4 Infatti la proprietá formale delle potenze implica, per ogni x e y razionali, a y a x = a x ( a y x 1 ) a y a x = a x a y x 1 Pertanto supponendo, ad esempio, x, y [, 1] Q, posto δ = y x, si ha a y a x a x a δ 1 a a δ 1 É evidente quindi che se proviamo che (2) lim δ a δ = 1
65 64 9. FUNZIONI CONTINUE se ne deduce che per ogni ε > esiste δ ε tale che δ δ ε : a a δ 1 ε ovvero x, y : x y δ ε a y a x ε che significa che la funzione esponenziale é uniformemente continua e quindi prolungabile, per continuitá da Q a R. Per provare la (2) ci serviamo della nota disuguaglianza x >, che implica ( 1 + a 1 ) n 1 + n a 1 n n (1 + x) n 1 + nx Ne segue pertanto lim a 1 n = 1 n Ne segue quindi, per ogni razionale δ = m n, m < n = a a 1 n 1 + a 1 n 1 a m n a 1 n 1 Il caso di δ equivale a quello precedente tenuto conto che a δ = 1 a δ 6. Il teorema di esistenza degli zeri 6.1. Insiemi connessi. Ricordiamo alcune definizioni (cfr. RUDIN, pag.4): Definizione 6.1. Due insiemi A, B si dicono separati se A B = e A B = Definizione 6.2. Un insieme E si dice connesso se non é unione di due insiemi separati e non vuoti. In R gli insiemi connessi sono tutti e soli gli intervalli (aperti, semiaperti, limitati, non limitati,...): essi sono anche tutti convessi. In R n gli insiemi convessi sono connessi, ma esistono anche insiemi connessi non convessi (si pensi ad una corona circolare, a un ferro di cavallo, ecc.)
66 6. IL TEOREMA DI ESISTENZA DEGLI ZERI Immagini di connessi. Teorema 6.3. Sia f : X Y continua e sia E X connesso: allora f(e) Y é connesso. Dimostrazione. Supponiamo, per assurdo, che f(e) non sia connesso, cioé f(e) = A B con A, B separati: A B = e A B =. Posto G = E f 1 (A), H = E f 1 (B) si ha E, G non vuoti e E = G H Riconosciamo adesso che i due insiemi G, H soddisferebbero alle due condizioni (3) G H = e G H = Cominciamo a provare la prima delle (3): Tenuto conto che A A riesce: f 1 (A) é chiuso perché f é continua, G f 1 (A) e, quindi, G f 1 (A). Le osservazioni precedenti implicano che G H = : infatti se esistesse x G H allora f(x ) A, f(x ) B e quindi f(x ) A B contrariamente all ipotesi A B =. Proviamo la seconda delle (3) Il procedimento é del tutto analogo al precedente. Tenuto conto che B B riesce: f 1 (B) é chiuso perché f é continua, H f 1 (B) e, quindi, H f 1 (B).
67 66 9. FUNZIONI CONTINUE Le osservazioni precedenti implicano che H G = : infatti se esistesse x 1 H G allora f(x 1 ) B, f(x 1 ) A e quindi f(x! ) B A contrariamente all ipotesi B A =. Quindi l ammissione fatta per assurdo che f(e) non sia connesso é da respingere, quindi risulta provato che f(e) é necessariamente connesso Applicazioni. Tenuto presente che i connessi di R sono intervalli (cfr. RUDIN, Teorema 2.47, pag. 4) si deducono dal precedente Teorema 6.3 i seguenti risultati Proposizione 6.4 (Teorema d esistenza degli zeri). Sia f : [a, b] R continua, se f(a)f(b) < allora esiste ξ (a, b) in cui riesce f(ξ) =. Proposizione 6.5 (Teorema dei valori intermedi). Sia f : I R R continua con I connesso (cioé un intervallo): siano a, b I k [f(a), f(b)] ξ [a, b] tale che f(ξ) = k 7. Funzioni monotone Ci occupiamo in questo paragrafo esclusivamente di funzioni f : (a, b) R R Punti di discontinuitá. Definizione 7.1. Limite sinistro e limite destro in un punto f(x ) = lim n f(t n ) t n x, t n < x f(x+) = lim n f(t n ) t n x, x < t n essendo tali limiti indipendenti dalle successioni {t n } scelte.
68 7. FUNZIONI MONOTONE 67 Definizione 7.2. Il punto x si dice punto di discontinuitá di prima specie, o semplice, se f(x ), f(x+), f(x ) f(x+) Si dice punto di discontinuitá di seconda specie se uno almeno dei due limiti sinistro o destro manca. Teorema 7.3. Le funzioni monotone f : (a, b) R R hanno, all interno dell intervallo in cui sono definite, solo discontinuitá di prima specie, l insieme dei punti di discontinuitá é finito o numerabile. Dimostrazione. Supponiamo f monotona crescente allora riesce, necessariamente, f(x ) = sup f(t), f(x+) = inf f(t) t (a,x) t (x,b) Sia E l insieme dei punti di discontinuitá: se x E allora riesce f(x ) < f(x+) associamo quindi ad ogni punto x E un numero razionale r(x) tale che f(x ) < r(x) < f(x+) Se x 1, x 2 E, x 1 x 2 allora essendo f monotona riesce r(x 1 ) r(x 2 ). La corrispondenza produce quindi un applicazione r : E r(e) Q. Considerato che Q é numerabile, tale sará anche r(e) e quindi E. Esempio 7.4. Si possono costruire funzioni monotone crescenti, limitate, con insieme di discontinuitá E assegnato (naturalmente con E finito o numerabile). Se E := {x 1 < x 2 <... < x m } allora basta scegliere m + 1 valori c 1 < c 2 <... < c m+1 e costruire la funzione f(x) Se E é una successione f(x) = c 1 x (a, x 1 ] c 2 x (x 1, x 2 ] c m+1 x (x m, b) E := {x 1 < x 2 < x 3 <... < x n <...} basta procurarsi una successione di numeri positivi a n tali che a n < n=1
69 68 9. FUNZIONI CONTINUE e definire f(x) = x n<x a n essendo la somma estesa a tutti gli indici n in corrispondenza ai quali riesce x n < x La funzione f(x) é certamente crescente: piú é grande x piú numerosi sono gli addendi positivi da sommare, ed é discontinua in tutti e soli i punti di E, traversando i quali si incontra un ulteriore addendo da sommare.
70 CAPITOLO 1 Integrali impropri di funzioni di una variabile 1. Le funzioni continue Consideriamo nel seguito una delle piú importanti applicazioni del teorema di uniforme continuitá delle funzioni continue su intervalli chiusi e limitati: la loro integrabilitá. Ricordiamo che l integrabilitá secondo Riemann su intervallo chiuso e limitato [a, b] é riconoscibile elementarmente per due sole classi di funzioni: quelle lipschitziane, quelle monotone e limitate. Teorema 1.1. Sia f : E R R continua, allora f é integrabile secondo Riemann in ogni intervallo chiuso e limitato [a, b] E. Dimostrazione. Essendo f continua in E e quindi anche in [a, b], f é, di conseguenza, uniformemente continua in [a, b]. Scelto ε > esiste pertanto un δ ε > tale che se la massima ampiezza degli intervallini della decomposizione verifica la disuguaglianza allora riesce a = x < x 1 < x 2 <... < x n 1 < x n = b max x i+1 x i δ ε i i : sup f(t) inf f(t) ε t [x i+1,x i ] t [x i+1,x i ] Indicate pertanto con S + e con S le somme di Riemann di f relative a tale decomposizione riesce S + S ε (b a) da cui l integrabilitá. 69
71 7 1. INTEGRALI IMPROPRI DI FUNZIONI DI UNA VARIABILE 2. Integrali impropri Il titolo di integrale improprio 1 si riferisce a integrali quali 1 ( ) sin dx, dx, e x sin(x) dx, dx x x x 2 riferiti a funzioni non continue agli estremi di intervalli, funzioni integrande non limitate, intervalli di integrazione non chiusi e limitati. Ricordiamo il seguente risultato fondamentale per l integrazione di funzioni f(x) continue su intervalli chiusi e limitati: Teorema 2.1. Sia f continua nell intervallo chiuso e limitato [a, b], siano {a n } e {b n } due successioni contenute in [a, b] e convergenti rispettivamente ad a e b allora bn (4) lim f(x)dx = n a n b a f(x)dx La proprietá indicata viene assunta come algoritmo di definizione dell integrale nei casi impropri precedentemente elencati: perché non definire come 1 1 lim a a sin( 1 x ) dx, sin( 1 x ) dx, una volta riconosciuta l esistenza di tale limite...? 3. Integrali su intervalli limitati 3.1. Funzioni continue e limitate. 1 Teorema 3.1. Sia f(x) continua sull intervallo aperto (a, b) e sia limitata in modulo: allora comunque si scelgano due successioni {a n } e {b n } contenute in (a, b) e convergenti rispettivamente ad a e a b esiste il bn (5) lim n a n 1 Vol. I, 3.15, pag, 31 f(x) dx
72 3. INTEGRALI SU INTERVALLI LIMITATI 71 il cui valore viene poi assunto come definizione di b a f(x) dx Dimostrazione. Sia f(x) M, posto I n = bn verifichiamo l esistenza del limite : a n f(x)dx lim I n n tramite il criterio di convergenza di Cauchy, valido per ogni successione numerica. Riesce I n I m M ( a n a m + b n b m ) Tenuto conto che {a n } e {b n } sono successioni convergenti, i due moduli a secondo membro saranno infinitesimi. Quindi infinitesimo riesce anche I n I m e quindi, verificato il criterio di convergenza, se ne deduce l esistenza del limite (5). Esempio 3.2. Il teorema precedente garantisce l esistenza dell integrale improprio di sin(1/x) sull intervallo (, π/2), come pure ovviamente su qualunque altro intervallo [, A]. Consideriamo, per altra via, l integrale improprio π/2 sin( 1 x Tenuto conto che, < a < π/2, si ha π/2 a π/2 a )dx = lim a π/2 a sin( 1 x )dx sin( 1 π/2 x )dx = x (cos( 2 1 ) x ) dx sin( 1 x )dx = x2 cos( 1 π/2 x ) 2 a a π/2 a x cos( 1 x )dx I due termini a secondo membro hanno limite per a : il primo perché esiste, ovviamente, lim a a 2 cos( 1 a ) = il secondo perché la funzione integranda é prolungabile per continuitá in tutto l intervallo chiuso [, π/2] É quindi riconosciuta l esistenza del limite π/2 lim a a sin( 1 x )dx
73 72 1. INTEGRALI IMPROPRI DI FUNZIONI DI UNA VARIABILE purtroppo, non é altrettanto semplice conoscerne il valore! 3.2. Numero finito di discontinuitá. Il precedente Teorema (3.1) copre anche il caso di alcuni punti di discontinuitá interni all intervallo di integrazione quali nel caso, vedi Figura 1,ad esempio di 1 1 sin( sin(x) ) dx Figura 1. 1 sin( 1 sin(x) ) dx 3.3. Funzioni continue in (a, b) non limitate. La questione 2 si riferisce al secondo esempio 1 1 dx x La costruzione degli integrali I n é la stessa del caso precedente: non altrettanto la loro convergenza che, dipende dall ordine di infinito che la funzione f presenta in uno o in entrambi gli estremi. Teorema 3.3. Sia f continua in (a, b], a escluso e b incluso, e riesca allora esiste il limite (6) lim f(x) M 1 x a α, α < 1 t a b t f(x)dx 2 Dire che f(x) continua in (a, b) aperto non é limitata equivale a dire che diverge in modulo in uno o in entrambi gli estremi.
74 3. INTEGRALI SU INTERVALLI LIMITATI 73 che puó essere quindi preso come valore dell integrale improprio b a f(x) dx Dimostrazione. Siano t 1, t 2 [a, a + ɛ], t 1 < t 2 b b t2 f(x)dx f(x)dx M 1 t 1 t 2 t 1 x a dx α = = M ( (t2 a) 1 α (t 1 a) 1 α) M 1 α 1 α ɛ1 α Figura 2. Sottografico di 1/ x (rosso) su [, 1] : regione illimitata (in alto...) ma area finita. Sottografico di 1/x (nero): area infinita. Esempio dx (1 x2 )(1 k 2 x 2 ), k 2 < 1 La funzione integranda f(x) é continua in [, 1), diverge in 1, ma ( ) 1 1 f(x) 1 k 2 1 x quindi presenta in x = 1 un ordine di divergenza con esponente α = 1/2 legittimo...! Un integrale di questo tipo si incontra nello studio delle oscillazioni del pendolo: vedi Courant-John, Introduction to Calculus and Analysis, Vol. I pag. 41.
75 74 1. INTEGRALI IMPROPRI DI FUNZIONI DI UNA VARIABILE 4. Integrali impropri di funzioni positive Proposizione 4.1. Sia positiva, f(x) : riesce lim c a b c f : (a, b] R R f(x)dx = sup c (a,b] 4.1. Teoremi di confronto. b c f(x)dx Teorema 4.2. Siano f e g due funzioni positive, continue in (a, b], e tali che f(x) g(x) allora se esiste l integrale improprio di g allora esiste anche quello di f, se non esiste l integrale improprio di f allora non esiste neanche quello di g Convergenza assoluta. Proposizione 4.3. Sia f continue in (a, b], se esiste l integrale improprio di f allora esiste anche quello di f. Dimostrazione. Indicate con f + ed f la parte positiva e la parte negativa di f riesce f(x) = f + (x) f (x), f + (x) f(x), f (x) f(x) Pertanto in base al precedente Teorema di confronto esistono gli integrali impropri sia di f + che di f e, quindi, per linearitá anche quello di f. 5. L indipendenza dalla successione I precedenti integrali impropri sono stati definiti come limiti di altri integrali: é importante riconoscere che i valori cosí assunti non dipendano tuttavia dalla successione scelta nel calcolo. Supponiamo per esempio che qualcuno parlasse dell integrale improprio + sin(x)dx dichiarando che esso vale in base al seguente ragionamento: la successione di punti x k = 2kπ tende a +
76 6. INTERVALLI ILLIMITATI 75 gli integrali xk sin(x)dx = quindi + xk sin(x)dx = lim sin(x)dx = k + L errore consiste nel fatto che occorre, per parlare di integrale improprio, poter riconoscere che qualsiasi successione x k + si prenda esista il limite degli integrali xk sin(x)dx e tale limite sia sempre lo stesso, cioé non cambi cambiando successione. Nel caso precedente se si scegliesse invece x k = (2k + 1)π successione ancora divergente a + si otterrebbero integrali xk sin(x)dx = 1 che porterebbero, con lo stesso diritto alla dichiarazione + sin(x)dx = 1 I teoremi dimostrati garantiscono condizioni sufficienti a tale indipendenza del limite dalla successione scelta per eseguire i calcoli. 6. Intervalli illimitati Funzioni continue da integrare su intervalli infiniti (semirette o tutto l asse reale): stesso procedimento basato sui casi precedenti, si integra su una successione di intervalli leciti e si assume come integrale improprio il loro limite. Teorema 6.1 (Criterio sufficiente di convergenza). Sia f(x) continua nell intervallo illimitato (a, + ) e infinitesima per x con un ordine di infinitesimo α > 1 allora esiste il limite f(x) lim x + 1/x = lim f(x) α x + xα = t lim t + a f(x) dx
77 76 1. INTEGRALI IMPROPRI DI FUNZIONI DI UNA VARIABILE e tale valore viene assunto come integrale improprio + a f(x) dx La dimostrazione é analoga a quella dei casi precedenti. Esempio 6.2. Il sottografico di ha area finita, π. Infatti + f(x) = x 2 1 dx = lim 1 + x2 a, b + b a x 2 dx = = lim (arctan(b) arctan(a)) = π a, b + Esempio 6.3. Il sottografico di f(x) = e x2, la campana di Gauss, ha area finita, valore π. Figura 3. In rosso 1/(1 + x 2 ), in nero, sotto, e x2 Esempi tratti dalle Note di Analisi Matematica I, Capitolo 3.
78 Assegnata f(x) = 6. INTERVALLI ILLIMITATI 77 1, x (, + )/{1} x log(x) α indicare in quali intervalli esiste l integrale b f(x)dx e per a quali α. (Cap. 3, pag.7) Assegnata la funzione R(x) = p(x) q(x) essendo p(x) e q(x) due polinomi, indicare in quali intervalli esiste l integrale b R(x)dx a Indipendenza del valore da attribuire ad un integrale improprio dalla successione usata per invadere l intervallo di integrazione: il caso di x dx (Cap. 3 pag. 8) Esistenza dell integrale improprio (Cap. 3 pag. 12) 1 1 (1 x2 )(1 k 2 x 2 ) dx k2 < 1 La funzione gamma: (Cap. 3 pag.14) Γ(x) = + e y y x 1 dx x > esistenza dell integrale improprio, Γ(x + 1) = xγ(x), Γ(n + 1) = n! Esempio di f(x) lineare a tratti per la quale esiste l integrale improprio su [, + ) mentre per il modulo f(x) l integrale improprio diverge. (Cap. 3 pag. 16) Sia f(x) una funzione non negativa, decrescente e infinitesima: riconoscere che esiste l integrale improprio (Cap. 3 pag. 18) + f(x) sin(x) dx il caso dell integrale improprio (Cap. 3 pag.1) + 1 cos(x) x dx
79 78 1. INTEGRALI IMPROPRI DI FUNZIONI DI UNA VARIABILE Gli integrali di Fresnel (Cap. 3, pag. 18) + sin(x 2 ) dx Una generalizzazione: per quali α esiste l integrale improprio + sin(x α ) dx Proposizione 6.4. Sia f(x) una funzione continua, non negativa, decrescente e infinitesima: esiste l integrale improprio + f(x) sin(x) dx Dimostrazione. L esistenza dell integrale improprio corrisponde all esistenza del limite (7) lim L + L Suddividiamo l intervallo [, L] in parti f(x) sin(x) dx [, π] [π, 2π] [2π, 3π]... [(n L 1)π, n L π] [n L π, L] l ultima delle quali lunga meno di π, cioé Posto riesce (8) L n L = [L/π], L + n L + a k = kπ (k 1)π f(x) sin(x) dx = n L k=1 f(x) sin(x) dx a k + L n L π f(x) sin(x) dx Tenuto conto che la funzione integranda ha segno costante in ciascuno degli intervallini [kπ, (k+1)π] si riconosce che i termini a k si presentano a segni alterni a 1, a 2, a 3,... Tenuto conto inoltre che f(x) é decrescente e infinitesima si riconosce che a k a k+1, lim a k = k + Quindi la serie k=1 a k
80 6. INTERVALLI ILLIMITATI 79 é convergente per il criterio di Leibnitz, cioé esiste lim L n L a k k=1 Esiste del resto anche il limite dell integrale L n L π L n L π f(x) sin(x) dx f (n Lπ) π f(x) sin(x) dx: infatti essendo f(x) infinitesima per x. Dalla (8) segue pertanto l esistenza del limite (7), cioé l esistenza dell integrale improprio + f(x) sin(x) dx
81
82 CAPITOLO 11 Successioni di funzioni 1. Primi esempi 1, x, x 2, x 3,..., x n,..., x [, 2] e x, e 2x, e 3x,..., e nx,..., x [ 1, 1] f n (x) = 1, n = 1, 2, 3,..., x R (n + 1) 2 + x2 f n (x) = sin(x), n = 1, 2, 3,..., x [, 2π] f n (x) = n 2, n = 1, 2, 3,..., x [, 1] I termini di una successione di funzioni {f n (x)} sono funzioni dipendenti da un parametro n a valori interi, che rappresenta l indice dell elemento, da una variabile x Serie di funzioni. Analogamente alle successioni di funzioni si possono considerare le Cosí ad esempio la serie serie di funzioni n= equivale a considerare la successione di funzioni s m (x) = 81 x n m n= x n
83 SUCCESSIONI DI FUNZIONI 1.2. Usare i grafici. Assegnare una funzione f : [a, b] R R equivale ad assegnare il suo grafico nel piano cartesiano (x, y). Assegnare una successione di funzioni equivale quindi ad assegnare una successione di grafici: un album da disegno con infinite pagine nella prima pagina c é il grafico della prima funzione della successione, la f 1 (x), nella seconda c é il grafico della seconda funzione della successione, la f 2 (x), ecc, Con mezzi piú moderni l album puó essere sostituito con una pellicola cinematografica, la prima pagina diventa il primo fotogramma, la seconda pagina il secondo, ecc. Osservazione 1.1. Questa x 1, x 2, x 3,... x n,... non é una successione di funzioni: infatti non c é alcun punto x nel quale possano essere calcolate tutte. Per poter calcolare la prima occorre che x 1, per poter calcolare anche la seconda occorre, in piú che riesca anche x 2, ecc. 2. Convergenza puntuale Assegnata la successione di funzioni {f n (x)}, x [a, b], n = 1, 2, 3,... ad essa risultano associate, per ogni scelta di x [a, b] le successioni numeriche {f n (x )}, n = 1, 2, 3,... Scelte di x diversi conducono a successioni numeriche {f n (x )} diverse: per alcuni x tali successioni possono risultare convergenti, per altri x tali successioni possono risultare non convergenti. Esempio 2.1. Sia f n (x) = x n, x [, 2]: scelto x = la successione numerica diventa {,,,...,,...}, convergente a l =, sia x = 1/3 la successione numerica diventa {1/3, 1/3 2, 1/3 3,..., 1/3 n,...}, convergente a l =, sia x = 1 la successione numerica diventa {1, 1, 1,..., 1,...}, convergente a l = 1, sia x = 2 la successione numerica diventa {2, 2 2, 2 3,..., 2 n,...}, non convergente.
84 2. CONVERGENZA PUNTUALE 83 Definizione 2.2. Una successione {f n (x)} assegnata per x [a, b] si dice convergente puntualmente in [a, b] alla funzione f(x) se per ogni x [a, b] la successione numerica associata {f n (x )} converge al valore f(x ). Il legame tra le f n (x) e la funzione limite f(x) si indica, come per tutti gli altri limiti, con la notazione lim f n(x) = f(x) n Una questione importante é la seguente: quali delle proprietá possedute dalle f n (x) si conservano nella f(x)? Proposizione 2.3. Riesca x [a, b] : lim f n (x) = f(x) allora: n se le f n (x) sono non negative sará non negativa anche f(x), se le f n (x) sono non decrescenti sará non decrescente anche f(x), se le f n (x) sono convesse sará convessa anche la f(x). Dimostrazione. x [a, b] : f n (x ) o lim f n (x ) = f(x ) n x 1 < x 2 [a, b] f n (x 2 ) f n (x 1 ) lim [f n (x 2 ) f n (x 1 )] = [f(x 2 ) f(x 1 )] n la convessitá significa che n, λ [, 1] : f n (λx 1 + (1 λ)x 2 ) λf n (x 1 ) + (1 λ)f n (x 2 ) passando al limite membro a membro, e tenuto conto che si mantengono le disuguaglianze, si ha λ [, 1] : f(λx 1 + (1 λ)x 2 ) λf(x 1 ) + (1 λ)f(x 2 ) 2.1. Esempi di proprietá che si possono perdere. la limitatezza: le funzioni f n (x) che compongono la successione possono essere ciascuna limitata e, tuttavia, ammettere un limite puntuale non limitato: x (, 1] : f n (x) = 1 x + 1 lim f n(x) = 1 n x n x > : f n (x) = { n 2 x se x [, 1/n) 1 x se x 1/n
85 SUCCESSIONI DI FUNZIONI continuitá: lim n xn = f(x) = { se x [, 1) 1 se x = 1 Pur essendo le funzioni della successione continue in [, 1] la funzione f(x) loro limite non lo é. integrabilitá: é noto come la funzione di Dirichlet d(x) { 1 se x Q d(x) = se x / Q non sia integrabile in [, 1]. Consideriamo la successione r 1, r 2, r 3,... dei razionali di [, 1] e consideriamo le funzioni { 1 se x {r1, r f n (x) = 2,..., r n } se x / {r 1, r 2,..., r n } É chiaro che le f n (x) hanno un numero finito di punti di discontinuitá e quindi sono integrabili in [, 1], ed é anche chiaro che riesce lim f n(x) = d(x) n passaggio al limite sotto il segno di integrale: b lim n a f n (x)dx = b a lim f n(x)dx? n in altri termini é (sempre) possibile scambiare le due operazioni, il passaggio al limite e il calcolo dell integrale? É chiaro che no: basta pensare alla situazione in Figura 7 a pag.3 del Cap.4 delle Note. la derivabilitá: il limite puntuale di una famiglia di funzioni derivabili puó essere non derivabile. Si consideri, ad esempio il grafico in Figura 1 due rette, una orizzontale, y = e una inclinata a 45 o, raccordate da un arco di circonferenza. La bontá del raccordo fa riconoscere nel disegno il grafico di una funzione derivabile: considerando tuttavia una successione di tali grafici con raccordi circolari sempre piú piccoli si riconosce una successione di funzioni i cui grafici tendono a quello rappresentato dalle due semirette. Grafico con angolo, quindi grafico di una funzione non derivabile!
86 2. CONVERGENZA PUNTUALE 85 Figura 1. Funzioni derivabili 2.2. La soglia n ε. La convergenza puntuale, indicata dalla notazione lim f n(x) = f(x), x [a, b] n corrisponde alla convergenza per ogni x numerica {f n (x )} al limite l = f(x ). Questo significa che ε > n ε tale che [a, b] della successione n n ε : f n (x ) f(x ) ε Non deve comunque essere trascurato il fatto che cambiando il punto x in un altro punto x 1 la successione numerica da considerare diventa la {f n (x 1 )} la quale puó convergere a f(x 1 ) con velocitá diversa, ovvero, in altri termini, anche riferendosi alla stessa scelta di ε si debba ricorrere ad una soglia n ε diversa da quella incontrata precedentemente. In altri termini ε > n ε (x ) n n ε (x ) : f n (x ) f(x ) ε ove risulta come la soglia possa dipendere dal punto x.
Serie prodotto. b k = B. a k = A,
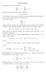 Assegnate due serie convergenti a k = A, Serie prodotto b k = B vogliamo occuparci di dare senso alla frase serie prodotto con la pretesa che tale serie prodotto converga e abbia somma il prodotto A B
Assegnate due serie convergenti a k = A, Serie prodotto b k = B vogliamo occuparci di dare senso alla frase serie prodotto con la pretesa che tale serie prodotto converga e abbia somma il prodotto A B
Università degli Studi di Palermo Facoltà di Economia. CdS Sviluppo Economico e Cooperazione Internazionale. Appunti del corso di Matematica
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 02 - I Numeri Reali Anno Accademico 2013/2014 D. Provenzano, M.
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 02 - I Numeri Reali Anno Accademico 2013/2014 D. Provenzano, M.
Federico Lastaria. Analisi e Geometria 1. Numeri reali 1/25
 Massimi e minimi Definizione (Massimo) Sia X R un sottoinsieme non vuoto. Si dice che M R è il massimo di X (e si scrive M = max X ) se: M X ; x X, x M. Definizione (Minimo) Sia X R un sottoinsieme non
Massimi e minimi Definizione (Massimo) Sia X R un sottoinsieme non vuoto. Si dice che M R è il massimo di X (e si scrive M = max X ) se: M X ; x X, x M. Definizione (Minimo) Sia X R un sottoinsieme non
Le funzioni continue
 Le funzioni continue Sia 1. Limiti di funzioni f : E X Y con X e Y spazi metrici. Indichiamo con d X e rispettivamente d Y rispettive espressioni della distanza. Se p D(E) allora ha senso parlare del (eventuale)
Le funzioni continue Sia 1. Limiti di funzioni f : E X Y con X e Y spazi metrici. Indichiamo con d X e rispettivamente d Y rispettive espressioni della distanza. Se p D(E) allora ha senso parlare del (eventuale)
Università degli Studi di Palermo Facoltà di Economia. Dipartimento di Scienze Economiche, Aziendali e Statistiche. Appunti del corso di Matematica
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 03 - I Numeri Reali Anno Accademico 2015/2016 M. Tumminello,
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 03 - I Numeri Reali Anno Accademico 2015/2016 M. Tumminello,
Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati siano stati dimostrati a lezione.
 Programma di Analisi Matematica 1 (Canale ICM) svolto per lezioni - A. Languasco - C. Vagnoni 1 Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati
Programma di Analisi Matematica 1 (Canale ICM) svolto per lezioni - A. Languasco - C. Vagnoni 1 Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati
Liceo Galilei - ROMA 27 maggio 2010
 Liceo Galilei - ROMA 27 maggio 2010 L. Lamberti Dipartimento di Matematica La Sapienza L. Lamberti Dipartimento di Matematica La Sapienza 27 maggio 2010 L. Lamberti Dipartimento di Matematica La Sapienza
Liceo Galilei - ROMA 27 maggio 2010 L. Lamberti Dipartimento di Matematica La Sapienza L. Lamberti Dipartimento di Matematica La Sapienza 27 maggio 2010 L. Lamberti Dipartimento di Matematica La Sapienza
Programma del corso di Analisi Matematica 1 Corso di Laurea in Matematica Prof. A. Garroni - Canale Dl-Pa
 Programma del corso di Analisi Matematica 1 Corso di Laurea in Matematica Prof. A. Garroni - Canale Dl-Pa 1. Elementi di spazi metrici e di topologia 1.1 Completezza di R. Richiami: Estremo superiore,
Programma del corso di Analisi Matematica 1 Corso di Laurea in Matematica Prof. A. Garroni - Canale Dl-Pa 1. Elementi di spazi metrici e di topologia 1.1 Completezza di R. Richiami: Estremo superiore,
ANALISI UNO (A.A. 2008/2009, Docente: S. Finzi Vita) Programma svolto settimanalmente
 ANALISI UNO (A.A. 2008/2009, Docente: S. Finzi Vita) Programma svolto settimanalmente 2-6 Marzo (8 ore) Gli assiomi dei numeri reali. Osservazioni sull assioma di continuità: altre formulazioni e loro
ANALISI UNO (A.A. 2008/2009, Docente: S. Finzi Vita) Programma svolto settimanalmente 2-6 Marzo (8 ore) Gli assiomi dei numeri reali. Osservazioni sull assioma di continuità: altre formulazioni e loro
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Successioni e loro limiti
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Successioni e loro limiti Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Successioni e loro limiti Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di
PROGRAMMA di Analisi Matematica 1 A.A , canale 3, prof.: Francesca Albertini Ingegneria area dell Informazione
 PROGRAMMA di Analisi Matematica A.A. 204-205, canale 3, prof.: Francesca Albertini Ingegneria area dell Informazione Testo Consigliato: - Analisi Matematica, Teoria e Applicazioni, A. Marson, P. Baiti,
PROGRAMMA di Analisi Matematica A.A. 204-205, canale 3, prof.: Francesca Albertini Ingegneria area dell Informazione Testo Consigliato: - Analisi Matematica, Teoria e Applicazioni, A. Marson, P. Baiti,
Università degli Studi di Palermo Facoltà di Economia. CdS Statistica per l Analisi dei Dati. Appunti del corso di Matematica I Numeri Reali
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 03 - I Numeri Reali Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina, A.
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 03 - I Numeri Reali Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina, A.
Diario del Corso Analisi Matematica I
 Diario del Corso Analisi Matematica I 1. Martedì 1 ottobre 2013 Presentazione del corso. Nozioni di Teoria degli Insiemi. Numeri Naturali, loro proprietà, rappresentazione geometrica, sommatoria, principio
Diario del Corso Analisi Matematica I 1. Martedì 1 ottobre 2013 Presentazione del corso. Nozioni di Teoria degli Insiemi. Numeri Naturali, loro proprietà, rappresentazione geometrica, sommatoria, principio
3. Successioni di insiemi.
 3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
Argomenti delle singole lezioni del corso di Analisi Matematica 1 (Laurea triennale di Matematica, A.A )
 Argomenti delle singole lezioni del corso di Analisi Matematica 1 (Laurea triennale di Matematica, A.A. 2018-19) NB. Le indicazioni bibliografiche si riferiscono al libro di testo. Lezione nr. 1, 1/10/2018.
Argomenti delle singole lezioni del corso di Analisi Matematica 1 (Laurea triennale di Matematica, A.A. 2018-19) NB. Le indicazioni bibliografiche si riferiscono al libro di testo. Lezione nr. 1, 1/10/2018.
CLASSE LIMITE DI UNA SUCCESSIONE DI NUMERI REALI C. MADERNA, G. MOLTENI, M. VIGNATI
 CLASSE LIMITE DI UNA SUCCESSIONE DI NUMERI REALI C. MADERNA, G. MOLTENI, M. VIGNATI Consideriamo l insieme R = R {, + } ottenuto aggiungendo all insieme dei numeri reali i simboli e +. Introduciamo in
CLASSE LIMITE DI UNA SUCCESSIONE DI NUMERI REALI C. MADERNA, G. MOLTENI, M. VIGNATI Consideriamo l insieme R = R {, + } ottenuto aggiungendo all insieme dei numeri reali i simboli e +. Introduciamo in
Successioni numeriche (II)
 Successioni numeriche (II) Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni (II) Analisi A 1 / 52 Forme indeterminate associate a funzioni razionali fratte:
Successioni numeriche (II) Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni (II) Analisi A 1 / 52 Forme indeterminate associate a funzioni razionali fratte:
Proposizioni. Negazione di una proposizione. Congiunzione e disgiunzione di due proposizioni. Predicati. Quantificatori.
 Corso di laurea in Ingegneria elettronica e informatica - A13 Programma di Analisi matematica 1 - A13106 Anno accademico 2015-2016 Prof. Giulio Starita 1 - Insiemi, logica, numeri I concetti primitivi.
Corso di laurea in Ingegneria elettronica e informatica - A13 Programma di Analisi matematica 1 - A13106 Anno accademico 2015-2016 Prof. Giulio Starita 1 - Insiemi, logica, numeri I concetti primitivi.
VERSIONE PRELIMINARE Lezioni di Analisi Matematica 3 corso di Laurea in Fisica a.a
 Lezioni di Analisi Matematica 3 corso di Laurea in Fisica a.a. 2005-06 G. Molteni, M. Vignati Notazioni I vettori di R n e le funzioni a valori in R n sono indicate in grassetto, per cui si dirà v R n
Lezioni di Analisi Matematica 3 corso di Laurea in Fisica a.a. 2005-06 G. Molteni, M. Vignati Notazioni I vettori di R n e le funzioni a valori in R n sono indicate in grassetto, per cui si dirà v R n
Corso di Laurea in Ingegneria, Settore Informazione (gruppi 2-3), A.A. 2007/2008 Docente: Antonio Ponno
 Programma del Corso di Matematica A Corso di Laurea in Ingegneria, Settore Informazione (gruppi 2-3), A.A. 2007/2008 Docente: Antonio Ponno Premessa (D) dopo un teorema o una proposizione citati sta ad
Programma del Corso di Matematica A Corso di Laurea in Ingegneria, Settore Informazione (gruppi 2-3), A.A. 2007/2008 Docente: Antonio Ponno Premessa (D) dopo un teorema o una proposizione citati sta ad
Il teorema di Ascoli-Arzelà
 Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
PARTE 1: Elementi di base. Simboli e operazioni sugli insiemi. Simboli logici. Prodotto cartesiano.
 PROGRAMMA di Analisi Matematica 1 A.A. 2008-2009, canale 1, prof.: Francesca Albertini, Claudio Marchi Ingegneria gestionale, meccanica e meccatronica, Vicenza Testo Consigliato: Analisi Matematica, M.
PROGRAMMA di Analisi Matematica 1 A.A. 2008-2009, canale 1, prof.: Francesca Albertini, Claudio Marchi Ingegneria gestionale, meccanica e meccatronica, Vicenza Testo Consigliato: Analisi Matematica, M.
Il campo ordinato completo R dei numeri reali. Federico Lastaria. Analisi e Geometria 1. Il campo ordinato completo R 1/13
 Il campo ordinato completo R dei numeri reali Federico Lastaria. Analisi e Geometria 1. Il campo ordinato completo R 1/13 Cosa significa campo? Significa che sono definite due operazioni: somma e prodotto,
Il campo ordinato completo R dei numeri reali Federico Lastaria. Analisi e Geometria 1. Il campo ordinato completo R 1/13 Cosa significa campo? Significa che sono definite due operazioni: somma e prodotto,
La convergenza uniforme
 La convergenza uniforme 1. Il tubo Sia {f n (x)} una successione convergente a f(x) per x E: disegniamo il grafico della funzione limite f(x) assegnato ε > 0 disegniamo la striscia - il tubo - intorno
La convergenza uniforme 1. Il tubo Sia {f n (x)} una successione convergente a f(x) per x E: disegniamo il grafico della funzione limite f(x) assegnato ε > 0 disegniamo la striscia - il tubo - intorno
Analisi 2. Roberto Monti. Appunti del Corso - Versione 5 Ottobre 2012
 Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Serie Borlini Alex
 Serie numerica >> Prefazione Progressione lista ordinata e finita di elementi. Successione lista ordinata e infinita di elementi (numeri reali chiamati termini), {a n }=a 1, a 2, a 3 Successione di Fibonacci:
Serie numerica >> Prefazione Progressione lista ordinata e finita di elementi. Successione lista ordinata e infinita di elementi (numeri reali chiamati termini), {a n }=a 1, a 2, a 3 Successione di Fibonacci:
Alcuni Teoremi sulle funzioni continue e uniforme continuità
 Alcuni Teoremi sulle funzioni continue e uniforme continuità Teorema 0. Una funzione f(x) è continua in x 0 se e solo se per ogni sucessione {x n } dom(f) con x n x 0 dom(f), risulta f(x n ) f(x 0 ). (Non
Alcuni Teoremi sulle funzioni continue e uniforme continuità Teorema 0. Una funzione f(x) è continua in x 0 se e solo se per ogni sucessione {x n } dom(f) con x n x 0 dom(f), risulta f(x n ) f(x 0 ). (Non
Funzioni analitiche secondo Weierstrass
 CAPITOLO 5 Funzioni analitiche secondo Weierstrass La maggior parte dei risultati illustrati in questo capitolo non saranno dimostrati.. Introduzione Consideriamo le due seguenti funzioni: ϕ(z) = k=0 z
CAPITOLO 5 Funzioni analitiche secondo Weierstrass La maggior parte dei risultati illustrati in questo capitolo non saranno dimostrati.. Introduzione Consideriamo le due seguenti funzioni: ϕ(z) = k=0 z
Problemi di topologia metrica.
 Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Successioni numeriche
 Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
PROGRAMMA di ANALISI MATEMATICA 1
 PROGRAMMA di ANALISI MATEMATICA Ingegneria gestionale, meccanica e meccatronica, Vicenza A.A. 200-20, Canale e matricole da 84 a 99 del Canale 3, docente: Monica Motta Testo Consigliato: Analisi Matematica,
PROGRAMMA di ANALISI MATEMATICA Ingegneria gestionale, meccanica e meccatronica, Vicenza A.A. 200-20, Canale e matricole da 84 a 99 del Canale 3, docente: Monica Motta Testo Consigliato: Analisi Matematica,
PROGRAMMA DI ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 15 CF A.A
 PROGRAMMA DI ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 15 CF A.A. 2018-19 Le indicazioni dei capitoli e dei paragrafi si riferiscono al libro: C.D. Pagani, S. Salsa. Analisi Matematica
PROGRAMMA DI ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 15 CF A.A. 2018-19 Le indicazioni dei capitoli e dei paragrafi si riferiscono al libro: C.D. Pagani, S. Salsa. Analisi Matematica
ESERCIZI SULLE SUCCESSIONI
 ESERCIZI SULLE SUCCESSIONI 8 marzo 2010 2 0.1 Esercizi sulle successioni di numeri reali Definizione 1 Una successione di numeri reali a n si dice convergente al limite l, e si scrive lim n a n = l se
ESERCIZI SULLE SUCCESSIONI 8 marzo 2010 2 0.1 Esercizi sulle successioni di numeri reali Definizione 1 Una successione di numeri reali a n si dice convergente al limite l, e si scrive lim n a n = l se
Analisi Matematica 1
 Analisi Matematica 1 Schema provvisorio delle lezioni A. A. 2015/16 1 Distribuzione degli argomenti delle lezioni Argomento ore tot Numeri reali 11 11 Numeri complessi 1 12 Spazio euclideo 2 14 Topologia
Analisi Matematica 1 Schema provvisorio delle lezioni A. A. 2015/16 1 Distribuzione degli argomenti delle lezioni Argomento ore tot Numeri reali 11 11 Numeri complessi 1 12 Spazio euclideo 2 14 Topologia
Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica), a.a. 2006/07. Notazioni, richiami sulla teoria degli insiemi.
 Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica, a.a. 2006/07 Notazioni, richiami sulla teoria degli insiemi. Introduzione e richiami di alcune notazioni (simboli matematiche.
Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica, a.a. 2006/07 Notazioni, richiami sulla teoria degli insiemi. Introduzione e richiami di alcune notazioni (simboli matematiche.
Generalizzazioni del Teorema di Weierstrass
 Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
1 PRELIMINARI 1.1 NOTAZIONI. denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A.
 1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
PROGRAMMA DI ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 15 CF A.A
 PROGRAMMA DI ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 15 CF A.A. 2017-18 Le indicazioni dei capitoli e dei paragrafi si riferiscono al libro: C.D. Pagani, S. Salsa. Analisi Matematica
PROGRAMMA DI ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 15 CF A.A. 2017-18 Le indicazioni dei capitoli e dei paragrafi si riferiscono al libro: C.D. Pagani, S. Salsa. Analisi Matematica
Spazi di Banach classici
 Spazi di Banach classici 1. Gli spazi L p ([, 1]) Le funzioni misurabili su [, 1] costituiscono uno spazio vettoriale V. Definizione 1.1. Due funzioni f, g V si dicono uguali quasi ovunque se esiste N
Spazi di Banach classici 1. Gli spazi L p ([, 1]) Le funzioni misurabili su [, 1] costituiscono uno spazio vettoriale V. Definizione 1.1. Due funzioni f, g V si dicono uguali quasi ovunque se esiste N
Analisi Matematica 1 (prof. G. Cupini) (CdS Astronomia - Univ. Bologna) REGISTRO DELLE LEZIONI A.A
 Analisi Matematica 1 (prof. G. Cupini) (CdS Astronomia - Univ. Bologna) REGISTRO DELLE LEZIONI A.A.2015-2016 22 SETTEMBRE 2015 3 ore 14-17 Insiemi e operazioni tra insiemi. Numeri reali. Assiomi dei numeri
Analisi Matematica 1 (prof. G. Cupini) (CdS Astronomia - Univ. Bologna) REGISTRO DELLE LEZIONI A.A.2015-2016 22 SETTEMBRE 2015 3 ore 14-17 Insiemi e operazioni tra insiemi. Numeri reali. Assiomi dei numeri
SPAZI COMPATTI. Proposizione 2 Sia (X, d) uno spazio metrico. Se esso è sequenzialmente compatto allora è completo.
 SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8/11/2013
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
PROGRAMMA DEL CORSO DI ANALISI (CANALE PF-Z) (versione del 18/01/2014)
 CORSO DI LAUREA in Fisica PROGRAMMA DEL CORSO DI ANALISI (CANALE PF-Z) AA 2013/14, CREDITI: 9 (versione del 18/01/2014) Il programma d esame comprende tutti gli argomenti svolti durante il corso. Dopo
CORSO DI LAUREA in Fisica PROGRAMMA DEL CORSO DI ANALISI (CANALE PF-Z) AA 2013/14, CREDITI: 9 (versione del 18/01/2014) Il programma d esame comprende tutti gli argomenti svolti durante il corso. Dopo
Corso di laurea: Ingegneria Civile Programma di Fondamenti di Analisi Matematica I a.a. 2011/2012 Docenti: Fabio Paronetto e Fabio Ancona
 Corso di laurea: Ingegneria Civile Programma di Fondamenti di Analisi Matematica I a.a. 2011/2012 Docenti: Fabio Paronetto e Fabio Ancona Gli argomenti denotati con un asterisco tra parentesi sono stati
Corso di laurea: Ingegneria Civile Programma di Fondamenti di Analisi Matematica I a.a. 2011/2012 Docenti: Fabio Paronetto e Fabio Ancona Gli argomenti denotati con un asterisco tra parentesi sono stati
Gli insiemi N, Z e Q. I numeri naturali
 Università Roma Tre L. Chierchia 1 Gli insiemi N, Z e Q Il sistema dei numeri reali (R, +,, ) può essere definito tramite sedici assiomi: quindici assiomi algebrici (si veda ad esempio 2.3 in [Giusti,
Università Roma Tre L. Chierchia 1 Gli insiemi N, Z e Q Il sistema dei numeri reali (R, +,, ) può essere definito tramite sedici assiomi: quindici assiomi algebrici (si veda ad esempio 2.3 in [Giusti,
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero
 IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
SUCCESSIONI E SERIE NUMERICHE E DI FUNZIONI
 SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
SPAZI TOPOLOGICI COMPATTI Note informali dalle lezioni
 SPAZI TOPOLOGICI COMPATTI Note informali dalle lezioni Sia X un insieme. Un ricoprimento di X è una famiglia U = {U j } j J di sottoinsiemi di X tali che X = j J U j. Un ricoprimento U = {U j } j J si
SPAZI TOPOLOGICI COMPATTI Note informali dalle lezioni Sia X un insieme. Un ricoprimento di X è una famiglia U = {U j } j J di sottoinsiemi di X tali che X = j J U j. Un ricoprimento U = {U j } j J si
ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 15 CF A.A
 ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 15 CF A.A. 2016-17 Programma Provvisorio del corso di Analisi Matematica A Il programma che segue è solo indicativo. Il programma definitivo
ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 15 CF A.A. 2016-17 Programma Provvisorio del corso di Analisi Matematica A Il programma che segue è solo indicativo. Il programma definitivo
SPAZI TOPOLOGICI. La nozione di spazio topologico è più generale di quella di spazio metrizzabile.
 SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
Corso di Analisi Matematica Successioni e loro limiti
 Corso di Analisi Matematica Successioni e loro limiti Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 30 1 Definizione di successione
Corso di Analisi Matematica Successioni e loro limiti Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 30 1 Definizione di successione
ESERCIZI DI ANALISI UNO
 ESERCIZI DI ANALISI UNO 4 marzo 2009 2 0.1 Esercizi sulle successioni di numeri reali Definizione 1 Una successione di numeri reali a n si dice convergente al limite l, e si scrive lim n a n = l se per
ESERCIZI DI ANALISI UNO 4 marzo 2009 2 0.1 Esercizi sulle successioni di numeri reali Definizione 1 Una successione di numeri reali a n si dice convergente al limite l, e si scrive lim n a n = l se per
COMPATTEZZA. i) X è compatto, cioè ogni ricoprimento aperto ammette un sottoricoprimento finito.
 1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
Analisi Matematica 1 Trentaquattresma lezione. Serie
 Analisi Matematica 1 Trentaquattresma lezione Serie prof. Claudio Saccon Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://saccon.blog.dma.unipi.it
Analisi Matematica 1 Trentaquattresma lezione Serie prof. Claudio Saccon Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://saccon.blog.dma.unipi.it
Limiti di successioni
 Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
A.A. 2016/17 - Analisi Matematica 1
 A.A. 2016/17 - Analisi Matematica 1 Argomenti svolti, libro di testo di riferimento: P. Marcellini, C. Sbordone: Elementi Calcolo. Liguori Editore. O. Bernardi: Temi d esame senza tema. Ed. Libreria Progetto.
A.A. 2016/17 - Analisi Matematica 1 Argomenti svolti, libro di testo di riferimento: P. Marcellini, C. Sbordone: Elementi Calcolo. Liguori Editore. O. Bernardi: Temi d esame senza tema. Ed. Libreria Progetto.
Serie Numeriche. Docente:Alessandra Cutrì
 Serie Numeriche Docente:Alessandra Cutrì Definizione di Serie Somma formale di un numero infinito di addendi. È un operazione che è in stretta relazione con quella di integrale improprio. data un successione
Serie Numeriche Docente:Alessandra Cutrì Definizione di Serie Somma formale di un numero infinito di addendi. È un operazione che è in stretta relazione con quella di integrale improprio. data un successione
Complemento 1 Gli insiemi N, Z e Q
 AM110 Mat, Univ. Roma Tre (AA 2010/11 L. Chierchia) 30/9/10 1 Complemento 1 Gli insiemi N, Z e Q Il sistema dei numeri reali (R, +,, ) può essere definito tramite sedici assiomi: quindici assiomi algebrici
AM110 Mat, Univ. Roma Tre (AA 2010/11 L. Chierchia) 30/9/10 1 Complemento 1 Gli insiemi N, Z e Q Il sistema dei numeri reali (R, +,, ) può essere definito tramite sedici assiomi: quindici assiomi algebrici
Serie numeriche. Riccarda Rossi. Analisi I. Università di Brescia
 Serie numeriche Riccarda Rossi Università di Brescia Analisi I Sommatoria Siano Con il simbolo I : insieme finito di indici (a i ) i I famiglia finita di numeri, al variare di i in I indichiamo la somma
Serie numeriche Riccarda Rossi Università di Brescia Analisi I Sommatoria Siano Con il simbolo I : insieme finito di indici (a i ) i I famiglia finita di numeri, al variare di i in I indichiamo la somma
PROGRAMMA. Capitolo 1 : Concetti di base: numeri reali, funzioni, funzioni reali di variabile reale.
 PROGRAMMA Capitolo 1 : Concetti di base: numeri reali, funzioni, funzioni reali di variabile reale. Gli insiemi numerici oggetto del corso: numeri naturali, interi relativi, razionali. Operazioni sui numeri
PROGRAMMA Capitolo 1 : Concetti di base: numeri reali, funzioni, funzioni reali di variabile reale. Gli insiemi numerici oggetto del corso: numeri naturali, interi relativi, razionali. Operazioni sui numeri
Successioni di funzioni
 Successioni di funzioni 1. Primi esempi 1, x, x 2, x 3,..., x n,..., x [0, 2] e x, e 2x, e 3x,..., e nx,..., x [ 1, 1] f n (x) = 1, n = 1, 2, 3,..., x R (n + 1) 2 + x2 f n (x) = sin(x), n = 1, 2, 3,...,
Successioni di funzioni 1. Primi esempi 1, x, x 2, x 3,..., x n,..., x [0, 2] e x, e 2x, e 3x,..., e nx,..., x [ 1, 1] f n (x) = 1, n = 1, 2, 3,..., x R (n + 1) 2 + x2 f n (x) = sin(x), n = 1, 2, 3,...,
COMPLETEZZA DELL INSIEME DEI NUMERI REALI R.
 COMPLETEZZA DELL INSIEME DEI NUMERI REALI R. FABIO CIPRIANI 1. Completezza dell insieme dei numeri reali R. Nell insieme dei numeri reali R la condizione di Cauchy e necessaria e sufficiente per la convergenza
COMPLETEZZA DELL INSIEME DEI NUMERI REALI R. FABIO CIPRIANI 1. Completezza dell insieme dei numeri reali R. Nell insieme dei numeri reali R la condizione di Cauchy e necessaria e sufficiente per la convergenza
Limiti di funzioni di una variabile
 Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
Diario del Corso Analisi Matematica I e Analisi Matematica
 Diario del Corso Analisi Matematica I e Analisi Matematica 1. Martedì 2 ottobre 2012 Nozioni di Teoria degli Insiemi. Numeri Naturali, loro proprietà, modello geometrico, sommatoria. 2. Mercoledì 3 ottobre
Diario del Corso Analisi Matematica I e Analisi Matematica 1. Martedì 2 ottobre 2012 Nozioni di Teoria degli Insiemi. Numeri Naturali, loro proprietà, modello geometrico, sommatoria. 2. Mercoledì 3 ottobre
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
tale differenza, detta resto di Lagrange è la seguente:
 . Le serie di Taylor Il teorema detto della formula di Taylor consiste nell espressione, quasi esplicita, fornita per la differenza Rx che intercorre tra i valori fx di una funzione indefinitamente derivabile
. Le serie di Taylor Il teorema detto della formula di Taylor consiste nell espressione, quasi esplicita, fornita per la differenza Rx che intercorre tra i valori fx di una funzione indefinitamente derivabile
1.5 Assioma di completezza
 1.5 Assioma di completezza Le proprietà 1-8 sin qui viste non sono prerogativa esclusiva di R, dato che sono ugualmente vere nell insieme dei numeri razionali Q. Ciò che davvero caratterizza R è la proprietà
1.5 Assioma di completezza Le proprietà 1-8 sin qui viste non sono prerogativa esclusiva di R, dato che sono ugualmente vere nell insieme dei numeri razionali Q. Ciò che davvero caratterizza R è la proprietà
Analisi vettoriale - A.A. 2003/04
 Soluzioni Analisi vettoriale - A.A. 2003/04 Foglio di esercizi n.7 1. Esercizio Studiare la convergenza delle seguenti serie di potenze: 2 n (n + 3)! x n 3(x 2) n, (2n)! log (n + 1). (1) 1.1. Soluzione.
Soluzioni Analisi vettoriale - A.A. 2003/04 Foglio di esercizi n.7 1. Esercizio Studiare la convergenza delle seguenti serie di potenze: 2 n (n + 3)! x n 3(x 2) n, (2n)! log (n + 1). (1) 1.1. Soluzione.
Massimo e minimo limite di successioni
 Massimo e minimo limite di successioni 1 Premesse Definizione 1.1. Definiamo R esteso l insieme R = R { } {+ }. In R si estende l ordinamento tra numeri reali ponendo < a < +, a R. In base a tale definizione,
Massimo e minimo limite di successioni 1 Premesse Definizione 1.1. Definiamo R esteso l insieme R = R { } {+ }. In R si estende l ordinamento tra numeri reali ponendo < a < +, a R. In base a tale definizione,
LICEO CLASSICO ANDREA DA PONTEDERA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
Insiemi, Numeri, Terminologia. Prof. Simone Sbaraglia
 Insiemi, Numeri, Terminologia Prof. Simone Sbaraglia Corso Rapido di Logica Matematica La logica formale definisce le regole cui deve obbedire qualsiasi teoria deduttiva. Una proposizione e` una affermazione
Insiemi, Numeri, Terminologia Prof. Simone Sbaraglia Corso Rapido di Logica Matematica La logica formale definisce le regole cui deve obbedire qualsiasi teoria deduttiva. Una proposizione e` una affermazione
Limiti e continuità. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68
 Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
2 Introduzione ai numeri reali e alle funzioni
 1 CORSO DI LAUREA in Fisica Canale A-CO (canale 4) docente P. Vernole Il programma d esame comprende tutti gli argomenti svolti durante il corso. Dopo ogni sezione sono indicate le parti delle Dispense
1 CORSO DI LAUREA in Fisica Canale A-CO (canale 4) docente P. Vernole Il programma d esame comprende tutti gli argomenti svolti durante il corso. Dopo ogni sezione sono indicate le parti delle Dispense
ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie
 ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
Matematica I. Francesco Bonsante e Giuseppe Da Prato
 Matematica I Francesco Bonsante e Giuseppe Da Prato 31 Maggio 2008 Contents 1 Numeri reali 1 1.1 Sottoinsiemi di Q......................... 1 1.1.1 Estremo superiore e estremo inferiore.......... 2 1.2
Matematica I Francesco Bonsante e Giuseppe Da Prato 31 Maggio 2008 Contents 1 Numeri reali 1 1.1 Sottoinsiemi di Q......................... 1 1.1.1 Estremo superiore e estremo inferiore.......... 2 1.2
I NUMERI. Si dice "radice quadrata" di un numero positivo a, quel numero positivo b che elevato al quadrato dà come risultato a.
 Questa dispensa rappresenta una breve introduzione ai numeri reali e alla loro Topologia, minimo necessario per affrontare serenamente lo studio dell ANALISI MATEMATICA. Inoltre non si ha la pretesa che
Questa dispensa rappresenta una breve introduzione ai numeri reali e alla loro Topologia, minimo necessario per affrontare serenamente lo studio dell ANALISI MATEMATICA. Inoltre non si ha la pretesa che
Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che
 1 Spazi metrici Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che 1) d(x, y) 0, x, y X; d(x, y) = 0 x = y, ) d(x, y) = d(y, x), x, y X, 3) d(x, z) d(x, y) +
1 Spazi metrici Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che 1) d(x, y) 0, x, y X; d(x, y) = 0 x = y, ) d(x, y) = d(y, x), x, y X, 3) d(x, z) d(x, y) +
7 Il Teorema di Bolzano - Weierstrass
 dimostrazione di (3.6). Supponiamo per esempio che f sia crescente e che x 0 < b Poniamo l + := inf f(x) x I,x 0
dimostrazione di (3.6). Supponiamo per esempio che f sia crescente e che x 0 < b Poniamo l + := inf f(x) x I,x 0
Pag. 151 Dimostrazioni dei criteri per lo studio della convergenza di serie numeriche
 C.7 Serie Pag. 151 Dimostrazioni dei criteri per lo studio della convergenza di serie numeriche Teorema 5.29 (Criterio del confronto) Siano e due serie numeriche a termini positivi e si abbia 0, per ogni
C.7 Serie Pag. 151 Dimostrazioni dei criteri per lo studio della convergenza di serie numeriche Teorema 5.29 (Criterio del confronto) Siano e due serie numeriche a termini positivi e si abbia 0, per ogni
Generalità - Insiemi numerici- Proprietà di completezza di R
 Generalità - Insiemi numerici- Proprietà di completezza di R Docente:Alessandra Cutrì Informazioni corso Sito docente: http://www.mat.uniroma2.it/~cutri/ Programma: vedi sito docente Testi consigliati:
Generalità - Insiemi numerici- Proprietà di completezza di R Docente:Alessandra Cutrì Informazioni corso Sito docente: http://www.mat.uniroma2.it/~cutri/ Programma: vedi sito docente Testi consigliati:
CAPITOLO 9. Le serie di potenze
 CAPITOLO 9 Le serie di potenze Ahlfors, pag. 33,..,45 Bozza da rivedere Le funzioni analitiche sono piú o meno polinomi in z, o i loro limiti, somme di serie di potenze in z. Prerequisiti fondamentali
CAPITOLO 9 Le serie di potenze Ahlfors, pag. 33,..,45 Bozza da rivedere Le funzioni analitiche sono piú o meno polinomi in z, o i loro limiti, somme di serie di potenze in z. Prerequisiti fondamentali
Soluzione esercizi 28 ottobre 2011
 ANALISI Soluzione esercizi 8 ottobre 0 4.. Esercizio. Siano α e β due numeri reali tali che la loro somma e la loro differenza siano razionali: provare che allora essi sono entrambi razionali. Il teorema
ANALISI Soluzione esercizi 8 ottobre 0 4.. Esercizio. Siano α e β due numeri reali tali che la loro somma e la loro differenza siano razionali: provare che allora essi sono entrambi razionali. Il teorema
Complementi di Analisi Matematica Ia. Carlo Bardaro
 Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Insiemi di numeri reali
 Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Funzione derivabile. La derivata.
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Diario del corso di Analisi Matematica 1 (a.a. 2017/18)
 Diario del corso di Analisi Matematica 1 (a.a. 2017/18) 22 settembre 2017 (2 ore) Presentazione del corso. Numeri naturali, interi, razionali, reali. 2 non è razionale. Come si risolve 2 + 1 = 0? 25 settembre
Diario del corso di Analisi Matematica 1 (a.a. 2017/18) 22 settembre 2017 (2 ore) Presentazione del corso. Numeri naturali, interi, razionali, reali. 2 non è razionale. Come si risolve 2 + 1 = 0? 25 settembre
Argomenti della Lezione
 ANALISI Argomenti della Lezione 5 ottobre 2011 1. I numeri reali 1.1. Naturali, Interi, Razionali. Gli insiemi dei numeri naturali N : 0, 1, 2,..., interi Z : 0, ±1, ±2,..., razionali Q = m/n, m, n Z sono
ANALISI Argomenti della Lezione 5 ottobre 2011 1. I numeri reali 1.1. Naturali, Interi, Razionali. Gli insiemi dei numeri naturali N : 0, 1, 2,..., interi Z : 0, ±1, ±2,..., razionali Q = m/n, m, n Z sono
1 Successioni di funzioni
 Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Insiemi numerici. Definizioni
 1 Insiemi numerici Gli insiemi numerici sono insiemi i cui elementi sono numeri, cioè appartengono all'insieme N dei naturali, degli interi Z, dei razionali Q, dei reali R o dei complessi C ( es.: A =
1 Insiemi numerici Gli insiemi numerici sono insiemi i cui elementi sono numeri, cioè appartengono all'insieme N dei naturali, degli interi Z, dei razionali Q, dei reali R o dei complessi C ( es.: A =
Modulo o "valore assoluto"
 Modulo o "valore assoluto" Dato x R definiamo modulo o valore assoluto di x il numero reale positivo x se x 0 x = x se x < 0 Sfrag replacements Es. 5 è 5. 2.34 è 2.34 Dal punto di vista geometrico x rappresenta
Modulo o "valore assoluto" Dato x R definiamo modulo o valore assoluto di x il numero reale positivo x se x 0 x = x se x < 0 Sfrag replacements Es. 5 è 5. 2.34 è 2.34 Dal punto di vista geometrico x rappresenta
n k. Confronto: se a n b n e b n tende a 0 allora lo stesso
 . DIARIO DELLE LEZIONI 28 settembre: Informazioni generali e presentazione. Insiemi numerici N, Z, Q. Rappresentazione sulla retta. Non esistenza della radice quadrata di 2 in Q. Sommatoria. Progressione
. DIARIO DELLE LEZIONI 28 settembre: Informazioni generali e presentazione. Insiemi numerici N, Z, Q. Rappresentazione sulla retta. Non esistenza della radice quadrata di 2 in Q. Sommatoria. Progressione
Analisi di Fourier e alcune equazioni della fisica matematica 1. TERZA LEZIONE Serie di funzioni Serie di potenze
 Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
 Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2017/18 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2017/18 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Successioni, massimo e minimo limite e compattezza in R
 Università di Roma Tor Vergata Corso di Laurea in Scienze e Tecnologie per i Media Successioni, massimo e minimo limite e compattezza in R Massimo A. Picardello BOZZA 10.11.2011 21:24 i CAPITOLO 1 Successioni
Università di Roma Tor Vergata Corso di Laurea in Scienze e Tecnologie per i Media Successioni, massimo e minimo limite e compattezza in R Massimo A. Picardello BOZZA 10.11.2011 21:24 i CAPITOLO 1 Successioni
Diario del corso di Analisi Matematica 1 (a.a. 2016/17)
 Diario del corso di Analisi Matematica 1 (a.a. 2016/17) 16 settembre 2016 (2 ore) Presentazione del corso. Numeri naturali, interi, razionali, reali. 2 non è razionale. Come si risolve 2 + 1 = 0? 19 settembre
Diario del corso di Analisi Matematica 1 (a.a. 2016/17) 16 settembre 2016 (2 ore) Presentazione del corso. Numeri naturali, interi, razionali, reali. 2 non è razionale. Come si risolve 2 + 1 = 0? 19 settembre
Argomento delle lezioni del corso di Analisi A.A
 Argomento delle lezioni del corso di Analisi A.A.2011-2012 30 gennaio 2012 Lezione 1-2 (5 ottobre 2011) Numeri naturali, interi, razionali. Definizione intuitiva dei reali attraverso la retta. Definizione
Argomento delle lezioni del corso di Analisi A.A.2011-2012 30 gennaio 2012 Lezione 1-2 (5 ottobre 2011) Numeri naturali, interi, razionali. Definizione intuitiva dei reali attraverso la retta. Definizione
Esempi. La successione {cos n} è limitata; {n ¾ } è limitata inferiormente ma non è limitata superiormente, quindi non è limitata.
 Analisi 2 Successioni numeriche -1- ÔÔÙÒØ Ô Ö Ð ÓÖ Ó Ò Ð ¾ º ËÙ ÓÒ ÒÙÑ Ö Proposizione (unicità del limite). Se {a n } è convergente, allora il limite è unico. Dimostrazione. Supponiamo che la tesi sia
Analisi 2 Successioni numeriche -1- ÔÔÙÒØ Ô Ö Ð ÓÖ Ó Ò Ð ¾ º ËÙ ÓÒ ÒÙÑ Ö Proposizione (unicità del limite). Se {a n } è convergente, allora il limite è unico. Dimostrazione. Supponiamo che la tesi sia
9 ottobre Esercizio. Verificare se le seguenti affermazioni sono valide per ogni scelta dei parametri in gioco:
 ANALISI Soluzioni del Foglio 1 9 ottobre 2009 1.1. Esercizio. Verificare se le seguenti affermazioni sono valide per ogni scelta dei parametri in gioco: x < a 2 a 2 < x < a 2 ; x y < x + y ; x y x y ;
ANALISI Soluzioni del Foglio 1 9 ottobre 2009 1.1. Esercizio. Verificare se le seguenti affermazioni sono valide per ogni scelta dei parametri in gioco: x < a 2 a 2 < x < a 2 ; x y < x + y ; x y x y ;
Esercitazione di Analisi Matematica I Esercizi e soluzioni 19/04/2013 TOPOLOGIA
 Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Serie numeriche
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Serie numeriche Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Serie numeriche Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi
