STATISTICA (2) ESERCITAZIONE Dott.ssa Antonella Costanzo
|
|
|
- Albano Masi
- 9 anni fa
- Visualizzazioni
Transcript
1 STATISTICA (2) ESERCITAZIONE Dott.ssa Antonella Costanzo Esercizio 1. Test di indipendenza tra mutabili In un indagine vengono rilevate le informazioni su settore produttivo (Y) e genere (X) su un campione casuale di occupati: X Y agricoltura artigianato industria servizi totale F M totale Testare ad un livello di significatività del 5% se i due caratteri possono essere considerati indipendenti. Soluzione Per stabilire se esiste indipendenza tra i caratteri oggetto di analisi dobbiamo utilizzare un test statistico basato sul chi-quadro χ. Il sistema di ipotesi da sottoporre a verifica è il seguente: H : X e Y sono indipendenti H : X e Y non sono indipendenti Livello di significatività α=0.05 Definizione della statistica test sotto l ipotesi nulla: dove E =.... χ = (O E ) i=1,..h, righe; j=1,..k, colonne E ~χ ;()() 1
2 Regola di decisione (regione di rifiuto) Con il livello di significatività α = 0.05 e con k= 4 e h = 2 otteniamo 2 χ 3;0.05 = dunque, se χ > χ 2 3;0.05 = si rifiuta l ipotesi nulla Calcolo il valore della statistica test sotto l ipotesi nulla Tabella teorica sotto l ipotesi di indipendenza (frequenze teoriche ) X Y agricoltura artigianato industria servizi totale F M totale χ = (O E ) E = (0 4.17) ( ) = Formula alternativa per il calcolo di χ ovvero: =.. ( 1).. 0 = = Decisione: Essendo >., si rifiuta l ipotesi nulla al livello di significatività α=5%. 2
3 Esercizio 2. Test sulla bontà di accostamento In 600 lanci di un dado si sono ottenuti i risultati riportati in tabella. Determinare con un livello di significatività del 5% se il dado può considerarsi truccato. Risultato Freq. osservate Soluzione Se il dado non è truccato dovremmo osservare una distribuzione uniforme dei risultati Risultato Freq. Osservate Freq. Teoriche = dove = Sistema di ipotesi : il dado non è truccato ( la distribuzione di frequenza osservata è una realizzazione di una v.c. uniforme discreta) : il dado è truccato ( la distribuzione di frequenza osservata non è una realizzazione di una v.c. uniforme discreta) Livello di significatività α=0.05 Costruzione della statistica test = ( ) ~ ;() dove k rappresenta il numero di modalità. 3
4 Regola di decisione (regione di rifuto): per il livello di significatività fissato il valore critico è in corrispondenza di:.;() =11.07 per cui se il valore della statistica test è maggiore di.;() l ipotesi nulla =11.07 si rifiuta Il valore della statistica test sotto l ipotesi nulla è data da: = (94 100) ( ) (88 100) =14.22 Decisione Siccome >.;() distribuzione uniforme discreta (il dado è truccato) =11.07 si rifiuta l ipotesi nulla, quindi rifiuto l ipotesi di 4
5 Esercizio 3. Test sulla bontà di accostamento (2) Nell arco di un triennio, sono stati registrati 1588 incidenti stradali capitati a 706 guidatori di una società di trasporto pubblico. La seguente tabella riporta come tali incidenti sono distribuiti tra i vari autisti: n. di incidenti n. di autisti Verificare al un livello di significatività del 5% se questi dati sono compatibili con l ipotesi che il numero di incidenti per autista abbia una distribuzione di Poisson? Soluzione Il primo passo nel test di buon adattamento consiste nello stimare il parametro della distribuzione di Poisson. Dalla tabella di frequenza si ottiene: = =2.25 Sistema di ipotesi H : i dati seguono una distribuzione di Poisson (=2.25) H : i dati non seguono una distribuzione di Poisson Livello di significatività α=0.05 5
6 Definizione della statistica test sotto l ipotesi nulla: χ = ( ) ~χ ;() dove = frequenze attese sotto l ipotesi che i dati seguano una legge di Poisson e k = numero di modalità Regola di decisione (Regione di Rifiuto) Il valore critico in corrispondenza di un livello di significatività del 5% con 8-1=7 gdl è dato da: χ., =14.07, per cui se χ >χ., rifiutiamo l ipotesi nulla. Calcoliamo le frequenze attese sotto l ipotesi che il numero di incidenti per autista segua una legge di Poisson di parametro, ricordando che: Distribuzione di probabilità di X: (=)= λ Es.! ~(λ); ()=()=λ (=0)=. = (=0)= =74.41 (=1)= = (=1)= = ! ( ) 6
7 n. di incidenti n. di autisti (freq.osservate) n. di autisti (freq.teoriche sotto ) = (=) Il valore della statistica test è pari a: Decisione χ = ( ) ( ) poiché χ >χ., rifiuto l ipotesi nulla. I dati non sono compatibili con l ipotesi che il numero di incidenti per autista segua una legge di Poisson. 7
8 Esercizio 4. Il modello di regressione: stima, bontà di adattamento, inferenza Si desidera studiare la relazione tra il voto Y conseguito all esame di statistica e il voto X conseguito nell esame di matematica. A partire da un campione casuale di n=200 studenti che hanno sostenuto entrambi gli esami in questione si osservano i seguenti risultati campionari: =27.87; 200 =25.24; =787.52; 200 =645.39; = a) Ricavare con il metodo dei minimi quadrati (OLS, Ordinary Least Squares), una stima dei parametri del modello di regressione con Y variabile dipendente e X variabile indipendente. b) Calcolare e interpretare il coefficiente di correlazione lineare e l indice di determinazione lineare c) Sulla base del modello stimato, qual è il voto atteso in statistica di uno studente che ha ottenuto un 24 in matematica? d) Valutare la significatività del modello di regressione (verifica di ipotesi sul coefficiente angolare) con α=0.05. Soluzione a) = + +ε è il modello di regressione lineare per la popolazione La stima della retta di regressione avviene sulla base del campione: = + + e sono rispettivamente gli stimatori per e della popolazione 8
9 : coefficiente angolare: inclinazione della retta di regressione, come varia in media Y a fronte di un incremento unitario della X : Intercetta della retta di regressione: indica il valore atteso della variabile di risposta Y quando il predittore X assume valore 0. Con il metodo dei minimi quadrati, il coefficiente angolare 1 risulta: = (,) 1 () = ( 1 ) ( 1 ) ( 1 ) = = =1.09 e l intercetta è pari a: ( 1 ) = = (25.24)=0.36 b) Per determinare, si può sfruttare la seguente relazione:, = (,) () () = ( ) = =0.96 dove ()= = ( ) Il valore prossimo a 1 di, indica la presenza di una forte relazione lineare positiva tra i due voti in questione. 1 Nota: è possibile, in alternativa, esprimere il coefficiente angolare della retta di regressione come: = (,) () = ( ) 9
10 L indice di determinazione lineare ( ) può essere calcolato anche come: =, =(0.96) =0.92 c) Il modello di regressione stimato è pari a: = per cui in corrispondenza di =24 il valore atteso di Y è dato da: = (24)=26.52 d) Valutare la significatività del modello stimato equivale a testare il seguente sistema di ipotesi: : =0 : 0 livello di significatività =0.05 Per costruire la statistica test dobbiamo studiare la distribuzione campionaria di. Siccome una delle ipotesi del modello di regressione lineare classico è allora si dimostra che 2 : ~(0, ).. ~, ( ) Tuttavia ciò sarebbe vero (e quindi lo stimatore per si distribuirebbe secondo una legge normale) se conoscessimo la varianza degli errori del modello. Nella realtà, gli errori del modello non sono osservabili, mentre è possibile osservare i residui. In particolare: = ( ) 2 2 Nota: gli stimatori OLS di e sono B.L.U.E (Teorema di Gauss-Markov). 10
11 per cui la varianza corretta dello stimatore per è pari a: ( ) = ( ) 2 ( ) = ( ) Sfrutto questo risultato per costruire la statistica test; infatti sotto essa risulta: = ( ) ~ ; Nota: per il TLC essendo n sufficientemente grande (n = 200) è ragionevole approssimare la distribuzione di ad una normale standardizzata, in particolare: = (0,1) Regola di decisione Con un livello di significatività del 5%, essendo il test bidirezionale e sfruttando l approssimazione normale (TLC) i valori critici da determinare sono in corrispondenza di: ± =±. =±1.96 per cui: se >. rifiuto l ipotesi nulla. Calcoli Dobbiamo determinare la quantità. Sapendo che: ( ) = = =1666 E, sfruttando il fatto che: =, =0.92 lo possiamo scrivere 3 come: 3 Ricorda la definizione dell indice di determinazione lineare 11
12 =1 ( ) ( ) dobbiamo risolvere rispetto alla quantità a numeratore del rapporto (in rosso), per cui: dove: ( ) =(1 ) ( ) ( ) = = =2156 quindi: ( ) =(1 0.92) 2156= Possiamo dunque calcolare: ( ) = ( ) 2 ( ) = ( ) = = E finalmente il valore della statistica test: Decisione = = =47.81 Siccome >. rifiuto l ipotesi nulla. 12
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6
 CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Associazione, correlazione e dipendenza tra caratteri In un collettivo di 11 famiglie è stata
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Associazione, correlazione e dipendenza tra caratteri In un collettivo di 11 famiglie è stata
Capitolo 12 La regressione lineare semplice
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
Esercizi di statistica
 Esercizi di statistica Test a scelta multipla (la risposta corretta è la prima) [1] Il seguente campione è stato estratto da una popolazione distribuita normalmente: -.4, 5.5,, -.5, 1.1, 7.4, -1.8, -..
Esercizi di statistica Test a scelta multipla (la risposta corretta è la prima) [1] Il seguente campione è stato estratto da una popolazione distribuita normalmente: -.4, 5.5,, -.5, 1.1, 7.4, -1.8, -..
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 2
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 2 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. La variabile Uniforme Continua Data una scheda telefonica da 5 euro di cui non si sa se sia
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 2 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. La variabile Uniforme Continua Data una scheda telefonica da 5 euro di cui non si sa se sia
Analisi della regressione multipla
 Analisi della regressione multipla y = β 0 + β 1 x 1 + β 2 x 2 +... β k x k + u 2. Inferenza Assunzione del Modello Classico di Regressione Lineare (CLM) Sappiamo che, date le assunzioni Gauss- Markov,
Analisi della regressione multipla y = β 0 + β 1 x 1 + β 2 x 2 +... β k x k + u 2. Inferenza Assunzione del Modello Classico di Regressione Lineare (CLM) Sappiamo che, date le assunzioni Gauss- Markov,
STATISTICA ESERCITAZIONE 13
 STATISTICA ESERCITAZIONE 13 Dott. Giuseppe Pandolfo 9 Marzo 2015 Errore di I tipo: si commette se l'ipotesi nulla H 0 viene rifiutata quando essa è vera Errore di II tipo: si commette se l'ipotesi nulla
STATISTICA ESERCITAZIONE 13 Dott. Giuseppe Pandolfo 9 Marzo 2015 Errore di I tipo: si commette se l'ipotesi nulla H 0 viene rifiutata quando essa è vera Errore di II tipo: si commette se l'ipotesi nulla
1.1 Obiettivi della statistica Struttura del testo 2
 Prefazione XV 1 Introduzione 1.1 Obiettivi della statistica 1 1.2 Struttura del testo 2 2 Distribuzioni di frequenza 2.1 Informazione statistica e rilevazione dei dati 5 2.2 Distribuzioni di frequenza
Prefazione XV 1 Introduzione 1.1 Obiettivi della statistica 1 1.2 Struttura del testo 2 2 Distribuzioni di frequenza 2.1 Informazione statistica e rilevazione dei dati 5 2.2 Distribuzioni di frequenza
Indice. centrale, dispersione e forma Introduzione alla Statistica Statistica descrittiva per variabili quantitative: tendenza
 XIII Presentazione del volume XV L Editore ringrazia 3 1. Introduzione alla Statistica 5 1.1 Definizione di Statistica 6 1.2 I Rami della Statistica Statistica Descrittiva, 6 Statistica Inferenziale, 6
XIII Presentazione del volume XV L Editore ringrazia 3 1. Introduzione alla Statistica 5 1.1 Definizione di Statistica 6 1.2 I Rami della Statistica Statistica Descrittiva, 6 Statistica Inferenziale, 6
Metodi statistici per la ricerca sociale Capitolo 7. Confronto tra Due Gruppi Esercitazione
 Metodi statistici per la ricerca sociale Capitolo 7. Confronto tra Due Gruppi Esercitazione Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università degli Studi di Firenze
Metodi statistici per la ricerca sociale Capitolo 7. Confronto tra Due Gruppi Esercitazione Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università degli Studi di Firenze
si tratta del test del chi-quadro di adattamento e di quello di indipendenza. 1 l ipotesi che la popolazione segua una legge fissata;
 di : dado : normale Finora abbiamo visto test d ipotesi per testare ipotesi differenti, ma tutte concernenti il valore atteso di una o due popolazioni. In questo capitolo vediamo come testare 1 l ipotesi
di : dado : normale Finora abbiamo visto test d ipotesi per testare ipotesi differenti, ma tutte concernenti il valore atteso di una o due popolazioni. In questo capitolo vediamo come testare 1 l ipotesi
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 5
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Approssimazione normale della Poisson (TLC) In un determinato tratto di strada il numero di incidenti
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Approssimazione normale della Poisson (TLC) In un determinato tratto di strada il numero di incidenti
Metodi statistici per l economia (Prof. Capitanio) Slide n. 10. Materiale di supporto per le lezioni. Non sostituisce il libro di testo
 Metodi statistici per l economia (Prof. Capitanio) Slide n. 10 Materiale di supporto per le lezioni. Non sostituisce il libro di testo 1 REGRESSIONE LINEARE Date due variabili quantitative, X e Y, si è
Metodi statistici per l economia (Prof. Capitanio) Slide n. 10 Materiale di supporto per le lezioni. Non sostituisce il libro di testo 1 REGRESSIONE LINEARE Date due variabili quantitative, X e Y, si è
STATISTICA A K (60 ore)
 STATISTICA A K (60 ore) Marco Riani [email protected] http://www.riani.it Richiami sulla regressione Marco Riani, Univ. di Parma 1 MODELLO DI REGRESSIONE y i = a + bx i + e i dove: i = 1,, n a + bx i rappresenta
STATISTICA A K (60 ore) Marco Riani [email protected] http://www.riani.it Richiami sulla regressione Marco Riani, Univ. di Parma 1 MODELLO DI REGRESSIONE y i = a + bx i + e i dove: i = 1,, n a + bx i rappresenta
Esercitazione 5 - Statistica (parte II) Davide Passaretti 9/3/2017
 Esercitazione 5 - Statistica (parte II) Davide Passaretti 9/3/2017 Contents 1 Inferenza sulla regressione semplice 1 1.1 Test sulla pendenza della retta................................... 1 1.2 Test sull
Esercitazione 5 - Statistica (parte II) Davide Passaretti 9/3/2017 Contents 1 Inferenza sulla regressione semplice 1 1.1 Test sulla pendenza della retta................................... 1 1.2 Test sull
Prova d'esame di Statistica I - Corso Prof.ssa S. Terzi
 Prova d'esame di Statistica I - Corso Prof.ssa S. Terzi Esercizio 1 Data la variabile casuale X con funzione di densità f(x) = 2x, per 0 x 1; f(x) = 0 per x [0, 1], determinare: a) P( - 0,5 < X< 0,7) b)
Prova d'esame di Statistica I - Corso Prof.ssa S. Terzi Esercizio 1 Data la variabile casuale X con funzione di densità f(x) = 2x, per 0 x 1; f(x) = 0 per x [0, 1], determinare: a) P( - 0,5 < X< 0,7) b)
Lezione 17. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 17. A. Iodice
 con Statistica Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () Statistica 1 / 29 Outline con 1 2 3 con 4 5 campioni appaiati 6 Indipendenza tra variabili () Statistica 2 /
con Statistica Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () Statistica 1 / 29 Outline con 1 2 3 con 4 5 campioni appaiati 6 Indipendenza tra variabili () Statistica 2 /
Regressione Lineare Semplice e Correlazione
 Regressione Lineare Semplice e Correlazione 1 Introduzione La Regressione è una tecnica di analisi della relazione tra due variabili quantitative Questa tecnica è utilizzata per calcolare il valore (y)
Regressione Lineare Semplice e Correlazione 1 Introduzione La Regressione è una tecnica di analisi della relazione tra due variabili quantitative Questa tecnica è utilizzata per calcolare il valore (y)
PROBABILITÀ ELEMENTARE
 Prefazione alla seconda edizione XI Capitolo 1 PROBABILITÀ ELEMENTARE 1 Esperimenti casuali 1 Spazi dei campioni 1 Eventi 2 Il concetto di probabilità 3 Gli assiomi della probabilità 3 Alcuni importanti
Prefazione alla seconda edizione XI Capitolo 1 PROBABILITÀ ELEMENTARE 1 Esperimenti casuali 1 Spazi dei campioni 1 Eventi 2 Il concetto di probabilità 3 Gli assiomi della probabilità 3 Alcuni importanti
COGNOME.NOME...MATR..
 STATISTICA 29.01.15 - PROVA GENERALE (CHALLENGE) Modalità A (A) ai fini della valutazione verranno considerate solo le risposte riportate dallo studente negli appositi riquadri bianchi: in caso di necessità
STATISTICA 29.01.15 - PROVA GENERALE (CHALLENGE) Modalità A (A) ai fini della valutazione verranno considerate solo le risposte riportate dallo studente negli appositi riquadri bianchi: in caso di necessità
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 4
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 4 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Stimatore media campionaria Il tempo in minuti necessario a un certo impiegato dell anagrafe
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 4 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Stimatore media campionaria Il tempo in minuti necessario a un certo impiegato dell anagrafe
ESAME. 9 Gennaio 2017 COMPITO B
 ESAME 9 Gennaio 2017 COMPITO B Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
ESAME 9 Gennaio 2017 COMPITO B Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
lezione n. 6 (a cura di Gaia Montanucci) Verosimiglianza: L = = =. Parte dipendente da β 0 e β 1
 lezione n. 6 (a cura di Gaia Montanucci) METODO MASSIMA VEROSIMIGLIANZA PER STIMARE β 0 E β 1 Distribuzione sui termini di errore ε i ε i ~ N (0, σ 2 ) ne consegue : ogni y i ha ancora distribuzione normale,
lezione n. 6 (a cura di Gaia Montanucci) METODO MASSIMA VEROSIMIGLIANZA PER STIMARE β 0 E β 1 Distribuzione sui termini di errore ε i ε i ~ N (0, σ 2 ) ne consegue : ogni y i ha ancora distribuzione normale,
Statistica multivariata Donata Rodi 17/10/2016
 Statistica multivariata Donata Rodi 17/10/2016 Quale analisi? Variabile Dipendente Categoriale Continua Variabile Indipendente Categoriale Chi Quadro ANOVA Continua Regressione Logistica Regressione Lineare
Statistica multivariata Donata Rodi 17/10/2016 Quale analisi? Variabile Dipendente Categoriale Continua Variabile Indipendente Categoriale Chi Quadro ANOVA Continua Regressione Logistica Regressione Lineare
R - Esercitazione 6. Andrea Fasulo Venerdì 22 Dicembre Università Roma Tre
 R - Esercitazione 6 Andrea Fasulo [email protected] Università Roma Tre Venerdì 22 Dicembre 2017 Il modello di regressione lineare semplice (I) Esempi tratti da: Stock, Watson Introduzione all econometria
R - Esercitazione 6 Andrea Fasulo [email protected] Università Roma Tre Venerdì 22 Dicembre 2017 Il modello di regressione lineare semplice (I) Esempi tratti da: Stock, Watson Introduzione all econometria
Statistica. Alfonso Iodice D Enza
 Statistica Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () Statistica 1 / 33 Outline 1 2 3 4 5 6 () Statistica 2 / 33 Misura del legame Nel caso di variabili quantitative
Statistica Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () Statistica 1 / 33 Outline 1 2 3 4 5 6 () Statistica 2 / 33 Misura del legame Nel caso di variabili quantitative
STATISTICA. Regressione-2
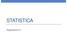 STATISTICA Regressione-2 Esempio Su un campione di =5unità sono state osservate due variabili, ed : x i 1 2 3 4 5 y i 1.5 2.5 3 2.5 3.5 1. Rappresentare l andamento congiunto di in funzione di mediante
STATISTICA Regressione-2 Esempio Su un campione di =5unità sono state osservate due variabili, ed : x i 1 2 3 4 5 y i 1.5 2.5 3 2.5 3.5 1. Rappresentare l andamento congiunto di in funzione di mediante
Test delle Ipotesi Parte I
 Test delle Ipotesi Parte I Test delle Ipotesi sulla media Introduzione Definizioni basilari Teoria per il caso di varianza nota Rischi nel test delle ipotesi Teoria per il caso di varianza non nota Test
Test delle Ipotesi Parte I Test delle Ipotesi sulla media Introduzione Definizioni basilari Teoria per il caso di varianza nota Rischi nel test delle ipotesi Teoria per il caso di varianza non nota Test
STATISTICA AZIENDALE Modulo Controllo di Qualità
 STATISTICA AZIENDALE Modulo Controllo di Qualità A.A. 009/10 - Sottoperiodo PROA DEL 14 MAGGIO 010 Cognome:.. Nome: Matricola:.. AERTENZE: Negli esercizi in cui sono richiesti calcoli riportare tutte la
STATISTICA AZIENDALE Modulo Controllo di Qualità A.A. 009/10 - Sottoperiodo PROA DEL 14 MAGGIO 010 Cognome:.. Nome: Matricola:.. AERTENZE: Negli esercizi in cui sono richiesti calcoli riportare tutte la
Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009)
 Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009) Quesito: Posso stimare il numero di ore passate a studiare statistica sul voto conseguito all esame? Potrei calcolare il coefficiente di correlazione.
Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009) Quesito: Posso stimare il numero di ore passate a studiare statistica sul voto conseguito all esame? Potrei calcolare il coefficiente di correlazione.
Statistica. Alfonso Iodice D Enza
 Statistica Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () Statistica 1 / 24 Outline 1 2 3 4 5 () Statistica 2 / 24 Dipendenza lineare Lo studio della relazione tra caratteri
Statistica Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () Statistica 1 / 24 Outline 1 2 3 4 5 () Statistica 2 / 24 Dipendenza lineare Lo studio della relazione tra caratteri
Indice. Prefazione. 4 Sintesi della distribuzione di un carattere La variabilità Introduzione La variabilità di una distribuzione 75
 00PrPag:I-XIV_prefazione_IAS 8-05-2008 17:56 Pagina V Prefazione XI 1 La rilevazione dei fenomeni statistici 1 1.1 Introduzione 1 1.2 Caratteri, unità statistiche e collettivo 1 1.3 Classificazione dei
00PrPag:I-XIV_prefazione_IAS 8-05-2008 17:56 Pagina V Prefazione XI 1 La rilevazione dei fenomeni statistici 1 1.1 Introduzione 1 1.2 Caratteri, unità statistiche e collettivo 1 1.3 Classificazione dei
STATISTICA (2) ESERCITAZIONE Dott.ssa Antonella Costanzo
 STATISTICA (2) ESERCITAZIONE 3 12.02.2014 Dott.ssa Antonella Costanzo Esercizio 1. Distribuzioni doppie di probabilità: applicazioni E stata svolta un indagine per studiare la relazione tra abitudine a
STATISTICA (2) ESERCITAZIONE 3 12.02.2014 Dott.ssa Antonella Costanzo Esercizio 1. Distribuzioni doppie di probabilità: applicazioni E stata svolta un indagine per studiare la relazione tra abitudine a
Esercizi su distribuzioni doppie, dipendenza, correlazione e regressione (Statistica I, IV Canale)
 Esercizi su distribuzioni doppie, dipendenza, correlazione e regressione (Statistica I, IV Canale) Esercizio 1: Un indagine su 10.000 famiglie ha dato luogo, fra le altre, alle osservazioni riportate nella
Esercizi su distribuzioni doppie, dipendenza, correlazione e regressione (Statistica I, IV Canale) Esercizio 1: Un indagine su 10.000 famiglie ha dato luogo, fra le altre, alle osservazioni riportate nella
Indipendenza, Dipendenza e interdipendenza
 Indipendenza, Dipendenza e interdipendenza In analisi bivariata la tabella di contingenza consente di esaminare congiuntamente due variabili consente di rilevare le relazioni esistenti tra le variabili
Indipendenza, Dipendenza e interdipendenza In analisi bivariata la tabella di contingenza consente di esaminare congiuntamente due variabili consente di rilevare le relazioni esistenti tra le variabili
Esercitazione 3 - Statistica II - Economia Aziendale Davide Passaretti 23/5/2017
 Esercitazione 3 - Statistica II - Economia Aziendale Davide Passaretti 3/5/017 Contents 1 Intervalli di confidenza 1 Intervalli su un campione 1.1 Intervallo di confidenza per la media................................
Esercitazione 3 - Statistica II - Economia Aziendale Davide Passaretti 3/5/017 Contents 1 Intervalli di confidenza 1 Intervalli su un campione 1.1 Intervallo di confidenza per la media................................
Prefazione Ringraziamenti dell'editore Il sito web dedicato al libro Test online: la piattaforma McGraw-Hill Education Guida alla lettura
 INDICE GENERALE Prefazione Ringraziamenti dell'editore Il sito web dedicato al libro Test online: la piattaforma McGraw-Hill Education Guida alla lettura XI XIV XV XVII XVIII 1 LA RILEVAZIONE DEI FENOMENI
INDICE GENERALE Prefazione Ringraziamenti dell'editore Il sito web dedicato al libro Test online: la piattaforma McGraw-Hill Education Guida alla lettura XI XIV XV XVII XVIII 1 LA RILEVAZIONE DEI FENOMENI
Nel modello omoschedastico la varianza dell errore non dipende da i ed è quindi pari a σ 0.
 Regressione [] el modello di regressione lineare si assume una relazione di tipo lineare tra il valore medio della variabile dipendente Y e quello della variabile indipendente X per cui Il modello si scrive
Regressione [] el modello di regressione lineare si assume una relazione di tipo lineare tra il valore medio della variabile dipendente Y e quello della variabile indipendente X per cui Il modello si scrive
Corso di Statistica Esercitazione 1.8
 Corso di Statistica Esercitazione.8 Test su medie e proporzioni Prof.ssa T. Laureti a.a. 202-203 Esercizio Un produttore vuole monitorare i valori dei livelli di impurità contenute nella merce che gli
Corso di Statistica Esercitazione.8 Test su medie e proporzioni Prof.ssa T. Laureti a.a. 202-203 Esercizio Un produttore vuole monitorare i valori dei livelli di impurità contenute nella merce che gli
Contenuti: Capitolo 14 del libro di testo
 Test d Ipotesi / TIPICI PROBLEMI DI VERIFICA DI IPOTESI SONO Test per la media Test per una proporzione Test per la varianza Test per due campioni indipendenti Test di indipendenza Contenuti Capitolo 4
Test d Ipotesi / TIPICI PROBLEMI DI VERIFICA DI IPOTESI SONO Test per la media Test per una proporzione Test per la varianza Test per due campioni indipendenti Test di indipendenza Contenuti Capitolo 4
Giorno n. clienti di attesa
 Esercizio 1 Un aspetto cruciale per la qualità del servizio ai clienti in un supermercato è il cosiddetto checkout (ovvero il tempo che il cliente impiega dal momento in cui si mette in fila alla cassa
Esercizio 1 Un aspetto cruciale per la qualità del servizio ai clienti in un supermercato è il cosiddetto checkout (ovvero il tempo che il cliente impiega dal momento in cui si mette in fila alla cassa
Esercitazione III Soluzione
 Esercitazione III Soluzione Esercizio 1 a) Frequenze congiunte assolute: n ij Reddito mensile Titolo di studio 1000-000 000-5000 5000-8000 Totale Laurea triennale 4 1 0 5 Laurea magistrale 1 4 7 Dottorato
Esercitazione III Soluzione Esercizio 1 a) Frequenze congiunte assolute: n ij Reddito mensile Titolo di studio 1000-000 000-5000 5000-8000 Totale Laurea triennale 4 1 0 5 Laurea magistrale 1 4 7 Dottorato
Statistica economica
 Statistica economica a.a. 013/14 Dr. Luca Secondi 10.a. Output tipico di un modello di regressione lineare multipla 1 Le analisi basate sul modello di regressione prevedono la stima dei coefficienti associati
Statistica economica a.a. 013/14 Dr. Luca Secondi 10.a. Output tipico di un modello di regressione lineare multipla 1 Le analisi basate sul modello di regressione prevedono la stima dei coefficienti associati
Σ (x i - x) 2 = Σ x i 2 - (Σ x i ) 2 / n Σ (y i - y) 2 = Σ y i 2 - (Σ y i ) 2 / n. 13. Regressione lineare parametrica
 13. Regressione lineare parametrica Esistono numerose occasioni nelle quali quello che interessa è ricostruire la relazione di funzione che lega due variabili, la variabile y (variabile dipendente, in
13. Regressione lineare parametrica Esistono numerose occasioni nelle quali quello che interessa è ricostruire la relazione di funzione che lega due variabili, la variabile y (variabile dipendente, in
Esercizi su Regressione e Connessione
 Esercizi su Regressione e Connessione Stefano Cabras 31 marzo 2009 Sommario Questa serie di esercizi è principalmente incentrata sulla regressione e la connessione, tuttavia in alcuni esercizi le soluzioni
Esercizi su Regressione e Connessione Stefano Cabras 31 marzo 2009 Sommario Questa serie di esercizi è principalmente incentrata sulla regressione e la connessione, tuttavia in alcuni esercizi le soluzioni
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazion
 Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
L'analisi bivariata (analisi della varianza e correlazione) Prof. Stefano Nobile. Corso di Metodologia della ricerca sociale
 L'analisi bivariata (analisi della varianza e correlazione) Prof. Stefano Nobile Corso di Metodologia della ricerca sociale L analisi della varianza (ANOVA) La tecnica con cui si esplorano le relazioni
L'analisi bivariata (analisi della varianza e correlazione) Prof. Stefano Nobile Corso di Metodologia della ricerca sociale L analisi della varianza (ANOVA) La tecnica con cui si esplorano le relazioni
Teorema del limite centrale TCL
 Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Intervalli di confidenza
 Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
METODI STATISTICI PER LA BIOLOGIA. Paolo Dai Pra e Francesco Caravenna
 METODI STATISTICI PER LA BIOLOGIA. Paolo Dai Pra e Francesco Caravenna 18 marzo 2008 NOME 1. Parte A 1.1. Sono stati raccolti 7 dati relativi ad una variabile x. Si sa che 3 dati hanno valore 5; 2 dati
METODI STATISTICI PER LA BIOLOGIA. Paolo Dai Pra e Francesco Caravenna 18 marzo 2008 NOME 1. Parte A 1.1. Sono stati raccolti 7 dati relativi ad una variabile x. Si sa che 3 dati hanno valore 5; 2 dati
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5
 CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Misura dell associazione tra due caratteri Uno store manager è interessato a studiare la relazione
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Misura dell associazione tra due caratteri Uno store manager è interessato a studiare la relazione
Esercitazione del
 Esercizi sulla regressione lineare. Esercitazione del 21.05.2013 Esercizio dal tema d esame del 13.06.2011. Si consideri il seguente campione di n = 9 osservazioni relative ai caratteri ed Y: 7 17 8 36
Esercizi sulla regressione lineare. Esercitazione del 21.05.2013 Esercizio dal tema d esame del 13.06.2011. Si consideri il seguente campione di n = 9 osservazioni relative ai caratteri ed Y: 7 17 8 36
SOLUZIONI ESERCITAZIONE NR. 8 Test statistici
 SOLUZIONI ESERCITAZIONE NR. 8 Test statistici ESERCIZIO nr. 1 Un campione casuale di dieci pazienti di sesso maschile in cura per comportamenti aggressivi nell ambito del contesto familiare è stato classificato
SOLUZIONI ESERCITAZIONE NR. 8 Test statistici ESERCIZIO nr. 1 Un campione casuale di dieci pazienti di sesso maschile in cura per comportamenti aggressivi nell ambito del contesto familiare è stato classificato
Variabilità e Concentrazione Esercitazione n 02
 Variabilità e Concentrazione Esercitazione n 02 ESERCIZIO 1 Nella tabella di seguito sono riportati i dati relativi al tempo necessario a 8 studenti per svolgere un test di valutazione (in ore): Tempo
Variabilità e Concentrazione Esercitazione n 02 ESERCIZIO 1 Nella tabella di seguito sono riportati i dati relativi al tempo necessario a 8 studenti per svolgere un test di valutazione (in ore): Tempo
REGRESSIONE E CORRELAZIONE
 REGRESSIONE E CORRELAZIONE Nella Statistica, per studio della connessione si intende la ricerca di eventuali relazioni, di dipendenza ed interdipendenza, intercorrenti tra due variabili statistiche 1.
REGRESSIONE E CORRELAZIONE Nella Statistica, per studio della connessione si intende la ricerca di eventuali relazioni, di dipendenza ed interdipendenza, intercorrenti tra due variabili statistiche 1.
Statistica Metodologica
 Statistica Metodologica Esercizi di Probabilita e Inferenza Silvia Figini e-mail: [email protected] Problema 1 Sia X una variabile aleatoria Bernoulliana con parametro p = 0.7. 1. Determinare la media
Statistica Metodologica Esercizi di Probabilita e Inferenza Silvia Figini e-mail: [email protected] Problema 1 Sia X una variabile aleatoria Bernoulliana con parametro p = 0.7. 1. Determinare la media
Statistica. Esercitazione 14. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice. Verifica di ipotesi
 Esercitazione 14 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 14 Ex.1: Verifica Ipotesi sulla media (varianza nota) Le funi prodotte da un certo macchinario hanno una
Esercitazione 14 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 14 Ex.1: Verifica Ipotesi sulla media (varianza nota) Le funi prodotte da un certo macchinario hanno una
Statistica. Alfonso Iodice D Enza
 Statistica Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () Statistica 1 / 1 Outline 1 () Statistica 2 / 1 Outline 1 2 () Statistica 2 / 1 Outline 1 2 3 () Statistica 2 / 1
Statistica Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () Statistica 1 / 1 Outline 1 () Statistica 2 / 1 Outline 1 2 () Statistica 2 / 1 Outline 1 2 3 () Statistica 2 / 1
Statistica. Esercitazione 16. Alfonso Iodice D Enza [email protected]. Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazione 16 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 24 Studio della relazione tra due variabili Commonly Asked Questions Qual è la relazione tra la spesa
Esercitazione 16 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 24 Studio della relazione tra due variabili Commonly Asked Questions Qual è la relazione tra la spesa
Statistica 1 A.A. 2015/2016
 Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 35 Il modello di regressione
Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 35 Il modello di regressione
Esercitazione 9 del corso di Statistica (parte seconda)
 Esercitazione 9 del corso di Statistica (parte seconda) Dott.ssa Paola Costantini 17 Marzo 9 Esercizio 1 Esercizio Un economista del Ministero degli Esteri desidera verificare se gli accordi di negoziazione
Esercitazione 9 del corso di Statistica (parte seconda) Dott.ssa Paola Costantini 17 Marzo 9 Esercizio 1 Esercizio Un economista del Ministero degli Esteri desidera verificare se gli accordi di negoziazione
Esercitazione 8 del corso di Statistica 2
 Esercitazione 8 del corso di Statistica Prof. Domenico Vistocco Dott.ssa Paola Costantini 6 Giugno 8 Decisione vera falsa è respinta Errore di I tipo Decisione corretta non è respinta Probabilità α Decisione
Esercitazione 8 del corso di Statistica Prof. Domenico Vistocco Dott.ssa Paola Costantini 6 Giugno 8 Decisione vera falsa è respinta Errore di I tipo Decisione corretta non è respinta Probabilità α Decisione
