Caos e complessita in natura. Guido Boffetta Dipartimento di Fisica Generale Universita di Torino
|
|
|
- Vanessa Pinto
- 6 anni fa
- Visualizzazioni
Transcript
1 Caos e complessita in natura Guido Boffetta Dipartimento di Fisica Generale Universita di Torino
2 Fisica e sistemi complessi La fisica si e sviluppata seguendo la linea riduzionista: lo studio di un fenomeno e riconducibile allo studio dei costituenti MOLECOLE Conseguenza: ATOMI NUCLEI QUARK? Attualmente conosciamo meglio il nucleo atomico che il moto turbolento dell acqua in un bicchiere Le equazioni della fluidodinamica viscosa sono note da 50 anni ma ancora una teoria completa della turbolenza non esiste. Sistemi complessi: il passaggio dalle equazioni costituenti alla fenomenologia non e ovvio
3 Fisica e predicibilita Una teoria fisica deve essere in grado di fare previsioni (esempio: astronomia) Per i sistemi complessi e difficile fare previsioni * Sistemi complicati (schedina totocalcio) L impredicibilita e dovuta al gran numero di cause in gioco che non riusciamo a controllare (non conosciamo le equazioni) * Sistemi caotici L impredicibilita e dovuta alla dinamica intrinsecamente instabile (conosciamo le equazioni, ma non basta)
4 PROPRIETA DEI SISTEMI CAOTICI SENSIBILITA ALLE CONDIZIONI INIZIALI (impredicibilita, effetto farfalla) ATTRATTORE DI PERIODO INFINITO (la sequenza non si ripete: es. meteorologia vs. astronomia) STRUTTURA FRATTALE DEGLI ATTRATTORI (dettagli a tutte le scale) LE SEQUENZE GENERATE DAI SISTEMI CAOTICI SONO COMPLESSE
5 PROPRIETA DEI SISTEMI CAOTICI SENSIBILITA ALLE CONDIZIONI INIZIALI (impredicibilita, effetto farfalla) Per colpa di un chiodo si perse lo zoccolo per colpa di uno zoccolo si perse il cavallo per colpa del cavallo si perse il cavaliere per colpa di un cavaliere si perse il messaggio per colpa di un messaggio si perse la battaglia per colpa di una battaglia si perse il regno (G. Herbert)
6 SISTEMI NON CAOTICI Gli attrattori (=luogo geometrico su cui avviene il moto a tempi lunghi) dei sistemi non caotici sono SEMPLICI: Pendolo smorzato PUNTO FISSO STABILE CICLO LIMITE (quasi periodico) Il moto futuro e predicibile: nel primo caso e banale, nel secondo un po meno (es. eclissi) Sistema solare
7 Nei sistemi non caotici, l impredicibilita e limitata a particolari condizioni iniziali Esempio: PUNTO FISSO INSTABILE?
8 SISTEMI CAOTICI: l impredicibilita e intrinseca, cioe per (quasi) tutte le condizioni iniziali Sistema caotico = sensibilita alle condizioni iniziali Due traiettorie, arbitrariamente vicine al tempo iniziale t=0, si separano (esponenzialmente) nel tempo futuro. Edward Lorenz ( ) Il battito d ali di una farfalla in Brasile puo provocare un tornado in Texas. FLIPPER DI LORENZ
9 CAOS: un semplice esempio meccanico Biliardo classico Biliardo caotico D(t) = D(0) + A t D(t) = D(0) eλ t
10 Sistema caotico elementare: mappa a tenda x(t+) x(t + = [ ] Esempio di evoluzione (rappresentazione binaria) x(t) 0 x(0)= x(0)= D(0)= x()= x()= D()= x(5)=0.0 x(5)=0. D(5)= D(t)=D(0) elog(2) t /2 Errore cresce esponenzialmente!
11 Sistema caotico in 2 dimensioni: la mappa del fornaio La mappa del fornaio e una trasformazione del quadrato in se stesso che mantiene l area (non si perde informazione). stiramento 2. ripiegamento Punti inizialmente vicini vengono allontanati esponenzialmente nel tempo Altri punti, inizialmente lontani, si avvicinano (mixing)
12 Esempio di applicazione della mappa del fornaio t= t=20 t=0 t=5 t=4 t=3 t=2 t= t=0
13 Il moto della Terra attorno al Sole segue orbite regolari (ellittiche) previste da Newton Se consideriamo pero piu di 2 corpi (Sole, Terra, Giove) il sistema matematicamente non e piu trattabile (Poincare ) In linea di principio il moto di 3 o piu corpi puo essere caotico. Il sistema solare e caotico?
14 Effetti caotici nel sistema solare sono osservabili nei corpi piu piccoli La distribuzione degli assi maggiori degli asteroidi nella fascia principale (tra Marte e Giove) rivela dei buchi detti intervalli di Kirkwood (867). Questi buchi corrispondono a periodi (Kepler: T2 R3) in risonanza col periodo di Giove. La teoria del caos spiega l assenza di asteroidi come conseguenza della risonanza. Simulazioni numeriche recenti del sistema solare con calcolatori dedicati han mostrato che anche il moto dei pianeti e caotico (e quindi anche la Terra) ma l impredicibilita avviene su tempi dell ordine dei 00 milioni di anni (eccentricita ) 3: 5:2 7:3 2:
15 PROPRIETA DEI SISTEMI CAOTICI ATTRATTORE DI PERIODO INFINITO (la sequenza non si ripete: es. meteorologia vs. astronomia) STRUTTURA FRATTALE DEGLI ATTRATTORI (dettagli a tutte le scale)
16 Pendolo ideale Moto armonico (periodico) Suono puro x(t) = ω
17 Pendolo con attrito Moto armonico smorzato (punto fisso) x(t) = τ ω
18 Pendolo con attrito e forzato Moto caotico (rumore non periodico) x(t) =
19 Esempio di sistema caotico: modelli di popolazioni * Modello molto semplice senza predatori e con potere riproduttivo costante r: n(t) = numero di n(t+)=r n(t) individui nell`anno t la soluzione e semplice: n(t)=r*n(t-) = r*r*n(t-2) =... = r*r*... *r n(0) = rt n(0) t crescita esponenziale (esplosione demografica) * Modello piu realistico: dobbiamo tenere conto dei limiti ambientali (cibo, spazio):il potere riproduttivo descresce con la popolazione r r (N - n(t)) n(t+)=r n(t) (N - n(t)) N = numero massimo di individui Introduciamo le nuove variabili: x(t)=n(t)/n e λ =r*n e otteniamo la x(t+) = λ x(t) ( - x(t)) MAPPA LOGISTICA
20 Comportamento della mappa logistica al variare del parametro λ λ =2.8 Punto fisso (x=0.65) La popolazione tende ad un valore costante di equilibrio λ =3.4 Ciclo periodico (x [0.5,0.8]) Alteranza periodica di popolazione λ =3.9 Dinamica caotica (x [0,]) La popolazione e instabile ed oscilla casualmente da un anno all altro
21 Diagramma di biforcazione della mappa logistica Forma dell attrattore in funzione del parametro λ ciclo limite periodo 2 ciclo limite periodo 4 moto caotico periodo infinito x t x =3.56 λλλ =3.5 =3.6 =3.7 =3.847 =3.575 =3.4 t x t
22 Modelli piu realistici di dinamica delle popolazioni devono tenere conto della presenza di altre specie (esempio: prede-predatori) Modello di Lotka - Volterra (93) n(t+)=r n(t) - b n(t) n2(t) n2(t+)= - r2 n2(t) + b2 n(t) n2(t) equazioni di questo tipo mostrano comportamenti complessi simili a quelli osservati in natura (o in laboratorio, con batteri) prede predatori
23 PROPRIETA DEI SISTEMI CAOTICI LE SEQUENZE GENERATE DAI SISTEMI CAOTICI SONO COMPLESSE
24 Caos e complessita Le serie temporali caotiche sono complesse regolare caotica Come misurare la complessita?
25 Teoria dell'informazione Consideriamo due esempi di schedine del totocalcio: entrambe hanno la stessa probabilitá: p = (/3)3 = ma ovviamente quella a sx é inverosimile quella a dx sembra plausibile (tipica) (Shannon) 2 X X 2 X 2 X X La probabilitá di un evento non é una buona misura della sua complessitá
26 Complessita algoritmica (Kolmogorov, Chaitin) Consideriamo degli esempi di serie temporali binarie: (a) (b) (c) semplici complessa Sia K(N) la lunghezza (misurata in qualche modo) del piu corto programma (insieme di istruzioni) in grado di generare la sequenza di N simboli La complessita algoritmica e definita, per grandi N come K= (NB: non dipende dal linguaggio)
27 Complessita algoritmica degli esempi: (a) scrivi N volte K=0 (b) scrivi 00 N/3 volte K=0 (c) Se la sequenza (c) e casuale (esempio, lancio moneta), allora l unico modo e : scrivi K= Questo e il modo in cui viene usualmente trasmessa l informazione (esempio: risultati di partite di calcio, oppure tavole per p)
28 Un sistema caotico e complesso? Apparentemente no, perche basta trasmettere la regola che genera la sequenza, ad esempio: x(t+) = λ x(t) ( - x(t)) Se pero voglio generare una specifica sequenza, devo dare anche la condizione iniziale x(0) Se il sistema e caotico, la condizione iniziale deve essere molto precisa per riprodurre una sequenza lunga. In generale si trova che in un sistema caotico la condizione iniziale deve avere un numero di cifre proporzionale a N (errore cresce esponenzialmente) I sistemi caotici hanno complessita algoritmica non nulla
29 Predire e difficile, specialmente il futuro. Mark Twain
30 Bibliografia James Gleick, Caos - La nascita di una nuova scienza Rizzoli SuperBUR Scienza, 2000 Edward Lorenz, The essence of Chaos University of Washington Press, 996 Angelo Vulpiani, Determinismo e caos Carrocci editore, 2004 David Ruelle, Caso e caos Bollati Boringhieri, 992
31
32 Caos ed impredicibilita Sistema caotico: l errore con cui predico lo stato del sistema cresce esponenzialmente nel tempo: D(t) = D(0) e λ t λ : esponente di Lyapunov dato errore iniziale D0 e tolleranza Dmax, il tempo di predicibilita vale T= λ quantita intrinseca del sistema (dipende poco da D0)
33 Caos ed impredicibilita in un semplice modello atmosferico atmosfera previsione numerica QuickTime and a YUV420 codec decompressor are needed to see this picture. Integrazione numerica di semplice modello di atmosfera Due realizzazioni con D(0)=0-6
34 Frattali Gli insiemi frattali sono luoghi geometrici intermedi tra gli insiemi classici (punto, retta, piano,...) La dimensione frattale D misura il grado di frastaglietá dell insieme (per gli insiemi classici D é intera) Caratteristica fondamentale dei frattali e l autosimilarita (si ripete a tutte le scale)
35 Costruzione dell insieme di Cantor
36 Costruzione dell insieme di Koch e cosi via
37 Dimensione frattale Generalizzazione del concetto ordinario di dimensione ad insiemi di punti non lisci. Sia N(n) il numero di segmenti di lunghezza r necessari a ricoprire l insieme di punti all iterazione n. La dimensione frattale e data da D = Cantor Segmento Koch N(n)= 2n 3n D= log(2)/log(3)= n log(4)/log(3)= n r 2 /3 3 /9 n /3n
Fisica e sistemi complessi
 Fisica e sistemi complessi La fisica si e sviluppata seguendo la linea riduzionista: lo studio di un fenomeno e riconducibile allo studio dei costituenti MOLECOLE ATOMI NUCLEI QUARK? E Il percorso inverso,
Fisica e sistemi complessi La fisica si e sviluppata seguendo la linea riduzionista: lo studio di un fenomeno e riconducibile allo studio dei costituenti MOLECOLE ATOMI NUCLEI QUARK? E Il percorso inverso,
Che cos'è il caos? Caos Dove comincia il caos si arresta la scienza classica (1987) L'aspetto irregolare della natura sono stati dei veri rompicapo
 Che cos'è il caos? Che cos'è il caos? Poincarè nel 1903 afferma che : una causa piccolissima che sfugga alla nostra attenzione determina un effetto considerevole che non possiamo mancare di vedere, e allora
Che cos'è il caos? Che cos'è il caos? Poincarè nel 1903 afferma che : una causa piccolissima che sfugga alla nostra attenzione determina un effetto considerevole che non possiamo mancare di vedere, e allora
Ordine e caos nel sistema solare
 Ordine e caos nel sistema solare Ugo Locatelli Dipartimento di Matematica, Università degli Studi di Roma Tor Vergata 15 febbraio 2017 Prima della formulazione della legge di gravitazione universale L
Ordine e caos nel sistema solare Ugo Locatelli Dipartimento di Matematica, Università degli Studi di Roma Tor Vergata 15 febbraio 2017 Prima della formulazione della legge di gravitazione universale L
ATTRATTORI CAOTICI. Attrattori. Classificazione degli attrattori: equilibri, cicli, tori, caos. Esponenti di Liapunov di attrattori
 ARAORI CAOICI Attrattori Classificazione degli attrattori: equilibri, cicli, tori, caos Esponenti di Liapunov di attrattori Sistemi dissipativi C. Piccardi e F. Dercole Politecnico di Milano - 06/12/2012
ARAORI CAOICI Attrattori Classificazione degli attrattori: equilibri, cicli, tori, caos Esponenti di Liapunov di attrattori Sistemi dissipativi C. Piccardi e F. Dercole Politecnico di Milano - 06/12/2012
Personaggi ed Interpreti in ordine di apparizione Atto I: I Modelli Atto II: Il Caos Atto III : Il Determinismo La Fisica La Matematica La Natura La r
 IL Caos e La Natura Fausto Borgonovi Dipartimento di Matematica e Fisica, Università Cattolica Personaggi ed Interpreti in ordine di apparizione Atto I: I Modelli Atto II: Il Caos Atto III : Il Determinismo
IL Caos e La Natura Fausto Borgonovi Dipartimento di Matematica e Fisica, Università Cattolica Personaggi ed Interpreti in ordine di apparizione Atto I: I Modelli Atto II: Il Caos Atto III : Il Determinismo
16 settembre 2017 Cantalupa
 16 settembre 2017 Cantalupa 16 settembre 2017 Cantalupa L imprevedibile viaggio matematico e storico che ci permette di portare l ombrello solo quando serve Gemma Gallino Matematica Matematica Talete 585
16 settembre 2017 Cantalupa 16 settembre 2017 Cantalupa L imprevedibile viaggio matematico e storico che ci permette di portare l ombrello solo quando serve Gemma Gallino Matematica Matematica Talete 585
INSIEMI FRATTALI. Dimensione di un insieme. Insiemi frattali elementari. Dimensioni frattali. Insiemi frattali e sistemi dinamici
 INSIEMI FRATTALI Dimensione di un insieme Insiemi frattali elementari Dimensioni frattali Insiemi frattali e sistemi dinamici C. Piccardi e F. Dercole Politecnico di Milano - 30/11/2011 1/29 Caratteristiche
INSIEMI FRATTALI Dimensione di un insieme Insiemi frattali elementari Dimensioni frattali Insiemi frattali e sistemi dinamici C. Piccardi e F. Dercole Politecnico di Milano - 30/11/2011 1/29 Caratteristiche
I FRATTALI. Chiara Mocenni. giovedì 15 dicembre 11
 I FRATTALI Chiara Mocenni (mocenni@dii.unisi.it) IL CAOS DETERMINISTICO Sistema deterministico Comportamento aperiodico Sensibilità alle condizioni iniziali Attrattori strani Infiniti cicli repulsivi GLI
I FRATTALI Chiara Mocenni (mocenni@dii.unisi.it) IL CAOS DETERMINISTICO Sistema deterministico Comportamento aperiodico Sensibilità alle condizioni iniziali Attrattori strani Infiniti cicli repulsivi GLI
Note sul sistema di Lotka-Volterra. Prima versione. Commenti e correzioni sono benvenuti.
 Ottobre 2016 Note sul sistema di Lotka-Volterra Prima versione. Commenti e correzioni sono benvenuti. 1 Introduzione Il sistema di Lotka Volterra (LV), o sistema preda predatore è probabilmente il primo
Ottobre 2016 Note sul sistema di Lotka-Volterra Prima versione. Commenti e correzioni sono benvenuti. 1 Introduzione Il sistema di Lotka Volterra (LV), o sistema preda predatore è probabilmente il primo
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
ANALISI DI SERIE TEMPORALI CAOTICHE (1)
 ANALISI DI SERIE TEMPORALI CAOTICHE (1) Problematiche Ricostruzione dello stato Dimensione di embedding C. Piccardi e F. Dercole Politecnico di Milano ver. 28/12/2009 1/15 Per studiare e comprendere appieno
ANALISI DI SERIE TEMPORALI CAOTICHE (1) Problematiche Ricostruzione dello stato Dimensione di embedding C. Piccardi e F. Dercole Politecnico di Milano ver. 28/12/2009 1/15 Per studiare e comprendere appieno
Capitolo 12. Moto oscillatorio
 Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Unità didattica 3. Terza unità didattica (Fisica) 1. Corso integrato di Matematica e Fisica per il Corso di Farmacia
 Unità didattica 3 Elasticità dei materiali Deformazione di un solido..2 Legge di Hooke.. 3 Forza elastica.. 4 Deformazione elastica di una molla... 5 Accumulo di energia attraverso la deformazione elastica..6
Unità didattica 3 Elasticità dei materiali Deformazione di un solido..2 Legge di Hooke.. 3 Forza elastica.. 4 Deformazione elastica di una molla... 5 Accumulo di energia attraverso la deformazione elastica..6
STRADE AL CAOS. Sistemi parametrizzati. Cascata di raddoppi di periodo (cascata di Feigenbaum) Rottura di toro. Caos alla Shilnikov.
 STRADE AL CAOS Sistemi parametrizzati Cascata di raddoppi di periodo (cascata di Feigenbaum) Rottura di toro Caos alla Shilnikov Intermittenza Crisi C. Piccardi e F. Dercole Politecnico di Milano ver.
STRADE AL CAOS Sistemi parametrizzati Cascata di raddoppi di periodo (cascata di Feigenbaum) Rottura di toro Caos alla Shilnikov Intermittenza Crisi C. Piccardi e F. Dercole Politecnico di Milano ver.
5. Applicazione ai dati sperimentali, un modello di previsione delle temperature
 5. Applicazione ai dati sperimentali, un modello di previsione delle temperature 5.1 Ricostruzione dello spazio delle fasi L utilizzo del teorema di embedding per ricostruire lo spazio delle fasi relativo
5. Applicazione ai dati sperimentali, un modello di previsione delle temperature 5.1 Ricostruzione dello spazio delle fasi L utilizzo del teorema di embedding per ricostruire lo spazio delle fasi relativo
Dinamica di sistemi non lineari
 Dinamica di sistemi non lineari DINAMICA: ANALISI DI SISTEMI CHE EVOLVONO NEL TEMPO ( in prima battuta, determinazione della presenza di equilibri e valutazione della loro stabilità). CENNI STORICI Metà
Dinamica di sistemi non lineari DINAMICA: ANALISI DI SISTEMI CHE EVOLVONO NEL TEMPO ( in prima battuta, determinazione della presenza di equilibri e valutazione della loro stabilità). CENNI STORICI Metà
COME APPARE IL CAOS DETERMINISTICO
 COME APPARE IL CAOS DETERMINISTICO Serie temporale Spettro di potenza Quadro delle traiettorie Sezione di Poincaré Auto-somiglianza Sensibilità alle condizioni iniziali C. Piccardi e F. Dercole Politecnico
COME APPARE IL CAOS DETERMINISTICO Serie temporale Spettro di potenza Quadro delle traiettorie Sezione di Poincaré Auto-somiglianza Sensibilità alle condizioni iniziali C. Piccardi e F. Dercole Politecnico
Che cos'è il caos? Caos Dove comincia il caos si arresta la scienza classica (1987) L'aspetto irregolare della natura sono stati dei veri rompicapo
 Poincarè nel 1903 afferma che : una causa piccolissima che sfugga alla nostra attenzione determina un effetto considerevole che non possiamo mancare di vedere, e allora diciamo che l'effetto è dovuto al
Poincarè nel 1903 afferma che : una causa piccolissima che sfugga alla nostra attenzione determina un effetto considerevole che non possiamo mancare di vedere, e allora diciamo che l'effetto è dovuto al
Dinamica del punto materiale
 Dinamica del punto materiale Formule fondamentali L. P. 5 Aprile 2010 N.B.: Le relazioni riportate sono valide in un sistema di riferimento inerziale. Princìpi della dinamica Secondo principio della dinamica
Dinamica del punto materiale Formule fondamentali L. P. 5 Aprile 2010 N.B.: Le relazioni riportate sono valide in un sistema di riferimento inerziale. Princìpi della dinamica Secondo principio della dinamica
Controlli Automatici e Teoria dei Sistemi Esempi di sistemi dinamici
 Controlli Automatici e Teoria dei Sistemi Esempi di sistemi dinamici Prof. Roberto Guidorzi Dipartimento di Elettronica, Informatica e Sistemistica Università di Bologna Viale del Risorgimento 2, 40136
Controlli Automatici e Teoria dei Sistemi Esempi di sistemi dinamici Prof. Roberto Guidorzi Dipartimento di Elettronica, Informatica e Sistemistica Università di Bologna Viale del Risorgimento 2, 40136
Andrea Carati Luigi Galgani. Appunti di Meccanica Analitica II
 Andrea Carati Luigi Galgani Appunti di Meccanica Analitica II Anno Accademico 2013 2014 ii Andrea Carati e Luigi Galgani Indice 1 Ordine e caos nei sistemi dinamici. 1 1. Introduzione. Poincaré e la rivoluzione
Andrea Carati Luigi Galgani Appunti di Meccanica Analitica II Anno Accademico 2013 2014 ii Andrea Carati e Luigi Galgani Indice 1 Ordine e caos nei sistemi dinamici. 1 1. Introduzione. Poincaré e la rivoluzione
Così Mandelbrot nel suo libro The Fractal Geometry of Nature descrive l'inadeguatezza della geometria euclidea nella descrizione della natura.
 Geometria frattale "Why is geometry often described as 'cold' and 'dry'? One reason lies in its inability to describe the shape of a cloud, a mountain, a coastiline or a tree. Clouds are not spheres, mountains
Geometria frattale "Why is geometry often described as 'cold' and 'dry'? One reason lies in its inability to describe the shape of a cloud, a mountain, a coastiline or a tree. Clouds are not spheres, mountains
Richiami sulle oscillazioni smorzate
 Richiami sulle oscillazioni smorzate Il moto armonico è il moto descritto da un oscillatore armonico, cioè un sistema meccanico che, quando perturbato dalla sua posizione di equilibrio, è soggetto ad una
Richiami sulle oscillazioni smorzate Il moto armonico è il moto descritto da un oscillatore armonico, cioè un sistema meccanico che, quando perturbato dalla sua posizione di equilibrio, è soggetto ad una
τ (O) r F è semplicemente l intensità della forza F dal polo O: = r F sinθ = bf
 5. Momenti, forze centrali e gravitazione Definizione di momento di una forza Si definisce momento della forza F rispetto al polo O la quantità data dal prodotto vettoriale τ (O) r F il cui modulo si misura
5. Momenti, forze centrali e gravitazione Definizione di momento di una forza Si definisce momento della forza F rispetto al polo O la quantità data dal prodotto vettoriale τ (O) r F il cui modulo si misura
Introduciamo il sistema di riferimento indicato in figura b) con F 1 = ( f, 0) ed F 2 = (f, 0). Se P = (x, y) la condizione (1) fornisce
 1 L ellisse 1.1 Definizione Consideriamo due punti F 1 ed F 2 e sia 2f la loro distanza. L ellisse è il luogo dei punti P tali che la somma delle distanze PF 1 e PF 2 da F 1 ed F 2 è costante. Se indichiamo
1 L ellisse 1.1 Definizione Consideriamo due punti F 1 ed F 2 e sia 2f la loro distanza. L ellisse è il luogo dei punti P tali che la somma delle distanze PF 1 e PF 2 da F 1 ed F 2 è costante. Se indichiamo
iv Indice c
 Indice Prefazione ix 1 Numeri 1 1 Insiemi e logica 1 1.1 Concetti di base sugli insiemi 1 1.2 Un po di logica elementare 9 2 Sommatorie e coefficienti binomiali 13 2.1 Il simbolo di sommatoria 13 2.2 Fattoriale
Indice Prefazione ix 1 Numeri 1 1 Insiemi e logica 1 1.1 Concetti di base sugli insiemi 1 1.2 Un po di logica elementare 9 2 Sommatorie e coefficienti binomiali 13 2.1 Il simbolo di sommatoria 13 2.2 Fattoriale
Applicazioni delle leggi della meccanica: moto armnico
 Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
CRESCITA DI POPOLAZIONI. Consideriamo una popolazione di esseri viventi e indichiamo con n(t) il numero di individui della popolazione al tempo t:
 CRESCITA DI POPOLAZIONI Consideriamo una popolazione di esseri viventi e indichiamo con n(t) il numero di individui della popolazione al tempo t: n : R N Questa è una funzione costante a tratti, cioè una
CRESCITA DI POPOLAZIONI Consideriamo una popolazione di esseri viventi e indichiamo con n(t) il numero di individui della popolazione al tempo t: n : R N Questa è una funzione costante a tratti, cioè una
Variabili aleatorie: parte 1. 1 Definizione di variabile aleatoria e misurabilitá
 Statistica e analisi dei dati Data: 11 Aprile 2016 Variabili aleatorie: parte 1 Docente: Prof. Giuseppe Boccignone Scriba: Noemi Tentori 1 Definizione di variabile aleatoria e misurabilitá Informalmente,
Statistica e analisi dei dati Data: 11 Aprile 2016 Variabili aleatorie: parte 1 Docente: Prof. Giuseppe Boccignone Scriba: Noemi Tentori 1 Definizione di variabile aleatoria e misurabilitá Informalmente,
La nascita di nuova scienza: dal determinismo al caos. Fausto Borgonovi
 La nascita di nuova scienza: dal determinismo al caos Fausto Borgonovi Dipartimento di Matematica e Fisica, Universitá Cattolica, Brescia Istituto Nazionale di Fisica Nucleare, Sezione di Pavia Il
La nascita di nuova scienza: dal determinismo al caos Fausto Borgonovi Dipartimento di Matematica e Fisica, Universitá Cattolica, Brescia Istituto Nazionale di Fisica Nucleare, Sezione di Pavia Il
ANALISI E SIMULAZIONE DI SISTEMI DINAMICI. Lezione XI: Stabilità interna
 ANALISI E SIMULAZIONE DI SISTEMI DINAMICI Lezione XI: Stabilità interna Stabilità interna e esterna Stabilità alla Lyapunov Stabilità asintotica I sistemi lineari Esempi 11-1 Tipi di Stabilità Idea intuitiva
ANALISI E SIMULAZIONE DI SISTEMI DINAMICI Lezione XI: Stabilità interna Stabilità interna e esterna Stabilità alla Lyapunov Stabilità asintotica I sistemi lineari Esempi 11-1 Tipi di Stabilità Idea intuitiva
Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori.
 ËÁËÌ ÅÁ ÈÁ ÆÁ ½ Queste note attualmente e probabilmente per un bel po ) sono altamente provvisorie e molto probabilmente) non prive di errori 41 Sistemi 2D Come abbiamo già detto tipicamente è impossibile
ËÁËÌ ÅÁ ÈÁ ÆÁ ½ Queste note attualmente e probabilmente per un bel po ) sono altamente provvisorie e molto probabilmente) non prive di errori 41 Sistemi 2D Come abbiamo già detto tipicamente è impossibile
Introduzione alla Meccanica: Cinematica
 Introduzione alla Meccanica: Cinematica La Cinematica si occupa della descrizione geometrica del moto, senza riferimento alle sue cause. E invece compito della Dinamica mettere in relazione il moto con
Introduzione alla Meccanica: Cinematica La Cinematica si occupa della descrizione geometrica del moto, senza riferimento alle sue cause. E invece compito della Dinamica mettere in relazione il moto con
e una frequenza = 0 /2 =1/T (misurata in Hertz). Infine è la fase, cioè un numero (radianti) che dipende dalla definizione dell istante t=0.
 8. Oscillazioni Definizione di oscillatore armonico libero Si tratta di un sistema soggetto ad un moto descrivibile secondo una funzione armonica (seno o coseno) del tipo x(t) = Acos( 0 t + ) A è l ampiezza
8. Oscillazioni Definizione di oscillatore armonico libero Si tratta di un sistema soggetto ad un moto descrivibile secondo una funzione armonica (seno o coseno) del tipo x(t) = Acos( 0 t + ) A è l ampiezza
Teoria delle catastrofi
 Teoria delle catastrofi Il caso precedente, studiato con PPLANE. Scelta dell algoritmo di discretezzazione (qui è importante che sia adattativo perché cambia la velocità) transizione rapida (catastrofe)
Teoria delle catastrofi Il caso precedente, studiato con PPLANE. Scelta dell algoritmo di discretezzazione (qui è importante che sia adattativo perché cambia la velocità) transizione rapida (catastrofe)
Pendolo senza attrito
 Pendolo senza attrito l m ϕ equazione del moto : mlϕ '' = mg sinϕ ϕ '' = y'' = k sin y, k > 0 g sinϕ l Pendolo senza attrito Trasformiamo l equazione in un sistema autonomo bidimensionale conservativo
Pendolo senza attrito l m ϕ equazione del moto : mlϕ '' = mg sinϕ ϕ '' = y'' = k sin y, k > 0 g sinϕ l Pendolo senza attrito Trasformiamo l equazione in un sistema autonomo bidimensionale conservativo
CAPITOLO 9: LA GRAVITAZIONE. 9.1 Introduzione.
 CAPITOLO 9: LA GRAVITAZIONE 9.1 Introduzione. Un altro tipo di forza piuttosto importante è la forza gravitazionale. Innanzitutto, è risaputo che nel nostro sistema di pianeti chiamato sistema solare il
CAPITOLO 9: LA GRAVITAZIONE 9.1 Introduzione. Un altro tipo di forza piuttosto importante è la forza gravitazionale. Innanzitutto, è risaputo che nel nostro sistema di pianeti chiamato sistema solare il
Modelli differenziali per le scienze della vita
 Modelli differenziali per le scienze della vita Andrea Susa Agenda Modelli Matematici Crescita delle popolazioni isolate crescita di una cellula Decadimento radioattivo Modello Malthus Modello a crescita
Modelli differenziali per le scienze della vita Andrea Susa Agenda Modelli Matematici Crescita delle popolazioni isolate crescita di una cellula Decadimento radioattivo Modello Malthus Modello a crescita
La Matematica nell Astronomia. Una (breve) introduzione. Roberto Ferretti
 La Matematica nell Astronomia Una (breve) introduzione Roberto Ferretti Il cielo: un fascino intramontabile Come si puó parlare di astronomia senza fermarsi un attimo a guardare il cielo? E un fascino
La Matematica nell Astronomia Una (breve) introduzione Roberto Ferretti Il cielo: un fascino intramontabile Come si puó parlare di astronomia senza fermarsi un attimo a guardare il cielo? E un fascino
Laboratorio di Calcolo B 68
 Generazione di numeri casuali Abbiamo già accennato all idea che le tecniche statistiche possano essere utili per risolvere problemi di simulazione di processi fisici e di calcoli numerici. Dobbiamo però
Generazione di numeri casuali Abbiamo già accennato all idea che le tecniche statistiche possano essere utili per risolvere problemi di simulazione di processi fisici e di calcoli numerici. Dobbiamo però
Le formule del cielo: la caotica armonia dei pianeti. Alessandra Celletti
 Le formule del cielo: la caotica armonia dei pianeti Alessandra Celletti Dipartimento di Matematica Università di Roma Tor Vergata celletti@mat.uniroma2.it Immagine: CICLOPS, JPL, ESA, NASA SOMMARIO 1.
Le formule del cielo: la caotica armonia dei pianeti Alessandra Celletti Dipartimento di Matematica Università di Roma Tor Vergata celletti@mat.uniroma2.it Immagine: CICLOPS, JPL, ESA, NASA SOMMARIO 1.
7. Forze elastiche. Nella figura 1 il periodo è T = 2s e corrisponde ad un moto unidimensionale limitato tra i valori x = 0 ed x = 1.
 1 Moti periodici 7. Forze elastiche Un caso particolare di moto accelerato è un moto periodico. In figura 1 è riportato un esempio di moto periodico unidimensionale. Un moto periodico si ripete identicamente
1 Moti periodici 7. Forze elastiche Un caso particolare di moto accelerato è un moto periodico. In figura 1 è riportato un esempio di moto periodico unidimensionale. Un moto periodico si ripete identicamente
PROBABILITÀ - SCHEDA N. 3 VARIABILI ALEATORIE CONTINUE E SIMULAZIONE
 PROBABILITÀ - SCHEDA N. 3 VARIABILI ALEATORIE CONTINUE E SIMULAZIONE (da un idea di M. Impedovo Variabili aleatorie continue e simulazione Progetto Alice n. 15, ) 1. La simulazione Nelle schede precedenti
PROBABILITÀ - SCHEDA N. 3 VARIABILI ALEATORIE CONTINUE E SIMULAZIONE (da un idea di M. Impedovo Variabili aleatorie continue e simulazione Progetto Alice n. 15, ) 1. La simulazione Nelle schede precedenti
Considerare il moto di un punto materiale di massa m = 1 soggetto ad un potenziale V (x):
 sercizio Considerare il moto di un punto materiale di massa m = soggetto ad un potenziale V (x): ẍ = V (x), dove V (x) = x x.. Scrivere esplicitamente l equazione del moto e verificare esplicitamente la
sercizio Considerare il moto di un punto materiale di massa m = soggetto ad un potenziale V (x): ẍ = V (x), dove V (x) = x x.. Scrivere esplicitamente l equazione del moto e verificare esplicitamente la
Risonanza magnetica nucleare
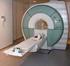 Risonanza magnetica nucleare Università di Firenze Corso di Tecnologie Biomediche Lezione del 31 ottobre 2003 Leonardo Bocchi Principi fisici Premessa Modello classico Visualizzazione semplificata Equazione
Risonanza magnetica nucleare Università di Firenze Corso di Tecnologie Biomediche Lezione del 31 ottobre 2003 Leonardo Bocchi Principi fisici Premessa Modello classico Visualizzazione semplificata Equazione
TEORIA DEI SISTEMI SISTEMI LINEARI
 TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
Matematica che terrorizza o affascina
 Matematica che terrorizza o affascina Emanuele Biolcati Dipartimento di Fisica dell Università di Torino Liceo Valsalice, Torino 1 febbraio 2011 Emanuele Biolcati (1/2/2011) Matematica che terrorizza o
Matematica che terrorizza o affascina Emanuele Biolcati Dipartimento di Fisica dell Università di Torino Liceo Valsalice, Torino 1 febbraio 2011 Emanuele Biolcati (1/2/2011) Matematica che terrorizza o
OLTRE LA BOTANICA. Numero 4 La sezione aurea in astronomia. = Cerchio Altazimutale di Ramsden, Osservatorio Astronomico "G.S.
 LA SEZIONE AUREA DAGLI ATOMI ALLE STELLE Numero 4 La sezione aurea in astronomia = Cerchio Altazimutale di Ramsden, Osservatorio Astronomico "G.S.Vaiana", Palermo = Rubrica curata da Francesco Di Noto
LA SEZIONE AUREA DAGLI ATOMI ALLE STELLE Numero 4 La sezione aurea in astronomia = Cerchio Altazimutale di Ramsden, Osservatorio Astronomico "G.S.Vaiana", Palermo = Rubrica curata da Francesco Di Noto
Il programma di formalizzazione matematica della realtà
 Angelo Vulpiani Caos deterministico Il programma di formalizzazione matematica della realtà inaugurato con la pubblicazione, nel 1687, dei Principia Mathematica di Isaac Newton è un punto di riferimento
Angelo Vulpiani Caos deterministico Il programma di formalizzazione matematica della realtà inaugurato con la pubblicazione, nel 1687, dei Principia Mathematica di Isaac Newton è un punto di riferimento
CALENDARIO BOREALE 1 EUROPA 2015 QUESITO 1
 www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE EUROPA 05 QUESITO La funzione f(x) è continua per x [ 4; 4] il suo grafico è la spezzata
www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE EUROPA 05 QUESITO La funzione f(x) è continua per x [ 4; 4] il suo grafico è la spezzata
Equazioni di Eulero del corpo rigido.
 Equazioni di Eulero del corpo rigido. In questa nota vogliamo scrivere e studiare le equazioni del moto di un corpo rigido libero, sottoposto alla sola forza di gravità. Ci occuperemo in particolare delle
Equazioni di Eulero del corpo rigido. In questa nota vogliamo scrivere e studiare le equazioni del moto di un corpo rigido libero, sottoposto alla sola forza di gravità. Ci occuperemo in particolare delle
Fractals. Anna Carbone Politecnico di Torino November 2, 2016
 Fractals Anna Carbone Politecnico di Torino www.polito.it/noiselab Caffé November 2, 2016 Fractals: Everywhere ever and ever (sempre e dovunque) Fractals: Everywhere ever and ever (sempre e dovunque) Middle
Fractals Anna Carbone Politecnico di Torino www.polito.it/noiselab Caffé November 2, 2016 Fractals: Everywhere ever and ever (sempre e dovunque) Fractals: Everywhere ever and ever (sempre e dovunque) Middle
Ricordiamo ora che a è legata ad x (derivata seconda) ed otteniamo
 Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
Grandezze fisiche e loro misura
 Grandezze fisiche e loro misura Cos è la fisica? e di che cosa si occupa? - Scienza sperimentale che studia i fenomeni naturali suscettibili di sperimentazione e che implicano grandezze misurabili. - Sono
Grandezze fisiche e loro misura Cos è la fisica? e di che cosa si occupa? - Scienza sperimentale che studia i fenomeni naturali suscettibili di sperimentazione e che implicano grandezze misurabili. - Sono
Macchine ricorsive lineari: alcune applicazioni
 Macchine ricorsive lineari: alcune applicazioni Marcello Colozzo http://www.extrabyte.info Le macchine ricorsive lineari hanno un costo computazionale molto basso, giacchè il corrispondente sistema dinamico
Macchine ricorsive lineari: alcune applicazioni Marcello Colozzo http://www.extrabyte.info Le macchine ricorsive lineari hanno un costo computazionale molto basso, giacchè il corrispondente sistema dinamico
Terza legge di Keplero, teoria e significato fisico della costante di Planck. m V p2
 estratto da : L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Terza legge di Keplero, teoria e significato fisico della costante di Planck La relazione E p h p p ci dice che all energia
estratto da : L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Terza legge di Keplero, teoria e significato fisico della costante di Planck La relazione E p h p p ci dice che all energia
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA. (Plank Einstein)
 L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
Modellistica e Simulazione: il sistema di Rossler a.a Chiara Mocenni
 Modellistica e Simulazione: il sistema di Rossler a.a. 007-008 Chiara Mocenni Il sistema di Rossler è il più semplice sistema di terzo ordine capace di manifestare comportamenti di tipo caotico. x = y
Modellistica e Simulazione: il sistema di Rossler a.a. 007-008 Chiara Mocenni Il sistema di Rossler è il più semplice sistema di terzo ordine capace di manifestare comportamenti di tipo caotico. x = y
Esperimentazioni di Fisica 1 Tracce delle lezioni di TERMOLOGIA
 Esperimentazioni di Fisica 1 Tracce delle lezioni di TERMOLOGIA AA 2015-2016 Temperatura Temperatura misura oggettiva della sensazione di caldo e freddo Grandezza intensiva Misura la direzione del trasferimento
Esperimentazioni di Fisica 1 Tracce delle lezioni di TERMOLOGIA AA 2015-2016 Temperatura Temperatura misura oggettiva della sensazione di caldo e freddo Grandezza intensiva Misura la direzione del trasferimento
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA
 DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
SCHEDA N 8 DEL LABORATORIO DI FISICA
 SCHEDA N 1 IL PENDOLO SEMPLICE SCHEDA N 8 DEL LABORATORIO DI FISICA Scopo dell'esperimento. Determinare il periodo di oscillazione di un pendolo semplice. Applicare le nozioni sugli errori di una grandezza
SCHEDA N 1 IL PENDOLO SEMPLICE SCHEDA N 8 DEL LABORATORIO DI FISICA Scopo dell'esperimento. Determinare il periodo di oscillazione di un pendolo semplice. Applicare le nozioni sugli errori di una grandezza
PREFAZIONE pag. 15 Capitolo 1 I NUMERI E LE FUNZIONI REALI 1. Premessa Gli assiomi dei numeri reali Alcune conseguenze degli assiomi dei
 PREFAZIONE pag. 15 Capitolo 1 I NUMERI E LE FUNZIONI REALI 1. Premessa 23 2. Gli assiomi dei numeri reali 24 3. Alcune conseguenze degli assiomi dei numeri reali 25 4. Cenni di teoria degli insiemi 30
PREFAZIONE pag. 15 Capitolo 1 I NUMERI E LE FUNZIONI REALI 1. Premessa 23 2. Gli assiomi dei numeri reali 24 3. Alcune conseguenze degli assiomi dei numeri reali 25 4. Cenni di teoria degli insiemi 30
Indice slides. 1 Oscillatore semplice 5. 2 Equazione caratteristica 6. 3 Radici complesse 7. 4 Integrale generale 8. 5 Forza Peso 9.
 Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Limiti di funzioni I. Limiti per x che tende all infinito
 Limiti di funzioni I. Limiti per x che tende all infinito 1 La crescita della popolazione mondiale La crescita della popolazione umana mondiale e il suo impatto sull ambiente: discussioni e studi matematici
Limiti di funzioni I. Limiti per x che tende all infinito 1 La crescita della popolazione mondiale La crescita della popolazione umana mondiale e il suo impatto sull ambiente: discussioni e studi matematici
Proprietà dei sistemi dinamici lineari
 Proprietà dei sistemi dinamici lineari Vediamo se le proprietà dei sistemi lineari ci possono essere utili per chiarire qualcosa sulla stabilità. Partiamo dal sistema dinamico lineare più semplice possibile:
Proprietà dei sistemi dinamici lineari Vediamo se le proprietà dei sistemi lineari ci possono essere utili per chiarire qualcosa sulla stabilità. Partiamo dal sistema dinamico lineare più semplice possibile:
OSCILLAZIONI SMORZATE E FORZATE
 OSCILLAZIONI SMORZATE E FORZATE Questo esperimento permette di studiare le oscillazioni armoniche di un pendolo e le oscillazioni smorzate e smorzate-forzate. Studiando il variare dell ampiezza dell oscillazione
OSCILLAZIONI SMORZATE E FORZATE Questo esperimento permette di studiare le oscillazioni armoniche di un pendolo e le oscillazioni smorzate e smorzate-forzate. Studiando il variare dell ampiezza dell oscillazione
5.4 Larghezza naturale di una riga
 5.4 Larghezza naturale di una riga Un modello classico più soddisfacente del processo di emissione è il seguente. Si considera una carica elettrica puntiforme in moto armonico di pulsazione ω 0 ; la carica,
5.4 Larghezza naturale di una riga Un modello classico più soddisfacente del processo di emissione è il seguente. Si considera una carica elettrica puntiforme in moto armonico di pulsazione ω 0 ; la carica,
Meccanica del punto materiale
 Meccanica del punto materiale Princìpi della dinamica. Forze. Momento angolare. Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro
Meccanica del punto materiale Princìpi della dinamica. Forze. Momento angolare. Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale
 Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Indice. Capitolo 1 Richiami di calcolo numerico 1. Capitolo 2 Rappresentazioni di dati 13
 Autori Prefazione Nota dell Editore e istruzioni per l uso Guida alla lettura XI XIII XV XVII Richiami di calcolo numerico 1 1.1 Unità di misura e fattori di conversione; potenze del 10; notazioni scientifiche
Autori Prefazione Nota dell Editore e istruzioni per l uso Guida alla lettura XI XIII XV XVII Richiami di calcolo numerico 1 1.1 Unità di misura e fattori di conversione; potenze del 10; notazioni scientifiche
DOCENTE: Lucio De Marcellis
 DOCENTE: CLASSE: 1 B PROGRAMMA svolto in MATEMATICA GLI INSIEMI NUMERICI I numeri naturali. I numeri relativi. L ordinamento dei numeri. I numeri frazionari e le relative operazioni. Le operazioni con
DOCENTE: CLASSE: 1 B PROGRAMMA svolto in MATEMATICA GLI INSIEMI NUMERICI I numeri naturali. I numeri relativi. L ordinamento dei numeri. I numeri frazionari e le relative operazioni. Le operazioni con
Fisica per scienze ed ingegneria
 Serway, Jewett Fisica per scienze ed ingegneria Capitolo 15 Blocchetto legato ad una molla in moto su un piano orizzontale privo di attrito. Forza elastica di richiamo: F x =-Kx (Legge di Hooke). Per x>0,
Serway, Jewett Fisica per scienze ed ingegneria Capitolo 15 Blocchetto legato ad una molla in moto su un piano orizzontale privo di attrito. Forza elastica di richiamo: F x =-Kx (Legge di Hooke). Per x>0,
UNIVERSITA' DEGLI STUDI DI CATANIA Facoltà di Scienze Matematiche, Fisiche, Naturali Corso di Laurea Specialistica in Fisica
 UNIVERSITA' DEGLI STUDI DI CATANIA Facoltà di Scienze Matematiche, Fisiche, Naturali Corso di Laurea Specialistica in Fisica CURRICULUM ASTROFISICA E FISICA DELLO SPAZIO Anno Accademico 2011-2012 PROGRAMMA
UNIVERSITA' DEGLI STUDI DI CATANIA Facoltà di Scienze Matematiche, Fisiche, Naturali Corso di Laurea Specialistica in Fisica CURRICULUM ASTROFISICA E FISICA DELLO SPAZIO Anno Accademico 2011-2012 PROGRAMMA
Liceo Artistico R. Cottini Torino
 INSIEMI NUMERICI Liceo Artistico R. Cottini Torino Programma di 1 a per l IDONEITÀ ALLA CLASSE 2 A L insieme dei numeri naturali le quattro operazioni in N multipli e divisori potenze espressioni con i
INSIEMI NUMERICI Liceo Artistico R. Cottini Torino Programma di 1 a per l IDONEITÀ ALLA CLASSE 2 A L insieme dei numeri naturali le quattro operazioni in N multipli e divisori potenze espressioni con i
Il metodo scientifico
 La Fisica è una scienza grazie a Galileo che a suo fondamento pose il metodo scientifico 1 Il metodo scientifico La Natura è complessa: non basta osservarla per capirla Intuizione di Galileo: bisogna porre
La Fisica è una scienza grazie a Galileo che a suo fondamento pose il metodo scientifico 1 Il metodo scientifico La Natura è complessa: non basta osservarla per capirla Intuizione di Galileo: bisogna porre
Struttura Elettronica degli Atomi Meccanica quantistica
 Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Analisi dei Dati Tabelle e Grafici
 Analisi dei Dati Tabelle e Grafici Spesso una misurazione consiste nello studio di una grandezza,y i in funzione di un altra, x i. Esempi: o lo spazio percorso da un oggetto in funzione di un intervallo
Analisi dei Dati Tabelle e Grafici Spesso una misurazione consiste nello studio di una grandezza,y i in funzione di un altra, x i. Esempi: o lo spazio percorso da un oggetto in funzione di un intervallo
La statistica. Elaborazione e rappresentazione dei dati Gli indicatori statistici. Prof. Giuseppe Carucci
 La statistica Elaborazione e rappresentazione dei dati Gli indicatori statistici Introduzione La statistica raccoglie ed analizza gruppi di dati (su cose o persone) per trarne conclusioni e fare previsioni
La statistica Elaborazione e rappresentazione dei dati Gli indicatori statistici Introduzione La statistica raccoglie ed analizza gruppi di dati (su cose o persone) per trarne conclusioni e fare previsioni
Iterando s impara. Modelli dinamici discreti
 Iterando s impara. Modelli dinamici discreti Scuola Estiva A (6 settembre 2017) Dipartimento di Matematica, Sapienza Università di Roma Stefano Finzi Vita Collaborano: R. Dalla Volta, A. Perrotta Finzi
Iterando s impara. Modelli dinamici discreti Scuola Estiva A (6 settembre 2017) Dipartimento di Matematica, Sapienza Università di Roma Stefano Finzi Vita Collaborano: R. Dalla Volta, A. Perrotta Finzi
La Bussola Magnetica di V. Croquette Dipartimento di Fisica, Università di Bologna Ghirardini Stefano Strumento reale:
 La Bussola Magnetica di V. Croquette Dipartimento di Fisica, Università di Bologna Ghirardini Stefano 01/06/2009 stefano.ghirardini@live.it Strumento reale: La bussola magnetica di Croquette consta di
La Bussola Magnetica di V. Croquette Dipartimento di Fisica, Università di Bologna Ghirardini Stefano 01/06/2009 stefano.ghirardini@live.it Strumento reale: La bussola magnetica di Croquette consta di
IL PROBLEMA DEI TRE CORPI
 IL PROBLEMA DEI TRE CORPI Il problema dei tre corpi consiste nel calcolare il moto di tre corpi soggetti alla loro reciproca attrazione. Il problema appassionò gli astronomi di tutta Europa tanto che il
IL PROBLEMA DEI TRE CORPI Il problema dei tre corpi consiste nel calcolare il moto di tre corpi soggetti alla loro reciproca attrazione. Il problema appassionò gli astronomi di tutta Europa tanto che il
Processi di Markov. Processi di Markov
 Processi Stocastici Processi Stocastici Processi Stocastici Catene o Catene o Catene di M Processi Stocastici Processi Stocastici Processi Stocastici Catene o Catene o Catene di M Processi Stocastici Un
Processi Stocastici Processi Stocastici Processi Stocastici Catene o Catene o Catene di M Processi Stocastici Processi Stocastici Processi Stocastici Catene o Catene o Catene di M Processi Stocastici Un
Esercitazioni di Meccanica Quantistica I
 Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
ISTITUTO PROFESSIONALE DI STATO PER L INDUSTRIA E L ARTIGIANATO I.P.S.I.A. L. B. ALBERTI
 ISTITUTO PROFESSIONALE DI STATO PER L INDUSTRIA E L ARTIGIANATO I.P.S.I.A. L. B. ALBERTI Via Clotilde Tambroni, RIMINI ( RN ) Anno scolastico 2016-2017 Classe I A Materia: FISICA Insegnante : Prof. GIUSEPPE
ISTITUTO PROFESSIONALE DI STATO PER L INDUSTRIA E L ARTIGIANATO I.P.S.I.A. L. B. ALBERTI Via Clotilde Tambroni, RIMINI ( RN ) Anno scolastico 2016-2017 Classe I A Materia: FISICA Insegnante : Prof. GIUSEPPE
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
EQUAZIONI DIFFERENZIALI
 Indice 1 EQUAZIONI DIFFERENZIALI 3 1.1 Equazioni fisicamente significative...................... 3 1.1.1 A cosa servono?............................. 3 1.1.2 Legge di Newton............................
Indice 1 EQUAZIONI DIFFERENZIALI 3 1.1 Equazioni fisicamente significative...................... 3 1.1.1 A cosa servono?............................. 3 1.1.2 Legge di Newton............................
ANALISI PICCO-PICCO. Diagramma picco-picco. Dinamica picco-picco. Diagramma dei tempi di ritorno. Calcolo del primo esponente di Liapunov
 ANALISI PICCO-PICCO Diagramma picco-picco Dinamica picco-picco Diagramma dei tempi di ritorno Calcolo del primo esponente di Liapunov C. Piccardi e F. Dercole Politecnico di Milano - 28/2/2009 /2 DIAGRAMMA
ANALISI PICCO-PICCO Diagramma picco-picco Dinamica picco-picco Diagramma dei tempi di ritorno Calcolo del primo esponente di Liapunov C. Piccardi e F. Dercole Politecnico di Milano - 28/2/2009 /2 DIAGRAMMA
TECNICHE DI SIMULAZIONE
 TECNICHE DI SIMULAZIONE Processi di Poisson Francesca Mazzia Dipartimento di Matematica Università di Bari a.a. 2004/2005 TECNICHE DI SIMULAZIONE p. 1 Consideriamo eventi casuali come gli arrivi di lavori
TECNICHE DI SIMULAZIONE Processi di Poisson Francesca Mazzia Dipartimento di Matematica Università di Bari a.a. 2004/2005 TECNICHE DI SIMULAZIONE p. 1 Consideriamo eventi casuali come gli arrivi di lavori
Enrico Silva - diritti riservati - Non è permessa, fra l altro, l inclusione anche parziale in altre opere senza il consenso scritto dell autore
 Particelle della presente identiche. opera. Principio di Pauli. 1 Particelle identiche: sommario Finora: proprietà di particella singola. Volendo ottenere il comportamento di più particelle, è necessario
Particelle della presente identiche. opera. Principio di Pauli. 1 Particelle identiche: sommario Finora: proprietà di particella singola. Volendo ottenere il comportamento di più particelle, è necessario
Il modello preda predatore. Modelli Matematici Ambientali, 2015/16 Dinamiche di Crescita:
 Modelli Matematici Ambientali, 2015/16 Dinamiche di Crescita: 2 popolazioni Il modello preda predatore Interazione di due popolazioni: il modello Preda-Predatore Il modello Preda-Predatore è stato sviluppato
Modelli Matematici Ambientali, 2015/16 Dinamiche di Crescita: 2 popolazioni Il modello preda predatore Interazione di due popolazioni: il modello Preda-Predatore Il modello Preda-Predatore è stato sviluppato
Numeri complessi e frattali 1
 Numeri complessi e frattali 1 Insiemi di Julia e di Mandelbrot 1) L 0 èilcerchio unitario 2) L c si deforma con continuità alvariare di c 3) J c =BdL c è una insieme frattale autosimile ricostruibile da
Numeri complessi e frattali 1 Insiemi di Julia e di Mandelbrot 1) L 0 èilcerchio unitario 2) L c si deforma con continuità alvariare di c 3) J c =BdL c è una insieme frattale autosimile ricostruibile da
Capitolo 6. Variabili casuali continue. 6.1 La densità di probabilità
 Capitolo 6 Variabili casuali continue Le definizioni di probabilità che abbiamo finora usato sono adatte solo per una variabile casuale che possa assumere solo valori discreti; vediamo innanzi tutto come
Capitolo 6 Variabili casuali continue Le definizioni di probabilità che abbiamo finora usato sono adatte solo per una variabile casuale che possa assumere solo valori discreti; vediamo innanzi tutto come
Esercitazione 2. Soluzione
 Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
Enrico Silva - diritti riservati - Non è permessa, fra l altro, l inclusione anche parziale in altre opere senza il consenso scritto dell autore
 Indeterminazione Finora si sono considerate le proprietà ondulatorie, lavorando sulla fase di una (per ora non meglio specificata) funzione. Si sono ricavate o ipotizzate relazioni per: - lunghezza d onda
Indeterminazione Finora si sono considerate le proprietà ondulatorie, lavorando sulla fase di una (per ora non meglio specificata) funzione. Si sono ricavate o ipotizzate relazioni per: - lunghezza d onda
Collisioni cosmiche. Civico Planetario di Milano Ulrico Hoepli 12 febbraio 2013
 Collisioni cosmiche Civico Planetario di Milano Ulrico Hoepli 12 febbraio 2013 Sommario L incontro ravvicinato con 2012 DA14 Gli asteroidi: che cosa sono, dove sono Orbite e determinazione orbitale Incontri
Collisioni cosmiche Civico Planetario di Milano Ulrico Hoepli 12 febbraio 2013 Sommario L incontro ravvicinato con 2012 DA14 Gli asteroidi: che cosa sono, dove sono Orbite e determinazione orbitale Incontri
Integrazione delle equazioni del moto
 Giorgio Pastore - note per il corso di Laboratorio di Calcolo Integrazione delle equazioni del moto In generale, le equazioni del moto della meccanica newtoniana si presentano nella forma di sistemi di
Giorgio Pastore - note per il corso di Laboratorio di Calcolo Integrazione delle equazioni del moto In generale, le equazioni del moto della meccanica newtoniana si presentano nella forma di sistemi di
EQUAZIONE LOGISTICA: MODELLO POLINOMIALE PER LA CRESCITA DEMOGRAFICA
 EQUAZIONE LOGISTICA: MODELLO POLINOMIALE PER LA CRESCITA DEMOGRAFICA L equazione logistica, anche nota come modello di Verhulst o curva di crescita logistica è un modello di crescita della popolazione,
EQUAZIONE LOGISTICA: MODELLO POLINOMIALE PER LA CRESCITA DEMOGRAFICA L equazione logistica, anche nota come modello di Verhulst o curva di crescita logistica è un modello di crescita della popolazione,
1 di 5 12/02/ :23
 Verifica: tibo5794_me08_test1 nome: classe: data: Esercizio 1. La traiettoria di un proiettile lanciato con velocità orizzontale da una certa altezza è: un segmento di retta obliqua percorso con accelerazione
Verifica: tibo5794_me08_test1 nome: classe: data: Esercizio 1. La traiettoria di un proiettile lanciato con velocità orizzontale da una certa altezza è: un segmento di retta obliqua percorso con accelerazione
LA GRAVITAZIONE. Legge di Gravitazione Universale 08/04/2015 =6, /
 LA GRAVITAZIONE Definizione (forza di attrazione gravitazionale) Due corpi puntiformi di massa e si attraggono vicendevolmente con una forza (forza che il corpo A esercita sul corpo B), o (forza che il
LA GRAVITAZIONE Definizione (forza di attrazione gravitazionale) Due corpi puntiformi di massa e si attraggono vicendevolmente con una forza (forza che il corpo A esercita sul corpo B), o (forza che il
il modello logistico
 LOTTA PER LA SOPRAVVIVENZA ovvero il modello logistico Circa 50 anni dopo l introduzione del modello di Malthus, il demografo belga Adolphe J. Quetelet (1796,1874) nella sua opera Sull uomo e sullo sviluppo
LOTTA PER LA SOPRAVVIVENZA ovvero il modello logistico Circa 50 anni dopo l introduzione del modello di Malthus, il demografo belga Adolphe J. Quetelet (1796,1874) nella sua opera Sull uomo e sullo sviluppo
