in cui le sommatorie sono fatte sugli elettroni dell atomo. Le componenti z di L e S sono date dalle somme scalari N
|
|
|
- Giustino Di Stefano
- 6 anni fa
- Visualizzazioni
Transcript
1 Termini atomici (o termini spettroscopici) e loro determinazione a partire dalla configurazione elettronica Le configurazioni elettroniche degli atomi sono ambigue nel senso che esiste un certo numero di insiemi di m l e m s in accordo con una data configurazione elettronica. Come esempio, si consideri la configurazione elettronica dello stato fondamentale di un atomo di carbonio, ls 2 2s 2 2p 2. I due elettroni 2p potrebbero trovarsi in uno qualsiasi dei tre orbitali 2p (2p x, 2p y, 2p z ) ed avere un qualsiasi spin che sia in accordo col principio di esclusione di Pauli. Le energie di questi diversi stati possono essere differenti, perciò richiedono una classificazione più dettagliata degli stati elettronici degli atomi. Lo schema che qui viene presentato è basato sull'idea di determinare il momento angolare orbitale totale L e il momento angolare totale di spin S, poi sommare vettorialmente L e S tra loro al fine di ottenere il momento angolare totale J. Il risultato di questo schema di calcolo, chiamato accoppiamento di Russell-Saunders, viene presentato come un simbolo di termine atomico o termine spettroscopico, il quale possiede la forma 2 S+ In un simbolo di termine L è il numero quantico del momento angolare orbitale totale, S è il numero quantico di spin totale e J è il numero quantico del momento angolare totale. In seguito vedremo che L assume necessariamente i valori 0,, 2, 3,.. Così come abbiamo assegnato le lettere s, p, d, f ai valori = 0,, 2, 3, del momento angolare orbitale per l'atomo di idrogeno, creiamo la corrispondenza L = S P D F G H... Osserveremo inoltre che il numero quantico di spin totale S deve assumere necessariamente i valori 0, ½,, 3/2, 2,.. e così l'indice 2S + che si trova in alto a sinistra nel simbolo di termine assume i valori, 2, 3, 4,... La grandezza 2S + viene chiamata molteplicità di spin. Quindi, ignorando per il momento l 'indice J, i simboli di termine sono del tipo 3 S 2 L D Il momento angolare orbitale totale e il momento angolare totale di spin, per un atomo a elettroni, sono dati rispettivamente dalle somme vettoriali J P L = l i e = S si () in cui le sommatorie sono fatte sugli elettroni dell atomo. Le componenti z di L e S sono date dalle somme scalari l zi = li e S z = szi = L z = m Così, nonostante il momento angolare si sommi vettorialmente come nelle equazioni (), le componenti z si sommano come scalari ( equazioni (2) ). Proprio come la componente z di l può m si (2)
2 assumere i 2l+ valori m l = l, l-,...,0,..., -l, la componente z di L può assumersi 2L+ valori M L = L, L-,...,0,..., -L. Similmente, a M S si possono attribuire i 2S + valori S, S -,..., -S +, -S. Quindi, la molteplicità di spin è semplicemente data dalle 2S + proiezioni che la componente z di S può assumere. Consideriamo la configurazione elettronica ns 2 (due elettroni in un orbitale ns). Esiste un solo insieme di valori di ml, m s, ml2 e m s2 : m l m s m l2 m s2 M L M S 0 ½ 0 -½ 0 0 Il fatto che l'unico valore di M L sia nullo implica che L = 0. Allo stesso modo, il fatto che il solo valore di M S sia nullo implica che S = 0. Il momento angolare totale J è dato da J = L + S (3) mentre la sua componente z é J z = Lz + S z = ( M L + M S ) = M J = 0 (4) e ciò implica che J = 0. Di conseguenza, per una configurazione elettronica ns 2, L = 0, S = 0, J = 0. Il valore L = 0 viene indicato come S nel simbolo del termine, perciò troviamo che il simbolo del termine corrispondente ad una configurazione elettronica ns 2 é S 0 (singoletto S zero). Dal momento che i due elettroni hanno spin opposti, il momento angolare totale di spin è nullo. Inoltre, entrambi gli elettroni occupano un orbitale che non possiede momento angolare, perciò il momento angolare totale deve essere nullo, che è ciò che il termine S 0 indica. Anche una configurazione elettronica np 6 possiederà uni simbolo di termine S 0. Per comprendere ciò, bisogna rendersi conto che i sei elettroni che si trovano nei tre orbitali np possiedono i numeri quantici (n,,, ±½), (n,, 0, ±½) e (n,, -, ±½). Quindi, nel sommare tutti gli mli, e gli m si, otteniamo M L = 0 e M S = 0, dando quindi un termine S 0. otare che M L e M S sono necessariamente uguali a zero per sottostrati elettronici completamente pieni, perché per ciascun elettrone avente un valore negativo di m li, vi è un altro elettrone con un valore corrispondente positivo che lo cancella; lo stesso vale per i valori di m si. Così, possiamo ignorare gli elettroni che si trovano in sottostrati elettronici completamente pieni quando consideriamo un'altra configurazione elettronica. Per esempio, quando in seguito discuteremo l'atomo di carbonio, potremo ignorare il contributo degli orbitali ls 2 2s 2 alla configurazione elettronica ls 2 2s 2 2p 2 di tale atomo. Una configurazione elettronica che possiede un simbolo di termine diverso da l S 0 è ns n s, in cui n n'. Un esempio è l'atomo di elio con la configurazione elettronica dello stato eccitato ls 2s. Per determinare i valori possibili di ml, m s, ml2 e m s2, costruiamo una tabella nella maniera seguente. Siccome ml, e ml2 possono avere entrambi il valore massimo 0, il valore massimo di M L è 0 (si 2
3 veda l'equazione 2), perciò 0 è il suo unico valore possibile. Analogamente, siccome m s e m s2 possono entrambi avere i valori +½ e -½, M S può essere -, 0, o. Ora costruiamo una tabella riportando nelle colonne i valori possibili di M S e nelle righe i valori possibili di M L, poi la riempiamola con gli insiemi di valori di ml, m s, ml2 e m s2, in accordo con ciascun valore di M L e M S come viene di seguito mostrato: M S M L La notazione 0 + significa che ml = 0 e m s = +/2, mentre 0 - significa che ml = 0 e m s = -/2. Gli insiemi possibili di valori di ml, m s, ml2 e m s2 corrispondenti a ciascun valore di M L e M S vengono chiamati microstati. In questa tabella vi sono quattro microstati perché esistono due possibili spin (+½ e -½) per l'elettrone nell'orbitale ns e due possibili spin (+½ e -½) per l'elettrone nell'orbitale n's. Bisogna osservare che abbiamo incluso sia sia perché gli elettroni si trovano in orbitali non equivalenti (cioè, s e 2s). Si noti che tutti i valori di M L della precedente tabella sono nulli, perciò essi devono corrispondere tutti a L = 0. Per di più, il massimo valore di M S è. Di conseguenza, S deve essere uguale ad ed i valori M S =, 0 e - corrispondono a L = 0, S =, equivalenti ad un termine 3 S. Questo termine 3 S tiene conto di un microstato per ciascuna colonna della tabella precedente. La colonna di mezzo contiene due microstati e non fa differenza quale dei due scegliamo. Dopo aver eliminato un microstato da ciascuna colonna ( ; ; e oppure ), rimaniamo soltanto con l'elemento avente M L = 0, M S = 0 (o oppure ), il che implica L = 0 e S = 0, corrispondenti ad un termine l S. Queste due coppie di valori L = 0, S = e L = 0, S = 0 assieme ai loro possibili valori di M J si possono riassumere nella seguente maniera L = 0, S = L = 0, S = 0 M L = 0, M S =, 0, - M L = 0, M S = 0 M J = M L + M S = l, 0, - M J = M L + M S = 0 Qui i valori di M J richiedono che J = nel caso L = 0, S = e che J = 0 nel caso L = 0, S = 0. I due simboli di termine corrispondenti alla configurazione elettronica ns l n's sono quindi 3 S e S 0 Il simbolo di temine 3 S viene chiamato tripletto S uno e il simbolo S 0 viene chiamato singoletto S zero. Questi due simboli di termine corrispondono a due stati elettronici diversi aventi energie diverse. Lo stato di tripletto ( 3 S ) possiede un'energia inferiore rispetto allo stato di singoletto ( S 0 ). Come esempio finale sulla deduzione dei simboli di termine atomici, consideriamo l'atomo di carbonio, la cui configurazione elettronica dello stato fondamentale è s 2 2s 2 2p 2. In precedenza abbiamo mostrato che non abbiamo bisogno di considerare i sottostrati elettronici completamente pieni perché in questo caso M L e M S sono per forza nulli. Di conseguenza, possiamo focalizzare l'attenzione sulla configurazione elettronica np 2. Come nel caso di ns l n's l considerato in 3
4 precedenza, costruiremo una tabella con i valori possibili di ml, m s, ml2 e m s2 Comunque, prima di fare ciò, vediamo quanti elementi vi sono nella tabella per np 2. Stiamo per assegnare due elettroni a due dei sei possibili spin-orbitali (o orbitali di spin) 2p x, 2p x, 2p y, 2p y, 2p z, 2p z. Esistono 6 scelte per il primo spin-orbitale e 5 scelte per il secondo, fornendo un totale di 6 x 5 = 30 scelte. Comunque, dato che gli elettroni sono indistinguibili, l'ordine dei due spin-orbitali scelti è irrilevante. Quindi, dobbiamo dividere le 30 scelte per un fattore 2 ottenendo 5 modi distinti di assegnare i due elettroni ai sei spin-orbitali. In generale, il numero dei modi distinti di assegnare elettroni a G spin-orbitali appartenenti allo stesso strato elettronico ( orbitali equivalenti, ad esempio tutti 2p) è dato da G! (per orbitali equivalenti) (5)!( G )! Si noti che l'equazione (5) fornisce il valore 5 ponendo G = 6 e = 2. Per trovare i 5 insiemi possibili di ml, m s, ml2 e m s2 nel caso di una configurazione elettronica np 2, per prima cosa determiniamo i valori possibili di M L e M S. Dal momento che ml e, ml2 possono entrambi raggiungere il valore massimo di, M L è al massimo 2 (vedere l'equazione 2), quindi i suoi valori possibili sono 2,, 0, - e -2. In maniera analoga, siccome m s e m s2 possono raggiungere il valore massimo di +/2, il massimo di M S è l (si veda l'equazione 2), perciò tutti i valori possibili di M S sono,0 e -. Sfruttando queste informazioni, costruiamo una tabella avente le colonne intestate con i valori possibili di M S e le righe intestate con i valori possibili di M L, poi riempiamola coi microstati che sono in accordo con ciascun valore di M L e M S, come mostrato nella seguente tabella: M L 0-2 +, + -, - -, - 0 +, + +,0 - ; -, , ,0 + ; +,- + +,- - ; - +, - ; 0 +,0 - -,- - ; 0 -, , ,- - ; 0 -, , , , ,- - Dove, ad esempio, la notazione +,- - vuol dire che ml =, m s = +½ e ml2 = -, m s2 = -½. Diversamente dall esempio precedente in cui abbiamo trattato orbitali non equivalenti, non includiamo entrambi +,0 - e 0 -, + nella posizione M S = 0, M L = perché in questo caso gli orbitali sono equivalenti (due orbitali 2p). Di conseguenza i due microstati +,0 - e 0 -, + sono indistinguibili. I sei microstati della tabella precedente eliminati con una croce violano il principio di esclusione di Pauli. I 5 microstati rimanenti costituiscono tutti i possibili microstati di una configurazione elettronica np 2. M S 4
5 Ora dobbiamo dedurre i valori possibili di L e di S da quelli tabulati di M L e M S. Il valore più grande di M L è 2, che compare soltanto quando M S = 0. Quindi, deve esistere uno stato con L = 2 e S = 0 ( l D). Dal momento che L = 2, si ha M L = 2,, 0, - e -2, perciò lo stato l D terrà conto di un microstato per ciascuna riga nella colonna di mezzo della tabella precedente. Per quelle righe che contengono più di un microstato (la seconda, la terza e la quarta), non importa quale microstato viene scelto. Possiamo scegliere arbitrariamente i microstati +,0 - ; +,- - ; e 0 +,- -. Eliminando questi microstati dalla tabella rimaniamo con la seguente: M L , + -, , - 0 +, , - ; 0 +,0 - -, , , , M S Il valore rimanente di M L più grande è M L =, che implica L =. Vi sono microstati con M L =, 0, - associati a M S = (0 +, + ; +,- + ; 0 +,- + ), con M S =0 ( -,0 + ; o - +, - o 0 +,0 - ; 0 -,- + ) e con M S = - (0 -, - ; -,- - ; 0 -,- - ). Quindi, questi nove microstati corrispondono a L = e a S =, ovvero ad un termine 3 P (tripletto P). Se eliminiamo questi nove microstati dalla tabella, allora rimaniamo soltanto con un microstato avente M L = 0 e M S = 0 al centro della tabella, il quale implica L = 0 e S = 0 ( S). Finora abbiamo trovato i simboli di termine D, 3 P e S, che sono determinati solo parzialmente. Per completare la loro specificazione dobbiamo calcolare, in ciascun caso, i valori possibili di J. Ricordiamoci che M J = M L + M S. Per i cinque elementi corrispondenti allo stato D, vale Ms = 0, quindi i valori di M J sono 2,, 0, - e -2, il che implica J = 2. Così il simbolo di termine completo dello stato D è D 2. otare che la degenerazione di questo stato è 5, cioè 2J +. I valori di M J per i nove elementi dello stato 3 P sono 2,,, 0, 0, -, 0, - e -2. Abbiamo ovviamente l'insieme di valori 2,, 0, -, -2 corrispondenti a J = 2. Eliminando questi cinque valori, rimaniamo con, 0, 0, -, che corrispondono a J = e J = 0. Perciò, lo stato 3 P possiede tre valori possibili di J, cosicché i simboli di termine sono 3 P 2, 3 P e 3 P 0. Lo stato S deve essere S 0. Riassumendo, quindi, gli stati elettronici associati ad una configurazione np 2 sono D 2, 3 P 0, 3 P, 3 P 2, e S 0 Le degenerazioni di tali stati sono rispettivamente 2J + = 5,, 3, 5 e. 5
6 I valori di J dei simboli di termine atomico possono essere determinati in relazione ai valori di L e di S se ricordiamo che J = L + S Il massimo valore che J può raggiungere è nel caso in cui L e S puntano entrambi nella medesima direzione, cioè J = L + S. Il minimo valore di J si ha quando L e S puntano in direzioni opposte, cioè J = L S. I valori di J che si trovano fra L + S e L S si ottengono da J = L+S, L+S, L+S 2,..., L - S (6) L'equazione 6 è dotata della seguente rappresentazione grafica. I vettori L e S vengono sommati fra loro in tutti i modi tali che la loro somma sia un vettore di lunghezza 0,, 2,.. se S è intero, oppure /2, 3/2, 5/2,... se S è /2, 3/2, 5/2, e così via. Per esempio, se L = 2 e S =, allora L e S possono essere sommati vettorialmente come segue. otare che il valore massimo di J corrisponde a L e S orientati nella stessa direzione e che il valore minino di J corrisponde a L e S orientati in direzioni opposte. Applicando l'equazione (6) al precedente simbolo di termine 3 P, si vede che i valori di J sono dati da J = ( + ), ( +), e così si ha J = 2,, 0, come ricavato in precedenza. Esiste un utile test per verificare la compatibilità tra l'equazione (5) e i simboli di termine associati ad una data configurazione elettronica. Un simbolo di termine 2S+ L avrà 2S + elementi per ciascun valore di M L nella tabella dei valori possibili di m li e m si (vedi la tabella di elementi per np 2 ). Dal momento che vi sono 2L + valori di M L per un dato valore di L, il numero totale di elementi per ciascun simbolo di termine (escludendo l'indice J) è (2S + )(2L + ). L'applicazione di questo risultato al caso np 2 dà S 3 P D ( ) + ( 3 3 ) + ( 5 ) = 5 6
Numeri quantici. Numero quantico principale n: determina l'energia dell'elettrone e può assumere qualsiasi valore intero positivo.
 Numeri quantici Numero quantico principale n: determina l'energia dell'elettrone e può assumere qualsiasi valore intero positivo. n= 1, 2, 3,. Numero quantico del momento angolare : Determina la forma
Numeri quantici Numero quantico principale n: determina l'energia dell'elettrone e può assumere qualsiasi valore intero positivo. n= 1, 2, 3,. Numero quantico del momento angolare : Determina la forma
CONFIGURAZIONE ELETTRONICA. In generale la configurazione elettronica indica come sono posizionati gli elettroni intorno al nucleo di un atomo.
 CONFIGURAZIONE ELETTRONICA In generale la configurazione elettronica indica come sono posizionati gli elettroni intorno al nucleo di un atomo. ORBITA : Zona intorno al nucleo di diversa energia dove ruotano
CONFIGURAZIONE ELETTRONICA In generale la configurazione elettronica indica come sono posizionati gli elettroni intorno al nucleo di un atomo. ORBITA : Zona intorno al nucleo di diversa energia dove ruotano
numeri quantici orbitale spin
 La funzione d onda ψ definisce i diversi stati in cui può trovarsi l elettrone nell atomo. Nella sua espressione matematica, essa contiene tre numeri interi, chiamati numeri quantici, indicati con le lettere
La funzione d onda ψ definisce i diversi stati in cui può trovarsi l elettrone nell atomo. Nella sua espressione matematica, essa contiene tre numeri interi, chiamati numeri quantici, indicati con le lettere
Dalle configurazioni ai termini
 Dalle configurazioni ai termini Introduzione Nello sviluppare i metodi di Thomas - Fermi, di Hartree e di Hartree - Fock, abbiamo sempre rappresentato gli autostati di un sistema costituito da due o più
Dalle configurazioni ai termini Introduzione Nello sviluppare i metodi di Thomas - Fermi, di Hartree e di Hartree - Fock, abbiamo sempre rappresentato gli autostati di un sistema costituito da due o più
I NUMERI QUANTICI. per l = orbitale: s p d f
 I NUMERI QUANTICI I numeri quantici sono quattro. I primi tre servono a indicare e a distinguere i diversi orbitali. Il quarto numero descrive una proprietà tipica dell elettrone. Esaminiamo in dettaglio
I NUMERI QUANTICI I numeri quantici sono quattro. I primi tre servono a indicare e a distinguere i diversi orbitali. Il quarto numero descrive una proprietà tipica dell elettrone. Esaminiamo in dettaglio
Particelle Subatomiche
 GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI I numeri quantici Le funzioni d onda Ψ n, soluzioni dell equazione d onda, sono caratterizzate da certe combinazioni di numeri quantici: n, l, m l, m s n = numero quantico principale,
GLI ORBITALI ATOMICI I numeri quantici Le funzioni d onda Ψ n, soluzioni dell equazione d onda, sono caratterizzate da certe combinazioni di numeri quantici: n, l, m l, m s n = numero quantico principale,
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Struttura del sistema periodico Stato fondamentale degli elementi
 Struttura del sistema periodico Stato fondamentale degli elementi Singolo elettrone: 1)Numero quantico principale n 2)Numero quantico del momento angolare orbitale l = 0, 1,, n-1 3)Numero quantico magnetico
Struttura del sistema periodico Stato fondamentale degli elementi Singolo elettrone: 1)Numero quantico principale n 2)Numero quantico del momento angolare orbitale l = 0, 1,, n-1 3)Numero quantico magnetico
CHIMICA: studio della struttura e delle trasformazioni della materia
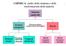 CHIMICA: studio della struttura e delle trasformazioni della materia 1 Materia (materali) Sostanze (omogenee) Processo fisico Miscele Elementi (atomi) Reazioni chimiche Composti (molecole) Miscele omogenee
CHIMICA: studio della struttura e delle trasformazioni della materia 1 Materia (materali) Sostanze (omogenee) Processo fisico Miscele Elementi (atomi) Reazioni chimiche Composti (molecole) Miscele omogenee
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
E. SCHRODINGER ( )
 E. SCHRODINGER (1887-1961) Elettrone = onda le cui caratteristiche possono essere descritte con un equazione simile a quella delle onde stazionarie le cui soluzioni, dette funzioni d onda ψ, rappresentano
E. SCHRODINGER (1887-1961) Elettrone = onda le cui caratteristiche possono essere descritte con un equazione simile a quella delle onde stazionarie le cui soluzioni, dette funzioni d onda ψ, rappresentano
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
1) Hamming bound, coset, codici equivalenti
 Argomenti della Lezione ) Hamming bound, coset, codici equivalenti 2) Esercizi sui codici lineari a blocchi Osservazione () Per effettuare la decodifica a rivelazione di errore si può seguire una delle
Argomenti della Lezione ) Hamming bound, coset, codici equivalenti 2) Esercizi sui codici lineari a blocchi Osservazione () Per effettuare la decodifica a rivelazione di errore si può seguire una delle
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
LA STRUTTURA DELLE MOLECOLE. Orbitali molecolari e legame chimico
 LA STRUTTURA DELLE MOLECOLE Orbitali molecolari e legame chimico GLI ORBITALI MOLECOLARI Quando degli atomi collidono tra di loro i loro nuclei ed elettroni vengono a trovarsi in prossimità influenzandosi
LA STRUTTURA DELLE MOLECOLE Orbitali molecolari e legame chimico GLI ORBITALI MOLECOLARI Quando degli atomi collidono tra di loro i loro nuclei ed elettroni vengono a trovarsi in prossimità influenzandosi
Elementi sulle diseguaglianze tra numeri relativi
 Elementi sulle diseguaglianze tra numeri relativi Dati due numeri disuguali a e b risulta a>b oppure ao oppure a-b
Elementi sulle diseguaglianze tra numeri relativi Dati due numeri disuguali a e b risulta a>b oppure ao oppure a-b
MATEMATICA PRIMO COMPITINO SOLUZIONE DI ALCUNI ESERCIZI PRIMA PARTE. Esercizio 1. (Testo B) Determina, motivando la risposta, se la funzione f : R R
 ANNO ACCADEMICO 25 6 SCIENZE GEOLOGICHE E SCIENZE NATURALI E AMBIENTALI MATEMATICA PRIMO COMPITINO SOLUZIONE DI ALCUNI ESERCIZI PROFF MARCO ABATE E MARGHERITA LELLI-CHIESA PRIMA PARTE Esercizio (Testo
ANNO ACCADEMICO 25 6 SCIENZE GEOLOGICHE E SCIENZE NATURALI E AMBIENTALI MATEMATICA PRIMO COMPITINO SOLUZIONE DI ALCUNI ESERCIZI PROFF MARCO ABATE E MARGHERITA LELLI-CHIESA PRIMA PARTE Esercizio (Testo
I 4 NUMERI QUANTICI. I numeri quantici consentono di definire forma, dimensioni ed energia degli orbitali.
 I 4 NUMERI QUANTICI I numeri quantici consentono di definire forma, dimensioni ed energia degli orbitali. n, numero quantico principale, indica il livello energetico e le dimensioni degli orbitali. Può
I 4 NUMERI QUANTICI I numeri quantici consentono di definire forma, dimensioni ed energia degli orbitali. n, numero quantico principale, indica il livello energetico e le dimensioni degli orbitali. Può
CONFIGURAZIONE ELETTRONICA DEGLI ELEMENTI
 CONFIGURAZIONE ELETTRONICA DEGLI ELEMENTI SOSTANZE: ELEMENTI E COMPOSTI Si definisce sostanza la materia che ha sempre la stessa composizione. Ogni campione di una sostanza ha le stesse propietà chimiche
CONFIGURAZIONE ELETTRONICA DEGLI ELEMENTI SOSTANZE: ELEMENTI E COMPOSTI Si definisce sostanza la materia che ha sempre la stessa composizione. Ogni campione di una sostanza ha le stesse propietà chimiche
2 2 2 A = Il Det(A) = 2 quindi la conica è non degenere, di rango 3.
 Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
GEOMETRIA PIANA. 1) sia verificata l uguaglianza di segmenti AC = CB (ossia C è punto medio del segmento AB);
 VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
ATOMI MONOELETTRONICI
 ATOMI MONOELETTRONICI L equazione di Schrödinger per gli atomi contenenti un solo elettrone (atomo di idrogeno, ioni He +, Li 2+ ) può essere risolta in maniera esatta e le soluzioni ottenute permettono
ATOMI MONOELETTRONICI L equazione di Schrödinger per gli atomi contenenti un solo elettrone (atomo di idrogeno, ioni He +, Li 2+ ) può essere risolta in maniera esatta e le soluzioni ottenute permettono
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
Dipendenza e indipendenza lineare (senza il concetto di rango)
 CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
COMPETENZE ABILITÀ CONOSCENZE. descrivere la. Comprendere ed applicare analogie relative ai concetti presi in analisi. struttura.
 ca descrivere la struttura dell atomo, la tavola periodica e le sue caratteristiche per spiegare le differenze tra i vari tipi di legami, descrivendoli e interpretandoli alla luce degli elettroni di valenza
ca descrivere la struttura dell atomo, la tavola periodica e le sue caratteristiche per spiegare le differenze tra i vari tipi di legami, descrivendoli e interpretandoli alla luce degli elettroni di valenza
Esercizi svolti. delle matrici
 Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
Gli orbitali atomici. Il modo più semplice di visualizzare un atomo. TUTTAVIA NON POSSO DIRE CON PRECISIONE DOVE SI TROVA OGNI e -
 Gli orbitali atomici Il modo più semplice di visualizzare un atomo TUTTAVIA NON POSSO DIRE CON PRECISIONE DOVE SI TROVA OGNI e - ORBITALI ATOMICI: regione di spazio (con forma tipica) dove c è una elevata
Gli orbitali atomici Il modo più semplice di visualizzare un atomo TUTTAVIA NON POSSO DIRE CON PRECISIONE DOVE SI TROVA OGNI e - ORBITALI ATOMICI: regione di spazio (con forma tipica) dove c è una elevata
Geometria e Topologia I (U1-4) 2006-mag-10 61
 Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
ATOMO POLIELETTRONICO. Numero quantico di spin m s
 ATOMO POLIELETTRONICO La teoria fisico-matematica che ha risolto esattamente il problema dell atomo di idrogeno non è in grado di descrivere con uguale precisione l atomo polielettronico. Problema: interazioni
ATOMO POLIELETTRONICO La teoria fisico-matematica che ha risolto esattamente il problema dell atomo di idrogeno non è in grado di descrivere con uguale precisione l atomo polielettronico. Problema: interazioni
Operazioni tra matrici e n-uple
 CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
Funzione d onda dello stato fondamentale (trascurando l interazione elettrone-elettrone)
 -e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
-e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
La teoria atomica moderna: il modello planetario L ELETTRONE SI MUOVE LUNGO UN ORBITA INTORNO AL NUCLEO
 La teoria atomica moderna: il modello planetario L ELETTRONE SI MUOVE LUNGO UN ORBITA INTORNO AL NUCLEO La luce La LUCE è una forma di energia detta radiazione elettromagnetica che si propaga nello spazio
La teoria atomica moderna: il modello planetario L ELETTRONE SI MUOVE LUNGO UN ORBITA INTORNO AL NUCLEO La luce La LUCE è una forma di energia detta radiazione elettromagnetica che si propaga nello spazio
Esercizi per Geometria II Geometria euclidea e proiettiva
 Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ALGEBRA 1 Secondo esonero 15 Giugno 2011 soluzioni
 ALGEBRA 1 Secondo esonero 15 Giugno 2011 soluzioni (1) Verificare che l anello quoziente Z 5 [x]/(x 3 2) possiede divisori dello zero, e determinare tutti i suoi ideali non banali. Soluzione: Il polinomio
ALGEBRA 1 Secondo esonero 15 Giugno 2011 soluzioni (1) Verificare che l anello quoziente Z 5 [x]/(x 3 2) possiede divisori dello zero, e determinare tutti i suoi ideali non banali. Soluzione: Il polinomio
Le disequazioni frazionarie (o fratte)
 Le disequazioni frazionarie (o fratte) Una disequazione si dice frazionaria (o fratta) se l'incognita compare al denominatore. Esempi di disequazioni fratte sono: 0 ; ; < 0 ; ; Come per le equazioni fratte,
Le disequazioni frazionarie (o fratte) Una disequazione si dice frazionaria (o fratta) se l'incognita compare al denominatore. Esempi di disequazioni fratte sono: 0 ; ; < 0 ; ; Come per le equazioni fratte,
Equazioni di 2 grado
 Equazioni di grado Tipi di equazioni: Un equazione (ad una incognita) è di grado se può essere scritta nella forma generale (o forma tipica o ancora forma canonica): a b c con a, b e c numeri reali (però
Equazioni di grado Tipi di equazioni: Un equazione (ad una incognita) è di grado se può essere scritta nella forma generale (o forma tipica o ancora forma canonica): a b c con a, b e c numeri reali (però
Configurazione elettronica e collegamento alla tavola periodica
 Configurazione elettronica e collegamento alla tavola periodica Modelli atomici a confronto Un elettrone che si trova in un certo livello possiede l energia associata a quel livello, in particolare al
Configurazione elettronica e collegamento alla tavola periodica Modelli atomici a confronto Un elettrone che si trova in un certo livello possiede l energia associata a quel livello, in particolare al
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Decomposizione LU di una matrice quadrata
 Appendice al Cap. 5 Decomposizione LU di una matrice quadrata Una qualunque matrice quadrata M = {m ij } di ordine N, reale, invertibile, i cui minori principali siano tutti non nulli, si può sempre decomporre
Appendice al Cap. 5 Decomposizione LU di una matrice quadrata Una qualunque matrice quadrata M = {m ij } di ordine N, reale, invertibile, i cui minori principali siano tutti non nulli, si può sempre decomporre
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Rette e piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
Precorso di Matematica
 UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
Gara Matematica. Dipartimento di Matematica Ulisse Dini. Viale Morgagni 67/a Firenze. Soluzioni edizione 2011
 Gara Matematica Dipartimento di Matematica Ulisse Dini Viale Morgagni 67/a - 50134 Firenze Soluzioni edizione 011 Esercizio 1. Determinare tutti gli interi positivi non nulli n che sono uguali alla somma
Gara Matematica Dipartimento di Matematica Ulisse Dini Viale Morgagni 67/a - 50134 Firenze Soluzioni edizione 011 Esercizio 1. Determinare tutti gli interi positivi non nulli n che sono uguali alla somma
I LEGAMI CHIMICI. Configurazione elettronica stabile: è quella in cui tutti i livelli energetici dell atomo sono pieni di elettroni
 I LEGAMI CIMICI In natura sono pochi gli elementi che presentano atomi allo stato libero. Gli unici elementi che sono costituiti da atomi isolati si chiamano gas nobili o inerti, formano il gruppo VIII
I LEGAMI CIMICI In natura sono pochi gli elementi che presentano atomi allo stato libero. Gli unici elementi che sono costituiti da atomi isolati si chiamano gas nobili o inerti, formano il gruppo VIII
Pagine di Algebra lineare. di premessa al testo Pagine di Geometria di Sara Dragotti. Parte terza: SISTEMI LINEARI
 Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Disequazioni di secondo grado
 Disequazioni di secondo grado. Disequazioni Definizione: una disequazione è una relazione di disuguaglianza tra due espressioni. Detti p() e g() due polinomi definiti in un insieme A, una disequazione
Disequazioni di secondo grado. Disequazioni Definizione: una disequazione è una relazione di disuguaglianza tra due espressioni. Detti p() e g() due polinomi definiti in un insieme A, una disequazione
La struttura elettronica degli atomi
 1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
= (cioè le due terne di numeri direttori ( devono essere ) proporzionali). Tale uguaglianza non è verificata, poiché risulta ρ
 Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
Lez. 3 Vettori e scalari
 Lez. 3 Vettori e scalari Prof. 1 Dott., PhD Dipartimento Scienze Fisiche Università di Napoli Federico II Compl. Univ. Monte S.Angelo Via Cintia, I-80126, Napoli mettivier@na.infn.it +39-081-676137 2 Un
Lez. 3 Vettori e scalari Prof. 1 Dott., PhD Dipartimento Scienze Fisiche Università di Napoli Federico II Compl. Univ. Monte S.Angelo Via Cintia, I-80126, Napoli mettivier@na.infn.it +39-081-676137 2 Un
Trapani. Dispensa di Geometria, x 1 x 2.x n. (x 1 y 1 ) (x n y n ) 2.
 2006 Trapani Dispensa di Geometria, 1 Distanze Siano P e Q punti di R n con P di coordinate allora la distanza tra P e Q e P Q = x 1 x 2 x n (x 1 y 1 ) 2 + (x n y n ) 2 e Q di coordinate Siano Σ 1 e Σ
2006 Trapani Dispensa di Geometria, 1 Distanze Siano P e Q punti di R n con P di coordinate allora la distanza tra P e Q e P Q = x 1 x 2 x n (x 1 y 1 ) 2 + (x n y n ) 2 e Q di coordinate Siano Σ 1 e Σ
Introduzione al Metodo del Simplesso. 1 Soluzioni di base e problemi in forma standard
 Introduzione al Metodo del Simplesso Giacomo Zambelli 1 Soluzioni di base e problemi in forma standard Consideriamo il seguente problema di programmazione lineare (PL), relativo all esempio di produzione
Introduzione al Metodo del Simplesso Giacomo Zambelli 1 Soluzioni di base e problemi in forma standard Consideriamo il seguente problema di programmazione lineare (PL), relativo all esempio di produzione
dipendenti. Cosa possiamo dire sulla dimensione di V?
 Esercizi Esercizi. In uno spazio vettoriale V ci sono tre vettori v, v 2, v linearmente indipendenti. Cosa possiamo dire sulla dimensione di V? 2. In uno spazio vettoriale V ci sono tre vettori v, v 2,
Esercizi Esercizi. In uno spazio vettoriale V ci sono tre vettori v, v 2, v linearmente indipendenti. Cosa possiamo dire sulla dimensione di V? 2. In uno spazio vettoriale V ci sono tre vettori v, v 2,
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione dei numeri relativi
 Codice BCD Prima di passare alla rappresentazione dei numeri relativi in binario vediamo un tipo di codifica che ha una certa rilevanza in alcune applicazioni: il codice BCD (Binary Coded Decimal). È un
Codice BCD Prima di passare alla rappresentazione dei numeri relativi in binario vediamo un tipo di codifica che ha una certa rilevanza in alcune applicazioni: il codice BCD (Binary Coded Decimal). È un
Corso di Laurea in Fisica. Geometria. a.a Canale 3 Prof. P. Piazza Magiche notazioni
 Corso di Laurea in Fisica. Geometria. a.a. 23-4. Canale 3 Prof. P. Piazza Magiche notazioni Siano V e W due spazi vettoriali e sia T : V W un applicazione lineare. Fissiamo una base B per V ed una base
Corso di Laurea in Fisica. Geometria. a.a. 23-4. Canale 3 Prof. P. Piazza Magiche notazioni Siano V e W due spazi vettoriali e sia T : V W un applicazione lineare. Fissiamo una base B per V ed una base
Equazioni di primo grado
 Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica,
 Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica, spin, ). Esempi: due elettroni, due protoni, due neutroni,
Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica, spin, ). Esempi: due elettroni, due protoni, due neutroni,
Struttura dell atomo atomo particelle sub-atomiche - protoni positiva - neutroni } nucleoni - elettroni negativa elemento
 Struttura dell atomo L atomo è la più piccola parte dell elemento che conserva le proprietà dell elemento Negli atomi ci sono tre diverse particelle sub-atomiche: - protoni (con carica positiva unitaria)
Struttura dell atomo L atomo è la più piccola parte dell elemento che conserva le proprietà dell elemento Negli atomi ci sono tre diverse particelle sub-atomiche: - protoni (con carica positiva unitaria)
Programma della I parte
 Programma della I parte Cenni alla meccanica quantistica: il modello dell atomo Dall atomo ai cristalli: statistica di Fermi-Dirac il modello a bande di energia popolazione delle bande livello di Fermi
Programma della I parte Cenni alla meccanica quantistica: il modello dell atomo Dall atomo ai cristalli: statistica di Fermi-Dirac il modello a bande di energia popolazione delle bande livello di Fermi
1 Equazioni parametriche e cartesiane di sottospazi affini di R n
 2 Trapani Dispensa di Geometria, Equazioni parametriche e cartesiane di sottospazi affini di R n Un sottospazio affine Σ di R n e il traslato di un sottospazio vettoriale. Cioe esiste un sottospazio vettoriale
2 Trapani Dispensa di Geometria, Equazioni parametriche e cartesiane di sottospazi affini di R n Un sottospazio affine Σ di R n e il traslato di un sottospazio vettoriale. Cioe esiste un sottospazio vettoriale
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Somma diretta di sottospazi vettoriali
 Capitolo 8 Somma diretta di sottospazi vettoriali 8.1 Introduzione Introduciamo un caso particolare di somma di due sottospazi vettoriali: la somma diretta. Anche questo argomento è stato visto nel corso
Capitolo 8 Somma diretta di sottospazi vettoriali 8.1 Introduzione Introduciamo un caso particolare di somma di due sottospazi vettoriali: la somma diretta. Anche questo argomento è stato visto nel corso
Piano cartesiano e Retta
 Piano cartesiano e Retta 1 Piano cartesiano e Retta 1. Richiami sul piano cartesiano 2. Richiami sulla distanza tra due punti 3. Richiami punto medio di un segmento 4. La Retta (funzione lineare) 5. L
Piano cartesiano e Retta 1 Piano cartesiano e Retta 1. Richiami sul piano cartesiano 2. Richiami sulla distanza tra due punti 3. Richiami punto medio di un segmento 4. La Retta (funzione lineare) 5. L
ˆ b, si usa la convenzione di prendere. come verso positivo quello antiorario e come verso negativo quello orario.
 Capitolo 4 Le rotazioni 4.1 Richiami di teoria E' opportuno ricordare che, dato un angolo orientato ao ˆ b, si usa la convenzione di prendere come verso positivo quello antiorario e come verso negativo
Capitolo 4 Le rotazioni 4.1 Richiami di teoria E' opportuno ricordare che, dato un angolo orientato ao ˆ b, si usa la convenzione di prendere come verso positivo quello antiorario e come verso negativo
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
Appunti di matematica per le Scienze Sociali Parte 1
 Appunti di matematica per le Scienze Sociali Parte 1 1 Equazioni 1.1 Definizioni preliminari 1.1.1 Monomi Si definisce monomio ogni prodotto indicato di fattori qualsiasi, cioè uguali o diseguali, numerici
Appunti di matematica per le Scienze Sociali Parte 1 1 Equazioni 1.1 Definizioni preliminari 1.1.1 Monomi Si definisce monomio ogni prodotto indicato di fattori qualsiasi, cioè uguali o diseguali, numerici
Geometria analitica del piano pag 12 Adolfo Scimone
 Geometria analitica del piano pag 12 Adolfo Scimone Fasci di rette Siano r e r' due rette distinte di equazioni r: ax + by + c r': a' x + b' y + c' Consideriamo la retta combinazione lineare delle due
Geometria analitica del piano pag 12 Adolfo Scimone Fasci di rette Siano r e r' due rette distinte di equazioni r: ax + by + c r': a' x + b' y + c' Consideriamo la retta combinazione lineare delle due
ALGEBRA I: SOLUZIONI QUINTA ESERCITAZIONE 9 maggio 2011
 ALGEBRA I: SOLUZIONI QUINTA ESERCITAZIONE 9 maggio 2011 Esercizio 1. Usando l algoritmo euclideo delle divisioni successive, calcolare massimo comune divisore e identità di Bézout per le seguenti coppie
ALGEBRA I: SOLUZIONI QUINTA ESERCITAZIONE 9 maggio 2011 Esercizio 1. Usando l algoritmo euclideo delle divisioni successive, calcolare massimo comune divisore e identità di Bézout per le seguenti coppie
= elemento che compare nella seconda riga e quinta colonna = -4 In generale una matrice A di m righe e n colonne si denota con
 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
1 Rette e piani in R 3
 POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
ax 1 + bx 2 + c = 0, r : 2x 1 3x 2 + 1 = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Chimica. Lezione 2 Il legame chimico Parte I
 Chimica Lezione 2 Il legame chimico Parte I GLI ATOMI TENDONO A LEGARSI SPONTANEAMENTE FRA DI LORO, PER FORMARE DELLE MOLECOLE, OGNI QUALVOLTA QUESTO PROCESSO PERMETTE LORO DI RAGGIUNGERE UNA CONDIZIONE
Chimica Lezione 2 Il legame chimico Parte I GLI ATOMI TENDONO A LEGARSI SPONTANEAMENTE FRA DI LORO, PER FORMARE DELLE MOLECOLE, OGNI QUALVOLTA QUESTO PROCESSO PERMETTE LORO DI RAGGIUNGERE UNA CONDIZIONE
Elementi di Algebra e di Matematica Discreta Numeri interi, divisibilità, numerazione in base n
 Elementi di Algebra e di Matematica Discreta Numeri interi, divisibilità, numerazione in base n Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra e di Matematica
Elementi di Algebra e di Matematica Discreta Numeri interi, divisibilità, numerazione in base n Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra e di Matematica
0.1 Condizione sufficiente di diagonalizzabilità
 0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
Complementi di Analisi per Informatica *** Capitolo 2. Numeri Complessi. e Circuiti Elettrici
 Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici Sergio Benenti Prima versione settembre 2013 Revisione settembre 2017? ndice 21 Circuito elettrico elementare
Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici Sergio Benenti Prima versione settembre 2013 Revisione settembre 2017? ndice 21 Circuito elettrico elementare
Studio del segno di un prodotto
 Studio del segno di un prodotto Consideriamo una disequazione costituita dal prodotto di più binomi, ad esempio: ( x 1 )( 4 x)( x + 3) > 0 Per risolverla possiamo studiare il segno del prodotto al variare
Studio del segno di un prodotto Consideriamo una disequazione costituita dal prodotto di più binomi, ad esempio: ( x 1 )( 4 x)( x + 3) > 0 Per risolverla possiamo studiare il segno del prodotto al variare
Esercizi svolti. Geometria analitica: rette e piani
 Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Alcuni esercizi sulla diagonalizzazione di matrici. campo dei reali. Se lo è calcolare una base spettrale e la relativa forma diagonale di A.
 Alcuni esercii sulla diagonaliaione di matrici Eserciio Dire se la matrice A 4 8 è diagonaliabile sul 3 3 campo dei reali Se lo è calcolare una base spettrale e la relativa forma diagonale di A Svolgimento
Alcuni esercii sulla diagonaliaione di matrici Eserciio Dire se la matrice A 4 8 è diagonaliabile sul 3 3 campo dei reali Se lo è calcolare una base spettrale e la relativa forma diagonale di A Svolgimento
L atomo. Il neutrone ha una massa 1839 volte superiore a quella dell elettrone. 3. Le particelle fondamentali dell atomo
 L atomo 3. Le particelle fondamentali dell atomo Gli atomi sono formati da tre particelle fondamentali: l elettrone con carica negativa; il protone con carica positiva; il neutrone privo di carica. Il
L atomo 3. Le particelle fondamentali dell atomo Gli atomi sono formati da tre particelle fondamentali: l elettrone con carica negativa; il protone con carica positiva; il neutrone privo di carica. Il
Risultati della teoria di Hartree
 Risultati della teoria di Hartree Il potenziale è a simmetria sferica, come nell atomo di idrogeno, quindi: ψ n, l, m = Rn, l ( r) Θ l, m ( θ ) Φ m ( ϕ ) l l l La dipendenza angolare delle autofunzioni
Risultati della teoria di Hartree Il potenziale è a simmetria sferica, come nell atomo di idrogeno, quindi: ψ n, l, m = Rn, l ( r) Θ l, m ( θ ) Φ m ( ϕ ) l l l La dipendenza angolare delle autofunzioni
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi
 La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
Matematica II,
 Matematica II 181111 1 Matrici a scala Data una riga R = [a 1 a 2 a n ] di numeri reali non tutti nulli il primo elemento non nullo di R si dice pivot di R Cosi il pivot di R compare come j mo elemento
Matematica II 181111 1 Matrici a scala Data una riga R = [a 1 a 2 a n ] di numeri reali non tutti nulli il primo elemento non nullo di R si dice pivot di R Cosi il pivot di R compare come j mo elemento
Graficazione qualitativa del luogo delle radici
 .. 1.1 1 Graficazione qualitativa del luogo delle radici Esempio. Si faccia riferimento al seguente sistema retroazionato: d(t) G(s) r(t) e(t) K 1(s 1) s(s+1)(s +8s+5) y(t) Per una graficazione qualitativa
.. 1.1 1 Graficazione qualitativa del luogo delle radici Esempio. Si faccia riferimento al seguente sistema retroazionato: d(t) G(s) r(t) e(t) K 1(s 1) s(s+1)(s +8s+5) y(t) Per una graficazione qualitativa
ALGEBRA VETTORIALE Corso di Fisica per la Facoltà di Farmacia, Università Gabriele D Annunzio, Chieti-Pescara, Cosimo Del Gratta 2008
 LGER VETTORILE DEFINIZIONE DI VETTORE (1) Sia E lo spazio tridimensionale della geometria euclidea. Consideriamo due punti e appartenenti a E Si chiama segmento orientato, e si indica con (,) il segmento
LGER VETTORILE DEFINIZIONE DI VETTORE (1) Sia E lo spazio tridimensionale della geometria euclidea. Consideriamo due punti e appartenenti a E Si chiama segmento orientato, e si indica con (,) il segmento
Soluzioni delle Esercitazioni VIII 21-25/11/2016. = lnx ln1 = lnx. f(t)dt.
 Esercitazioni di Matematica Esercitazioni VIII -5//6 Soluzioni delle Esercitazioni VIII -5//6 A. Funzione integrale. La funzione integrale di f nell intervallo [, ] è per definizione F() = dt con [,].
Esercitazioni di Matematica Esercitazioni VIII -5//6 Soluzioni delle Esercitazioni VIII -5//6 A. Funzione integrale. La funzione integrale di f nell intervallo [, ] è per definizione F() = dt con [,].
ESERCIZI DI ALGEBRA LINEARE E COMPLEMENTI DI GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E COMPLEMENTI DI GEOMETRIA Foglio Esempio. Determinare le soluzioni del sistema lineare Ax = B, in cui 4 A = 6 6, B = Sol. Consideriamo la matrice aumentata C = 4 6 6 6 5 e
ESERCIZI DI ALGEBRA LINEARE E COMPLEMENTI DI GEOMETRIA Foglio Esempio. Determinare le soluzioni del sistema lineare Ax = B, in cui 4 A = 6 6, B = Sol. Consideriamo la matrice aumentata C = 4 6 6 6 5 e
Note sulle Catene di Markov
 Note sulle Catene di Markov ELAUT Prof. Giuseppe C. Calafiore Sommario Queste note contengono un estratto schematico ridotto di parte del materiale relativo alle Catene di Markov a tempo continuo e a tempo
Note sulle Catene di Markov ELAUT Prof. Giuseppe C. Calafiore Sommario Queste note contengono un estratto schematico ridotto di parte del materiale relativo alle Catene di Markov a tempo continuo e a tempo
Punti di massimo o di minimo per funzioni di n variabili reali
 Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
4 0 = 4 2 = 4 4 = 4 6 = 0.
 Elementi di Algebra e Logica 2008. Esercizi 4. Gruppi, anelli e campi. 1. Determinare la tabella additiva e la tabella moltiplicativa di Z 6. (a) Verificare dalla tabella moltiplicativa di Z 6 che esistono
Elementi di Algebra e Logica 2008. Esercizi 4. Gruppi, anelli e campi. 1. Determinare la tabella additiva e la tabella moltiplicativa di Z 6. (a) Verificare dalla tabella moltiplicativa di Z 6 che esistono
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
