Rappresentazione delle informazioni
|
|
|
- Adriano Ventura
- 8 anni fa
- Visualizzazioni
Transcript
1 Rappresentazione delle informazioni Rappresentazione delle informazioni L informatica si occupa di rappresentare ed elaborare informazioni diverse: numeri caratteri audio immagini video I caratteri: ASCII standard Rappresentazione dei caratteri I simboli o caratteri appartenenti ad un alfabeto vengono codificati (cioè rappresentati ) mediante sequenze di bit: una diversa sequenza per ciascun diverso carattere. Uno dei codici più noti e usati è il codice ASCII (American Standard Code for Information Interchange), usa una sequenza di 7 bit per ciascun carattere: ci sono 128 (=2 7 ) sequenze diverse, utilizzate anche per lettere, segni di punteggiatura, cifre decimali, ecc. 1
2 I caratteri: ASCII esteso Dato che l unità elementare di informazione nei calcolatori è il byte (= 8 bit), si è passati ad usare, quasi sempre, il codice ASCII esteso, che usa una sequenza di 8 bit per ciascun carattere degli alfabeti occidentali: ci sono 256 (=2 8 ) sequenze diverse, utilizzate anche per vocali accentate e altre lettere speciali (es. ß tedesca, ç francese) le sequenze con la prima cifra uguale a zero coincidono con il codice ASCII. (Appendice G) I caratteri: ASCII esteso La codifica è: posizione n il primo carattere il secondo l ultimo La sequenza di simboli Ciao viene codificata in ASCII nel modo seguente: C i a o n Le lettere sono rappresentabili in 7 bit. I caratteri: ASCII esteso I primi 32 caratteri del codice ASCII (con codice da 0 a 31) sono caratteri di controllo: 9 tabulatore \t 10 nuova riga \n 13 invio \r I caratteri da 32 a 127 sono caratteri stampabili: 32 spazio da 48 a 57 caratteri numerici, le cifre decimali 0, 1 da 65 a 90, da 97 a 122 caratteri alfabetici (maiuscoli e minuscoli) da 33 a 47, da 58 a 64, da 91 a 96, da 123 a 127 caratteri di interpunzione e simboli speciali. I caratteri: Unicode Per rappresentare i segni grafici utilizzati da tutti gli alfabeti del mondo servono molti più simboli diversi codifica Unicode usa una sequenza di 16 bit per ciascun segno grafico: ci sono (= 2 16 ) sequenze diverse le sequenze con le prime otto cifre uguali a zero coincidono con il codice ASCII esteso. 2
3 I caratteri (codice Unicode) Rappresentazione delle informazioni Il linguaggio Java utilizza Unicode come insieme di simboli; in ogni linguaggio di programmazione i simboli servono per costruire le unità lessicali. Ogni informazione che vogliamo rappresentare è caratterizzata da un valore e da un suo tipo (tipo di dato). Non sempre possiamo o vogliamo rappresentare direttamente il valore, ma vogliamo poterci riferire ad esso tramite un nome. Astrazione Astrazione L evoluzione dei linguaggi di programmazione (basso ad alto livello) ha portato all introduzione del concetto di variabile: la locazione di memoria viene nascosta all utente, che vi accede tramite il nome della variabile. Le operazioni che si possono fare sulla variabile dipendono dal suo tipo: l utente non sa come avviene realmente la somma tra due numeri interi (reali) o il loro confronto. Si ha una astrazione sul dato e sul suo tipo. 3
4 Astrazione L evoluzione successiva dei linguaggi permetterà all utente di inventare dei nuovi tipi di dati, dei nuovi concetti. Tipo di Dato Astratto 1. è un insieme di elementi chiamato dominio 2. ha un nome 3. possiede delle funzioni che operano sul dominio 4. possono esserci costanti che lo caratterizzano. Variabile e Tipi base Variabile e Tipi base Nei corsi di matematica quando scriviamo x R e diciamo x è una variabile reale intendiamo dire che x è un nome che indica un elemento generico dell insieme R dei numeri reali. Nei corsi di informatica con x è una variabile reale intendiamo dire che x è un nome che indica una posizione di memoria che conterrà un elemento generico di R (con R R R). Variabile e Tipi base R insieme dei numeri reali (infinito e continuo). R insieme dei numeri reali rappresentabili nel calcolatore (finito e discreto). La posizione di memoria è caratterizzata dal tipo, che è l insieme da cui la variabile può estrarre i suoi valori 3 reale è diverso da 3 intero 4
5 Variabile e Tipi base Ogni linguaggio ha dei tipi base per rappresentare informazione numerica e non numerica (caratteri, valori logici). Anche il linguaggio Java possiede dei tipi base che non sono tipi di dato astratto, dal momento che sono predefiniti: non sono concetti nuovi, ma sono concetti fondamentali sui quali i concetti nuovi si baseranno. Variabile e Tipi base Tipi base o primitivi (par. 2.1, 2.5) numeri interi byte, short, int, long numeri reali float, double caratteri char logici boolean Definizione di una variabile Sintassi: nometipo nomevariabile; nometipo nomevar1, nomevar2; Esempi. Variabile e Tipi base int n, numeroanni; int dimensione; double area, saldo; boolean errore; char lettera; Variabile e Tipi base Le operazioni che possiamo fare su una variabile sono: accesso : individuare la posizione di memoria ed estrarre il valore (lettura) assegnamento : individuare la posizione di memoria e introdurre il valore (scrittura) 5
6 Variabile e Tipi base Nelle istruzioni di un programma, si ha: accesso: quando la variabile compare in una istruzione e se ne utilizza il valore assegnamento: quando il valore le viene attribuito: lettura del valore in una acquisizione di dati dall esterno in una istruzione di assegnazione (par. 2.2) Assegnazione Assegnazione Sintassi: (par. 2.2) nomevariabile = espressione; Esempi. //con riferimento alle dichiarazioni precedenti n = 3+5; area = 25.67; saldo = 20000; lettera = 'x'; lettera = x ; //Errore Assegnazione Quando una variabile viene definita le viene associata un area di memoria del tipo attribuito con la definizione: int a; double b; a b Non si possono ridefinire le variabili. 6
7 Assegnazione Quando si esegue l assegnazione, il valore viene inserito nell area corrispondente a=3; b=3; 3 3 a Le due aree di memoria sono di tipo diverso e la sequenza di bit contenuta è diversa, anche con uguale numero di bit. b Assegnazione Il simbolo per l istruzione di assegnazione è = NON lo si deve confondere con un simbolo matematico di uguaglianza o di confronto. Il suo significato è: il valore dell espressione a destra del simbolo = viene inserito nella locazione corrispondente alla variabile che sta a sinistra. Nel Pascal, il simbolo è := proprio per distinguerlo dal simbolo di uguaglianza Assegnazione Definizione e assegnazione in un unica istruzione: si può eseguire una assegnazione anche in fase di definizione: int k=25; La definizione di una variabile può essere fatta in un qualunque punto del programma ma deve essere sempre prima del suo uso. Assegnazione Osserviamo queste due assegnazioni e osserviamo che la variabile a è a destra o a sinistra del simbolo di assegnazione: ciò implica un diverso significato per l utilizzo di a: a=5; //assegnamento su a (scrittura) //a è a sinistra k=a; //accesso per a //a è a destra (lettura) 7
8 Assegnazione Osserviamo queste assegnazioni: a = 5; //assegnamento a = a + 1; /*accesso e assegnamento*/ Quanto valea? 5 a = a + 1; 6 In alcuni linguaggi di pseudocodifica, il simbolo per l assegnazione è Assegnazione Nei primi linguaggi le variabili avevano per il tipo una definizione di default. In Java una variabile può essere usata solo se è stata precedentemente definita, ossia se è stata dichiarata con il suo tipo. Esempio. int c=7; c1=c; //Errore: c1 non è definita Il compilatore segnala: cannot find symbol Assegnazione Diversamente da altri linguaggi, in Java una variabile definita in un metodo può essere usata (accesso) solo se è stata precedentemente inizializzata, ossia se ha un valore. Esempio. int c2; a=c2; //Errore: c2 non ha valore Il compilatore segnala: variable c2 might not have been initialized Assegnazione Nell assegnazione si deve rispettare il tipo di dato. Esempio. int m; double y = 23.75; m = y; //Errore: m è intero Il compilatore segnala: possible loss of precision 8
9 Tipo Intero Tipi base Si rappresenta un intervallo limitato, quindi finito, dei numeri interi (par. 4.1) Dominio: Z Z Il nome del dominio varia a seconda del numero di bit destinati alla rappresentazione: si hanno nomi diversi e anche insiemi diversi bit byte byte 8 1 short 16 2 int 32 4 long 64 8 Tipo Intero Il tipo di rappresentazione su n bit è 1 n-1 il primo è il bit del segno, i successivi n-1 sono per il numero. Dal momento che ogni bit assume due valori (0,1), avendo a disposizione n-1 bit si possono rappresentare 2 n-1 valori diversi. Tipo Intero Per il segno del numero si assume: 0 per il positivo 1 per il negativo Il numero 0, che non ha segno, viene scritto con il bit del segno 0 ed è rappresentato da una sequenza di bit tutti nulli. In tale modo, lo zero occupa un posto nell intervallo dei numeri positivi. 9
10 Tipo Intero Si vuole rappresentare la struttura algebrica dell insieme Z dei numeri interi: (Z, +) Z insieme + operazione esiste un elemento neutro, lo zero ogni numero ha un inverso, chiamato opposto L insieme Z è dato dall intervallo [-2 n-1, 2 n-1-1] Tipo Intero I vari domini per gli interi sono: (Cap.4 Tabella 1) byte n=8 [-2 7, 2 7-1] = [-128, 127] short n=16 [-2 15, ] = [-32768, 32767] int n=32 [-2 31, ] long n=64 [-2 63, ] Tipo Intero Le costanti che caratterizzano il dominio sono gli estremi dell intervallo: -2 n-1 e 2 n-1-1. In Java esistono dei nomi che rappresentano questi estremi dell intervallo, e sono legati al nome del tipo: Byte.MIN_VALUE Byte.MAX_VALUE Short.MIN_VALUE Short. MAX_VALUE Integer.MIN_VALUE Integer. MAX_VALUE Long.MIN_VALUE Long. MAX_VALUE Tipo Intero Le operazioni che possiamo fare sono: + somma sottrazione prodotto / divisione (troncata) % resto della divisione Operatori di confronto: < > <= >= ==!= 10
11 Tipo Intero La divisione tra interi è troncata. Esempi. 32 /64 e 1 /2 in aritmetica sono frazioni equivalenti 32 / 64 è 0 nell aritmetica del calcolatore, perché il risultato deve essere intero Se si vuole ottenere il valore corretto, si devono usare costanti reali, indicate dal punto decimale : 32. / Tipo Intero Analogamente con le variabili: int a,b; a/b è troncata double c,d; c/d è reale, con gli eventuali decimali Si può volere una divisione troncata e avere quoziente e resto: 7 /4 1 7 %4 3 Tipo reale Tipo Reale Si rappresenta un intervallo limitato e finito dei numeri reali Dominio: R R Il nome del dominio varia a seconda del numero di bit destinati alla rappresentazione: si hanno nomi diversi e anche insiemi diversi bit byte float 32 4 semplice precisione double 64 8 doppia precisione 11
12 Tipo reale I numeri reali vengono chiamati numeri in virgola mobile, floating point. Secondo la notazione anglosassone la separazione tra parte intera e parte decimale è il punto (nella notazione italiana è la virgola). Quando si moltiplica o si divide un numero per la base 10, la posizione del punto si sposta: = = virgola fissa Tipo reale La notazione scientifica viene scritta in Java utilizzando la lettera E (esponente), che rappresenta il prodotto per la base 10, seguita da un numero intero E E-1 Per la parte intera non si usa la separazione con il punto (in alto) per gruppi di cifre: non ma Tipo reale I numeri reali sono rappresentati in modulo e segno: significa che un numero a e il suo opposto a hanno di diverso solo il bit del segno. Il primo bit è il bit del segno ed è: 0 per i positivi 1 per i negativi I rimanenti bit rappresentano la mantissa e l esponente: 3.25 = mantissa 1 esponente riferito alla base 10 Tipo Reale Il tipo di rappresentazione per i float è con n = 32 bit il primo è il bit del segno, i successivi 8 sono per l esponente, i successivi 23 per la mantissa. Per i double, n = 64, la ripartizione è: 1(segno) 11(esponente) 52(mantissa) 12
13 Tipo Reale Si vuole rappresentare la struttura algebrica dell insieme R dei numeri reali: (R, +, ) R insieme + operazioni esiste un elemento neutro per la somma, lo zero 0 l inverso di a per la somma, opposto -a esiste un elemento neutro per il prodotto, l uno 1 l inverso di a 0 per il prodotto, reciproco 1/a Tipo Reale Oltre agli estremi dell intervallo di rappresentazione (il massimo reale e il suo opposto), dobbiamo conoscere quale è il più piccolo reale positivo: il più piccolo reale distinguibile dallo 0. Avendo a disposizione un numero finito di cifre i numeri reali minori del minimo positivo, sono rappresentati dallo 0. Le cifre decimali a disposizione: float: 6 cifre semplice precisione double: 15 cifre doppia precisione Tipo Reale Le costanti che caratterizzano il dominio sono il minimo positivo e il massimo reale. Anche per i reali le costanti significative sono rappresentate da dei nomi: Float.MIN_VALUE Double.MIN_VALUE Float.MAX_VALUE Double.MAX_VALUE Tipo Reale I numeri reali della macchina rappresentano esattamente se stessi e rappresentano in maniera approssimata un intervallo di numeri reali. I numeri reali della macchina hanno tutti un numero finito di cifre decimali (6, 15), pertanto tutti i numeri con un numero maggiore di cifre non possono essere rappresentati esattamente. 13
14 Tipo Reale Esempio. x = y = x, y R Se abbiamo a disposizione 6 cifre decimali, x e y sono rappresentati esattamente, mentre α = β = saranno approssimati con x e y rispettivamente. Tipo Reale I numeri reali sono approssimati per arrotondamento. Se la cifra che si trascura è allora il numero viene approssimato al reale macchina più piccolo (per difetto); se la cifra è il numero è approssimato al reale macchina più grande (per eccesso): α = è approssimato da y. Tipo Reale I numeri reali della macchina non sono distribuiti in maniera uniforme sulla retta reale: sono più fitti verso il minimo reale e più radi verso il massimo reale. Esempio. a = b = a = b = Tipo Reale I numeri a e b vengono approssimati con a 1 = * 10-2 b 1 = * La settima cifra di a e b (1) che si trascura ha una grandezza diversa: 10-9 in a e 10 5 in b. Il rappresentante a 1 è vicino ad a mentre il rappresentante b 1 è lontano da b. 14
15 Tipo Reale I numeri reali della macchina sono pertanto dei rappresentanti di intervalli, perché approssimano (per eccesso e per difetto) infiniti numeri reali (che non ci stanno ): y è il rappresentante di α α < y : eccesso β β > y : difetto E se ci servissero tutte le cifre di α e di β? Tipo Reale Nell esempio visto abbiamo utilizzato 6 cifre decimali e quindi la semplice precisione; se abbiamo bisogno di più cifre utilizziamo la doppia precisione: definiamo le variabili con il tipo double, con il quale si rappresentano 15 decimali. In Java useremo sempre il tipo double per i reali e il tipo int per gli interi. Tipo Reale L insieme dei numeri del tipo double contiene l insieme dei numeri di tipo float: I double rappresentano un insieme più grande: maxfloat~10 38 maxdouble~ i rappresentanti sono più fitti tra due rappresentanti x e y (float) ci sono molti, ma in quantità finita, numeri esatti (rappresentanti) in doppia precisione Tipo Reale Le operazioni che possiamo fare sono: prodotto / divisione + somma sottrazione Operatori di confronto: < > <= >= ==!= 15
16 Operatori e precedenza Il simbolo della divisione è / (par. 4.4) a + b 2 no, invece (a+b) / 2 Priorità degli operatori aritmetici: (Appendice E) come nell algebra, moltiplicazione e divisione hanno più alta priorità rispetto alla addizione e sottrazione: nell esempio precedente le parentesi sono obbligatorie. Operatori e precedenza Le due scritture producono diversi risultati: 1. (a+b) / 2 2. a+b / 2 1. prima si effettua la somma (a+b) e poi la divisione 2. prima si effettua la divisione b/2 e poi la somma A parità di priorità le operazioni vengono effettuate da sinistra verso destra: 3. a b/c = (a b)/c Interi o reali? Perché ci sono due tipi di numeri: interi e i reali? I reali sono necessari per rappresentare valori con i decimali: lira (intero), euro (reale). Se vogliamo avere una divisione non troncata dobbiamo usare i numeri reali. Gli interi sono più efficienti : occupano meno spazio di memoria, le operazioni tra interi sono più veloci, e non producono errori di arrotondamento (maxint ha 10 cifre). Tipo Carattere 16
17 Tipo Carattere Il nome del tipo è char 2 byte 16 bit L insieme dei caratteri è UNICODE Esempi. char s = '0'; char x = 'a'; Operatori di confronto: < > <= >= ==!= Tipo Logico Il nome del tipo è boolean L insieme è Tipo Logico 1 bit B = {false, true} false 0 true 1 Operatori logici && (and) (or)! (not) Esercizio Problema. Calcolare la somma dei reciproci dei primi 10 numeri naturali. Soluzione. Dobbiamo calcolare la somma /2 + 1/ /10 Ricopiando questa somma in una istruzione, otterremo un risultato corretto? Attenzione: 1 /2 = 0 mentre 1. /2 =
18 Tipo di Dato Astratto Tipo di Dato Astratto I tipi base non sono TDA: sono tipi predefinti che l utente può usare ma non modificare e non può aggiungerne altri. Un TDA deve poter rappresentare un nuovo concetto e si basa su concetti già esistenti. Nei linguaggi orientati agli oggetti si possono definire e realizzare dei nuovi concetti. Insiemi numerici L invenzione dei numeri risale a molti secoli fa: Naturali N = {1, 2, 3, } Interi Z = {., -3, -2, -1, 0, 1, 2, 3.} Razionali Q ={ a/b a,b interi e b 0} Irrazionali es. π, e, Reali R visualizzati sulla retta Complessi C visualizzati sul piano x 2 +1 = 0 ha soluzione? Java non possiede il tipo di dato complex. Tipo di Dato Astratto Vogliamo definire un nuovo concetto: Numero Complesso. Definizione. Indichiamo con C l insieme dei numeri complessi: C = {(a,b) a, b R } Si vuole rappresentare la struttura algebrica dell insieme C dei numeri complessi: (C, +, ) C insieme + operazioni 18
19 Tipo di Dato Astratto Un numero complesso è definito come coppia di reali (i numeri reali sono un concetto già esistente): z = (a, b) La forma algebrica di z C è z = a + i b a parte reale b parte immaginaria i = (0, 1) unità immaginaria Tipo di Dato Astratto Per costruire il nuovo concetto dobbiamo descrivere: la sua forma: quali sono i dati (campi) le sue proprietà: quali operazioni possiamo fare (metodi) Il nuovo concetto viene descritto all interno di una classe: class NuovoConcetto { <descrizione della sua forma> <descrizione delle sue proprietà> } //fine classe Tipo di Dato Astratto Per il TDA NumeroComplesso avremo: class NumeroComplesso{ //forma o campi double partere; double parteim; //proprietà o metodi /* somma, prodotto, sottrazione, divisione,.*/ }//fine classe NumeroComplesso Tipo di Dato Astratto La classe NumeroComplesso dovrà sviluppare gli algoritmi (metodi) che rappresentano le operazioni con le quali si possono usare oggetti di tipo NumeroComplesso: somma, prodotto, Ogni oggetto di tipo NumeroComplesso sarà una realizzazione del nuovo concetto e potrà essere utilizzato tramite i suoi metodi. Un utente della nostra classe NumeroComplesso potrà utilizzare il metodo somma senza conoscere i dettagli descritti nella classe, così come noi eseguiamo la somma di due numeri interi senza sapere come ciò avviene realmente. 19
20 Oggetti, classi, metodi Oggetti, classi, metodi Un oggetto è un entità che si può usare invocando (chiamando) i metodi della sua classe. (par. 2.3) Un metodo è una sequenza di istruzioni che può accedere ai dati dell oggetto. I metodi della classe esprimono la funzionalità dell oggetto e la loro realizzazione è nascosta all utente. Oggetti, classi, metodi Il concetto NuovoConcetto che si va a descrivere nella classe è solo un prototipo : ossia non è funzionante. Per sapere se il nostro concetto è realizzato correttamente è necessario provarlo. Si dovrà pertanto costruire un programma, con un metodo main, che costruisce l oggetto e verifica la correttezza dei suoi metodi. Oggetti, classi, metodi Pertanto per ogni TDA costruiremo una classe di collaudo class ProvaNuovoConcetto{//classe di prova //per la classe NuovoConcetto //metodomain{ /* istruzioni per creare e utilizzare un oggetto di tipo NuovoConcetto */ }//fine main }//fine classe ProvaNuovoConcetto 20
21 Tipo di dati String Tipo di dati String Una stringa è una sequenza di caratteri. Diversamente dai numeri, in Java le stringhe sono oggetti. (par. 4.6) Una costante (letterale) stringa si scrive racchiusa tra virgolette: "benvenuto" e le virgolette non fanno parte della stringa. Letterale o costante letterale: sequenza di simboli che rappresenta un valore di un certo tipo di dato. Tipo di dati String Analogamente agli altri tipi di dato definiamo una stringa e le assegniamo un valore. Il tipo di dato è rappresentato dalla classe String: String nome; //definizione nome = "Maria"; //assegnazione Le stringhe hanno una sintassi diversa dagli altri oggetti. Tipo di dati String String è il nome di una classe: inizia con la maiuscola. Una variabile di tipo String può quindi essere utilizzata richiamando i metodi della sua classe. La lunghezza di una stringa è il numero di caratteri presenti in essa (senza contare le virgolette). Ogni carattere ha una sua posizione, o indice, all interno della stringa. 21
22 Tipo di dati String La posizione dei caratteri nelle stringhe viene numerata a partire da 0 (deriva da C e C++). F i l i p p o La posizione dell ultimo carattere di una stringa corrisponde alla lunghezza della stringa meno 1. la lettera o di Filippo è in posizione 6 = 7-1 Tipo di dati String Per sapere di quanti caratteri è composta una stringa, utilizziamo il metodo length. (par. 2.3) Come si invoca un metodo (che agisce su oggetti)? nomeoggetto.nomemetodo(parametri); String saluto = "Ciao"; nome = "Filippo"; Tipo di dati String Il metodo length non ha parametri e restituisce un valore di tipo int. Pertanto memorizziamo questo valore in una variabile di tipo int: int n1 = saluto.length(); //n1=4 int n2 = nome.length(); //n2=7 //visualizziamo i valori di n1 e n2 System.out.println("n1= " + n1 + " n2= " + n2); Tipo di dati String Concatenazione tra stringhe. Le stringhe si possono concatenare utilizzando l operatore + String s1 = "Ciao"; String s2 = "mondo"; String s3 = s1 + s2; Il valore memorizzato in s3 è "Ciaomondo" Se si voglio gli spazi, questi devono essere inseriti esplicitamente: String s4 = s1 + " " + s2 22
23 Tipo di dati String Se una delle espressioni a destra o sinistra dell operatore + è una stringa, l altra espressione viene convertita a stringa e si ha la concatenazione. Questa concatenazione è utile nelle stampe: System.out.print("area = "); System.out.println(25.6); System.out.println("area = " ); Tipo di dati String Una stringa di lunghezza zero, che non contiene caratteri, si chiama stringa vuota e si indica con due caratteri virgolette consecutivi, senza spazi interposti: String vuota = ""; Poiché il metodo length restituisce un valore numerico, tale valore di ritorno può essere passato come parametro al metodoprintln: System.out.println(vuota.length()); //stampa 0 Tipo di dati String Vogliamo estrarre una sottostringa da una stringa data, utilizziamo il metodo substring: oggettostringa.substring(n1, n2); il primo parametro di substring è la posizione del primo carattere che si vuole estrarre; il secondo parametro è la posizione successiva all ultimo carattere che si vuole estrarre (il primo che non si vuole). Esempio. Tipo di dati String String saluto1 = "Ciao mondo!"; String subs1 = saluto1.substring(0,4); // subs1 contiene "Ciao" Il metodo restituisce una nuova stringa. La differenza tra i due parametri di substring corrisponde alla lunghezza della sottostringa estratta: la lunghezza disubs1 è 4 =
24 Tipo di dati String String subs2 = saluto1.substring(5,6); // subs2 contiene "m" di lunghezza 1 Attenzione: "m" è una stringa non un carattere. Il metodo substring può essere anche invocato con un solo parametro che indica il primo da estrarre; si estraggono i rimanenti fino alla fine: String subs3 = saluto1.substring(7); // subs3 contiene "ndo!" Tipo di dati String Metodo replace: ha due parametri di tipo stringa e restituisce una stringa dove è stato sostituito il primo con il secondo. String nome1 = "Maria"; String nome2 = nome1.replace("i","t"); //nome2 è "Marta" Metodi touppercase e tolowercase: convertono tutto in maiuscolo e in minuscolo rispettivamente. Tipo di dati String I metodi visti non modificano la stringa con la quale si invoca il metodo, ma restituiscono una nuova stringa (parametro di ritorno). Nessun metodo della classe String modifica l oggetto con cui viene invocato. Per tale motivo si dice che gli oggetti di tipo String sono oggetti immutabili. Tipo di dati String Se si fornisce un parametro errato a substring, il programma viene compilato correttamente, ma viene generato un errore in esecuzione. Esempio. public class Errore{ public static void main (String[] arg){ String nome = "Filippo"; String nome1 = nome.substring(5,10); System.out.println(nome1);} } 24
25 Tipo di dati String Questo errore non viene segnalato dal compilatore, ma si ha un errore durante l esecuzione del programma, che si interrompe segnalando: StringIndexOutOfBoundsException Si tratta di un errore logico, di cui però ci si accorge dato che l esecuzione viene interrotta. Sequenze di escape Come possiamo stampare una stringa che contiene delle virgolette? Ciao, "Mondo"! System.out.println("Ciao, "Mondo"!"); //ERRATO Il compilatore identifica le seconde virgolette come la fine della prima stringa "Ciao, ", ma poi non capisce il significato della parola Mondo. Si deve inserire una barra rovesciata \ (backslash) prima delle virgolette all interno della stringa System.out.println ("Ciao, \"Mondo\"!"); Sequenze di escape Il carattere backslash all interno di una stringa non rappresenta se stesso, ma si usa per codificare altri caratteri: sequenza di escape (di uscita). Per inserire veramente un carattere backslash in una stringa, si usa la sequenza di escape \\ Per scrivere parole italiane con lettere accentate senza avere a disposizione una tastiera italiana, si inserisce \u seguito dalla codifica Unicode del carattere. Esempio. Stampare la parola Perché System.out.println("Perch\u00E9"); Esercizio Dato un gruppo di tre parole, utilizzando i metodi visiti, costruirne l acronimo. Esempio. Date le parole random access memory, costruire l acronimo RAM. Soluzione. Dobbiamo estrarre da ogni parola la sottostringa iniziale di lunghezza 1, concatenarle tra loro e trasformarle poi in maiuscolo. 25
26 Esercizio public class Acronimo{//costruzione acronimo public static void main(string[] arg){ String parola1 = "random"; String parola2 = "access"; String parola3 = "memory"; // estrai le iniziali String tmp = parola1.substring(0, 1) + parola2.substring(0, 1) + parola3.substring(0, 1); // converti in maiuscolo String acro = tmp.touppercase(); System.out.println("L'acronimo e' " + acro); }//fine main }//fine main 26
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Informatica. Rappresentazione dei numeri Numerazione binaria
 Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
Variabili e tipi di dato
 Variabili e tipi di dato Tutte le variabili devono essere dichiarate, specificandone il tipo La dichiarazione deve precedere l uso Il tipo è un concetto astratto che esprime: L allocazione di spazio per
Variabili e tipi di dato Tutte le variabili devono essere dichiarate, specificandone il tipo La dichiarazione deve precedere l uso Il tipo è un concetto astratto che esprime: L allocazione di spazio per
Alessandro Pellegrini
 Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
3 - Variabili. Programmazione e analisi di dati Modulo A: Programmazione in Java. Paolo Milazzo
 3 - Variabili Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica, Università di Pisa http://www.di.unipi.it/ milazzo milazzo di.unipi.it Corso di
3 - Variabili Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica, Università di Pisa http://www.di.unipi.it/ milazzo milazzo di.unipi.it Corso di
Java:Struttura di Programma. Fabio Scanu a.s. 2014/2015
 Java:Struttura di Programma Fabio Scanu a.s. 2014/2015 Altre Attenzioni da riservare Java è Case Sensitive: La variabile «a» e la variabile «A» sono diverse Java ha alcune regole di scrittura: I nomi delle
Java:Struttura di Programma Fabio Scanu a.s. 2014/2015 Altre Attenzioni da riservare Java è Case Sensitive: La variabile «a» e la variabile «A» sono diverse Java ha alcune regole di scrittura: I nomi delle
Le variabili. Olga Scotti
 Le variabili Olga Scotti Cos è una variabile Le variabili, in un linguaggio di programmazione, sono dei contenitori. Possono essere riempiti con un valore che poi può essere riletto oppure sostituito.
Le variabili Olga Scotti Cos è una variabile Le variabili, in un linguaggio di programmazione, sono dei contenitori. Possono essere riempiti con un valore che poi può essere riletto oppure sostituito.
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione in virgola mobile
 Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Informazione analogica e digitale
 L informazione L informazione si può: rappresentare elaborare gestire trasmettere reperire L informatica offre la possibilità di effettuare queste operazioni in modo automatico. Informazione analogica
L informazione L informazione si può: rappresentare elaborare gestire trasmettere reperire L informatica offre la possibilità di effettuare queste operazioni in modo automatico. Informazione analogica
Introduzione alla programmazione in C
 Introduzione alla programmazione in C Testi Consigliati: A. Kelley & I. Pohl C didattica e programmazione B.W. Kernighan & D. M. Ritchie Linguaggio C P. Tosoratti Introduzione all informatica Materiale
Introduzione alla programmazione in C Testi Consigliati: A. Kelley & I. Pohl C didattica e programmazione B.W. Kernighan & D. M. Ritchie Linguaggio C P. Tosoratti Introduzione all informatica Materiale
Rappresentazione dell informazione Codifica Binaria
 Fondamenti di Informatica Rappresentazione dell informazione Codifica Binaria Fondamenti di Informatica - D. Talia - UNICAL 1 Rappresentazione dell informazione Tutta l'informazione in un calcolatore è
Fondamenti di Informatica Rappresentazione dell informazione Codifica Binaria Fondamenti di Informatica - D. Talia - UNICAL 1 Rappresentazione dell informazione Tutta l'informazione in un calcolatore è
Tipi di dato-prima parte
 Corso di Fondamenti di Informatica Corso di Laurea in Ingegneria Meccanica (A-K) Tipi di dato-prima parte Ing. Agnese Pinto 1 di 15 Tipi di dato Sommario Tipi di dato Classificazione dei tipi di dato Tipi
Corso di Fondamenti di Informatica Corso di Laurea in Ingegneria Meccanica (A-K) Tipi di dato-prima parte Ing. Agnese Pinto 1 di 15 Tipi di dato Sommario Tipi di dato Classificazione dei tipi di dato Tipi
Gli array. Gli array. Gli array. Classi di memorizzazione per array. Inizializzazione esplicita degli array. Array e puntatori
 Gli array Array e puntatori Laboratorio di Informatica I un array è un insieme di elementi (valori) avente le seguenti caratteristiche: - un array è ordinato: agli elementi dell array è assegnato un ordine
Gli array Array e puntatori Laboratorio di Informatica I un array è un insieme di elementi (valori) avente le seguenti caratteristiche: - un array è ordinato: agli elementi dell array è assegnato un ordine
Logica e codifica binaria dell informazione
 Politecnico di Milano Corsi di Laurea in Ingegneria Matematica e Ingegneria Fisica Dipartimento di Elettronica ed Informazione Logica e codifica binaria dell informazione Anno Accademico 2002 2003 L. Muttoni
Politecnico di Milano Corsi di Laurea in Ingegneria Matematica e Ingegneria Fisica Dipartimento di Elettronica ed Informazione Logica e codifica binaria dell informazione Anno Accademico 2002 2003 L. Muttoni
Dall Algoritmo al Programma. Prof. Francesco Accarino IIS Altiero Spinelli Sesto San Giovanni
 Dall Algoritmo al Programma Prof. Francesco Accarino IIS Altiero Spinelli Sesto San Giovanni IL PROGRAMMA Gli algoritmi sono modelli di descrizione astratti e per controllarne il funzionamento devono essere
Dall Algoritmo al Programma Prof. Francesco Accarino IIS Altiero Spinelli Sesto San Giovanni IL PROGRAMMA Gli algoritmi sono modelli di descrizione astratti e per controllarne il funzionamento devono essere
Informatica Generale 02 - Rappresentazione numeri razionali
 Informatica Generale 02 - Rappresentazione numeri razionali Cosa vedremo: Rappresentazione binaria dei numeri razionali Rappresentazione in virgola fissa Rappresentazione in virgola mobile La rappresentazione
Informatica Generale 02 - Rappresentazione numeri razionali Cosa vedremo: Rappresentazione binaria dei numeri razionali Rappresentazione in virgola fissa Rappresentazione in virgola mobile La rappresentazione
2. Codifica dell informazione
 2. Codifica dell informazione Codifica Una codifica è una regola per associare in modo univoco i valori di un dato da codificare con sequenze di simboli. La corrispondenza definita dalla codifica è arbitraria,
2. Codifica dell informazione Codifica Una codifica è una regola per associare in modo univoco i valori di un dato da codificare con sequenze di simboli. La corrispondenza definita dalla codifica è arbitraria,
Informatica B a.a 2005/06 (Meccanici 4 squadra) PhD. Ing. Michele Folgheraiter
 Informatica B a.a 2005/06 (Meccanici 4 squadra) Scaglione: da PO a ZZZZ PhD. Ing. Michele Folgheraiter Architettura del Calcolatore Macchina di von Neumann Il calcolatore moderno è basato su un architettura
Informatica B a.a 2005/06 (Meccanici 4 squadra) Scaglione: da PO a ZZZZ PhD. Ing. Michele Folgheraiter Architettura del Calcolatore Macchina di von Neumann Il calcolatore moderno è basato su un architettura
Rappresentazione di informazioni con un alfabeto finito
 Rappresentazione di informazioni con un alfabeto finito Sia A = { a 1,, a k } un insieme (alfabeto) di k simboli, detti anche lettere. Quante sono le sequenze composte da n simboli (anche ripetuti) di
Rappresentazione di informazioni con un alfabeto finito Sia A = { a 1,, a k } un insieme (alfabeto) di k simboli, detti anche lettere. Quante sono le sequenze composte da n simboli (anche ripetuti) di
Alcune regole di base per scrivere un programma in linguaggio C
 Alcune regole di base per scrivere un programma in linguaggio C Un programma il linguaggio C (listato) viene scritto in formato testo ed archiviato in un file: *.c Per scrivere un listato C si utilizza
Alcune regole di base per scrivere un programma in linguaggio C Un programma il linguaggio C (listato) viene scritto in formato testo ed archiviato in un file: *.c Per scrivere un listato C si utilizza
Obiettivi dell Analisi Numerica. Avviso. Risoluzione numerica di un modello. Analisi Numerica e Calcolo Scientifico
 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p. 3/43 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p.
M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p. 3/43 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p.
Rappresentazione delle informazioni
 Rappresentazione delle informazioni Abbiamo informazioni (numeri, caratteri, immagini, suoni, video... ) che vogliamo rappresentare (e poter elaborare) in un calcolatore. Per motivi tecnologici un calcolatore
Rappresentazione delle informazioni Abbiamo informazioni (numeri, caratteri, immagini, suoni, video... ) che vogliamo rappresentare (e poter elaborare) in un calcolatore. Per motivi tecnologici un calcolatore
Sistemi di Numerazione Binaria NB.1
 Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Funzioni in C. Violetta Lonati
 Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Funzioni - in breve: Funzioni Definizione di funzioni
Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Funzioni - in breve: Funzioni Definizione di funzioni
Elementi di informatica
 Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Rappresentazione dei numeri nei calcolatori rappresentazioni finalizzate ad algoritmi efficienti per le operazioni
Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Rappresentazione dei numeri nei calcolatori rappresentazioni finalizzate ad algoritmi efficienti per le operazioni
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Corso di Laurea Ingegneria Informatica Fondamenti di Informatica
 Corso di Laurea Ingegneria Informatica Fondamenti di Informatica Dispensa 05 La rappresentazione dell informazione Carla Limongelli Ottobre 2011 http://www.dia.uniroma3.it/~java/fondinf/ La rappresentazione
Corso di Laurea Ingegneria Informatica Fondamenti di Informatica Dispensa 05 La rappresentazione dell informazione Carla Limongelli Ottobre 2011 http://www.dia.uniroma3.it/~java/fondinf/ La rappresentazione
LINGUAGGI DI PROGRAMMAZIONE
 LINGUAGGI DI PROGRAMMAZIONE Il potere espressivo di un linguaggio è caratterizzato da: quali tipi di dati consente di rappresentare (direttamente o tramite definizione dell utente) quali istruzioni di
LINGUAGGI DI PROGRAMMAZIONE Il potere espressivo di un linguaggio è caratterizzato da: quali tipi di dati consente di rappresentare (direttamente o tramite definizione dell utente) quali istruzioni di
Esempi ed esercizi Aritmetica degli elaboratori e algebra di commutazione
 Esempi ed esercizi Aritmetica degli elaboratori e algebra di commutazione Fondamenti di Informatica Michele Ceccarelli Università del Sannio ceccarelli@unisannio.it Angelo Ciaramella DMI-Università degli
Esempi ed esercizi Aritmetica degli elaboratori e algebra di commutazione Fondamenti di Informatica Michele Ceccarelli Università del Sannio ceccarelli@unisannio.it Angelo Ciaramella DMI-Università degli
Università di Torino Facoltà di Scienze MFN Corso di Studi in Informatica. Programmazione I - corso B a.a. 2009-10. prof.
 Università di Torino Facoltà di Scienze MFN Corso di Studi in Informatica Programmazione I - corso B a.a. 009-10 prof. Viviana Bono Blocco 9 Metodi statici: passaggio parametri, variabili locali, record
Università di Torino Facoltà di Scienze MFN Corso di Studi in Informatica Programmazione I - corso B a.a. 009-10 prof. Viviana Bono Blocco 9 Metodi statici: passaggio parametri, variabili locali, record
Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013
 Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013 In questo documento vengono illustrate brevemente le operazioni aritmetiche salienti e quelle logiche ad esse strettamente collegate.
Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013 In questo documento vengono illustrate brevemente le operazioni aritmetiche salienti e quelle logiche ad esse strettamente collegate.
Lezione 2 OPERAZIONI ARITMETICHE E LOGICHE ARCHITETTURA DI UN ELABORATORE. Lez2 Informatica Sc. Giuridiche Op. aritmetiche/logiche arch.
 Lezione 2 OPERAZIONI ARITMETICHE E LOGICHE ARCHITETTURA DI UN ELABORATORE Comunicazione importante dalla prossima settimana, la lezione del venerdì si terrà: dalle 15:00 alle 17.15 in aula 311 l orario
Lezione 2 OPERAZIONI ARITMETICHE E LOGICHE ARCHITETTURA DI UN ELABORATORE Comunicazione importante dalla prossima settimana, la lezione del venerdì si terrà: dalle 15:00 alle 17.15 in aula 311 l orario
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
I sistemi di numerazione
 I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
SISTEMI DI NUMERAZIONE DECIMALE E BINARIO
 SISTEMI DI NUMERAZIONE DECIMALE E BINARIO Il sistema di numerazione decimale (o base dieci) possiede dieci possibili valori (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) utili a rappresentare i numeri. Le cifre possiedono
SISTEMI DI NUMERAZIONE DECIMALE E BINARIO Il sistema di numerazione decimale (o base dieci) possiede dieci possibili valori (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) utili a rappresentare i numeri. Le cifre possiedono
Concetto di Funzione e Procedura METODI in Java
 Fondamenti di Informatica Concetto di Funzione e Procedura METODI in Java Fondamenti di Informatica - D. Talia - UNICAL 1 Metodi e Sottoprogrammi Mentre in Java tramite le classi e gli oggetti è possibile
Fondamenti di Informatica Concetto di Funzione e Procedura METODI in Java Fondamenti di Informatica - D. Talia - UNICAL 1 Metodi e Sottoprogrammi Mentre in Java tramite le classi e gli oggetti è possibile
Appunti di informatica. Lezione 2 anno accademico 2015-2016 Mario Verdicchio
 Appunti di informatica Lezione 2 anno accademico 2015-2016 Mario Verdicchio Sistema binario e logica C è un legame tra i numeri binari (0,1) e la logica, ossia la disciplina che si occupa del ragionamento
Appunti di informatica Lezione 2 anno accademico 2015-2016 Mario Verdicchio Sistema binario e logica C è un legame tra i numeri binari (0,1) e la logica, ossia la disciplina che si occupa del ragionamento
Sistemi di Numerazione
 Fondamenti di Informatica per Meccanici Energetici - Biomedici 1 Sistemi di Numerazione Sistemi di Numerazione I sistemi di numerazione sono abitualmente posizionali. Gli elementi costitutivi di un sistema
Fondamenti di Informatica per Meccanici Energetici - Biomedici 1 Sistemi di Numerazione Sistemi di Numerazione I sistemi di numerazione sono abitualmente posizionali. Gli elementi costitutivi di un sistema
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Elementi di Informatica. ( Lezione II, parte I ) Sistemi di numerazione: binario, ottale ed esadecimale
 Elementi di Informatica ( Lezione II, parte I ) Sistemi di numerazione: binario, ottale ed esadecimale Il sistema di numerazione posizionale decimale Nella numerazione posizionale ogni cifra del numero
Elementi di Informatica ( Lezione II, parte I ) Sistemi di numerazione: binario, ottale ed esadecimale Il sistema di numerazione posizionale decimale Nella numerazione posizionale ogni cifra del numero
Esercitazione Informatica I AA 2012-2013. Nicola Paoletti
 Esercitazione Informatica I AA 2012-2013 Nicola Paoletti 4 Gigno 2013 2 Conversioni Effettuare le seguenti conversioni, tenendo conto del numero di bit con cui si rappresenta il numero da convertire/convertito.
Esercitazione Informatica I AA 2012-2013 Nicola Paoletti 4 Gigno 2013 2 Conversioni Effettuare le seguenti conversioni, tenendo conto del numero di bit con cui si rappresenta il numero da convertire/convertito.
Corso di Informatica
 Corso di Informatica Modulo T3 1-Sottoprogrammi 1 Prerequisiti Tecnica top-down Programmazione elementare 2 1 Introduzione Lo scopo di questa Unità è utilizzare la metodologia di progettazione top-down
Corso di Informatica Modulo T3 1-Sottoprogrammi 1 Prerequisiti Tecnica top-down Programmazione elementare 2 1 Introduzione Lo scopo di questa Unità è utilizzare la metodologia di progettazione top-down
Codifica binaria e algebra di Boole
 Codifica binaria e algebra di Boole Corso di Programmazione A.A. 2008/09 G. Cibinetto Contenuti della lezione Codifica binaria dell informazione Numeri naturali, interi, frazionari, in virgola mobile Base
Codifica binaria e algebra di Boole Corso di Programmazione A.A. 2008/09 G. Cibinetto Contenuti della lezione Codifica binaria dell informazione Numeri naturali, interi, frazionari, in virgola mobile Base
La codifica delle informazioni
 La codifica delle informazioni Bit e byte Come già visto l elaboratore è in grado di rappresentare informazioni al proprio interno solo utilizzando cifre binarie (bit) che solitamente vengono manipolate
La codifica delle informazioni Bit e byte Come già visto l elaboratore è in grado di rappresentare informazioni al proprio interno solo utilizzando cifre binarie (bit) che solitamente vengono manipolate
LA RAPPRESENTAZIONE DELLE INFORMAZIONI
 ISTITUTO TECNICO E LICEO SCIENTIFICO TECNOLOGICO ANGIOY LA RAPPRESENTAZIONE DELLE INFORMAZIONI Prof. G. Ciaschetti DATI E INFORMAZIONI Sappiamo che il computer è una macchina stupida, capace di eseguire
ISTITUTO TECNICO E LICEO SCIENTIFICO TECNOLOGICO ANGIOY LA RAPPRESENTAZIONE DELLE INFORMAZIONI Prof. G. Ciaschetti DATI E INFORMAZIONI Sappiamo che il computer è una macchina stupida, capace di eseguire
Codifica binaria dei numeri
 Codifica binaria dei numeri Caso più semplice: in modo posizionale (spesso detto codifica binaria tout court) Esempio con numero naturale: con 8 bit 39 = Codifica in virgola fissa dei numeri float: si
Codifica binaria dei numeri Caso più semplice: in modo posizionale (spesso detto codifica binaria tout court) Esempio con numero naturale: con 8 bit 39 = Codifica in virgola fissa dei numeri float: si
Laboratorio di Informatica
 per chimica industriale e chimica applicata e ambientale LEZIONE 2 Rappresentazione delle informazioni: numeri e caratteri 1 Codice La relazione che associa ad ogni successione ben formata di simboli di
per chimica industriale e chimica applicata e ambientale LEZIONE 2 Rappresentazione delle informazioni: numeri e caratteri 1 Codice La relazione che associa ad ogni successione ben formata di simboli di
Codifica dei numeri negativi
 E. Calabrese: Fondamenti di Informatica Rappresentazione numerica-1 Rappresentazione in complemento a 2 Codifica dei numeri negativi Per rappresentare numeri interi negativi si usa la cosiddetta rappresentazione
E. Calabrese: Fondamenti di Informatica Rappresentazione numerica-1 Rappresentazione in complemento a 2 Codifica dei numeri negativi Per rappresentare numeri interi negativi si usa la cosiddetta rappresentazione
Informatica. Rappresentazione binaria Per esempio +101010000 diventa +0.10101 10 18/10/2007. Introduzione ai sistemi informatici 1
 Informatica Pietro Storniolo storniolo@csai.unipa.it http://www.pa.icar.cnr.it/storniolo/info200708 Numeri razionali Cifre più significative: : sono le cifre associate ai pesi maggiori per i numeri maggiori
Informatica Pietro Storniolo storniolo@csai.unipa.it http://www.pa.icar.cnr.it/storniolo/info200708 Numeri razionali Cifre più significative: : sono le cifre associate ai pesi maggiori per i numeri maggiori
12 - Introduzione alla Programmazione Orientata agli Oggetti (Object Oriented Programming OOP)
 12 - Introduzione alla Programmazione Orientata agli Oggetti (Object Oriented Programming OOP) Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica,
12 - Introduzione alla Programmazione Orientata agli Oggetti (Object Oriented Programming OOP) Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica,
ESTRAZIONE DI RADICE
 ESTRAZIONE DI RADICE La radice è l operazione inversa dell elevamento a potenza. L esponente della potenza è l indice della radice che può essere: quadrata (); cubica (); quarta (4); ecc. La base della
ESTRAZIONE DI RADICE La radice è l operazione inversa dell elevamento a potenza. L esponente della potenza è l indice della radice che può essere: quadrata (); cubica (); quarta (4); ecc. La base della
Algebra di Boole: Concetti di base. Fondamenti di Informatica - D. Talia - UNICAL 1. Fondamenti di Informatica
 Fondamenti di Informatica Algebra di Boole: Concetti di base Fondamenti di Informatica - D. Talia - UNICAL 1 Algebra di Boole E un algebra basata su tre operazioni logiche OR AND NOT Ed operandi che possono
Fondamenti di Informatica Algebra di Boole: Concetti di base Fondamenti di Informatica - D. Talia - UNICAL 1 Algebra di Boole E un algebra basata su tre operazioni logiche OR AND NOT Ed operandi che possono
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
Convertitori numerici in Excel
 ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
(71,1), (35,1), (17,1), (8,1), (4,0), (2,0), (1,0), (0,1) 0, 7155 2 = 1, 431 0, 431 2 = 0, 862 0, 896 2 = 1, 792 0, 724 2 = 1, 448 0, 448 2 = 0, 896
 2 Esercizio 2.2 La rappresentazione esadecimale prevede 16 configurazioni corrispondenti a 4 bit. Il contenuto di una parola di 16 bit può essere rappresentato direttamente con 4 digit esadecimali, sostituendo
2 Esercizio 2.2 La rappresentazione esadecimale prevede 16 configurazioni corrispondenti a 4 bit. Il contenuto di una parola di 16 bit può essere rappresentato direttamente con 4 digit esadecimali, sostituendo
Richiesta pagina PHP (es: index.php)
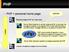 PHP PHP = personal home page SERVER Richiesta pagina PHP (es: index.php) Server Web (Apache) in ascolto sulla porta 80, si accorge che la pagina richiesta è una pagina PHP in base all'estensione o con
PHP PHP = personal home page SERVER Richiesta pagina PHP (es: index.php) Server Web (Apache) in ascolto sulla porta 80, si accorge che la pagina richiesta è una pagina PHP in base all'estensione o con
Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri
 Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri 1 Da base 2 a base 10 I seguenti esercizi richiedono di convertire in base 10 la medesima stringa binaria codificata rispettivamente
Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri 1 Da base 2 a base 10 I seguenti esercizi richiedono di convertire in base 10 la medesima stringa binaria codificata rispettivamente
Parte II Indice. Operazioni aritmetiche tra valori rappresentati in binario puro. Rappresentazione di numeri con segno
 Parte II Indice Operazioni aritmetiche tra valori rappresentati in binario puro somma sottrazione Rappresentazione di numeri con segno modulo e segno complemento a 2 esercizi Operazioni aritmetiche tra
Parte II Indice Operazioni aritmetiche tra valori rappresentati in binario puro somma sottrazione Rappresentazione di numeri con segno modulo e segno complemento a 2 esercizi Operazioni aritmetiche tra
Introduzione agli algoritmi e alla programmazione in VisualBasic.Net
 Lezione 1 Introduzione agli algoritmi e alla programmazione in VisualBasic.Net Definizione di utente e di programmatore L utente è qualsiasi persona che usa il computer anche se non è in grado di programmarlo
Lezione 1 Introduzione agli algoritmi e alla programmazione in VisualBasic.Net Definizione di utente e di programmatore L utente è qualsiasi persona che usa il computer anche se non è in grado di programmarlo
Lez. 3 L elaborazione (II parte) Prof. Pasquale De Michele Gruppo 2
 Lez. 3 L elaborazione (II parte) Prof. Pasquale De Michele Gruppo 2 1 Dott. Pasquale De Michele Dipartimento di Matematica e Applicazioni Università di Napoli Federico II Compl. Univ. Monte S.Angelo Via
Lez. 3 L elaborazione (II parte) Prof. Pasquale De Michele Gruppo 2 1 Dott. Pasquale De Michele Dipartimento di Matematica e Applicazioni Università di Napoli Federico II Compl. Univ. Monte S.Angelo Via
Tipi elementari, costanti. Tipi di dati. VALORI: un insieme dei valori del tipo OPERAZIONI: per operare su tali valori. Tipi. intero reale carattere
 Tipi elementari, costanti 1 Tipi di dati VALORI: un insieme dei valori del tipo OPERAZIONI: per operare su tali valori Tipi Semplici intero reale carattere Strutturati 2 1 Tipo intero Gli interi servono
Tipi elementari, costanti 1 Tipi di dati VALORI: un insieme dei valori del tipo OPERAZIONI: per operare su tali valori Tipi Semplici intero reale carattere Strutturati 2 1 Tipo intero Gli interi servono
APPUNTI DI MATEMATICA ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1)
 ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
Struttura di un programma Java
 Struttura di un programma Java Un programma in Java è un insieme di dichiarazioni di classi. Una classe non può contenere direttamente delle istruzioni, ma può contenere la dichiarazione di metodi, che
Struttura di un programma Java Un programma in Java è un insieme di dichiarazioni di classi. Una classe non può contenere direttamente delle istruzioni, ma può contenere la dichiarazione di metodi, che
Fasi di creazione di un programma
 Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo 41 Sviluppo di programmi Per la costruzione di un programma
Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo 41 Sviluppo di programmi Per la costruzione di un programma
Introduzione allo Scilab Parte 1: numeri, variabili ed operatori elementari
 Introduzione allo Scilab Parte 1: numeri, variabili ed operatori elementari Felice Iavernaro Dipartimento di Matematica Università di Bari http://dm.uniba.it/ iavernaro 6 Giugno 2007 Felice Iavernaro (Univ.
Introduzione allo Scilab Parte 1: numeri, variabili ed operatori elementari Felice Iavernaro Dipartimento di Matematica Università di Bari http://dm.uniba.it/ iavernaro 6 Giugno 2007 Felice Iavernaro (Univ.
Rappresentazione dei numeri in un calcolatore
 Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri in un calcolatore Lezione 2 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione dei numeri
Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri in un calcolatore Lezione 2 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione dei numeri
Codifica binaria dei numeri relativi
 Codifica binaria dei numeri relativi Introduzione All interno di un calcolatore, è possibile utilizzare solo 0 e 1 per codificare qualsiasi informazione. Nel caso dei numeri, non solo il modulo ma anche
Codifica binaria dei numeri relativi Introduzione All interno di un calcolatore, è possibile utilizzare solo 0 e 1 per codificare qualsiasi informazione. Nel caso dei numeri, non solo il modulo ma anche
CODIFICA BINARIA. ... sono rappresentati ricorrendo a simboli che sintezzano il concetto di numerosità.
 I METODI DI NUMERAZIONE I numeri naturali... sono rappresentati ricorrendo a simboli che sintezzano il concetto di numerosità. Il numero dei simboli usati per valutare la numerosità costituisce la base
I METODI DI NUMERAZIONE I numeri naturali... sono rappresentati ricorrendo a simboli che sintezzano il concetto di numerosità. Il numero dei simboli usati per valutare la numerosità costituisce la base
3. La sintassi di Java
 pag.9 3. La sintassi di Java 3.1 I tipi di dati statici In Java, come in Pascal, esistono tipi di dati statici predefiniti e sono i seguenti: byte 8 bit da -128 a 127 short 16 bit coincide con l integer
pag.9 3. La sintassi di Java 3.1 I tipi di dati statici In Java, come in Pascal, esistono tipi di dati statici predefiniti e sono i seguenti: byte 8 bit da -128 a 127 short 16 bit coincide con l integer
La gestione dell input/output da tastiera La gestione dell input/output da file La gestione delle eccezioni
 La gestione dell input/output da tastiera La gestione dell input/output da file La gestione delle eccezioni Autore: Prof. Agostino Sorbara ITIS "M. M. Milano" Autore: Prof. Agostino Sorbara ITIS "M. M.
La gestione dell input/output da tastiera La gestione dell input/output da file La gestione delle eccezioni Autore: Prof. Agostino Sorbara ITIS "M. M. Milano" Autore: Prof. Agostino Sorbara ITIS "M. M.
ALGEBRA DELLE PROPOSIZIONI
 Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
Dispense di Informatica per l ITG Valadier
 La notazione binaria Dispense di Informatica per l ITG Valadier Le informazioni dentro il computer All interno di un calcolatore tutte le informazioni sono memorizzate sottoforma di lunghe sequenze di
La notazione binaria Dispense di Informatica per l ITG Valadier Le informazioni dentro il computer All interno di un calcolatore tutte le informazioni sono memorizzate sottoforma di lunghe sequenze di
I file di dati. Unità didattica D1 1
 I file di dati Unità didattica D1 1 1) I file sequenziali Utili per la memorizzazione di informazioni testuali Si tratta di strutture organizzate per righe e non per record Non sono adatte per grandi quantità
I file di dati Unità didattica D1 1 1) I file sequenziali Utili per la memorizzazione di informazioni testuali Si tratta di strutture organizzate per righe e non per record Non sono adatte per grandi quantità
Aritmetica: operazioni ed espressioni
 / A SCUOLA DI MATEMATICA Lezioni di matematica a cura di Eugenio Amitrano Argomento n. : operazioni ed espressioni Ricostruzione di un abaco dell epoca romana - Museo RGZ di Magonza (Germania) Libero da
/ A SCUOLA DI MATEMATICA Lezioni di matematica a cura di Eugenio Amitrano Argomento n. : operazioni ed espressioni Ricostruzione di un abaco dell epoca romana - Museo RGZ di Magonza (Germania) Libero da
Appunti del corso di Informatica 1 (IN110 Fondamenti) 6 Introduzione al linguaggio C
 Università di Roma Tre Facoltà di Scienze M.F.N. Corso di Laurea in Matematica Appunti del corso di Informatica 1 (IN110 Fondamenti) 6 Introduzione al linguaggio C Marco Liverani (liverani@mat.uniroma3.it)
Università di Roma Tre Facoltà di Scienze M.F.N. Corso di Laurea in Matematica Appunti del corso di Informatica 1 (IN110 Fondamenti) 6 Introduzione al linguaggio C Marco Liverani (liverani@mat.uniroma3.it)
Tipi primitivi. Ad esempio, il codice seguente dichiara una variabile di tipo intero, le assegna il valore 5 e stampa a schermo il suo contenuto:
 Tipi primitivi Il linguaggio Java offre alcuni tipi di dato primitivi Una variabile di tipo primitivo può essere utilizzata direttamente. Non è un riferimento e non ha senso tentare di istanziarla mediante
Tipi primitivi Il linguaggio Java offre alcuni tipi di dato primitivi Una variabile di tipo primitivo può essere utilizzata direttamente. Non è un riferimento e non ha senso tentare di istanziarla mediante
Programmazione in Java Parte I: Fondamenti
 Programmazione in Java Parte I: Fondamenti Lezione 1 Dott. Marco Faella Riferimenti Testi consigliati: Progettazione del software e design pattern in Java di C.S. Horstmann Apogeo Gli esempi di codice
Programmazione in Java Parte I: Fondamenti Lezione 1 Dott. Marco Faella Riferimenti Testi consigliati: Progettazione del software e design pattern in Java di C.S. Horstmann Apogeo Gli esempi di codice
Laboratorio di Informatica
 Laboratorio di Informatica Introduzione a Python Dottore Paolo Parisen Toldin - parisent@cs.unibo.it Argomenti trattati Che cosa è python Variabili Assegnazione Condizionale Iterazione in una lista di
Laboratorio di Informatica Introduzione a Python Dottore Paolo Parisen Toldin - parisent@cs.unibo.it Argomenti trattati Che cosa è python Variabili Assegnazione Condizionale Iterazione in una lista di
Excel. A cura di Luigi Labonia. e-mail: luigi.lab@libero.it
 Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
Nascita di Java. Che cos e Java? Caratteristiche di Java. Java: linguaggio a oggetti
 Nascita di Java L uscita di Java, verso la metà degli anni novanta, fu accolta con molto entusiasmo dalla comunità dei programmatori e dei provider di servizi internet perché permetteva agli utenti del
Nascita di Java L uscita di Java, verso la metà degli anni novanta, fu accolta con molto entusiasmo dalla comunità dei programmatori e dei provider di servizi internet perché permetteva agli utenti del
Fondamenti di Informatica e Laboratorio T-AB Ingengeria dell Automazione a.a. 2008/2009. Lab 02 Tipi semplici in C
 Fondamenti di Informatica e Laboratorio T-AB Ingengeria dell Automazione a.a. 2008/2009 Lab 02 Tipi semplici in C Obiettivo dell esercitazione Acquistare familiarità con i tipi di dato semplici supportati
Fondamenti di Informatica e Laboratorio T-AB Ingengeria dell Automazione a.a. 2008/2009 Lab 02 Tipi semplici in C Obiettivo dell esercitazione Acquistare familiarità con i tipi di dato semplici supportati
INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI
 INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
Gian Luca Marcialis studio degli algoritmi programma linguaggi LINGUAGGIO C
 Università degli Studi di Cagliari Corso di Laurea in Ingegneria Biomedica (Industriale), Chimica, Elettrica, e Meccanica FONDAMENTI DI INFORMATICA 1 http://www.diee.unica.it/~marcialis/fi1 A.A. 2010/2011
Università degli Studi di Cagliari Corso di Laurea in Ingegneria Biomedica (Industriale), Chimica, Elettrica, e Meccanica FONDAMENTI DI INFORMATICA 1 http://www.diee.unica.it/~marcialis/fi1 A.A. 2010/2011
Arduino: Programmazione
 Programmazione formalmente ispirata al linguaggio C da cui deriva. I programmi in ARDUINO sono chiamati Sketch. Un programma è una serie di istruzioni che vengono lette dall alto verso il basso e convertite
Programmazione formalmente ispirata al linguaggio C da cui deriva. I programmi in ARDUINO sono chiamati Sketch. Un programma è una serie di istruzioni che vengono lette dall alto verso il basso e convertite
Appunti del corso di Informatica 1. 6 Introduzione al linguaggio C
 Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica 1 (IN110 Fondamenti) 6 Introduzione al linguaggio C Marco Liverani (liverani@mat.uniroma3.it)
Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica 1 (IN110 Fondamenti) 6 Introduzione al linguaggio C Marco Liverani (liverani@mat.uniroma3.it)
Dati testuali. Caratteri e stringhe. Tipi di dato testuali. Dati testuali. Il sistema dei tipi C. Rappresentazione dei testi
 Tipi di dato testuali Caratteri Stringhe Caratteri e stringhe 5 Tipi di dato testuali I programmi visti finora erano in grado di elaborare esclusivamente informazioni numeriche Numeri eri (), numeri reali
Tipi di dato testuali Caratteri Stringhe Caratteri e stringhe 5 Tipi di dato testuali I programmi visti finora erano in grado di elaborare esclusivamente informazioni numeriche Numeri eri (), numeri reali
Strutturazione logica dei dati: i file
 Strutturazione logica dei dati: i file Informazioni più complesse possono essere composte a partire da informazioni elementari Esempio di una banca: supponiamo di voler mantenere all'interno di un computer
Strutturazione logica dei dati: i file Informazioni più complesse possono essere composte a partire da informazioni elementari Esempio di una banca: supponiamo di voler mantenere all'interno di un computer
FORMULE: Operatori matematici
 Formule e funzioni FORMULE Le formule sono necessarie per eseguire calcoli utilizzando i valori presenti nelle celle di un foglio di lavoro. Una formula inizia col segno uguale (=). La formula deve essere
Formule e funzioni FORMULE Le formule sono necessarie per eseguire calcoli utilizzando i valori presenti nelle celle di un foglio di lavoro. Una formula inizia col segno uguale (=). La formula deve essere
razionali Figura 1. Rappresentazione degli insiemi numerici Numeri reali algebrici trascendenti frazionari decimali finiti
 4. Insiemi numerici 4.1 Insiemi numerici Insieme dei numeri naturali = {0,1,,3,,} Insieme dei numeri interi relativi = {..., 3,, 1,0, + 1, +, + 3, } Insieme dei numeri razionali n 1 1 1 1 = : n, m \{0}
4. Insiemi numerici 4.1 Insiemi numerici Insieme dei numeri naturali = {0,1,,3,,} Insieme dei numeri interi relativi = {..., 3,, 1,0, + 1, +, + 3, } Insieme dei numeri razionali n 1 1 1 1 = : n, m \{0}
Linguaggio C. Fondamenti. Struttura di un programma.
 Linguaggio C Fondamenti. Struttura di un programma. 1 La storia del Linguaggio C La nascita del linguaggio C fu dovuta all esigenza di disporre di un Linguaggio ad alto livello adatto alla realizzazione
Linguaggio C Fondamenti. Struttura di un programma. 1 La storia del Linguaggio C La nascita del linguaggio C fu dovuta all esigenza di disporre di un Linguaggio ad alto livello adatto alla realizzazione
Utilizzo delle formule in Excel
 Utilizzo delle formule in Excel Excel è dotato di un potente motore di calcolo che può essere utilizzato per elaborare i dati immessi dagli utenti. I calcoli sono definiti mediante formule. Ogni formula
Utilizzo delle formule in Excel Excel è dotato di un potente motore di calcolo che può essere utilizzato per elaborare i dati immessi dagli utenti. I calcoli sono definiti mediante formule. Ogni formula
Lezione 1. Gli Insiemi. La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme:
 Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Esempio: dest = parolagigante, lettere = PROVA dest (dopo l'invocazione di tipo pari ) = pprrlogvgante
 Esercizio 0 Scambio lettere Scrivere la funzione void scambiolettere(char *dest, char *lettere, int p_o_d) che modifichi la stringa destinazione (dest), sostituendone i caratteri pari o dispari (a seconda
Esercizio 0 Scambio lettere Scrivere la funzione void scambiolettere(char *dest, char *lettere, int p_o_d) che modifichi la stringa destinazione (dest), sostituendone i caratteri pari o dispari (a seconda
EXCEL PER WINDOWS95. sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area di lavoro, detta foglio di lavoro,
 EXCEL PER WINDOWS95 1.Introduzione ai fogli elettronici I fogli elettronici sono delle applicazioni che permettono di sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area
EXCEL PER WINDOWS95 1.Introduzione ai fogli elettronici I fogli elettronici sono delle applicazioni che permettono di sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area
la scienza della rappresentazione e della elaborazione dell informazione
 Sistema binario Sommario informatica rappresentare informazioni la differenza Analogico/Digitale i sistemi di numerazione posizionali il sistema binario Informatica Definizione la scienza della rappresentazione
Sistema binario Sommario informatica rappresentare informazioni la differenza Analogico/Digitale i sistemi di numerazione posizionali il sistema binario Informatica Definizione la scienza della rappresentazione
I NUMERI DECIMALI. che cosa sono, come si rappresentano
 I NUMERI DECIMALI che cosa sono, come si rappresentano NUMERI NATURALI per contare bastano i numeri naturali N i numeri naturali cominciano con il numero uno e vanno avanti con la regola del +1 fino all
I NUMERI DECIMALI che cosa sono, come si rappresentano NUMERI NATURALI per contare bastano i numeri naturali N i numeri naturali cominciano con il numero uno e vanno avanti con la regola del +1 fino all
I PROBLEMI ALGEBRICI
 I PROBLEMI ALGEBRICI La risoluzione di problemi è una delle attività fondamentali della matematica. Una grande quantità di problemi è risolubile mediante un modello algebrico costituito da equazioni e
I PROBLEMI ALGEBRICI La risoluzione di problemi è una delle attività fondamentali della matematica. Una grande quantità di problemi è risolubile mediante un modello algebrico costituito da equazioni e
ESAME SCRITTO DI ELEMENTI DI INFORMATICA E PROGRAMMAZIONE. 27 Gennaio 2015
 COGNOME E NOME: MATRICOLA: Civile Ambiente e Territorio Non si possono consultare manuali, appunti e calcolatrici. Esercizio 1: [3 punto] Rappresentare i numeri 36 e 91 (in base 10) in notazione binaria
COGNOME E NOME: MATRICOLA: Civile Ambiente e Territorio Non si possono consultare manuali, appunti e calcolatrici. Esercizio 1: [3 punto] Rappresentare i numeri 36 e 91 (in base 10) in notazione binaria
La selezione binaria
 Andrea Marin Università Ca Foscari Venezia Laurea in Informatica Corso di Programmazione part-time a.a. 2011/2012 Introduzione L esecuzione di tutte le istruzioni in sequenza può non è sufficiente per
Andrea Marin Università Ca Foscari Venezia Laurea in Informatica Corso di Programmazione part-time a.a. 2011/2012 Introduzione L esecuzione di tutte le istruzioni in sequenza può non è sufficiente per
