Esercizio 1. Si consideri il sistema di equazioni differenziali lineari. ẋ = Ax, x R 4, A =
|
|
|
- Costanzo Leoni
- 4 anni fa
- Visualizzazioni
Transcript
1 Tutorato I - Roberto Feola e Luca Battaglia ( ) Esercizio. Si consideri il sistema di equazioni differenziali lineari ẋ = Ax, x R 3, A = 2 0, 5 3 con dato iniziale x(0) = (,,0). Se ne trovi la soluzione. Esercizio 2. Si consideri il sistema di equazioni differenziali lineari ẋ = x y + z ẏ = x y z ż = 2x 2y con condizioni iniziali generiche (x(0),y(0),z(0)) = (x 0,y 0,z 0 ). Se ne trovi la soluzione e si verifichi in particolare che il moto descritto dal sistema avviene in un piano, individuando al variare dei dati iniziali il piano su cui si svolge. Esercizio 3. Si consideri il sistema di equazioni differenziali lineari ẋ = Ax, x R 4, A = , con dato iniziale x(0) = (,0,,2). Se ne trovi la soluzione. Esercizio 4.Si consideri il sistema di equazioni differenziali lineari ( ) = Ax 0 A =, x(0) = (,) α 2 Se ne trovi la soluzione al variare del parametro α R. Esercizio 5. Si consideri il sistema di equazioni differenziali lineari ẋ = Ax, x R n A = con condizioni iniziali x(0) = (2,...,2). Se ne determini la soluzione. Esercizio 6. Dimostrare che se, data una matrice A, esistono λ R e n 2 tale che A n = λa, allora expa è un polinomio di grado n in A, e calcolare esplicitamente i coefficienti.
2 Tutorato 2 - Roberto Feola e Luca Battaglia (/03/2009) Esercizio. Si dica per quali λ R il problema ẍ + λx = 0 x(0) = 0 x() = 0 ammette soluzioni non banali, e per tali λ determinare queste soluzioni. Esercizio 2. Risolvere il seguente problema di Cauchy... x 5ẍ + 8ẋ 4x = 0 x(0) = ẋ(0) = 0 ẍ(0) = 2 Esercizio 3.Si consideri il seguente problema di Cauchy ẍ εẋ 4x = εe t x(0) = ẋ(0) = 0 Se ne determini la soluzione al variare di ε 0. Esercizio 4.Determinare le equazioni della curva piana γ(t) = (x(t), y(t)) tale che le sue componenti verificano = y + cos t e passante per il punto (, 0). ẏ = x 3 sint Esercizio 5.Si consideri il seguente sistema di equazioni differenziali lineari { ẋ = Ax x(0) = x 0 x R 3. Si dimostri che se deta = 0 il moto descritto dal sistema avviene in un piano per qualunque scelta del dato iniziale x 0 R 3 Esercizio 6. Si determini la soluzione dell equazione differenziale lineare non omogenea ẋ = x + f(t) in funzione del dato iniziale x(0) = x 0. Si usi tale risultato per dimostrare che la soluzione del sistema di equazioni differenziali lineari x = x x 2 = x + x 2 k x 3 = x 2 + x 3 con condizioni iniziali x k (0) = k =,...,n è x k (t) = e t t j k =,...,n. j!... j=0 x n = x n + x n Si calcoli infine lim x n(t). n (Suggerimento: per il secondo punto, può essere utile procedere per induzione)
3 Tutorato 3 - Roberto Feola e Luca Battaglia ( ) Esercizio. Risolvere il seguente problema di Cauchy: = x 2 + 2tx + t 2 x(0) = (Suggerimento:si consideri il cambio di variabile y = x + t) Esercizio 2. Risolvere il seguente problema di Cauchy: ẋ = tx2 e t t 2 xe t x() = 2 (Suggerimento:considerare la sostituzione y = tx) Esercizio 3. Risolvere il seguente problema di Cauchy: t ẋ = x(2t 2 t 4 2) π x(0) = 2 Mostrare che l intervallo massimale di esistenza della soluzione è un chiuso e spiegare perchè questo non contraddice quanto visto a lezione. Esercizio 4.Risolvere il seguente problema di Cauchy ẋ = t(x + 2t) + (x + t)(4x t) 2 x(0) = α al variare di α R.Determinare l intervallo di definizione della soluzione. (Suggerimento.Si cerchino soluzioni della forma x(t) = y(t) t 2 ) Esercizio 5.Usando il metodo della variazione delle costanti, trovare una formula risolutiva per il problema di Cauchy: ẍ + ω 2 x = f(t) x(0) = 0 ẋ(0) = 0 Esercizio 6. Risolvere il seguente problema di Cauchy... x ẍ + 4ẋ 4x = 3e t x(0) = 0 ẋ(0) = ẍ(0) = 2
4 Tutorato 4 - Roberto Feola e Luca Battaglia ( ) Esercizio. Sia dato il sistema dinamico planare = 2y( x 2 ) ẏ = 2x(y 2 ) (.)Determinare una costante del moto H(x,y) per il sistema tale che H(0,0) = 0. (.2)Determinare i punti di equilibrio del sistema e discuterne la stabilità. (.3)Studiare qualitativamente le traiettorie del sistema. (.4)Individuare i dati iniziali che danno origine a traiettorie periodiche. Dimostrare in particolare che la traiettoria con dato iniziale ( 2,0) lo è e scriverne il periodo come integrale definito. (.5)Determinare esplicitamente la soluzione con dato iniziale (x,y) = (,0). Esercizio 2.Sia dato il sistema dinamico planare = x 3 + 9y 2 x x ẏ = 3x 2 y 3y 3 + y (2.)Determinare una costante del moto per il sistema. (2.2)Determinare i punti d equilibrio e discuterne la stabilità (2.3)Studiare qualitativamente le curve di livello Γ E = {(x,y) R 2 : H(x, y) = E} (2.4)Individuare i dati iniziali che danno origine a traiettorie periodiche. Esercizio 3.Sia dato il sistema dinamico planare = e xy (2y 2) ẏ = e xy (4x 3 4x) (3.)Si mostri che la funzione H(x,y) = (y x 2 )(y + x 2 2) è una costante del moto per il sistema. (3.2)Si determinino i punti di equilibrio del sistema. (3.3)Se ne discuta la stabilità. (3.4)Si studino qualitativamente le traiettorie del sistema. Esercizio 4. Sia dato il sistema dinamico planare = x 2y 2 ẏ = 2y 2x 2 (4.)Determinare i punti di equilibrio e discuterne la natura. (4.2)Stimare il bacino di attrazione di eventuali punti d equilibrio asintoticamente stabili.
5 Tutorato 5 - Roberto Feola e Luca Battaglia ( ) Esercizio.Sia dato il sistema gradiente della forma dove ż = V (z), z = (x,y) R 2 V (x,y) = y 2 + x 2 (x + 2) 2 (.)Determinare i punti di equilibrio e discuterne la stabilità. (.2)Analizzare qualitativamente le curve di livello. (.3)Stimare il bacino di attrazione di eventuali punti asintoticamente stabili. Esercizio 2.Sia dato il sistema dinamico planare ẋ = H y ẏ = H x dove H(x,y) = x 2 y(x + y 2 + )(x y 2 ) (2.)Si determinino i punti di equilibrio del sistema. (2.2)Se ne discuta la stabilità. (2.3)Si studino qualitativamente le traiettorie del sistema. (2.4)Si dimostri che non esistono traiettorie periodiche. Esercizio 3.Si consideri il sistema di equazioni differenziali non lineari = y x 3 xy 2 ẏ = x x 2 y y 3 (3.)Si dimostri che l origine è un punto asintoticamente stabile. (3.2)Si dimostri che il suo bacino d attrazione è tutto il piano. (3.3)Si trovi la forma esplicita di ρ(t) = x 2 (t) + y 2 (t). (3.4)Si determinino esplicitamente le soluzioni del sistema. (Suggerimento:per l ultimo punto può essere conveniente utilizzare coordinate polari (ρ,θ).) Esercizio 4.Sia dato il sistema gradiente ẋ = V x, ẏ = V y, V (x,y) = e (x2 +y 2). (4.)Si determinino i punti di equilibrio e studiarne la stabilità. (4.2)Studiare qualitativamente le traiettorie del sistema. (4.3)Studiare il bacino d attrazione di eventuali punti di equilibrio asintoticamente stabili. Esercizio d esame 5/09/2008
6 Tutorato 6 - Roberto Feola e Luca Battaglia ( ) Esercizio.Si consideri il sistema di equiazioni differenziali lineari 2 0 ẋ = Ax, x R 3, A = 0 0, con dato iniziale x(0) = (2,,0).Se ne trovi la soluzione. Esercizio 2.Dato il problema di Cauchy in R = x x x(0) = x 0 si risponda alle seguenti domande: (2.)Quante soluzioni esistono? (2.2)Si trovi esplicitamente una soluzione e se e discuta la regolarità in t (2.3)Si verifichi che x 0 = 0 è un punto di equilibrio asintoticamente stabile e si studi il suo bacino di attrazione. Esercizio 3.Sia dato il sistema dinamico planare = 2xy xe x 2 (3.)Verificare che la funzione ẏ = ye x2 2x 2 ye x2 y 2 H(x,y) = xy(y e x2 ) è una costante del moto per il sistema. (3.2)Determinare i punti di equilibrio del sistema e discuterne la stabilità. (3.3)Studiare qualitativamente le curve di livello Γ E = {(x, y) R 2 : H(x,y) = E} nel piano delle fasi e analizzare i versi di percorrenza delle corrispondenti traiettorie. (3.4)Individuare i dati iniziali che danno origine a traiettorie periodiche. Esercizio 4.Sia dato il sistema gradiente planare ẋ = V x ẏ = V V (x,y) = y 2 x 6 + 6x 4 9x 2 y (4.)Determinare i punti di equilibrio del sistema. (4.2)Studiarne la stabilità. (4.3)Studiare qualitativamente le traiettorie del sistema. (4.4)Stimare il bacino di attrazione di eventuali punti asintoticamente stabili.
7 Tutorato 7 - Roberto Feola e Luca Battaglia ( ) Esercizio.Si consideri il sistema meccanico unidimensionale che descrive un punto materiale di massa m =, soggetto alla forza di energia potenziale V (x) = x(x2 2) x 2 (.)Scrivere le equazioni del sistema dinamico associato. (.2)Determinare eventuali punti d equilibrio e discuterne la stabilità. (.3)Studiare qualitativamente il grafico dell energia potenziale. (.4)Analizzare qualitativamente il moto nel piano delle fasi. Esercizio 2.Si consideri il sistema meccanico unidimensionale che descrive un punto materiale di massa m = soggetto alla forza di energia potenziale V (x) = e x2 (2x 3 3x 2 + ) (2.)Scrivere le equazioni del sistema dinamico associato. (2.2)Verificare che l energia E(x,y) = 2 y2 + V (x) con y = ẋ, è una costante del moto. (2.3)Studiare qualitativamente il grafico dell energia potenziale. (2.4)Determinare eventuali punti di equilibrio e discuterne la stabilità. (2.5)Analizzare qualitativamente il moto nel piano (x,ẋ). (2.6)Determinare l insieme dei dati iniziali che danno origine a traiettorie periodiche. Esercizio 3.Si consideri il sistema meccanico unidimensionale che descrive un punto materiale di massa m = soggetto alla forza di energia potenziale V (x) = 3x 4 8αx 3 + 6x 2 Al variare del parametro α 0, rispondere alle seguenti domande: (2.)Scrivere le equazioni del sistema dinamico associato. (2.2)Determinare eventuali punti di equilibrio e discuterne la stabilità. (2.3)Studiare qualitativamente il grafico dell energia potenziale. (2.4)Discutere qualitativamente il moto nel piano (x,y) = (x,ẋ).
8 Tutorato 8 - Roberto Feola e Luca Battaglia ( ) Esercizio.Si consideri il sistema meccanico unidimensionale che descrive un punto materiale di massa m = soggetto alla forza di energia potenziale V (x) = x 3 e x (.)Scrivere le equazioni del sistema dinamico associato. (.2)Determinare eventuali punti di equilibrio e discuterne la stabilità. (.3)Studiare qualitativamente il grafico dell energia potenziale. (.4)Discutere qualitativamente il moto nel piano (x,y) = (x,ẋ). (.5)Determinare l insieme dei dati iniziali che danno origine a traiettorie periodiche. Esercizio 2.Si consideri il sistema meccanico unidimensionale che descrive un punto materiale di massa m = soggetto alla forza F(x) = 5x 3 2x 7 (2.)Scrivere le equazioni del moto e le equazioni del sistema dinamico associato. (2.2)Determinare eventuali punti di equilibrio del sistema dinamico e discuterne la stabilità. (2.3)Studiare qualitativamente il grafico dell energia potenziale V (x) corrispondente alla forza F(x) e tale che V (0) = 0. (2.4)Discutere qualitativamente il moto nel piano (x,y) = (x,ẋ). (2.5)Verificare che la traiettoria con dati iniziali ( x, x) = (, 0) è periodica, scriverne il periodo come integrale definito e darne una stima. Esercizio 3.Si consideri il sistema meccanico unidimensionale che descrive un punto materiale di massa m = soggetto alla forza di energia potenziale V (x) = x 3 4x + α x al variare di α R rispondere alle seguenti domande: (3.)Scrivere le equazioni del sistema dinamico associato. (3.2)Determinare eventuali punti di equilibrio e discuterne la stabilità. (3.3)Studiare qualitativamente il grafico dell energia potenziale. (3.4)Discutere qualitativamente il moto nel piano (x,y) = (x,ẋ).
9 Tutorato 9 - Roberto Feola e Luca Battaglia ( ) Esercizio.Si considerino due punti materiali di massa m = m 2 = 2 che interagiscono attraverso una forza centrale di energia potenziale V (ρ) = log ρ ρ 4 dove ρ = r e r = r r 2 è il vettore che individua la posizione relativa dei due punti. (.)Descrivere il moto nel sistema del centro di massa, in modo da ricondursi a un sistema a due gradi di libert a nelle variabili polari (ρ,θ). (.2)Determinare eventuali punti di equilibrio e discuterne la stabilità. (.3)Studiare qualitativamente il grafico del potenziale efficace. (.4)Discutere qualitativamente il moto nel piano (ρ, ρ). (.5)Determinare le traiettorie periodiche nel piano (ρ, ρ). (.6)Scrivere la variazione di θ(t) in funzione di ρ(t) e dire sotto quali condizioni il moto complessivo del sistema è periodico. Esercizio 2.Si considerino due punti materiali di massa m = m 2 = 2,che interagiscono mediante una forza centrale di energia potenziale V (ρ) = log ρ 2α ρ dove ρ = r e r = r r 2 è il vettore che individua la posizione relativa dei due punti e α R. Rispondere alle domande seguenti al variare del parametro α e del modulo L 0 del momento angolare del sistema. (2.)Scrivere le equazioni di Newton e il sistema dinamico associato. (2.2)Determinare eventuali punti di equilibrio e discuterne la stabilità. (2.3)Studiare qualitativamente il grafico del potenziale efficace. (2.4)Analizzare qualitativamente il moto nel piano (ρ, ρ). (2.5)Determinare le traiettorie periodiche nel piano (ρ, ρ) Esercizio 3.Si consideri il sistema meccanico unidimensionale che descrive un punto materiale di massa m = soggetto alla forza di energia potenziale V (x) = 4 sin 3 x + 3 sin 2 x, x T = R/2πZ (3.)Scrivere le equazioni del sistema dinamico associato. (3.2)Determinare eventuali punti di equilibrio e discuterne la stabilità. (3.3)Studiare qualitativamente il grafico dell energia potenziale. (3.4)Discutere qualitativamente il moto nel piano (x,y) = (x,ẋ). (3.5)Determinare l insieme dei dati iniziali che danno origine a traiettorie periodiche. (3.6)Verificare in particolare che esiste una traiettoria periodica per E = 0 e scriverne il periodo come integrale definito.
10 Tutorato 0 - Roberto Feola e Luca Battaglia ( ) Esercizio.Si consideri un punto materiale di massa m = soggetto a una forza centrale di energia potenziale V (ρ) = ρ2 2 2 log ρ α ρ 2 Rispondere alle seguenti domande al variare di α 0. (.)Scrivere le equazioni di Newton e il sistema dinamico associato. (.2)Determinare eventuali punti di equilibrio e discuterne la stabilità. (.3)Studiare qualitativamente il grafico del potenziale efficace. (.4)Discutere qualitativamente il moto nel piano (ρ, ρ). (.5)Determinare le traiettorie periodiche nel piano (ρ, ρ). Esercizio 2.Si consideri un punto materiale di massa m = soggetto a una forza centrale di energia potenziale V (ρ) = 2ρ αρ 4 Rispondere alle seguenti domande al variare di α 0 (2.)Scrivere le equazioni di Newton e il sistema dinamico associato. (2.2)Determinare eventuali punti di equilibrio e discuterne la stabilità. (2.3)Studiare qualitativamente il grafico del potenziale efficace. (2.4)Analizzare qualitativamente il moto nel piano (ρ, ρ). (2.5)Determinare le traiettorie periodiche nel piano (ρ, ρ). Esercizio 3.Si consideri un punto materiale di massa m = soggetto ad una forza centrale di energia potenziale ( 3ρ 2 ) + 2 V (ρ) = log 2ρ (3.)Scrivere le equazioni di Newton e il sistema dinamico associato. (3.2)Determinare eventuali punti di equilibrio e discuterne la stabilità. (3.3)Studiare qualitativamente il grafico del potenziale efficace. (3.4)Studiare qualitativamente il moto nel piano (ρ, ρ). (3.5)Determinare le traiettorie periodiche nel piano (ρ, ρ).
11 Tutorato - Roberto Feola e Luca Battaglia ( ) Esercizio.Dato un sistema di riferimento κ = Oxyz (sistema assoluto), si consideri un sistema di riferimento mobile K = O ξηζ (sistema relativo), la cui origine si muove nel piano (x,y) lungo la parabole di equazioni y = x 2 in modo tale che la sua componente lungo l asse x sia x O (t) = t. L asse ζ di K si mantiene parallelo all asse z di κ, mentre l asse ξ si mantiene sempre tangente alla parabola.un punto P di massa m = si muove nel sistema K lungo l asse ξ secondo la legge oraria ξ(t) = e t. (.)Scrivere la trasformazione rigida D : K κ come composizione di una traslazione C con una rotazione B, D = C B, e determinare la forma di C e B. (.2)Determinare il moto q(t) nel sistema di riferimento assoluto κ e il moto Q(t) nel sistema di riferimento relativo K. (.3)Determinare la velocità assoluta v. (.4)Determinare la velocità relativa v. (.5)Determinare la componente traslatoria della velocità di trascinamento v 0. (.6)Determinare la componente rotatoria della velocità di trascinamento v T. (.7)Determinare la forza centrifuga e la forza di Coriolis che agiscono sul punto P. Suggerimento: si ricorda che cos(arctan x) = + x 2 e sin(arctanx) = x + x 2 Esercizio 2.Dato un sistema di riferimento κ = Oxyz (sistema assoluto), si consideri un sistema di riferimento mobile K = O ξηζ (sistema relativo) che all istante t = 0 coincide con κ e ruota attorno all asse ζ, parallelo a z, con velocità angolare costante ω.l origine O si muove lungo l asse z con legge oraria z O (t) = t. Un punto P di massa m = si muove nel sistema K secondo le equazioni ξ = η η = ξ ζ = α dove α è un parametro reale, e al tempo t = 0 si trova nel punto (ξ(0),η(0),ζ(0)) = (,0, 0). (2.)Scrivere la trasformazione rigida D : K κ come composizione di una traslazione C con una rotazione B, D = C B, e determinare la forma di C e B. (2.2)Determinare il moto q(t) nel sistema di riferimento assoluto κ e il moto Q(t) nel sistema di riferimento relativo K. (2.3)Determinare la velocità assoluta v. (2.4)Determinare la velocità relativa v. (2.5)Determinare la componente traslatoria della velocità di trascinamento v 0. (2.6)Determinare la componente rotatoria della velocità di trascinamento v T. (2.7)Determinare la forza centrifuga e la forza di Coriolis che agiscono sul punto P. (2.8)Discutere sotto quali condizioni sui parametri ω e α il punto P ha un moto periodico nel sistema κ. (2.9)Discutere sotto quali condizioni sui parametri ω e α il punto P risulta fermo nel sistema κ. Suggerimento: si ricorda che cos(x + y) = cos xcos y sin xsin y e sin(x + y) = sin xcos y + cos xsin y Esercizio 3.Dato un sistema di riferimento κ = Oxyz (sistema assoluto) si consideri un sistema di riferimento mobile K = O ξηζ (sistema relativo), la cui origine si muove lungo la curva γ(t) = (x(t),y(t),0) tale che le sue componenti verificano = 2y x 2 + ẏ = 2xy L asse ξ di K si mantiene tangente alla curva q O (t), mentre l asse ζ si mantiene parallelo all asse z di κ; all istante iniziale O occupa la posizione q O (0) = (0,,0) e gli assi ξ e η sono diretti come gli assi x e
12 y rispettivamente. Un punto P di massa m = si muove in K lungo l asse ξ sotto l azione di una forza conservativa di energia potenziale V (ξ) = ξ 2 con dato iniziale ξ(0) = 0 ed energia meccanica E = 0. (3.)Scrivere la trasformazione rigida D : K κ come composizione di una traslazione con una rotazione D = C B e determinare la forma di C e B. (3.2)Scrivere la legge del moto nei sistemi K e κ. (3.3)Determinare la velocità assoluta v e la velocità relativa v. (3.4)Scrivere la componente traslatoria della velocità di trascinamento v 0. (3.5)Scrivere la componente rotatoria della velocità di trascinamento v T. (3.6)Determinare la forza centrifuga e la forza di Coriolis che agiscono sul punto P. 2
13 Tutorato 2 - Roberto Feola e Luca Battaglia ( ) Esercizio.Si consideri un sistema meccanico unidimensionale che descrive un punto materiale di massa m = soggetto alla forza di energia potenziale V (x) = x n Al variare del parametro n N, si risponda alle seguenti domande: (.)Si studi il grafico dell energia potenziale. (.2)Si determinino i punti di equilibrio del sistema dinamico associato. (.3)Se ne discuta la stabilità. (.4)Si studino qualitativamente le traiettorie del sistema. (.5)In particolare di dimostri che, al variare di n,o tutti i dati iniziali che non siano punti di equilibrio danno luogo a traiettorie periodiche o non esistono traiettorie periodiche.nel primo caso si scriva il periodo T come integrale definito. (.6)Si espliciti la dipendenza dall energia E del periodo trovato al punto precedente. (.7)Si dica per quale valore di n il periodo T non dipende da E, e calcolarlo esplicitamente. Esercizio 2.Dato un sistema di riferimento κ = Oxyz (sistema assoluto) si consideri un sistema mobile K = O ξηζ la cui origine si muove lungo la curva piana γ(t) = (γ (t),γ 2 (t)) tale che le sue componenti verificano { γ = 2γ 2γ 2 γ 2 = 2γ + 2γ 2 La componente lungo l asse x che individua il punto O varia secondo la legge oraria x O (t) = γ (t).l asse ζ di K si mantiene parallelo all asse z di κ mentre l asse ξ di K si mantiene tangente a γ(t).all istante iniziale il punto O occupa la posizione q O = (,0,0).Un punto P di massa m = si muove nel sistema K lungo l asse ξ sotto l azione di una molla di costante elastica λ > 0. (2.)Scrivere la trasformazione rigida D : K κ come composizione di una traslazione con una rotazione D = C B e determinare la forma di C e B. (2.2)Scrivere la legge del moto nei sistemi κ e K. (2.3)Determinare la velocità assoluta v e la velocità relativa v. (2.4)Scrivere la componente traslatoria della velocità di trascinamento v 0. (2.5)Scrivere la componente rotatoria della velocità di trascinamento v T. (2.6)Determinare la forza centrifuga che agisce sul punto P. (2.7)Determinare la forza di Coriolis che agisce sul punto P. Esercizio 3.Si consideri un punto materiale di massa µ soggetto a una forza centrale di energia potenziale V (ρ) = ρ4 4 α 8ρ 8 dove α R.Al variare del parametro e del momento angolare L,si risponda alle seguenti domande. (3.)Si scriva l equazione del moto per la variabile ρ e il sistema dinamico associato. (3.2)Si determinino i punti di equilibrio. (3.3)Si discuta la stabilità dei punti di equilibrio. (3.4)Si disegni il grafico dell energia potenziale efficace. (3.5)Si analizzino qualitativamente le orbite nel piano (ρ, ρ). (3.6)Si determinino le traiettorie periodiche nel piano (ρ, ρ). (3.7)Si discutano le condizioni sotto le quali il moto complessivo del sistema è periodico. Esercizio esame 07/06/2007
Esercizi di preparazione alla PFB
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Esercizi di preparazione alla PFB A.A. 0-03 - Docenti: A. Bruno e G. Gentile Tutori: Sara Lamboglia e Maria Chiara Timpone Parte : Analisi
Università degli Studi Roma Tre - Corso di Laurea in Matematica Esercizi di preparazione alla PFB A.A. 0-03 - Docenti: A. Bruno e G. Gentile Tutori: Sara Lamboglia e Maria Chiara Timpone Parte : Analisi
Esercizi di preparazione alla PFB
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Esercizi di preparazione alla PFB.. 2012-2013 - Docente:. Bruno e G. Gentile Tutori: Sara Lamboglia e Maria Chiara Timpone 1. Dato p > 0
Università degli Studi Roma Tre - Corso di Laurea in Matematica Esercizi di preparazione alla PFB.. 2012-2013 - Docente:. Bruno e G. Gentile Tutori: Sara Lamboglia e Maria Chiara Timpone 1. Dato p > 0
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
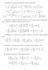 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
II compito di esonero di Meccanica Razionale per fisici del 2 maggio 1989 Università dell Aquila
 II compito di esonero di Meccanica Razionale per fisici del 2 maggio 1989 Università dell Aquila Agli estremi di una sbarretta di lunghezza 2l e massa trascurabile sono saldate due particelle puntiformi
II compito di esonero di Meccanica Razionale per fisici del 2 maggio 1989 Università dell Aquila Agli estremi di una sbarretta di lunghezza 2l e massa trascurabile sono saldate due particelle puntiformi
FM210 - Fisica Matematica I
 Corso di laurea in Matematica - Anno Accademico 11/1 FM1 - Fisica Matematica I Soluzioni al tutorato del 9-1-1 1. Due particelle di massa m e coordinate x, y R si muovono sotto l effetto di una forza centrale
Corso di laurea in Matematica - Anno Accademico 11/1 FM1 - Fisica Matematica I Soluzioni al tutorato del 9-1-1 1. Due particelle di massa m e coordinate x, y R si muovono sotto l effetto di una forza centrale
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017
 Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017 ẋ = x(µ x 2 )(x µ + 2) 2. Si calcoli la matrice esponenziale della matrice [ ] 2 4. 0 2 3. Dato il sistema differenziale lineare non omogeneo
Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017 ẋ = x(µ x 2 )(x µ + 2) 2. Si calcoli la matrice esponenziale della matrice [ ] 2 4. 0 2 3. Dato il sistema differenziale lineare non omogeneo
Esercizi proposti di Meccanica Razionale
 Esercizi proposti di Meccanica Razionale Docente Alessandro Teta a.a. 2015/16 1 Equazioni differenziali ordinarie Esercizio 1.1. Si consideri il sistema ẋ = ax (1 y) ẏ = cy (1 x) definito in D = {(x, y)
Esercizi proposti di Meccanica Razionale Docente Alessandro Teta a.a. 2015/16 1 Equazioni differenziali ordinarie Esercizio 1.1. Si consideri il sistema ẋ = ax (1 y) ẏ = cy (1 x) definito in D = {(x, y)
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
Foglio di Esercizi 7 Meccanica Razionale a.a. 2018/19 Canale A-L (P. Buttà)
 Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Corso di Laurea in Ingegneria Gestionale - Sede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame
 Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
FM210 - Fisica Matematica I
 Corso di laurea in Matematica - Anno Accademico 03/4 FM0 - Fisica Matematica I Primo appello scritto [0-0-04]. (0 punti). Si consideri il sistema lineare { ẋ = αx + y + ẏ = α x + 3y con α R. (a) Si discuta
Corso di laurea in Matematica - Anno Accademico 03/4 FM0 - Fisica Matematica I Primo appello scritto [0-0-04]. (0 punti). Si consideri il sistema lineare { ẋ = αx + y + ẏ = α x + 3y con α R. (a) Si discuta
Equazioni Differenziali
 Università degli Studi di Udine Anno Accademico 2012/2013 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Equazioni Differenziali Appello del 5 febbraio 2013 N.B.: scrivere
Università degli Studi di Udine Anno Accademico 2012/2013 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Equazioni Differenziali Appello del 5 febbraio 2013 N.B.: scrivere
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione
![Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione](/thumbs/88/116749009.jpg) Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 30 Gennaio 2009
 Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 30 Gennaio 2009 Dipartimento di Matematica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli, G. Gentile Istruzioni (a) La sufficienza
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 30 Gennaio 2009 Dipartimento di Matematica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli, G. Gentile Istruzioni (a) La sufficienza
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
, con x =, y. 3. Si disegni il grafico delle curve di livello sul piano delle fasi (x, ẋ) al variare di E e si discuta la natura qualitativa del moto.
 7 o tutorato - MA - Prova Pre-Esonero - 8/4/5 Esercizio Una massa puntiforme m è vincolata a muoversi nel piano verticale xy (con x l asse orizzontale e y l asse verticale orientato verso l alto), su una
7 o tutorato - MA - Prova Pre-Esonero - 8/4/5 Esercizio Una massa puntiforme m è vincolata a muoversi nel piano verticale xy (con x l asse orizzontale e y l asse verticale orientato verso l alto), su una
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 3 Ottobre 2007
 Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 3 Ottobre 2007 Dipartimento di Matematica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli, G. Gentile Istruzioni (a) La sufficienza
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 3 Ottobre 2007 Dipartimento di Matematica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli, G. Gentile Istruzioni (a) La sufficienza
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12. Corsi di laurea in Ingegneria Elettronica ed Informatica
 Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
Esame di ammissione al Dottorato in Matematica, XXIV Ciclo Università di Firenze Tema n. 1.
 Esame di ammissione al Dottorato in Matematica, XXIV Ciclo Università di Firenze Tema n. 1. Esercizio 1. Un punto materiale di massa m si muove su un piano orizzontale, vincolato senza attrito alla curva
Esame di ammissione al Dottorato in Matematica, XXIV Ciclo Università di Firenze Tema n. 1. Esercizio 1. Un punto materiale di massa m si muove su un piano orizzontale, vincolato senza attrito alla curva
Prova scritta di Analisi Matematica III
 18 luglio 2016 f n (x) = 1 n e (x n)2 (x R, n N ). 2. Si scriva la disuguaglianza di Bessel per la funzione f, periodica di periodo 2π, tale che 0 x [ π, 0) f (x) = 2 x x [0, π). 3. Si consideri l equazione
18 luglio 2016 f n (x) = 1 n e (x n)2 (x R, n N ). 2. Si scriva la disuguaglianza di Bessel per la funzione f, periodica di periodo 2π, tale che 0 x [ π, 0) f (x) = 2 x x [0, π). 3. Si consideri l equazione
Soluzioni del Tutorato 4 (29/03/2017)
 1 Soluzioni del Tutorato 4 (29/3/217) Esercizio 1 Si consideri il moto di una particella di massa m = 1 soggetta a una forza centrale di potenziale V ( r ) = log( r ) Si studi qualitativamente il moto
1 Soluzioni del Tutorato 4 (29/3/217) Esercizio 1 Si consideri il moto di una particella di massa m = 1 soggetta a una forza centrale di potenziale V ( r ) = log( r ) Si studi qualitativamente il moto
ESERCIZI DI ANALISI MATEMATICA II. sin(tv) v. f(v) dv = (1 + t) (e 1/t + 1)
 ESERCIZI DI ANALISI MATEMATICA II Equazioni differenziali ED 1 Stabilire se l equazione integrale f(t) 1/2 0 sin(tv) v f(v) dv = (1 + t) (e 1/t + 1) ammette una soluzione nello spazio C([0, 1/2]). (Suggerimento:
ESERCIZI DI ANALISI MATEMATICA II Equazioni differenziali ED 1 Stabilire se l equazione integrale f(t) 1/2 0 sin(tv) v f(v) dv = (1 + t) (e 1/t + 1) ammette una soluzione nello spazio C([0, 1/2]). (Suggerimento:
Analisi Matematica 3
 Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
FM210 - Fisica Matematica I
 Corso di laurea in Matematica - Anno Accademico 2/4 FM2 - Fisica Matematica I Prima Prova di Esonero [--2]. (2 punti). Si consideri il sistema lineare ẋ = αx + x 2 + α, ẋ 2 = x + 2α, ẋ = α 2 x 2 con α
Corso di laurea in Matematica - Anno Accademico 2/4 FM2 - Fisica Matematica I Prima Prova di Esonero [--2]. (2 punti). Si consideri il sistema lineare ẋ = αx + x 2 + α, ẋ 2 = x + 2α, ẋ = α 2 x 2 con α
FM210 - Fisica Matematica 1 Tutorato VI - Roberto Feola (soluzioni degli esercizi)
 Corso di laurea in Matematica - Anno Accademico 011/01 FM10 - Fisica Matematica 1 Tutorato VI - Roberto Feola (soluzioni degli esercizi) Esercizio 1. Poniamo r = x e notiamo che l equazione che descrive
Corso di laurea in Matematica - Anno Accademico 011/01 FM10 - Fisica Matematica 1 Tutorato VI - Roberto Feola (soluzioni degli esercizi) Esercizio 1. Poniamo r = x e notiamo che l equazione che descrive
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI
 SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
Foglio di Esercizi 5 Meccanica Razionale a.a. 2017/18 Canale A-L (P. Buttà)
 Foglio di Esercizi 5 Meccanica Razionale a.a. 017/18 Canale A-L (P. Buttà) Esercizio 1. Su un piano orizzontale sono poste due guide immateriali circolari di centri fissi O 1 e O e uguale raggio r; sia
Foglio di Esercizi 5 Meccanica Razionale a.a. 017/18 Canale A-L (P. Buttà) Esercizio 1. Su un piano orizzontale sono poste due guide immateriali circolari di centri fissi O 1 e O e uguale raggio r; sia
Corsi di laurea in Matematica e Fisica - Anno Accademico 2017/18 FM210 / MA. Prima Prova di Esonero [ ]
![Corsi di laurea in Matematica e Fisica - Anno Accademico 2017/18 FM210 / MA. Prima Prova di Esonero [ ] Corsi di laurea in Matematica e Fisica - Anno Accademico 2017/18 FM210 / MA. Prima Prova di Esonero [ ]](/thumbs/97/134636190.jpg) Corsi di laurea in Matematica e Fisica - Anno Accademico 017/18 FM10 / MA Prima Prova di Esonero [9-4-018] 1. Un punto materiale di massa m si muove in una dimensione sotto l effetto di una forza posizionale,
Corsi di laurea in Matematica e Fisica - Anno Accademico 017/18 FM10 / MA Prima Prova di Esonero [9-4-018] 1. Un punto materiale di massa m si muove in una dimensione sotto l effetto di una forza posizionale,
Prova Finale di Tipo B e Prova di Accesso alla Laura Special. Dip. Matematica - Università Roma Tre. 2 febbraio 2005
 Prova Finale di Tipo B e Prova di Accesso alla Laura Special Dip. Matematica - Università Roma Tre 2 febbraio 2005 Istruzioni. a) La sufficienza viene raggiunta con un punteggio di almeno 20 punti in ciascuno
Prova Finale di Tipo B e Prova di Accesso alla Laura Special Dip. Matematica - Università Roma Tre 2 febbraio 2005 Istruzioni. a) La sufficienza viene raggiunta con un punteggio di almeno 20 punti in ciascuno
Sistemi Dinamici e Meccanica Classica A/A Alcuni Esercizi
 Sistemi Dinamici e Meccanica Classica A/A 2008 2009. Alcuni Esercizi G.Falqui, P. Lorenzoni, Dipartimento di Matematica e Applicazioni, Università di Milano Bicocca. Versione del 23 Dicembre 2008 con esercizi
Sistemi Dinamici e Meccanica Classica A/A 2008 2009. Alcuni Esercizi G.Falqui, P. Lorenzoni, Dipartimento di Matematica e Applicazioni, Università di Milano Bicocca. Versione del 23 Dicembre 2008 con esercizi
FM1 - Equazioni differenziali e meccanica
 Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x).
![x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x). x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x).](/thumbs/102/153351382.jpg) Funzioni Esercizio Siano f, g due funzioni definite da fx) = x x 2, gx) = ln x Trovare l insieme di definizione di f e g 2 Determinare le funzioni composte f g e g f, precisandone insieme di definizione
Funzioni Esercizio Siano f, g due funzioni definite da fx) = x x 2, gx) = ln x Trovare l insieme di definizione di f e g 2 Determinare le funzioni composte f g e g f, precisandone insieme di definizione
FM210 - Fisica Matematica 1 Tutorato VII - Martha Faraggiana e Enzo Livrieri (soluzioni degli esercizi)
 Corso di laurea in Matematica - Anno Accademico 0/0 FM0 - Fisica Matematica Tutorato VII - Martha Faraggiana e Enzo Livrieri (soluzioni degli esercizi) Esercizio. Problema del secondo esonero A.A. 0-0
Corso di laurea in Matematica - Anno Accademico 0/0 FM0 - Fisica Matematica Tutorato VII - Martha Faraggiana e Enzo Livrieri (soluzioni degli esercizi) Esercizio. Problema del secondo esonero A.A. 0-0
FM210 - Fisica Matematica 1. Esercizio 1. Si consideri il sistema di equazioni differenziali lineari
 TUTORATO 1 (5-03-2019) FM210 - Fisica Matematica 1 sercizio 1. Si consideri il sistema di equazioni differenziali lineari ( ) ẋ = Ax, x R 2 3 2, A = 6 1 1. Si calcolino gli autovalori e gli autovettori.
TUTORATO 1 (5-03-2019) FM210 - Fisica Matematica 1 sercizio 1. Si consideri il sistema di equazioni differenziali lineari ( ) ẋ = Ax, x R 2 3 2, A = 6 1 1. Si calcolino gli autovalori e gli autovettori.
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 22 Settembre 2017
 Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 22 Settembre 2017 Dipartimento di Matematica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli, A. Giuliani Istruzioni (a) La sufficienza
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 22 Settembre 2017 Dipartimento di Matematica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli, A. Giuliani Istruzioni (a) La sufficienza
x = t y = t z = t 3 1 A = B = 1 2
 11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
Politecnico di Torino II Facoltà di Architettura Esame di Istituzioni di Matematiche I 15 gennaio 2004
 Esame di Istituzioni di Matematiche I 5 gennaio 2004 Monaco 02BJVa W0034 60 De ngelis 02BJVb W003 630 Pieraccini 0BJU Biglio 03BJV Esame completo Prova intermedia Teoria: teoremi sulle funzioni continue.
Esame di Istituzioni di Matematiche I 5 gennaio 2004 Monaco 02BJVa W0034 60 De ngelis 02BJVb W003 630 Pieraccini 0BJU Biglio 03BJV Esame completo Prova intermedia Teoria: teoremi sulle funzioni continue.
Raccolta di esercizi di Calcolo Numerico Prof. Michela Redivo Zaglia
 Raccolta di esercizi di Calcolo Numerico Prof. Michela Redivo Zaglia Nota Bene: Gli esercizi di questa raccolta sono solo degli esempi. Non sono stati svolti né verificati e servono unicamente da spunto
Raccolta di esercizi di Calcolo Numerico Prof. Michela Redivo Zaglia Nota Bene: Gli esercizi di questa raccolta sono solo degli esempi. Non sono stati svolti né verificati e servono unicamente da spunto
; c) log 3 5 (x 2 1) log 5 (x + 1). 1 log(x + 4) ; c) f(x) =
 Corso di Analisi Matematica I per Ingegneria Gestionale, a.a. 25-6 Esercizi per il ricevimento del 3 ottobre 25. Semplificare il più possibile le seguenti espressioni: a) 32x+4 9 ; b) x3 x 2 x+ ( x) 4
Corso di Analisi Matematica I per Ingegneria Gestionale, a.a. 25-6 Esercizi per il ricevimento del 3 ottobre 25. Semplificare il più possibile le seguenti espressioni: a) 32x+4 9 ; b) x3 x 2 x+ ( x) 4
Sistemi Dinamici 2. Esercitazioni
 Sistemi Dinamici Laurea Triennale in Matematica Applicata - II anno - II semestre Esercitazioni Es. 1 Stabilità Esercizio 1 Dimostrare che per un sistema autonomo ẋ = f(x) in R valgono le seguenti proprietà:
Sistemi Dinamici Laurea Triennale in Matematica Applicata - II anno - II semestre Esercitazioni Es. 1 Stabilità Esercizio 1 Dimostrare che per un sistema autonomo ẋ = f(x) in R valgono le seguenti proprietà:
Sistemi Dinamici e Meccanica Classica A/A Alcuni Esercizi
 Sistemi Dinamici e Meccanica Classica A/A 2008 2009. Alcuni Esercizi G.Falqui, P. Lorenzoni, Dipartimento di Matematica e Applicazioni,Università di Milano Bicocca. Seconda versione preliminare, 15 Dicembre
Sistemi Dinamici e Meccanica Classica A/A 2008 2009. Alcuni Esercizi G.Falqui, P. Lorenzoni, Dipartimento di Matematica e Applicazioni,Università di Milano Bicocca. Seconda versione preliminare, 15 Dicembre
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017
 Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
FM210 / MA - Prima prova pre-esonero ( )
 FM10 / MA - Prima prova pre-esonero (4-4-018) 1. Una particella di massa m si muove in una dimensione sotto l effetto di una forza posizionale, come descritto dalla seguente equazione: mẍ = A x xx 0 3x
FM10 / MA - Prima prova pre-esonero (4-4-018) 1. Una particella di massa m si muove in una dimensione sotto l effetto di una forza posizionale, come descritto dalla seguente equazione: mẍ = A x xx 0 3x
Tutorato Calcolo 2 Simone La Cesa, 15/11/2017
 1 Tutorato Calcolo Simone La Cesa, 15/11/017 Esercizi stabilità dei sistemi di equazioni differenziali e Funzioni di Lyapunov 1. Si consideri l equazione: mx + k(x + x 3 ) = 0 moto di una particella di
1 Tutorato Calcolo Simone La Cesa, 15/11/017 Esercizi stabilità dei sistemi di equazioni differenziali e Funzioni di Lyapunov 1. Si consideri l equazione: mx + k(x + x 3 ) = 0 moto di una particella di
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 1 Febbraio 2007
 Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 1 Febbraio 27 Dipartimento di Matematica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli, G. Gentile Istruzioni (a) La sufficienza
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 1 Febbraio 27 Dipartimento di Matematica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli, G. Gentile Istruzioni (a) La sufficienza
Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014
 Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014 MATRICOLA:...NOME e COGNOME:............................................. Desidero sostenere la prova orale al prossimo appello
Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014 MATRICOLA:...NOME e COGNOME:............................................. Desidero sostenere la prova orale al prossimo appello
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del sesto appello, 16 luglio 2018 Testi 1
 Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
Soluzione del Compitino di Sistemi Dinamici del 21 dicembre 2016
 Soluzione del Compitino di Sistemi Dinamici del dicembre 06 Esercizio Si consideri il sistema newtoniano con dissipazione ẍ = x cosx γẋ, γ 0, ed il sistema dinamico continuo ad esso associato a Si trasformi
Soluzione del Compitino di Sistemi Dinamici del dicembre 06 Esercizio Si consideri il sistema newtoniano con dissipazione ẍ = x cosx γẋ, γ 0, ed il sistema dinamico continuo ad esso associato a Si trasformi
es.1 es.2 es.3 es.4 es.5 es. 6 somma Meccanica Razionale 1: Scritto Generale: Cognome e nome:...matricola:...
 es.1 es.2 es.3 es.4 es.5 es. 6 somma 6 6 6 6 6 6 30 Meccanica Razionale 1: Scritto Generale: 07.09.2012 Cognome e nome:....................................matricola:......... Gli studenti che hanno seguito
es.1 es.2 es.3 es.4 es.5 es. 6 somma 6 6 6 6 6 6 30 Meccanica Razionale 1: Scritto Generale: 07.09.2012 Cognome e nome:....................................matricola:......... Gli studenti che hanno seguito
Esercizio: pendolo sferico. Soluzione
 Esercizio: pendolo sferico Si consideri un punto materiale di massa m vincolato a muoversi senza attrito sulla superficie di una sfera di raggio R e soggetto alla forza di gravita. Ridurre il moto alle
Esercizio: pendolo sferico Si consideri un punto materiale di massa m vincolato a muoversi senza attrito sulla superficie di una sfera di raggio R e soggetto alla forza di gravita. Ridurre il moto alle
Anno accademico
 Scuola Normale Superiore Ammissione al 4 anno della Classe di Scienze Prova di Analisi per l ammissione alla Laurea Specialistica in Fisica applicata, Informatica, Matematica, Scienze fisiche, Tecnologie
Scuola Normale Superiore Ammissione al 4 anno della Classe di Scienze Prova di Analisi per l ammissione alla Laurea Specialistica in Fisica applicata, Informatica, Matematica, Scienze fisiche, Tecnologie
Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018)
 Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018) Esercizio 1 Si consideri l insieme Esercizi sulla funzione implicita e superfici Z = {(x, y) R 2 2y xe y
Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018) Esercizio 1 Si consideri l insieme Esercizi sulla funzione implicita e superfici Z = {(x, y) R 2 2y xe y
Statistica Matematica e Trattamento Informatico dei Dati. Analisi Matematica 3. Esercizi svolti nelle lezioni. V. Del Prete
 Statistica Matematica e Trattamento Informatico dei Dati A.A.00-0 Analisi Matematica 3 Esercizi svolti nelle lezioni V. Del Prete Numeri complessi Argomenti ed esercizi svolti nelle lezioni 30.09.00 e
Statistica Matematica e Trattamento Informatico dei Dati A.A.00-0 Analisi Matematica 3 Esercizi svolti nelle lezioni V. Del Prete Numeri complessi Argomenti ed esercizi svolti nelle lezioni 30.09.00 e
Esercizi. Misti iniziali. Più variabili. 1. Data la funzione. F (x) = x3 3 + x e t2 dt. se ne studino massimi, minimi, flessi, limiti a ±.
 Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A Prof. G.Cupini
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
Università di Trieste Facoltà d Ingegneria. Esercizi sulle equazioni differenziali. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria Esercizi sulle equazioni differenziali Dott Franco Obersnel Esercizio 1 Si classifichino le seguenti equazioni, come ordinarie o alle derivate parziali si dica
Università di Trieste Facoltà d Ingegneria Esercizi sulle equazioni differenziali Dott Franco Obersnel Esercizio 1 Si classifichino le seguenti equazioni, come ordinarie o alle derivate parziali si dica
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 20 Settembre 2013
 Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 20 Settembre 2013 Corso di Laurea in Matematica Dipartimento di Matematica e Fisica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli,
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 20 Settembre 2013 Corso di Laurea in Matematica Dipartimento di Matematica e Fisica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli,
Matematica II - ING ELT Appello del 27/7/2009. Nome e cognome:... Recupero I parte Recupero II parte Scritto completo. { x log y. se y > 0 f(x, y) :=
 Matematica II - ING ELT Appello del 27/7/2009 Nome e cognome:...... Scegliere una delle opzioni sottostanti Matricola:... Recupero I parte Recupero II parte Scritto completo Esercizio 1 Si consideri la
Matematica II - ING ELT Appello del 27/7/2009 Nome e cognome:...... Scegliere una delle opzioni sottostanti Matricola:... Recupero I parte Recupero II parte Scritto completo Esercizio 1 Si consideri la
Corsi di laurea in Matematica e Fisica - Anno Accademico 2016/17 FM210 / MA. Prima Prova di Esonero [ ]
![Corsi di laurea in Matematica e Fisica - Anno Accademico 2016/17 FM210 / MA. Prima Prova di Esonero [ ] Corsi di laurea in Matematica e Fisica - Anno Accademico 2016/17 FM210 / MA. Prima Prova di Esonero [ ]](/thumbs/101/150162749.jpg) Corsi di laurea in Matematica e Fisica - Anno Accademico 016/17 FM10 / MA Prima Prova di Esonero [10-4-017] 1. (14 punti). Un punto materiale di massa m si muove in una dimensione sotto l effetto di una
Corsi di laurea in Matematica e Fisica - Anno Accademico 016/17 FM10 / MA Prima Prova di Esonero [10-4-017] 1. (14 punti). Un punto materiale di massa m si muove in una dimensione sotto l effetto di una
Esercizi. f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 )
 Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
1 Limiti e continuità
 Calcolo infinitesimale e differenziale Gli esercizi indicati con l asterisco (*) sono più impegnativi. Limiti e continuità Si ricorda che per una funzione di più variabili, la definizione di continuità
Calcolo infinitesimale e differenziale Gli esercizi indicati con l asterisco (*) sono più impegnativi. Limiti e continuità Si ricorda che per una funzione di più variabili, la definizione di continuità
EQUAZIONI DIFFERENZIALI Esercizi con soluzione
 EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
Considerare il moto di un punto materiale di massa m = 1 soggetto ad un potenziale V (x):
 sercizio Considerare il moto di un punto materiale di massa m = soggetto ad un potenziale V (x): ẍ = V (x), dove V (x) = x x.. Scrivere esplicitamente l equazione del moto e verificare esplicitamente la
sercizio Considerare il moto di un punto materiale di massa m = soggetto ad un potenziale V (x): ẍ = V (x), dove V (x) = x x.. Scrivere esplicitamente l equazione del moto e verificare esplicitamente la
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Prima Prova Scritta 18/03/1997
 Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Scritto d esame di Analisi Matematica
 116 Prove d Esame di Analisi Matematica Versione 2006 Pisa, 15 Gennaio 2000 x 0 sin x 4 x 4 (arctan x x) 4. 2. eterminare, al variare del parametro λ R, il numero di soluzioni dell equazione 2x 2 = λe
116 Prove d Esame di Analisi Matematica Versione 2006 Pisa, 15 Gennaio 2000 x 0 sin x 4 x 4 (arctan x x) 4. 2. eterminare, al variare del parametro λ R, il numero di soluzioni dell equazione 2x 2 = λe
Registro dell insegnamento. Scienze Matematiche Fisiche e Naturali Analisi Matematica IV modulo Settore:... Corsi di studio:...
 UNIVERSITÀ DEGLI STUDI DI FIRENZE Registro dell insegnamento Anno Accademico 2007/2008 Facoltà: Insegnamento: Scienze Matematiche Fisiche e Naturali Analisi Matematica IV modulo Settore:..........................
UNIVERSITÀ DEGLI STUDI DI FIRENZE Registro dell insegnamento Anno Accademico 2007/2008 Facoltà: Insegnamento: Scienze Matematiche Fisiche e Naturali Analisi Matematica IV modulo Settore:..........................
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del , se (x, y) = (0, 0) ( x e. + y x e (y2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
FM210 / MA - Seconda prova pre-esonero ( ) R cos u. dove h è una costante positiva. Oltre alla forza peso, l asta è soggetta ad una forza
 FM10 / MA - Seconda prova pre-esonero (6-5-017) Esercizio 1. Un asta rigida omogenea AB di lunghezza R e massa M è vincolata ad avere l estremo A sull asse fisso x, orientato verticalmente verso l alto,
FM10 / MA - Seconda prova pre-esonero (6-5-017) Esercizio 1. Un asta rigida omogenea AB di lunghezza R e massa M è vincolata ad avere l estremo A sull asse fisso x, orientato verticalmente verso l alto,
Equazioni differenziali del II ordine. y 5y + 6y = 0 y(0) = 0 y (0) = 1
 Equazioni differenziali del II ordine 1. Risolvere il seguente problema di Cauchy: y 5y + 6y = 0 y (0) = 1. Determinare l integrale generale della seguente equazione differenziale: y 5y + 6y = f(x), con
Equazioni differenziali del II ordine 1. Risolvere il seguente problema di Cauchy: y 5y + 6y = 0 y (0) = 1. Determinare l integrale generale della seguente equazione differenziale: y 5y + 6y = f(x), con
FM210 - Fisica Matematica I
 Corso di laurea in Matematica - Anno Accademico 212/13 FM21 - Fisica Matematica I Soluzioni della Seconda Prova Pre-esonero [9-1-213] Esercizio 2 (a) Osserviamo che il sistema è conservativo e il potenziale
Corso di laurea in Matematica - Anno Accademico 212/13 FM21 - Fisica Matematica I Soluzioni della Seconda Prova Pre-esonero [9-1-213] Esercizio 2 (a) Osserviamo che il sistema è conservativo e il potenziale
Corsi di laurea in Matematica e Fisica - Anno Accademico 2017/18 FM210 / MA. Primo Scritto [ ]
![Corsi di laurea in Matematica e Fisica - Anno Accademico 2017/18 FM210 / MA. Primo Scritto [ ] Corsi di laurea in Matematica e Fisica - Anno Accademico 2017/18 FM210 / MA. Primo Scritto [ ]](/thumbs/93/112641904.jpg) Corsi di laurea in Matematica e Fisica - Anno Accademico 017/18 FM10 / MA Primo Scritto [1-6-018] 1. Si consideri il sistema meccanico bidimensionale per x R. ẍ = ( x 4 1)x, (a) Si identifichino due integrali
Corsi di laurea in Matematica e Fisica - Anno Accademico 017/18 FM10 / MA Primo Scritto [1-6-018] 1. Si consideri il sistema meccanico bidimensionale per x R. ẍ = ( x 4 1)x, (a) Si identifichino due integrali
Corsi di laurea in Matematica e Fisica - Anno Accademico 2017/18 FM210 / MA
 Corsi di laurea in Matematica e Fisica - Anno Accademico 07/8 FM0 / MA Seconda Prova di Esonero [8-5-08]. Un sistema meccanico è costituito da due sbarre uguali, rettilinee, omogenee, pesanti, di massa
Corsi di laurea in Matematica e Fisica - Anno Accademico 07/8 FM0 / MA Seconda Prova di Esonero [8-5-08]. Un sistema meccanico è costituito da due sbarre uguali, rettilinee, omogenee, pesanti, di massa
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Prima Prova Scritta [26-1-212] Soluzioni Problema 1 1. Riscriviamo il sistema come e risolviamo la prima equazione: xt) = x e 3t + 2 ẋ = 3x + 2, ẏ = y + z 3, ż = 2x + z, Inserendo
FM21 - Fisica Matematica I Prima Prova Scritta [26-1-212] Soluzioni Problema 1 1. Riscriviamo il sistema come e risolviamo la prima equazione: xt) = x e 3t + 2 ẋ = 3x + 2, ẏ = y + z 3, ż = 2x + z, Inserendo
MP. Moti rigidi piani
 MP. Moti rigidi piani Quanto abbiamo visto a proposito dei moti rigidi e di moti relativi ci consente di trattare un esempio notevole di moto rigido come il moto rigido piano. Un moto rigido si dice piano
MP. Moti rigidi piani Quanto abbiamo visto a proposito dei moti rigidi e di moti relativi ci consente di trattare un esempio notevole di moto rigido come il moto rigido piano. Un moto rigido si dice piano
{ x + 2y = 3 αx + 2y = 1 αx + y = 0. f(x) = e x 2 +3x+4 x 5. f(x) = x 3 e 7x.
 0 Gennaio 006 Teoria: Definizione di derivata puntuale e suo significato geometrico Esercizio Determinare l equazione del piano contenente i vettori u = (,, 3 e v = (,, e passante per P o = (,, Scrivere
0 Gennaio 006 Teoria: Definizione di derivata puntuale e suo significato geometrico Esercizio Determinare l equazione del piano contenente i vettori u = (,, 3 e v = (,, e passante per P o = (,, Scrivere
Matematica - Prova d esame (25/06/2004)
 Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
FM210 - Fisica Matematica I
 FM10 - Fisica Matematica I Seconda Prova di Esonero [13-01-01] Soluzioni Problema 1 1. Il moto si svolge in un campo di forze centrale in assenza di attrito. Pertanto si avranno due integrali primi del
FM10 - Fisica Matematica I Seconda Prova di Esonero [13-01-01] Soluzioni Problema 1 1. Il moto si svolge in un campo di forze centrale in assenza di attrito. Pertanto si avranno due integrali primi del
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Provetta scritta di Calcolo I Corsi di laurea in Fisica - Scienza e Tecnologia dei Materiali Prova scritta del 7/12/2005 Fila A
 Provetta scritta di Calcolo I Prova scritta del 7/2/25 Fila A ) Calcolare i limiti 3 x 3 x 4 ; b) lim sin(2x) + x2 x( cos(3x)) c) lim + 5 x 7 x 4 x 2 + x. 2) Determinare il massimo di x 3 (2 + x 4 ) 3/2,
Provetta scritta di Calcolo I Prova scritta del 7/2/25 Fila A ) Calcolare i limiti 3 x 3 x 4 ; b) lim sin(2x) + x2 x( cos(3x)) c) lim + 5 x 7 x 4 x 2 + x. 2) Determinare il massimo di x 3 (2 + x 4 ) 3/2,
Analisi Matematica II. Prove Parziali A.A. 1992/2017
 Complementi di Analisi Polo di Savona Analisi Matematica II Complementi di Analisi Matematica Prove Parziali A.A. 1992/2017 1- PrPzCa.TEX [] Complementi di Analisi Polo di Savona Prima Prova Parziale 92/93
Complementi di Analisi Polo di Savona Analisi Matematica II Complementi di Analisi Matematica Prove Parziali A.A. 1992/2017 1- PrPzCa.TEX [] Complementi di Analisi Polo di Savona Prima Prova Parziale 92/93
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 3 Ottobre 2008
 Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 3 Ottobre 2008 Dipartimento di Matematica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli, G. Gentile Istruzioni (a) La sufficienza
Prova Finale di Tipo B e Prova di Accesso alla Laurea Magistrale 3 Ottobre 2008 Dipartimento di Matematica Università di Roma Tre U. Bessi, A. Bruno, S. Gabelli, G. Gentile Istruzioni (a) La sufficienza
Complementi di Analisi Matematica. Foglio di esercizi n.9 10/04/2017 (Aggiornamento del 26/04/2017)
 Complementi di Analisi Matematica. Foglio di esercizi n.9 0/04/207 (Aggiornamento del 26/04/207) Esercizi su equazioni differenziali Esercizio Tracciare i grafici qualitativi delle soluzioni dell equazione
Complementi di Analisi Matematica. Foglio di esercizi n.9 0/04/207 (Aggiornamento del 26/04/207) Esercizi su equazioni differenziali Esercizio Tracciare i grafici qualitativi delle soluzioni dell equazione
Compito del 14 giugno 2004
 Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
Equazioni Differenziali
 Università degli Studi di Udine Anno Accademico 2015/2016 Dipartimento di Scienze Matematiche, Informatiche e Fisiche Corso di Laurea in Matematica Equazioni Differenziali Appello del 26 gennaio 2016 N.B.:
Università degli Studi di Udine Anno Accademico 2015/2016 Dipartimento di Scienze Matematiche, Informatiche e Fisiche Corso di Laurea in Matematica Equazioni Differenziali Appello del 26 gennaio 2016 N.B.:
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 2010
 Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
Derivate parziali, derivate direzionali, differenziabilità. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) =
 Derivate parziali, derivate direzionali, differenziabilità 1. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) = 3 x (y 1) + 1. b) Calcolare D v f(0, 1), dove v è il versore
Derivate parziali, derivate direzionali, differenziabilità 1. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) = 3 x (y 1) + 1. b) Calcolare D v f(0, 1), dove v è il versore
ANALISI MATEMATICA 3. esercizi assegnati per la prova scritta del 31 gennaio 2011
 esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 6 Giugno 08 (usare fogli diversi per esercizi diversi) Primo Esercizio i) Assumiamo che Q sia un punto di un corpo rigido piano
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 6 Giugno 08 (usare fogli diversi per esercizi diversi) Primo Esercizio i) Assumiamo che Q sia un punto di un corpo rigido piano
