Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12. Corsi di laurea in Ingegneria Elettronica ed Informatica
|
|
|
- Orsola Mancini
- 5 anni fa
- Visualizzazioni
Transcript
1 Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy x, b) log(1 xy 2 ), c) x 2 y y 2, d) log(2x 2 + xy y 2 ). 2) Calcolare nel punto ( 2, 1) la derivata direzionale della funzione in 1b) nella direzione della retta 2y x = 4, orientata nel verso delle x crescenti. 3) Si considerino le funzioni nulle nell origine che nei punti (x, y) (0, 0) sono definite dalle seguenti leggi, e se ne studino, nell origine, le derivate parziali e la derivata nella direzione della retta y = x, orientata nel verso delle x crescenti. a) x 2 y x 2 + y 2, b) x 2 + y 4, c) sin(xy) x 2 + y 2, d) y 3 x4 + y 4. 4) Determinare, qualora esista, l equazione del piano tangente al grafico della funzione f(x, y) = x 2 + xy + 2y 2 nei seguenti punti: a) (1, 1, 2) b) (0, 0, 0) 5) Determinare i punti di minimo e di massimo locale delle seguenti funzioni: a) xy x2 1 3 y3, b) x 2 y 3, c) 1 2 x + y x2 y 2, d) x 2 y 2xy 2, e) log(y x 2 ) + (2x/y) 6) Stabilire se l origine è un punto di estremo locale per le seguenti funzioni: a) x 2 y + y 3, b) x 2 + y 2 cos x, c) y 2 x 4, d) y 2 2x 2 y + 2x 4. 1
2 7) Determinare i valori di estremo assoluto di f su E nei seguenti casi. a) f(x, y) = x 2 + y 2 2y, E = {(x, y) IR 2 : x 2 y 2 x 2 } b) f(x, y) = 2y 3 x 2 y 2, E = triangolo di vertici (0, 0), (2, 0), (1, 1) c) f(x, y) = xy x 2 log y, E = [0, 2] [1, e] d) f(x, y) = x 2 + y 2 y 2, E = {(x, y) IR 2 : 1 2 (x2 1) y 1} e) f(x, y) = ye x, E = {(x, y) IR 2 : x 2 + y 2 2, y 0} f) f(x, y) = xy 2y, E = {(x, y) IR 2 : x 2 + y 2 2x, y x} g) f(x, y) = arctg 4 x 2 + y 2, E = [1, 2] [0, 5] h) f(x, y) = x 3 y, E = {(x, y) IR 2 : x 2 + y 2 4, 0 y 2 x} i) f(x, y) = x + xy, E = {(x, y) IR 2 : 3x 2 + y 2 3, y x + 1} j) f(x, y) = xy 2, E = {(x, y) IR 2 : 1 x 2 + y 2 2x} 8) Determinare, qualora esista, l equazione della retta tangente alla curva Γ = {(x, y) IR 2 x 3 + y 4 = 2xy} nel punto (1, 1). 9) Sia Γ = {(x, y) IR 2 x e 3 xy = 4y}: determinare gli eventuali punti di Γ in cui la retta tangente è parallela all asse x. 10) Determinare i valori di estremo assoluto della funzione f(x, y) = x+y sulla circonferenza di equazione x 2 + y 2 = 2x ) Sia Γ l arco di iperbole Γ = {(x, y) IR 2 : x 2 y 2 = 1, 0 x 2}. Determinare i punti di Γ a distanza minima e massima dal punto (0, 1). 12) Un triangolo isoscele (simmetrico rispetto all asse y) è inscritto nell ellisse di equazione 4x 2 + 3y 2 = 12, ed ha un vertice nel punto (0, 2). Quanto può valere, al massimo, la sua area? 2
3 13) Calcolare f(x, y) dxdy, dove f ed E sono dati come segue. E a) f(x, y) = 1 + x 2, E = triangolo di vertici (0, 0), (1, 0), (1, 1) b) f(x, y) = x 3, E = {(x, y) IR 2 : x 2 + y 2 1, y x } c) f(x, y) = y, E = {(x, y) IR 2 : x y 2, 0 y 2 x} d) f(x, y) = sin(x 2 y 2 ), E = triangolo di vertici (1, 0), (2, 2), (0, 1) e) f(x, y) = x 2 (1 + y 2 ) 1, E = {(x, y) IR 2 : x 0, x 3 y 1} f) f(x, y) = xe 2y, E = {(x, y) IR 2 : x 2 + y 2 1, y x/ 3} g) f(x, y) = x, E = {(x, y) IR 2 : x 2 + y 2 4x 3, y 0} h) f(x, y) = y 1 log(2 xy), E = {(x, y) IR 2 : 0 xy 1, 1 y 2} i) f(x, y) = x (1 + y) 1, E = {(x, y) IR 2 : 1 x 2 + y 2 4, y 0} j) f(x, y) = x 2, E = {(x, y) IR 2 : x 2 + y 2 2, x 1} k) f(x, y) = (y + xy 2 ) 1, E = {(x, y) IR 2 : 1 y x, xy 3} l) f(x, y) = 4 x 2 y 2, E = {(x, y) IR 2 : 1 x 2 + y 2 2y} 14) Si calcoli l area dei seguenti insiemi, utilizzando: in a) la sostituzione ξ = 2x + y, η = x + 2y, in b) le coordinate polari riferite all origine. a) E = {(x, y) R 2 : 2x + y x + 2y 2} b) E = {(x, y) IR 2 : x 2 + y 2 2x + y, 0 y x} 15) Sia E = {(x, y) IR 2 : y 2 2x 3 x 4, x 1}: tramite la sostituzione ξ = x, η = y/x si calcoli E x 1 dxdy. 3
4 16) Calcolare il volume dei seguenti solidi: a) E = {(x, y, z) IR 3 : x 2 + y 2 4, z y} b) E = {(x, y, z) IR 3 : 0 z 1, 0 y z 2 x 2 } c) E = {(x, y, z) IR 3 : x 2 + z 2 1, y 2 + z 2 1} d) E = {(x, y, z) IR 3 : x 2 2x z 3 y 2, x 1} 17) Nei seguenti casi, calcolare il volume del solido generato dalla rotazione di A attorno agli assi indicati a lato. a) A = {(x, y) IR 2 : 1 y 2, y x }, asse x b) A = {(x, y) IR 2 : 0 x π/2, 0 y cos x}, entrambi gli assi c) A = {(x, y) IR 2 : x 2 + y 2 3 2x, x 0}, asse y 18) Calcolare i baricentri dei seguenti solidi a) E come in 16a b) E = {(x, y, z) IR 3 : 1 x 2 + y 2 + z 2 4, z 0}. 19) Calcolare f(x, y, z) dxdydz, dove f ed E sono dati come segue. E a) f(x, y, z) = z 3, E = {(x, y, z) IR 3 : x 2 y 1, 0 z 1 y} b) f(x, y, z) = xy, E = {(x, y, z) IR 3 : x 2 + y 2 + z 2 4, 0 y x} c) f(x, y, z) = x 1, E = {(x, y, z) IR 3 : x 2 + y 2 + 4z 2 4x} 20) Determinare,qualora esista, la retta tangente alla curva di equazione polare ρ = e θ, θ IR, nel punto (1, 0). 21) Calcolare la lunghezza dell arco γ(t) = (t 3, (4 t 2 ) 3/2 ), t [0, 2]. 4
5 22) Sull arco dell esercizio precedente si determini un punto che lo divida in due archi di uguale lunghezza. 23) Calcolare γ yexy dy, dove la traccia di γ è definita dalle condizioni x 2 = e xy, 1 x e, ed il suo verso di percorrenza è quello in cui cresce x. 24) Calcolare γ x4 ds, dove γ(t) = (2e t/2, t 1 2 et ), t [0, log 2]. 25) Calcolare F (u) du, dove γ è il segmento che va da (0, 2) a (2, 1) γ ed F (x, y) = (x + y, 2x y). 26) Calcolare γ F (u) du, dove γ(t) = (t2 log t, t), t [1, e], ed F (x, y) = (x y 2, x/y). 27) Calcolare F (u) du, dove E è il trapezio del piano xy definito + E dalle condizioni 0 y 2 x, y 1 ed F (x, y) = (2y + cos x, x 4 sin y). 28) Calcolare l area della regione piana racchiusa dall arco γ e dal segmento che ne congiunge gli estremi, nei seguenti due casi: a) γ(t) = (cos(πt), t t 2 ), b) γ(t) = (te t 1, te 1 t ), t [0, 1]. 29) Calcolare l area della regione piana racchiusa dall arco γ di equazione polare ρ = sin 2 θ, θ [0, π]. 30) Posto F (x, y) = ( 4 x 3 + 3y, x y 4 e 2y ) e γ(t) = (cos t, 2 + sin t), t [0, 2π], calcolare F (u) du. γ 31) Posto F (x, y) = (y 3 y log x, 3xy 2 x log x) e γ(t) = (1+2 cos t, 2 sin t), t [ π/2, π/2], calcolare F (u) du. γ 32) Stabilire se i seguenti campi vettoriali risultano conservativi e, in caso affermativo, calcolarne un potenziale. Salvo diversa indicazione a lato, si consideri ciascun campo definito sul suo dominio di esistenza. a) F (x, y) = (x + 2y, y 2x), b) F (x, y) = (x + xy 2, y 2 + x 2 y), c) F (x, y) = (y log y, x + x log y), d) F (x, y) = (1 xy) 1/2 (y 2, 3xy 2), e) F (x, y) = (x + y) 2 (y 2, x 2 ), x + y > 0. 5
6 33) Nei casi che seguono, stabilire se F è conservativo sul proprio dominio di esistenza, sapendo che ivi risulta irrotazionale. a) F (x, y) = (x 2 + y 2 ) 3/2 (x, y), b) F (x, y) = (x 2 + y 2 ) 1 (x + 2y, y 2x). 34) Nei casi che seguono, calcolare F (u) du, sapendo che F è irrotazionale sul proprio dominio di γ esistenza. a) γ(t) = (2 log(t/2), sin 2 (π/t)), t [2, 4], F (x, y) = e x/y (y, 2y x) b) γ(t) = (1 + t, 1 + t 2 ), t [0, 1], F (x, y) = (log(x 2 + y 2 ), 2 arctg (x/y)) c) γ(t) = (2 + cos t, sin t), t [0, π], F (x, y) = (x + 2y) 1/2 (3x + 4y, 2x) d) γ(t) = (t, 2 t), t [0, 2], F (x, y) come in 33b 35) Calcolare l area delle seguenti superfici ordinarie: a) Σ = {(x, y, z) IR 3 : z = 1 2 x + y, 0 y 1 x2 }, b) Σ = {(x, y, z) IR 3 : z = y 2, x y 1}, c) Σ = {(x, y, z) IR 3 : z = x 2 + y 2, x 2 + y 2 4y 3}. 36) Calcolare l area della superficie Σ generata dalla rotazione dell arco Γ attorno all asse x, nei seguenti casi: a) Γ = segmento di estremi (1, 2), (2, 1) b) Γ = {(x, y) IR 2 : 2 x 6, y = x} c) Γ = {(x, y) IR 2 : y 0, x 2 + y 2 = x y}. 6
7 37) Scelto un orientamento su Σ, calcolare F νdσ nei casi che seguono. Σ a) Σ = {(x, y, z) IR 3 : x 2 + y 2 1, z = x + y}, F (x, y, z) = (3x, 2 y, z) b) Σ = triangolo di vertici (1, 0, 0), (0, 1, 0), (0, 0, 2), F (x, y, z) = (2y, z, x) c) Σ = {(x, y, z) IR 3 : z = x 2 + y 2, z 2y}, F (x, y, z) = ( x, y, 2z) 38) Come sopra, utilizzando il teorema della divergenza. a) Σ = {(x, y, z) IR 3 : x 2 + y 2 + z 2 = 1}, F (x, y, z) = (x + cos z, 4y x 3, e xy z) b) Σ = {(x, y, z) IR 3 : 0 z = log(3 x 2 y 2 )}, F (x, y, z) = (y 2, 2yz, 1 z 2 ) c) Σ = {(x, y, z) IR 3 : x 2 + y 2 + z 2 = 4, z 2x y}, F (2, 3, 1) d) Σ = {(x, y, z) IR 3 : x 2 + y 2 = 2yz, 1 z 2}, F (x, y, z) = (x, y, 2 2z). 39) Risolvere i seguenti problemi di Cauchy, determinandone la soluzione in forma esplicita, ed indicando il dominio su cui viene considerata. (a) e 2t y = y 2, y(0) = 1 (b) 2tyy = y 2 1, y( 1) = 2 (c) t 2 y = ty 2, y(1) = 3 7
8 (d) yy = e t y 2 3, y(0) = 2 (e) y = 1 + y 3, y(2) = 1 (f) (t + 1)y = ty + 1, y(0) = 1 (g) t + y e y+t = 0, y(0) = 0 (h) 2t(y t y 2 ) = (1 2t 2 )y, y(1) = 1 (i) (y + 1)y = y 3 (t + 1), y(1) = 1/3 (j) yy = (4 y 2 )tg t, y(π/4) = 2 (k) (2y 3t)(1 + t) = y, y(0) = 2 (l) y = y y 1, y(0) = 2 (m) ty (2 + y) = y 2 2y, y(1/2) = 1 (n) (t 2 1)(y t) = ty, y(0) = 1 (o) y + (y log y)tg t = 0, y(0) = 1/ e (p) (t t 2 )y = y + t, y(1/4) = 1 40) Determinare l integrale generale delle seguenti equazioni. (a) y + y = y, (b) y 2y = 0, (c) 2y = y + y, (d) y + y + 6 = (t 2 y)/4, (e) y y = cos t, (f) y + y 2y = e 2t, (g) y + y = te t, (h) y 2y + y = t 1 e t, t > 0. 41) Risolvere il problema di Cauchy relativo all equazione 40e) ed alle condizioni iniziali y(0) = 1, y (0) = 1/2. 8
9 42) Nelle equazioni che seguono, stabilire per quali valori del parametro ρ tutte le soluzioni sono periodiche. (a) y + ρy + y = 0, (b) y + ρy = 0. 43) Nelle equazioni che seguono, stabilire per quali valori del parametro ρ tutte le soluzioni non banali sono oscillanti e tendenti a zero per t +. (a) y + ρy + y = 0, (b) y y + ρy = 0. 44) Determinare le trasformate di Laplace delle seguenti funzioni: (a) 2e t + e 2t, (b) 3t 2 + cos(2t), (c) t 3 e t, (d) t sin(t/2), (e) e 2t cos(3t), (f) max (t 2 2t, 0), (g) sin 3 t. 45) Determinare, qualora esistano, le antitrasformate di Laplace delle seguenti funzioni: (a) 2 3z z 4, (b) e 2z z 2, (c) z z + 1, (d) 1 z 2 1, (e) z 4z 2 + 1, (f) 1 z 2 + 9, (g) z (2z + 1), (h) 2z z 2 4z + 8, (i) 3z 1 z 2 2z 3, (j) z z 4 + 4, (k) 1 z 2 + z, (l) 4z z 2 4 z 4 3z ) Utilizzando la trasformata di Laplace, risolvere i seguenti problemi di Cauchy su [0, + [. (a) y 2y + 5y = 0, y(0) = 2, y (0) = 1 (b) y 4y + 4y = e 2t cos(t), y(0) = 0, y (0) = 0 (c) y 4y = 3te t, y(0) = 0, y (0) = 0 9
10 47) Determinare le trasformate di Fourier delle seguenti funzioni. (a) f(t) = 1, se 1 t 2, f(t) = 0, altrove, (b) 1 t 2 + 9, (c) e 2t 3, (d) (f) t 2 sin 3t, (e) t (t 2 + 1), (g) t /4 2 e t2, (h) sin2 t, t 1 2t 2 2t + 5, Risposte agli esercizi ) Il campo di esistenza richiesto è l insieme dei punti (x, y) IR 2 che verificano, rispettivamente, le seguenti condizioni: a - [ (x 0 y 1) (x 0 y 1) ], b - [ (x 0) (x > 0 1/ x < y < 1/ x) ], c - [ 0 y x 2 ], d - [ (x < 0 2x < y < x) (x > 0 x < y < 2x) ]. 2) [ 2/(3 5) ] 3) Ci si riferisce, nell ordine, alle tre derivate direzionali richieste: a - [ 0; 0; 1/(2 2) ], b - [ ; 0; ], c - [ 0; 0; ], d - [ 0; 1; 1/2 ] 4) a - [ 3x + 5y 4z = 0 ]; b - [ ]; 5) Ci si riferisce, nell ordine, ai punti di minimo locale, massimo locale ed ai punti sella (ovvero ai punti stazionari che non sono di estremo locale). a - [ (1, 1); ; (0, 0) ]; b - [ (0, y), y > 0; (0, y), y < 0; (x, 0), x IR ]; c - [ ; ; (1, 1/2) ]; d - [ ; ; (0, 0) ]; e - [ ; ; (1/2, 1/2) ]; 6) a - [ no ]; b - [ sì (minimo) ]; c - [ no ]; d - [ sì (minimo) ]; 7) Ci si riferisce, nell ordine, ai valori di minimo e massimo assoluti. 10
11 a - [ 1 = f(0, 1); 0 = f(0, 0) = f(0, 2) = f(±1, 1) ] b - [ 5/16 = f(3/2, 1/2); 1 = f(1, 1) ] c - [ 0 = f(0, y), 1 y e; 2 = f(2, 1) ] d - [ 0 = f(0, 0) = f(0, 1); 5/4 = f(± 2, 1/2) ] e - [ 0 = f(x, 0), 2 x 2; e = f(1, 1) ] f - [ 1 = f(1, 1); 3 3/4 = f(1/2, 3/2) ] g - [ π/4 = f(1, 0); π/3 = f(2, 5) ] h - [ 3 3 = f( 3, 1); 27/16 = f(3/2, 1/2) ] i - [ 1 = f( 1, 0); 2 2/3 = f( 2/3, 1) ] j - [ 0 = f(x, 0), 1 x 2; 32/27 = f(4/3, ±2 2/3) ] 8) [ x + 2y 3 = 0 ] 9) [ ±(2/e, e/2) ] 10) [ 1 = f(0, 1); 3 = f(2, 1) ] 11) [ ( 5/2, 1/2) è il punto più vicino; (2, 3) è il più lontano ] 12) [ 9/2, area del triangolo di vertici (0, 2), (±3/2, 1) ] 13) a - [ (2 2 1)/3 ], b - [ 0 ], c - [ 5/12 ], d - [ 0 ], e - [ (log 2)/6 ], f - [ 1/e ], g - [ π ], h - [ (log 4 1)/2 ], i - [ 3 log 3 (1/2) ], j - [ π/4 ], k - [ log 2 (π/6) ], l - [ (2π/ 3) (10/9) ] 14) a - [ 4/3 ], b - [ (5π/16) + (7/8) ] 15) [ π/2 ] 16) a - [ 32/3 ], b - [ 1/3 ], c - [ 16/3 ], d - [ 4π ] 17) a - [ 28π/3 ], b - [ asse x : π 2 /4; asse y : π(π 2) ], 11
12 c - [ 6π 3 (8π 2 /3) ] 18) a - [ (0, 3π/8, 0) ], b - [ (0, 0, 45/56) ] 19) a - [ (7/6) (π/4) ], b - [ 32/15 ], c - [ 16π/3 ] 20) [ y = x 1 ] 21) [ 12 ] 22) [ (2 2, 2 2) = γ( 2) ] 23) [ 2/3 ] 24) [ (8/3)( ) ] 25) [ 9/2 ] 26) [ 1 ] 27) [ 6 ] 28) a - [ 4π 2 ], b - [ 1/3 ] 29) [ 3π/16 ] 30) [ 2π ] 31) [ 16 2π ] 32) a - [ F non è conservativo ], b - [ V (x, y) = 1 3 y x2 y x2 + c, c IR, (x, y) R 2 ], c - [ V (x, y) = xy log y + c, c IR, y > 0 ]. d - [ V (x, y) = 2y 1 xy + c, c IR, xy < 1 ]. e - [ V (x, y) = (x + y) 1 xy + c, c IR, x + y > 0 ]. 12
13 33) a - [ sì ], b - [ no ]. Nota: nel punto (a), a meno di un fattore scalare, F è il campo elettrico generato da una carica puntiforme situata nell origine (ristretto al piano). Un suo potenziale è dato da V (x, y) = (x 2 + y 2 ) 1/2. 34) a - [ 3 ], b - [ 5 log 2 + (π/2) 2 ], c - [ ], d - [ π ]. 35) a - [ 2 ], b - [ (5 5 1)/6 ], c - [ π 2 ]. 36) a - [ 3π 2 ], b - [ 49π/3 ], c - [ π(4 π)/2 2 ]. 37) a - [ ± 2π ], b - [ ± 3/2 ], c - [ ± π ]. 38) a - [ ± 16π/3 ], b - [ ± 2π ], c - [ ± 8π/ 6 ], d - [ ± 8π ]. 39) Le soluzioni sono le seguenti: a - [ y(t) = 2(e 2t + 1) 1, t IR ], b - [ y(t) = 1 3t, t < 0 (prolungabile a t < 1/3) ], c - [ y(t) = 2t + t 1, t > 0 ], d - [ y(t) = 3 + e 2t, t IR ], e - [ y(t) 1, t IR ], f - [ y(t) = (2e t 1)/(t + 1), t > 1 ], g - [ y(t) = log(1 + t) t, t > 1 ], h - [ y(t) = t, t > 0 ], i - [ y(t) = (t + 2) 1, t > 2 ], j - [ y(t) = 2 sin t, π/2 < t < π/2 ], k - [ y(t) = t 2 t 2, t > 1 (prolungabile a tutto IR) ], l - [ y(t) = 1 + tg 2 ((2t + π)/4), π/2 < t < π/2 ], m - [ y(t) = t + 2 t 2 + 4t, t > 0 ], 13
14 n - [ y(t) = t t 2, 1 < t < 1 ], o - [ y(t) = e 1 2 cos t, π/2 < t < π/2 ], p - [ y(t) = (t 2 t)/(1 t), 0 < t < 1 ], 40) Le soluzioni sono le seguenti (definite su tutto l asse reale, tranne l ultima), al variare di c 1, c 2 IR. a - [ y(t) = e t/2 (c 1 cos( 3t/2) + c 2 sin( 3t/2)) ], b - [ y(t) = c 1 + c 2 e 2t ], c - [ y(t) = c 1 e t/2 + c 2 e t ], d - [ y(t) = e t/2 (c 1 + c 2 t) + t 2 8t ], e - [ y(t) = c 1 e t + c 2 e t 1 cos t ], 2 f - [ y(t) = (c t)e 2t + c 2 e t ], g - [ y(t) = c 1 cos t + c 2 sin t (t + 1)e t ], h - [ y(t) = e t (c 1 + c 2 t + t log t), t > 0 ] 41) [ e t et 1 cos t, t IR ] 2 42) a - [ ρ = 0 ], b - [ ρ > 0 ] 43) a - [ 0 < ρ < 2 ], b - [ nessun valore di ρ ] 44) a - [ 3(z + 1)(z 2 + z 2) 1, Re z > 1 ], b - [ 6z 3 + z(z 2 + 4) 1, Re z > 0 ], c - [ 6(z + 1) 4, Re z > 1 ], d - [ 16z(4z 2 + 1) 2, Re z > 0 ], e - [ (z 2)(z 2 4z + 13) 1, Re z > 2 ], f - [ 2z 3 e 2z (1 + z), Re z > 0 ], g - [ 6(z z 2 + 9) 1, Re z > 0 ], 14
15 45) a - [ (t 3 /3) (3t 2 /2) ], b - [ max(0, t 2) ], c - [ ], d - [ (e t e t )/2 ], e - [ (1/4) cos(t/2) ], f - [ (1/3) sin(3t) ], g - [ (1/8)e t/2 (2 t) ], h - [ (e 2t /2)(4 cos(2t) + 5 sin(2t)) ], i - [ 2e 3t + e t ], j - [ (1/4)(e t e t ) sin t ], k - [ t sin t ], l - [ (1/5)(3e 2t + e 2t 4 cos t sin t) ]. 46) a - [ y(t) = (e t /2)(4 cos(2t) 3 sin(2t)) ], b - [ y(t) = e 2t (1 cos t) ], c - [ y(t) = (e 2t /12) (3e 2t /4)+(2 3t)(e t /3) ]. 47) a - [ ˆf(s) = (2/s)(sin(2s) sin(s)) per s 0, ˆf(0) = 2 ], b - [ ˆf(s) = (π/3)e 3s ) ], c - [ ˆf(s) = 4(s 2 + 4) 1 e 3is/2 ], d - [ ˆf(s) = π se 3 < s < 3, ˆf(±3) = π/2, ˆf(s) = 0 altrove ], e - [ ˆf(s) = (π/3)e (is+ 3s )/2 ], f - [ ˆf(s) = (π/2)e s (1 s ) ], g - [ ˆf(s) = 4 π is e s 2 ], h - [ ˆf(s) = πi/2 se 2 < s < 0, ˆf(s) = πi/2 se 0 < s < 2, ˆf(s) = 0 altrove ]. 15
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
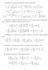 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
a) 1 n b) n cos(nx) n 2 + x 2, c) nx n2 x nx 2 (su IR), 1 + nx x x 2 e) n + x 2, f) nx (come sopra), n sin x g) 2n2 x 2 1 n 2 x + n,
 1. Determinare, ove esista, il limite puntuale delle seguenti successioni di funzioni, e stabilire se esse convergono uniformemente sugli insiemi indicati alla fine della riga. 1 n 1 + n2 x 2, b) n cos(nx)
1. Determinare, ove esista, il limite puntuale delle seguenti successioni di funzioni, e stabilire se esse convergono uniformemente sugli insiemi indicati alla fine della riga. 1 n 1 + n2 x 2, b) n cos(nx)
9/11/2010 (I prova in itinere): solo test a risposta multipla
 9/11/2010 (I prova in itinere): solo test a risposta multipla 23/12/2010 (II prova in itinere, II parte) Esercizio 1. Posto Σ = {(x, y, z) R 3 x 2 + y 2 + z 2 = 4, z 1}, si chiede di calcolare il flusso
9/11/2010 (I prova in itinere): solo test a risposta multipla 23/12/2010 (II prova in itinere, II parte) Esercizio 1. Posto Σ = {(x, y, z) R 3 x 2 + y 2 + z 2 = 4, z 1}, si chiede di calcolare il flusso
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione
![Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione](/thumbs/88/116749009.jpg) Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
CODICE= Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A , Appelli 1, 2, 3 e 4
 Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
Analisi Matematica 3
 Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 2017/2018 Codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
D : 0 E : arctan 2 1 F : 2 arctan 1. 3y + 3y y = 0 y(0) = 3 y (0) = 0.
 Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
Esercizi. f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 )
 Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Corso di Laurea in Ingegneria Gestionale - Sede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame
 Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Esercizi 17.XI.2017 1. Verificare che le curve definite dalle seguenti parametrizzazioni sono regolari, o regolari
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Esercizi 17.XI.2017 1. Verificare che le curve definite dalle seguenti parametrizzazioni sono regolari, o regolari
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
b) Dimostrare che se f(x) è differenziabile in x 0, allora è continua in x 0.
 Analisi Matematica II - Calcolo in più variabili Nome, Cognome, Matricola: Corso di Laurea: Versione A Avvertenza: La prova d esame si compone di due esercizi e di due quesiti. La risposta ai quesiti va
Analisi Matematica II - Calcolo in più variabili Nome, Cognome, Matricola: Corso di Laurea: Versione A Avvertenza: La prova d esame si compone di due esercizi e di due quesiti. La risposta ai quesiti va
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
Quesito 1. f(x, y) = xy log (x 2 + y 2 ) Quesito 2. Quesito 3. y = 2y3 +x 3. xy 2 y(1) = 1. Quesito 4
 Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Esercizi sull integrazione II
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Analisi Matematica II Corso di Ingegneria Gestionale Compito del
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -09-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -09-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Prima prova di verifica in itinere di ANALISI MATEMATICA II. 12 Marzo 2008 Compito A. 1 (punti 3)
 anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
Foglio 3 Esercizi su forme differenziali lineari ed integrali di seconda specie (alcuni con cenno di soluzione).
 Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Raccolta esami di Analisi II
 Esame del 18 gennaio 2011 Raccolta esami di Analisi II Corsi di laurea in Ing. Edile-Architettura e Civile-Ambientale V = x,, z : x 2 + 2 4, x 2 + 2 z x 2 + 2 } a disegnare l intersezione di V con il piano
Esame del 18 gennaio 2011 Raccolta esami di Analisi II Corsi di laurea in Ing. Edile-Architettura e Civile-Ambientale V = x,, z : x 2 + 2 4, x 2 + 2 z x 2 + 2 } a disegnare l intersezione di V con il piano
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 2010
 Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Analisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 2018
 nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
Esempi di esercizi d esame A.A. 2006/07 Analisi Matematica 2 Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli
 Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Analisi Matematica 2. Prove Parziali A.A. 2012/2017
 Analisi 2 Polo di Savona Analisi Matematica 2 Prove Parziali A.A. 2012/2017 1- PrPzAmT.TEX [] Analisi 2 Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale 23/11/2011 Si consideri la funzione
Analisi 2 Polo di Savona Analisi Matematica 2 Prove Parziali A.A. 2012/2017 1- PrPzAmT.TEX [] Analisi 2 Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale 23/11/2011 Si consideri la funzione
Prove d Esame A.A. 2012/2013
 Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Campi vettoriali. 1. Sia F (x, y) = ye x i + (e x cos y) j un campo vettoriale. Determinare un potenziale per F, se esiste.
 Campi vettoriali. Sia F (x, y = ye x i + (e x cos y j un campo vettoriale. Determinare un potenziale per F, se esiste.. Sia F (x, y = xy i + x j un campo vettoriale. Determinare un potenziale per F, se
Campi vettoriali. Sia F (x, y = ye x i + (e x cos y j un campo vettoriale. Determinare un potenziale per F, se esiste.. Sia F (x, y = xy i + x j un campo vettoriale. Determinare un potenziale per F, se
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Corso di Analisi Matematica 2
 Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2016 Versione del 27 ottobre 2016 Appello del 15 gennaio 2016 Tempo: 150 minuti 1. Enunciare le definizioni di campo
Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2016 Versione del 27 ottobre 2016 Appello del 15 gennaio 2016 Tempo: 150 minuti 1. Enunciare le definizioni di campo
3 ) (5) Determinare la proiezione ortogonale del punto (2, 1, 2) sul piano x + 2y + 3z + 4 = 0.
 1 Calcolo vettoriale 1 Scrivere il vettore w =, 6 sotto forma di combinazione lineare dei vettori u = 1, e v = 3, 1 R w = v 4u Determinare la lunghezza o il modulo del vettore, 6, 3 R 7 3 Determinare la
1 Calcolo vettoriale 1 Scrivere il vettore w =, 6 sotto forma di combinazione lineare dei vettori u = 1, e v = 3, 1 R w = v 4u Determinare la lunghezza o il modulo del vettore, 6, 3 R 7 3 Determinare la
Analisi Vettoriale A.A Soluzioni del Foglio 4
 Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
Quarto appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano A.A. 2017/2018. Prof. M. Bramanti. y = 1+y2
 Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 7/8. Prof. M. Bramanti Es. 3 5 6 7 Tot. Punti Cognome e nome in stampatello) codice persona o n di matricola) n d
Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 7/8. Prof. M. Bramanti Es. 3 5 6 7 Tot. Punti Cognome e nome in stampatello) codice persona o n di matricola) n d
Analisi Vettoriale - Primo esonero - 26 ottobre 2006
 Analisi Vettoriale - Primo esonero - 26 ottobre 26 Esercizio 1. ia F (x, y) = e xy + x 2 y 2x 2y + 1. a) imostrare che l equazione F (x, y) = definisce implicitamente, in un intorno del punto P = (1, ),
Analisi Vettoriale - Primo esonero - 26 ottobre 26 Esercizio 1. ia F (x, y) = e xy + x 2 y 2x 2y + 1. a) imostrare che l equazione F (x, y) = definisce implicitamente, in un intorno del punto P = (1, ),
Es. 1 Es. 2 Es. 3 Es. 4 Totale
 Es. Es. Es. Es. 4 Totale Analisi e Geometria Seconda prova in itinere Docente: luglio Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio
Es. Es. Es. Es. 4 Totale Analisi e Geometria Seconda prova in itinere Docente: luglio Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio
Corso di Analisi Matematica 2. Corso di Laurea in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015
 Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015 Appello del 21 novembre 2014 Tempo: 150 minuti 1. Enunciare la definizione di forma differenziale esatta
Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015 Appello del 21 novembre 2014 Tempo: 150 minuti 1. Enunciare la definizione di forma differenziale esatta
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Prove scritte dell esame di Analisi Matematica II a.a. 2013/2014
 Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Esercizi sull integrazione I
 ANALII MAEMAICA -2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. I ANALII MAEMAICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione I (Grazie agli studenti del corso
ANALII MAEMAICA -2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. I ANALII MAEMAICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione I (Grazie agli studenti del corso
Analisi Matematica 2 5 febbraio Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es.
 Analisi Matematica 2 5 febbraio 2013 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es. 7 1 Esercizio 1.
Analisi Matematica 2 5 febbraio 2013 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es. 7 1 Esercizio 1.
Politecnico di Bari - A.A. 2012/2013 Corso di Laurea in Ingegneria Elettrica Esame di ANALISI MATEMATICA - 3 Luglio 2013.
 Esame di ANALISI MATEMATICA - 3 Luglio 2013 (1) Studiare il carattere della serie numerica n 1( 1) n F 0 (n), dove F (x) = Z x 0 log(1 + e t2 ) dt (x 1). (6 punti) log(1 + e t2 ) (2) ata la funzione f(x,
Esame di ANALISI MATEMATICA - 3 Luglio 2013 (1) Studiare il carattere della serie numerica n 1( 1) n F 0 (n), dove F (x) = Z x 0 log(1 + e t2 ) dt (x 1). (6 punti) log(1 + e t2 ) (2) ata la funzione f(x,
ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.
 ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.Patrizia Pera Parte 2 Funzioni reali di più variabili 1. Stabilire se i
ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.Patrizia Pera Parte 2 Funzioni reali di più variabili 1. Stabilire se i
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = 3x 2 x 2 y + y + 1
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del --5 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del --5 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = (x 2 2y 2 ) e x y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--5 - È obbligatorio consegnare tutti i fogli anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--5 - È obbligatorio consegnare tutti i fogli anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
(a) Le derivate parziali f x. f y = x2 + 2xy + 3 si annullano contemporaneamente in (1, 2) e ( 1, 2). Le derivate seconde di f valgono.
 Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
Analisi Matematica II Corso di Ingegneria Biomedica Compito A del f(x, y) = x 2 + y 2
 Analisi Matematica II Corso di Ingegneria Biomedica Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Biomedica Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
1) i) Rappresentare sia attraverso disequazioni, sia attraverso un disegno, il dominio della funzione
 Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II.7.8 SOLUZIONE
Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II.7.8 SOLUZIONE
(a) è chiuso; (b) il punto (1, 1/e) è punto di accumulazione di A; (c) è convesso.
 Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
ESAMI E ESERCITAZIONI A.A. 2010/11. Calcolare la lunghezza del grafico di f. Suggerimento: ricordare che, se h(u) è una funzione continua e.
 ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
Università degli Studi di Salerno - Facoltà di Ingegneria Matematica II - Prova Scritta - 09/06/2006
 Matematica II - Prova Scritta - 09/06/2006 f(x, y) = (y x)e x2 y 2, 2. Risolvere le seguenti equazioni differenziali: y 2 = 1 1 (2x y) 2, y 2y + y 2y = e x (x 1). 3. Calcolare il seguente integrale curvilineo
Matematica II - Prova Scritta - 09/06/2006 f(x, y) = (y x)e x2 y 2, 2. Risolvere le seguenti equazioni differenziali: y 2 = 1 1 (2x y) 2, y 2y + y 2y = e x (x 1). 3. Calcolare il seguente integrale curvilineo
Analisi Matematica 2: Secondo Parziale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Secondo Parziale, 6.6.7, Versione A Cognome e nome:....................................matricola:......... es. es. es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica : Secondo Parziale, 6.6.7, Versione A Cognome e nome:....................................matricola:......... es. es. es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Politecnico di Torino II Facoltà di Architettura Esame di Istituzioni di Matematiche II
 Politecnico di Torino II Facoltà di Architettura Esame di Istituzioni di Matematiche II 5 Gennaio 008 Teoria: Scrivere l espressione della lunghezza dell arco di curva grafico della funzione f(x) = x +
Politecnico di Torino II Facoltà di Architettura Esame di Istituzioni di Matematiche II 5 Gennaio 008 Teoria: Scrivere l espressione della lunghezza dell arco di curva grafico della funzione f(x) = x +
es.1 es.2 es.3 es.4 es.5 somma Analisi Matematica 2: Primo Parziale, , Versione A Cognome e nome:...matricola:...
 es. es. es. es.4 es.5 somma 5 4 8 8 5 Analisi Matematica : Primo Parziale,.4.7, Versione A Cognome e nome:....................................matricola:.......... Calcolare la lunghezza della curva di
es. es. es. es.4 es.5 somma 5 4 8 8 5 Analisi Matematica : Primo Parziale,.4.7, Versione A Cognome e nome:....................................matricola:.......... Calcolare la lunghezza della curva di
calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1), calcolare rot ( E ), determinare un potenziale U(x, y, z) per E.
 ANALISI VETTORIALE Soluzione esonero.1. Esercizio. Assegnato il campo E (x, y, z) = x(y + z ), y(x + z ), z(x + y ) } 1111 calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1),
ANALISI VETTORIALE Soluzione esonero.1. Esercizio. Assegnato il campo E (x, y, z) = x(y + z ), y(x + z ), z(x + y ) } 1111 calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1),
Prove scritte dell esame di Analisi Matematica II a.a. 2011/2012
 Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
Quarto appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2016/2017. Prof. M. Bramanti.
 Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/. Prof. M. Bramanti Tema n 6 Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine
Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/. Prof. M. Bramanti Tema n 6 Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine
Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 2013/14 scheda 1
 Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 203/4 scheda ) Calcolare l integrale doppio ZZ dove A = {(x, y) : x + y apple}. xy dx dy, A 2) Sia la curva nello spazio
Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 203/4 scheda ) Calcolare l integrale doppio ZZ dove A = {(x, y) : x + y apple}. xy dx dy, A 2) Sia la curva nello spazio
Contents. 1. Funzioni di più variabili.
 RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
Prove scritte dell esame di Analisi Matematica II a.a. 2015/2016
 Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Analisi Matematica II Corso di Ingegneria Gestionale Compito del A
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013
 Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Università degli Studi di Roma Tre Corso di Laurea in Ingegneria civile a.a. 2015/2016 Complementi di Matematica (A-K) Secondo Appello 5 Luglio 2016.
 Università degli Studi di Roma Tre Corso di Laurea in Ingegneria civile a.a. 5/6 Complementi di Matematica (A-K) Secondo Appello 5 Luglio 6. Cognome e nome Matricola Specificare quale esame si deve sostenere:
Università degli Studi di Roma Tre Corso di Laurea in Ingegneria civile a.a. 5/6 Complementi di Matematica (A-K) Secondo Appello 5 Luglio 6. Cognome e nome Matricola Specificare quale esame si deve sostenere:
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
si ha La lunghezza L si calcola per ciascun tratto L = (2t)2 + (3t 2 ) dt+ 2 (3t2 ) 2 + (2t) 2 dt = 4t2 + 9t 4 dt = t
 ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 2013/14 17/05/2014
 Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 203/4 7/05/204 ) Calcolare l integrale doppio ZZ ( x + y ) dx dy, A A è il quadrato di vertici (, 0), (, 2), (, 2),
Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 203/4 7/05/204 ) Calcolare l integrale doppio ZZ ( x + y ) dx dy, A A è il quadrato di vertici (, 0), (, 2), (, 2),
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Curve e integrali curvilinei
 6 Curve e integrali curvilinei 6.1. Esempi ed esercizi svolti e/o proposti Esempio 6.1.1. Si consideri la curva parametrica ϕ: t [0,2π] ϕ(t) = (acos(t),asin(t),bt) R 3 dove a e b sono due costanti positive.
6 Curve e integrali curvilinei 6.1. Esempi ed esercizi svolti e/o proposti Esempio 6.1.1. Si consideri la curva parametrica ϕ: t [0,2π] ϕ(t) = (acos(t),asin(t),bt) R 3 dove a e b sono due costanti positive.
Prima Prova Scritta 18/03/1997
 Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 19/06/2010 A
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Esame di Analisi Matematica 2 25/2/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 2 25/2/203 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 202/203 A Esercizio 0. Riportare esclusivamente la risposta a ciascuno dei questi a-d di sotto. Gli elaborati
Esame di Analisi Matematica 2 25/2/203 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 202/203 A Esercizio 0. Riportare esclusivamente la risposta a ciascuno dei questi a-d di sotto. Gli elaborati
Corso di Analisi Matematica 2
 Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof A Iannizzotto Prove d esame 2017 Versione del 17 settembre 2017 Appello del 9 gennaio 2017 Tempo: 150 minuti 1 Determinare gli estremi globali
Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof A Iannizzotto Prove d esame 2017 Versione del 17 settembre 2017 Appello del 9 gennaio 2017 Tempo: 150 minuti 1 Determinare gli estremi globali
Secondo appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2017/2018. Prof. M. Bramanti. Tema n 1.
 Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 17/18. Prof. M. Bramanti 1 Tema n 1 5 6 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 17/18. Prof. M. Bramanti 1 Tema n 1 5 6 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Versione preliminare si prega di segnalare eventuali errori
 Analisi matematica (I mod) Ing. Elettronica PROFF. GIACOMELLI e VERGARA CAFFARELLI ESEMPI DI ESERCIZI D ESAME A.A.8/9 Versione preliminare si prega di segnalare eventuali errori *) Determinare (purché
Analisi matematica (I mod) Ing. Elettronica PROFF. GIACOMELLI e VERGARA CAFFARELLI ESEMPI DI ESERCIZI D ESAME A.A.8/9 Versione preliminare si prega di segnalare eventuali errori *) Determinare (purché
Compiti di Analisi Matematica 2
 UNIVERSITÀ DEGLI STUDI DEL SALENTO FACOLTÀ DI INGEGNERIA Compiti di Analisi Matematica 2 per il C.d.L. in Ingegneria dell Informazione Angela Albanese Informazioni legali: Questi appunti sono prodotti
UNIVERSITÀ DEGLI STUDI DEL SALENTO FACOLTÀ DI INGEGNERIA Compiti di Analisi Matematica 2 per il C.d.L. in Ingegneria dell Informazione Angela Albanese Informazioni legali: Questi appunti sono prodotti
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2014 2015 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2014 2015 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014
 Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014 MATRICOLA:...NOME e COGNOME:............................................. Desidero sostenere la prova orale al prossimo appello
Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014 MATRICOLA:...NOME e COGNOME:............................................. Desidero sostenere la prova orale al prossimo appello
Analisi Matematica II Corso di Ingegneria Gestionale Compito del (x y) log
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -6-4 Esercizio. punti Data la funzione { x y log +, fx, y = x +y 4 x, y,, x, y =, i dire in quali punti del dominio è continua; ii dire
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -6-4 Esercizio. punti Data la funzione { x y log +, fx, y = x +y 4 x, y,, x, y =, i dire in quali punti del dominio è continua; ii dire
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
ISTITUZIONI DI MATEMATICHE II
 ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
Esame di Analisi Matematica 2 24/7/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta del I MODULO di ANALISI MATEMATICA II - 14 gennaio 2000) Compito A
 CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta del I MODULO di ANALISI MATEMATICA II - 14 gennaio 000) Compito A COGNOME... NOME... Data l equazione differenziale y 3 cos
CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta del I MODULO di ANALISI MATEMATICA II - 14 gennaio 000) Compito A COGNOME... NOME... Data l equazione differenziale y 3 cos
Analisi Matematica II Corso di Ingegneria Gestionale Compito del
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del --9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del --9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica 2: Secondo Parziale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Alcuni esercizi risolti da esami di anni passati
 Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
es.1 es.2 es.3 es.4 es.5 somma Analisi Matematica 2: Secondo Parziale, , Versione A Cognome e nome:...matricola:...
 es.1 es. es.3 es. es.5 somma 6 6 6 6 6 3 Analisi Matematica : Secondo Parziale, 3.5.16, Versione A Cognome e nome:....................................matricola:......... 1. Dimostrare che la forma differenziale
es.1 es. es.3 es. es.5 somma 6 6 6 6 6 3 Analisi Matematica : Secondo Parziale, 3.5.16, Versione A Cognome e nome:....................................matricola:......... 1. Dimostrare che la forma differenziale
Ricordiamo che l operatore divergenza agisce su un campo vettoriale F ed è definito come segue: div F (x) = x i. i=1. x 2 + y 2
 Capitolo 4 Campi vettoriali Ultimo aggiornamento: 3 maggio 2017 Ricordiamo che l operatore divergenza agisce su un campo vettoriale F ed è definito come segue: div F x = n F i x. x i i=1 Esercizio 4.1
Capitolo 4 Campi vettoriali Ultimo aggiornamento: 3 maggio 2017 Ricordiamo che l operatore divergenza agisce su un campo vettoriale F ed è definito come segue: div F x = n F i x. x i i=1 Esercizio 4.1
