Rappresentazione dell informazione
|
|
|
- Regina Vecchi
- 7 anni fa
- Visualizzazioni
Transcript
1 Rappresentazione dell informazione Prof. Alberto Borghese Dipartimento di Scienze dell Informazione Università degli Studi di Milano Riferimenti al testo: Paragrafi 2.4, 2.9, 3.1, 3.2, 3.5 (codifica IEEE754) 1/56 Sommario Rappresentazione binaria dell Informazione Sistema di numerazione binario Conversione in e da un numero binario Operazioni elementari su numeri binari: somma, sottrazioni. I numeri decimali Codifica IEEE754 dei numeri reali anche in forma denormalizzata. 2/56 1
2 Il linguaggio Per farsi capire da un calcolatore, occorre parlare la sua stessa lingua. 3/56 Proprietà di potenze e logaritmi 2 K x 2 M = 2 (K+M) M K K K* M M 2 2 = = 2 K = K Il logaritmo è l operazione inversa dell elevamento a potenza. log 2 (2 M ) = M log 2 KM = log2 K + log2 M 1 log2 K = log2 K 4/56 2
3 Rappresentazione dell informazione Non solo conteggio, ma anche enumerazione di oggetti. Noi rappresentiamo gli oggetti tramite parole composte da un alfabeto di simboli: A,B,,Z,0,1,,9, Diversi alfabeti possono essere usati per rappresentare gli stessi oggetti. I simboli degli alfabeti possono assumere diverse forme. Segni su carta, livelli di tensione, fori su carta, segnali di fumo.... 5/56 Codifica dei caratteri alfanumerici Quanti bit devono avere le parole binarie usate per identificare i 26 caratteri diversi dell alfabeto inglese (es: A,B,,Z)? 2 4 < 26 < 2 5 Quanti bit devono avere le parole binarie usate per identificare oggetti diversi (es: A,B,,Z, a,b,.... z)? 2 5 < 52 < 2 6 Quanti bit servono per 100 oggetti? ceil [log 2 100] 6/56 3
4 Il codice ASCII e la rappresentazione dell informazione alfanumerica 8 bit 0-31 codici di controllo extended ASCII 7/56 L UNICODE Codifica su 8, 16, 32 bit alfabeti diversi. 8/56 4
5 Sommario Rappresentazione binaria dell Informazione Sistema di numerazione binario Conversione in e da un numero binario Operazioni elementari su numeri binari: somma, sottrazioni. I numeri decimali Codifica IEEE754 dei numeri reali anche in forma denormalizzata. 9/56 Tassonomia ed unità di misura Hertz - numero di ciclo al secondo nei moti periodici (clock). MIPS - Milioni di istruzioni per secondo. MFLOPS - Milioni di istruzioni in virgola mobile (FLOating point) al secondo. Prefissi: k - chilo (mille:10 3 ). m - milli (un millesimo: 10-3 ) M - mega (un milione:10 6 ). µ - micro (un milionesimo: 10-6 ) G - giga (un miliardo: 10 9 ). n - nano (un miliardesimo: 10-9 ) T tera (1000 miliardi: ) p pico (un millesimo di P peta (1,000,000 miliardi: ) miliardo: ) f femto (un milionesimo di miliardo: ) 10/56 5
6 Terminologia Bit = binary digit. 1 byte = 8 bit. 1kbyte = 2 10 byte = 1,024 byte 1Mbyte = 2 20 byte = 1,048,576 byte. 1Gbyte =2 30 byte = 1,073,741,824 byte. 1Tbyte =2 40 byte = 1,099,511,627,776 byte. Parola (word) numero di bit trattati come un unicum dall elaboratore. Le parole oggi arrivano facilmente a 64bit (Itanium). 11/56 Numerazione Simbolica Sistema di numerazione mediante simboli (numerazione romana: I, V, X, L, C, M) il cui valore non dipende dalla posizione: e.g. XXXI = 31, XI = Sistema di numerazione posizionale (decimale): cifra + peso. Il peso è la base elevata alla posizione della cifra. 1 ha un valore diverso nelle due scritture: /56 6
7 Numerazione Posizionale Alfabeto della numerazione: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} numerazione araba decimale. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F} numerazione esadecimale. {0, 1} numerazione binaria. Sistemi di numerazione binario, ottale ed esadecimale. Conversioni decimale -> binario e viceversa. 13/56 Codifica posizionale di un numero Fondata sul concetto di base: B = [b 0, b 1, b 2, b 3,...]. Ciasun elemento, N, può essere rappresentato come combinazione lineare degli elementi della base: N c b k Esempi: = k k 764,3 10 = 7x x x x10-1 = 764,3 12,21 10 = 1x x x x10-2 = 12,21 100,11 2 = 1x x x x x2-2 = 4,75 b k = B k = 10 k b k = B k = 10 k b k = B k = 2 k 14/56 7
8 Osservazioni sulla numerazione binaria Il linguaggio di un elaboratore elettronico è fatto di due segnali: on e off, rappresentati dai simboli 1 e 0 (alfabeto binario). Sia le istruzioni che i dati sono rappresentati da parole di numeri binari. Un alfabeto binario non limita le funzionalità di un elaboratore a patto di avere parole di lunghezza sufficiente rappresenta un istruzione di addizione in MIPS su 32 bit (add $k0, $t0, $t9). 15/56 Codifica binaria Quanti oggetti diversi possiamo rappresentare con parole binarie di k bit? Con una parola di 1 bit rappresentiamo 2 oggetti (1 bit ha due possibili valori). Supponiamo di avere parole di k-1 bit. Quanti oggetti riescono a rappresentare? 2 k-1 oggetti. 16/56 8
9 Esempio di codifica binaria Quanti oggetti diversi possiamo rappresentare con parole binarie di 3 bit? A B C D E F G H 17/56 Sommario Sistema di numerazione binario Rappresentazione binaria dell Informazione Conversione in e da un numero binario Operazioni elementari su numeri binari (somma, sottrazione e moltiplicazione intera). I numeri decimali Codifica IEEE754 dei numeri reali anche in forma denormalizzata. 18/56 9
10 Conversione da base n a base 10 Un numero N=[c 0, c 1, c 2, c 3,...] in base 10, B = [b 0, b 1, b 2, b 3...] si trasforma in base n, R = [r 0, r 1, r 2, r 3...], facendo riferimento alla formula: N 1 N = k c k b ciascuna cifra k-esima viene moltiplicata per la base corrispondente: r k = n k. i valori così ottenuti sono sommati per ottenere il numero in notazione decimale due = 1x x x x x x x x x x x2 0 = = 1493 k = k = 0 d k r k A.A /45 borghese Spelling di un numero Vogliamo rappresentare 1493 dieci Unità Decine Centinaia Migliaia 1493 = 10 x (10x) 149 = 10 x (100x) 14 = 10 x (1000x) 1 = 10 x Cifra meno significativa Cifra più significativa 1493 = 3x1 + 9x10 + 4x x /56 10
11 estrazione delle cifre decimali Vogliamo estrarre le cifre di 1493 dieci. Porto le cifre alla destra della virgola: 1493 / 10 = 149,3 esamino unità 149 / 10 =14,9 esamino 14 9 decine 14 / 10 = 1,4 esamino 1 4 centinaia 1 / 10 = 0,1 termina 1 migliaia 21/56 Meccanismo di estrazione Vogliamo estrarre le cifre di 1493 dieci. Porto le cifre alla destra della virgola. Utilizzo la divisione intera per la base 10, il resto rappresenta la cifra decimale meno significativa / 10 = 149 con R = 3 3 unità 149 / 10 =14 con R = 9 9 decine 14 / 10 = 1 con R = 4 4 centinaia 1 / 10 = 0 con R = 1 1 migliaia Termina perchè non è rimasto nulla del numero. 22/56 11
12 Conversione base 10 -> base 2 estrazione delle cifre binarie Vogliamo rappresentare 1493 dieci in binario: due 1493 / 2 = / 2 = *2 + 0 = / 2 = *2 + 1 = 373 => (186*2+1)*2 = / 2 = / 2 = / 2 = / 2 = / 2 = / 2 = / 2 = / 2 = Bit meno significativo (LSB) Bit più significativo (MSB) 23/56 Perché funziona? Prendiamo il numero E0 e dividiamo per 2. Se E0 è pari il resto, R0, sarà 0, altrimenti sarà 1. Infatti: int (E0 / 2) * 2 + R0 = E0. Esempio: E0 = 5 10 =? 2 R0 = resto(5/2) = 1 Chiamiamo E1 = int( E0 / 2 ) e procediamo. Prendiamo E1 e dividiamo per 2. Chiamiamo E2 = int(e1 / 2). Se E1 è pari il resto, R1, sarà 0, altrimenti sarà 1. E1 = int (E1 / 2) * 2 + R1 Chiamiamo E2 = int(e1 / 2) e procediamo. Prendiamo E2 e dividiamo per 2. Se E2 è pari il resto, R2, sarà 0, altrimenti sarà 1. E2 = int (E2 / 2) * 2 + R2. E1 = quoz(5/2) = 2 R1 = resto(2/2) = 0 E2 = quoz(2/2) = 1 R2 = resto(1/2) = 0 Si procede fino a quando Ei non è < 2 (=1). E0 = R0 + R1 * 2 + R2 *2 2 E0 = int [ E0 / 2] * 2 + R0. = E0 = int [ E1] * 2 + R0. E0 = int [ int ( E1 / 2) * 2 + R1] * 2 + R0. E0 = int [ int(e2) * 2 + R1] * 2 + R0. E0 = int [ int[int(e2 / 2)*2 +R2] * 2 + R1] * 2 + R0. int(e2 / 2) = 0 24/56 12
13 Conversione base 10 -> base n: algoritmo Un numero x in base 10 si trasforma in base n usando il seguente procedimento: Dividere il numero x per n Il resto della divisione è la cifra di posto 0 in base n Il quoziente della divisione è a sua volta diviso per n Il resto ottenuto a questo passo è la cifra di posto 1 in base n Si prosegue con le divisioni dei quozienti ottenuti al passo precedente fino a che l ultimo quoziente è 0. l ultimo resto è la cifra più significativa in base n 25/56 Esercizi Dati i numeri decimali 23456, 89765, 67489, , 2453, si trasformino in base 3 si trasformino in base 7 si trasformino in base 2 Dati i numeri , , , convertire ciascuno in decimale e in binario 26/56 13
14 Codifica esadecimale Il codice esadecimale viene utilizzato come forma compatta per rappresentare numeri binari: 16 simboli: 0,1,,9,A,B,,F Diverse notazioni equivalenti: 0x9F 9F 16 9Fhex 0x9F = 9x x16 0 = /56 Conversione esadecimale -> binario Vogliamo rappresentare 9Fhex in binario. E semplice. Ogni simbolo viene convertito in un numero binario di 4 cifre: 9hex --> 1001 due Fhex --> 1111 due 9Fhex --> due È sufficiente ricordarsi come si rappresentano in binario i numeri decimali da 0 a 15 (o derivarli) 28/56 14
15 Conversione binario -> esadecimale Da binario ad esadecimale si procede in modo analogo: Ogni gruppo di 4 cifre viene tradotto nel simbolo corrispondente: Esempio: convertire due in esadecimale: 1011 due --> B hex 110 due --> 6 hex Viene aggiunto un leading due --> 6B hex add $k0, $t0, $t9 0x0328d020 29/56 Codifica dei numeri interi Viene replicato il bit più significativo Codifica su 16 bit: Numeri naturali: = = Replico il primo bit, parte integrante del numero Numeri relativi: = = Numeri relativi: = = Replico il primo bit, quello del segno 30/56 15
16 Capacità di rappresentazione: Numeri Interi Interi con segno su N bit. Range: -2 N-1 n 2 N-1-1. Esempio: Visual C++. Intero è su 4byte (word di 32 bit): = n = /56 Sommario Sistema di numerazione binario Rappresentazione binaria dell Informazione Conversione in e da un numero binario Operazioni elementari su numeri binari: somma, sottrazione I numeri decimali Codifica IEEE754 dei numeri reali anche in forma denormalizzata. 32/56 16
17 Somma = Riporto Vorrei definire solo l operazione di somma e non utilizzare la sottrazione 33/56 Numeri negativi: complemento a 1 I numeri negativi sono complementari ai numeri positivi: a + (-a) = 0 Codifica in complemento a 1: il numero negativo si ottiene cambiando 0 con 1 e viceversa. Problema: Doppia codifica per lo /56 17
18 Numeri negativi: complemento a 2 I numeri negativi sono complementari ai numeri positivi: a + (-a) = 0 Codifica in complemento a 2: il numero negativo si ottiene cambiando 0 con 1 e viceversa, e sommando negativo: = 111 = negativo: = 110 = negativo: = 101 = (x 31 x )+ (x 30 x 2 30 ) + (x 29 x 2 29 )+ + (x 1 x 2 1 ) + (x 0 x 2 0 ) NB La prima cifra è il bit di segno. 35/56 Perché complemento a 2? La rappresentazione in complemento a due deve il suo nome alla proprietà in base alla quale la somma senza segno di un numero di n bit e del suo complemento è pari a 2 n (peso del bit n+1) 7 + (-7) = = (-5) = = e quindi il complemento (o negazione) di un numero x in complemento a due è pari a 2 n x, ovvero il suo complemento a = = /56 18
19 Doppia negazione I numeri negativi sono complementari ai numeri positivi: a + (-a) = 0 Segue che -(-a) = +a Codifica in complemento a 2: il numero negativo si ottiene cambiando 0 con 1 e viceversa, e sommando = Esempio: -(-2) 10 = (10) 2 => Complemento a 1 => 01 => Sommo 1 (complemento a 2) => 10 2 = 2 10 c.v.d. 37/56 Sottrazione Sommo i seguenti 2 numeri 11 + (-13): = = E equivalente ad effettuare la differenza: = /56 19
20 Sommario Sistema di numerazione binario Rappresentazione binaria dell Informazione Conversione in e da un numero binario Operazioni elementari su numeri binari: somma, sottrazione. I numeri decimali Codifica IEEE754 dei numeri reali anche in forma denormalizzata. 39/56 Numeri decimali rappresentazione in fixed point Numeri reali per il computer non sono i numeri reali per la matematica!! E meglio chiamarli float (numeri decimali), sono in numero finito. Dato un certo numero di bit (stringa) per codificare il numero float, esistono due tipi di codifiche possibili: Rappresentazione in fixed point. La virgola è in posizione fissa all interno della stringa. Supponiamo di avere una stringa di 8 cifre, con virgola in 3a posizione: 27,35 = + 27, ,7 = - 18, , = + 00,00145(6) 40/56 20
21 Numeri decimali rappresentazione floating point Rappresentazione come mantissa + esponente. E = Esempio di rappresentazioni equivalenti: 627,35 = 62,735 x 10 1 = 6,2735 x 10 2 = 0,62735 x 10 3 = 10 1 x (6x x x x x10-4 ) = 10 2 x 1,2735 In grassetto viene evidenziata la rappresentazione normalizzata. Vengono rappresentati numeri molto grandi e molto piccoli. Supponiamo di avere una stringa di 8 cifre. 5 per la mantissa, 2 per l esponente: 0, = k c b k k = N c k k= M B k E in virgola mobile, perchè la prima cifra prima della virgola ha un peso diverso a seconda dell esponente. 41/56 Conversione base 10 -> base n: algoritmo Un numero x.y in base 10 si trasforma in base n usando il seguente procedimento. Per la parte intera, x, si applica l algoritmo visto in precedenza: Dividere il numero x per n Il resto della divisione è la cifra di posto 0 in base n Il quoziente della divisione è a sua volta diviso per n Il resto ottenuto a questo passo è la cifra di posto 1 in base n Si prosegue con le divisioni dei quozienti ottenuti al passo precedente fino a che l ultimo quoziente è 0. l ultimo resto è la cifra più significativa in base n 42/56 21
22 «Estrazione» delle cifre decimali contenute dopo la virgola Vogliamo estrarre le cifre di 0,3672 dieci. Porto le cifre alla sinistra della virgola: 0,3672 * 10 = 3,67 esamino 0,672 3 decimi 0,672 * 10 =6,7 esamino 0,72 6 centesimi 0,72 * 10 = 7,2 esamino 0,2 7 millesimi 0,2 * 10 = 2,0 termina 2 decimillesimi 43/56 Conversione base 10 -> base 2 estrazione delle cifre binarie dopo la virgola Vogliamo rappresentare 0,625 dieci in binario: 0,101 due 0,625 * 2 = 1,250 => 1 0,250 * 2 = 0,500 => 0 0,500 * 2 = 1,000 => 1 0,0000 1* * *2-3 = ½ + 1/8 = 0,5 + 0,125 = 0,625 44/56 22
23 Conversione base 10 -> base n: algoritmo per la parte frazionaria Un numero x,y in base 10 si trasforma in base n usando il seguente procedimento. Per la parte frazionaria, y: Moltiplicare il numero y per n La prima cifra del risultato coincide con la cifra di posto 1 dopo la virgola. Si elimina la parte intera ottenuta e si considera la nuova parte frazionaria. La parte frazionaria ottenuta viene moltiplicata per la base n. La prima cifra del risultato coincide con la cifra di posto 2 dopo la virgola. Si prosegue con le moltiplicazioni della parte frazionaria fino a quando non diventa 0 o non si esaurisce la capacità di rappresentazione. 45/56 Conversione base 10 -> base n: algoritmo per la parte frazionaria Un numero x,y in base 10 si trasforma in base n usando il seguente procedimento. Per la parte frazionaria, y: Moltiplicare il numero y per n La prima cifra del risultato coincide con la cifra di posto 1 dopo la virgola. Si elimina la parte intera ottenuta e si considera la nuova parte frazionaria. La parte frazionaria ottenuta viene moltiplicata per la base n. La prima cifra del risultato coincide con la cifra di posto 2 dopo la virgola. Si prosegue con le moltiplicazioni della parte frazionaria fino a quando non diventa 0 o non si esaurisce la capacità di rappresentazione. 46/56 23
24 Errori di approssimazione Esempio: 10,75 10 = 1010,11 2 Esempio: 10,76 10 = 1010, : 2 => 0 5 : 2 => 1 2 : 2 => 0 1 : 2 => 1 ###### 1010, 0,75 *2 => 1 (1),50 *2 => 1 (1),00 => ###### 11 Errori di approssimazione: arrotondamento e troncamento. 0,76 *2 => 1x2-1 (1),52*2 => 1x2-2 (1),04*2 => 0x2-3 (0),08 *2 => 0x2-4 (0),16 *2 => 0x2-5 (0),32 *2 => 0x2-6 (0),64 *2 => 1x2-7 (1),28.. (2-7 = 0, ) Con 7 bit di parte fraz, rappresento: 0,5+0,25+0, = 0, Errore = 0, /56 Sommario Sistema di numerazione binario Rappresentazione binaria dell Informazione Conversione in e da un numero binario Operazioni elementari su numeri binari: somma, sottrazione. I numeri decimali Codifica IEEE754 dei numeri reali anche in forma denormalizzata 48/56 24
25 Standard IEEE 754 (1980) Rappresentazione polarizzata dell esponente: Polarizzazione pari a 127 per singola precisione => 1 viene codificato come Polarizzazione pari a 1023 in doppia precisione. 1 viene codificato come /56 Codifica mediante lo standard IEEE 754 Sign Esempio: N = -10,75 10 = -1010,11 2 1) Normalizzazione: ±1,xxxxxx Esempio: -1,01011 x 2 3 2) Codifica del segno 1 = - 0 = + 3) Calcolo dell esponente, exp. s Exp+127 Parte Frazionaria 50/56 25
26 Calcolo dell esponente in notazione polarizzata Sign Esempio: N = -10,75 10 = -1010,11 2 = -1, x 2 3 Calcolo dell esponente, e, in rappresentazione polarizzata (si considerano solo 254 esponenti sui 256 possibili): Codifica Exp effettivo del numero = 255 Codifica riservata = = = = Polarizzazione: = = = = 0 Codifica riservata 51/56 N = Configurazioni notevoli nello Standard IEEE 754 Configurazioni notevoli: 0 Mantissa: 0 Esponente: Mantissa: 0 Esponente: NaN Mantissa: 0. Esponente: Range degli esponenti (8 bit): => -126 exp Numeri float: 1.0 x = x x10 38 = x /56 26
27 Capacità dello Standard IEEE 754 Range degli esponenti (8 bit): => -126 exp Minimo float (in valore assoluto!): 1.0 x Massimo float: x Capacità float: Minimo: x ( e-038) Massimo: e+038 x ( e+038) Discontinuità tra Minimo_float e 0 il delta è x Si può fare di meglio? Numero denormalizzato Mantissa: 0 Esponente: /56 Denormalizzazione nello Standard IEEE 754 Esempio di numero denormalizzato: 0, x Range degli esponenti (8 bit): => -126 exp Minimo float (in valore assoluto!): 1.0 x = x Tuttavia abbiamo anche la mantissa a disposizione. Se troviamo una codifica per cui possiamo scrivere 0, , otteniamo un numero più piccolo (in valore assoluto!) pari a : 2 ( ) = x Discontinuità tra Minimo_float e 0 diventa = x Configurazioni notevoli: 0 Mantissa: 0 Esponente: Mantissa: 0 Esponente: NaN Mantissa: 0. Esponente: Numero denormalizzato Mantissa: 0 Esponente: /56 27
28 Risoluzione della codifica dei reali Distanza tra due numeri vicini. Fixed point: Risoluzione fissa, pari al peso del bit meno significativo. Esempio su 8 bit: +1111,101 la risoluzione per tutti i numeri sarà: 1 x 2-3 = 0,125 Floating point: Risoluzione relativa fissa, pari al peso del bit meno significativo. Il bit meno significativo è in 23a posizione in singola precisione => 2-23, ne consegue che la risoluzione sarà 2-23 volte il numero descritto. Esempi: 100,... = 1,000 x 2 2 => La risoluzione sarà 2-23 x 2 2 = x => La risoluzione sarà 2-23 x = /56 Sommario Sistema di numerazione binario Rappresentazione binaria dell Informazione Conversione in e da un numero binario Operazioni elementari su numeri binari: somma, sottrazione I numeri decimali Codifica IEEE754 dei numeri reali anche in forma denormalizzata. 56/56 28
La codifica binaria. Sommario
 La codifica binaria Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@dsi.unimi.it Università degli Studi di Milano 1/44 Sommario Rappresentazione binaria dell Informazione Conversione
La codifica binaria Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@dsi.unimi.it Università degli Studi di Milano 1/44 Sommario Rappresentazione binaria dell Informazione Conversione
Rappresentazione dell informazione
 Rappresentazione dell informazione Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@di.unimi.it Università degli Studi di Milano Riferimenti al testo: Paragrafi 2.4, 2.9, 3.1,
Rappresentazione dell informazione Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@di.unimi.it Università degli Studi di Milano Riferimenti al testo: Paragrafi 2.4, 2.9, 3.1,
Numerazione Simbolica. Sommario
 Numerazione Simbolica Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@dsi.unimi.it Università degli Studi di Milano Riferimenti al testo: Paragrafi 2.4, 2.9, 3.1, 3.2, 3.5 (codifica
Numerazione Simbolica Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@dsi.unimi.it Università degli Studi di Milano Riferimenti al testo: Paragrafi 2.4, 2.9, 3.1, 3.2, 3.5 (codifica
Rappresentazione dell informazione
 Rappresentazione dell informazione Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@di.unimi.it Università degli Studi di Milano Riferimenti al testo: Paragrafi 2.4, 2.9, 3.1,
Rappresentazione dell informazione Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@di.unimi.it Università degli Studi di Milano Riferimenti al testo: Paragrafi 2.4, 2.9, 3.1,
Numerazione Simbolica
 Numerazione Simbolica Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@dsi.unimi.it Università degli Studi di Milano Riferimenti al testo: capitolo 3 (escluso 3.5,del paragrafo
Numerazione Simbolica Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@dsi.unimi.it Università degli Studi di Milano Riferimenti al testo: capitolo 3 (escluso 3.5,del paragrafo
Rappresentazione dell informazione
 Rappresentazione dell informazione Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@di.unimi.it Università degli Studi di Milano Riferimenti al testo: Paragrafi 2.4, 2.9, 3.1,
Rappresentazione dell informazione Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@di.unimi.it Università degli Studi di Milano Riferimenti al testo: Paragrafi 2.4, 2.9, 3.1,
Architetture dei calcolatori e delle reti. Lezione 2
 Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Scienze dell Informazione Università degli Studi di Milano L 2 1/32 Alcune unità di
Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Scienze dell Informazione Università degli Studi di Milano L 2 1/32 Alcune unità di
Lezione 2. Rappresentazione dell informazione
 Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Scienze dell Informazione (DSI) Università degli Studi di Milano L 2 1/30 Alcune unità
Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Scienze dell Informazione (DSI) Università degli Studi di Milano L 2 1/30 Alcune unità
Lezione 2. Rappresentazione dell informazione
 Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Scienze dell Informazione (DSI) Università degli Studi di Milano L 2 1/29 Terminologia!
Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Scienze dell Informazione (DSI) Università degli Studi di Milano L 2 1/29 Terminologia!
Lezione 2. Rappresentazione dell informazione
 Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Informatica (DI) Università degli Studi di Milano L 2 1/24 Rappresentazione dell informazione
Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Informatica (DI) Università degli Studi di Milano L 2 1/24 Rappresentazione dell informazione
Lezione 2. Rappresentazione dell informazione
 Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Informatica (DI) Università degli Studi di Milano 1 Rappresentazione dell informazione
Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Informatica (DI) Università degli Studi di Milano 1 Rappresentazione dell informazione
Lezione 2. Rappresentazione dell informazione
 Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Informatica (DI) Uniersità degli Studi di Milano 1 Rappresentazione dell informazione
Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Informatica (DI) Uniersità degli Studi di Milano 1 Rappresentazione dell informazione
Lezione 2. Rappresentazione dell informazione
 Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Informatica (DI) Uniersità degli Studi di Milano 1 Rappresentazione dell informazione
Architetture dei calcolatori e delle reti Lezione 2 Rappresentazione dell informazione A. Borghese, F. Pedersini Dip. Informatica (DI) Uniersità degli Studi di Milano 1 Rappresentazione dell informazione
1-Rappresentazione dell informazione
 1-Rappresentazione dell informazione Informazioni: testi, numeri, immagini, suoni, etc.; Come viene rappresentata l informazione in un calcolatore? Uso di tecnologia digitale: tutto ciò che viene rappresentato
1-Rappresentazione dell informazione Informazioni: testi, numeri, immagini, suoni, etc.; Come viene rappresentata l informazione in un calcolatore? Uso di tecnologia digitale: tutto ciò che viene rappresentato
Aritmetica dei Calcolatori Elettronici
 Aritmetica dei Calcolatori Elettronici Prof. Orazio Mirabella L informazione Analogica Segnale analogico: variabile continua assume un numero infinito di valori entro l intervallo di variazione intervallo
Aritmetica dei Calcolatori Elettronici Prof. Orazio Mirabella L informazione Analogica Segnale analogico: variabile continua assume un numero infinito di valori entro l intervallo di variazione intervallo
Conversione binario-ottale/esadecimale. Conversione binario-ottale/esadecimale. Rappresentazione di Numeri Interi Positivi (numeri naturali)
 Conversione binario-ottale/esadecimale Conversione binario-ottale/esadecimale Nella rappresentazione ottale (B=8) si usano gli 8 simboli,, 2, 3, 4, 5, 6, 7 In quella esadecimale (B=6) i 6 simboli,, 2,
Conversione binario-ottale/esadecimale Conversione binario-ottale/esadecimale Nella rappresentazione ottale (B=8) si usano gli 8 simboli,, 2, 3, 4, 5, 6, 7 In quella esadecimale (B=6) i 6 simboli,, 2,
UD 1.2e: La codifica Digitale dei Numeri CODIFICA DIGITALE DEI NUMERI
 Modulo 1: Le I.C.T. : La codifica Digitale dei Numeri CODIFICA DIGITALE DEI NUMERI Prof. Alberto Postiglione Corso di Informatica Generale (AA 07-08) Corso di Laurea in Scienze della Comunicazione Università
Modulo 1: Le I.C.T. : La codifica Digitale dei Numeri CODIFICA DIGITALE DEI NUMERI Prof. Alberto Postiglione Corso di Informatica Generale (AA 07-08) Corso di Laurea in Scienze della Comunicazione Università
Modulo 1: Le I.C.T. UD 1.2e: La codifica Digitale dei Numeri
 Modulo 1: Le I.C.T. : La codifica Digitale dei Numeri Prof. Alberto Postiglione Corso di Informatica Generale (AA 07-08) Corso di Laurea in Scienze della Comunicazione Università degli Studi di Salerno
Modulo 1: Le I.C.T. : La codifica Digitale dei Numeri Prof. Alberto Postiglione Corso di Informatica Generale (AA 07-08) Corso di Laurea in Scienze della Comunicazione Università degli Studi di Salerno
Rappresentazione di dati: numerazione binaria. Appunti per la cl. 3 Di A cura del prof. Ing. Mario Catalano
 Rappresentazione di dati: numerazione binaria Appunti per la cl. 3 Di A cura del prof. Ing. Mario Catalano Rappresentazione binaria Tutta l informazione interna ad un computer è codificata con sequenze
Rappresentazione di dati: numerazione binaria Appunti per la cl. 3 Di A cura del prof. Ing. Mario Catalano Rappresentazione binaria Tutta l informazione interna ad un computer è codificata con sequenze
Rappresentazione binaria
 Rappresentazione binaria Per informazione intendiamo tutto quello che viene manipolato da un calcolatore: numeri (naturali, interi, reali,... ) caratteri immagini suoni programmi... La più piccola unità
Rappresentazione binaria Per informazione intendiamo tutto quello che viene manipolato da un calcolatore: numeri (naturali, interi, reali,... ) caratteri immagini suoni programmi... La più piccola unità
Sistemi di Elaborazione delle Informazioni
 Sistemi di Elaborazione delle Informazioni Rappresentazione dell Informazione 1 Il bit Si consideri un alfabeto di 2 simboli: 0, 1 Che tipo di informazione si può rappresentare con un bit? 2 Codifica binaria
Sistemi di Elaborazione delle Informazioni Rappresentazione dell Informazione 1 Il bit Si consideri un alfabeto di 2 simboli: 0, 1 Che tipo di informazione si può rappresentare con un bit? 2 Codifica binaria
Rappresentazione numeri reali
 Rappresentazione numeri reali I numeri reali rappresentabili in un calcolatore sono in realtà numeri razionali che approssimano i numeri reali con un certo grado di precisione Per rappresentare un numero
Rappresentazione numeri reali I numeri reali rappresentabili in un calcolatore sono in realtà numeri razionali che approssimano i numeri reali con un certo grado di precisione Per rappresentare un numero
Codifica dell Informazione per il Calcolo Scientifico
 Alfredo Cuzzocrea per il Calcolo Scientifico CODIFICA BINARIA Codifica binaria: usa un alfabeto di 2 simboli Utilizzata nei sistemi informatici Si utilizza una grandezza fisica (luminosità, tensione elettrica,
Alfredo Cuzzocrea per il Calcolo Scientifico CODIFICA BINARIA Codifica binaria: usa un alfabeto di 2 simboli Utilizzata nei sistemi informatici Si utilizza una grandezza fisica (luminosità, tensione elettrica,
I.4 Rappresentazione dell informazione
 I.4 Rappresentazione dell informazione Università di Ferrara Dipartimento di Economia e Management Insegnamento di Informatica Ottobre 13, 2015 Argomenti Introduzione 1 Introduzione 2 3 L elaboratore Introduzione
I.4 Rappresentazione dell informazione Università di Ferrara Dipartimento di Economia e Management Insegnamento di Informatica Ottobre 13, 2015 Argomenti Introduzione 1 Introduzione 2 3 L elaboratore Introduzione
N= a i b i. Numeri e numerali. Sistemi di Numerazione Binaria. Sistemi posizionali. Numeri a precisione finita
 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Sistemi di Numerazione Binaria Lo stesso numero è rappresentato da
Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Sistemi di Numerazione Binaria Lo stesso numero è rappresentato da
Sistemi di Numerazione Binaria
 Sistemi di Numerazione Binaria BIN.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Sistemi di Numerazione Binaria BIN.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Rappresentazione binaria
 Rappresentazione binaria Per informazione intendiamo tutto quello che viene manipolato da un calcolatore: numeri (naturali, interi, reali,... ) caratteri immagini suoni programmi... La più piccola unità
Rappresentazione binaria Per informazione intendiamo tutto quello che viene manipolato da un calcolatore: numeri (naturali, interi, reali,... ) caratteri immagini suoni programmi... La più piccola unità
Elementi di informatica
 1 2 Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri 3 Sistemi di numerazione posizionali La rappresentazione dei numeri richiede ovviamente una codifica, ovvero la
1 2 Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri 3 Sistemi di numerazione posizionali La rappresentazione dei numeri richiede ovviamente una codifica, ovvero la
Fondamenti di informatica
 Fondamenti di informatica Alessandro GORI a.gori@unifi.it informottica.webnode.it A.Gori - Fondamenti di informatica 1 Bibliografia Introduzione ai Sistemi Informatici IV edizione, Sciuto et alt., McGraw-Hill
Fondamenti di informatica Alessandro GORI a.gori@unifi.it informottica.webnode.it A.Gori - Fondamenti di informatica 1 Bibliografia Introduzione ai Sistemi Informatici IV edizione, Sciuto et alt., McGraw-Hill
Numeri frazionari nel sistema binario
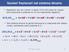 Numeri frazionari nel sistema binario Sappiamo che nei numeri in base 10 le cifre dopo la virgola sono associate a potenze di 10 con esponente negativo: 675,93 (10) = 6 10 2 +7 10 1 +5 10 0 +9 10-1 +3
Numeri frazionari nel sistema binario Sappiamo che nei numeri in base 10 le cifre dopo la virgola sono associate a potenze di 10 con esponente negativo: 675,93 (10) = 6 10 2 +7 10 1 +5 10 0 +9 10-1 +3
Architettura degli Elaboratori e Laboratorio. Matteo Manzali Università degli Studi di Ferrara Anno Accademico
 Architettura degli Elaboratori e Laboratorio Matteo Manzali Università degli Studi di Ferrara Anno Accademico 2016-2017 Numeri razionali Sono numeri esprimibili come rapporto di due numeri interi. L insieme
Architettura degli Elaboratori e Laboratorio Matteo Manzali Università degli Studi di Ferrara Anno Accademico 2016-2017 Numeri razionali Sono numeri esprimibili come rapporto di due numeri interi. L insieme
La codifica. dell informazione
 00010010101001110101010100010110101000011100010111 00010010101001110101010100010110101000011100010111 La codifica 00010010101001110101010100010110101000011100010111 dell informazione 00010010101001110101010100010110101000011100010111
00010010101001110101010100010110101000011100010111 00010010101001110101010100010110101000011100010111 La codifica 00010010101001110101010100010110101000011100010111 dell informazione 00010010101001110101010100010110101000011100010111
Codifica. Rappresentazione di numeri in memoria
 Codifica Rappresentazione di numeri in memoria Rappresentazione polinomiale dei numeri Un numero decimale si rappresenta in notazione polinomiale moltiplicando ciascuna cifra a sinistra della virgola per
Codifica Rappresentazione di numeri in memoria Rappresentazione polinomiale dei numeri Un numero decimale si rappresenta in notazione polinomiale moltiplicando ciascuna cifra a sinistra della virgola per
Elementi di informatica
 Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Sistemi di numerazione posizionali La rappresentazione dei numeri richiede ovviamente una codifica, ovvero la definizione
Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Sistemi di numerazione posizionali La rappresentazione dei numeri richiede ovviamente una codifica, ovvero la definizione
I sistemi di numerazione. Informatica - Classe 3ª, Modulo 1
 I sistemi di numerazione Informatica - Classe 3ª, Modulo 1 1 La rappresentazione interna delle informazioni ELABORATORE = macchina binaria Informazione esterna Sequenza di bit Spett. Ditta Rossi Via Roma
I sistemi di numerazione Informatica - Classe 3ª, Modulo 1 1 La rappresentazione interna delle informazioni ELABORATORE = macchina binaria Informazione esterna Sequenza di bit Spett. Ditta Rossi Via Roma
Notazione posizionale. Codifica binaria. Rappresentazioni medianti basi diverse. Multipli del byte
 Codifica binaria Rappresentazione di numeri Notazione di tipo posizionale (come la notazione decimale). Ogni numero è rappresentato da una sequenza di simboli Il valore del numero dipende non solo dalla
Codifica binaria Rappresentazione di numeri Notazione di tipo posizionale (come la notazione decimale). Ogni numero è rappresentato da una sequenza di simboli Il valore del numero dipende non solo dalla
Codifica di informazioni numeriche
 Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica Codifica di informazioni numeriche Fondamenti di Informatica - Ingegneria Elettronica Leonardo Querzoni querzoni@dis.uniroma1.it
Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica Codifica di informazioni numeriche Fondamenti di Informatica - Ingegneria Elettronica Leonardo Querzoni querzoni@dis.uniroma1.it
Rappresentazione e Codifica dell Informazione
 Rappresentazione e Codifica dell Informazione Capitolo 1 Chianese, Moscato, Picariello, Alla scoperta dei fondamenti dell informatica un viaggio nel mondo dei BIT, Liguori editore. Sistema di numerazione
Rappresentazione e Codifica dell Informazione Capitolo 1 Chianese, Moscato, Picariello, Alla scoperta dei fondamenti dell informatica un viaggio nel mondo dei BIT, Liguori editore. Sistema di numerazione
Rappresentazione dell informazione
 Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica Rappresentazione dell informazione Fondamenti di Informatica Ingegneria Gestionale Leonardo Querzoni querzoni@dis.uniroma1.it A.A.
Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica Rappresentazione dell informazione Fondamenti di Informatica Ingegneria Gestionale Leonardo Querzoni querzoni@dis.uniroma1.it A.A.
CdL in Medicina Veterinaria - STPA AA
 CdL in Medicina Veterinaria - STPA AA 2007-08 La rappresentazione delle informazioni Che cosa è un informazione? "Per la teoria dell'informazione è abbastanza facile identificare alcune delle ipotesi che
CdL in Medicina Veterinaria - STPA AA 2007-08 La rappresentazione delle informazioni Che cosa è un informazione? "Per la teoria dell'informazione è abbastanza facile identificare alcune delle ipotesi che
Rappresentazione dell Informazione
 Rappresentazione dell Informazione Gli strumenti di elaborazione e memorizzazione a cui un computer ha accesso hanno solo 2 stati Rappresentazione delle informazioni in codice binario: Caratteri, Naturali
Rappresentazione dell Informazione Gli strumenti di elaborazione e memorizzazione a cui un computer ha accesso hanno solo 2 stati Rappresentazione delle informazioni in codice binario: Caratteri, Naturali
Calcolatori Elettronici Parte III: Sistemi di Numerazione Binaria
 Anno Accademico 2001/2002 Calcolatori Elettronici Parte III: Sistemi di Numerazione Binaria Prof. Riccardo Torlone Università di Roma Tre Numeri e numerali! Numero: entità astratta! Numerale: stringa di
Anno Accademico 2001/2002 Calcolatori Elettronici Parte III: Sistemi di Numerazione Binaria Prof. Riccardo Torlone Università di Roma Tre Numeri e numerali! Numero: entità astratta! Numerale: stringa di
Codifica dell informazione numerica. Matteo Re, Nicola Basilico,
 Codifica dell informazione numerica Matteo Re, matteo.re@unimi.it Nicola Basilico, nicola.basilico@unimi.it Informazioni (edizione 2017-2018) Turno A (cognomi A - F) Nicola Basilico, dip. via Comelico,
Codifica dell informazione numerica Matteo Re, matteo.re@unimi.it Nicola Basilico, nicola.basilico@unimi.it Informazioni (edizione 2017-2018) Turno A (cognomi A - F) Nicola Basilico, dip. via Comelico,
Rappresentazione dell informazione
 Rappresentazione dell informazione RAPPRESENTAZIONE DELL INFORMAZIONE Per poter rappresentare le informazioni è necessario codificare le informazioni per poterne garantire l'affidabilità. I simboli per
Rappresentazione dell informazione RAPPRESENTAZIONE DELL INFORMAZIONE Per poter rappresentare le informazioni è necessario codificare le informazioni per poterne garantire l'affidabilità. I simboli per
Informatica di Base - 6 c.f.u.
 Università degli Studi di Palermo Dipartimento di Ingegneria Informatica Informatica di Base - 6 c.f.u. Anno Accademico 27/28 Docente: ing. Salvatore Sorce Rappresentazione delle informazioni Sistemi di
Università degli Studi di Palermo Dipartimento di Ingegneria Informatica Informatica di Base - 6 c.f.u. Anno Accademico 27/28 Docente: ing. Salvatore Sorce Rappresentazione delle informazioni Sistemi di
Programma del corso. Rappresentazione delle Informazioni. Introduzione agli algoritmi. Architettura del calcolatore
 Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori (Reti Locali, Internet) Elementi di Programmazione Rappresentazione
Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori (Reti Locali, Internet) Elementi di Programmazione Rappresentazione
modificato da andynaz Cambiamenti di base Tecniche Informatiche di Base
 Cambiamenti di base Tecniche Informatiche di Base TIB 1 Il sistema posizionale decimale L idea del sistema posizionale: ogni cifra ha un peso Esempio: 132 = 100 + 30 + 2 = 1 10 2 + 3 10 1 + 2 10 0 Un numero
Cambiamenti di base Tecniche Informatiche di Base TIB 1 Il sistema posizionale decimale L idea del sistema posizionale: ogni cifra ha un peso Esempio: 132 = 100 + 30 + 2 = 1 10 2 + 3 10 1 + 2 10 0 Un numero
Esercitazione del 2/3/2010- Numeri binari e conversione
 Esercitazione del 2/3/2010- Numeri binari e conversione 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero indica il peso della cifra stessa, cioè
Esercitazione del 2/3/2010- Numeri binari e conversione 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero indica il peso della cifra stessa, cioè
Sistemi di Numerazione Binaria
 Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
La Rappresentazione dell Informazione
 La Rappresentazione dell Informazione Maurizio Palesi Sommario In questo documento sarà trattato il modo in cui, in un calcolatore, vengono rappresentati i vari generi di informazione (testi, numeri interi,
La Rappresentazione dell Informazione Maurizio Palesi Sommario In questo documento sarà trattato il modo in cui, in un calcolatore, vengono rappresentati i vari generi di informazione (testi, numeri interi,
Sistemi di Numerazione Binaria a i b i. a m a m-1... a 0. a -1 a a -k
 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Sistemi di Numerazione Binaria Lo stesso numero è rappresentato da
Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Sistemi di Numerazione Binaria Lo stesso numero è rappresentato da
Corso di Architettura degli Elaboratori
 Corso di Architettura degli Elaboratori Codifica dell'informazione: Numeri Binari (lucidi originali della Prof.ssa Zacchi e del Prof. Balossino) Dipartimento di Informatica Università degli Studi di Torino
Corso di Architettura degli Elaboratori Codifica dell'informazione: Numeri Binari (lucidi originali della Prof.ssa Zacchi e del Prof. Balossino) Dipartimento di Informatica Università degli Studi di Torino
Sistemi di Numerazione Binaria
 Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Informatica e Laboratorio di Programmazione Sistema Binario Alberto Ferrari. Alberto Ferrari Informatica e Laboratorio di Programmazione
 Informatica e Laboratorio di Programmazione Sistema Binario Alberto Ferrari Alberto Ferrari Informatica e Laboratorio di Programmazione analogico e digitale una grandezza (fisica o astratta) può essere
Informatica e Laboratorio di Programmazione Sistema Binario Alberto Ferrari Alberto Ferrari Informatica e Laboratorio di Programmazione analogico e digitale una grandezza (fisica o astratta) può essere
Aritmetica dei Calcolatori
 Aritmetica dei Calcolatori Luca Abeni e Luigi Palopoli February 25, 2015 Informazione nei Computer Un computer è un insieme di circuiti elettronici......in ogni circuito, la corrente può passare o non
Aritmetica dei Calcolatori Luca Abeni e Luigi Palopoli February 25, 2015 Informazione nei Computer Un computer è un insieme di circuiti elettronici......in ogni circuito, la corrente può passare o non
Unità aritmetica e logica
 Aritmetica del calcolatore Capitolo 9 Unità aritmetica e logica n Esegue le operazioni aritmetiche e logiche n Ogni altra componente nel calcolatore serve questa unità n Gestisce gli interi n Può gestire
Aritmetica del calcolatore Capitolo 9 Unità aritmetica e logica n Esegue le operazioni aritmetiche e logiche n Ogni altra componente nel calcolatore serve questa unità n Gestisce gli interi n Può gestire
Programma del corso. Rappresentazione delle Informazioni. Introduzione agli algoritmi. Architettura del calcolatore
 Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori (Reti Locali, Internet) Elementi di Programmazione Codifica dell informazione
Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori (Reti Locali, Internet) Elementi di Programmazione Codifica dell informazione
Esercitazione 1 del 9/10/2013
 Esercitazione 1 del 9/10/2013 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero è associata al peso della cifra stessa, cioè il moltiplicatore da
Esercitazione 1 del 9/10/2013 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero è associata al peso della cifra stessa, cioè il moltiplicatore da
Rappresentazione di Numeri Reali. Rappresentazione in virgola fissa (fixed-point) Rappresentazione in virgola fissa (fixed-point)
 Rappresentazione di Numeri Reali Un numero reale è una grandezza continua Può assumere infiniti valori In una rappresentazione di lunghezza limitata, deve di solito essere approssimato. Esistono due forme
Rappresentazione di Numeri Reali Un numero reale è una grandezza continua Può assumere infiniti valori In una rappresentazione di lunghezza limitata, deve di solito essere approssimato. Esistono due forme
1.2 Concetti base dell Informatica: Informazione
 1.2 Concetti base dell Informatica: Informazione Insegnamento di Informatica Elisabetta Ronchieri Corso di Laurea di Economia, Universitá di Ferrara I semestre, anno 2014-2015 Elisabetta Ronchieri (Universitá)
1.2 Concetti base dell Informatica: Informazione Insegnamento di Informatica Elisabetta Ronchieri Corso di Laurea di Economia, Universitá di Ferrara I semestre, anno 2014-2015 Elisabetta Ronchieri (Universitá)
Corso di Architettura degli Elaboratori
 Corso di Architettura degli Elaboratori Codifica dell'informazione: Numeri Binari (lucidi originali della Prof.ssa Zacchi e del Prof. Balossino, rivisti dal Prof. Baldoni) 1 Codifica dell'informazione?
Corso di Architettura degli Elaboratori Codifica dell'informazione: Numeri Binari (lucidi originali della Prof.ssa Zacchi e del Prof. Balossino, rivisti dal Prof. Baldoni) 1 Codifica dell'informazione?
Firmware Division & Floating pointer adder
 Firmware Division & Floating pointer adder Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@di.unimi.it Università degli Studi di Milano Riferimenti sul Patterson: 3.4, 3.5 1/47
Firmware Division & Floating pointer adder Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@di.unimi.it Università degli Studi di Milano Riferimenti sul Patterson: 3.4, 3.5 1/47
Esercitazione 1 del 8/10/2014
 Esercitazione 1 del 8/10/2014 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero è associata al peso della cifra stessa, cioè il moltiplicatore da
Esercitazione 1 del 8/10/2014 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero è associata al peso della cifra stessa, cioè il moltiplicatore da
Sistema Numerico Decimale
 Sistema Numerico Decimale 10 digits d = [0,1,2,3,4,5,6,7,8,9] 734 = 7 * 10 2 + 3 * 10 1 + 4 * 10 0 0.234 = 2 * 10-1 + 3 * 10-2 + 8 * 10-3 In generale un numero N con p digits(d) interi ed n digits frazionari
Sistema Numerico Decimale 10 digits d = [0,1,2,3,4,5,6,7,8,9] 734 = 7 * 10 2 + 3 * 10 1 + 4 * 10 0 0.234 = 2 * 10-1 + 3 * 10-2 + 8 * 10-3 In generale un numero N con p digits(d) interi ed n digits frazionari
Aritmetica dei Calcolatori
 Aritmetica dei Calcolatori Luca Abeni e Luigi Palopoli February 18, 2016 Informazione nei Computer Un computer è un insieme di circuiti elettronici......in ogni circuito, la corrente può passare o non
Aritmetica dei Calcolatori Luca Abeni e Luigi Palopoli February 18, 2016 Informazione nei Computer Un computer è un insieme di circuiti elettronici......in ogni circuito, la corrente può passare o non
Rappresentazione dell informazione
 Rappresentazione dell informazione La codifica delle informazioni codifica forma adatta per essere trattata dall elaboratore INFORMAZIONI DATI interpretazione 2 Informazioni Numeri Immagini fisse Interi
Rappresentazione dell informazione La codifica delle informazioni codifica forma adatta per essere trattata dall elaboratore INFORMAZIONI DATI interpretazione 2 Informazioni Numeri Immagini fisse Interi
Rappresentazione dell informazione
 Corso di Laurea in Informatica Rappresentazione dell informazione Architettura dei Calcolatori Prof. Andrea Marongiu andrea.marongiu@unimore.it Anno accademico 2018/19 Rappresentazione binaria Tutta l
Corso di Laurea in Informatica Rappresentazione dell informazione Architettura dei Calcolatori Prof. Andrea Marongiu andrea.marongiu@unimore.it Anno accademico 2018/19 Rappresentazione binaria Tutta l
Programma del corso. Rappresentazione delle Informazioni. Introduzione agli algoritmi. Architettura del calcolatore
 Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori (Reti Locali, Internet) Elementi di Programmazione Rappresentazione
Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori (Reti Locali, Internet) Elementi di Programmazione Rappresentazione
Informazione e Registri - 2
 Informazione e Registri Le informazioni (dati e/o istruzioni) trattate da una macchina sono memorizzate in elementi detti registri Il registro può essere visto come un contenitore di informazione individuato
Informazione e Registri Le informazioni (dati e/o istruzioni) trattate da una macchina sono memorizzate in elementi detti registri Il registro può essere visto come un contenitore di informazione individuato
Rappresentazione dell' informazione. Cenni, necessari per capire le caratteristiche dei tipi di dato e delle limitazioni dell'aritmetica del computer
 Rappresentazione dell' informazione Cenni, necessari per capire le caratteristiche dei tipi di dato e delle limitazioni dell'aritmetica del computer Cos'è l'informazione? Tutto quello che viene manipolato
Rappresentazione dell' informazione Cenni, necessari per capire le caratteristiche dei tipi di dato e delle limitazioni dell'aritmetica del computer Cos'è l'informazione? Tutto quello che viene manipolato
Esercitazione 1 del 10/10/2012
 Esercitazione 1 del 10/10/2012 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero è associata al peso della cifra stessa, cioè il moltiplicatore
Esercitazione 1 del 10/10/2012 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero è associata al peso della cifra stessa, cioè il moltiplicatore
Codifica dell informazione
 Programmazione M-Z Ingegneria e Scienze Informatiche - Cesena A.A. 2016-2017 Codifica dell informazione Pietro Di Lena - pietro.dilena@unibo.it There are 10 types of people in this world: understand binary
Programmazione M-Z Ingegneria e Scienze Informatiche - Cesena A.A. 2016-2017 Codifica dell informazione Pietro Di Lena - pietro.dilena@unibo.it There are 10 types of people in this world: understand binary
Analogico vs. Digitale. LEZIONE II La codifica binaria. Analogico vs digitale. Analogico. Digitale
 Analogico vs. Digitale LEZIONE II La codifica binaria Analogico Segnale che può assumere infiniti valori con continuità Digitale Segnale che può assumere solo valori discreti Analogico vs digitale Il computer
Analogico vs. Digitale LEZIONE II La codifica binaria Analogico Segnale che può assumere infiniti valori con continuità Digitale Segnale che può assumere solo valori discreti Analogico vs digitale Il computer
Rappresentazione binaria
 Codifica digitale delle informazioni Argomenti - Rappresentazione binaria delle informazioni - Codifica di informazioni enumerative - Codifiche di numeri naturali, interi, razionali Rappresentazione binaria
Codifica digitale delle informazioni Argomenti - Rappresentazione binaria delle informazioni - Codifica di informazioni enumerative - Codifiche di numeri naturali, interi, razionali Rappresentazione binaria
Esercitazione del 05/03/ Soluzioni
 Esercitazione del 05/03/2009 - Soluzioni. Conversione binario decimale ( Rappresentazione dell Informazione Conversione in e da un numero binario, slide 0) a. 0 2? 0 2 Base 2 La posizione della cifra all
Esercitazione del 05/03/2009 - Soluzioni. Conversione binario decimale ( Rappresentazione dell Informazione Conversione in e da un numero binario, slide 0) a. 0 2? 0 2 Base 2 La posizione della cifra all
Fondamenti di Informatica - 1. Prof. B.Buttarazzi A.A. 2011/2012
 Fondamenti di Informatica - 1 Prof. B.Buttarazzi A.A. 2011/2012 I numeri reali Sommario Conversione dei numeri reali da base 10 a base B Rappresentazione dei numeri reali Virgola fissa Virgola mobile (mantissa
Fondamenti di Informatica - 1 Prof. B.Buttarazzi A.A. 2011/2012 I numeri reali Sommario Conversione dei numeri reali da base 10 a base B Rappresentazione dei numeri reali Virgola fissa Virgola mobile (mantissa
La codifica. dell informazione. (continua) Codifica dei numeri. Codifica dei numeri. Sono stati pertanto studiati codici alternativi per
 La codifica dell informazione (continua) Codifica dei numeri Il codice ASCII consente di codificare le cifre decimali da 0 a 9 fornendo in questo modo un metodo per la rappresentazione dei numeri Il numero
La codifica dell informazione (continua) Codifica dei numeri Il codice ASCII consente di codificare le cifre decimali da 0 a 9 fornendo in questo modo un metodo per la rappresentazione dei numeri Il numero
Elementi di informatica
 Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Sistemi di numerazione posizionali La rappresentazione dei numeri richiede ovviamente una codifica, ovvero la definizione
Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Sistemi di numerazione posizionali La rappresentazione dei numeri richiede ovviamente una codifica, ovvero la definizione
La codifica. dell informazione. Codifica dei numeri. (continua) Codifica dei numeri. Codifica dei numeri: il sistema decimale
 La codifica dell informazione Il codice ASCII consente di codificare le cifre decimali da a 9 fornendo in questo modo un metodo per la rappresentazione dei numeri Il numero 324 potrebbe essere rappresentato
La codifica dell informazione Il codice ASCII consente di codificare le cifre decimali da a 9 fornendo in questo modo un metodo per la rappresentazione dei numeri Il numero 324 potrebbe essere rappresentato
Esercitazione 1 del 07/10/2011
 Esercitazione 1 del 07/10/2011 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero indica il peso della cifra stessa, cioè il moltiplicatore da usare
Esercitazione 1 del 07/10/2011 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero indica il peso della cifra stessa, cioè il moltiplicatore da usare
DIPARTIMENTO DI MATEMATICA E INFORMATICA SISTEMI OPERATIVI. Anno Accademico 2017/2018. Docente: ing. Salvatore Sorce
 DIPARTIMENTO DI MATEMATICA E INFORMATICA SISTEMI OPERATIVI Anno Accademico 27/28 Docente: ing. Salvatore Sorce Rappresentazione numerica delle informazioni I parte: i bit e i sistemi di numerazione Obiettivi
DIPARTIMENTO DI MATEMATICA E INFORMATICA SISTEMI OPERATIVI Anno Accademico 27/28 Docente: ing. Salvatore Sorce Rappresentazione numerica delle informazioni I parte: i bit e i sistemi di numerazione Obiettivi
La codifica digitale
 La codifica digitale Codifica digitale Il computer e il sistema binario Il computer elabora esclusivamente numeri. Ogni immagine, ogni suono, ogni informazione per essere compresa e rielaborata dal calcolatore
La codifica digitale Codifica digitale Il computer e il sistema binario Il computer elabora esclusivamente numeri. Ogni immagine, ogni suono, ogni informazione per essere compresa e rielaborata dal calcolatore
Esercitazione del 09/03/ Soluzioni
 Esercitazione del 09/03/2006 - Soluzioni. Conversione binario decimale ( Rappresentazione dell Informazione Conversione in e da un numero binario, slide 0) a. 0 2? 0 2 Base 2 Si cominciano a contare le
Esercitazione del 09/03/2006 - Soluzioni. Conversione binario decimale ( Rappresentazione dell Informazione Conversione in e da un numero binario, slide 0) a. 0 2? 0 2 Base 2 Si cominciano a contare le
Introduzione e Nozioni di Base. Prof. Thomas Casali
 Università degli studi di Bologna Facoltà di Economia Sede di Forlì Introduzione e Nozioni di Base Corso di Laurea in Economia di Internet Prof. Thomas Casali thomas@casali.biz La rappresentazione digitale
Università degli studi di Bologna Facoltà di Economia Sede di Forlì Introduzione e Nozioni di Base Corso di Laurea in Economia di Internet Prof. Thomas Casali thomas@casali.biz La rappresentazione digitale
Firmware Division & Floating gpointer adder
 Firmware Division & Floating gpointer adder Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@di.unimi.it it Università degli Studi di Milano Riferimenti sul Patterson: 3.4, 3.5
Firmware Division & Floating gpointer adder Prof. Alberto Borghese Dipartimento di Scienze dell Informazione borghese@di.unimi.it it Università degli Studi di Milano Riferimenti sul Patterson: 3.4, 3.5
Codifica dell informazione numerica
 Codifica dell informazione numerica Nicola Basilico, nicola.basilico@unimi.it Architetture degli Elaboratori I, Laboratorio - Corso di Laurea in Informatica, A.A. 201-2018 Informazioni (edizione 2017-2018)
Codifica dell informazione numerica Nicola Basilico, nicola.basilico@unimi.it Architetture degli Elaboratori I, Laboratorio - Corso di Laurea in Informatica, A.A. 201-2018 Informazioni (edizione 2017-2018)
Esercitazione del 03/03/ Soluzioni
 Esercitazione del 03/03/2005 - Soluzioni. Conversione binario decimale ( Rappresentazione dell Informazione Conversione da base n a base 0, slide 0) a. 0 2? 0 2 Base 2 Si cominciano a contare le posizioni
Esercitazione del 03/03/2005 - Soluzioni. Conversione binario decimale ( Rappresentazione dell Informazione Conversione da base n a base 0, slide 0) a. 0 2? 0 2 Base 2 Si cominciano a contare le posizioni
Somma di numeri binari
 Fondamenti di Informatica: Codifica Binaria dell Informazione 1 Somma di numeri binari 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 Esempio: 10011011 + 00101011 = 11000110 in base e una base Fondamenti di
Fondamenti di Informatica: Codifica Binaria dell Informazione 1 Somma di numeri binari 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 Esempio: 10011011 + 00101011 = 11000110 in base e una base Fondamenti di
Programma del corso. Introduzione Rappresentazione delle Informazioni Calcolo proposizionale Architettura del calcolatore Reti di calcolatori
 Programma del corso Introduzione Rappresentazione delle Informazioni Calcolo proposizionale Architettura del calcolatore Reti di calcolatori Codifica dell informazione Il calcolatore memorizza ed elabora
Programma del corso Introduzione Rappresentazione delle Informazioni Calcolo proposizionale Architettura del calcolatore Reti di calcolatori Codifica dell informazione Il calcolatore memorizza ed elabora
Codifica dell informazione
 Codifica dell informazione Informatica B Come memorizzo l informazione nel calcolatore? 1 bit di informazione 1 bit di informazione La memoria del calcolatore L informazione nel calcolatore q Il calcolatore
Codifica dell informazione Informatica B Come memorizzo l informazione nel calcolatore? 1 bit di informazione 1 bit di informazione La memoria del calcolatore L informazione nel calcolatore q Il calcolatore
Rappresentazione dei numeri reali in un calcolatore
 Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri reali in un calcolatore Lezione 3 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione di numeri
Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri reali in un calcolatore Lezione 3 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione di numeri
Programma del corso. Rappresentazione delle Informazioni. Introduzione agli algoritmi. Architettura del calcolatore
 Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori (Reti Locali, Internet) Elementi di Programmazione Rappresentazione
Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori (Reti Locali, Internet) Elementi di Programmazione Rappresentazione
= = = Codifica dell informazione
 Rappresentazione dell informazione Paolo Bison Fondamenti di Informatica AA 2006/07 Università di Padova Codifica dell informazione rappresentazione dell informazione con una sequenza finita di bit differenti
Rappresentazione dell informazione Paolo Bison Fondamenti di Informatica AA 2006/07 Università di Padova Codifica dell informazione rappresentazione dell informazione con una sequenza finita di bit differenti
Algebra di Boole e porte logiche
 Algebra di Boole e porte logiche Dott.ssa Isabella D'Alba Corso PENTEST MIND PROJECT 2016 Algebra di Boole e porte logiche (I parte) Algebra di Boole I Sistemi di Numerazione (Posizionali, Non posizionali)
Algebra di Boole e porte logiche Dott.ssa Isabella D'Alba Corso PENTEST MIND PROJECT 2016 Algebra di Boole e porte logiche (I parte) Algebra di Boole I Sistemi di Numerazione (Posizionali, Non posizionali)
Laboratorio del 21/10/2010- Numeri binari e conversione
 Laboratorio del 21/10/2010- Numeri binari e conversione 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero indica il peso della cifra stessa, cioè
Laboratorio del 21/10/2010- Numeri binari e conversione 1. Conversione binario decimale a. 1101 2? 10 1 1 2 Base 2 La posizione della cifra all interno del numero indica il peso della cifra stessa, cioè
Paolo Bison. Fondamenti di Informatica A.A. 2006/07 Università di Padova
 Rappresentazione dell informazione Paolo Bison Fondamenti di Informatica A.A. 2006/07 Università di Padova Rappresentazione dell informazione, Paolo Bison, FI06, 2007-01-30 p.1 Codifica dell informazione
Rappresentazione dell informazione Paolo Bison Fondamenti di Informatica A.A. 2006/07 Università di Padova Rappresentazione dell informazione, Paolo Bison, FI06, 2007-01-30 p.1 Codifica dell informazione

 Rappresentazione dell informazione Paolo Bison Fondamenti di Informatica AA 2006/07 Università di Padova Codifica dell informazione rappresentazione dell informazione con una sequenza finita di bit differenti
Rappresentazione dell informazione Paolo Bison Fondamenti di Informatica AA 2006/07 Università di Padova Codifica dell informazione rappresentazione dell informazione con una sequenza finita di bit differenti