Simulazione di II prova di Matematica Classe V
|
|
|
- Gioacchino Corona
- 7 anni fa
- Visualizzazioni
Transcript
1 Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 09/02/2018 Simulazione di II prova di Matematica Classe V Studente/ssa Risolvi uno dei due problemi. 1. Nel sito web della stazione meteorologica cittadina sono stati pubblicati, come ogni giorno, due grafici. Il primo grafico visualizza la distribuzione locale della pressione atmosferica al suolo mediante linee di livello (isobare) che uniscono i punti aventi la stessa pressione (misurata in chilopascal, kpa). Le linee di livello corrispondono a valori consecutivi della pressione atmosferica (100, 101, 102, ). La diagonale AB passa per i punti L e H, dove la pressione assume rispettivamente un minimo (100 kpa) e un massimo (120 kpa). Il secondo grafico rappresenta l andamento della pressione p( x) in funzione della posizione x lungo la diagonale AB (x è espresso in chilometri, con origine in A). i. Utilizzando i dati del primo grafico, individua sul secondo grafico il punto corrispondente ad H, fornendone ascissa e ordinata. ii. Una delle seguenti funzioni rappresenta la funzione p( x) nell intervallo 0 x 30, con a, b costanti reali non nulle: f ( x)= 500( a + be x ) ; g x ( )= 300 ( 2x + a ) ( 2x + a) b. Stabilisci quale, in base ai dati forniti nei grafici. Per la funzione così determinata, ricava i valori delle costanti a e b. 1 di 5
2 iii. iv. Verificato che è la seconda funzione a rappresentare i dati riportati nel grafico, con a = 25 e b = 110, studia la corrispondente funzione p( x) nel suo dominio naturale, indicando in particolare quanti e quali punti di flesso ammette. Esponi un modo per stimare accuratamente il valore medio della pressione atmosferica lungo il tratto AB e applicalo per determinare tale valore. 2. Nella figura sottostante è riportato il grafico della funzione f ( x), derivata prima della funzione reale f x ( ) definita e continua nell intervallo 0; 8. ( ) sono note le coordinate dei punti evidenziati e le seguenti caratte- Del grafico di f x ristiche: i tratti AB 1 e FG sono segmenti di retta; i punti B 1 e B 2 non appartengono al grafico; il tratto B 2 F ha un andamento di tipo sinusoidale e si raccorda col tratto FG senza presentare un punto angoloso. i. Traccia in due distinti riferimenti cartesiani i grafici plausibili delle funzioni f ( x) e f ( x) nell intervallo 0; 8, nell ipotesi che sia f ( 0)= 0, motivando in modo esauriente i passaggi. Quanto vale f ( 6)? Qual è il massimo valore assunto da f ( x), e in corrispondenza a quale o a quali valori di x viene assunto? ii. iii. Giustifica il fatto che la funzione f ( x) presenta un punto di non derivabilità di tipo angoloso nell intervallo 0; 8, quindi determina la misura in gradi, minuti e secondi dell angolo acuto α individuato dalle tangenti al grafico di f ( x) in tale punto angoloso. Date tutte le precedenti ipotesi sulla funzione f x ( ), indica quali tra le seguenti affermazioni sono vere, motivando la risposta. 2 di 5
3 a. Come conseguenza del teorema di Lagrange, deve esistere necessariamente almeno un valore x nell intervallo 0; 6 tale che f ( x)= 1 3. b. Poiché f x ( ) non soddisfa tutte le ipotesi del teorema di Lagrange nell intervallo 0; 6, non può esistere alcun valore x interno a tale intervallo tale che f ( x)= 1 3. c. Benché f x ( ) non soddisfi tutte le ipotesi del teorema di Lagrange nell intervallo 0; 6, esistono più valori x interni a tale intervallo tali che f ( x)= 1 3. iv. Di tutti i valori assunti dalla funzione f x ( ), esponi un metodo per determinare il valore medio. Utilizza tale metodo per determinare tale valore. 3 di 5
4 Risolvi cinque dei dieci quesiti. 1. Discuti la continuità e la derivabilità della seguente funzione reale: f ( x)= x x se x 0 1 se x = 0. Valuta la funzione all infinito. 2. Data la funzione f ( x)= 4, ricava le equazioni di tutte le rette tangenti al suo grafico passanti per il punto A( 0; 4). x Determina tipo e carattere della serie ( 1) n. 2 n+3 4. Due punti materiali si muovono nello stesso verso su una retta secondo le leggi orarie s 1 ( t)= 4t 2 + 5t + 4 e s 2 ( t)= 2( t +1) (le s i, i = 1,2, sono espresse in metri, t in secondi). i. Determina le posizioni iniziali dei due punti e stabilisci la distanza tra loro dopo un tempo infinito. ii. Determina la velocità dei due punti materiali all infinito. 5. Enuncia il Teorema di esistenza degli zeri. Supponi che f sia una funzione definita e continua in I = a;, che f ( a )< 0 e lim f ( x )=. Dimostra che esiste almeno x una soluzione dell equazione f ( x)= 0 in I. 6. Verifica che i punti A( 1; 1; 1), B( 3; 3; 1) e C( 3; 1; 0) sono i vertici di un triangolo isoscele e determinane l area. Qual è l equazione del piano perpendicolare al triangolo passante per A e per B? 7. Considera il triangolo T 0, rettangolo isoscele di cateto di lunghezza 4 cm. Uno dei due cateti è l ipotenusa di un triangolo rettangolo isoscele T 1. Uno dei sue cateti è l ipotenusa di un triangolo rettangolo isoscele T 2. Così via. Sia a ( n) la successione delle aree dei triangoli e p ( n) la successione dei perimetri dei triangoli. Individua la tipologia di successioni e determina i caratteri di p n. a n e di 4 di 5
5 8. Dato nel riferimento Oxyz il piano π di equazione 2 2x + 3y + 2 2z 4 = 0 e dette A, B, C le sue intersezioni con gli assi x, y e z, calcola l area del triangolo ABC e la distanza di O dal piano π. Determina infine il volume della piramide ABCO Si vuole costruire una stanza a forma di parallelepipedo di volume 96 m 3, la cui base sia un quadrato. Per rifinire la stanza è necessario tappezzare le pareti laterali e costruire il pavimento. Per l acquisto e la posa delle piastrelle per il pavimento è previsto un costo di 16 al metro quadrato; per l acquisto e la posa della tappezzeria è previsto un costo di 18 al metro quadrato. Quali devono essere le dimensioni della stanza affinché il costo complessivo di rifinitura sia il minimo possibile? 10. Nella figura a fianco sono riportati i grafici di una funzione f ( x), della sua derivata prima f x f ( ) e della derivata seconda ( x) (tutte e tre le funzioni sono derivabi- ( ), f ( x) e f ( x) al li in! ). Associa f x giusto grafico, motivando la tua scelta. NOTE: i. È ammesso l uso del calcolatore elettronico o di tavole numeriche; ii. Punteggio massimo 15 p.ti. Per la sufficienza è necessario raggiungere il punteggio di 10 p.ti. 1 Il volume di una piramide di area di base A e altezza h è V = 1 3 A h. 5 di 5
SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO. Il candidato risolva uno dei problemi e risponda a 5 quesiti del questionario.
 ANNO SCOLASTICO 06/7 SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei problemi e risponda a 5 quesiti del questionario. Problema Modello in
ANNO SCOLASTICO 06/7 SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei problemi e risponda a 5 quesiti del questionario. Problema Modello in
SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO. Il candidato risolva uno dei problemi e risponda a 5 quesiti del questionario.
 Simulazione 06/7 ANNO SCOLASTICO 06/7 SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei problemi e risponda a 5 quesiti del questionario. Problema
Simulazione 06/7 ANNO SCOLASTICO 06/7 SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei problemi e risponda a 5 quesiti del questionario. Problema
Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/01/2019. Verifica scritta di Matematica Classe V
 Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/01/2019 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 25 p.ti. 1. Un corpo
Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/01/2019 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 25 p.ti. 1. Un corpo
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 2015/2016 CLASSI 2 I SISTEMI LINEARI
 PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI I SISTEMI LINEARI Stabilisci se il sistema è determinato, indeterminato o impossibile senza risolverlo [determinato] [impossibile] Determina per
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI I SISTEMI LINEARI Stabilisci se il sistema è determinato, indeterminato o impossibile senza risolverlo [determinato] [impossibile] Determina per
Test di Matematica di base
 Test di Matematica di base Geometria Il rapporto tra la superficie di un quadrato e quella di un triangolo equilatero di eguale lato è a. 4 b. 4 d. [ ] Quali sono le ascisse dei punti della curva di equazione
Test di Matematica di base Geometria Il rapporto tra la superficie di un quadrato e quella di un triangolo equilatero di eguale lato è a. 4 b. 4 d. [ ] Quali sono le ascisse dei punti della curva di equazione
Verifica scritta di Matematica Classe V
 Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/1/018 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 5 p.ti. 1. Determina
Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/1/018 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 5 p.ti. 1. Determina
Simulazione di II prova di Matematica Classe V
 Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 03/05/2018 Simulazione di II prova di Matematica Classe V Studente/ssa Risolvi uno dei due problemi. 1. Il tasso alcolemico T a misura
Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 03/05/2018 Simulazione di II prova di Matematica Classe V Studente/ssa Risolvi uno dei due problemi. 1. Il tasso alcolemico T a misura
1) Qual è il parallelogrammo di area massima tra quelli di lati assegnati? Giustificare la risposta.
 TEMA PROBLEMA k Sono assegnate le funzioni di equazione y = e, essendo k un numero reale. a. stabilire al variare di k il numero di punti stazionari e la loro natura b. stabilire per quali valori di k
TEMA PROBLEMA k Sono assegnate le funzioni di equazione y = e, essendo k un numero reale. a. stabilire al variare di k il numero di punti stazionari e la loro natura b. stabilire per quali valori di k
2. Calcola, enunciando, descrivendo e applicando la definizione, la derivata della 2
 Domande di matematica per l esame di stato per il liceo classico Analisi matematica 1. Spiega quando una funzione è un infinitesimo e quando è un infinito per x che tende a x 0. Quali sono i possibili
Domande di matematica per l esame di stato per il liceo classico Analisi matematica 1. Spiega quando una funzione è un infinitesimo e quando è un infinito per x che tende a x 0. Quali sono i possibili
f(x) = sin cos α = k2 2 k
 28 Maggio 2015 Il punteggio viene attribuito in base alla correttezza e completezza nella risoluzione dei quesiti, nonché alle caratteristiche dell esposizione: chiarezza, ordine ed organicità. La sufficienza
28 Maggio 2015 Il punteggio viene attribuito in base alla correttezza e completezza nella risoluzione dei quesiti, nonché alle caratteristiche dell esposizione: chiarezza, ordine ed organicità. La sufficienza
12 Simulazione di prova d Esame di Stato
 2 Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario È assegnata la funzione = f() =( +2)e 2 +, essendo una variabile reale.
2 Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario È assegnata la funzione = f() =( +2)e 2 +, essendo una variabile reale.
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 2015/2016 CLASSI 3
 PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI DISEQUAZIONI Risolvi le seguenti disequazioni numeriche intere. ) ) 9 ) ) 9 ( ) ) ) non esiste R non esiste R Risolvi le seguenti disequazioni
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI DISEQUAZIONI Risolvi le seguenti disequazioni numeriche intere. ) ) 9 ) ) 9 ( ) ) ) non esiste R non esiste R Risolvi le seguenti disequazioni
8 Simulazione di prova d Esame di Stato
 8 Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario Si consideri la famiglia di funzioni f α () = a e a con a parametro reale
8 Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario Si consideri la famiglia di funzioni f α () = a e a con a parametro reale
1) Ricava il dominio di ciascuna delle due funzioni e scrivilo attraverso intervalli
 1) Ricava il dominio di ciascuna delle due funzioni e scrivilo attraverso intervalli A) 1 2 B) [ A) 2 x 1; B) (-, - 3) ( - 3, 0) ( 0, + ) ] 2) Riferendoti al grafico rappresentato completa a) Il dominio
1) Ricava il dominio di ciascuna delle due funzioni e scrivilo attraverso intervalli A) 1 2 B) [ A) 2 x 1; B) (-, - 3) ( - 3, 0) ( 0, + ) ] 2) Riferendoti al grafico rappresentato completa a) Il dominio
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE
 1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
VERIFICA DI MATEMATICA. Classe 3P 02/10/2018
 Non utilizzare matita e bianchetto. Classe 3P 02/10/2018 Il punteggio viene attribuito in base alla correttezza e alla completezza nella risoluzione dei quesiti, al metodo risolutivo adottato e alle caratteristiche
Non utilizzare matita e bianchetto. Classe 3P 02/10/2018 Il punteggio viene attribuito in base alla correttezza e alla completezza nella risoluzione dei quesiti, al metodo risolutivo adottato e alle caratteristiche
ESAME DI STATO DI LICEO SCIENTIFICO Sessione suppletiva
 ESAME DI STATO DI LICEO SCIENTIFICO Sessione suppletiva PROBLEMA Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. Si consideri la funzione reale f m di variabile
ESAME DI STATO DI LICEO SCIENTIFICO Sessione suppletiva PROBLEMA Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. Si consideri la funzione reale f m di variabile
Matematica classe 5 C a.s. 2012/2013
 Matematica classe 5 C a.s. 2012/2013 Asintoti e grafici 1) Una funzione y = f(x) gode delle seguenti caratteristiche: D / 4, y 0 se x 0 x 2, lim, 3. Rappresentare un grafico qualitativo della funzione.
Matematica classe 5 C a.s. 2012/2013 Asintoti e grafici 1) Una funzione y = f(x) gode delle seguenti caratteristiche: D / 4, y 0 se x 0 x 2, lim, 3. Rappresentare un grafico qualitativo della funzione.
ULTERIORI ESERCIZI SUL CALCOLO DIFFERENZIALE
 ULTERIORI ESERCIZI SUL CALCOLO DIFFERENZIALE 1 Scrivi l equazione della retta tangente al grafico di f(x) = (1 + 2x) 4 nel suo punto di intersezione con l asse y 2 Scrivi l equazione della retta tangente
ULTERIORI ESERCIZI SUL CALCOLO DIFFERENZIALE 1 Scrivi l equazione della retta tangente al grafico di f(x) = (1 + 2x) 4 nel suo punto di intersezione con l asse y 2 Scrivi l equazione della retta tangente
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT
 1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
SISTEMI DI RIFERIMENTO SU UNA RETTA E SU UN PIANO
 DIPARTIMENTO DI INGEGNERIA CIVILE PRECORSO DI MATEMATICA ANNO ACCADEMICO 013-014 ESERCIZI RELATIVI A SISTEMI DI RIFERIMENTO SU UNA RETTA E SU UN PIANO Esercizio 1: Fissato su una retta un sistema di riferimento
DIPARTIMENTO DI INGEGNERIA CIVILE PRECORSO DI MATEMATICA ANNO ACCADEMICO 013-014 ESERCIZI RELATIVI A SISTEMI DI RIFERIMENTO SU UNA RETTA E SU UN PIANO Esercizio 1: Fissato su una retta un sistema di riferimento
Prepararsi alla Prova di matematica
 Scuola Media E. Fermi Prepararsi alla Prova di matematica Prove d esame di matematica Prof. Vincenzo Loseto 2013/ 2014 PROVA NUMERO 1 QUESITO 1 In un triangolo rettangolo la somma di un cateto e dell ipotenusa
Scuola Media E. Fermi Prepararsi alla Prova di matematica Prove d esame di matematica Prof. Vincenzo Loseto 2013/ 2014 PROVA NUMERO 1 QUESITO 1 In un triangolo rettangolo la somma di un cateto e dell ipotenusa
Rilevazione degli apprendimenti
 Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATICA Scuola secondaria di II grado Classe... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATICA Scuola secondaria di II grado Classe... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
Precorso 2000 Test finale
 42 Esercizi di Analisi Matematica Versione 2006 Precorso 2000 Test finale Tempo concesso: 120 minuti Valutazione: risposta esatta +1, errata 1, mancante 0 punti (per 32 domande) Trovare i valori di a che
42 Esercizi di Analisi Matematica Versione 2006 Precorso 2000 Test finale Tempo concesso: 120 minuti Valutazione: risposta esatta +1, errata 1, mancante 0 punti (per 32 domande) Trovare i valori di a che
Esame di maturità scientifica, corso di ordinamento a. s
 Problema 1 Esame di maturità scientifica, corso di ordinamento a. s. -4 Sia f la funzione definita da: f()=- Punto 1 Disegnate il grafico G di f()=-. La funzione f()=- è una funzione polinomiale (una cubica).
Problema 1 Esame di maturità scientifica, corso di ordinamento a. s. -4 Sia f la funzione definita da: f()=- Punto 1 Disegnate il grafico G di f()=-. La funzione f()=- è una funzione polinomiale (una cubica).
D4. Circonferenza - Esercizi
 D4. Circonferenza - Esercizi Trasformare l equazione della circonferenza nell altra forma e rappresentare graficamente la circonferenza trovandone prima centro e raggio. 1) + --=0 [(-1) +(-1) =, C(1;1),
D4. Circonferenza - Esercizi Trasformare l equazione della circonferenza nell altra forma e rappresentare graficamente la circonferenza trovandone prima centro e raggio. 1) + --=0 [(-1) +(-1) =, C(1;1),
Esame di Stato di Liceo Scientifico Corso di Ordinamento
 Corso di Ordinamento Soluzione dei Temi di Matematica proposti nella Sessione Ordinaria 006 Sessione Ordinaria 006 Corso di Ordinamento Sommario Problema Punto a) Punto b) Punto c) Punto Finale 4 Problema
Corso di Ordinamento Soluzione dei Temi di Matematica proposti nella Sessione Ordinaria 006 Sessione Ordinaria 006 Corso di Ordinamento Sommario Problema Punto a) Punto b) Punto c) Punto Finale 4 Problema
Rappresenta nel piano cartesiano l insieme dei punti P(x; y) le cui coordinate soddisfano le seguenti condizioni:
 ultima modifica /0/0 ESERCIZI PROPOSTI IL PIANO CARTESIANO LE COORDINATE DI UN PUNTO NEL PIANO CARTESIANO A Quali sono le coordinate dei punti indicati in figura? B Quali sono le coordinate dei punti indicati
ultima modifica /0/0 ESERCIZI PROPOSTI IL PIANO CARTESIANO LE COORDINATE DI UN PUNTO NEL PIANO CARTESIANO A Quali sono le coordinate dei punti indicati in figura? B Quali sono le coordinate dei punti indicati
IL PIANO CARTESIANO E LA RETTA
 IL PIANO CARTESIANO E LA RETTA ESERCIZI 1. Le coordinate di un punto su un piano 1 A Scrivi le coordinate dei punti indicati in figura. 1 B Scrivi le coordinate dei punti indicati in figura. Rappresenta
IL PIANO CARTESIANO E LA RETTA ESERCIZI 1. Le coordinate di un punto su un piano 1 A Scrivi le coordinate dei punti indicati in figura. 1 B Scrivi le coordinate dei punti indicati in figura. Rappresenta
PROGRAMMA SVOLTO II LB Matematica 2015/2016
 PROGRAMMA SVOLTO II LB Matematica 2015/2016 Sistemi di equazioni lineari: metodo di sostituzione, metodo del confronto, riduzione e Cramer. Cenni a matrici e operazioni con esse. Interpretazione grafica
PROGRAMMA SVOLTO II LB Matematica 2015/2016 Sistemi di equazioni lineari: metodo di sostituzione, metodo del confronto, riduzione e Cramer. Cenni a matrici e operazioni con esse. Interpretazione grafica
Chi non risolve esercizi non impara la matematica.
 2.8 esercizi 31 2.8 esercizi hi non risolve esercizi non impara la matematica. 1 Vero o falso? a. I punti (0, 2), (4, 4), (6, 0) e (2, 2) sono i vertici di un quadrato. V F b. Non esiste il coefficiente
2.8 esercizi 31 2.8 esercizi hi non risolve esercizi non impara la matematica. 1 Vero o falso? a. I punti (0, 2), (4, 4), (6, 0) e (2, 2) sono i vertici di un quadrato. V F b. Non esiste il coefficiente
ESERCIZI. 1.2 Dire quali dei seguenti insiemi sono vuoti e descriverne il complementare nell insieme dei numeri reali: C:= {x R x 1 3 e x 1 2 };
 ESERCIZI. INSIEMISTICA. Sia l insieme dei punti dello spazio, Γ una sfera e N il suo polo nord. Quali delle seguenti relazioni sono corrette? N Γ; N ; Γ ; Γ ; N ; Γ N.. Dire quali dei seguenti insiemi
ESERCIZI. INSIEMISTICA. Sia l insieme dei punti dello spazio, Γ una sfera e N il suo polo nord. Quali delle seguenti relazioni sono corrette? N Γ; N ; Γ ; Γ ; N ; Γ N.. Dire quali dei seguenti insiemi
2. Determina l equazione della circonferenza passante per i punti A ( 2; 4), B ( 1; 3) ed avente centro sulla retta di equazione 2x 3y + 2 = 0.
 CLASSE 3^ C LICEO SCIENTIFICO Novembre 01 La circonferenza 1. Ricava l equazione di ciascuna delle circonferenze rappresentate, spiegando in maniera esauriente il procedimento che seguirai, prima di svolgere
CLASSE 3^ C LICEO SCIENTIFICO Novembre 01 La circonferenza 1. Ricava l equazione di ciascuna delle circonferenze rappresentate, spiegando in maniera esauriente il procedimento che seguirai, prima di svolgere
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2007 Sessione suppletiva
 ESAME DI STAT DI LIE SIENTIFI RS DI RDINAMENT 7 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Rispetto a un sistema di assi cartesiani
ESAME DI STAT DI LIE SIENTIFI RS DI RDINAMENT 7 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Rispetto a un sistema di assi cartesiani
Verifica di matematica. Nel piano riferito a coordinate ortogonali monometriche (x; y) è assegnata la curva Γ di equazione: 2
 0 Marzo 00 Verifica di matematica roblema Si consideri l equazione ln( + ) 0. a) Si dimostri che ammette due soluzioni reali. Nel piano riferito a coordinate ortogonali monometriche (; ) è assegnata la
0 Marzo 00 Verifica di matematica roblema Si consideri l equazione ln( + ) 0. a) Si dimostri che ammette due soluzioni reali. Nel piano riferito a coordinate ortogonali monometriche (; ) è assegnata la
c) Determina per quali valori di k il segmento BC ha misura 2. 3) Ricava l equazione della spezzata rappresentata in figura
 VERIFICHE TERZA C a.s. 2010 2011 1) Sono assegnati i punti A(0; 10) B(8; - 6) C(0; 0). Rappresentali. a) Verifica che il triangolo ABC è isoscele e calcola la sua area b) Tra i punti P che hanno ordinata
VERIFICHE TERZA C a.s. 2010 2011 1) Sono assegnati i punti A(0; 10) B(8; - 6) C(0; 0). Rappresentali. a) Verifica che il triangolo ABC è isoscele e calcola la sua area b) Tra i punti P che hanno ordinata
LA GEOMETRIA DELLO SPAZIO
 LA GEOMETRIA ELLO SPAZIO 1 alcola l area e il perimetro del triangolo individuato dai punti A ; 0; 4, ; 1; 5 e 0; ;. ( ) ( ) ( ) 9 ; + 6 Stabilisci se il punto A ( 1;1; ) appartiene all intersezione dei
LA GEOMETRIA ELLO SPAZIO 1 alcola l area e il perimetro del triangolo individuato dai punti A ; 0; 4, ; 1; 5 e 0; ;. ( ) ( ) ( ) 9 ; + 6 Stabilisci se il punto A ( 1;1; ) appartiene all intersezione dei
Verifica del 8 febbraio 2018
 Verifica del 8 febbraio 018 Esercizio 1 (15 punti) Risolvi le seguenti disequazioni: 1 x 1 a) x + 6x + 8 x 3 b) x + 1 + 1 c) d) Esercizio (0 punti) 3 x 8 x 4 x 3 ax 9 Considera la funzione f ( x) = x 3x
Verifica del 8 febbraio 018 Esercizio 1 (15 punti) Risolvi le seguenti disequazioni: 1 x 1 a) x + 6x + 8 x 3 b) x + 1 + 1 c) d) Esercizio (0 punti) 3 x 8 x 4 x 3 ax 9 Considera la funzione f ( x) = x 3x
Indirizzo: Tema di Il candidato risolva uno dei due problemi e 4 quesiti del questionario. PROBLEMA 1 PROBLEMA 2
 Sessione ordinaria all estero (EUROPA) 8-9 ESAMI DI STATO DI LICEO SCIENTIFICO SCUOLE ITALIANE ALL ESTERO: EUROPA CORSO DI ORDINAMENTO Indirizzo: SCIENTIFICO Tema di: MATEMATICA Il candidato risolva uno
Sessione ordinaria all estero (EUROPA) 8-9 ESAMI DI STATO DI LICEO SCIENTIFICO SCUOLE ITALIANE ALL ESTERO: EUROPA CORSO DI ORDINAMENTO Indirizzo: SCIENTIFICO Tema di: MATEMATICA Il candidato risolva uno
Liceo Scientifico di ordinamento anno ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO anno PROBLEMA 1
 Liceo Scientifico di ordinamento anno 00-00 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO anno 00-00 PROBLEMA Punto a Indicati rispettivamente con V ed S il volume e l area totale di T e con
Liceo Scientifico di ordinamento anno 00-00 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO anno 00-00 PROBLEMA Punto a Indicati rispettivamente con V ed S il volume e l area totale di T e con
M557 - ESAME DI STATO DI LICEO SCIENTIFICO
 Pag. 1/1 Sessione ordinaria 2001 $$$$$.2.1/1 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1. Si consideri la seguente relazione tra le variabili
Pag. 1/1 Sessione ordinaria 2001 $$$$$.2.1/1 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1. Si consideri la seguente relazione tra le variabili
LICEO SCIENTIFICO PROBLEMA 2
 www.matefilia.it LICEO SCIENTIFICO 2018 - PROBLEMA 2 Consideriamo f k (x): R R così definita: f k (x) = x + kx + 9, con k Z 1) Detto Γ k il grafico della funzione, verifica che per qualsiasi valore del
www.matefilia.it LICEO SCIENTIFICO 2018 - PROBLEMA 2 Consideriamo f k (x): R R così definita: f k (x) = x + kx + 9, con k Z 1) Detto Γ k il grafico della funzione, verifica che per qualsiasi valore del
a) Perché posso affermare che sono complanari? b) Determina l equazione del piano che li contiene
 Esercizi svolti Esercizio 1. Dati i punti: A(1, 1, 0), B( 1, 1, 4), C(1, 1, 3), D(2, 2, 8) dello spazio R 3 a) Perché posso affermare che sono complanari? b) Determina l equazione del piano che li contiene
Esercizi svolti Esercizio 1. Dati i punti: A(1, 1, 0), B( 1, 1, 4), C(1, 1, 3), D(2, 2, 8) dello spazio R 3 a) Perché posso affermare che sono complanari? b) Determina l equazione del piano che li contiene
( ) 2. Determina il resto della divisione fra il polinomio P ( x) 2 2x. 3. Per quale valore del parametro m il polinomio P(
 ALGEBRA E ANALITICA. Determina il resto della divisione fra il polinomio P ( ) e il binomio D ( ). [ R ( ) ] + + + ( ) Detto D() il polinomio divisore, Q() il polinomio quoziente, R() il resto, il polinomio
ALGEBRA E ANALITICA. Determina il resto della divisione fra il polinomio P ( ) e il binomio D ( ). [ R ( ) ] + + + ( ) Detto D() il polinomio divisore, Q() il polinomio quoziente, R() il resto, il polinomio
2) Riferendoti al grafico riportato rispondi alle seguenti domande y
 Verifiche 5 C a. s. 007/008 009/000 ) Di una funzione di equazione y = f() si sa che: D 0, f() 0 se, la retta y = è asintoto obliquo, f() < 0,. Rappresenta un grafico qualitativo della funzione. y 3 0-7
Verifiche 5 C a. s. 007/008 009/000 ) Di una funzione di equazione y = f() si sa che: D 0, f() 0 se, la retta y = è asintoto obliquo, f() < 0,. Rappresenta un grafico qualitativo della funzione. y 3 0-7
Liceo Scientifico G. Galilei Trebisacce Anno Scolastico Prova di Matematica : Piano cartesiano e retta Alunno: Classe: 2 C
 Liceo Scientifico G. Galilei Trebisacce Anno Scolastico 010-011 Prova di Matematica : Piano cartesiano e retta Alunno: Classe: C 10.03.011 prof. Mimmo Corrado Dato il triangolo di vertici: 6; 3, ; 1, 4;
Liceo Scientifico G. Galilei Trebisacce Anno Scolastico 010-011 Prova di Matematica : Piano cartesiano e retta Alunno: Classe: C 10.03.011 prof. Mimmo Corrado Dato il triangolo di vertici: 6; 3, ; 1, 4;
Silvia Braschi PROGRAMMA SVOLTO 2 i Matematica 2017/2018
 Silvia Braschi PROGRAMMA SVOLTO 2 i Matematica 2017/2018 1. Sistemi di equazioni lineari: metodo di sostituzione, metodo del confronto, riduzione e Cramer. Interpretazione grafica dei sistemi di I grado.
Silvia Braschi PROGRAMMA SVOLTO 2 i Matematica 2017/2018 1. Sistemi di equazioni lineari: metodo di sostituzione, metodo del confronto, riduzione e Cramer. Interpretazione grafica dei sistemi di I grado.
Geometria analitica pagina 1 di 5
 Geometria analitica pagina 1 di 5 GEOMETRIA LINEARE NEL PIANO È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 01. Scrivere due diverse rappresentazioni parametriche
Geometria analitica pagina 1 di 5 GEOMETRIA LINEARE NEL PIANO È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 01. Scrivere due diverse rappresentazioni parametriche
LICEO PEDAGOGICO-ARTISTICO G. Pascoli di Bolzano VERIFICA SCRITTA DI MATEMATICA CLASSE 4a P-FILA A 04/11/2010- Tempo 100
 LICEO PEDAGOGICO-ARTISTICO G. Pascoli di Bolzano VERIFICA SCRITTA DI MATEMATICA CLASSE 4a P-FILA A 4//- Tempo Ogni risposta ai quesiti va opportunamente motivata (con calcoli, grafici, ecc.) pena la sua
LICEO PEDAGOGICO-ARTISTICO G. Pascoli di Bolzano VERIFICA SCRITTA DI MATEMATICA CLASSE 4a P-FILA A 4//- Tempo Ogni risposta ai quesiti va opportunamente motivata (con calcoli, grafici, ecc.) pena la sua
Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto
 La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
Rilevazione degli apprendimenti
 Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATICA Scuola secondaria di II grado Classe... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATICA Scuola secondaria di II grado Classe... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
. Imponiamo la validità del teorema di Carnot: =
 PROBLEMA 1 Nel piano riferito a coordinate cartesiane, ortogonali e monometriche, si considerino i triangoli ABC con A(1, 0), B(, 0) e C variabile sulla retta d equazione y =. 1. Si provi che i punti (1,
PROBLEMA 1 Nel piano riferito a coordinate cartesiane, ortogonali e monometriche, si considerino i triangoli ABC con A(1, 0), B(, 0) e C variabile sulla retta d equazione y =. 1. Si provi che i punti (1,
Test su geometria. 1. una circonferenza. 2. un iperbole. 3. una coppia di iperboli. 4. una coppia di rette. 5. una coppia di circonferenze
 Test su geometria Domanda 1 Fissato nel piano un sistema di assi cartesiani ortogonali Oxy, il luogo dei punti le cui coordinate (x; y) soddisfano l equazione x y = 1 è costituita da una circonferenza.
Test su geometria Domanda 1 Fissato nel piano un sistema di assi cartesiani ortogonali Oxy, il luogo dei punti le cui coordinate (x; y) soddisfano l equazione x y = 1 è costituita da una circonferenza.
2. Verificare che la equazione +x+3=0 ammette una e una sola soluzione nell intervallo 10,0
 1 Compito 1. 08 - a 1. Studiare e rappresentare in Oxy la funzione. Verificare che la equazione +x+3=0 ammette una e una sola soluzione nell intervallo 10,0 3. Determinare la equazione della parabola passante
1 Compito 1. 08 - a 1. Studiare e rappresentare in Oxy la funzione. Verificare che la equazione +x+3=0 ammette una e una sola soluzione nell intervallo 10,0 3. Determinare la equazione della parabola passante
Rilevazione degli apprendimenti
 Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATICA Scuola secondaria di II grado Classe... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATICA Scuola secondaria di II grado Classe... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
Applicazioni dei teoremi di Pitagora ed Euclide
 Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo rettangolo: Teorema di Pitagora: 1 + c i c = 1 Teorema di Euclide: c p i 1 = 1 c =
Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo rettangolo: Teorema di Pitagora: 1 + c i c = 1 Teorema di Euclide: c p i 1 = 1 c =
Geometria analitica - Testo pagina 1 di 5 67
 Geometria analitica - Testo pagina di 5 67 5. GEOMETRI NLITI: Geometria lineare nel piano È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 50. 502. 503. 504. Scrivere
Geometria analitica - Testo pagina di 5 67 5. GEOMETRI NLITI: Geometria lineare nel piano È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 50. 502. 503. 504. Scrivere
PROGRAMMA SVOLTO E INDICAZIONI LAVORO ESTIVO. a. s CLASSE 3Cs. Insegnante: prof.ssa Franca TORCHIA Disciplina: MATEMATICA
 PROGRAMMA SVOLTO E INDICAZIONI LAVORO ESTIVO a s 07-08 CLASSE Cs Insegnante: profssa Franca TORCHIA Disciplina: MATEMATICA PROGRAMMA SVOLTO EQUAZIONI E DISEQUAZIONI - Disequazioni e princìpi di equivalenza
PROGRAMMA SVOLTO E INDICAZIONI LAVORO ESTIVO a s 07-08 CLASSE Cs Insegnante: profssa Franca TORCHIA Disciplina: MATEMATICA PROGRAMMA SVOLTO EQUAZIONI E DISEQUAZIONI - Disequazioni e princìpi di equivalenza
Testi verifiche 3 C 3 I a. s. 2008/2009
 Testi verifiche 3 C 3 I a. s. 2008/2009 1) Sono assegnati i punti A(- 1; 3) C(3; 0) M ;1 a) Ricavare le coordinate del simmetrico di A rispetto a M e indicarlo con B. Verificare che il segmento congiungente
Testi verifiche 3 C 3 I a. s. 2008/2009 1) Sono assegnati i punti A(- 1; 3) C(3; 0) M ;1 a) Ricavare le coordinate del simmetrico di A rispetto a M e indicarlo con B. Verificare che il segmento congiungente
Allenamenti di Matematica
 rescia, 3-4 febbraio 2006 llenamenti di Matematica Geometria 1. Il trapezio rettangolo contiene una circonferenza di raggio 1 metro, tangente a tutti i suoi lati. Sapendo che il lato obliquo è lungo 7
rescia, 3-4 febbraio 2006 llenamenti di Matematica Geometria 1. Il trapezio rettangolo contiene una circonferenza di raggio 1 metro, tangente a tutti i suoi lati. Sapendo che il lato obliquo è lungo 7
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2006
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 6 PRBLEMA Si considerino le funzioni f e g determinate da f () log e g () a, essendo a un parametro reale e il logaritmo di base e.. Si discuta,
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 6 PRBLEMA Si considerino le funzioni f e g determinate da f () log e g () a, essendo a un parametro reale e il logaritmo di base e.. Si discuta,
Problemi sui teoremi di Euclide e Pitagora
 Appunti di Matematica GEOMETRIA EUCLIDEA Problemi sui teoremi di Euclide e Pitagora Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo
Appunti di Matematica GEOMETRIA EUCLIDEA Problemi sui teoremi di Euclide e Pitagora Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo
Protocollo dei saperi imprescindibili Ordine di scuola: professionale
 Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. - IMPERATORE D. CLASSE/INDIRIZZO: prima servizi commerciali calcolo numerico (N,
Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. - IMPERATORE D. CLASSE/INDIRIZZO: prima servizi commerciali calcolo numerico (N,
4 Simulazione di prova d Esame di Stato
 Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario Si consideri una sfera di centro O e raggio R; sia SS un suo diametro. Un
Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario Si consideri una sfera di centro O e raggio R; sia SS un suo diametro. Un
Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04/11/ 13
 Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04// 3 Esercizio. Si consideri la funzione ) se 0 f) e se 0. e si verifichi che non è continua in 0. Che tipo di discontinuità presenta in
Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04// 3 Esercizio. Si consideri la funzione ) se 0 f) e se 0. e si verifichi che non è continua in 0. Che tipo di discontinuità presenta in
PIANO CARTESIANO. NB: attenzione ai punti con una coordinata nulla: si trovano sugli assi
 PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
D2. Problemi sulla retta - Esercizi
 D. Problemi sulla retta - Esercizi Per tutti gli esercizi è OBBLIGATORIO tracciare il grafico. 1) Trovare il perimetro del triangolo ABC, con A(1;0), B(-1;1), C(0;-). [ 5 + 10 ) Trovare il perimetro del
D. Problemi sulla retta - Esercizi Per tutti gli esercizi è OBBLIGATORIO tracciare il grafico. 1) Trovare il perimetro del triangolo ABC, con A(1;0), B(-1;1), C(0;-). [ 5 + 10 ) Trovare il perimetro del
LAVORO ESTIVO di MATEMATICA Classi Terze Scientifico Moderno N.B. DA CONSEGNARE ALLA PRIMA LEZIONE DI MATEMATICA DI SETTEMBRE
 LAVORO ETIVO di MATEMATICA Classi Terze cientifico Moderno N.B. A CONEGNARE ALLA PRIMA LEZIONE I MATEMATICA I ETTEMBRE PROBLEMI I ALGEBRA APPLICATA ALLA GEOMETRIA ) In un cerchio di raggio r si determini
LAVORO ETIVO di MATEMATICA Classi Terze cientifico Moderno N.B. A CONEGNARE ALLA PRIMA LEZIONE I MATEMATICA I ETTEMBRE PROBLEMI I ALGEBRA APPLICATA ALLA GEOMETRIA ) In un cerchio di raggio r si determini
COMPITI DELLE VACANZE A.S. 2015/16 MATEMATICA
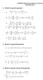 1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Verifiche di matematica classe 3 C 2012/2013
 Verifiche di matematica classe 3 C 2012/2013 1) È assegnato il punto P 1 (3; 1), calcolare le coordinate dei punti: P 2 simmetrico di P 1 rispetto alla bisettrice del primo e terzo quadrante P 3 simmetrico
Verifiche di matematica classe 3 C 2012/2013 1) È assegnato il punto P 1 (3; 1), calcolare le coordinate dei punti: P 2 simmetrico di P 1 rispetto alla bisettrice del primo e terzo quadrante P 3 simmetrico
Problemi sull ellisse
 1 equazione dell ellisse Determina l equazione di un ellisse che ha i fuochi sull asse delle ascisse, semiasse maggiore lungo 6 e distanza focale uguale a 6 + yy Scrivi l equazione dell ellisse con i fuochi
1 equazione dell ellisse Determina l equazione di un ellisse che ha i fuochi sull asse delle ascisse, semiasse maggiore lungo 6 e distanza focale uguale a 6 + yy Scrivi l equazione dell ellisse con i fuochi
QUESITO 1. Lanciando due dadi, qual è il numero che ha maggiore probabilità di uscita? Qual è la probabilità che esca un numero primo?
 www.matefilia.it PNI 29 SESSIONE STRAORDINARIA - QUESITI QUESITO 1 Lanciando due dadi, qual è il numero che ha maggiore probabilità di uscita? Qual è la probabilità che esca un numero primo? Nel lancio
www.matefilia.it PNI 29 SESSIONE STRAORDINARIA - QUESITI QUESITO 1 Lanciando due dadi, qual è il numero che ha maggiore probabilità di uscita? Qual è la probabilità che esca un numero primo? Nel lancio
ESAME DI STATO 2017 TEMA DI MATEMATICA. Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario.
 ESAME DI STATO 217 TEMA DI MATEMATICA Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. Problema 1 Si può pedalare agevolmente su una bicicletta a ruote quadrate? A New
ESAME DI STATO 217 TEMA DI MATEMATICA Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. Problema 1 Si può pedalare agevolmente su una bicicletta a ruote quadrate? A New
ESAME DI STATO 2016 INDIRIZZO SCIENTIFICO E OPZIONE SCIENZE APPLICATE
 ESAME DI STATO 2016 INDIRIZZO SCIENTIFICO E OPZIONE SCIENZE APPLICATE Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario 1. PROBLEMA 1 L amministratore di un piccolo condominio
ESAME DI STATO 2016 INDIRIZZO SCIENTIFICO E OPZIONE SCIENZE APPLICATE Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario 1. PROBLEMA 1 L amministratore di un piccolo condominio
ORDINAMENTO 2003 SESSIONE STRAORDINARIA - QUESITI QUESITO 1
 www.matefilia.it ORDINAMENTO 3 SESSIONE STRAORDINARIA - QUESITI QUESITO 1 Nell insieme delle rette dello spazio si consideri la relazione così definita: «due rette si dicono parallele se sono complanari
www.matefilia.it ORDINAMENTO 3 SESSIONE STRAORDINARIA - QUESITI QUESITO 1 Nell insieme delle rette dello spazio si consideri la relazione così definita: «due rette si dicono parallele se sono complanari
Kangourou della Matematica 2019 Coppa Kangourou a squadre Semifinale turno A Cervia, 3 maggio Quesiti
 Kangourou della Matematica 209 Coppa Kangourou a squadre Semifinale turno A Cervia, 3 maggio 209 Quesiti. La sostituzione Se sostituite i numeri N =, 2, 3, nell espressione N 2 209N + 209 ottenete una
Kangourou della Matematica 209 Coppa Kangourou a squadre Semifinale turno A Cervia, 3 maggio 209 Quesiti. La sostituzione Se sostituite i numeri N =, 2, 3, nell espressione N 2 209N + 209 ottenete una
y = [Sol. y 2x = 4x Verifica n.1
 Verifica n.1 disegnare curve, con valori assoluti e radicali luoghi geometrici (con retta, parabola, circonferenza) funzione omografica parabola aree (ellisse, segmento parabolico) formule goniometriche:
Verifica n.1 disegnare curve, con valori assoluti e radicali luoghi geometrici (con retta, parabola, circonferenza) funzione omografica parabola aree (ellisse, segmento parabolico) formule goniometriche:
D. 1 Il prodotto di a = 12,37 e b = 25,45
 Settembre 005 Aritmetica D. Il prodotto di a =,7 e b = 5,45 A 4, 867 B 4, 65 C 45, 650 D 4, 865 E 4, 8655 D. L inverso del numero numero: A 5 B 5 + 5 C + 5 D E D. I numeri 5 è il,4,5,0,00, si ordinano
Settembre 005 Aritmetica D. Il prodotto di a =,7 e b = 5,45 A 4, 867 B 4, 65 C 45, 650 D 4, 865 E 4, 8655 D. L inverso del numero numero: A 5 B 5 + 5 C + 5 D E D. I numeri 5 è il,4,5,0,00, si ordinano
Dato un triangolo ABC, è il segmento che partendo dal vertice opposto al lato, incontra il lato stesso formando due angoli retti.
 Anno 2014 1 Sommario Altezze, mediane, bisettrici dei triangoli... 2 Altezze relativa a un vertice... 2 Mediane relative a un lato... 2 Bisettrici relativi a un lato... 2 Rette perpendicolari... 3 Teorema
Anno 2014 1 Sommario Altezze, mediane, bisettrici dei triangoli... 2 Altezze relativa a un vertice... 2 Mediane relative a un lato... 2 Bisettrici relativi a un lato... 2 Rette perpendicolari... 3 Teorema
ESAME DI STATO DI LICEO SCIENTIFICO Sessione suppletiva
 ESAME DI STATO DI LICEO SCIENTIFICO Sessione suppletiva 00 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PROBLEMA Se il polinomio f () si divide per si
ESAME DI STATO DI LICEO SCIENTIFICO Sessione suppletiva 00 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PROBLEMA Se il polinomio f () si divide per si
SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO. t ed è nulla per t 0. Vale il limite:
 Simulazione /6 ANNO SCOLASTICO /6 SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Risoluzione Problema Conversazioni telefoniche a) La funzione f t è continua e derivabile
Simulazione /6 ANNO SCOLASTICO /6 SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Risoluzione Problema Conversazioni telefoniche a) La funzione f t è continua e derivabile
Y557 ESAME DI STATO DI LICEO SCIENTIFICO
 Pag. / Sessione ordinaria 008 Seconda prova scritta Y557 ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE Indirizzo: PIANO INTERNAZIONALE INFORMATICA Tema di: MATEMATICA Il candidato risolva uno
Pag. / Sessione ordinaria 008 Seconda prova scritta Y557 ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE Indirizzo: PIANO INTERNAZIONALE INFORMATICA Tema di: MATEMATICA Il candidato risolva uno
