Silvia Braschi PROGRAMMA SVOLTO 2 i Matematica 2017/2018
|
|
|
- Sofia Giorgi
- 7 anni fa
- Visualizzazioni
Transcript
1 Silvia Braschi PROGRAMMA SVOLTO 2 i Matematica 2017/ Sistemi di equazioni lineari: metodo di sostituzione, metodo del confronto, riduzione e Cramer. Interpretazione grafica dei sistemi di I grado. Semplici problemi risolvibili con sistemi di equazioni. 2. Piano cartesiano e retta: distanza tra due punti, punto medio di un segmento; equazione della retta, fasci propri e impropri e significato dei parametri (m e q), retta passante per due punti, rette parallele e perpendicolari, distanza di un punto da una retta. 3. Geometria: i quadrilateri particolari; il teorema di Talete 4. Disequazioni ed equazioni con valori assoluti: disequazioni di I grado intere, disequazioni di grado superiore scomponibili, fratte, sistemi di disequazioni di I grado; semplici equazioni e disequazioni con i valori assoluti; interpretazioni grafiche. Semplici problemi di scelta e modelli matematici (cenni). 5. Trasformazioni geometriche: le isometrie; equazioni delle traslazioni, delle simmetrie assiali ad asse verticale e orizzontale, delle simmetrie centrali. Luoghi geometrici e asse del segmento e bisettrice di un angolo. 6. I radicali: introduzione ai numeri reali, radicali aritmetici e algebrici: confronto, proprietà e operazioni con essi; domini e razionalizzazione dei denominatori (solo i più semplici). Equazioni e disequazioni e sistemi con coefficienti irrazionali. 7. Equazioni di II grado: equazioni incomplete e complete, formula risolutiva e formula ridotta; radicali nel discriminante (semplici esempi), ovvero radicali doppi; equazioni fratte ed equazioni di grado superiore scomponibili; scomposizione di un trinomio di II grado. Discussione sui parametri e relazioni tra soluzioni e coefficienti. Semplici problemi di II grado. Semplici modelli matematici. 8. La parabola: definizione come luogo geometrico, equazione della parabola con asse verticale con vertice nell origine e in un punto qualsiasi; significato dei parametri (a, b, c), intersezione tra retta e parabola, tra due parabole, condizione di tangenza e rette tangenti; interpretazione grafica dei sistemi di II grado. Semplici problemi di massimo e minimo. 9. Equazioni di grado superiore: equazioni binomie e trinomie, equazioni scomponibili. 10. Disequazioni di II grado: disequazioni numeriche intere, fratte e di grado superiore al II scomponibili. Sistemi di disequazioni. Interpretazione grafica di una disequazione. 11. Geometria: circonferenza come luogo geometrico, corde e diametri e proprietà, archi, definizione di radiante, angoli al centro e alla circonferenza; posizioni reciproche di circonferenze e rette, di circonferenze e circonferenze.
2 12. La circonferenza: equazione della circonferenza con centro nell origine. Semplici sistemi di IV grado e interpretazione grafica. 13. Geometria: poligoni inscritti e circoscritti, quadrilateri e poligoni regolari. Le similitudini e le proporzioni. Triangoli simili e criteri di similitudine. I teoremi di Pitagora e Euclide. 14. Probabilità: eventi aleatori e probabilità (definizione classica e statistica); legge dei grandi numeri; probabilità della somma logica di eventi; probabilità condizionata e del prodotto logico di eventi. 15. Equazioni irrazionali: cenni alle equazioni irrazionali e condizioni di esistenza. COMPITI per le vacanze per chi ha il debito a settembre o è promosso con aiuto tutti gli esercizi (solo quelli in grassetto per chi è promosso!) SISTEMI LINEARI MATRICI E DETERMINANTI: pag. 612 es. n 14, 17, 19, 20, n 23, 24 pag. 614 n 29, 35, n 31, 45 pag. 616 PROVA C n 2, 3; PROVA D n 1, 2, n 6 pag. 646 n 23, 27, 28, 29, 36, 42 pag. 650 PROVA D n 2, 3, 4, n 5 IL PIANO CARTESIANO E LA RETTA: pag. 786 n 1, 2, 3, 4, 5; n 18, 19 pag. 788 n 20, 23, n 24 pag. 790 PROVA C n 2, 3, 4, 5; PROVA F I RADICALI: pag. 681 n 1, 6, 7, 8, 9, 12, n 13, 15, 17 pag. 682 n 27, 28, 33, 69 pag. 728 n 5, 6, 7, 8, 10, 11; n 12, 16, 19, 31, 41, 42, 43, 48, 58 pag. 732 n 2, n 3, PROVA E LE EQUAZIONI DI II GRADO: pag. 854 es. dal n 3 al 10; n 12, 16, 17 pag. 856 n 41, 42, 43; n 44, 49, 50 pag. 858 PROVA C n 2, 3, 4, 6; PROVA D n 1, 2, 4, n 5, PROVA E n 2 LE PARABOLE: pag. 874 dal n 15 al 19, 26, n 27, 28 pag. 876 dal n 55 al 59, n 60 pag. 878 dal n 68 al 72, n 76, 77, 78 pag. 880 n 94, 97
3 pag. 897 dal n 348 al 352 pag. 920 n 1, 2, 3, 5, n 7, 8, 9; EQUAZIONI DI GRADO SUPERIORE E SISTEMI: pag. 920 dal n 12 al 20; n 24, 25, 27 pag. 924 PROVA C n 1, 2, 3; n 5, 6; PROVA D n 1; n 2, 5, 6 DISEQUAZIONI DI II GRADO: pag. 976 dal n 2 al 6, n 7, 8; dal n 14 al 17; n 18, 22, 27 pag. 978 PROVA C dal n 1 al 5; PROVA D n 1, 2, 3; n 5 EQUAZIONI IRRAZIONALI E VALORI ASSOLUTI : pag dal n 2 al 5; n 7, 12, 30, 41 PROBABILITÀ: pag PROVA C n 1, 2, 4; PROVA D n 1, 2, 3; n 5; PROVA E n 1, 3; n 2 GEOMETRIA: pag. G 180 n 2, 3, n 4, 5, 8; n 24 pag. G184 PROVA C n 4, 5; PROVA D n 2, 4; n 5, 6 pag. G 205 n 117, 119, n 121, 122 pag. G 262 PROVA C n 1, 2, n 3, 4, 5; PROVA D n 1, 2, 3 ; PROVA E Sarà vostra cura inoltre svolgere accuratamente alcuni esercizi dalle verifiche scritte fatte durante l anno scolastico 1) Fra le rette parallele a quella di equazione 3x +4y -8 = 0 determina: a. quella passante per il punto A(2;-1) b. quella passante per l origine c. quella che ha ordinata all origine -18 d. quella passante per il punto B(-4;5) 2) Trova i valori del paramento k in modo che la retta di equazione (k+1)x-(2k-1)y+1=0 sia: a. parallela a quella di equazione 2x-y+3=0 b. intersechi l asse x nel punto di ascissa 1 c. abbia ordinata all origine uguale a -2 3) Determina il valore di m in modo che la retta di equazione y = (m+1)x m+2 sia: a. parallela all asse delle ascisse b. parallela all asse delle ordinate c. parallela alla bisettrice del I e III quadrante d. perpendicolare alla retta di equazione 2x 5y=0 e. passante per l origine degli assi f. passante per il punto di coordinate (9;2)
4 1. Scrivi l equazione delle rette utilizzando le informazioni fornite dal grafico. 2. Verifica che il triangolo di vertici A(5;0), B(-1;4) e C(3;-2) è isoscele e calcolane l area. 3. Date le rette di equazione k 1 x y 3k 0 a) parallela all asse x; b) parallela all asse y; c) parallela alla retta di equazione 2x 3y 1 0; d) perpendicolare alla retta di equazione 4x 2y 1 0., determina fra esse quella che risulta: 4. Determina per quale valore del parametro a le due rette 2 x 3y 4a 0 2x 2 3a y 1 0 sono perpendicolari. a e 5. Trova la distanza tra i punti A, di ascissa 1, e B, di ordinata 6, appartenenti alla retta 2 di equazione y 5x 4. Individua sulla semiretta sotto riportata i seguenti numeri: 4 1, Inserisci gli stessi numeri nel diagramma di Eulero-Venn riportato qui dietro. R gira.. Q Z
5 7. Risolvi i seguenti problemi (fai anche il grafico con cura): a) Paolo vuole frequentare la palestra di arrampicata per un mese e si trova a dover scegliere tra le seguenti tre possibilità; - la palestra A ha un costo fisso mensile di 25 euro e 5 euro per ogni ingresso - la palestra B ha un costo fisso di 15 euro e 7 euro per ogni ingresso - la palestra C ha un costo mensile di 85 euro, senza limiti di ingresso Qual è la scelta più conveniente per Paolo? b) Le correnti d aria salendo verso l alto si espandono e si raffreddano. Una corrente d aria ha, a terra, una temperatura di 15 C e a 1 Km di altitudine, una temperatura di 5 C. - esprimi mediante un modello lineare la temperatura T della corrente d aria (in C) in funzione dell altitudine h (in Km) - disegna il grafico e spiega il significato del coefficiente angolare della retta, in relazione a questo problema - stabilisci qual è la temperatura della corrente d aria a un altitudine di 5 Km - determina a quale altitudine la temperatura della corrente d aria sarà di - 45 C. c) Paolo e Barbara stanno progettando un viaggio in Grecia e vorrebbero noleggiare un auto ad Atene per i loro spostamenti; stanno valutando le offerte di tre compagnie. - La I chiede una quota fissa di 10 euro più 20 euro per ogni giorno di noleggio - La II chiede una quota fissa di 40 euro più 15 euro per ogni giorno di noleggio - La III chiede 25 euro al giorno senza quote fisse Scrivi le equazione delle funzioni che esprimono la spesa complessiva y necessaria a noleggare l auto per x giorni presso ognuna delle tre compagnie e confrontale (grafico). Supponendo che desiderino avere l auto a noleggio per almeno una settimana, quindi, quale compagnia gli conviene scegliere? a) Svolgi le seguenti espressioni e semplifica se necessario il risultato: i. ii. b) Trasporta fuori dal segno di radice ciò che puoi:
6 c) Esegui i seguenti calcoli e semplifica: i. ii. iii. iv. d) Razionalizza i denominatori: e) Dato il fascio di rette di equazione y=px+2p+3 valuta se è un fascio di rette proprio e in tal caso trova il centro per cui tutte le rette passano. Determina poi tra queste la retta s che passa per l origine degli assi e l equazione di r parallela a uno degli assi coordinati. f) Dati i punti A=(-1;1), B=(5;-2), C=(2;7): Verifica che il triangolo ABC è isoscele e rettangolo, poi trovane area e lunghezza dell altezza relativa all ipotenusa Determina il quarto vertice D del parallelogramma ABCD a) Risolvi la seguente equazione (scomponibile): b) Risolvi la seguente disequazione: 1) La parabola di equazione y=-x 2 +2x+1 ha fuoco in F e interseca la retta di equazione x+y-1=0 in A e B. Trova l area del triangolo ABF (Fai un grafico accurato). 2) Sono date la parabola Γ: y =-x 2 +4x e la retta r passante per A(1;3) e B(3;2). Per quali valori di x il grafico della retta r è al di sotto del grafico della parabola Γ? (Fai un grafico accurato). 3) Siano A e B i punti in cui la parabola di equazione y=-x 2 +4x+5 interseca l asse x; fai il grafico preciso. Trova le equazioni delle rette tangenti alla parabola in A e B, le coordinate del loro punto di intersezione C e verifica che il triangolo ABC è isoscele di base AB. Trova quindi perimetro e area di questo triangolo.
7 4) Risolvi i seguenti sistemi: 5) Risolvi le seguenti disequazioni: a) b) 6) Risolvi le seguenti equazioni: 7) Si vuole costruire un recinto della forma indicata in figura, adiacente a un lato di una casa (i 3 lati x sono congruenti). Si vogliono utilizzare 45 m di rete. Stabilisci per quali valori di x è possibile costruire il recinto e per quale x si ha l area massima possibile. x x x Risolvi il seguente sistema di disequazioni: Risolvi le seguenti disequazioni:
8 Geometria - G1) In un triangolo sia e l altezza misura 12 cm. Determina area e perimetro. G2) Calcola perimetro di un triangolo rettangolo avente l ipotenusa di 50 cm e un cateto uguale a 5/4 della sua proiezione sull ipotenusa. G3) Date una circonferenza di centro O e una sua corda AB, dopo aver costruito il punto medio M della corda, scegliere su essa due punti C e D, equidistanti da M. Dimostrare che C e D sono anche equidistanti da O. Varie ed eventuali V1) Una palla lanciata verticalmente verso l alto da un altezza di 1 m con una velocità iniziale v 0 = 10 m/s, dopo t secondi dal lancio si trova a un altezza, in metri, espressa dalla funzione h(t) = 1+ 10t 9,81/2 t 2. In quale istante la palla raggiunge la massima altezza? A che altezza si trova? Dopo quanto tempo cade a terra? Pavia, 15 giugno 2018 L insegnante. Silvia Braschi.
PROGRAMMA SVOLTO II LB Matematica 2015/2016
 PROGRAMMA SVOLTO II LB Matematica 2015/2016 Sistemi di equazioni lineari: metodo di sostituzione, metodo del confronto, riduzione e Cramer. Cenni a matrici e operazioni con esse. Interpretazione grafica
PROGRAMMA SVOLTO II LB Matematica 2015/2016 Sistemi di equazioni lineari: metodo di sostituzione, metodo del confronto, riduzione e Cramer. Cenni a matrici e operazioni con esse. Interpretazione grafica
Programma di matematica Classe: II BL Docente: Alessandra Mancini Anno scolastico: 2015/2016
 Programma di matematica Classe: II BL Docente: Alessandra Mancini Anno scolastico: 2015/2016 NUCLEI DISCIPLINARI OBIETTIVI SPECIFICI 1. RIPASSO Saper operare con: 0.1 scomposizioni 0.2 frazioni algebriche
Programma di matematica Classe: II BL Docente: Alessandra Mancini Anno scolastico: 2015/2016 NUCLEI DISCIPLINARI OBIETTIVI SPECIFICI 1. RIPASSO Saper operare con: 0.1 scomposizioni 0.2 frazioni algebriche
PROGRAMMA DI MATEMATICA
 A.S. 2015/2016 ALGEBRA - Equazioni letterali fratte PROGRAMMA DI MATEMATICA - Disequazioni di 1 grado ad una incognita intere e frazionarie - Sistemi di disequazioni di 1 o grado in una incognita - Sistemi
A.S. 2015/2016 ALGEBRA - Equazioni letterali fratte PROGRAMMA DI MATEMATICA - Disequazioni di 1 grado ad una incognita intere e frazionarie - Sistemi di disequazioni di 1 o grado in una incognita - Sistemi
PROGRAMMA DI MATEMATICA PER LA CLASSE 2^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA I.I.S
 PROGRAMMA DI MATEMATICA PER LA CLASSE 2^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA I.I.S. VIA SILVESTRI ANNO SCOLASTICO 2015-2016 INSEGNANTE: MASCI ORNELLA ALGEBRA - Equazioni letterali fratte
PROGRAMMA DI MATEMATICA PER LA CLASSE 2^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA I.I.S. VIA SILVESTRI ANNO SCOLASTICO 2015-2016 INSEGNANTE: MASCI ORNELLA ALGEBRA - Equazioni letterali fratte
PROGRAMMA DI MATEMATICA SVOLTO NELL A.S. 2016/2017 ALGEBRA
 LICEO SCIENTIFICO STATALE «CARLO CATTANEO» Sede: Via Sostegno 41/10-10146 TORINO Tel. 011 773 2013 fax: 011 7732014 Succursale: via Postumia 57/60 10142 TORINO Tel. 011 7071984 fax 011 7078256 PROGRAMMA
LICEO SCIENTIFICO STATALE «CARLO CATTANEO» Sede: Via Sostegno 41/10-10146 TORINO Tel. 011 773 2013 fax: 011 7732014 Succursale: via Postumia 57/60 10142 TORINO Tel. 011 7071984 fax 011 7078256 PROGRAMMA
risoluzione di problemi da risolvere tramite la risoluzione di sistemi ed equazioni di 1^ grado. 5 R ed i Radicali
 ORD. MODULO MODULO ARGOMENTO 1 Disequazioni disequazioni di 1^ grado disequazioni fratte disequazioni di grado superiore da risolvere con la scomposizione in fattori sistemi di disequazioni 2 Geometria
ORD. MODULO MODULO ARGOMENTO 1 Disequazioni disequazioni di 1^ grado disequazioni fratte disequazioni di grado superiore da risolvere con la scomposizione in fattori sistemi di disequazioni 2 Geometria
LICEO SCIENTIFICO STATALE ANTONIO LABRIOLA. PROGRAMMA DI MATEMATICA Anno Scolastico 2017/2018
 LICEO SCIENTIFICO STATALE ANTONIO LABRIOLA PROGRAMMA DI MATEMATICA Anno Scolastico 2017/2018 CLASSE 2I DOCENTE: prof.ssa Maria De Sanctis LIBRO DI TESTO: Matematica multimediale.blu con tutor vol 2 Massimo
LICEO SCIENTIFICO STATALE ANTONIO LABRIOLA PROGRAMMA DI MATEMATICA Anno Scolastico 2017/2018 CLASSE 2I DOCENTE: prof.ssa Maria De Sanctis LIBRO DI TESTO: Matematica multimediale.blu con tutor vol 2 Massimo
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S
 PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S. VIA SILVESTRI 301 ANNO SCOLASTICO 2017-20178 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: -
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S. VIA SILVESTRI 301 ANNO SCOLASTICO 2017-20178 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: -
SOMMARIO I SISTEMI LINEARI CAPITOLO 13 CAPITOLO 14 I RADICALI CAPITOLO 15 LE OPERAZIONI CON I RADICALI III. Riepilogo: Metodi di risoluzione 704
 SOMMARIO T E CAPITOLO 13 3 video ( Metodo di riduzione Metodo di Cramer Un problema con tre incognite) e inoltre 9 animazioni I SISTEMI LINEARI 1 I sistemi di due equazioni in due incognite 670 688 2 Il
SOMMARIO T E CAPITOLO 13 3 video ( Metodo di riduzione Metodo di Cramer Un problema con tre incognite) e inoltre 9 animazioni I SISTEMI LINEARI 1 I sistemi di due equazioni in due incognite 670 688 2 Il
Silvia Braschi PROGRAMMA SVOLTO 3 i Matematica 2017/2018
 Silvia Braschi PROGRAMMA SVOLTO i Matematica 017/018 Geometria Analitica (vol A) Ripasso delle disequazioni di secondo grado intere e fratte Disequazioni di grado superiore al secondo Sistemi di disequazioni
Silvia Braschi PROGRAMMA SVOLTO i Matematica 017/018 Geometria Analitica (vol A) Ripasso delle disequazioni di secondo grado intere e fratte Disequazioni di grado superiore al secondo Sistemi di disequazioni
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 2015/2016 CLASSI 2 I SISTEMI LINEARI
 PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI I SISTEMI LINEARI Stabilisci se il sistema è determinato, indeterminato o impossibile senza risolverlo [determinato] [impossibile] Determina per
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI I SISTEMI LINEARI Stabilisci se il sistema è determinato, indeterminato o impossibile senza risolverlo [determinato] [impossibile] Determina per
PROGRAMMA DI MATEMATICA PER LA CLASSE 3^C LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA I.I.S
 PROGRAMMA DI MATEMATICA PER LA CLASSE 3^C LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA I.I.S. VIA SILVESTRI ANNO SCOLASTICO 2017-2018 INSEGNANTE: NEGRI MARINA ALGEBRA Equazioni e disequazioni di grado
PROGRAMMA DI MATEMATICA PER LA CLASSE 3^C LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA I.I.S. VIA SILVESTRI ANNO SCOLASTICO 2017-2018 INSEGNANTE: NEGRI MARINA ALGEBRA Equazioni e disequazioni di grado
ANNO SCOLASTICO CLASSE II E DISCIPLINA: MATEMATICA DOCENTE: Romio Silvana A. PROGRAMMA SVOLTO A.S
 ANNO SCOLASTICO 2014-2015 CLASSE II E DISCIPLINA: MATEMATICA DOCENTE: Romio Silvana A. PROGRAMMA SVOLTO A.S. 2014-2015 ALGEBRA Ripasso sulle equazioni di I grado (tutti i tipi). Disequazioni intere (numeriche
ANNO SCOLASTICO 2014-2015 CLASSE II E DISCIPLINA: MATEMATICA DOCENTE: Romio Silvana A. PROGRAMMA SVOLTO A.S. 2014-2015 ALGEBRA Ripasso sulle equazioni di I grado (tutti i tipi). Disequazioni intere (numeriche
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 2015/2016 CLASSI 3
 PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI DISEQUAZIONI Risolvi le seguenti disequazioni numeriche intere. ) ) 9 ) ) 9 ( ) ) ) non esiste R non esiste R Risolvi le seguenti disequazioni
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI DISEQUAZIONI Risolvi le seguenti disequazioni numeriche intere. ) ) 9 ) ) 9 ( ) ) ) non esiste R non esiste R Risolvi le seguenti disequazioni
Programma di matematica classe II sez. F a.s
 Programma di matematica classe II sez. F a.s. 2018-2019 Testo in adozione: LA matematica a colori - EDIZIONE BLU per il primo biennio vol.2 Autore: Leonardo Sasso Ed Petrini -------------------------------------------------------------------------
Programma di matematica classe II sez. F a.s. 2018-2019 Testo in adozione: LA matematica a colori - EDIZIONE BLU per il primo biennio vol.2 Autore: Leonardo Sasso Ed Petrini -------------------------------------------------------------------------
Come orientarsi nel libro 573 SISTEMI LINEARI. Metodo di riduzione Metodo di Cramer. e inoltre 7 animazioni e 65 esercizi in più
 INDICE Come orientarsi nel libro 573 Un'equazione in due incognite, a pagina 585 100 animali, 100 denari, a pagina 644 18 19 SISTEMI LINEARI 1. Sistemi di equazioni 574 584 2. Metodo di sostituzione 577
INDICE Come orientarsi nel libro 573 Un'equazione in due incognite, a pagina 585 100 animali, 100 denari, a pagina 644 18 19 SISTEMI LINEARI 1. Sistemi di equazioni 574 584 2. Metodo di sostituzione 577
Rappresenta nel piano cartesiano l insieme dei punti P(x; y) le cui coordinate soddisfano le seguenti condizioni:
 ultima modifica /0/0 ESERCIZI PROPOSTI IL PIANO CARTESIANO LE COORDINATE DI UN PUNTO NEL PIANO CARTESIANO A Quali sono le coordinate dei punti indicati in figura? B Quali sono le coordinate dei punti indicati
ultima modifica /0/0 ESERCIZI PROPOSTI IL PIANO CARTESIANO LE COORDINATE DI UN PUNTO NEL PIANO CARTESIANO A Quali sono le coordinate dei punti indicati in figura? B Quali sono le coordinate dei punti indicati
COMPITI DELLE VACANZE A.S. 2015/16 MATEMATICA
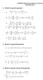 1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
PROGRAMMA DI MATEMATICA
 Docente: Rosinella Cuomo Classe: IID Anno scolastico 2017/2018 ALGEBRA PROGRAMMA DI MATEMATICA 1. Le disequazioni di primo grado Insiemi di numeri sulla retta Disuguaglianze numeriche Disequazioni equivalenti
Docente: Rosinella Cuomo Classe: IID Anno scolastico 2017/2018 ALGEBRA PROGRAMMA DI MATEMATICA 1. Le disequazioni di primo grado Insiemi di numeri sulla retta Disuguaglianze numeriche Disequazioni equivalenti
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S
 PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S. VIA SILVESTRI 301 ANNO SCOLASTICO 2016-2017 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: - Ripetizione
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S. VIA SILVESTRI 301 ANNO SCOLASTICO 2016-2017 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: - Ripetizione
LICEO SCIENTIFICO STATALE A. VOLTA PROGRAMMA DI MATEMATICA CLASSE 2 SEZ.D A.S
 LICEO SCIENTIFICO STATALE A. VOLTA PROGRAMMA DI MATEMATICA CLASSE 2 SEZ.D A.S. 2015-2016 Testi: M.Bergamini-A.Trifone-G.Barozzi Algebra.Blu con probabilità vol.2, ed.zanichelli M.Bergamini-A.Trifone-G.Barozzi
LICEO SCIENTIFICO STATALE A. VOLTA PROGRAMMA DI MATEMATICA CLASSE 2 SEZ.D A.S. 2015-2016 Testi: M.Bergamini-A.Trifone-G.Barozzi Algebra.Blu con probabilità vol.2, ed.zanichelli M.Bergamini-A.Trifone-G.Barozzi
INDICE SISTEMI LINEARI
 INDICE Come orientarsi nel libro 375 Un'equazione in due incognite, a pagina 387 14 SISTEMI LINEARI 1. Sistemi di equazioni 376 386 2. Metodo di sostituzione 379 389 3. Metodo del confronto 380 391 4.
INDICE Come orientarsi nel libro 375 Un'equazione in due incognite, a pagina 387 14 SISTEMI LINEARI 1. Sistemi di equazioni 376 386 2. Metodo di sostituzione 379 389 3. Metodo del confronto 380 391 4.
CONVITTO NAZIONALE CARLO ALBERTO Scuole annesse: Primaria Secondaria I grado Liceo Scientifico
 CONVITTO NAZIONALE CARLO ALBERTO Scuole annesse: Primaria Secondaria I grado Liceo Scientifico Baluardo Partigiani n 6 28100 - Novara Tel. 0321/620047 - Fax. 0321/620622 Email: [email protected]
CONVITTO NAZIONALE CARLO ALBERTO Scuole annesse: Primaria Secondaria I grado Liceo Scientifico Baluardo Partigiani n 6 28100 - Novara Tel. 0321/620047 - Fax. 0321/620622 Email: [email protected]
PROGRAMMA SVOLTO DI MATEMATICA A.S DOCENTE: MARTINA RIGATO CLASSE 1E
 PROGRAMMA SVOLTO DI MATEMATICA A.S. 2018-19 DOCENTE: MARTINA RIGATO CLASSE 1E I numeri naturali e i numeri interi I numeri razionali Gli insiemi e le relazioni Logica I monomi e i polinomi Le equazioni
PROGRAMMA SVOLTO DI MATEMATICA A.S. 2018-19 DOCENTE: MARTINA RIGATO CLASSE 1E I numeri naturali e i numeri interi I numeri razionali Gli insiemi e le relazioni Logica I monomi e i polinomi Le equazioni
CLASSE I D. Anno scolastico 2017/2018
 PROGRAMMA DI MATEMATICA Prof. MINARDA ELISABETTA CLASSE I D Anno scolastico 2017/2018 ARITMETICA: L insieme dei numeri naturali- Operazioni- Calcolo del M.C.D e del m.c.m- I sistemi di numerazione. L insieme
PROGRAMMA DI MATEMATICA Prof. MINARDA ELISABETTA CLASSE I D Anno scolastico 2017/2018 ARITMETICA: L insieme dei numeri naturali- Operazioni- Calcolo del M.C.D e del m.c.m- I sistemi di numerazione. L insieme
PROGRAMMAZIONE DEL GRUPPO DISCIPLINARE A.S. 2016/17 INDIRIZZO SCOLASTICO: LICEO SCIENZE UMANE
 ISTITUTO D ISTRUZIONE SUPERIORE Enrico Mattei ISTITUTO TECNICO COMMERCIALE LICEO SCIENTIFICO LICEO dellescienze UMANE LICEO ECONOMICO SOCIALE Via delle Rimembranze, 26 40068 San Lazzaro di Savena BO Tel.
ISTITUTO D ISTRUZIONE SUPERIORE Enrico Mattei ISTITUTO TECNICO COMMERCIALE LICEO SCIENTIFICO LICEO dellescienze UMANE LICEO ECONOMICO SOCIALE Via delle Rimembranze, 26 40068 San Lazzaro di Savena BO Tel.
PROGRAMMAZIONE DEL GRUPPO DISCIPLINARE A.S. 2016/2017 INDIRIZZO SCOLASTICO: LICEO SCIENTIFICO DISCIPLINA: MATEMATICA ORE SETT.
 ISTITUTO D ISTRUZIONE SUPERIORE Enrico Mattei ISTITUTO TECNICO COMMERCIA LICEO SCIENTIFICO LICEO dellescienze UMANE Via delle Rimembranze, 26 40068 San Lazzaro di Savena BO Tel. 051 464510 464545 fax 452735
ISTITUTO D ISTRUZIONE SUPERIORE Enrico Mattei ISTITUTO TECNICO COMMERCIA LICEO SCIENTIFICO LICEO dellescienze UMANE Via delle Rimembranze, 26 40068 San Lazzaro di Savena BO Tel. 051 464510 464545 fax 452735
Programma di Matematica svolto durante l anno scolastico nella classe 2 sez.e
 Programma di Matematica svolto durante l anno scolastico 2015-2016 nella classe 2 sez.e ALGEBRA 1) Richiami sul calcolo letterale e sulle equazioni algebriche lineari ad una incognita. 2) Disequazioni
Programma di Matematica svolto durante l anno scolastico 2015-2016 nella classe 2 sez.e ALGEBRA 1) Richiami sul calcolo letterale e sulle equazioni algebriche lineari ad una incognita. 2) Disequazioni
CLASSE II A LICEO LINGUISTICO A.S. 2015/2016. Prof.ssa ANNA CARLONI
 CLASSE II A LICEO LINGUISTICO A.S. 2015/2016 Prof.ssa ANNA CARLONI OBIETTIVI la scomposizione dei polinomi le frazioni algebriche X X X scomposizione in fattori dei Scomporre a fattor comune polinomi Calcolare
CLASSE II A LICEO LINGUISTICO A.S. 2015/2016 Prof.ssa ANNA CARLONI OBIETTIVI la scomposizione dei polinomi le frazioni algebriche X X X scomposizione in fattori dei Scomporre a fattor comune polinomi Calcolare
LICEO SCIENTIFICO E. CURIEL Anno scolastico 2018/2019
 LICEO SCIENTIFICO E. CURIEL Anno scolastico 2018/2019 Classe 1^ B PROGRAMMA CONSUNTIVO DEL DOCENTE DI: MATEMATICA PROF. FILIPPO SCARSO ALGEBRA I numeri naturali e i numeri interi I numeri razionali Insiemi
LICEO SCIENTIFICO E. CURIEL Anno scolastico 2018/2019 Classe 1^ B PROGRAMMA CONSUNTIVO DEL DOCENTE DI: MATEMATICA PROF. FILIPPO SCARSO ALGEBRA I numeri naturali e i numeri interi I numeri razionali Insiemi
ANNO SCOLASTICO 2013/2014 CLASSE 1^B S DISCIPLINA FISICA DOCENTE PROF. FAGGIAN GIULIANA PROGRAMMA DI FISICA
 CLASSE 1^B S DISCIPLINA FISICA PROGRAMMA DI FISICA Le grandezze fisiche: grandezze fondamentali e derivate, la misura delle grandezze e il sistema di misura, i sistemi M.K.S., C.G.S. e il S.I., le potenze
CLASSE 1^B S DISCIPLINA FISICA PROGRAMMA DI FISICA Le grandezze fisiche: grandezze fondamentali e derivate, la misura delle grandezze e il sistema di misura, i sistemi M.K.S., C.G.S. e il S.I., le potenze
A.S. 2015/2016 Programma svolto classe III Q
 A.S. 2015/2016 Programma svolto classe III Q Circonferenza e cerchio Lunghezza della circonferenza e area del cerchio. Lunghezza di un arco. Area di un settore circolare e di un segmento circolare. Raggio
A.S. 2015/2016 Programma svolto classe III Q Circonferenza e cerchio Lunghezza della circonferenza e area del cerchio. Lunghezza di un arco. Area di un settore circolare e di un segmento circolare. Raggio
Liceo scientifico Leonardo da Vinci PROGRAMMA DI MATEMATICA ANNO SCOLASTICO 2013/2014 II A LE EQUAZIONI LINEARI
 Liceo scientifico Leonardo da Vinci PROGRAMMA DI MATEMATICA ANNO SCOLASTICO 2013/2014 II A LE EQUAZIONI LINEARI Le identità; Le equazioni; Le equazioni equivalenti; I principi di equivalenza; Le equazioni
Liceo scientifico Leonardo da Vinci PROGRAMMA DI MATEMATICA ANNO SCOLASTICO 2013/2014 II A LE EQUAZIONI LINEARI Le identità; Le equazioni; Le equazioni equivalenti; I principi di equivalenza; Le equazioni
Programma Didattico Annuale
 LICEO STATALE SCIENTIFICO - LINGUISTICO - CLASSICO GALILEO GALILEI - LEGNANO PdQ - 7.06 Ediz.: 1 Rev.: 0 Data 02/09/05 Alleg.: D01 PROG. M2 PROCEDURA della QUALITA' Programma Didattico Annuale Anno Scolastico
LICEO STATALE SCIENTIFICO - LINGUISTICO - CLASSICO GALILEO GALILEI - LEGNANO PdQ - 7.06 Ediz.: 1 Rev.: 0 Data 02/09/05 Alleg.: D01 PROG. M2 PROCEDURA della QUALITA' Programma Didattico Annuale Anno Scolastico
I monomi: definizione e determinazione del grado. Operazioni tra monomi. Ricerca del mcm e del MCD tra monomi
 PROGRAMMA DI MATEMATICA CLASSE I Au SCIENZE UMANE. ANNO SCOLASTICO 2015/16 ISTITUTO MARGHERITA DI SAVOIA I NUMERI I numeri naturali. I numeri interi. I numeri razionali. Operazioni, proprietà. Espressioni.
PROGRAMMA DI MATEMATICA CLASSE I Au SCIENZE UMANE. ANNO SCOLASTICO 2015/16 ISTITUTO MARGHERITA DI SAVOIA I NUMERI I numeri naturali. I numeri interi. I numeri razionali. Operazioni, proprietà. Espressioni.
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT
 1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE
 1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
f(x) = sin cos α = k2 2 k
 28 Maggio 2015 Il punteggio viene attribuito in base alla correttezza e completezza nella risoluzione dei quesiti, nonché alle caratteristiche dell esposizione: chiarezza, ordine ed organicità. La sufficienza
28 Maggio 2015 Il punteggio viene attribuito in base alla correttezza e completezza nella risoluzione dei quesiti, nonché alle caratteristiche dell esposizione: chiarezza, ordine ed organicità. La sufficienza
PROGRAMMAZIONE MODULARE
 PROGRAMMAZIONE MODULARE Classe: 2 I.P.S.S. Sezione A Anno Scolastico: 2016-2017 Materia: MATEMATICA Docente: Danilo Latini FINALITÀ EDUCATIVE Far acquisire coscienza di se stessi, lavorando sull autostima
PROGRAMMAZIONE MODULARE Classe: 2 I.P.S.S. Sezione A Anno Scolastico: 2016-2017 Materia: MATEMATICA Docente: Danilo Latini FINALITÀ EDUCATIVE Far acquisire coscienza di se stessi, lavorando sull autostima
PROGRAMMA SVOLTO E INDICAZIONI LAVORO ESTIVO. a. s CLASSE: 2^Bs. Insegnante : POCHETTI LUISA. Disciplina : MATEMATICA
 PROGRAMMA SVOLTO E INDICAZIONI LAVORO ESTIVO a. s. 2017-2018 CLASSE: 2^Bs Insegnante : POCHETTI LUISA Disciplina : MATEMATICA PROGRAMMA SVOLTOPROGRAMMA SVOLTO: 1) SISTEMI LINEARI Sistemi di equazioni Metodo
PROGRAMMA SVOLTO E INDICAZIONI LAVORO ESTIVO a. s. 2017-2018 CLASSE: 2^Bs Insegnante : POCHETTI LUISA Disciplina : MATEMATICA PROGRAMMA SVOLTOPROGRAMMA SVOLTO: 1) SISTEMI LINEARI Sistemi di equazioni Metodo
Ore annue: 132 MODULO 1
 Liceo B. Russell VIA IV NOVEMBRE 35, 38023 CLES Indirizzo: Liceo Linguistico CLASSI 2 e Programmazione Didattica Disciplina: Ore annue: 132 Matematica Settembre ottobre MODULO 1 novembre Disequazioni numeriche
Liceo B. Russell VIA IV NOVEMBRE 35, 38023 CLES Indirizzo: Liceo Linguistico CLASSI 2 e Programmazione Didattica Disciplina: Ore annue: 132 Matematica Settembre ottobre MODULO 1 novembre Disequazioni numeriche
LICEO SCIENTIFICO E. CURIEL PROGRAMMA DI MATEMATICA ANNO SCOLASTICO 2018/2019
 LICEO SCIENTIFICO E. CURIEL PROGRAMMA DI MATEMATICA ANNO SCOLASTICO 2018/2019 CLASSE I F SCIENZE APPLICATE GLI INSIEMI NUMERICI Gli insiemi dei Naturali N, degli interi Z e dei razionali Q. Il valore assoluto
LICEO SCIENTIFICO E. CURIEL PROGRAMMA DI MATEMATICA ANNO SCOLASTICO 2018/2019 CLASSE I F SCIENZE APPLICATE GLI INSIEMI NUMERICI Gli insiemi dei Naturali N, degli interi Z e dei razionali Q. Il valore assoluto
PROGRAMMA EFFETTIVAMENTE SVOLTO DAL DOCENTE
 Ministero dell istruzione, dell università e della ricerca Istituto d Istruzione Superiore Severi-Correnti IIS Severi-Correnti 02-318112/1 via Alcuino 4-20149 Milano 02-33100578 codice fiscale 97504620150
Ministero dell istruzione, dell università e della ricerca Istituto d Istruzione Superiore Severi-Correnti IIS Severi-Correnti 02-318112/1 via Alcuino 4-20149 Milano 02-33100578 codice fiscale 97504620150
Programma di MATEMATICA
 Classe 1 a E Indirizzo COSTRUZIONI, AMBIENTE E TERRITORIO Cap. 1 I NUMERI NATURALI I numeri naturali le quattro operazioni multipli e divisori le potenze e le relative proprietà espressioni numeriche la
Classe 1 a E Indirizzo COSTRUZIONI, AMBIENTE E TERRITORIO Cap. 1 I NUMERI NATURALI I numeri naturali le quattro operazioni multipli e divisori le potenze e le relative proprietà espressioni numeriche la
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI ANNO SCOLASTICO INSEGNANTE: MASCI ORNELLA
 PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI ANNO SCOLASTICO 2014-2015 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: - Ripetizione dei numeri naturali e delle quattro operazioni
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI ANNO SCOLASTICO 2014-2015 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: - Ripetizione dei numeri naturali e delle quattro operazioni
Modulo 1: Insiemi numerici
 A.S. 2013/2014 Programma di Matematica svolto nella classe 1^G Modulo 1: Insiemi numerici 1 Numeri naturali e numeri interi: Numeri naturali: definizioni Operazioni in N Potenza dei numeri naturali Criteri
A.S. 2013/2014 Programma di Matematica svolto nella classe 1^G Modulo 1: Insiemi numerici 1 Numeri naturali e numeri interi: Numeri naturali: definizioni Operazioni in N Potenza dei numeri naturali Criteri
OBIETTIVI GENERALI OBIETTIVI SPECIFICI ALGEBRA
 Revisione dei contenuti in data 21 aprile 2015 OBIETTIVI GENERALI Imparare a lavorare in classe (saper ascoltare insegnante e compagni, intervenire con ordine e nei momenti opportuni). Concepire il lavoro
Revisione dei contenuti in data 21 aprile 2015 OBIETTIVI GENERALI Imparare a lavorare in classe (saper ascoltare insegnante e compagni, intervenire con ordine e nei momenti opportuni). Concepire il lavoro
LICEO SCIENTIFICO STATALE G. GALILEI - SIENA
 ANNO SCOLASTICO 2015 / 2016 LICEO SCIENTIFICO STATALE G. GALILEI - SIENA PROGRAMMA DI MATEMATICA SVOLTO NELLA CLASSE I sez. E TEORIA DEGLI INSIEMI * definizioni * rappresentazioni di un insieme * operazioni
ANNO SCOLASTICO 2015 / 2016 LICEO SCIENTIFICO STATALE G. GALILEI - SIENA PROGRAMMA DI MATEMATICA SVOLTO NELLA CLASSE I sez. E TEORIA DEGLI INSIEMI * definizioni * rappresentazioni di un insieme * operazioni
LICEO SCIENTIFICO - OPZIONE DELLE SCIENZE APPLICATE MATEMATICA
 LICEO SCIENTIFICO - OPZIONE DELLE SCIENZE APPLICATE MATEMATICA OBIETTIVI SPECIFICI DEL BIENNIO 1) utilizzare consapevolmente le tecniche e le procedure di calcolo basilari studiate; 2) riconoscere nei
LICEO SCIENTIFICO - OPZIONE DELLE SCIENZE APPLICATE MATEMATICA OBIETTIVI SPECIFICI DEL BIENNIO 1) utilizzare consapevolmente le tecniche e le procedure di calcolo basilari studiate; 2) riconoscere nei
Liceo G.B. Vico Corsico a.s
 Liceo G.B. Vico Corsico a.s. 2018-19 Programma svolto durante l anno scolastico Classe: 2F Materia: MATEMATICA Insegnante: CALDI SILVIA Testo utilizzato: Nuova matematica a colori - Volume 1 La matematica
Liceo G.B. Vico Corsico a.s. 2018-19 Programma svolto durante l anno scolastico Classe: 2F Materia: MATEMATICA Insegnante: CALDI SILVIA Testo utilizzato: Nuova matematica a colori - Volume 1 La matematica
Liceo Scientifico A. Romita Programma di Matematica Anno scolastico 2016/2017 Prof.ssa Santella Mariagrazia
 Liceo Scientifico A. Romita Programma di Matematica Anno scolastico 2016/2017 Prof.ssa Santella Mariagrazia Classe III sez. A Modulo 1 Unità didattica 1 Ripetizione della risoluzione delle equazioni di
Liceo Scientifico A. Romita Programma di Matematica Anno scolastico 2016/2017 Prof.ssa Santella Mariagrazia Classe III sez. A Modulo 1 Unità didattica 1 Ripetizione della risoluzione delle equazioni di
PROGRAMMA SVOLTO E INDICAZIONI LAVORO ESTIVO. a. s CLASSE 3Cs. Insegnante: prof.ssa Franca TORCHIA Disciplina: MATEMATICA
 PROGRAMMA SVOLTO E INDICAZIONI LAVORO ESTIVO a s 07-08 CLASSE Cs Insegnante: profssa Franca TORCHIA Disciplina: MATEMATICA PROGRAMMA SVOLTO EQUAZIONI E DISEQUAZIONI - Disequazioni e princìpi di equivalenza
PROGRAMMA SVOLTO E INDICAZIONI LAVORO ESTIVO a s 07-08 CLASSE Cs Insegnante: profssa Franca TORCHIA Disciplina: MATEMATICA PROGRAMMA SVOLTO EQUAZIONI E DISEQUAZIONI - Disequazioni e princìpi di equivalenza
I.I.S. Via Silvestri 301 Roma. Liceo Scientifico M. Malpighi. Anno scolastico
 I.I.S. Via Silvestri 301 Roma Liceo Scientifico M. Malpighi Anno scolastico 2018-19 Programma di MATEMATICA svolto nella classe I sezione A Docente prof.ssa Ornella Masci ALGEBRA NUMERI NATURALI: - Ripetizione
I.I.S. Via Silvestri 301 Roma Liceo Scientifico M. Malpighi Anno scolastico 2018-19 Programma di MATEMATICA svolto nella classe I sezione A Docente prof.ssa Ornella Masci ALGEBRA NUMERI NATURALI: - Ripetizione
Ripasso della scomposizione di un polinomio in fattori primi, M.C.D. e m.c.m. di polinomi.
 Anno scolastico 2010 11 Classe V Ginnasio (sez.a) Ripasso della scomposizione di un polinomio in fattori primi, M.C.D. e m.c.m. di polinomi. Frazioni algebriche. Operazioni. Espressioni. Equazioni numeriche
Anno scolastico 2010 11 Classe V Ginnasio (sez.a) Ripasso della scomposizione di un polinomio in fattori primi, M.C.D. e m.c.m. di polinomi. Frazioni algebriche. Operazioni. Espressioni. Equazioni numeriche
(Prof.ssa Dessì Annalisa)
 LICEO SCIENTIFICO PITAGORA - SELARGIUS CLASSE 1 SEZ. E - ANNO SCOLASTICO 2014 / 2015 PROGRAMMA DI MATEMATICA Libro di testo: Bergamini Barozzi Matematica multimediale.blu con tutor, vol. 1 Zanichelli L
LICEO SCIENTIFICO PITAGORA - SELARGIUS CLASSE 1 SEZ. E - ANNO SCOLASTICO 2014 / 2015 PROGRAMMA DI MATEMATICA Libro di testo: Bergamini Barozzi Matematica multimediale.blu con tutor, vol. 1 Zanichelli L
LICEO SCIENTIFICO STATALE G. D. CASSINI PROGRAMMAZIONE DI MATEMATICA BIENNIO
 PROGRAMMAZIONE DI MATEMATICA BIENNIO I nuclei tematici contenuti nelle Indicazioni nazionali per il primo biennio dei licei scientifici sono: A - Aritmetica e algebra B - Geometria C - Relazioni e funzioni
PROGRAMMAZIONE DI MATEMATICA BIENNIO I nuclei tematici contenuti nelle Indicazioni nazionali per il primo biennio dei licei scientifici sono: A - Aritmetica e algebra B - Geometria C - Relazioni e funzioni
Istituto di Istruzione Superiore L. da Vinci Civitanova Marche. Anno scolastico PROGRAMMA SVOLTO. Materia: Matematica
 Anno scolastico 2015-2016 PROGRAMMA SVOLTO Materia: Matematica Docente: Massimiliano Iori Classe : 2F Indirizzo: Linguistico Disequazioni lineari Le diseguaglianze: definizioni e proprietà. Disequazioni
Anno scolastico 2015-2016 PROGRAMMA SVOLTO Materia: Matematica Docente: Massimiliano Iori Classe : 2F Indirizzo: Linguistico Disequazioni lineari Le diseguaglianze: definizioni e proprietà. Disequazioni
