Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Belzoni, Padova
|
|
|
- Agnese Mattioli
- 4 anni fa
- Visualizzazioni
Transcript
1 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Belzoni, Padova Programma del corso Alcune lezioni svolte (metà corso) 3 Esercizi tipo svolti 4 Esercizi teorici svolti 5 Testi delle esercitazioni a gruppi Typeset by AMS-TEX
2 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Corso di ALGEBRA LINEARE (A), SEF - SGI Programma aa / 4/3 Matrici Esempi: diagonali e scalari Moltiplicazione di una matrice per uno scalare e sue proprietà 4/3 Addizione di matrici e sue proprietà Prodotto di matrici righe per colonne e sue proprietà 5/3 Matrici non singolari Trasposte e H-trasposte e loro proprietà Matrici simmetriche, hermitiane, anti-simmetriche, anti-hermitiane 5/3 Parte hermitiana e parte anti-hermitiana di una matrice quadrata Decomposizione a blocchi Applicazioni al prodotto 6/3 Matrici elementari e loro inverse Operazioni elementari sulle righe di una matrice 6/3 Eliminazione di Gauss senza scambi di righe /3 Eliminazione di Gauss con scambi di righe Forma ridotta di Gauss di una matrice Colonne dominanti e colonne libere /3 Scrittura matriciale di un sistema lineare Risoluzione di un sistema lineare (con una o infinite soluzioni), sistemi lineari senza soluzione 3/3 Esercizi tipo e 3/3 Inverse destre, sinistre e bilatere Criteri per l esistenza Inverse di matrici 4/3 Esercizi tipo 3 e 4 4/3 Matrici triangolari Decomposizione A = LU, determinazione di L 8/3 Decomposizione A = P T LU 8/3 Esercizi tipo 5 e 6 /3 Spazi vettoriali reali e complessi Esempi /3 Sottospazi di uno spazio vettoriale Esempi I sottospazi fondamentali di una matrice /3 Insiemi di generatori Insiemi linearmente indipendenti Lemma della scrematura /3 Esercizi tipo 7 e 8 5/3 Esercizi teorici e 5/3 Lemma del rimpiazzo Esistenza ed equipotenza delle basi 6/3 Caratterizzazioni delle basi Basi degli spazi delle righe e delle colonne di una matrice in forma ridotta di Gauss 6/3 Basi di C(A) e di R(A) Rango di una matrice 7/3 Esercizio tipo 9
3 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI3 7/3 Proprieta del rango di una matrice Decomposizioni a rango pieno Coordinate di un vettore rispetto ad una base ordinata 8/4 Mappa delle coordinate e sue proprieta Matrice di passaggio tra due basi ordinate Trasformazioni lineari Spazio nullo e spazio immagine 8/4 Il caso della moltiplicazione per una matrice Teorema nullita +rango Matrice associata ad una trasformazione lineare 9/4 Esercizi tipo,, 9/4 Come cambia la matrice associata ad una trasformazione lineare quando si cambiano le basi /4 Esercizio tipo 3 Interpretazione geometrica di R ed R 3 Regola del parallelogramma /4 Norme su spazi vettoriali Le norme, e 5/4 Rotazioni in R ed angoli tra vettori di R Prodotti scalari e norme indotte 5/4 Diseguaglianza di Schwarz per i prodotti scalari Esercizio tipo 4 6/4 Intorni dell origine in R rispetto alle norme, e Esercizi tipo 5 e 6 6/4 Angolo tra vettori Ortogonalita Ortogonalita di vettori non nulli implica indipendenza Proiezione ortogonale su di una retta Proiezione ortogonale su un sottospazio 7/4 Proprieta della proiezione ortogonale del piano su di una retta Complemento ortogonale di un sottospazio Complementarieta dei sottospazi fondamentali di una matrice (senza dimostrazione) 7/4 Algoritmo di Gram-Schmidt (senza dimostrazione) Esercizio tipo 7 /4 Matrice di proiezione su di un sottospazio di C n Decomposizioni Q R - non-normalizzata e QR-normalizzata per una matrice /4 Esercizi tipo 8 e 9 3/4 Determinanti Esempi 3/4 Esercizio tipo ( modo) Esercizio teorico 3 4/4 Proprietà del determinante Polinomio caratteristico, autovalori e loro molteplicità algebriche Esercizi tipo e 4/4 Determinante di una matrice triangolare Esercizio teorico 4
4 4ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI LEZIONE Matrici ed esempi Def Una matrice m n ad elementi reali (risp ad elementi complessi) è una tabella di numeri reali (risp complessi) disposti in m righe ed n colonne Una matrice ad elementi reali (risp complessi) è detta anche una matrice reale (risp complessa) Le matrici vengono indicate con lettere maiuscole ( 5 3 Esempio Siano A = 4 ), B = i 7 + i 3, C = 3 π 9 6 4, 5 D = ( 8 i ) ed E = 3 A è una matrice 3 ad elementi reali (oppure: A è una 5 matrice 3 reale), B è una matrice 3 complessa, C è una matrice 3 3 reale, D è una matrice complessa ed E è una matrice 3 reale ( ) 5 3 NB Si puó scrivere indifferentemente A =, oppure A = 4 oppure A = [ ] 5 3, 4 La a riga di A è ( ( 5 3 ) ), la a riga di A è ( 4 ( ) ), la a colonna di A è 5 3, la 4 a colonna di A è, la 3 a colonna di A è Def Data una matrice m n reale (risp complessa) A, il numero che si trova nella i-esima riga e nella j-esima colonna di A, dove i m e j n, si dice l elemento di posto (i, j) di A Esso viene di solito indicato con il simbolo a ij Si scrive allora: a a a n a n a a a n a n A = a m a m a m n a m n a m a m a mn a mn, oppure, in forma compatta, A = [a ij ] i=,,m;j=,,n (anche: A = [a ij ], m n) Quindi se A e B sono le matrici dell Esempio, a =, a = 5, ecc, b =, b 3 = 3, ecc
5 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI5 Def 3 Due matrici A = [a ij ], m n, e B = [b ij ], r t, sono uguali se m = r n = t a ij = b ij per ogni i m, j n ossia se hanno uguale numero di righe, uguale numero di colonne, e gli elementi corrispondenti uguali Def 4 Si chiama matrice nulla m n la matrice m n ogni cui elemento è Il simbolo usato per indicarla è O m n (oppure O quando dal contesto si puó dedurre quante righe e quante colonne ha) Def 5 Una matrice con una sola riga ed n colonne si dice vettore riga con n componenti Ad esempio la matrice D dell Esempio è un vettore riga con componenti Def 6 Una matrice con una sola colonna ed m righe si dice vettore colonna con m componenti Ad esempio la matrice E dell Esempio è un vettore colonna con 3 componenti NB Per indicare i vettori colonna si preferiscono usare lettere in carattere corsivo minuscolo con un segno sotto: e piuttosto che E Def 7 Una matrice in cui il numero delle righe è uguale al numero delle colonne si dice quadrata Se A è una matrice quadrata, il numero delle righe di A (che è uguale al numero delle colonne di A) si chiama l ordine di A Ad esempio la matrice C dell Esempio è una matrice quadrata di ordine 3 Notazioni L insieme delle matrici reali m n si indica con il simbolo M mn (R), l insieme delle matrici complesse m n si indica con il simbolo M mn (C) NB Si usano il simbolo R n (risp C n ) al posto del simbolo M n (R) (risp M n (C)), il simbolo R m (risp C m ) al posto del simbolo M m (R) (risp M m (C)), il simbolo M m (R) (risp M m (C)) al posto del simbolo M mm (R (risp M mm (C)) Quindi se A, B, C, D ed E sono le matrici dell Esempio, allora A M 3 (R), B M 3 (C), C M 3 (R), D C ed E R 3 Def 8 Sia A = [a ij ] una matrice m n Gli elementi a ii si chiamano elementi diagonali di A Ad esempio, se A, B e C sono le matrici dell Esempio, gli elementi diagonali di A
6 6ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI sono e, gli elementi diagonali di B sono e, gli elementi diagonali di C sono 3, 6 e 5 Def 9 Una matrice quadrata A = [a ij ] si dice diagonale se a ij = per ogni (i, j) con i j (ossia se gli elementi di A che non sono diagonali sono tutti nulli) Esempio A = diagonali, mentre D = 7, B = 3 i 7 ed E = i, C = 3 sono matrici 3 non sono matrici diagonali Def Una matrice diagonale si dice scalare se i suoi elementi diagonali sono tra loro uguali 7 Esempio 3 A = è una matrice scalare, mentre B = C = e D = non sono matrici scalari 7 7, 7 Def Si chiama matrice identica di ordine m la matrice scalare m m i cui elementi diagonali sono tutti uguali ad Il simbolo usato per indicarla è I m (oppure I quando dal contesto si puó dedurre il suo numero di righe e di colonne) La sua colonna i-esima, quando i m, è indicata con il simbolo e i Dunque e i è il vettore colonna con m componenti: e i = i Prodotto di una matrice per uno scalare Def Siano A = [a ij ] una matrice complessa (risp reale) m n ed α un numero complesso (risp reale) α viene chiamato scalare Sia B = [b ij ] la matrice m n definita da b ij = αa ij per ogni i =,, m; j =,, n,
7 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI7 ossia la matrice che si ottiene da A moltiplicando ciascun elemento di A per lo scalare α Allora B si chiama il prodotto della matrice A per lo scalare α B viene indicata con il simbolo αa Esempio 4 Se B la matrice considerata nell Esempio, allora ( + i)b = ( + i) 7 + i ( + i) ( + i)(7 + i) i = ( + i)( i) ( + i) = 3 ( + i) ( + i)3 + i 7 + 7i + i = i + i = + i 6 + 8i + i 3 + 3i 3 + 3i Si definisce così su M mn (C) (risp su M mn (R)) un operazione di moltiplicazione di matrici per scalari C M mn (C) M mn (C) (risp R M mn (R) M mn (R)) (α, A) αa Proprietà della moltiplicazione di matrici per scalari () α(βa) = (αβ)a per ogni scalare α e β ed ogni matrice A, () A = A per ogni matrice A Dimostrazione Sia A = [a ij ] una matrice m n Si ponga B := βa e si indichi con b ij l elemento di posto (i, j) di B (per cui B = [b ij ]) Si ponga C := αb e si indichi con c ij l elemento di posto (i, j) di C (per cui C = [c ij ]) Si ponga infine D := (αβ)a e si indichi con d ij l elemento di posto (i, j) di D (per cui D = [d ij ]) Si noti che B e D sono m n essendolo A, e che C è m n essendolo B Per ogni i m e j n si ha c ij = αb ij = α(βa ij ) = (αβ)a ij = d ij quindi C = D ossia αb = D Poichè B = βa e D = (αβ)a si ottiene () Per provare () si ponga E = A e si indichi con e ij l elemento di posto (i, j) di E (per cui E = [e ij ]) E è m n essendolo A Per ogni i m e j n si ha e ij = a ij = a ij, quindi E = A, ossia A = A
8 8ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI LEZIONE Somma di due matrici m n Def Siano A = [a ij ] e B = [b ij ] due matrici (reali o complesse) ENTRAMBE m n Sia C = [c ij ] la matrice m n definita da c ij = a ij + b ij per ogni i =,, m; j =,, n, (ossia la matrice i cui elementi si ottengono sommando gli elementi corrispondenti di A e B) La matrice C si chiama la somma delle matrici A e B Per indicare C si usa il simbolo A + B i Esempio Siano A = e B = i i + 3 A + B = ( i 3 = ) Allora ( + i 3 + i 4 3 NB NON ESISTE la somma di due matrici che non abbiano lo stesso numero di righe oppure che non abbiano lo stesso numero di colonne ) Si definisce cosìsu M mn (C) (risp su M mn (R)) un operazione di addizione di matrici M mn (C) M mn (C) M mn (C) (risp M mn (R) M mn (R) M mn (R)) Proprietà dell addizione di matrici (A, B) A + B Per ogni A, B, C M mn (C) (risp M mn (R)) ed ogni α, β C (risp R) si ha: () associatività: A + (B + C) = (A + B) + C; () commutatività: A + B = B + A; (3) elemento neutro: A + O = A(= O + A); (4) matrice opposta: se si indica con A la matrice ( )A, si ha A + ( A) = O (la matrice A si chiama l opposta della matrice A; (5) α(a + B) = αa + αb; (6) (α + β)a = αa + βa Le proprietà (5) e (6) sono proprietà ditributive che collegano l addizione di matrici con la moltiplicazione per scalari Dimostrazione Siano A = [a ij ], B = [b ij ] e C = [c ij ] Per ogni i m e j n si ha:
9 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI9 () : a ij + (b ij + c ij ) = (a ij + b ij ) + c ij ; () : a ij + b ij = b ij + a ij ; (3) : a ij + = a ij = + a ij ; (4) : a ij + ( a ij ) = a ij a ij = ; (5) : α(a ij + b ij ) = αa ij + αb ij ; (6) : (α + β)a ij = αa ij + βa ij Notazione Per indicare la somma di A con l opposta di B si scrive A B, al posto di A + ( B) b Def Siano A = ( a a a n ) e B = b b n un vettore riga ed un vettore colonna con lo stesso numero di componenti, n Si chiama prodotto del vettore riga con n componenti A ed il vettore colonna con n componenti B il numero ( a a a n ) b b b n = a b + a b + + a n b n = a i b i i n
10 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI NB Quando si vuole metter in evidenza che i numeri sono matrici, si scrive [a b + a b + + a n b n ] al posto di a b + a b + + a n b n Nel caso di vettori riga si preferisce scrivere ( a a a n ) piuttosto che ( a a a n ), ed analogamente per i vettori colonna Esempio ( 3 i ) i = 3 ( ) + i i + 6 = 6 + = 4 6 Def 3 Siano A = [a ij ] una matrice m n e B = [b ij ] una matrice n r Il prodotto delle due matrici, A e B, di cui la prima, A, ha un numero di colonne uguale al numero delle righe della seconda, B è la matrice C = [c ij ], m r, ove c ij = ( a i a i a in ) b j b j b nj = a ib j + a i b j + + a in b nj = k n a ik b kj, ossia la matrice m r il cui elemento di posto (i, j) è il prodotto della i-esima riga di A e la j-esima colonna di B Per indicare C si usa il simbolo AB 3 Esempio Siano A = e B = 3 4 Allora AB = 6 C = [c ij ] è la matrice 4 ove c = ( 3 ) = + ( ) + 3 = + =, c = ( 3 ) 3 = 3 + ( ) + 3 = = 7, c 3 = ( 3 ) 4 = = = 4, c 4 = ( 3 ) = ( ) = =, c = ( 6 ) = 6 + ( ) + = = 6,
11 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI c = ( 6 ) 3 = ( ) + = = 9, c 3 = ( 6 ) 4 = = + + =, c 4 = ( 6 ) = ( ) = + =, 7 4 ossia C = 6 9 NB Il prodotto AB di due matrici A e B ESISTE SOLO SE IL NUMERO DELLE COLONNE DI A E UGUALE AL NUMERO DELLE RIGHE DI B Si definisce cosìun operazione di moltiplicazione di matrici M mn (C) M nr (C) M mr (C) (risp M mn (R) M nr (R) M mr (R)) (A, B) AB Proprietà della moltiplicazione di matrici () associatività: A(BC) = (AB)C, se A, B e C sono matrici tali che tutte le moltiplicazioni scritte siano possibili; () distributività rispetto alla somma: A(B + C) = AB + AC, se A, B e C sono matrici tali che tutti i prodotti e tutte le somme scritte siano possibili, e (B + C)A = BA + CA, se A, B e C sono matrici tali che tutti i prodotti e tutte le somme scritte siano possibili; (3) α(ab) = (αa)b = A(αB), se A e B sono matrici tali che il prodotto AB esista ed α è uno scalare; (4) I m A = A = AI n per ogni matrice A, m n; (5) O k m A = O k n e AO n k = O m k per ogni matrice A, m n, ed ogni numero naturale k NB la moltiplicazione di matrici NON gode della proprietà commutativa: date due matrici A, m n, e B, r t, () se esiste AB (ossia se r = n) non è detto che esista BA (perchè BA esista occorre che m = t)
12 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI () Se sia AB che BA esistono, ossia se A è m n, e B è n m, allora AB è m m e BA è n n Se m n, senz altro AB BA (3) Se anche A e B sono entrambe m m, per cui AB e BA entrambe esistono ed entrambe sono m m, non è egualmente detto che AB e BA siano uguali Ad esempio: ( 3 ) = = 9 ( 3 ) 3 Per la moltiplicazione di matrici NON vale la legge di cancellazione per il prodotto: esistono matrici A e B, con A O B e AB = O Ad esempio: = Esercizio Per ogni a R sia S a = ai = () S a A = AS a per ogni A M (R) a Si provi: a () Se B M (R) è tale che BA = AB per ogni A M (R), allora B = S a per un opportuno a R
13 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 3 Svolgimento () Sia A M (R) Allora S a A = (ai )A = a(i A) = aa = a(ai a ) Poichè per la proprietà (3) della moltiplicazione di matrici si ha che a(ai a ) = A(aI a ), si conclude che S a A = AS a a b () Sia B = M c d (R) tale che ( ) BA = AB per ogni A M (R) In particolare prendendo in ( ) come matrice A la matrice à =, si ottiene: a = c ( a b c d ) = ( ) a b = c d a b Se ne( deduce) che b = c =, ossia che la matrice B deve essere una matrice diagonale: a B = d Tenendo conto del fatto che B = matrice A = si ottiene: a a = d d ( a d Se ne deduce che d = a, e quindi che ) = B = a e prendendo in ( ) come matrice A la d ( a = S a a ) a = d a d a d Nell esercizio si è provato che le matrici reali che commutano con ogni matrice reale sono esattamente le matrici reali scalari di ordine Allo stesso modo si può vedere che le matrici complesse che commutano con ogni matrice complessa sono esattamente le matrici complesse scalari di ordine In generale è possibile provare: le matrici reali (risp complesse) m m che commutano con ogni matrice reale (risp complessa) m m sono esattamente le matrici reali (risp complesse) scalari di ordine m Def 4 Sia A una matrice quadrata Si definisce la potenza n-esima di A, dove n è un numero naturale, nel seguente modo: A = A, A = AA, A 3 = AA, A n = AA n
14 4 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Si pone poi A = I Come per le potenze dei numeri, si ha la seguente proprietà delle potenze: per ogni coppia di numeri naturali m ed n ed ogni matrice quadrata A si ha A m A n = A m+n = A n A m Def 5 Una matrice A si dice non singolare (o anche invertibile), se esiste una matrice B tale che AB = I = BA Vedremo che se una tale B esiste, allora è unica Essa si chiama l inversa di A e si indica con il simbolo A Proposizione Se A e B sono due matrici non singolari tali che esista AB, allora anche il prodotto AB è una matrice non singolare e (AB) = B A In generale se A, A,, A r, A r sono matrici non singolari tali che esista il prodotto A A A r A r, allora anche il prodotto A A A r A r è non singolare e si ha (A A A r A r ) = A r A r A A Dimostrazione Facciamo la dimostrazione supponendo che il prodotto abbia solo due fattori Osserviamo innanzitutto che se A e B sono matrici non singolari tali che esista AB, allora A, B, A e B sono tutte matrici m m per un opportuno m Si ha poi: (AB)B A = A(BB )A = AIA = AA = I, (B A )(AB) = B (A A)B = B IB = B B = I La dimostrazione del risultato quando il numero dei fattori nel prodotto è r è analoga
15 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 5 LEZIONE 3 Trasposte, coniugate, H-trasposte Def Data una matrice A = [a ij ], m n, si chiama trasposta di A la matrice n m B = [b ij ] definita da: La matrice B si indica con il simbolo A T Esempio Se A = b ij = a ji per ogni i m, j n 4i 3, allora la trasposta di A è 5i 4i A T = 3 5i Def Data una matrice A = [a ij ], m n, si chiama coniugata di A la matrice m n B = [b ij ] definita da: b ij = a ij per ogni i m, j n, ove se z = a + ib è un numero complesso espresso in forma algebrica (cioè a e b sono numeri reali), z = a ib è il suo coniugato La matrice B si indica con il simbolo A Esempio Se A = A = 4i 3, allora la coniugata di A è 5i 4i 3 = 5i 4i 3 + 5i Def 3 Data una matrice A = [a ij ], m n, si chiama H-trasposta di A la matrice n m B = [b ij ] definita da: La matrice B si indica con il simbolo A H b ij = a ji per ogni i m, j n Si noti che per ottenere la H-trasposta di A si può procedere indifferentemente in uno dei due seguenti modi: o si calcola prima la trasposta di A e di quest ultima si calcola poi la coniugata (ossia A H = A T ), oppure si calcola prima la coniugata di A e di quest ultima si calcola poi la trasposta (ossia A H = (A) T )
16 6 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Esempio 3 Se A = ma anche A H = (A) T = 4i 3, allora la H-trasposta di A è 5i A H = A T = 4i 3 5i = 4i 3 + 5i, T 4i 3 = 5i T 4i 3 = 4i + 5i 3 + 5i Proprietà delle coniugate Siano A e B matrici per cui siano possibili le operazioni indicate, e sia α uno scalare Allora si ha: () A = A; () (A + B) = A + B, e (A B) = A B; (3) αa = αa; (4) AB = AB Le proprietà delle coniugate seguono dalla definizione di coniugata di una matrice, e dalle definizioni di prodotto di una matrice per uno scalare e di prodotto di due matrici
17 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 7 Proprietà delle trasposte e delle H-trasposte Siano A e B matrici per cui siano possibili le operazioni indicate, e sia α uno scalare Allora si ha: () : (A T ) T = A; (A H ) H = A; () : (A + B) T = A T + B T ; (A + B) H = A H + B H ; (A B) T = A T B T ; (A + B) H = A H + B H ; (3) : (αa) T = αa T ; (αa) H = αa H ; (4) : (AB) T = B T A T ; (AB) H = B H A H Dimostrazione Per provare (),() e (3) basta applicare le definizioni di trasposta, di H-trasposta, di somma di matrici e di prodotto di matrici per scalari Per provare la prima uguaglianza di (4), supponiamo che A = [a ij ] sia m n e B = [b ij ] sia n r, e poniamo AB = C = [c ij ] e B T A T = D = [d ij ] Poichè B T è r n ed A T è n m, allora D è r m, come C T L elemento di posto (i, j) di D è il prodotto della i-esima riga di B T per la j-esima colonna di A T Poichè la i-esima riga di B T è la i-esima colonna di B pensata come vettore riga, e la j-esima colonna di A T è la j-esima riga di A pensata come vettore colonna, allora d ij = ( b i b i a b ni ) j = a jn b i = b li a jl = b a jl b li = ( a j a j a jn ) i = c ji l n l n b ni Dalla definizione di trasposta (di C) si ottiene la prima uguaglianza di (4) Per la seconda, si noti che la definizione di H-trasposta, la proprietà (4) delle coniugate e la proprietà (AB) T = B T A T che abbiamo già dimostrato implicano: (AB) H = (AB) T = (A B) T = B T A T = B H A H a j Definizioni 4,5,6,7 Una matrice A si dice: simmetrica se coincide con la sua trasposta (ossia se A = A T ); hermitiana se coincide con la sua H-trasposta (ossia se A = A H ); anti-simmetrica se coincide con l opposta della sua trasposta (ossia se A = A T, oppure, ed è lo stesso, se A T = A); anti-hermitiana se coincide con l opposta della sua H-trasposta (ossia se A = A H, oppure, ed è lo stesso, se A H = A)
18 8 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Si noti che se A è simmetrica, o hermitiana, o anti-simmetrica, o infine anti-hermitiana, allora A è quadrata Esempio 4 Siano 3, B = A = ( 3 + i i ), C =, D = + i + i Allora A è simmetrica, B è hermitiana, C è anti-simmetrica e D è anti-hermitiana Dalla proprietà (4) della trasposta e della H-trasposta segue che la somma di due matrici simmetriche è una matrice simmetrica; la somma di due matrici hermitiane è una matrice hermitiana; la somma di due matrici anti-simmetriche è una matrice anti-simmetrica; la somma di due matrici anti-hermitiane è una matrice anti-hermitiana 3 3 Esempio 5 A = e B = sono simmetriche, ma AB = non è simmetrica Dunque il prodotto di due matrici simmetriche puó essere una matrice non simmetrica i i Esempio 6 A = e B = sono hermitiane, ma AB = i i 3 3i non è hermitiana Dunque il prodotto di due matrici hermitiane i puó essere una matrice non hermitiana Esempio 7 A = è anti-simmetrica, ma A = AA = non è anti-simmetrica Dunque il prodotto di due matrici anti-simmetriche puó essere una matrice non anti-simmetrica i i i i Esempio 8 A = e B = sono anti-hermitiane, ma AB = non è anti-hermitiana Dunque il prodotto di due matrici anti-hermitiane puó essere una matrice non anti-hermitiana Esercizio: (Decomposizione di una matrice quadrata nella parte hermitiana ed anti-hermitiana) Sia A una matrice quadrata m m Allora esistono B = (A+AH ) e C = (A AH ) Si provi che:
19 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 9 B è hermitiana, C è antihermitiana, A = B + C, se D ed E sono due matrici tali che D è hermitiana E è anti-hermitiana D + E = A allora D = (A + AH ) ed E = (A AH ) Ossia: ogni matrice quadrata A si puó scrivere in un modo unico come somma di una matrice hermitiana, (A+AH ), ed una matrice anti-hermitiana, (A-AH ) (A + AH ) si chiama la parte hermitiana di A e (A AH ) si chiama la parte anti-hermitiana di A
20 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Svolgimento: Poichè A è m m, anche A H è m m, per cui esistono sia A + A H che A A H, entrambe m m, e dunque esistono anche B = (A + AH ) e C = (A AH ) Allora, poichè B e C sono entrambe m m, esiste B + C, ed è: B + C = (A + AH ) + (A AH ) = A + AH + A AH = A La matrice B è hermitiana: B H = ( (A + AH )) H = (A + AH ) H = (AH + (A H ) H ) = (AH + A) = B La matrice C è anti-hermitiana: C H = ( (A AH )) H = (A AH ) H = (AH (A H ) H ) = (AH A) = C Abbiamo quindi visto per ogni matrice quadrata A esistono una matrice hermitiana, (A + AH ), ed una matrice antihermitiana (A AH ) tali che A sia la loro somma Vogliamo ora provare che se A è una matrice quadrata e D ed E sono matrici tali che D è hermitiana E è anti-hermitiana D + E = A allora D = (A + AH ) ed E = (A AH ) Poniamo B = (A + AH ) e C = (A AH ) Poichè abbiamo visto che A = B + C e stiamo supponendo che A = D + E, allora ( ) B + C = D + E Da (*) segue che anche (B + C) H = (D + E) H Poichè abbiamo visto che B H = B e C H = C, allora (B + C) H = B H + C H = B C Poichè stiamo supponendo che D H = D ed E H = E, allora Quindi da (B + C) H = (D + E) H segue (D + E) H = D H + E H = D E ( ) B C = D E Sommando membro a membro (*) e (**) otteniamo B = D, da cui, moltiplicando entrambi i membri dell uguaglianza per, D = B = (A + AH ) Sottraendo membro a membro (*) e (**) otteniamo C = E, da cui, moltiplicando entrambi i membri dell uguaglianza per, E = C = (A AH )
21 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Abbiamo quindi provato che data una matrice quadrata A, esistono un unica matrice hermitiana B ed un unica matrice anti-hermitiana C tali che A = B + C (inoltre B = (A + AH ) e C = (A AH )) ( + i 6i Esempio 9 Se A = 4 per cui la parte hermitiana di A è (A + AH ) = e la parte anti-hermitiana di A è (A AH ) = ), allora A H = A T = ( + i + i 6i i + ( + i + i 6i i ) = ) = + i 4 = 6i + 3i, 3i i + 3i + 3i i 4, 6i Quanto detto generalizza ció che già sappiamo per i numeri, ossia le matrici Sappiamo infatti che per ogni numero complesso z esistono e sono unici due numeri reali a e b tali che z = a + ib (tale espressione si chiama la forma algebrica di z) Ogni numero reale a è una matrice hermitiana: a H = a T = a = a Ogni numero immaginario puro ib (ove b è un numero reale) è una matrice anti-hermitiana: (ib) H = (ib) T = ib = i b = ( i)b = (ib) Quindi la forma algebrica di z, ossia l espressione z = a + ib con a e b numeri reali, è l espressione della matrice z come somma di una matrice hermitiana, a, ed una matrice anti-hermitiana, ib Un calcolo diretto mostra che a e b sono proprio la parte hermitiana e la parte anti-hermitiana di z: poichè z H = z T = z = a ib, allora (z + zh ) = (a + ib + a ib) = a e (z zh ) = (a + ib a + ib) = ib LEZIONE 4 Matrici a blocchi Def Data una matrice A si chiama sottomatrice di A ogni matrice che si ottiene da A sopprimendo alcune righe ed alcune colonne di A
22 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 4i 3 9 Esempio Se A = 5i 4, allora i 9 5i 4i 3 9 B =, C = e D = sono tre sottomatrici di A: B si ottiene da A sopprimendo la a riga e la 4 a colonna, C si ottiene da A sopprimendo la a riga, la 3 a e la 5 a colonna, D si ottiene da sopprimendo solo la a colonna Ripartire una matrice A in blocchi significa tracciare delle linee orizzontali (lunghe tanto quanto lo è la matrice) e delle righe verticali (alte tanto quanto lo è la matrice): i blocchi della ripartizione effettuata sono le sottomatrici di A che le linee tracciate delimitano 4i 3 9 Esempio Se A = 5i 4 è la matrice considerata nell Esempio i 3 9 5i 4, allora A = è una ripartizione di A in blocchi I blocchi di questa ripartizione sono: 4i 3 9 A =, A 5i =, A 3 =, 4 A = ( 6 7 ), A =, A 3 = ( 8 ) Per indicare che A è stata ripartita nei blocchi A, A, A 3, A, A, ed A 3 si scrive A A A = A 3 A A A 3 Le notazioni scelte suggeriscono che quando si ripartisce una matrice A in blocchi, si puó pensare ad A come ad una matrice i cui elementi sono i blocchi della ripartizione effettuata Quando una matrice è ripartita in blocchi si dice che è una matrice a blocchi Prodotto di una matrice a blocchi per uno scalare A A A r A Siano A = A A r una matrice a blocchi ed α uno scalare Allora A t A t A tr αa αa αa r αa αa = αa αa r αa t αa t αa tr
23 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 3 A A Esempio 3 Se A = A 3 è la matrice a blocchi considerata A A A 3 ia ia nell Esempio, ed α = i, allora αa = ia = ia 3 Poichè ia ia ia 3 ia = 4 3i, ia i 5 = i 9i, ( i)a 3 =, 4i i ( i)a = ( 6i 7i ), ( i)a = ( i ), ( i)a 3 = ( 8i ), 4 3i i 9i allora A = i 5 4i i 6i 7i i 8i Somma di due matrici a blocchi Siano A = a blocchi Se A A A n A m A m A mn e B = B B B s B r B r B rs m = r n = s esiste A ij + B ij per ogni i m, j n due matrici (l ultima condizione è verificata se e solo se A ij ha lo stesso numero di righe e lo stesso numero di colonne di B ij, per ogni i m, j n), allora A + B = Esempio 4 Se A = con blocchi A = A + B A + B A n + B n A m + B m A m + B m A mn + B mn A A B B e B = sono le matrici a blocchi A A B B, A 3 = B =, B = ( 4), A = ( ), B = ( 3 ), B = O e A = O, allora A + B A + B = A + B A A = = 4 3 A + B A + B B B 4 3 Prodotto di due matrici a blocchi
24 4 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Siano A = A A A n A m A m A mn e B = B B B s B r B r B rs due matrici a blocchi C C C s Se r = n allora AB = C è la matrice a blocchi C = con C n C n C ns C ij = A i B j + A i B j + + A in B nj = k n A ik B kj, A CONDIZIONE CHE TUTTE LE OPERAZIONI SCRITTE SIANO DEFINITE Esempio 5 Se A è la matrice 4 a blocchi A = I,A = I,A = 3I,A = 4I, e B è la matrice 4 a blocchi B = con B = B = B = B = allora AB = = A A con A A A = B B B B A A B B = A A B B A B + A B A B + A B I B = + I B I B + I B = A B + A B A B + A B 3I B + 4I B 3I B + 4I B = 3B 3B = 7B 7B Applicazione del prodotto a blocchi al prodotto di due matrici () Ripartizione della seconda matrice in colonne Siano A e B due matrici tali che esista il loro prodotto AB (quindi se A è una matrice m n allora B è una matrice n r) Ripartiamo B in blocchi prendendo come blocchi le sue colonne: B = ( B B B r ) = ( b b b r ) dove B j = b j è la j-esima colonna di B per ogni j r Si puó allora calcolare il prodotto AB pensando A come ad un unico blocco, e si ottiene AB = A ( B B B r ) = A ( b b b r ) = ( Ab Ab Ab r )
25 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 5 Per ogni j r, Ab j è un vettore colonna con m componenti, ed è la j-esima colonna di AB () Ripartizione della prima matrice in righe Come in (), siano A e B due matrici tali che esista il loro prodotto AB (quindi se A è una matrice m n allora B è una matrice n r) Ripartiamo A in blocchi prendendo come blocchi le sue righe: A r T A A = = r T A m dove A i = r T i è la i-esima riga di A per ogni i m Si noti che indicando con r T i un vettore riga con n componenti, ossia una matrice n, stiamo indicando con r i un vettore colonna con n componenti, ossia una matrice n Si puó allora calcolare il prodotto AB pensando B come ad un unico blocco, e si ottiene A r T r T A AB = B = r T B B = r T B A m r T mb Per ogni i m, r T i B è un vettore riga con r componenti, ed è la i-esima riga di AB r T m r T m (3) Il prodotto di una matrice per un vettore colonna Siano A una matrice m n e v = v v v n un vettore colonna con n componenti Allora esiste Av e puó essere calcolato come prodotto a blocchi, pensando A ripartita nei suoi blocchi colonna A = ( a a a n ) e v ripartito nei suoi blocchi riga (quindi v ha n blocchi riga, ciascuno dei quali è una matrice, ossia un numero v j ): Ab = ( a a a n ) v v v n = v a + v a + + v n a n In particolare Ae i = i-esima colonna di A (e i è la i-esima colonna di I n ) (4) Il prodotto di vettore riga per una matrice
26 6 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Siano B una matrice n r e w T = ( w w w n ) un vettore riga con n componenti Allora esiste w T B e puó essere calcolato come prodotto a blocchi, pensando s T B ripartita nei suoi blocchi riga B = s T s T n e wt ripartito nei suoi blocchi colonna (quindi w T ha n blocchi riga, ciascuno dei quali è una matrice, ossia un numero w j ): s T s T w T B = ( w w w n ) s T n = w s T + w s T + + w ns T n In particolare e T i B = i-esima riga di B ( e i è la i-esima colonna di I n ) Siano A una matrice m n e B una matrice n r Da () e (3) si ricava che la j-esima colonna di AB è b j a + b j a + + b nj a n ove a, a, a n sono le colonne di A e b j b j b nj è la j-esima colonna di B Da () e (4) si ricava che la i-esima riga di AB è a i s T + a i s T + + a in s T n s T, s T, s T n sono le righe di B e ( a i a i a in ) è la i-esima riga di A ove (5) Ripartizione della prima matrice in colonne e della seconda in righe Siano A e B due matrici tali che esista il loro prodotto AB (quindi se A è una matrice m n allora B è una matrice n r) Ripartiamo A in blocchi prendendo come blocchi le sue colonne: A = ( a a a n ), e B prendendo come blocchi le sue righe: s T s T B = s T n
27 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 7 Allora AB puó essere calcolato come prodotto a blocchi: s T s T AB = ( a a a n ) s T n = a s T + a s T + + a n s T n Si noti che ciascun addendo a i s T i è una matrice m r LEZIONE 5 Matrici elementari e loro inverse Si fissi m un numero naturale Per ogni i, j m con i j siano E ij (c) (ove c è uno scalare ) la matrice m m con tutti gli elementi diagonali uguali ad, l elemento di posto (i, j) uguale a c ed ogni altro elemento nullo se k = r In simboli: E ij (c) = [e kr ] dove e kr = c se (k, r) = (i, j) altrimenti j i c = E ij (c) Si noti che E ij (c) è la matrice che si ottiene da I m sommando alla i-esima riga di I m la j-esima riga di I m moltiplicata per c se c, E i (c) la matrice m m diagonale con tutti gli elementi diagonali uguali ad tranne quell di posto (i, i), uguale a c In simboli: E i (c) = [e kr ] dove se k = r i e kr = c se k = r = i altrimenti
28 8 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI i O O c = E i (c) Si noti E i (c) è la matrice che si ottiene da I m moltiplicando la i-esima riga di I m per c E ij la matrice m m che si ottiene da I m scambiando la i-esima con la j-esima se k = r / {i, j} se (k, r) = (i, j) riga In simboli: E ij = [e kr ] dove e kr = se (k, r) = (j, i) altrimenti
29 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 9 i j i j = E ij NB In genere si deduce dal contesto quante quante righe (e quindi quante colonne, dal momento che si tratta di matrici quadrate) hanno le matrici elementari Def Si chiama matrice elementare ogni matrice del tipo E ij (c), oppure del tipo E i (c), o infine del tipo E ij Un calcolo diretto mostra che se E ij (c) è m m, allora per ogni i, j m con i j si ha: E ij (c)e ij ( c) = I m = E ij ( c)e ij (c) Quindi E ij (c) è non singolare e E ij (c) = E ij ( c) se E i (c) è m m e c, allora per ogni i m si ha: E i (c)e i ( c ) = I m = E i ( c )E i(c) Quindi E i (c) è non singolare e E i (c) = E i ( c ) se E ij è m m, allora per ogni i, j m con i j si ha: Quindi E ij è non singolare e E ij = E ij E ij E ij = I m
30 3 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Operazioni elementari sulle righe di una matrice m n Sia A una matrice m n E ij (c)a è la matrice che si ottiene da A sommando alla i-esima riga di A la j-esima riga di A moltiplicata per lo scalare c Quindi se A = [a kr ], E ij (c)a ha tutte le righe diverse dalla i-esima uguali alle corrispondenti righe di A, ed ha come i-esima riga ( a i + ca j a i + ca j a in + ca jn ) E i (c)a è la matrice che si ottiene da A moltiplicando la i-esima riga di A per lo scalare c (c ) Quindi se A = [a kr ], E i (c)a ha tutte le righe diverse dalla i-esima uguali alle corrispondenti righe di A, ed ha come i-esima riga ( ca i ca i ca in ) E ij A è la matrice che si ottiene da A scambiando la i-esima riga di A con la j-esima Quindi se A = [a kr ], E ij A ha tutte le righe diverse dalla i-esima e dalla j-esima uguali alle corrispondenti righe di A, ed ha come i-esima e come j-esima riga rispettivamente: ( a j a j a jn ) e ( a i a i a in ) Def operazioni: Si chiamano operazioni elementari sulle righe di A le tre seguenti sommare ad una riga un altra riga di A moltiplicata per uno scalare, moltiplicare una riga di A per uno scalare non nullo, scambiare due righe di A Ciascuna di esse corrisponde alla premoltiplicazione di A per un opportuna matrice elementare Eliminazione di Gauss senza scambi di righe Sia A una matrice m n, con A O m n Illustriamo ora un algoritmo che consiste in un insieme di operazioni sulle righe di A e che viene chiamato un eliminazione di Gauss senza scambi di righe su A L obiettivo di tale algoritmo è costruire a partire da A una matrice m n U con le prime k-righe non nulle e le rimanenti m k righe nulle (dove k è un opportuno numero compreso tra ed m che dipende da A),
31 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 3 gli elementi non nulli disposti come sopra ad una scala che scende da sinistra a destra, a partire dalla prima riga fino alla k-esima riga, ogni cui gradino è alto una riga ed è lungo una o piú colonne (la scala ha quindi k gradini), gli elementi alla base di ciascun gradino di questa scala uguali ad, ossia una matrice del tipo: dove gli elementi al di sotto della scalinata sono tutti nulli, e gli eventuali elementi non nulli si trovano al di sopra della scalinata (in questo disegno la scala ha 3 gradini) Le operazioni lecite in questo algoritmo sono solo di due tipi: sommare ad una riga di A un altra riga di A moltiplicata per un scalare, moltiplicare una riga di A per uno scalare non nullo L applicazione di questo algoritmo facilita la soluzione di alcuni problemi, come ad esempio la risoluzione dei sistemi lineari Esistono matrici per cui questo algoritmo fallisce, ossia per le quali questo algoritmo non porta alla costruzione di U Per tali matrici introdurremo nella prossima lezione un algoritmo piú ricco (in cui è lecita anche la terza operazione elementare sulle righe di A) Esempio Per A = l eliminazione di Gauss senza scambi di righe fallisce: non ( è possibile, ) utilizzando ( le due ) operazioni lecite, ( arrivare ) ad una matrice del tipo U =, oppure U =, oppure U = Supponiamo che la prima riga di A non sia nulla (per le matrici non nulle con la prima riga nulla l eliminazione di Gauss senza scambi di righe fallisce) o Passaggio L obiettivo del o passaggio è trasformare la j -esima colonna nella prima colonna di I m (il numero j è definito nel seguente punto ()) () Percorrendo la prima riga di A da sinistra a destra, sia a j il primo elemento non nullo (quindi se j > allora a = a = = a,j = e a j ; il piú delle volte, peró, j =, ossia a ) a j è detto il pivot della a riga Se a j, moltiplichiamo la prima riga di A per a j, ottenendo cosí una matrice m n A = [a ij ] che ha tutte le righe uguali a quelle di A, tranne la prima, i cui elementi sono gli elementi della prima riga di A moltiplicati
32 3 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI per a j, ossia divisi per a j In particolare a = a = = a,j = e a j = Poichè l operazione che abbiamo fatto corrisponde a premoltiplicare A per la matrice elementare E (a j ), m m, scriviamo: A E (a j ) A () Percorriamo la colonna j -esima dall alto in basso, e tenendo in considerazione solo gli elementi a ij che siano diversi da, per ciascun a ij che troviamo, partendo da i = e arrivando fino a i = m, sommiamo alla riga i-esima di A la prima riga di A moltiplicata per a ij, (per ogni i =,, m tale che a ij ) Otteniamo cosí una matrice B = [b ij ] in cui la j -esima colonna è la prima colonna di I m Poichè le operazioni che abbiamo fatto corrispondono a premoltiplicare A per il prodotto di matrici elementari scriviamo: E m ( a mj )E m, ( a m,j ) E 3 ( a 3j )E ( a j ), E m( a mj )E m,( a m,j )E 3( a 3j )E ( a j ) A B Esempio Sia A = Poichè a, allora j = L operazione richiesta al punto () è moltiplicare la prima riga di A per a = 3 La matrice A che si ottiene ha come prima riga ( e le altre righe uguali alle righe di B, quindi 5 3 ) = ( 5), A = a a Consideriamo la prima (qui j = ) colonna di A, a = 3 a 4 Le operazioni richieste al punto () sono: poiché a =, sommare alla seconda riga di A la prima riga di A moltiplicata per a =,
33 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 33 poiché a 3 =, sommare alla terza riga di A la prima riga di A moltiplicata per a 3 = Non occorrono altre operazioni, poichè a 4 = La matrice B che si ottiene ha come seconda riga ( 5 5 ) + ( ) ( 5 ) = ( ), ha come terza riga ( 3 3 ) + ( ) ( 5) = ( 3 6 ), ed ha la prima e la quarta riga uguali rispettivamente alla prima e alla quarta riga di A Quindi 5 B = Supponiamo che la matrice A da cui siamo partiti sia tale che, dopo aver effettuato sulle sue righe le operazioni descritte nel o passaggio, si ottenga una matrice B in cui se j > allora le prime j colonne sono nulle, ed inoltre o tutte le righe diverse dalla prima sono nulle, oppure la seconda riga è non nulla (per le matrici in cui questa situazione non si presenta, l eliminazione di Gauss senza scambi di righe fallisce) Se tutte le righe di B diverse dalla prima sono nulle, l algoritmo si ferma a B (ossia B è la U cercata) Altrimenti la seconda riga di B è non nulla e si procede o Passaggio L obiettivo del o passaggio è trasformare la j -esima colonna in una colonna del tipo (il numero j è definito nel seguente punto ()) () Percorrendo la seconda riga di B da sinistra a destra, sia b j il primo elemento non nullo (quindi b = b = = b,j = e b j ) b j è detto il pivot della a riga Se b j, moltiplichiamo la seconda riga di B per b j, ottenendo cosí una matrice m n B = [b ij ] che ha tutte le righe uguali a quelle di B, tranne la seconda, i cui elementi sono gli elementi della seconda riga di B moltiplicati per b j, ossia divisi per b j In particolare b = b = = b,j = e b j =
34 34 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Poichè l operazione che abbiamo fatto corrisponde a premoltiplicare B per la matrice elementare E (b j ), m m, scriviamo: B E (b j ) B () Percorriamo la colonna j -esima dall alto in basso, e tenendo in considerazione solo gli elementi b ij che siano diversi da, per ciascun b ij che troviamo, partendo da i = 3 e arrivando fino a i = m, sommiamo alla riga i-esima di B la seconda riga di B moltiplicata per b ij, (per ogni i = 3,, m tale che b ij ) Otteniamo cosí una matrice C = [c ij ] in cui la j -esima colonna è del tipo:, come ci eravamo prefissati Poichè le operazioni che abbiamo fatto corrispondono a premoltiplicare B per il prodotto di matrici elementari scriviamo: E m ( b mj )E m, ( b m,j ) E 3 ( b 3j ), E m( b mj )E m,( b m,j )E 3( b 3j ) B C Esempio 3 Riprendiamo la matrice B ottenuta alla fine dell Esempio : 5 B = Poichè b, allora j =, ma poichè b = non è richiesta alcuna operazione al punto (), per cui B = B b b Consideriamo la seconda (qui j = ) colonna di B, b = 3 b 4 5 Le operazioni richieste al punto () sono: poiché b 3 =, sommare alla terza riga di B la seconda riga di B moltiplicata per b 3 =, poiché b 4 = 5, sommare alla quarta riga di B la seconda riga di B moltiplicata per b 4 = 5
35 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 35 La matrice C che si ottiene ha come terza riga ( 3 6 ) + ( ) ( ) = ( 6), ha come quarta riga ( ) + ( 5) ( ) = ( 6), ed ha la prima e la seconda riga uguali rispettivamente alla prima e alla srconda riga di B Quindi 5 C = 6 6 Supponiamo che la matrice A da cui siamo partiti sia tale che, dopo aver effettuato sulle sue righe le operazioni descritte nel o passaggio, si ottenga una matrice C in cui se j > j + allora TUTTE le colonne comprese tra la j + -esima e la j -esima sono del tipo, ed inoltre o tutte le righe diverse dalle prime due sono nulle, oppure la terza riga è non nulla (per le matrici in cui questa situazione non si presenta, l eliminazione di Gauss senza scambi di righe fallisce) Se tutte le righe di C diverse dalle prime due sono nulle, l algoritmo si ferma a C (ossia C è la U cercata) Altrimenti la terza riga di C è non nulla e si procede 3, 4,, k-esimo Passaggio Si itera il procedimento illustrato nei primi due passaggi L obiettivo del passaggio i-esimo, se i k, è di trasformare la colonna j i -esima in una colonna del tipo, dove il numero sta nella riga i-esima Se la matrice A da cui parte è tale che dopo aver effettuato il passaggio i-esimo si ottiene che TUTTE le colonne comprese
36 36 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI tra la j i + -esima e la j i -esima (se ce ne sono ) sono del tipo, (dove il piú basso sta nella riga i -esima) ed inoltre o tutte le righe diverse dalle prime i sono nulle, oppure la i + -esima riga è non nulla (per le matrici in cui questa situazione non si presenta, l algoritmo di Gauss senza scambi di righe fallisce), allora l algoritmo si ferma (ottenendo U) quando si raggiunge una riga nulla, oppure, se non si raggiunge mai una riga nulla, quando si raggiunge l ultima riga Esempio 4 Riprendiamo la matrice C ottenuta alla fine dell Esempio 3, e mostriamo il procedimento per C Poichè la terza riga di C è non nulla, l algoritmo non si ferma a C Il primo elemento non nullo della terza riga di C è d 34, quindi j 3 = 4 Si chiama C la matrice che si ottiene da C moltiplicando la terza riga di C per c 34 = Dunque 5 C = 3 6 Per sistemare la j 3 -esima colonna di C, ossia per ottenere a partire da C una matrice con la terza colonna del tipo, basta sommare alla quarta riga di C la terza riga di C moltiplicata per Si ottiene 5 D = 3 Poichè la quarta riga di D è nulla, l algoritmo si ferma a D, ossia U = D Per riassumere il procedimento si scrive: A = E3( )E( )E( 3 ) E 4( 5)E 3( ) E43( )E3( ) = U 6 3 6
37 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 37 LEZIONE 6 Eliminazione di Gauss con scambi di righe Sia A O una matrice m n Abbiamo illustrato nella Lezione 5 un algoritmo che ha come obiettivo quello di costruire a partire da A una matrice U, m n, che abbia il seguente aspetto U =, eseguendo sulle righe di A un insieme di operazioni del tipo: sommare ad una riga un altra riga di A moltiplicata per uno scalare, moltiplicare una riga di A per uno scalare non nullo Def Una matrice che sia o nulla, oppure abbia l aspetto di U, si dice una matrice in forma ridotta di Gauss Abbiamo anche visto nell Esempio della lezione precedente che l eliminazione di Gauss senza scambi di righe fallisce per certe matrici Vediamolo con un altro esempio 4 3 Esempio Sia A = Volendo applicare l eliminazione di Gauss senza scambi di righe ad A, si ottiene che poichè il primo elemento non nullo nella prima riga di A è a 3, allora j = 3 Ma poichè non è vero che tutte le colonne prima della j -esima, ossia prima della terza, sono nulle (la seconda non lo è), allora l eliminazione di Gauss senza scambi di righe applicata ad A non porta ad una matrice in forma ridotta di Gauss Analogamente applicando l eliminazione di Gauss senza scambi di righe a B = 4 6 8, otteniamo 4 B = E3( )E( )E( ) In questo caso j = 4 Poichè nelle righe seguenti alla seconda ci sono elementi non nulli che stanno in colonne precedenti alla j -esima, allora anche in questo caso l eliminazione di Gauss senza scambi di righe applicata ad B non porta ad una matrice in forma ridotta di Gauss
38 38 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Introduciamo allora un altro algoritmo, che chiamiamo eliminazione di Gauss con scambi di righe (o piú semplicemente eliminazione di Gauss), che differisce da quello descritto nella Lezione 5 soltanto nel fatto che tutte le volte che è necessario si possa fare anche uno scambio di righe, ossia un algoritmo in cui è lecita anche la terza operazione elementare sulle righe della matrice In questo modo si puó arrivare ad una matrice in forma ridotta di Gauss a partire da qualunque matrice A O Def Una matrice in forma ridotta di Gauss che si ottenga a partire da una matrice A applicandovi l eliminazione di Gauss con o senza scambi di righe si dice una forma ridotta di Gauss per la matrice A Si dice poi che la matrice nulla m n è una forma ridotta di Gauss di sè stessa Esempio Sia A = 4 3 la prima matrice considerata nell Esempio L operazione da fare è scambiare la a con la a riga Poichè ció corrispone a premoltiplicare A per la matrice elementare E, si scrive: 4 3 E A = A = 4 3 quindi si procede con l algoritmo su A Quello che si ottiene è: 4 3 E A = 4 3 ( E ( 4 ) 4 3 ed U è una forma ridotta di Gauss per A E ( ) ) = U Sia B = la seconda matrice considerata nell Esempio Un eliminazione 4 di Gauss su B è: B = E3( )E( )E( ) E 3 3 E3( 5 ) 3 = Ũ 5 Sia C = In questo caso si puó scegliere: 4
39 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI 39 C = E E3( )E( 3 ) E3 4 4 E( ) oppure E3( ) = U ; 4 C = E E( 3)E( ) 3 4 E ( 3 ) E3( ) Entrambe U ed U sono forme ridotte di Gauss per C = U NB U ed U sono due matrici diverse, ma entrambe sono forme ridotte di Gauss per la stessa matrice C Quindi non c e in generale un unica forma ridotta di Gauss per una matrice Def 3 Sia U una matrice m n in forma ridotta di Gauss, e siano k le sue righe non nulle (quindi le prime k righe di U sono non nulle e le ultime m k righe di U sono non nulle) Allora U ha esattamente k colonne che corrispondono all inizio di ogni gradino: la j -esima, che è la prima colonna di I m, la j -esima, che è del tipo ( ) T, la j 3 -esima, che è del tipo ( ) T, la j 4 -esima, che è del tipo ( ) T, inoltre la j k -esima, che è un vettore riga con m componenti del tipo ( ) T k tutte le eventuali colonne comprese tra la j + -esima e la j -esima sono del tipo ( ) T,
40 4 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI tutte le eventuali colonne comprese tra la j + -esima e la j 3 -esima sono del tipo ( ) T, tutte le eventuali colonne comprese tra la j 3 + -esima e la j 4 -esima sono del tipo ( ) T, tutte le eventuali colonne comprese tra la j k + -esima e la j k -esima sono del tipo ( ) T (il numero di è k ) Le colonne j -esima, j -esima, j 3 -esima,, j k -esima si chiamano le colonne dominanti della matrice in forma ridotta di Gauss U Le altre colonne di U si chiamano le colonne libere della matrice in forma ridotta di Gauss U Esempio 3 Siano A, B e C le matrici considerate nell Esempio e siano U ed Ũ le forme ridotte di Gauss trovate per A e B rispettivamente, ed inoltre U ed U le due forme ridotte di Gauss trovate per C colonne dominanti di U: la a e la 3 a ; colonne libere di U: la a e la 4 a ; colonne dominanti di Ũ: la a, la 3 a e la 4 a ; unica colonna libera di Ũ: la a ; U ed U hanno tutte le colonne dominanti e nessuna colonna libera Def 4 Una matrice U, m n si dice in forma ridotta di Gauss-Jordan se U è in forma ridotta di Gauss e, se u, u, u k sono le colonne dominanti di U allora u = e, u = e, u k = e k, dove e, e,, e k sono le prime k colonne di I m Come ottenere una forma ridotta di Gauss-Jordan di una matrice Esempio 4 Si trovi una forma ridotta di Gauss-Jordan per B = Troviamo una forma ridotta di Gauss per B, ad esempio, come abbiamo già calcolato nell Esempio, Ũ = 3 Partendo da Ũ procediamo a ritroso nel seguente modo: 3 E3( 3)E3( ) E( ) = V V è una forma ridotta di Gauss-Jordan per B
1 se k = r i. 0 altrimenti. = E ij (c)
 Facoltà di Scienze Statistiche, Algebra Lineare A, G.Parmeggiani LEZIONE 5 Matrici elementari e loro inverse Si fissi m un numero naturale. Per ogni i, j m con i j siano E ij (c) (ove c è uno scalare )
Facoltà di Scienze Statistiche, Algebra Lineare A, G.Parmeggiani LEZIONE 5 Matrici elementari e loro inverse Si fissi m un numero naturale. Per ogni i, j m con i j siano E ij (c) (ove c è uno scalare )
ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, A.A. 2002/03, GEMMA PARMEGGIANI
 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Belzoni, 7 353 Padova Typeset by AMS-TEX ALGEBRA
ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Belzoni, 7 353 Padova Typeset by AMS-TEX ALGEBRA
Def. 1. Si chiamano operazioni elementari sulle righe di A le tre seguenti operazioni:
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 5 Operazioni elementari sulle righe di una matrice Sia A una matrice m n. Def. 1. Si chiamano operazioni elementari sulle righe
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 5 Operazioni elementari sulle righe di una matrice Sia A una matrice m n. Def. 1. Si chiamano operazioni elementari sulle righe
ha come obiettivo quello di costruire a partire da A una matrice U, m n, che abbia il
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 6 Eliminazione di Gauss con scambi di righe Sia A O una matrice m n. Abbiamo illustrato nella Lezione 5 un algoritmo che ha come
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 6 Eliminazione di Gauss con scambi di righe Sia A O una matrice m n. Abbiamo illustrato nella Lezione 5 un algoritmo che ha come
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G. Parmeggiani - Programma
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G. Parmeggiani - Programma Il testo di riferimento è: Appunti di Algebra Lineare, Gregorio, Parmeggiani, Salce 06/12/04 Matrici. Esempi. Tipi particolari
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G. Parmeggiani - Programma Il testo di riferimento è: Appunti di Algebra Lineare, Gregorio, Parmeggiani, Salce 06/12/04 Matrici. Esempi. Tipi particolari
Def. 2. Si dice che una matrice A, m n, ha un inversa sinistra se esiste una matrice L,
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 8 Inverse destre, sinistre e bilatere Def. 1. Si dice che una matrice A, m n, ha un inversa destra se esiste una matrice R, n
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 8 Inverse destre, sinistre e bilatere Def. 1. Si dice che una matrice A, m n, ha un inversa destra se esiste una matrice R, n
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
3x 2 = 6. 3x 2 x 3 = 6
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
Matrici e sistemi. Geometria. Matrici e operazioni tra matrici. Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante
 Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
Fattorizzazione QR e matrici di Householder
 Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
LeLing9: Prodotto tra matrici.
 Geometria Lingotto LeLing9: Prodotto tra matrici Ārgomenti svolti: Prodotto tra matrici Dimostrazione del teorema del rango L algebra delle matrici quadrate: Il prodotto tra matrici non e commutativo Rotazioni
Geometria Lingotto LeLing9: Prodotto tra matrici Ārgomenti svolti: Prodotto tra matrici Dimostrazione del teorema del rango L algebra delle matrici quadrate: Il prodotto tra matrici non e commutativo Rotazioni
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
MATRICI E OPERAZIONI
 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Elementi di Algebra Matriciale. (richiami)
 Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Anno Accademico 2015/2016
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI
 DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
Operazioni tra matrici. Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia c = 3
 Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
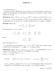 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
Corso di Matematica per la Chimica. Dott.ssa Maria Carmela De Bonis a.a
 Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Spazio dei vettori Il primo oggetto matematico che definiamo sarà il vettore. Partendo dai numeri reali come rappresentazione dei punti della retta reale R,
Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Spazio dei vettori Il primo oggetto matematico che definiamo sarà il vettore. Partendo dai numeri reali come rappresentazione dei punti della retta reale R,
Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, Padova
 ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, A.A. 8/9, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso. Nota
ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, A.A. 8/9, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso. Nota
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Piccola rassegna di Algebra delle Matrici
 Piccola rassegna di Algebra delle Matrici 1 Introduzione Questa nota va intesa semplicemente come un brevissimo sommario di alcuni concetti relativi alle Matrici, che dovete utilizzare nell ambito dello
Piccola rassegna di Algebra delle Matrici 1 Introduzione Questa nota va intesa semplicemente come un brevissimo sommario di alcuni concetti relativi alle Matrici, che dovete utilizzare nell ambito dello
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, SGI, A.A. 2010/2011, GEMMA PARMEGGIANI
 ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, SGI, A.A. /, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso.
ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, SGI, A.A. /, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso.
a.a MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI
 aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
LEZIONE 1 C =
 LEZIONE 1 11 Matrici a coefficienti in R Definizione 111 Siano m, n Z positivi Una matrice m n a coefficienti in R è un insieme di mn numeri reali disposti su m righe ed n colonne circondata da parentesi
LEZIONE 1 11 Matrici a coefficienti in R Definizione 111 Siano m, n Z positivi Una matrice m n a coefficienti in R è un insieme di mn numeri reali disposti su m righe ed n colonne circondata da parentesi
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
MATRICI e DETERMINANTI. Prof.ssa Maddalena Dominijanni
 MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
Matrici. Prof. Walter Pugliese
 Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Introduzione all algebra delle matrici. Appunti a cura di Lara Ercoli
 Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
= elemento che compare nella seconda riga e quinta colonna = -4 In generale una matrice A di m righe e n colonne si denota con
 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
, è Det(A) = a 11 a 22 a 12 a 21. ( il determinante della matrice che si ottiene da A. la 1 a riga e la 2 a colonna di A
 G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2015 Rossi Algebra Lineare 2015 1 / 41 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2015 Rossi Algebra Lineare 2015 1 / 41 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Matematica II
 Matematica II 241110 Matrice inversa 1 Per n 1, l insieme R n n delle matrici quadrate di ordine n diventa l insieme R dei numeri reali, e la moltiplicazione di matrici diventa la moltiplicazione di numeri
Matematica II 241110 Matrice inversa 1 Per n 1, l insieme R n n delle matrici quadrate di ordine n diventa l insieme R dei numeri reali, e la moltiplicazione di matrici diventa la moltiplicazione di numeri
Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza.
 Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5. Indice. 2. Esercizi 5
 ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
Le matrici. Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1.
 Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Lezione 4 - Esercitazioni di Algebra e Geometria - Anno accademico
 Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Lezioni di Algebra Lineare. II. Aritmetica delle matrici e eliminazione di Gauss. versione ottobre 2008
 versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
Definizione 1. Una matrice n m a coefficienti in K é una tabella del tipo. ... K m, detto vettore riga i-esimo, ed a im
 APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. 2011/2012
 6// G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. / Algebra Lineare A, Svolgimento degli Esercizi per casa 7 Sia V = a+bx+cx a,b,c C} lo spazio dei polinomi a coefficienti complessi
6// G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. / Algebra Lineare A, Svolgimento degli Esercizi per casa 7 Sia V = a+bx+cx a,b,c C} lo spazio dei polinomi a coefficienti complessi
Richiami di Algebra Lineare
 Appendice A Richiami di Algebra Lineare In questo capitolo sono presentati alcuni concetti di algebra lineare L algebra lineare è quella branca della matematica che si occupa dello studio di vettori, spazi
Appendice A Richiami di Algebra Lineare In questo capitolo sono presentati alcuni concetti di algebra lineare L algebra lineare è quella branca della matematica che si occupa dello studio di vettori, spazi
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
ossia può anche essere localizzato univocamente sul piano complesso con la sua forma polare.
 ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
G. Parmeggiani, 17/5/2018 Algebra Lineare, a.a. 2017/2018, numero di MATRICOLA PARI
 G Parmeggiani, 17/5/2018 Algebra Lineare, aa 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA
G Parmeggiani, 17/5/2018 Algebra Lineare, aa 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni 2. MATRICI
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 2 MATRICI Siano m, n N \ {0}, sia K un campo Una matrice m n a coefficienti in K è una
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 2 MATRICI Siano m, n N \ {0}, sia K un campo Una matrice m n a coefficienti in K è una
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Richiami di Algebra Lineare
 Università di Pavia Richiami di Algebra Lineare Eduardo Rossi Vettori a : (n 1) b : (n 1) Prodotto interno a b = a 1 b 1 + a 2 b 2 +... + a n b n Modulo (lunghezza): a = a 2 1 +... + a2 n Vettori ortogonali:
Università di Pavia Richiami di Algebra Lineare Eduardo Rossi Vettori a : (n 1) b : (n 1) Prodotto interno a b = a 1 b 1 + a 2 b 2 +... + a n b n Modulo (lunghezza): a = a 2 1 +... + a2 n Vettori ortogonali:
0. Introduzione al linguaggio matematico
 Prof. Lidia Angeleri Università di Verona, 2009/2010 Algebra Lineare ed Elementi di Geometria Programma svolto nel Modulo Algebra Lineare 0. Introduzione al linguaggio matematico 1. Insiemi 1.1 Esempi
Prof. Lidia Angeleri Università di Verona, 2009/2010 Algebra Lineare ed Elementi di Geometria Programma svolto nel Modulo Algebra Lineare 0. Introduzione al linguaggio matematico 1. Insiemi 1.1 Esempi
G. Parmeggiani, 28/4/2016 Algebra Lineare, a.a. 2015/2016, numero di MATRICOLA PARI. Svolgimento degli Esercizi per casa 7
 G. Parmeggiani, 8/4/6 Algebra Lineare, a.a. 5/6, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA PARI
G. Parmeggiani, 8/4/6 Algebra Lineare, a.a. 5/6, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA PARI
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
3 Soluzione di sistemi lineari
 3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
Elementi di Algebra Lineare
 Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
2 Sistemi lineari. Metodo di riduzione a scala.
 Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Spazi vettoriali euclidei.
 Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
PROGRAMMA DEL CORSO DI GEOMETRIA E ALGEBRA. A.A
 PROGRAMMA DEL CORSO DI GEOMETRIA E ALGEBRA. A.A. 2011-12 DOCENTE TITOLARE: FRANCESCO BONSANTE 1. Geometria analitica dello spazio (1) vettori applicati e lo spazio E 3 O: operazioni su vettori e proprietà.
PROGRAMMA DEL CORSO DI GEOMETRIA E ALGEBRA. A.A. 2011-12 DOCENTE TITOLARE: FRANCESCO BONSANTE 1. Geometria analitica dello spazio (1) vettori applicati e lo spazio E 3 O: operazioni su vettori e proprietà.
TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI
 TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI 2 Direttore Beatrice VENTURI Università degli Studi di Cagliari Comitato scientifico Umberto NERI University of
TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI 2 Direttore Beatrice VENTURI Università degli Studi di Cagliari Comitato scientifico Umberto NERI University of
G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. 2012/2013., w 3 = α se e solo se.
 7// G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. /3 Algebra Lineare A, Svolgimento degli Esercizi per casa 6 Si dica quale dei seguenti sottoinsiemi di R 3 è linearmente indipendente:
7// G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. /3 Algebra Lineare A, Svolgimento degli Esercizi per casa 6 Si dica quale dei seguenti sottoinsiemi di R 3 è linearmente indipendente:
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
Parte 8. Prodotto scalare, teorema spettrale
 Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
La forma normale di Schur
 La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
G. Parmeggiani, 29/3/2018 Algebra Lineare, a.a. 2017/2018, numero di MATRICOLA PARI. Svolgimento degli Esercizi per casa 4
 G. Parmeggiani, 29/3/2018 Algebra Lineare, a.a. 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MARICOLA
G. Parmeggiani, 29/3/2018 Algebra Lineare, a.a. 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MARICOLA
Matrici e Sistemi di Equazioni Lineari
 CAPITOLO 1 Matrici e Sistemi di Equazioni Lineari Il primo obiettivo di questo Capitolo è quello di introdurre le matrici a coefficienti complessi e le loro principali operazioni: la somma di due matrici,
CAPITOLO 1 Matrici e Sistemi di Equazioni Lineari Il primo obiettivo di questo Capitolo è quello di introdurre le matrici a coefficienti complessi e le loro principali operazioni: la somma di due matrici,
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010
 Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010 In quetsa dispensa: V è uno spazio vettoriale di dimensione d sul campo complesso C generato dai vettori v 1,..., v d. Le variabili m,
Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010 In quetsa dispensa: V è uno spazio vettoriale di dimensione d sul campo complesso C generato dai vettori v 1,..., v d. Le variabili m,
Matematica II
 Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
A.A. 2014/2015 Corso di Algebra Lineare
 A.A. 2014/2015 Corso di Algebra Lineare Stampato integrale delle lezioni Massimo Gobbino Indice Lezione 01: Vettori geometrici nel piano cartesiano. Operazioni tra vettori: somma, prodotto per un numero,
A.A. 2014/2015 Corso di Algebra Lineare Stampato integrale delle lezioni Massimo Gobbino Indice Lezione 01: Vettori geometrici nel piano cartesiano. Operazioni tra vettori: somma, prodotto per un numero,
