ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, A.A. 2002/03, GEMMA PARMEGGIANI
|
|
|
- Riccardo Franco
- 5 anni fa
- Visualizzazioni
Transcript
1 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Belzoni, Padova Typeset by AMS-TEX
2 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI LEZIONE Matrici ed esempi Def Una matrice m n ad elementi reali (risp ad elementi complessi è una tabella di numeri reali (risp complessi disposti in m righe ed n colonne Una matrice ad elementi reali (risp complessi è detta anche una matrice reale (risp complessa Le matrici vengono indicate con lettere maiuscole Esempio Siano A = ( 5 3, B = 4 i 7 + i 3, C = 3 π 9 6 4, 5 D = ( 8 i ed E = 3 A è una matrice 3 ad elementi reali (oppure: A è una matrice 5 3 reale, B è una matrice 3 complessa, C è una matrice 3 3 reale, D è una matrice complessa ed E è una matrice 3 reale NB Si puó scrivere indifferentemente A = oppure A = La a riga di A è ( 5 3, la a riga di A è ( 4 ( 5 3 a colonna di A è, la 3 a colonna di A è ( 5 3, oppure A = 4, la a colonna di A è [ ] 5 3, 4 ( 4, la Def Data una matrice m n reale (risp complessa A, il numero che si trova nella i-esima riga e nella j-esima colonna di A, dove i m e j n, si dice l elemento di posto (i, j di A Esso viene di solito indicato con il simbolo a ij Si scrive allora: a a a n a n a a a n a n A = a m a m a m n a m n a m a m a mn a mn, oppure, in forma compatta, A = [a ij ] i=,,m;j=,,n (anche: A = [a ij ], m n Quindi se A e B sono le matrici dell Esempio, a =, a = 5, ecc, b =, b 3 = 3, ecc
3 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 3 Def 3 Due matrici A = [a ij ], m n, e B = [b ij ], r t, sono uguali se m = r n = t a ij = b ij per ogni i m, j n ossia se hanno uguale numero di righe, uguale numero di colonne, e gli elementi corrispondenti uguali Def 4 Si chiama matrice nulla m n la matrice m n ogni cui elemento è Il simbolo usato per indicarla è O m n (oppure O quando dal contesto si puó dedurre quante righe e quante colonne ha Def 5 Una matrice con una sola riga ed n colonne si dice vettore riga con n componenti Ad esempio la matrice D dell Esempio è un vettore riga con componenti Def 6 Una matrice con una sola colonna ed m righe si dice vettore colonna con m componenti Ad esempio la matrice E dell Esempio è un vettore colonna con 3 componenti NB Per indicare i vettori colonna si preferiscono usare lettere in carattere corsivo minuscolo con un segno sotto: e piuttosto che E Def 7 Una matrice in cui il numero delle righe è uguale al numero delle colonne si dice quadrata Se A è una matrice quadrata, il numero delle righe di A (che è uguale al numero delle colonne di A si chiama l ordine di A Ad esempio la matrice C dell Esempio è una matrice quadrata di ordine 3 Notazioni L insieme delle matrici reali m n si indica con il simbolo M mn (R, l insieme delle matrici complesse m n si indica con il simbolo M mn (C NB Si usano il simbolo R n (risp C n al posto del simbolo M n (R (risp M n (C, il simbolo R m (risp C m al posto del simbolo M m (R (risp M m (C, il simbolo M m (R (risp M m (C al posto del simbolo M mm (R (risp M mm (C Quindi se A, B, C, D ed E sono le matrici dell Esempio, allora A M 3 (R, B M 3 (C, C M 3 (R, D C ed E R 3 Def 8 Sia A = [a ij ] una matrice m n Gli elementi a ii si chiamano elementi diagonali di A Ad esempio, se A, B e C sono le matrici dell Esempio, gli elementi diagonali di A sono e, gli elementi diagonali di B sono e, gli elementi diagonali di C sono 3, 6 e 5
4 4 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Def 9 Una matrice quadrata A = [a ij ] si dice diagonale se a ij = per ogni (i, j con i j (ossia se gli elementi di A che non sono diagonali sono tutti nulli 7 Esempio A =, B = 3, C = 3 sono matrici diagonali, i 3 7 mentre D = ed E = non sono matrici diagonali i Def Una matrice diagonale si dice scalare se i suoi elementi diagonali sono tra loro uguali 7 Esempio 3 A = è una matrice scalare, mentre B = C = e D = non sono matrici scalari 7 7, 7 Def Si chiama matrice identica di ordine m la matrice scalare m m i cui elementi diagonali sono tutti uguali ad Il simbolo usato per indicarla è I m (oppure I quando dal contesto si puó dedurre il suo numero di righe e di colonne La sua colonna i-esima, quando i m, è indicata con il simbolo e i Dunque e i è il vettore colonna con m componenti: e i = i Prodotto di una matrice per uno scalare Def Siano A = [a ij ] una matrice complessa (risp reale m n ed α un numero complesso (risp reale α viene chiamato scalare Sia B = [b ij ] la matrice m n definita da b ij = αa ij per ogni i =,, m; j =,, n,
5 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 5 ossia la matrice che si ottiene da A moltiplicando ciascun elemento di A per lo scalare α Allora B si chiama il prodotto della matrice A per lo scalare α B viene indicata con il simbolo αa Esempio 4 Se B la matrice considerata nell Esempio, allora ( + ib = ( + i 7 + i ( + i ( + i(7 + i i = ( + i( i ( + i = 3 ( + i ( + i3 + i 7 + 7i + i + i 6 + 8i = i + i = + i 3 + 3i 3 + 3i Si definisce così su M mn (C (risp su M mn (R un operazione di moltiplicazione di matrici per scalari C M mn (C M mn (C (risp (α, A αa R M mn (R M mn (R Proprietà della moltiplicazione di matrici per scalari ( α(βa = (αβa per ogni scalare α e β ed ogni matrice A, ( A = A per ogni matrice A Dimostrazione Sia A = [a ij ] una matrice m n Si ponga B := βa e si indichi con b ij l elemento di posto (i, j di B (per cui B = [b ij ] Si ponga C := αb e si indichi con c ij l elemento di posto (i, j di C (per cui C = [c ij ] Si ponga infine D := (αβa e si indichi con d ij l elemento di posto (i, j di D (per cui D = [d ij ] Si noti che B e D sono m n essendolo A, e che C è m n essendolo B Per ogni i m e j n si ha c ij = αb ij = α(βa ij = (αβa ij = d ij quindi C = D ossia αb = D Poichè B = βa e D = (αβa si ottiene ( Per provare ( si ponga E = A e si indichi con e ij l elemento di posto (i, j di E (per cui E = [e ij ] E è m n essendolo A Per ogni i m e j n si ha e ij = a ij = a ij, quindi E = A, ossia A = A
6 6 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI LEZIONE Somma di due matrici m n Def Siano A = [a ij ] e B = [b ij ] due matrici (reali o complesse ENTRAMBE m n Sia C = [c ij ] la matrice m n definita da c ij = a ij + b ij per ogni i =,, m; j =,, n, (ossia la matrice i cui elementi si ottengono sommando gli elementi corrispondenti di A e B La matrice C si chiama la somma delle matrici A e B Per indicare C si usa il simbolo A + B Esempio Siano A = A + B = i e B = i i + 3 = i 3 Allora + i 3 + i 4 3 NB NON ESISTE la somma di due matrici che non abbiano lo stesso numero di righe oppure che non abbiano lo stesso numero di colonne Si definisce così su M mn (C (risp su M mn (R un operazione di addizione di matrici M mn (C M mn (C M mn (C (risp M mn (R M mn (R M mn (R (A, B A + B Proprietà dell addizione di matrici Per ogni A, B, C M mn (C (risp M mn (R ed ogni α, β C (risp R si ha: ( associatività: A + (B + C = (A + B + C; ( commutatività: A + B = B + A; (3 elemento neutro: A + O = A(= O + A; (4 matrice opposta: se si indica con A la matrice ( A, si ha A + ( A = O (la matrice A si chiama l opposta della matrice A; (5 α(a + B = αa + αb; (6 (α + βa = αa + βa Le proprietà (5 e (6 sono proprietà ditributive che collegano l addizione di matrici con la moltiplicazione per scalari Dimostrazione Siano A = [a ij ], B = [b ij ] e C = [c ij ] Per ogni i m e j n si ha:
7 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 7 ( : a ij + (b ij + c ij = (a ij + b ij + c ij ; ( : a ij + b ij = b ij + a ij ; (3 : a ij + = a ij = + a ij ; (4 : a ij + ( a ij = a ij a ij = ; (5 : α(a ij + b ij = αa ij + αb ij ; (6 : (α + βa ij = αa ij + βa ij Notazione Per indicare la somma di A con l opposta di B si scrive A B, al posto di A + ( B Def Siano A = ( a a a n e B = b b un vettore riga ed un vettore colonna con lo stesso numero di componenti, n Si chiama prodotto del vettore riga con n componenti A ed il vettore colonna con n componenti B il numero b b ( a a a n b n b n = a b + a b + + a n b n = i n a i b i NB Quando si vuole metter in evidenza che i numeri sono matrici, si scrive [a b + a b + + a n b n ] al posto di a b + a b + + a n b n Nel caso di vettori riga si preferisce scrivere ( a a a n piuttosto che ( a a a n, ed analogamente per i vettori colonna Esempio ( 3 i i = 3 ( + i i + 6 = 6 + = 4 6 Def 3 Siano A = [a ij ] una matrice m n e B = [b ij ] una matrice n r Il prodotto delle due matrici, A e B, di cui la prima, A, ha un numero di colonne uguale al numero delle righe della seconda, B, è la matrice C = [c ij ], m r, ove c ij = ( a i a i a in b j b j b nj = a ib j + a i b j + + a in b nj = k n a ik b kj, ossia la matrice m r il cui elemento di posto (i, j è il prodotto della i-esima riga di A e la j-esima colonna di B Per indicare C si usa il simbolo AB Typeset by AMS-TEX
8 8 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Esempio 3 Siano A = 3 4 ove c = 3 c = 3 c 3 = 3 c 4 = 3 c = 6 c = e B = 3 4 = + ( + 3 = + =, = 3 + ( + 3 = = 7, = = = 4, = ( = =, = 6 + ( + = = 6, = ( + = = 9, Allora AB = C = [c ij ] è la matrice c 3 = 6 4 c 4 = 6 = = + + =, ossia C = = ( = + =, NB Il prodotto AB di due matrici A e B ESISTE SOLO SE IL NUMERO DELLE COLONNE DI A E UGUALE AL NUMERO DELLE RIGHE DI B Si definisce così un operazione di moltiplicazione di matrici M mn (C M nr (C M mr (C (risp (A, B AB M mn (R M nr (R M mr (R Proprietà della moltiplicazione di matrici Typeset by AMS-TEX
9 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 9 ( associatività: A(BC = (ABC, se A, B e C sono matrici tali che tutte le moltiplicazioni scritte siano possibili; ( distributività rispetto alla somma: A(B + C = AB + AC, se A, B e C sono matrici tali che tutti i prodotti e tutte le somme scritte siano possibili, e (B + CA = BA + CA, se A, B e C sono matrici tali che tutti i prodotti e tutte le somme scritte siano possibili; (3 α(ab = (αab = A(αB, se A e B sono matrici tali che il prodotto AB esista ed α è uno scalare; k (4 I m A = A = AI n per ogni matrice A, m n; (5 O k m A = O k n e AO n k = O m k per ogni matrice A, m n, ed ogni numero naturale NB la moltiplicazione di matrici NON gode della proprietà commutativa: date due matrici A, m n, e B, r t, ( se esiste AB (ossia se r = n non è detto che esista BA (perchè BA esista occorre che m = t ( Se sia AB che BA esistono, ossia se A è m n, e B è n m, allora AB è m m e BA è n n Se m n, senz altro AB BA (3 Se anche A e B sono entrambe m m, per cui AB e BA entrambe esistono ed entrambe sono m m, non è egualmente detto che AB e BA siano uguali Ad esempio: ( 3 = = 9 ( 3 3 Per la moltiplicazione di matrici NON vale la legge di cancellazione per il prodotto: esistono matrici A e B, con A O B e AB = O Ad esempio: = Esercizio Per ogni a R sia S a = ai = ( S a A = AS a per ogni A M (R a Si provi: a ( Se B M (R è tale che BA = AB per ogni A M (R, allora B = S a per un opportuno a R Typeset by AMS-TEX
10 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Svolgimento ( Sia A M ( Allora S aa = (ai A = a(i A = aa = a(ai Poichè per la proprietà (3 della moltiplicazione di matrici si ha che a(ai a = A(aI, si conclude che S aa = AS a ( Sia B = a b M c d ( tale che ( BA = AB per ogni A M ( In particolare prendendo in ( come matrice A la matrice à =, si ottiene: a = c a b c d = a b = c d a b Se ne deduce che b = c =, ossia che la matrice B deve essere una matrice diagonale: B = a d Tenendo conto del fatto che B = a d e prendendo in ( come matrice A la matrice A = si ottiene: a a = d d a d = a = d a d a d Se ne deduce che d = a, e quindi che B = a a = S a Nell esercizio si è provato che le matrici reali che commutano con ogni matrice reale sono esattamente le matrici reali scalari di ordine Allo stesso modo si può vedere che le matrici complesse che commutano con ogni matrice complessa sono esattamente le matrici complesse scalari di ordine In generale è possibile provare: le matrici reali (risp complesse m m che commutano con ogni matrice reale (risp complessa m m sono esattamente le matrici reali (risp complesse scalari di ordine m Def 4 Sia A una matrice quadrata Si definisce la potenza n-esima di A, dove n è un numero naturale, nel seguente modo: A = I, A = A, A = AA, A 3 = AA, A n = AA n Typeset by AMS-TEX
11 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Come per le potenze dei numeri, si ha la seguente proprietà delle potenze: per ogni coppia di numeri naturali m ed n ed ogni matrice quadrata A si ha A m A n = A m+n = A n A m Def 5 Una matrice A si dice non singolare (o anche invertibile, se esiste una matrice B tale che AB = I = BA Vedremo che se una tale B esiste, allora è unica Essa si chiama l inversa di A e si indica con il simbolo A Osservazione Se A è non singolare allora sia A che A sono quadrate Proposizione Se A e B sono due matrici non singolari tali che esista AB, allora anche il prodotto AB è una matrice non singolare e (AB = B A In generale se A, A,, A r, A r sono matrici non singolari tali che esista il prodotto A A A r A r, allora anche il prodotto A A A r A r è non singolare e si ha (A A A r A r = A r A r A A Dimostrazione Facciamo la dimostrazione supponendo che il prodotto abbia solo due fattori Osserviamo innanzitutto che se A e B sono matrici non singolari tali che esista AB, allora A, B, A e B sono tutte matrici m m per un opportuno m Si ha poi: (ABB A = A(BB A = AIA = AA = I, (B A (AB = B (A AB = B IB = B B = I La dimostrazione del risultato quando il numero dei fattori nel prodotto è r è analoga
12 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI LEZIONE 3 Trasposte, coniugate, H-trasposte Def Data una matrice A = [a ij ], m n, si chiama trasposta di A la matrice n m B = [b ij ] definita da: b ij = a ji per ogni i m, j n La matrice B si indica con il simbolo A T 4i 3 Esempio Se A =, allora la trasposta di A è A 5i T = 4i 3 5i Def Data una matrice A = [a ij ], m n, si chiama coniugata di A la matrice m n B = [b ij ] definita da: b ij = a ij per ogni i m, j n, ove se z = a + ib è un numero complesso espresso in forma algebrica (cioè a e b sono numeri reali, z = a ib è il suo coniugato La matrice B si indica con il simbolo A Esempio Se A = A = 4i 3, allora la coniugata di A è 5i 4i 3 = 5i 4i 3 + 5i Def 3 Data una matrice A = [a ij ], m n, si chiama H-trasposta di A la matrice n m B = [b ij ] definita da: b ij = a ji per ogni i m, j n La matrice B si indica con il simbolo A H Si noti che per ottenere la H-trasposta di A si può procedere indifferentemente in uno dei due seguenti modi: o si calcola prima la trasposta di A e di quest ultima si calcola poi la coniugata (ossia A H = A T, oppure si calcola prima la coniugata di A e di quest ultima si calcola poi la trasposta (ossia A H = (A T Esempio 3 Se A = 4i 3, allora la H-trasposta di A è 5i A H = A T = 4i 3 5i = 4i 3 + 5i,
13 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 3 ma anche A H = (A T = T 4i 3 = 5i T 4i 3 = + 5i 4i 3 + 5i Proprietà delle coniugate: Siano A e B matrici per cui siano possibili le operazioni indicate, e sia α uno scalare Allora si ha: ( A = A; ( (A + B = A + B, e (A B = A B; (3 αa = αa; (4 AB = AB Le proprietà delle coniugate seguono dalla definizione di coniugata di una matrice, e dalle definizioni di prodotto di una matrice per uno scalare e di prodotto di due matrici Proprietà delle trasposte e delle H-trasposte: Siano A e B matrici per cui siano possibili le operazioni indicate, e sia α uno scalare Allora si ha: ( : (A T T = A; (A H H = A; ( : (A + B T = A T + B T ; (A + B H = A H + B H ; (A B T = A T B T ; (A B H = A H B H ; (3 : (αa T = αa T ; (αa H = αa H ; (4 : (AB T = B T A T ; (AB H = B H A H Typeset by AMS-TEX
14 4 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Dimostrazione Per provare (,( e (3 basta applicare le definizioni di trasposta, di H-trasposta, di somma di matrici e di prodotto di matrici per scalari Per provare la prima uguaglianza di (4, supponiamo che A = [a ij ] sia m n e B = [b ij ] sia n r, e poniamo AB = C = [c ij ] e B T A T = D = [d ij ] Poichè B T è r n ed A T è n m, allora D è r m, come C T L elemento di posto (i, j di D è il prodotto della i-esima riga di B T per la j-esima colonna di A T Poichè la i-esima riga di B T è la i-esima colonna di B pensata come vettore riga, e la j-esima colonna di A T è la j-esima riga di A pensata come vettore colonna, allora d ij = b i b i b ni = b li a jl = a jl b li = a j a j a l n l n jn Dalla definizione di trasposta (di C si ottiene la prima uguaglianza di (4 b i b i b ni = c ji a j a j a jn Per la seconda, si noti che la definizione di H-trasposta, la proprietà (4 delle coniugate e la proprietà (AB T = B T A T che abbiamo già dimostrato implicano: = (AB H = (AB T = (A B T = B T A T = B H A H Definizioni 4,5,6,7 Una matrice A si dice: simmetrica se coincide con la sua trasposta (ossia se A = A T ; hermitiana se coincide con la sua H-trasposta (ossia se A = A H ; anti-simmetrica se coincide con l opposta della sua trasposta (ossia se A = A T, oppure, ed è lo stesso, se A T = A; anti-hermitiana se coincide con l opposta della sua H-trasposta (ossia se A = A H, oppure, ed è lo stesso, se A H = A Si noti che se A è simmetrica, o hermitiana, o anti-simmetrica, o infine anti-hermitiana, allora A è quadrata Typeset by AMS-TEX
15 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 5 Esempio 4 Siano A = 3, B = 3 + i i, C =, D = + i + i Allora A è simmetrica, B è hermitiana, C è anti-simmetrica e D è anti-hermitiana Dalla proprietà (4 della trasposta e della H-trasposta segue che la somma di due matrici simmetriche è una matrice simmetrica; la somma di due matrici hermitiane è una matrice hermitiana; la somma di due matrici anti-simmetriche è una matrice anti-simmetrica; la somma di due matrici anti-hermitiane è una matrice anti-hermitiana Esempio 5 A = e B = sono simmetriche, ma AB = 3 3 non è simmetrica Dunque il prodotto di due matrici simmetriche puó essere una matrice non simmetrica Esempio 6 A = i e B = i i 3 3i sono hermitiane, ma AB = non è hermitiana Dunque il prodotto di due matrici hermitiane puó essere una matrice non i i hermitiana Esempio 7 A = è anti-simmetrica, ma A = AA = non è anti-simmetrica Dunque il prodotto di due matrici anti-simmetriche puó essere una matrice non anti-simmetrica Esempio 8 A = i i e B = i sono anti-hermitiane, ma AB = i non è anti-hermitiana Dunque il prodotto di due matrici anti-hermitiane puó essere una matrice non anti-hermitiana Esercizio: (Decomposizione di una matrice quadrata nella parte hermitiana ed antihermitiana Sia A una matrice quadrata m m Allora esistono B = (A + AH e C = (A AH Si provi che: B è hermitiana, C è antihermitiana, A = B + C, se D ed E sono due matrici tali che allora D = (A + AH ed E = (A AH D è hermitiana E è anti-hermitiana D + E = A Ossia: ogni matrice quadrata A si puó scrivere in un modo unico come somma di una matrice hermitiana, (A+AH, ed una matrice anti-hermitiana, (A-AH (A+AH si chiama la parte hermitiana di A e (A AH si chiama la parte anti-hermitiana di A
16 6 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Svolgimento Poichè A è m m, anche A H è m m, per cui esistono sia A+A H che A A H, entrambe m m, e dunque esistono anche B = (A + AH e C = (A AH Allora, poichè B e C sono entrambe m m, esiste B + C, ed è: B + C = (A + AH + (A AH = A + AH + A AH = A La matrice B è hermitiana: B H = ( (A + AH H = (A + AH H = (AH + (A H H = (AH + A = B La matrice C è anti-hermitiana: C H = ( (A AH H = (A AH H = (AH (A H H = (AH A = C Abbiamo quindi visto per ogni matrice quadrata A esistono una matrice hermitiana, (A+AH, ed una matrice antihermitiana (A AH tali che A sia la loro somma Vogliamo ora provare che se A è una matrice quadrata e D ed E sono matrici tali che allora D = (A + AH ed E = (A AH D è hermitiana E è anti-hermitiana D + E = A Poniamo B = (A + AH e C = (A AH Poichè abbiamo visto che A = B + C e stiamo supponendo che A = D + E, allora ( B + C = D + E Da (* segue che anche (B + C H = (D + E H Poichè abbiamo visto che B H = B e C H = C, allora (B + C H = B H + C H = B C Poichè stiamo supponendo che D H = D ed E H = E, allora Quindi da (B + C H = (D + E H segue (D + E H = D H + E H = D E ( B C = D E Sommando membro a membro (* e (** otteniamo B = D, da cui, moltiplicando entrambi i membri dell uguaglianza per, D = B = (A + AH Sottraendo membro a membro (* e (** otteniamo C = E, da cui, moltiplicando entrambi i membri dell uguaglianza per, E = C = (A AH Abbiamo quindi provato che data una matrice quadrata A, esistono un unica matrice hermitiana B ed un unica matrice anti-hermitiana C tali che A = B + C (inoltre B = (A + AH e C = (A AH Typeset by AMS-TEX
17 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 7 Esempio 9 Se A = + i 6i, allora A 4 H = A T = + i 4 = 6i i 4, per cui la parte 6i hermitiana di A è (A + AH = e la parte anti-hermitiana di A è (A AH = + i + i 6i i + = + i + i 6i i = + 3i 3i, i + 3i + 3i Quanto detto generalizza ció che già sappiamo per i numeri, ossia le matrici Sappiamo infatti che per ogni numero complesso z esistono e sono unici due numeri reali a e b tali che z = a + ib (tale espressione si chiama la forma algebrica di z Ogni numero reale a è una matrice hermitiana: a H = a T = a = a Ogni numero immaginario puro ib (ove b è un numero reale è una matrice anti-hermitiana: (ib H = (ib T = ib = i b = ( ib = (ib Quindi la forma algebrica di z, ossia l espressione z = a+ib con a e b numeri reali, è l espressione della matrice z come somma di una matrice hermitiana, a, ed una matrice anti-hermitiana, ib Un calcolo diretto mostra che a e b sono proprio la parte hermitiana e la parte anti-hermitiana di z: poichè z H = z T = z = a ib, allora (z + zh = (a + ib + a ib = a e (z zh = (a + ib a + ib = ib Typeset by AMS-TEX
18 8 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI LEZIONE 4 Matrici a blocchi Def Data una matrice A si chiama sottomatrice di A ogni matrice che si ottiene da A sopprimendo alcune righe ed alcune colonne di A Esempio Se A = 4i 3 9 5i , allora B = 5i 6 7, C = 4i e D = 4i sono tre sottomatrici di A: B si ottiene da A sopprimendo la a riga e la 4 a colonna, C si ottiene da A sopprimendo la a riga, la 3 a e la 5 a colonna, D si ottiene da sopprimendo solo la a colonna Ripartire una matrice A in blocchi significa tracciare delle linee orizzontali (lunghe tanto quanto lo è la matrice e delle righe verticali (alte tanto quanto lo è la matrice: i blocchi della ripartizione effettuata sono le sottomatrici di A che le linee tracciate delimitano 4i 3 9 Esempio Se A = 5i 4 è la matrice considerata nell Esempio, allora A = i 3 9 5i 4 è una ripartizione di A in blocchi I blocchi di questa ripartizione sono: A = 4i 3 5i, A =, A 3 = 9 4, A = 6 7, A =, A 3 = 8 Per indicare che A è stata ripartita nei blocchi A, A, A 3, A, A, ed A 3 si scrive A = A A A 3 A A A 3 Le notazioni scelte suggeriscono che quando si ripartisce una matrice A in blocchi, si puó pensare ad A come ad una matrice i cui elementi sono i blocchi della ripartizione effettuata Quando una matrice è ripartita in blocchi si dice che è una matrice a blocchi Typeset by AMS-TEX Typeset by AMS-TEX
19 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 9 Prodotto di una matrice a blocchi per uno scalare A A A r A Siano A = A A r una matrice a blocchi ed α uno scalare Allora A t A t A tr αa αa αa r αa αa = αa αa r αa t αa t αa tr Esempio 3 Se A = A A A 3 A A A 3 è la matrice a blocchi considerata nell Esempio, ed α = i, allora αa = ia = ia ia ia 3 ia ia ia 3 Poichè allora A = ia = 4 3i i 5, ia = i, ( ia 3 = 9i 4i i, ( ia = 6i 7i, ( ia = i, ( ia 3 = 8i, 4 3i i 9i i 5 4i i 6i 7i i 8i Somma di due matrici a blocchi Siano A = Se A A A n A m A m A mn e B = B B B s B r B r B rs m = r n = s esiste A ij + B ij per ogni i m, j n due matrici a blocchi (l ultima condizione è verificata se e solo se A ij ha lo stesso numero di righe e lo stesso numero di colonne di B ij, per ogni i m, j n, allora A + B = A + B A + B A n + B n A m + B m A m + B m A mn + B mn Typeset by AMS-TEX
20 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Esempio 4 Se A = A A e B = A A B B sono le matrici a blocchi con blocchi B B A = 3, A = B =, B = 4, A =, B = 3, B = e A =, allora A + B = A + B A + B A + B A + B = A A B B = Prodotto di due matrici a blocchi Siano A = A A A n A m A m A mn e B = Se r = n allora AB = C è la matrice a blocchi C = B B B s B r B r B rs C ij = A i B j + A i B j + + A in B nj = C C C s C m C m C ms k n A ik B kj, due matrici a blocchi con A CONDIZIONE CHE TUTTE LE OPERAZIONI SCRITTE SIANO DEFINITE Esempio 5 Se A è la matrice 4 a blocchi A = A A A A con A = I,A = I,A = 3I,A = 4I, e B è la matrice 4 a blocchi B = B B allora AB = A A A A B B B B = B B con B = B = B = B = = A B + A B A B + A B A B + A B A B + A B = I B + I B I B + I B 3I B + 4I B 3I B + 4I B = = 3B 3B 7B 7B = Typeset by AMS-TEX Typeset by AMS-TEX
21 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Applicazione del prodotto a blocchi al prodotto di due matrici ( Ripartizione della seconda matrice in colonne Siano A e B due matrici tali che esista il loro prodotto AB (quindi se A è una matrice m n allora B è una matrice n r Ripartiamo B in blocchi prendendo come blocchi le sue colonne: B = ( B B B r = ( b b b r dove B j = b j è la j-esima colonna di B per ogni j r Si puó allora calcolare il prodotto AB pensando A come ad un unico blocco, e si ottiene AB = A ( B B B r = A ( b b b r = ( Ab Ab Ab r Per ogni j r, Ab j è un vettore colonna con m componenti, ed è la j-esima colonna di AB A = ( Ripartizione della prima matrice in righe b b b r Ab Ab r Come in (, siano A e B due matrici tali che esista il loro prodotto AB (quindi se A è una matrice m n allora B è una matrice n r Ripartiamo A in blocchi prendendo come blocchi le sue righe: A = A A A m = r T r T dove A i = r T i è la i-esima riga di A per ogni i m Si noti che indicando con r T i un vettore riga con n componenti, ossia una matrice n, stiamo indicando con r i un vettore colonna con n componenti, ossia una matrice n Si puó allora calcolare il prodotto AB pensando B come ad un unico blocco, e si ottiene AB = A A A m B = r T r T r T m r T m B = r T B r T B r T mb
22 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Per ogni i m, r T i B è un vettore riga con r componenti, ed è la i-esima riga di AB r T r T r T m B = r T B r T B r T mb (3 Il prodotto di una matrice per un vettore colonna Siano A una matrice m n e v = v v v n un vettore colonna con n componenti Allora esiste Av e puó essere calcolato come prodotto a blocchi, pensando A ripartita nei suoi blocchi colonna A = ( a a a n e v ripartito nei suoi blocchi riga (quindi v ha n blocchi riga, ciascuno dei quali è una matrice, ossia un numero v j : Ab = ( a a a n v v v n = v a + v a + + v n a n v v v n = v + v + + v n a a a n a a a n NB In particolare Ae i = i-esima colonna di A (e i è la i-esima colonna di I n (4 Il prodotto di vettore riga per una matrice Siano B una matrice n r e w T = ( w w w n un vettore riga con n componenti Allora esiste w T B e puó essere calcolato come prodotto a blocchi, pensando B ripartita nei suoi s T s T blocchi riga B = s T n e wt ripartito nei suoi blocchi colonna (quindi w T ha n blocchi colonna,
23 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 3 ciascuno dei quali è una matrice, ossia un numero w j : s T s T w T B = ( w w w n s T n = w s T + w s T + + w n s T n [w w w n ] s T s T = w s T +w s T + +w n s T n s T n NB In particolare e T i B = i -esima riga di B (e i è la i-esima colonna di I n Siano A una matrice m n e B una matrice n r Da (3 si ricava che la j-esima colonna di AB è (ABe j = propr assoc A(Be j = 3 dove a, a, a n sono le colonne di A e b j = Ab j = 3 b j b j b nj b j a + b j a + + b nj a n è la j-esima colonna di B Da (4 si ricava che la i-esima riga di AB è e T i (AB = (e T i AB = propr assoc 4 r T i B = 4 a i s T + a i s T + + a in s T n dove s T, st, st n sono le righe di B e rt i = ( a i a i a in è la i-esima riga di A (5 Ripartizione della prima matrice in colonne e della seconda in righe Siano A e B due matrici tali che esista il loro prodotto AB (quindi se A è una matrice m n allora B è una matrice n r Ripartiamo A in blocchi prendendo come blocchi le sue colonne: A = ( a a a n,
24 4 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI e B prendendo come blocchi le sue righe: s T s T B = s T n Allora AB puó essere calcolato come prodotto a blocchi: s T s T AB = ( a a a n s T n = a s T + a s T + + a n s T n s T s T s T n = s T + s T + + s T n a a a n a a a n Si noti che ciascun addendo a i s T i è una matrice m r
25 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 5 ESERCIZIO TIPO Definizione Sia A una matrice quadrata Un numero λ si dice un autovalore di A se esiste un vettore v tale che Av = λv (NB v! In tal caso v si dice un autovettore di A relativo all autovalore λ a b T ESERCIZIO Siano A = una matrice complessa n n ripartita in D blocchi Si provi: a è un autovalore di A a C,, b C n (per cui b T C n, D M n (C Se A possiede un autovalore λ a e x v = Cn, ove x C e w C n, w è un autovettore di A relativo all autovalore λ, allora λ è anche un autovalore di D e w è un autovettore di D relativo a λ (dunque v è un vettore colonna con n componenti, ripartito in due blocchi, dei quali quello superiore è un numero, e quello inferiore è w Per provare che a è un autovalore di A dobbiamo trovare un vettore z tale che Az = az a Osserviamo che la prima colonna di A è il vettore, ossia, per definizione di prodotto per uno scalare, il vettore a = ae, ove e è la prima colonna della matrice identica I n Ricordiamo (il NB del punto (3 nella Lezione 4 che la i-esima colonna di A è Ae i, e quindi, in particolare, la prima colonna di A è Ae Dunque Ae = ae, e poichè e, si puó prendere z = e Poichè v è un autovettore di A relativo a λ allora v e Av = λv
26 6 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI Calcolando i prodotti Av e λv a blocchi si ottiene: a b T x ax + b T w ax + b T w Av = = =, D w x + Dw Dw x λx λv = λ = ; w λw per cui dall uguaglianza Av = λv ricaviamo (II comporta: (I ax + b T w = λx (II Dw = λw [ λ è un autovalore di D e ] w è un autovettore di D relativo a λ w Supponiamo per assurdo w = Allora b T w = b T = e da (I ricaviamo ax = λx = λx x x Inoltre w = implica v = = w Poichè v, allora x, per cui esiste x Moltiplicando ambo i membri dell uguaglianza ax = λx per x otteniamo a = λ, mentre per ipotesi λ a La contraddizione deriva dall aver supposto w = Dunque w, ossia λ è un autovalore di D e w è un autovettore di D relativo a λ
27 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 7 LEZIONE 5 Operazioni elementari sulle righe di una matrice Sia A una matrice m n Def Si chiamano operazioni elementari sulle righe di A le tre seguenti operazioni: sommare ad una riga un altra riga di A moltiplicata per uno scalare, moltiplicare una riga di A per uno scalare non nullo, scambiare due righe di A Notazioni Sia B la matrice che si ottiene da A sommando alla i-esima riga di A la j-esima riga di A moltiplicata per lo scalare c, ossia sia B = [b kr ] la matrice con tutte le righe diverse dalla i-esima uguali alle corrispondenti righe di A = [a kr ], e con i-esima riga il vettore riga ( b i b i b in = ( a i + ca j a i + ca j a in + ca jn Per indicare che B è la matrice ottenuta dalla matrice A eseguendo l operazione elementare sommare alla i-esima riga la j-esima riga moltiplicata per lo scalare c, scriviamo: A E ij (c B Sia B la matrice che si ottiene da A moltiplicando la i-esima riga di A per lo scalare c (c, ossia sia B = [b kr ] la matrice con tutte le righe diverse dalla i-esima uguali alle corrispondenti righe di A = [a kr ], ed con i-esima riga il vettore riga ( b i b i b in = ( ca i ca i ca in Per indicare che B è la matrice ottenuta dalla matrice A eseguendo l operazione elementare moltiplicare la i-esima riga per lo scalare (non nullo c, scriviamo: A E i(c B Sia B la matrice che si ottiene da A scambiando la i-esima riga di A con la j-esima, ossia sia B = [b kr ] la matrice con tutte le righe diverse dalla i-esima e dalla j-esima uguali alle corrispondenti righe di A, e con i-esima e j-esima riga rispettivamente: ( b i b i b in = ( a j a j a jn, ( b j b j b jn = ( a i a i a in Per indicare che B è la matrice ottenuta dalla matrice A eseguendo l operazione elementare scambiare la i-esima riga con la j-esima riga, scriviamo: A E ij B
28 8 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI NB I simboli E ij (c, E i (c e E ij rappresentano in realtà opportune matrici, dette matrici elementari Abbiamo scelto, con abuso di notazione, di indicare le operazioni elementari sulle righe di una matrice con gli stessi simboli con cui vengono indicate le matrici elementari poichè, come si vedrà in un corso superiore, vi è tra esse una stretta connessione Eliminazione di Gauss senza scambi di righe Sia A una matrice m n, con A O m n Illustriamo ora un algoritmo che consiste in un insieme di operazioni sulle righe di A e che viene chiamato un eliminazione di Gauss senza scambi di righe su A L obiettivo di tale algoritmo è costruire a partire da A una matrice m n U con le prime k-righe non nulle e le rimanenti m k righe nulle (dove k è un opportuno numero compreso tra ed m che dipende da A, gli elementi non nulli disposti come sopra ad una scala che scende da sinistra a destra, a partire dalla prima riga fino alla k-esima riga, ogni cui gradino è alto una riga ed è lungo una o piú colonne (la scala ha quindi k gradini, gli elementi alla base di ciascun gradino di questa scala uguali ad, ossia una matrice del tipo: dove gli elementi al di sotto della scalinata sono tutti nulli, e gli eventuali elementi non nulli si trovano al di sopra della scalinata (in questo disegno la scala ha 3 gradini Le operazioni lecite in questo algoritmo sono solo di due tipi: sommare ad una riga di A una riga di A che la precede moltiplicata per un scalare, moltiplicare una riga di A per uno scalare non nullo Esistono matrici per cui questo algoritmo fallisce, ossia per le quali questo algoritmo non porta alla costruzione di U Esempio Per A = l eliminazione di Gauss senza scambi di righe fallisce: non, è possibile, utilizzando le due operazioni lecite, arrivare ad una matrice del tipo U = oppure U =, oppure U = Per tali matrici introdurremo nella prossima lezione un algoritmo piú ricco (in cui è lecita anche la terza operazione elementare sulle righe di A
29 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 9 Applicazioni L algoritmo descritto in questa lezione e la sua generalizzazione esposta nella successiva, hanno diverse applicazioni In questo corso verranno utilizzati per la risoluzione di sistemi lineari, per il calcolo del rango di una matrice e di basi di spazi delle righe e delle colonne In un corso successivo, verranno utilizzati per il calcolo di decomposizioni A = P T LU, e per quello di decomposizioni a rango pieno Supponiamo che la prima riga di A non sia nulla (per le matrici non nulle con la prima riga nulla l eliminazione di Gauss senza scambi di righe fallisce o Passaggio L obiettivo del o passaggio è trasformare la j -esima colonna nella prima colonna di I m (il numero j è definito nel seguente punto ( ( Percorrendo la prima riga di A da sinistra a destra, sia a j il primo elemento non nullo (quindi se j > allora a = a = = a,j = e a j ; il piú delle volte, peró, j =, ossia a a j è detto il pivot della a riga Se a j, moltiplichiamo la prima riga di A per a j, ottenendo cosí una matrice m n A = [a ij ] che ha tutte le righe uguali a quelle di A, tranne la prima, i cui elementi sono gli elementi della prima riga di A moltiplicati per a j, ossia divisi per a j In particolare a = a = = a,j = e a j = Scriviamo: A E (a j A ( Percorriamo la colonna j -esima dall alto in basso, e tenendo in considerazione solo gli elementi a ij che siano diversi da, per ciascun a ij che troviamo, partendo da i = e arrivando fino a i = m, sommiamo alla riga i-esima di A la prima riga di A moltiplicata per a ij, (per ogni i =,, m tale che a ij Otteniamo cosí una matrice B = [b ij ] in cui la j -esima colonna è la prima colonna di I m Scriviamo: E m( a mj E m, ( a m,j E 3( a 3j E ( a j A B Esempio Sia A = Poichè a, allora j = L operazione richiesta al punto ( è moltiplicare la prima riga
30 3 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI di A per a = 3 La matrice A che si ottiene ha come prima riga ( = ( 5, e le altre righe uguali alle righe di B, quindi A = a a Consideriamo la prima (qui j = colonna di A, a = 3 a 4 Le operazioni richieste al punto ( sono: poiché a =, sommare alla seconda riga di A la prima riga di A moltiplicata per a =, poiché a 3 =, sommare alla terza riga di A la prima riga di A moltiplicata per a 3 = Non occorrono altre operazioni, poichè a 4 = La matrice B che si ottiene ha come seconda riga ha come terza riga ( ( ( 5 = (, ( ( ( 5 = ( 3 6, ed ha la prima e la quarta riga uguali rispettivamente alla prima e alla quarta riga di A Quindi 5 B = Supponiamo che la matrice A da cui siamo partiti sia tale che, dopo aver effettuato sulle sue righe le operazioni descritte nel o passaggio, si ottenga una matrice B in cui se j > allora le prime j colonne sono nulle, ed inoltre o tutte le righe diverse dalla prima sono nulle, oppure la seconda riga è non nulla (per le matrici in cui questa situazione non si presenta, l eliminazione di Gauss senza scambi di righe fallisce Se tutte le righe di B diverse dalla prima sono nulle, l algoritmo si ferma a B (ossia B è la U cercata Altrimenti la seconda riga di B è non nulla e si procede
31 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 3 o Passaggio L obiettivo del o passaggio è trasformare la j -esima colonna in una colonna del tipo (il numero j è definito nel seguente punto ( ( Percorrendo la seconda riga di B da sinistra a destra, sia b j il primo elemento non nullo (quindi b = b = = b,j = e b j b j è detto il pivot della a riga Se b j, moltiplichiamo la seconda riga di B per b j, ottenendo cosí una matrice m n B = [b ij] che ha tutte le righe uguali a quelle di B, tranne la seconda, i cui elementi sono gli elementi della seconda riga di B moltiplicati per b j, ossia divisi per b j In particolare b = b = = b,j = e b j = Scriviamo: B E (b j B ( Percorriamo la colonna j -esima dall alto in basso, e tenendo in considerazione solo gli elementi b ij che siano diversi da, per ciascun b ij che troviamo, partendo da i = 3 e arrivando fino a i = m, sommiamo alla riga i-esima di B la seconda riga di B moltiplicata per b ij, (per ogni i = 3,, m tale che b ij Otteniamo cosí una matrice C = [c ij ] in cui la j -esima colonna è del tipo:, come ci eravamo prefissati Scriviamo: E m( b mj E m, ( b m,j E 3( b 3j B C Esempio 3 Riprendiamo la matrice B ottenuta alla fine dell Esempio : 5 B = Poichè b, allora j =, ma poichè b = non è richiesta alcuna operazione al punto (, per cui B = B
32 3 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI b b Consideriamo la seconda (qui j = colonna di B, b = 3 b 4 5 Le operazioni richieste al punto ( sono: poiché b 3 =, sommare alla terza riga di B la seconda riga di B moltiplicata per b 3 =, poiché b 4 = 5, sommare alla quarta riga di B la seconda riga di B moltiplicata per b 4 = 5 La matrice C che si ottiene ha come terza riga ha come quarta riga ( ( ( = ( 6, ( ( 5 ( = ( 6, ed ha la prima e la seconda riga uguali rispettivamente alla prima e alla srconda riga di B Quindi 5 C = 6 6 Supponiamo che la matrice A da cui siamo partiti sia tale che, dopo aver effettuato sulle sue righe le operazioni descritte nel o passaggio, si ottenga una matrice C in cui se j > j + allora TUTTE le colonne comprese tra la j +-esima e la j -esima sono del tipo, ed inoltre o tutte le righe diverse dalle prime due sono nulle, oppure la terza riga è non nulla (per le matrici in cui questa situazione non si presenta, l eliminazione di Gauss senza scambi di righe fallisce Se tutte le righe di C diverse dalle prime due sono nulle, l algoritmo si ferma a C (ossia C è la U cercata Altrimenti la terza riga di C è non nulla e si procede 3, 4,, k-esimo Passaggio Si itera il procedimento illustrato nei primi due passaggi L obiettivo del passaggio i-esimo, se i k, è di trasformare la colonna j i -esima in una colonna del tipo, dove il numero
33 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 33 sta nella riga i-esima Se la matrice A da cui parte è tale che dopo aver effettuato il passaggio i-esimo si ottiene che TUTTE le colonne comprese tra la j i +-esima e la j i -esima (se ce ne sono sono del tipo, (dove il piú basso sta nella riga i -esima ed inoltre o tutte le righe diverse dalle prime i sono nulle, oppure la i + -esima riga è non nulla (per le matrici in cui questa situazione non si presenta, l algoritmo di Gauss senza scambi di righe fallisce, allora l algoritmo si ferma (ottenendo U quando si raggiunge una riga nulla, oppure, se non si raggiunge mai una riga nulla, quando si raggiunge l ultima riga Esempio 4 Riprendiamo la matrice C ottenuta alla fine dell Esempio 3, e mostriamo il procedimento per C Poichè la terza riga di C è non nulla, l algoritmo non si ferma a C Il primo elemento non nullo della terza riga di C è d 34, quindi j 3 = 4 Si chiama C la matrice che si ottiene da C moltiplicando la terza riga di C per c 34 = Dunque 5 C = 3 6 Per sistemare la j 3 -esima colonna di C, ossia per ottenere a partire da C una matrice con la terza colonna del tipo, basta sommare alla quarta riga di C la terza riga di C moltiplicata per Si ottiene 5 D = 3 Poichè la quarta riga di D è nulla, l algoritmo si ferma a D, ossia U = D Per riassumere il procedimento si scrive: A = E3( E( E(
34 34 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 5 5 E 4( 5E 3( E43( E3( = U 6 3 6
35 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 35 LEZIONE 6 Eliminazione di Gauss con scambi di righe Sia A O una matrice m n Abbiamo illustrato nella Lezione 5 un algoritmo che ha come obiettivo quello di costruire a partire da A una matrice U, m n, che abbia il seguente aspetto U =, eseguendo sulle righe di A un insieme di operazioni del tipo: sommare ad una riga di A una riga che la precede moltiplicata per uno scalare, moltiplicare una riga di A per uno scalare non nullo Def Una matrice che sia o nulla, oppure abbia l aspetto di U, si dice una matrice in forma ridotta di Gauss Abbiamo anche visto nell Esempio della lezione precedente che l eliminazione di Gauss senza scambi di righe fallisce per certe matrici Vediamolo con un altro esempio 4 3 Esempio Sia A = Volendo applicare l eliminazione di Gauss senza scambi di righe ad A, si ottiene che poichè il primo elemento non nullo nella prima riga di A è a 3, allora j = 3 Ma poichè non è vero che tutte le colonne prima della j -esima, ossia prima della terza, sono nulle (la seconda non lo è, allora l eliminazione di Gauss senza scambi di righe applicata ad A non porta ad una matrice in forma ridotta di Gauss Analogamente applicando l eliminazione di Gauss senza scambi di righe a B = 4 6 8, otteniamo 4 B = E3( E( E( In questo caso j = 4 Poichè nelle righe seguenti alla seconda ci sono elementi non nulli che stanno in colonne precedenti alla j -esima, allora anche in questo caso l eliminazione di Gauss senza scambi di righe applicata ad B non porta ad una matrice in forma ridotta di Gauss Introduciamo allora un altro algoritmo, che chiamiamo eliminazione di Gauss con scambi
36 36 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI di righe (o piú semplicemente eliminazione di Gauss, che differisce da quello descritto nella Lezione 5 soltanto nel fatto che tutte le volte che è necessario si possa fare anche uno scambio di righe, ossia un algoritmo in cui è lecita anche la terza operazione elementare sulle righe della matrice In questo modo si puó arrivare ad una matrice in forma ridotta di Gauss a partire da qualunque matrice A O Def Una matrice in forma ridotta di Gauss che si ottenga a partire da una matrice A applicandovi l eliminazione di Gauss con o senza scambi di righe si dice una forma ridotta di Gauss per la matrice A Si dice poi che la matrice nulla m n è una forma ridotta di Gauss di sè stessa Esempio Sia A = 4 3 la prima matrice considerata nell Esempio L operazione da fare è scambiare la a con la a riga: A = ( 4 3 E A = quindi si procede con l algoritmo su A Quello che si ottiene è: 4 3 A = 4 3 ed U è una forma ridotta di Gauss per A ( E 4 3 ( E ( 4, 4 3 E ( = U Sia B = la seconda matrice considerata nell Esempio Un eliminazione di 4 Gauss su B è: B = E3( E( E( E 3 3 E3( 5 3 = Ũ 5 Sia C = In questo caso si puó scegliere: 4
37 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 37 C = oppure E E( E3( E( 3 E3( = U ; E3 C = E E( 3E( 3 4 E ( 3 E3( = U Entrambe U ed U sono forme ridotte di Gauss per C NB U ed U sono due matrici diverse, ma entrambe sono forme ridotte di Gauss per la stessa matrice C Quindi non c e in generale un unica forma ridotta di Gauss per una matrice Def 3 Sia U una matrice m n in forma ridotta di Gauss, e siano k le sue righe non nulle (quindi le prime k righe di U sono non nulle e le ultime m k righe di U sono nulle Allora U ha esattamente k colonne che corrispondono all inizio di ogni gradino: la j -esima, che è la prima colonna di I m, la j -esima, che è del tipo ( T, la j 3 -esima, che è del tipo ( T, la j 4 -esima, che è del tipo ( T, inoltre la j k -esima, che è un vettore riga con m componenti del tipo ( T k tutte le eventuali colonne comprese tra la j + -esima e la j -esima sono del tipo ( T, tutte le eventuali colonne comprese tra la j + -esima e la j 3 -esima sono del tipo ( T, tutte le eventuali colonne comprese tra la j 3 + -esima e la j 4 -esima sono del tipo ( T,
38 38 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI tutte le eventuali colonne comprese tra la j k + -esima e la j k -esima sono del tipo ( T (il numero di è k Le colonne j -esima, j -esima, j 3 -esima,, j k -esima si chiamano le colonne dominanti della matrice in forma ridotta di Gauss U Le altre colonne di U si chiamano le colonne libere della matrice in forma ridotta di Gauss U Esempio 3 Siano A, B e C le matrici considerate nell Esempio e siano U ed Ũ le forme ridotte di Gauss trovate per A e B rispettivamente, ed inoltre U ed U le due forme ridotte di Gauss trovate per C colonne dominanti di U: la a e la 3 a ; colonne libere di U: la a e la 4 a ; colonne dominanti di Ũ: la a, la 3 a e la 4 a ; unica colonna libera di Ũ: la a ; U ed U hanno tutte le colonne dominanti e nessuna colonna libera NB E possibile provare che se U è una forma ridotta di Gauss per A allora esiste una matrice non singolare F tale che U = F A Osservazione Il numero delle colonne dominanti di una matrice in forma ridotta di Gauss U è uguale al numero delle sue righe non nulle Def 4 Una matrice U, m n si dice in forma ridotta di Gauss-Jordan se U è in forma ridotta di Gauss e, se u, u, u k sono le colonne dominanti di U allora u = e, u = e, u k = e k, dove e, e,, e k sono le prime k colonne di I m Come ottenere una forma ridotta di Gauss-Jordan di una matrice 4 6 Esempio 4 Si trovi una forma ridotta di Gauss-Jordan per B = 8 4 Troviamo una forma ridotta di Gauss per B, ad esempio, come abbiamo già calcolato nell Esempio, Ũ = 3 In questa prima parte del procedimento, come sappiamo, è lecita l operazione elementare E ij (c solo quando i > j
39 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 39 Partendo da Ũ procediamo a ritroso nel seguente modo: 3 E3( 3E3( E( = V V è una forma ridotta di Gauss-Jordan per B Dunque in questa seconda parte del procedimento stiamo permettendo anche l operazione elementare E ij (c quando i < j
40 4 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI ESERCIZIO TIPO α Sia A α = 3α α α 3, dove α R α α Per ogni α R si trovi una forma ridotta di Gauss U α per A α e si dica quali sono le colonne dominanti e quali sono le colonne libere di U α o CASO α α A α = 3α α α 3 α α /α /α /α E 3 α α α + 3 α 3 E(3αE( /α E3( α 3E(/α /α /α /α α + 3 α 3 α α /α /α /α = B α 3(α + / / / o sottocaso del caso α = B = = U Le colonne dominanti di U sono la a e la a, quelle libere la 3 a e la 4 a o sottocaso del caso α e α B α E 3( 3(α+ /α /α /α = U α Le colonne dominanti di U α (per α, sono la a, la a e la 3 a ; l unica libera è la 4 a o CASO α = A = 3 E( 3 E(/3 Le colonne dominanti di U sono la a e la 4 a, quelle libere la a e la 3 a = U
41 ALGEBRA LINEARE I (A PER SCIENZE STATISTICHE, AA /3, GEMMA PARMEGGIANI 4 ESERCITAZIONI* + i Siano A =, B = 8i 9i, C = i 3 5 i i i Si calcoli A + D(CA + ib Siano A = 3i + i i, B = ( + i, C = 3 + 5i 6 i i e D = ( i, D = ( 7 + i + 3i 3 i (a Di ciascuna delle precedenti matrici si calcolino la trasposta, la coniugata e la H-trasposta (b Si calcoli (A H C + ib T B + ( + 3iD H AB = O x y 3 Sia A = Si trovino tutte le matrici reali B = tali che z t BA = O T 4 Sia A =, dove è il vettore colonna con n componenti I n v uguali a e v è il vettore colonna con n componenti uguali a (quindi A ha tutte le componenti dell ultima colonna uguali a Sia B una matrice n n in cui la prima colonna ha tutte le componenti uguali a Si provi che la matrice AB ha come autovalore, ed e come autovettore ad esso relativo (Suggerimento: si suddivida B a blocchi mettendo in evidenza la sua ultima riga e la sua prima colonna e si calcoli il prodotto AB a blocchi 5 Siano A = e B = 4 Si trovino forme ridotte di Gauss per 4 3 A e B i i iα 6 Sia A α = α + 4 α, dove α C Per ogni α C si trovi una forma α + 4 α ridotta di Gauss U α per A α e si dica quali sono le colonne dominanti e quali sono le colonne libere di U α
Def. 1. Si chiamano operazioni elementari sulle righe di A le tre seguenti operazioni:
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 5 Operazioni elementari sulle righe di una matrice Sia A una matrice m n. Def. 1. Si chiamano operazioni elementari sulle righe
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 5 Operazioni elementari sulle righe di una matrice Sia A una matrice m n. Def. 1. Si chiamano operazioni elementari sulle righe
1 se k = r i. 0 altrimenti. = E ij (c)
 Facoltà di Scienze Statistiche, Algebra Lineare A, G.Parmeggiani LEZIONE 5 Matrici elementari e loro inverse Si fissi m un numero naturale. Per ogni i, j m con i j siano E ij (c) (ove c è uno scalare )
Facoltà di Scienze Statistiche, Algebra Lineare A, G.Parmeggiani LEZIONE 5 Matrici elementari e loro inverse Si fissi m un numero naturale. Per ogni i, j m con i j siano E ij (c) (ove c è uno scalare )
Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Belzoni, Padova
 ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Belzoni, 7 353 Padova Programma del corso Alcune
ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, AA /, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Belzoni, 7 353 Padova Programma del corso Alcune
ha come obiettivo quello di costruire a partire da A una matrice U, m n, che abbia il
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 6 Eliminazione di Gauss con scambi di righe Sia A O una matrice m n. Abbiamo illustrato nella Lezione 5 un algoritmo che ha come
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 6 Eliminazione di Gauss con scambi di righe Sia A O una matrice m n. Abbiamo illustrato nella Lezione 5 un algoritmo che ha come
Def. 2. Si dice che una matrice A, m n, ha un inversa sinistra se esiste una matrice L,
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 8 Inverse destre, sinistre e bilatere Def. 1. Si dice che una matrice A, m n, ha un inversa destra se esiste una matrice R, n
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 8 Inverse destre, sinistre e bilatere Def. 1. Si dice che una matrice A, m n, ha un inversa destra se esiste una matrice R, n
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
3x 2 = 6. 3x 2 x 3 = 6
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Matrici e sistemi. Geometria. Matrici e operazioni tra matrici. Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante
 Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
MATRICI E OPERAZIONI
 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Matematica II
 Matematica II 241110 Matrice inversa 1 Per n 1, l insieme R n n delle matrici quadrate di ordine n diventa l insieme R dei numeri reali, e la moltiplicazione di matrici diventa la moltiplicazione di numeri
Matematica II 241110 Matrice inversa 1 Per n 1, l insieme R n n delle matrici quadrate di ordine n diventa l insieme R dei numeri reali, e la moltiplicazione di matrici diventa la moltiplicazione di numeri
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5. Indice. 2. Esercizi 5
 ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
LEZIONE 1 C =
 LEZIONE 1 11 Matrici a coefficienti in R Definizione 111 Siano m, n Z positivi Una matrice m n a coefficienti in R è un insieme di mn numeri reali disposti su m righe ed n colonne circondata da parentesi
LEZIONE 1 11 Matrici a coefficienti in R Definizione 111 Siano m, n Z positivi Una matrice m n a coefficienti in R è un insieme di mn numeri reali disposti su m righe ed n colonne circondata da parentesi
Elementi di Algebra Matriciale. (richiami)
 Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Lezioni di Algebra Lineare. II. Aritmetica delle matrici e eliminazione di Gauss. versione ottobre 2008
 versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni 2. MATRICI
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 2 MATRICI Siano m, n N \ {0}, sia K un campo Una matrice m n a coefficienti in K è una
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 2 MATRICI Siano m, n N \ {0}, sia K un campo Una matrice m n a coefficienti in K è una
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
Le matrici. Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1.
 Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Operazioni tra matrici. Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia c = 3
 Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
a.a MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI
 aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
LeLing9: Prodotto tra matrici.
 Geometria Lingotto LeLing9: Prodotto tra matrici Ārgomenti svolti: Prodotto tra matrici Dimostrazione del teorema del rango L algebra delle matrici quadrate: Il prodotto tra matrici non e commutativo Rotazioni
Geometria Lingotto LeLing9: Prodotto tra matrici Ārgomenti svolti: Prodotto tra matrici Dimostrazione del teorema del rango L algebra delle matrici quadrate: Il prodotto tra matrici non e commutativo Rotazioni
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
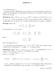 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
G. Parmeggiani, 17/5/2018 Algebra Lineare, a.a. 2017/2018, numero di MATRICOLA PARI
 G Parmeggiani, 17/5/2018 Algebra Lineare, aa 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA
G Parmeggiani, 17/5/2018 Algebra Lineare, aa 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA
Matrici e sistemi. Sistemi lineari. Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer
 Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
, è Det(A) = a 11 a 22 a 12 a 21. ( il determinante della matrice che si ottiene da A. la 1 a riga e la 2 a colonna di A
 G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Determinante, autovalori e autovettori
 Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta. Metodi per il calcolo del rango di una matrice
 Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
3 Soluzione di sistemi lineari
 3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
Lezione 4 - Esercitazioni di Algebra e Geometria - Anno accademico
 Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Introduzione all algebra delle matrici. Appunti a cura di Lara Ercoli
 Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Definizione 1. Una matrice n m a coefficienti in K é una tabella del tipo. ... K m, detto vettore riga i-esimo, ed a im
 APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
ALGEBRA DELLE MATRICI
 ALGEBRA DELLE MATRICI March 8, 2015 1 Definizioni e notazioni Una matrice è una tabella rettangolare le cui entrate sono numeri organizzati in righe orizzontali e colonne verticali. Esempio 1 2 A = 4 0
ALGEBRA DELLE MATRICI March 8, 2015 1 Definizioni e notazioni Una matrice è una tabella rettangolare le cui entrate sono numeri organizzati in righe orizzontali e colonne verticali. Esempio 1 2 A = 4 0
Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.
![Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe. Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.](/thumbs/100/147138366.jpg) Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI
 CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Matrici. Prof. Walter Pugliese
 Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Matrici e Sistemi di Equazioni Lineari
 CAPITOLO 1 Matrici e Sistemi di Equazioni Lineari Il primo obiettivo di questo Capitolo è quello di introdurre le matrici a coefficienti complessi e le loro principali operazioni: la somma di due matrici,
CAPITOLO 1 Matrici e Sistemi di Equazioni Lineari Il primo obiettivo di questo Capitolo è quello di introdurre le matrici a coefficienti complessi e le loro principali operazioni: la somma di due matrici,
La forma normale di Schur
 La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
Matematica II
 Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. 2011/2012
 6// G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. / Algebra Lineare A, Svolgimento degli Esercizi per casa 7 Sia V = a+bx+cx a,b,c C} lo spazio dei polinomi a coefficienti complessi
6// G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. / Algebra Lineare A, Svolgimento degli Esercizi per casa 7 Sia V = a+bx+cx a,b,c C} lo spazio dei polinomi a coefficienti complessi
1. Consideriamo un sistema lineare. E piuttosto naturale aspettarsi che
 Algebra Lineare (Matematica CI) 151113 1 Consideriamo un sistema lineare E piuttosto naturale aspettarsi che (a) se il numero delle equazioni e minore del numero delle incognite allora il sistema e indeterminato;
Algebra Lineare (Matematica CI) 151113 1 Consideriamo un sistema lineare E piuttosto naturale aspettarsi che (a) se il numero delle equazioni e minore del numero delle incognite allora il sistema e indeterminato;
LEZIONE 4. { x + y + z = 1 x y + 2z = 3
 LEZIONE 4 4.. Operazioni elementari di riga. Abbiamo visto, nella precedente lezione, quanto sia semplice risolvere sistemi di equazioni lineari aventi matrice incompleta fortemente ridotta per righe.
LEZIONE 4 4.. Operazioni elementari di riga. Abbiamo visto, nella precedente lezione, quanto sia semplice risolvere sistemi di equazioni lineari aventi matrice incompleta fortemente ridotta per righe.
G. Parmeggiani, 29/3/2018 Algebra Lineare, a.a. 2017/2018, numero di MATRICOLA PARI. Svolgimento degli Esercizi per casa 4
 G. Parmeggiani, 29/3/2018 Algebra Lineare, a.a. 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MARICOLA
G. Parmeggiani, 29/3/2018 Algebra Lineare, a.a. 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MARICOLA
= elemento che compare nella seconda riga e quinta colonna = -4 In generale una matrice A di m righe e n colonne si denota con
 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Sistemi Lineari II. March 18, 2015
 Sistemi Lineari II March 18, 2015 1 Operazioni elementari Abbiamo visto nell esempio 1 come sia utile manipolare le equazioni di un sistema senza cambiare le soluzioni del sistema in modo da ottenere un
Sistemi Lineari II March 18, 2015 1 Operazioni elementari Abbiamo visto nell esempio 1 come sia utile manipolare le equazioni di un sistema senza cambiare le soluzioni del sistema in modo da ottenere un
Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, Padova
 ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, A.A. 8/9, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso. Nota
ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, A.A. 8/9, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso. Nota
TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI
 TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI 2 Direttore Beatrice VENTURI Università degli Studi di Cagliari Comitato scientifico Umberto NERI University of
TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI 2 Direttore Beatrice VENTURI Università degli Studi di Cagliari Comitato scientifico Umberto NERI University of
Geometria BAER PRIMO CANALE Foglio esercizi 1
 Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
Vettori e matrici. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 27-28 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 27-28 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Operazioni tra matrici e n-uple
 CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI)
 Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, SGI, A.A. 2010/2011, GEMMA PARMEGGIANI
 ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, SGI, A.A. /, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso.
ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, SGI, A.A. /, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso.
MATRICI e DETERMINANTI. Prof.ssa Maddalena Dominijanni
 MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
Geometria BIAR Esercizi 2
 Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Piccola rassegna di Algebra delle Matrici
 Piccola rassegna di Algebra delle Matrici 1 Introduzione Questa nota va intesa semplicemente come un brevissimo sommario di alcuni concetti relativi alle Matrici, che dovete utilizzare nell ambito dello
Piccola rassegna di Algebra delle Matrici 1 Introduzione Questa nota va intesa semplicemente come un brevissimo sommario di alcuni concetti relativi alle Matrici, che dovete utilizzare nell ambito dello
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
0 0 c. d 1. det (D) = d 1 d n ;
 Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Analisi dei dati corso integrato - Algebra lineare, e a b c 0. le soluzioni del sistema lineare omogeneo x d e f 2. a b c.
 Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
Corso di Matematica per la Chimica. Dott.ssa Maria Carmela De Bonis a.a
 Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Spazio dei vettori Il primo oggetto matematico che definiamo sarà il vettore. Partendo dai numeri reali come rappresentazione dei punti della retta reale R,
Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Spazio dei vettori Il primo oggetto matematico che definiamo sarà il vettore. Partendo dai numeri reali come rappresentazione dei punti della retta reale R,
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. 2012/2013., w 3 = α se e solo se.
 7// G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. /3 Algebra Lineare A, Svolgimento degli Esercizi per casa 6 Si dica quale dei seguenti sottoinsiemi di R 3 è linearmente indipendente:
7// G. Parmeggiani, Facoltà di Scienze Statistiche, corso di laurea SGI, a.a. /3 Algebra Lineare A, Svolgimento degli Esercizi per casa 6 Si dica quale dei seguenti sottoinsiemi di R 3 è linearmente indipendente:
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI
 DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
