ESTENSIONE DELLA TECNICA DEGLI ALBERI
|
|
|
- Luigina Ruggeri
- 5 anni fa
- Visualizzazioni
Transcript
1 ROMA TRE UNIVERSITÀ DEGLI STUDI DI ROMA TRE DIPARTIMENTO DI ECONOMIA ESTENSIONE DELLA TECNICA DEGLI ALBERI BI/TRI NOMIALI AD ALBERI N NOMIALI. APPLICAZIONE AI PROCESSI DIFFUSIVI CON SALTO Massimiliano Corradini Working paper n ARACNE
2 I Working Papers del Dipartimento di Economia svolgono la funzione di divulgare tempestivamente, in forma definitiva o provvisoria, i risultati di ricerche scientifiche originali. La loro pubblicazione è soggetta all approvazione del Comitato Scientifico. Per ciascuna pubblicazione vengono soddisfatti gli obblighi previsti dall art.1 del D.L.L , n. 660 e successive modifiche. Copie della presente pubblicazione possono essere richieste alla Redazione Università degli Studi di Roma Tre Dipartimento di Economia Via Ostiense, Roma Tel Fax dip_eco@uniroma3.it Comitato scientifico Alessandra Carleo Marisa Cenci Valentina Guizzi Loretta Mastroeni Carlo Mottura Copyright MMIII ARACNE EDITRICE S.R.L Roma, via Raffaele Garofalo, 133 A/B (06) (06) telefax (06) info@aracne-editrice.it ISBN I diritti di traduzione, di memorizzazione elettronica, di riproduzione e di adattamento anche parziale, con qualsiasi mezzo, sono riservati per tutti i Paesi. I edizione: maggio 2004
3 Estensione della tecnica degli alberi bi/tri-nomiali ad alberi N-nomiali. Applicazione ai processi diffusivi con salto. Massimiliano Corradini Università degli Studi Roma Tre Sommario Nel presente articolo è proposta un estensione della tecnica degli alberi bi/tri-nomiali, largamente usata per la valutazione di titoli derivati, ad una tecnica basata sulla costruzione di alberi N-nomiali, con N intero arbitrario. Il vantaggio di tale tecnica consiste essenzialmente in 1) utilizzo di probabilità di transizione da un nodo ad un altro deducibili direttamente dall evoluzione del sottostante in ambito risk-neutral; 2) facilità di realizzazione del codice per il calcolo numerico e notevole precisione di calcolo in tempi brevi; 3) agevole trattazione dei processi diffusivi con salto. I risultati ottenuti nel presente articolo sono simili a quelli ottenibili tramite uno schema di calcolo basato sull integrazione in spazi di dimensione infinita (integrali di cammino di Feynmann). Si confrontino, relativamente al caso di processi stocastici puramente diffusivi, i riferimenti bibliografici [1, 2, 3].
4 Indice 1 Introduzione 9 2 Il metodo degli alberi N-nomiali Processi di diffusione Processi diffusivi con salto Risultati 18
5 Introduzione 9 1 Introduzione Nella teoria moderna del pricing di titoli derivati sono comunemente usate, laddove non esistano soluzioni analitiche in forma chiusa, tecniche numeriche basate sulla costruzione di alberi binomiali o trinomiali. Più in particolare, si supponga di dover determinare il valore all istante t 0 di un titolo derivato F su un sottostante S(t), con maturity T e valore a scadenza φ(s T ). Si ricorda che, se il valore del sottostante S(t) soddisfa l equazione differenziale stocastica ds(t) = µ(s(t), t)dt + σ(s(t), t)dz(t), (1) S(t 0 ) = S dove µ(s(t), t) e σ(s(t), t) sono, rispettivamente, il drift e la volatilità del processo S(t), dz(t) è un processo di Wiener standard e t [t 0, T ], il valore F(S(t), t) di un generico titolo derivato che dipenda soltanto dal tempo t e dal sottostante S(t), e il cui valore a scadenza sia F(S T, T ) = φ(s T ), deve soddisfare, in condizioni di assenza di arbitraggio, l equazione differenziale ( si confronti, per maggiori dettagli, il riferimento bibliografico [4]). F(S,t) + (µ(s, t) q(s, t)σ(s, t)) F(S,t) + 1 t S 2 σ2 (S, t) 2 F(S,t) = S 2 = rf(s, t). F(S, T ) = φ(s) (2) Nell equazione (2), r rappresenta l intensità istantanea di interesse priva di rischio, considerata per semplicità costante, mentre q(s, t) è il valore di mercato del rischio associato al sottostante S(t). La soluzione dell equazione (2) può essere ottenuta utilizzando il teorema di Feynmann-Kač, il quale asserisce che (per maggiori dettagli si confronti ad esempio il riferimento bibliografico [5]), data un equazione alle derivate parziali in forma parabolica, f(x, t) t f(x, t) + α(x, t) + 1 x 2 β2 (x, t) 2 f(x, t) x 2 = r(x, t)f(x, t), con t [t 0, T ] e con condizione al contorno f(x, T ) = g(x), e dato il processo stocastico
6 10 Capitolo 1 dx(t) = α(x(t), t)dt + β(x(t), t)dz(t), (3) con t [t 0, T ] e condizione al contorno x(t 0 ) = x, sussiste la seguente identità: f(x, t) = E M [e R T t 0 r(x(s),s)ds g(x(t )) x(t 0 ) = x], (4) in cui la media va calcolata secondo la misura M generata dal processo (3). Applicando tale teorema all equazione (2), tenendo conto che r è costante e, quindi, si ottiene: e R T t 0 r(x(s),s)ds = e r(t t 0), F(S, t 0 ) = e r(t t 0) E Q [φ(s T ) S(t 0 ) = S], (5) ovvero il valore attuale del derivato, F(S, t 0 ), può essere ottenuto scontando il valore atteso del suo valore a scadenza, calcolato rispetto la misura Q (la cosiddetta misura risk-neutral generalizzata) generata dal processo stocastico ds(t) = µ(s(t), t)dt + σ(s(t), t)dz(t), (6) S(t 0 ) = S dove µ(s(t), t) = µ(s(t), t) q(s(t), t)σ(s(t), t). (7) Si osservi che, detta P la misura generata dall evoluzione reale del processo, data dall equazione (1), il passaggio dall ambiente reale a quello risk-neutral o, equivalentemente, il passaggio dalla misura P alla misura Q, modifica soltanto il termine di drift del processo in esame mentre la volatilità rimane invariata: tale risultato può essere visto come caso particolare di un teorema molto più generale dovuto a Girsanov. Si può osservare ancora che se il sottostante S(t) è esso stesso un bene di investimento deve valere (si confronti il riferimento bibliografico [4]) µ(s(t), t) = rs(t) : in tal caso la misura Q è nota come misura risk-neutral tradizionale.
7 Introduzione 11 Per effettuare numericamente il calcolo del valore del titolo derivato dato dall equazione (5), è opportuno dapprima suddividere l intervallo temporale [t 0, T ] in M sottointervalli, ciascuno di ampiezza t = T t 0, M cosicché la variabile temporale t possa assumere solo i valori discreti t i = t 0 + i t, i = 0,..., M. In tal modo è possibile approssimare l evoluzione del processo in ambiente risk-neutral data dall equazione (6) con il processo discreto Si+1 = S i + µ(s i, t i ) t + σ(s i, t i ) tɛ i, (8) S 0 = S dove S i = S(t i ) e ɛ i è una variabile casuale con distribuzione gaussiana standard. L essenza del metodo degli alberi binomiali o trinomiali consiste nell approssimare l evoluzione del processo dato dall equazione (8) supponendo che ad un dato istante temporale t i+1 la variabile stocastica S i+1 possa assumere soltanto i valori Si+1 = S i + α S, (9) α = 1, 0, 1} dove la variabile aleatoria α è definita da Prob(α = 1) = p u, Prob(α = 0) = 0 e Prob(α = 1) = p d nel caso di alberi binomiali e da Prob(α = 1) = p u, Prob(α = 0) = p m e Prob(α = 1) = p d nel caso di alberi trinomiali. In entrambi i casi le probabilità p u, p d e p m possono essere definite in base a considerazioni di consistenza interna del metodo mentre il passo spaziale S deve dipendere dal passo temporale t secondo una relazione ben definita come ad esempio, nel caso di alberi trinomiali, S σ 3 t (si confronti il riferimento bibliografico [6]). Dalla conoscenza della struttura degli alberi binomiali o trinomiali si può poi calcolare il valore del derivato (5) (per maggiori dettagli si confrontino i riferimenti bibliografici [7, 8]). Nel presente articolo si propone un metodo di calcolo che elimini la restrizione presente nella relazione (9) in modo tale che, se il processo continuo S(t) definito dall equazione (6) è a valori in un determinato intervallo I = [S min, S max ], allora il processo discreto S i definito dall equazione (8) assume gli N valori S min, S min + S, S min + 2 S,..., S min + (N 2) S,
8 12 Capitolo 1 S min + (N 1) S = S max }, dove S = Smax S min. Nella Fig. 1 si mostra la costruzione di un N 1 albero pentanomiale con 2 passi temporali. S max S i S S min t 0 t 1 t 2 =T t i Figura 1 Nel metodo proposto nel presente articolo, inoltre, la probabilità di transizione da un nodo (t i, S i ) al nodo (t i+1, S i+1 ) può, essere calcolata direttamente a partire dall evoluzione del processo S(t) in ambito riskneutral, a meno di infinitesimi di ordine superiore a t. Infine, come si discuterà più in dettaglio nel seguito, la trattazione di processi stocastici con salti, rilevanti ad esempio nello studio dei titoli derivati energetici (elettricità, petriolo o gas), si può effettuare attraverso una semplice modifica del formalismo relativo a processi stocastici puramente diffusivi. I risultati ottenuti nel presente articolo sono simili a quelli ottenibili tramite uno schema di calcolo del valore dell opzione (5) basato sull integrazione in spazi di dimensione infinita (integrali di cammino di Feynmann). Si confrontino, relativamente al caso di processi stocastici puramente diffusivi, i riferimenti bibliografici [1, 2, 3].
9 Il metodo degli alberi N-nomiali 13 2 Il metodo degli alberi N-nomiali 2.1 Processi di diffusione Nel calcolo del valore del titolo derivato F definito dall equazione (5), che di seguito riscriviamo per comodità, F(S, t 0 ) = e r(t t 0) E Q [φ(s T ) S(t 0 ) = S], (10) occorre calcolare la media del valore a scadenza φ(s T ), con condizione iniziale S(t 0 ) = S, relativamente alla probabilità Q associata all evoluzione del processo stocastico in ambito risk-neutral, definito dall equazione (6), ds(t) = µ(s(t), t)dt + σ(s(t), t)dz(t). (11) S(t 0 ) = S Tale media può essere calcolata attraverso la relazione F(S, t 0 ) = e r(t t 0) ds T φ(s T )f(t, S T ; t 0, S), (12) essendo f(t, S T ; t 0, S) la densità della probabilità che il processo S(t) assuma all istante T il valore S T, posto che all istante t 0 esso aveva assunto il valore S. Discretizzando l intervallo temporale [t 0, T ], secondo quanto visto nel paragrafo 1, t i = t 0 + i t, con i = 0,..., M e t = T t 0, è M possibile approssimare l equazione differenziale stocastica (11) attraverso il seguente processo discreto: Si+1 = S i + µ(s i, t i ) t + σ(s i, t i ) tɛ i, (13) S 0 = S ed approssimare di conseguenza la densità della probabilità di transizione f(t, S T ; t 0, S 0 ). Si osservi infatti che detta f(t 2, S 2 ; t 0, S 0 ) la densità della probabilità che S(t) assuma all istante t 2 il valore S 2, posto che all istante t 0 aveva assunto il valore S 0, essa può essere riscritta come (t 0 < t 1 < t 2 ) f(t 2, S 2 ; t 0, S 0 ) = S 1 f(t 2, S 2 ; t 1, S 1 )f(t 1, S 1 ; t 0, S 0 ) S, (14)
10 14 Capitolo 2 S max S 2 S 0 S min cioè 1 la probabilità che, dato il valore del sottostante in t 0 pari a S 0 esso assuma il valore S 2 al tempo t 2, è pari alla probabilità che dal valore S 0 al tempo t 0 esso assuma il valore S 1 al tempo t 1, per la probabilità che dal valore S 1 al tempo t 1 esso assuma il valore S 2 al tempo t 2, somt 0 t 1 t 2 Figura 2 mando poi su tutti i possibili valori S 1 = S min +k 1 S, k 1 = 0,..., N 1 (si confronti la Fig. 2 relativamente al caso N = 5). Applicando ripetutamente M 1 volte la relazione (14), otteniamo: f(t, S T ; t 0, S 0 ) = S M 1...S 1 ( S) M 1 f(t, S T ; t M 1, S M 1 ) f(t M 1, S M 1 ; t M 2, S M 2 )... f(t 2, S 2 ; t 1, S 1 )f(t 1, S 1 ; t 0, S 0 ) > (15) ovvero, f(t, S T ; t 0, S 0 ) = 1 S S M 1...S 2,S 1 M 1 i=0 f(t i+1, S i+1 ; t i, S i ) S, (16) avendo posto S M modo che t = T t 0 M superiore a t, = S T. Scegliendo M sufficientemente grande, in 0, si può porre, a meno di infinitesimi di ordine 1 Tale relazione è nota in teoria della probabilità come equazione di Chapman- Kolmogorov.
11 Il metodo degli alberi N-nomiali 15 f(t i+1, S i+1 ; t i, S i ) = 1 2πσ2 (t i, S i ) t (S 2 i+1 S i µ(t i,s i) t) 2σ e( 2 (t i,s i ) t ), (17) essendo la variabile casuale S i+1 distribuita secondo una gaussiana di media S i + µ(t i, S i ) t e varianza σ 2 (t i, S i ) t, come si può evincere dall equazione (13). Dalla relazione (16) e dalla relazione (12), si ottiene: F(S 0, t 0 ) e r(t t 0) ds T φ(s T ) 1 S S M 1...,S 2,S 1 (18) f(t i+1, S i+1 ; t i, S i ) S. M 1 i=0 Calcolando in modo approssimato l integrale nell equazione (18) tramite la relazione ds T g(s T ) g(s M ) S, S M si ottiene, infine, F(t 0, S 0 ) e r(t t 0) S M φ(s M ) ovvero 2 S M 1...S 2,S 1 M 1 i=0 f(t i+1, S i+1 ; t i, S i ) S, (19) F(t 0, S 0 ) e r(t t 0) S 1 f(t 1, S 1 ; t 0, S 0 ) S 2 f(t 2, S 2 ; t 1, S 1 )... S M 1 f(t M 1, S M 1 ; t M 2, S M 2 ) S M f(t M, S M ; t M 1, S M 1 )φ(s M ) (20) con f(t i+1, S i+1 ; t i, S i ) data dall equazione (17). 2 Per un confronto tra il risultato ottenuto nel presente articolo e quello ottenibile tramite una formulazione del problema basata sugli integrali di cammino di Feynmann, si confronti l equazione (19) del presente testo con l equazione (42) del riferimento bibliografico [2].
12 16 Capitolo 2 Dalle relazioni (19) o (20) si evince che il calcolo del valore F di un titolo derivato può essere ricondotto al calcolo di M somme, corrispondenti al numero di passi temporali in cui si suddivide l intervallo di tempo [t 0, T ], che non presenta, in generale, particolari difficoltà sia dal punto di vista della stesura del codice sia dal punto di vista del tempo di calcolo. 2.2 Processi diffusivi con salto Si consideri ora il problema del calcolo del valore F di un titolo derivato su un sottostante S(t), nel caso in cui il valore di quest ultimo possa subire salti improvvisi 3. Si supponga che l evoluzione del valore del sottostante S(t) sia definita dall equazione differenziale stocastica (t [t 0, T ]) ds(t) = µ(s(t), t)dt + σ(s(t), t)dz(t) + u(s(t), t)dq(t) S(t 0 ) = S, (21) in cui dq è un processo di Poisson: Prob(dq = 1) = λdt Prob(dq = 0) = 1 λdt. Tale processo, in effetti, è in grado di simulare la presenza di salti improvvisi: tra t e t + dt, con probabilità pari a λdt, il processo S(t) subisce un salto di ampiezza pari a u(s(t), t). Il valore F di un titolo derivato con maturity T e valore a scadenza φ(s T ), è dato, in completa analogia con quanto visto nel paragrafo precedente, dalla relazione F(S, t 0 ) = e r(t t 0) E Q [φ(s T ) S(t 0 ) = S], (22) in cui Q è la misura generata dall evoluzione del processo S(t) in ambiente risk-neutral, data dall equazione (per maggiori dettagli si confronti il riferimento bibliografico [9]) ds(t) = µ(s(t), t)dt + σ(s(t), t)dz(t) + u(s(t), t)dq(t) S(t 0 ) = S, (23) 3 Tale comportamento è particolarmente rilevante, ad esempio, nel caso in cui il sottostante S(t) rappresenti un bene di natura energetica, come l elettricità, il petrolio o il gas (si confrontino i riferimenti bibliografici [9, 10] per maggiori dettagli in proposito)
13 Il metodo degli alberi N-nomiali 17 in cui µ(s(t), t) = µ(s(t), t) σ(s(t), t)q(s(t), t), (24) essendo q(s(t), t) il valore di mercato del rischio associato a S(t). Per il calcolo della media nell equazione (22) si può utilizzare un procedimento simile a quello proposto nel paragrafo precedente (equazioni (15), (16) e (18)-(20)). In questo caso però la densità della probabilità di transizione dal nodo (t i, S i ) al nodo (t i+1, S i+1 ), f(t i+1, S i+1 ; t i, S i ), non è più una semplice funzione gaussiana. Si osservi tuttavia che, per definizione stessa di processo di Poisson, tra t i e t i + t il processo S i, risultante dalla discretizzazione del processo dato nell equazione (23), può subire, al più, un salto e, quindi, 1 f(t i+1, S i+1 ; t i, S i ) = 2πσ 2 (t i,s i ) t e( + (S i+1 S i µ(t i,s i ) t) 2 2σ 2 (t i,s i ) t (S i+1 S i µ(t i,s i ) t u(t i,s i )) 2 1 2πσ 2 (t i,s i ) t e( 2σ 2 (t i,s i ) t ) (1 λ t). ) λ t (25) In conclusione, nel caso in cui il processo S(t) subisca salti improvvisi e tali salti possano essere descritti tramite un processo di Poisson, come supposto nell equazione (21), è possibile utilizzare per il calcolo del valore di un titolo derivato ancora l approssimazione (20) trovata nel caso di processo puramente diffusivo, in cui però la densità della probabilità di transizione f(t i+1, S i+1 ; t i, S i ) è data dalla somma di due distribuzioni gaussiane con opportuni pesi (equazione (25)). Si osservi pertanto che nell ambito dello schema di calcolo proposto nel presente articolo l inclusione di un termine di Poisson nell evoluzione del sottostante non aumenta né la difficoltà della stesura del codice né tantomeno il tempo necessario per il calcolo numerico. In particolare gli alberi N-nomiali qui presentati non subiscono alcuno shift nel momento in cui il sottostante S(t) subisce un salto, contrariamente a quanto avviene nel caso degli alberi bi/trinomiali ordinariamente considerati in letteratura, essendo l effetto del salto incorporato direttamente nelle probabilità (25) associate ai vari valori del sottostante.
Comitato scientifico
 ROMA TRE UNIVERSITÀ DEGLI STUDI DI ROMA TRE DIPARTIMENTO DI ECONOMIA UN MODELLO PER LA DINAMICA DEL PREZZO A PRONTI DELL ELETTRICITÀ Massimiliano Corradini Working paper n. 40 2004 ARACNE I Working Papers
ROMA TRE UNIVERSITÀ DEGLI STUDI DI ROMA TRE DIPARTIMENTO DI ECONOMIA UN MODELLO PER LA DINAMICA DEL PREZZO A PRONTI DELL ELETTRICITÀ Massimiliano Corradini Working paper n. 40 2004 ARACNE I Working Papers
ESTENSIONE DELLA TECNICA DEGLI ALBERI
 ISBN 88-7999-752-1 9 788879 997522 ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMA TRE UNIVERSITÀ DEGLI
ISBN 88-7999-752-1 9 788879 997522 ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMATRE ROMA TRE UNIVERSITÀ DEGLI
SELEZIONE DI PORTAFOGLI OTTIMI
 ROMA TRE UNIVERSITÀ DEGLI STUDI DI ROMA TRE DIPARTIMENTO DI ECONOMIA SELEZIONE DI PORTAFOGLI OTTIMI CON VINCOLO DI SHORTFALL Valentina Guizzi Working paper n. 37 2004 ARACNE I Working Papers del Dipartimento
ROMA TRE UNIVERSITÀ DEGLI STUDI DI ROMA TRE DIPARTIMENTO DI ECONOMIA SELEZIONE DI PORTAFOGLI OTTIMI CON VINCOLO DI SHORTFALL Valentina Guizzi Working paper n. 37 2004 ARACNE I Working Papers del Dipartimento
RETI DI TELECOMUNICAZIONE
 RETI DI TELECOMUNICAZIONE CATENE DI MARKOV TEMPO CONTINUE Definizioni Sia dato un processo stocastico x(t) che può assumere valori discreti appartenenti ad un insieme se accade che il processo è una catena
RETI DI TELECOMUNICAZIONE CATENE DI MARKOV TEMPO CONTINUE Definizioni Sia dato un processo stocastico x(t) che può assumere valori discreti appartenenti ad un insieme se accade che il processo è una catena
Corsi di Laurea Magistrale in Matematica, A.A Calcolo stocastico e applicazioni (Docente: Bertini) Esercizi settimanali
 Settimana 1 Esercizio 1. [Unicità della misura di Wiener] Sia C([0, 1]) l insieme delle funzioni continue sull intervallo [0, 1] con la topologia (metrizzabile) indotta dalla convergenza uniforme. Sia
Settimana 1 Esercizio 1. [Unicità della misura di Wiener] Sia C([0, 1]) l insieme delle funzioni continue sull intervallo [0, 1] con la topologia (metrizzabile) indotta dalla convergenza uniforme. Sia
Introduzione al modello Uniforme
 Introduzione al modello Uniforme Esempio: conversione Analogico/Digitale Errore di quantizzazione Ampiezza Continua Discreta x () t x ( t ) q Tempo Discreto Continuo Segnale Analogico ( ) x t k t t Segnale
Introduzione al modello Uniforme Esempio: conversione Analogico/Digitale Errore di quantizzazione Ampiezza Continua Discreta x () t x ( t ) q Tempo Discreto Continuo Segnale Analogico ( ) x t k t t Segnale
Ciclo di seminari: Metodi Computazionali per la Finanza
 Ciclo di seminari: Metodi Computazionali per la Finanza C.d.L.M. Finanza e Assicurazioni a.a. 2018/2019 Lezione 4: Simulazione Moti Browniani e con Monte Carlo Cos è il Metodo Monte Carlo? Dinamica di
Ciclo di seminari: Metodi Computazionali per la Finanza C.d.L.M. Finanza e Assicurazioni a.a. 2018/2019 Lezione 4: Simulazione Moti Browniani e con Monte Carlo Cos è il Metodo Monte Carlo? Dinamica di
Indice. Notazioni generali... 1
 Notazioni generali............................................. 1 1 Derivati e arbitraggi....................................... 5 1.1 Opzioni................................................ 5 1.1.1 Finalità..........................................
Notazioni generali............................................. 1 1 Derivati e arbitraggi....................................... 5 1.1 Opzioni................................................ 5 1.1.1 Finalità..........................................
Esercizi di Fondamenti di Sistemi Dinamici
 Giuseppe Fusco Esercizi di Fondamenti di Sistemi Dinamici ARACNE Copyright MMVIII ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133 a/b 00173 Roma (06 93781065
Giuseppe Fusco Esercizi di Fondamenti di Sistemi Dinamici ARACNE Copyright MMVIII ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133 a/b 00173 Roma (06 93781065
Introduzione al Metodo agli Elementi Finiti (FEM) (x, y) Γ Tale formulazione viene detta Formulazione forte del problema.
 Introduzione al Metodo agli Elementi Finiti (FEM) Consideriamo come problema test l equazione di Poisson 2 u x 2 + 2 u = f(x, y) u = f y2 definita su un dominio Ω R 2 avente come frontiera la curva Γ,
Introduzione al Metodo agli Elementi Finiti (FEM) Consideriamo come problema test l equazione di Poisson 2 u x 2 + 2 u = f(x, y) u = f y2 definita su un dominio Ω R 2 avente come frontiera la curva Γ,
Note sulle Catene di Markov
 Note sulle Catene di Markov ELAUT Prof. Giuseppe C. Calafiore Sommario Queste note contengono un estratto schematico ridotto di parte del materiale relativo alle Catene di Markov a tempo continuo e a tempo
Note sulle Catene di Markov ELAUT Prof. Giuseppe C. Calafiore Sommario Queste note contengono un estratto schematico ridotto di parte del materiale relativo alle Catene di Markov a tempo continuo e a tempo
λ è detto intensità e rappresenta il numero di eventi che si
 ESERCITAZIONE N 1 STUDIO DI UN SISTEMA DI CODA M/M/1 1. Introduzione Per poter studiare un sistema di coda occorre necessariamente simulare gli arrivi, le partenze e i tempi di ingresso nel sistema e di
ESERCITAZIONE N 1 STUDIO DI UN SISTEMA DI CODA M/M/1 1. Introduzione Per poter studiare un sistema di coda occorre necessariamente simulare gli arrivi, le partenze e i tempi di ingresso nel sistema e di
MATEMATICA E STATISTICA CORSO A III COMPITINO 20 Marzo 2009
 MATEMATICA E STATISTICA CORSO A III COMPITINO Marzo 9 SOLUZIONI. () Sia X una variabile aleatoria binomiale con valor medio uguale a 5/; la varianza di X può valere? Giustificare la risposta. Il valor
MATEMATICA E STATISTICA CORSO A III COMPITINO Marzo 9 SOLUZIONI. () Sia X una variabile aleatoria binomiale con valor medio uguale a 5/; la varianza di X può valere? Giustificare la risposta. Il valor
MICROECONOMIA MATEMATICA
 A13 363 Gianluca Dari MICROECONOMIA MATEMATICA TRECENTO ESERCIZI SVOLTI Copyright MMX ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133/A B 00173 Roma (06)
A13 363 Gianluca Dari MICROECONOMIA MATEMATICA TRECENTO ESERCIZI SVOLTI Copyright MMX ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133/A B 00173 Roma (06)
Zero-coupon bond e tassi di interesse a breve termine
 Zero-coupon bond e tassi di interesse a breve termine Definizione. Uno zero-coupon bond con data di maturità T > 0, detto anche T -bond, è un contratto che prevede il pagamento alla scadenza T del suo
Zero-coupon bond e tassi di interesse a breve termine Definizione. Uno zero-coupon bond con data di maturità T > 0, detto anche T -bond, è un contratto che prevede il pagamento alla scadenza T del suo
Michele Angelaccio / Berta Buttarazzi. Reti logiche. PARTE SECONDA Reti sequenziali
 A09 37 Michele Angelaccio / Berta Buttarazzi Reti logiche PARTE SECONDA Reti sequenziali Copyright MMIV ARACNE EDITRICE S.r.l. www.aracneeditrice.it info@aracneeditrice.it 00173 Roma via Raffaele Garofalo,
A09 37 Michele Angelaccio / Berta Buttarazzi Reti logiche PARTE SECONDA Reti sequenziali Copyright MMIV ARACNE EDITRICE S.r.l. www.aracneeditrice.it info@aracneeditrice.it 00173 Roma via Raffaele Garofalo,
Variabili aleatorie n-dim
 Sessione Live #6 Settimana dal 6 maggio al giugno 003 Variabili aleatorie n-dim Funzioni di ripartizione e di densità (F.D.R. e f.d.d.) congiunte e marginali, valori medi e momenti misti, funzione generatrice
Sessione Live #6 Settimana dal 6 maggio al giugno 003 Variabili aleatorie n-dim Funzioni di ripartizione e di densità (F.D.R. e f.d.d.) congiunte e marginali, valori medi e momenti misti, funzione generatrice
Equazioni di Evoluzione
 Equazioni di Evoluzione Le equazioni di evoluzione descrivono fenomeni che variano in funzione del tempo, tra gli altri per esempio fenomeni di onde, termodinamici, di dinamica delle popolazioni. Le equazioni
Equazioni di Evoluzione Le equazioni di evoluzione descrivono fenomeni che variano in funzione del tempo, tra gli altri per esempio fenomeni di onde, termodinamici, di dinamica delle popolazioni. Le equazioni
Capitolo 6. Variabili casuali continue. 6.1 La densità di probabilità
 Capitolo 6 Variabili casuali continue Le definizioni di probabilità che abbiamo finora usato sono adatte solo per una variabile casuale che possa assumere solo valori discreti; vediamo innanzi tutto come
Capitolo 6 Variabili casuali continue Le definizioni di probabilità che abbiamo finora usato sono adatte solo per una variabile casuale che possa assumere solo valori discreti; vediamo innanzi tutto come
METODI NUMERICI. Metodo delle differenze finite
 METOI NUMERICI Lo sviluppo dei moderni calcolatori ha consentito di mettere a disposizione della scienza e della tecnica formidabili strumenti che hanno permesso di risolvere numerosi problemi la cui soluzione
METOI NUMERICI Lo sviluppo dei moderni calcolatori ha consentito di mettere a disposizione della scienza e della tecnica formidabili strumenti che hanno permesso di risolvere numerosi problemi la cui soluzione
Capitolo 6 La distribuzione normale
 Levine, Krehbiel, Berenson Statistica Casa editrice: Pearson Capitolo 6 La distribuzione normale Insegnamento: Statistica Corso di Laurea Triennale in Economia Dipartimento di Economia e Management, Università
Levine, Krehbiel, Berenson Statistica Casa editrice: Pearson Capitolo 6 La distribuzione normale Insegnamento: Statistica Corso di Laurea Triennale in Economia Dipartimento di Economia e Management, Università
Outline. 1 v.c. continue. 2 v.c. Normale. 3 v.c. Esponenziale. Lezione 13. A. Iodice. v.c. continue. v.c. Normale. v.c.
 Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 48 Outline 1 2 3 () Statistica 2 / 48 Variabili casuali continue Una variabile casuale X è continua
Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 48 Outline 1 2 3 () Statistica 2 / 48 Variabili casuali continue Una variabile casuale X è continua
Esercizi 6 - Variabili aleatorie vettoriali, distribuzioni congiunte
 Esercizi - Variabili aleatorie vettoriali, distribuzioni congiunte Esercizio. X e Y sono v.a. sullo stesso spazio di probabilità (Ω, E, P). X segue la distribuzione geometrica modificata di parametro p
Esercizi - Variabili aleatorie vettoriali, distribuzioni congiunte Esercizio. X e Y sono v.a. sullo stesso spazio di probabilità (Ω, E, P). X segue la distribuzione geometrica modificata di parametro p
Variabili casuali. - di Massimo Cristallo -
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
Definizione di Sistema Dinamico
 Capitolo 1. INTRODUZIONE 1.1 Definizione di Sistema Dinamico Un sistema dinamico è definito dai seguenti oggetti: Un insieme ordinato dei tempi T, Un insieme di valori di ingresso U, Un insieme di funzioni
Capitolo 1. INTRODUZIONE 1.1 Definizione di Sistema Dinamico Un sistema dinamico è definito dai seguenti oggetti: Un insieme ordinato dei tempi T, Un insieme di valori di ingresso U, Un insieme di funzioni
SISTEMI CASUALI DINAMICI (PROCESSI) ESEMPIO: I GUASTI (Ipotesi Markoviana) Frequenza dei guasti: N Guasti = N/T X X X X X X X
 CATENE DI MARKOV SISTEMI CASUALI DINAMICI (PROCESSI) ESEMPIO: I GUASTI (Ipotesi Markoviana) Frequenza dei guasti: N Guasti = N/T X X X X X X X X X 0 T 0 T! Δ 0, 1,, 0 Δ 1 Δ Δ 1Δ Δ Δ ESEMPIO: I GUASTI (Ipotesi
CATENE DI MARKOV SISTEMI CASUALI DINAMICI (PROCESSI) ESEMPIO: I GUASTI (Ipotesi Markoviana) Frequenza dei guasti: N Guasti = N/T X X X X X X X X X 0 T 0 T! Δ 0, 1,, 0 Δ 1 Δ Δ 1Δ Δ Δ ESEMPIO: I GUASTI (Ipotesi
Spazio di probabilità
 Spazio di probabilità Uno spazio di probabilità è una terna (Ω, A, P), dove Ω è un insieme qualunque (in genere pensato come l insieme dei risultati possibili di un esperimento casuale), A è detta σ-algebra,
Spazio di probabilità Uno spazio di probabilità è una terna (Ω, A, P), dove Ω è un insieme qualunque (in genere pensato come l insieme dei risultati possibili di un esperimento casuale), A è detta σ-algebra,
Valutazione in tempo continuo (formula di Black e Scholes)
 Valutazione in tempo continuo (formula di Black e Scholes) Federico Marchetti (Politecnico di Milano) Dipartimento di Economia e Produzione 5/6/000 1 Calcolo stocastico Ci limitiamo al caso unidimensionale,
Valutazione in tempo continuo (formula di Black e Scholes) Federico Marchetti (Politecnico di Milano) Dipartimento di Economia e Produzione 5/6/000 1 Calcolo stocastico Ci limitiamo al caso unidimensionale,
Introduzione al modello Uniforme
 Teoria dei Fenomeni Aleatori 1 AA 01/13 Introduzione al modello Uniforme Esempio: conversione Analogico/Digitale Errore di quantizzazione Ampiezza Continua Discreta x t x q t Tempo Discreto Continuo 0
Teoria dei Fenomeni Aleatori 1 AA 01/13 Introduzione al modello Uniforme Esempio: conversione Analogico/Digitale Errore di quantizzazione Ampiezza Continua Discreta x t x q t Tempo Discreto Continuo 0
Capitolo 6. La distribuzione normale
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 6 La distribuzione normale Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 6 La distribuzione normale Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
Esercitazione del 16/04/2019 Istituzioni di Calcolo delle Probabilità
 Esercitazione del 6/04/09 Istituzioni di Calcolo delle Probabilità David Barbato Nozioni di riepilogo con esercizi Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile
Esercitazione del 6/04/09 Istituzioni di Calcolo delle Probabilità David Barbato Nozioni di riepilogo con esercizi Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A Alberto Perotti, Roberto Garello
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
VETTORI DI VARIABILI ALEATORIE
 VETTOI DI VAIABILI ALEATOIE E. DI NADO 1. Funzioni di ripartizione congiunte e marginali Definizione 1.1. Siano X 1, X 2,..., X n v.a. definite su uno stesso spazio di probabilità (Ω, F, P ). La n-pla
VETTOI DI VAIABILI ALEATOIE E. DI NADO 1. Funzioni di ripartizione congiunte e marginali Definizione 1.1. Siano X 1, X 2,..., X n v.a. definite su uno stesso spazio di probabilità (Ω, F, P ). La n-pla
PROBABILITA. Distribuzione di probabilità
 DISTRIBUZIONI di PROBABILITA Distribuzione di probabilità Si definisce distribuzione di probabilità il valore delle probabilità associate a tutti gli eventi possibili connessi ad un certo numero di prove
DISTRIBUZIONI di PROBABILITA Distribuzione di probabilità Si definisce distribuzione di probabilità il valore delle probabilità associate a tutti gli eventi possibili connessi ad un certo numero di prove
1 Serie temporali. 1.1 Processi MA
 1 Serie temporali Un processo stocastico 1 {X t, t T }, dove T = N o T = Z, si dice stazionario se (X 1,..., X n ) e (X k+1,...,x k+n ) hanno la stessa distribuzione per ogni n 1 e per ogni k T. Un processo
1 Serie temporali Un processo stocastico 1 {X t, t T }, dove T = N o T = Z, si dice stazionario se (X 1,..., X n ) e (X k+1,...,x k+n ) hanno la stessa distribuzione per ogni n 1 e per ogni k T. Un processo
f(x) dx = F (b) F (a) Formula di quadratura o di integrazione numerica c i f(x i ) + R n (f)
 INTEGRAZIONE NUMERICA Integrale di funzione I(f) = a f(x) dx = F (b) F (a) Formula di quadratura o di integrazione numerica a f(x) dx = n i=0 c i f(x i ) + R n (f) dove le {x i } sono i nodi e {c i } sono
INTEGRAZIONE NUMERICA Integrale di funzione I(f) = a f(x) dx = F (b) F (a) Formula di quadratura o di integrazione numerica a f(x) dx = n i=0 c i f(x i ) + R n (f) dove le {x i } sono i nodi e {c i } sono
Calcolo delle probabilità (3/7/2001) (Ing. Elettronica, Informatica, Telecomunicazioni - Latina)
 Calcolo delle probabilità (3/7/00). La distribuzione di probabilità di un numero aleatorio X non negativo soddisfa la condizione P (X > x + y X > y) = P (X > x), x > 0, y > 0. Inoltre la previsione di
Calcolo delle probabilità (3/7/00). La distribuzione di probabilità di un numero aleatorio X non negativo soddisfa la condizione P (X > x + y X > y) = P (X > x), x > 0, y > 0. Inoltre la previsione di
Università di Roma Tor Vergata Corso di Teoria dei Fenomeni Aleatori, AA 2012/13. Catene di Markov
 Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Frequenza dei guasti: N GUASTI 0 T N T 0 T! Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Campionando
Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Frequenza dei guasti: N GUASTI 0 T N T 0 T! Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Campionando
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
CURVE E SUPERFICI DIFFERENZIABILI
 Giulio Campanella CURVE E SUPERFICI DIFFERENZIABILI ESERCIZI SVOLTI Copyright MMIII, ARACNE EDITRICE S.R.L. 00173 Roma, via R. Garofalo, 133 A B tel. (06) 72672222 telefax 72672233 ISBN 978-88-7999-281-7
Giulio Campanella CURVE E SUPERFICI DIFFERENZIABILI ESERCIZI SVOLTI Copyright MMIII, ARACNE EDITRICE S.R.L. 00173 Roma, via R. Garofalo, 133 A B tel. (06) 72672222 telefax 72672233 ISBN 978-88-7999-281-7
Esercitazione del 21/02/2012 Istituzioni di Calcolo delle Probabilità
 Esercitazione del /0/0 Istituzioni di Calcolo delle Probabilità David Barbato Funzione di ripartizione Sia F X una funzione da in. consideriamo le seguenti condizioni: F X è non decrescente lim ( ) x F
Esercitazione del /0/0 Istituzioni di Calcolo delle Probabilità David Barbato Funzione di ripartizione Sia F X una funzione da in. consideriamo le seguenti condizioni: F X è non decrescente lim ( ) x F
0.1 P(A n ) Quindi stiamo cercando n che soddisfa la seguente relazione: n + 180
 Esercizio 1 Alcuni ingegneri civili ritengono che il peso in tonnellate che un braccio di ponte può sopportare senza avere cedimenti strutturali possa descriversi mediante una variabile aleatoria Y con
Esercizio 1 Alcuni ingegneri civili ritengono che il peso in tonnellate che un braccio di ponte può sopportare senza avere cedimenti strutturali possa descriversi mediante una variabile aleatoria Y con
a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre gli zeri di f e studiarne il segno.
 1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
Corso di Laurea Magistrale in Ingegneria Informatica A.A. 2016/17 Processi stocastici e analisi di serie temporali
 Corso di Laurea Magistrale in Ingegneria Informatica A.A. 206/7 Processi stocastici e analisi di serie temporali PROVA DI ESONERO SUI PROCESSI DI MARKOV DEL 6 DICEMBRE 206 Punteggi: : + + 4 2; 2: 2 5;
Corso di Laurea Magistrale in Ingegneria Informatica A.A. 206/7 Processi stocastici e analisi di serie temporali PROVA DI ESONERO SUI PROCESSI DI MARKOV DEL 6 DICEMBRE 206 Punteggi: : + + 4 2; 2: 2 5;
DISTRIBUZIONI DI PROBABILITA
 DISTRIBUZIONI DI PROBABILITA La distribuzione di probabilità e un modello matematico, uno schema di riferimento, che ha caratteristiche note e che può essere utilizzato per rispondere a delle domande derivate
DISTRIBUZIONI DI PROBABILITA La distribuzione di probabilità e un modello matematico, uno schema di riferimento, che ha caratteristiche note e che può essere utilizzato per rispondere a delle domande derivate
Indici di posizione e dispersione per distribuzioni di variabili aleatorie
 Indici di posizione e dispersione per distribuzioni di variabili aleatorie 12 maggio 2017 Consideriamo i principali indici statistici che caratterizzano una distribuzione: indici di posizione, che forniscono
Indici di posizione e dispersione per distribuzioni di variabili aleatorie 12 maggio 2017 Consideriamo i principali indici statistici che caratterizzano una distribuzione: indici di posizione, che forniscono
Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari"
 Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
SOMMARIO DELLE MISURE DIRETTE
 p. 1/21 SOMMARIO DELLE MISURE DIRETTE Studio delle caratteristiche degli strumenti usati, evidenziare possibili errori sistematici, correggerli. p. 1/21 SOMMARIO DELLE MISURE DIRETTE Studio delle caratteristiche
p. 1/21 SOMMARIO DELLE MISURE DIRETTE Studio delle caratteristiche degli strumenti usati, evidenziare possibili errori sistematici, correggerli. p. 1/21 SOMMARIO DELLE MISURE DIRETTE Studio delle caratteristiche
Corso Integrato di Statistica Informatica e Analisi dei Dati Sperimentali. Esercitazione E
 Corso Integrato di Statistica Informatica e Analisi dei Dati Sperimentali A.A 2009-2010 Esercitazione E Scopo dell esercitazione Applicazioni del teorema del limite centrale. Rappresentazione delle incertezze
Corso Integrato di Statistica Informatica e Analisi dei Dati Sperimentali A.A 2009-2010 Esercitazione E Scopo dell esercitazione Applicazioni del teorema del limite centrale. Rappresentazione delle incertezze
VIII Indice 2.6 Esperimenti Dicotomici Ripetuti: Binomiale ed Ipergeometrica Processi Stocastici: Bernoul
 1 Introduzione alla Teoria della Probabilità... 1 1.1 Introduzione........................................ 1 1.2 Spazio dei Campioni ed Eventi Aleatori................ 2 1.3 Misura di Probabilità... 5
1 Introduzione alla Teoria della Probabilità... 1 1.1 Introduzione........................................ 1 1.2 Spazio dei Campioni ed Eventi Aleatori................ 2 1.3 Misura di Probabilità... 5
PROF. ING. UMBERTO CRISALLI Dipartimento di Ingegneria dell Impresa.
 corso di Teoria e Tecnica della Circolazione + Trasporti e Territorio a.a. 2012-2013 ELEMENTI DI TEORIA DELLE CODE PROF. ING. UMBERTO CRISALLI Dipartimento di Ingegneria dell Impresa crisalli@ing.uniroma2.it
corso di Teoria e Tecnica della Circolazione + Trasporti e Territorio a.a. 2012-2013 ELEMENTI DI TEORIA DELLE CODE PROF. ING. UMBERTO CRISALLI Dipartimento di Ingegneria dell Impresa crisalli@ing.uniroma2.it
Facoltà di Ingegneria Calcolo delle Probabilità e Statistica Ingegneria Civile e A&T e Informatica
 Facoltà di Ingegneria Calcolo delle Probabilità e Statistica Ingegneria Civile e A&T e Informatica Prima prova scritta A.A. 8-9 Durata della prova h Punteggi: ) + + ; ) + + + ; ) +. Totale. Esercizio Sia
Facoltà di Ingegneria Calcolo delle Probabilità e Statistica Ingegneria Civile e A&T e Informatica Prima prova scritta A.A. 8-9 Durata della prova h Punteggi: ) + + ; ) + + + ; ) +. Totale. Esercizio Sia
METODI DI COLLOCAZIONE POLINOMIALE (Metodi di Runge-Kutta continui) November 30, 2004
 METODI DI COLLOCAZIONE POLINOMIALE (Metodi di Runge-Kutta continui) November, Nell approssimare numericamente un problema di Cauchy, puo capitare di essere interessati a valori della soluzione in punti
METODI DI COLLOCAZIONE POLINOMIALE (Metodi di Runge-Kutta continui) November, Nell approssimare numericamente un problema di Cauchy, puo capitare di essere interessati a valori della soluzione in punti
VARIABILI CASUALI CONTINUE
 p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale continua può assumere tutti gli infiniti valori appartenenti ad un intervallo di numeri reali. p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale
p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale continua può assumere tutti gli infiniti valori appartenenti ad un intervallo di numeri reali. p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale
ESAME. 9 Gennaio 2017 COMPITO B
 ESAME 9 Gennaio 2017 COMPITO B Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
ESAME 9 Gennaio 2017 COMPITO B Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
Calcolo delle Probabilità 2
 Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
Corso di Calcolo Numerico
 Prof. L. Brandolini Corso di Calcolo Numerico Dott.ssa N. Franchina Laboratorio 5 Equazioni differenziali ordinarie: metodi espliciti 25 Novembre 215 Esercizi di implementazione Un equazione differenziale
Prof. L. Brandolini Corso di Calcolo Numerico Dott.ssa N. Franchina Laboratorio 5 Equazioni differenziali ordinarie: metodi espliciti 25 Novembre 215 Esercizi di implementazione Un equazione differenziale
Computazione per l interazione naturale: fondamenti probabilistici (1)
 Computazione per l interazione naturale: fondamenti probabilistici (1) Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Computazione per l interazione naturale: fondamenti probabilistici (1) Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Mauro Piccioni PROBABILITÀ DI BASE CON 136 ESERCIZI SVOLTI. II edizione
 A01 164 Mauro Piccioni PROBABILITÀ DI BASE CON 136 ESERCIZI SVOLTI II edizione Copyright MMXI ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133/A B 00173 Roma
A01 164 Mauro Piccioni PROBABILITÀ DI BASE CON 136 ESERCIZI SVOLTI II edizione Copyright MMXI ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133/A B 00173 Roma
ESAME. 9 Gennaio 2017 COMPITO A
 ESAME 9 Gennaio 2017 COMPITO A Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
ESAME 9 Gennaio 2017 COMPITO A Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
con distribuzione gaussiana standard e si ponga
 Laurea Triennale in Matematica, Università La Sapienza Corso di Probabilità, AA 6/7 Prova di Esonero Maggio 7 Testi e soluzioni degli esercizi proposti Siano Z, Z, Z variabili aleatorie indipendenti e
Laurea Triennale in Matematica, Università La Sapienza Corso di Probabilità, AA 6/7 Prova di Esonero Maggio 7 Testi e soluzioni degli esercizi proposti Siano Z, Z, Z variabili aleatorie indipendenti e
Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha. P {X = a, Y = b} = P {X = a}p {Y = b}
 Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha P {X = a, Y = b} = P {X = a}p {Y = b} Una variabile aleatoria χ che assume i soli valori 1, 2,..., n
Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha P {X = a, Y = b} = P {X = a}p {Y = b} Una variabile aleatoria χ che assume i soli valori 1, 2,..., n
Corso di Calcolo Numerico
 Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 9 - EQUAZIONI DIFFERENZIALI ORDINARIE valori iniziali Valori iniziali Ci occuperemo della soluzione numerica di equazioni del prim ordine
Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 9 - EQUAZIONI DIFFERENZIALI ORDINARIE valori iniziali Valori iniziali Ci occuperemo della soluzione numerica di equazioni del prim ordine
Istituzioni di Probabilità Laurea magistrale in Matematica a.a. 2013/14 Registro delle lezioni
 Istituzioni di Probabilità Laurea magistrale in Matematica a.a. 2013/14 Registro delle lezioni Lezione 1 (25/2). Introduzione al corso. Prime definizioni sui processi stocastici (processo stocastico, distribuzioni
Istituzioni di Probabilità Laurea magistrale in Matematica a.a. 2013/14 Registro delle lezioni Lezione 1 (25/2). Introduzione al corso. Prime definizioni sui processi stocastici (processo stocastico, distribuzioni
Analisi Numerica: quadratura
 Analisi Numerica: quadratura S. Maset Dipartimento di Matematica e Geoscienze, Università di Trieste In situazioni come queste, si ricorrerà a metodi numerici come quelli che presenteremo per calcolare
Analisi Numerica: quadratura S. Maset Dipartimento di Matematica e Geoscienze, Università di Trieste In situazioni come queste, si ricorrerà a metodi numerici come quelli che presenteremo per calcolare
Presentazione dell edizione italiana
 1 Indice generale Presentazione dell edizione italiana Prefazione xi xiii Capitolo 1 Una introduzione alla statistica 1 1.1 Raccolta dei dati e statistica descrittiva... 1 1.2 Inferenza statistica e modelli
1 Indice generale Presentazione dell edizione italiana Prefazione xi xiii Capitolo 1 Una introduzione alla statistica 1 1.1 Raccolta dei dati e statistica descrittiva... 1 1.2 Inferenza statistica e modelli
Complementi di Matematica e Calcolo Numerico A.A Laboratorio 11 - Metodi numerici per equazioni differenziali ordinarie
 Complementi di Matematica e Calcolo Numerico A.A. 2010-2011 Laboratorio 11 - Metodi numerici per equazioni differenziali ordinarie Cosideriamo il seguente Problema di Cauchy: Trovare una funzione y : I
Complementi di Matematica e Calcolo Numerico A.A. 2010-2011 Laboratorio 11 - Metodi numerici per equazioni differenziali ordinarie Cosideriamo il seguente Problema di Cauchy: Trovare una funzione y : I
Project Scheduling: PERT. Il PERT ha potenzialità superiori rispetto a quelle di un semplice mezzo per la pianificazione ed il controllo.
 1. Introduzione Project Scheduling: PERT Il PERT è una tecnica introdotta per la pianificazione ed il controllo di progetti in cui le durate t ij delle singole attività sono delle variabili aleatorie.
1. Introduzione Project Scheduling: PERT Il PERT è una tecnica introdotta per la pianificazione ed il controllo di progetti in cui le durate t ij delle singole attività sono delle variabili aleatorie.
E (X 2 ) = E (G) + E (E 2 ) = 1, V ar (X 2 ) = V ar (G) + V ar (E 2 ) = 5, Cov(X 1, X 2 ) = Cov(G + E 1, G + E 2 ) = V ar (G) = 4,
 Laurea Triennale in Matematica, Università La Sapienza Corso di Probabilità, AA 04/05 Prova di Esonero Maggio 05 degli esercizi proposti Siano G, E, E tre variabili aleatorie gaussiane indipendenti, rispettivamente
Laurea Triennale in Matematica, Università La Sapienza Corso di Probabilità, AA 04/05 Prova di Esonero Maggio 05 degli esercizi proposti Siano G, E, E tre variabili aleatorie gaussiane indipendenti, rispettivamente
5. Distribuzioni. Corso di Simulazione. Anno accademico 2009/10
 Anno accademico 2009/10 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Anno accademico 2009/10 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Esercizi su formula di Itô
 Esercizi su formula di Itô 1. Scrivere il differenziale stocastico dei seguenti processi: (i) X t = B t (ii) X t = t + e B t (iii) X t = B 3 t 3tB t (iv) X t = 1 + t + e B t (v) X t = [B 1 (t)] + [B (t)]
Esercizi su formula di Itô 1. Scrivere il differenziale stocastico dei seguenti processi: (i) X t = B t (ii) X t = t + e B t (iii) X t = B 3 t 3tB t (iv) X t = 1 + t + e B t (v) X t = [B 1 (t)] + [B (t)]
assuma valori in un determinato intervallo è data dall integrale della sua densità ( = )=
 VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
Capitolo Trasformata di Laplace
 Capitolo Trasformata di Laplace. Segnali lo studio dei sistemi. Trasformata di Laplace.3 Antitrasformata di Laplace.4 Antitrasformata di Laplace: metodo delle frazioni parziali . SEGNALI PER LO STUDIO
Capitolo Trasformata di Laplace. Segnali lo studio dei sistemi. Trasformata di Laplace.3 Antitrasformata di Laplace.4 Antitrasformata di Laplace: metodo delle frazioni parziali . SEGNALI PER LO STUDIO
DISTRIBUZIONI DI PROBABILITA
 DISTRIBUZIONI DI PROBABILITA Nell associare ai risultati di un esperimento un valore numerico si costruisce una variabile casuale (o aleatoria, o stocastica). Ogni variabile casuale ha una corrispondente
DISTRIBUZIONI DI PROBABILITA Nell associare ai risultati di un esperimento un valore numerico si costruisce una variabile casuale (o aleatoria, o stocastica). Ogni variabile casuale ha una corrispondente
Raccolta di Esercizi d esame ( di Calcolo Numerico) Prof. Laura Pezza. Equazioni non lineari
 Raccolta di Esercizi d esame ( di Calcolo Numerico) Prof. Laura Pezza Equazioni non lineari ESERCIZIO 1 Data l equazione ln(e + x) = 1 (1 + 4x) + 1 2 1.1 verificare analiticamente se sono soddisfatte le
Raccolta di Esercizi d esame ( di Calcolo Numerico) Prof. Laura Pezza Equazioni non lineari ESERCIZIO 1 Data l equazione ln(e + x) = 1 (1 + 4x) + 1 2 1.1 verificare analiticamente se sono soddisfatte le
Metodi e Modelli dei Mercati Finanziari
 Diario delle lezioni di Metodi e Modelli dei Mercati Finanziari a.a. 2018/2019 www.mat.uniroma2.it/~caramell/did 1819/mmmf.htm Parte I: Opzioni Europee e Metodi Monte Carlo Lezioni 1, 2-02/10/2018 Breve
Diario delle lezioni di Metodi e Modelli dei Mercati Finanziari a.a. 2018/2019 www.mat.uniroma2.it/~caramell/did 1819/mmmf.htm Parte I: Opzioni Europee e Metodi Monte Carlo Lezioni 1, 2-02/10/2018 Breve
3. Distribuzioni. Corso di Simulazione. Anno accademico 2006/07
 Anno accademico 2006/07 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Anno accademico 2006/07 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Statistica. Alfonso Iodice D Enza
 Statistica Alfonso Iodice D Enza iodicede@unina.it Università degli studi di Cassino () Statistica 1 / 27 Outline 1 () Statistica 2 / 27 Outline 1 2 () Statistica 2 / 27 Outline 1 2 3 () Statistica 2 /
Statistica Alfonso Iodice D Enza iodicede@unina.it Università degli studi di Cassino () Statistica 1 / 27 Outline 1 () Statistica 2 / 27 Outline 1 2 () Statistica 2 / 27 Outline 1 2 3 () Statistica 2 /
Corso di Analisi Numerica
 Corso di Laurea in Ingegneria Informatica Corso di Analisi Numerica 9 - EQUAZIONI DIFFERENZIALI ORDINARIE Lucio Demeio Dipartimento di Scienze Matematiche 1 2 3 Problemi ai valori iniziali Problemi ai
Corso di Laurea in Ingegneria Informatica Corso di Analisi Numerica 9 - EQUAZIONI DIFFERENZIALI ORDINARIE Lucio Demeio Dipartimento di Scienze Matematiche 1 2 3 Problemi ai valori iniziali Problemi ai
Alessio Russo Numeri, gruppi, polinomi. Un introduzione all Algebra Nuova edizione
 A1 Alessio Russo Numeri, gruppi, polinomi Un introduzione all Algebra Nuova edizione Copyright MMXIII ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133/A B
A1 Alessio Russo Numeri, gruppi, polinomi Un introduzione all Algebra Nuova edizione Copyright MMXIII ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133/A B
Corso di Analisi Numerica
 Corso di Laurea in Ingegneria Informatica Corso di Analisi Numerica 9 - EQUAZIONI DIFFERENZIALI ORDINARIE Lucio Demeio Dipartimento di Scienze Matematiche 1 Problemi ai Valori Iniziali: metodo di Eulero
Corso di Laurea in Ingegneria Informatica Corso di Analisi Numerica 9 - EQUAZIONI DIFFERENZIALI ORDINARIE Lucio Demeio Dipartimento di Scienze Matematiche 1 Problemi ai Valori Iniziali: metodo di Eulero
()Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Riassunto Abbiamo introdotto le equazioni differenziali stocastiche, equazioni del tipo dx t = b (t, X t ) dt + σdb t (o un po più generali) dove B t è il moto
Probablità, Statistica e Processi Stocastici Riassunto Abbiamo introdotto le equazioni differenziali stocastiche, equazioni del tipo dx t = b (t, X t ) dt + σdb t (o un po più generali) dove B t è il moto
Matematica con elementi di Informatica
 Teoria dell integrazione Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche. () Teoria
Teoria dell integrazione Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche. () Teoria
ESERCITAZIONE 23 : PREPARAZIONE AL COMPITINO
 ESERCITAZIONE 23 : PREPARAZIONE AL COMPITINO e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 28 Maggio 2013 Esercizio
ESERCITAZIONE 23 : PREPARAZIONE AL COMPITINO e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 28 Maggio 2013 Esercizio
7 - Distribuzione Poissoniana
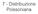 7 - Distribuzione Poissoniana Probabilita' (poissoniana) o densita' di probabilita' (gaussiana) 0.7 Poisson, λ=0.5 Gaussiana, µ=λ=0.5, σ= 0.6 0.5 0.4 0.3 0.2 0.1 0 0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 n = numero
7 - Distribuzione Poissoniana Probabilita' (poissoniana) o densita' di probabilita' (gaussiana) 0.7 Poisson, λ=0.5 Gaussiana, µ=λ=0.5, σ= 0.6 0.5 0.4 0.3 0.2 0.1 0 0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 n = numero
Analisi Stocastica Programma del corso 2008/09
 Analisi Stocastica Programma del corso 2008/09 [13/01] Introduzione. 0. Preludio (1 ora) [1] Descrizione del corso: obiettivi, prerequisiti, propedeuticità. Un esempio euristico: lavoro di una forza, valore
Analisi Stocastica Programma del corso 2008/09 [13/01] Introduzione. 0. Preludio (1 ora) [1] Descrizione del corso: obiettivi, prerequisiti, propedeuticità. Un esempio euristico: lavoro di una forza, valore
Distribuzioni di probabilità nel continuo
 Distribuzioni di probabilità nel continuo Prof.ssa Fabbri Francesca Classe 5C Variabili casuali continue Introduzione: Una Variabile Casuale o Aleatoria è una grandezza che, nel corso di un esperimento
Distribuzioni di probabilità nel continuo Prof.ssa Fabbri Francesca Classe 5C Variabili casuali continue Introduzione: Una Variabile Casuale o Aleatoria è una grandezza che, nel corso di un esperimento
Corso di Analisi Numerica - AN410. Parte 5: formule di quadratura. Roberto Ferretti
 Corso di Analisi Numerica - AN410 Parte 5: formule di quadratura Roberto Ferretti UNIVERSITÀ DEGLI STUDI ROMA TRE Formule di quadratura interpolatorie: teoria generale Formule di Newton Cotes semplici
Corso di Analisi Numerica - AN410 Parte 5: formule di quadratura Roberto Ferretti UNIVERSITÀ DEGLI STUDI ROMA TRE Formule di quadratura interpolatorie: teoria generale Formule di Newton Cotes semplici
Variabili aleatorie continue
 Variabili aleatorie continue Per descrivere la distribuzione di una variabile aleatoria continua, non si può più assegnare una probabilità positiva ad ogni valore possibile. Si assume allora di poter specificare
Variabili aleatorie continue Per descrivere la distribuzione di una variabile aleatoria continua, non si può più assegnare una probabilità positiva ad ogni valore possibile. Si assume allora di poter specificare
CP110 Probabilità: Esonero 2. Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 212-13, II semestre 23 maggio, 213 CP11 Probabilità: Esonero 2 Testo e soluzione 1. (7 punti) Una scatola contiene 1 palline, 5 bianche e 5 nere. Ne vengono
Dipartimento di Matematica, Roma Tre Pietro Caputo 212-13, II semestre 23 maggio, 213 CP11 Probabilità: Esonero 2 Testo e soluzione 1. (7 punti) Una scatola contiene 1 palline, 5 bianche e 5 nere. Ne vengono
Equazioni Iperboliche
 Equazioni Iperboliche Le equazioni iperboliche rappresentano probabilmente la classe che descrive il più ampio numero di fenomeni in diversi campi della fisica fisica (fluidodinamica, acustica, elettromagnetismo
Equazioni Iperboliche Le equazioni iperboliche rappresentano probabilmente la classe che descrive il più ampio numero di fenomeni in diversi campi della fisica fisica (fluidodinamica, acustica, elettromagnetismo
CAPITOLO 3 LA LEGGE DI GAUSS
 CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
Università di Foggia - Facoltà di Economia. Prova scritta di Matematica Generale - Vecchio Ordinamento - 04 giugno 2002
 Università di Foggia - Facoltà di Economia Prova scritta di Matematica Generale - Vecchio Ordinamento - 04 giugno 00 Cognome e nome............................................ Numero di matricola...........
Università di Foggia - Facoltà di Economia Prova scritta di Matematica Generale - Vecchio Ordinamento - 04 giugno 00 Cognome e nome............................................ Numero di matricola...........
RICHIAMI DI CALCOLO DELLE PROBABILITÀ
 UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
ESAME SCRITTO DI FISICA MODERNA. 22 giugno Traccia di soluzione
 ESAME SCRITTO DI FISICA MODERNA giugno 08 Traccia di soluzione ) Ponendo α = /σ ), il valore medio della posizione è + ψ ˆx ψ = dx ψ ˆx x x ψ = dx ψ x)xψx) = α + dx x e αx x 0), ) e con un semplice cambio
ESAME SCRITTO DI FISICA MODERNA giugno 08 Traccia di soluzione ) Ponendo α = /σ ), il valore medio della posizione è + ψ ˆx ψ = dx ψ ˆx x x ψ = dx ψ x)xψx) = α + dx x e αx x 0), ) e con un semplice cambio
