3 a 11 a a 1n a 21 a a 2n a 31 a a 3n ...
|
|
|
- Federica Lillo
- 4 anni fa
- Visualizzazioni
Transcript
1 Matrici n n n n n Nozioni fondamentali Algebra delle matrici Determinanti di matrici quadrate Inversa di una matrice Rango di una matrice n Nozioni fondamentali Introduzione In questo capitolo affronteremo lo studio delle matrici, che sono tabelle di elementi ordinati per righe e colonne. Dopo aver visto alcune definizioni fondamentali, ci occuperemo dell algebra delle matrici, imparando quindi le operazioni tra matrici e le relative proprietà: studieremo la somma e il prodotto scalare tra matrici, che (come vedremo) non va confuso con il prodotto di una matrice per uno scalare, cioè per un numero. Assoceremo quindi a ogni matrice quadrata una quantità fondamentale, il suo determinante, di cui vedremo diversi utilizzi, e scopriremo inoltre come calcolare l inversa di una matrice invertibile. Infine, affronteremo il concetto di rango di una matrice. Spesso le matrici costituiscono un argomento che lo studente non apprezza pienamente, a causa forse dell artificiosità di alcune definizioni, come quella ad esempio del prodotto tra matrici. Proseguendo negli studi, si può invece comprendere l enorme utilità delle matrici, che, permettendo di esprimere in maniera sintetica ed elegante i concetti più svariati, hanno consentito ai matematici di arrivare a importanti generalizzazioni in diverse teorie matematiche. Definizioni DEFINIZIONE MATRICE Detti m ed n due numeri interi positivi e considerati m n numeri reali, si chiama matrice (rettangolare) di tipo ðm nþ l insieme degli m n numeri considerati, disposti ordinatamente su m righe e su n colonne, come nello schema che segue: a a... a n a a... a n a a... a n a m a m... a mn I numeri reali racchiusi nella tabella si dicono elementi della matrice e sono rappresentati da una lettera munita di due indici: il primo indice fornisce la riga a cui appartiene l elemento e il secondo la colonna. Ad esempio, l elemento a si trova all incrocio tra la terza riga e la seconda colonna le righe e le colonne si contano rispettivamente a partire dall alto e da sinistra, come è naturale. & 0 De Agostini Scuola SpA Novara
2 Matrici Le matrici si indicano di solito con lettere maiuscole e si scrive, sinteticamente, A ¼½a ik Š con i ¼ ::: m k ¼ ::: n Se m ¼ n si ha una matrice quadrata (di ordine n). ESEMPIO A ¼ pffiffiffi 0 e B ¼ 0 pffiffiffiffiffiffi 0 sono rispettivamente una matrice rettangolare di tipo ð Þ p e una matrice quadrata di ordine. Con ovvio significato dei simboli si ha, ad esempio: a ¼, a ¼ ffiffiffi p, b ¼ 0, b ¼ ffiffiffiffiffiffi,... DEFINIZIONI MATRICE RIGA, MATRICE COLONNA Si chiama matrice riga o vettore riga una matrice di ordine ð nþ, cioè formata da una sola riga si chiama matrice colonna o vettore colonna una matrice di ordine ðm Þ, cioè formata da una sola colonna. DEFINIZIONE MATRICE NULLA La matrice nulla o matrice zero è la matrice i cui elementi sono tutti uguali a zero si indica con Z ¼½z ik Š z ik ¼ 0 con i ¼ ::: m k ¼ ::: n DEFINIZIONE MATRICI UGUALI Due matrici dello stesso tipo sono uguali, e scriveremo A ¼ B, se hanno uguali tutti gli elementi corrispondenti. DEFINIZIONE MATRICE OPPOSTA La matrice opposta di A, che viene indicata con il simbolo A, èla matrice, dello stesso tipo di A, i cui elementi sono gli opposti dei corrispondenti elementi di A. DEFINIZIONE MATRICE TRASPOSTA Data una matrice A di tipo ðm nþ si definisce trasposta di A, e si indica con A T, la matrice di tipo ðn mþ che si ottiene da A scambiando ordinatamente le righe con le colonne. È del tutto evidente che ða T Þ T ¼ A, cioè la trasposta della trasposta di A, èla stessa matrice A. ESEMPIO Data la matrice A ¼ 0 si ha 0 A ¼ A T ¼ 0 e ða TÞ T ¼ ¼ A 0 & 0 De Agostini Scuola SpA Novara
3 Matrici Diagonale principale e diagonale secondaria di una matrice quadrata DEFINIZIONI DIAGONALE PRINCIPALE, DIAGONALE SECONDARIA Se A è una matrice quadrata di ordine n, si chiama diagonale principale di A l insieme degli elementi a, a ::: a nn che hanno i due indici uguali. La diagonale secondaria di A è l insieme degli elementi a n, a n,..., a n i cui indici hanno per somma n þ. ESEMPIO Consideriamo la seguente matrice: 0 = A ¼ 0 0 diagonale secondaria diagonale principale Si tratta di una matrice quadrata di ordine. La sua diagonale principale è costituita dagli elementi,,,, mentre la sua diagonale secondaria ha per elementi,, 0,. Matrici diagonali e triangolari. Matrice unità DEFINIZIONE MATRICE DIAGONALE Si dice che una matrice quadrata è diagonale se sono nulli tutti i suoi elementi tranne quelli che costituiscono la diagonale principale. DEFINIZIONE MATRICE TRIANGOLARE Una matrice quadrata si dice triangolare superiore se tutti gli elementi al di sotto della diagonale principale sono nulli. Una matrice quadrata è detta triangolare inferiore se tutti gli elementi al di sopra della diagonale principale sono nulli. DEFINIZIONE MATRICE UNITÀ Si chiama matrice unità o matrice identica (di ordine n) quella matrice diagonale i cui elementi, sulla diagonale principale, sono tutti uguali a. Indicheremo la matrice unità con il simbolo I o, eventualmente, I n per specificarne l ordine. ESEMPIO Delle seguenti matrici A è una matrice diagonale di ordine, B è triangolare superiore di ordine e I è la matrice unità di ordine A ¼ 0 0 B ¼ I ¼ & 0 De Agostini Scuola SpA Novara
4 Matrici n Algebra delle matrici Somma delle matrici Consideriamo ora l operazione di addizione tra matrici, la cui definizione è molto intuitiva. DEFINIZIONE SOMMA DI MATRICI Si definisce somma di due matrici A e B dello stesso tipo (ossia con lo stesso numero di righe e lo stesso numero di colonne), la matrice, dello stesso tipo di A edib, i cui elementi sono la somma dei corrispondenti elementi delle matrici date. Tale matrice somma viene indicata con A þ B. La differenza di due matrici si può definire come somma della prima matrice con l opposto della seconda: A B ¼ A þð BÞ: ESEMPIO 0 Se è A ¼ e B ¼, risulta 0 þ þ þ 0 A þ B ¼ ¼ 0 þ þ e 0 A B ¼ ¼ 0 ð Þ 8 Prodotto di una matrice per uno scalare Anche la definizione di prodotto di una matrice per uno scalare è intuitiva. DEFINIZIONE PRODOTTO DI UNA MATRICE PER UNO SCALARE Si chiama prodotto della matrice A per uno scalare (cioè per il numero reale ) la matrice che si ottiene da A moltiplicando tutti i suoi elementi per. ESEMPIO Sia A ¼. Risulta: A ¼ ¼ A ¼ ¼ Prodotto scalare di una matrice riga per una matrice colonna Affrontiamo adesso la definizione del prodotto tra matrici che, come vedremo, è alquanto laboriosa. Per prima cosa è necessario introdurre il prodotto di una matrice riga per una matrice colonna. Consideriamo nell ordine una matrice riga A di tipo ð sþ e una matrice colonna B di tipo ðs Þ: b A ¼½a a ::: a s Š B ¼ b. b s & 0 De Agostini Scuola SpA Novara
5 Matrici Definiamo prodotto scalare di A per B la matrice P di tipo ð Þ che ha per elemento il numero che si ottiene sommando i prodotti del tipo a j b j con j ¼,,..., s. Osserviamo che tale matrice è costituita da un solo numero, cioè è uno scalare. P ¼ A B ¼½a b þ a b þ ::: þ a s b s Š¼ Xs j¼ a j b j NOTA BENE X s j¼ a j b j si legge sommatoria per j che va da a s di a j b j. ESEMPIO Date le matrici A ¼½ Š e B ¼, si ottiene P ¼ A B ¼½ Š ¼½þþŠ ¼½Š 8 Prodotto di matrici Siano A una matrice di tipo ðm sþ e B una matrice di tipo ðs nþ. Le due matrici siano dunque tali che il numero delle colonne della prima sia uguale al numero delle righe della seconda (matrici conformabili rispetto alla moltiplicazione). Si definisce prodotto (righe per colonne) della matrice A di tipo ðm sþ per la matrice B di tipo ðs nþ la matrice P di tipo ðm nþ il cui generico elemento p ik si ottiene moltiplicando scalarmente la i-esima riga di A per la k-esima colonna di B: X s P ¼ A B ¼½p ik Š¼ a ij b jk, j¼ ATTENZIONE! Il prodotto righe per colonne tra matrici si può effettuare solo se il numero di colonne della prima matrice è uguale al numero di righe della seconda. con i ¼ ::: m e k ¼ ::: n Schematicamente si ha b k b k >< >= >= m righe s righe ¼ m righe. ::::::::p a i a i ::: a ik :::::::: is >: > > riga i b sk. colonna k fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl} fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} s colonne n colonne n colonne Osserviamo che il punto che indica il prodotto tra matrici può anche essere omesso, come si usa fare con il punto che indica il prodotto tra numeri. Si noti, inoltre, che potrebbe essere definito il prodotto colonne per righe di matrici di tipo ðs mþ per matrici di tipo ðn sþ. ESEMPIO Calcoliamo il prodotto delle matrici A ¼ 0 B ¼ 0 & 0 De Agostini Scuola SpA Novara
6 Matrici Osserviamo che le due matrici sono conformabili rispetto alla moltiplicazione essendo A di tipo ð Þ e B di tipo ð Þ. La matrice prodotto P sarà quindi di tipo ð Þ. Calcoliamo dunque i elementi di P l elemento p sarà il prodotto scalare della prima riga di A per la prima colonna di B, l elemento p sarà il prodotto scalare della prima riga di A per la seconda colonna di B e così via...: p ¼½ Š ¼ þ ¼ p ¼½ Š ¼ þ ¼ ecc: Proseguendo in questo modo, possiamo calcolare gli altri elementi della matrice prodotto e verificare che si ottiene P ¼ A B ¼ Proprietà delle operazioni Le operazioni ora definite godono delle seguenti proprietà.. Proprietà distributiva del prodotto di una matrice per uno scalare rispetto alla somma di matrici: ða þ BÞ ¼A þ B. Proprietà distributiva del prodotto di una matrice per uno scalare rispetto alla somma di scalari: ð þ ÞA ¼ A þ A. Proprietà associativa del prodotto di una matrice per uno scalare:. Prodotto per e per :. Proprietà commutativa della somma: ðþa ¼ ð AÞ A ¼ A ð ÞA ¼ A A þ B ¼ B þ A. Proprietà associativa della somma e del prodotto: A þðb þ CÞ ¼ðA þ BÞþC A ðb CÞ ¼ðA BÞC. Proprietà distributive (sinistra e destra) del prodotto rispetto alla somma: A ðb þ CÞ ¼A B þ A C ðb þ CÞA ¼ B A þ C A Le proprietà dalla alla e la prima delle sono conseguenza immediata delle proprietà delle operazioni aritmetiche. Dimostriamo, a titolo di esempio, la. Occorre dimostrare che è ð þ ÞA ¼ A þ A. n Dimostrazione Consideriamo il generico elemento di riga i e colonna k della matrice ð þ ÞA: esso è ð þ Þa ik. Il corrispondente elemento della matrice A þ A è dato dalla somma degli elementi di riga i e colonna k delle matrici A e A essi sono rispettivamente a ik e a ik e la loro somma è a ik þ a ik ¼ðþÞa ik : Pertanto le due matrici ð þ ÞA e A þ A, avendo uguali tutti gli elementi corrispondenti, sono uguali. c.v.d. Analoghe sono le dimostrazioni delle proprietà,,, che lasciamo al lettore per esercizio. Più complesse sono le dimostrazioni della seconda delle e delle. Dimostriamo la prima della, lasciando come esercizio la dimostrazione delle altre. Occorre dimostrare che è AðB þ CÞ ¼AB þ AC. & 0 De Agostini Scuola SpA Novara
7 Matrici n Dimostrazione Consideriamo il generico elemento di riga i e colonna k della matrice A ðbþcþ. Esso è il prodotto scalare della riga i della matrice A per la colonna k della matrice B þ C, ossia b k þ c k b ½a i a i... a in Š k þ c k... ¼ a iðb k þ c k Þþa i ðb k þ c k Þþ...þ a in ðb nk þ c nk Þ b nk þ c nk Il generico elemento di riga i e colonna k della matrice AB þ AC è dato dalla somma dei corrispondenti elementi delle matrici AB e AC, ossia b k c k b ½a i a i... a in Š k... þ½a c i a i... a in Š k... ¼ b nk c nk ¼ða i b k þ a i b k þ...þ a in b nk Þþða i c k þ a i c k þ...þ a in c nk Þ¼ ¼ a i ðb k þ c k Þþa i ðb k þ c k Þþ...þ a in ðb nk þ c nk Þ Pertanto le due matrici AðB þ CÞ e AB þ AC, avendo uguali tutti gli elementi corrispondenti, sono uguali. c.v.d. È importante rilevare che il prodotto tra matrici non gode della proprietà commutativa, ossia, in generale è A B ¼ B A (si veda il successivo ESEMPIO ). Ciò non esclude che in casi particolari sia A B ¼ B A. Per tale motivo è necessario formulare due proprietà distributive distinte: infatti, in mancanza della proprietà commutativa del prodotto, non è lecito dedurre l una dall altra. Inoltre, non vale per le matrici la legge di annullamento del prodotto, ossia il prodotto di due matrici può essere la matrice nulla senza che nessuno dei fattori sia la matrice nulla (ESEMPIO ). Infine la matrice unità, definita al PARAGRAFO, è elemento neutro rispetto al prodotto, ossia non muta le matrici con cui viene moltiplicata: A I n ¼ A I n B ¼ B ESEMPI Verifichiamo con un esempio che il prodotto di matrici non gode della proprietà commutativa. 0 Consideriamo le matrici A ¼, B ¼ 0 Si ha A B ¼ ¼ 8 0 B A ¼ ¼ e quindi è A B ¼ B A: Ricordiamo però che, in casi particolari, può risultare A B ¼ B A. Possiamo verificare che ciò accade, ad esempio, se A e B sono matrici diagonali dello stesso ordine. Si ha ¼. Si verifica così che il prodotto di due matrici, nessuna 0 0 delle quali è la matrice nulla, può essere la matrice nulla: per il prodotto tra matrici non vale la legge di annullamento del prodotto. Siano A, B, C le seguenti matrici: A ¼ B ¼ C ¼ 0 0 & 0 De Agostini Scuola SpA Novara
8 Matrici Calcoliamo A C þ B C e verifichiamo che risulta uguale a ða þ BÞC (proprietà distributiva destra del prodotto rispetto alla somma). Si ha A C þ B C ¼ þ ¼ ¼ þ ¼ 0! ða þ BÞC ¼ þ ¼ 0 0 ¼ ¼ 0 Si ha quindi ða þ BÞC ¼ A C þ B C: Si può verificare che è anche C ðaþbþ ¼C A þ C B: 0 Potenza di una matrice quadrata Si può definire la potenza n-esima di una matrice quadrata nel modo seguente: A n ¼ fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl} A A ::: A ðn Þ n volte n Determinanti di matrici quadrate Definizione A una matrice quadrata può essere associato un valore numerico, detto determinante, secondo le modalità che vedremo tra poco. Alle matrici rettangolari di tipo (m, n), con m ¼ n, invece, non viene associato alcun valore numerico. Sia dunque A ¼½a ij Š i j ¼ ::: n una matrice quadrata di ordine n. Il suo determinante verrà indicato con uno dei seguenti simboli a a... a n a a... a n ATTENZIONE! det A ¼jAj ¼ Non confondere il simbolo di de-. terminante con quello di modulo. a n a n... a nn Nel caso particolare di matrice (quadrata) di ordine, cioè A ¼½a Š, si pone det A ¼jAj ¼ja j¼a Nel caso delle matrici quadrate di ordine, il determinante si definisce nel seguente modo: a a ¼ a a a a a a 8 & 0 De Agostini Scuola SpA Novara
9 Matrici ESEMPI Se A ¼½ Š allora jaj ¼ : Se B ¼ allora jbj ¼ð Þ ð Þ ¼ 0 sen cos Se C ¼ allora jcj ¼sen ð cos Þ¼sen þ cos ¼ cos sen Risolvere l equazione x x x ¼ 0 Sviluppando il determinante, si ottiene x x ðx Þ ¼0, ossia xð x þ xþ ¼0! x ¼ 0 _ x ¼ _ x ¼ Minore complementare. Complemento algebrico Per estendere la definizione di determinante a una matrice di ordine superiore al secondo, occorre premettere le seguenti definizioni. DEFINIZIONE MINORE COMPLEMENTARE Si dice minore complementare di un elemento di una matrice quadrata di ordine n il determinante che si ottiene sopprimendo dalla matrice data la riga e la colonna alle quali l elemento appartiene. Il minore complementare di un elemento di una matrice di ordine n risulta quindi un determinante di ordine ðn Þ. DEFINIZIONE COMPLEMENTO ALGEBRICO Si dice complemento algebrico di un elemento a ik di una matrice A di ordine n il minore complementare di a ik, preceduto dal segno þ o dal segno, a seconda che, rispettivamente, ði þ kþ sia pari o dispari. Per il complemento algebrico di a ik useremo il simbolo A ik. Avremo così che A ik è il prodotto del minore complementare dell elemento a ik per ð Þ iþk. ESEMPIO 0 Se è A ¼ 0,sihaA ¼þ ¼þ A ¼ ¼ A ¼þ ¼ ::: Determinanti del terzo ordine DEFINIZIONE DETERMINANTE DI UNA MATRICE DEL TERZO ORDINE Il determinante di una matrice del terzo ordine è la somma dei prodotti degli elementi di una riga o di una colonna qualsiasi per i rispettivi complementi algebrici. 9 & 0 De Agostini Scuola SpA Novara
10 Matrici La definizione appena data ha significato in quanto, come si potrebbe verificare facilmente, il valore numerico ottenuto è indipendente dalla riga o dalla colonna scelta. ESEMPIO Se A ¼ 0 si ha, sviluppando secondo la terza colonna, 0 jaj ¼þ þ ¼ ð Þ ð þ Þþ ¼ 0 Se si sviluppa secondo la prima colonna, si ha jaj ¼þ 0 þ ¼ ð þ Þþð Þ ¼ Si noti che, sviluppando secondo la riga o la colonna con il maggior numero di zeri, i calcoli sono semplificati. Regola di Sarrus Applicando la definizione formulata nel precedente paragrafo, si ha a a a a a a ¼ a a a þ a a a þ a a a a a a a a a a a a a a a Si può verificare che si ottiene la medesima espressione sviluppando il determinante secondo una riga o una colonna qualsiasi. La formula precedente può essere facilmente ricordata mediante il seguente schema che costituisce la regola di Sarrus (valida solo per i determinanti del o ordine): þ þ þ a a a a a a a a a a a a a a a A destra della matrice data si riscrivono, di seguito e nell ordine, la prima e la seconda colonna si calcola il prodotto degli elementi della diagonale principale della matrice e quello degli elementi delle due diagonali parallele lo stesso si fa con la diagonale secondaria e le sue parallele, ma prendendo, questa volta, i prodotti con il segno cambiato: la somma algebrica dei sei prodotti fornisce il determinante. ESEMPIO Calcolare, con la regola di Sarrus, il determinante della matrice A ¼ þ þ þ Si ottiene jaj ¼ þ ¼ 0 & 0 De Agostini Scuola SpA Novara
11 Matrici Determinanti di ordine n Il procedimento seguito per definire un determinante del terzo ordine vale anche per determinanti di ordine superiore si può infatti dire che il determinante di una qualsiasi matrice di ordine n è dato dalla somma dei prodotti degli elementi di una linea qualsiasi (riga o colonna) per i rispettivi complementi algebrici. Si noti che, in tale definizione, rientra anche il caso del determinante del secondo ordine. Per ricordare il segno che compete a ciascun complemento algebrico, si può ricorrere alla cosiddetta regola della scacchiera. 0 þ þ ::: þ þ ::: B þ þ ::: A ::: ::: ::: ::: ::: È importante rilevare che, come già osservato nel PARAGRAFO per i determinanti del terzo ordine, anche nel caso dei determinanti di ordine n la scelta della riga, o colonna, non influenza il risultato. In particolare, scambiando tra loro le righe con le colonne, il determinante non cambia, cioè ja T j¼jaj: È ovvio infatti che sviluppare ja T j, ad esempio, secondo la riga i-esima, equivale a sviluppare j Aj secondo la colonna i-esima. OSSERVAZIONE Ovviamente, matrici diverse possono avere lo stesso determinante. ESEMPIO Calcolare il determinante della matrice 0 0 A ¼ 0 Conviene sviluppare il determinante secondo la prima colonna, che è la linea che contiene il maggior numero di zeri: 0 jaj ¼ I due determinanti del terzo ordine si possono calcolare con la regola di Sarrus: jaj ¼ ð þ þ 0 0 Þ ðþ8þ0 0 Þ ¼ Proprietà dei determinanti I determinanti delle matrici quadrate godono delle seguenti proprietà.. Se tutti gli elementi di una linea sono nulli, il determinante è zero.. Il determinante della matrice unità, I n, di qualsiasi ordine, è.. Moltiplicando tutti gli elementi di una linea per uno scalare k, il determinante della matrice viene moltiplicato per k.. Se in una matrice una riga (o una colonna) è la somma di due matrici riga (o matrici colonna), il suo determinante è la somma dei due determinanti che si ottengono sostituendo a quella riga (o colonna) rispettivamente le due matrici riga (o matrici colonna) di cui è somma.. Se una matrice ha due linee uguali, o proporzionali, il suo determinante è zero. & 0 De Agostini Scuola SpA Novara
12 Matrici. Se si scambiano tra loro due righe (o due colonne) di una matrice, il determinante cambia segno.. Se agli elementi di una linea si sommano gli elementi di un altra linea a essa parallela, tutti moltiplicati per uno stesso numero, il determinante non cambia. 8. Il determinante del prodotto di due matrici è il prodotto dei loro determinanti (TEOREMA DI BINET). 9. Se una linea è combinazione lineare di due o più altre linee a essa parallele, il determinante è nullo. OSSERVAZIONE Precisiamo che una linea si dice combinazione lineare di due o più altre linee date, se i suoi elementi si ottengono sommando gli elementi corrispondenti delle linee date, dopo aver moltiplicato gli elementi di ciascuna di tali linee per un numero. Questi numeri si dicono coefficienti della combinazione lineare. Ad esempio, nella seguente matrice quadrata di ordine la terza riga è combinazione lineare della prima e della seconda riga, rispettivamente secondo i coefficienti h e k: a b c a 0 b 0 c 0 ha þ ka 0 hb þ kb 0 hc þ kc 0 Per motivi di spazio non daremo tutte le dimostrazioni delle proprietà enunciate, in quanto alcune di esse sono molto laboriose. Proponiamo a titolo di esempio la dimostrazione della PROPRIETÀ, lasciando la dimostrazione di alcune delle altre come esercizio. n Dimostrazione Supponiamo che sia la prima riga a essere la somma di due matrici riga sviluppiamo allora secondo la prima riga: a þ b a þ b... a n þ b n a a... a n. ¼ a n a n... a nn ¼ða þ b ÞA þða þ b ÞA þ...þða n þ b n ÞA n ¼ ¼ a A þ b A þ a A þ b A þ...þ a n A n þ b n A n ¼ ¼ða A þ a A þ...þ a n A n Þþðb A þ b A þ...þ b n A n Þ¼ a a... a n b b... b n a a... a n a a... a n ¼... þ a n a n... a nn a n a n... a nn c.v.d. Calcolo dei determinanti Il calcolo di un qualunque determinante può essere notevolmente semplificato ricorrendo alla PROPRIE- TÀ. Infatti, applicandola ripetutamente, possiamo rendere nulli tutti gli elementi di una linea tranne uno. Il determinante così ottenuto può essere facilmente sviluppato secondo questa linea. In questo modo, il problema del calcolo di un determinante di ordine n viene ridotto al calcolo di un determinante di ordine n, a cui si può applicare ancora il procedimento descritto fino a giungere al calcolo di determinanti di ordine o. & 0 De Agostini Scuola SpA Novara
13 Matrici ESEMPI Calcoliamo il seguente determinante: jaj ¼ 0 9 In questo caso notiamo che la quarta colonna è uguale alla prima moltiplicata per. Dunque, per la PRO- PRIETÀ, è jaj ¼0 OSSERVA CHE il determinante è nullo se tutti gli elementi di una linea sono nulli due linee parallele sono proporzionali una linea è combinazione lineare di altre due o più ad essa parallele. Calcolare il seguente determinante del quarto ordine: 0 jaj ¼ Applicando la PROPRIETÀ, addizioniamo agli elementi della prima riga quelli della terza moltiplicati per ð Þ, cioè sostituiamo alla prima riga la differenza tra la prima e la terza: il determinante non cambia sommiamo poi agli elementi della terza colonna quelli della quarta moltiplicati per : jaj ¼ ¼ Come si vede, si è fatto in modo di avere gli elementi della prima riga tutti nulli tranne l ultimo sviluppando ora il determinante, in base alla definizione, secondo la prima riga, si ottiene un determinante di ordine. A esso possiamo ancora applicare la PROPRIETÀ, sommando alla prima riga la terza, il che equivale a sostituire alla prima riga la somma della prima e della terza: 0 0 jaj ¼ ¼ Sviluppiamo il determinante così ottenuto secondo la prima riga: jaj ¼ ¼ ð þ Þ ¼ 0 n Inversa di una matrice 8 Definizioni DEFINIZIONE MATRICE INVERSA Si chiama matrice inversa di una matrice quadrata A di ordine n, e si indica con il simbolo A, una matrice (se esiste), anch essa quadrata e dello stesso ordine, tale che A A ¼ A A ¼ I n & 0 De Agostini Scuola SpA Novara
14 Matrici Enunciamo il seguente teorema. TEOREMA L inversa di una matrice quadrata, se esiste, è unica. Non tutte le matrici quadrate hanno un inversa. Se di una matrice quadrata A esiste un inversa, A si dice invertibile o non singolare. Se tale inversa non esiste, A si dice non invertibile o singolare. Le matrici con determinante nullo non sono invertibili. Infatti, se A è invertibile, allora A A ¼ I Per la PROPRIETÀ dei determinanti (PARAGRAFO ), è jij ¼, e quindi ja A j¼ Ma per la PROPRIETÀ 8 (TEOREMA DI BINET), si ha ja A j¼jajja j e perciò jajja j¼ da cui ja j¼ jaj Le ultime due uguaglianze sono assurde se è jaj ¼0. Possiamo perciò concludere che condizione necessaria affinché una matrice sia invertibile è che il suo determinante sia diverso da zero. Inoltre, se una matrice è invertibile, il determinante della sua inversa è il reciproco del suo determinante. Nel PARAGRAFO 9 vedremo che la condizione che il determinante sia diverso da zero è, oltre che necessaria, anche sufficiente per l invertibilità di una matrice. 9 Calcolo dell inversa di una matrice Il seguente teorema, che ci limitiamo a enunciare, fornisce un metodo per determinare l inversa di una data matrice. TEOREMA Sia A una matrice quadrata il cui determinante sia diverso da zero sia A la matrice formata con i complementi algebrici degli elementi di A. La matrice inversa di A esiste ed è la trasposta di A divisa per il determinante di A. Siha A A A... n jaj jaj jaj A ¼ jaj A T! a a... a n a a... a n a n a n... a nn A A A... n ¼ jaj jaj jaj A n A n A... nn jaj jaj jaj OSSERVAZIONE Questo teorema, insieme a quanto osservato nel PARAGRAFO 8, ci permette di affermare che condizione necessaria e sufficiente affinché una matrice quadrata sia invertibile è che il suo determinante sia diverso da zero. In pratica, per determinare l inversa di una matrice, dobbiamo:. calcolare il determinante di A (se jaj ¼0 l inversa non esiste). costruire la matrice A dei complementi algebrici di A & 0 De Agostini Scuola SpA Novara
15 Matrici. formare la trasposta A T di tale matrice. dividere ciascun elemento della matrice così ottenuta per il determinante di A. ESEMPIO Determinare l inversa della matrice 0 A ¼. Calcoliamo jaj, applicando la regola di Sarrus: jaj ¼ þ þ 0 0 þ ¼. Costruiamo la matrice dei complementi algebrici: A ¼ ¼ A ¼ ¼ A ¼ ¼ A ¼ 0 ¼ A ¼ 0 ¼ A ¼ ¼ A ¼ 0 ¼ A ¼ 0 ¼ A ¼ ¼ A ¼. Formiamone la trasposta: A T ¼. Dividiamone ciascun elemento per jaj ¼: A ¼ Ti lasciamo il compito di verificare che A A ¼ A A ¼ I : n Rango di una matrice 0 Minori Sia A una matrice di tipo ðm nþ. Possiamo estrarre da essa una sottomatrice, scegliendo p righe e q colonne di A ð0 < p m 0 < q nþ e considerando la matrice formata dagli elementi che appartengono contemporaneamente alle righe e alle colonne prescelte. DEFINIZIONE MINORE D ORDINE p Si dice minore d ordine p della matrice A il determinante di una sottomatrice quadrata di tipo ðp pþ estratta da A. Evidentemente, l ordine di un minore estratto da una matrice di tipo ðm nþ non può superare il più piccolo dei due numeri m, n. Si noti che un qualsiasi elemento della matrice può essere considerato un suo minore di ordine e che, in generale, una stessa matrice ammette diversi minori dello stesso ordine. & 0 De Agostini Scuola SpA Novara
16 Matrici ESEMPIO Consideriamo la seguente matrice: 0 A ¼ 0 0 I seguenti sono minori d ordine : jj ¼, j0j ¼0, j j ¼, ecc. Scegliendo gli elementi della prima e seconda riga e della seconda e quarta colonna, si ha il seguente minore di ordine : 0 ¼ Infine un minore di ordine è, ad esempio, 0 0 ¼ 0 La matrice A ovviamente non ha minori di ordine superiore a. Rango DEFINIZIONE RANGO DI UNA MATRICE Si dice rango o caratteristica di una matrice A il massimo ordine dei minori non nulli che si possono estrarre da A. Se gli elementi di A sono tutti nulli, risulta nullo qualsiasi minore estratto da A. Si conviene in tal caso che il rango di A sia zero. Se A è una matrice di tipo ðm nþ, il suo rango, evidentemente, non può superare il più piccolo dei due numeri m e n. ESEMPI Consideriamo la matrice A ¼ 8 Essa ha rango. Infatti essa ha minori non nulli di ordine : ad esempio jj ¼: D altra parte, la prima e la seconda riga di A, e così pure la seconda e la terza, sono proporzionali e quindi qualunque minore di ordine o di A, avendo due righe proporzionali, risulta nullo (PROPRIETÀ del PARAGRAFO ). Consideriamo la matrice B ¼ 0 0 Essa ha rango. Infatti essa ha un minore non nullo di ordine : 0 ¼ d altra parte l unico minore di ordine di B è jbj e risulta jbj ¼0, essendo la terza riga di B uguale alla somma delle prime due (PROPRIETÀ 9 del PARAGRAFO ). Si osservi che dire che una matrice A di tipo ðm nþ ha rango r equivale ad affermare che. esiste un minore di A, di ordine r, diverso da zero. tutti i minori di A di ordine maggiore di r sono nulli. & 0 De Agostini Scuola SpA Novara
17 Matrici Queste considerazioni suggeriscono anche un metodo per determinare il rango di una data matrice: individuato un minore di ordine r non nullo, si calcolano tutti i minori di ordine maggiore di r (in particolare se r ¼ min ðm nþ, non esistendo minori di ordine superiore, il rango è r). Se questi risultano tutti nulli, il rango della matrice è r in caso contrario si sarà individuato un minore non nullo di ordine maggiore di r e si dovrà quindi riprendere il procedimento descritto. In pratica però tale metodo è molto laborioso. Il teorema di Kronecker, che enunceremo nel paragrafo seguente, permette di determinare il rango di una matrice in modo più rapido. Osserviamo infine che, se A è una matrice quadrata di ordine n, il suo rango è n se e solo se è jaj ¼ 0 ovviamente il suo rango non può essere maggiore di n. Teorema di Kronecker DEFINIZIONE MATRICE ORLATA Orlare una matrice di tipo ðm nþ significa aggiungerle successivamente una riga e una colonna, in modo da trasformarla in una matrice di tipo ðm þ n þ Þ. La matrice così ottenuta conterrà dunque la matrice data come sottomatrice. TEOREMA TEOREMA DI KRONECKER Il rango di una matrice A è r se e solo se:. esiste un minore A 0 non nullo di A, di ordine r. sono nulli tutti i minori di ordine r þ, ottenuti orlando in ogni modo possibile il minore A 0 con righe e colonne di A. ESEMPI Determinare il rango della matrice 0 0 A ¼ Osserviamo che l elemento della prima riga e della prima colonna costituisce un minore di ordine non nullo: jj ¼ ¼ 0 Tale minore verifica la condizione del teorema. Per controllare la validità della condizione, cominciamo orlandolo con la ª riga e la ª colonna: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: :::! ¼ 0 ::: ::: ::: ::: ::: Orliamolo ora con la ª riga e la ª colonna: ::: 0 ::: ::: ::: ::: ::: ::: ::: ::: ::: :::! 0 ¼ ¼ 0 ::: ::: ::: ::: ::: La condizione non è perciò soddisfatta. Abbiamo però determinato un minore di ordine non nullo, formato con gli elementi della ª e ª riga e della ª e ª colonna. Per quest ultimo minore la condizione del teorema è soddisfatta. & 0 De Agostini Scuola SpA Novara
18 Matrici Per controllare la validità della condizione dovremo calcolare minori di ordine, e precisamente formati orlando il minore considerato con la terza riga e, rispettivamente, con la ª, ª e ª colonna: 0 ::: ::: ::: 0 ::: ::: 0 ::: ::: ::: ::: 0 ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: 0 ¼ 0 ::: ::: ::: ::: :::? y 0 0 ¼ 0 ::: ::: ::: ::: :::? y 0 ¼ 0 e altri formati orlando il minore dato con la ª riga e, ancora, con la ª, ª e ª colonna: 0 ::: ::: ::: 0 ::: ::: 0 ::: ::: ::: ::: 0 ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: ::: :::? y 0 ¼ 0 ::: :::? y 0 0 ¼ 0 ::: :::? y 0 ¼ 0 NOTA BENE Una sottomatrice si può orlare anche aggiungendo all interno della sottomatrice stessa righe e colonne della matrice da cui è stata estratta. È fondamentale però inserire tali righe e colonne nei rispettivi posti in modo che la matrice orlata mantenga l ordinamento della matrice di partenza. I primi tre minori di ordine hanno la terza riga che è somma delle prime due negli altri tre la terza riga è somma della prima e del doppio della seconda. Quindi, poiché tutti i sei minori di ordine così ottenuti sono nulli, è verificata anche la condizione del teorema. La matrice A ha perciò rango. 8 & 0 De Agostini Scuola SpA Novara
19 Esercizi n n n n n Nozioni fondamentali Algebra delle matrici Determinanti di matrici quadrate Inversa di una matrice quadrata Rango di una matrice Nozioni fondamentali RICORDIAMO LA TEORIA n Matrice di tipo ðm nþ: tabella formata da m n elementi di R posti su m righe e n colonne. Si scrive A ¼½a ik Š i ¼ ::: m k ¼ ::: n. Se m ¼ parliamo di matrice riga, sen ¼ dimatrice colonna. Se m ¼ n la matrice è quadrata di ordine n. n Matrice nulla: tutti i suoi elementi sono 0. n Matrici uguali: matrici che hanno tutti gli elementi corrispondenti uguali A ¼ B () a ik ¼ b ik i ¼ ::: m k ¼ ::: n n Matrice opposta di una matrice A: matrice indicata con A, i cui elementi sono gli opposti dei corrispondenti elementi di A. n Matrice trasposta della matrice A: matrice indicata con A T, che si ottiene da A scambiando le righe con le colonne. n Diagonale principale di una matrice quadrata: insieme degli elementi che hanno i due indici uguali. n Diagonale secondaria di una matrice quadrata di ordine n: insieme degli elementi i cui indici hanno per somma n þ. n Matrice diagonale: matrice quadrata i cui elementi al di fuori della diagonale principale sono nulli. n Matrice triangolare superiore (inferiore): matrice quadrata i cui elementi al di sotto (sopra) della diagonale principale sono nulli. n Matrice unità di ordine n: matrice diagonale, indicata con I n, i cui elementi sulla diagonale principale sono tutti uguali a. QUESITI A RISPOSTA MULTIPLA 0 È data la matrice A ¼ Qual è l elemento a? &a &b &c &d Qual è l elemento a? &a &b &c 0 &d Quali sono gli elementi della diagonale principale? &a &b 0 &c 0 9 & 0 De Agostini Scuola SpA Novara
20 Esercizi COMPLETARE... L opposta di una matrice è quella matrice dello stesso tipo i cui elementi sono... dei corrispondenti elementi della matrice data. Una matrice si dice triangolare superiore se sono nulli tutti gli elementi La matrice identica è una matrice... di ordine n formata da n... disposti sulla diagonale principale e n negli altri posti. ESERCIZIO SVOLTO x þ y x y 0 Determina per quali valori di x, y, z la matrice 0 x y yþ z risulta diagonale. x þ z 0 z Come sappiamo una matrice è diagonale quando gli elementi non appartenenti alla diagonale principale sono tutti nulli. Dovrà quindi essere: ( x y ¼ 0 ( x ¼ y þ z ¼ 0 x þ z ¼ 0 da cui risolvendo si ottiene y ¼ z ¼ 0 0 Sostituendo nella matrice data i valori trovati, otteniamo 0 0 che è evidentemente una matrice diagonale Determina x e y in modo che siano uguali le due matrici A ¼ x y B ¼ x ¼ ^ y ¼ A ¼ B ¼ y x 9 Determina x, y, z in modo che siano opposte le due matrici A ¼ þ x 0 B ¼ z y z x y z 0 x þ y yþ x x ¼ ^ y ¼ ^ z ¼ A ¼ B ¼ 0 0 Determina x e y in modo che siano uguali le due matrici x þ y x y x ¼ 0 y x x þ y y ¼ 0 Determina x e y in modo che siano opposte le matrici x þ y x y þ 0 x þ y 0 x þ y _ x ¼ 0 y ¼ x ¼ 0 y ¼ 0 Determina x, y e z in modo che la seguente matrice sia triangolare superiore. x y x þ z 0 0 x þ y z x ¼ ^ y ¼ ^ z ¼ 0 y z 0 y Determina x e y in modo che sia diagonale la matrice x y 0 y x x y x þ 0 x y y 8 >< x ¼ >: y ¼ _ 8 x ¼ >< >: y ¼ 0 & 0 De Agostini Scuola SpA Novara
21 Esercizi Date le due matrici A ¼ x þ y x þ y 0 z B ¼ z z 0 x þ y determina x, y, z in modo che A T ¼ B. ½x ¼ ^ y ¼ 0 ^ z ¼ Š Esistono valori di a per i quali le due matrici A ¼ a þ e B ¼ risultano uguali? a þ a þ Algebra delle matrici RICORDIAMO LA TEORIA n Somma di due matrici A stesso tipo: matrice, indicata con A þ B, i cui elementi sono la somma dei corrispondenti elementi delle matrici date. n n Prodotto di una matrice A per uno scalare : matrice i cui elementi sono il prodotto di per i corrispondenti elementi di A. Prodotto scalare di una matrice riga A di tipo (, s) per una matrice colonna B di tipo (s, ): matrice di tipo ð Þ che ha per elemento il numero che si ottiene sommando i prodotti del tipo a j b j con j ¼ ::: s. n Prodotto righe per colonne della matrice A di tipo (m, s) per la matrice B di tipo (s, n): matrice di tipo ðm nþ il cui elemento generico è dato da p ik ¼ Xs n Proprietà delle operazioni tra matrici Date le matrici A, B, C e gli scalari,, 8A B C e 8, si ha:. ða þ BÞ ¼A þ B. ð þ ÞA ¼ A þ A. ðþa ¼ ðaþ. A ¼ A ð ÞA ¼ A. A þ B ¼ B þ A. A þðb þ CÞ ¼ðA þ BÞþC A ðb CÞ ¼ðA BÞC. A ðb þ CÞ ¼A B þ A C ðb þ CÞA ¼ B A þ C A j¼ a ij b jk i ¼ ::: m k ¼ ::: n. ½noŠ VERO O FALSO? Il prodotto di due matrici può essere una matrice nulla se e solo se una delle due matrici è una matrice nulla. La somma di due matrici si può eseguire solo se le due matrici sono dello stesso tipo. 8 Il prodotto di due matrici si può eseguire solo se le due matrici sono dello stesso tipo. 9 L addizione di matrici gode delle proprietà associativa e commutativa. 0 La moltiplicazione di matrici gode delle proprietà associativa e commutativa. Il prodotto righe per colonne di due matrici è possibile solo se la prima matrice ha un numero di righe uguale al numero di colonne della seconda. La moltiplicazione tra matrici diagonali è un operazione commutativa. QUESITI A RISPOSTA MULTIPLA Il prodotto ½ 0 Š è &a ½Š &b ½ Š &c ½Š &d ½ Š & 0 De Agostini Scuola SpA Novara
22 Esercizi Il prodotto delle matrici A ¼ 0 &a 0 0 COMPLETARE... &b 0 e B ¼ 0 è la matrice &c 8 0 &d 0 La differenza di due matrici è la somma della prima matrice con La proprietà distributiva del prodotto di uno scalare per una matrice rispetto alla somma di matrici è espressa dalla seguente uguaglianza: ða þ BÞ ¼.... Siano A, B, C le seguenti matrici: A ¼ 0 B ¼ C ¼ 0 Calcola le seguenti espressioni ESERCIZIO SVOLTO A B. Ricordando la definizione di prodotto di una matrice per uno scalare e di differenza tra matrici possiamo scrivere: 0 9 ¼ ¼ A þ B A B. 9 A þ B þ C A B þ C. 0 0 A þ B A B þ C. 0 Determina una matrice X tale che ða þ BÞ ¼X þ C X ¼ 9 Determina una matrice X tale che ða þ XÞ ¼C B A X ¼ 0 0 Calcola 0 0 cos sen cos sen cosð þ Þ senð þ Þ Calcola sen cos sen cos senð þ Þ cosð þ Þ Determina x in modo che sia Determina x e y in modo che sia x 0 0 Sia A ¼. Calcola A e A. 0 8 Verifica che ¼ ¼ x y ¼ ½x ¼ Š ½x ¼ ^ y ¼ Š & 0 De Agostini Scuola SpA Novara
23 9 Determina x in modo che ¼ 0 0 x 0 0 Esercizi ½x ¼ 9Š Considera le seguenti matrici: A ¼ 0 0 Calcola A B B A: Calcola A B A B: B ¼ C ¼ Calcola A C B C. 8 0 Calcola A B C C B A: 0 Determina una matrice X tale che sia A X ¼ B. Calcola A ðb þ CÞ, A B þ A C e verifica che i risultati sono uguali. Calcola (B þ CÞA, B A þ C A e verifica che i risultati sono uguali. Considera le matrici A ¼ 0 B ¼ C ¼ Calcola A B B A e verifica che A B ¼ B A. 8 Verifica che ða BÞC ¼ A ðbcþ. 9 Verifica che A ðbþcþ ¼A B þ A C. 0 Verifica che ða þ BÞC ¼ A C þ B C. Verifica che ða BÞ T ¼ A T B T, mentre ða BÞ T ¼ B T A T. Calcola A, B, C. Calcola 0 0 Calcola ½ Š 0 Calcola 0 0 Calcola Calcola ½½ 8 ŠŠ & 0 De Agostini Scuola SpA Novara
24 Esercizi log x log y log z 8 Calcola log x log y log z log x log y log z 9 Calcola cos sen sen cos sen 0 sen cos cos sen cos 0 sen cos 0 0 logðxyzþ log x yz log y xz log x yz logðxyzþ log z xy log y xz log z xy logðxyzþ cos sen sen sen cos cos 0 ESERCIZIO SVOLTO tan 0 Sia A ¼ calcola A ¼ A A. tan Eseguendo il solito prodotto righe per colonne otteniamo tan tan ¼ tan tan tan tan tan tan þ Notando che è tan ¼ sen cos ¼ cos sen cos cos tan possiamo scrivere A cos ¼ tan cos cos ¼ cos cos Sia A ¼ A ¼ calcola A ¼ A A e A ¼ A A. ATTENZIONE! A n ¼ A A n 8n n N. cos sen calcola A sen cos ¼ A A e A ¼ A A. Sia A ¼ x calcola A e A. x x Date le matrici A ¼ 0 B ¼ 0 ða þ BÞ ¼ A þ AB þ B ða þ BÞ ¼ A þ AB þ BA þ B ða þ BÞðA BÞ ¼ A B, verifica che è Ricorda però che il prodotto di matrici non è commutativo. cos sen sen cos x ð þ x Þ x x cos sen sen cos ð þ x Þ x x x ða þ BÞðA BÞ ¼A þ BA AB B Determina x in modo che risulti ¼ x 0 Determina x e y in modo che risulti 0 x x þ y 0 ¼ 0 ½x ¼ Š ½x ¼ ^ y ¼ Š & 0 De Agostini Scuola SpA Novara
25 Esercizi COMPLETARE... Siano A una matrice di tipo ðm nþ e B una matrice di tipo ðn pþ. Dimostra che ðabþ T ¼ B T A T, ossia la trasposta del prodotto di due matrici è il prodotto, in ordine inverso, delle loro trasposte. Cominciamo con l osservare che la matrice AB, essendo il prodotto di una matrice di tipo ðm nþ con una di tipo ðn pþ, èuna matrice di tipo ðm pþ e quindi la sua trasposta ðabþ T è di tipo... d altra parte le matrici B T e A T sono rispettivamente di tipo... e... e quindi il loro prodotto B T A T è di tipo.... Dunque le matrici ðabþ T e B T A T sono dello stesso tipo. Poniamo AB ¼ C e B T A T ¼ D. Occorre dimostrare che C T ¼ D, ossia che c ki ¼ d ik. L elemento c ki è il prodotto scalare della riga k della matrice A con la colonna i della matrice B, ossia c ki ¼ ½a k a k ::: a kn Š b i b i ::: b ni ¼ a kb i þ a k b i þ ::: þ a kn b ni D altra parte d ik è il prodotto scalare della riga i della matrice B T, ossia della... della matrice B, con la colonna... della matrice A T, ossia... della matrice A, quindi si ha: d ik ¼ :::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: Si può dunque concludere che... c.v.d. Determinanti di matrici quadrate RICORDIAMO LA TEORIA n Determinante di una matrice quadrata A: si indica con jaj e se A è di ordine, jaj ¼a se A è di ordine, jaj ¼a a a a. n Minore complementare di un elemento di una matrice quadrata: determinante della matrice che si ottiene sopprimendo dalla matrice data la riga e la colonna alle quali l elemento appartiene. n Complemento algebrico A ik dell elemento a ik : minore complementare di a ik, moltiplicato per ð Þ iþk : n Determinante di una matrice di ordine n: somma dei prodotti degli elementi di una linea qualsiasi per i rispettivi complementi algebrici n Proprietà dei determinanti: A Il determinante è nullo se: jaj ¼ Xn k¼ a ik A ik ¼ Xn i¼ a ik A ik tutti gli elementi di una linea sono nulli due linee parallele sono proporzionali una linea è combinazione lineare di altre due, o più, ad essa parallele. B Il determinante della matrice unità di qualsiasi ordine è. C D E F G Moltiplicando tutti gli elementi di una linea per uno scalare k, il determinante della matrice viene moltiplicato per k. Se in una matrice una riga (o una colonna) è la somma di due matrici riga (o matrici colonna), il suo determinante è la somma dei due determinanti che si ottengono sostituendo a quella riga (o colonna) rispettivamente le due matrici riga (o matrici colonna) di cui è somma. Se si scambiano tra loro due righe (o due colonne) di una matrice, il determinante cambia segno. Se agli elementi di una linea si sommano gli elementi di un altra linea ad essa parallela, tutti moltiplicati per uno stesso numero, il determinante non cambia. Il determinante del prodotto di due matrici è il prodotto dei loro determinanti (teorema di Binet). & 0 De Agostini Scuola SpA Novara
26 Esercizi VERO O FALSO? 8 Per calcolare il determinante di una matrice si può sempre ricorrere alla regola di Sarrus. 9 Il determinante si definisce solo per le matrici quadrate. 0 Il determinante della somma di due matrici è la somma dei loro determinanti. Il determinante del prodotto di due matrici è il prodotto dei loro determinanti. Il determinante di una matrice è zero se e soltanto se la matrice è nulla. Il determinante di una matrice è se e solo se si tratta di una matrice unità. Il determinante del prodotto di una matrice A per uno scalare k è il prodotto del determinante di A per k. Una matrice diagonale e una triangolare superiore (o inferiore), aventi gli elementi della diagonale principale uguali, hanno lo stesso determinante. QUESITI A RISPOSTA MULTIPLA Qual è il determinante della matrice? &a 0 &b &c 0 &d &e In quali dei seguenti casi il determinante di una matrice è sicuramente zero? &a &b &c &d &e &f &g &h Se una riga ha tutti gli elementi nulli Se una riga ha tutti gli elementi uguali tra loro Se due colonne sono uguali Se la matrice è triangolare Se gli elementi di una riga sono uguali ai corrispondenti elementi di una colonna Se gli elementi di una colonna sono tutti multipli di uno stesso intero k Se gli elementi della diagonale principale sono tutti nulli Se due colonne sono proporzionali ESERCIZI SVOLTI 8 Calcola il seguente determinante 0 Utilizzando la regola di Sarrus, otteniamo þ 0 þð 8Þ ¼ Calcola Osservando che la terza riga è uguale alla prima moltiplicata per lo scalare, possiamo immediatamente concludere che il determinante della matrice è nullo. Applicando le definizioni, calcola il valore dei seguenti determinanti. 80 ½ Š & 0 De Agostini Scuola SpA Novara
27 cos sen sen cos cos sen sen cos x y x x x x þ y x y x y xþ y x x x x x x a x a x a sen sen cos cos sen sen cos cos sen sen sen sen x y z w a b 0 sen cos cos cos sen sen 0 c 0 sen cos sen 0 0 d Esercizi ½ cos Š ½x y 0Š ½xy Š ½ a senð ÞŠ ½ sen sen Š ½0 8Š ½ 0 0Š ½0 x wš ½ðac Þðbd Þ sen þ cos Š Applicando la regola di Sarrus, calcola i seguenti determinanti x x 9 9 a a a b b b b a c c ab ab ½ 0Š ðx Þðx ) ½0 ða bþða þ b abþš Applicando le proprietà studiate, calcola i seguenti determinanti ½0 infatti... 8Š ½0 infatti...š & 0 De Agostini Scuola SpA Novara
28 Esercizi a b c d a b c d ½0 infatti... 0Š a a 0 b b ½ða Þðb Þðb aþ 0Š y þ z xþ z xþ y x y z ½0 Š ½ Š a 0 0 x 0 b 0 x : 0 0 c x d 0 0 x ½ abcd ðx Þ ðx þ ÞŠ a x y x y 0 b c 0 y x y x d e ½ðx yþ ðx þ y þ Þðx þ y Þ þ abcdeš Risolvi le seguenti equazioni ESERCIZIO SVOLTO x x x x þ ¼ 0 Per definizione di determinante abbiamo xðx þ Þ xð xþ ¼ x x x þ x ¼ x x ¼ xðx Þ da cui possiamo ricavare, per la legge di annullamento del prodotto, x ¼ 0 _ x ¼. x x x x ¼ 0 ¼ 0 _ x ¼ x 0 0 x ¼ 0 ½x ¼ Š 0 x x x x ¼ 0 x x x x x x x x x x ¼ 0 0 x x 0 0 x ½x ¼ 0 _ x ¼ Š ½x ¼ 0 _ x ¼ _ x ¼ _ x ¼ Š 8 & 0 De Agostini Scuola SpA Novara
29 Esercizi Risolvi le seguenti disequazioni. x x 0 x x 0 x x x x x x x 0 < 0 ½impossibileŠ x x x x pffiffiffi 08 x x < 0 ½x < _ x > Š pffiffiffi pffiffiffi x Inversa di una matrice quadrata RICORDIAMO LA TEORIA n Matrice inversa di una matrice quadrata A: matrice, indicata con A dello stesso ordine di A, tale che A A ¼ A A ¼ I n A A A ::: n jaj jaj jaj Se jaj ¼ 0, si ha A ¼ jaj A T ¼ A A A ::: n jaj jaj jaj ::: ::: ::: ::: A n A n A ::: nn jaj jaj jaj essendo A T la trasposta della matrice A formata dai complementi algebrici degli elementi di A. QUESITI 09 Qual è l inversa della matrice unità I? 0 Qual è l inversa della matrice? QUESITI A RISPOSTA MULTIPLA L inversa della matrice è &a &b &c &d La matrice A ha determinante. Qual è il determinante della sua inversa? &a &b &c &d 0 &e Non esiste la matrice inversa. Moltiplicando una matrice A per la sua inversa, si ottiene &a la matrice A &b la matrice nulla &c la matrice unità &d l inversa di A Qual è l inversa della matrice unità I n? &a La stessa matrice I n &b La matrice nulla &c L opposta della matrice unità, cioè ð I n Þ &d Non esiste l inversa di I n 9 & 0 De Agostini Scuola SpA Novara
30 Esercizi Una matrice quadrata è invertibile &a se ha il determinante diverso da &b se ha il determinante positivo &c se ha il determinante diverso da zero &d sempre ESERCIZIO SVOLTO Determina l inversa della matrice A ¼ 0 Per prima cosa controlliamo che la matrice sia invertibile, verificando che il suo determinante sia diverso da 0. Utilizzando ad esempio la regola di Sarrus otteniamo jaj ¼0 þ þ þ 0 ¼ 9 ¼ 0 Dato che la matrice è invertibile, calcoliamo i complementi algebrici dei suoi elementi. A ¼ 0 ¼ A ¼ 0 ¼ A ¼ ¼ A ¼ 0 ¼ A ¼ 0 ¼ A ¼ ¼ 8 A ¼ ¼ A ¼ ¼ A ¼ ¼ Formiamo quindi la matrice dei complementi algebrici A ¼ 8 la sua trasposta sarà A T ¼ Concludendo, l inversa di A sarà la matrice A ¼ Determina l inversa delle seguenti matrici, verificando poi, per ognuna di esse, che il prodotto per la corrispondente inversa dà la matrice unità & 0 De Agostini Scuola SpA Novara
31 Esercizi sen cos cos cos sen sen sen cos sen Per quali valori di esiste la matrice inversa? cos sen sen cos cos 0 sen 0 0 sen 0 cos cos sen 0 0 sen cos cos sen 0 0 sen cos 0 a b a 0 c con a b c ¼ 0 b c 0 a a a 0 con a ¼ a sen cos 0 sen sen sen cos sen þ cos sen þ cos cos sen sen cos sen þ cos sen þ cos cos sen sen cos cos 0 sen 0 0 sen 0 cos cos sen 0 0 sen cos cos sen 0 0 sen cos c ab a b b a ac c a b c bc a a a a COMPLETARE... 0 Siano A e B due matrici quadrate invertibili. Dimostra che ½ABŠ ¼ B A ossia l inversa della matrice prodotto di due matrici è il prodotto, in ordine inverso, delle loro inverse. Occorre dimostrare che il prodotto delle matrici ðabþðb A Þ e il prodotto delle matrici ðb A ÞðABÞ sono la matrice unità. Si ha infatti, per la proprietà associativa del prodotto tra matrici: ðabþðb A Þ¼Að::: :::ÞA ¼ A :::::::::: A ¼ :::::::::::::::::::: ðb A ÞðA BÞ ¼B ð::: :::ÞB ¼ B ::::::: B ¼ ::::::::::::: c.v.d. Sia A una matrice quadrata invertibile. Dimostra che ½A T Š ¼½A Š T ossia che l inversa della trasposta di una matrice è la trasposta della sua inversa (occorre dimostrare che si ha A T ½A Š T ¼ I e che ½A Š T A T ¼ I). & 0 De Agostini Scuola SpA Novara
32 Esercizi Dimostra che, se A è una matrice quadrata invertibile, A ¼ ja x Considera la matrice A ¼ x p Determina x in modo che A ¼ A: ½x ¼ ffiffiffi Š j Rango di una matrice RICORDIAMO LA TEORIA n Minore d ordine p della matrice A: determinante di una sottomatrice di ordine ðp pþ estratta da A. n Rango di una matrice A: massimo ordine dei minori non nulli di A. n Orlare una matrice di tipo (m, n): significa aggiungerle una riga e una colonna in modo che diventi una matrice di tipo ðm þ n þ Þ. n Teorema di Kronecker: la matrice A ha rango r se e solo se esiste un minore ja 0 j di ordine r estratto da A sono tutti nulli i minori di ordine r þ ottenuti orlando A 0 con righe e colonne di A in tutti i modi possibili. VERO O FALSO? Il rango si può definire solo per le matrici quadrate. Una matrice non nulla non può avere rango zero. Se una matrice ha un minore di ordine k non nullo, il suo rango è sicuramente maggiore o uguale a k. Il massimo rango di una matrice con righe e colonne è. ESERCIZIO SVOLTO 8 Determina il rango della matrice A ¼ a La matrice è quadrata di ordine. Il suo rango è se e solo se il suo determinante è diverso da zero. Si ha jaj ¼a þ e quindi jaj ¼0 () a ¼. Si hanno quindi due possibilità. Se è a ¼, essendo jaj ¼ 0, il rango di A è. Se è a ¼, si ha A ¼. Tale matrice, avendo determinante zero, non può avere rango del resto ciascuno dei suoi elementi costituisce un minore non nullo di ordine e quindi il rango di A è. Riassumendo, si ha se a ¼ il rango di A è se a ¼ il rango di A è. Determina il rango delle seguenti matrici mediante semplici considerazioni sui determinanti e sulle loro proprietà ½ Š ½ Š & 0 De Agostini Scuola SpA Novara
33 Esercizi ½ Š Applicando il teorema di Kronecker, determina il rango delle seguenti matrici. 0 0 ½ Š ½ Š ½ Š 8 8 ½ Š ½ Š 0 0 & 0 De Agostini Scuola SpA Novara
34 Laboratorio di matematica Eseguire operazioni con le matrici usando il foglio elettronico Utilizziamo il foglio elettronico per eseguire le operazioni tra matrici quadrate di ordine : somma, differenza, prodotto di due matrici prodotto di una matrice per uno scalare calcolo del determinante. In questa esercitazione facciamo riferimento a Excel, ma lo stesso procedimento può essere impiegato in altri fogli elettronici. La tabella in FIGURA è una proposta di soluzione. FIGURA & 0 De Agostini Scuola SpA Novara
35 Laboratorio di matematica Dopo aver scritto le intestazioni come illustrato nella tabella proposta immettiamo gli elementi della prima matrice nelle celle B, B, C, C, mentre nelle celle F, F, G, G immettiamo gli elementi della seconda matrice. Per ottenere la somma delle due matrici, dopo aver selezionato la cella B scriviamo la formula: e la copiamo nelle celle B, C, C. ¼ B þ F Per ottenere la differenza delle due matrici, immettiamo nella cella F la formula: copiandola quindi nelle celle F, G, G. ¼ B F Per ottenere il prodotto delle due matrici si può utilizzare l apposita funzione di Excel, che ha la sintassi seguente: MATR.PRODOTTO(matrice matrice) Per usare questa funzione occorre selezionare preventivamente tutte le celle che conterranno gli elementi della matrice prodotto. Selezioniamo quindi le celle B0, B, C0, C e scriviamo: =MATR.PRODOTTO(B:CF:G) A questo punto, invece di premere Invio come si fa di solito, premiamo CtrlþMaiuscþInvio: in questo modo nelle celle selezionate compaiono gli elementi della matrice prodotto. Osserviamo che se dopo aver scritto la formula si preme solo Invio, Excel fornisce soltanto l elemento appartenente alla prima riga e alla prima colonna (in questo caso ), e non l intera matrice. Per calcolare il determinante delle due matrici utilizziamo la funzione di Excel corrispondente essa ha la sintassi: Digitiamo dunque nella cella C la formula e copiamola nella cella G. ESERCIZI MATR.DETERM(matrice) ¼ MATR.DETERM(BC) Utilizza il foglio elettronico per eseguire le operazioni tra matrici quadrate di ordine. Utilizza il foglio elettronico per calcolare il determinante di una matrice quadrata di ordine. Eseguire operazioni con le matrici usando Derive Il programma Derive consente di eseguire le operazioni tra le matrici studiate in questo capitolo, compreso il calcolo del determinante e dell inversa di una matrice quadrata, con estrema semplicità. Inseriamo ad esempio le matrici A ¼ 0 B ¼ 0 pffiffiffi C ¼ 0 0 Facciamo clic sul pulsante : appare una finestra (FIGURA ) intitolata Crea matrice... scriviamo nelle apposite caselle il numero di righe e di colonne di cui è composta la matrice che vogliamo definire (oppure impostiamo tali valori mediante i pulsanti con le freccine a destra delle caselle) e quindi clicchiamo su OK. FIGURA & 0 De Agostini Scuola SpA Novara
36 Laboratorio di matematica Compare una seconda finestra (FIGURA ) con una tabella già predisposta per l inserimento degli elementi della matrice: non dobbiamo fare altro che riempirla e cliccare su OK. FIGURA La matrice così definita apparirà nella finestra Derive (espressione di FIGURA ). Ripetiamo poi la procedura descritta per inserire le altre due matrici. In alternativa al metodo descritto, le matrici si possono introdurre mediante la procedura con cui si inserisce una qualsiasi espressione: occorre tenere presente che per Derive una matrice non è altro che un vettore colonna i cui elementi sono vettori riga. Perciò per inserire la matrice A è sufficiente inserire l espressione [,0,,,] Le operazioni tra le matrici si indicano con i comuni simboli aritmetici. Naturalmente Derive può eseguire le operazioni tra le matrici solo se il numero di righe e di colonne di esse rende possibile l operazione. Calcoliamo ad esempio la matrice A B. Cominciamo con il selezionare la matrice cliccando sopra di essa quindi premiamo il tasto F: in tal modo la matrice selezionata viene inserita nella riga di inserimento delle espressioni. Scriviamo quindi il segno e spostiamo il mouse nella finestra algebrica cliccando sulla matrice al fine di selezionarla premiamo nuovamente il tasto F per inserire la nuova matrice. Per immettere l espressione e ottenere il risultato dell operazione facciamo clic sul pulsante (FIGURA ). FIGURA Dovendo eseguire diverse operazioni su alcune matrici date è preferibile, per semplificare il lavoro, associare un nome a ciascuna di esse. Ad esempio, per assegnare i nomi m, m, m alle matrici già inserite procediamo nel modo seguente. & 0 De Agostini Scuola SpA Novara
37 Laboratorio di matematica Scriviamo m:=, selezioniamo la matrice e premiamo il tasto F per inserire la matrice selezionata. Premiamo infine il tasto Invio. Ripetiamo il procedimento per le altre due matrici. Da questo momento sarà possibile inserire nelle espressioni di Derive m, m, m anziché scrivere per esteso le componenti della matrice. Calcoliamo ad esempio i prodotti m*m e m*m: è sufficiente inserire tali espressioni e semplificare (FIGURA ). FIGURA Con Derive è possibile calcolare rapidamente il determinante e l inversa di una matrice quadrata. Dopo aver inserito la matrice m (FIGURA ), per calcolarne il determinante immettiamo l espressione det(m) e semplifichiamo per calcolarne l inversa immettiamo l espressione m^ e semplifichiamo. FIGURA & 0 De Agostini Scuola SpA Novara
3 a 11 a a 1n a 21 a a 2n a 31 a a 3n. 5 a m1 a m2... a mn
 Matrici n n n Nozioni fondamentali Algebra delle matrici Determinanti di matrici quadrate n Nozioni fondamentali Definizioni DEFINIZIONE MATRICE Detti m ed n due numeri interi positivi e considerati m
Matrici n n n Nozioni fondamentali Algebra delle matrici Determinanti di matrici quadrate n Nozioni fondamentali Definizioni DEFINIZIONE MATRICE Detti m ed n due numeri interi positivi e considerati m
MATRICI e DETERMINANTI. Prof.ssa Maddalena Dominijanni
 MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
= elemento che compare nella seconda riga e quinta colonna = -4 In generale una matrice A di m righe e n colonne si denota con
 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
Matrici. Prof. Walter Pugliese
 Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Elementi di Algebra Matriciale. (richiami)
 Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
Scheda per il recupero 1
 A Ripasso Le operazioni in N e le loro proprietà OPERAZIONE PROPRIETÀ ESEMPI Addizione Interna a N (ovvero la somma di due numeri naturali è sempre un numero naturale) Commutativa a þ b ¼ b þ a Associativa
A Ripasso Le operazioni in N e le loro proprietà OPERAZIONE PROPRIETÀ ESEMPI Addizione Interna a N (ovvero la somma di due numeri naturali è sempre un numero naturale) Commutativa a þ b ¼ b þ a Associativa
M. TROVATO. algebra lineare. elementi di goniometria e trigonometria
 M. TROVATO C algebra lineare 4 elementi di goniometria e trigonometria UNITÀ VETTORI Contenuti vettori e confronto fra vettori operazioni sui vettori combinazione lineare di vettori dipendenza lineare
M. TROVATO C algebra lineare 4 elementi di goniometria e trigonometria UNITÀ VETTORI Contenuti vettori e confronto fra vettori operazioni sui vettori combinazione lineare di vettori dipendenza lineare
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
VETTORI E MATRICI. De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali. x 1 x 2. x n
 VETTORI E MATRICI De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali x 1 x. x n 5 L insieme di tutti i vettori con n componenti reali si indica con R n :I numeri reali si possono pensare
VETTORI E MATRICI De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali x 1 x. x n 5 L insieme di tutti i vettori con n componenti reali si indica con R n :I numeri reali si possono pensare
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
Introduzione all algebra delle matrici. Appunti a cura di Lara Ercoli
 Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
L insieme dei numeri interi relativi
 n L insieme dei numeri interi relativi [p. 61] n Le operazioni aritmetiche con i numeri interi relativi [p. 64] n Le potenze [p. 71] n Espressioni [p. 77] L insieme dei numeri interi relativi RICORDIAMO
n L insieme dei numeri interi relativi [p. 61] n Le operazioni aritmetiche con i numeri interi relativi [p. 64] n Le potenze [p. 71] n Espressioni [p. 77] L insieme dei numeri interi relativi RICORDIAMO
Sui determinanti e l indipendenza lineare di vettori
 Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
08 - Matrici, Determinante e Rango
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 08 - Matrici, Determinante e Rango Anno Accademico 2013/2014 D.
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 08 - Matrici, Determinante e Rango Anno Accademico 2013/2014 D.
MATRICI E OPERAZIONI
 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Geometria BIAR Esercizi 2
 Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Operazioni tra matrici. Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia c = 3
 Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Determinante. Elisabetta Colombo. Determinante. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico ,
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, 1 n=2 2 3 con le 4 n=2 n=2 con le Ad ogni matrice quadrata A = (a ij ) j=1...n i=1...n di ordine n si può associare
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, 1 n=2 2 3 con le 4 n=2 n=2 con le Ad ogni matrice quadrata A = (a ij ) j=1...n i=1...n di ordine n si può associare
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Lezione Determinanti
 Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
G. Parmeggiani, 17/5/2018 Algebra Lineare, a.a. 2017/2018, numero di MATRICOLA PARI
 G Parmeggiani, 17/5/2018 Algebra Lineare, aa 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA
G Parmeggiani, 17/5/2018 Algebra Lineare, aa 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
, è Det(A) = a 11 a 22 a 12 a 21. ( il determinante della matrice che si ottiene da A. la 1 a riga e la 2 a colonna di A
 G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Lezione 11. Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale
 Lezione Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale Matrici. Somma Date due matrici n x m, A = A ij e B = B ij, con i =,,,
Lezione Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale Matrici. Somma Date due matrici n x m, A = A ij e B = B ij, con i =,,,
Lezione 4 - Esercitazioni di Algebra e Geometria - Anno accademico
 Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Matematica II
 Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Monomi L insieme dei monomi
 Monomi 10 10.1 L insieme dei monomi Definizione 10.1. Un espressione letterale in cui numeri e lettere sono legati dalla sola moltiplicazione si chiama monomio. Esempio 10.1. L espressione nelle due variabili
Monomi 10 10.1 L insieme dei monomi Definizione 10.1. Un espressione letterale in cui numeri e lettere sono legati dalla sola moltiplicazione si chiama monomio. Esempio 10.1. L espressione nelle due variabili
MATRICI Vol.1. Pag. 1/24
 MATRICI Vol.1 Sommario ALGEBRA DELLE MATRICI... 3 Matrici nulla, diagonale e unità... 3 Matrice simmetrica e matrice trasposta... 3 Combinazioni lineari e differenza tra matrici. Matrice emisimmetrica...
MATRICI Vol.1 Sommario ALGEBRA DELLE MATRICI... 3 Matrici nulla, diagonale e unità... 3 Matrice simmetrica e matrice trasposta... 3 Combinazioni lineari e differenza tra matrici. Matrice emisimmetrica...
Determinanti. Definizione ed esempi. Definizione ed esempi. Proprietà dei determinanti Rango di matrici
 Introduzione S S S Rango di matrici Si dice sottomatrice d'una matrice data la matrice ottenuta selezionando un certo numero di righe e di colonne della matrice iniziale. Lezione 24.wpd 08/01/2011 XXIV
Introduzione S S S Rango di matrici Si dice sottomatrice d'una matrice data la matrice ottenuta selezionando un certo numero di righe e di colonne della matrice iniziale. Lezione 24.wpd 08/01/2011 XXIV
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI
 MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO
 UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
Anno 4 Matrice inversa
 Anno 4 Matrice inversa 1 Introduzione In questa lezione parleremo della matrice inversa di una matrice quadrata: definizione metodo per individuarla Al termine della lezione sarai in grado di: descrivere
Anno 4 Matrice inversa 1 Introduzione In questa lezione parleremo della matrice inversa di una matrice quadrata: definizione metodo per individuarla Al termine della lezione sarai in grado di: descrivere
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI
 CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
Introduciamo ora un altro campo, formato da un numero finito di elementi; il campo delle classi resto modulo n, con n numero primo.
 Capitolo 3 Il campo Z n 31 Introduzione Introduciamo ora un altro campo, formato da un numero finito di elementi; il campo delle classi resto modulo n, con n numero primo 32 Le classi resto Definizione
Capitolo 3 Il campo Z n 31 Introduzione Introduciamo ora un altro campo, formato da un numero finito di elementi; il campo delle classi resto modulo n, con n numero primo 32 Le classi resto Definizione
EQUAZIONI LINEARI. Attività di recupero ATTIVITÀ DI RECUPERO. A. Rivedere il ripasso punto per punto nel testo e on line
 Attività di recupero A. Rivedere il ripasso punto per punto nel testo e on line B. Esercizi da completare e domande. Completare l uguaglianza: a þ a :::::, a) in modo che risulti un identità; b) in modo
Attività di recupero A. Rivedere il ripasso punto per punto nel testo e on line B. Esercizi da completare e domande. Completare l uguaglianza: a þ a :::::, a) in modo che risulti un identità; b) in modo
Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.
![Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe. Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.](/thumbs/100/147138366.jpg) Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
1 Introduzione alle matrici quadrate 2 2 a coefficienti in R.
 1 Introduzione alle matrici quadrate 2 2 a coefficienti in R Per introdurre il concetto di matrice, a 2 righe e 2 colonne, iniziamo col considerare griglie o tabelle di numeri Gli elementi della griglia,
1 Introduzione alle matrici quadrate 2 2 a coefficienti in R Per introdurre il concetto di matrice, a 2 righe e 2 colonne, iniziamo col considerare griglie o tabelle di numeri Gli elementi della griglia,
Sottospazi vettoriali
 Capitolo 6 Sottospazi vettoriali 6.1 Introduzione Riprendiamo un argomento già studiato ampiamente nel corso di Geometria, i sottospazi vettoriali di uno spazio vettoriale. Ci limiteremo a darne la definizione,
Capitolo 6 Sottospazi vettoriali 6.1 Introduzione Riprendiamo un argomento già studiato ampiamente nel corso di Geometria, i sottospazi vettoriali di uno spazio vettoriale. Ci limiteremo a darne la definizione,
Il prodotto tra matrici non è commutativo. Nelle notazioni precedenti, ponendo n = p e m = q si hanno:
 L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Corso di Calcolo Numerico
 Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 7 - CALCOLO NUMERICO CON MATRICI Richiami teorici Operazioni fondamentali Siano A = {a ij } e B = {b ij }, i = 1,..., m, j = 1,..., n due
Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 7 - CALCOLO NUMERICO CON MATRICI Richiami teorici Operazioni fondamentali Siano A = {a ij } e B = {b ij }, i = 1,..., m, j = 1,..., n due
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
SISTEMI DI EQUAZIONI LINEARI
 SISTEMI DI EQUAZIONI LINEARI Date le rette di equazioni ax + by + c = 0 e a x + b y + c = 0 quanti punti hanno in comune? Per rispondere devo risolvere il sistema ax + by + c = 0 ቊ a x + b y + c = 0 e
SISTEMI DI EQUAZIONI LINEARI Date le rette di equazioni ax + by + c = 0 e a x + b y + c = 0 quanti punti hanno in comune? Per rispondere devo risolvere il sistema ax + by + c = 0 ቊ a x + b y + c = 0 e
ALGEBRA LINEARE PARTE II
 DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 27-28 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 27-28 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
1 Identità ed equazioni
 90. Le equazioni 1 Identità ed equazioni Consideriamo due tipi di uguaglianze. La somma di un numero con il suo triplo è uguale al quadruplo del numero stesso. Scriviamo questa frase con i simboli matematici
90. Le equazioni 1 Identità ed equazioni Consideriamo due tipi di uguaglianze. La somma di un numero con il suo triplo è uguale al quadruplo del numero stesso. Scriviamo questa frase con i simboli matematici
Matematica II,
 Matematica II,.05.04 Diamo qui la nozione di determinante di una matrice quadrata, le sue prime proprieta, e ne deriviamo una caratterizzazione delle matrici non singolari e una formula per l inversa di
Matematica II,.05.04 Diamo qui la nozione di determinante di una matrice quadrata, le sue prime proprieta, e ne deriviamo una caratterizzazione delle matrici non singolari e una formula per l inversa di
Vettori e matrici. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
ALGEBRA DELLE MATRICI
 ALGEBRA DELLE MATRICI March 8, 2015 1 Definizioni e notazioni Una matrice è una tabella rettangolare le cui entrate sono numeri organizzati in righe orizzontali e colonne verticali. Esempio 1 2 A = 4 0
ALGEBRA DELLE MATRICI March 8, 2015 1 Definizioni e notazioni Una matrice è una tabella rettangolare le cui entrate sono numeri organizzati in righe orizzontali e colonne verticali. Esempio 1 2 A = 4 0
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
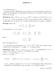 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Matrici quadrate particolari
 Matrici quadrate particolari Sia A Mn(K) una matrice quadrata. Gli elementi (a 1,1, a 2,2,, a n,n ) costituiscono la diagonale principale di A. Gli elementi (a 1,n, a 2,n-1,, a n-1,2, a n,1 ) costituiscono
Matrici quadrate particolari Sia A Mn(K) una matrice quadrata. Gli elementi (a 1,1, a 2,2,, a n,n ) costituiscono la diagonale principale di A. Gli elementi (a 1,n, a 2,n-1,, a n-1,2, a n,1 ) costituiscono
Matrici e sistemi. Geometria. Matrici e operazioni tra matrici. Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante
 Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
1 PRELIMINARI 1.1 NOTAZIONI. denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A.
 1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
Operazioni tra matrici e n-uple
 CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma:
 SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
Lezioni di Algebra Lineare. II. Aritmetica delle matrici e eliminazione di Gauss. versione ottobre 2008
 versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
PROBLEMA. Costruire matrici quadrate contenute. Fare i determinanti delle matrici quadrate contenute in A
 A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
determinante della sottomatrice ottenuta da A cancellando la i-esima riga e la j-esima colonna
 Data una matrice quadrata A di ordine n si definisce minore complementare m ij dell elemento generico a ij della matrice A il determinante della sottomatrice ottenuta da A cancellando la i-esima riga e
Data una matrice quadrata A di ordine n si definisce minore complementare m ij dell elemento generico a ij della matrice A il determinante della sottomatrice ottenuta da A cancellando la i-esima riga e
Capitolo 3. Determinante e rango Permutazioni
 Capitolo 3 Determinante e rango 303 Permutazioni Ricordiamo innanzitutto che, dato un insieme, l insieme S () delle applicazioni biunivoche da in sè stesso, può essere munito di una operazione, indicata
Capitolo 3 Determinante e rango 303 Permutazioni Ricordiamo innanzitutto che, dato un insieme, l insieme S () delle applicazioni biunivoche da in sè stesso, può essere munito di una operazione, indicata
1.1 Matrici a coefficienti in R. Vi sono alcuni casi particolari che vale la pena evidenziare:
 Lezione Matrici a coefficienti in R Definizione Siano m, n Z numeri interi positivi Una matrice m n acoefficientiinrèuninsiemedimn numeri reali disposti su m righe ed n colonne circondata da parentesi
Lezione Matrici a coefficienti in R Definizione Siano m, n Z numeri interi positivi Una matrice m n acoefficientiinrèuninsiemedimn numeri reali disposti su m righe ed n colonne circondata da parentesi
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche. Appunti del corso di Matematica
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 19 - Determinante Anno Accademico 2015/2016 M. Tumminello,
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 19 - Determinante Anno Accademico 2015/2016 M. Tumminello,
