Manuale di Orientamento e Topografia
|
|
|
- Anna Pinna
- 9 anni fa
- Просмотров:
Транскрипт
1 argomenti Orientamento cosa serve l orientamento Orientamento punti cardinali Topografia longitudine, latitudine Topografia cartografia Topografia le curve di livello Topografia declinazione magnetica o nord magnetico Topografia l orientamento della mappa Topografia l azimut Orientamento la bussola Topografia misura di distanze e altezze Orientamento 1. orientarsi con il sole ( bastone, scout americano) 2. con orologio ( fiammifero e non) 3. con luna 4. con le stelle 5. con coltellino 6. con i segni della natura Manuale di Orientamento e Topografia L orientamento L orientamento e la topografia cosa servono a noi scout? Ci servono a sapere dove siamo in ogni momento e che direzione prendere per raggiungere la nostra meta. I punti cardinali La posizione è sempre relativa ad un punto di riferimento. Come molti sanno il punto in cui sorge il sole è l EST indicato con E, mentre quello in cui tramonta si chiama OVEST indicato con W. Se uniamo questi due punti con una linea e si traccia una perpendicolare a questa avremo la linea che congiunge il NORD, indicato con N, e il SUD indicato con S. Questi quattro punti sono chiamati punti cardinali perché fanno da cardine all orientamento. Scout Evangelici di San Bonifacio (VR) Rev. 0 Apr.2014 autore: GB La linea che congiunge il nord al sud viene chiamato asse terrestre Longitudine e Latitudine
2 I semicerchi che uniscono i due poli si chiamano Meridiani e viene definito come fondamentale quello di Greenwich. L Equatore divide, invece, la terra in due emisferi, quello Boreale e quello Australe. I cerchi paralleli all equatore si chiamano appunto Paralleli. La maglia che si crea fra meridiani e paralleli viene chiamata Reticolo Geografico. Queste sono molto importanti perché ci permettono di definire la posizione assoluta di dove ci troviamo. Ogni intersezione si può individuare con un angolo che lo separa dall equatore e dal meridiano di Greenwich. I due angoli che si formano si chiamano: Latitudine e Longitudine. LA CARTA TOPOGRAFICA Una carta topografica è una rappresentazione grafica ridotta e simbolica di una parte della superficie terrestre su un piano N.B. In questa scala 1cm = 250 m ovvero 1 km = 4 cm Apprestandosi a leggere una carta topografica oltre alla scala, si deve tenere in considerazione che, salvo diversa indicazione, vengono tutte stampate con il Nord Geografico verso l alto.
3 Le cartine hanno una loro colorazione che ci aiuta a capire dove ci troviamo, azzurro = acque, marrone per le caratteristiche altimetriche, verde per la vegetazione, rosso per le strade, nero per le scritte e simboli. I sentieri facili sono rappresentati da trattini Quelli difficili da una serie di puntini Le mulattiere da tratti e punti _._._._._._ Le curve di livello o Isoipse La declinazione Magnetica
4 Orientare la carta con la bussola
5
6 LaBussola Calcolo dell azimut
7 ORIENTARE UNA CARTA Orientare una carta significa disporla in modo che il nord della stessa coincida con il nord individuato dalla bussola. In particolare dovremmo disporla secondo il nord geografico, il che significa, individuato il nord magnetico, correggere l'orientamento in base alla declinazione magnetica del luogo. In alcuni tipi di bussole è possibile impostare la declinazione (mediante una vite di regolazione che in pratica sposta l'indice della scala e lo blocca sul valore impostato) per tenerne conto automaticamente (attenzione: se utilizziamo un goniometro al posto della bussola per misurare gli angoli dovremo ogni volta considerare anche la declinazione magnetica). Alle nostre latitudini e per spostamenti relativamente brevi la declinazione magnetica può essere trascurata. Un orientamento rapido è comunque possibile anche senza bussola a parte conoscere il territorio, basta individuare un punto noto (ad esempio una vetta ben visibile ed identificabile) e ruotare la carta in modo che lo stesso sopra rappresentato sia nella direzionedel punto osservato. L'operazione di orientamento, che ci consente di guardare la carta con immediato riscontro di quel che rappresenta nell'ambiente circostante, è una operazione molto semplice. Con la BUSSOLA DA CARTEGGIO occorre ruotare la corona in modo che lo 0 della scala e l'indice sul fondo della cassa siano allineati con l'asse della bussola (questa operazione non è necessaria con la bussola a traguardo poichè l'ago magnetizzato è sempre allineato con lo 0 della scala in quanto solidale con essa). Poi dobbiamo posare la bussola sulla carta con lo 0 della scala dalla parte del nord della carta, come nella foto successiva, ed allineare la stessa al bordo della carta. In genere nella carte il nord è in alto (intendendo per l'alto quello con la carta disposta nel modo che possiamo leggere le scritte) per cui la direzione al nord è parallela al bordo destro o sinistro ed al reticolo dei meridiani geografici (non al reticolo UTM), se presente. A questo punto occorre ruotare carta e bussola senza muovere l'una rispetto all'altra e senza muovere la corona in modo che l'ago della bussola vada a puntare lo zero della scala, ossia si sovrapponga con l'indice sul fondo della cassa. In questo modo avremo che il bordo della carta (direzione del nord della carta, ovvero parallela al reticolo geografico) è parallelo al nord della bussola (che coincide con l'asse della stessa) e contemporaneamente il nord della carta da lato del nord indicato dall'ago della bussola. Orientamento della carta con la bussola da carteggio MISURARE ANGOLI (AZIMUT) SU UNA CARTA, INDIVIDUARE LA ROTTA SULLA CARTA E LA DIREZIONE DI MARCIA SUL TERRENO Per individuare la direzione di marcia da tenere per raggiungere un punto noto, presente sulla carta, a partire dalla posizione in cui ci troviamo (supponendo per il momento di conoscerla) dobbiamo misurare l'azimut di questo punto, ossia l'angolo che la direzione al nord geografico forma con la direzione al punto da raggiungere, a partire dalla nostra posizione (che sarà la direzione di marcia da tenere), misurato crescente in senso orario a partire dalla direzione al nord che costituisce lo 0 della scala. Questo è il senso di misura dei goniometri e degli strumenti topografici. L'angolo così rilevato sulla carta sarà quello che sul terreno, dovremo tenere durante la marcia rispetto alla direzione al nord geografico che andremo ad individuare con la bussola (a meno dell'errore dovuto alla declinazione magnetica che, come detto, potremo trascurare nella maggiorr parte dei casi). Una volta misurato il valore dell'azimut, occorre annotarlo. Esistono bussole che dispongono di un meccanismo che blocca la ghiera in modo che l'indice di lettura della scala dei gradi resti sul valore trovato, anche richiudendo la bussola e mettendola in tasca. Per misurare l'azimut di un punto rispetto ad un altro sulla carta, ossia la direzione che dobbiamo tenere per raggiungere un punto noto a partire dalla nostra posizione, il metodo più semplice è utilizzare un goniometro. Misura dell'azimut sulla carta con il goniometro Tracciamo una retta parallela al bordo della carta a partire dalla nostra posizione P1, individuando il nord geografico. Posto il goniometro con centro sul punto P1
8 con l'origine della scala sulla direzione al nord, la congiungente con la posizione da raggiungere P2 individua sulla scala il valore dell'azimut cercato, in questo esempio pari a 101 (se il goniometro, come quello in foto, riporta sia scala sessagesimale che centesimale dovremmo leggere in genere leggere l'angolo in gradi sessagesimali o centesimali in base al tipo di scala che abbiamo sulla bussola, in genere sessagesimale ma vi sono bussole che riportano entrambi i tipi di scala). In mancanza del goniometro è possibile utilizzare una bussola, da carteggio o da rilevamento con due tipi di procedimento leggermente diversi. Con la BUSSOLA DA CARTEGGIO (che in questo caso si rivela la più comoda da usare) dobbiamo posizionare la base trasparente sulla carta allineando il lato lungo (con la parte più larga della bussola, ove si trova l'indice di puntamento verso la nostra destinazione) e successivamente ruotare la corona in modo che lo 0 della scala e l'indice sul fondo della capsula siano allineati con il nord della carta (ossia paralleli al bordo o reticolo geografico). Misura dell'azimut su carta con la bussola da carteggio A questo punto la lettura dell'angolo in corrispondenza dell'indice di puntamento della bussola (parallelo al bordo della base trasparente e quindi alla direzione verso il punto da raggiungere P2) ci darà l'azimut cercato. Notare che non è assolutamente necessario preoccuparsi di orientare la carta e non ha nessun interesse, in questa operazione, che direzione assuma l'ago magnetizzato. Mi pare superfluo annotare che queste operazioni debbono essere fatte usufruendo di un piano di appoggio e che lo stesso, perché la bussola lavori correttamente, deve essere orizzontale (questo problema ovviamente non si ha col goniometro). Una volta che abbiamo letto l'azimut basterà sollevare la bussola dalla carta senza più muovere la corona. Con la bussola da carteggio, l'indice di lettura rimarrà sopra lo 0 della scala e l'indice di puntamento (asse della base e della bussola stessa) rimarrà sul valore dell'azimut. Se abbiamo misurato l'azimut sulla carta con il goniometro o in un momento precedente quando cominceremo a muoverci sul campo occorrerà egualmente annotarlo per poi ruotare la ghiera sino a che l'indice di puntamento segnerà il valore dell'azimut stesso (in pratica lo reimpostiamo). A questo punto, tenendo la bussola in mano orizzontale, ruoteremo noi stessi e la bussola sino a che l'ago magnetico non si sovrapporà all'indice di lettura sul fondo della capsula. Avremo così lo 0 della scala corrispondente al nord (magnetico) mentre l'indice di puntamento forma un angolo pari al nostro azimut con la direzione al nord. Facendo in modo che l'ago non si sposta da questa posizione potremo traguardare lungo l'indice di puntamento e visualizzare la direzione sul terreno. E' buona cosa prendere a riferimento, per la marcia, degli elementi del territorio facilmente individuabili (rocce, alberi, fabbricati, ecc.), per non dover sempre ricontrollare la direzione. Traguardare con la bussola da carteggio non è una cosa molto agevole, occorre tenere la bussola in orizzontale davanti agli occhi e guardare la che direzione assume l'indice di puntamento mantenendo contemporaneamente l'ago della bussola allineato con l'indice in fondo alla capsula. La cosa più semplice è appoggiare la bussola su una superficie piana. Come traguardare con la bussola da carteggio (vedi anche foto del paragrafo successivo) Queste operazioni sono agevolate nelle bussole ibride a specchio che consentono di traguardare attraverso indice di puntamento e contemporaneamente vedere il quadrante della bussola riflesso nello specchio (posto sopra o sotto la base, inclinato a 45 verso chi osserva) per poter
9 verificare l'allineamento dell'ago con l'indice mobile della bussola senza spostare la bussola e riducendo il pericolo di disallineare l'ago. Misurare l'azimut sulla carta e "riportarlo" sul terreno è utile non solo per individuare la direzione di marcia ma anche per individuare la direzione in cui osserviamo unn qualsiasi punto di interesse, ad esempio una vetta: basta misurare sulla carta l'azimut del punto che ci interessa e poi traguardare sul terreno finchè non troviamo la direzione individuata dall'azimut stesso. In quella direzione dovremo vedere il punto cercato. L'operazione inversa (riconoscere ad esempio una vetta rilevandone l'azimut sul terreno) è descritta nel paragrafo successivo. MISURARE ANGOLI DI DIREZIONE (AZIMUT) SUL TERRENO E RIPORTARLI SULLA CARTA Queste operazioni non sono che quelle inverse alle precedenti in cui, partendo da un azimut misurato sulla carta, lo riportavamo sul terreno per individuare la direzione di marcia, di una montagna, ecc.. Anche in questo caso rilevare gli azimut è più semplice ed agevole con la bussola da puntamento che con quella da carteggio, a meno di non disporre di una ibrida a specchio. Con la BUSSOLA DA CARTEGGIO dobbiamo tenerla orizzontale dinanzi a noi e traguardare il punto "bersaglio" (una vetta da identificare, la nostra destinazione, ecc.) con l'indice di puntamento. Successivamente, senza muovere la bussola dobbiamo ruotare la corona in modo che l'indice sul fondo della capsula (origine della scala degli angoli) non si sovrappone all'ago magnetizzato, dalla parte del nord. A questo punto leggeremo il valore dell'azimut in corrispondenza dell'indice di puntamento, sulla scala degli angoli. Traguardando con la bussola da carteggio verso una lontanissima Becca Mortens Come già detto in questa operazione le difficoltà sono allineare bene l'indice di puntamento con il punto "bersaglio" che può essere molto più alto o più basso di noi (occorre "visualizzare" la verticale come in foto) e spostarsi per ruotare la corona ed allineare l'indice (freccia di direzione) con l'ago magnetizzato senza spostare la bussola (in questo modo lo 0 della scala coincide con la direzione al nord, come deve essere per misurare l'azimut). Non è molto agevole farlo con la bussola in mano, se possibile è meglio appoggiarla su una superficie orizzontale. Una soluzione potrebbe farsi aiutare da un compagno, che guarda quando l'ago si soprappone all'indice sul fondo della capsula, mentre noi guardiamo di taglio il punto da collimare e ruotiamo la corona. Lo specchio, se presente, risolve i problemi in quanto entrambe le operazioni vengono effettuate senza dover spostare l'occhio. Una volta letto l'azimut, il valore resta fisso sull'indice a meno che non ruotiamo di nuovo la corona. Per riportarlo su una carta dovremo solo posare la bussola su di essa SENZA RUOTARE LA CORONA, posizionarla con l'indice sul fondo della capsula parallelo al nord della carta (orientato verso il nord), spostare la bussola in modo che il lato lungo passi per il punto che rappresenta la nostra posizione e tracciare la linea passante per il lato lungo che formerà con il nord della carta un angolo pari all'azimut rilevato (questa operazione non è altro che l'inverso di quella già vista per misurare gli angoli sulla carta). La determinazione dell'azimut, nota la propria posizione sulla carta (ad esempio se ci troviamo su una vetta o presso un punto comunque noto, come un rifugio) si rivela utile per individuare ad esempio i nomi delle vette e altri luoghi segnati in carta che osserviamo: basta misurare l'azimut della vetta incognita e riportarlo sulla carta a partire dalla nostra posizione. Individueremo cosi sulla carta la vetta, alpeggio o altro che incontriamo sulla retta data dall'azimut misurato.
10
11
12 Valutazione delle distanze e principali misure personali Qualcuno ha detto: "Per misurare il mondo inizia a misurare te stesso!" Qualcuno ha detto: "Per misurare il mondo inizia a misurare te stesso!" Calcolo distanze e altezze Misurazione delle altezze Per misurare un'altezza o una distanza puoi utilizzare le proprietà dei triangoli simili e le proporzioni. Metodo dei triangoli Pianta un bastone a qualche distanza dal piede dell albero del quale vuoi misurare l altezza. Mettendoti faccia a terra, spostati opportunamente per trovare sul terreno il punto dal quale vedi allineate l a sommità del bastone e quella dell albero. Se è necessario, sposta il bastone per facilitare la ricerca. L'altezza sarà: È utile imparare a memoria le seguenti misure personali: Statura. Altezza da terra agli occhi. Larghezza braccia spalancate. Distanza da terra al ginocchio. Distanza dal gomito al polso. Lunghezza dell'indice disteso. Distanza tra mignolo e pollice divaricati (spanna). Larghezza del polso. Numero di passi per percorrere 100 metri al passo. Numero di passi per percorrere 100 metri di corsa. Metodo delle 10 volte Misura 1 8 metri dal piede dell albero e pianta il bastone in terra. Spostati di altri 2 metri e, faccia a terra, traguarda la sommità dell albero, segnando dove la linea di mira taglia il bastone. Misura ora sul bastone la distanza " h" tra il segno e il terreno e moltiplicala per 10. Essendo la base del triangolo maggiore, 10 volte più grande di quella del triangolo minore, (20 m e 2 m) è evidente che l altezza da misurare sarà dieci volte maggiore di quella segnata sul bastone. Metodo dell ombra Se c è il sole pianta in terra il bastone, poi misura l ombra del bastone e quella dell albero. Con delle semplici proporzioni otterrai:
13 Metodo della matita Metti ai piedi dell'albero una persona della quale conosci l altezza. Stando a una distanza presumibilmente almeno doppia di quella ricercata, conta, con l aiuto di una matita o di un bastoncino tenuto in mano con il braccio teso, quante volte l altezza dell oggetto conosciuto sta nell altezza dell albero. Moltiplica questo numero per la lunghezza dell oggetto e otterrai l altezza desiderata. Metodo indiano Volgi le spalle all albero che vuoi misurare, poi piegati e guardalo attra verso le gambe, tenendo le cavi glie con le mani. Avanza, o indietreggia, finché non vedi tutto l albero. Misura la distanza fra te e la base dell albero. L'altezza dell albero è la metà di questa distanza. Per ottenere dei buoni risultati, però, devi fare prima diverse prove, misurando un oggetto del quale conosci l altezza, in maniera da determinare esattamente la posizione che devi assumere: mani sulle caviglie, o un po più in alto o più in basso, gambe tese o ginocchia leggermente fesse, ecc. Metodo della rotazione Mettiti a una certa distanza dall oggetto che vuoi misurare. Tenendo un ba stoncino con il braccio teso, traguarda in maniera da vedere l oggetto compreso fra la sommità del bastoncino e il tuo pollice. Ruota ora il bastoncino di 90 in posizione orizzontale. Mantieni il pollice alla base dell oggetto e guarda dove la sommità del bastoncino tocca ora il suolo. La distanza X da questo punto alla base del palo è uguale all altezza X del palo.
14 Valutazione delle distanze Con un po di esperienza e con molto esercizio, potrai imparare a valutare le distanze a colpo d occhio. Ricorda, però, che ci sono condizioni che fanno sembrare gli oggetti più vicini, mentre ve ne sono altre che li fanno sembrare più lontani: Gli oggetti ti sembrano più vicini quando: l atmosfera è molto limpida (ad esempio dopo un temporale); la luce è viva e vi batte sopra; fra te ed essi c'è una superficie di acqua, di neve, o di sabbia; il terreno è piatto; da mezza costa di una collina guardi verso l alto o verso il basso. Gli oggetti ti sembrano più lontani quando: il terreno è accidentato; sono in ombra; fa molto caldo e c è umidità nell aria; c è poca luce (sei al crepuscolo o c è foschia); guardi attraverso una valle; lo sfondo è del loro medesimo colore; sono in fondo a un viale o a una lunga strada dritta; sei disteso o in ginocchio. Esercizio per l'occhio alle varie distanze: 50 m Si vedono gli occhi e la bocca di una persona. 100 m Gli occhi sembrano puntini. 200 m Si distinguono bene tutte le parti del corpo umano ed alcuni particolari dell'abito. 300 m Si vede ancora un po' la faccia. 400 m Si distingue il movimento delle gambe. 500 m Si distingue, con luce adatta, il colore del vestito, la testa e il cappello dal resto del corpo. 600 m La testa diviene un punto. 700 m E' molto difficile distinguere la testa dal tronco. 800 m La testa non si distingue più dal tronco m Si possono ancora distinguere i movimenti delle braccia e delle gambe m Si distingue bene un uomo a cavallo da un uomo a piedi m Si distingue ancora un palo telefonico m Si distinguono i tronchi di grossi alberi isolati m Possono distinguersi soltanto i campanili delle chiese. A più di 500 m: conviene accorciare la distanza scegliendo un punto a 250 m, valutare questa distanza e raddoppiarla. In mare: l'orizzonte serve a stabilire la distanza. Con l'occhio ad 1,5 metri dal livello dell'acqua una nave all'orizzonte è lontana 4,5 km. Valutare le distanze con il suono Il suono ti può permettere di calcolare una distanza perché, come sai, esso si propaga alla velocità di circa 340 metri al secondo. Se riesci a calcolare il tempo che il suono impiega per arrivare fino a te, puoi conoscere la distanza che esiste fra te e il punto di origine del suono stesso. Se vuoi valutare una distanza, ad esempio, fra te e un taglialegna, dovrai moltiplicare per 340 il numero di secondi che passano fra quando lo vedi vibrare il colpo di scure e quando senti il rumore relativo. Con lo stesso sistema puoi anche misurare la distanza di una parete di roccia che rimandi l eco. Ricordati poi di dividere per due, perché il suono compie il tragitto di andata e ritorno. Se non hai un orologio con l indicazione dei secondi, puoi valutare i secondi contando lentamente milleuno, milledue, milletre, ecc. Esercitati con un orologio. Il metodo del pollice Il tuo pollice può esserti molto utile per valutare con buona approssimazione le distanze. Puoi adoperarlo in due modi, uno è valido per distanze inferiori a 3 km, l altro per distanze maggiori. FINO A 3 KM Stendi il braccio con il pollice alzato davanti agli occhi e copri con esso un oggetto che si trovi alla distanza cercata e che sia facilmente valutabile, ad esempio la larghezza di una finestra, la facciata di una casa, ecc. La distanza tra te e quell oggetto si ottiene moltiplicando per 25 la larghezza dello spazio coperto dal pol lice. OLTRE 3 KM Stendi il braccio con il pollice (oppure con una matita) alzato davanti agli occhi.traguarda prima con l occhio destro, poi con il sinistro sempre tenendo immobile la mano. Valuta la distanza tra i due punti traguardati e moltiplicala per 9. otterrai la distanza che c è fra te e i punti traguardati. Esercitati in varie
15 circostanze e su terreni differenti perché se la teoria è semplice non sempre lo è anche la pratica. N.B. Nelle figure non sono rispettate le proporzioni. Metodo delle perpendicolari Individua un oggetto (A) ben visibile sull altro lato del fiume. In corrispondenza ad esso, pianta un bastone (B) sulla tua riva. Cammina lungo l a riva, perpendicolarmente all a direzione AB, per una certa distanza, ad es. 50 metri. Pianta qui un altro bastone (C). Continua a camminare per una distan za uguale alla precedente (altri 50 metri). Pianta qui un terzo bastone (D). Ora cammina perpendicolarmente alla direzione BD. Quando vedrai allineati il bastone C con il punto A fermati, La distanza DE è uguale alla larghezza del fiume. Se sulla riva del fiume vi è poco spazio (vedi disegno), puoi percorrere una distanza CD pari alla metà di BC. In tal caso la distanza DE sarà pari ala metà della larghezza del fiume. Metodo del cappellone Stando sulla riva del fiume individua un oggetto ben visibile sull altra sponda. Inclina il cappellone in modo da traguardare il punto prescelto con la tesa dello stesso cappellone. Senza alzare ne abbassare la testa, girati su te stesso fino a trovare sulla tua riva un punto che sia allineato con la "tesa" del cappellone. La distanza fra te e questo punto è uguale alla larghezza del fiume. Metodo del sasso Per valutare la larghezza di un corso d acqua, mettiti sulla sua riva nel punto O, e lascia cadere un sasso verticalmente nell acqua. Se l acqua è calma, dal punto O dov è caduto il sasso, partono dei cerchi concentrici che si allontaneranno sempre più. Segui con gli occhi uno di questi cerchi e, nel momento preciso in cui esso tocca la riva opposta nel punto K, cerca il punto M in corrispondenza della ava lungo la quale sei tu. Misura la distanza OH, essa sarà uguale alla distanza OK. Metodo della bussola Stando su un lato del fiume (punto B) individua un punto evidente dall altro lato (roccia A). Rileva l azimut della direzione BA (ad es. 120 ). Aggiungi 45 all azimut della direzione BA ( = 165 ). Cammina lungo il fiume perpendicolarmente alla direzione BA tenendo la bussola orientata verso l azimut di 165. Quando con questo azimut riuscirai a vedere nel mirino la roccia A, fermati. La distanza CB è uguale alla larghezza del fiume. Valutazione della profondità Per misurare la profondità di un pozzo, lascia cadere un sasso e misura quanti secondi occorrono per sentirne il rumore della caduta sul fondo. La tabella seguente ti dà la profondità del pozzo. TEMPO PROFONDITA' 0,5 1,20 m 1 5 m 1,5 11 m 2 19 m 2,5 30 m 3 44 m 3,5 60 m
16 COME ORIENTARSI SENZA LA BUSSOLA Non voglio credere che vi ritroviate a non avere una bussola perché l'avete dimenticata (dato che sono sicuro non vi succederà mai), ma comunque mettiamo il caso che vi sia scivolata e sia caduta in un burrone. Come ci si può orientare senza questo prezioso strumento? Qui esaminiamo diversi sistemi, la cui scelta sta nelle condizioni ambientali e nel materiale che si ha a disposizione. ORIENTARSI DI GIORNO CON UNA BUONA VISIBILITA' Metodo dell'orologio a lancette (figura 3.1) Innanzitutto se è in vigore l'ora legale mettete indietro l'orologio di un'ora. Puntate adesso in direzione del sole la lancetta delle ore ed osservate l'angolo che quest'ultima forma con il numero 12. La linea immaginaria che divide a metà questo angolo indica il sud. Figura 3.2: il metodo dell'orologio e del fiammifero Figura 3.1: il metodo dell'orologio a lancette Metodo dell'orologio e del fiammifero (figura 3.2) E' meno immediato del precedente, ma ugualmente efficace. Sistemate l'orologio ben orizzontale e appoggiatevi sopra un fiammifero, al centro, ben verticale. Ruotate ora l'orologio finché l'ombra del fiammifero si trova esattamente a metà tra l'angolo formato dalla lancetta delle ore ed il numero 12: in questa posizione il 12 indica il nord. Metodo del bastone (figura 3.3) Richiede più tempo, ma si può usare se non si ha un orologio a lancette. Scegliete un tratto di terreno pianeggiante (anche di pochi metri quadrati) e piantateci ben verticale un bastone che sporga di almeno un metro. Segnate con una pietra o qualcos'altro l'estremità dell'ombra sul terreno e prendete nota dell'ora esatta. Dopo un quarto d'ora segnate la nuova estremità dell'ombra, che nel frattempo si sarà spostata, e riunite con una linea i due punti così ottenuti: quella è la direzione est ovest ed il secondo punto indica l'est. Figura 3.3: il metodo del bastone Metodo del bastoncino (figura 3.4) E' una variante del sistema precedente, che si può usare se non si riesce a trovare un bastone abbastanza lungo. Piantate nel terreno un bastoncino, puntandolo inclinato verso il sole, in modo che non faccia ombra. Aspettate quindi che l'ombra compaia e che sia lunga almeno 15 centimetri: la sua estremità indica l'est. Figura 3.4: il metodo del bastoncino Osservazione della posizione del sole (figura 3.5) Sapendo che il sole alle ore 12 si trova a sud e che in 24 ore la Terra deve compiere un giro completo intorno ad esso, si ha che: alle 6 è ad est, alle 9 a sudest, alle 12 a sud, alle 15 a sud ovest, alle 18 ad ovest. Questa osservazione però è piuttosto approssimativa, perché in realtà il sole sorge esattamente ad est e tramonta esattamente ad ovest solo negli equinozi, mentre negli altri periodi dell'anno si sposta gradualmente: verso nord fino al solstizio d'estate e verso sud fino al solstizio d'inverno. Figura 3.5: la posizione del sole nelle ore della giornata Metodo della carta topografica Se avete a disposizione la cartina della zona in cui vi trovate, basta orientarla "a vista" per trovare i punti cardinali. ORIENTARSI DI GIORNO CON UNA SCARSA VISIBILITA' Metodo del coltello (figura 3.6) Se il cielo è coperto ed è difficile stabilire la posizione esatta del sole, si può appoggiare un foglio di carta bianca per terra e metterci sopra verticalmente un coltello. Ruotandolo, quando la lama produce l'ombra, nella direzione opposta c'è il sole. Figura 3.6: il metodo del coltello ORIENTARSI DI NOTTE Individuazione della Stella Polare (figura 3.7) La Stella Polare è l'unica del cielo ad essere sempre fissa ed indica con una buona approssimazione il nord. E' anche facile da trovare, essendo l'ultima della costellazione dell'orsa Minore (o Piccolo Carro). L'Orsa Maggiore (o Grande Carro) è comunque più visibile e per arrivare alla Polare bisogna osservare le prime due stelle del carro (Merak e Dubhe) e prolungare la loro distanza per cinque volte. Dalla parte opposta si trova invece Cassiopea, che ha una forma a W e la cui stella centrale è rivolta verso la Polare. Anche Orione, evidentissima, ma solo nei mesi invernali, ci può aiutare nell'orientamento: le tre stelle della spada, che sono allineate, portano verso il nord. Se queste non sono visibili, bisogna unire la stella centrale della cintura con quella che simboleggia la testa e prolungare la linea fino ad
17 incrociare la Polare. Per ragioni di spazio, nella figura 3.7 Orione è disegnata molto più vicina di quanto sia nella realtà alle altre tre costellazioni. Figura 3.7: come individuare la Stella Polare Orientamento con la Luna LaLuna,ruotando intorno alla Terra(un giro completo ogni29 giorni),é: Luna nuova (che non vediamo) primo quarto (la gobba é a destra) Luna piena (tutta illuminata dal Sole) Ultimo quarto (la gobba é a sinistra) U so dell'orologio con la Luna piena:orientare la lancetta delle ore verso la Luna;la bisettrice dell'angolo formato dalla lancetta delle ore con le ore 12 indica il S ud,dalla parte opposta si troverà il Nord. U so dell'orologio con la Luna al primo quarto:dirigere la lancetta delle ore verso la Luna;la bisettrice formata fra la direzione della Luna e le ore 12 indica l'ovest, ruotando di 90 in senso orario (cioè 3 ore dopo quella che segna l'ovest)si ottiene la direzione del Nord. U so dell'orologio con la Luna all'ultimo quarto:posizionando l'orologio come prima la bisettrice indicherà la direzione Est,ruotandodi90 (cioèdi3 ore) in senso antiorario si ottiene la direzione Nord. Un altro metodo (più approssimativo) per trovare il Nord con la Luna consiste nell'orientamento con le fasi della Luna secondo la tabella La tabella si legge nel modo seguente: alle 24 la luna indica il Sud quando è piena, l'ovest quando è al primo quarto,l'est all'ultimo quarto,ecc. Dice un proverbio: Gobba a levante (est) luna calante Gobba a ponente (ovest) luna crescente. Orientamento con l'osservazione diretta del terreno Facendo attenzione ai significativi punti di riferimento si commettono meno errori. i traccia una mappa per avere un'idea abbastanza esatta del terreno circa le costruzioni varie,i bivi,i sentieri,i fiumi,le rocce,le baite,i tronchi abbattuti,le croci,ecc. Anche senza carta topografica e bussola si riesce a trovare la strada del ritorno,pur trovandosi in zona sconosciuta a patto di prestare molta attenzione ai possibili oggetti di riferimento. Può essere di grande aiuto servirsi di un semplice schizzo fatto all'andata. L'orientamento diventa più difficile nel deserto,su terreno coperto da neve,durante una bufera di neve,nelle notti senza stelle,con la nebbia o in zone boscose. Sono di aiuto questi particolari: La corteccia degli alberi ad alto fusto che hanno la parte rivolta a Nord generalmente è coperta di muschio per la maggiore umidità. Sui ceppi di un albero abbattuto gli anelli di crescita sono più ampi nel lato Sud. Il fogliame è più folto sul lato Sud dell'albero. Il Sole scioglie la neve più velocemente verso la parte esposta a Sud. Presenza di muschio sul lato delle rocce orientate a Nord. Maggiore umidità nel sottobosco esposto a Nord. A Sud si trovano pietrame più pulito e rocce più asciutte.
18 Osservazione di fenomeni naturali Questi sistemi è meglio utilizzarli se siete proprio disperati perché non sono sempre affidabili. Il muschio alla base degli alberi cresce preferibilmente sul lato più esposto all'umidità, che è il nord, ma anche il nord ovest. Se vi trovate in un bosco fitto, però, noterete che gli alberi sono ricoperti quasi interamente di muschio e quindi non potete usare questo metodo. La corteccia degli alberi, nell'emisfero boreale, è più spessa sul lato a nord. Le foglie ed i fiori generalmente si rivolgono verso il sud, per ricevere la massima insolazione. In inverno la neve si mantiene più a lungo sui versanti nord e nord ovest delle montagne e le rocce esposte a nord sono spesso coperte di ghiaccio. Conoscendo il vento dominante della zona, cioè quello che soffia più spesso, basta osservare la direzione in cui sono incurvati i rami e le cime degli alberi e ribaltarla: ad esempio, se c'è spesso il maestrale, gli alberi sono piegati verso sud est. Materiale di squadriglia per la topografia Ciò che serve per una attività di esplorazione o topografia...ogni squadriglia che si rispetti deve avere fra il proprio materiale anche quello per la topografia, da contenere in una sacca apposita. bussola righello coordinatometro squadra goniometro compasso matita gomma biro pastelli e pennarelli di almeno tre colori diversi ben distinguibili fra loro carta millimetrata carta da lucido.
Orientarsi Bussola e Azimut Carte e scale Misure. Topografia. Basi minime di topografia. Reparto Aquile Randage. Chirignago 1
 Basi minime di topografia. Chirignago 1 2008 Contenuti 1 Orientarsi La bussola Orientarsi con il sole Orientarsi con le stelle 2 Marcia all azimut Percorso rettificato 3 Paralleli e meridiani Scala 4 La
Basi minime di topografia. Chirignago 1 2008 Contenuti 1 Orientarsi La bussola Orientarsi con il sole Orientarsi con le stelle 2 Marcia all azimut Percorso rettificato 3 Paralleli e meridiani Scala 4 La
MANUALE DI TOPOGRAFIA
 GRUPPO SCOUT AGESCI CANDA 1 Reparto Grande Magnolia MANUALE DI TOPOGRAFIA Sq: I punti cardinali I punti cardinali sono detti così perché servono da "cardine" per l orientamento e per gli antichi rappresentavano
GRUPPO SCOUT AGESCI CANDA 1 Reparto Grande Magnolia MANUALE DI TOPOGRAFIA Sq: I punti cardinali I punti cardinali sono detti così perché servono da "cardine" per l orientamento e per gli antichi rappresentavano
Il taccuino dell esploratore
 Il taccuino dell esploratore a cura di ORESTE GALLO (per gli scout: Lupo Tenace) QUINTA CHIACCHIERATA L ORIENTAMENTO (prima parte) Un buon escursionista fra le proprie conoscenze teoriche deve perlomeno
Il taccuino dell esploratore a cura di ORESTE GALLO (per gli scout: Lupo Tenace) QUINTA CHIACCHIERATA L ORIENTAMENTO (prima parte) Un buon escursionista fra le proprie conoscenze teoriche deve perlomeno
Topografia e orientamento
 CAI - ALPINISMO GIOVANILE Secondo Corso Di Avvicinamento Alla Montagna 2012 Topografia e orientamento C A I B o r g o m a n e r o A l p i n i s m o G i o v a n i l e 2 0 1 2 Pagina 1 Introduzione Per un
CAI - ALPINISMO GIOVANILE Secondo Corso Di Avvicinamento Alla Montagna 2012 Topografia e orientamento C A I B o r g o m a n e r o A l p i n i s m o G i o v a n i l e 2 0 1 2 Pagina 1 Introduzione Per un
Società alpina delle Giulie Sezione di Trieste del Club Alpino Italiano. Topografia e orientamento
 Società alpina delle Giulie Sezione di Trieste del Club Alpino Italiano Topografia e orientamento Introduzione Per un alpinista sapersi orientare in montagna è altrettanto importante che saper arrampicare
Società alpina delle Giulie Sezione di Trieste del Club Alpino Italiano Topografia e orientamento Introduzione Per un alpinista sapersi orientare in montagna è altrettanto importante che saper arrampicare
CORSO DI CARTOGRAFIA LIVELLO I
 CORSO DI CARTOGRAFIA LIVELLO I L ORIENTAMENTO ORIENTARSI vuol dire trovare la strada. In geografia orientarsi vuol dire trovare l ORIENTE, cioè il punto dove nasce il sole. L oriente è uno dei 4 PUNTI
CORSO DI CARTOGRAFIA LIVELLO I L ORIENTAMENTO ORIENTARSI vuol dire trovare la strada. In geografia orientarsi vuol dire trovare l ORIENTE, cioè il punto dove nasce il sole. L oriente è uno dei 4 PUNTI
Orientamento. Scuola di Sci Alpinismo M. Righini. Programma:
 Orientamento Programma: Ripasso carta: scala, curve livello, reticolo, orientamento carta Descrizione strumenti: altimetro e bussola Uso della bussola Azimut Rilevazione dell azimut sulla carta Rilevazione
Orientamento Programma: Ripasso carta: scala, curve livello, reticolo, orientamento carta Descrizione strumenti: altimetro e bussola Uso della bussola Azimut Rilevazione dell azimut sulla carta Rilevazione
L utilizzo della bussola
 San Nicolò di Celle 1 L utilizzo della bussola La bussola La bussola a prisma 1) Coperchi ribaltabile 2) Finestrella del coperchio 3) Linea di mira incisa sul vetro 4) Disco graduato girevole immerso nel
San Nicolò di Celle 1 L utilizzo della bussola La bussola La bussola a prisma 1) Coperchi ribaltabile 2) Finestrella del coperchio 3) Linea di mira incisa sul vetro 4) Disco graduato girevole immerso nel
TOPOGRAFIA E ORIENTAMENTO
 TOPOGRAFIA E ORIENTAMENTO Sq: Realizzato da Fabio Duò 2012 LA BUSSOLA La bussola è uno strumento per l'individuazione dei punti cardinali. È provvista di un ago calamitato che, libero di girare su di un
TOPOGRAFIA E ORIENTAMENTO Sq: Realizzato da Fabio Duò 2012 LA BUSSOLA La bussola è uno strumento per l'individuazione dei punti cardinali. È provvista di un ago calamitato che, libero di girare su di un
LEZIONI DI CARTOGRAFIA
 LEZIONI DI CARTOGRAFIA by Andrea ErDuca Palladino PART. 2 LA CARTA TOPOGRAFICA IMPORTANTE: QUESTA GUIDA E STATA REDATTA ESCLUSIVAMENTE PER UN USO INTERNO DELL ASSOCIAZIONE E PERTANTO VIETATA LA DIVULGAZIONE
LEZIONI DI CARTOGRAFIA by Andrea ErDuca Palladino PART. 2 LA CARTA TOPOGRAFICA IMPORTANTE: QUESTA GUIDA E STATA REDATTA ESCLUSIVAMENTE PER UN USO INTERNO DELL ASSOCIAZIONE E PERTANTO VIETATA LA DIVULGAZIONE
OTTO ORGANO TECNICO TERRITORIALE OPERATIVO CAI SAT 2 LEZIONE: USO
 OTTO ORGANO TECNICO TERRITORIALE OPERATIVO CAI SAT 2 LEZIONE: USO e UTILIZZO della BUSSOLA 1 SAT 2 Lezione aggiornata al 24 Settembre 2015 (ultima) 1 Poli Magnetici. 2 Longitudine e Latitudine. 3 Bussole.
OTTO ORGANO TECNICO TERRITORIALE OPERATIVO CAI SAT 2 LEZIONE: USO e UTILIZZO della BUSSOLA 1 SAT 2 Lezione aggiornata al 24 Settembre 2015 (ultima) 1 Poli Magnetici. 2 Longitudine e Latitudine. 3 Bussole.
Impariamo ad orientarci
 Impariamo ad orientarci A cura di Paola Gagliardi Docente dell ITC A. Serra Quaderno dei senti Corso di Orientamento e sentstica Quaderno dei sent Quaderno dei senti La carta topografica è un disegno che
Impariamo ad orientarci A cura di Paola Gagliardi Docente dell ITC A. Serra Quaderno dei senti Corso di Orientamento e sentstica Quaderno dei sent Quaderno dei senti La carta topografica è un disegno che
LA TERRA. La TERRA ha la forma di una grande sfera un po schiacciata alle estremità, chiamate POLI.
 LA TERRA La TERRA ha la forma di una grande sfera un po schiacciata alle estremità, chiamate POLI. Per poterla studiare possiamo rappresentare la TERRA per mezzo di un mappamondo (globo). Su di esso possiamo
LA TERRA La TERRA ha la forma di una grande sfera un po schiacciata alle estremità, chiamate POLI. Per poterla studiare possiamo rappresentare la TERRA per mezzo di un mappamondo (globo). Su di esso possiamo
Il punto di stazione. Corso di orientamento e Cenni di topografia Dario Tommasi IW0QNL
 Il punto di stazione Abbiamo visto tanti modi per usare la bussola, abbiamo visto come trovare un punto sulla carta e come darne le coordinate, come seguire un percorso, ma la cosa più importante è sapere
Il punto di stazione Abbiamo visto tanti modi per usare la bussola, abbiamo visto come trovare un punto sulla carta e come darne le coordinate, come seguire un percorso, ma la cosa più importante è sapere
Unità 4 Paragrafo 1 La forma e le dimensioni della Terra
 Unità 4 Paragrafo 1 La forma e le dimensioni della Terra forma ellissoide di rotazione più precisamente geoide sfera schiacciata ai poli solido più gonio dove ci sono i continenti e un po depresso nelle
Unità 4 Paragrafo 1 La forma e le dimensioni della Terra forma ellissoide di rotazione più precisamente geoide sfera schiacciata ai poli solido più gonio dove ci sono i continenti e un po depresso nelle
GLI STRUMENTI DELLA GEOGRAFIA
 GLI STRUMENTI DELLA GEOGRAFIA Che cos è la geografia La geografia (dal greco géo, Terra, e graphìa, scrittura, disegno) è la disciplina che studia e descrive la Terra e il rapporto che esiste fra l uomo
GLI STRUMENTI DELLA GEOGRAFIA Che cos è la geografia La geografia (dal greco géo, Terra, e graphìa, scrittura, disegno) è la disciplina che studia e descrive la Terra e il rapporto che esiste fra l uomo
22 gennaio 2014 TOPOGRAFIA e ORIENTAMENTO
 22 gennaio 2014 TOPOGRAFIA e ORIENTAMENTO Per chi non sa dove andare qualunque strada é quella giusta! Topografia: Scienza della rappresentazione del territorio al fine di consentire l esatta individuazione
22 gennaio 2014 TOPOGRAFIA e ORIENTAMENTO Per chi non sa dove andare qualunque strada é quella giusta! Topografia: Scienza della rappresentazione del territorio al fine di consentire l esatta individuazione
INDICE. Italiano. [Rotella motrice sbloccata] Bloccaggio (rotazione in senso antiorario) Rotella motrice
![INDICE. Italiano. [Rotella motrice sbloccata] Bloccaggio (rotazione in senso antiorario) Rotella motrice INDICE. Italiano. [Rotella motrice sbloccata] Bloccaggio (rotazione in senso antiorario) Rotella motrice](/thumbs/57/40024819.jpg) INDICE Pag. MISURAZIONE DELLA DISTANZA SULLE MAPPE... 31 PRECAUZIONI PER L USO DELL OROLOGIO CON FUNZIONE DI MISURAZIONE DELLA DISTANZA SULLE MAPPE... 34 BUSSOLA A CALOTTA ROTANTE... 36 PRECAUZIONI PER
INDICE Pag. MISURAZIONE DELLA DISTANZA SULLE MAPPE... 31 PRECAUZIONI PER L USO DELL OROLOGIO CON FUNZIONE DI MISURAZIONE DELLA DISTANZA SULLE MAPPE... 34 BUSSOLA A CALOTTA ROTANTE... 36 PRECAUZIONI PER
COME USARE LA BUSSOLA NEL PERCORSO DIDATTICO Supponiamo di voler andare dal punto 2 al punto 3 del percorso indicato dalla mappa.
 COME USARE LA BUSSOLA NEL PERCORSO DIDATTICO Supponiamo di voler andare dal punto 2 al punto 3 del percorso indicato dalla mappa. Metodo delle 3 Frecce Questo metodo non memorizza l azimut del punto di
COME USARE LA BUSSOLA NEL PERCORSO DIDATTICO Supponiamo di voler andare dal punto 2 al punto 3 del percorso indicato dalla mappa. Metodo delle 3 Frecce Questo metodo non memorizza l azimut del punto di
Le carte geografiche
 Le carte geografiche Definizione delle carte geografiche Le carte sono rappresentazioni approssimate,simboliche e ridotte della terra oppure di una parte della terra. Esse concentrano in un foglio di dimensioni
Le carte geografiche Definizione delle carte geografiche Le carte sono rappresentazioni approssimate,simboliche e ridotte della terra oppure di una parte della terra. Esse concentrano in un foglio di dimensioni
Cartografia, topografia e orientamento
 Cartografia, topografia e orientamento Esercitazioni Mi sono portato la carta UTM, il goniometro, la bussola, l altimetro, lo scalimetro, il righello, il coordinatometro, la matita, ed ho pure l alpestoc,
Cartografia, topografia e orientamento Esercitazioni Mi sono portato la carta UTM, il goniometro, la bussola, l altimetro, lo scalimetro, il righello, il coordinatometro, la matita, ed ho pure l alpestoc,
sfera celeste e coordinate astronomiche
 sfera celeste e coordinate astronomiche sfera celeste La sfera celeste appare come una grande sfera che ruota su se stessa, al cui centro sta la Terra immobile, e sulla cui superficie stanno le stelle
sfera celeste e coordinate astronomiche sfera celeste La sfera celeste appare come una grande sfera che ruota su se stessa, al cui centro sta la Terra immobile, e sulla cui superficie stanno le stelle
Scuola Alpinismo "Cosimo Zappelli" CAI Viareggio 10 Corso Arrampicata su roccia LEZIONE DI ORIENTAMENTO
 Scuola Alpinismo "Cosimo Zappelli" CAI Viareggio 10 Corso Arrampicata su roccia LEZIONE DI ORIENTAMENTO Viareggio 06/10/2011 Introduzione Cos è l orientamento? L'orientamento è l'insieme delle tecniche
Scuola Alpinismo "Cosimo Zappelli" CAI Viareggio 10 Corso Arrampicata su roccia LEZIONE DI ORIENTAMENTO Viareggio 06/10/2011 Introduzione Cos è l orientamento? L'orientamento è l'insieme delle tecniche
Cartografia, topografia e orientamento
 Cartografia, topografia e orientamento Soluzioni delle esercitazioni Mi sono portato la carta UTM, il goniometro, la bussola, l altimetro, lo scalimetro, il righello, il coordinatometro, la matita, ed
Cartografia, topografia e orientamento Soluzioni delle esercitazioni Mi sono portato la carta UTM, il goniometro, la bussola, l altimetro, lo scalimetro, il righello, il coordinatometro, la matita, ed
Come costruire una meridiana equatoriale
 Pagina 1 di 5 Come costruire una meridiana equatoriale La meridiana equatoriale è l'orologio solare più semplice da costruire. Per capire come funziona, supponiamo che la Terra sia disposta in modo che
Pagina 1 di 5 Come costruire una meridiana equatoriale La meridiana equatoriale è l'orologio solare più semplice da costruire. Per capire come funziona, supponiamo che la Terra sia disposta in modo che
Disegnare Linee Rette ed Angoli
 Disegnare Linee Rette ed Angoli (a cura Prof. E. Bocca C. P.) Linea retta La retta o linea retta è uno degli enti geometrici fondamentali. Un filo di cotone o di spago ben teso tra due punti è un modello
Disegnare Linee Rette ed Angoli (a cura Prof. E. Bocca C. P.) Linea retta La retta o linea retta è uno degli enti geometrici fondamentali. Un filo di cotone o di spago ben teso tra due punti è un modello
LA TERRA. La Terra studiata come copro celeste, risulta essere un PIANETA un copro celeste di forma sferica che ruota attorno ad una stella il SOLE
 IL PIANETA TERRA LA TERRA La Terra studiata come copro celeste, risulta essere un PIANETA un copro celeste di forma sferica che ruota attorno ad una stella il SOLE FORMA E DIMENSIONI DELLA TERRA Agli
IL PIANETA TERRA LA TERRA La Terra studiata come copro celeste, risulta essere un PIANETA un copro celeste di forma sferica che ruota attorno ad una stella il SOLE FORMA E DIMENSIONI DELLA TERRA Agli
In prima approssimazione, guardandoci intorno. Note su Nord-Sud-Est-Ovest Enrica Giordano e Nicoletta Lanciano febbraio 2008
 Note su Nord-Sud-Est-Ovest Enrica Giordano e Nicoletta Lanciano febbraio 2008 Le cose devono essere apprese solo per essere nuovamente disimparate, oppure, cosa più probabile, per essere corrette R. Feynman
Note su Nord-Sud-Est-Ovest Enrica Giordano e Nicoletta Lanciano febbraio 2008 Le cose devono essere apprese solo per essere nuovamente disimparate, oppure, cosa più probabile, per essere corrette R. Feynman
Le Coordinate Astronomiche
 Le Stelle vanno a scuola Le Coordinate Astronomiche Valentina Alberti Novembre 2003 1 2 INDICE Indice 1 Coordinate astronomiche 3 1.1 Sistema dell orizzonte o sistema altazimutale.......... 3 1.2 Sistema
Le Stelle vanno a scuola Le Coordinate Astronomiche Valentina Alberti Novembre 2003 1 2 INDICE Indice 1 Coordinate astronomiche 3 1.1 Sistema dell orizzonte o sistema altazimutale.......... 3 1.2 Sistema
3. Le coordinate geografiche: latitudine e longitudine
 Introduzione 3. Le coordinate geografiche: latitudine e longitudine Ogni volta che vogliamo individuare un punto sulla superficie terrestre gli associamo due numeri, le coordinate geografiche: la latitudine
Introduzione 3. Le coordinate geografiche: latitudine e longitudine Ogni volta che vogliamo individuare un punto sulla superficie terrestre gli associamo due numeri, le coordinate geografiche: la latitudine
Stefania Ferrari a.s. 2003/2004. Stefania Ferrari, Scuola Media di Bomporto,
 Stefania Ferrari a.s. 2003/2004 1 1 - GLI ELEMENTI NATURALI La geografia studia gli elementi naturali, cioè le cose della natura. I fiumi, i mari, le montagne e le pianure sono elementi naturali. Anche
Stefania Ferrari a.s. 2003/2004 1 1 - GLI ELEMENTI NATURALI La geografia studia gli elementi naturali, cioè le cose della natura. I fiumi, i mari, le montagne e le pianure sono elementi naturali. Anche
ESEMPIO DI CALCOLO DELL INVOLUCRO SOLARE
 ESEMPIO DI CALCOLO DELL INVOLUCRO SOLARE 1 Suggerimenti sul calcolo dell involucro solare Nel calcolo della distanza reciproca che dovranno mantenere i nuovi è consigliato e valutato nelle Linee Guida
ESEMPIO DI CALCOLO DELL INVOLUCRO SOLARE 1 Suggerimenti sul calcolo dell involucro solare Nel calcolo della distanza reciproca che dovranno mantenere i nuovi è consigliato e valutato nelle Linee Guida
Una balestra un po più complessa: la balestriglia
 MISURE ANGOLARI 1 2 Una balestra un po più complessa: la balestriglia Uno strumento utilissimo in astronomia è la balestriglia, chiamata un tempo bastone di Giacobbe oppure raggio astronomico o croce astronomica
MISURE ANGOLARI 1 2 Una balestra un po più complessa: la balestriglia Uno strumento utilissimo in astronomia è la balestriglia, chiamata un tempo bastone di Giacobbe oppure raggio astronomico o croce astronomica
LE CURVE DI LIVELLO O ISOPSE
 Lettura ed interpretazione delle carte topografiche LE CURVE DI LIVELLO O ISOPSE Rilievo Depressione Lettura ed interpretazione delle carte topografiche LE CURVE DI LIVELLO O ISOPSE Lettura ed interpretazione
Lettura ed interpretazione delle carte topografiche LE CURVE DI LIVELLO O ISOPSE Rilievo Depressione Lettura ed interpretazione delle carte topografiche LE CURVE DI LIVELLO O ISOPSE Lettura ed interpretazione
Illustrazioni tratte in parte dal testo: Ecosistema Terra ST1 Minerva Scuola
 http://digilander.libero.it/glampis64 Illustrazioni tratte in parte dal testo: Ecosistema Terra ST1 Minerva Scuola Prove della sfericità della Terra Salendo su un alta montagna l orizzonte si amplia Man
http://digilander.libero.it/glampis64 Illustrazioni tratte in parte dal testo: Ecosistema Terra ST1 Minerva Scuola Prove della sfericità della Terra Salendo su un alta montagna l orizzonte si amplia Man
Topografia Orientamento
 Club Alpino Italiano Sezione di Bozzolo Scuola Sesto Gnaccarini XXIV CORSO DI ALPINISMO Topografia Orientamento 03 settembre 2015 Topografia 03/09/2015 Scuola Sesto Gnaccarini - CAI Bozzolo 2 CARTA GEOGRAFICA
Club Alpino Italiano Sezione di Bozzolo Scuola Sesto Gnaccarini XXIV CORSO DI ALPINISMO Topografia Orientamento 03 settembre 2015 Topografia 03/09/2015 Scuola Sesto Gnaccarini - CAI Bozzolo 2 CARTA GEOGRAFICA
CONTROLLO DELLA RADIAZIONE SOLARE
 CAPITOLO 11 11.1 Generalità La localizzazione e l orientamento di un edificio per ridurre l esposizione solare estiva e valorizzare quella invernale, sono obiettivi fondamentali per una corretta progettazione.
CAPITOLO 11 11.1 Generalità La localizzazione e l orientamento di un edificio per ridurre l esposizione solare estiva e valorizzare quella invernale, sono obiettivi fondamentali per una corretta progettazione.
Il reticolato geografico. Meridiani e paralleli.
 Il reticolato geografico. Meridiani e paralleli. Per localizzare un punto qualsiasi sulla superficie terrestre, cioè per individuarne la posizione esatta, i geografi hanno tracciato sul globo terrestre
Il reticolato geografico. Meridiani e paralleli. Per localizzare un punto qualsiasi sulla superficie terrestre, cioè per individuarne la posizione esatta, i geografi hanno tracciato sul globo terrestre
L illuminazione della Terra
 L illuminazione della Terra I moti della Terra nello spazio Sole Mercurio Venere Terra La Terra e gli altri pianeti orbitano intorno al Sole, che è una stella con un raggio di circa 700 000 km e dista
L illuminazione della Terra I moti della Terra nello spazio Sole Mercurio Venere Terra La Terra e gli altri pianeti orbitano intorno al Sole, che è una stella con un raggio di circa 700 000 km e dista
TOPOGRAFIA e CARTOGRAFIA
 1. Un ettometro corrisponde a : a. 100 m ; b. 1.000 m ; c. 10.000 m ; 2. Un chilometro corrisponde a : a. 100 m ; b. 1.000 m ; c. 10.000 m ; 3. Un decametro corrisponde a : a. 0,1 m ; b. 0,01 m ; c. 10
1. Un ettometro corrisponde a : a. 100 m ; b. 1.000 m ; c. 10.000 m ; 2. Un chilometro corrisponde a : a. 100 m ; b. 1.000 m ; c. 10.000 m ; 3. Un decametro corrisponde a : a. 0,1 m ; b. 0,01 m ; c. 10
LA LATITUDINE E LA LONGITUDINE
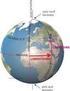 LC.06.02.06 LA LATITUDINE E LA LONGITUDINE Prerequisiti: nozioni scientifiche e matematiche acquisite durante la scuola secondaria di primo grado Obiettivi: studio della latitudine e della longitudine
LC.06.02.06 LA LATITUDINE E LA LONGITUDINE Prerequisiti: nozioni scientifiche e matematiche acquisite durante la scuola secondaria di primo grado Obiettivi: studio della latitudine e della longitudine
ESPERIENZA 6 La legge della riflessione
 ESPERIENZA 6 La legge della riflessione 1. Argomenti Determinare la direzione del raggio riflesso sulla superficie di uno specchio piano a diversi angoli di incidenza. Confrontare gli angoli di incidenza
ESPERIENZA 6 La legge della riflessione 1. Argomenti Determinare la direzione del raggio riflesso sulla superficie di uno specchio piano a diversi angoli di incidenza. Confrontare gli angoli di incidenza
CLUB ALPINO ITALIANO Scuola Intersezionale di Escursionismo VERONESE SIEV
 CLUB ALPINO ITALIANO Scuola Intersezionale di Escursionismo VERONESE SIEV Cartografia e Orientamento Argomenti che tratteremo: Orientamento Leggere una carta escursionistica Gli strumenti per l orientamento
CLUB ALPINO ITALIANO Scuola Intersezionale di Escursionismo VERONESE SIEV Cartografia e Orientamento Argomenti che tratteremo: Orientamento Leggere una carta escursionistica Gli strumenti per l orientamento
Programma Didattico Annuale
 LICEO SCIENTIFICO STATALE GALILEO GALILEI PdQ - 7.06 Ediz.: 1 Rev.: 0 Data 02/09/05 Alleg.: D01 PROG. M2 PROCEDURA della QUALITA' Programma Didattico Annuale Anno Scolastico 2011/2012 MATERIA : Scienze
LICEO SCIENTIFICO STATALE GALILEO GALILEI PdQ - 7.06 Ediz.: 1 Rev.: 0 Data 02/09/05 Alleg.: D01 PROG. M2 PROCEDURA della QUALITA' Programma Didattico Annuale Anno Scolastico 2011/2012 MATERIA : Scienze
GEOMETRIA ANALITICA. Il Piano cartesiano
 GEOMETRIA ANALITICA La geometria analitica consente di studiare e rappresentare per via algebrica informazioni di tipo geometrico. Lo studio favorisce una più immediata visualizzazione di informazioni,
GEOMETRIA ANALITICA La geometria analitica consente di studiare e rappresentare per via algebrica informazioni di tipo geometrico. Lo studio favorisce una più immediata visualizzazione di informazioni,
IL MOTO di ROTAZIONE. CONSEGUENZE del MOTO di ROTAZIONE
 IL MOTO di ROTAZIONE moto di rotazione: il moto di rotazione è il movimento che la Terra compie attorno al proprio asse, da ovest verso est, in senso antiorario per un osservatore posto al polo nord celeste;
IL MOTO di ROTAZIONE moto di rotazione: il moto di rotazione è il movimento che la Terra compie attorno al proprio asse, da ovest verso est, in senso antiorario per un osservatore posto al polo nord celeste;
Topografia e orientamento SA1 2012
 Topografia e orientamento SA1 2012 Di cosa stiamo parlando Topografia Rappresentazione schematica e in scala del territorio attraverso la quale è possibile consentire l esatta individuazione dei luoghi
Topografia e orientamento SA1 2012 Di cosa stiamo parlando Topografia Rappresentazione schematica e in scala del territorio attraverso la quale è possibile consentire l esatta individuazione dei luoghi
GEOMETRIA. Elementi geometrici
 GEOMETRIA Elementi geometrici Ripasso dei principali elementi geometrici e relative definizioni A)Una scatola di gessetti, un barattolo, una palla sono corpi Ogni cosa che occupa uno spazio è, quindi un
GEOMETRIA Elementi geometrici Ripasso dei principali elementi geometrici e relative definizioni A)Una scatola di gessetti, un barattolo, una palla sono corpi Ogni cosa che occupa uno spazio è, quindi un
OLIMPIADI ITALIANE DI ASTRONOMIA 2014 FINALE NAZIONALE Prova Teorica - Categoria Junior
 OLIMPIADI ITALIANE DI ASTRONOMIA 2014 FINALE NAZIONALE Prova Teorica - Categoria Junior 1. Le quattro stagioni Si scrivano gli intervalli entro cui variano l ascensione retta ( ) e la declinazione ( )
OLIMPIADI ITALIANE DI ASTRONOMIA 2014 FINALE NAZIONALE Prova Teorica - Categoria Junior 1. Le quattro stagioni Si scrivano gli intervalli entro cui variano l ascensione retta ( ) e la declinazione ( )
Gli indizi a favore di questa ipotesi erano molteplici:
 La forma della Terra Nell antichità la forma della Terra è stata oggetto di numerose ipotesi. Nonostante la limitatezza degli strumenti di osservazione di allora, già gli antichi svilupparono l idea che
La forma della Terra Nell antichità la forma della Terra è stata oggetto di numerose ipotesi. Nonostante la limitatezza degli strumenti di osservazione di allora, già gli antichi svilupparono l idea che
Misurare l'altezza del sole: il sestante
 PARTE CONCLUSIVA DELL'UNITA' DIDATTICA "SOLE E TERRA" Misurare l'altezza del sole: il sestante Ad oggi si sono sperimentate due tipi di gestione dell'attività. La modalità A fa riferimento all'attività
PARTE CONCLUSIVA DELL'UNITA' DIDATTICA "SOLE E TERRA" Misurare l'altezza del sole: il sestante Ad oggi si sono sperimentate due tipi di gestione dell'attività. La modalità A fa riferimento all'attività
CONTROLLO DELLA RADIAZIONE SOLARE
 Corso di Fisica tecnica e ambientale a.a. 211/212 - Docente: Prof. Carlo Isetti CAPITOLO 11 CONTROLLO DELLA RADIAZIONE OLARE La localizzazione e l orientamento di un edificio per ridurre l esposizione
Corso di Fisica tecnica e ambientale a.a. 211/212 - Docente: Prof. Carlo Isetti CAPITOLO 11 CONTROLLO DELLA RADIAZIONE OLARE La localizzazione e l orientamento di un edificio per ridurre l esposizione
1 La traslazione. 2 La composizione di traslazioni. 3 La rotazione
 1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
Come misurare la declinazione della parete utilizzando il programma Orologi Solari
 Come misurare la declinazione della parete utilizzando il programma Orologi Solari Un passo fondamentale per il progetto di un orologio solare verticale è la misura della declinazione della parete. Orologi
Come misurare la declinazione della parete utilizzando il programma Orologi Solari Un passo fondamentale per il progetto di un orologio solare verticale è la misura della declinazione della parete. Orologi
LA MISURA DI GRANDI DISTANZE CON LA TRIANGOLAZIONE
 L MISUR DI GRNDI DISTNZE ON L TRINGOLZIONE ome si può misurare l altezza di un lampione senza doversi arrampicare su di esso? Se è una giornata di sole, è possibile sfruttare l ombra del lampione. on un
L MISUR DI GRNDI DISTNZE ON L TRINGOLZIONE ome si può misurare l altezza di un lampione senza doversi arrampicare su di esso? Se è una giornata di sole, è possibile sfruttare l ombra del lampione. on un
unità 5. L orientamento e la misura del tempo
 giorno Sole osservazione del cielo notte Stella Polare/Croce del sud longitudine in base all ora locale Orientamento coordinate geografiche latitudine altezza della stella Polare altezza del Sole bussola
giorno Sole osservazione del cielo notte Stella Polare/Croce del sud longitudine in base all ora locale Orientamento coordinate geografiche latitudine altezza della stella Polare altezza del Sole bussola
Carte Topografiche. La Terra
 Carte Topografiche Le carte vengono denominate in base alla scala. Geografiche se hanno una scala maggiore di 1:1.000.000; Corografiche se la scala è compresa fra 1:1000.000, Topografiche se la scala è
Carte Topografiche Le carte vengono denominate in base alla scala. Geografiche se hanno una scala maggiore di 1:1.000.000; Corografiche se la scala è compresa fra 1:1000.000, Topografiche se la scala è
Orientarsi con un bastone
 Orientarsi con un bastone Pianta in terra un bastone, puntandolo verso il sole in maniera che non faccia ombra sul terreno. Dopo almeno una ventina di minuti apparirà l ombra alla base del bastone, questa
Orientarsi con un bastone Pianta in terra un bastone, puntandolo verso il sole in maniera che non faccia ombra sul terreno. Dopo almeno una ventina di minuti apparirà l ombra alla base del bastone, questa
ESPERIENZE CON GLI SPECCHI PIANI
 1. Qual è la posizione dell immagine fornita da uno specchio piano? Di che tipo di immagine si tratta? Disponi il cilindro giallo dietro lo specchio, in modo che coincida con l immagine riflessa del cilindro
1. Qual è la posizione dell immagine fornita da uno specchio piano? Di che tipo di immagine si tratta? Disponi il cilindro giallo dietro lo specchio, in modo che coincida con l immagine riflessa del cilindro
Scientifico Tecnologico
 Scientifico Tecnologico Compiti vacanze estive giugno 2016 La Terra nel sistema solare S.L.Murialdo Pinerolo Materiale didattico co-finanziato dal POR FSE 2014-2020 PERIODO DI RIFERIMENTO OBIETTIVO VALUTATO
Scientifico Tecnologico Compiti vacanze estive giugno 2016 La Terra nel sistema solare S.L.Murialdo Pinerolo Materiale didattico co-finanziato dal POR FSE 2014-2020 PERIODO DI RIFERIMENTO OBIETTIVO VALUTATO
INDICE ITALIANO. Italiano. Italiano. [Rotella motrice sbloccata]
![INDICE ITALIANO. Italiano. Italiano. [Rotella motrice sbloccata] INDICE ITALIANO. Italiano. Italiano. [Rotella motrice sbloccata]](/thumbs/39/20316297.jpg) ITALIAO IDIC Pag. FUZIO DI MIURAZIO DLLA DITAZA ULL MAPP (I KILOMTRI O MIGLIA)... 31 PRCAUZIOI PR L UO DLL OROLOGIO CO FUZIO DI MIURAZIO DLLA DITAZA ULL MAPP... 35 BUOLA A CALOTTA ROTAT... 36 PRCAUZIOI
ITALIAO IDIC Pag. FUZIO DI MIURAZIO DLLA DITAZA ULL MAPP (I KILOMTRI O MIGLIA)... 31 PRCAUZIOI PR L UO DLL OROLOGIO CO FUZIO DI MIURAZIO DLLA DITAZA ULL MAPP... 35 BUOLA A CALOTTA ROTAT... 36 PRCAUZIOI
Preparazione al compito di geometria (Semiretta, Retta, Angoli)
 Preparazione al compito di geometria (Semiretta, Retta, Angoli) Semiretta Per definire una semiretta, prendiamo una retta ed un punto P su di essa: Tale punto dividerà la retta in due parti; ciascuna di
Preparazione al compito di geometria (Semiretta, Retta, Angoli) Semiretta Per definire una semiretta, prendiamo una retta ed un punto P su di essa: Tale punto dividerà la retta in due parti; ciascuna di
Questo paragrafo e quello successivo trattano gli stessi argomenti del capitolo B6 relativo alla soluzione grafica dei sistemi di primo grado.
 D1. Retta D1.1 Equazione implicita ed esplicita Ogni equazione di primo grado in due incognite rappresenta una retta sul piano cartesiano (e viceversa). Si può scrivere un equazione di primo grado in due
D1. Retta D1.1 Equazione implicita ed esplicita Ogni equazione di primo grado in due incognite rappresenta una retta sul piano cartesiano (e viceversa). Si può scrivere un equazione di primo grado in due
CARTOGRAFIA e ORIENTAMENTO
 CARTOGRAFIA e ORIENTAMENTO Elemento fondamentale per potersi orientare è la capacità e la possibilità di determinazione dei punti cardinali ROSA DEI VENTI Per definire la posizione di un punto sulla superficie
CARTOGRAFIA e ORIENTAMENTO Elemento fondamentale per potersi orientare è la capacità e la possibilità di determinazione dei punti cardinali ROSA DEI VENTI Per definire la posizione di un punto sulla superficie
Grandezze scalari e vettoriali
 VETTORI Grandezze scalari e vettoriali Tra le grandezze misurabili alcune sono completamente definite da un numero e da un unità di misura, altre invece sono completamente definite solo quando, oltre ad
VETTORI Grandezze scalari e vettoriali Tra le grandezze misurabili alcune sono completamente definite da un numero e da un unità di misura, altre invece sono completamente definite solo quando, oltre ad
Progetto Laboratori Lauree Scientifiche
 Progetto Laboratori Lauree Scientifiche Laboratorio sulle funzioni trigonometriche Le ore di insolazione giornaliera in funzione della latitudine Bozza di progetto Nel seguito verrà presentata la descrizione
Progetto Laboratori Lauree Scientifiche Laboratorio sulle funzioni trigonometriche Le ore di insolazione giornaliera in funzione della latitudine Bozza di progetto Nel seguito verrà presentata la descrizione
L Astrolabio. di Alberto Nicelli. GAE Gruppo Astrofili Eporediesi
 L Astrolabio di Alberto Nicelli GAE Gruppo Astrofili Eporediesi L Astrolabio (vedi kit allegato) è così costituito: Il Piatto, che riproduce in proiezione stereografica: o l Orizzonte Locale, relativo
L Astrolabio di Alberto Nicelli GAE Gruppo Astrofili Eporediesi L Astrolabio (vedi kit allegato) è così costituito: Il Piatto, che riproduce in proiezione stereografica: o l Orizzonte Locale, relativo
TOPOGRAFIA: GLI STRUMENTI TAVOLETTA TOPOGRAFICA MULTIUSO
 Pagina 1 di 8 TOPOGRAFIA: GLI STRUMENTI TAVOLETTA TOPOGRAFICA MULTIUSO Al giorno d oggi, quando ormai tutti gli strumenti di rilevamento sono elettronici e precisissimi, è ancora possibile recuperare,
Pagina 1 di 8 TOPOGRAFIA: GLI STRUMENTI TAVOLETTA TOPOGRAFICA MULTIUSO Al giorno d oggi, quando ormai tutti gli strumenti di rilevamento sono elettronici e precisissimi, è ancora possibile recuperare,
Codice Morse. Semaforico
 Codice Morse & Semaforico Il Codice Morse, detto comunemente anche Alfabeto Morse, è un sistema per trasmettere lettere, numeri e segni di punteggiatura per mezzo di un segnale in codice ad intermittenza.
Codice Morse & Semaforico Il Codice Morse, detto comunemente anche Alfabeto Morse, è un sistema per trasmettere lettere, numeri e segni di punteggiatura per mezzo di un segnale in codice ad intermittenza.
PIANO CARTESIANO e RETTE classi 2 A/D 2009/2010
 PIANO CARTESIANO e RETTE classi 2 A/D 2009/2010 1) PIANO CARTESIANO serve per indicare, identificare, chiamare... ogni PUNTO del piano (ente geometrico) con una coppia di valori numerici (detti COORDINATE).
PIANO CARTESIANO e RETTE classi 2 A/D 2009/2010 1) PIANO CARTESIANO serve per indicare, identificare, chiamare... ogni PUNTO del piano (ente geometrico) con una coppia di valori numerici (detti COORDINATE).
Calcolo dell altezza di un rilievo lunare: l esempio di Arzachel
 Calcolo dell altezza di un rilievo lunare: l esempio di Arzachel Lo scopo della suddetta esperienza è il calcolo dell altezza di un particolare rilievo lunare, scelto appositamente per la conformazione
Calcolo dell altezza di un rilievo lunare: l esempio di Arzachel Lo scopo della suddetta esperienza è il calcolo dell altezza di un particolare rilievo lunare, scelto appositamente per la conformazione
L UNIVERSO L UNIVERSO È IMMENSO. CONTIENE TUTTE LE STELLE E TUTTI I PIANETI CHE ESISTONO (MOLTI SONO COSÌ LONTANI CHE NOI NON LI CONOSCIAMO).
 L UNIVERSO L UNIVERSO È IMMENSO. CONTIENE TUTTE LE STELLE E TUTTI I PIANETI CHE ESISTONO (MOLTI SONO COSÌ LONTANI CHE NOI NON LI CONOSCIAMO). LA SCIENZA CHE STUDIA I CORPI CELESTI (CIOE' LE STELLE E I
L UNIVERSO L UNIVERSO È IMMENSO. CONTIENE TUTTE LE STELLE E TUTTI I PIANETI CHE ESISTONO (MOLTI SONO COSÌ LONTANI CHE NOI NON LI CONOSCIAMO). LA SCIENZA CHE STUDIA I CORPI CELESTI (CIOE' LE STELLE E I
Capitolo 6. I poligoni. (Ob. 4, 5, 6, 7, 9, 11, 12, 14, 15)
 (Ob. 4, 5, 6, 7, 9, 11, 12, 14, 15) (vertici, lati, diagonali, convessità, angoli, perimetro) 6.2 I triangoli 6.3 I quadrilateri 6.4 I poligoni regolari 6.5 Le altezze 6.6 Le aree Un poligono è la parte
(Ob. 4, 5, 6, 7, 9, 11, 12, 14, 15) (vertici, lati, diagonali, convessità, angoli, perimetro) 6.2 I triangoli 6.3 I quadrilateri 6.4 I poligoni regolari 6.5 Le altezze 6.6 Le aree Un poligono è la parte
asse fuoco vertice direttrice Fig. D3.1 Parabola.
 D3. Parabola D3.1 Definizione di parabola come luogo di punti Definizione: una parabola è formata dai punti equidistanti da un punto detto fuoco e da una retta detta direttrice. L equazione della parabola
D3. Parabola D3.1 Definizione di parabola come luogo di punti Definizione: una parabola è formata dai punti equidistanti da un punto detto fuoco e da una retta detta direttrice. L equazione della parabola
prof.a.battistelli PROIEZIONI ORTOGONALI
 PROIEZIONI ORTOGONALI PROIEZIONI ORTOGONALI È il disegno delle viste, da davanti, da sopra e di fianco di un oggetto tridimensionale disegnate in un foglio bidimensionale. Trasformiamoci in designer Per
PROIEZIONI ORTOGONALI PROIEZIONI ORTOGONALI È il disegno delle viste, da davanti, da sopra e di fianco di un oggetto tridimensionale disegnate in un foglio bidimensionale. Trasformiamoci in designer Per
Punti nel piano cartesiano
 Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
STUDIO della RIFRAZIONE
 STUDIO della RIFRAZIONE Presentazione Possiamo vedere ogni oggetto anche se non emette luce propria. I corpi, infatti, sono in grado di riflettere la luce che li "colpisce", verso i nostri occhi. Talvolta,
STUDIO della RIFRAZIONE Presentazione Possiamo vedere ogni oggetto anche se non emette luce propria. I corpi, infatti, sono in grado di riflettere la luce che li "colpisce", verso i nostri occhi. Talvolta,
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
Risposte ai quesiti D E H D
 Perugia, dic. 2009/gen. 2010 Risposte ai quesiti 1. Dati i quadrati CD e C D, come in figura, provare che la perpendicolare uscente da alla retta DD passa per il punto medio del segmento quale che sia
Perugia, dic. 2009/gen. 2010 Risposte ai quesiti 1. Dati i quadrati CD e C D, come in figura, provare che la perpendicolare uscente da alla retta DD passa per il punto medio del segmento quale che sia
Risolutore NxNxN. Notazione
 Risolutore NxNxN Il Risolutore NxNxN risolve Cubi di Rubik di qualsiasi dimensione: dal 2x2x2 all' NxNxN. La risoluzione avviene in 3 fasi ed ogni fase è a sua volta suddivisa in tappe atte al compimento
Risolutore NxNxN Il Risolutore NxNxN risolve Cubi di Rubik di qualsiasi dimensione: dal 2x2x2 all' NxNxN. La risoluzione avviene in 3 fasi ed ogni fase è a sua volta suddivisa in tappe atte al compimento
L errore percentuale di una misura è l errore relativo moltiplicato per 100 ed espresso in percentuale. Si indica con e p e risulta: e ( e 100)%
 UNITÀ L ELBORZIONE DEI DTI IN FISIC 1. Gli errori di misura.. Errori di sensibilità, errori casuali, errori sistematici. 3. La stima dell errore. 4. La media, la semidispersione e lo scarto quadratico
UNITÀ L ELBORZIONE DEI DTI IN FISIC 1. Gli errori di misura.. Errori di sensibilità, errori casuali, errori sistematici. 3. La stima dell errore. 4. La media, la semidispersione e lo scarto quadratico
LA RETE DI ERATOSTENE
 LA RETE DI ERATOSTENE CHE COS È LA RETE DI ERATOSTENE? La Rete di Eratostene ha come uno delle principali la misurazione della terra. Questo lavoro si svolge attraverso una collaborazione tra più scuole.
LA RETE DI ERATOSTENE CHE COS È LA RETE DI ERATOSTENE? La Rete di Eratostene ha come uno delle principali la misurazione della terra. Questo lavoro si svolge attraverso una collaborazione tra più scuole.
Approfondimento A2.1 La cartografia applicata allo sport 1
 Approfondimento A2.1 La cartografia applicata allo sport 1 Cos è e come si pratica l orienteering L orienteering (sport dei boschi) è una disciplina sportiva nata all inizio del 900 nei Paesi scandinavi,
Approfondimento A2.1 La cartografia applicata allo sport 1 Cos è e come si pratica l orienteering L orienteering (sport dei boschi) è una disciplina sportiva nata all inizio del 900 nei Paesi scandinavi,
LE TRASFORMAZIONI GEOMETRICHE
 LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
LE SCALE DI RIDUZIONE
 LE SCALE DI RIDUZIONE la prima cosa che si deve osservare in una carta, insieme all'equidistanza fra le curve di livello, è la scala di riduzione che è sempre in primo piano, é altresì importante osservare
LE SCALE DI RIDUZIONE la prima cosa che si deve osservare in una carta, insieme all'equidistanza fra le curve di livello, è la scala di riduzione che è sempre in primo piano, é altresì importante osservare
NAVIGAZIONE ASTRONOMICA parte 3. Circolo Astrofili di Mestre Guido Ruggieri
 parte 3 3 Novembre 2008, ore 21:00 Introduzione. Orientamento sulla Terra. Coordinate orizzontali degli astri, azimuth e altezza. Coordinate equatoriali degli astri, Ascensione Retta e Declinazione. 17
parte 3 3 Novembre 2008, ore 21:00 Introduzione. Orientamento sulla Terra. Coordinate orizzontali degli astri, azimuth e altezza. Coordinate equatoriali degli astri, Ascensione Retta e Declinazione. 17
Le coniche: circonferenza, parabola, ellisse e iperbole.
 Le coniche: circonferenza, parabola, ellisse e iperbole. Teoria in sintesi Queste curve si chiamano coniche perché sono ottenute tramite l intersezione di una superficie conica con un piano. Si possono
Le coniche: circonferenza, parabola, ellisse e iperbole. Teoria in sintesi Queste curve si chiamano coniche perché sono ottenute tramite l intersezione di una superficie conica con un piano. Si possono
LE ALTEZZE. Sandra Taccetti, Antonio Moro, Classe quarta o quinta delle scuola primaria
 LE ALTEZZE Sandra Taccetti, Antonio Moro, 2013 Classe quarta o quinta delle scuola primaria 1. Oggi misuriamo le nostre altezze: esperienza in classe con l uso del metro e dei grafici (già fatta lo scorso
LE ALTEZZE Sandra Taccetti, Antonio Moro, 2013 Classe quarta o quinta delle scuola primaria 1. Oggi misuriamo le nostre altezze: esperienza in classe con l uso del metro e dei grafici (già fatta lo scorso
Momento delle forze e equilibrio di un corpo rigido
 Momento delle forze e equilibrio di un corpo rigido F r r F + F = 0 Equilibrio? NO Il corpo può ruotare F Perche un corpo esteso sia in equilibrio non basta imporre che la somma delle forze che agiscono
Momento delle forze e equilibrio di un corpo rigido F r r F + F = 0 Equilibrio? NO Il corpo può ruotare F Perche un corpo esteso sia in equilibrio non basta imporre che la somma delle forze che agiscono
Topografia e Orientamento. Scuola Intersezionale di Alpinismo e scialpinismo C.Giorda - Topografia e Orientamento
 Topografia e Orientamento Di cosa parliamo Topografia: scienza che si occupa della rappresentazione del territorio al fine di consentire l esatta individuazione dei luoghi per mezzo di modelli semplificati
Topografia e Orientamento Di cosa parliamo Topografia: scienza che si occupa della rappresentazione del territorio al fine di consentire l esatta individuazione dei luoghi per mezzo di modelli semplificati
Quadro riassuntivo di geometria analitica
 Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
MISURA DI LUNGHEZZE D ONDA CON UNO SPETTROSCOPIO A RETICOLO DI DIFFRAZIONE
 MISURA DI LUNGHEZZE D ONDA CON UNO SPETTROSCOPIO A RETICOLO DI DIFFRAZIONE Il reticolo di diffrazione può essere utilizzato per determinare la lunghezza d onda di una radiazione monocromatica. Detto d
MISURA DI LUNGHEZZE D ONDA CON UNO SPETTROSCOPIO A RETICOLO DI DIFFRAZIONE Il reticolo di diffrazione può essere utilizzato per determinare la lunghezza d onda di una radiazione monocromatica. Detto d
