Fatica dei materiali Dati di fatica di base
|
|
|
- Leonzio Lamberti
- 8 anni fa
- Просмотров:
Транскрипт
1 atica dei materiali Curve SN e SNP Metodo stair-case Effetto della tensione media: diagrammi di fatica Stima dei diagrammi SN 006 Politecnico di Torino 1
2 Introduzione (1/3) I dati di fatica di base sono ottenuti da prove con sollecitazioni nominali uniassiali ad ampiezza costante Politecnico di Torino
3 Introduzione (/3) I dati di fatica di base sono ottenuti da prove con sollecitazioni nominali uniassiali ad ampiezza costante Le prove possono essere condotte sia su provette sia su componenti in grandezza naturale o in scala 5 Introduzione (3/3) I dati di fatica di base sono ottenuti da prove con sollecitazioni nominali uniassiali ad ampiezza costante Le prove possono essere condotte sia su provette sia su componenti in grandezza naturale o in scala I dati di fatica di base sono rappresentati nei diagrammi di Wöhler o diagrammi delle curve S-N Politecnico di Torino 3
4 August Wöhler (1/) August Wöhler ( ) Dal 1854 al 1869 direttore delle ferrovie imperiali prussiane, dove, per primo, affrontò in modo sistematico e sperimentale lo studio della fatica degli assali ferroviari, costruendo apposite macchine di prova da 7 August Wöhler (/) Per primo indicò il concetto di limite di fatica e i principali parametri che lo influenzano August Wöhler ( ) Dal 1854 al 1869 direttore delle ferrovie imperiali prussiane, dove, per primo, affrontò in modo sistematico e sperimentale lo studio della fatica degli assali ferroviari, costruendo apposite macchine di prova da Politecnico di Torino 4
5 Diagramma di Wöhler (1/6) a Acciaio N 9 Diagramma di Wöhler (/6) atica oligociclica a Acciaio N Politecnico di Torino 5
6 Diagramma di Wöhler (3/6) a atica oligociclica Resistenza a termine Acciaio N 11 Diagramma di Wöhler (4/6) a atica oligociclica atica (ad alto numero di cicli) Resistenza a termine Resistenza o vita infinita Acciaio N Politecnico di Torino 6
7 Diagramma di Wöhler (5/6) a atica oligociclica atica (ad alto numero di cicli) Resistenza a termine Resistenza o vita infinita N D Limite di fatica Acciaio N 13 Diagramma di Wöhler (6/6) a atica oligociclica atica (ad alto numero di cicli) Resistenza a termine Resistenza o vita infinita N D Limite di fatica Acciaio Leghe Al N Politecnico di Torino 7
8 lessione rotante max ω t 15 Macchine di prova in flessione rotante (1/3) ω P P M f Provetta su quattro appoggi Politecnico di Torino 8
9 Macchine di prova in flessione rotante (/3) ω P P M f Provetta su quattro appoggi 17 Macchine di prova in flessione rotante (3/3) ω P P M f M f Provetta su quattro appoggi ω P Provetta a sbalzo Politecnico di Torino 9
10 Macchine di prova in flessione piana (1/3) ω ω 19 Macchine di prova in flessione piana (/3) ω ω Politecnico di Torino 10
11 Macchine di prova in flessione piana (3/3) ω ω Reg. ω m Regolazione a 1 Macchine di prova assiali (1/) Macchina idraulica 006 Politecnico di Torino 11
12 Macchine di prova assiali (/) Macchina idraulica Vibroforo 3 Condizioni standard (1/3) lessione rotante ( m = 0, corrispondente a R = -1) Politecnico di Torino 1
13 Condizioni standard (/3) lessione rotante ( m = 0, corrispondente a R = -1) Provetta di diametro 10mm circa 5 Condizioni standard (3/3) lessione rotante ( m = 0, corrispondente a R = -1) Provetta di diametro 10mm circa Superficie lucidata Politecnico di Torino 13
14 Dispersione dei dati (1/3) I dati di fatica sono dispersi sia come durata, sia come limite di fatica 7 Dispersione dei dati (/3) I dati di fatica sono dispersi sia come durata, sia come limite di fatica Sono necessari metodi statistici per elaborare i dati Politecnico di Torino 14
15 Dispersione dei dati (3/3) I dati di fatica sono dispersi sia come durata, sia come limite di fatica Sono necessari metodi statistici per elaborare i dati I risultati dovrebbero essere dati con riferimento ad una probabilità di sopravvivenza (o di rottura) 9 Elaborazione dei dati (1/4) A rigore il metodo dei minimi quadrati per tracciare le curve è utilizzabile solo se: Non ci sono runouts Politecnico di Torino 15
16 Elaborazione dei dati (/4) A rigore il metodo dei minimi quadrati per tracciare le curve è utilizzabile solo se: Non ci sono runouts La dispersione delle durate a una data sollecitazione è descrivibile con una distribuzione normale o lognormale 31 Elaborazione dei dati (3/4) A rigore il metodo dei minimi quadrati per tracciare le curve è utilizzabile solo se: Non ci sono runouts La dispersione delle durate a una data sollecitazione è descrivibile con una distribuzione normale o lognormale La dispersione è costante al variare della sollecitazione Politecnico di Torino 16
17 Elaborazione dei dati (4/4) A rigore il metodo dei minimi quadrati per tracciare le curve è utilizzabile solo se: Non ci sono runouts La dispersione delle durate a una data sollecitazione è descrivibile con una distribuzione normale o lognormale La dispersione è costante al variare della sollecitazione In caso contrario si devono usare metodi più sofisticati come quello della Massima Verosimiglianza (ML MLL) 33 Curve SNP a (Mpa) X = rottura 0 = runout M1 m =30 MPa MLL - Weibull B 90 B 50 B N NB: la variabile dipendente è N! N = f( a ) Politecnico di Torino 17
18 Limite di fatica e caratteristiche statiche D-1 (Mpa) D 1 = R m =0.50 =0.45 = =0.3 Acciai da bonifica R m (Mpa) 35 Criteri di Bach e di uchs (1/) Per stimare il limite di fatica si possono, utilizzare in prima approssimazione, relazioni con il carico unitario di rottura del materiale: Criterio di Bach (1900) D 1 D0 = 0.5 R = 0.3 R m m ( R = 1 m = 0) ( R = 0 = 0) min Politecnico di Torino 18
19 Criteri di Bach e di uchs (/) Per stimare il limite di fatica si possono, utilizzare in prima approssimazione, relazioni con il carico unitario di rottura del materiale: Criterio di Bach (1900) D 1 D0 = 0.5 R = 0.3 R m m ( R = 1 m = 0) ( R = 0 = 0) min Criterio di uchs (1980) (Acciai legati) D 1 D 1 = 0.5 R m = 700 MPa ( Rm < 1400 MPa) ( R 1400 MPa) m Politecnico di Torino 19
20 Il metodo I (1/3) Metodo statistico introdotto da W.J. Dixon durante la II guerra mondiale per studi su esplosivi 39 Il metodo I (/3) Metodo statistico introdotto da W.J. Dixon durante la II guerra mondiale per studi su esplosivi Molto utilizzato in campo biomedico Politecnico di Torino 0
21 Il metodo I (3/3) Metodo statistico introdotto da W.J. Dixon durante la II guerra mondiale per studi su esplosivi Molto utilizzato in campo biomedico Utilizzato per la valutazione della resistenza a termine (limite di fatica se nella zona asintotica della curva SN) eseguendo un numero limitato di prove 41 Il metodo II (1/) Previsto dalla norma italiana UNI 3964/85 Prove meccaniche dei materiali metallici. Prove di fatica a temperatura ambiente. Principi generali Politecnico di Torino 1
22 Il metodo II (/) Previsto dalla norma italiana UNI 3964/85 Prove meccaniche dei materiali metallici. Prove di fatica a temperatura ambiente. Principi generali. Permette di valutare il valore mediano N(50%) (coincide con la media per la distribuzione normale) e lo scarto tipo s in termini di tensione 43 Procedura di prova I (1/3) Si scelgono: Un numero di cicli di riferimento N Politecnico di Torino
23 Procedura di prova I (/3) Si scelgono: Un numero di cicli di riferimento N Un livello di tensione di partenza, possibilmente nei dintorni del valore presunto della resistenza a N cicli 45 Procedura di prova I (3/3) Si scelgono: Un numero di cicli di riferimento N Un livello di tensione di partenza, possibilmente nei dintorni del valore presunto della resistenza a N cicli Un gradino d; il valore del gradino dovrebbe essere circa uguale allo scarto tipo (incognito). La UNI UNI 3964/85 suggerisce 10-0 MPa Politecnico di Torino 3
24 Procedura di prova II (1/4) Si eseguono le prove in modo sequenziale seguendo la seguente regola: i : rotta i+1 = i d 47 Procedura di prova II (/4) Si eseguono le prove in modo sequenziale seguendo la seguente regola: i : rotta i+1 = i d i : non rotta i+1 = i + d Politecnico di Torino 4
25 Procedura di prova II (3/4) Si eseguono le prove in modo sequenziale seguendo la seguente regola: i : rotta i+1 = i d i : non rotta i+1 = i + d NB: i provini devono essere scelti in modo casuale 49 Procedura di prova II (4/4) Si eseguono le prove in modo sequenziale seguendo la seguente regola: i : rotta i+1 = i d i : non rotta i+1 = i + d NB: i provini devono essere scelti in modo casuale La procedura può essere interrotta quando si raggiungono almeno 15 prove utili Politecnico di Torino 5
26 Esito delle prove M8 Prove di fatica m = 400 MPa "senza difetti" d= 10 MPa 1 = Rotta; 0 = Non rotta N = a Range delle prove utili M8 Prove di fatica m = 400 MPa "senza difetti" d= 10 MPa 1 = Rotta; 0 = Non rotta N = a Politecnico di Torino 6
27 Elaborazione I M8 Prove di fatica m = 400 MPa "senza difetti" d= 10 MPa 1 = Rotta; 0 = Non rotta N = a esito Evento meno frequente Non Rotta tot Elaborazione II (1/) Si considerano solo le prove relative all evento meno frequente ( non rotta ) i n in iin N = 7 A = 7 B = Politecnico di Torino 7
28 Elaborazione II (/) Si considerano solo le prove relative all evento meno frequente ( non rotta ) i n in iin N = 7 A = 7 B = 11 A N(50%) = 0 + d ± 0. 5 N (= 45 MPa) + : evento meno frequente non rotta : evento meno frequente rotta 55 Elaborazione III (1/4) se NB-A N > 0.3 s NB - A = 1.6d N Politecnico di Torino 8
29 Elaborazione III (/4) se se NB-A N NB-A N > s s NB - A = 1.6d N = 0.53 d Elaborazione III (3/4) se se NB-A N NB-A N > s s NB-A =0.6 N NB - A = 1.6d N = 0.53 d s=9.7mpa Politecnico di Torino 9
30 Elaborazione III (4/4) se se NB-A N NB-A N > s s NB-A =0.6 N NB - A = 1.6d N = 0.53 d s=9.7mpa N(10%) N(90%) = = N(50%) N(50%) 1.8 s s (= 57 Mpa) (= 33 Mpa) Politecnico di Torino 30
31 Effetto della tensione media (1/3) La nucleazione di una cricca avviene su un piano (π) inclinato di 45 rispetto alla sollecitazione assiale applicata 61 Effetto della tensione media (/3) π τ π La nucleazione di una cricca avviene su un piano (π) inclinato di 45 rispetto alla sollecitazione assiale applicata Su questo piano agiscono, istante per istante una τ π, responsabile della nucleazione, e una π Politecnico di Torino 31
32 Effetto della tensione media (3/3) π τ π La nucleazione di una cricca avviene su un piano (π) inclinato di 45 rispetto alla sollecitazione assiale applicata Su questo piano agiscono, istante per istante una τ π, responsabile della nucleazione, e una π. Intuitivamente: Se π >0 nucleazione favorita; Se π <0 nucleazione ostacolata. 63 Cicli con R =-1 max m =0 t min τ τ πmin = τ πmax s πmin s πmax Politecnico di Torino 3
33 Cicli con R > 0 max m τ τ πmax τ πmin min t La π èsempre positiva. Rispetto ad R =-1 la nucleazione è facilitata s πmin s πmax 65 Cicli con R > 1 max t m min s πmin τ s πmax τ πmax τ πmin La π èsempre negativa. Rispetto ad R =-1 la nucleazione è ostacolata Inoltre, se non vi è parte del ciclo in trazione, non può avvenire la propagazione Politecnico di Torino 33
34 Diagramma di Haigh a R p0. punti sperimentali D-1 R p0. R m m 67 Ipotesi di Goodman a R p0. D-1 retta di Goodman D R p0. R m m D D 1 + R m m = 1 D = D 1 R D 1 m m Politecnico di Torino 34
35 Limitazione della tensione massima a R p0. D-1 R p0. R m m D D 1 + R m m = 1 D = D 1 R D 1 m m 69 Diagramma di Haigh completo a R=- R p0. D-1 R=0 R p0. R m m Politecnico di Torino 35
36 Diagramma di Goodman (1/6) R m R p0. max, min D-1 R p0. R m m D-1 71 Diagramma di Goodman (/6) R m R p0. max, min D-1 R p0. R m m D Politecnico di Torino 36
37 Diagramma di Goodman (3/6) R m R p0. max, min D-1 R p0. R m m D-1 73 Diagramma di Goodman (4/6) R m R p0. max, min D-1 R p0. R m m D Politecnico di Torino 37
38 Diagramma di Goodman (5/6) R m R p0. max, min D-1 R p0. R m m D-1 75 Diagramma di Goodman (6/6) R m R p0. max, min D-1 a a m R p0. R m m D Politecnico di Torino 38
39 Diagramma di Moore-Kommer-Jasper max R m R p0. D / 0 1/ 1 R 77 Diagramma di Ros o Diagramma Master R a =1 max R= a 160 R = - R a = R= MPa m min Politecnico di Torino 39
40 Dati necessari (1/3) I diagrammi SN possono essere di tipo: Doppio logaritmico (log-log) Semilogaritmici (semilog) Politecnico di Torino 40
41 Dati necessari (/3) I diagrammi SN possono essere di tipo: Soppio logaritmico (log-log) Semilogaritmici (semilog) Per la stima si devono conoscere: Il carico di rottura R m Il limite di fatica D ad una data tensione media m (eventualmente stimati) 81 Dati necessari (3/3) I diagrammi SN possono essere di tipo: Doppio logaritmico (log-log) Semilogaritmici (semilog) Per la stima si devono conoscere: Il carico di rottura R m Il limite di fatica D ad una data tensione media m (eventualmente stimati) Oppure Il limite in termini di tensione massima max per un dato rapporto di tensione R Politecnico di Torino 41
42 Idea base - m = cost (1/3) Si suppone che la curva SN passi per due punti: G: ginocchio della curva SN ( N, ) = ( N ) G G G, D 83 Idea base - m = cost (/3) Si suppone che la curva SN passi per due punti: G: ginocchio della curva SN ( N, ) = ( N ) G G G, Se non si hanno maggiori informazioni N G = D Politecnico di Torino 4
43 Idea base - m = cost (3/3) Si suppone che la curva SN passi per due punti: G: ginocchio della curva SN Se non si hanno maggiori informazioni N G = : punto al limite della fatica oligocilica (N = 10 3 ) corrispondente ad una a pari al 90% di quella che porta ad una max = R m ( ) 3 ( N, ) = 10,0.9( R ) ( N, ) = ( N ) G G G, m D m 85 Diagramma log-log - m = cost (1/) 1000 a 500 m = G N a = AN b Politecnico di Torino 43
44 Diagramma log-log - m = cost (/) 1000 a 500 m = G N b a = AN N = B k a 87 Calcolo coefficienti I b a = AN ovvero log( a) = log(a) + b log(n) b = log( log(n D G ) log( ) log(n ) ) log(a) = log( D log( ) log(n D G ) log( ) log(n ) log(n ) G ) Politecnico di Torino 44
45 Calcolo coefficienti II N k a = B ovvero log(n) = log(b) k log( a ) k = log(n log( G ) log(n ) log( D ) ) = 1 b log(b) = log(n G log(n ) + log( G ) log(n ) log( D ) log( ) D ) 89 Diagramma semilog - m = cost (1/) 1000 a m = 400 G N a = logn G D logn (logn logn ) Politecnico di Torino 45
46 Diagramma semilog - m = cost (/) 1000 a m = 400 G N a = logn logn = logn G + D logn a D (logn logn (logn G logn ) ) 91 Diagrammi ad R = cost max R = 400 max G N 3 ( N, ) = ( N, ' ) ( N, ) = 10 ;0.9 R G G G max m 1 R Politecnico di Torino 46
Comportamento meccanico dei materiali
 Comportamento meccanico dei materiali Fatica dei materiali Propagazione delle cricche Dati di fatica di base Dai provini ai componenti, fatica uniassiale Fatica con sollecitazioni ad ampiezza variabile
Comportamento meccanico dei materiali Fatica dei materiali Propagazione delle cricche Dati di fatica di base Dai provini ai componenti, fatica uniassiale Fatica con sollecitazioni ad ampiezza variabile
FATICA. FATICA: curva di Wohler
 FATICA Flessione rotante CURVA DI WOHLER 1 FATICA: curva di Wohler 2 1 FATICA: curva di Wohler 3 FATICA: curva di Wohler an f b f N f 1 1 m m f K N f f a 1 b 4 2 FATICA: curva di Wohler la curva viene
FATICA Flessione rotante CURVA DI WOHLER 1 FATICA: curva di Wohler 2 1 FATICA: curva di Wohler 3 FATICA: curva di Wohler an f b f N f 1 1 m m f K N f f a 1 b 4 2 FATICA: curva di Wohler la curva viene
17/03/2014. Le prove meccaniche distruttive. Tipologie di deformazione. Sistemi di Produzione D. Antonelli, G. Murari C.L.U.T.
 Le prove meccaniche distruttive Le prove meccaniche distruttive Sistemi di Produzione D. Antonelli, G. Murari C.L.U.T. Editrice, 2008 capitolo 3 Tecnologia meccanica S. Kalpakjian, S. R. Schmid Pearson
Le prove meccaniche distruttive Le prove meccaniche distruttive Sistemi di Produzione D. Antonelli, G. Murari C.L.U.T. Editrice, 2008 capitolo 3 Tecnologia meccanica S. Kalpakjian, S. R. Schmid Pearson
Calcolo a fatica di componenti meccanici. Prima parte
 Calcolo a fatica di componenti meccanici Prima parte Calcolo a fatica di componenti meccanici L esperienza, nella pratica costruttiva, di rotture improvvise, dovute a carichi che si ripetono ciclicamente,
Calcolo a fatica di componenti meccanici Prima parte Calcolo a fatica di componenti meccanici L esperienza, nella pratica costruttiva, di rotture improvvise, dovute a carichi che si ripetono ciclicamente,
FATICA OLIGOCICLICA TEORIA E APPLICAZIONI. Fatica Oligociclica Costruzione di Macchine 3
 FATICA OLIGOCICLICA TEORIA E APPLICAZIONI 1 RICHIAMI La fatica è il complesso dei fenomeni per cui un elemento strutturale, soggetto a sollecitazioni cicliche, mostra una resistenza inferiore a quella
FATICA OLIGOCICLICA TEORIA E APPLICAZIONI 1 RICHIAMI La fatica è il complesso dei fenomeni per cui un elemento strutturale, soggetto a sollecitazioni cicliche, mostra una resistenza inferiore a quella
Esempi domande CMM pagina 1
 : omande di Statica - - -3-4 -5-6 -7-8 Nel diagramma σ - ε di un materiale duttile, secondo la simbologia UNI-ISO la tensione di scostamento dalla proporzionalità R P0 è: [A] il valore limite per cui la
: omande di Statica - - -3-4 -5-6 -7-8 Nel diagramma σ - ε di un materiale duttile, secondo la simbologia UNI-ISO la tensione di scostamento dalla proporzionalità R P0 è: [A] il valore limite per cui la
La verifica di resistenza a fatica dei materiali metallici 1: il provino. Andrea Manes
 La verifica di resistenza a fatica dei materiali metallici 1: il provino La fatica nei materiali metallici 2 Nel corso della storia dell industria moderna sono avvenute rotture improvvise e inaspettate
La verifica di resistenza a fatica dei materiali metallici 1: il provino La fatica nei materiali metallici 2 Nel corso della storia dell industria moderna sono avvenute rotture improvvise e inaspettate
Elementi Costruttivi delle Macchine. Soluzione - Verifica di un albero di trasmissione 3.1. Politecnico di Torino CeTeM
 Si richiede la verifica di un albero di che riceve il moto da una ruota dentata calettata sull albero stesso il quale trasmette moto alternato a una puleggia. 40 50 20 20 R.5 R.1 R.5 R.2 R.1 Ø65 Ø46 Ø41
Si richiede la verifica di un albero di che riceve il moto da una ruota dentata calettata sull albero stesso il quale trasmette moto alternato a una puleggia. 40 50 20 20 R.5 R.1 R.5 R.2 R.1 Ø65 Ø46 Ø41
Comportamento Meccanico dei Materiali. 4 Soluzione degli esercizi proposti. Esercizio 4-1
 Esercizio 4-1 Una piastra in S355 EN 1007/1 (Fe510 UNI 7070) delle dimensioni indicate in figura viene sollecitata da un carico assiale T 64 kn. Con riferimento alla sezione con intaglio, calcolare i coefficienti
Esercizio 4-1 Una piastra in S355 EN 1007/1 (Fe510 UNI 7070) delle dimensioni indicate in figura viene sollecitata da un carico assiale T 64 kn. Con riferimento alla sezione con intaglio, calcolare i coefficienti
Dipartimento di Meccanica Politecnico di Torino
 Fatica in - Local strain approach Low Cycle Fatigue (LCF) ilosoia del metodo P Zona critica Innesco cricca di atica cedimento della provetta Alla radice dell intaglio sono presenti deormazioni plastiche.
Fatica in - Local strain approach Low Cycle Fatigue (LCF) ilosoia del metodo P Zona critica Innesco cricca di atica cedimento della provetta Alla radice dell intaglio sono presenti deormazioni plastiche.
La frattura nei materiali ceramici
 Giornata di studio Analisi del comportamento a frattura di materiali ceramici e compositi per applicazioni industriali Comportamento a fatica ciclica di compositi ceramici C/C SiC M. Labanti, G. L. Minoccari,
Giornata di studio Analisi del comportamento a frattura di materiali ceramici e compositi per applicazioni industriali Comportamento a fatica ciclica di compositi ceramici C/C SiC M. Labanti, G. L. Minoccari,
Ingegneria del vetro V.M. Sglavo UNITN Proprietà meccaniche. elasticità! resistenza! densità di legami chimici! forza del legame!
 Proprietà meccaniche elasticità! r 0 resistenza! densità di legami chimici! forza del legame! Durezza! P! profilo impronta scala Mohs diamante 10 zaffiro 9 topazio 8 quarzo ortoclasio apatite fluorite
Proprietà meccaniche elasticità! r 0 resistenza! densità di legami chimici! forza del legame! Durezza! P! profilo impronta scala Mohs diamante 10 zaffiro 9 topazio 8 quarzo ortoclasio apatite fluorite
LE PROVE DI AFFIDABILITA
 4. LE PROVE DI AFFIDABILITA Ed.1 del 14/09/98 Rev. 3 del 08/09/00 AFFIDABILITA' DI COMPONENTI E SCHEDE ELETTRONICHE-sez 4 1 LE PROVE DI AFFIDABILITA SI RICAVANO INFORMAZIONI RELATIVE AD UN CAMPIONE E SI
4. LE PROVE DI AFFIDABILITA Ed.1 del 14/09/98 Rev. 3 del 08/09/00 AFFIDABILITA' DI COMPONENTI E SCHEDE ELETTRONICHE-sez 4 1 LE PROVE DI AFFIDABILITA SI RICAVANO INFORMAZIONI RELATIVE AD UN CAMPIONE E SI
Università del Salento Facoltà di Ingegneria Costruzione di Macchine
 Università del Salento Facoltà di Ingegneria Costruzione di Macchine Lezione 3 Prova di trazione a cura del prof. ing. Vito Dattoma e dell ing. Riccardo Nobile 1 Prove di caratterizzazione meccanica Prova
Università del Salento Facoltà di Ingegneria Costruzione di Macchine Lezione 3 Prova di trazione a cura del prof. ing. Vito Dattoma e dell ing. Riccardo Nobile 1 Prove di caratterizzazione meccanica Prova
IL LEGNO COME MATERIALE STRUTTURALE E LE SUE PROPRIETA MECCANICHE
 Corso di formazione: SISTEMI COSTRUTTIVI DI COPERTURA IN LEGNO LAMELLARE Ordine degli Ingegneri di Napoli 5 e 6 maggio 2014 IL LEGNO COME MATERIALE STRUTTURALE E LE SUE PROPRIETA MECCANICHE Parte 2: IL
Corso di formazione: SISTEMI COSTRUTTIVI DI COPERTURA IN LEGNO LAMELLARE Ordine degli Ingegneri di Napoli 5 e 6 maggio 2014 IL LEGNO COME MATERIALE STRUTTURALE E LE SUE PROPRIETA MECCANICHE Parte 2: IL
COSTRUZIONI IN CEMENTO ARMATO PROF.RIZZO
 Parte da stralciare portandola a me tematica Parte da stralciare portandola a me tematica COSTRUZIONI IN CEMENTO ARMATO PROF.RIZZO LEZIONE ARGOMENTI note 1. Introduzione Presentazione del corso 2. Cenni
Parte da stralciare portandola a me tematica Parte da stralciare portandola a me tematica COSTRUZIONI IN CEMENTO ARMATO PROF.RIZZO LEZIONE ARGOMENTI note 1. Introduzione Presentazione del corso 2. Cenni
Classificazione generica delle prove meccaniche in base alla legge di applicazione del carico nel tempo
 Classificazione generica delle prove meccaniche in base alla legge di applicazione del carico nel tempo carico 1 2 min.1 s.1.1 s 1 1 h tempo statiche dinamiche dinamiche periodiche di scorrimento Prova
Classificazione generica delle prove meccaniche in base alla legge di applicazione del carico nel tempo carico 1 2 min.1 s.1.1 s 1 1 h tempo statiche dinamiche dinamiche periodiche di scorrimento Prova
Problema. caso uniassiale prova di trazione. caso multiassiale (carico generico)
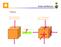 Criteri di Rottura Problema caso uniassiale prova di trazione caso multiassiale (carico generico)? criterio di rottura 1 Criteri di Rottura ASSUNZIONE BASE: Il collasso di un componente avviene quando
Criteri di Rottura Problema caso uniassiale prova di trazione caso multiassiale (carico generico)? criterio di rottura 1 Criteri di Rottura ASSUNZIONE BASE: Il collasso di un componente avviene quando
TEORIA DEGLI ERRORI DI MISURA, IL CALCOLO DELLE INCERTEZZE
 TEORIA DEGLI ERRORI DI MISURA, IL CALCOLO DELLE INCERTEZZE Errore di misura è la differenza fra l indicazione fornita dallo strumento e la dimensione vera della grandezza. Supponendo che la grandezza vera
TEORIA DEGLI ERRORI DI MISURA, IL CALCOLO DELLE INCERTEZZE Errore di misura è la differenza fra l indicazione fornita dallo strumento e la dimensione vera della grandezza. Supponendo che la grandezza vera
Costruzione di Macchine Verifica a fatica degli elementi delle macchine
 Costruzione di Macchine Verifica a fatica degli elementi delle macchine In figura 1 è rappresentato schematicamente un mescolatore: l albero con la paletta è mosso da un motore elettrico asincrono trifase
Costruzione di Macchine Verifica a fatica degli elementi delle macchine In figura 1 è rappresentato schematicamente un mescolatore: l albero con la paletta è mosso da un motore elettrico asincrono trifase
Sforzo e Deformazione nei Metalli
 Sforzo e Deformazione nei Metalli I metalli vanno incontro a deformazione sotto l azione di una forza assiale a trazione Deformazione elastica: il metallo ritorna alla sua dimensione iniziale quando la
Sforzo e Deformazione nei Metalli I metalli vanno incontro a deformazione sotto l azione di una forza assiale a trazione Deformazione elastica: il metallo ritorna alla sua dimensione iniziale quando la
Curva di Taratura.xls
 Seconda fase: INDAGINI IN SITU PROVE SUL CALCESTRUZZO PROVE SCLEROMETRICHE COSTRUZIONE DELLE CURVE DI TARATURA: ESEMPIO Costruzione Curva di Taratura.xls Seconda fase: INDAGINI IN SITU PROVE SUL CALCESTRUZZO
Seconda fase: INDAGINI IN SITU PROVE SUL CALCESTRUZZO PROVE SCLEROMETRICHE COSTRUZIONE DELLE CURVE DI TARATURA: ESEMPIO Costruzione Curva di Taratura.xls Seconda fase: INDAGINI IN SITU PROVE SUL CALCESTRUZZO
ESERCITAZIONE SUL CRITERIO
 TECNOLOGIE DELLE COSTRUZIONI AEROSPAZIALI ESERCITAZIONE SUL CRITERIO DI JUVINALL Prof. Claudio Scarponi Ing. Carlo Andreotti Ing. Carlo Andreotti 1 IL CRITERIO DI JUVINALL La formulazione del criterio
TECNOLOGIE DELLE COSTRUZIONI AEROSPAZIALI ESERCITAZIONE SUL CRITERIO DI JUVINALL Prof. Claudio Scarponi Ing. Carlo Andreotti Ing. Carlo Andreotti 1 IL CRITERIO DI JUVINALL La formulazione del criterio
Lezioni di Costruzione di Macchine
 Università del Salento Facoltà di Ingegneria Corso di laurea in Ingegneria Industriale Lezioni di Costruzione di Macchine a.a. 2015/16 Fatica Random Fatica ad ampiezza di sollecitazione variabile 2 Modalità
Università del Salento Facoltà di Ingegneria Corso di laurea in Ingegneria Industriale Lezioni di Costruzione di Macchine a.a. 2015/16 Fatica Random Fatica ad ampiezza di sollecitazione variabile 2 Modalità
TOPOGRAFIA 2013/2014. Prof. Francesco-Gaspare Caputo
 TOPOGRAFIA 2013/2014 L operazione di misura di una grandezza produce un numero reale che esprime il rapporto della grandezza stessa rispetto a un altra, a essa omogenea, assunta come unità di misura. L
TOPOGRAFIA 2013/2014 L operazione di misura di una grandezza produce un numero reale che esprime il rapporto della grandezza stessa rispetto a un altra, a essa omogenea, assunta come unità di misura. L
CURVE DI DURATA: Introduzione e Rappresentazione analitica
 CURVE DI DURATA: Introduzione e Rappresentazione analitica Premesse Si definisce durata di una portata Q riferita ad una sezione di misura, l'intervallo di tempo in cui le portate naturali del corso d
CURVE DI DURATA: Introduzione e Rappresentazione analitica Premesse Si definisce durata di una portata Q riferita ad una sezione di misura, l'intervallo di tempo in cui le portate naturali del corso d
-gdl>gdv il sistema è staticamente labile (trave labile, cioè in grado di muoversi);
 Meccanica a trave Trave in equilibrio con due vincoli I gradi di libertà per un corpo sul piano sono 3, mentre quelli di un corpo nello spazio sono 6. Consideriamo un sistema di riferimento formato da:
Meccanica a trave Trave in equilibrio con due vincoli I gradi di libertà per un corpo sul piano sono 3, mentre quelli di un corpo nello spazio sono 6. Consideriamo un sistema di riferimento formato da:
ESERCIZIO 1. Fig. 1. Si ricava a = m = 14.6 mm. Ricalcolando per a/w= 14.6/50= 0.29, si ottiene Procedendo, si ricava:
 ESERCIZIO 1 Una piastra di larghezza totale 100 mm e spessore 5 mm, con cricca centrale passante (ig. 1), è soggetta ad una orza di trazione P=50 kn. 1) Determinare le condizioni di cedimento della piastra.
ESERCIZIO 1 Una piastra di larghezza totale 100 mm e spessore 5 mm, con cricca centrale passante (ig. 1), è soggetta ad una orza di trazione P=50 kn. 1) Determinare le condizioni di cedimento della piastra.
MATERIALI PER L INGEGNERIA (Corso di Laurea in Ingegneria Gestionale) Prof. Tommaso Pastore TEST ORIENTATIVO del 8 giugno 2007
 L MATERIALI PER L INGEGNERIA (Corso di Laurea in Ingegneria Gestionale) Prof. Tommaso Pastore TEST ORIENTATIVO del 8 giugno 2007 Esercizio 1 In un cantiere, è richiesto il collaudo di una barra di ancoraggio
L MATERIALI PER L INGEGNERIA (Corso di Laurea in Ingegneria Gestionale) Prof. Tommaso Pastore TEST ORIENTATIVO del 8 giugno 2007 Esercizio 1 In un cantiere, è richiesto il collaudo di una barra di ancoraggio
Circuito RC con d.d.p. sinusoidale
 Circuito C con d.d.p. sinusoidale Un circuito C-serie ha la seguente configurazione: G è la resistenza interna del generatore. Misura dello sfasamento della tensione ai capi del condensatore rispetto alla
Circuito C con d.d.p. sinusoidale Un circuito C-serie ha la seguente configurazione: G è la resistenza interna del generatore. Misura dello sfasamento della tensione ai capi del condensatore rispetto alla
Prove sperimentali a rottura di travi rettangolari in cemento armato con staffatura tipo Spirex e staffatura tradizionale
 Università degli Studi di Firenze DIPARTIMENTO DI INGEGNERIA CIVILE E AMBIENTALE LABORATORIO PROVE STRUTTURE E MATERIALI Via di Santa Marta, 3-50139 Firenze Prove sperimentali a rottura di travi rettangolari
Università degli Studi di Firenze DIPARTIMENTO DI INGEGNERIA CIVILE E AMBIENTALE LABORATORIO PROVE STRUTTURE E MATERIALI Via di Santa Marta, 3-50139 Firenze Prove sperimentali a rottura di travi rettangolari
Questi appunti costituiscono soltanto una traccia sintetica del Corso di Laboratorio di Fisica, a prescindere dalle opportune spiegazioni e dai
 Questi appunti costituiscono soltanto una traccia sintetica del Corso di Laboratorio di Fisica, a prescindere dalle opportune spiegazioni e dai necessari chiarimenti forniti a lezione. 1 MISURA DI UNA
Questi appunti costituiscono soltanto una traccia sintetica del Corso di Laboratorio di Fisica, a prescindere dalle opportune spiegazioni e dai necessari chiarimenti forniti a lezione. 1 MISURA DI UNA
Il fenomeno della frattura ha assunto una notevole importanza solo in tempi relativamente recenti.
 Il fenomeno della frattura ha assunto una notevole importanza solo in tempi relativamente recenti. In passato, infatti, i materiali e le tecnologie di costruzione non avevano mai messo in luce questo fenomeno.....finché
Il fenomeno della frattura ha assunto una notevole importanza solo in tempi relativamente recenti. In passato, infatti, i materiali e le tecnologie di costruzione non avevano mai messo in luce questo fenomeno.....finché
Scopo delle prove RAPPORTO DI PROVA N
 Scopo delle prove Le prove sono state eseguite su impianti dentali intraossei (i-fix F1 3.8mm x 12mm) (i-fix FN 3.0mm x 12mm, Titanio Gr.4 ASTM F67) allo scopo di determinare la sollecitazione Dinamica
Scopo delle prove Le prove sono state eseguite su impianti dentali intraossei (i-fix F1 3.8mm x 12mm) (i-fix FN 3.0mm x 12mm, Titanio Gr.4 ASTM F67) allo scopo di determinare la sollecitazione Dinamica
Corso di Laurea Ingegneria Meccanica Costruzione di Macchine 2. Dimensionamento di una sospensione
 Corso di Laurea Ingegneria Meccanica Dimensionamento di una sospensione Un esempio storico Ford Model T Altri esempi 3 Sospensione a quadrilatero basso MacPherson Sospensione a quadrilatero alto Molle:
Corso di Laurea Ingegneria Meccanica Dimensionamento di una sospensione Un esempio storico Ford Model T Altri esempi 3 Sospensione a quadrilatero basso MacPherson Sospensione a quadrilatero alto Molle:
Cauchy (XIX secolo) Introduce il concetto di deformazione relativa (ε = l/l o ) e la mette in relazione con lo sforzo applicato (σ = F/A o ):
 Cauchy (XIX secolo) Introduce il concetto di deformazione relativa (ε = l/l o ) e la mette in relazione con lo sforzo applicato (σ = F/A o ): σ = E ε LEGGE DI HOOKE A o l o Δl Young (XIX secolo) Il valore
Cauchy (XIX secolo) Introduce il concetto di deformazione relativa (ε = l/l o ) e la mette in relazione con lo sforzo applicato (σ = F/A o ): σ = E ε LEGGE DI HOOKE A o l o Δl Young (XIX secolo) Il valore
Lezioni di Costruzione di Macchine
 Università del Salento Facoltà di Ingegneria Corso di laurea in Ingegneria Industriale Lezioni di Costruzione di Macchine a.a. 014/15 1 FATICA NEI METALLI Introduzione La meccanica dei materiali è l area
Università del Salento Facoltà di Ingegneria Corso di laurea in Ingegneria Industriale Lezioni di Costruzione di Macchine a.a. 014/15 1 FATICA NEI METALLI Introduzione La meccanica dei materiali è l area
Meccanica della Frattura Lecture 10 Temperatura di transizione duttile-fragile
 Lecture 10 Temperatura di transizione duttile-fragile Introduzione I metalli e le leghe (acciai) mostrano una dipendenza della tensione di snervamento e della rottura dalla temperatura. 2 1 rv Tensione
Lecture 10 Temperatura di transizione duttile-fragile Introduzione I metalli e le leghe (acciai) mostrano una dipendenza della tensione di snervamento e della rottura dalla temperatura. 2 1 rv Tensione
5.4 Caratterizzazione in regime quasi statico e ad elevata velocità di deformazione di un acciaio per applicazione Oil and Gas
 5.4 Caratterizzazione in regime quasi statico e ad elevata velocità di deformazione di un acciaio per applicazione Oil and Gas Si riportano in questa sezione i risultati relativi ai test sperimentali effettuati
5.4 Caratterizzazione in regime quasi statico e ad elevata velocità di deformazione di un acciaio per applicazione Oil and Gas Si riportano in questa sezione i risultati relativi ai test sperimentali effettuati
Principi e Metodologie della Progettazione Meccanica
 Principi e Metodologie della Progettazione Meccanica ing. F. Campana a.a. 06-07 Lezione 13: Robust Design Robust Design significato ed esempi Le tecniche di ottimizzazione fin qui viste hanno un ampio
Principi e Metodologie della Progettazione Meccanica ing. F. Campana a.a. 06-07 Lezione 13: Robust Design Robust Design significato ed esempi Le tecniche di ottimizzazione fin qui viste hanno un ampio
Introduzione a Matlab Costruzione di Macchine 2 Prof. Sergio Baragetti
 Esercitazioni del corso di Costruzione di Macchine 2 a cura dell ing. Francesco Villa Introduzione a Matlab Costruzione di Macchine 2 Prof. Sergio Baragetti Dalmine - 27/02/2013 Introduzione a Matlab FONDAMENTI
Esercitazioni del corso di Costruzione di Macchine 2 a cura dell ing. Francesco Villa Introduzione a Matlab Costruzione di Macchine 2 Prof. Sergio Baragetti Dalmine - 27/02/2013 Introduzione a Matlab FONDAMENTI
STATISTICA DESCRITTIVA. Elementi di statistica medica GLI INDICI INDICI DI DISPERSIONE STATISTICA DESCRITTIVA
 STATISTICA DESCRITTIVA Elementi di statistica medica STATISTICA DESCRITTIVA È quella branca della statistica che ha il fine di descrivere un fenomeno. Deve quindi sintetizzare tramite pochi valori(indici
STATISTICA DESCRITTIVA Elementi di statistica medica STATISTICA DESCRITTIVA È quella branca della statistica che ha il fine di descrivere un fenomeno. Deve quindi sintetizzare tramite pochi valori(indici
Ministero dell Istruzione dell Università e della Ricerca M552 ESAME DI STATO DI ISTITUTO TECNICO INDUSTRIALE
 Pag. 1/1 Sessione ordinaria 2010 Seconda prova scritta Ministero dell Istruzione dell Università e della Ricerca M552 ESAME DI STATO DI ISTITUTO TECNICO INDUSTRIALE CORSO DI ORDINAMENTO Indirizzo: MECCANICA
Pag. 1/1 Sessione ordinaria 2010 Seconda prova scritta Ministero dell Istruzione dell Università e della Ricerca M552 ESAME DI STATO DI ISTITUTO TECNICO INDUSTRIALE CORSO DI ORDINAMENTO Indirizzo: MECCANICA
Caratteristiche di materiali
 Caratteristiche di materiali Caratteristiche macroscopiche Lavorazione Microstruttura Formula chimica Legami chimici Struttura atomica Meccaniche Materiale Fisiche Elettriche Megnetiche Termiche Meccaniche
Caratteristiche di materiali Caratteristiche macroscopiche Lavorazione Microstruttura Formula chimica Legami chimici Struttura atomica Meccaniche Materiale Fisiche Elettriche Megnetiche Termiche Meccaniche
Scale Logaritmiche. Matematica con Elementi di Statistica a.a. 2015/16
 Scale Logaritmiche Scala Logaritmica: sull asse prescelto (ad esempio, l asse x) si rappresenta il punto di ascissa = 0 0 nella direzione positiva si rappresentano, a distanze uguali fra di loro, i punti
Scale Logaritmiche Scala Logaritmica: sull asse prescelto (ad esempio, l asse x) si rappresenta il punto di ascissa = 0 0 nella direzione positiva si rappresentano, a distanze uguali fra di loro, i punti
Lezioni del Corso di Fondamenti di Metrologia
 Facoltà di Ingegneria Lezioni del Corso di Fondamenti di Metrologia 11. Taratura nel settore dimensionale Indice Taratura di Calibri (UNI 9313) Taratura di comparatori (UNI 9191) Taratura di micrometri
Facoltà di Ingegneria Lezioni del Corso di Fondamenti di Metrologia 11. Taratura nel settore dimensionale Indice Taratura di Calibri (UNI 9313) Taratura di comparatori (UNI 9191) Taratura di micrometri
P: potenza in kw, n: numero di giri R: raggio puleggia in metri B = 1,1 b + 10 mm dove: B: larghezza corona l = B dove l : lunghezza mozzo puleggia
 ESERCIZIO Si deve provvedere all accoppiamento, con un riduttore a ruote dentate cilindriche a denti diritti, tra un motore asincrono trifase e un albero, rappresentato nello schema, che a sua volta trasmette
ESERCIZIO Si deve provvedere all accoppiamento, con un riduttore a ruote dentate cilindriche a denti diritti, tra un motore asincrono trifase e un albero, rappresentato nello schema, che a sua volta trasmette
CAPITOLO 7 Frattura DUTTILE o FRAGILE
 CAPITOLO 7 Frattura DUTTILE o FRAGILE La frattura causa la separazione di un solido stressato in due o più parti. Comportamento duttile e fragile Frattura dei Metalli Frattura Duttile La frattura causa
CAPITOLO 7 Frattura DUTTILE o FRAGILE La frattura causa la separazione di un solido stressato in due o più parti. Comportamento duttile e fragile Frattura dei Metalli Frattura Duttile La frattura causa
Università degli studi Roma Tre Facoltà di Ingegneria Corso di Laurea Magistrale in Ingegneria Civile
 Università degli studi Roma Tre Facoltà di Ingegneria Corso di Laurea Magistrale in Ingegneria Civile RELAZIONE DI FINE TIROCINIO PROVE DI CARATTERIZZAZIONE DEL CALCESTRUZZO UTILIZZATO PER I CAMPIONI IN
Università degli studi Roma Tre Facoltà di Ingegneria Corso di Laurea Magistrale in Ingegneria Civile RELAZIONE DI FINE TIROCINIO PROVE DI CARATTERIZZAZIONE DEL CALCESTRUZZO UTILIZZATO PER I CAMPIONI IN
Esami di Stato ª sessione - Settore ingegneria Industriale sez. Meccanica
 Esami di Stato 2004-1ª sessione - Settore ingegneria Industriale sez. Meccanica Effetto DOPPLER Verifica di una sezione a flessione Diagramma carichi-deformazioni Linea con retta iso. Curva motore Definizione
Esami di Stato 2004-1ª sessione - Settore ingegneria Industriale sez. Meccanica Effetto DOPPLER Verifica di una sezione a flessione Diagramma carichi-deformazioni Linea con retta iso. Curva motore Definizione
f yd = f yk ; s 0, 7 f yk calcestruzzo armato. Le caratteristiche degli acciai, conformi con le Norme Tecniche, vengono presentate più avanti.
 Acciaio per cemento armato ordinario. Le barre di armatura sono caratterizzate dal diametro della barra tonda equipesante, calcolato nell ipotesi che il peso specifico dell acciaio sia 7850 kg/m 3. Secondo
Acciaio per cemento armato ordinario. Le barre di armatura sono caratterizzate dal diametro della barra tonda equipesante, calcolato nell ipotesi che il peso specifico dell acciaio sia 7850 kg/m 3. Secondo
RELAZIONE ESERCITAZIONI AUTODESK INVENTOR
 20 Ottobre 2015 RELAZIONE ESERCITAZIONI AUTODESK INVENTOR Corso di Costruzione di Macchine e Affidabilità C.d.L.M. in Ingegneria Meccanica Docente: Prof.ssa Cosmi Francesca Assistente: Dott.ssa Ravalico
20 Ottobre 2015 RELAZIONE ESERCITAZIONI AUTODESK INVENTOR Corso di Costruzione di Macchine e Affidabilità C.d.L.M. in Ingegneria Meccanica Docente: Prof.ssa Cosmi Francesca Assistente: Dott.ssa Ravalico
Prove eseguite su connettori Tecnaria MINICEM h=20mm per travetti in calcestruzzo e solette in calcestruzzo fibrorinforzato.
 Prove eseguite su connettori Tecnaria MINICEM h=20mm per travetti in calcestruzzo e solette in calcestruzzo fibrorinforzato. Introduzione Viene riportato il risultato di una indagine sperimentale avente
Prove eseguite su connettori Tecnaria MINICEM h=20mm per travetti in calcestruzzo e solette in calcestruzzo fibrorinforzato. Introduzione Viene riportato il risultato di una indagine sperimentale avente
Introduzione. Piattaforma petrolifera Alexander Kielland 27 Marzo morti. SS John P. Gaines 24 Novembre morti
 La fatica Introduzione Piattaforma petrolifera Alexander Kielland 27 Marzo 1980 123 morti SS John P. Gaines 24 Novembre 1943 10 morti Boston 15 Gennaio 1919 11 morti Fatica nei dispositivi medici Fratture
La fatica Introduzione Piattaforma petrolifera Alexander Kielland 27 Marzo 1980 123 morti SS John P. Gaines 24 Novembre 1943 10 morti Boston 15 Gennaio 1919 11 morti Fatica nei dispositivi medici Fratture
Caratteristiche di materiali
 Caratteristiche di materiali Caratteristiche macroscopiche Lavorazione Microstruttura Formula chimica Legami chimici Struttura atomica Meccaniche Materiale Fisiche Elettriche Megnetiche Termiche Meccaniche
Caratteristiche di materiali Caratteristiche macroscopiche Lavorazione Microstruttura Formula chimica Legami chimici Struttura atomica Meccaniche Materiale Fisiche Elettriche Megnetiche Termiche Meccaniche
a) determinare le fasi presenti, la loro quantità (percentuale) e la loro composizione in una lega Pb30% - Sn a 300, 200 e 184, 180 e 20 C.
 ESERCIZIO 1 E dato il diagramma di stato del sistema Pb-Sn (figura). a) determinare le fasi presenti, la loro quantità (percentuale) e la loro composizione in una lega Pb30% - Sn a 300, 200 e 184, 180
ESERCIZIO 1 E dato il diagramma di stato del sistema Pb-Sn (figura). a) determinare le fasi presenti, la loro quantità (percentuale) e la loro composizione in una lega Pb30% - Sn a 300, 200 e 184, 180
RELAZIONE DI CALCOLO
 RELAZIONE DI CALCOLO CONDOTTA IN ACCIAIO Premessa La costruzione della Strada Provinciale in oggetto prevede la realizzazione di una rotatoria sul tracciato esistente attraversato dal canale di bonifica
RELAZIONE DI CALCOLO CONDOTTA IN ACCIAIO Premessa La costruzione della Strada Provinciale in oggetto prevede la realizzazione di una rotatoria sul tracciato esistente attraversato dal canale di bonifica
PROGRAMMAZIONE DIDATTICA DIPARTIMENTO MECCANICO. Tecnologia meccanica e applicazioni. Classe 4 MT A.S
 PROGRAMMAZIONE DIDATTICA DIPARTIMENTO MECCANICO Tecnologia meccanica e applicazioni Classe 4 MT A.S.2016-2017 Rev. 0 del 08-03-04 pag. 1 di 6 1 Caratteristiche meccaniche e tecnologiche dei materiali metallici
PROGRAMMAZIONE DIDATTICA DIPARTIMENTO MECCANICO Tecnologia meccanica e applicazioni Classe 4 MT A.S.2016-2017 Rev. 0 del 08-03-04 pag. 1 di 6 1 Caratteristiche meccaniche e tecnologiche dei materiali metallici
Franco Ferraris Marco Parvis Generalità sulle Misure di Grandezze Fisiche. Prof. Franco Ferraris - Politecnico di Torino
 Generalità sulle Misure di Grandezze Fisiche Prof. - Politecnico di Torino - La stima delle incertezze nel procedimento di misurazione -modello deterministico -modello probabilistico - La compatibilità
Generalità sulle Misure di Grandezze Fisiche Prof. - Politecnico di Torino - La stima delle incertezze nel procedimento di misurazione -modello deterministico -modello probabilistico - La compatibilità
I materiali. I materiali. Introduzione al corso. Tecnologia di produzione I materiali La misura della durezza. Le prove meccaniche distruttive
 I materiai I materiai Introduzione a corso Tecnoogia di produzione I materiai La misura dea durezza Prove non distruttive La meccanica dei materiai 2 26 Poitecnico di Torino 1 Obiettivi dea ezione Conoscere
I materiai I materiai Introduzione a corso Tecnoogia di produzione I materiai La misura dea durezza Prove non distruttive La meccanica dei materiai 2 26 Poitecnico di Torino 1 Obiettivi dea ezione Conoscere
Esame di Stato di Istituto Tecnico Industriale Seconda prova scritta
 Esame di Stato di Istituto Tecnico Industriale Seconda prova scritta L'albero conduttore di un piccolo cambio a due velocità deve trasmettere una potenza di 4kW a 78rad/s. Due ruote dentate cilindriche
Esame di Stato di Istituto Tecnico Industriale Seconda prova scritta L'albero conduttore di un piccolo cambio a due velocità deve trasmettere una potenza di 4kW a 78rad/s. Due ruote dentate cilindriche
Metallurgia e Materiali non Metallici. Prova di trazione. Marco Colombo.
 Metallurgia e Materiali non Metallici Prova di trazione Marco Colombo [email protected] 16/03/2016 La prova di trazione uniassiale Una delle più comuni e importanti prove distruttive, si ricavano
Metallurgia e Materiali non Metallici Prova di trazione Marco Colombo [email protected] 16/03/2016 La prova di trazione uniassiale Una delle più comuni e importanti prove distruttive, si ricavano
TECNOLOGIA DELL ARCHITETTURA 2009/10 PROF. SERGIO RINALDI
 SISTEMI STRUTTURALI PRINCIPALI NELLA STORIA DELL ARCHITETTURA Esiste una stretta relazione tra il sistema strutturale e i materiali scelti per la costruzione sistema a telaio sistema trilitico sistema
SISTEMI STRUTTURALI PRINCIPALI NELLA STORIA DELL ARCHITETTURA Esiste una stretta relazione tra il sistema strutturale e i materiali scelti per la costruzione sistema a telaio sistema trilitico sistema
ESERCIZIO 1. Fig. 1. Si ricava a = m = 14.6 mm. Ricalcolando b per a/w= 14.6/50= 0.29, si ottiene b Procedendo, si ricava:
 ESERCIZIO 1 Una piastra di larghezza totale 100 mm e spessore 5 mm, con cricca centrale passante (fig. 1), è soggetta ad una forza di trazione P50 kn. 1) Determinare le condizioni di cedimento della piastra.
ESERCIZIO 1 Una piastra di larghezza totale 100 mm e spessore 5 mm, con cricca centrale passante (fig. 1), è soggetta ad una forza di trazione P50 kn. 1) Determinare le condizioni di cedimento della piastra.
Tecnologia dei Materiali e Chimica Applicata Soluzione Esercitazione IV Prof. Dott. Bernhard Elsener
 Tecnologia dei Materiali e Chimica Applicata Soluzione Esercitazione IV ESERCIZIO 4.1 E dato il diagramma di stato del sistema Pb-Sn (figura 1). Figura 1 Diagramma di stato Pb-Sn 1. Determinare le fasi
Tecnologia dei Materiali e Chimica Applicata Soluzione Esercitazione IV ESERCIZIO 4.1 E dato il diagramma di stato del sistema Pb-Sn (figura 1). Figura 1 Diagramma di stato Pb-Sn 1. Determinare le fasi
Fatica (HCF): conteggio dei cicli Lecture 5 Conteggio dei cicli
 Fatica Conteggio dei cicli Fatica (HCF): conteggio dei cicli Lecture 5 Conteggio dei cicli Fatica Conteggio dei cicli Introduzione Le strutture reali sono soggette a stati di sollecitazione che variano
Fatica Conteggio dei cicli Fatica (HCF): conteggio dei cicli Lecture 5 Conteggio dei cicli Fatica Conteggio dei cicli Introduzione Le strutture reali sono soggette a stati di sollecitazione che variano
Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009)
 Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009) Quesito: Posso stimare il numero di ore passate a studiare statistica sul voto conseguito all esame? Potrei calcolare il coefficiente di correlazione.
Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009) Quesito: Posso stimare il numero di ore passate a studiare statistica sul voto conseguito all esame? Potrei calcolare il coefficiente di correlazione.
La verifica di resistenza a fatica
 La verifica di resistenza a fatica 1 La verifica di resistenza a fatica Gli elementi delle macchine se soggetti a carichi variabili nel tempo presentano rotture precoci anche per carichi inferiori rispetto
La verifica di resistenza a fatica 1 La verifica di resistenza a fatica Gli elementi delle macchine se soggetti a carichi variabili nel tempo presentano rotture precoci anche per carichi inferiori rispetto
Le proprietà meccaniche
 Antonio Licciulli, Antonio Greco Corso di scienza e ingegneria dei materiali Le proprietà meccaniche Proprietà meccaniche L effetto delle forze è di indurre delle deformazioni nei materiali Le relazioni
Antonio Licciulli, Antonio Greco Corso di scienza e ingegneria dei materiali Le proprietà meccaniche Proprietà meccaniche L effetto delle forze è di indurre delle deformazioni nei materiali Le relazioni
Distribuzione Normale
 Distribuzione Normale istogramma delle frequenze di un insieme di misure di una grandezza che può variare con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata di
Distribuzione Normale istogramma delle frequenze di un insieme di misure di una grandezza che può variare con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata di
TUBI DI POLIETILENE ALTA DENSITA PE 80 SCHEDA TECNICA
 TUBI DI POLIETILENE ALTA DENSITA PE 80 SCHEDA TECNICA Tubi Unidelta di polietilene alta densità PE 80 per fluidi in pressione I tubi Unidelta di polietilene alta densità PE 80, realizzati con materia prima
TUBI DI POLIETILENE ALTA DENSITA PE 80 SCHEDA TECNICA Tubi Unidelta di polietilene alta densità PE 80 per fluidi in pressione I tubi Unidelta di polietilene alta densità PE 80, realizzati con materia prima
UNI EN :2001 (penultima normativa) UNI EN ISO :2009 (ultima normativa: recepimento a livello internazionale della normativa UNI-EN)
 UNI EN 10002-1:2001 (penultima normativa) UNI EN ISO 6892-1:2009 (ultima normativa: recepimento a livello internazionale della normativa UNI-EN) 1 E' la più importante prova meccanica convenzionale. Si
UNI EN 10002-1:2001 (penultima normativa) UNI EN ISO 6892-1:2009 (ultima normativa: recepimento a livello internazionale della normativa UNI-EN) 1 E' la più importante prova meccanica convenzionale. Si
UNIVERSITA DEGLI STUDI DI PADOVA
 UNIVERSITA DEGLI STUDI DI PADOVA Facoltà di Ingegneria Corso di Laurea Magistrale in Ingegneria Civile Ponti metallici ferroviari rivettati Valutazione del danno a fatica e corrosione Metallic riveted
UNIVERSITA DEGLI STUDI DI PADOVA Facoltà di Ingegneria Corso di Laurea Magistrale in Ingegneria Civile Ponti metallici ferroviari rivettati Valutazione del danno a fatica e corrosione Metallic riveted
LA DISTRIBUZIONE NORMALE
 LA DISTRIBUZIONE NORMALE Italo Nofroni Statistica medica - Facoltà di Medicina Sapienza - Roma La più nota ed importante distribuzione di probabilità è, senza alcun dubbio, la Distribuzione normale, anche
LA DISTRIBUZIONE NORMALE Italo Nofroni Statistica medica - Facoltà di Medicina Sapienza - Roma La più nota ed importante distribuzione di probabilità è, senza alcun dubbio, la Distribuzione normale, anche
Fondamenti di Infrastrutture Viarie
 Politecnico di Torino Fondamenti di Infrastrutture Viarie Relazione esercitazioni. Anno Accademico 2011/2012 Corso di Fondamenti di Infrastrutture Viarie Professore: Marco Bassani Esercitatore: Pier Paolo
Politecnico di Torino Fondamenti di Infrastrutture Viarie Relazione esercitazioni. Anno Accademico 2011/2012 Corso di Fondamenti di Infrastrutture Viarie Professore: Marco Bassani Esercitatore: Pier Paolo
Nucleo Fondante Competenze-Conoscenze-Abilità Contenuti Metodi Materiali - Strumenti Raccordi disciplinari
 Nucleo Fondante Competenze-Conoscenze-Abilità Contenuti Metodi Materiali - Strumenti Raccordi disciplinari NUMERI Concetto di insieme e sua rappresentazione Operazioni con gli insiemi Eseguire le quattro
Nucleo Fondante Competenze-Conoscenze-Abilità Contenuti Metodi Materiali - Strumenti Raccordi disciplinari NUMERI Concetto di insieme e sua rappresentazione Operazioni con gli insiemi Eseguire le quattro
ESERCITAZIONI 1 e 2: calcoli
 ESERCITAZIONI 1 e 2: calcoli L uso del foglio elettronico nel laboratorio di ispezione degli alimenti. Funzioni utilizzate negli esercizi e traduzione in inglese americano per l utilizzo su computer con
ESERCITAZIONI 1 e 2: calcoli L uso del foglio elettronico nel laboratorio di ispezione degli alimenti. Funzioni utilizzate negli esercizi e traduzione in inglese americano per l utilizzo su computer con
Obiettivo. Leghe a memoria di forma
 Attuazione con lega a memoria di forma: fondamenti e potenziale applicazione nel settore aeronautico (Progetto SISA) Ing. Pietro Bisci, Dipartimento di Chimica IFM e CoE NIS, Università di Torino Obiettivo
Attuazione con lega a memoria di forma: fondamenti e potenziale applicazione nel settore aeronautico (Progetto SISA) Ing. Pietro Bisci, Dipartimento di Chimica IFM e CoE NIS, Università di Torino Obiettivo
PROPRIETÀ MECCANICHE DEI MATERIALI
 PROPRIETÀ MECCANICHE DEI MATERIALI Il comportamento meccanico di un materiale rappresenta la risposta ad una forza o ad un carico applicato 1. Comportamento elastico 2. Comportamento plastico 3. Comportamento
PROPRIETÀ MECCANICHE DEI MATERIALI Il comportamento meccanico di un materiale rappresenta la risposta ad una forza o ad un carico applicato 1. Comportamento elastico 2. Comportamento plastico 3. Comportamento
Fatica oligociclica (LCF) Lecture 6 Strain controlled fatigue
 Fatica oligociclica (LCF) Lecture 6 Strain controlled fatigue Introduzione La retta di Basquin descrive la relazione tra durata e ampiezza della sollecitazione. A sforzi elevati (basse durate) la retta
Fatica oligociclica (LCF) Lecture 6 Strain controlled fatigue Introduzione La retta di Basquin descrive la relazione tra durata e ampiezza della sollecitazione. A sforzi elevati (basse durate) la retta
Unità 2 Diagrammi di stato e proprietà dei materiali UNITA 2 DIAGRAMMI DI STATO E PROPRIETA DEI MATERIALI
 Esercizio.1 UNITA DIAGRAMMI DI STATO E PROPRIETA DEI MATERIALI Tracciare un diagramma di stato binario in cui sia presente un composto intermedio A x B y a fusione congruente e un composto intermedio A
Esercizio.1 UNITA DIAGRAMMI DI STATO E PROPRIETA DEI MATERIALI Tracciare un diagramma di stato binario in cui sia presente un composto intermedio A x B y a fusione congruente e un composto intermedio A
σ a σ R σ S σ N σ LF Tensione alterna La Curva di Wöhler N Numero di cicli log N Fatica oligociclica
 Fatica oligociclica a Tensione alterna R S N Zona di progettazione a tempo (fatica ad alto numero di cicli) LF La Curva di Wöhler Vita infinita 10 4 N Numero di cicli 10 7 10 8 log N 1 a Fatica oligociclica
Fatica oligociclica a Tensione alterna R S N Zona di progettazione a tempo (fatica ad alto numero di cicli) LF La Curva di Wöhler Vita infinita 10 4 N Numero di cicli 10 7 10 8 log N 1 a Fatica oligociclica
Corso di Biomeccanica
 Corso di Laurea in Ingegneria Biomedica Corso di Biomeccanica Parte 3: prove di trazione F. Auricchio [email protected] http://www.unipv.it/dms/auricchio Università degli Studi di Pavia Dipartimento di
Corso di Laurea in Ingegneria Biomedica Corso di Biomeccanica Parte 3: prove di trazione F. Auricchio [email protected] http://www.unipv.it/dms/auricchio Università degli Studi di Pavia Dipartimento di
Scale di Misurazione Lezione 2
 Last updated April 26, 2016 Scale di Misurazione Lezione 2 G. Bacaro Statistica CdL in Scienze e Tecnologie per l'ambiente e la Natura II anno, II semestre Tipi di Variabili 1 Scale di Misurazione 1. Variabile
Last updated April 26, 2016 Scale di Misurazione Lezione 2 G. Bacaro Statistica CdL in Scienze e Tecnologie per l'ambiente e la Natura II anno, II semestre Tipi di Variabili 1 Scale di Misurazione 1. Variabile
Collegamenti filettati
 Collegamenti filettati Carmine Napoli Si possono dividere i collegamenti filettati in due tipologie: 1. di serraggio (collegamento forzato tra due elementi) 2. viti di manovra ( tornio movimento torretta)
Collegamenti filettati Carmine Napoli Si possono dividere i collegamenti filettati in due tipologie: 1. di serraggio (collegamento forzato tra due elementi) 2. viti di manovra ( tornio movimento torretta)
Cenni di resistenza dei materiali
 Università degli Studi di Bergamo Corso di Laurea in Ingegneria Tessile Corso di Elementi di Meccanica Cenni di resistenza dei materiali Un corpo soggetto a dei carichi presenta modificazioni più o meno
Università degli Studi di Bergamo Corso di Laurea in Ingegneria Tessile Corso di Elementi di Meccanica Cenni di resistenza dei materiali Un corpo soggetto a dei carichi presenta modificazioni più o meno
Valutare le proprietà meccaniche di rivestimenti thermal spray: come e con quali prospettive per le applicazioni
 Valutare le proprietà meccaniche di rivestimenti thermal spray: come e con quali prospettive per le applicazioni Elisabetta. Gariboldi, Nora Lecis Politecnico di Milano Dip. Meccanica Walter Cerri, Paolo
Valutare le proprietà meccaniche di rivestimenti thermal spray: come e con quali prospettive per le applicazioni Elisabetta. Gariboldi, Nora Lecis Politecnico di Milano Dip. Meccanica Walter Cerri, Paolo
