Calcolo di precisione e simulazione Monte Carlo del processo Bhabha
|
|
|
- Beata Anna Maria Benedetti
- 5 anni fa
- Visualizzazioni
Transcript
1 UNIVERSITÀ DEGLI STUDI DI PAVIA FACOLTÀ DI SCIENZE MM. FF. NN. Dipartimento di Fisica Nucleare e Teorica - Corso di Laurea Specialistica in Scienze Fisiche Calcolo di precisione e simulazione Monte Carlo del processo Bhabha Relatore Chiar.mo Prof. Guido Montagna Correlatore Dott. Carlo M. Carloni Calame Tesi di Laurea Specialistica di Giovanni Balossini Anno Accademico 4/5
2
3 Indice Indice iii Introduzione 1 1 Misura di R e luminosità Il rapporto R e suoi metodi di misura Parametri del Modello Standard e rapporto R Determinazione della luminosità e processo Bhabha Correzioni radiative di QED e Parton Shower 11.1 Singolarità collineari e infrarosse Cancellazione infrarossa Vertice di Altarelli-Parisi Equazioni di Altarelli-Parisi Metodi risolutivi e Parton Shower Matching e BABAYAGA Correzioni radiative esatte O (α) Parton Shower e correzioni O (α): il matching Generazione di eventi con BABAYAGA Risultati numerici Indipendenza dal separatore infrarosso Criteri di selezione degli eventi Contributi alla sezione d urto totale Distribuzioni Confronto con calcoli indipendenti Conclusioni 57 A Calcoli 59 A.1 Somma sulle polarizzazioni per il fotone A. Elementi di matrice con correzioni radiative esatte O (α) Bibliografia 63 Ringraziamenti 67
4
5 Introduzione Gran parte della ricerca in fisica delle alte energie degli ultimi anni è stata incentrata sulla validazione del Modello Standard ([1]). Della teoria delle interazioni elettrodeboli con la sua estensione alla Cromodinamica Quantistica (QCD) si ha, ormai, una conoscenza estremamente precisa. Dopo i successi degli anni Ottanta e Novanta, con la scoperta dei bosoni W e Z e del quark top, rimane sostanzialmente ancora un importante obiettivo da raggiungere: l osservazione diretta del bosone di Higgs. Pur avendo informazioni indirette e pur potendo stimare un intervallo di masse plausibili mediante effetti virtuali ad osservabili di precisione, ancora non si hanno prove dirette della sua esistenza, cruciale per la verifica del Modello Standard. Un aiuto a tale ricerca viene dalla valutazione dei valori di massa maggiormente probabili, ma tale modo di procedere è vincolato alla conoscenza del valore il più possibile esatto della costante di accoppiamento elettromagnetica α al picco della Z. La conoscenza dell andamento di α ad alte energie richiede la misura della sezione d urto di produzione di adroni ad energie più basse, tra qualche centinaio di MeV e la decina di GeV. Questa viene effettuata mediante lo studio dei processi di interazione tra positroni ed elettroni e la determinazione del parametro R. Come si mostrerà nel capitolo 1, R è dato dal rapporto tra la sezione d urto del processo e + e in adroni e quella del processo e + e in muoni e l accuratezza nella sua determinazione richiede un attentissima analisi della luminosità degli acceleratori utilizzati, chiamati in gergo flavour factory. Nel seguito sarà spiegato in dettaglio come si rende, dunque, necessario il calcolo di precisione della sezione d urto teorica del processo Bhabha e + e e + e, utilizzato ai fini della valutazione della luminosità. Un ulteriore importante motivazione per lo studio di R è il calcolo di precisione del momento magnetico anomalo del muone a µ. Lo studio di questo parametro potrebbe, infatti, evidenziare limiti di validità del Modello Standard stesso, mostrando, nel confronto tra i valori attesi della teoria e i dati sperimentali, che già sono noti con elevata precisione, effetti riconducibili a nuova fisica ([]). Il presente lavoro è stato realizzato nell ambito delle attività del gruppo di ricerca in fisica teorica delle alte energie del Dipartimento di Fisica Nucleare e Teorica dell Università e della Sezione di Pavia dell Istituto Nazionale di Fisica Nucleare. Si è trattato del prosieguo di un attività pluriennale, che ha visto, nel, la preparazione della prima versione di un generatore di eventi Monte Carlo, BABAYAGA, ormai largamente utilizzato a DAΦNE, CESR, VEPP-M. Questo programma è stato migliorato nel 5 includendo contributi teorici assenti nella versione originale e necessari per raggiungere l accuratezza oggi richiesta. Si è, quindi, reso opportuno validare il nuovo codice per verificare che lo scopo sia stato effettivamente raggiunto. L incertezza del calcolo teorico è, infatti, la principale fonte di errore nella deter-
6 Introduzione. minazione della luminosità, essendo attualmente superiore a quella sperimentale. L obiettivo da raggiungere è quello un errore relativo che si aggiri attorno all 1. Nelle prossime pagine si discuterà delle basi teoriche da cui si è partiti per affrontare il problema e della soluzione che si è proposta, basata essenzialmente sull utilizzo di un algoritmo Monte Carlo, alla cui formulazione si è pervenuti adattando in QED alcuni risultati noti in QCD, le equazioni di Altarelli-Parisi. In particolare, il primo capitolo è dedicato all esposizione delle motivazioni del lavoro. Si partirà dalla definizione formale di R e dall illustrazione dei principali approcci sperimentali adottati per misurare questa quantità, con particolare riferimento alla tecnica del ritorno radiativo, per poi spiegare come da R si possono ottenere informazioni sulla costante di accoppiamento elettromagnetica e sul momento magnetico anomalo del muone. Questo porterà a comprendere la necessità di una valutazione precisa della luminosità e dell utilità del calcolo di precisione del processo Bhabha, la cui sezione d urto in approssimazione di Born è presentata in un ultimo paragrafo. Il secondo capitolo è dedicato alla discussione dei principali risultati della teoria delle correzioni radiative, partendo dalla Bremsstrahlung in approssimazione soffice, per poi passare ad un estesa presentazione delle equazioni di Altarelli-Parisi applicate all elettrodinamica quantistica. La loro risoluzione può essere effettuata con un metodo chiamato Parton Shower che, per le sue caratteristiche di ricorsività, si presta bene ad essere realizzato al calcolatore mediante un algoritmo Monte Carlo. In conclusione sarà, quindi, dedicato ampio spazio a questo sistema e ai suoi vantaggi. Nel capitolo 3 fa la sua apparizione BABAYAGA. Sarà illustrata per prima la sua versione originale, anche se l oggetto di analisi del presente lavoro è stata, come già detto, una versione migliorata del programma. Questa in più comprende i risultati O (α) esatti, noti in letteratura, che precedentemente non erano considerati. Sarà quindi mostrato il metodo originale seguito per includere gli elementi di matrice del processo Bhabha a questo ordine nel Parton Shower. Il quarto ed ultimo capitolo è dedicato ai risultati numerici. Si è fatton ampio uso delle risorse informatiche messe a disposizione dalla Sezione INFN e dal Dipartimento, in particolare del cluster Beowulf. La flessibilità di BABAYAGA è stata sfruttata per calcolare la sezione d urto in quattro configurazioni dei dati in ingresso, scelte in modo tale da ricondursi alle condizioni sperimentali tipiche delle flavour factory per la misura della luminosità. La simulazione del processo Bhabha si è effettuata con diversi gradi di approssimazione, allo scopo di valutare la gerarchia dei vari contributi che la compongono e determinare la loro incidenza relativa. Questa operazione ha avuto lo scopo di stimare il livello di accuratezza raggiunto dal generatore di eventi e confrontarlo con quello richiesto.
7 Capitolo 1 Misura di R e luminosità Questo primo capitolo è dedicato alla definizione del rapporto R e all illustrazione dei principali metodi sperimentali oggi utilizzati per la sua misura. Verranno, quindi, mostrati i principali parametri del Modello Standard calcolabili per mezzo di questa quantità. In ultimo sarà spiegata l importanza di una valutazione precisa della luminosità, come conseguenza di quanto esposto precedentemente, e sarà sviluppato il calcolo esplicito della sezione d urto Born del processo Bhabha. 1.1 Il rapporto R e suoi metodi di misura Uno degli obiettivi dell attuale ricerca in fisica delle alte energie è la determinazione del rapporto: (1.1) R (s) σ e + e adroni (s) σ e + e µ + µ (s). Le motivazioni per cui tale quantità riveste particolare importanza sono brevemente illustrate nel paragrafo 1.. In questo paragrafo, invece, si intende dare un idea dei metodi utilizzati per valutare sperimentalmente σ e + e adroni. Gli acceleratori utilizzati vengono usualmente chiamati flavour factory perché vi si producono con elevata statistica stati legati di quark u, d, c, s e b. Le energie tipiche per queste macchine sono approssimativamente comprese tra.5 GeV e 1 GeV e le strategie sperimentali utilizzate possono essere grosso modo classificate in due tipologie. Alcuni acceleratori lavorano ad un energia nel centro di massa prefissata e praticano una misura diretta di R da quei processi che prevedono nello stato finale solamente adroni. A BEPC (Pechino, Cina), CESR (Cornell University, Ithaca, USA), VEPP-M (Novosibirsk, Russia), la sezione d urto σ e + e adroni viene misurata mediante la tecnica dell energy scan. Un altro e differente sistema è utilizzato a DAΦNE, presso i Laboratori Nazionali di Frascati dell INFN, che opera ad un energia nel centro di massa di circa 1. GeV. L esperimento attualmente operativo è KLOE (figura 1.1), il cui( detector è formato ) σp sostanzialmente da una camera di deriva ad alta risoluzione p.4% e da un calorimetro elettromagnetico con risoluzione σ E 5.7% E =. L analisi viene E( GeV) effettuata su quegli eventi in cui gli adroni (π + π ) vengono emessi con angolo polare ϑ π compreso tra 5 e 13 gradi ([3]).
8 4 Capitolo 1. Misura di R e luminosità Figura 1.1: Esperimento KLOE presso DAΦNE ( e γ e e + (a) e γ γ γ e + γ (b) ISR e + (c) FSR Figura 1.: Diagrammi di Feynman del processo e + e adroni con contributi radiativi di stato iniziale (1.(b)) e di stato iniziale (1.(c)). A DAΦNE, ma anche alle b-factory, come PEP-II (SLAC, Stanford University, USA) e KEK-B (Giappone), si procede con il metodo del ritorno radiativo ([4, 5]), in cui non si prendono in considerazione solo i processi di figura 1.(a), ma anche tutti quelli in cui vi è emissione di fotone. Questi, in particolare, sono di due tipi: vi può essere radiazione dagli stati iniziali (ISR, figura 1.(b)), oppure dagli stati finali (FSR, figura 1.(c)), ma solo la prima è di interesse, perché il suo contributo è dominante. Il vantaggio insito nell osservare una classe più ampia di eventi sta nel fatto che, mentre la macchina opera ad un energia nel centro di massa e + e prefissata, l emissione di fotoni riduce la massa invariante del sistema adronico. In questo modo è possibile ampliare lo studio alle risonanze diverse da quella nominale dell acceleratore (la Φ nel caso di DAΦNE), aventi s inferiore (si veda a tal proposito figura 1.3). Accorgimenti particolari vanno, poi, utilizzati in fase di analisi dei dati per estrarre dalla sezione d urto σ e + e adroni+γ quella di effettivo interesse
9 1.. Parametri del Modello Standard e rapporto R 5 σ e + e adroni. Queste sono, in generale, legate dalla relazione ([6]): s dσ e + e adroni+γ ds = H (s) σ e + e adroni, dove s è il quadrato della massa invariante del sistema adronico e H (s) è il radiatore che descrive l emissione di fotoni. 7 ρ,ω,φ Ψ s Υ s Burkhardt, Pietrzyk Rhad % s in GeV Bacci et al. Cosme et al. PLUTO CESR, DORIS MARK I CRYSTAL BALL MD-1 VEPP-4 VEPP-M ND DM BES 1999 BES 1 CMD- 4 KLOE 5 15% 5.9% 6% 1.4% rel. err. cont. Figura 1.3: Spettro di R con risonanze (da [7]). 1. Parametri del Modello Standard e rapporto R Uno dei più importanti parametri del Modello Standard è la costante di accoppiamento elettromagnetica che, alla scala s, è data dalla costante di struttura fine risommata: α α (s) = 1 α (s),
10 6 Capitolo 1. Misura di R e luminosità dove (1.) α (s) = Π γ (s) Π γ (), con Π γ (s) funzione di polarizzazione del vuoto o self-energia del fotone. In teoria delle perturbazioni la (1.) si scrive: f (1.3) α (s) = f = α 3π f = f ( Q f N cf ln = α l + α (5) quark + α top s m 5 ) = f 3 q q Figura 1.4: Polarizzazione del vuoto in quark. La (1.3), tuttavia, presenta un problema. Infatti, mentre la determinazione dei contributi α l e α top non presenta particolari problemi (per i dettagli si vedano [8, 9, 1]), i contributi di figura 1.4 non sono calcolabili, perché la Cromodinamica Quantistica non è affidabile a basse energie, dunque le masse dei quark leggeri non sono ben definite. Il problema si risolve facendo uso della relazione di dispersione: Dal teorema ottico si ha: Re [ Π γ (s) Π γ () ] = s π Re ds Im Π γ (s ) s s (s s iɛ). Im Π γ (s) = s e σ e + e adroni (s). Facendo uso della (1.1) e ricordando che, a livello albero, σ e + e µ + 4πα µ (s) = 3s, in definitiva si ha: α (5) quark (s) α(5) adroni (s) = αs 3π Re 4m π ds R (s ) s (s s iɛ). Il momento magnetico anomalo del muone a µ è un altra quantità che si può calcolare in termini di R (s). Analogamente al caso della costante di accoppiamento, i contributi derivanti dalla creazione e dal successivo riassorbimento di particelle fortemente interagenti (vedi figura 1.5) non possono essere calcolati con l aiuto della cromodinamica quantistica perturbativa. Si può, tuttavia, usare ancora la relazione di dispersione: a adroni µ = ( αmµ ) ds R (s) ˆK (s) 3π 4m π s,
11 1.3. Determinazione della luminosità e processo Bhabha 7 γ µ µ Figura 1.5: Contributo da particelle fortemente interagenti al momento magnetico anomalo del muone. dove il kernel ˆK (s) è una funzione limitata e monotòna crescente tra.63 alla soglia s = 4m π e 1 per s. Risulta, così, evidente l importanza di una determinazione sperimentale il più possibile precisa del rapporto definito dalla (1.1), in quanto sta alla base di alcune tra le più importanti verifiche del Modello Standard elettrodebole. 1.3 Determinazione della luminosità e processo Bhabha La luminosità (o normalizzazione) L dell apparato sperimentale è il coefficiente che lega il numero N di eventi osservati alla sezione d urto σ del processo studiato: (1.4) N = Lσ. Il linea di massima questo parametro può essere calcolato conoscendo le caratteristiche della macchina acceleratrice e dei rivelatori; tuttavia, procedendo in questo modo, si giunge ad un risultato piuttosto impreciso. Le misure sperimentali più precise richiedono, invece, di conoscere la luminosità con un errore dell ordine dello.1% o inferiore. Alternativamente è possibile procedere invertendo la (1.4) e sostituendo a σ (sperimentale) la sezione d urto teorica di un processo ben conosciuto e sperimentalmente misurabile con elevata accuratezza: L = N σ teor.. Particolarmente adatto a questo scopo risulta essere il Bhabha scattering ([11]), studiato grandi angoli, e non a piccoli come veniva fatto a LEP, sia per motivi legati alla realizzazione sperimentale, sia grazie alla trascurabilità dei processi deboli a bassa energia. La sua sezione d urto teorica risulta, poi, essere ben quantificabile, nonché elevata, alle energie tipiche delle flavour factory. Occorre anche ricordare che elettroni e positroni sono particelle facilmente rilevabili. Si indica con Bhabha scattering il processo di diffusione elastica e + e e + e. All elemento di matrice M contribuiscono i diagrammi di figura 1.6(a) e di figura 1.6(b): M = M a + M b.
12 8 Capitolo 1. Misura di R e luminosità e + e + p 1 r 1 µ q 1 s 1 e e q p 1 q 1 p r p 1 r 1 q p 1 + p q s µ ν q 1 s 1 p r ν q s e + (a) Canale s. e + e (b) Canale t. e Figura 1.6: Diagrammi di Feynman del processo Bhabha. Applicando le regole di Feynman si ottiene: (1.5a) M a = per il processo in canale s, e ie (p 1 + p ) ū (q, s ) γ µ v (q 1, s 1 ) v (p 1, r 1 ) γ µ u (p, r ), (1.5b) M b = ie (p 1 q 1 ) ū (q, s ) γ µ u (p, r ) v (p 1, r 1 ) γ µ v (q 1, s 1 ), per il processo in canale t. Il modulo quadro di M, mediato sulle polarizzazioni degli stati iniziali e sommato su quelle degli stati finali, ha la forma: M 1 4 r 1, r, s 1, s M = M a + M b + M ab + M ab dove si è definito M ab 1 4 r 1, r, s 1, s M a M b. Utilizzando la (1.5a), la (1.5b) e ricordando le relazioni di completezza per le soluzioni dell equazione di Dirac si ha immediatamente: (1.6a) M a = 1 e 4 ( 4 (p 1 + p ) 4 Tr π α m e 4 t + u s, (1.6b) M b = 1 e 4 ( 4 (p 1 q 1 ) 4 Tr π α m e 4 u + s t, γ ν /p 1 m e γ µ /p + m e m e m e γ ν /p 1 m e γ µ /q 1 m e m e m e ) ( Tr ) ( Tr, /q 1 + m e /q m e γ ν γ µ m e m e /q + m e /p + m e γ ν γ µ m e m e ) )
13 1.3. Determinazione della luminosità e processo Bhabha 9 dove nell ultimo passaggio di entrambe le equazioni ci si è posti nel limite ultrarelativistico per trascurare le masse al numeratore, e (1.6c) M ab = 1 4 = 1 4 e 4 ( (p 1 + p ) (p 1 q 1 ) Tr /q + m e m e ( /q + m e e 4 (p 1 + p ) (p 1 q 1 ) Tr m e γ µ /q 1 m e m e γ µ /p + m e m e γ ν /p 1 m e m e γ ν /p 1 m e m e γ µ /p ) + m e γ ν = m e ) γ µ /q 1 m e γ ν m e Il calcolo esplicito della (1.6c) si può semplificare se si utilizzano le identità di contrazione per le matrici γ. Il risultato finale è: M ab π α m e 4 La sezione d urto differenziale nel centro di massa per il Bhabha scattering ha, dunque, la forma: ( dσ (1.7) dω = α t + u 8E s + u + s ) t + u. ts Si fissi, ora, la cinematica: p 1 = (E,,, E) p = (E,,, E) u ts q 1 = (E,, E sin ϑ, E cos ϑ) q = (E,, E sin ϑ, E cos ϑ). Di conseguenza gli invarianti cinematici di Mandelstam sono: s = 4E t = E (1 cos ϑ) u = E (1 + cos ϑ) e la (1.7) si riscrive: (1.8) dσ dω = α 8E 1 + cos ϑ } {{ } s + cos4 ϑ + 1 sin 4 ϑ } {{ } t cos4 ϑ sin 4 ϑ } {{ } st. Dalla (1.8) risulta evidente che a piccoli angoli di diffusione (ϑ ) il termine t relativo allo scambio di un fotone tra positrone ed elettrone è dominante su quello di annichilazione s e su quello di interferenza tra i due diagrammi st (vedi figura 1.7). Questo fatto si riflette in un comportamento divergente per la sezione d urto nel limite ϑ. Vale la pena notare che per energie nel centro di massa dell ordine di 1 GeV, tipiche delle cosiddette B-factories, gli effetti di natura debole sulla sezione d urto Bhabha dovuti allo scambio di un bosone Z non sono trascurabili alla scala dello.1% e vanno, pertanto, tenuti in considerazione. Il contributo dominante in questi casi è dato dall interferenza [ Z (s), γ (t) ] tra il diagramma di Feynman corrispondente allo scambio di uno Z in canale s e quello di scambio di un fotone in canale t..
14 1 Capitolo 1. Misura di R e luminosità dσ dω (nb/gradi) dσ dω tot ṡ t st ϑ (gradi) Figura 1.7: Contributi s, t e st alla sezione d urto differenziale del processo Bhabha. 1 1 σ (nb) s (GeV) Figura 1.8: Andamento della sezione d urto Bhabha totale (integrata su angoli di diffusione compresi tra 55 e 15 gradi) in funzione dell energia nel centro di massa.
15 Capitolo Correzioni radiative di QED e Parton Shower In questo capitolo verranno presentati gli aspetti teorici delle correzioni radiative di QED alla teoria perturbativa. In primo luogo si procederà con lo studio di un processo di annichilazione fermionica con emissione di un fotone reale dagli stati iniziali. Si mostrerà, in particolare, l insorgenza del problema della divergenza infrarossa e il metodo per cancellarla. In seguito, dopo aver illustrato la possibilità di operare una particolare fattorizzazione della sezione d urto, si introdurrà un approccio alternativo alle correzioni radiative dominanti che, partendo da una cinematica approssimata, porterà a scrivere delle equazioni integro-differenziali per la cosiddetta funzione di struttura dell elettrone (equazioni di Altarelli-Parisi). In ultimo si presenteranno le principali tecniche risolutive per questa equazione, concentrandosi, in particolare, su quella denominata Parton Shower e basata sul metodo Monte Carlo..1 Singolarità collineari e infrarosse Un tipico esempio di correzione radiativa è quello in cui, in un generico processo di annichilazione e + e γ l + l preso all ordine più basso di approssimazione, si considera anche l emissione di fotoni dagli stati iniziali, la cosiddetta Bremsstrahlung 1. I diagrammi di Feynman che contribuisicono alla sezione d urto sono quelli in figura.1. e γ l e l p σ p k p + k ν µ q q q + σ p ν k p + q µ q q + e + l + e + p +k γ l + Figura.1: Diagrammi di Bremsstrahlung. 1 Dal tedesco: Bremse (freno) + Strahlung (radiazione). Letteralmente: radiazione di frenamento
16 1 Capitolo. Correzioni radiative di QED e Parton Shower L elemento di matrice M B risulta, dunque, uguale alla somma dei due contributi: ( M (1) = ū (q ) ( ieγ µ ) v (q + ) i g ) νµ q v (p + ) ( ieγ ν ) ( i /p /k + m ) ( ieγ σ ) u (p ) ε σ (k) = p k = i ( ie)3 q ū (q ) γ µ /p v (q + ) v (p + ) γ /k + m µ p k γσ u (p ) ε σ (k) e M () = i ( ie)3 q ū (q ) γ µ v (q + ) v (p + ) γ σ /p + + /k + m γ µ u (p ) ε σ (k). p + k Si ha, quindi: M B = M (1) + M () = i ( ie)3 q ū (q ) γ µ v (q + ) v (p + ) [ γ µ /p /k + m p k γσ + γ σ /p + + /k + m ] γ µ u (p ) ε σ (k). p + k Si considerino, ora, separatamente gli addendi del termine tra parentesi quadre e si sviluppino: e p ρ /p p k γσ u (p ) ε σ (k) = p k γρ γ σ u (p ) ε σ (k) = 1 = p k (gρσ γ σ γ ρ ) p ρ u (p ) ε σ (k) = = 1 p k (ε (k) p ) u (p ) = = ε (k) p p k u (p ) p + ρ v (p + ) γ σ /p + p + k ε σ (k) = v (p + ) γ σ γ ρ p + k = p + ρ = v (p + ) (g σρ γ ρ γ σ ) p + k ε σ (k) = = v (p + ) (ε (k) p + ) = v (p + ) ε (k) p + p + k. 1 p + k = In entrambi i casi si è fatto uso dell equazione di Dirac, considerando anche che ci si pone nel limite ultrarelativistico per cui le masse degli elettroni sono trascurabili. Si
17 .1. Singolarità collineari e infrarosse 13 ottiene, infine: (.1) M B = M (1) + M () = i ( ie)3 q ū (q ) γ µ v (q + ) v (p + ) γ µ u (p ) [ ε (k) p + ε (k) p ] + = p k p + k = M eε µ (k) [ p µ p k + p ] µ +, p + k }{{} j µ (k) dove M è l elemento di matrice del processo al livello di Born. Nella (.1) si è definita la corrente iconale j µ (k), che soddisfa la relazione: [ k µ j µ (k) = k p p k + k p ] + =. p + k Passando dallo spazio dei momenti a quello delle posizioni con una trasformata di Fourier si verifica, così, che la corrente iconale è conservata: µ j µ (x) =. I diagrammi di figura.1 costituiscono, dunque, un sottoinsieme gauge-invariante dell intero insieme dei diagrammi di correzione radiativa. Il modulo quadro dell elemento di matrice è: M B = M e ε µ (k) j µ (k) ε ν (k) j ν (k). Per sommare sulle polarizzazioni si possono utilizzare le relazioni di completezza: ε µ (k, λ) ε ν (k, λ) = g µν, λ=1, giungendo, quindi, a scrivere: (.) M B = M e j µ (k) j µ (k) = = M [ m e (p k) + m ] e (p + k) p p +. (p k) (p + k) La sezione d urto differenziale si ricava inserendo la (.) nell espressione: dσ = (π) 4 δ (4) (q + + q + k p + p + ) d3 q + E + (π) 3 d 3 q E (π) 3 d 3 k E γ (π) 3 M B 4p + p (per sapere come si giunge a questa relazione si veda [1]), da cui discende: ( ) [ dσ dσ = e p p + dω (p k) (p + k) m e (p k) m ] e d 3 k (p + k) E γ (π) 3 = (.3) ( ) [ dσ α p p + = dω π (p k) (p + k) m e (p k) m ] e (p + k) E γ de γ d cos ϑ γ,
18 14 Capitolo. Correzioni radiative di QED e Parton Shower dove si è utilizzato: d 3 k = E γ de γ d cos ϑ γ dφ γ. e si è integrato su dφ γ. In altre parole, l approssimazione di Born viene corretta da un opportuno coefficiente al prim ordine in α. Per studiare la cinematica del processo è opportuno fissare: p = (E,,, βe) p + = (E,,, βe) k = ( ) E γ, E γ sin ϑ γ cos φ γ, E γ sin ϑ γ sin φ γ, E γ cos ϑ γ, con β e ( 1 me ) 1 E. I prodotti scalari di interesse sono: p + p = E + E p + p = E + β E = E ( 1 + β ) E, p k = EE γ βee γ cos ϑ γ = EE γ ( 1 β cos ϑγ ) p + k = EE γ + βee γ cos ϑ γ = EE γ ( 1 + β cos ϑγ ) Sostituendo questi risultati nella (.3) si giunge a: d ( ) [ σ dσ α 1 4 ( ) ( )+ de γ d cos ϑ γ dω π E γ 1 + β cos ϑγ 1 β cos ϑγ (.5) ] 1 β 1 β ( ) ( ). 1 β cos ϑγ 1 + β cos ϑγ Per β = 1 (cioè per fermioni carichi a massa nulla) la sezione d urto differenziale diverge per ϑ γ = o per ϑ γ = π. Questa divergenza è, pertanto, detta collineare. Per β 1 non c è una vera e propria divergenza, ma la sezione d urto differenziale cresce comunque all approssimarsi di ϑ γ a e a π. Un altra singolarità (non integrabile) è quella che si ha per E γ =, viene detta infrarossa e per la sua trattazione si rimanda al paragrafo successivo. Per procedere all integrazione della (.5) su ϑ γ si calcoli innanzi tutto (c cos ϑ γ ): +1 1 Gli altri integrali sono: 1 dc (1 βc) (1 + βc) = dc 1 βc + 1 = 1 [ln (1 βc)]+1 β = 1 β ln ( ) 1 + β 1 β ). = 1 β ln ( 1 + β 1 β 1 dc (1 βc) = ± 1 [ 1 β 1 βc dc 1 + βc = [ln (1 + βc)]+1 β 1 ( ) 1 β β ln = 1 + β ] +1 1 = 1 β. 1 =
19 .. Cancellazione infrarossa 15 Si sviluppi, poi: β = (1 m e E ) m e E Effettuando le sostituzioni, valide nel limite ultrarelativistico β 1, si ha: (.6) dσ α 1 = σ (L 1), de γ π E γ dove L ln s m e è detto logaritmo collineare.. Cancellazione infrarossa Come si accennava nel paragrafo precedente, la divergenza infrarossa nella (.6) non è integrabile sullo spettro dell energia. Infatti: σ B (s) E de γ dσ de γ [ ln E γ ] E. Il problema è aggirabile a patto di dare una definizione fenomenologicamente corretta di evento elastico. Questo, infatti, nella realtà non è dato soltanto dal processo e + e γ l + l all ordine più basso, ma anche da quei processi (detti di Bremsstrahlung elastica) per cui l energia dei fotoni emessi si trova ad essere inferiore alla risoluzione (finita) dell apparato sperimentale (fotoni sotto-soglia). In altre parole vanno considerati tutti i processi del tipo e + e l + l + (γ) con E γ < E, dove E è l energia minima rilevabile. In termini di sezione d urto: σ elast. (s) = σ (s) + σ B ( s; Eγ < E ). L integrazione della (.6) può avvenire, quindi, tra un opportuno cut-off λ, che verrà poi fatto tendere a zero al termine dei calcoli, e E. Risulta, dunque: σ B (L 1) ln E λ Se, ora, si considera che i diagrammi con emissione di un fotone virtuale di figura. contribuiscono allo stesso ordine della Bremsstrahlung elastica, si può eliminare il parametro λ. Si ha, infatti: e, di conseguenza: σ virt. (s) (L 1) ln E λ ( σ elast. (s) = σ (s) + σ B s; Eγ < E ) + σ virt. (s) = ( = σ (s) 1 + α ) E (L 1) ln. π E
20 16 Capitolo. Correzioni radiative di QED e Parton Shower e p l e p k q l q k q + q + e + p + e l + e + q p + l l + p q + e + p + k l + Figura.: Inserimento di fotoni virtuali nell annichilazione e + e. ln E E viene detto logaritmo infrarosso. Il procedimento di cancellazione infrarossa non si applica solo al prim ordine nella teoria delle perturbazioni. Si può, infatti, dimostrare che, in ogni teoria di gauge con bosoni di campo non massivi, le probabilità di transizione non presentano divergenze collineari o infrarosse, a patto che si sommino tutti gli stati iniziali e finali degeneri. Quanto fatto più sopra si estende infatti ad n fotoni reali emessi, con n arbitrario. Ne segue l espressione della sezione d urto esponenziata nella forma: (.7) σ ( ) (s) = σ (s) n=.3 Vertice di Altarelli-Parisi ( ) 1 α E n ( ) α E π (L 1) (L 1) ln = σ (s). n! π E E Nei precedenti paragrafi ci si è posti nell approssimazione (piuttosto restrittiva) di fotone estremamente soffice, cioè con tutte le componenti di k tendenti a. Ora si vuole rilassare questa condizione, mostrando che la sezione d urto di un processo con emissione di fotone, come quello in figura.3(a), è ancora fattorizzabile se si considera piccola solo la componente trasversa k di k, ferma restando la trascurabilità rispetto al quadrimpulso dell elettrone ([13, 14]). Indicando con M l elemento di matrice dell intero processo e con M 1 e M quelli dei due sottoprocessi di figura.3(b) e.3(c) rispettivamente si vuole dimostrare che: (.8) 1 1 N X ( M 1 k p q σ 1, σ, ρ 1, ρ ) [ 1 s, σ 1, σ M 1 ] [ 1 dove N X è la molteplicità degli spin dello stato iniziale X. Si ha: M 1 = ū (q, s) ( ieγ µ ) u (p, σ 1 ) ε µ (k, σ ), da cui segue come al solito: 1 1 N X s, σ 1, σ M 1 = e Tr (γµ /pγ ν /q) σ ε µ (k, σ ) ε ν (k, σ ). s, ρ 1, ρ M ],
21 .3. Vertice di Altarelli-Parisi 17 e γ p σ 1 k σ q s q 1 ρ 1 X q ρ (a) Y γ e k σ q s e p σ 1 q ρ Y q s q 1 ρ 1 (b) e X (c) Figura.3: Generico processo con emissione di fotone e suoi sottoprocessi fattorizzati.
22 18 Capitolo. Correzioni radiative di QED e Parton Shower Il calcolo della traccia: (.9) Tr (γ µ /pγ ν /q) = 4 [q µ p ν g µν (p q) + q ν p µ ] e la relazione di completezza, valida per un fotone reale (n = (1,,, )) (si veda l Appendice A.1): σ ε µ (k, σ ) ε ν (k, σ ) = g µν 1 k [k µk ν k (k µ n ν + k ν n µ )], dove si è sommato sulle sole polarizzazioni trasversali e si è posto k k n, permettono di arrivare a scrivere: (.1) 1 s, σ 1, σ M 1 = 4 e [qµ p ν g µν (p q) + q ν p µ ] { g µν 1 = 4 e } k [k µk ν k (k µ n ν + k ν n µ )] = { (p q) 1 k {(p k) (q k) k [(q k) p + + (p k) q ]} + 4 (p q) + 1 k { k (p q) k [(p q) k + + (p q) k ] } (p q) 1 k {(p k) (q k) k [(p k) q + } + (q k) p ]} = = 4 e k [(q k) p + (p k) q ] con p p n e q q n. Per il diagramma di figura.3(c), invece, si scrive genericamente: Si calcoli, ora: M = Γ (q 1, ρ 1 ; q, ρ ) u (q, s). M = Γ (q 1, ρ 1 ; q, ρ ) i (/q + m e) q m ( ieγµ ) u (p, σ 1 ) ε µ (k, σ ) e k p Γ (q 1, ρ 1 ; q, ρ ) i (/p + m e) k p p ( ieγ µ ) u (p, σ 1 ) ε µ (k, σ ) = = e p Γ (q 1, ρ 1 ; q, ρ ) p µ u (p, σ 1 ) ε µ (k, σ ), dove, nell ultimo passaggio, si sono sfruttati il commutatore delle γ e l equazione di Dirac. Se, ancora una volta, si approssima q con p, si, ha Γ (q 1, ρ 1 ; q, ρ ) u (p, σ 1 ) Γ (q 1, ρ 1 ; q, ρ ) u (q, s) = k p σ 1, ρ 1, ρ s, ρ 1, ρ 1 = M, s, ρ 1, ρ 1
23 .3. Vertice di Altarelli-Parisi 19 dunque: 1 1 N X ( ) [ M 1 1 k p q σ 1, σ, ρ 1, ρ 1 N X ] M s, ρ 1, ρ ] [4e σ p µ ε µ (k, σ ) ε ν (k, σ ) p ν. Se si osserva che, adottando la solita approssimazione q p nella (.9), si ha: 4p µ p ν 1 k p Tr (γµ /pγ ν /q), allora la (.8) è immediatamente dimostrata. Utilizzando questo risultato si può passare al calcolo della sezione d urto del processo e + X γ + Y, che ha la forma generale: 1 (.11) σ = (1 + v X ) p q 1 d 3 k 1 (π) 3 k dπ Y ( 1 q ) M1 M, dove v X è la velocità della particella relativamente al centro di massa e dπ X è l elemento di spazio delle fasi delle particelle di stato finale Y. In approssimazione ultra-relativistica si può assumere la seguente cinematica: p = (E,,, E) k = (ze, k,, ze k ) (.1) q = p k = Il fotone deve essere quasi on-shell, quindi: e, con questa approssimazione: ze ( (1 z) E, k,, (1 z) E k = z E k z E + k k 4 4z E O(k ) k 3 = [ ( ze k O(k ) ze ) ] 1 O(k ) ( z E k ) 1 = ) 1 = ze (1 k z E (1 O(k ) ze k ) z E O(k ) ) k. (1 z) E
24 Capitolo. Correzioni radiative di QED e Parton Shower Di conseguenza: e Tenendo, inoltre, conto che q 3 O(k ) (1 z) E k ze q O(k ) k z. d 3 k = dzeπd k la (.11) si riscrive: dzπdk z (1 z) σ = 16π 4 M 1 1 dπ Y M = k (1 + v X ) p q 1 (.13) dzπdk z (1 z) = 16π 4 M 1 σ, k dove con σ si è indicata la sezione d urto del processo di figura.3(c). Dalla cinematica (.1) discendono i prodotti scalari: e Inoltre: q k = k + zk O(k ) k + p k = k z, (1 z) + (1 z) k z zk (1 z) + (1 z) k z + O ( k 4 ) O(k ) p n = E p, q n = (1 z) E q, k n = ze k. Questi risultati si possono sostituire nella (.1), ottenendo: M 1 = 4 [(k e + zk z (1 z) + (1 z) k ) + k z z e = z (1 z) k z (1 z) + z + (1 z) (.14) = z = 8πα k 1 + (1 z). z (1 z) z con Si ha: d 3 k = d k dk 3, dk 3 dze. ] (1 z) = a meno di termini proporzionali a k, trascurabili per via della successiva moltiplicazione per d k. Rimane da calcolare: dove si è sfruttato il fatto che dk = k dk. d k = k dk dφ = πk dk = = π 1 dk = πdk,
25 .4. Equazioni di Altarelli-Parisi 1 Si giunge, infine, a calcolare la sezione d urto per l intero processo di figura.3(a) se si sostituisce la (.14) nella (.13): dzdk 1 + (1 z) σ = σ = π z = dx dk α 1 + x k π 1 x σ, con x 1 z frazione di momento rimanente all elettrone. Si definisce vertice di Altarelli-Parisi: P e e +γ (x) α 1 + x π 1 x, divergente per x 1, in accordo con la divergenza infrarossa. Per comprenderne il significato fisico è opportuno notare che, utilizzando l espressione approssimata per q, si ha q = k + O ( 4 k ) k z O(k ) z, dunque: dk k = dq q. Da quanto illustrato fino ad ora risulta, quindi, abbastanza evidente che α 1 + x dq π 1 x q rappresenta la probabilità che l elettrone emetta un fotone conservando una frazione x di energia e variando la propria virtualità di dq..4 Equazioni di Altarelli-Parisi Per quanto visto fino ad ora è lecito pensare che un elettrone (o un positrone) coinvolto in un processo di scattering risenta del campo delle altre particelle cariche ed emetta radiazione per Bremsstrahlung, risultando, quindi, accompagnato da uno sciame di fotoni. Di conseguenza, si può considerare la densità di probabilità di trovare all interno di questo sciame, ovvero dentro all elettrone originario, un elettrone avente una frazione x del quadrimpulso totale, alla scala di virtualità s. Tale densità di probabilità è descritta dalla funzione di struttura D (x, s), soluzione di un equazione differenziale che ne descrive l evoluzione al variare di s ([15, 16, 17, 18, 19, ]). Per ricavare questa equazione, si cominci con il notare che la probabilità differenziale D (x, s + ds) di trovare nello sciame un elettrone con una frazione x del momento orginario e con virtualità s + ds è data dalla somma della probabilità che l elettrone vari la propria virtualità di ds lasciando x inalterata e di quella che, al contrario, lo faccia irraggiando un fotone. In quest ultimo caso si ha x = zy, dove 1 z è la frazione di quadrimpulso del fotone emesso, rispetto a quello dell elettrone prima dell irraggiamento. Si possono, quindi, sfruttare i risultati acquisiti nel paragrafo precedente e osservare che la probabilità di emissione di un fotone con variazione di virtualità ds è: α ds x+ dzp (z), π s
26 Capitolo. Correzioni radiative di QED e Parton Shower con x + 1 per dare un senso all integrale nonostante la singolarità (infrarossa) del vertice di Altarelli-Parisi in z = 1. La probabilità di non emissione è, di conseguenza: (.15) 1 α π ds s x+ dzp (z). Osservando che δ (zy x) = 1 z δ ( y x ) z impone la condizione x = zy, valida per il caso di emissione di un fotone, si scrive: ( D (x, s + ds) = 1 α ds x+ ) dzp (z) D (x, s) + π s 1 + α ds dy π s x ( = 1 α ds π s x+ x+ + + α ds π s ( = 1 α ds π s + α π ds s x+ x+ dzp (z) D (y, s) δ (zy x) = ) dzp (z) D (x, s) + x+ dyθ (y x) θ (1 y) ) dzp (z) D (x, s) + dz z P (z) D ( x z, s ) θ Portando D (x, s) al primo membro e dividendo per ds s s D (x, s) = α π + α π = α π + α π x+ x+ x+ x+ dzp (z) D (x, s) + dz ( x ) z P (z) D z, s dzp (z) dzp (z) D (y, s) δ (zy x) = ( x ) ( z x θ 1 x ). z s si ottiene: ( x ) ( θ z x θ 1 x ) = z [ ( x ) ( x ) ( D z, s θ z x θ 1 x )] z dz ( x ) ( x ) ( z P (z) D z, s θ z x θ 1 x ), z z=1 + dove nell ultimo passaggio si sono sfruttate le proprietà della distribuzione θ. Si definisca, ora, il vertice di Altarelli-Parisi regolarizzato P + (z) come quella distribuzione che soddisfa a (.16) 1 dzp + (z) f (z) = 1 dzp (z) [f (z) f (1)] per ogni generica test-funzione f (z). Sfruttando nuovamente le proprietà della θ, si giunge, infine, all equazione di Altarelli-Parisi ([1,, 3]): (.17) s s D (x, s) = α 1 dz ( x ) π z P + (z) D z, s, x dove si è potuto eseguire il limite x + 1 perché la (.16) garantisce l esistenza dell integrale al secondo membro della (.17). Si può, poi, verificare che l espressione analitica (.18) P + (z) = P (z) δ (1 z) soddisfa alla (.16). 1 dtp (t)
27 .5. Metodi risolutivi e Parton Shower 3.5 Metodi risolutivi e Parton Shower Esistono vari metodi risolutivi per l equazione di Altarelli-Parisi, alcuni analitici ed altri numerici. Si può, ad esempio, ricordare brevemenete l utilizzo della trasformata di Mellin di una generica funzione f (x) (.19a) F (n) = e della sua inversa (.19b) f (x) = 1 c+i c i dxx n 1 f (x) dn πi x n F (n). Applicando la (.19a) alla (.17) si ottiene l equazione: s s D (n, s) = α π D (n, s) P + (n), la cui soluzione, con la condizione iniziale: D ( n, m ) ( ( e = 1 D x, ) me = δ (1 x) ) è: (.) D (n, s) = exp [ α π P + (n) ln s ] [ η ] = exp m e 4 P + (n), dove si è posto η = α π L e la trasformata del vertice di Altarelli-Parisi regolarizzato è: P + (n) = n (n + 1) 1 n. La funzione di struttura D (x, s) viene banalmente ottenuta dalla (.) facendone l antitrasformata (.19b). Alternativamente, si può, sotto opportune condizioni, cercare una soluzione analitica approssimata. Nella regione di radiazione debole (x 1), vale, ad esempio, la soluzione di Gribov-Lipatov: (.1) D GL (x, s) = exp [ 1 η ( 3 4 γ E Γ ( η) η(1 x) 1 η 1, )] k=1 dove γ E lim n + [ n i=1 ] 1 n ln n è la costante di Eulero-Mascheroni. Si noti che il termine η(1 x) 1 η 1 fa sì che la (.1) tenga conto del contributo di logaritmo dominante esponenziato a tutti gli ordini, come già visto nella (.7). Un ulteriore approccio risolutivo è si basa sul porre la (.17) nella forma: D (x, s) = δ (1 x) + s ds m s 1 x dz ( x z P + (z) D z, s )
28 4 Capitolo. Correzioni radiative di QED e Parton Shower e nel risolverla iterativamente. A differenza della soluzione di Gribov-Lipatov, l espressione per la funzione di struttura che si ottiene così è valida per ogni x, ma risulta troncata ad un ordine perturbativo finito. Insieme alla (.1), può essere però utilizzata per costruire soluzioni miste o ibride, in cui la soluzione di Gribov- Lipatov viene utilizzata per approssimare al limite di fotone soffice tutti quei termini che non vengono calcolati iterativamente. Un altro metodo per avvicinarsi all equazione di Altarelli-Parisi si fonda sull utilizzo del metodo Monte Carlo e va sotto il nome di algoritmo di Parton Shower. Prima di poterlo presentare, tuttavia, va introdotto il fattore di forma di Sudakov Π (s f, s i ), cioè la probabilità che l elettrone nella sua evoluzione da virtualità s i a virtualità s f emetta fotoni con frazione di energia solo sotto una certa soglia ε. Dalla (.15) si può facilmente riconoscere che: [ (.) Π (s f + ds f, s i ) = Π (s f, s i ) 1 α ds f π s f da cui segue: (.3) Π (s f, s i ) = exp dove si è posto: I + 1 ε 1 ε [ α sf ds ] π s i s I +, ] dzp (z), dzp (z) = ln ε 1 (1 ε) 1 ε. Ricordando l espressione (.18) per il vertice di Altarelli-Parisi regolarizzato, la (.17) si riscrive esplicitamente: (.4) s s D (x, s) = α π α π = α π = α π α π 1 x 1 x 1 x dz ( x ) z P (z) D z, s + dz ( x ) 1 z δ (1 z) D z, s dtp (t) = dz z P (z) D ( x z, s ) α π [ x+ 1 ε x x+ x 1 dz z P (z) D ( x z, s ) + dtp (t) }{{} I 1 dz z P (z) D ( x z, s ) α π I +D (x, s), ( x ) D z, s = x + dz z P (z) D ( x z, s ) ] D (x, s) I dove, nell ultimo passaggio, si è posto z 1 per poter approssimare gli ultimi due termini per mezzo della relazione I + = I 1 x + dzp (z). In conclusione, la (.4) risulta essere in forma analoga alla (.17), a patto di assumere una diversa regolarizzazione del vertice di Altarelli-Parisi che obbedisca alla relazione: P + (x) = P (x) θ (x + x) δ (1 x) x+ dzp (z).
29 .5. Metodi risolutivi e Parton Shower 5 Si ottiene, dunque: (.5) s s D (x, s) = α π Dalla (.3) discende che: x+ x dz ( x ) z P (z) D z, s α x+ dzp (z). π x dπ (s, s ) Π (s, s ) = α π I ds + s ; Sostituendo quest ultima relazione nella (.4) si arriva a scrivere: cioè s s D ( x, s ) = α π x+ d [ D (x, s) Π ( s, s )] = α π x dz ( x z P (z) D z, s ) 1 s s Π (s, s ) x+ x s Π ( s, s ) D ( x, s ), dz z P (z) D ( x z, s ) Π ( s, s ) ds s, che porta a scrivere una soluzione implicita per l equazione di Altarelli-Parisi: (.6) D (x, s) = Π ( s, m e ) D ( x, m e ) + + α π s m e ds s Π ( s, s ) La soluzione iterativa formale della (.6) [4] (.7) D (x, s) = Π ( s, m e ) δ (1 x) + + s m e s Π ( s, s ) ds x+ x s Π ( s, m ) α e π s dz z D ( x z, s ). x+ dyp (y) δ (x y) + + Π ( s, s ) ds m e s Π ( s, s ) ds m e s Π ( s, m ) e ( α ) x+ x+ dx 1 dx P (x 1 ) P (x ) δ (x x 1 x ) + = π = Π ( s, m ) ( α ) k 1 e π k! k= k i=1 x+ L dx i P (x i ) δ (x x 1 x k ) ha la seguente interpretazione fisica ([5]): il contributo di ordine α n alla funzione di struttura D (x, s) è dato dal prodotto delle n probabilità di evoluzione da virtualità m e a s 1, da s 1 a s, e così via, senza emissione di fotoni più energetici di ε = 1 x + e delle n probabilità di emissione di un fotone che lascia una frazione x i di energia all elettrone e ne varia la virtualità da s i a s i + ds i. La particolare forma della (.7) suggerisce l idea di utilizzare un metodo Monte Carlo per calcolare e simulare gli effetti dell emissione di radiazione ([6]). Questo fatto è, del resto, pienamente compatibile con la visione probabilistica che sta alla base di tutto il formalismo di Altarelli-Parisi, nel senso che una soluzione numerica esatta della (.5) ad una data virtualità s consente di generare la variabile x distribuita come D (x, s). L algoritmo che fa questo va sotto il nome di Parton Shower e può essere schematizzato come segue ([4, 7]): 1. si fissano le condizioni iniziali K = m e e x = 1 per la virtualità dell elettrone e per la sua frazione di energia;
30 6 Capitolo. Correzioni radiative di QED e Parton Shower. si estrae, con distribuzione uniforme, un numero casuale ξ compreso tra e 1; 3. si confronta ξ con la probabilità Π ( s, K ) : se ξ Π ( s, K ) l algoritmo si interrompe; se ξ > Π ( s, K ) c è stata emissione di fotoni: ) si calcola la nuova virtualità K invertendo l equazione ξ = Π (K, K ; 4. nell intervallo tra e x + 1 ε si estrae, secondo la distribuizione data dal vertice di Altarelli-Parisi P (z), la frazione z di energia rimanente all elettrone; 5. si effettuano le sostituzioni K K e x zx e si ritorna al punto. Figura.4: Distribuzione della x ottenuta mediante Parton Shower. In ordinata è riportato il numero di eventi. Si è posto s = 19 GeV e si è effettuata la simulazione di eventi con ε = 1 5. Una caratteristica piuttosto importante dell algoritmo appena enunciato è quella di restituire ad ogni passaggio non solo la frazione di energia x, ma anche la virtualità K dell elettrone, così che risulta possibile ricostruire una cinematica approssimata del processo. Questo non è, invece, possibile se ci si limita allo studio, ancorché esatto, della funzione di struttura. Come, infatti, si può notare dalla (.6), la risoluzione dell equazione di Altarelli-Parisi (.5) prevede che l integrazione sia su questi parametri, con conseguente perdita di informazione.
31 .5. Metodi risolutivi e Parton Shower 7 L affidabilità del Parton Shower viene verificata applicando una variante troncata a O (α) dell algoritmo. In questo modo, i risultati ottenuti possono essere direttamente confrontati con quelli derivanti dall usuale calcolo in teoria delle perturbazioni al prim ordine. In termini di funzioni di struttura, la sezione d urto da calcolare è: [ ( σ O(α) = dx 1 dx dy 1 dy dσ D x1, Q ) D ( x, Q ) D ( y 1, Q ) D ( y, Q )] O(α) Ω Troncando la serie nella (.7) al primo ordine in α (e sviluppando allo stesso ordine i fattori di forma di Sudakov) è possibile valutare il prodotto ([4]) (per semplicità si considera il prodotto di due sole funzioni di struttura): (.8) [D (x, s) D (y, s)] O(α) = correttamente normalizzato a 1: 1 [ 1 α π I + ln s + α π ln s m e [ +δ (1 y) m e ] δ (1 x) δ (1 y) + [ δ (1 x) x+ x+ dxdy[d (x, s) D (y, s)] O(α) = 1. dzp (z) δ (y z) + ] dzp (z) δ (x z), I passi dell algoritmo Parton Shower per ottenere x e y distribuite secondo la (.8) sono i seguenti: 1. si fissano le condizioni iniziali K 1, = m e e x = y = 1;. si estrae, con distribuzione uniforme, un numero casuale ξ compreso tra e 1; 3. si confronta ξ con la probabilità [ Π ( s, m e )] O(α) : se ξ [ Π ( s, m )] e l algoritmo si interrompe; O(α) se ξ > [ Π ( s, m )] e c è stata emissione di un fotone: nell intervallo O(α) tra e x + 1 ε si estrae, secondo la distribuizione data dal vertice di Altarelli-Parisi P (z), la frazione z di energia rimanente all elettrone e si pone con uguale probabilità x = z oppure y = z; a seconda della scelta operata si calcola la nuova virtualità K 1, della particella che ha emesso il fotone invertendo l equazione ξ = [ Π ( s, m )] e O(α). Si può utilizzare il Parton Shower per convincersi dell indipendenza da ε della funzione di struttura (.7) nella regione [, 1 ε]. Si osservi figura.5: la curva continua è stata ottenuta simulando con ε = 1 1, mentre quella tratteggiata è la stessa di figura.4 (ε = 1 5 ). A meno di differenze statistiche dovute all utilizzo di un metodo Monte Carlo, esse sono sovrapponibili. La dipendenza da ε, tramite Π ( s, m e ), è limitata alle x comprese nell intervallo (1 ε, 1] e determina un errore O (ε), trascurabile per ε. Come si accennava in precedenza, ogni passo dell algoritmo restituisce la virtualità e la frazione di energia di un elettrone immediatamente dopo l emissione di ciascun
32 8 Capitolo. Correzioni radiative di QED e Parton Shower Figura.5: Confronto tra distribuzioni di x ottenute mediante Parton Shower con ε diversi: ε = 1 1, linea continua, e ε = 1 5, linea tratteggiata.
33 .5. Metodi risolutivi e Parton Shower 9 fotone. Questo permette di ricostruire passo a passo la cinematica del processo. Si può, ad esempio, porre: p = (E,, p z ) p = ( ze, p, p ) z q = ((1 z) E, p, q z ). Imponendo le virtualità del fermione rispettivamente prima e dopo l emissione del fotone p = K e p = K, quella del fotone q = e considerando anche la conservazione della componente z del momento si può scrivere il sistema: E p z = K Segue: z E p p z = K (1 z) E p q z = p z + q z = p z. p z = ( E K ) 1 p 1 z = [ze ] K K (E K ) 1 1 q z = (E K ) 1 p = (1 z) E [ ] K K + E (1 z) [ ] K K + E (1 z) 4 (E K ) Questa soluzione, tuttavia, non garantisce la positività di p per ogni possibile scelta di x, di K e di K. L imposizione delle opportune condizioni fisiche, inoltre, fa sì che il Parton Shower non generi più la corretta distribuzione D ( x, Q ). Alternativamente è possibile cercare una cinematica approssimata consistentemente con quanto già fatto nel paragrafo.3. Si considera, dunque, E p e E K e si sviluppano le precedenti soluzioni al prim ordine in p E, K E e in K E, in modo da ottenere: (.9) p z = E K E p z = ze (1 z) K + K E q z = (1 z) E zk K ( E ) p = (1 z) zk K. Ancora non è garantito p >, però ora il problema si può aggirare ponendo p. La cinematica (.9) va sotto il nome di pure Parton Shower. La discussione appena fatta si basa su un assunzione di assoluta affidabilità del Parton Shower nella ricostruzione della cinematica. Una scelta alternativa, però, può essere, invece, quella di ritenere, tra i dati provenienti dall algoritmo, solo la frazione.
34 3 Capitolo. Correzioni radiative di QED e Parton Shower di energia z e di riprendere invece i risultati di pag. 14. Si suppone, quindi, che ogni particella carica contribuisca indipendentemente allo spettro del fotone come ([8]): (.3) P ( cos ϑ γ ) 1 1 β cos ϑ γ f, dove β è la velocità del fermione e cos ϑ γ f è l angolo di emissione del fotone rispetto all elettrone. Questa distribuzione viene utilizzata per ottenere p e quindi risalire all intera cinematica. Questo particolare modo di procedere viene chiamato prescrizione di polo dominante, leading pole in inglese. Le cinematiche mostrate fino ad ora non tengono in realtà conto di un fatto importante. Quando più particelle cariche sono coinvolte nel processo, fenomeni di interferenza della radiazione emessa da ciascuna di esse influiscono sulla distribuzione angolare dei fotoni. Questo implica la necessità di correggere in maniera appropriata la (.3). Dalla formula di Yennie-Frautchi-Suura ([9]), valida in approssimazione soffice, riscritta all ordine α n : e n dσ O(α n ) dσ n! n d 3 q l l=1 (π) 3 q l N i, j=1 p i p j η i η j (p i q l ) (p j q l ), dove N è il numero di fermioni emittenti, è possibile ricavare informazioni sullo spettro angolare dell l-simo fotone: (.31) cos ϑ l N i, j=1 1 β i β j cos ϑ ij η i η j (1 β i cos ϑ il ) (1 β j cos ϑ il ), dove β k è la velocità del k-esimo fermione e ϑ kl è l angolo tra questo e l l-esimo fotone.
35 Capitolo 3 Matching e BABAYAGA Nel capitolo sono stati illustrati gli aspetti teorici delle correzioni radiative ai processi e + e e, in particolare, nel paragrafo.5, l algoritmo Parton Shower per la generazione di eventi in accordo con l equazione di Altarelli-Parisi. Il Parton Shower è stato applicato allo sviluppo di un generatore di eventi Monte Carlo per il calcolo di precisione del processo Bhabha, BABAYAGA 1, realizzato a Pavia presso la locale Sezione dell INFN e il Dipartimento di Fisica Nucleare e Teorica dell Università. Scopo di questo capitolo è quello di illustrare le caratteristiche salienti di questo programma, comprese le ultime migliorie apportate per tener conto anche dei risultati esatti a O (α). Il Parton Shower, infatti, calcola i termini a tale ordine soltanto in maniera approssimata, mentre, in realtà, questi sono noti in letteratura in forma completa. Risulta, quindi, doveroso, prima di passare alla discussione su BABAYAGA, aggiungere alcune ultime considerazioni teoriche a quanto già enunciato nei precedenti capitoli. 3.1 Correzioni radiative esatte O (α) Prima di procedere è opportuno riassumere brevemente i principali risultati relativi al calcolo della sezione d urto esatta a O (α) per il processo e + e e + e (γ). Questa è data dalla somma di un contributo soffice-virtuale e da uno reale: (3.1) σ esatta (α) = σ esatta SV (α) ( ) Eγ < k + σ esatta(α) ( ) R Eγ > k. Il parametro k è il cut-off di energia del fotone scelto per separare la regione di radiazione soffice da quella di radiazione dura (reale). Se E è l energia dell elettrone incidente, è immediato notare che il rapporto k E è equivalente al parametro ε introdotto nel paragrafo.5 discutendo del Parton Shower. La forma esplicita dei termini che appaiono nella (3.1) è data in Appendice A. a pag Da Baba ga, nome di una strega del folklore russo, che ha ispirato, tra gli altri, il compositore Modest Mussorgsky ( ) (si veda [4, pag. 17]).
Problemi per il corso di teoria delle interazioni fondamentali gennaio 2013
 Problemi per il corso di teoria delle interazioni fondamentali gennaio 203 Primo Modulo. Urto Bhabha in QED Considerare il processo e + e e + e nella regione di energia per cui la massa degli elettroni
Problemi per il corso di teoria delle interazioni fondamentali gennaio 203 Primo Modulo. Urto Bhabha in QED Considerare il processo e + e e + e nella regione di energia per cui la massa degli elettroni
20 giugno La sezione d urto invariante impolarizzata per il processo (1) è
 20 giugno 2002 e (p 1 ) + e + (p 2 ) γ(k) + Z 0 (q) (1) (i tetra-impulsi delle particelle sono indicati in parentesi). 1. Si scrivano i diagrammi di Feynman rilevanti per il processo, e si scriva l espressione
20 giugno 2002 e (p 1 ) + e + (p 2 ) γ(k) + Z 0 (q) (1) (i tetra-impulsi delle particelle sono indicati in parentesi). 1. Si scrivano i diagrammi di Feynman rilevanti per il processo, e si scriva l espressione
la forma esplicita delle correzioni
 la forma esplicita delle correzioni al leading order (ma nei programmi di fit le correzioni si spingono, a seconda dei casi, ad ordini superiori) e per m H >m W le correzioni dipendenti dal flavour sono
la forma esplicita delle correzioni al leading order (ma nei programmi di fit le correzioni si spingono, a seconda dei casi, ad ordini superiori) e per m H >m W le correzioni dipendenti dal flavour sono
Programma del corso di Particelle Elementari
 Programma del corso di Particelle Elementari 1. Le interazioni fondamentali 1.1 Costituenti elementari 1.2 Quark e colore 1.3 Il colore come carica dell interazione nucleare 1.4 Unità naturali 1.5 Interazione
Programma del corso di Particelle Elementari 1. Le interazioni fondamentali 1.1 Costituenti elementari 1.2 Quark e colore 1.3 Il colore come carica dell interazione nucleare 1.4 Unità naturali 1.5 Interazione
Problemi per il corso di teoria delle interazioni fondamentali giugno 2005
 Problemi per il corso di teoria delle interazioni fondamentali giugno 2005 Primo Modulo 1. Urto Bhabha Determinare la sezione d urto differenziale per l urto e + e e + e, nel limite di alta energia in
Problemi per il corso di teoria delle interazioni fondamentali giugno 2005 Primo Modulo 1. Urto Bhabha Determinare la sezione d urto differenziale per l urto e + e e + e, nel limite di alta energia in
interpretazione del modello a partoni
 interpretazione del modello a partoni Nel modello a partoni, la sezione d urto per un partone con frazione di momento longitudinale pari a z sarà: " # $ dz q( z)" parton ( zp + q) z D altra parte, per
interpretazione del modello a partoni Nel modello a partoni, la sezione d urto per un partone con frazione di momento longitudinale pari a z sarà: " # $ dz q( z)" parton ( zp + q) z D altra parte, per
Misura diretta al LEP del numero di famiglie di neutrini
 Misura diretta al LEP del numero di famiglie di neutrini Anno Accademico 2005-2006 - Presentazione a cura di F. Orio Quanti tipi diversi di neutrino esistono? Spettro continuo del decadimento β ν e _ ν
Misura diretta al LEP del numero di famiglie di neutrini Anno Accademico 2005-2006 - Presentazione a cura di F. Orio Quanti tipi diversi di neutrino esistono? Spettro continuo del decadimento β ν e _ ν
Riassunto della lezione precedente
 Riassunto della lezione precedente regola di somma GDH: test di transizione da regime perturbativo a nonperturbativo regola di somma di Bjorken polarizzata: rapporto g A /g V necessità di introdurre correzioni
Riassunto della lezione precedente regola di somma GDH: test di transizione da regime perturbativo a nonperturbativo regola di somma di Bjorken polarizzata: rapporto g A /g V necessità di introdurre correzioni
Fisica Quantistica III Esercizi Natale 2009
 Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Fenomenologia del Modello Standard Prof. A. Andreazza. Lezione 13. La scoperta del W
 Fenomenologia del Modello Standard Prof. A. Andreazza Lezione 13 La scoperta del W Premio Nobel 1984 Articolo 12.5, Collaborazione UA1, Experimental observation of isolated large transverse electrons with
Fenomenologia del Modello Standard Prof. A. Andreazza Lezione 13 La scoperta del W Premio Nobel 1984 Articolo 12.5, Collaborazione UA1, Experimental observation of isolated large transverse electrons with
LABORATORIO DI FISICA I
 UNIVERSITA DEGLI STUDI DI PALERMO CORSO DI LAUREA IN SCIENZE FISICHE A.A. 2018/2019 13 Dicembre 2018 LABORATORIO DI FISICA I RELAZIONE TERZA ESPERIENZA DI LABORATORIO GRUPPO 1 Nigrelli Giulia Valenti Giuseppe
UNIVERSITA DEGLI STUDI DI PALERMO CORSO DI LAUREA IN SCIENZE FISICHE A.A. 2018/2019 13 Dicembre 2018 LABORATORIO DI FISICA I RELAZIONE TERZA ESPERIENZA DI LABORATORIO GRUPPO 1 Nigrelli Giulia Valenti Giuseppe
Conteggi e sezione d urto
 Capitolo 1 Conteggi e sezione d urto Consideriamo la reazione a due corpi: a + X b + Y (1.1) che comprende come caso particolare lo scattering elastico. La sezione d urto differenziale per la reazione
Capitolo 1 Conteggi e sezione d urto Consideriamo la reazione a due corpi: a + X b + Y (1.1) che comprende come caso particolare lo scattering elastico. La sezione d urto differenziale per la reazione
Evidenza delle diverse famiglie di neutrini
 Fenomenologia del Modello Standard Prof. A. Andreazza Lezione 2 Evidenza delle diverse famiglie di neutrini Diversi tipi di neutrini Agli inizi degli anni 60 si sapeva che il numero leptonico era conservato
Fenomenologia del Modello Standard Prof. A. Andreazza Lezione 2 Evidenza delle diverse famiglie di neutrini Diversi tipi di neutrini Agli inizi degli anni 60 si sapeva che il numero leptonico era conservato
TEORIA DELLE INTERAZIONI FONDAMENTALI PROBLEMI
 TEORIA DELLE INTERAZIONI FONDAMENTALI PROBLEMI Cenni di teoria quantistica dei campi (1) I generatori delle traslazioni P µ e delle trasformazioni di Lorentz J µν soddisfano le relazioni di commutazione
TEORIA DELLE INTERAZIONI FONDAMENTALI PROBLEMI Cenni di teoria quantistica dei campi (1) I generatori delle traslazioni P µ e delle trasformazioni di Lorentz J µν soddisfano le relazioni di commutazione
8.1 Problema della diffusione in meccanica quantistica
 8.1 Problema della diffusione in meccanica quantistica Prima di procedere oltre nello studio dell interazione puntuale, in questo paragrafo vogliamo dare un breve cenno alle nozioni di base della teoria
8.1 Problema della diffusione in meccanica quantistica Prima di procedere oltre nello studio dell interazione puntuale, in questo paragrafo vogliamo dare un breve cenno alle nozioni di base della teoria
Effetto Compton. Nicola Cabibbo 27 Novembre 2000
 Effetto Compton Nicola Cabibbo 27 Novembre 2000 In questa nota consideriano il processo Compton di diffusione di un fotone su un elettrone,γ + e γ + e. La nota integra la trattazione che si trova in Mandl
Effetto Compton Nicola Cabibbo 27 Novembre 2000 In questa nota consideriano il processo Compton di diffusione di un fotone su un elettrone,γ + e γ + e. La nota integra la trattazione che si trova in Mandl
Test 1 - Teoria dei Campi 2010
 Test - Teoria dei Campi 200 Discutere il path-integral della QCD in gauge assiale (nell Euclideo) n µ A a µ = 0, a =,..., 8, () dove n µ e un vettore assegnato. Derivare: - regole di Feynman; - identitaà
Test - Teoria dei Campi 200 Discutere il path-integral della QCD in gauge assiale (nell Euclideo) n µ A a µ = 0, a =,..., 8, () dove n µ e un vettore assegnato. Derivare: - regole di Feynman; - identitaà
PROBLEMA A DUE CORPI: STATI DEL CONTINUO
 Capitolo 10 PROBLEMA A DUE CORPI: STATI DEL CONTINUO Riprendiamo l equazione di Schrödinger per il sistema di due particelle interagenti con l intento di cercare la classe di soluzioni che descrivono stati
Capitolo 10 PROBLEMA A DUE CORPI: STATI DEL CONTINUO Riprendiamo l equazione di Schrödinger per il sistema di due particelle interagenti con l intento di cercare la classe di soluzioni che descrivono stati
Note di Teoria della Probabilità.
 Note di Teoria della Probabilità. In queste brevi note, si richiameranno alcuni risultati di Teoria della Probabilità, riguardanti le conseguenze elementari delle definizioni di probabilità e σ-algebra.
Note di Teoria della Probabilità. In queste brevi note, si richiameranno alcuni risultati di Teoria della Probabilità, riguardanti le conseguenze elementari delle definizioni di probabilità e σ-algebra.
Fisica Nucleare e Subnucleare III. Le violazioni di scaling e la QCD. mercoledì 11 novembre 2009
 Fisica Nucleare e Subnucleare III Le violazioni di scaling e la QCD 1 Variazione di α s con Q 2 Come la QED, la costante di accoppiamento della QCD deve essere rinormalizzata, e in conseguenza, varia con
Fisica Nucleare e Subnucleare III Le violazioni di scaling e la QCD 1 Variazione di α s con Q 2 Come la QED, la costante di accoppiamento della QCD deve essere rinormalizzata, e in conseguenza, varia con
LIMITI SPERIMENTALI SUL BOSONE DI HIGGS A LEP II
 LIMITI SPERIMENTALI SUL BOSONE DI HIGGS A LEP II Chiara Orlandi Tutor: Stefano Giagu Corso di Fisica Nucleare e Subnucleare II Prof. Carlo Dionisi A.A. 008/09 1 Il bosone di Higgs Il bosone di Higgs è
LIMITI SPERIMENTALI SUL BOSONE DI HIGGS A LEP II Chiara Orlandi Tutor: Stefano Giagu Corso di Fisica Nucleare e Subnucleare II Prof. Carlo Dionisi A.A. 008/09 1 Il bosone di Higgs Il bosone di Higgs è
La struttura elettronica degli atomi
 1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
Teoria delle interazioni fondamentali Ricerca e Didattica a Pavia
 Teoria delle interazioni fondamentali Ricerca e Didattica a Pavia Oreste Nicrosini Istituto Nazionale Fisica Nucleare, Sezione di Pavia & Dipartimento Fisica Nucleare e Teorica, Università degli Studi
Teoria delle interazioni fondamentali Ricerca e Didattica a Pavia Oreste Nicrosini Istituto Nazionale Fisica Nucleare, Sezione di Pavia & Dipartimento Fisica Nucleare e Teorica, Università degli Studi
Se la funzione è analiticamente invertibile, estratto q, si può ricavare x = x(q).
 La tecnica Monte Carlo Il metodo Monte Carlo è basato sulla scelta di eventi fisici con una probabilità di accadimento nota a priori. sia p(x) la distribuzione di probabilità con la quale si manifesta
La tecnica Monte Carlo Il metodo Monte Carlo è basato sulla scelta di eventi fisici con una probabilità di accadimento nota a priori. sia p(x) la distribuzione di probabilità con la quale si manifesta
Misura del momento magnetico dell elettrone
 FACOLTÀ Università degli Studi di Roma Tre DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea in Fisica Misura del momento magnetico dell elettrone Candidato: Andrea Sciandra Matricola 4480 Relatore:
FACOLTÀ Università degli Studi di Roma Tre DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea in Fisica Misura del momento magnetico dell elettrone Candidato: Andrea Sciandra Matricola 4480 Relatore:
Sistemi relativistici
 Sistemi relativistici Corso di laurea magistrale 2017 18 F. Becattini Sommario lezione Insieme microcanonico gas ideale relativistico Corpo nero microcanonico Caso massivo generale: sviluppo in molteplicita'
Sistemi relativistici Corso di laurea magistrale 2017 18 F. Becattini Sommario lezione Insieme microcanonico gas ideale relativistico Corpo nero microcanonico Caso massivo generale: sviluppo in molteplicita'
ed infine le interazioni nucleari forte e debole? dove E rappresenta l energia cinetica della particella α, e K è: K = e2 2Z
 Introduzione 1. Stima il valore delle energie dei fotoni necessarie per risolvere distanze atomiche, e poi nucleari. 2. Per quali ragioni fisiche le interazioni fondamentali sono state storicamente identificate
Introduzione 1. Stima il valore delle energie dei fotoni necessarie per risolvere distanze atomiche, e poi nucleari. 2. Per quali ragioni fisiche le interazioni fondamentali sono state storicamente identificate
CAPITOLO 3 LA LEGGE DI GAUSS
 CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
04 - Numeri Complessi
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
Riassunto della lezione precedente
 Riassunto della lezione precedente necessità di introdurre correzioni radiative a QPM IQPM inglobato nella pqcd rinormalizzazione di teoria di gauge: cancellazione divergenze ultraviolette; eq. di Callan-Symanzik;
Riassunto della lezione precedente necessità di introdurre correzioni radiative a QPM IQPM inglobato nella pqcd rinormalizzazione di teoria di gauge: cancellazione divergenze ultraviolette; eq. di Callan-Symanzik;
H = H 0 + V. { V ti t t f 0 altrove
 Esercizio 1 (Regola d oro di Fermi Determinare la probabilità di transizione per unità di tempo da uno stato a ad uno stato b al primo ordine perturbativo di un sistema per cui si suppone di aver risolto
Esercizio 1 (Regola d oro di Fermi Determinare la probabilità di transizione per unità di tempo da uno stato a ad uno stato b al primo ordine perturbativo di un sistema per cui si suppone di aver risolto
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Test 1 - Teoria dei Campi 2010
 Test - Teoria dei Campi 200 Discutere il path-integral della QCD in gauge assiale (nell Euclideo) n µ A a µ = 0, a =,..., 8, () dove n µ e un vettore assegnato. Derivare: - regole di Feynman; - identitaà
Test - Teoria dei Campi 200 Discutere il path-integral della QCD in gauge assiale (nell Euclideo) n µ A a µ = 0, a =,..., 8, () dove n µ e un vettore assegnato. Derivare: - regole di Feynman; - identitaà
Simulazione dei dati
 Simulazione dei dati Scopo della simulazione Fasi della simulazione Generazione di numeri casuali Esempi Simulazione con Montecarlo 0 Scopo della simulazione Le distribuzioni di riferimento usate per determinare
Simulazione dei dati Scopo della simulazione Fasi della simulazione Generazione di numeri casuali Esempi Simulazione con Montecarlo 0 Scopo della simulazione Le distribuzioni di riferimento usate per determinare
Esperimento ATLAS INFN ed Università di Bologna PROPOSTA PER SVOLGERE IL TIROCINIO-MONDO LAVORO PRESSO L ESPERIMENTO ATLAS
 i Esperimento ATLAS INFN ed Università di Bologna PROPOSTA PER SVOLGERE IL TIROCINIO-MONDO LAVORO PRESSO L ESPERIMENTO ATLAS Il guppo di Bologna dell esperimento ATLAS propone un tirocinio di lavoro nel
i Esperimento ATLAS INFN ed Università di Bologna PROPOSTA PER SVOLGERE IL TIROCINIO-MONDO LAVORO PRESSO L ESPERIMENTO ATLAS Il guppo di Bologna dell esperimento ATLAS propone un tirocinio di lavoro nel
MECCANICA QUANTISTICA. Corso di laurea in fisica PROGRAMMA DEL CORSO E PROGRAMMA D ESAME. Anno accademico 2011/2012
 MECCANICA QUANTISTICA Corso di laurea in fisica PROGRAMMA DEL CORSO E PROGRAMMA D ESAME Anno accademico 2011/2012 Argomenti facenti parte del programma d esame. Argomenti facenti parte del programma d
MECCANICA QUANTISTICA Corso di laurea in fisica PROGRAMMA DEL CORSO E PROGRAMMA D ESAME Anno accademico 2011/2012 Argomenti facenti parte del programma d esame. Argomenti facenti parte del programma d
Raccolta di esercizi di Calcolo Numerico Prof. Michela Redivo Zaglia
 Raccolta di esercizi di Calcolo Numerico Prof. Michela Redivo Zaglia Nota Bene: Gli esercizi di questa raccolta sono solo degli esempi. Non sono stati svolti né verificati e servono unicamente da spunto
Raccolta di esercizi di Calcolo Numerico Prof. Michela Redivo Zaglia Nota Bene: Gli esercizi di questa raccolta sono solo degli esempi. Non sono stati svolti né verificati e servono unicamente da spunto
2.3 Percorso residuo (range)
 Figure 13: Determinazione del range a partire da una curva di trasmissione (I èil numero di particelle tramesse per unità di tempo in funzione delle spessore t essendo I 0 il numero di particelle entranti)
Figure 13: Determinazione del range a partire da una curva di trasmissione (I èil numero di particelle tramesse per unità di tempo in funzione delle spessore t essendo I 0 il numero di particelle entranti)
APPUNTI ASTROFISICA Processi radiativi
 APPUNTI ASTROFISICA Processi radiativi Claudio Chiuderi June 20, 2007 1 1 Processi radiativi Descriveremo brevemente le caratteristiche dei processi radiativi che non coinvolgono l emissione di righe da
APPUNTI ASTROFISICA Processi radiativi Claudio Chiuderi June 20, 2007 1 1 Processi radiativi Descriveremo brevemente le caratteristiche dei processi radiativi che non coinvolgono l emissione di righe da
Costanti di Accoppiamento
 Costanti di Accoppiamento Fenomenologia delle Interazioni Elettrodeboli Diego Bettoni Anno Accademico 8-9 La costante di struttura fine in realtà non è una costante, ma varia in funzione del uadrimpulso
Costanti di Accoppiamento Fenomenologia delle Interazioni Elettrodeboli Diego Bettoni Anno Accademico 8-9 La costante di struttura fine in realtà non è una costante, ma varia in funzione del uadrimpulso
vita media risonanze matrice S e probabilità di transizione regola d oro di Fermi QED e diagrammi di Feynman
 sezione d urto durto vita media risonanze matrice S e probabilità di transizione regola d oro di Fermi QED e diagrammi di Feynman 0 Che cosa si misura: sezioni d urto durto a + b qualunque cosa proiettile
sezione d urto durto vita media risonanze matrice S e probabilità di transizione regola d oro di Fermi QED e diagrammi di Feynman 0 Che cosa si misura: sezioni d urto durto a + b qualunque cosa proiettile
05. Errore campionario e numerosità campionaria
 Statistica per le ricerche di mercato A.A. 01/13 05. Errore campionario e numerosità campionaria Gli schemi di campionamento condividono lo stesso principio di fondo: rappresentare il più fedelmente possibile,
Statistica per le ricerche di mercato A.A. 01/13 05. Errore campionario e numerosità campionaria Gli schemi di campionamento condividono lo stesso principio di fondo: rappresentare il più fedelmente possibile,
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Istituzioni di Fisica Nucleare e Subnucleare Prof. A. Andreazza. Lezione 8. I decadimenti γ
 Istituzioni di Fisica Nucleare e Subnucleare Prof. A. Andreazza Lezione 8 I decadimenti γ Decadimenti γ (Cenni da cap. 9 del Krane) I decadimenti γ consistono nel passaggio di un nucleo da uno stato eccitato
Istituzioni di Fisica Nucleare e Subnucleare Prof. A. Andreazza Lezione 8 I decadimenti γ Decadimenti γ (Cenni da cap. 9 del Krane) I decadimenti γ consistono nel passaggio di un nucleo da uno stato eccitato
di Higgs a LHC b-tagging per la ricerca Scuola Normale Superiore e INFN, Pisa Incontri sulla Fisica delle Alte Energie Andrea Bocci
 b-tagging per la ricerca di Higgs a LHC Incontri sulla Fisica delle Alte Energie Pavia Scuola Normale Superiore e INFN, Pisa Sommario - b-tagging per la ricerca del bosone di Higgs - Caratteristiche degli
b-tagging per la ricerca di Higgs a LHC Incontri sulla Fisica delle Alte Energie Pavia Scuola Normale Superiore e INFN, Pisa Sommario - b-tagging per la ricerca del bosone di Higgs - Caratteristiche degli
G.Battistoni Neutrini Atmosferici
 Neutrini Atmosferici Interazione dei cosmici in atmosfera Sciame adronico Cosmico primario Raggi cosmici secondari Sciame atmosferico Il flusso di neutrini p In un regime in cui tutti i π decadono ν µ
Neutrini Atmosferici Interazione dei cosmici in atmosfera Sciame adronico Cosmico primario Raggi cosmici secondari Sciame atmosferico Il flusso di neutrini p In un regime in cui tutti i π decadono ν µ
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
8π c 3 ν2. dx x 2 /(e x 1) fotoni/m 2 /sec,
 Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 8 Giugno 7 - (tre ore a disposizione) Soluzione 1.) Una stazione radio trasmette emettendo una potenza di un kilowatt alla frequenza di 9
Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 8 Giugno 7 - (tre ore a disposizione) Soluzione 1.) Una stazione radio trasmette emettendo una potenza di un kilowatt alla frequenza di 9
Ricerca del Bosone di Higgs
 Ricerca del Bosone di iggs Fenomenologia delle nterazioni Forti Diego Bettoni Anno Accademico 008-09 Produzione e Rivelazione del Bosone di iggs La teoria elettrodebole dipende in modo cruciale dal meccanismo
Ricerca del Bosone di iggs Fenomenologia delle nterazioni Forti Diego Bettoni Anno Accademico 008-09 Produzione e Rivelazione del Bosone di iggs La teoria elettrodebole dipende in modo cruciale dal meccanismo
Corso di Laurea Specialistica in Ingegneria Meccanica e Ingegneria Energetica Progetto numerico al calcolatore
 Corso di Laurea Specialistica in Ingegneria Meccanica e Ingegneria Energetica Progetto numerico al calcolatore Soluzione di un sistema non lineare con la Regula Falsi generalizzata per la determinazione
Corso di Laurea Specialistica in Ingegneria Meccanica e Ingegneria Energetica Progetto numerico al calcolatore Soluzione di un sistema non lineare con la Regula Falsi generalizzata per la determinazione
Bosone. Particella a spin intero, che obbedisce alla statistica di Bose-Einstein, che è opposta a quella di Fermi-Dirac.
 Particelle ed Interazioni fondamentali Fermione. Particella a spin semintero, che obbedisce alla statistica di Fermi-Dirac, cioè due fermioni con gli stessi numeri quantici non possono coesistere in uno
Particelle ed Interazioni fondamentali Fermione. Particella a spin semintero, che obbedisce alla statistica di Fermi-Dirac, cioè due fermioni con gli stessi numeri quantici non possono coesistere in uno
Calcolo Numerico. Corso di Laurea in Ingegneria Elettronica Appello del 17 gennaio A(x) =
 Calcolo Numerico Corso di Laurea in Ingegneria Elettronica Appello del 7 gennaio 204 Sia M = F (2, 3). Dopo aver mostrato che 20 M, determinare tutti gli elementi ξ M tali che: ξ > 20 Per ogni x R, sia:
Calcolo Numerico Corso di Laurea in Ingegneria Elettronica Appello del 7 gennaio 204 Sia M = F (2, 3). Dopo aver mostrato che 20 M, determinare tutti gli elementi ξ M tali che: ξ > 20 Per ogni x R, sia:
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA
 Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Interazioni Elettrodeboli. Lezione n. 15
 Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 15 28.11.2017 Corrente adronica debole Decadimento del mesone π Decadimento del leptone τ: τ π ν τ Proprietà isotopiche
Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 15 28.11.2017 Corrente adronica debole Decadimento del mesone π Decadimento del leptone τ: τ π ν τ Proprietà isotopiche
Sezione d urto classica
 Capitolo Sezione d urto classica In meccanica classica, ogni particella del fascio incidente segue una traiettoria ben definita sotto l azione del potenziale. Se V (r) è centrale, il momento angolare è
Capitolo Sezione d urto classica In meccanica classica, ogni particella del fascio incidente segue una traiettoria ben definita sotto l azione del potenziale. Se V (r) è centrale, il momento angolare è
Effetto Stark (1) H 0 nlm > = E n nlm > (4) Ricordiamo che. E n = me4 2 h 2 n 2 = E 1
 Effetto Stark Studiamo l equazione di Schrödinger per l atomo di idrogeno in presenza di un campo elettrico costante e diretto lungo l asse z, E = E k. La hamiltoniana di Schrödinger per l atomo di idrogeno
Effetto Stark Studiamo l equazione di Schrödinger per l atomo di idrogeno in presenza di un campo elettrico costante e diretto lungo l asse z, E = E k. La hamiltoniana di Schrödinger per l atomo di idrogeno
Teorema di Thevenin generalizzato
 Teorema di Thevenin generalizzato Si considerino due reti elettriche lineari, A e B, aventi rispettivamente N A e N B nodi interni. Esse si interfacciano attraverso n (n 3) fili di collegamento, in cui
Teorema di Thevenin generalizzato Si considerino due reti elettriche lineari, A e B, aventi rispettivamente N A e N B nodi interni. Esse si interfacciano attraverso n (n 3) fili di collegamento, in cui
Scattering inelastico con neutrini
 Fenomenologia del Modello Standard Prof. A. Andreazza Lezione 6 Scattering inelastico con neutrini Deep Inelastic Scattering con neutrini I neutrini sono delle sonde eccezionali per studiare il nucleone:
Fenomenologia del Modello Standard Prof. A. Andreazza Lezione 6 Scattering inelastico con neutrini Deep Inelastic Scattering con neutrini I neutrini sono delle sonde eccezionali per studiare il nucleone:
Interazioni Elettrodeboli. Lezione n. 4. Equazione di Dirac 3 Interazione E.M. Scattering di Coulomb
 Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 4 12.10.2017 Equazione di Dirac 3 Interazione E.M. Scattering di Coulomb anno accademico 2017-2018 Scattering Coulombiano:
Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 4 12.10.2017 Equazione di Dirac 3 Interazione E.M. Scattering di Coulomb anno accademico 2017-2018 Scattering Coulombiano:
Problemi attuali di fisica delle particelle
 Problemi attuali di fisica delle particelle Incontri di Fisica 2007 LNF, Frascati, 1/3 Ottobre 2007 Riccardo Barbieri SNS Pisa Le particelle elementari in una pagina L SM = 1 4 Fa µνf aµν + i ψ Dψ +ψ i
Problemi attuali di fisica delle particelle Incontri di Fisica 2007 LNF, Frascati, 1/3 Ottobre 2007 Riccardo Barbieri SNS Pisa Le particelle elementari in una pagina L SM = 1 4 Fa µνf aµν + i ψ Dψ +ψ i
Fisica dei mesoni. Mesoni sono particelle con spin intero e interagisce coi barioni (nucleoni) attraverso le forze forti, elettromagnetiche e deboli
 Fisica dei mesoni Mesone π e quello piu leggero nella famiglia dei mesoni E la particella che viene scambiato nell interazione forte nucleone-nucleone ed e quindi responsabile della maggiore componente
Fisica dei mesoni Mesone π e quello piu leggero nella famiglia dei mesoni E la particella che viene scambiato nell interazione forte nucleone-nucleone ed e quindi responsabile della maggiore componente
SCHEDA DIDATTICA N 7
 FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA CIVILE CORSO DI IDROLOGIA PROF. PASQUALE VERSACE SCHEDA DIDATTICA N 7 LA DISTRIBUZIONE NORMALE A.A. 01-13 La distribuzione NORMALE Uno dei più importanti
FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA CIVILE CORSO DI IDROLOGIA PROF. PASQUALE VERSACE SCHEDA DIDATTICA N 7 LA DISTRIBUZIONE NORMALE A.A. 01-13 La distribuzione NORMALE Uno dei più importanti
Rivelatori Caratteristiche generale e concetti preliminari
 Rivelatori Caratteristiche generale e concetti preliminari Stage Residenziale 2012 Indice Caratteristiche generali sensibilità, risposta, spettro d ampiezza, risoluzione energetica, efficienza, tempo morto
Rivelatori Caratteristiche generale e concetti preliminari Stage Residenziale 2012 Indice Caratteristiche generali sensibilità, risposta, spettro d ampiezza, risoluzione energetica, efficienza, tempo morto
Fisica dell alto pt a Tevatron (jets e top)
 Fisica dell alto pt a Tevatron (jets e top) 1 2 Ad un collider adronico.. Partoni all interno di un (anti-) protone si scontrano hanno una frazione x1 ed x2 degli impulsi vertice d interazione calcolabile
Fisica dell alto pt a Tevatron (jets e top) 1 2 Ad un collider adronico.. Partoni all interno di un (anti-) protone si scontrano hanno una frazione x1 ed x2 degli impulsi vertice d interazione calcolabile
Elaborazione statistica di dati
 Elaborazione statistica di dati CONCETTI DI BASE DI STATISTICA ELEMENTARE Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Collaudo sistemi di produzione IPOTESI:
Elaborazione statistica di dati CONCETTI DI BASE DI STATISTICA ELEMENTARE Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Collaudo sistemi di produzione IPOTESI:
Università della Calabria
 Università della Calabria FACOLTA DI INGEGNERIA Corso di Laurea in Ingegneria Civile CORSO DI IDROLOGIA N.O. Prof. Pasquale Versace SCHEDA DIDATTICA N 3 CURVE DI PROBABILITÀ PLUVIOMETRICA A.A. 00- CURVE
Università della Calabria FACOLTA DI INGEGNERIA Corso di Laurea in Ingegneria Civile CORSO DI IDROLOGIA N.O. Prof. Pasquale Versace SCHEDA DIDATTICA N 3 CURVE DI PROBABILITÀ PLUVIOMETRICA A.A. 00- CURVE
Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica), a.a. 2007/08. Insiemi numerici: sup A, inf A
 Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica, a.a. 2007/08 Esercizi: Parte 1 Insiemi numerici: sup A, inf A 1. Verificare se A, nel caso sia non vuoto, è limitato superiormente,
Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica, a.a. 2007/08 Esercizi: Parte 1 Insiemi numerici: sup A, inf A 1. Verificare se A, nel caso sia non vuoto, è limitato superiormente,
, B con probabilità 1 4 e C con probabilità 1 4.
 Laurea triennale in MATEMATICA, Corso di PROBABILITÀ Prof. L. Bertini - G. Nappo - F. Spizzichino Esonero del 0.06.00 N.B. Scrivere le soluzioni degli esercizi su questi fogli giustificando brevemente
Laurea triennale in MATEMATICA, Corso di PROBABILITÀ Prof. L. Bertini - G. Nappo - F. Spizzichino Esonero del 0.06.00 N.B. Scrivere le soluzioni degli esercizi su questi fogli giustificando brevemente
Considerare il moto di un punto materiale di massa m = 1 soggetto ad un potenziale V (x):
 sercizio Considerare il moto di un punto materiale di massa m = soggetto ad un potenziale V (x): ẍ = V (x), dove V (x) = x x.. Scrivere esplicitamente l equazione del moto e verificare esplicitamente la
sercizio Considerare il moto di un punto materiale di massa m = soggetto ad un potenziale V (x): ẍ = V (x), dove V (x) = x x.. Scrivere esplicitamente l equazione del moto e verificare esplicitamente la
Università degli Studi di Palermo Facoltà di Economia. Dipartimento di Scienze Economiche, Aziendali e Statistiche. Appunti del corso di Matematica
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 09 - Derivate II Limiti di forme indetermate e derivate
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 09 - Derivate II Limiti di forme indetermate e derivate
Misura della sezione d urto di produzione di Z 0 Z 0 nel canale di decadimento quadrileptonico all esperimento CDF
 Misura della sezione d urto di produzione di Z 0 Z 0 nel canale di decadimento quadrileptonico all esperimento CDF UNIVERSITÀ DEGLI STUDI DI PADOVA LAUREA SPECIALISTICA IN FISICA Relatrice: D. Lucchesi
Misura della sezione d urto di produzione di Z 0 Z 0 nel canale di decadimento quadrileptonico all esperimento CDF UNIVERSITÀ DEGLI STUDI DI PADOVA LAUREA SPECIALISTICA IN FISICA Relatrice: D. Lucchesi
Oscillazioni libere e risonanza di un circuito RLC-serie (Trattazione analitica del circuito RLC-serie)
 III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
La struttura del nucleone
 La struttura del nucleone 90% del materiale dai proff. Ragusa e Mandelli Scattering elettrone-nucleone Capitolo 8: The Structure of the Nucleon Negli anni 50 con la formulazione del modello a quark (statico)
La struttura del nucleone 90% del materiale dai proff. Ragusa e Mandelli Scattering elettrone-nucleone Capitolo 8: The Structure of the Nucleon Negli anni 50 con la formulazione del modello a quark (statico)
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Istituzioni di Fisica Nucleare e Subnucleare Prof. A. Andreazza. Lezione 14. Il Modello Standard
 Istituzioni di Fisica Nucleare e Subnucleare Prof. A. Andreazza Lezione 14 Il Modello Standard Simmetria di gauge Abbiamo visto diversi tipi di simmetrie: Simmetrie per traslazione (anche temporale), rotazione
Istituzioni di Fisica Nucleare e Subnucleare Prof. A. Andreazza Lezione 14 Il Modello Standard Simmetria di gauge Abbiamo visto diversi tipi di simmetrie: Simmetrie per traslazione (anche temporale), rotazione
G.V. Margagliotti. Appunti di Introduzione alla Fisica Nucleare e Subnucleare a.a. 2017/18
 G.V. Margagliotti Appunti di Introduzione alla Fisica Nucleare e Subnucleare a.a. 2017/18 2017 Indice 1 Preambolo 11 1.1 I costituenti fondamentali della materia............ 12 1.2 Elementarietà...........................
G.V. Margagliotti Appunti di Introduzione alla Fisica Nucleare e Subnucleare a.a. 2017/18 2017 Indice 1 Preambolo 11 1.1 I costituenti fondamentali della materia............ 12 1.2 Elementarietà...........................
Effetto Zeeman. p q c A) 2. i h ψ t. = Hψ (2)
 Effetto Zeeman Effetto Zeeman normale La hamiltoniana di una particella in presenza di un campo elettromagnetico, descritto dal potenziale vettore A e dal potenziale scalare Φ é H = 2M e l euazione di
Effetto Zeeman Effetto Zeeman normale La hamiltoniana di una particella in presenza di un campo elettromagnetico, descritto dal potenziale vettore A e dal potenziale scalare Φ é H = 2M e l euazione di
Note sulla probabilità
 Note sulla probabilità Maurizio Loreti Dipartimento di Fisica Università degli Studi di Padova Anno Accademico 2002 03 1 La distribuzione del χ 2 0.6 0.5 N=1 N=2 N=3 N=5 N=10 0.4 0.3 0.2 0.1 0 0 5 10 15
Note sulla probabilità Maurizio Loreti Dipartimento di Fisica Università degli Studi di Padova Anno Accademico 2002 03 1 La distribuzione del χ 2 0.6 0.5 N=1 N=2 N=3 N=5 N=10 0.4 0.3 0.2 0.1 0 0 5 10 15
Limiti di successioni
 Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Studio sperimentale del decadimento del nucleo eccitato 88 Mo prodotto in reazioni di fusione
 Società Italiana di Fisica 100 Congresso Nazionale Simone Valdré Studio sperimentale del decadimento del nucleo eccitato 88 Mo prodotto in reazioni di fusione Università degli studi di Firenze e INFN -
Società Italiana di Fisica 100 Congresso Nazionale Simone Valdré Studio sperimentale del decadimento del nucleo eccitato 88 Mo prodotto in reazioni di fusione Università degli studi di Firenze e INFN -
Esercitazione 05: Trasformata di Laplace e funzione di trasferimento
 Esercitazione 05: Trasformata di Laplace e funzione di trasferimento 28 marzo 208 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state
Esercitazione 05: Trasformata di Laplace e funzione di trasferimento 28 marzo 208 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state
La radiazione elettromagnetica nucleare deve avere una lunghezza d onda dell ordine delle dimensioni del nucleo, e pertanto: c A 1/ 3
 Emissione gamma La radiazione γ è l emissione spontanea di quanti da parte del nucleo. Emettendo fotoni il nucleo passa da uno stato eccitato ed uno stato meno eccitato. Vi possono essere transizioni radiative
Emissione gamma La radiazione γ è l emissione spontanea di quanti da parte del nucleo. Emettendo fotoni il nucleo passa da uno stato eccitato ed uno stato meno eccitato. Vi possono essere transizioni radiative
Corso di Fenomenologia delle Interazioni Fondamentali LM in Fisica, AA Silvia Arcelli
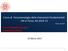 Corso di Fenomenologia delle Interazioni Fondamentali LM in Fisica, AA 2014-15 Silvia Arcelli Verso il Modello Standard: Scoperta del charm 10 Marzo 2015 1 Scoperta del charm, del tau e del beuty Il quarto
Corso di Fenomenologia delle Interazioni Fondamentali LM in Fisica, AA 2014-15 Silvia Arcelli Verso il Modello Standard: Scoperta del charm 10 Marzo 2015 1 Scoperta del charm, del tau e del beuty Il quarto
Introduzione alla Fisica Moderna - a.a
 Introduzione alla Fisica Moderna - a.a. 2016-17 18/12/2017 Nome Cognome Matricola: 1) Si consideri il sistema dinamico nonlineare ẋ = y x 2, ẏ = x + y 2, Si determinino i punti di equilibrio, si caratterizzi
Introduzione alla Fisica Moderna - a.a. 2016-17 18/12/2017 Nome Cognome Matricola: 1) Si consideri il sistema dinamico nonlineare ẋ = y x 2, ẏ = x + y 2, Si determinino i punti di equilibrio, si caratterizzi
Il Principio di Indeterminazione di Heisenberg
 Il Principio di Indeterminazione di Heisenberg Il Principio di Indeterminazione di Heisenberg è uno dei fondamenti della meccanica quantistica, e stabilisce che non è possibile ottenere nello stesso tempo
Il Principio di Indeterminazione di Heisenberg Il Principio di Indeterminazione di Heisenberg è uno dei fondamenti della meccanica quantistica, e stabilisce che non è possibile ottenere nello stesso tempo
Lezione 4 Quadratura Numerica. Fernando Palombo
 Lezione 4 Quadratura Numerica http://idefix.mi.infn.it/~palombo/didattica/lab-tnds/corsolab/lezionifrontali Fernando Palombo Scopo della Quadratura Numerica Calcolare con metodi numerici un integrale definito
Lezione 4 Quadratura Numerica http://idefix.mi.infn.it/~palombo/didattica/lab-tnds/corsolab/lezionifrontali Fernando Palombo Scopo della Quadratura Numerica Calcolare con metodi numerici un integrale definito
Diffusione da elettroni legati elasticamente
 Diffusione da elettroni legati elasticamente Nell ipotesi di elettroni legati elasticamente nella materia, il moto del singolo elettrone è determinato dall equazione del moto classica r + γṙ + ω 0r F ext
Diffusione da elettroni legati elasticamente Nell ipotesi di elettroni legati elasticamente nella materia, il moto del singolo elettrone è determinato dall equazione del moto classica r + γṙ + ω 0r F ext
Definizione della variabile c 2 Distribuzione della variabile c 2
 Definizione della variabile c Distribuzione della variabile c In queste definizioni ho N variabili indipendenti, nessun vincolo e quindi N coincide con i gradi di libertà In un sistema fisico dove il numero
Definizione della variabile c Distribuzione della variabile c In queste definizioni ho N variabili indipendenti, nessun vincolo e quindi N coincide con i gradi di libertà In un sistema fisico dove il numero
Disuguaglianza di Cramér-Rao
 Disuguaglianza di Cramér-Rao (Appunti per gli studenti Silvano Holzer Dipartimento di Scienze Economiche, Aziendali, Matematiche e Statistiche Bruno de Finetti Università degli studi di Trieste Un esperimento
Disuguaglianza di Cramér-Rao (Appunti per gli studenti Silvano Holzer Dipartimento di Scienze Economiche, Aziendali, Matematiche e Statistiche Bruno de Finetti Università degli studi di Trieste Un esperimento
FAM A+B C. Considera la disintegrazione di una particella A in due particelle B e C: A B +C.
 Serie 19: Relatività VIII FAM C. Ferrari Esercizio 1 Collisione completamente anelastica Considera la collisione frontale di due particelle A e B di massa M A = M B = M e v A = v B = 3/5c, tale che alla
Serie 19: Relatività VIII FAM C. Ferrari Esercizio 1 Collisione completamente anelastica Considera la collisione frontale di due particelle A e B di massa M A = M B = M e v A = v B = 3/5c, tale che alla
Problema Cosmologico e Modello Standard Fernando Palombo
 Problema Cosmologico e Modello Standard Fernando Palombo Per queste trasparenze: http://idefix.mi.infn.it/~palombo/didattica/cpviolation/ Lezione3-Cosmologia-ModelloStandard.pdf Bibliografia BaBar Physics
Problema Cosmologico e Modello Standard Fernando Palombo Per queste trasparenze: http://idefix.mi.infn.it/~palombo/didattica/cpviolation/ Lezione3-Cosmologia-ModelloStandard.pdf Bibliografia BaBar Physics
Corso di Laurea: Numero di Matricola: Esame del 31 maggio 2018 Tempo consentito: 120 minuti
 Corso di Laurea: Numero di Matricola: Esame del 31 maggio 2018 Tempo consentito: 120 minuti Professor Paolo Vitale Anno Accademico 2017-8 UdA, Scuola d Economia Domanda 1 [6 punti]. (a) La multi-collineartità
Corso di Laurea: Numero di Matricola: Esame del 31 maggio 2018 Tempo consentito: 120 minuti Professor Paolo Vitale Anno Accademico 2017-8 UdA, Scuola d Economia Domanda 1 [6 punti]. (a) La multi-collineartità
CALCOLO NUMERICO Prof. L. Gori Prova d esame
 CALCOLO NUMERICO Prof. L. Gori Prova d esame 2-7-998 ESERCIZIO. Data la seguente formula di quadratura: f(x)dx = ( ) 3 3 2 f + Af( x) + R 6 0 (.) Determinare A e x in modo che il grado di precisione sia.
CALCOLO NUMERICO Prof. L. Gori Prova d esame 2-7-998 ESERCIZIO. Data la seguente formula di quadratura: f(x)dx = ( ) 3 3 2 f + Af( x) + R 6 0 (.) Determinare A e x in modo che il grado di precisione sia.
Analisi multivariata per osservazioni appaiate. Analisi multivariata per osservazioni appaiate
 Introduzione Notazione Modello additivo Verifica d ipotesi Sia X una variabile q-dimensionale, a valori reali, non degenere, osservata in k tempi diversi (τ 1, τ 2,..., τ k ), sulle stesse n unità statistiche
Introduzione Notazione Modello additivo Verifica d ipotesi Sia X una variabile q-dimensionale, a valori reali, non degenere, osservata in k tempi diversi (τ 1, τ 2,..., τ k ), sulle stesse n unità statistiche
Introduzione agli acceleratori Parte III: Emissione di sincrotrone
 Introduzione agli acceleratori Parte III: Emissione di sincrotrone Gabriele Chiodini Istituto Nazionale di Fisica Nucleare Sezione di Lecce Corso di Laurea Magistrale in Fisica dell Università del Salento
Introduzione agli acceleratori Parte III: Emissione di sincrotrone Gabriele Chiodini Istituto Nazionale di Fisica Nucleare Sezione di Lecce Corso di Laurea Magistrale in Fisica dell Università del Salento
METODI NUMERICI. Metodo delle differenze finite
 METOI NUMERICI Lo sviluppo dei moderni calcolatori ha consentito di mettere a disposizione della scienza e della tecnica formidabili strumenti che hanno permesso di risolvere numerosi problemi la cui soluzione
METOI NUMERICI Lo sviluppo dei moderni calcolatori ha consentito di mettere a disposizione della scienza e della tecnica formidabili strumenti che hanno permesso di risolvere numerosi problemi la cui soluzione
