Forme aggiunte su varietà algebriche
|
|
|
- Filippa Palma
- 5 anni fa
- Visualizzazioni
Transcript
1 Forme aggiunte su varietà algebriche Luca Rizzi Università degli studi di Udine Genova 31 Maggio 2018
2 Famiglia di Varietà Definizione Una famiglia di varietà n-dimensionali è un morfismo proprio sommersivo π : X B tale che la fibra X b := π 1 (b) sopra un punto b B ha dimensione n. La varietà B è detta base della famiglia.
3 Famiglia di Varietà Definizione Una famiglia di varietà n-dimensionali è un morfismo proprio sommersivo π : X B tale che la fibra X b := π 1 (b) sopra un punto b B ha dimensione n. La varietà B è detta base della famiglia. Fissiamo un punto 0 B e chiamiamo X := X 0 la fibra sopra tale punto. Possiamo interpretare la famiglia π : X B come una deformazione della struttura complessa di X. In pratica interpretiamo le fibre X b := π 1 (b) con b B come deformazione della fibra centrale X = X 0.
4 La mappa dei periodi Consideriamo una famiglia π : X B. Ad ogni fibra X b possiamo associare la struttura di Hodge sulla coomologia k-esima. Più in dettaglio: ad ogni punto della base associamo il pezzo p-esimo della filtrazione di Hodge b F p H k (X b, C) < H k (X b, C).
5 La mappa dei periodi Consideriamo una famiglia π : X B. Ad ogni fibra X b possiamo associare la struttura di Hodge sulla coomologia k-esima. Più in dettaglio: ad ogni punto della base associamo il pezzo p-esimo della filtrazione di Hodge b F p H k (X b, C) < H k (X b, C). Per il Teorema di Ehresmann, eventualmente restringendo la base B, otteniamo che lo spazio vettoriale H k (X b, C) è isomorfo a V := H k (X, C), per ogni b B. Denotiamo con b p,k la dimensione dim C F p H k (X b, C).
6 La mappa dei periodi Definizione La mappa dei periodi P p,k : B G = Grass(b p,k, V ) è la mappa che a b B associa il sottospazio F p H k (X b, C) di V. Teorema (P. Griffiths) La mappa P p,k è olomorfa per ogni p, k con p k. Mettendo insieme le mappe P p,k per p = 1,..., k, otteniamo una mappa, anch essa chiamata mappa dei periodi, P k : B k Grass(b p,k, V ) p=1 b (P 1,k (b),..., P k,k (b)).
7 Il differenziale della mappa dei periodi Lo spazio tangente alla varietà Grassmanniana Grass(r, V ) in un punto W è Hom(W, V /W ), quindi il differenziale della mappa dei Periodi è: dp p,k : T B,b Hom(F p H k (X b, C), H k (X b, C)/F p H k (X b, C)) Denotiamo con Θ X il fascio dei vettori tangenti ad X e con Ω p X il fascio delle p-forme olomorfe. Teorema (P. Griffiths) Il differenziale della mappa dei periodi dp p,k assume valori in Hom(H q (X b, Ω p X b ), H q+1 (X b, Ω p 1 X b )) ed è dato dalla composizione della mappa di Kodaira-Spencer con la mappa data dal prodotto cup: dp p,k : T B,b H 1 (X b, Θ Xb ) Hom(H q (X b, Ω p X b ), H q+1 (X b, Ω p 1 X b )).
8 La famiglia di Kuranishi Teorema (M. Kuranishi) Per ogni varietà complessa compatta X esiste una famiglia π : X B con π 1 (0) = X e tale che la mappa di Kodaira-Spencer T B,0 H 1 (X, Θ X ) è un isomorfismo. Tale famiglia è detta famiglia di Kuranishi di X. Quindi, per la famiglia di Kuranishi, la prima parte del differenziale della mappa dei periodi è un isomorfismo: dp p,k : T B,b = H 1 (X b, Θ Xb ) Hom(H q (X b, Ω p X b ), H q+1 (X b, Ω p 1 X b )).
9 Problemi di tipo Torelli Ci sono vari problemi di Torelli: Il problema di Torelli globale indaga l iniettività della mappa dei periodi, cioè se è possibile ricostruire la struttura complessa della varietà X a partire dalla sua struttura di Hodge. Il problema di Torelli generico indaga l iniettività generica della mappa dei periodi. Infine il problema di Torelli infinitesimale studia l iniettività del differenziale della mappa dei periodi per la famiglia di Kuranishi π : X B nel punto 0 B. La teoria dell aggiunta risulta utile per lo studio di quest ultimo problema.
10 Il problema infinitesimale di Torelli: alcuni dettagli Dobbiamo studiare l iniettività del differenziale della mappa dei periodi dp p,k : T B,0 = H 1 (X, Θ X ) Hom(H q (X, Ω p X ), Hq+1 (X, Ω p 1 X )). Poiché la Kodaira-Spencer è un isomorfismo per la famiglia di Kuranishi, è sufficiente far vedere l iniettività di H 1 (X, Θ X ) Hom(H q (X, Ω p X ), Hq+1 (X, Ω p 1 X )) per opportuni p e q. D ora in poi considereremo q = 0 e p = 1.
11 Il problema infinitesimale di Torelli: alcuni risultati noti Nel caso delle curve lisce, il risultato del problema di Torelli è ben noto: Teorema Il teorema di Torelli infinitesimale vale per ogni curva liscia C con g(c) pari a 1, 2 o g(c) 3 e C non iperellittica. In dimensione più alta la situazione non è così chiara: ci sono sia risultati positivi (ipersuperfici lisce dello spazio proiettivo, divisori lisci sufficientemente ampi di una varietà liscia, intersezioni complete) ma anche controesempi (superfici di tipo generale con H 0 (X, Ω 1 X ) = H0 (X, Ω 2 X ) = 0, prodotto simmetrico di curve iperellittiche).
12 Interpretazione via estensioni Definizione Siano F, G fasci di O X -moduli. Una estensione di F con G è una sequenza esatta corta di O X -moduli 0 G E F 0. Se fissiamo F e G, tutte le classi di isomorfismo di estensioni di F con G formano un gruppo abeliano denotato con Ext 1 (F, G). Se i fasci sono localmente liberi e G è O X abbiamo: Ext 1 (F, O X ) = H 1 (X, F ).
13 Interpretazione via estensioni Per studiare l iniettività di H 1 (X, Θ X ) Hom(H 0 (X, Ω 1 X ), H1 (X, O X )) prendiamo un elemento ξ H 1 (X, Θ X ). Poiché H 1 (X, Θ X ) = Ext 1 (Ω 1 X, O X ), ξ è unicamente associato (a meno di isomorfismo) ad una estensione del fascio delle 1-forme olomorfe Ω 1 X : 0 O X Ω 1 X X Ω1 X 0. Questa sequenza esatta corta dà in coomologia una sequenza lunga H 0 (X, Ω 1 X X ) H0 (X, Ω 1 X ) δ ξ H 1 (X, O X )
14 Il problema di Torelli infinitesimale si riduce alla seguente domanda: se l omomorfismo di cobordo δ ξ è zero, possiamo dire che ξ = 0, cioè che Ω 1 X X = O X Ω 1 X? In maggior generalità studiamo il problema: sia 0 O X E F 0 una sequenza esatta di fasci localmente liberi associata ad un elemento ξ H 1 (X, F ) tale che la mappa in coomologia H 0 (X, F) δ ξ H 1 (X, O X ) sia zero. Cosa possiamo dire di ξ? La teoria delle forme aggiunte è particolarmente adatta per lo studio di tale problema.
15 Forma aggiunta Consideriamo una sequenza esatta di fasci localmente liberi su X : 0 O X E F 0. Assumiamo che F sia di rango n e che il nucleo dell omomorfismo di connessione δ ξ : H 0 (X, F) H 1 (X, O X ) abbia dimensione n + 1.
16 Forma aggiunta Consideriamo una sequenza esatta di fasci localmente liberi su X : 0 O X E F 0. Assumiamo che F sia di rango n e che il nucleo dell omomorfismo di connessione δ ξ : H 0 (X, F) H 1 (X, O X ) abbia dimensione n + 1. Prendiamo un sottospazio n + 1-dimensionale W ker δ ξ e una base B = {η 1,..., η n+1 } di W. Poiché η 1,..., η n+1 sono elementi di ker δ ξ, dalla sequenza esatta lunga in coomologia H 0 (X, E) H 0 (X, F) δ ξ H 1 (X, O X )... possiamo scegliere dei sollevamenti s i H 0 (X, E) di η i, per i = 1,..., n + 1.
17 Consideriamo il prodotto wedge s 1... s n+1 n+1 H 0 (X, E) e chiamiamo Ω la sua immagine in H 0 (X, det E) tramite la mappa naturale n+1 H 0 (X, E) H 0 (X, det E) s 1... s n+1 Ω Poiché det E = det F otteniamo da Ω una sezione globale ω di det F, che dipende dai sollevamenti scelti e da B. H 0 (X, det E) = H 0 (X det F) Ω ω Definizione Chiamiamo ω H 0 (X, det F) una forma aggiunta di ξ, W, B.
18 Chiamiamo ω i per i = 1,..., n + 1 l immagine di η 1... η i... η n+1 n H 0 (X, F) tramite l applicazione n H 0 (X, F) H 0 (X, det F). Chiamiamo λ n W = ω 1,..., ω n+1 < H 0 (X, det F) lo spazio vettoriale generato dalle sezioni ω i. Denotiamo con D W e Z W la parte fissa e il luogo base del sistema lineare λ n W.
19 L espressione locale della forma aggiunta Sia U X un aperto su cui i fasci E e F della sequenza 0 O X E F 0 sono banali. Prendiamo generatori (σ 1,..., σ n ) di F. Quindi E è generato su U da (σ 1,..., σ n, dɛ). Possiamo scrivere le sezioni η i e n η i U = bj i σ j j=1 n s i U = bj i σ j + c i dɛ. j=1
20 Risulta che b bn 1 c 1 ω U = σ b1 n+1 1 σ n. (1)... bn n+1 c n+1 e b bn ω i U = b1 i 1... bn i 1 b1 i+1... bn i b1 n+1... bn n+1 σ 1 σ n L espressione locale delle sezioni ω i dà delle entrate della matrice aggiunta di (1), questo spiega il nome della teoria.
21 Il risultato principale Problema La forma aggiunta ω appartiene al sottospazio λ n W = ω 1,..., ω n+1? Se questo accade, cosa possiamo dire della classe di estensione ξ?
22 Il risultato principale Problema La forma aggiunta ω appartiene al sottospazio λ n W = ω 1,..., ω n+1? Se questo accade, cosa possiamo dire della classe di estensione ξ? Il teorema dell aggiunta risponde a questo problema: Teorema (Teorema dell aggiunta) Siano ω una forma aggiunta associata al sottospazio W H 0 (X, det F). Se ω λ n W allora ξ ker(h 1 (X, F ) H 1 (X, F (D W ))). Viceversa, se ξ sta in questo nucleo e h 0 (X, O X (D W )) = 1, allora ω λ n W. Corollario Se D W = 0 abbiamo che ω λ n W se e solo se ξ = 0.
23 Il risultato principale 0 O X Ê F( D W ) 0 0 O X E F 0
24 Ritorniamo al problema di Torelli Il teorema dell aggiunta può essere usato per dimostrare il teorema infinitesimale di Torelli in certe classi di varietà. Prendiamo la sequenza 0 O X Ω 1 X X Ω1 X 0 e ricordiamo che abbiamo ridotto il problema allo studio della seguente: se la mappa di cobordo δ ξ è zero, possiamo dire che ξ = 0?
25 Ritorniamo al problema di Torelli Il teorema dell aggiunta può essere usato per dimostrare il teorema infinitesimale di Torelli in certe classi di varietà. Prendiamo la sequenza 0 O X Ω 1 X X Ω1 X 0 e ricordiamo che abbiamo ridotto il problema allo studio della seguente: se la mappa di cobordo δ ξ è zero, possiamo dire che ξ = 0? Scegliamo un sottospazio opportuno W H 0 (X, Ω 1 X ) (dato che stiamo assumendo δ ξ = 0, la sollevabilità delle sezioni η i è garantita) Verifichiamo che ω è un elemento di λ n W Verifichiamo che D W = 0. Per il corollario precedente otteniamo che ξ = 0.
26 Esempio di applicazione Corollario Sia X una varietà n-dimensionale primitiva di tipo generale tale che p g = q = n + 1. Se Ω 1 X è generato da sezioni globali allora il teorema di Torelli infinitesimale vale per X. In questo caso prendiamo W = H 0 (X, Ω 1 X ) (q = n + 1) ω è un elemento di λ n W perché λ n W = ω 1,..., ω n+1 = H 0 (X, ω X ) (X è primitiva e p g = n + 1) D W = 0 (Ω 1 X è generato dalle sezioni globali).
27 Quadriche aggiunte La seguente nozione risulta essere importante per ottenere soluzioni positive al problema infinitesimale di Torelli. Definizione Una quadrica aggiunta per ω è una quadrica in P(H 0 (X, det F) ) della forma ω 2 L i ω i, dove ω è una forma aggiunta di W H 0 (X, F), le sezioni ω i sono come sopra e L i H 0 (X, det F), i = 1,..., n + 1.
28 Nel caso di problemi di Torelli in cui F = Ω 1 X, le quadriche aggiunte sono quadriche nello spazio proiettivo P(H 0 (X, ω X ) ). In particolare ci possiamo chiedere che relazione abbiano con l immagine canonica della varietà X. Risulta che Teorema Se non ci sono quadriche aggiunte che svaniscono sull immagine canonica di X, allora la forma aggiunta ω appartiene al sottospazio generato dalle ω i, λ n W. Quindi lo studio delle quadriche che passano per l immagine canonica di X può essere utile per lo studio della condizione ω λ n W e quindi anche per la soluzione del problema infinitesimale di Torelli.
29 Esempi di applicazione La tecnica delle quadriche aggiunte risulta efficiente nel caso in cui ci siano poche (o meglio ancora nessuna) quadriche che svaniscono sull immagine canonica di X. Esempio L immagine canonica di X è una ipersuperficie di grado > 2 o una intersezione completa di ipersuperfici di grado > 2. Esempio Superfici di Schoen. Una superficie di Schoen ha p g = 5 e q = 4. La sua mappa canonica S P 4 è un morfismo 2:1 su una superficie che è l intersezione completa di una quadrica ed una quartica. La sua immagine canonica è singolare con 40 nodi.
30 È possibile dimostrare che la quadrica che contiene l immagine canonica di una superficie di Schoen non è una quadrica aggiunta, ottenendo quindi il seguente risultato: Teorema Il teorema infinitesimale di Torelli vale per superfici di Schoen. Con questa tecnica dovrebbe essere possibile studiare altri esempi simili.
31 È possibile dimostrare che la quadrica che contiene l immagine canonica di una superficie di Schoen non è una quadrica aggiunta, ottenendo quindi il seguente risultato: Teorema Il teorema infinitesimale di Torelli vale per superfici di Schoen. Con questa tecnica dovrebbe essere possibile studiare altri esempi simili. Per studiare il problema di Torelli tramite la teoria dell aggiunta è necessario avere almeno dim X + 1 forme differenziali. Cosa fare se non ci troviamo in questo caso?
32 Una generalizzazione della teoria Consideriamo l estensione 0 O X E F 0. Se vogliamo applicare la teoria come presentata finora abbiamo bisogno dell ipotesi h 0 (X, F) n + 1 dove n è il rango di F. Questo può essere restrittivo. La prima idea che viene in mente è tensorizzare questa sequenza con un fascio invertibile sufficientemente ampio L ed ottenere la sequenza 0 L E L F L 0. Scegliendo L opportunamente avremo h 0 (X, F L) n + 1. Inoltre questa sequenza è ancora associata alla stessa estensione ξ. Dobbiamo quindi estendere la teoria dell aggiunta a sequenze esatte in cui il primo fascio non è necessariamente O X.
33 Prendiamo la sequenza esatta su X : 0 L E F 0. Assumiamo che F sia di rango n e che il nucleo dell omomorfismo di connessione δ ξ : H 0 (X, F) H 1 (X, O X ) abbia dimensione n + 1. Scegliamo un sottospazio n + 1-dimensionale W ker δ ξ ed una sua base B = {η 1,..., η n+1 }. Scegliamo sollevamenti s i H 0 (X, E) di η i, per i = 1,..., n + 1. Definizione La sezione Ω H 0 (X, det E) che corrisponde a s 1... s n+1 tramite n+1 H 0 (X, E) H 0 (X, det E) è detta forma aggiunta generalizzata.
34 Differenze con la teoria classica La forma aggiunta ω è un elemento di H 0 (X, det F), la forma aggiunta generalizzata Ω è un elemento di H 0 (X, det E) Per la teoria classica la giusta condizione da studiare è ω λ n W, per la teoria generalizzata invece Ω Im (H 0 (X, L) λ n W H 0 (X, det E)). Notiamo che se L = O X, allora det F = det E e H 0 (X, L) = C, quindi la teoria generalizzata si riduce a quella classica.
35 Il teorema dell aggiunta generalizzata Teorema (Dell aggiunta generalizzata) Se Ω Im (H 0 (X, L) λ n W H 0 (X, det E)) allora ξ ker(h 1 (X, F L) H 1 (X, F L(D W ))). Viceversa assumiamo che ξ è in questo nucleo e che H 0 (X, L) = H 0 (X, L(D W )), allora Ω Im (H 0 (X, L) λ n W H 0 (X, det E)). Corollario Se D W = 0 abbiamo che Ω Im (H 0 (X, L) λ n W H 0 (X, det E)) se e solo se ξ = 0.
36 Applicazioni: ipersuperfici di P n Sia X P n una ipersuperficie liscia di grado d definita dal polinomio omogeneo F. Ricordiamo che, dato il polinomio F C[x 0,..., x n ], l ideale Jacobiano di F è l ideale J C[x 0,..., x n ] generato dalle derivate parziali F x i per i = 0,..., n. Poichè l anello C[x 0,..., x n ] e l ideale Jacobiano J sono graduati, il loro quoziente R := C[x 0,..., x n ]/J, chiamato anello Jacobiano, ha una graduazione naturale. Denotiamo con R k gli elementi di grado k.
37 Il differenziale della mappa dei periodi per ipersuperfici Proposizione Se n 4 o n = 3 e d 4 c è un isomorfismo Inoltre per ogni p H 1 (X, Θ X ) = R d. H n p,p 1 (X ) = R dp n 1. Una deformazione infinitesima ξ H 1 (X, Θ X ) è data da una classe [G] C[x 0,..., x n ]/J dove G è un polinomio omogeneo di grado d. Intuitivamente, la famiglia di deformazione data da [G] ha equazione F + tg = 0. Per t = 0 otteniamo la varietà X di partenza e per t 0 sufficientemente piccolo abbiamo una nuova ipersuperficie liscia di P n che è una deformazione di X.
38 P. Griffiths ha dimostrato che: Teorema Grazie alle identificazioni precedenti, il differenziale della mappa dei periodi H 1 (X, Θ X ) Hom(H n p,p 1 (X ), H n p 1,p (X )) è data dalla moltiplicazione polinomiale R d Hom(R dp n 1, R d(p+1) n 1 ). Ciò significa che il problema infinitesimale di Torelli è ricondotto al livello di polinomi.
39 Il teorema di Macaulay Teorema (Macaulay) Dati due interi a, b tali che b 0 e a + b (n + 1)(d 2), la mappa data dal prodotto è iniettiva. R a Hom(R b, R a+b ) Questo risultato permette di dimostrare il teorema di Torelli infinitesimale per ipersuperfici lisce.
40 Aggiunta generalizzata e Torelli infinitesimale Sia X P n Una ipersuperficie liscia definita da un polinomio omogeneo F C[x 0,..., x n ] di grado deg F = d. Una deformazione infinitesimale ξ Ext 1 (Ω 1 X, O X ) di X dà una sequenza esatta per il fascio di forme differenziali Ω 1 X : 0 O X Ω 1 X X Ω1 X 0. (2) Assumiamo che n 3, quindi H 0 (X, Ω 1 X ) = 0 e non possiamo applicare direttamente la teoria della forma aggiunta classica. Come abbiamo visto l idea è di tensorizzare (2) per un intero a in modo che Ω 1 X (a) abbia almeno n sezioni globali. Non è difficile vedere che a = 2 è sufficiente. L aggiunta generalizzata funziona perfettamente con la sequenza 0 O X (2) Ω 1 X X (2) Ω1 X (2) 0.
41 Usando l aggiunta generalizzata otteniamo il seguente risultato. Teorema Per una ipersuperficie liscia X di grado d in P n con n 3 e d > 3 le seguenti sono equivalenti: i) Il differenziale della mappa dei periodi è zero sulla deformazione infinitesima [G] R d = H 1 (X, Θ X ) ii) G è un elemento dell ideale J iii) Ω Im (H 0 (X, O X (2)) λ n W H 0 (X, O X (n + d 1))) per la generica aggiunta generalizzata Ω iv) La generica aggiunta generalizzata Ω appartiene all ideale J. Questo teorema è il teorema infinitesimale di Torelli per ipersuperfici proiettive riformulato nel linguaggio della teoria delle forme aggiunte. Un risultato simile vale anche per divisori ampi sufficientemente lisci di una varietà razionale omogenea con numero di Picard pari a uno.
42 Il teorema dell aggiunta per curve Gorenstein La teoria dell aggiunta può essere estesa anche a varietà singolari. Il caso che consideriamo è quello di una curva Gorenstein. Definizione Una curva di Gorenstein è una curva proiettiva C tale che il fascio dualizzante ω C è invertibile. Possiamo estendere la teoria dell aggiunta a curve Gorenstein irriducibili. Consideriamo una sequenza di fasci localmente liberi con F e L di rango 1. 0 L E F 0
43 Il problema principale Sia δ ξ : H 0 (C, F) H 1 (C, L) il suo omomorfismo di connessione, e sia W ker δ ξ un sottospazio vettoriale di dimensione 2. Scegliamo una base B := {η 1, η 2 } di W. Possiamo scegliere sollevamenti s 1, s 2 H 0 (C, E) delle sezioni η 1, η 2. Consideriamo il luogo base di W. Consiste di un numero finito di punti lisci e singolari. Denotiamo con D W il divisore di Cartier associato ai punti lisci nel luogo base e con I W l ideale dei punti singolari. L ideale I W è un divisore effettivo generalizzato sulla curva C.
44 Una nuova definizione di aggiunta Proposizione Abbiamo il seguente diagramma 0 F (D W ) I 1 W W O C F( D W ) I W 0 ω (s 1,s 2 ) 0 L E F 0 che può essere completato con una mappa ω Hom(F (D W ) I 1 W, L). Definizione Il morfismo ω Hom(F (D W ) I 1 W, L) è detto aggiunto di W e ξ.
45 Una nuova definizione di aggiunta Nel caso liscio il diagramma è 0 F (D W ) W O C F( D W ) 0 (s 1,s 2 ) 0 L E F 0 e la prima freccia verticale è data per contrazione con l aggiunta generalizzata Ω H 0 (X, det E). Nel caso singolare studiamo la condizione ω Im Φ B dove Φ B : Hom(W O C, L) Hom(F (D W ) I 1 W, L).
46 Una nuova definizione di aggiunta Nel caso liscio il diagramma è 0 F (D W ) W O C F( D W ) 0 (s 1,s 2 ) 0 L E F 0 e la prima freccia verticale è data per contrazione con l aggiunta generalizzata Ω H 0 (X, det E). Nel caso singolare studiamo la condizione ω Im Φ B dove Φ B : Hom(W O C, L) Hom(F (D W ) I 1 W, L).
47 Teorema dell aggiunta per curve Gorenstein Teorema Sia C una curva Gorenstein irriducibile. Siano F, L fasci invertibili su C. Consideriamo ξ Ext 1 (F, L) associata all estensione 0 L E F 0. Abbiamo che ω Im Φ B se e solo se ξ è nel nucleo di Ext 1 (F, L) Ext 1 (F( D W ) I W, L). Come applicazione abbiamo Teorema Sia C una curva di Gorenstein irriducibile di genere 2 o non iperellittica di genere 3, ξ H 1 (C, ω C ) tale che δ ξ = 0. Allora ξ = 0.
48 Questo teorema è sostanzialmente il teorema di Torelli infinitesimale per deformazioni di curve Gorenstein che non rimuovono le singolarità. Infatti abbiamo la sequenza esatta 0 H 1 (C, Hom(Ω 1 C, O C )) Ext 1 (Ω 1 C, O C ) R 0. Questa sequenza ci dice che ci sono due tipi di deformazioni al primo ordine di C. Quelle che vengono da R sono quelle che rimuovono le singolarità. D altra parte le deformazioni di H 1 (C, Hom(Ω 1 C, O C )) sono localmente banali intorno ad i punti singolari.
49 GRAZIE PER L ATTENZIONE
Appunti per il corso di Algebraic Geometry 2. Claudio Fontanari
 Appunti per il corso di Algebraic Geometry 2 Claudio Fontanari Trento, maggio 2014 Definizione: la dimensione di Kodaira κ(x) di una varietà proiettiva X è la massima dimensione dell immagine di X in P
Appunti per il corso di Algebraic Geometry 2 Claudio Fontanari Trento, maggio 2014 Definizione: la dimensione di Kodaira κ(x) di una varietà proiettiva X è la massima dimensione dell immagine di X in P
Mattia Talpo. 24 Luglio 2009
 24 Luglio 2009 : studio locale di famiglie di oggetti. Oggetti=, con eventuale struttura aggiuntiva: punti marcati, sotto chiusi, fasci, fibrati,... Famiglie=morfismi f : X S, con eventuale struttura aggiuntiva
24 Luglio 2009 : studio locale di famiglie di oggetti. Oggetti=, con eventuale struttura aggiuntiva: punti marcati, sotto chiusi, fasci, fibrati,... Famiglie=morfismi f : X S, con eventuale struttura aggiuntiva
Superficie K3 e spazi di moduli. Claudio Fontanari
 Superficie K3 e spazi di moduli Claudio Fontanari Trento, maggio 2014 Definizione: la dimensione di Kodaira κ(x) di una varietà proiettiva X è la massima dimensione dell immagine di X in P N tramite la
Superficie K3 e spazi di moduli Claudio Fontanari Trento, maggio 2014 Definizione: la dimensione di Kodaira κ(x) di una varietà proiettiva X è la massima dimensione dell immagine di X in P N tramite la
Corso di Superfici di Riemann e curve algebriche. Programma
 Corso di Superfici di Riemann e curve algebriche Programma (1) Carta complessa, compatibilità di carte complesse, atlante complesso. Definizione di superficie di Riemann. Primi esempi di superfici di Riemann:
Corso di Superfici di Riemann e curve algebriche Programma (1) Carta complessa, compatibilità di carte complesse, atlante complesso. Definizione di superficie di Riemann. Primi esempi di superfici di Riemann:
Geometria Algebrica A.A Esercizi. Insiemi algebrici affini, Insiemi algebrici irriducibili.
 Geometria Algebrica A.A. 2014 2015 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non scritto al contrario, che il campo k sia algebricamente chiuso di
Geometria Algebrica A.A. 2014 2015 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non scritto al contrario, che il campo k sia algebricamente chiuso di
Spazio degli omomorfismi
 Capitolo 13 Spazio degli omomorfismi 13.1 Introduzione Ecco un argomento totalmente nuovo. Abbiamo visto che ad ogni omomorfismo tra spazi vettoriali di dimensione finita possiamo associare una matrice
Capitolo 13 Spazio degli omomorfismi 13.1 Introduzione Ecco un argomento totalmente nuovo. Abbiamo visto che ad ogni omomorfismo tra spazi vettoriali di dimensione finita possiamo associare una matrice
Geometria Algebrica A.A Esercizi. Insiemi algebrici affini, Insiemi algebrici irriducibili.
 Geometria Algebrica A.A. 2017 2018 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non scritto al contrario, che il campo k sia algebricamente chiuso di
Geometria Algebrica A.A. 2017 2018 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non scritto al contrario, che il campo k sia algebricamente chiuso di
Algebra Lineare. a.a Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/12/2004
 Algebra Lineare. a.a. 004-05. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/1/004 Esercizio 1. Siano V e W due spazi vettoriali e sia F : V W un isomorfismo (quindi F è lineare e
Algebra Lineare. a.a. 004-05. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/1/004 Esercizio 1. Siano V e W due spazi vettoriali e sia F : V W un isomorfismo (quindi F è lineare e
Geometria Superiore. A.A. 2014/2015 CdL in Matematica Università degli Studi di Salerno. May 28, 2015
 Geometria Superiore A.A. 2014/2015 CdL in Matematica Università degli Studi di Salerno Luca Vitagliano May 28, 2015 Programma Prerequisiti. Spazi affini. Anelli commutativi con unità. Ideali. Anelli quoziente.
Geometria Superiore A.A. 2014/2015 CdL in Matematica Università degli Studi di Salerno Luca Vitagliano May 28, 2015 Programma Prerequisiti. Spazi affini. Anelli commutativi con unità. Ideali. Anelli quoziente.
SUPERFICI DI RIEMANN (settima parte) anno acc. 2008/2009
 (settima parte) anno acc. 2008/2009 Divisori molto ampi Sia X una superficie di Riemann compatta, D Div(X) un divisore su X e Φ D l applicazione associata. Si dice che D è molto ampio se Φ = Φ D è un immersione
(settima parte) anno acc. 2008/2009 Divisori molto ampi Sia X una superficie di Riemann compatta, D Div(X) un divisore su X e Φ D l applicazione associata. Si dice che D è molto ampio se Φ = Φ D è un immersione
Spazi proiettivi. 16 novembre Completamento proiettivo di uno spazio affine
 Spazi proiettivi 16 novembre 2009 1 Completamento proiettivo di uno spazio affine Definizione 1. Una geometria è una coppia ordinata (P, L) di insiemi con: 1. Ogni elemento di L è un sottoinsieme di P;
Spazi proiettivi 16 novembre 2009 1 Completamento proiettivo di uno spazio affine Definizione 1. Una geometria è una coppia ordinata (P, L) di insiemi con: 1. Ogni elemento di L è un sottoinsieme di P;
Teoremi di struttura per divisori su superifici K3
 Teoremi di struttura per divisori su superifici K3 Emiliano Ambrosi 9 agosto 2015 1 Richiarmi generali sulla teoria delle superfici e sulle K3 In questa sezione richiamiamo alcuni teoremi e osservazioni
Teoremi di struttura per divisori su superifici K3 Emiliano Ambrosi 9 agosto 2015 1 Richiarmi generali sulla teoria delle superfici e sulle K3 In questa sezione richiamiamo alcuni teoremi e osservazioni
Algebre di Lie, formule di Cartan e cicli algebrici.
 Sapienza Università di Roma Milano, 27 febbraio 2012 Un algebra di Lie è uno spazio vettoriale L dotato di un applicazione bilineare (bracket) che soddisfa le condizioni [, ]: L L L Antisimmetria [a, b]
Sapienza Università di Roma Milano, 27 febbraio 2012 Un algebra di Lie è uno spazio vettoriale L dotato di un applicazione bilineare (bracket) che soddisfa le condizioni [, ]: L L L Antisimmetria [a, b]
e la funzione meromorfa f su C, (detta proiezione stereografica), definita da f = Y Z e h = X Z.
 Esercizi su Superfici di Riemann e curve algebriche 1) Siano X, Y, Z coordinate omogenee in P 2 C. Sia C = {[X, Y, Z] P 2 C X 4 + XY 3 + Z 4 = 0}. Si consideri su C la funzione meromorfa f = X/Z. a)calcolare
Esercizi su Superfici di Riemann e curve algebriche 1) Siano X, Y, Z coordinate omogenee in P 2 C. Sia C = {[X, Y, Z] P 2 C X 4 + XY 3 + Z 4 = 0}. Si consideri su C la funzione meromorfa f = X/Z. a)calcolare
n+1 i=1 Sia D la superficie di Riemann della curva algebrica piana:
 ESERCIZI 1) Sia C una superficie di Riemann di genere 1. Sia p C. a) Dimostrare che l(2p) = 2 e l(3p) = 3. b) Siano {1, f} e {1, f, g} basi per L(2p) e L(3p), rispettivamente. Dimostrare che esistono costanti
ESERCIZI 1) Sia C una superficie di Riemann di genere 1. Sia p C. a) Dimostrare che l(2p) = 2 e l(3p) = 3. b) Siano {1, f} e {1, f, g} basi per L(2p) e L(3p), rispettivamente. Dimostrare che esistono costanti
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Fra le applicazioni definite tra spazi vettoriali sono particolarmente significative quelle che conservano le operazioni, dette applicazioni lineari. Definizione Siano V, W due k-s.v.
APPLICAZIONI LINEARI Fra le applicazioni definite tra spazi vettoriali sono particolarmente significative quelle che conservano le operazioni, dette applicazioni lineari. Definizione Siano V, W due k-s.v.
Analisi a più variabili: Integrazione sulle curve e superfici, forme differenziali
 Analisi a più variabili: Integrazione sulle curve e superfici, forme differenziali 1 Definizione (Parametrizzazione di T): T R n, una sua parametrizzazione è una coppia φ, con = a, b intervallo di R e
Analisi a più variabili: Integrazione sulle curve e superfici, forme differenziali 1 Definizione (Parametrizzazione di T): T R n, una sua parametrizzazione è una coppia φ, con = a, b intervallo di R e
Curve Ellittiche, Forme Modulari e Rappresentazioni di Galois
 Curve Ellittiche, Forme Modulari e Rappresentazioni di Galois Una breve introduzione Daniele Masoero Università degli studi di Genova, Dipartimento di Matematica 18 Maggio, 2015 Daniele Masoero Curve Ellittiche,
Curve Ellittiche, Forme Modulari e Rappresentazioni di Galois Una breve introduzione Daniele Masoero Università degli studi di Genova, Dipartimento di Matematica 18 Maggio, 2015 Daniele Masoero Curve Ellittiche,
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura. Complementi di Geometria Proiettiva Docente F.
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Complementi di Geometria Proiettiva Docente F. Flamini POLARITA DEFINITA DA UNA CONICA 1 Spazio vettoriale duale.
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Complementi di Geometria Proiettiva Docente F. Flamini POLARITA DEFINITA DA UNA CONICA 1 Spazio vettoriale duale.
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Il luogo iperellittico nello stack dei moduli delle curve lisce di dato genere
 Scuola Normale Superiore di Pisa Esame di licenza Il luogo iperellittico nello stack dei moduli delle curve lisce di dato genere 29 Maggio 2013 Allievo Andrea Petracci Relatore Prof. Angelo Vistoli Piano
Scuola Normale Superiore di Pisa Esame di licenza Il luogo iperellittico nello stack dei moduli delle curve lisce di dato genere 29 Maggio 2013 Allievo Andrea Petracci Relatore Prof. Angelo Vistoli Piano
SUPERFICI DI RIEMANN (terza parte) anno acc. 2008/2009
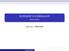 (terza parte) anno acc. 2008/2009 Sia C = V(F) P 2 una curva algebrica piana non singolare, con F(z 0, z 1, z 2 ) polinomio omogeneo di grado d. Supponiamo che il sistema di riferimento sia stato scelto
(terza parte) anno acc. 2008/2009 Sia C = V(F) P 2 una curva algebrica piana non singolare, con F(z 0, z 1, z 2 ) polinomio omogeneo di grado d. Supponiamo che il sistema di riferimento sia stato scelto
Geometria Algebrica Esercizi. Insiemi algebrici affini, Insiemi algebrici irriducibili.
 Geometria Algebrica 2009 2010 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non detto al contrario, che il campo k è algebraicamente chiuso. Sia V A n
Geometria Algebrica 2009 2010 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non detto al contrario, che il campo k è algebraicamente chiuso. Sia V A n
The Chow ring of double EPW sextics
 The Chow ring of double EPW sextics Andrea Ferretti Max Planck Institute for Mathematics Bonn 28 maggio 2010 Andrea Ferretti (MPIM) The Chow ring of double EPW sextics 28 maggio 2010 1 / 38 Piano della
The Chow ring of double EPW sextics Andrea Ferretti Max Planck Institute for Mathematics Bonn 28 maggio 2010 Andrea Ferretti (MPIM) The Chow ring of double EPW sextics 28 maggio 2010 1 / 38 Piano della
a.a ESAME DI GEOMETRIA PER INFORMATICA il sottospazio di R 4 costituito dalle soluzioni del x 1 +2x 2 x 4 =0 x + y 2x V = {
 a.a. 2005-2006 24..2007 ESAME DI GEOMETRIA PER INFORMATICA Per ogni quesito dare adeguate spiegazioni. () Sia V λ, al variare di λ R il sottospazio di R 4 costituito dalle soluzioni del x +2x 2 x 4 =0
a.a. 2005-2006 24..2007 ESAME DI GEOMETRIA PER INFORMATICA Per ogni quesito dare adeguate spiegazioni. () Sia V λ, al variare di λ R il sottospazio di R 4 costituito dalle soluzioni del x +2x 2 x 4 =0
LEZIONE 12. Y = f(x) = f( x j,1 f(e j ) = x j,1 A j = AX = µ A (X),
 LEZIONE 1 1.1. Matrice di un applicazione lineare. Verifichiamo ora che ogni applicazione lineare f: R n R m è della forma µ A per un unica A R m,n. Definizione 1.1.1. Per ogni j 1,..., n indichiamo con
LEZIONE 1 1.1. Matrice di un applicazione lineare. Verifichiamo ora che ogni applicazione lineare f: R n R m è della forma µ A per un unica A R m,n. Definizione 1.1.1. Per ogni j 1,..., n indichiamo con
Ψ(U i ). Dalla proposizione 0.3 segue che per ogni i R h esiste c i ( δ, δ) n k tale che ϕ 2 Ψ(U i ) c i, quindi ϕ 2 (L h ) = i R h
 Foliazioni Definition 0.1 Siano date una varieta M, C, una distribuzione involutiva di dimensione k ed una immersione iniettiva Ψ : N M con N varieta connessa di dimensione k. Diremo che N e una sottovarieta
Foliazioni Definition 0.1 Siano date una varieta M, C, una distribuzione involutiva di dimensione k ed una immersione iniettiva Ψ : N M con N varieta connessa di dimensione k. Diremo che N e una sottovarieta
Classe di Chern di un fibrato lineare
 Classe di Chern di un fibrato lineare Silvia Ghinassi 30 aprile 2013 (Per gli argomenti trattati si veda Griffiths-Harris, Ch.1, Sect.1.) Prima di iniziare a parlare di fibrati lineari abbiamo bisogno
Classe di Chern di un fibrato lineare Silvia Ghinassi 30 aprile 2013 (Per gli argomenti trattati si veda Griffiths-Harris, Ch.1, Sect.1.) Prima di iniziare a parlare di fibrati lineari abbiamo bisogno
Superfici di Riemann, teorema di Riemann-Roch e applicazioni
 Scuola Normale Superiore - Colloquio del terzo anno Superfici di Riemann, teorema di Riemann-Roch e applicazioni Denis Nardin Divisori su di una superficie di Riemann Definizione di divisore. Grado di
Scuola Normale Superiore - Colloquio del terzo anno Superfici di Riemann, teorema di Riemann-Roch e applicazioni Denis Nardin Divisori su di una superficie di Riemann Definizione di divisore. Grado di
AL210 - Appunti integrativi - 7
 AL210 - Appunti integrativi - 7 Prof. Stefania Gabelli - a.a. 2016-2017 Fattorizzazione in anelli di polinomi Poiché l anello dei polinomi K[X] in una indeterminata X su un campo K è un dominio euclideo,
AL210 - Appunti integrativi - 7 Prof. Stefania Gabelli - a.a. 2016-2017 Fattorizzazione in anelli di polinomi Poiché l anello dei polinomi K[X] in una indeterminata X su un campo K è un dominio euclideo,
Scuola Normale Superiore Ammissione al IV anno del corso ordinario Prova scritta di Algebra e Geometria per matematici
 Scuola Normale Superiore Ammissione al IV anno del corso ordinario Prova scritta di Algebra e Geometria per matematici 27 agosto 2010 Esercizio 1. Siano n e d due interi positivi, e sia φ(x) C[x] un polinomio
Scuola Normale Superiore Ammissione al IV anno del corso ordinario Prova scritta di Algebra e Geometria per matematici 27 agosto 2010 Esercizio 1. Siano n e d due interi positivi, e sia φ(x) C[x] un polinomio
Deformazioni di fibrati di Higgs e mappa di Hitchin
 Deformazioni di fibrati di Higgs e mappa di Hitchin Elena Martinengo Università La Sapienza - Roma Gargnano del Garda, 28 Maggio 2010 1. Definizioni iniziali e risultati classici. 2. Introduzione alla
Deformazioni di fibrati di Higgs e mappa di Hitchin Elena Martinengo Università La Sapienza - Roma Gargnano del Garda, 28 Maggio 2010 1. Definizioni iniziali e risultati classici. 2. Introduzione alla
Soluzione degli esercizi di algebra lineare (del 26 ottobre 2018)
 Soluzione degli esercizi di algebra lineare (del 26 ottobre 28) Esercizio. Siano V un K-spazio vettoriale con base B = (v,..., v n ) e W un K-spazio vettoriale con base C = (w,..., w m ), e sia f : V W
Soluzione degli esercizi di algebra lineare (del 26 ottobre 28) Esercizio. Siano V un K-spazio vettoriale con base B = (v,..., v n ) e W un K-spazio vettoriale con base C = (w,..., w m ), e sia f : V W
Proposizione 2 Il polinomio minimo di t corrisponde all annullatore minimale di M V.
 Fogli NON riletti. Grazie per ogni segnalazione di errori. L esempio qui sviluppato vuole mostrare in concreto il significato dei risultati trattati a lezione e qui velocemente riassunti. Si assume che
Fogli NON riletti. Grazie per ogni segnalazione di errori. L esempio qui sviluppato vuole mostrare in concreto il significato dei risultati trattati a lezione e qui velocemente riassunti. Si assume che
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Complessi di Catene e Gruppi di Omologia. 28 febbraio 2007
 Complessi di Catene e Gruppi di Omologia 28 febbraio 2007 Complessi di Catene Definizione Un complesso di catene è una successione C di gruppi abeliani con i loro omomorfismi n+1 C n+1 n Cn Cn 1 infinita
Complessi di Catene e Gruppi di Omologia 28 febbraio 2007 Complessi di Catene Definizione Un complesso di catene è una successione C di gruppi abeliani con i loro omomorfismi n+1 C n+1 n Cn Cn 1 infinita
Algebra Commutativa a Genova
 Algebra Commutativa a Genova Matteo Varbaro Workshop di presentazione Dottorato Parte del gruppo di Algebra Commutativa Postdoc: Figure : Aldo Conca - Hop D. Nguyen - Shreedevi K. Masuti Ph.D.: Figure
Algebra Commutativa a Genova Matteo Varbaro Workshop di presentazione Dottorato Parte del gruppo di Algebra Commutativa Postdoc: Figure : Aldo Conca - Hop D. Nguyen - Shreedevi K. Masuti Ph.D.: Figure
1. Funzioni implicite
 1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
I parte. Nome e cognome: Matricola: Attenzione: riportare i dati personali su ogni foglio consegnato
 Prova di geometria complessa del 8-2-202 I parte Nome e cognome: Attenzione: riportare i dati personali su ogni foglio consegnato Esercizio.. Si dia la definizione di funzione olomorfa in più variabili
Prova di geometria complessa del 8-2-202 I parte Nome e cognome: Attenzione: riportare i dati personali su ogni foglio consegnato Esercizio.. Si dia la definizione di funzione olomorfa in più variabili
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Applicazioni lineari tra spazi euclidei. Cambi di base.
 pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
14 febbraio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
0.1 Coordinate in uno spazio vettoriale
 0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
Soluzione: La matrice M cercata è quella formata dagli autovettori di A. Il polinomio caratteristico di A è: p t (A) = (t 1)(t 3) 0 4 V 1 = Ker
 Compito di Algebra Lineare - Ingegneria Biomedica 4 luglio 7 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non si può
Compito di Algebra Lineare - Ingegneria Biomedica 4 luglio 7 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non si può
x + 2y = 0 Soluzione. La retta vettoriale di equazione cartesiana x + 2y = 0.
 Algebra Lineare. a.a. 4-5. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del //5 Esercizio. Sia V = R il piano vettoriale euclideo con base ortonormale standard {e, e }. Determinare le
Algebra Lineare. a.a. 4-5. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del //5 Esercizio. Sia V = R il piano vettoriale euclideo con base ortonormale standard {e, e }. Determinare le
Omomorfismi tra spazi vettoriali
 Capitolo 6 Omomorfismi tra spazi vettoriali 61 Omomorfismi Nei capitoli precedenti abbiamo studiato omomorfismi tra gruppi e omomorfismi tra anelli Si tratta di funzioni tra insiemi dotati di una struttura
Capitolo 6 Omomorfismi tra spazi vettoriali 61 Omomorfismi Nei capitoli precedenti abbiamo studiato omomorfismi tra gruppi e omomorfismi tra anelli Si tratta di funzioni tra insiemi dotati di una struttura
GEOMETRIA COMPLESSA (Superfici di Riemann - terza parte) anno acc. 2010/2011
 (Superfici di Riemann - terza parte) anno acc. 2010/2011 Divisori effettivi e sistemi lineari Sia D un divisore su una superficie di Riemann X. Si dice sistema lineare completo D associato a D, l insieme
(Superfici di Riemann - terza parte) anno acc. 2010/2011 Divisori effettivi e sistemi lineari Sia D un divisore su una superficie di Riemann X. Si dice sistema lineare completo D associato a D, l insieme
APPLICAZIONI LINEARI O OMOMORFISMI
 42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
Per le risposte utilizza gli spazi predisposti. Quando richiesto, il procedimento va esposto brevemente, ma in maniera comprensibile.
 COGNOME............................... NOME..................................... Punti ottenuti Esame di geometria Scrivi cognome e nome negli spazi predisposti in ciascuno dei tre fogli. Per ogni domanda
COGNOME............................... NOME..................................... Punti ottenuti Esame di geometria Scrivi cognome e nome negli spazi predisposti in ciascuno dei tre fogli. Per ogni domanda
CdL in Ingegneria Industriale (F-O)
 CdL in Ingegneria Industriale (F-O Prova scritta di Algebra lineare e Geometria- 0 Giugno 07 Durata della prova: tre ore. È vietato uscire dall aula prima di aver consegnato definitivamente il compito.
CdL in Ingegneria Industriale (F-O Prova scritta di Algebra lineare e Geometria- 0 Giugno 07 Durata della prova: tre ore. È vietato uscire dall aula prima di aver consegnato definitivamente il compito.
1 Estensioni di Campi
 1 Estensioni di Campi Siano K, F campi. F si dice estensione di K se F K. Definizione 1.1. Un elemento α F si dice algebrico su K se f(x) K[x] \ {0} tale che f(α) = 0. α F si dice trascendente su K se
1 Estensioni di Campi Siano K, F campi. F si dice estensione di K se F K. Definizione 1.1. Un elemento α F si dice algebrico su K se f(x) K[x] \ {0} tale che f(α) = 0. α F si dice trascendente su K se
Dipartimento di Matematica Corso di laurea in Matematica Compiti di Geometria II assegnati da dicembre 2000 a dicembre 2003
 Dipartimento di Matematica Corso di laurea in Matematica Compiti di Geometria assegnati da dicembre 2000 a dicembre 2003 11/12/2000 n R 4 sono assegnati i punti A(3, 0, 1, 0), B(0, 0, 1, 0), C(2, 1, 0,
Dipartimento di Matematica Corso di laurea in Matematica Compiti di Geometria assegnati da dicembre 2000 a dicembre 2003 11/12/2000 n R 4 sono assegnati i punti A(3, 0, 1, 0), B(0, 0, 1, 0), C(2, 1, 0,
p(ϕ) = a 0 Id + a 1 ϕ + + a n ϕ n,
 1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
Soluzioni della prova scritta di Geometria 1 del 27 giugno 2019 (versione I)
 Soluzioni della prova scritta di Geometria 1 del 7 giugno 019 (versione I) Esercizio 1. Sia R 4 lo spazio quadridimensionale standard munito del prodotto scalare standard con coordinate canoniche (x 1,
Soluzioni della prova scritta di Geometria 1 del 7 giugno 019 (versione I) Esercizio 1. Sia R 4 lo spazio quadridimensionale standard munito del prodotto scalare standard con coordinate canoniche (x 1,
Foglio di esercizi di Istituzioni di Geometria
 Foglio di esercizi di Istituzioni di Geometria 11 ottobre 2017 Esercizio 1 Sia M varietà differenziabile, p M e si consideri un funzionale lineare D : C (M) R tale che D(fg) = f(p)d(g) + g(p)d(f). 1. Si
Foglio di esercizi di Istituzioni di Geometria 11 ottobre 2017 Esercizio 1 Sia M varietà differenziabile, p M e si consideri un funzionale lineare D : C (M) R tale che D(fg) = f(p)d(g) + g(p)d(f). 1. Si
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
Corso di Laurea in Fisica. Geometria. a.a Prof. P. Piazza Soluzione compito a casa del 24/10/09
 Corso di Laurea in Fisica. Geometria. a.a. 29-. Prof. P. Piazza Soluzione compito a casa del 24//9 Soluzione esercizio. Siano A e B due matrici simmetriche e λ un numero reale. Dobbiamo mostrare che anche
Corso di Laurea in Fisica. Geometria. a.a. 29-. Prof. P. Piazza Soluzione compito a casa del 24//9 Soluzione esercizio. Siano A e B due matrici simmetriche e λ un numero reale. Dobbiamo mostrare che anche
REGISTRO DELLE LEZIONI
 UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE LEZIONI del Corso UFFICIALE di GEOMETRIA B tenute dal prof. Domenico AREZZO nell anno accademico 2006/2007
UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE LEZIONI del Corso UFFICIALE di GEOMETRIA B tenute dal prof. Domenico AREZZO nell anno accademico 2006/2007
(E) : 4x 181 mod 3. h(h 1)x + 4hy = 0
 Dipartimento di Matematica e Informatica Anno Accademico 206-207 Corso di Laurea in Informatica (L-3) Prova scritta di Matematica Discreta (2 CFU) 6 Settembre 207 Parte A [0 punti] Sia data la successione
Dipartimento di Matematica e Informatica Anno Accademico 206-207 Corso di Laurea in Informatica (L-3) Prova scritta di Matematica Discreta (2 CFU) 6 Settembre 207 Parte A [0 punti] Sia data la successione
DIARIO DELLE LEZIONI DI ALGEBRA I Canale Dl-Pa A.A
 DIARIO DELLE LEZIONI DI ALGEBRA I Canale Dl-Pa A.A. 2011-12 Lunedì 5 Marzo Introduzione alla teoria degli insiemi: nozioni e notazioni fondamentali. Criterio di uguaglianza tra insiemi. Unione, intersezione
DIARIO DELLE LEZIONI DI ALGEBRA I Canale Dl-Pa A.A. 2011-12 Lunedì 5 Marzo Introduzione alla teoria degli insiemi: nozioni e notazioni fondamentali. Criterio di uguaglianza tra insiemi. Unione, intersezione
GEOMETRIA 1 terza parte
 GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
Corso di Laurea in Matematica - Esame di Geometria 1. Prova scritta del 7 settembre 2015
 Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
dipendenti. Cosa possiamo dire sulla dimensione di V?
 Esercizi Esercizi. In uno spazio vettoriale V ci sono tre vettori v, v 2, v linearmente indipendenti. Cosa possiamo dire sulla dimensione di V? 2. In uno spazio vettoriale V ci sono tre vettori v, v 2,
Esercizi Esercizi. In uno spazio vettoriale V ci sono tre vettori v, v 2, v linearmente indipendenti. Cosa possiamo dire sulla dimensione di V? 2. In uno spazio vettoriale V ci sono tre vettori v, v 2,
Esercitazione n. 35 (24/02/2016)
 Esercitazione n 35 (24/02/206) Argomenti Morfismo di Frobenius Esercizi vari sugli anelli II Teorema di isomorfismo, applicazioni Anelli di funzioni Esercizio (Morfismo di Frobenius) Sia p un numero primo
Esercitazione n 35 (24/02/206) Argomenti Morfismo di Frobenius Esercizi vari sugli anelli II Teorema di isomorfismo, applicazioni Anelli di funzioni Esercizio (Morfismo di Frobenius) Sia p un numero primo
Corso di Geometria BIAR, BSIR Esercizi 4: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Matrici jordanizzabili
 Capitolo 17 Matrici jordanizzabili 17.1 Introduzione Abbiamo visto che non tutte le matrici sono simili a matrici diagonali. Mostreremo in questo capitolo che alcune matrici sono simili a matrici di Jordan.
Capitolo 17 Matrici jordanizzabili 17.1 Introduzione Abbiamo visto che non tutte le matrici sono simili a matrici diagonali. Mostreremo in questo capitolo che alcune matrici sono simili a matrici di Jordan.
un sistema di coordinate affini su T e f K[x 1,..., x n ]. Studieremo i sottoinsiemi di T definiti come segue:
![un sistema di coordinate affini su T e f K[x 1,..., x n ]. Studieremo i sottoinsiemi di T definiti come segue: un sistema di coordinate affini su T e f K[x 1,..., x n ]. Studieremo i sottoinsiemi di T definiti come segue:](/thumbs/97/132853275.jpg) Capitolo 10 Ipersuperfici Sia T uno spazio affine sul campo K. Sia X : T un sistema di coordinate affini su T e f K[x 1,..., x n ]. Studieremo i sottoinsiemi di T definiti come segue: V (f) := {p T f(x(p))
Capitolo 10 Ipersuperfici Sia T uno spazio affine sul campo K. Sia X : T un sistema di coordinate affini su T e f K[x 1,..., x n ]. Studieremo i sottoinsiemi di T definiti come segue: V (f) := {p T f(x(p))
Vale: I (J 1 + J 2 ) = IJ 1 + IJ 2. (Si prova verificando la doppia inclusione). Def. Due ideali I, J di A si dicono coprimi se I + J = (1).
 Operazioni con gli ideali Sia A un anello (commutativo, unitario). Se I e J sono due ideali di A, si definisce I + J come il pi`piccolo ideale che contiene sia I, sia J. Si verifica che vale: I + J = {a
Operazioni con gli ideali Sia A un anello (commutativo, unitario). Se I e J sono due ideali di A, si definisce I + J come il pi`piccolo ideale che contiene sia I, sia J. Si verifica che vale: I + J = {a
Equazioni differenziali Problema di Cauchy
 Equazioni differenziali Problema di Cauch Primo esempio - Risolvere l equazione '( ) = g( ) con g( ) :[ a, b] R continua Teor. fondamentale del calcolo integrale ( ) = + g ( t )dt Primo esempio - Osserviamo
Equazioni differenziali Problema di Cauch Primo esempio - Risolvere l equazione '( ) = g( ) con g( ) :[ a, b] R continua Teor. fondamentale del calcolo integrale ( ) = + g ( t )dt Primo esempio - Osserviamo
SUPERFICI DI RIEMANN ALCUNI ESERCIZI
 SUPERFICI DI RIEMANN 2013-14 ALCUNI ESERCIZI FUNZIONI DI PIÚ VARIABILI COMPLESSE. 1.1. Si consideri la funzione f : C 2 C, f(z 1, z 2 ) = z 3 1z 2 + z 1 z 2 + z 2 1z 2 2 + z 2 2 + z 1 z 3 2. Trovare una
SUPERFICI DI RIEMANN 2013-14 ALCUNI ESERCIZI FUNZIONI DI PIÚ VARIABILI COMPLESSE. 1.1. Si consideri la funzione f : C 2 C, f(z 1, z 2 ) = z 3 1z 2 + z 1 z 2 + z 2 1z 2 2 + z 2 2 + z 1 z 3 2. Trovare una
Algebra lineare Geometria 1 15 luglio 2009
 Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
Aritmetica 2009/10 Compitino 3/11/ x 16 mod 23 3x 2 mod 5
 Aritmetica 2009/10 Compitino 3/11/2009 1. Trovare le soluzioni intere del sistema 4 x 16 mod 23 3x 2 mod 5 Esempio risoluzione: Cerchiamo di riportarci ad un sistema di congruenze lineari. Calcoliamo l
Aritmetica 2009/10 Compitino 3/11/2009 1. Trovare le soluzioni intere del sistema 4 x 16 mod 23 3x 2 mod 5 Esempio risoluzione: Cerchiamo di riportarci ad un sistema di congruenze lineari. Calcoliamo l
LEZIONE 21 [ ] D [ ] 1. k n. k m. k n,1 k m,1
![LEZIONE 21 [ ] D [ ] 1. k n. k m. k n,1 k m,1 LEZIONE 21 [ ] D [ ] 1. k n. k m. k n,1 k m,1](/thumbs/92/110228368.jpg) LEZIONE 21 21.1. Matrice di un applicazione lineare. Siano V e W spazi vettoriali su k = R, C finitamente generati e siano = (v 1,..., v n ) e = (w 1,..., w m ) basi di V e W rispettivamente. Come abbiamo
LEZIONE 21 21.1. Matrice di un applicazione lineare. Siano V e W spazi vettoriali su k = R, C finitamente generati e siano = (v 1,..., v n ) e = (w 1,..., w m ) basi di V e W rispettivamente. Come abbiamo
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
ALCUNI ESEMPI DI ALGEBRA
 ALCUNI ESEMPI DI ALGEBRA a cura di Lorenzo Ruffoni Indice 1 Premessa 1 2 Teorema fondamentale di omomorfismo 2 3 Divisibilità nei PID & co. 2 4 Morfismi di anelli e spazi vettoriali 6 1 Premessa Questo
ALCUNI ESEMPI DI ALGEBRA a cura di Lorenzo Ruffoni Indice 1 Premessa 1 2 Teorema fondamentale di omomorfismo 2 3 Divisibilità nei PID & co. 2 4 Morfismi di anelli e spazi vettoriali 6 1 Premessa Questo
4. Sottospazi vettoriali Piani e rette in E 3 O
 Indice Prefazione i Capitolo 0. Preliminari 1 1. Insiemistica e logica 1 1.1. Insiemi 1 1.2. Insiemi numerici 2 1.3. Logica matematica elementare 5 1.4. Ancora sugli insiemi 7 1.5. Funzioni 10 1.6. Composizione
Indice Prefazione i Capitolo 0. Preliminari 1 1. Insiemistica e logica 1 1.1. Insiemi 1 1.2. Insiemi numerici 2 1.3. Logica matematica elementare 5 1.4. Ancora sugli insiemi 7 1.5. Funzioni 10 1.6. Composizione
10. Il gruppo Speciale Lineare SL(V )
 1 2 3 4 5 6 7 8 9 1 10. Il gruppo Speciale Lineare SL(V ) Siano F un campo e V uno spazio vettoriale di dimensione n su F. Indichiamo con GL(V ) l insieme delle applicazioni lineari biiettive di V in sé.
1 2 3 4 5 6 7 8 9 1 10. Il gruppo Speciale Lineare SL(V ) Siano F un campo e V uno spazio vettoriale di dimensione n su F. Indichiamo con GL(V ) l insieme delle applicazioni lineari biiettive di V in sé.
Funzioni di n variabili a valori vettoriali
 Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 20 Gennaio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
A = e 1 = e 2 + e 3, e 2 = e 1 + e 3, e 3 = e 1, ; e 3 =
 aa -6 Soluzioni Esercizi Applicazioni lineari Sia data l applicazione lineare F : R R, F X A X, dove A i Sia {e, e, e } la base canonica di R Far vedere che i vettori e e + e, e e + e, e e, formano una
aa -6 Soluzioni Esercizi Applicazioni lineari Sia data l applicazione lineare F : R R, F X A X, dove A i Sia {e, e, e } la base canonica di R Far vedere che i vettori e e + e, e e + e, e e, formano una
1 Indipendenza lineare e scrittura unica
 Geometria Lingotto. LeLing7: Indipendenza lineare, basi e dimensione. Ārgomenti svolti: Indipendenza lineare e scrittura unica. Basi e dimensione. Coordinate. Ēsercizi consigliati: Geoling. Indipendenza
Geometria Lingotto. LeLing7: Indipendenza lineare, basi e dimensione. Ārgomenti svolti: Indipendenza lineare e scrittura unica. Basi e dimensione. Coordinate. Ēsercizi consigliati: Geoling. Indipendenza
ATTENZIONE: : giustificate le vostre argomentazioni! Geometria Canale 3. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A.
 Geometria Canale. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A. Nome e Cognome: Numero di Matricola: Esercizio Punti totali Punteggio 1 7 2 6 6 4 6+1 5 6+2 Totale 1+ ATTENZIONE:
Geometria Canale. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A. Nome e Cognome: Numero di Matricola: Esercizio Punti totali Punteggio 1 7 2 6 6 4 6+1 5 6+2 Totale 1+ ATTENZIONE:
Algebra lineare e geometria AA Appunti sul cambio di base in uno spazio vettoriale
 Algebra lineare e geometria AA. -7 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Algebra lineare e geometria AA. -7 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Capitolo 6: Campi di spezzamento:
 Capitolo 6: Campi di spezzamento: Idea: Studiare i polinomi a coefficienti in un campo. Definizione (Algebrico e trascendente): Dati campi, un elemento si dice algebrico su se Dati campi, un elemento si
Capitolo 6: Campi di spezzamento: Idea: Studiare i polinomi a coefficienti in un campo. Definizione (Algebrico e trascendente): Dati campi, un elemento si dice algebrico su se Dati campi, un elemento si
Algebra Commutativa a Genova
 Algebra Commutativa a Genova Matteo Varbaro Workshop di presentazione Dottorato Parte del gruppo di Algebra Commutativa Figure : Aldo Conca Postdocs: - Dang Hop Nguyen - Ramakrishna Nanduri - Oscar Fernandez
Algebra Commutativa a Genova Matteo Varbaro Workshop di presentazione Dottorato Parte del gruppo di Algebra Commutativa Figure : Aldo Conca Postdocs: - Dang Hop Nguyen - Ramakrishna Nanduri - Oscar Fernandez
Sul Cono dei 2-cicli effettivi su M 0,7
 Sul Cono dei 2-cicli effettivi su M 0,7 Luca Schaffler 4 giugno 2015 1 Preliminari e contesto n 3, k = k, caratteristica qualsiasi. caratteristica. Farò notare quando dovremo stare attenti alla L oggetto
Sul Cono dei 2-cicli effettivi su M 0,7 Luca Schaffler 4 giugno 2015 1 Preliminari e contesto n 3, k = k, caratteristica qualsiasi. caratteristica. Farò notare quando dovremo stare attenti alla L oggetto
XI Settimana. 2. Elementi basilari della teoria degli anelli (II parte)
 XI Settimana 2. Elementi basilari della teoria degli anelli (II parte) Dati due anelli (, +, ) e (, +, ), un applicazione f : si dice un omomorfismo di anelli se: f(x + y) = f(x) + f(y) e f(x y) = f(x)
XI Settimana 2. Elementi basilari della teoria degli anelli (II parte) Dati due anelli (, +, ) e (, +, ), un applicazione f : si dice un omomorfismo di anelli se: f(x + y) = f(x) + f(y) e f(x y) = f(x)
Capitolo 4: Teoria degli anelli:
 Capitolo 4: Teoria degli anelli: Definizione (Anello): È un insieme munito di due operazioni che indicheremo con in modo che: 1- è un gruppo abeliano rispetto a 2- è un monoide associativo rispetto al
Capitolo 4: Teoria degli anelli: Definizione (Anello): È un insieme munito di due operazioni che indicheremo con in modo che: 1- è un gruppo abeliano rispetto a 2- è un monoide associativo rispetto al
Quasifibrazione e flock parziali di un cono infinito
 CAPITOLO 22 Quasifibrazione e flock parziali di un cono infinito De Clerck e Van Maldeghem [27] hanno studiato i flock infiniti di un cono quadratico, i piani di traslazione corrispondenti e la possibilità
CAPITOLO 22 Quasifibrazione e flock parziali di un cono infinito De Clerck e Van Maldeghem [27] hanno studiato i flock infiniti di un cono quadratico, i piani di traslazione corrispondenti e la possibilità
20 gennaio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 0 gennaio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
0 gennaio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
Varietà di Grassmann in Geometria Algebrica
 Varietà di Grassmann in Geometria Algebrica Scuola di Dottorato, Gargnano 10-14 Aprile 2007 Giorgio Ottaviani ottavian@math.unifi.it www.math.unifi.it/ottavian Università di Firenze Grassmanniane come
Varietà di Grassmann in Geometria Algebrica Scuola di Dottorato, Gargnano 10-14 Aprile 2007 Giorgio Ottaviani ottavian@math.unifi.it www.math.unifi.it/ottavian Università di Firenze Grassmanniane come
Esercizi di Algebra commutativa e omologica
 Esercizi di Algebra commutativa e omologica Esercizio 1. Sia A un anello non nullo. Dimostrare che A è un campo se e solo se ogni omomorfismo di A in un anello non nullo B è iniettivo. Esercizio 2. Sia
Esercizi di Algebra commutativa e omologica Esercizio 1. Sia A un anello non nullo. Dimostrare che A è un campo se e solo se ogni omomorfismo di A in un anello non nullo B è iniettivo. Esercizio 2. Sia
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
Spazi affini e combinazioni affini.
 Spazi affini e combinazioni affini. Morfismi affini. Giorgio Ottaviani Abstract Introduciamo il concetto di combinazione affine in uno spazio affine, e in base a questo, ne caratterizziamo i sottospazi.
Spazi affini e combinazioni affini. Morfismi affini. Giorgio Ottaviani Abstract Introduciamo il concetto di combinazione affine in uno spazio affine, e in base a questo, ne caratterizziamo i sottospazi.
NOTE SUL TEOREMA DI DE RHAM
 NOTE SUL TEOREMA DI DE RHAM MAURIZIO CORNALBA Sia K, un complesso doppio di gruppi abeliani con differenziali d : K p,q K p+1,q e d : K p,q K p,q+1, dove d 2 = d 2 = d d + d d = Indichiamo con K il corrispondente
NOTE SUL TEOREMA DI DE RHAM MAURIZIO CORNALBA Sia K, un complesso doppio di gruppi abeliani con differenziali d : K p,q K p+1,q e d : K p,q K p,q+1, dove d 2 = d 2 = d d + d d = Indichiamo con K il corrispondente
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
