Esercitazione 01: Calcolo degli spostamenti mediante il teorema del Castigliano
|
|
|
- Emma Pesce
- 8 anni fa
- Visualizzazioni
Transcript
1 Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 01: Calcolo degli spostamenti mediante il teorema del Castigliano Indice 1 Flessione fra tre punti 1 Flessione generata da più carichi 3 3 Utilizzo del carico fittizio 4 1 Flessione fra tre punti In Fig.1 è mostrato lo schema di una trave in flessione su tre punti, carico in mezzeria e supporti verticali alle estremità. T b h P P / P / P / l M f Pl /4 Figura 1: Trave in flessione su tre punti. 1
2 Considerando il contributo della sola flessione e applicando il teorema del Castigliano, si può calcolare lo spostamento del punto di mezzeria: δ M = P U M = P = P l/ 0 l 0 M f EI dξ 1 EI Pξ Pξ dξ = P P 4EI [ ξ 3 3 ] l/ 0 = 1 Pl 3 48 EI Considerando il contributo della flessione e anche quello del taglio (per la sezione rettangole il fattore di taglio è: χ = 6/5): (1) δ = δ M + δ T δ T = P U T = P l 0 χ T GA dξ = P l 0 6 (P/) 5 GA dξ = 3 10 Pl GA () (3) A questo punto è interessante valutare quantitativamente il peso dei due contributi. Considerando una trave snella : l = 1000 mm, b = 1 mm, h = 0 mm, sollecitata con un carico P = 100 N (materiale acciaio, costanti elastiche: E = MPa, ν = 0.3, G = MPa 1 ), si ottiene: δ M = 1.70 mm e δ T = 0.00 mm. Il contributo del taglio è minore dell 1%. Considerando, invece, una trave tozza : l = 80 mm, b = 1 mm, h = 0 mm (stesso materiale e stesso carico) si ottiene: δ M = mm e δ T = mm. In questo caso i due contributi sono dello stesso ordine di grandezza, tuttavia la freccia totale è molto piccola. Da notare che nello svolgimento dell esempio precedente è stata determinata l energia elastica e successivamente è stata eseguita l operazione di derivazione. Tuttavia si può osservare che vale il teorema: l P 0 M f EI = l 0 M f M f P EI (4) Ritrovare la soluzione δ M relativa al caso precedente, sfruttando il teorema di derivazione introdotto. Notare come l onere di calcolo sia minore. 1 Il modulo tangenziale G è legato al modulo di Young E e al modulo di Poisson ν attraverso la relazione: E G = (1 + ν)
3 Flessione generata da più carichi In Fig. è mostrato lo schema di un telaio caricato da due forze, che entrambe produco un contributo sullo spostamento orizzontale δ 1 del punto C. A l 1 B l P 1 C 1 P Figura : Telaio sollecitato da due carichi, o forze attive. Determinare lo spostamento δ 1, considerando soltanto i termini flessionali. δ 1 = 1 EI [l 1 l (P 1 l + 1 ) P l ] 3 P 1l 3 (5) Trovare lo spostamento δ 1 dello stesso telaio di Fig., nel caso in cui non ci sia la forza P 1 Sostituire P 1 = 0 nell equazione del risultato precedente: δ 1 = 1 P l1 l EI (6) 3
4 3 Utilizzo del carico fittizio La possibilità di introdurre un carico e successivamente imporre tale carico nullo, al fine di trovare una componente di spostamento in un punto, suggerisce la tecnica del carico fittizio. Determinare lo spostamento di rotazione ϕ B, per effetto del carico P 1, nello schema di telaio di Fig.3 A l 1 B B l P 1 C Figura 3: Utilizzo del carico fittizio. Suggerimento: Determinare il momento flettente sui vari tratti, introducendo un momento fittizio M B (con direzione e verso secondo ϕ B ), eseguire la derivata rispetto a M B, eseguire l integrale sulla struttura ed infine imporre M B = 0. È anche possibile imporre M B = 0 prima di eseguire l integrale, ottenendo calcoli più veloci. ϕ B = P 1l 1 l EI (7) 4
5 Determinare la componente, secondo la direzione indicata, dello spostamento del punto C, dove è applicata la forza P 1, Fig.4 A l 1 B l P 1 C Figura 4: Componente di spostamento non allineata con il carico applicato. Suggerimento: Trovare il vettore spostamento ed infine la componente secondo la direzione indicata. δ α = P 1l EI ( l ) 3 l cos(α)+ P 1l1 l sin(α) (8) EI 5
6 Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 0: Calcolo degli spostamenti mediante il metodo degli integrali di Mohr Indice 1 Flessione fra tre punti 1 Flessione generata da più carichi 3 Determinazione dello spostamento di generico punto 3 4 Equazione della linea elastica mediante l integrale di Mohr 4 5 Risoluzione dell equazione differenziale della linea elastica 5 1 Flessione fra tre punti In Fig.1(a) è mostrato lo schema di una trave in flessione su tre punti, carico in mezzeria e supporti verticali alle estremità. Al fine di determinare lo spostamento verticale in mezzeria, utilizzando il teorema dei lavori virtuali si applica un carico unitario (esploratore) avente punto di applicazione, direzione e verso, coincidenti con lo spostamento che si intende valutare, Fig.1(b). È importante sottolineare che il carico esploratore unitario ha punto di applicazione direzione e verso secondo lo spostamento che si intende determinare, indipendentemente dal carico applicato. Nel caso considerato il carico esploratore ha direzione e verso del carico reale che sollecita la struttura, ma questo è dovuto solo al fatto che si cerca lo spostamento esattamente in quel punto. Considerando il contributo della sola flessione, si determina lo spostamento del punto di mezzeria, combinando spostamento e deformazioni dello schema di carico generato da P, con caratteristiche e sollecitazioni del carico unitario, ottenendo la seguente forma (integrale di Mohr): l 1 δ(= L.V.E.)= 0 M(P) M(1)dξ (= L.V.I.) (1) EI 1
7 b h P l P / P / P / N l 1 T T M f M f Pl /4 (a) (b) l /4 Figura 1: (a) Trave in flessione su tre punti. (b) Carico esploratore unitario. Essendo il carico unitario, il primo termine è esattamente lo spostamento cercato. Conoscendo le caratteristiche della sollecitazione è quindi possibile risolvere l integrale: l/ δ = 0 Pξ / ξ EI dξ = P EI [ ξ 3 3 ] l/ 0 = 1 Pl 3 48 EI Considerando il contributo della flessione e anche quello del taglio (per la sezione rettangolare il fattore di taglio è: χ = 6/5): () δ = δ M + δ T l δ T = χ T (P) l/ 0 GA T (1)= P/ 1 GA dξ = 3 Pl 10 GA (3) (4) Notare che si ritrovano gli stessi risultati ottenuti nell esercitazione precedente, utilizzando il teorema di Castigliano. Infatti, il teorema dei lavori virtuali e quello di castigliano, anche se hanno una formulazione diversa, si implicano a vicenda. Più precisamente si può notare che la distribuzione di momento flettente (ed eventuali altre caratteristiche della sollecitazione che hanno un peso significativo nel calcolo dello spostamento) ottenuta applicando lo spostamento esploratore unitario (Mohr) coincide con la derivata del momento rispetto alla forza che agisce sul punto e secondo la direzione dello spostamento cercato (Castigliano). Secondo la notazione dell esercizio mostrato: M(1)= M/ P. Quindi gli argomenti di integrazione di Castigliano e di Mohr coincidono, come era lecito attendersi dal momento che il risultato finale deve essere lo stesso. Flessione generata da più carichi In Fig. è mostrato lo schema di un telaio caricato da due forze, che entrambe producono un contributo sullo spostamento orizzontale δ 1 del punto C. Determinare lo spostamento δ 1, considerando soltanto i termini flessionali, utilizzando il metodo dell integrale di Mohr.
8 A l 1 B l P 1 C 1 P Figura : Telaio sollecitato da due carichi, o forze attive. δ 1 = 1 EI [l 1 l (P 1 l + 1 ) P l ] 3 P 1l 3 (5) 3 Determinazione dello spostamento di generico punto Il metodo degli integrali di Mohr fa sempre riferimento a due sistemi di carico: quello effettivamente agente sulla struttura e quello esploratore unitario, che ha la funzione di porre in evidenza lo spostamento cercato. A differenza del metodo del Castigliano, non c è nessuna differenza formale nell utilizzo di tale metodo per determinare lo spostamento in un punto secondo la direzione di una forza effettivamente presente, piuttosto che lo spostamento in un qualsiasi punto della struttura non caricato. Determinare lo spostamento di rotazione ϕ B, per effetto del carico P 1, nello schema di telaio di Fig.3. A l 1 B B l P 1 C Figura 3: Utilizzo del carico fittizio. Suggerimento: Introdurre un momento esploratore unitario in corrispondenza di B, con direzione e verso secondo ϕ B. 3
9 ϕ B = P 1l 1 l EI (6) 4 Equazione della linea elastica mediante l integrale di Mohr Mediante l integrale di Mohr (ma anche attraverso il metodo del Castigliano) si può determinare le componenti di spostamento in tutti i punti di una struttura, secondo una direzione, ottenendo quindi l equazione della linea elastica. Determinare la linea elastica della trave incastrata (con carico non all estremità, Fig.4), mediante l integrale di Mohr. P A l 1 B z l uz ( ) A z 1 B Figura 4: Trave incastrata con carico non di estremità, condizione di carico esploratore unitario nella generica posizione z. Suggerimento: Introdurre un carico esploratore unitario in una generica posizione z. Tenere presente che la variabile z non deve essere confusa con la variabile di integrazione ξ. Per z l 1 : u(z)= Pz ( l 1 z ) EI 3 Per z > l 1 : u(z)= Pl 1 EI ( z l ) 1 3 (7) (8) 4
10 5 Risoluzione dell equazione differenziale della linea elastica Una trave sollecitata a flessione nel piano (trascurando l effetto del taglio) si deforma secondo l equazione differenziale ordinaria lineare del secondo ordine: d u(z) dz = M EI (9) Conoscendo le caratteristiche della sollecitazione è quindi possibile risolvere l equazione differenziale della linea elastica, ed imporre le condizioni al contorno: in corrispondenza di un vincolo di spostamento nullo, in un punto z, la condizione da imporre è: u( z)=0; un vincolo di incastro, inoltre elimina anche la rotazione, per cui le condizioni da imporre sono: u( z)= 0, du( z)/dz = 0; in un punto in cui il momento flettente è nullo (ad esempio una cerniera o un appoggio di estremità) la condizione da imporre è: d u( z)/dz = 0; Risolvere l equazione differenziale appena mostrata, nel caso di trave incastrata e sollecitata da un carico P non di estremità, Fig.4. Suggerimento: Risolvere prima il tratto di sinistra, successivamente utilizzare spostamento e derivata prima per risolvere il tratto di destra. Per z l 1 : u(z)= Pz ( l 1 z ) EI 3 Per z > l 1 : u(z)= Pl 1 EI ( z l ) 1 3 (10) (11) 5
11 Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 03: Calcolo della linea elastica e carico critico di strutture a trave Indice 1 Trave incastrata in flessione a sezione variabile 1 Trave appoggiata su due punti, caricata a sbalzo 3 Instabilità dell equilibrio di strutture a trave caricate di punta Sistemi ad elasticità concentrata Trave ad elasticità distribuita Trave incastrata in flessione a sezione variabile In Fig.1 è mostrato lo schema di una trave incastrata, sollecitata da un carico flettente di estremità, la cui sezione b è variabile lungo l asse della trave, ed è pari a b 0 in corrispondenza dell incastro. z F h uz ( ) b 0 Figura 1: Trave incastrata, sollecitata da un carico flettente di estremità, con sezione variabile. Determinare l abbassamento dell asse della trave u in funzione della coordinata curvilinea z, considerando soltanto i termini flessionali. Confrontare la soluzione ottenuta con quella relativa al caso notevole di trave incastrata e caricata all estremità, con sezione uniforme. 1
12 u(z)= 6Fl Eb 0 h 3 z (1) Trave appoggiata su due punti, caricata a sbalzo In Fig. è mostrato lo schema di una trave appoggiata su due punti e sollecitata da un carico flettente posto a sbalzo. z z ' F A uz ( ) a B b C Figura : Trave su due appoggi con carico a sbalzo. Determinare l abbassamento dell asse della trave u in funzione della coordinata curvilinea z, considerando soltanto i termini flessionali. Suggerimento: Trovare l integrale generale nei due tratti AB e BC, imporre spostamento nullo in corrispondenza degli appoggi B e C ed infine imporre la condizione di continuità e di tangenza in corrispondenza del punto B. Utilizzare la coordinata z nel primo tratto, mentre risulta più comodo introdurre un altra coordinata z per il secondo tratto. Tratto AB: u(z)= Fz3 6EI Fa EI ( a + b )z + Fa (a + b) () 3 3EI Tratto BC: u (z )= Fz 3 a 6EI b + Faz EI Fab 3EI z (3)
13 3 Instabilità dell equilibrio di strutture a trave caricate di punta 3.1 Sistemi ad elasticità concentrata In Fig.3 è mostrato lo schema di una trave dotata di una sconnessione in mezzeria, sostenuta da un elemento ad elasticità concentrata (molla flessionale) e caricata da una forza P secondo l asse della trave. l l C B A P k v P P C k l Figura 3: Trave caricata di punta con sconnessione in mezzeria ed elasticità concentrata. La condizione indeformata è di equilibrio, ma, tale equilibrio perde di stabilità ad un certo valore del carico, detto carico critico P C. Al fine di valutare l entità del carico critico è necessario considerare la struttura in una configurazione diversa da quella indeformata. Tuttavia, è di interesse soltanto il carico critico e non il comportamento successivo alla perdita di stabilità. Per cui è possibile sfruttare tutte le semplificazioni relative alla linearizzazione e scrivere la condizione di equilibrio nella configurazione deformata: v Pv k ϕ = 0 (4) l Al fine di avere tale condizione soddisfatta, con spostamento v non nullo, è necessario che: P k ϕ = 0 (5) l per cui il carico critico è pari a: P C = k ϕ (6) l Avendo sfruttato la linearizzazione non è possibile avere nessuna informazione circa il comportamento dopo aver raggiunto il carico critico. Spesso non è di interesse tale informazione, in quanto è bene che la struttura rimanga lontana dalla condizione di perdita di stabilità. 3
14 Determinare il carico critico relativo alla struttura di Fig.4. l 1 C B P k l A Figura 4: Trave caricata di punta con sconnessione non in mezzeria ed elasticità concentrata. P C = k ϕ l, 1 l = 1 l l (7) Determinare il carico critico relativo alla struttura di Fig.5. B l P A k Figura 5: Trave caricata di punta, incernierata alla base con elasticità concentrata. P C = k ϕ l 4 (8)
15 Osservazione: Notare che il carico critico della struttura di Fig.5 è lo stesso di quella della struttura di Fig.4, nel caso in cui: l l 1. Determinare il carico critico relativo alla struttura di Fig.6, in cui compaiono due sconnessioni elastiche. P a a a k k Figura 6: Trave caricata di punta, dotata di due sconnessioni ad elasticità concentrata. Suggerimento: Notare che la generica configurazione deformata è funzione di due parametri, ad esempio gli spostamenti orizzontali dei due punti intermedi. La condizione di equilibrio diventa quindi un sistema. L equilibrio perde la stabilità in corrispondenza del carico per il quale il sistema ammette infinite soluzioni, ossia determinante della matrice del sistema nullo. P C = k ϕ a (9) 5
16 3. Trave ad elasticità distribuita Le strutture mostrate in precedenza hanno interesse didattico, tuttavia, le travi sono caratterizzate da elasticità distribuita, piuttosto che concentrata. Il caso più semplice di calcolo di carico critico con struttura a trave (elasticità distribuita) è fornito dalla trave caricata di punta con estremità vincolata lateralmente (trave di Eulero), Fig.7. B l A P v( ) EI d v d P v 0 Figura 7: Trave caricata di punta ed incernierata alla base. C è una profonda differenza fra il calcolo della linea elastica per strutture che non si discostano molto dalla loro configurazione di riferimento ed invece problemi di instabilità, dove la minima perturbazione dalla configurazione di riferimento è la causa stessa della perdita di stabilità. Il momento flettente Pv è appunto generato dalla deformazione stessa della struttura. Imponendo l equazione della linea elastica, nella configurazione deformata rispetto all equilibrio: EI d v + Pv = 0 (10) dξ ponendo: P λ = (11) EI ed utilizzando l apice per intendere la derivata rispetto all ascissa curvilinea ξ,sipuò riscrivere l equazione della linea elastica secondo la forma: v + λ v = 0 (1) che ammette come integrale generale: v(ξ )=Asin(λξ)+Bcos(λξ) (13) Imponendo la condizione al contorno: v(ξ = 0)=0 (14) segue che: B = 0. Infine, imponendo l altra condizione di spostamento nullo all estremità, si ottiene: A sin(λ l)=0 (15) Anche in questo caso si ripresenta la soluzione indeformata: A = 0, ma anche la possibilità di avere una soluzione deformata che soddisfi le condizioni al contorno: sin(λ l)=0 (16) 6
17 che è risolta da: λl = nπ (17) È opportuno determinare soltanto la prima delle soluzioni (n = 1), dato che se la struttura perde la stabilità ad un certo carico non ha interesse il comportamento a carichi più alti. Quindi in definitiva il carico critico è dato dalla condizione precedente sostituendo n = 1 (carico di critico di Eulero): P C = π EI l (18) Il risultato appena trovato è corretto, tuttavia, l imposizione dell equazione differenziale della linea elastica, Eq.10, è valida solo nei casi particolari in cui è possibile scrivere il momento flettente in funzione dello spostamento incognito. Nel caso di Fig.8, invece, il carico P genera un momento flettente variabile lungo la trave che è funzione dello spostamento v(ξ ) ma anche dello spostamento dell estremità v(l). B l A P v( ) d v EI P[() v l v()] 0 d Figura 8: Trave caricata di punta, incastro alla base ed estremità libera. L equazione della linea elastica è: EI d v + Pv = Pv(l) (19) dξ che è a differenza della precedente presenta un termine noto. Questa equazione differenziale può essere riscritta introducendo λ, con lo stesso significato del caso precedente: v + λ v = λ v(l) (0) ed ammette la soluzione: v(ξ )=Asin(λξ)+Bcos(λξ)+c 1 (1) 7
18 Determinare il carico critico, di perdita di stabilità a carico di punta, per il caso di Fig.8. Suggerimento: Utilizzare la soluzione dell equazione differenziale Eq.1, ed imporre le condizioni al contorno. P C = π EI 4l () Osservazione: Si può ritrovare la stessa soluzione per similitudine geometrica dal caso di Eulero, precedentemente risolto. 8
19 Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 04: Collegamenti bullonati Indice 1 Flangia bullonata sottoposta a sollecitazione generica Calcolo delle azioni sui bulloni Verifica statica bullone, criterio di locale aderenza fra le piastre... Collegamento bullonato fra due travi 4 3 Collegamento con distribuzione dei bulloni non a doppia simmetria 5 1 Flangia bullonata sottoposta a sollecitazione generica 1.1 Calcolo delle azioni sui bulloni In Fig.1 si mostra una flangia bullonata che collega due piastre, di cui una è vincolata al suolo, mentre l altra è saldata ad un telaio sollecitato da carichi esterni. h 1 N.8 bulloni h L 1 L P Figura 1: Flangia bullonata. Al fine di determinare le sollecitazioni che agiscono sui singoli bulloni, il piano della flangia può essere visto come la sezione di una trave, in cui l area è sostituita da elementi puntiformi in corrispondenza delle posizioni dei bulloni. Nelle zone di competenza dei bulloni agiscono dei carichi tali da garantire l equilibrio. Facendo alcune ipotesi sulla distribuzione di tali carichi e imponendo l equilibrio è possibile stimarli. In Fig. si mostrano le distribuzioni di carichi sui bulloni, per effetto delle sollecitazioni di: azione normale, taglio, momento flettente e momento 1
20 torcente. N i N n T i T n N T d i y i M f M t Ti di I0 I0 d j j M t M f Ni yi I x Ix yj j Figura : Distribuzioni dei carichi sui bulloni, per effetto delle varie sollecitazioni. Nel caso di azione normale o taglio, semplicemente il carico si ripartisce equamente sui vari bulloni. Nel caso di flessione o torsione si assume l ipotesi di piastra molto più rigida dei bulloni e quindi le forze sono proporzionali alla distanza dall asse neutro, per la flessione, e dal baricentro, per la torsione. Determinare le sollecitazioni che agiscono sui singoli bulloni relativi alla condizione di carico di Fig.1. I dati del problema sono: P = 10 kn L 1 = 3m L = m h 1 = 00 mm h = 150 mm (1) Individuare il bullone che subisce l azione tangenziale maggiore (in modulo) e quello che subisce l azione di forza normale maggiore (con segno, ossia quello che subisce un azione di trazione maggiore). Uno dei bulloni della flangia subisce la massima azione tangenziale di T max = 14.4 kn, e anche la massima azione di trazione di N max = 33.3 kn. 1. Verifica statica bullone, criterio di locale aderenza fra le piastre I bulloni vengono preserrati con un carico relativamente elevato, altrimenti la loro condizione di esercizio non è corretta. Il preserraggio dei bulloni genera una condizione di compressione fra
21 le piastre. Prima dell applicazione di carichi esterni la forza di preserraggio sui bulloni è uguale all azione di compressione fra le piastre. Successivamente, la presenza di azione di trazione genera una riduzione della forza locale di compressione fra le piastre, Fig.3. F i N T T F i N Aderenza: ( F N) f T i s Figura 3: Azioni che agiscono nella zona intorno al bullone. N è l azione di trazione, le piastre sono quindi in compressione di una forza pari a: F i N, in cui F i è la forza di preserraggio iniziale. T è l azione tangenziale da garantire, la condizione di aderenza che deve essere soddisfatta è: (F i N) f s > T in cui f s è il coefficiente di attrito di primo distacco o di aderenza. Il precarico da imporre al bullone F i è pari a: F i = 0.9S p A t in cui: S p è la massima tensione di precarico che è molto alta, pari al 90% del carico di snervamento, e A t è l area della sezione resistente. Il diametro con il quale si valuta la sezione resistente è circa diametro esterno della filettatura (cresta dei filetto) meno il passo della fillettatura, per tenere di conto che il diametro della vite non è pieno. Tipicamente non si sfrutta al massimo la tensione di precarico, da cui il coefficiente 0.9 nella formula di F i. Verificare la condizione di aderenza fra le due piastre del bullone relativo all esercitazione precedente su cui agisce azione tangenziale e forza di trazione massime (ipotizzando che sia stato applicato il serraggio opportuno). Assumere: f s = 0., Classe del bullone buona: SAE 8.8, S p = 600 MPa (pari a circa 0.9S Y ), Diametro esterno della vite, d = mm, passo p =.5 mm. La condizione di aderenza fra le piastre risulta verificata. 3
22 Collegamento bullonato fra due travi In Fig.4 si mostra un collegamento bullonato, al fine di realizzare un incastro fra due travi. y N.6 bulloni b L h x P y P z z Figura 4: Collegamento bullonato fra due travi. La forza ha una direzione generica per cui, nella sezione di bullonatura, si ha: forza normale, taglio, flessione e torsione. I dati del problema sono: P y = 1000 N P z = 500 N L = 800 mm b = 50 mm h = 50 mm Classe bullone SAE: 5.8, S p = 380 MPa () Determinare il bullone che presenta la situazione più sfavorevole di azione di tangenziale / azione di trazione. Verificare la condizione di aderenza, considerando stesso materiale dell esercizio precedente e diametro vite d = 10 mm, passo p = 1.5 mm. Suggerimento: Verificare che le azioni tangenziale e normale sui bulloni generate da forza normale e taglio sono trascurabili, rispetto a quelle generate da flessione torsione. La condizione di aderenza risulta verificata, anche se con un margine ridotto. Quindi si suggerisce di utilizzare un altra classe di materiale del bullone, o un diametro d maggiore, al fine di avere un preserraggio più elevato. 4
23 3 Collegamento con distribuzione dei bulloni non a doppia simmetria In Fig.5 si mostra una flangia bullonata che realizza l incastro di una trave a flessione. In questo caso lo schema dei bulloni non ammette due simmetrie. N.9 bulloni h 1 h y x G L b P Figura 5: Flangia bullonata trave a flessione, schema dei bulloni non simmetrico. La disposizione dei bulloni di Fig.5 è ottimizzata. La densità dei bulloni superiori è doppia rispetto ai bulloni inferiori. Essendo i bulloni superiori in trazione si trovano in condizioni peggiori rispetto a quelli inferiori, per cui una migliore ripartizione delle azioni di trazione è vantaggiosa. La disposizione dei bulloni di Fig.5 ammette tuttavia una simmetria. Risultano quindi definite le due direzioni principali della sezione: una è la direzione di simmetria è l altra è la direzione ortogonale. Si possono quindi facilmente valutare i momenti secondi baricentrici principali. Inoltre il momento flettente che agisce è secondo una delle direzioni principali. Verificare la condizione di aderenza fra piastre per il bullone che presenta la peggiore condizione azione tangenziale / trazione. I dati del problema sono: P = N b = 100 mm h 1 = 50 mm h = 100 mm L = 500 mm (3) Suggerimento: Determinare il baricentro della distribuzione di bulloni, e successivamente calcolare il momento secondo baricentrico principale. 5
24 Sollecitazione di taglio (uguale su tutti i bulloni) pari a: T i = 1111 N, trazione sulla fila superiore di bulloni pari a: N max = 954 N. Scegliendo un diametro esterno della vite pari a d = 10 mm, p = 1.5 mm, classe di materiale SAE 5.8, S p = 380 MPa, ed assumendo un tipico coefficiente di attrito di primo distacco fra due piastre in acciaio pari a f s = 0., la condizione di aderenza risulta soddisfatta: (F i N) f s = 1977 N > T i = 1111 N 6
25 Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 05: Collegamenti bullonati e saldature Indice 1 Collegamenti bullonati con schema complesso 1 Collegamenti saldati 4 1 Collegamenti bullonati con schema complesso In precedenza è stato affrontato il problema di determinare le forze che agiscono in corrispondenza dei bulloni, per flange con schemi simmetrici, Fig.1(a). In questo caso le direzioni principali sono ovviamente gli assi di simmetria dello schema dei bulloni. Anche nel caso di un solo asse di simmetria, tale asse è principale (quindi il suo perpendicolare è a sua volta principale). y Y Y y h h 1 M t G M f x X h h 1 M t G M f x X b N.1 bulloni b N.8 bulloni Figura 1: (a) Flangia bullonata con schema a doppia simmetria. (b) Flangia bullonata con schema non simmetrico. Nel caso di schema non simmetrico, le direzioni principali non sono immediatamente evidenti, Fig.1(b). Presi due assi baricentrici generici x, y, gli assi principali X,Y sono ruotati di un angolo 1
26 ϕ, in genere, non nullo. Inizialmente si possono calcolare i momenti secondi rispetto agli assi x,y: I x = y i i I y = xi i I xy = x i y i i in cui x i,y i sono le coordinate delle posizioni dei bulloni (ad esempio, nello schema di Fig.1(b): i = 1...8). Successivamente si determina l angolo di rotazione invertendo la relazione: I xy tan(ϕ)= I x I y e si possono trovare i momenti secondi principali: I X = I (Ix ) x + I y I y + + I xy I Y = I x + I y (Ix ) I y + I xy Ovviamente, qualora fosse I xy = 0, le direzioni x,y sarebbero già le principali, per definizione. Tale situazione può accadere anche se lo schema non è simmetrico, dato che x,y sono semplicemente direzioni qualsiasi. Le direzioni principali e i momenti secondi principali sono necessari per la determinazione delle azioni normali generate da una sollecitazione di flessione (M f in Fig.1). Nel caso in cui il vettore M f sia allineato con una delle direzioni principali, si ha flessione retta. Invece, nel caso in cui non sia allineato con nessuna direzione principale si ha flessione deviata. In quest ultimo caso è necessario scomporre M f nelle componenti secondo X e Y, eseguire i due calcoli di flessione rette ed applicare il principio di sovrapposizione degli effetti. Determinare le azioni che agiscono sui bulloni (sia tangenziali che normali), per effetto dei momenti M f e M t, dello schema di Fig.1(a). In particolare determinare la massima azione normale e la massima azione tangenziale. I dati del problema sono: M t = 100 Nm M f = 3500 Nm α = 0 h 1 = 75 mm h = 0 mm b = 50 mm (1)
27 Un bullone dello schema di Fig.1(a) subisce sia la massima azione normale N max sia la massima azione tangenziale T max : N max = 6501 N T max = 1179 N Dimensionare il bullone più sollecitato, scegliendo fra le dimensioni (diametro esterno e passo) riportate in Tab.1, classe SAE 5.8, S p = 380 MPa, e coefficiente di attrito statico f s = 0.. Φ [mm] p [mm] Φ [mm] p [mm] Tabella 1: Diametro esterno e passo di alcuni bulloni unificati. La combinazione Φ = 10 mm, p = 1.5 mm, garantisce la condizione di aderenza, con un margine di sicurezza superiore a : (F i N max ) f s = 581 N T max = 1179 N. Si supponga che le due coppie di bulloni laterali vengano eliminate, ottenendo la configurazione di Fig.1(b). Determinare azione normale massima e tangenziale massima, e verificare se il dimensionamento fatto in precedenza garantisce anche in questa configurazione l aderenza fra le piastre. Suggerimento: Notare che la posizione del baricentro non cambia, individuare le nuove direzioni principali, infine, scomporre la sollecitazione di flessione nelle due componenti di flessione retta e applicare il principio di sovrapposizione degli effetti. Notare inoltre che la direzione di M f è circa la stessa del nuovo asse principale. Sfruttare tale semplificazione. Le azioni che agiscono sul bullone più sollecitato sono: N max = 577 N T max = 1851 N 3
28 Utilizzando le stesse dimensioni del bullone trovate per il caso precedente, la verifica di aderenza viene soddisfatta anche se con margine ridotto. Osservazione: Nonostante siano stati eliminati due bulloni il margine di sicurezza è lo stesso verificato. Tale situazione può sembrare paradossale. Da notare che i bulloni eliminati hanno allineato l asse di sollecitazione (ossia l asse perpendicolare all asse neutro) con la diagonale contente gli altri bulloni rimasti. Invece, eliminare i bulloni dell altra diagonale avrebbe prodotto un effetto molto negativo. Collegamenti saldati Analogamente ai collegamenti bullonati una soluzione dello stato di tensione, nella sezione di saldatura, si può ottenere assumendo il cordone molto più cedevole rispetto ai due elementi saldati fra loro, ed imponendo l equilibrio, Fig.. N A T A N T y d M f M t d I A 0 I0 d da M t M I A x f y I x y da Figura : Stato di tensione nella sezione di saldatura, generato dalle varie caratteristiche di sollecitazione. Anche per il calcolo delle tensioni nella sezione di saldatura si presentano le eventuali difficoltà di flessione deviata e sezione non simmetrica. L area A è quella del cordone proiettata sul piano della saldatura, e I 0, I x (I y ) sono i momenti secondi di area rispettivamente polare ed assiale. Nel caso di giunto saldato a cordone d angolo, si individua come sezione resistente il ribaltamento dello spessore di gola sul piano della sezione della saldatura, Fig3. Analogamente ai collegamenti bullonati, le differenti componenti della tensione nel cordone hanno ruoli diversi. Per il caso di cordone d angolo, considerando la direzione del cordone, si individuano le componenti di tensione: σ (tensione normale perpendicolare), τ (tensione tangenziale perpendicolare), τ (tensione tangenziale parallela). È importante sottolineare che la componente τ non esiste secondo la teoria dello stato di sollecitazione della trave, dato che implica uno stato di tensione su un bordo libero. Nella trattazione della sollecitazione della saldatura a cordone d angolo invece tale tensione è ammessa in quanto è una media di uno stato di tensione fortemente variabile. Nel caso di cordone a piena penetrazione fra due lembi, lo stato di sollecitazione è lo stesso di quello nella sezione di una trave, ed 4
29 Si può assumere: a s a a s Figura 3: Giunto a cordone d angolo, componenti di tensione. infatti la componente τ non è presente. La procedura di calcolo descritta nella norma italiana CNR , permette di valutare la resistenza del giunto saldato a cordone d angolo sulla base dei valori di σ,τ,τ, della qualità della saldatura e della tensione ammissibile del materiale. In Fig.4 è mostrata una mensola sollecitata da un azione normale posta all estremità. d s L F Figura 4: Mensola saldata sollecitata da una forza normale all estremità. La sezione di saldatura è ricavata all interno di un foro, ed è sollecitata a trazione e a flessione. Notare che in corrispondenza della sezione di saldatura è presente solo la componente σ. Determinare lo stato di sollecitazione nel cordone della saldatura, in particolare determinare la massima tensione normale σ. 5
30 I dati del problema sono: F = 70 N L = 1300 mm d = 50 mm s = mm () Nella sezione della saldatura la massima tensione normale σ è: σ (max)=139 MPa In Fig.5 è mostrata una mensola sollecitata da un azione tangenziale posta all estremità. b h s F L Figura 5: Mensola saldata sollecitata da una forza tangenziale all estremità. La sezione di saldatura è su due cordoni ed è sollecitata a torsione e a taglio. Nel cordone agiscono soltanto tensioni tangenziali normale e parallela τ,τ. Determinare lo stato di sollecitazione nella sezione della saldatura di Fig.5, in particolare individuare il punto in cui τ + τ è maggiore, eivalori di τ,τ in tale punto. I dati del problema sono: F = 1.8kN L = 1300 mm b = 10 mm h = 00 mm s = mm (3) Nel punto più sollecitato della saldatura le componenti di tensione tangenziale sono: τ = 146 MPa τ = 0 MPa 6
31 Infine, si può eseguire la verifica statica del punto più sollecitato del collegamento. Secondo la normativa CNR è necessario verificare che: σ + τ + τ 0.70σ adm nel caso si utilizzi Fe 510, per il quale σ adm = 40 MPa. Considerando lo stato di sollecitazione dell esempio precedente: σ + τ + τ = 147 MPa < 0.70σ adm = 168 MPa la verifica risulta quindi soddisfatta. 7
32 Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 06: Verifica di strutture sollecitate a fatica Indice 1 Verifica della resistenza a fatica Resistenza statica Resistenza a fatica Effetto della tensione media Sensibilità all intaglio... 3 Struttura sollecitata da carico ripetuto 5 1 Verifica della resistenza a fatica 1.1 Resistenza statica La resistenza statica di un materiale è determinata attraverso la semplice prova di trazione. La prova viene eseguita sollecitando un provino, in genere cilindrico, mediante un carico crescente nel tempo molto lentamente. Durante la prova vengono misurati carico applicato al provino e deformazione e riportati su un grafico, Fig.1. La perdita di linearità della curva σ ε rappresenta il limite di snervamento S Y mentre S U è la tensione di rottura del materiale. S U S Y P A E Area A l l P Lunghezza l Allungamento l Figura 1: Curva di resistenza statica del materiale. 1
33 L andamento mostrato in Fig.1 è tipico di materiali metallici che riescono a deformarsi molto, dopo aver superato lo snervamento, prima di arrivare a rottura. 1. Resistenza a fatica Un componente sollecitato in modo ciclico può tuttavia rompersi, dopo un numero elevato di ripetizioni del carico, anche se l entità della sollecitazione è inferiore a S Y. Questa modalità di rottura viene detta a fatica. Solitamente si fissa un numero di cicli molto elevato (ad esempio 10 6 o10 7 ) e si individua il limite di fatica, ossia il valore di variazione di tensione ΔS e per il quale il materiale resiste alla sollecitazione di fatica, Fig.. (log) S e Prove Linea media 6 10 N f (log) max tempo min max min max min m 0 Figura : Curva di fatica e limite di fatica. Una stima del limite di fatica, valido per gli acciai, è: ΔS e S U (1) In realtà si corregge il valore fornito da tale relazione con fattori cautelativi (inferiori all unità) per tenere di conto di eventuali effetti che riducono la resistenza a fatica, ad esempio lo stato della superficie. 1.3 Effetto della tensione media Nella Fig. è stato mostrato un carico ciclico di fatica a tensione media σ m nulla. La presenza di tensione media positiva tende a ridurre la resistenza a fatica del componente. Un modello che riproduce questo effetto è l equazione di Soderberg. Si corregge la variazione di tensione Δσ individuando una variazione di tensione maggiorata Δσ, che tenga di conto della presenza della tensione media positiva: Δσ = Δσ 1 σ m S Y () Δσ potrà quindi essere confrontato con il limite di fatica ΔS e a tensione media nulla. Se Δσ < ΔS e allora il componente garantisce una resistenza di 10 6 cicli altrimenti è probabile che si rompa. Infine, si definisce Coefficiente di Sicurezza C S il rapporto fra il limite di fatica e la variazione di tensione corretta: C S = ΔS e Δσ (3) Nel caso di verifica positiva della resistenza a fatica, C S è maggiore dell unità e quindi fornisce una misura del margine di sicurezza che il componente ha rispetto alla rottura a fatica.
34 S e * m SY * 1 m 1 S Y max max tempo min min max min m 0 Figura 3: Modello di Soderberg per considerare l effetto della tensione media sulla resistenza a fatica. 1.4 Sensibilità all intaglio Fin ora sono state considerate prove di fatica eseguite su provini cilindrici, tuttavia i componenti meccanici sono spesso caratterizzati da forme complesse, che introducono una locale concentrazione di tensioni, ossia un aumento della sollecitazione confinato in una zona, ma che favorisce l innescarsi della sollecitazione di fatica. Considerando ad esempio un foro in una lastra sollecitata da un carico assiale F alternato, Fig.4, è possibile definire una tensione nominale σ n, nell ipotesi di distribuzione uniforme. Per effetto del presenza del foro lo stato di tensione subisce una locale concentrazione che viene quantificata dal parametro k t definito come fattore di concentrazione delle tensioni: k t = σ 0 (4) σ n in cui σ 0 è la tensione locale massima. Il fattore di concentrazione k t dipende unicamente della geometria. In particolare, per il caso di lastra con foro circolare piccolo rispetto alla larghezza, b D, vale k t = 3.0. F F 0 tempo n b D F h F n hb ( D) k t 0 n 3.0 Figura 4: Lastra con foro centrale sollecitata da un carico remoto alternato. In queste condizioni di geometria e carico, si esegue la verifica a fatica semplicemente moltiplicando la tensione nominale per k t, e ripetendo la procedura esposta precedentemente valutando 3
35 in definitiva il coefficiente di sicurezza C S. La lastra di Fig.5, con fori vicini alle estremità, è sollecitata a flessione ripetuta nel tempo da zero ad un valore massimo. M f b 1 b b 1 M f M (max) f f tempo M (min) D kt 3.0 h M f Figura 5: Lastra con fori vicino alle estremità, sollecitata da un momento flettente ripetuto. I dati del problema sono: Geometria : D = 10 mm b 1 = 30 mm b = 100 mm h = 5mm Materiale : S U = 900 MPa S Y = 650 MPa Carico : M f (max)=3000 Nm M f (min)=0nm (5) Determinare il coefficiente di sicurezza C S a fatica. Nel punto più sollecitato il coefficiente di sicurezza è pari a: C S = Essendo maggiore dell unità la struttura garantisce resistenza a fatica. 4
36 Struttura sollecitata da carico ripetuto In Fig.6 si mostra una piccola gru che sostiene un carico P, il quale oscilla fra due posizioni. Nonostante il carico non cambi, per effetto della variazione di configurazione, le travi della gru risultano sollecitate a fatica. l 3 l l 1 s d l 4 d 1 x P x l l 1 tempo I dati del problema sono: Figura 6: Gru sollecitata da un carico di posizione variabile. Geometria : l 1 = 1m l = m l 3 = 4m l 4 = 1m d 1 = 300 mm d = 400 mm s = 10 mm Materiale : S U = 50 MPa S Y = 345 MPa Carico : P = 50 kn (6) Verificare se la trave orizzontale, che sostiene il carico P, è in sicurezza rispetto alla sollecitazione di fatica. Nel punto critico della trave il coefficiente di sicurezza (minimo) è: C S =
37 Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 07: Progettazione di strutture meccaniche Indice 1 Progettazione e dimensionamento di strutture meccaniche Verifica e dimensionamento Progettazione e dimensionamento Utilizzo di valori tabulati di proprietà di sezione... 3 Dimensionamento di un asse sollecitato a fatica 6 1 Progettazione e dimensionamento di strutture meccaniche La progettazione di strutture meccaniche consiste nell individuare una configurazione in grado di sostenere il carico a cui la struttura è sottoposta ed evitare il verificarsi di cedimenti di ogni tipo. Le modalità di cedimento, analizzato in precedenza, sono: rottura statica, raggiungimento del limite di rottura o anche soltanto del limite di snervamento; instabilità elastica, la soluzione elastica non è stabile, la struttura si deforma notevolmente causando quindi una rottura; rottura per fatica, in una zona della struttura (tipicamente in corrispondenza di concentrazione di tensioni) la sollecitazione ciclica, ripetuta per un numero molto elevato di volte (dell ordine di 10 6 ), genera una sezione di frattura sul componente. altre forme di cedimento. 1.1 Verifica e dimensionamento Nelle esercitazioni precedenti le modalità di cedimento appena elencate erano già state presentate. In particolare era stata svolta la verifica. La configurazione geometrica, le dimensioni, e le condizioni di carico erano date e quindi era necessario individuare la sezione critica e verificare che il coefficiente di sicurezza fosse maggiore dell unità. 1
38 Il dimensionamento consiste, invece, nel trovare le dimensioni della struttura, data la configurazione geometrica e i carichi. Un modo di dimensionamento è quello di fare delle verifiche partendo da dimensioni di tentativo e iterativamente trovare la condizione di coefficiente di sicurezza maggiore dell unità. La linea guida per il metodo di dimensionamento iterativo è che: maggiore è la dimensione della sezione e maggiore è anche la sua capacità di sostenere il carico. In alcuni casi è tuttavia possibile risolvere il problema del dimensionamento in modo diretto, piuttosto che iterativamente. In questi casi semplici, infatti, è possibile imporre la condizione di coefficiente di sicurezza pari all unità e determinare per formula inversa la dimensione della sezione che soddisfi tale condizione. Ovviamente è poi necessario considerare una dimensione maggiore in modo da avere un certo margine di sicurezza. In Fig.1 si mostra una travatura reticolare, che sostiene un carico all estremità. Dimensionare la sezione delle aste (ipotizzando di realizzare tutte le aste con lo stesso diametro). L 1 d? P L1 1m P 1000 N Materiale: S S U Y 500 MPa 35 MPa Figura 1: Dimensionamento di una travatura reticolare. Suggerimento: Notare che le modalità di rottura sono: il superamento del limite elastico delle travi, ma anche la perdita di stabilità delle travi in compressione. Diametro minimo, per il quale coefficiente di sicurezza è pari all unità: d = 13.0mm Applicando una maggiorazione cautelativa: d = 15.0mm 1. Progettazione e dimensionamento Talvolta i termini dimensionamento e progettazione vengono considerati come sinonimi. Tuttavia, è bene puntualizzare che per dimensionamento si intende la determinazione delle dimensioni di una struttura meccanica al fine di sostenere una certo livello di carico (ad esempio l esercizio precedente), mentre per progettazione si intende, in modo più ampio, pensare una configurazione della struttura migliore, ai fini della resistenza, e quindi successivamente farne il dimensionamento.
39 Individuare una configurazione di maggiore resistenza al fine di sostenere il carico della Fig.1. Dato che la modalità di cedimento più critica è l instabilità (a carico di punta) si può suggerire di considerare la configurazione speculare, nella quale i versi delle forze si invertono (puntoni diventano tiranti e viceversa). I questo modo si ottiene come diametro minimo: d = 11.9mm Applicando una maggiorazione cautelativa: d = 13.0mm quindi il diametro richiesto è (leggermente) minore. 1.3 Utilizzo di valori tabulati di proprietà di sezione Molto spesso vengono utilizzate sezioni standardizzate, per le quali sono disponibili i valori tabulati delle proprietà di sezione. In questo caso, il dimensionamento mediante formula inversa non è fattibile, mentre è immediato il procedimento di dimensionamento iterativo. Si consideri la struttura di Fig., in cui una traversa, caricata da un peso che grava sopra, è sostenuto da 3 pilastri allineati. P P /3 P /3 P /3 h Figura : Traversa sostenuta da 3 pilastri. In Fig.3 si mostrano i due possibili modi di cedimento, per instabilità elastica, che ammette la struttura. In particolare il secondo modo, Fig.3(b), ammette un carico critico più basso di 4 volte, dato che nel senso laterale la struttura ha una lunghezza di libera inflessione (da punto di flesso a punto di flesso) doppia. Tuttavia, non è detto che la sezione sia isotropa (stesso momento d inerzia I nelle due direzioni). 3
40 h / h / h h P C1 L0 L 0 EI h (a) P EI C L0 0 h L (b) Figura 3: Modi di cedimento della struttura per instabilità elastica. Il progetto della struttura, in questo caso, consiste nel decidere di utilizzare una sezione con anisotropia (momenti d inerzia diversi, ad esempio I x > I y ), in modo da compensare la disparità di carico critico in una direzione. Scegliendo di utilizzare una trave a doppio T, la configurazione più favorevole è quella mostrata in Fig.4. Maggiore rigidezza sezione, per contrastare minore resistenza strutturale Figura 4: Disposizione migliore di sezione a doppio T. A questo punto si può procedere con il dimensionamento della sezione. In Fig.5 vengono riportate le proprietà di sezione di profilati IPE, fra cui scegliere quale usare, sfruttando la configurazione favorevole di Fig.4. 4
41 h mm b mm a mm e mm r mm Peso kg/m Sezione cm Momenti di inerzia Moduli di resistenza Raggi di inerzia Jx cm ,8 5, 5 6,0 7,64 80,14 8,49 0,03 3,69 3,4 1, ,1 5,7 7 8,1 10,3 171,0 15,9 34,0 5,79 4,07 1, ,4 6,3 7 10,4 13,1 317,8 7,67 5,96 8,65 4,90 1, ,9 7 1,9 16,43 541, 44,9 77,3 1,31 5,74 1, ,0 7,4 9 15,8 0,09 869,3 68,31 108,7 16,66 6,58 1, ,3 8,0 9 18,8 3, ,9 146,3,16 7,4, ,6 8,5 1,4 8, ,4 194,3 8,47 8,6, ,9 9, 1 6, 33, ,9 5,0 37,5 9,11, , 9, ,7 39, ,6 34,3 47,7 9,97, ,6 10, 15 36,1 45, ,9 48,9 6,0 11,3 3, ,1 10,7 15 4, 53, ,8 557,1 80,50 1,46 3, ,5 11, ,1 6, ,1 713,1 98,5 13,71 3, ,0 1, ,1 7, ,6 1,8 14,95 3, ,6 13,5 1 66,3 84, ,4 16,55 3, ,4 14,6 1 77,6 98, ,4 18,48 4, , 16,0 1 90,7 115, , 0,43 4, ,1 17, , ,1,35 4, ,0 19, , ,9 4,30 4,66 Jy cm4 Wx cm3 Wy cm3 ix cm iy cm (a) (b) Figura 5: Profilati IPE. Scegliere la sezione IPE più piccola, in grado di garantire resistenza ad entrambi i tipi di cedimento elastico. Essendo J x > 4J y per tutte le sezioni, sfruttando la configurazione di Fig.4, il tipo di cedimento più pericoloso è quello di Fig.3(a). La sezione più piccola in grado di sostenere il carico è la IPE 0 (altezza della sezione: 0 mm). Con tale sezione si ha: P C1 = 41kN > P 3 = 33kN 5
42 Dimensionamento di un asse sollecitato a fatica In Fig.6 si mostra un asse, sostenuto da cuscinetti radiali, alla cui estremità è collocata una puleggia su cui si avvolge una cinghia precaricata. Sezione critica d? T T 0 0 Figura 6: Puleggia folle. Sollecitazione sull asse e sui supporti, generato dal precarico della cinghia. Essendo i rami delle cinghie sollecitate dal precarico, tale sollecitazione si scarica sull asse e quindi sui cuscinetti (o supporti). In corrispondenza della sezione critica (momento massimo, sezione minima) si ha flessione rotante, e concentrazione di tensione k t, dovuta ad una variazione di sezione, anche se mitigata da un evidente raggio di raccordo. Determinare il diametro d tale che l asse sia in grado di sostenere la sollecitazione di flessione rotante. Dati: L S U = 900MPa S Y = 800MPa k t =.0 L = 370mm T 0 = 100N α = 30 Il diametro che garantisce un coefficiente di sicurezza unitario è pari a: d = 36.8 mm. Tuttavia, nella fatica è particolarmente importante sovradimensionare. Un valore affidabile di diametro è pertanto: d = 50 mm, a cui corrisponde un coefficiente di sicurezza pari a.5. 6
43 Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 08: Introduzione alla cinematica e dinamica del punto materiale e del corpo rigido Indice 1 Dinamica del punto materiale 1 Cinematica del corpo rigido 4 1 Dinamica del punto materiale Il punto materiale è un astrazione concettuale di un sistema le cui dimensioni sono piccole rispetto alle dimensioni della traiettoria del moto che realizza. Addirittura la terra può essere considerata un punto materiale studiandone il moto intorno al sole. Il punto materiale è caratterizzato da dimensioni di ingombro nulle, per cui la sua posizione (rispetto ad un qualsiasi sistema di riferimento) è definita, semplicemente, da una terna di coordinate: x,y,z. Il punto materiale inoltre è caratterizzato da una massa m. Le note definizioni della cinematica sono: Velocità v x,v y,v z : v x = dx dt in cui t è il tempo. v y = dy dt v z = dz dt Accelerazione a x,a y,a z : a x = dv x dt = d x dt a y = dv y dt = d y dt a z = dv z dt = d z dt La legge fondamentale della dinamica lega le componenti della risultante delle forze che agiscono sul punto materiale alle componenti dell accelerazione rispetto ad un sistema di coordinate inerziale: F x = ma x F y = ma y F z = ma z 1
44 Per le applicazioni di interesse del presente corso, un sistema di coordinate inerziale è il suolo terrestre, e quindi anche un qualsiasi altro sistema che trasla, in modo uniforme e senza ruotare, rispetto al suolo. In Fig.1 si mostra un punto materiale di massa m che si muove lungo una traiettoria circolare, sul quale agisce l azione F esercitata da un filo. v m F r Figura 1: Punto materiale in moto lungo una traiettoria circolare. Nel caso in cui il moto circolare sia uniforme, determinare: 1. l angolo formato dal cavo con la tangente della traiettoria;. la massima velocità di rotazione senza causare il cedimento del cavo (resistenza materiale S U, diametro filo Φ). I dati del problema sono: m = 10 kg r = 1m S U = 300 MPa Φ = mm La velocità periferica a cui il filo si rompe è pari a: v r = 9.71 m/s.
RESISTENZA DEI MATERIALI TEST
 RESISTENZA DEI MATERIALI TEST 1. Nello studio della resistenza dei materiali, i corpi: a) sono tali per cui esiste sempre una proporzionalità diretta tra sollecitazione e deformazione b) sono considerati
RESISTENZA DEI MATERIALI TEST 1. Nello studio della resistenza dei materiali, i corpi: a) sono tali per cui esiste sempre una proporzionalità diretta tra sollecitazione e deformazione b) sono considerati
Dimensionamento delle strutture
 Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Per prima cosa si determinano le caratteristiche geometriche e meccaniche della sezione del profilo, nel nostro caso sono le seguenti;
 !""##"!$%&'((""!" )**&)+,)-./0)*$1110,)-./0)*!""##"!$%&'((""!" *&)23+-0-$4--56%--0.),0-,-%323 -&3%/ La presente relazione ha lo scopo di illustrare il meccanismo di calcolo che sta alla base del dimensionamento
!""##"!$%&'((""!" )**&)+,)-./0)*$1110,)-./0)*!""##"!$%&'((""!" *&)23+-0-$4--56%--0.),0-,-%323 -&3%/ La presente relazione ha lo scopo di illustrare il meccanismo di calcolo che sta alla base del dimensionamento
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE LE FONDAZIONI
 LE FONDAZIONI Generalità sulle fondazioni Fondazioni dirette Plinti isolati Trave rovescia Esecutivi di strutture di fondazione Generalità Le opere di fondazione hanno il compito di trasferire le sollecitazioni
LE FONDAZIONI Generalità sulle fondazioni Fondazioni dirette Plinti isolati Trave rovescia Esecutivi di strutture di fondazione Generalità Le opere di fondazione hanno il compito di trasferire le sollecitazioni
Le molle. Costruzione di Macchine 2 Prof. Stefano Beretta Chiara Colombo
 Le molle Costruzione di Macchine 2 Prof. Stefano Beretta Chiara Colombo Le molle 2 Le molle sono elementi in grado di deformarsi elasticamente, assorbendo energia. Applicazioni caratteristiche: accumulatore
Le molle Costruzione di Macchine 2 Prof. Stefano Beretta Chiara Colombo Le molle 2 Le molle sono elementi in grado di deformarsi elasticamente, assorbendo energia. Applicazioni caratteristiche: accumulatore
DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE
 DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE Per un corretto dimensionamento del martinetto a ricircolo di sfere è necessario operare come segue: definizione dei dati del dell applicazione (A)
DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE Per un corretto dimensionamento del martinetto a ricircolo di sfere è necessario operare come segue: definizione dei dati del dell applicazione (A)
LEZIONI N 24 E 25 UNIONI SALDATE
 LEZIONI N 24 E 25 UNIONI SALDATE Le saldature si realizzano prevalentemente con il metodo dell arco elettrico, utilizzando elettrodi rivestiti, che forniscono il materiale di apporto. Il collegamento è
LEZIONI N 24 E 25 UNIONI SALDATE Le saldature si realizzano prevalentemente con il metodo dell arco elettrico, utilizzando elettrodi rivestiti, che forniscono il materiale di apporto. Il collegamento è
Sussidi didattici per il corso di COSTRUZIONI EDILI. Prof. Ing. Francesco Zanghì TRAVI RETICOLARI AGGIORNAMENTO DEL 7/11/2011
 Sussidi didattici per il corso di COSTRUZIONI EDILI Prof. Ing. Francesco Zanghì TRAVI RETICOLARI AGGIORNAMENTO DEL 7/11/2011 Le travi reticolari sono strutture formate da aste rettilinee, mutuamente collegate
Sussidi didattici per il corso di COSTRUZIONI EDILI Prof. Ing. Francesco Zanghì TRAVI RETICOLARI AGGIORNAMENTO DEL 7/11/2011 Le travi reticolari sono strutture formate da aste rettilinee, mutuamente collegate
ANALISI STRUTTURALE DELLA TRAVE PORTA-PARANCO IN ACCIAIO (sala C LNGS - INFN)
 ANALISI STRUTTURALE DELLA TRAE PORTA-PARANCO IN ACCIAIO (sala C LNGS - INFN) SALA C SALA A SALA B Ing. FRANCESCO POTENZA Ing. UBERTO DI SABATINO 1 1. PREESSA La presente relazione illustra i risultati
ANALISI STRUTTURALE DELLA TRAE PORTA-PARANCO IN ACCIAIO (sala C LNGS - INFN) SALA C SALA A SALA B Ing. FRANCESCO POTENZA Ing. UBERTO DI SABATINO 1 1. PREESSA La presente relazione illustra i risultati
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
I.T.I.S. «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: 049.80.40.211 Fax 049.80.40.277 e-mail: marconi@provincia.padova.it ww.itismarconipadova.
 PAG. 1/5 I.T.I.S. «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: 049.80.40.211 Fax 049.80.40.277 e-mail: marconi@provincia.padova.it ww.itismarconipadova.it DIPARTIMANTO DI MECCANICA E MACCHINE A FLUIDO Rev.
PAG. 1/5 I.T.I.S. «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: 049.80.40.211 Fax 049.80.40.277 e-mail: marconi@provincia.padova.it ww.itismarconipadova.it DIPARTIMANTO DI MECCANICA E MACCHINE A FLUIDO Rev.
. Si determina quindi quale distanza viene percorsa lungo l asse y in questo intervallo di tempo: h = v 0y ( d
 Esercizio 1 Un automobile viaggia a velocità v 0 su una strada inclinata di un angolo θ rispetto alla superficie terrestre, e deve superare un burrone largo d (si veda la figura, in cui è indicato anche
Esercizio 1 Un automobile viaggia a velocità v 0 su una strada inclinata di un angolo θ rispetto alla superficie terrestre, e deve superare un burrone largo d (si veda la figura, in cui è indicato anche
Collegamenti nelle strutture
 1 Collegamenti nelle strutture Le tipologie delle unioni bullonate o saldate sono molteplici e dipendono essenzialmente da: caratteristiche dell unione: nell ambito di quelle bullonate si possono avere
1 Collegamenti nelle strutture Le tipologie delle unioni bullonate o saldate sono molteplici e dipendono essenzialmente da: caratteristiche dell unione: nell ambito di quelle bullonate si possono avere
Strutture in Acciaio:
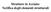 Strutture in Acciaio: i Verifica degli elementi strutturali STATI LIMITE DI ESERCIZIO STATI LIMITE ULTIMI DELLE SEZIONI (RESISTENZA DELLE SEZIONI) Si possono considerare due stati limite: 1. Stato
Strutture in Acciaio: i Verifica degli elementi strutturali STATI LIMITE DI ESERCIZIO STATI LIMITE ULTIMI DELLE SEZIONI (RESISTENZA DELLE SEZIONI) Si possono considerare due stati limite: 1. Stato
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
F 2 F 1. r R F A. fig.1. fig.2
 N.1 Un cilindro di raggio R = 10 cm e massa M = 5 kg è posto su un piano orizzontale scabro (fig.1). In corrispondenza del centro del cilindro è scavata una sottilissima fenditura in modo tale da ridurre
N.1 Un cilindro di raggio R = 10 cm e massa M = 5 kg è posto su un piano orizzontale scabro (fig.1). In corrispondenza del centro del cilindro è scavata una sottilissima fenditura in modo tale da ridurre
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012
 Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Documento #: Doc_a8_(9_b).doc
 10.10.8 Esempi di progetti e verifiche di generiche sezioni inflesse o presso-tensoinflesse in conglomerato armato (rettangolari piene, circolari piene e circolari cave) Si riportano, di seguito, alcuni
10.10.8 Esempi di progetti e verifiche di generiche sezioni inflesse o presso-tensoinflesse in conglomerato armato (rettangolari piene, circolari piene e circolari cave) Si riportano, di seguito, alcuni
7 Applicazioni ulteriori
 7 Applicazioni ulteriori 7 Applicazioni ulteriori 7.1 Strutture con maglie chiuse 7.1.1 Analisi cinematica Si consideri la struttura in figura 7.1: i gradi di libertà sono pari a l =3n c v =3 0 3 = 0,
7 Applicazioni ulteriori 7 Applicazioni ulteriori 7.1 Strutture con maglie chiuse 7.1.1 Analisi cinematica Si consideri la struttura in figura 7.1: i gradi di libertà sono pari a l =3n c v =3 0 3 = 0,
SETTI O PARETI IN C.A.
 SETTI O PARETI IN C.A. Parete Pareti accoppiate SETTI O PARETI IN C.A. Na 20% Fh i i h i Na/M tot >=0.2 SETTI O PARETI IN C.A. IL FATTORE DI STRUTTURA VERIFICHE SETTI O PARETI IN C.A. SOLLECITAZIONI -FLESSIONE
SETTI O PARETI IN C.A. Parete Pareti accoppiate SETTI O PARETI IN C.A. Na 20% Fh i i h i Na/M tot >=0.2 SETTI O PARETI IN C.A. IL FATTORE DI STRUTTURA VERIFICHE SETTI O PARETI IN C.A. SOLLECITAZIONI -FLESSIONE
11 Teorema dei lavori virtuali
 Teorema dei lavori virtuali Teorema dei lavori virtuali Si consideri una trave ad asse rettilineo figura.). Per essa si definisce sistema carichi sollecitazioni CS) l insieme di tutte le grandezze di tipo
Teorema dei lavori virtuali Teorema dei lavori virtuali Si consideri una trave ad asse rettilineo figura.). Per essa si definisce sistema carichi sollecitazioni CS) l insieme di tutte le grandezze di tipo
UNIVERSITA DEGLI STUDI DI BRESCIA
 UNIVERSITA DEGLI STUDI DI BRESCIA ESAME DI STATO DI ABILITAZIONE ALL'ESERCIZIO DELLA PROFESSIONE DI INGEGNERE (Lauree di primo livello D.M. 509/99 e D.M. 270/04 e Diploma Universitario) SEZIONE B - Prima
UNIVERSITA DEGLI STUDI DI BRESCIA ESAME DI STATO DI ABILITAZIONE ALL'ESERCIZIO DELLA PROFESSIONE DI INGEGNERE (Lauree di primo livello D.M. 509/99 e D.M. 270/04 e Diploma Universitario) SEZIONE B - Prima
Prova d esame del 30 giugno 2010 Soluzione
 UNIVERSITÀ I PIS Facoltà di Ingegneria Meccanica nalitica e dei Continui (CS Ing. Nucleare e della Sicurezza Industriale) Scienza delle Costruzioni (C Ing. Nucleare e della Sicurezza e Protezione) Scienza
UNIVERSITÀ I PIS Facoltà di Ingegneria Meccanica nalitica e dei Continui (CS Ing. Nucleare e della Sicurezza Industriale) Scienza delle Costruzioni (C Ing. Nucleare e della Sicurezza e Protezione) Scienza
Forze, leggi della dinamica, diagramma del. 28 febbraio 2009 (PIACENTINO - PREITE) Fisica per Scienze Motorie
 Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
ESAME DI STATO 2009/10 INDIRIZZO MECCANICA TEMA DI : MECCANICA APPLICATA E MACCHINE A FLUIDO
 ESAME DI STATO 2009/10 INDIRIZZO MECCANICA TEMA DI : MECCANICA APPLICATA E MACCHINE A FLUIDO Lo studio delle frizioni coniche si effettua distinguendo il caso in cui le manovre di innesto e disinnesto
ESAME DI STATO 2009/10 INDIRIZZO MECCANICA TEMA DI : MECCANICA APPLICATA E MACCHINE A FLUIDO Lo studio delle frizioni coniche si effettua distinguendo il caso in cui le manovre di innesto e disinnesto
Horae. Horae Software per la Progettazione Architettonica e Strutturale
 1 IL MATERIALE X-LAM Nel programma CDSWin il materiale X-LAM pu ò essere utilizzato solo come elemento parete verticale. Quindi, dal punto di vista strutturale, il suo comportamento è prevalentemente a
1 IL MATERIALE X-LAM Nel programma CDSWin il materiale X-LAM pu ò essere utilizzato solo come elemento parete verticale. Quindi, dal punto di vista strutturale, il suo comportamento è prevalentemente a
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
Lezione. Tecnica delle Costruzioni
 Lezione Tecnica delle Costruzioni 1 Flessione composta tensoflessione Risposta della sezione Campo elastico σ + A I Risposta della sezione Al limite elastico el, Per calcolare el, : σ A + el, I f f + el,
Lezione Tecnica delle Costruzioni 1 Flessione composta tensoflessione Risposta della sezione Campo elastico σ + A I Risposta della sezione Al limite elastico el, Per calcolare el, : σ A + el, I f f + el,
Q 1 = +3 10-5 C carica numero 1 Q 2 = +4 10-5 C carica numero 2 forza esercitata tra le cariche distanza tra le cariche, incognita
 Problema n 1 A quale distanza, una dall'altra bisogna porre nel vuoto due cariche (Q 1 =3 10-5 C e Q 2 =4 10-5 C) perché esse esercitino una sull'altra la forza di 200 N? Q 1 = +3 10-5 C carica numero
Problema n 1 A quale distanza, una dall'altra bisogna porre nel vuoto due cariche (Q 1 =3 10-5 C e Q 2 =4 10-5 C) perché esse esercitino una sull'altra la forza di 200 N? Q 1 = +3 10-5 C carica numero
Esercitazione 5 Dinamica del punto materiale
 Problema 1 Un corpo puntiforme di massa m = 1.0 kg viene lanciato lungo la superficie di un cuneo avente un inclinazione θ = 40 rispetto all orizzontale e altezza h = 80 cm. Il corpo viene lanciato dal
Problema 1 Un corpo puntiforme di massa m = 1.0 kg viene lanciato lungo la superficie di un cuneo avente un inclinazione θ = 40 rispetto all orizzontale e altezza h = 80 cm. Il corpo viene lanciato dal
MODULO GRAT PROCEDURA TRASFXY TEST CASES
 TC GRAT/TrasfXY 1 MODULO GRAT PROCEDURA TRASFXY TEST CASES 1 TC TRASFXY 1 - Graticcio a 17 aste carico nel perimetro aste ripartizione in direz. Y Trave 1 Trave 2 Trave 3 Traverso 1 Traverso 2 Traverso
TC GRAT/TrasfXY 1 MODULO GRAT PROCEDURA TRASFXY TEST CASES 1 TC TRASFXY 1 - Graticcio a 17 aste carico nel perimetro aste ripartizione in direz. Y Trave 1 Trave 2 Trave 3 Traverso 1 Traverso 2 Traverso
TRAVE SU SUOLO ELASTICO
 Capitolo 3 TRAVE SU SUOLO ELASTICO (3.1) Combinando la (3.1) con la (3.2) si ottiene: (3.2) L equazione differenziale può essere così riscritta: (3.3) La soluzione dell equazione differenziale di ordine
Capitolo 3 TRAVE SU SUOLO ELASTICO (3.1) Combinando la (3.1) con la (3.2) si ottiene: (3.2) L equazione differenziale può essere così riscritta: (3.3) La soluzione dell equazione differenziale di ordine
15 febbraio 2010 - Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a. 2009-2010 COGNOME... NOME... N. MATRICOLA...
 15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
Calcola l allungamento che subisce un tirante di acciaio lungo l=2,5m (a sez.circolare) con φ =20mm sottoposto ad un carico (in trazione) F=40.000N.
 Edutecnica.it Azioni interne esercizi risolti 1 razione Esercizio no.1 soluzione a pag.7 Determina il diametro di un tirante (a sezione circolare in acciaio Fe0 da sottoporre ad una forza F10.000N di lunghezza
Edutecnica.it Azioni interne esercizi risolti 1 razione Esercizio no.1 soluzione a pag.7 Determina il diametro di un tirante (a sezione circolare in acciaio Fe0 da sottoporre ad una forza F10.000N di lunghezza
6. Unioni bullonate. 6.1 Tecnologia delle unioni bullonate. 6.1.1 Classificazione dei bulloni. (aggiornamento 24-09-2009)
 6. Unioni bullonate (aggiornamento 24-09-2009) 6.1 Tecnologia delle unioni bullonate 6.1.1 Classificazione dei bulloni NTC - D.M. 14-1-2008 1 N.B. Il primo numero x 100 = f ub il secondo per il primo =f
6. Unioni bullonate (aggiornamento 24-09-2009) 6.1 Tecnologia delle unioni bullonate 6.1.1 Classificazione dei bulloni NTC - D.M. 14-1-2008 1 N.B. Il primo numero x 100 = f ub il secondo per il primo =f
Lezione. Tecnica delle Costruzioni
 Lezione Tecnica delle Costruzioni Classificazione dei collegamenti Tipi di collegamenti 1. Collegamento a parziale ripristino di resistenza In grado di trasmettere le caratteristiche di sollecitazione
Lezione Tecnica delle Costruzioni Classificazione dei collegamenti Tipi di collegamenti 1. Collegamento a parziale ripristino di resistenza In grado di trasmettere le caratteristiche di sollecitazione
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
McGraw-Hill. Tutti i diritti riservati
 Copyright 004 The Companies srl e Corbusier - Progetto per il palazzo dei Soviet a Mosca 1931 Problema 1. Arco Trave di copertura Tirante bielle Membrana di copertura Fig. P1.1 Analizzare il sistema in
Copyright 004 The Companies srl e Corbusier - Progetto per il palazzo dei Soviet a Mosca 1931 Problema 1. Arco Trave di copertura Tirante bielle Membrana di copertura Fig. P1.1 Analizzare il sistema in
Strutture in acciaio. Unioni
 Strutture in acciaio Unioni Tipologie di unioni Chiodi o bulloni Sono puntuali Indeboliscono le sezioni Ripristinano solo parzialmente la continuità Si eseguono in opera con relativa facilità Saldatura
Strutture in acciaio Unioni Tipologie di unioni Chiodi o bulloni Sono puntuali Indeboliscono le sezioni Ripristinano solo parzialmente la continuità Si eseguono in opera con relativa facilità Saldatura
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
FORMULE UTILIZZATE NEI CALCOLI
 OGGETTO LAVORI Committente: FORMULE UTILIZZATE NEI CALCOLI Il Progettista Strutturale VERIFICA DELLE RIGIDEZZE. La rigidezza iniziale (K in ) si calcola con la formula: K = GAEl 2 h 3 G1,2hEl 2 dove: E,G
OGGETTO LAVORI Committente: FORMULE UTILIZZATE NEI CALCOLI Il Progettista Strutturale VERIFICA DELLE RIGIDEZZE. La rigidezza iniziale (K in ) si calcola con la formula: K = GAEl 2 h 3 G1,2hEl 2 dove: E,G
IL TRACCIAMENTO QUALITATIVO DEL MOMENTO FLETTENTE NEI PORTALI
 IL TRACCIAMENTO QUALITATIVO DEL MOMENTO FLETTENTE NEI PORTALI Alcune proprietà della deformata dei portali Si esaminano nel seguito alcune proprietà della deformata dei portali. Queste proprietà permettono
IL TRACCIAMENTO QUALITATIVO DEL MOMENTO FLETTENTE NEI PORTALI Alcune proprietà della deformata dei portali Si esaminano nel seguito alcune proprietà della deformata dei portali. Queste proprietà permettono
Appunti sulle funi. Le Funi Carmine Napoli
 Appunti sulle funi DEFINIZIONE Fune: è un organo flessibile formato da un insieme di fili di acciaio, di forma e dimensioni appropriate, avvolti elicoidalmente in uno o più gruppi concentrici attorno ad
Appunti sulle funi DEFINIZIONE Fune: è un organo flessibile formato da un insieme di fili di acciaio, di forma e dimensioni appropriate, avvolti elicoidalmente in uno o più gruppi concentrici attorno ad
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Carichi unitari. Dimensionamento delle sezioni e verifica di massima. Dimensionamento travi a spessore. Altri carichi unitari. Esempio.
 Carichi unitari delle sezioni e verifica di massima Una volta definito lo spessore, si possono calcolare i carichi unitari (k/m ) Solaio del piano tipo Solaio di copertura Solaio torrino scala Sbalzo piano
Carichi unitari delle sezioni e verifica di massima Una volta definito lo spessore, si possono calcolare i carichi unitari (k/m ) Solaio del piano tipo Solaio di copertura Solaio torrino scala Sbalzo piano
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
LA FORZA. Il movimento: dal come al perché
 LA FORZA Concetto di forza Principi della Dinamica: 1) Principio d inerzia 2) F=ma 3) Principio di azione e reazione Forza gravitazionale e forza peso Accelerazione di gravità Massa, peso, densità pag.1
LA FORZA Concetto di forza Principi della Dinamica: 1) Principio d inerzia 2) F=ma 3) Principio di azione e reazione Forza gravitazionale e forza peso Accelerazione di gravità Massa, peso, densità pag.1
24 - Strutture simmetriche ed antisimmetriche
 24 - Strutture simmetriche ed antisimmetriche ü [.a. 2011-2012 : ultima revisione 1 maggio 2012] In questo capitolo si studiano strutture piane che presentano proprieta' di simmetria ed antisimmetria sia
24 - Strutture simmetriche ed antisimmetriche ü [.a. 2011-2012 : ultima revisione 1 maggio 2012] In questo capitolo si studiano strutture piane che presentano proprieta' di simmetria ed antisimmetria sia
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Insegnamento di Progetto di Infrastrutture viarie
 Insegnamento di Progetto di Infrastrutture viarie Opere in terra Caratteristiche di un terreno Compressibilità e costipamento delle terre Portanza sottofondi e fondazioni stradali Instabilità del corpo
Insegnamento di Progetto di Infrastrutture viarie Opere in terra Caratteristiche di un terreno Compressibilità e costipamento delle terre Portanza sottofondi e fondazioni stradali Instabilità del corpo
Analisi e consolidamento di colonne e pilastri in muratura
 CORSO DI RECUPERO E CONSERVAZIONE DEGLI EDIFICI A.A. 2010-2011 Analisi e consolidamento di colonne e pilastri in muratura Resistenza a compressione (1) I materiali lapidei naturali ed artificiali raggiungono
CORSO DI RECUPERO E CONSERVAZIONE DEGLI EDIFICI A.A. 2010-2011 Analisi e consolidamento di colonne e pilastri in muratura Resistenza a compressione (1) I materiali lapidei naturali ed artificiali raggiungono
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
UNIVERSITA DEGLI STUDI DI CAGLIARI FACOLTA DI INGEGNERIA DIPARTIMENTO DI INGEGNERIA STRUTTURALE PROVE SPERIMENTALI SU PIGNATTE IN PSE RELAZIONE
 UNIVERSITA DEGLI STUDI DI CAGLIARI FACOLTA DI INGEGNERIA DIPARTIMENTO DI INGEGNERIA STRUTTURALE PROVE SPERIMENTALI SU PIGNATTE IN PSE RELAZIONE Il Responsabile Scientifico Dott. Ing. Fausto Mistretta Il
UNIVERSITA DEGLI STUDI DI CAGLIARI FACOLTA DI INGEGNERIA DIPARTIMENTO DI INGEGNERIA STRUTTURALE PROVE SPERIMENTALI SU PIGNATTE IN PSE RELAZIONE Il Responsabile Scientifico Dott. Ing. Fausto Mistretta Il
Forza. Forza. Esempi di forze. Caratteristiche della forza. Forze fondamentali CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA
 Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
DIMENSIONAMENTO DI UN PILASTRO
 DIMENSIONAMENTO DI UN PILASTRO Si dimensioni un pilastro nelle tre diverse tecnologie: legno, acciaio e cemento armato. Osservando una generica pianta di carpenteria, il pilastro centrale sarà quello maggiormente
DIMENSIONAMENTO DI UN PILASTRO Si dimensioni un pilastro nelle tre diverse tecnologie: legno, acciaio e cemento armato. Osservando una generica pianta di carpenteria, il pilastro centrale sarà quello maggiormente
(7) Nel calcolo della resistenza di un collegamento ad attrito il coefficiente di attrito µ dipende: (punti 3)
 Domande su: taglio, flessione composta e collegamenti. Indica se ciascuna delle seguenti affermazioni è vera o falsa (per ciascuna domanda punti 2) (1) L adozione di un gioco foro-bullone elevato semplifica
Domande su: taglio, flessione composta e collegamenti. Indica se ciascuna delle seguenti affermazioni è vera o falsa (per ciascuna domanda punti 2) (1) L adozione di un gioco foro-bullone elevato semplifica
Rette e curve, piani e superfici
 Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Verifica di sicurezza di un capannone industriale in acciaio
 Verifica di sicurezza di un capannone industriale in acciaio 1 Elementi strutturali Travi principali reticolari (capriate); travi secondarie (arcarecci); pilastri; controventi di falda; controventi longitudinali
Verifica di sicurezza di un capannone industriale in acciaio 1 Elementi strutturali Travi principali reticolari (capriate); travi secondarie (arcarecci); pilastri; controventi di falda; controventi longitudinali
Nome..Cognome.. Classe 4G 4 dicembre 2008. VERIFICA DI FISICA: lavoro ed energia
 Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
FAM. 1. Sistema composto da quattro PM come nella tabella seguente
 Serie 11: Meccanica IV FAM C. Ferrari Esercizio 1 Centro di massa: sistemi discreti Determina il centro di massa dei seguenti sistemi discreti. 1. Sistema composto da quattro PM come nella tabella seguente
Serie 11: Meccanica IV FAM C. Ferrari Esercizio 1 Centro di massa: sistemi discreti Determina il centro di massa dei seguenti sistemi discreti. 1. Sistema composto da quattro PM come nella tabella seguente
Istruzioni per l uso dei programmi MomCad, TraveCon, TraveFon
 Istruzioni per l uso dei programmi MomCad, TraveCon, TraveFon I tre programmi sono utility generali preparate appositamente per gli studenti (ma che potrebbero essere utili anche per professionisti). MomCad
Istruzioni per l uso dei programmi MomCad, TraveCon, TraveFon I tre programmi sono utility generali preparate appositamente per gli studenti (ma che potrebbero essere utili anche per professionisti). MomCad
Dimensioni Altezza del telaio di protezione dai supporti: Larghezza del telaio di protezione:
 Scheda 23: TELAIO ANTERIORE ABBATTIBILE SALDATO PER MOTOAGRICOLE CON STRUTTURA PORTANTE DI TIPO ARTICOLATO O RIGIDO CON POSTO DI GUIDA ARRETRATO CON MASSA MAGGIORE DI 2000 kg E FINO A 3500 kg SPECIFICHE
Scheda 23: TELAIO ANTERIORE ABBATTIBILE SALDATO PER MOTOAGRICOLE CON STRUTTURA PORTANTE DI TIPO ARTICOLATO O RIGIDO CON POSTO DI GUIDA ARRETRATO CON MASSA MAGGIORE DI 2000 kg E FINO A 3500 kg SPECIFICHE
TRAVI SU SUOLO ALLA WINKLER, INTERAZIONE TERRENO-FONDAZIONE
 Università degli Studi di Palermo Facoltà di Ingegneria Dipartimento di Ingegneria Strutturale e Geotecnica TRAVI SU SUOO AA WINKER, INTERAZIONE TERRENO-FONDAZIONE Prof.. Cavaleri Ing. F. Di Trapani TRAVI
Università degli Studi di Palermo Facoltà di Ingegneria Dipartimento di Ingegneria Strutturale e Geotecnica TRAVI SU SUOO AA WINKER, INTERAZIONE TERRENO-FONDAZIONE Prof.. Cavaleri Ing. F. Di Trapani TRAVI
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Modulo di Meccanica e Termodinamica
 Modulo di Meccanica e Termodinamica 1) Misure e unita di misura 2) Cinematica: + Moto Rettilineo + Moto Uniformemente Accelerato [+ Vettori e Calcolo Vettoriale] + Moti Relativi 3) Dinamica: + Forza e
Modulo di Meccanica e Termodinamica 1) Misure e unita di misura 2) Cinematica: + Moto Rettilineo + Moto Uniformemente Accelerato [+ Vettori e Calcolo Vettoriale] + Moti Relativi 3) Dinamica: + Forza e
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
www.rodacciai.it PROVA DI TRAZIONE L 0 = 5.65 S 0 PROVE MECCANICHE
 PROVA DI TRAZIONE La prova, eseguita a temperatura ambiente o più raramente a temperature superiori o inferiori, consiste nel sottoporre una provetta a rottura per mezzo di uno sforzo di trazione generato
PROVA DI TRAZIONE La prova, eseguita a temperatura ambiente o più raramente a temperature superiori o inferiori, consiste nel sottoporre una provetta a rottura per mezzo di uno sforzo di trazione generato
Problemi di dinamica del punto materiale (moto oscillatorio) A Sistemi di riferimento inerziali
 Problemi di dinamica del punto materiale (moto oscillatorio) A Sistemi di riferimento inerziali Problema n. 1: Un corpo puntiforme di massa m = 2.5 kg pende verticalmente dal soffitto di una stanza essendo
Problemi di dinamica del punto materiale (moto oscillatorio) A Sistemi di riferimento inerziali Problema n. 1: Un corpo puntiforme di massa m = 2.5 kg pende verticalmente dal soffitto di una stanza essendo
RELAZIONE STRUTTURALE
 RELAZIONE STRUTTURALE DESCRIZIONE DELL OPERA. Si prevede di realizzare una passerella pedonale in acciaio per l accesso secondario alla grotta. La struttura è costituita da due travi parallele in acciaio
RELAZIONE STRUTTURALE DESCRIZIONE DELL OPERA. Si prevede di realizzare una passerella pedonale in acciaio per l accesso secondario alla grotta. La struttura è costituita da due travi parallele in acciaio
LA LEGGE DI GRAVITAZIONE UNIVERSALE
 GRAVIMETRIA LA LEGGE DI GRAVITAZIONE UNIVERSALE r La legge di gravitazione universale, formulata da Isaac Newton nel 1666 e pubblicata nel 1684, afferma che l'attrazione gravitazionale tra due corpi è
GRAVIMETRIA LA LEGGE DI GRAVITAZIONE UNIVERSALE r La legge di gravitazione universale, formulata da Isaac Newton nel 1666 e pubblicata nel 1684, afferma che l'attrazione gravitazionale tra due corpi è
2 R = mgr + 1 2 mv2 0 = E f
 Esercizio 1 Un corpo puntiforme di massa m scivola lungo la pista liscia di raggio R partendo da fermo da un altezza h rispetto al fondo della pista come rappresentato in figura. Calcolare: a) Il valore
Esercizio 1 Un corpo puntiforme di massa m scivola lungo la pista liscia di raggio R partendo da fermo da un altezza h rispetto al fondo della pista come rappresentato in figura. Calcolare: a) Il valore
bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo
 Momento di una forza Nella figura 1 è illustrato come forze uguali e contrarie possono non produrre equilibrio, bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo esteso.
Momento di una forza Nella figura 1 è illustrato come forze uguali e contrarie possono non produrre equilibrio, bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo esteso.
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA. Dinamica: studio delle forze che causano il moto dei corpi
 DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA Dinamica: studio delle forze che causano il moto dei corpi 1 Forza Si definisce forza una qualunque causa esterna che produce una variazione dello stato
DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA Dinamica: studio delle forze che causano il moto dei corpi 1 Forza Si definisce forza una qualunque causa esterna che produce una variazione dello stato
Ricordiamo ora che a è legata ad x (derivata seconda) ed otteniamo
 Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
Generalità e note di teoria
 Capitolo 1 Generalità e note di teoria In questo capitolo sono riportate alcune note delle teorie utilizzate, riguardanti: Verifiche di resistenza. Dati del problema e convenzioni. Ipotesi fondamentali.
Capitolo 1 Generalità e note di teoria In questo capitolo sono riportate alcune note delle teorie utilizzate, riguardanti: Verifiche di resistenza. Dati del problema e convenzioni. Ipotesi fondamentali.
Cap 3.1- Prima legge della DINAMICA o di Newton
 Parte I Cap 3.1- Prima legge della DINAMICA o di Newton Cap 3.1- Prima legge della DINAMICA o di Newton 3.1-3.2-3.3 forze e principio d inerzia Abbiamo finora studiato come un corpo cambia traiettoria
Parte I Cap 3.1- Prima legge della DINAMICA o di Newton Cap 3.1- Prima legge della DINAMICA o di Newton 3.1-3.2-3.3 forze e principio d inerzia Abbiamo finora studiato come un corpo cambia traiettoria
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Le piastre Precompresse
 Corso di Progetto di Strutture POTENZA, a.a. 2012 2013 Le piastre Precompresse Dott. Marco VONA Scuola di Ingegneria, Università di Basilicata marco.vona@unibas.it http://www.unibas.it/utenti/vona/ PIASTRE
Corso di Progetto di Strutture POTENZA, a.a. 2012 2013 Le piastre Precompresse Dott. Marco VONA Scuola di Ingegneria, Università di Basilicata marco.vona@unibas.it http://www.unibas.it/utenti/vona/ PIASTRE
Scelta e verifica dei motori elettrici per gli azionamenti di un mezzo di trazione leggera
 Scelta e verifica dei motori elettrici per gli azionamenti di un mezzo di trazione leggera Si consideri un convoglio ferroviario per la trazione leggera costituito da un unità di trazione, la quale è formata
Scelta e verifica dei motori elettrici per gli azionamenti di un mezzo di trazione leggera Si consideri un convoglio ferroviario per la trazione leggera costituito da un unità di trazione, la quale è formata
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 2015
 SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
Combinazione dei carichi
 Combinazione dei carichi Un passo fondamentale del progetto di un opera civile è sicuramente l analisi delle forze agenti su essa che sono necessarie per l individuazione delle corrette sollecitazioni
Combinazione dei carichi Un passo fondamentale del progetto di un opera civile è sicuramente l analisi delle forze agenti su essa che sono necessarie per l individuazione delle corrette sollecitazioni
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
Corso di Componenti e Impianti Termotecnici LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE
 LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE 1 PERDITE DI CARICO LOCALIZZATE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE 1 PERDITE DI CARICO LOCALIZZATE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Progetto delle armature longitudinali del solaio
 prof. Renato Giannini Progetto delle armature longitudinali del solaio (arch. Lorena Sguerri) orrezioni del diagramma di momento flettente Prescrizioni di normativa specifiche per il solaio Progetto delle
prof. Renato Giannini Progetto delle armature longitudinali del solaio (arch. Lorena Sguerri) orrezioni del diagramma di momento flettente Prescrizioni di normativa specifiche per il solaio Progetto delle
19 Il campo elettrico - 3. Le linee del campo elettrico
 Moto di una carica in un campo elettrico uniforme Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice se il campo elettrico è uniforme,
Moto di una carica in un campo elettrico uniforme Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice se il campo elettrico è uniforme,
Cosa determina il moto? Aristotele pensava che occorresse uno sforzo per mantenere un corpo in movimento. Galileo non era d'accordo.
 Introduzione Cosa determina il moto? Aristotele pensava che occorresse uno sforzo per mantenere un corpo in movimento. Galileo non era d'accordo. riassunto Cosa determina il moto? Forza - Spinta di un
Introduzione Cosa determina il moto? Aristotele pensava che occorresse uno sforzo per mantenere un corpo in movimento. Galileo non era d'accordo. riassunto Cosa determina il moto? Forza - Spinta di un
Capitolo 4: Ottimizzazione non lineare non vincolata parte II. E. Amaldi DEIB, Politecnico di Milano
 Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti];
![1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti]; 1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti];](/thumbs/24/2314490.jpg) 1 Esercizio Una ruota di raggio R = 15 cm e di massa M = 8 Kg può rotolare senza strisciare lungo un piano inclinato di un angolo θ 2 = 30 0, ed è collegato tramite un filo inestensibile ad un blocco di
1 Esercizio Una ruota di raggio R = 15 cm e di massa M = 8 Kg può rotolare senza strisciare lungo un piano inclinato di un angolo θ 2 = 30 0, ed è collegato tramite un filo inestensibile ad un blocco di
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
