Analisi stocastica. Dispense del corso 2009/10. Versione 2.1 Ultima modifica: 21 dicembre FRANCESCO CARAVENNA
|
|
|
- Massimo Ferrante
- 4 anni fa
- Visualizzazioni
Transcript
1 Aalisi socasica Dispese del corso 9/1 Versioe.1 Ulima modifica: 1 dicembre 1. FRANCESCO CARAVENNA fracesco.caravea@mah.uipd.i hp:// DIPARIMENO DI MAEMAICA PURA E APPLICAA UNIVERSIÀ DEGLI SUDI DI PADOVA VIA RIESE 63, 3511 PADOVA, IALY Sommario. Quese oe rifleoo il coeuo del corso di aalisi socasica da me euo ell ao accademico 9/1 presso l Uiversià degli Sudi di Padova per il corso di laurea magisrale i maemaica. Le pari del eso o svole a lezioe, o solao acceae, soo i corpo miore. Le pricipali foi di ispirazioe soo sai (i ordie grossomodo decrescee) i esi di Comes e Meyre [6], Baldi [], Karazas e Shreve [1998], Mörers eperes[9]elegall[8]. Segalazioi di errori, osservazioi, suggerimei e criiche soo molo gradii. Il cervo che palleggia (lo vedee?) raffigurao i coperia è u segmeo di raieoria del moo browiao el piao, oeuo mediae ierpolazioe lieare di ua passeggiaa aleaoria co icremei ormali cerai (5 passi).
2 Idice Preludio Capiolo 1. Richiami di probabilià Spazi misurabili Probabilià e variabili aleaorie Legge di ua variabile aleaoria Idipedeza e misura prodoo Nozioi di covergeza Fuzioi caraerisiche Leggi ormali Quesioi eciche Gli spazi M e M loc Capiolo 6. Calcolo socasico e applicazioi Formula di Iô per il moo browiao Processi di Iô e formula di Iô geerale Il caso mulidimesioale Moo browiao e laplaciao Il eorema di Girsaov Capiolo 7. Equazioi differeziali socasiche Defiizioi Esiseza e uicià di soluzioi fori La formula di Feyma-Kac Capiolo 8. Rimorsi Le diffusioi come processi di Marov L iegrale di Sraoovich eoremi di rappreseazioe per marigale Capiolo. Moo browiao Processi socasici gaussiai Moo browiao Esiseza del moo browiao (Ir)regolarià delle raieorie La filrazioe aurale Moo browiao mulidimesioale La misura di Wieer Capiolo 3. Filrazioi e empi d arreso Processi socasici e filrazioi Moo browiao rispeo a ua filrazioe La proprieà di Marov semplice del moo browiao empi d arreso La proprieà di Marov fore del moo browiao Capiolo 4. Speraza codizioale e marigale Speraza codizioale Marigale Variazioe quadraica di ua marigala coiua Capiolo 5. Iegrale socasico Prolugameo di isomerie L iegrale socasico i M [,] L iegrale socasico come processo L iegrale socasico i Mloc [,]
3 PRELUDIO Preludio Sia x() R la posizioe all isae [, ) di ua paricella vicolaa a muoversi lugo ua rea su cui agisce u campo di forze. Idichiamo co F (, x) l iesià della forza all isae el puo x R. Se la fuzioe x( ) è derivabile, il lavoro compiuo dalla forza sulla paricella ell iervallo di empo [,] è dao dall iegrale F (, x()) dx() := F (, x()) x ()d, (.1) dove x () := dx() d idica la derivaa prima di x. Lo sesso iegrale ammee alre possibili ierpreazioi. Suppoiamo ad esempio che x() idichi il valore di u cero iolo azioario all isae e che F (, x) rappresei la mia sraegia di ivesimeo, ossia la quaià di azioi che possiedo all isae se il iolo vale x. L iegrale i (.1) rappresea allora il guadago (co sego!) che oego delle azioi i mio possesso ra gli isai e. Cosideriamo ora il caso i cui x( ) o sia derivabile. È possibile dare u seso all iegrale F (, x()) dx() ache i quesa circosaza? Cosideriamo per semplicià il caso i cui la fuzioe F (, x) =F () o dipede espliciamee da x ed è coiua. Quado x( ) è derivabile co coiuià, l iegrale F ()dx() defiio i (.1) può essere espresso come limie di somme di Riema, el modo seguee: F ()dx() = lim N 1 N i= F i N x i+1 N x i N. (.) Dao che i quesa espressioe o compare la derivaa prima di x( ), si porebbe sperare di usarla come defiizioe dell iegrale F ()dx() quado la fuzioe x( ) o è derivabile. I effei, è possibile mosrare (eorema 56 del capiolo I i [Proer, 4]) che daa ua fuzioe x( ) coiua, o ache solo coiua a desra, il limie i (.) esise per ogi F ( ) coiua se e solao se x( ) è a variazioe fiia, cioè sup N N N 1 i= x i+1 N x i N <. I queso caso, usado la eoria dell iegrazioe asraa, è possibile esedere l iegrale a fuzioi F (, x) boreliae (o come limie delle somme i (.)). Il problema è che, per descrivere l adameo di u iolo fiaziario o il moo di ua paricella sooposa a uri casuali, si usao ipicamee modelli i cui x = x(, ω) è ua fuzioe aleaoria, ovvero u processo socasico, a variazioe ifiia. U risulao fodameale di Iô [1944], eseso e geeralizzao successivamee da diversi auori, afferma che è effeivamee possibile dare u seso all iegrale F dx() per ua vasa classe di processi socasici x() =x(, ω) a variazioe ifiia i paricolare per il moo browiao, l esempio più imporae di processo socasico a empo coiuo, al cui sudio dedicheremo ua buoa pare del corso. La defiizioe di queso uovo iegrale, deo iegrale socasico, è irisecamee probabilisica: esso o è defiio puualmee per ogi ω, cioè per ogi raieoria x(, ω), ma solo come limie i probabilià. L iegrado F o deve essere ecessariamee della forma F (, x(, ω)) ma può essere più i geerale u processo socasico F (, ω), co opporue e imporai resrizioi (F deve essere adaao al processo x, come vedremo). Se le raieorie F (, ω) soo coiue per ogi ω, l iegrale socasico può essere defiio come limie (i probabilià) di somme di Riema, aalogamee a (.): F (, ω)dx(, ω) := lim N 1 N i= F i N, ω x i+1 N, ω x i N, ω. (.3) Le proprieà di queso iegrale soo peculiari. Per esempio, se ella somma di Riema i (.3) si sosiuisce F ( i i+1 N, ω) co F ( N, ω) u cambio appareemee iocuo, daa la coiuià di F (, ω) il valore dell iegrale risula i geerale diverso, a differeza di quao accade per l iegrale ordiario. Occorre duque decidere quale defiizioe usare. Noi ci cocereremo sull iegrale di Iô, defiio proprio come i (.3), che è quello più aurale per le applicazioi fiaziarie e ha iolre fodameali legami co la eoria delle equazioi differeziali alle derivae parziali del secodo ordie. Alre defiizioi risulao più coveiei i coesi diversi: acceeremo brevemee all iegrale di Sraoovich, usao elle applicazioi fisiche e ella geomeria socasica, i cui il ermie F ( i N, ω) è sosiuio da 1 (F ( i i+1 N, ω)+f ( N, ω)). Per ua fuzioe x() derivabile, segue dal eorema fodameale del calcolo che per ogi fuzioe G : R R derivabile si ha G(x( )) G(x()) = d G(x()) d =: d G (x()) dx(). Per l iegrale di Iô quesa relazioe o è più valida. Più precisamee, se x(, ω) è il moo browiao e se G : R R è ua fuzioe derivabile due vole co coiuià, mosreremo che G(x(,ω)) G(x(, ω)) = G (x(, ω)) dx(, ω) + 1 G (x(, ω)) d, che può essere riscria i forma differeziale (soiededo la dipedeza da ω) come dg(x()) = G (x()) dx() + 1 G (x()) d. Quesa è la celebre formula di Iô, che cosiuisce il cuore del calcolo socasico. Come vedremo, la preseza del ermie aggiuivo coeee G è dovua precisamee al fao che le raieorie del moo browiao soo a variazioe ifiia. 1
4 PRELUDIO 3 4 PRELUDIO Noazioi. Idicheremo co N := {1,, 3,...} e co N := N {} = {, 1,,...}. Useremo gli aggeivi crescee, decrescee, posiivo e egaivo i seso debole: ua fuzioe f : R R è crescee se per ogi x, y R co x<ysi ha f(y) f(x), mere è sreamee crescee se si ha f(y) >f(x); aalogamee, f è posiiva se per ogi x R si ha f(x), mere è sreamee posiiva se si ha f(x) >.
5 6 1. RICHIAMI DI PROBABILIÀ 1. Richiami di probabilià Foriamo u compedio delle ozioi basilari di probabilià che ci sarao uili. Per maggiori deagli, si possoo cosulare i esi [Billigsley, 1995], [Williams, 1991] Spazi misurabili σ-algebre. Ua σ-algebra E su u isieme o vuoo E è ua famiglia di pari (sooisiemi) di E che coiee E e che sia chiusa per uioi umerabili e passaggio al complemeare. La coppia (E,E) è dea spazio misurabile. I due casi esremi di σ-algebre soo quella baale E = {,E} e quella discrea E = P(E). Daa ua famiglia o vuoa I P(E) di pari di E, si idica co σ(i) la più piccola σ-algebra che coega I, cioè l iersezioe di ue le σ-algebre che coegoo I. La famiglia I è dea u geeraore di σ(i). SeiolreI è chiusa per iersezioi fiie, I è dea ua base di σ(i). Se (E,τ) è uo spazio opologico, si dice boreliaa la σ-algebra su E geeraa dagli isiemi aperi (equivaleemee, dagli isiemi chiusi). L esempio più imporae è dao da E = R d, la cui σ-algebra boreliaa, idicaa co B(R d ), è geeraa dai reagoli aperi (a 1,b 1 ) (a d,b d ), che e cosiuiscoo ua base. U alro esempio imporae è la rea reale esesa R := R {, + }. Iederemo sempre R d e R come spazi misurabili, muii della σ-algebra boreliaa. Soolieiamo che, a differeza di quao accade per la opologia, o è i geerale possibile descrivere espliciamee gli elemei della σ-algebra σ(i) geeraa da ua famiglia I. Per quesa ragioe, è ecessario lavorare co geeraori e basi (si veda la sezioe 1.8.1) Applicazioi misurabili. Sia X : E F ua applicazioe ra due spazi misurabili (E,E) e (F, F) (scriveremo sieicamee X :(E,E) (F, F)). L applicazioe X è dea misurabile se X 1 (F) E, cioè se X 1 (B) E per ogi B F. SeJ è u geeraore di F, cioè se F = σ(j), èsufficiee richiedere che X 1 (J) E. Qualuque sia la σ-algebra F su F, X 1 (F) è sempre ua σ-algebra su E, dea la σ-algebra geeraa da X e idicaa co σ(x): si raa della più piccola σ-algebra su E che reda X misurabile. I effei σ(x) rede misurabile qualuque fuzioe di X: per ogi g :(F, F) (G, G) misurabile, la composizioe g(x) =g X è σ(x)-misurabile, cioè è misurabile come applicazioe da (E,σ(X)) i (G, G). Vale u parziale viceversa, oo come lemma di misurabilià di Doob: se X : E (F, F) èua applicazioe geerica e Y : E R d è σ(x)-misurabile, allora esise g :(F, F) R d misurabile ale che Y = g(x) (si veda la sezioe 1.8.). Si oi che l iersezioe di ua famiglia arbiraria di σ-algebre è acora ua σ-algebra, mere i geerale l uioe (ache fiia) di σ-algebre o lo è. Se X :(E,E) (F, F) e Y :(F, F) (G, G) soo applicazioi misurabili, lo è la loro composizioe Y X :(E,E) (G, G). SeE, F soo spazi opologici e E, F le rispeive σ-algebre boreliae, ogi applicazioe X : E F coiua è ache misurabile. Segue che se X, Y :(E,E) R soo applicazioi misurabili, lo soo ache X + Y, X Y, X, X + := max(x, ), ecc. Iolre soo misurabili le applicazioi (a valori i R) sup X, N if X, N lim sup X, N lim if N X, X, purché X :(E,E) R sia misurabile per ogi N. Soolieiamo che per quesi risulai è fodameale che la famiglia {X } sia (al più) umerabile Spazi prodoo. Dai due spazi misurabili (F, F), (G, G), sul loro prodoo caresiao F G si defiisce la σ-algebra prodoo F G := σ(f G), cioè la σ-algebra geeraa dalla famiglia F G := {A B : A F,B G} (si oi che F G o è ua σ-algebra). U applicazioe X :(E,E) (F G, F G) si può sempre scrivere come X =(X 1,X ), co X 1, X avaloriif, G rispeivamee, ed è misurabile se e solo se lo soo le sue compoei X 1 e X. Aaloghe proprieà valgoo per il prodoo di u umero fiio di spazi misurabili. Quesi risulai si possoo esedere ache al caso di ua famiglia arbiraria di spazi misurabili {(F i, F i)} i I: illoroprodoo i I Fi èmuiodellaσ-algebra i IFi := σ(fi1 F i : N, i 1,...,i I) eu applicazioex = {X i} i I :(E,E) ( i I Fi, i IFi) èmisurabileseesolose lo soo le sigole compoei X i. 1.. Probabilià e variabili aleaorie Misure e probabilià. Dao uo spazio misurabile (E,E), ua misura µ è ua fuzioe µ : E [, + ] ale che µ( ) =e co la proprieà di σ-addiivià, cioè µ( N A )= N µ(a ) per ogi successioe {A } N di elemei di E adue aduedisgiui(a A m = per m = ). La era (E,E,µ) è dea spazio di misura o spazio misurao. Lamisuraµ è dea fiia se µ(e) < e σ-fiia se si può scrivere E = N A co µ(a ) < per ogi N. U esempio classico di misura fiia è dao dalla dela di Dirac δ x,dovex E è u qualuque puo fissao, defiia da δ x (A) =1se x A e δ x (A) =alrimei. L esempio più imporae di misura σ-fiia è dao dalla misura di Lebesgue su (R d, B(R d )). Ua misura P su uo spazio misurabile (Ω, F) ale che P(Ω) =1è dea probabilià (o misura di probabilià o ache legge). La era (Ω, F, P) è dea spazio di probabilià e gli elemei di F soo dei evei. U eveo A F si dice quasi cero se P(A) =1. Ricordiamo alcue imporai proprieà che ci sarao uili. Per ogi coppia di evei A B si ha P(A) P(B) [moooia]. Per ogi successioe di evei {A } N vale la relazioe P( N A ) N P(A ) [subaddiivià]. N 5
6 1.. PROBABILIÀ E VARIABILI ALEAORIE RICHIAMI DI PROBABILIÀ Per ogi successioe crescee (risp. decrescee) di evei {A } N, idicado l eveo limie co A = lim A = N A (risp. A = lim A = N A ), si ha che P(A ) P(A) [coiuià dal basso e dall alo]. Se {A } N è ua famiglia di evei quasi ceri, cioè P(A )=1per ogi N, ache N A è u eveo quasi cero. Se {B } N è q.c. ua parizioe dello spazio di probabilià, cioè se P( N B )=1 e P(B B m )=per m =, vale la relazioe P(A) = N P(A B ), per ogi eveo A [formula di disiegrazioe]. Osserviamo che se I è ua base di F (cioè F = σ(i) e I è chiusa per iersezioi fiie), due probabilà P, P su (Ω, F) che coicidoo su I soo ecessariamee uguali, cioè P(A) =P (A) per ogi A F, come segue dal Lemma di Dyi (vedi sezioe 1.8) Spazi di misura complei. Uo spazio di misura (E,E,µ) è deo compleo se, per ogi C E ale che µ(c) =, si ha che ogi sooisieme N C è misurabile, cioè N E (e di cosegueza µ(n) =). Se (E,E,µ) o è compleo, è sempre possibile complearlo, cioè cosruire uo spazio di misura compleo (E,E, µ) ale che E E e µ coicida co µ su E. Si defiisce iaziuo la famiglia degli isiemi rascurabili (o µ-rascurabili, se si vuole efaizzare la misura): N := N E : C E ale che N C e µ(c) = e si esede la σ-algebra E poedo E := σ(e, N ). Si può mosrare (esercizio) che A E se e solao se esise A E ale che A A N,doveA A := (A \ A ) (A \ A) idica la differeza simmerica, e i queso caso si defiisce µ(a) :=µ(a ). Si verifica che ale defiizioe è be posa, cioè o dipede dalla scela di A,esimosracheµ defiisce ua misura su E e che (E,E, µ) è uo spazio di misura compleo (esercizio). Gli isiemi di E di misura µ ulla soo esaamee gli elemei di N. Ua applicazioe X :(E,E) (F, F) è misurabile se e solo se è µ-q.c. uguale a ua applicazioe misurabile X :(E,E) (F, F), cioè se e solo se vale che {x E : X (x) = X(x)} N. Lavorare co spazi complei risula spesso coveiee. Per esempio, dao uo spazio di probabilià (Ω, F, P), suppoiamo di sapere che esise A E, co P(A) =1,aleche per ogi ω A vale ua cera proprieà (ad esempio l esiseza di u cero limie). Se idichiamo co A l isieme di ui gli ω Ω per cui vale la proprieà i quesioe, si ha duque A A. Se lo spazio (Ω, F, P) è compleo, si può cocludere che A F e quidi µ( A)=1, mere quesa coclusioe i geerale è falsa se lo spazio o è compleo. Soolieiamo che il compleameo E della σ-algebra E dipede dalla misura µ. Per esempio, se sullo spazio misurabile (R, B(R)) si sceglie la misura di Dirac δ,laσ-algebra compleaa è l isieme delle pari P(R), come si verifica facilmee Variabili aleaorie. Cosideriamo ua applicazioe X : Ω E, dove (Ω, F, P) è uo spazio di probabilià e (E,E) è uo spazio misurabile (scriveremo sieicamee X :(Ω, F, P) (E,E)). Se l applicazioe X è misurabile, essa è dea variabile aleaoria. Nel caso i cui lo spazio di arrivo E coicida co R ocor d,siparla rispeivamee di variabile aleaoria reale (dea ache scalare) o di veore aleaorio. Daa ua variabile aleaoria X :(Ω, F, P) (E,E) e u isieme A E, è cosueudie idicare co {X A} l eveo X assume valori i A, cioè {X A} := X 1 (A) = {ω Ω : X(ω) A}. Aalogamee, per ua variabile aleaoria reale X si poe {X a} := {X [a, )} = X 1 ([a, )), ecc. Useremo quese oazioi cosaemee. Si oi che la σ-algebra σ(x) geeraa da X cosise esaamee degli evei della forma {X A} al variare di A E. La fuzioe idicarice 1 B di u isieme B è defiia da 1 B (x) =1se x B mere 1 B (x) =se x B. I paricolare, per A E si ha che 1 {X A} = 1 A X (si oi che 1 {X A} è ua fuzioe defiia su Ω mere 1 A è defiia su E) Iegrale e valore aeso. Dao uo spazio di misura (E,E,µ) e ua fuzioe misurabile posiiva g : E R +, è sempre be defiio l iegrale g dµ = g(x) µ(dx) [, + ]. Ricordiamo ua proprieà imporae: se g, g dµ = se e solo se µ(g >) =, cioè g =µ-q.c.. U arbiraria fuzioe misurabile reale g è dea iegrabile se g dµ < e i queso caso si defiisce g dµ := g + dµ g dµ, dovesièposog ± (x) :=max{±g(x), }, da cui g = g + g.sihache g dµ g dµ. Specializzado quese defiizioi al caso di uo spazio di probabilià (Ω, F, P), per ua variabile aleaoria reale posiiva Y :(Ω, F, P) R + è sempre be defiio il valore aeso E(Y ):= Y (ω)p(dω) [, + ] e si ha che E(Y )= se e solo se P(Y = ) = 1. U arbiraria variabile aleaoria reale X è dea iegrabile se E( X ) <, el qual caso si defiisce E(X) :=E(X + ) E(X ) e vale la relazioe E(X) E( X ) Spazi L p. Per ogi variabile aleaoria reale X defiia su (Ω, F, P) si defiisce X p := (E( X p )) 1/p [, + ], per p 1, e si idica co L p = L p (Ω, P) l isieme delle variabili aleaorie reali X ali che X p <. Vale la disuguagliaza riagolare X + Y p X p + Y p, da cui segue che L p è uo spazio veoriale su R e p è ua semiorma su L p. Ifai X p =o implica che X =ma solao che P (X = ) = 1. Iroducedo su L p la relazioe di equivaleza X Y se P (X = Y )=1, p divea ua vera orma sull isieme delle classi di equivaleza, che co radizioale abuso di oazioe sarà idicao sempre co L p (quado sarà imporae disiguere ra fuzioi e classi di equivaleza, lo soolieeremo). I queso modo (L p, p ) divea uo spazio di Baach, cioè uo spazio ormao compleo: ue le successioi di Cauchy hao limie. Dalla disuguagliaza di Jese, richiamaa più i basso, segue che, per ogi variabile Si defiisce iaziuo 1 A dµ := µ(a) per A E esiesedeladefiizioeperlieariàalle fuzioi semplici ci1a i,perai F e ci R+.Peruafuzioemisurabileoegaivaarbiraria, si defiisce il valore aeso come il limie dei valori aesi di ua qualuque successioe crescee di fuzioi semplici che coverge alla variabile aleaoria (ua ale successioe esise sempre, e il limie dei valori aesi o dipede dalla successioe scela).
7 1.. PROBABILIÀ E VARIABILI ALEAORIE RICHIAMI DI PROBABILIÀ aleaoria X, sihax q X p se p q, da cui segue che L p L q (quesa proprieà o vale se P è ua misura o fiia). Lo spazio più imporae è ceramee L,cheèieffei uo spazio di Hilber, poiché la orma è idoa dal prodoo scalare X, Y := E(XY ). Per X L,laquaià Var(X) :=E[(X E(X)) ]=E(X ) E(X) [, ) è dea variaza di X. Ricordiamo che Var(X) =se e solao se esise c R ale che P (X = c) =1. Per X, Y L, l operaore bilieare Cov(X, Y ):=E[(X E(X))(Y E(Y ))] = E(XY ) E(X)E(Y ) R è deo covariaza. Si verifica facilmee che e iolre Var(X) =Cov(X, X). Var(X + Y ) = Var(X) + Var(Y )+Cov(X, Y ) U veore aleaorio X =(X 1,...,X d ) avaloriir d è per defiizioe i L p se e solo se lo soo ue le sue compoei. Poedo X p =(E( X p )) 1/p,dove idica la orma euclidea su R d,sihachex L p se e solo se X p <. IolreX q X p se p q, quidil p L q ache el caso veoriale. Dao u veore aleaorio X =(X 1,...,X d ) avaloriir d ale che X L 1, si defiisce il veore media poedo E(X) :=(E(X 1 ),...,E(X d )) R d.seiolrex L, si defiisce la marice delle covariaze Γ ij := Cov(X i,x j ), per 1 i, j d. La marice Γ è simmerica e semi-defiia posiiva: per ogi u R d si ha u, Γu, dove idichiamo co Γu l ordiario prodoo marice-veore, cioè (Γu) i = d j=1 Γ iju j,edovex, y := d x iy i deoa il prodoo scalare sadard per x, y R d. Si ha ifai u, Γu = = d u i (Γu) i = d Γ ij u i u j = i,j=1 d Cov(X i,x j )u i u j i,j=1 d Cov(u i X i,u j X j )=Cov(u, X, u, X) = Var(u, X), i,j=1 avedo usao la biliearià dell operaore Cov(, ). Vedremo el paragrafo 1.7 che ogi marice reale Γ simmerica e semi-defiia posiiva è la marice delle covariaze di u opporuo veore aleaorio eoremi di covergeza. Ricordiamo di seguio i pricipali risulai di covergeza (validi i realà ache ell ipoesi che P sia ua misura o di probabilià). eorema 1.1 (Covergeza moooa). Sia {X } N ua successioe q.c. crescee di variabili aleaorie reali posiive, defiie sullo sesso spazio di probabilià (Ω, F, P), che coverge q.c. verso la variabile aleaoria X; suppoiamo cioè che X (ω) X(ω) per q.o. ω Ω. AlloraE(X ) E(X). eorema 1. (Lemma di Faou). Sia {X } N ua successioe di variabili aleaorie reali, defiie sullo sesso spazio di probabilià (Ω, F, P), alichex (ω) per q.o. ω Ω (o più i geerale X (ω) Y (ω), coy variabile aleaoria reale iegrabile). Allora E(lim if X ) lim if E(X ). eorema 1.3 (Covergeza domiaa). Siao {X } N, X variabili aleaorie reali, defiie sullo sesso spazio di probabilià (Ω, F, P), alichex (ω) X(ω) per q.o. ω Ω. Suppoiamo che esisa ua variabile aleaoria posiiva Y iegrabile, ale cioè che E(Y ) <, chesoddisfi X (ω) Y (ω) per ogi N e per q.o. ω Ω. Allora E( X X ), cioè X X i L 1 ; i paricolare E(X ) E(X) Disuguagliaze. Ricordiamo la disuguagliaza di Marov: per ogi variabile aleaoria posiiva X e per ogi δ > si ha che P(X δ) E(X), (1.1) δ da cui segue la disuguagliaza di Chebychev: per ogi variabile aleaoria X L e per ogi δ > si ha che P( X E(X) > δ) Var(X) δ. (1.) La disuguagliaza di Jese afferma che per ogi variabile aleaoria reale iegrabile X e per ogi fuzioe covessa ϕ : R R {+ } ale che E(ϕ(X)) < si ha ϕ(e(x)) E(ϕ(X)). (1.3) Dae due variabili aleaorie X L p e Y L q, co 1 p + 1 q =1,ladisuguagliaza di Hölder afferma che XY L 1 e si ha XY 1 X p Y q, o più espliciamee E( XY ) E( X p ) 1/p E( Y q ) 1/q. (1.4) Nel caso speciale p = q = 1 si ha la disuguagliaza di Cauchy-Schwarz Legge di ua variabile aleaoria Ua variabile aleaoria X :(Ω, F, P) (E,E) iduce su (E,E) ua probabilià µ X, dea legge o misura immagie, defiia da µ X (A) :=P(X 1 (A)) = P(X A). La legge µ X descrive la probabilià co cui i possibili valori di X vegoo assui ed è alvola idicaa co P X 1 o co X (P ), dovex idica l operaore che a ua misura ν su (Ω, F) associa la misura X (ν) :=ν X 1 su (E,E). Ua rappreseazioe schemaica dell azioe di X è la seguee: Ω F M 1 (Ω, F) X X 1 E E X M 1 (E,E)
8 1.3. LEGGE DI UNA VARIABILE ALEAORIA RICHIAMI DI PROBABILIÀ dove M 1 (Ω, F) idica l isieme delle probabilià su (Ω, F), e aalogamee per E. Se le variabili aleaorie X, Y :(Ω, F, P) (E,E) soo q.c. uguali, cioè P(X = Y )=1, allora hao la sessa legge: ifai da X = Y q.c. segue che 1 {X A} = 1 {Y A} q.c. e duque µ X (A) =E(1 {X A} )=E(1 {Y A} )=µ Y (A), per ogi A E. Si oi che, daa ua misura di probabilià µ sullo spazio misurabile (E,E), la fuzioe ideià id : (E,E,µ) (E,E) èuavariabilealeaoriadileggeµ. Quesoèilprocedimeocaoicopercosruireua variabile aleaoria di legge assegaa. I paricolare, daa ua variabile aleaoria X :(Ω, F, P) (E, E), la fuzioe ideià id :(E,E,µ X) (E,E) èuavariabilealeaoriachehalasessaleggedix. Se X :(Ω, F, P) (E,E) èuavariabilealeaoriaey :(E,E) (G, G) èu applicazioemisurabile, si verifica facilmee che la legge della variabile aleaoria Y X :(Ω, F, P) (G, G) coicide co la legge della variabile aleaoria Y :(E,E,µ X) R. Ialreparole,sihache(Y X) (P )=Y (X (P )). Fodameale è il seguee eorema, oo ache come cambio di variabili. eorema 1.4 (Cambio di variabili). Sia X :(Ω, F, P) (E,E) ua variabile aleaoria e f :(E,E) R u applicazioe misurabile. La variabile aleaoria f(x) : (Ω, F, P) R è iegrabile se e solo se lo è la variabile aleaoria f :(E,E,µ X ) R, el qual caso si ha E(f(X)) = f(x(ω)) P(dω) = f(x) µ X (dx). Ω Leggi su R d. Dae due misure µ, ν sullo sesso spazio misurabile (E,E), si dice che µ è assoluamee coiua rispeo a ν, e si idica co µ ν, se esise ua fuzioe misurabile f :(E,E) [, ) ale che µ(a) = E 1 A(x) f(x) ν(dx) per ogi A E, o equivaleemee g(x) µ(dx) = g(x) f(x) ν(dx), E per ogi fuzioe misurabile o-egaiva g :(E,E) R +. La fuzioe f è dea desià oachederivaa di Rado-Niodym. Noazioi aleraive per la relazioe di assolua coiuià soo µ = f ν, dµ = f dν, dµ dν = f. Chiaramee se µ ν allora per ogi A ale che ν(a) =si ha µ(a) =. Il celebre eorema di Rado-Niodym afferma che ache il viceversa è vero. Il caso che a oi ieressa di più è dao dalle leggi su R d che soo assoluamee coiue rispeo alla misura di Lebesgue, dee leggi assoluamee coiue ou cour. Per ua ale legge µ esise cioè ua desià f : R d [, ) ale che µ(a) = R 1 d A (x) f(x)dx per ogi A B(R), dovedx idica la misura di Lebesgue su R d. U veore aleaorio X avalorii R d è deo assoluamee coiuo se la sua legge µ X lo è. Idicado co f X la sua desià, dal eorema di passaggio alla misura immagie si oiee E(g(X)) = R g(x) f d X (x)dx, per ogi fuzioe misurabile e limiaa g : R d R. Ua legge µ su R d èdeadiscreadiscrea se è ua sovrapposizioe di misure di Dirac, cioè se esisoo {x i} i N, {p i} i N, cox i R d e p i [, 1], alicheµ = i N pi δx (chiaramee i i N pi =1). U veore aleaorio X avaloriir d èdeodiscreoseloèlasualeggeµ X,elqualcasosihacheE(g(X)) = g(x) µ R X(dx) = d i N pi g(xi). La fuzioe px : R [, 1] defiia da px(x) := i N pi 1 {x i}(x) (cioè p X(x) =p i se x = x i per qualche i N e p X(x) =alrimei) è dea desià discrea o fuzioe di massa. E E Sia X u veore aleaorio d-dimesioale assoluamee coiuo, co desià f X.Se A è ua marice d d iveribile e b R d, il veore aleaorio Y := AX + b è acora assoluamee coiuo, co desià f Y (y) := de A 1 f X (A 1 (y b)). Quesa formula si può geeralizzare al caso i cui la rasformazioe affie x Ax + b sia sosiuia da u diffeomorfismo, ma o e avremo bisogo. Ricordiamo ifie che le misure di probabilià µ su R soo i corrispodeza biuivoca co le fuzioi F : R [, 1] crescei, coiue a desra e ali che lim x F (x) =e lim x + F (x) =1: la corrispodeza è semplicemee quella che associa a ua probabilià µ la sua fuzioe di riparizioe F (x) :=µ((,x]) Idipedeza e misura prodoo Idipedeza. La ozioe basilare di idipedeza riguarda σ-algebre, variabili aleaorie ed evei. Fissiamo uo spazio di probabilià (Ω, F, P). Daa le σ-algebre F 1,...,F coeue i F, esse si dicoo idipedei se per ogi scela di evei A 1 F 1,...,A F,sihache P(A 1 A ) = P(A j ). (1.5) Dae le variabili aleaorie X 1,...,X, defiie su Ω a valori rispeivamee egli spazi (E 1, E 1 ),...,(E, E ), esse si dicoo idipedei se lo soo le σ-algebre da esse geerae σ(x 1 ),...,σ(x ). Ricordado che σ(x) ={{X B}, B E}, ciò sigifica che per ogi scela di evei B 1 E 1,...,B E si deve avere P(X 1 B 1,...,X B ) = j=1 P(X j B j ). Dai gli evei A 1,...,A di F, essi si dicoo idipedei se lo soo le σ-algebre σ({a 1 }),...,σ({a }) da essi geerae. Dao che σ({a}) ={, A, A c, Ω}, queso equivale a richiedere che per ogi scela di σ 1,...,σ {1,c} P(A σ1 1 Aσ ) = j=1 j=1 P(A σj j ), dove poiamo A 1 i := A i. Si può mosrare che quesa corrispode alla defiizioe classica di idipedeza, cioè che per ogi sooisieme J {1,...,} si abbia P A j = P(A j ). j J j J Soo ache possibili euciai misi: per esempio, ua variabile aleaoria X si dice idipedee dalla σ-algebra G se le σ-algebre {σ(x), G} soo idipedei, ecc.
9 1.4. INDIPENDENZA E MISURA PRODOO RICHIAMI DI PROBABILIÀ Abbiamo defiio l idipedeza per u umero fiio di di σ-algebre F 1,...,F. L esesioe a ua famiglia ifiia {F i } i I, co I isieme arbirario, è immediaa: per defiizioe, diremo che le σ-algebre {F i } i I soo idipedei se ogi soofamiglia fiia è idipedee, cioè se F i1,...,f i soo idipedei per ogi N e per ogi scela di i 1,...,i I. I modo aalogo si defiisce l idipedeza di famiglie arbirarie di variabili aleaorie {X i } i I ed evei {A i } i I. U osservazioe molo uile i praica è la seguee: siao dae le σ-algebre F 1,..., F,esiaJ i ua base di F i, per 1 i ; aliσ-algebre soo idipedei se e solo se lo soo J 1,...,J, cioè se vale la relazioe (1.5) per A 1 J 1,...,A J (queso segue dal Lemma di Dyi; si veda la sezioe 1.8.1) Idipedeza e scorrelazioe. U risulao imporae è che se X e Y soo variabili aleaorie reali iegrabili idipedei, allora il prodoo XY è iegrabile e si ha E(XY ) =E(X) E(Y ); duque Cov(X, Y ) =, cioè le variabili soo scorrelae. I paricolare, se X, Y L soo idipedei si ha che Var(X + Y )=Var(X)+Var(Y ). Il viceversa è falso i geerale. Soolieiamo che se X e Y soo variabili aleaorie reali iegrabili o idipedei, o è deo che XY sia iegrabile. Noiamo ache che se X e Y soo variabili aleaorie idipedei, lo soo ache ϕ(x) e ψ(y ), qualuque siao le applicazioi misurabili ϕ, ψ. I paricolare, se ϕ, ψ soo fuzioi reali misurabili e limiae, si ha E(ϕ(X)ψ(Y )) = E(ϕ(X)) E(ψ(Y )) Covoluzioe. Dae due probabilià µ, ν su R d e due variabili aleaorie X e Y idipedei, le cui leggi siao rispeivamee µ e ν, la covoluzioe di µ e ν, idicaa co µ ν, è per defiizioe la legge della variabile aleaoria X + Y. Per ogi isieme A boreliao di R d si ha µ ν(a) = R d µ(a y)ν(dy) = R d ν(a y)µ(dy), chemosrara l alro come µ ν dipeda solo da µ e ν e o dalle variabili X e Y. Il caso più imporae è quello i cui le leggi µ e ν siao assoluamee coiue, co desià rispeivamee f e g. I queso caso la legge di µ ν è ach essa assoluamee coiua, co desià h(x) = R d f(x y)g(y)dy = R d g(x y)f(y)dy, dea covoluzioe di f e g e idicaa co h = f g Misura prodoo. Dai due spazi di misura (E 1, E 1,µ 1 ), (E, E,µ ) fiii o σ-fiii, esise ua misura µ = µ 1 µ sullo spazio (E 1 E, E 1 E ), dea misura prodoo, co la proprieà µ(a B) =µ 1 (A)µ (B) per ogi A E 1 e B E.alemisura è uica, perchè gli isiemi della forma A B, alvariaredia E 1 e B E, cosiuiscoo ua base di E 1 E. Nel caso i cui E 1 = E = R e le misure µ 1, µ siao assoluamee coiue, co desià rispeive f 1, f, la misura prodoo è ach essa assoluamee coiua, co desià f(x 1,x ):=f 1 (x 1 ) f (x ). Quesi risulai si esedoo seza difficolà al prodoo di u umero fiio di spazi. Richiamiamo ora il eorema di Fubii. Se f :(E 1 E, E 1 E ) R è misurabile allora, per ogi x 1 E 1 fissao, la fuzioe x f(x 1,x ) è misurabile da (E, E ) i R; aalogamee, per ogi x E fissao, la fuzioe x 1 f(x 1,x ) è misurabile da (E 1, E 1 ) i R. Soolieiamo che o vale il viceversa: per la misurabilià dell applicazioe f o è sufficiee che siao misurabili le applicazioi x 1 f(x 1,x ) e x f(x 1,x ). Siao ora µ 1 e µ misure σ-fiie su (E 1, E 1 ) e (E, E ) rispeivamee e poiamo µ := µ 1 µ. Se la fuzioe f è µ-iegrabile (cioè E 1 E f dµ < ), oppure se f, vale che f dµ = f(x 1,x ) µ (dx ) µ 1 (dx 1 ) E 1 E E 1 E (1.6) = f(x 1,x ) µ 1 (dx 1 ) µ (dx ). E 1 E U applicazioe direa del eorema di Fubii è la seguee: per ogi variabile aleaoria reale posiiva Y, scrivedo Y (ω) = 1 {Y (ω)>} d e applicado (1.6), si oiee l uile formula E(Y )= P (Y > )d. Dae due variabili aleaorie X 1, X defiie su (Ω, F, P) a valori rispeivamee i (E 1, E 1 ), (E, E ), idichiamo le loro leggi co µ X1, µ X. La coppia X =(X 1,X ) è ua variabile aleaoria a valori i (E 1 E, E 1 E ), la cui legge idichiamo co µ X. È facile vedere che X 1 e X soo idipedei se e solao se µ X = µ X1 µ X. Lo sesso vale per u umero fiio di variabili aleaorie X 1,...,X a valori egli spazi (E i, E i ):levariabili soo idipedei se e solao se la loro legge cogiua su ( E i, E i) è daa dal prodoo delle leggi margiali Successioi idipedei. È oo che, assegaa u arbiraria successioe di probabilià {µ } N su R, esise u opporuo spazio di probabilià (Ω, F, P) su cui è defiia ua successioe {X } N di variabili aleaorie reali idipedei ali che la legge di X sia µ. Ua cosruzioe ipica è richiamaa ella sezioe Si può vedere X := {X } N come ua variabile aleaoria defiia su (Ω, F, P) avaloriellospazio X := (R N, B(R) N ): ifai X èuaapplicazioemisurabile,perchélesuecompoeilosoo.la legge µ X di X sullo spazio X èalvoladeaprodoo(ifiio)delleleggi{µ } N, edèidicaaco µ X = i Nµ i.ieffei, µ X èl uicamisurasux ale che, per ogi N eperogia 1,...,A B(R), si abbia µ(a 1 A R N )=µ 1(A 1) µ (A ) Lemma di Borel-Caelli. Daa ua successioe di evei {A } N di uo spazio di probabilià (Ω, F, P), si defiisce l eveo lim sup A := A = {ω Ω : ω A per ifiii } = 1 A =. N N Si ha allora l uilissimo Lemma 1.5 (Borel-Caelli). Sia {A } N ua successioe di evei di uo spazio di probabilià (Ω, F, P). Se N P(A ) <, allorap(lim sup A )=. Se N P(A )= e iolre se A i e A j soo idipedei per ogi i = j, allora P(lim sup A )=1. Esercizio 1.6. Se {X } N soo variabili aleaorie i.i.d. co X Exp(λ), allora q.c. si ha lim sup X / log = λ 1.
10 1.5. NOZIONI DI CONVERGENZA RICHIAMI DI PROBABILIÀ 1.5. Nozioi di covergeza Covergeza di misure. Sia (E,E) uo spazio merico, co disaza d(, ), muio della σ-algebra boreliaa E = B(E). Il caso ipico è dao da R d, co la disaza d idoa dalla orma euclidea: d(x, y) = x y = (x i y i ). Daa ua successioe di probabilià {µ } N su E, si dice che essa coverge debolmee verso la probabilià µ su E se per ogi fuzioe f :(E,E) R coiua e limiaa si ha che f dµ f dµ. Sebbee esisao alre ozioi di covergeza per successioi di misure, quesa è la più imporae e sarà l uica che cosidereremo Covergeza di variabili aleaorie. Cosideriamo ua famiglia di variabili aleaorie X :(Ω, F, P ) (E,E), per N, ex :(Ω, F, P) (E,E), defiie o ecessariamee sullo sesso spazio di probabilià, ma ue a valori ello sesso spazio merico E. Diremo che la successioe {X } N coverge i legge (o i disribuzioe) verso X se la successioe delle leggi µ X di X coverge debolmee verso la legge µ X di X. Usado il eorema di passaggio alla misura immagie, ciò sigifica che E (f(x )) E(f(X)) per ogi fuzioe f : E R coiua e limiaa. Suppoiamo ora che le variabili aleaorie {X } N, X siao ue defiie sullo sesso spazio di probabilià (Ω, F, P) e assumao valori ello spazio merico (E,E). Diremo che la successioe {X } N coverge i probabilià verso X se per ogi ε > si ha che P(d(X,X) > ε). Diremo che la successioe {X } N coverge quasi ceramee (q.c.) verso X se esise A F co P(A) =1ale che per ogi ω A si ha X (ω) X(ω), cioè d(x (ω),x(ω)). Cosideriamo ifie il caso i cui le variabili aleaorie {X } N, X siao defiie sullo sesso spazio (Ω, F, P) e assumao valori i R d. Diremo che la successioe {X } N coverge verso X i L p se X X p, cioè se E( X X p ), dove idica la orma euclidea su R d. Si oi che, essedo X X q X X p se p q (Jese), la covergeza di X verso X i L p implica quella i L q. Dalla disuguagliaza riagolare si ha iolre che X p X p X X p, da cui si ricava che la covergeza i L p implica quella del momeo p-esimo. I defiiiva, X X i L p = E( X q ) E( X q ), per ogi 1 q p. (1.7) Proposizioe 1.7. Dae le variabili aleaorie X,X a valori i uo spazio merico E, valgoo le seguei relazioi: se X X q.c., allora X X i probabilià; se X X i L p,allorax X i probabilià; se X X i probabilià, allora esise ua soosuccessioe { } N ale che X X q.c.; se X X i probabilià, allora X X i legge. Dimosrazioe. Se X X q.c., si ha d(x,x) q.c. e duque 1 {d(x,x)>ε} q.c., per ogi ε >. PercovergezadomiaasioieeduqueP(d(X,X) > ε) =E(1 {d(x,x)>ε}), poiché 1 {d(x,x)>ε} 1. DicoseguezaX X i probabilià. Suppoiamo ora che X X i L p.iquesocasoe = R d e d(x, y) = x y. Applicadola disuguagliaza di Marov, si ha P(d(X,X) > ε) =P( X X > ε) ε p E( X X p ) per ogi ε >, duquex X i probabilià. Facciamo ora l ipoesi che X X i probabilià. Fissiamo arbirariamee ua successioe {ε } N posiiva e ifiiesima, per esempio ε := 1.Perogi fissao si ha P(d(X,X) > ε) per, quidi possiamo defiire come il più piccolo valore di N per cui P(d(X,X) > ε ) 1.Per cosruzioe N P(d(X,X) > ε) 1 N <, quidiperillemmadiborel-caellisihache q.c. d(x,x) ε = 1 per grade, da cui segue che d(x,x) q.c. per.abbiamoduque deermiao ua successioe ( ) N per cui X X q.c.. Suppoiamo ifie che X X i probabilià e sia f : E R ua qualuque fuzioe coiua elimiaa.vogliamomosrarechee(f(x )) E(f(X)), dacuiseguechex X i legge. Per u argomeo classico (vedi Esercizio 1.8 più giù), è sufficiee mosrare che per ogi soosuccessioe { } N esise ua soo-soosuccessioe { } N ale che E(f(X )) E(f(X)). Visocheperipoesi X X i probabilià, ache X X i probabilià. Per quao viso sopra, possiamo duque esrarre ua soosuccessioe { } N di { } N ale che X X q.c.. Di cosegueza ache f(x ) f(x) q.c., perché f ècoiua,elacovergezae(f(x )) E(f(X)) segue dal eorema di covergeza domiaa, poiché f èlimiaa. Esercizio 1.8. Sia {x } N ua successioe i uo spazio opologico E. Suppoiamo esisa x E co la seguee proprieà: per ogi soosuccessioe {x } N esise ua soo-soosuccessioe {x } N di {x } N che coverge verso x. Allora la successioe complea {x } N coverge verso x Uleriori osservazioi. Se X X i legge e lo spazio d arrivo è polacco (cioè merico compleo e separabile), è possibile defiire su u opporuo spazio di probabilià (Ω, F, P) variabili aleaorie { X } { N} e X,colasessaleggerispeivameediX e X, aliche X X q.c. (eorema di Sorood). Dae leggi µ, µ su R le cui fuzioi di riparizioe siao rispeivamee F ( ), F ( ), lacovergeza debole di µ verso µ èequivaleeallacovergezadif (x) verso F (x) per ogi x R i cui F ( ) è coiua. Ricordiamo ifie l euciao del eorema Limie Cerale: se {X } N èuasuccessioei.i.d.di variabili aleaorie reali co E(X )=, E(X )=1,alloraP(X X x ) Φ(x) per ogi x R, doveφ( ) idica la fuzioe di riparizioe della legge ormale sadard (si oi che Φ( ) ècoiua i ogi x R). Possiamo duque riformulare il eorema Limie Cerale el modo seguee: la legge della variabile aleaoria (X X )/ coverge debolmee verso la legge ormale sadard Fuzioi caraerisiche Daa ua veore aleaorio X i R d e dea µ la sua legge, la fuzioe caraerisica (o rasformaa di Fourier) di µ (o, per esesioe, di X) è la fuzioe ˆµ : R d C defiia da ˆµ(ϑ) := E(e iϑ,x ) = e iϑ,x µ(dx), R d dove ricordiamo che a, b := d a ib i idica il prodoo scalare sadard su R d. È facile verificare che ˆµ( ) è ua fuzioe uiformemee coiua su R d e che ˆµ( ) 1.
11 1.7. LEGGI NORMALI RICHIAMI DI PROBABILIÀ Le proprieà fodameali delle fuzioi caraerisiche soo le seguei: La fuzioe caraerisica ideifica la legge, cioè se due leggi µ, ν su R d soo ali che ˆµ(ϑ) =ˆν(ϑ) per ogi ϑ R d,alloraµ = ν. Siao X 1,...,X d variabili casuali reali co legge rispeivamee µ 1,...,µ d e idichiamo co µ la legge del veore aleaorio (X 1,...,X d ) su R d.alloralevariabili X 1,...,X d soo idipedei (equivaleemee µ = µ 1 µ d ) se e solo se per ogi ϑ =(ϑ 1,...,ϑ d ) R d si ha che ˆµ(ϑ) =ˆµ 1 (ϑ 1 ) ˆµ (ϑ d ). Se ua successioe {µ } N di leggi su R d coverge debolmee verso la legge µ, siha auralmee ˆµ (ϑ) ˆµ(ϑ) per ogi ϑ R d. Viceversa, se ˆµ (ϑ) ψ(ϑ) per ogi ϑ R d e se la fuzioe ψ( ) è coiua i zero, allora ψ( ) è la fuzioe caraerisica di ua probabilià µ su R d e µ µ debolmee (eorema di covergeza di Lévy) Leggi ormali Leggi ormali uivariae. Dai µ R e σ (, ), la legge ormale (o gaussiaa) di media µ e variaza σ, idicaa co N (µ, σ ),èlaprobabiliàsur assoluamee coiua co desià f(x) = 1 πσ e (x µ) σ. Si verifica che effeivamee la media e la variaza di quesa legge valgoo rispeivamee µ e σ, mere la fuzioe caraerisica vale R e iϑx f(x)dx = e iϑµ 1 σ ϑ. Ua variabile aleaoria reale X è dea ormale di media µ R e variaza σ, e scriveremo X N (µ, σ ), se lo è la sua legge, cioè se E(e iϑx ) = e iϑµ 1 σ ϑ. (1.8) Per esesioe, quado σ =defiiremo la legge N (µ, ) come la misura di Dirac coceraa el puo µ. Aalogamee, per ua variabile aleaoria X scriviamo X N (µ, ) se P (X = µ) =1. Si oi che media, variaza e fuzioe caraerisica soo cosisei co la oazioe. Quado µ =e σ =1parleremo di legge ormale sadard. Se X N (µ, σ ),alloraax + b N (aµ + b, a σ ), come si verifica facilmee. Se X N (µ x, σx) e Y N (µ y, σy) soo variabili aleaorie idipedei, essedo E(e iϑ(x+y ) )= E(e iϑx ) E(e iϑy ), segue facilmee che X + Y N (µ x + µ y, σx + σy). Aalogamee, se X 1,...,X soo variabili aleaorie idipedei e X i N (µ i, σi ),allora X i N ( µ i, σ i ). Ogi combiazioe lieare di variabili ormali idipedei è duque ormale Leggi ormali mulivariae. U veore aleaorio X = (X 1,...,X d ) avaloriir d è deo ormale (o gaussiao) se ogi combiazioe lieare u, X := d u ix i delle sue compoei, dove u R d, è ua variabile aleaoria reale ormale. Ua probabilià su R d è dea ormale se è la legge di u veore aleaorio ormale. U esempio imporae: se X 1,...,X d soo variabili aleaorie reali ormali idipedei, allora X =(X 1,...,X d ) è u veore aleaorio ormale: ifai, come abbiamo viso, ogi combiazioe lieare delle variabili X 1,...,X d è ormale. I geerale, se X =(X 1,...,X d ) è u veore aleaorio ormale, segue dalla defiizioe che ciascua compoee X i è ua variabile aleaoria reale ormale. I paricolare, X i L e soo duque be defiii il veore media µ = E(X) =(E(X 1 ),...,E(X d )) e la marice delle covariaze Γ ij := Cov(X i,x j ) di X. Diremo allora che il veore aleaorio X su R d (e, per esesioe, la sua legge) è ormale di media µ emaricedellecovariazeγ e scriveremo X N (µ, Γ). La fuzioe caraerisica di X si calcola facilmee: per defiizioe ϑ,x è ua variabile aleaoria reale ormale, per ogi ϑ R d, per cui applicado (1.8) si oiee E(e iϑ,x ) = e i E(ϑ,X) 1 Var(ϑ,X) = e iϑ,µ 1 ϑ,γϑ, (1.9) poiché E(ϑ,X) =ϑ,µ e Var(ϑ,X) =ϑ, Γϑ. Queso mosra che, se u veore aleaorio X è ormale, la sua fuzioe caraerisica (e duque la sua legge) è deermiaa dal veore media µ e dalla marice delle covariaze Γ. Mosriamo ora che, per ogi µ R d e per ogi marice Γ d d simmerica e semidefiia posiiva, è effeivamee possibile cosruire u veore aleaorio X N (µ, Γ). Cosideriamo iaziuo d variabili aleaorie reali Z 1,...,Z d idipedei, ciascua ormale sadard. Iroducedo il veore Z =(Z 1,...,Z d ), per ϑ R d si ha d d E(e iϑ,z )= E(e iϑizi )= e 1 ϑ i = e 1 d ϑ i = e 1 ϑ,ϑ. (1.1) Queso sigifica, i base a (1.9), chez N (,I d ),dovei d idica la marice ideià: (I d ) ij := δ ij per 1 i, j d. Si dice che Z è u veore aleaorio ormale sadard. Daa ua marice Γ simmerica d d e semi-defiia posiiva, essa ammee, per il eorema sperale, ua base oroormale {v 1,...,v d } di auoveori: v i,v j = δ ij e Γv i = λ i v i,doveλ i perché Γ è semi-defiia posiiva. Idichiamo co A la rasposa della marice A. Defiedo l operaore lieare Γ 1/ ramie Γ 1/ v i := λ i v i, si verifica facilmee che Γ 1/ =(Γ 1/ ) e Γ 1/ (Γ 1/ ) =(Γ 1/ ) = Γ.SeorapoiamoX := Γ 1/ Z+µ, cioè X i := d j=1 (Γ1/ ) ij Z j + µ j, grazie a (1.1) si ha E(e iϑ,x )=e iϑ,µ E(e i(γ1/ ) ϑ,z )=e iϑ,µ 1 (Γ1/ ) ϑ,(γ 1/ ) ϑ = e iϑ,µ 1 ϑ,γϑ. Grazie a (1.9), si ha duque che X N (µ, Γ) Proprieà delle leggi ormali. Dall equazioe (1.9) è facile deermiare il comporameo dei veori ormali per rasformazioi affii: se X N (µ, Γ) è u veore aleaorio ormale i R d e Y = AX + b, co A marice reale m d e b R m,
12 1.7. LEGGI NORMALI RICHIAMI DI PROBABILIÀ allora Y è u veore aleaorio ormale i R m la cui legge è N (Aµ + b, AΓA ). Ifai per ogi ϑ R m possiamo scrivere E(e iϑ,y )=e iϑ,b E(e ia ϑ,x )=e iϑ,b e ia ϑ,µ 1 A ϑ,γa ϑ = e iϑ,aµ+b 1 ϑ,aγa ϑ. Espoiamo ora ua proprieà fodameale delle variabili ormali. Suppoiamo che X, Y siao due variabili aleaorie reali ormali ali che il veore aleaorio bidimesioale (X, Y ) sia ormale. Diremo i queso caso che X e Y soo cogiuamee ormali. Allora X e Y soo idipedei se (e solo se) soo scorrelae, cioè se (e solo se) Cov(X, Y )=. Ifai i queso caso la marice di covariaza Γ del veore (X, Y ) è diagoale. Ricordado la relazioe (1.9), possiamo allora scrivere E(e i(ϑ1x+ϑy ) )=e i(ϑ1µ X+ϑ µ Y ) e 1 (Var(X)ϑ 1 +Var(Y )ϑ ) =E(e iϑ1x )E(e iϑy ), e l idipedeza segue dalle proprieà delle fuzioi caraerisiche. L esesioe al caso i cui le variabili siao più di due è immediaa. Lemma 1.9. Dae X 1,...,X variabili aleaorie reali cogiuamee ormali, ali cioè che il veore aleaorio X =(X 1,...,X ) avaloriir sia ormale, esse soo idipedei se e solo se soo scorrelae, cioè Cov(X i,x j )=per ogi i = j. Soolieiamo che quesa proprieà i geerale o è valida se le variabili ormali X 1,...,X o soo cogiuamee ormali. Il Lemma 1.9 può essere riformulao el modo seguee: dao u veore aleaorio ormale X =(X 1,...,X ) avaloriir, le sue compoei X 1,...,X soo idipedei se e solo se la marice di covariaza di X è diagoale, cioè Γ ij =per ogi i = j. No è difficile esedere il Lemma 1.9 al caso i cui X 1,...,X siao veori aleaori cogiuamee ormali, cioè X i =(X (1) i,...,x (di) i ) è a valori i R di, co d i N, ex = {X (j) i },...,, j=1,...,di sia u veore ormale i R d1+...+d. L idipedeza di X 1,...,X equivale i queso caso alla scorrelazioe delle rispeive compoei: Cov(X (a) i,x (b) j )= per ogi i = j e per ogi 1 a d i e 1 b d j. Soolieiamo che o si richiede che Cov(X (a) i,x (b) i )=. Se X N (µ, Γ) è u veore aleaorio ormale i R d, el caso i cui de(γ) = il veore X è assoluamee coiuo co desià f X (x) = 1 (π) d/ de(γ) e 1 x µ,γ 1 (x µ), (1.11) come segue dalla già mezioaa rappreseazioe X = Γ 1/ Z + µ co Z N (,I d ), applicado la legge di rasformazioe per la desià f X (x) = de(γ) 1/ f Z (Γ 1/ (x µ)) e osservado che f Z (z) =(π) / e 1 z,z. Se ivece de(γ) =, il veore X o è assoluamee coiuo. Dimosriamo ifie u uile risulao di covergeza. Proposizioe 1.1. Sia {X } N ua successioe di veori aleaori che coverge i L verso u veore aleaorio X. SeX è ormale per ogi N, X N (µ, Γ ), allora ache X è ormale: X N (µ, Γ); iolreµ =lim µ e Γ = lim Γ. Dimosrazioe. Scrivedo X =(X (1) X X = E d,...,x (d) ) e X =(X (1),...,X (d) ) si ha (X (i) X (i) ) = d X (i) X (i), da cui segue che la covergeza i L di X X implica (è azi equivalee a) la covergeza i L di ue le compoei: X (i) X (i), per ogi 1 i d. Grazie alla relazioe (1.7), si ha i paricolare E((X (i) ) ) E((X (i) ) ), per ogi 1 i d. Noiamo ora che E(X (i) X (j) ) E(X (i) X (j) ), per ogi 1 i, j d: ifai, usado le disuguagliaze riagolare e di Cauchy-Schwarz, possiamo scrivere E(X (i) X (j) ) E(X (i) X (j) ) E((X (i) X (i) X (i) )X (j) ) + E(X (i) (X (j) X (j) )) X (i) X (j) + X (i) X (j) X (j). Aalogamee E(X (i) ) E(X (i) ), per ogi 1 i d, poiché E(X (i) ) E(X (i) ) E( X (i) X (i) )=X (i) X (i) 1 X (i) X (i). I defiiiva, abbiamo dimosrao la covergeza di µ (i) := E(X (i) ) verso µ (i) := E(X (i) ) e di (Γ ) ij := Cov(X (i) ) verso Γ ij := Cov(X (i),x (j) ), da cui segue che,x (j) E(e iϑx ) = e iϑ,µ 1 ϑ,γϑ e iϑ,µ 1 ϑ,γϑ. (1.1) Dao che la covergeza i L implica quella i legge, per la Proposizioe 1.7, la fuzioe caraerisica di X è il limie delle fuzioi caraerisiche delle X. Segue duque da (1.1) che E(e iϑx )=e iϑ,µ 1 ϑ,γϑ per ogi ϑ R,cioèX N (µ, Γ). Osservazioe La Proposizioe 1.1 resa vera ache quado la covergeza i L è sosiuia dalla covergeza i legge. Queso sigifica che se ua successioe di veori aleaori ormali X coverge verso X i uo qualuque dei modi descrii el paragrafo 1.5 (i legge, i probabilià, quasi ceramee, i L p ), il veore aleaorio X è auomaicamee ormale; iolre, veore media e marice delle covariaze di X soo dai dal limie delle aaloghe quaià di X. La dimosrazioe di quesa geeralizzazioe o è difficile ma presea qualche aspeo ecico e la omeiamo per brevià (si veda l esercizio.16 i Baldi []).
13 1.8. QUESIONI ECNICHE 1 1. RICHIAMI DI PROBABILIÀ 1.8. Quesioi eciche Classi di Dyi. A differeza di quao accade co la opologia, la σ-algebra E = σ(i) geeraa da ua famiglia I o ammee ua descrizioe esplicia. Si porebbe pesare di cosiderare la famiglia I (1) coeee gli elemei di I, ilorocomplemearielelorouioiumerabili,mai geerale I (1) o è ua σ-algebra. Aggiugedo agli elemei di I (1) ilorocomplemearielelorouioi umerabili, si oiee ua famiglia più ampia I (),eieradolaprocedurasidefiiscei () per N. Chiaramee I (1) I ()... euoporebbesperarecheσ(i) =I () per qualche N, operlomeo che σ(i) = N I(). Purroppo queso è falso i geerale: per esempio, quado E = R e I è la famiglia degli iervalli aperi, σ(i) èsreameepiùgradedi N I() (cf. la fie della sezioe el capiolo 1 i [Billigsley, 1995], pagg. 3 e seguei). No essedo dispoibile ua descrizioe esplicia degli elemei di E = σ(i), siredooecessarie eciche per dimosrare che ua cera proprieà è verificaa per ogi elemeo di E. Dao u isieme E, ua famiglia D P(E) di pari di E èdeauaclasse di Dyi (o ache classe moooa) secoiee E eseèchiusaperuioiumerabilidisgiueeperpassaggioalcomplemeare: A D = A c D ; A D N, A i A j = se i = j = N A D. Ua defiizioe aleraiva equivalee è che, olre a coeere E, laclassed sia chiusa per differeze proprie eperuioiumerabilicrescei,cioè A, B D, A B = B \ A D ; A D N, A A +1 = N A D. Si ha allora il seguee Lemma 1.1 (Dyi). Sia D ua classe di Dyi su u isieme E esiai P(E) ua famiglia chiusa per iersezioi fiie. Se D coiee I, allora D coiee σ(i). Per dimosrare che ua cera proprieà è soddisfaa da ui gli elemei di ua σ-algebra E, si dimosra iaziuo che gli isiemi che hao quesa proprieà formao ua classe di Dyi, quidi si dimosra che quesa proprieà è soddisfaa dagli elemei di ua base I di E. DallemmadiDyisegueduque che godoo di quesa proprieà ui gli elemei di E. Nellosessospirio,sihailsegueerisulaoper fuzioi misurabili. Lemma 1.13 (Classe Moooa). Sia H ua famiglia di fuzioi reali limiae, defiie su u isieme E, e sia I P(E) ua famiglia di pari di E chiusa per iersezioi fiie. Siao iolre soddisfae le seguei codizioi: H è uo spazio veoriale che coiee le fuzioi cosai; se {f } N è ua successioe di fuzioi di H ale che f (x) f(x) per ogi x E, cof limiaa, si ha che f H; H coiee 1 A per ogi A I. Allora H coiee ue le fuzioi reali limiae e misurabili rispeo a σ(i) Cosruzioe di successioi idipedei. Mosriamo che è sempre possibile cosruire ua successioe di variabili aleaorie reali idipedei co leggi assegae {µ } N. Uilizzeremocome spazio di probabilià ([, 1), B[, 1), dx), dovedx idica la misura di Lebesgue. Per ω [, 1), idichiamo co Y (ω) l -esima cifra ello sviluppo i base due, cioè ω =.Y 1(ω)Y (ω)y 3(ω)... co Y (ω) {, 1}; ei casi ambigui, per es..1 =.1, scegliamolosviluppofiio.piùprecisamee,poiamoperω [, 1) Y (ω) := 1 =1 1 [ 1, )(ω). È facile verificare che la successioe di variabili aleaorie {Y } N è i.i.d., cioèlevariabilisooidipedei ehaolasessalegge:piùprecisameep(y =)=P(Y =1)= 1.EssedoY l -esima cifra ello sviluppo i base due, si ha che per ogi ω [, 1) =1 Y (ω) = ω, cioè =1 Y = id, dove id idica l ideià su [, 1). Iparicolare,lavariabilealeaoriaZ := N disribuia su [, 1), cioèhacomeleggelamisuradilebesguesu[, 1). Idicado co {p i} i N la successioe dei umeri primi, poiamo per N X := =1 Y (p ). Y è uiformemee Per fissao, la successioe {Y (p ) } N èi.i.d.coleggemargialep(y (p ) =)=P(Y (p ) =1)= 1, esaamee come la successioe origiale {Y } N. Dicosegueza,lavariabileX ha la sessa legge della variabile Z, cioè è uiformemee disribuia sull iervallo [, 1). (Sioicheoèveroche Y (p ) =1 = id.) Dao che, per p, p primi disii, le successioi {p } e {(p ) } soo disgiue, segue che per 1,..., disii le variabili {X 1,...,X } soo idipedei (iuiivamee, soo cosruie a parire da famiglie disgiue di variabili Y i). Di cosegueza abbiamo cosruio ua successioe {X } N di variabili aleaorie reali idipedei, ciascua co legge uiforme sull iervallo [, 1). Ifie, basa osservare che ua variabile aleaoria reale co legge assegaa µ si può sempre oeere come immagie di ua variabile aleaoria uiforme su [, 1). Piùprecisamee,seZ èuavariabile aleaoria uiforme su [, 1) e se F (x) =µ((,x]) è la fuzioe di riparizioe di µ, idicado co G(y) :=if{x : F (x) y} la pseudo-iversa di F ( ), defiiapery [, 1), si verifica facilmee che G(Z) è ua variabile aleaoria co fuzioe di riparizioe F ( ), cioè co legge µ. Se idichiamo co F ( ) la fuzioe di riparizioe di µ ecog ( ) la corrispodee pseudo-iversa, abbiamo che {W := G (Y )} N èuasuccessioedivariabilialeaorierealiidipedeicoleggimargiali{µ } N Lemma di misurabilià di Doob. U risulao alvola uile è il seguee: Lemma 1.14 (Doob). Siao X :(E,E) (F, F) e Y :(E,E) R d applicazioi misurabili e sia σ(x) la σ-algebra su E geeraa da X. L applicazioey èmisurabilerispeoaσ(x) se e solao se esise u applicazioe misurabile g :(F, F) R d ale che Y = g(x).
Moto browniano e analisi stocastica
 Moo browiao e aalisi socasica Versioe 3.3 Ulima modifica: 9 giugo 11. FRANCESCO CARAVENNA fracesco.caravea@uimib.i hp://www.maapp.uimib.i/~fcarave DIPARIMENO DI MAEMAICA E APPLICAZIONI UNIVERSIÀ DEGLI
Moo browiao e aalisi socasica Versioe 3.3 Ulima modifica: 9 giugo 11. FRANCESCO CARAVENNA fracesco.caravea@uimib.i hp://www.maapp.uimib.i/~fcarave DIPARIMENO DI MAEMAICA E APPLICAZIONI UNIVERSIÀ DEGLI
Esercizio 1. Sia N un processo di Poisson di parametro λ. Dimostrare che, per ogni t > 0,
 Esercizi di Calcolo delle Probabilià della 9 a seimaa Corso di Laurea i Maemaica, Uiversià degli Sudi di Padova. Esercizio 1. Sia N u processo di Poisso di paramero λ. Dimosrare che, per ogi > 0, N P oλ.
Esercizi di Calcolo delle Probabilià della 9 a seimaa Corso di Laurea i Maemaica, Uiversià degli Sudi di Padova. Esercizio 1. Sia N u processo di Poisso di paramero λ. Dimosrare che, per ogi > 0, N P oλ.
2. Moto browniano: prime proprietà Il moto browniano Processi stocastici gaussiani
 6. MOTO BROWNIANO: PRIME PROPRIETÀ. Moo browiao: prime proprieà I queso capiolo sviluppiamo la raazioe maemaica del moo browiao. Queso processo prede il ome dal boaico scozzese Rober Brow, che el 87 descrisse
6. MOTO BROWNIANO: PRIME PROPRIETÀ. Moo browiao: prime proprieà I queso capiolo sviluppiamo la raazioe maemaica del moo browiao. Queso processo prede il ome dal boaico scozzese Rober Brow, che el 87 descrisse
Il modello di Black e Scholes come limite del modello binomiale multiperiodale
 Capiolo Il modello di Blac e Scholes come limie del modello biomiale muliperiodale. Il Modello Biomiale Muliperiodale Ricordiamo brevemee il Modello Biomiale Muliperiodale o Cox-Ross-Rubisei IPOTESI e
Capiolo Il modello di Blac e Scholes come limie del modello biomiale muliperiodale. Il Modello Biomiale Muliperiodale Ricordiamo brevemee il Modello Biomiale Muliperiodale o Cox-Ross-Rubisei IPOTESI e
Lezione 3 Proprietà statistiche degli stimatori OLS - 1. Anche in questo capitolo si considera il modello di regressione lineare.
 Lezioe 3 Proprieà saisiche degli simaori OLS - Ache i queso capiolo si cosidera il modello di regressioe lieare y x β + u co E( u Ω ) 0, x appariee a Ω per,,, e si assume che sia assegao il processo (fiio)
Lezioe 3 Proprieà saisiche degli simaori OLS - Ache i queso capiolo si cosidera il modello di regressioe lieare y x β + u co E( u Ω ) 0, x appariee a Ω per,,, e si assume che sia assegao il processo (fiio)
Istituzioni di Analisi Superiore, secondo modulo
 Uiversià degli Sudi di Udie Ao Accademico 997/98 Facolà di Scieze aemaiche, Fisiche e Naurali Corso di Laurea i aemaica Isiuzioi di Aalisi Superiore, secodo modulo Cogome e Nome: Prova Scria del 4 giugo
Uiversià degli Sudi di Udie Ao Accademico 997/98 Facolà di Scieze aemaiche, Fisiche e Naurali Corso di Laurea i aemaica Isiuzioi di Aalisi Superiore, secodo modulo Cogome e Nome: Prova Scria del 4 giugo
(x + 1) α (1 x) 3 α per x ( 1, 1) 0 per x / [ 1, 1]
![(x + 1) α (1 x) 3 α per x ( 1, 1) 0 per x / [ 1, 1] (x + 1) α (1 x) 3 α per x ( 1, 1) 0 per x / [ 1, 1]](/thumbs/103/160377773.jpg) Corsi di Probabilià, Saisica e Processi socasici per Ig dell Auomazioe, Iformaica e If Ges Azieda // Esercizio Si osserva l iesià del veo el poro di Maria regisrado uo ogi gioro i cui il veo o supera ua
Corsi di Probabilià, Saisica e Processi socasici per Ig dell Auomazioe, Iformaica e If Ges Azieda // Esercizio Si osserva l iesià del veo el poro di Maria regisrado uo ogi gioro i cui il veo o supera ua
Teoria delle distribuzioni Parte quinta Limiti nel senso delle distribuzioni
 ezioi di Maemaica e disribuzioi pare 5 Teoria delle disribuzioi Pare quia imii el seso delle disribuzioi operazioe di limie i seso disribuzioale Passiamo a raare, araverso ua serie di esempi precedui da
ezioi di Maemaica e disribuzioi pare 5 Teoria delle disribuzioi Pare quia imii el seso delle disribuzioi operazioe di limie i seso disribuzioale Passiamo a raare, araverso ua serie di esempi precedui da
I appello - 8 Gennaio 2019
 Aalisi Maemaica - A.A. 08/9 Prove scrie di Aalisi Maemaica - A.A. 08/09 Corso di Laurea i Igegeria Civile Corso di Laurea i Igegeria Iformaica ed Eleroica I appello - 8 Geaio 09 Svolgere i seguei esercizi,
Aalisi Maemaica - A.A. 08/9 Prove scrie di Aalisi Maemaica - A.A. 08/09 Corso di Laurea i Igegeria Civile Corso di Laurea i Igegeria Iformaica ed Eleroica I appello - 8 Geaio 09 Svolgere i seguei esercizi,
0 per x / ( 1, ). i) (4 p) Trovare per quali valori di α la funzione f è una densità di probabilità (non si chiede di calcolare C α ).
 Corsi di Probabilià, Saisica e Processi socasici per Ig dell Auomazioe, Iformaica e If Ges Azieda /5/ Esercizio U sisema di preallarme su u velivolo segala ua A allarme oppure ua N o allarme ogi dieci
Corsi di Probabilià, Saisica e Processi socasici per Ig dell Auomazioe, Iformaica e If Ges Azieda /5/ Esercizio U sisema di preallarme su u velivolo segala ua A allarme oppure ua N o allarme ogi dieci
****** FUNZIONI MISURABILI E INTEGRAZIONE ******
 ****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
Il modello di Black e Scholes come limite del modello binomiale multiperiodale
 Capiolo Il modello di Blac e Scholes come limie del modello biomiale muliperiodale. Il Modello Biomiale Muliperiodale Ricordiamo brevemee il Modello Biomiale Muliperiodale o Cox-Ross-Rubisei.. Ipoesi e
Capiolo Il modello di Blac e Scholes come limie del modello biomiale muliperiodale. Il Modello Biomiale Muliperiodale Ricordiamo brevemee il Modello Biomiale Muliperiodale o Cox-Ross-Rubisei.. Ipoesi e
1. Richiami di probabilità
 1. Richiami di probabilità Forniamo un compendio delle nozioni basilari di probabilità che ci saranno utili. Per maggiori dettagli, si possono consultare i testi [Billingsley, 1995], [Williams, 1991].
1. Richiami di probabilità Forniamo un compendio delle nozioni basilari di probabilità che ci saranno utili. Per maggiori dettagli, si possono consultare i testi [Billingsley, 1995], [Williams, 1991].
Università di Roma Tor Vergata - Corso di Laurea in Ingegneria Analisi Matematica I - Prova scritta del 30 Gennaio 2019
 Uiversià di Roma Tor Vergaa - Corso di Laurea i Igegeria Aalisi Maemaica I - Prova scria del 3 Geaio 9 Esercizio. [5 pui] Calcolare lo sviluppo di Taylor dell ordie = 5 el puo x = per la seguee fuzioe:
Uiversià di Roma Tor Vergaa - Corso di Laurea i Igegeria Aalisi Maemaica I - Prova scria del 3 Geaio 9 Esercizio. [5 pui] Calcolare lo sviluppo di Taylor dell ordie = 5 el puo x = per la seguee fuzioe:
Università di Camerino Corso di Laurea in Fisica: indirizzo Tecnologie per l Innovazione Appunti di Calcolo Prof. Angelo Angeletti
 Iegrali idefiii Geeralià Si è viso come, daa ua fuzioe di equazioe y = f(), si possa rovare la sua derivaa prima f (). Si è ache osservao che esise ua codizioe ecessaria, ma o sufficiee, affiché ua fuzioe
Iegrali idefiii Geeralià Si è viso come, daa ua fuzioe di equazioe y = f(), si possa rovare la sua derivaa prima f (). Si è ache osservao che esise ua codizioe ecessaria, ma o sufficiee, affiché ua fuzioe
Serie e trasformate di Fourier brevi richiami
 UNIVERSIÀ DEGLI SUDI DI FIRENZE DIPARIMENO DI INGEGNERIA CIVILE e AMBIENALE Sezioe Geoecica Serie e rasformae di Fourier brevi richiami Do. Ig. Albero Pulii eorema di Fourier U qualsiasi segale periodico
UNIVERSIÀ DEGLI SUDI DI FIRENZE DIPARIMENO DI INGEGNERIA CIVILE e AMBIENALE Sezioe Geoecica Serie e rasformae di Fourier brevi richiami Do. Ig. Albero Pulii eorema di Fourier U qualsiasi segale periodico
Esercitazione IV Complementi di Probabilità a.a. 2011/2012
 Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Equazioni differenziali: formule
 Equazioi differeziali: formule Equazioi a variabili separabili y ' A B y Vale eorema esiseza e uicià locale y ' dy Ad B y y y ' A B y y Si applicao le codizioi alla fie dei due iegrali idefiii, oppure
Equazioi differeziali: formule Equazioi a variabili separabili y ' A B y Vale eorema esiseza e uicià locale y ' dy Ad B y y y ' A B y y Si applicao le codizioi alla fie dei due iegrali idefiii, oppure
ESAME DI STATO DI LICEO SCIENTIFICO Corso Sperimentale P.N.I. Tema di MATEMATICA - 23 giugno 2005
 ESAME DI STATO DI LICEO SCIENTIFICO -5 Corso Sperimeale PNI Tema di MATEMATICA - giugo 5 Svolgimeo a cura della profssa Sadra Berecoli e del prof Luigi Tomasi (luigiomasi@liberoi) RISPOSTE AI QUESITI DEL
ESAME DI STATO DI LICEO SCIENTIFICO -5 Corso Sperimeale PNI Tema di MATEMATICA - giugo 5 Svolgimeo a cura della profssa Sadra Berecoli e del prof Luigi Tomasi (luigiomasi@liberoi) RISPOSTE AI QUESITI DEL
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 2007/2008
 UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
INTEGRAZIONE INDEFINITA DI ALCUNE CLASSI DI FUNZIONI
 Adolfo Scimoe FORMULE INTEGRAZIONE Pag INTEGRAZIONE INDEFINITA DI ALCUNE CLASSI DI FUNZIONI Iegrazioe delle fuzioi razioali frae Se la frazioe è impropria, cioè il grado del umeraore è maggiore o uguale
Adolfo Scimoe FORMULE INTEGRAZIONE Pag INTEGRAZIONE INDEFINITA DI ALCUNE CLASSI DI FUNZIONI Iegrazioe delle fuzioi razioali frae Se la frazioe è impropria, cioè il grado del umeraore è maggiore o uguale
Modelli'di'Variabili'Aleatorie'
 ModellidiVariabiliAleaorie! VariabilialeaoriediBeroulli: " X èdiberoullidiparamero p (,) se P( X ) p e P( X ) p. " Proprieà: # E X # Var X : p X ( ) + p X ( ) p. E( X ) E( X) masiccome X X $ E( X) E( X)
ModellidiVariabiliAleaorie! VariabilialeaoriediBeroulli: " X èdiberoullidiparamero p (,) se P( X ) p e P( X ) p. " Proprieà: # E X # Var X : p X ( ) + p X ( ) p. E( X ) E( X) masiccome X X $ E( X) E( X)
Esercitazione X Complementi di Probabilità a.a. 2011/2012
 Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Analisi Stocastica. Note del corso 2008/09. Francesco Caravenna.
 Analisi Stocastica Note del corso 28/9 Francesco Caravenna francesco.caravenna@math.unipd.it Dipartimento di Matematica Pura e Applicata Università degli Studi di Padova via Trieste 63, 35121 Padova, Italy
Analisi Stocastica Note del corso 28/9 Francesco Caravenna francesco.caravenna@math.unipd.it Dipartimento di Matematica Pura e Applicata Università degli Studi di Padova via Trieste 63, 35121 Padova, Italy
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
Sforzo all interfaccia fra due regioni con differente permeabilità magnetica
 Sforzo all ierfaccia fra due regioi co differee permeabilià mageica Si cosideri l ierfaccia fra due regioi, Ω e Ω, avei diversa permeabilià mageica, rispeivamee e. Si limii ora lo sudio ad ua porzioe ifiiesima
Sforzo all ierfaccia fra due regioi co differee permeabilià mageica Si cosideri l ierfaccia fra due regioi, Ω e Ω, avei diversa permeabilià mageica, rispeivamee e. Si limii ora lo sudio ad ua porzioe ifiiesima
OPERAZIONI SUI SEGNALI DETERMINISTICI, ENERGIA, VALOR MEDIO, POTENZA, ANALISI DI FOURIER, CONVOLUZIONE. A cos 2 / 2
 OPERAZIONI SUI SEGNALI DEERMINISICI, ENERGIA, VALOR MEDIO, POENZA, ANALISI DI FOURIER, CONVOLUZIONE Esercizio Calcolare la poeza, l eergia e il valor medio dei seguei segali a) x()a; b) x()u() ; c) x()acos(oφ)
OPERAZIONI SUI SEGNALI DEERMINISICI, ENERGIA, VALOR MEDIO, POENZA, ANALISI DI FOURIER, CONVOLUZIONE Esercizio Calcolare la poeza, l eergia e il valor medio dei seguei segali a) x()a; b) x()u() ; c) x()acos(oφ)
Nozioni elementari di Analisi Matematica applicate alla Fisica Generale
 Nozioi elemeari di alisi Maemaica applicae alla Fisica Geerale Nozioe di iegrale ideiio La derivazioe può essere ierpreaa come ua regola che, per ogi uzioe assegaa (primiiva), ci permee di deermiare u
Nozioi elemeari di alisi Maemaica applicae alla Fisica Geerale Nozioe di iegrale ideiio La derivazioe può essere ierpreaa come ua regola che, per ogi uzioe assegaa (primiiva), ci permee di deermiare u
Ammortamento di un debito
 Ammorameo di u debio /35 Ammorameo di u debio Che cosa si iede per ammorameo? Ammorameo coabile La quoa di ammorameo cosiuisce la pare del coso di u bee maeriale o immaeriale di ivesimeo da aribuire all
Ammorameo di u debio /35 Ammorameo di u debio Che cosa si iede per ammorameo? Ammorameo coabile La quoa di ammorameo cosiuisce la pare del coso di u bee maeriale o immaeriale di ivesimeo da aribuire all
Analisi stocastica. Dispense del corso 2010/11. FRANCESCO CARAVENNA
 Analisi stocastica Dispense del corso 21/11 FRANCESCO CARAVENNA francesco.caravenna@unimib.it http://www.matapp.unimib.it/~fcaraven DIPARTIMENTO DI MATEMATICA E APPLICAZIONI UNIVERSITÀ DEGLI STUDI DI MILANO-BICOCCA
Analisi stocastica Dispense del corso 21/11 FRANCESCO CARAVENNA francesco.caravenna@unimib.it http://www.matapp.unimib.it/~fcaraven DIPARTIMENTO DI MATEMATICA E APPLICAZIONI UNIVERSITÀ DEGLI STUDI DI MILANO-BICOCCA
ELEMENTI DI TEORIA DELLE PROBABILITA
 ELEMENTI DI TEORIA DELLE PROBABILITA Nozioi base Spazio S S è l isieme di ui i possibili esii di u esperimeo. Esempio 1. Nel lacio di u dado abbiamo S{1,2,3,4,5,6}. Esempio 2. La duraa di ua lampadia S{x
ELEMENTI DI TEORIA DELLE PROBABILITA Nozioi base Spazio S S è l isieme di ui i possibili esii di u esperimeo. Esempio 1. Nel lacio di u dado abbiamo S{1,2,3,4,5,6}. Esempio 2. La duraa di ua lampadia S{x
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 07/02/2017
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
Esercizi 2 Pietro Caputo 14 dicembre se ξ n > log n
 Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
TRASFORMATA DI FOURIER. A.1 Segnali analogici, deterministici ed aleatori. A p p e n d i c e A
 A p p e d i c e A RASFORMAA DI FOURIER Uo degli aspei più imporai di uo il seore dell igegeria è sicuramee l aalisi di segali el domiio del empo e della frequeza. I segali aalogici si disiguoo i segali
A p p e d i c e A RASFORMAA DI FOURIER Uo degli aspei più imporai di uo il seore dell igegeria è sicuramee l aalisi di segali el domiio del empo e della frequeza. I segali aalogici si disiguoo i segali
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 22/01/2018
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Analisi stocastica. Dispense del corso 2010/11. Versione 3.1 Ultima modifica: 15 aprile FRANCESCO CARAVENNA
 Alisi socsic Dispese del corso 1/11 Versioe 3.1 Ulim modific: 15 prile 11. FRANCESCO CARAVENNA frcesco.crve@uimib.i hp://www.mpp.uimib.i/~fcrve DIPARIMENO DI MAEMAICA E APPLICAZIONI UNIVERSIÀ DEGLI SUDI
Alisi socsic Dispese del corso 1/11 Versioe 3.1 Ulim modific: 15 prile 11. FRANCESCO CARAVENNA frcesco.crve@uimib.i hp://www.mpp.uimib.i/~fcrve DIPARIMENO DI MAEMAICA E APPLICAZIONI UNIVERSIÀ DEGLI SUDI
ALTRI ESERCIZI SULL INTEGRALE DI LEBESGUE. A. Figà Talamanca
 ALTRI SRCIZI SULL INTGRAL DI LBSGU A. Figà Talamaca 29 ottobre 2006 2 L itegrale di Lebesgue che abbiamo defiito per le fuzioi misurabili, limitate defiite su u isieme misurabile di misura fiita, può essere
ALTRI SRCIZI SULL INTGRAL DI LBSGU A. Figà Talamaca 29 ottobre 2006 2 L itegrale di Lebesgue che abbiamo defiito per le fuzioi misurabili, limitate defiite su u isieme misurabile di misura fiita, può essere
Il Teorema di Markov. 1.1 Analisi spettrale della matrice di transizione. Il teorema di Markov afferma che
 1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
ESERCITAZIONE: FEM. Consideriamo un elemento triangolare. y 3
 ESERCITAZIONE: FEM L aalisi agli elemei fiii è u ipo di aalisi che si rifà alla meccaica dei solidi e rasforma il coiuo i u discreo composo da umerosi elemei dei quali se e cooscoo le proprieà. Le relazioi
ESERCITAZIONE: FEM L aalisi agli elemei fiii è u ipo di aalisi che si rifà alla meccaica dei solidi e rasforma il coiuo i u discreo composo da umerosi elemei dei quali se e cooscoo le proprieà. Le relazioi
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Si dice che f è infinitesima o che è un infinitesimo per x x0 Un infinitesimo, quindi è una variabile che tende a zero.
 pag Appui elaborai dal collega Prof. Vicezo De Pasquale Ifiiesimi Si dice che f è ifiiesima o che è u ifiiesimo per se f ( ) U ifiiesimo, quidi è ua variabile che ede a zero. Es. - π y cos è u ifiiesimo
pag Appui elaborai dal collega Prof. Vicezo De Pasquale Ifiiesimi Si dice che f è ifiiesima o che è u ifiiesimo per se f ( ) U ifiiesimo, quidi è ua variabile che ede a zero. Es. - π y cos è u ifiiesimo
Il logaritmo e l esponenziale
 Il logarimo e l espoeziale 6 marzo 2009 La defiizioe di logarimo che si impara ella scuola secodaria è la seguee: Defiizioe Il logarimo i base b di x è l espoee cui si deve elevare b per oeere x. I formule:
Il logarimo e l espoeziale 6 marzo 2009 La defiizioe di logarimo che si impara ella scuola secodaria è la seguee: Defiizioe Il logarimo i base b di x è l espoee cui si deve elevare b per oeere x. I formule:
Algebra delle matrici
 Algebra delle matrici Prodotto di ua matrice per uo scalare Data ua matrice A di tipo m, e dato uo scalare r R, moltiplicado r per ciascu elemeto di A si ottiee ua uova matrice di tipo m, detta matrice
Algebra delle matrici Prodotto di ua matrice per uo scalare Data ua matrice A di tipo m, e dato uo scalare r R, moltiplicado r per ciascu elemeto di A si ottiee ua uova matrice di tipo m, detta matrice
IV Appello di Calcolo delle Probabilità Cognome: Laurea Triennale in Matematica 2011/12 Nome: 17 luglio
 IV Appello di Calcolo delle Probabilità Cogome: Laurea Trieale i Matematica / Nome: 7 luglio Email: Quado o è espressamete idicato il cotrario, per la soluzioe degli esercizi è possibile usare tutti i
IV Appello di Calcolo delle Probabilità Cogome: Laurea Trieale i Matematica / Nome: 7 luglio Email: Quado o è espressamete idicato il cotrario, per la soluzioe degli esercizi è possibile usare tutti i
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
1.10 La funzione esponenziale
 6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
0.1 Il teorema limite centrale
 0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
R chi h ami m sul u cana n le di d com o u m n u i n cazion o e n radi d o
 Richiami sul caale di comuicazioe radio 1 Fadig leo shadowig è causao da osacoli di gradi dimesioi palazzi ra TX e RX Il pah loss è proporzioale a r α, dove α è i geere ra 2.5 e 5 i ambiee urbao Erambi
Richiami sul caale di comuicazioe radio 1 Fadig leo shadowig è causao da osacoli di gradi dimesioi palazzi ra TX e RX Il pah loss è proporzioale a r α, dove α è i geere ra 2.5 e 5 i ambiee urbao Erambi
Convergenza di variabili aleatorie
 Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER
 TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO
 Simulazioe 14/15 ANNO SCOLASTICO 14/15 SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Risoluzioe Problema 1 - Trekkig i moaga a) Disegiamo il grafico b) Calcoliamo la
Simulazioe 14/15 ANNO SCOLASTICO 14/15 SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Risoluzioe Problema 1 - Trekkig i moaga a) Disegiamo il grafico b) Calcoliamo la
Soluzione CPS 22/6/04. I parte. (1). Chiamiamo C l evento l individuo scelto ha il colesterolo alto, V, O e NL rispettivamente
 Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica I del c.1.
 Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
SMSMW#300#130#1#220#210W#300#130#1#140#130W#220#13
 Marice icideza La marice d'icideza complea A c di u grafo orieao G co N odi ed R rami, è ua marice reagolare di N righe ed R coloe che si cosruisce come segue: si umerao co =1,2,...,N ui i odi e co r=1,2,...,r
Marice icideza La marice d'icideza complea A c di u grafo orieao G co N odi ed R rami, è ua marice reagolare di N righe ed R coloe che si cosruisce come segue: si umerao co =1,2,...,N ui i odi e co r=1,2,...,r
Il logaritmo e l esponenziale
 Il logarimo e l espoeziale 2 geaio 202 La defiizioe di logarimo che si impara ella scuola secodaria è la seguee: Defiizioe Il logarimo i base b di x è l espoee cui si deve elevare b per oeere x. I formule:
Il logarimo e l espoeziale 2 geaio 202 La defiizioe di logarimo che si impara ella scuola secodaria è la seguee: Defiizioe Il logarimo i base b di x è l espoee cui si deve elevare b per oeere x. I formule:
Statistica Inferenziale Soluzioni 1. Stima puntuale
 ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
Istituzioni di Analisi Superiore Esercizi
 Istituzioi di Aalisi Superiore Esercizi G.P.Leoardi 13 aprile 2010 Nota: gli esercizi delle sezioi 2 4 soo stati tratti i buoa parte da ua raccolta di esercizi di Aalisi Fuzioale ad opera di H.Brezis e
Istituzioi di Aalisi Superiore Esercizi G.P.Leoardi 13 aprile 2010 Nota: gli esercizi delle sezioi 2 4 soo stati tratti i buoa parte da ua raccolta di esercizi di Aalisi Fuzioale ad opera di H.Brezis e
y(t) o complesse non tutte nulle, fa corrispondere un'uscita data dalla:
 Capiolo V TRASFORMAZIOI LIEARI DEI SEGALI V. - Defiizioi. Proprieà geerali. x( ) S y() Fig. VI. Trasformazioe di segali S ed è simbolicamee rappreseaa dalla relazioe: y () = S x () I (V..) { } U sisema
Capiolo V TRASFORMAZIOI LIEARI DEI SEGALI V. - Defiizioi. Proprieà geerali. x( ) S y() Fig. VI. Trasformazioe di segali S ed è simbolicamee rappreseaa dalla relazioe: y () = S x () I (V..) { } U sisema
Appendice 2. Norme di vettori e matrici
 Appedice 2. Norme di vettori e matrici La ozioe esseziale per poter defiire il cocetto di distaza e lughezza i uo spazio vettoriale lieare è quello di orma. Il cocetto di orma è ua geeralizzazioe del cocetto
Appedice 2. Norme di vettori e matrici La ozioe esseziale per poter defiire il cocetto di distaza e lughezza i uo spazio vettoriale lieare è quello di orma. Il cocetto di orma è ua geeralizzazioe del cocetto
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
Lezione 2. . Gruppi isomorfi. Gruppi S n e A n. Sottogruppi normali. Gruppi quoziente. , ossia, equivalentemente, se x G Hx = xh.
 Prerequisiti: Lezioe Gruppi Lezioe 2 Z Gruppi isomorfi Gruppi S e A Riferimeti ai testi: [FdG] Sezioe ; [H] Sezioe 26; [PC] Sezioe 58 Sottogruppi ormali Gruppi quoziete L Esempio 7 giustifica la seguete
Prerequisiti: Lezioe Gruppi Lezioe 2 Z Gruppi isomorfi Gruppi S e A Riferimeti ai testi: [FdG] Sezioe ; [H] Sezioe 26; [PC] Sezioe 58 Sottogruppi ormali Gruppi quoziete L Esempio 7 giustifica la seguete
Soluzione. La curva di equazione y = 6 x è una parabola con vertice in V = (0,6)
 Sessioe ordiaria LS_ORD 5 Soluzioe ) La curva di equazioe y è ua parabola co verice i (,) e cocavià rivola verso il basso, ed ierseca l asse delle ascisse ei pui (,), B (,) come soo rappreseao: La figura
Sessioe ordiaria LS_ORD 5 Soluzioe ) La curva di equazioe y è ua parabola co verice i (,) e cocavià rivola verso il basso, ed ierseca l asse delle ascisse ei pui (,), B (,) come soo rappreseao: La figura
UN INTRODUZIONE ALL INFERENZA SU PROCESSI STOCASTICI
 UN INTRODUZIONE ALL INFERENZA SU PROCESSI STOCASTICI Il piu semplice problema (saico) di ifereza saisica paramerica e quello i cui la disribuzioe di probabilia comue a ui i umeri aleaori (a) osservabili
UN INTRODUZIONE ALL INFERENZA SU PROCESSI STOCASTICI Il piu semplice problema (saico) di ifereza saisica paramerica e quello i cui la disribuzioe di probabilia comue a ui i umeri aleaori (a) osservabili
1 Famiglia delle densità gamma
 olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
Tecnica delle misurazioni applicate Esame del 7 gennaio 2008
 Tecica delle misurazioi applicae Esame del 7 geaio 008 Problema 1. La Beloiglio rl è u impresa che alleva idusrialmee coigli e da lugo empo uilizza il magime ProRabbi 10% che ha sempre garaio, i u presabilio
Tecica delle misurazioi applicae Esame del 7 geaio 008 Problema 1. La Beloiglio rl è u impresa che alleva idusrialmee coigli e da lugo empo uilizza il magime ProRabbi 10% che ha sempre garaio, i u presabilio
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
2.5 Convergenza assoluta e non
 .5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
.5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
Il caso di coefficienti decrescenti e infinitesimi
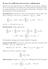 Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
1-Econometria, a.a Breve introduzione
 -Ecoomeria, a.a. 0-. Breve iroduzioe Lezioe Breve Iroduzioe. L Ecoomeria e ua disciplia che uilizza i meodi saisici per dare risposa a problemi di aura ecoomica.. I dai ecoomici o soo di aura sperimeale.
-Ecoomeria, a.a. 0-. Breve iroduzioe Lezioe Breve Iroduzioe. L Ecoomeria e ua disciplia che uilizza i meodi saisici per dare risposa a problemi di aura ecoomica.. I dai ecoomici o soo di aura sperimeale.
v = ( v 1,..., v n ).
 Lezioe del 21 ovembre. Sistemi lieari 1. Spaio vettoriale R Sia u itero positivo. ssatoمح Cosideriamo lلاiisieme R delle ple ordiate di umeri reali u (u 1, u 2,..., u ), u i R. Al posto di pla ordiata
Lezioe del 21 ovembre. Sistemi lieari 1. Spaio vettoriale R Sia u itero positivo. ssatoمح Cosideriamo lلاiisieme R delle ple ordiate di umeri reali u (u 1, u 2,..., u ), u i R. Al posto di pla ordiata
Fondamenti Segnali e Trasmissione IOL Prova in presenza 23/02/2006
 Fodamei Segali e rasmissioe IOL Prova i preseza 0006 è l igresso di u sisema lieare empo ivariae caraerizzao dalla risposa all impulso h () rec 0. 5. Disegare ale risposa all impulso e valuare quale y
Fodamei Segali e rasmissioe IOL Prova i preseza 0006 è l igresso di u sisema lieare empo ivariae caraerizzao dalla risposa all impulso h () rec 0. 5. Disegare ale risposa all impulso e valuare quale y
Def. R si dice raggio di convergenza; nel caso i) R = 0, nel caso ii)
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
2 Criteri di convergenza per serie a termini positivi
 Uiversità Roma Tre L. Chierchia 65 (29//7) 2 Criteri di covergeza per serie a termii positivi I questo paragrafo cosideriamo serie a termii positivi ossia serie a co a > 0. Si ricordi che ua serie a termii
Uiversità Roma Tre L. Chierchia 65 (29//7) 2 Criteri di covergeza per serie a termii positivi I questo paragrafo cosideriamo serie a termii positivi ossia serie a co a > 0. Si ricordi che ua serie a termii
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
2. FUNZIONE D ONDA, OSSERVABILI QUANTISTICHE ED EQUAZIONE DI SCHROEDINGER Ovvero: Gli strumenti della Meccanica Quantistica
 . FUNZIONE D ONDA OSSERVABILI QUANTISTICHE ED EQUAZIONE DI SCHROEDINGER Ovvero: Gli srumei della Meccaica Quaisica Sisema di ieresse (cosiderao come isolao: aomo/molecola Cofigurazioe del sisema: isieme
. FUNZIONE D ONDA OSSERVABILI QUANTISTICHE ED EQUAZIONE DI SCHROEDINGER Ovvero: Gli srumei della Meccaica Quaisica Sisema di ieresse (cosiderao come isolao: aomo/molecola Cofigurazioe del sisema: isieme
0.1 Esercitazioni V, del 18/11/2008
 1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 Sulla dimostrazione del Teorema di Carathéodory
 Sulla dimostrazioe del Teorema di Carathéodory Ricordiamo che la dimostrazioe del Teorema di Carathéodory procede secodo diversi passi, riassuti dal seguete diagramma: (A, P ) (B, P ) (P (Ω), P ) (C, P
Sulla dimostrazioe del Teorema di Carathéodory Ricordiamo che la dimostrazioe del Teorema di Carathéodory procede secodo diversi passi, riassuti dal seguete diagramma: (A, P ) (B, P ) (P (Ω), P ) (C, P
Sia dato un esperimento casuale individuato da uno spazio di probabilità S=
 Capiolo II CARATTERIZZAZIONE STATISTICA DEI SEGNALI II. - Fuzioi di proailià del primo ordie. Sia dao u eperimeo cauale idividuao da uo pazio di proailià S (, F,Pr) Ω. Per egale aleaorio reale iede u applicazioe
Capiolo II CARATTERIZZAZIONE STATISTICA DEI SEGNALI II. - Fuzioi di proailià del primo ordie. Sia dao u eperimeo cauale idividuao da uo pazio di proailià S (, F,Pr) Ω. Per egale aleaorio reale iede u applicazioe
Esponenziale complesso
 Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
Metodi Matematici per l Ingegneria
 Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
SUCCESSIONI SERIE NUMERICHE pag. 1
 SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
Esercitazione di AM310
 Uiversità degli Studi Roma Tre - Corso di Laurea i Matematica Esercitazioe di AM3 A.A. 8-9 - Esercitatore: Luca Battaglia Soluzioi dell esercitazioe 6 del Dicembre 8 Argometo: Misure prodotto, operatori
Uiversità degli Studi Roma Tre - Corso di Laurea i Matematica Esercitazioe di AM3 A.A. 8-9 - Esercitatore: Luca Battaglia Soluzioi dell esercitazioe 6 del Dicembre 8 Argometo: Misure prodotto, operatori
ECONOMIA MONETARIA (parte generale) Prof. Guido Ascari LEZIONE 7 LA STRUTTURA A TERMINE DEI TASSI D INTERESSED
 ECONOMIA MONETARIA (pare geerale) Prof. Guido Ascari Ao 2006-2007 2007 LEZIONE 7 LA STRUTTURA A TERMINE DEI TASSI D INTERESSED LA STRUTTURA A TERMINE DEI TASSI D INTERESSED Tioli di debio hao diverse scadeze
ECONOMIA MONETARIA (pare geerale) Prof. Guido Ascari Ao 2006-2007 2007 LEZIONE 7 LA STRUTTURA A TERMINE DEI TASSI D INTERESSED LA STRUTTURA A TERMINE DEI TASSI D INTERESSED Tioli di debio hao diverse scadeze
1-Econometria, a.a Capitolo 1
 -Ecoomeria, a.a. 04-5 Capiolo - Breve Iroduzioe - Modello di regressioe lieare -3 Due meodi di sima: Il Meodo dei Momei e il Meodo dei Miimi Quadrai -4 Proprieà geomeriche delle sime OLS -5 Le sime OLS
-Ecoomeria, a.a. 04-5 Capiolo - Breve Iroduzioe - Modello di regressioe lieare -3 Due meodi di sima: Il Meodo dei Momei e il Meodo dei Miimi Quadrai -4 Proprieà geomeriche delle sime OLS -5 Le sime OLS
(a 0, a 1, a 2,..., a n,...) (0, a 0 ), (1, a 1 ), (2, a 2 ),... (1, 3, 5, 7,...) Lezione del 26 settembre. 1. Successioni.
 Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
Tab. 1 - Studenti presenti alla lezione di statistica del per voto alla maturità
 53 Idici di variabilià 531 Iervalli di variazioe Sosiuire ua disribuzioe co u valore medio, per quao esso possa essere rappreseaivo, causa comuque ua fore perdia di iformazioe Divea perciò ecessario rovare
53 Idici di variabilià 531 Iervalli di variazioe Sosiuire ua disribuzioe co u valore medio, per quao esso possa essere rappreseaivo, causa comuque ua fore perdia di iformazioe Divea perciò ecessario rovare
Analisi Matematica I Soluzioni del tutorato 2
 Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
P(X = k) = (k 1). 2 Infatti, le uniche sequenze di lunghezza k (di T e C) possibili sono
 Prima Prova Itermedia testo co soluzioi 5 Aprile 09 Elemeti di Probabilità e Statistica, Laurea Trieale i Matematica, 08-9 M Romito, M Rossi Problema 0 Ua moeta equa viee laciata fio alla prima volta i
Prima Prova Itermedia testo co soluzioi 5 Aprile 09 Elemeti di Probabilità e Statistica, Laurea Trieale i Matematica, 08-9 M Romito, M Rossi Problema 0 Ua moeta equa viee laciata fio alla prima volta i
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
SOLUZIONI COMPITO del 10/01/2014 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A
 SOLUZIONI COMPITO del //4 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio Poedo z = x + iy, otteiamo iz + z = ix y + x xy y, da cui si ricava e iz +z = 3 e xy y = 3 xy y = log 3 Pertato, avremo
SOLUZIONI COMPITO del //4 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio Poedo z = x + iy, otteiamo iz + z = ix y + x xy y, da cui si ricava e iz +z = 3 e xy y = 3 xy y = log 3 Pertato, avremo
Capitolo Parte V
 Capitolo 1 1.1 Parte V Exercise 1.1. Sia X ua variabile aleatoria, defiita su (Ω,P a valori i E, quasi certamete costate, ossia esiste c E tale che P(X = c = 1. Si mostri che esiste u uico elemeto c E
Capitolo 1 1.1 Parte V Exercise 1.1. Sia X ua variabile aleatoria, defiita su (Ω,P a valori i E, quasi certamete costate, ossia esiste c E tale che P(X = c = 1. Si mostri che esiste u uico elemeto c E
Si estendono, in modo non banale, le operazioni di somma e prodotto da Q ad R; con queste operazioni R e un campo.
 1 Numeri reali 1.1 Numeri reali Per umero reale itediamo u qualsiasi umero decimale, co u umero di cifre dopo la virgola fiito o ifiito, periodico o o periodico; possiamo pesare u umero decimale co u umero
1 Numeri reali 1.1 Numeri reali Per umero reale itediamo u qualsiasi umero decimale, co u umero di cifre dopo la virgola fiito o ifiito, periodico o o periodico; possiamo pesare u umero decimale co u umero
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Proprietà asintotiche stimatori OLS e statistiche collegate
 Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE
 DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 21 DICEMBRE 2010 1. Sviluppi di Laplace Proposizioe 1.1. Sia A M, (K), allora per ogi idice i = 1,..., fissato vale lo sviluppo
DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 21 DICEMBRE 2010 1. Sviluppi di Laplace Proposizioe 1.1. Sia A M, (K), allora per ogi idice i = 1,..., fissato vale lo sviluppo
