FISICA TECNICA INDUSTRIALE
|
|
|
- Cesare Miele
- 9 anni fa
- Visualizzazioni
Transcript
1 UNIVERSITA DI CATANIA FACOLTA DI INGEGNERIA FISICA TECNICA INDUSTRIALE VOLUME SECONDO: TERMOFLUIDODINAMICA DEFLUSSO MONODIMENSIONALE MOTO ADIABATICO NEI CONDOTTI A SEZIONE VARIABILE MOTO ADIABATICO NEI CONDOTTI CILINDRICI MOTO ISOTERMO NEI CONDOTTI CILINDRICI MOTO DI RAYLEIGT CIRCOLAZIONE DEI FLUIDI BIFASE STABILITA DEI TUBI BOLLITORI PROF. ING. GIULIANO CAMMARATA PROF. ING. LUIGI CAMMARATA DIPARTIMENTO DI INGEGNERIA INDUSTRIALE E MECCANICA SEZIONE DI ENERGETICA INDUSTRIALE ED AMBIENTALE AGGIORNAMENTO DEL //
2 ii FILE: FISICA TECNICA VOL - COMPLEMENTI DI TERMOFLUIDODINAMICA.doc AUTORI: GIULIANO CAMMARATA E LUIGI CAMMARATA DATA: OTTOBRE [email protected] [email protected] Il reente volume uò eere liberamente coiato e diffuo dagli Allievi er uo didattico e a condizione che rimangano invariati i riferimenti ora indicati. PROF. ING. GIULIANO CAMMARATA
3 iii INTRODUZIONE Le moderne macchine er generazione di otenza meccanica i baano emre iù ulle turbine, ia a vaore che a ga. Quete ono organi di notevole comleità rogettuale che coinvolge numeroi diciline quali la Fiica Tecnica, le Macchine e la Fluidodinamica. Quet ultima dicilina non è inerita nell ordinamento della notra Facoltà e ertanto reta al di fuori dei normali ercori di tudio che gli Allievi Ingegneri Meccanici oono cegliere. La Meccanica dei Fluidi è toricamente imotata come Idraulica con nome aarentemente cambiato e non core gli argomenti relativi ai fluidi comrimibili e quindi tiici della Fluidodinamica. In queto breve oucolo i deidera affrontare alcuni dei concetti fondamentali della Fluidodinamica neceari er le alicazioni imiantitiche e macchinitiche. Si affronteranno, ertanto, i roblemi della comrimibilità dei fluidi e dei loro effetti nel moto in condotti a ezione variabile (equazioni di Hugoniot) e a ezione cotante. Sono intereanti i moti di Fanno e di Raileigth e i concetti di arametri di attrito e di lunghezza maima nel moto dei fluidi comreibili. Si laciano fuori da queta trattazione tutti gli altri (numeroi) roblemi di fluidodinamica che intereano altri cami dell Ingegneria (quale, ad eemio, aeronautica e/o aziale). Gli argomenti qui elezionati, quindi, ono il minimo indienabile er la moderna formazione di un ingegnere meccanico e trovano immediata alicazione nei cori di Macchine ed Imianti.. Del tutto nuovo è oi il caitolo u fluidi bifae (cioè di liquidi in reenza di una fae aeriforme o anche del rorio vaore) che trova alicazioni imortanti e fondamentali nel rogetto di imianti (ad eemio caldaie, generatori di vaore, turbine, ). Si oerva ubito che gli argomenti trattati richiederebbero da oli interi cori annuali. Tuttavia, data la natura del Coro, i ono viluati olamente gli argomenti ritenuti fondamentali rimandando l arofondimento ai teti in letteratura. Catania //. PROF. ING. GIULIANO CAMMARATA
4 . FLUIDI COMPRIMIBILI - DEFLUSSO MONODIMENSIONALE Le grandezze fiiche che caratterizzato il moto di un mezzo fluido variano, in generale, tridimenionalmente ertanto elaborare una teoria del moto a tre variabili euleriane riulta di enorme comleità anche nell iotei di regime tazionario. Sovente i fa riferimento allo tudio del defluo bidimenionale cegliendo con oortuno criterio la giacitura del iani di riferimento in modo che le variazioni del comortamento del fluido lungo la terza dimenione iano tracurabili. Frequentemente quanto detto riulta oibile o tutt al iù i rende necearia qualche correzione da aortare ai riultati lungo la dimenione tracurata; diveramente i uò interretare il fenomeno u iù iani aralleli interolando oi i riultati a quote intermedie, coì facendo il moto viene a erdere una dimenione, e quindi una variabile euleriana, coicché le variazioni delle grandezze fiiche caratterizzanti il moto del fluido vengono coniderati olo lungo le linee di corrente e erendicolarmente ad ee. Tutte le volte che le variazioni del comortamento del fluido in direzione erendicolare alle linee di corrente non ono rilevanti di uò fare riferimento alla teoria monodimenionale del defluo alvo, anche in queto cao, ad aortare oortune correzioni di tio bidimenionale; è in genere lecito ricorrere a queta emlificazione nel moto lungo i condotti, emre a condizione che le dimenioni traverali iano iuttoto iccole rietto alla lunghezza del condotto teo e ciò equivale a uorre che lungo le linee di corrente congruenti i fenomeni avvengano identicamente, in tale iotei è ufficiente tudiare quel che avviene lungo la linea mediana dell effluo (eo coincidente con l ae del condotto) er oi etraolare i riultati, eventualmente corretti, a tutte le altre linee di corrente. La teoria monodimenionale imlica nel regime tazionario una ola variabile euleriana e i reenta emlice ed efficace, caace di fornire una viione eenziale dei fenomeni; occorre erò dire che ea i reenta concettualmente inufficiente in quanto nel moto di un fluido non uò eere tracurata l eitenza degli attriti i quali roducono variazioni di quantità di moto che ono caua di indeiderate ditribuzioni di velocità nella direzione normale a quella del defluo. D altra arte le forze d attrito, avendo carattere deciamente non conervativo, non ono funzione della ola oizione er cui, anche nel regime tazionario, non ono direttamente valutabili alla maniera euleriana ne tanto meno a quella lagrangiana ne conegue che entrambi i criteri di analii cinematica debbano limitari in ratica, ur mantenendo il loro rigore, al olo tudio dei moti ideali. Tale limitazione uò eere tuttavia uerata mediante certi artifici conitenti nel coniderare a otenziale, lungo la regione intereata al defluo, anche le forze di attrito valutandone globalmente, e erimentalmente, il lavoro diiato. Ma e tale criterio uò eere accettato ai fini del bilancio energetico eo non i reta a definire con emlicità i riflei degli attriti ulla ditribuzione delle velocità coicché l artificio rimane valido olo a condizione di limitare il camo di moto ad un eiguo tubo di fluo (che al limite degeneri in una linea di corrente) u ogni ezione del quale la velocità oa riteneri cotante. Queta è robabilmente la ragione che orta a definire euleriana la teoria monodimenionale del defluo mentre in realtà il criterio euleriano è di carattere generale in quanto i etende alle tre dimenioni dello azio; in effetti olo in forma monodimenionale il metodo euleriano riulta alicabile, quando i tratta di defluo con attrito, in virtù della redetta oibilità di valutare, ia ure er via emirica, il lavoro diiato in funzione della ucceione delle velocità nel camo di moto. Facendo riferimento al ga erfetto, aroimazione valida er ga a media e baa denità, viene qui reo in eame il moto monodimenionale con e enza attrito nei deflui interni er i quali le variazioni di denità ono della maima imortanza er individuare la natura della corrente; queto modello fiico anche e, come già detto, embra iuttoto limitato aroima molto bene la realtà di molte correnti fluide. L iotei di monodimenionalità reuone quindi che tutte le grandezze fiiche intereate (reione, denità, temeratura, velocità, ecc.) abbiano ditribuzione uniforme in qualiai ezione del condotto.
5 .. COMPRIMIBILITÀ ED ESPANSIONE La variazione volumetrica di un fluido influice ull andamento del moto in maniera alquanto comlea ed anche nel defluo in condotti cilindrici, dove er fluidi a denità cotante il moto uò eere coniderato mediamente uniforme, i cambiamenti di denità fanno variare la velocità anche lungo la direzione di avanzamento; rorio quete variazioni di denità e velocità ono quelle che determinano la neceità di una trattazione di tale defluo ditinta da quella volta er i fluidi incomrimibili in quanto in tale circotanza il camo dinamico e quello termico interagicono mutuamente. Lo tudio del comortamento di un fluido comrimibile in moto neceita ertanto della conocenza dell equazione cinetica di tato e quella del roceo termodinamico reonabile della variazione volumetrica uddetta. Viene qui dedicata articolare attenzione ad defluo adiabatico, ia nei condotti a ezione variabile che in quelli cilindrici, vito che nella gran arte dei roblemi tecnici è quello che reenta interee maggiore; viene erò anche analizzato il moto iotermo nei condotti cilindrici anche e la realizzazione di tale defluo, come i avrà modo di vedere, uò avvenire olo a articolari condizioni. E noto dalla Termodinamica che lo tato fiico di una otanza ura ed omogenea è decritto attravero l equazione: f (, v, T) [.] oure in forma elicita da una delle equazioni: v v (, T ) le quali differenziate divengono: ( v, T ) T T (, v) ovvero in termini di variazione relativa: che oono eere critte nella forma: [.] v v dv dt d T T d dt dv T v v T T dt dv d v v dv v v dt v v T v T T v d d dt dv T v v T dt dv d T T v T T T
6 3 nelle quali il termine: dv dt T d v d dt dv v dt dv T T T T v v T rende il nome di coefficiente di eanione iobara ed erime la variazione relativa di volume ecifico al variare della temeratura in un roceo a reione cotante; il termine: v T v T viene denominato coefficiente di comrimibilità ioterma, eo indica la variazione relativa di volume ecifico al variare della reione in un roceo a temeratura cotante; inoltre: [.6] T v rareenta il coefficiente di tenione iovolumico ed erime, in una traformazione a volume cotante, l effetto della temeratura ulla reione. Tale coefficiente e quello di eanione iobara ono in generale funzioni della reione e della temeratura. Le [.3] cotituicono le equazioni differenziali di tato relative ad un fluido qualiai allo tato termodinamico monofae. I coefficienti termodinamici ora definiti non ono indiendenti tra loro, infatti tenuto conto che er una funzione del tio (.) i uò crivere: ovvero anche: d v T v T T v v T v T T v [.4] [.5] e quindi dalle (.4), (.5) e (.6) i ottiene: [.7] T [.3] relazione che conente il calcolo di uno dei coefficienti noti che iano gli altri due. Se il fluido in eame è un ga erfetto er i coefficienti eanione e di tenione i crive: RT R v T v RT R T v v v Seo detto anche coefficiente di dilatazione cubica dei materiali.
7 4 il che equivale a crivere: [.8] T oia tali coefficienti ono indiendenti dalla reione. Integrando la rima delle [.3] lungo un roceo iobaro e la econda lungo un roceo iovolumico i ottiene riettivamente: T v v ex dt T T ex dt T i oerva che e l intervallo di temeratura non è grande i coefficienti e oono riteneri con buona aroimazione cotanti ertanto le uddette relazioni divengono: v v ex T T ex T T [.9] inoltre viluando in erie e tracurando i termini di ordine ueriore i uò crivere: v v T T T T [.] come temeratura iniziale i uò coniderare quella del ghiaccio fondente ari a 73,5 K. Per grandi intervalli di temeratura le uddette ereioni oono ancora eere ritenute valide a condizione che e iano da intendere come valori medi lungo tali intervalli. Semre nel cao di ga erfetto er il coefficiente di comrimibiltà iotermo i ha: RT RT T v v ovvero anche: T [.] eo quindi non diende dalla temeratura. La comrimibilità di un fluido uò anche avvenire ioentroicamente, in tal cao dalle equazioni del rimo e econdo rinciio della termodinamica riulta: du dv dh v d T ovvero nella forma equivalente: u h v v quindi effettuando il raorto: e crivendo nella forma: h h v v u u v
8 5 v h v u i uò definire un altro coefficiente termodinamico di variazione volumetrica dato dalla: v v [.] denominato coefficiente di comrimibilità ioentroica il quale rareenta la variazione di volume ecifico al variare della reione in un roceo ad entroia cotante; tale coefficiente, come i avrà modo di vedere oco iù avanti, è legato alla velocità di roagazione delle onde di reione in un mezzo fluido. Pertanto la relazione: h [.3] u rareenta l equazione differenziale di una traformazione ioentroica, nota dalla termodinamica, ed erime la variazione delle rorietà calorifiche, entalia ed energia interna, del fluido in funzione delle ue rorietà termiche, reione e volume ecifico, in un roceo ioentroico. La quantità: h u rareenta aunto l eonente dell ioentroica, icché er un fluido qualiai il coefficiente di comrimibilità ioentroico aume la forma: [.4] e il fluido è un ga erfetto riulta: h dh c u du c ertanto la [.4] diviene: v [.5] e dal confronto con la [.] ne riulta: T [.6] oia il coefficiente adiabatico è dato dal raorto tra i due coefficienti di comrimibilità iotermo ed ioentroico, riettivamente. Si oerva altreì che la uddetta ereione, come i uò dimotrare, ha validità anche er un fluido qualiai. I ga hanno la tendenza a comrimeri molto iù elevata rietto a quella dei liquidi, in condizioni tandard di reione e temeratura riulta dell ordine di -5 m²/n. I liquidi oongono maggiore reitenza alle azioni che tendono a comrimerli. Integrando la rima delle [.3] er un roceo iotermo i ottiene: v v ex T d anche qui coniderando non ecceivo l intervallo di reione i uò crivere: v v ex T [.7] quindi viluando in erie e tracurando i termini di ordine ueriore al rimo i ha:
9 6 v v T [.8] 9 Per i liquidi iù comuni T è dell ordine di m / N, in articolare nel cao dell acqua, alle medeime condizioni di reione e temeratura, eo vale circa 5 m / N oia ventimila volte iù iccolo del corriondente valore che comete al ga, di coneguenza atteo il iccolo valore di T dalla [.8] i deduce che il valore di v è raticamente coincidente con quello di v e ciò conente di coniderare i liquidi come fluidi incomrimibili. Tuttavia anche i ga oono eere trattati allo teo modo dei liquidi tutte le volte che il loro movimento non comorta enibili variazioni di reione. L iotei di incomrimibilità orta ovviamente ad una fondamentale emlificazione negli vilui analitici e fornice al temo teo riultati di comleta attendibilità er molti roblemi ratici. Non i deve erò dimenticare che il fluido incomrimibile cotituice una emlice atrazione, analoga a quella del coro rigido; in un fluido reale e er rocei iotermici ad ogni variazione di reione i aocia una variazione dell energia otenziale elatica connea ai corriondenti cambiamenti di volume e tale variazione di energia equivale al lavoro meccanico comiuto dalle reioni eterne ulla uerficie di contorno durante la variazione volumetrica. L iotei di incomrimibilità reuorrebbe che la reione del fluido otee variare indiendentemente da un effettivo lavoro delle reioni eterne; aume ertanto una certa imortanza tabilire entro quali limiti è effettivamente lecito ammettere l incomrimibilità dei fluidi... VELOCITÀ DEL SUONO E NUMERO DI MACH Si conideri un tubo cilindrico nel quale un itone viene otato con un imrovvio movimento x da initra vero detra; a eguito di tale otamento i viene a generare nel fluido immediatamente vicino al itone un aumento di reione il quale non i manifeta all itante in tutti i unti del condotto, eendo il fluido dotato di inerzia e di elaticità, benì i roaga, vero detra, con velocità c; tale velocità di roagazione di queta erturbazione rovocata nel fluido viene denominata velocità del uono. dw d d c a c - dw c.b Figura
10 7 Per otere determinare queta velocità i conideri un riferimento olidale con l onda di reione, in tal cao il fluido corre da detra vero initra e aando attravero il fronte d onda la ua velocità aa dal valore c al valore c dw. Nell iotei che il fluido i muove di moto tazionario rietto al riferimento olidale col fronte d onda alicando l equazione di bilancio di quantità di moto in due ezioni immediatamente a monte ed a valle di queto i ha: c d ( d)( c dw) e tracurando infiniteimi di ordine ueriore i uò crivere: d c d c dw Alicando inoltre l equazione di bilancio di maa i crive: c ( d)( c dw) che diviene: c d dw e otituita nella recedente fornice: d c d c d dalla quale i ottiene: d c [.9] d Se i tiene conto che la velocità di roagazione delle vibrazioni onore nel mezzo fluido è molto grande neuno cambio di calore, anche e iccolo, riece a roduri nelle zone di comreione e di dereione dell onda da una arte ed il mezzo dall altra coicché le vibrazioni del mezzo dovute alla roagazione dell onda i oono coniderare adiabatiche ed ioentroiche, ertanto la [.9] deve eere critta: c [.] nota come equazione di Lalace. L iotei che ha condotto alla [.] è che l ecceo di reione ia iccolo, al limite infiniteimo; in realtà i dimotra che non eendo tale incremento infiniteimo la velocità di roagazione effettiva c ' differice dal valore fornito dalla uddetta ereione, ovvero i verifica che c' c er incrementi di reione oitivi e vicevera er incrementi negativi. Il valore di c calcolato con la [.] viene anche denominato velocità del uono di frequenza zero, infatti quando le vibrazioni onore di frequenza ufficientemente alta i roagano in un mezzo fluido l iotei ulla loro natura ioentroica cea di eere valida, er tali ituazioni la velocità del uono diende anche dalla frequenza. Tuttavia er un intervallo di frequenze che reentano ratico interee l equazione di Lalace fornice valori di c che, a meno di qualche centeimo di ercento, coincidono con i dati erimentali. Erimendo la [.] in termini di volume ecifico i ha: e tramite la [.4] i ottiene: c v v v c [.] Se il fluido è un ga erfetto, tenuto conto dell equazione di tato, la uddetta relazione diviene: c R T [.]
11 8 la velocità del uono diende in tal cao dalla ola temeratura, mentre in un ga reale c è funzione anche della reione. Oervando la [.] i deduce che ammettere l incomrimibilità equivale ad aegnare valore infinito alla velocità del uono, ciò ignifica che ogni iccola variazione di reione rovocata in un unto qualiai della maa fluida venga itantaneamente rientita in tutti gli altri unti. Nell eemio citato il fluido è comrimibile er cui eo non i ota ubito alla velocità del itone, come ciò invece avrebbe luogo e al oto del fluido il itone ingee un cilindro di metallo. Affinché l iotei di incomrimibilità non dia luogo a contraddizioni troo evidenti le dimenioni della maa fluida devono eere abbatanza limitate in modo tale da otere ritenere tracurabile il temo effettivamente neceario er la tramiione delle variazioni di reione fino ai unti iù lontani, oure tali variazioni riultino coì lente e graduali ed il temo redetto ia breviimo. Nel cao di liquidi arà allora neceario mettere in conto la comrimibilità nello tudio dei fenomeni che riguardano l inizio e l arreto del movimento entro lunghi condotti (colo d ariete) e non e ne otrà recindere nemmeno nel cao di condotti brevi quando l avviamento o l arreto del moto avvengono in un intervallo di temo etremamente breve. La comrimibilità deve orattutto eere rea in coniderazione allorquando il fluido acquita velocità che i avvicina al valore di c, ciò i verifica con relativa frequenza nei rocei gadinamici ed aerodinamici ia erché la velocità del uono negli aeriformi è aai minore di quella che comete ai liquidi (da un quarto ad un quinto, circa, di quella dell acqua) e ia erché in eno all aria è iù facile raggiungere velocità di traorto molto elevate. L eitenza di queta velocità di roagazione è reonabile di una fondamentale ditinzione tra il regime ubonico (w < c) ed il regime ueronico (w > c), tale ditinzione i rende necearia in quanto il comortamento termodinamico del fluido nei due regimi di moto è aai divero. Si conideri a tal rooito una corrente fluida in moto a ia w la velocità in un unto qualiai in corriondenza del quale lo tato termodinamico è caratterizzato dai valori di,v,t ; allora il raorto adimenionale: w M [.3] c viene denominato numero di Mach e ta ad indicare il raorto tra la velocità del fluido in un unto, in un dato tato termodinamico, e la velocità del uono nel medeimo unto e allo teo tato; ertanto il regime di defluo di un fluido, al variare della velocità, viene coì claificato: M < regime ubonico M = regime onico M << regime incomrimibile M > regime ueronico M >> regime ieronico Come vito olo er M (in ratica all incirca M,3 ) i uò ritenere accettabile l iotei di incomrimibilità; er valori elevati della velocità w non i uò tracurare lo tato termodinamico del fluido il quale arà ottooto ad eanioni e comreioni..3. STATI TERMODINAMICI PARTICOLARI E noto che i valori di,v,t individuano lo tato termodinamico di un fluido e queta terna di grandezze in un unto qualiai, in corriondenza del quale il fluido è dotato di velocità w, rareenta uno tato termodinamico generico comunemente chiamato tato locale; queto tato non mette in evidenza neun articolare circa il comortamento fiico del fluido. Si conideri adeo un defluo adiabatico enza cambio di lavoro e con variazione di energia otenziale tracurabile; alicando l equazione di bilancio energetico fra uno tato locale (h,w) ed uno tato ( h, w ) riulta:
12 9 h w h [.4] queto tato fiico articolare viene denominato tato di ritagno ovvero anche tato di arreto adiabatico ed h rareenta l entalia di ritagno oia quel valore di entalia che il fluido avrebbe e a artire da condizioni locali foe ortato adiabaticamente fino alla condizione di velocità nulla. Se ( h, w) e ( h, w ) ono due tati locali e e il fluido cambia calore l equazione di bilancio energetico, tenuto conto della recedente, i uò crivere: w w q h h h h [.5] dalla quale i oerva che l entalia di ritagno rimane cotante e non vi è cambio di calore con l eterno, anche in reenza di fenomeni diiativi; ea aumenta, o diminuice, nel cao di omminitrazione, o ottrazione, di calore al fluido. L entalia di ritagno è quindi una grandezza rareentativa del contenuto energetico del fluido, recindendo dall effettiva utilizzazione di tale energia al fine di ottenere lavoro. Nel cao di ga erfetto la [.4] diviene: T w T [.6] c che rareenta la temeratura di ritagno, definita in maniera analoga a quanto fatto er l entalia; in tal cao dalla [.5] i ha: q c T T [.7] ertanto anche la temeratura di ritagno è rareentativa del contenuto energetico er un ga erfetto e varia olo e vi è cambio di calore con l eterno. In un defluo adiabatico i ha emre: h co t. T co t. Scrivendo la [.6] nella forma: T w w T c T RT e quindi er le [.] e [.3] riulta: T M [.8] T oia er un dato ga il raorto tra la temeratura di ritagno e quella locale è funzione del numero di Mach. Inoltre eendo: dalla [.8] i ottiene: T T M [.9] che rareenta la reione di ritagno, oia quella reione che il ga avrebbe e artendo da condizioni locali (,w) foe ortato ioentroicamente fino alla condizione di velocità nulla. Facendo riferimento all equazione di bilancio energetico in forma meccanica e tracurando ancora variazioni di energia otenziale i uò crivere:
13 w w d lr e uoto che gli etremi di integrazione iano due tati di ritagno tale ereione diviene: d lr [.3] tale eguaglianza è dovuta al fatto che calcolare l integrale uddetto nelle condizioni di ritagno equivale ad eeguire il calcolo coniderando, ad ogni ao di integrazione, reione e denità nelle condizioni di ritagno. Nel cao di ga erfetto e e queto non cambia calore la [.3] i crive: d lr RT RTln [.3] dalla quale riulta: R ex l RT [.3] ertanto nel moto adiabatico la reione di ritagno non è una cotante, lo diviene olo che il defluo avviene ioentroicamente, ovvero: l R icché la reione di ritagno è una grandezza rareentativa del contenuto entroico del ga e quindi dalla ua caacità di traformare in lavoro meccanico l energia oeduta. Eendo inoltre: ancora dalla (.8) riulta: T T M [.33] i ottiene la denità di ritagno, definita allo teo modo della reione di ritagno e come tale è una cotante olo nel defluo ioentroico. In queto cao arebbe: T T ed eendo cotante la temeratura di ritagno arà anche: Le equazioni [.8], [.9] e [.33] dimotrano che nel cao di deflui adiabatici reveribili eite un legame univoco tra il numero di Mach ed i raorti fra le grandezze termodinamiche locali e quelle di ritagno. Si uò concludere che lo tato di ritagno cotituice uno tato di arreto adiabatico er entalia e temeratura mentre er reione e denità eo è uno tato di arreto ioentroico. Si faccia ancora riferimento alla [.6] che uò eere mea nella forma: ovvero anche: w RT RT w c c [.34]
14 dalla quale i oerva che la velocità locale del ga diminuice all aumentare della velocità del uono e vicevera; da qui i deduce che in corriondenza di un dato unto, caratterizzato da un dato tato termodinamico, le due velocità hanno eguale valore icché: w c w c in tale tato il numero di Mach diviene unitario ed il valore comune alle due velocità vale: wc c [.35] che rende il nome di velocità critica. Eendo noto lo tato di ritagno la temeratura critica i uò determinare dalla [.8], icché: Tc T [.36] ed è ovvio che tale valore da olo non è ufficiente a definire uno tato termodinamico, ono neceari i valori di reione e denità er i quali, come i è vito, i rende necearia la condizione di ioentroicità del defluo; ertanto dalla [.9] i erviene alla: e dalla [.33] i ha: c c [.37] [.38] Quete ultime tre equazioni individuano lo tato termodinamico corriondente alla condizione di M che viene coì denominato tato critico. Partendo da uno tato locale (,, T, w) combinando le uddette relazioni con le [.8], [.9] e [.33] i uò crivere: Tc T M c M c M [.39] lo tato critico ioentroico è ertanto uno tato termodinamico corriondente alla condizione M ottenuto a artire da condizioni locali o di ritagno. Eendo il defluo ioentroico i valori di Tc, c, c ono cotanti in ogni unto del camo di moto. Queto articolare tato termodinamico è fondamentale nello tudio dell effluo dei ga lungo i condotti a ezione variabile (ugelli e diffuori) nei quali, come i avrà modo di vedere qui di eguito, ia er geometria ia er condizioni di moto l entroia i uò ritenere cotante, almeno in rima aroimazione. Dalla [.34] i oerva che nel moto ioentroico la velocità ha un limite ueriore che i ottiene allorquando la velocità locale del uono diviene nulla, in cao i uò crivere: w c max [.4]
15 queta velocità in ratica arebbe realizzata olo allo zero aoluto di temeratura in corriondenza del quale l entalia del ga arebbe totalmente traformata in energia cinetica; tale valore in condizioni ioentroiche non uò quindi eere raggiunto. Facendo riferimento alla [.4] la [.34] aume la forma: w w c [.4] c max la quale motra come tutti i oibili regimi di moto ora decritti er un ga erfetto giacciono u un ellie di ai ( wc, ), come è illutrato nella Figura. c c M M M M M w max w Figura.4. FATTORE DI COMPRIMIBILITÀ Si faccia riferimento all equazione energetica er un fluido incomrimibile la quale, tracurando variazioni di energia otenziale e le reitenze er attrito, i crive: w eendo la reione di ritagno del fluido; crivendo tale equazione nella forma: w [.4] i oerva che la reione dinamica del fluido i identifica come differenza tra la reione di ritagno e quella locale; non i uò dire altrettanto nel cao di un fluido comrimibile. Si conideri infatti il raorto: f [.43] w che viene denominato fattore di comrimibilità, da eo i deduce che e il fluido è incomrimibile i ha f mentre e il fluido è comrimibile deve eere f e ertanto i ha: w [.44]
16 3 Al fine di valutare la differenza di reione i conideri un ga erfetto che i muove ioentroicamente, in tal cao i uò crivere: di coneguenza la [.43] diviene: e quindi er la [.9] riulta: f f w M M M M [.45] ertanto er un dato ga, ovvero er un aegnato valore di, il fattore di comrimibilità è funzione del olo numero di Mach locale. Sviluando in erie binomiale il termine in arentei i uò crivere: e la [.45] diviene: ( ) M M M M O( M ) 8 48 M 4 6 f M O( M ) [.46] 4 4 icché dalla [.43] i ottiene la differenza di reione richieta, oia: w M 4 6 M O( M ) 4 [.47] Se il moto del ga è lontano dal regime onico, oia er M, i termini alla econda ed alla quarta otenza delle ultime due relazioni divengono iccoliimi di coneguenza dalla [.46] riulterebbe che f, oia il fluido i uò coniderare incomrimibile, mentre la i identificherebbe con la [.4]. Tale riultato riulta alquanto ignificativo, il defluo adiabatico dei ga attorno ad oggetti e lungo i condotti i uò ritenere incomrimibile finché il numero di Mach è iccolo, M,3 circa, ottenendo coì nel modello a denità cotante una indubbia emlificazione di calcolo.
17 4. MOTO ADIABATICO NEI CONDOTTI A SEZIONE VARIABILE Allorquando i fluidi i comortano come comrimibili i hanno intereanti comortamenti er il loro moto all interno di condotti a ezione variabile che qui i reentano... MOTO ISOENTROPICO: VELOCITÀ E PORTATA SPECIFICA Nello tudio dei condotti a ezione variabile il roblema che in ratica i one è quello di analizzare la loro conformazione e le condizioni oerative necearie al fine di ottenere mentre il fluido cambia lavoro, ed eventualmente calore, che eo ubica determinate traformazioni; vicevera di individuare le traformazioni che il fluido ubice nell attraverare un condotto di forma aegnata ed in determinate condizioni. I condotti che vengono qui eaminati ono uddivii in due clai fondamentali dove il fluido egue un comortamento totalmente divero, i definice infatti: - ugello un condotto che, a recindere dalla ua forma geometrica, conente di ottenere un incremento della velocità a ee di una diminuzione di reione e denità; - diffuore un condotto che, recindendo dalla forma geometrica, conente di realizzare una diminuzione della velocità a vantaggio di un aumento di reione e di denità. Si vedrà nel roimo aragrafo che la modalità del defluo in queti articolari condotti diende ecluivamente dal regime di artenza della corrente fluida ur conervando la tea geometria. Si conideri allora un fluido che viaggia in regime tazionario in un condotto a ezione variabile er il quale iano riettate le eguenti iotei: - areti termicamente iolate, - non vi ia cambio di lavoro meccanico, - le variazioni di energia otenziale dovute al camo gravitazionale iano tracurabili, - defluo monodimenionale. La rima iotei è enz altro verificata in quanto trattandoi di condotti corti ed avendo a che fare con velocità elevate ne riulta che la quantità di calore cambiata attravero le areti è molto iccola ed in ratica quai emre tracurabile, la terza iotei i ritiene accettabile aunto erché le alte velocità danno luogo a variazioni di energia cinetica molto grandi rietto e quelle di energia otenziale, anche la quarta iotei i ritiene valida e il condotto è ad ae rettilineo o comunque oco incurvato di modo che i filetti fluidi iano aralleli e diretti econdo l ae. La econda iotei non viene er il momento rea in coniderazione. Sotto le uddette condizioni l equazione di bilancio di energia nella forma termodinamica i crive: dalla quale i ricava: w w h h w w h h [.] che conente la determinazione della velocità del fluido in una ezione generica del condotto a artire da uno tato locale noto, caratterizzato dai valori ( h, w ), e viene denominata velocità adiabatica; mentre l equazione di bilancio di energia nella forma meccanica i crive: dalla quale riulta: w w d l R d w w l R [.]
18 5 che conente di determinare la velocità in una generica ezione del condotto a artire dallo tato locale noto caratterizzato dai valori (, w ). Le equazioni [.] e [.] ono di carattere generale nel eno che ono valide er qualiai fluido, anche e er dare forma riolutiva alla econda ono necearie la conocenza del roceo termodinamico e del lavoro delle forze d attrito altrimenti il roblema riulta due volte indeterminato. Se il condotto, ugello o diffuore, è convenientemente breve e la uerficie lambita dal fluido è ben levigata la traformazione i uò coniderare raticamente reveribile in quanto il termine l R diviene iuttoto iccolo rietto al valore che aume l energia cinetica nella ezione finale e ertanto uò eere coniderato tracurabile, almeno in rima aroimazione, di coneguenza la (.) diviene: d w w [.3] Si uò dire ertanto che la [.] è valida nel cao di roceo reveribile ed irreveribile ma neceariamente adiabatico mentre la [.3] è alicabile a qualunque roceo urché neceariamente reveribile il quale e è anche adiabatico la uddetta ereione viene denominata velocità ioentroica. Facendo riferimento alla [.] e e il fluido è un ga erfetto i uò crivere: ovvero anche: w w c T T T w w RT T e tenuto conto ia dell equazione di tato che l equazione di traformazione in funzione di reione e temeratura i ottiene: w w RT ovvero la velocità ioentroica del ga erfetto; è immediato verificare che alla uddetta equazione i uò ervenire anche attravero la [.3] otituendo nell integrale l equazione di traformazione in funzione di reione e denità. La ortata di maa ecifica i uò ottenere dalla relazione: m w A nella quale eendo: RT e tenuto conto della (.4) i erviene alla relazione: m A RT w RT oia la ortata ecifica ioentroica di un ga erfetto. Si oerva che qualora la velocità w non ia nota i uò mettere la [.4] nella forma: [.4] [.5]
19 6 inoltre otendo crivere: w w RT w w w tenuto conto dell equazione di bilancio di maa: w w w A w A e dell equazione di traformazione la recedente ereione diviene: e otituendo nella [.6] i ottiene: A w w w A RT w A A in tal cao la velocità ioentroica viene mea in relazione con la geometria del condotto; er la ortata di maa i uò allora crivere: A A m A R T tale ereione conente anche di riolvere il roblema invero, oia quello di determinare l area della ezione di ucita del condotto, nota che ia quella in ingreo, affinché ia garantita una data ortata di maa di ga comatibile con lo tato termodinamico iniziale e la reione finale. Per emlificare le ereioni uddette i otrebbe coniderare una articolare ezione del condotto ove vi iano condizioni tali er le quali ia nulla, o quanto meno tracurabile, la velocità del fluido; nella maggior arte delle ituazioni reali tale ezione non eite erò ad ea i uò emre fare riferimento in quanto noto che ia il uo tato termodinamico (,, T, w ) i uò emre determinare lo tato di ritagno ad ea aociato (,, T ) attravero le equazioni [.8], [.9] e [.33] icché la [.4] w RT mentre er la ortata di maa ecifica riulta: [.6] [.7] [.9] [.8]
20 7 m A R T Se i tiene conto della [.9] er la uddetta equazione i uò crivere: R T m A R e quindi emlificando ed ordinando i ottiene: [.] T M m M A R T M M ( ) [.] la quale erime la ortata ecifica in funzione dello tato termodinamico di ritagno e del numero di Mach; tale relazione cotituice una forma alternativa alla [.] ed ha un imortanza notevole nel camo della termofluidodinamica alicata alle macchine. Uno dei roblemi fondamentali nello tudio del comortamento degli ugelli e diffuori è quello di determinare il valore maimo di ortata ecifica che uò defluire nel condotto in eame e iù reciamente a quale tato termodinamico tale valore corrionde. Con riferimento alla [.] i oerva che la ortata ecifica varia al variare della reione ed il valore maimo i ottiene allorquando riulta maimo il termine in arentei quadra er il quale, in corriondenza di una data reione, deve eere nulla la derivata rima: dalla quale i ottiene: c ertanto la maima ortata ecifica i raggiunge in corriondenza dello tato critico icché otituendo queto valore di reione nella [.] i erviene all ereione: m m A A R T max c ( ) [.] Dalla [.] i oerva che la ortata aumenta al diminuire della reione fino al valore fornito dalla [.] er oi decrecere fino ad annullari addirittura laddove la velocità aume valore maimo, è evidente che queto dicoro è inaccettabile; in ratica attravero l oervazione erimentale i è vito che una volta raggiunta la reione critica la ortata conerva cotantemente il valore maimo icché l andamento della funzione [.] è quello riortato nella figura 3 dove il ramo di curva tratteggiato ha olo un ignificato matematico ma non corrionde ad alcuna ituazione reale.
21 8 F m A m I HG A K J max Figura 3 Queto fatto one enz altro un limite alla validità della [.] in quanto non eendo fiicamente giutificabile il econdo ramo della curva uddetta tale equazione è accettabile olo er... TEOREMA DI HUGONIOT L iotei di coniderare reveribile il defluo adiabatico negli ugelli e diffuori cotituice ovviamente olo un aroimazione anche e abbatanza accettabile vito che, er quanto detto in recedenza, i tratta di condotti di caratteritiche geometriche tali che i fenomeni diiativi non hanno ne lo azio ne il temo ufficiente er far entire in modo arezzabile i loro effetti; nella realtà erò queta è una emlificazione che viene fatta olo in una rima fae di calcolo, o di verifica, al fine di determinare i valori teorici di velocità, ortata di maa e le altre grandezze fiiche e ucceivamente, in un econda fae, vengono mee in conto le irreveribilità, fra l altro inevitabili, modificando i valori delle uddette grandezze mediante oortuni coefficienti correttivi determinabili olo attravero l oervazione erimentale. Coniderando in una rima aroimazione il moto ioentroico attravero le equazioni differenziali di bilancio di maa ed energia i uò analizzare il comortamento di un fluido comrimibile che attravera un condotto a ezione variabile. Per le condizioni ote inizialmente l equazione differenziale di bilancio energetico i crive: d w dw [.3] che i uò anche mettere nella forma: dw d d w w d ovvero er la [.] e la [.3]. dw d w M [.4] inoltre differenziando l equazione di continuità: w A co t. riulta: c d da dw A w [.5] c
22 9 quindi otituendo nella [.4] ed ordinando i ha: da dw M [.6] A w quindi otituendo nella [.3] i ha: da d M A w [.7] otituendo ancora la [.5] nella [.4] i ottiene: da d A M [.8] Le [.6], [.7] e [.8]ono le equazioni di Hugoniot le quali decrivono il moto di un fluido comrimibile qualiai lungo un condotto a ezione variabile, iù reciamente attravero le uddette equazioni è oibile rialire al comortamento totalmente ooto del fluido nei riguardi dei due regimi di defluo. Nel cao di defluo ubonico le variazioni della ezione del condotto cauerebbero la variazione delle grandezze fiiche nel modo eguente: dw dw da d da d d d mentre in regime ueronico i avrebbe: dw dw da d da d d d Da quete condizioni i vede che er oter incrementare la velocità del fluido, a ee di una diminuzione di reione e denità, occorre un condotto convergente in regime ubonico ed un divergente in regime ueronico ertanto in un convergente non uò eere realizzato il regime ueronico, al limite i raggiunge il regime onico; un condotto che realizza queta condizione di moto viene denominato rareenta ugello e uò eere cotituito da un olo convergente o da un convergente collegato ad un divergente, come è illutrato nella Figura 4a. Per decelerare il fluido, con recuero di reione e denità, occorre un convergente in regime ueronico ed un divergente in regime ubonico; un condotto che realizza queto defluo rareenta un diffuore, illutrato nella Figura 4b. Si oerva quindi come la denominazione, ovvero la caratteritica del condotto, non diende dalla forma geometrica benì dal regime di moto della corrente. Da quete coniderazioni i uò enunciare il teorema di Hugoniot econdo il quale nel moto ioentroico in un condotto a ezione variabile il aaggio da moto ubonico a ueronico, e vicevera, uò avvenire olo in una ezione di area minima che viene chiamata ezione di gola. Con riferimento al ga erfetto che fluice in regime tazionario è oibile ricavare una relazione fra il numero di Mach e l area della ezione traverale del condotto; in tal cao i fa riferimento alla ezione di gola in corriondenza della quale i è raggiunta la velocità del uono, ovvero la condizione M, e che ertanto viene definita ezione critica A. c L equazione di bilancio di maa tra la ezione uddetta ed una ezione generica conente di crivere: w A w A ovvero anche: c c c
23 A c w RT c c c c Tc Ac w M RT M T / Ugello M M M M a Diffuore M M M M b Figura 4 Tenuto conto della rima e terza delle [.39] i ottiene: A M A M c ( ) [.9] queta funzione, rareentata nella Figura, reenta un minimo er M dove i ha A A, er A ogni altro valore del raorto i hanno due valori del numero di Mach: uno er il regime A c A A ubonico ed uno di regime ueronico e quindi er aumentare il numero di Ac A M c M Mach la ezione traverale deve diminuire, nel eno del defluo, a velocità uboniche ed aumentare a velocità ueroniche; vicevera er diminuire il numero di Mach. A Tutto ciò è in accordo con quanto dedotto dalle equazioni di Hugoniot. I valori del raorto Ac ono tabulati ed anche diagrammati er dato numero di Mach ma anche er un dato valore di il quale, come i oerva ancora dal diagramma di Figura 5, influenza il uddetto raorto olo er elevati valori del numero di Mach e iù reciamente nel cao di regimi ueronici. c
24 A A c A A c M< M= M> M Figura 5 A Nello tudio del funzionamento degli ugelli e diffuori riulta conveniente erime il raorto Ac in funzione del raorto di reione, infatti facendo riferimento alle [.] e [.] dal loro raorto riulta: A A c [.] A dalla quale ad ogni valore del raorto corriondono due oluzioni ioentroiche: una di A c moto ubonico ed una di moto ueronico ; er A Ac i ha la oluzione c M. M Si oerva che er dato condotto, ugello o diffuore, e a econda del regime di moto, ubonico o ueronico, in cui i trova il fluido una delle due oluzioni uddette dovrà neceariamente eere cartata in quanto riulterebbe incomatibile con il comortamento caratteritico del condotto in eame, iù in articolare i oono fare le eguenti coniderazioni concluive er ciacuno dei due condotti. Nel cao di un ugello i uò dire che e il fluido arriva alla ezione di gola con moto ubonico il defluo nel divergente, er il teorema di Hugoniot, roegue ubonicamente e queta è una condizione da non rendere in coniderazione in quanto il condotto funzionerebbe come un tubo di Venturi, il fluido nella ezione di gola deve neceariamente arrivare con velocità onica in tal cao nel divergente il moto o ritorna ubonico, oluzione da cartare, come uò divenire ueronico che rareenta la condizione che i vuole realizzare; queta ituazione di moto è chematicamente illutrata nella Figura 6.
25 Ugello M M M M M Figura 6 x Diffuore M M M M M Figura 7 Ooto è il comortamento del diffuore in quanto e il fluido erviene alla ezione di gola con moto ueronico eo nel divergente rocede ueronicamente, condizione da non rendere in coniderazione, il fluido deve arrivare nella ezione di gola con velocità è onica allora nel divergente il x
26 3 moto uò ritornare ueronico, oluzione da cartare, come uò divenire ubonico e queta rareenta la condizione che i vuole realizzare; la ituazione di moto è illutrata nella Figura 7. Una articolare equazione di Hugoniot i uò ottenere artendo dall equazione differenziale di bilancio energetico nella forma: wdw dh la quale er un ga erfetto diviene: R wdw dt ovvero crivendo in termini di variazioni relative: dw RT dt w w T ed ordinando i ottiene: dt T dw w ( M ) [.] tale equazione, a differenza delle tre recedenti, vale er moto adiabatico con attrito ma il fluido deve eere un ga erfetto, ea mette in evidenza che nei fenomeni di effluo la variazione di temeratura è emre oota in egno alla variazione di velocità e ertanto ad una diminuzione di velocità corrionde un aumento di temeratura, il ga i comrime, coì come ad un aumento di velocità conegue una diminuzione di temeratura, il ga i eande; i uò quindi affermare che, in valore aoluto, ad una variazione di velocità egue una variazione di temeratura tanto iù raida quanto iù è elevato il numero di Mach..3. CONDIZIONE DI FUNZIONAMENTO DI UN UGELLO Si è vito attravero il teorema di Hugoniot come la traformazione termodinamica che un fluido ubice nell attraverare un ugello o un diffuore diende, ovviamente er un dato fluido, olo dalla legge con cui la ezione del condotto varia lungo l ae, tale teorema cotituice ertanto la bae er otere effettuare una analii qualitativa del comortamento di un ugello, o di un diffuore, di caratteritiche geometriche refiate una volta aegnato lo tato termodinamico del fluido a monte e facendo variare la reione a valle. Queto tudio viene qui condotto facendo riferimento al moto ioentroico di un ga erfetto che i eande in un ugello coniderando earatamente i cai in cui eo è cotituito da un olo convergente o da un convergente -divergente in quanto il funzionamento di quet ultimo è leggermente iù comleo del rimo. Analoghe coniderazioni ma nel vero ooto, ovvero a diagrammi caovolti, i oono oi fare nel cao del diffuore.... UGELLO CONVERGENTE Nella Figura 8 è rareentato un ugello convergente dove il ga a artire da uno tato termodinamico di ritagno a monte fluice in un ambiente la cui reione viene fatta decrecere con continuità a artire dal valore. Il funzionamento di queto condotto è caratterizzato da quattro ituazioni fondamentali: a) Se non i ha defluo in quanto non i realizza alcun gradiente di reione in eno al fluido ed è quindi nulla la ortata di maa; l andamento della reione egue ovviamente la linea orizzontale del diagramma di fig..7. b) Se c i viene ad avere un gradiente di reione in eno al ga ed eendo il moto ubonico i ha anche e quindi la velocità nella ezione di ucita vale:
27 4 mentre la ortata di maa ecifica è: w RT m A R T T a b o c o c M= c d c c x Figura 8 un ulteriore abbaamento di reione ma emre comreo nell intervallo uddetto del diagramma, non farebbe altro che aumentare la velocità e la ortata ma il regime di moto nella ezione di ucita rimane ubonico. c) Se c il regime di moto nella ezione di ucita è onico: w w R T ertanto la ortata di maa raggiunge il valore maimo: max c m A R T d) Se c il gradiente di reione nel convergente rimane come nella curva c coì come rimangono inalterate velocità e ortata nella ezione di ucita ma il fluido all ucita del condotto ubice delle onde di eanione e olo iù a valle i adegua alla reione dell ambiente. c ( )
28 5 L aenza di un divergente a valle di A imedice ertanto al fluido di raggiungere il regime ueronico e ciò è in erfetto accordo con il teorema di Hugoniot.... UGELLO CONVERGENTE - DIVERGENTE Si è detto che il funzionamento di queto condotto è un o iù comleo del recedente e non altro nel divergente vito che dovendoi qui realizzare il regime ueronico è oibile la formazione di onde d urto anche e queto fenomeno non verrà qui reo in coniderazione. Partendo da una reione a valle uguale a quella a monte, condizione corriondente al valore di ortata nulla, la reione di carico viene al olito ridotta con continuità dal valore di ritagno a valori via via decrecenti e er ogni valore di i calcola un valore di reione g in corriondenza della ezione di gola. Finché riulta g c la velocità del fluido il tale ezione è ubonica e ertanto il moto riulta ubonico anche nel divergente icché il condotto i comorta come un tubo di Venturi. Allorquando i ha g c la ezione di gola diviene critica e la ortata del fluido diviene maima a queto unto il moto nel tratto convergente è comletamente definito mentre il moto nel divergente diende dalle condizioni imote a valle. Si è vito che in queta ituazione le oluzioni nel divergente oono eere due in tal cao la (.) deve erò eere critta: A A c da queta equazione i oono ricavare i due valori di reione e M M nella ezione di ucita del divergente. Per cui i uò trarre una rima concluione: a) er il moto del fluido nel divergente riulta ubonico ioentroico, che rareenta la oluzione da cartare; b) er i ottiene nel divergente il moto ueronico ioentroico, che arebbe la oluzione ottimale. Reta adeo da chiarire che coa accade al fluido quando i verifica ed ancora quando i ha. Si è detto che e il moto è ueronico è neceario revenire la formazione di onde d urto le quali oono aver luogo all interno del divergente ed anche nell ambiente dove il fluido avrà lo bocco. A caua della formazione di un onda d urto la reione di ritagno diminuice brucamente dal valore a monte, dove i ha M, a quello a valle, dove i verifica M. Se il fronte d onda uò formari in una ezione qualiai del divergente i uonga che queto avvenga nella ezione di ucita e ertanto, enza eraltro entrare nei dettagli di queto argomento, i dimotra che: M nella quale è la reione che i ha nella ezione rima della formazione dell onda mentre è la reione immediatamente a valle del fronte d onda, M è il numero di Mach a monte del fronte d onda, non viene coniderato quello a valle M.
29 6 T M M M Figura 9 M Figura 9 Calcolata la reione a valle dell onda d urto con l equazione uddetta i oono fare le eguenti coniderazioni: c) er il moto non è ioentroico con formazione di un onda d urto in una ezione interna al divergente; er il moto è ioentroico nel divergente con formazione di un onda d urto in corriondenza della ezione di ucita; e) er il moto è ioentroico nel divergente ma con formazione di onde d urto eterne di comreione, ovvero il fluido è oraeano; f) er il moto è ioentroico nel divergente ma con formazione di onde d urto eterne di eanione, ovvero il fluido è ottoeano. La curva dicreta tracciata nel divergente rareenta il luogo dei unti in corriondenza dei quali i manifeta un onda d urto normale, tutti i unti di tale curva rareentano reioni a valle del fronte d onda...3. OSSERVAZIONI In tutto ciò che i è detto, anche ull ugello convergente, i oerva che non è tata rea in coniderazione la lunghezza del condotto ertanto l ugello otrebbe teoricamente avere qualunque lunghezza, è evidente che e il condotto è molto breve la diminuzione di reione avviene con forti gradienti nella direzione aiale mentre e eo è lungo i avrebbero gradienti di reione minori; nella realtà queta lunghezza viene fiata da diveri criteri di carattere cotruttivo. x
30 7 Per lo tato termodinamico a monte è tato convenientemente celto quello di ritagno al quale, come già detto, i uò emre rialire da uno tato locale noto in quanto una velocità nulla all inizio dell eanione ignificherebbe coniderare infinita l area della ezione, i uò erò in ratica tendere a queta condizione cotruendo le areti dell ugello tangenti alle areti del erbatoio di monte, come è illutrato nella Figura, coicché la velocità riulta iccola e quindi tracurabile e non è neceario oi che la arte convergente dell ugello abbia un rofilo articolare, qualunque forma è accettabile urché l area decreca gradualmente fino alla ezione di gola; il tronco convergente uò avere una lunghezza abbatanza breve e queto ignifica che le erdite er attrito fra fluido e arete ono coniderate quai nulle. Figura Molto iù delicato è invece il divergente il quale deve eere realizzato iù accuratamente in quanto qui il fluido ha uerato la barriera del uono, inoltre allorquando il fluido ece dall ugello le areti del divergente devono avere curvatura molto graduale fino a divenire arallele in corriondenza della ezione di ucita. Inoltre e er ridurre gli attriti occorre che il tratto divergente ia breve l angolo di divergenza non uò eere troo grande altrimenti i avrebbe il ditacco della vena fluida dalle areti con formazione di vortici e coneguenti fenomeni diiativi. Nella maggior arte dei cai ratici il rofilo di un ugello ha forma tronco-conica con angolo convergente fino a circa 45 mentre l angolo di aertura nel divergente è in genere comreo tra i 7 e i. Da quete coniderazioni i uò dire che er un ugello convergente - divergente le dimenioni fondamentali, cioè quelle da calcolare, i riducono alle aree della ezione di gola ed alla ezione di ucita mentre e l ugello è cotituito da un olo convergente il calcolo riguarda olo l area della ezione di ucita. Figura
31 8.4. MOTO ADIABATICO CON ATTRITO Il defluo ioentroico ha una notevole imortanza teorica in quanto cotituice un riferimento limite mentre il moto adiabatico irreveribile rivete grande imortanza ratica in quanto qualunque movimento fluido lungo un condotto di qualivoglia geometria è emre accomagnato da erdite di energia anche in condotti corti e ben rofilati come lo ono gli ugelli e i diffuori, rinciale reonabile di tali erdite è l attrito dovuto revalentemente alla vicoità del fluido ed alla rugoità delle areti nonché, con riferimento ai fluidi che qui vengono trattati, all effetto della comrimibilità. Gli effetti dovuti alla vicoità del fluido i manifetano in due modi: - formazione di uno trato limite in una zona a ridoo delle areti er cui anche uonendo ioentroico il defluo i valori delle aree introdurre nelle ereioni della ortata no arebbero iù quelli geometrici; - er effetto dell attrito in eno al fluido e tra fluido e arete i avrà nel cao di un ugello una riduzione della velocità di effluo e di ortata rietto ai corriondenti valori ioentroici, nel cao di un diffuore una arte della variazione di energia cinetica verrà convertita in calore di coneguenza a arità di variazione di entalia e di energia cinetica l aumento di reione riulterà minore di quello che i avrebbe nella corriondente comreione ioentroica. Si conideri il defluo di un fluido in un ugello dove a caua delle erdite er attrito l entroia crece nella direzione del moto, inoltre tenuto conto che durante il defluo, con o enza attrito, il fluido i eande ino alla reione all ucita dell ugello il unto r corriondente allo tato termodinamico reale i troverà ulla tea iobara ma iù a detra del unto e oiché le iobare nel diagramma h- hanno endenza oitiva i ha che hr h e ertanto durante il defluo i ha emre h h r h h coneguentemente la velocità del ga w irr all ucita dall ugello arà emre inferiore di quella ioentroica. Si criva l equazione di bilancio energetico tra uno tato locale generico ed uno tato locale noto la quale e il moto è ioentroico allora i crive: mentre er il moto adiabatico i ha: w w h h wirr w hirr h il rendimento ioentroico dell ugello è dato dall ereione: wirr w h hirr ie h h w w ovvero e la velocità iniziale i ritiene tracurabile, er quanto è tato fatto oervare in recedenza, i uò ancora crivere: wirr ie [.] w in tal cao il rendimento ioentroico di un ugello è dato dal raorto tra l energia cinetica adiabatica e quella ioentroica nella ezione di ucita, ertanto riulta: che i uò anche crivere come: w irr w ie
32 9 w irr w [.3] w icché la velocità adiabatica w irr i ottiene da quella ioentroica, fornita dalla [.4], moltilicando queta er il fattore w ie che viene denominato coefficiente di velocità, è un coefficiente di riduzione erimentale che, nella maggior arte dei cai, è oco dicoto dall unità e diende dalla forma e dalla rugoità delle areti. Nel cao di ugelli convergenti w ha un influenza tracurabile ulla velocità in quanto aume valori comrei fra,97,99 ed il moto i conidera abbondantemente ioentroico; nel cao di ugelli convergenti - divergenti i valori di w ono comrei fra,94,96 e ciò erché il condotto è iù lungo e ia erché nella arte divergente i realizzano velocità iù elevate. La erdita di energia er attrito uò eere erea come la differenza tra l energia cinetica ioentroica nella ezione di ucita dell ugello e quella adiabatica irreveribile in corriondenza della tea ezione, oia: che attravero la [.] diviene: w wirr Eattr [.4] w w Eattr ie [.5] nella quale il termine viene chiamato coefficiente di erdita di energia. Se e ono gli tati termodinamici in cui i trova il fluido, riettivamente, all ingreo e all ucita dell ugello la differenza tra la velocità ioentroica in ucita: e quella adiabatica nella medeima ezione: w h h w h h irr irr la erdita di energia uò eere critta: E h h [.6] attr irr ed è dunque erea come differenza tra l entalia adiabatica e quella ioentroica nella ezione di ucita dell ugello. Inoltre tenuto conto della [.5] ed utilizzando la velocità ioentroica la uddetta relazione aume la forma: E h h [.7] attr e quindi eguagliando i econdi membri di quete ereioni i uò determinare il valore dell entalia adiabatica nella ezione di ucita: h h h h [.8] irr Nel diagramma di Figura è rareentato il defluo adiabatico dell ugello, i oerva che l area otto la curva irr rareenta il lavoro neceario er vincere le forze d attrito che i traforma irreveribilmente in calore aorbito dal fluido icché la temeratura del ga nella ezione di ucita dell ugello è maggiore di quella ioentroica; d altra lungo l adiabatica riulta: q attr irr T d irr
33 3 T irr Figura i oerva dal diagramma T che l area ottea dalla curva iobarica irr rareenta la erdita di energia cinetica er attrito Eattr ; infatti tenuto conto che er lungo un iobara reveribile i ha: Td dh allora integrando tra i unti e irr riulta: T irr T d hirr h [.9] T nella quale il rimo membro rareenta rorio l area della curva tratteggiata oramenzionata, dal confronto con l area ottea dalla curva i oerva che la erdita di energia cinetica er attrito irr E attr rareenta olo una arte del calore di attrito la rimanente arte, non tratteggiata, viene aorbita dal fluido e i traforma di nuovo in lavoro meccanico. Pertanto vale emre la diuguaglianza: h h q [.3] irr attr ne conegue che la forma della curva irr, erimente convenzionalmente un adiabatica irreveribile, non ha alcuna imortanza er l analii del defluo con attrito. Nel cao un defluo adiabatico con attrito eendo qet riulta: dh vd dq attr quindi integrando: irr attr [.3] h h vd q D altra arte tenuto conto che er un roceo ioentroico i ha: h h vd i uò affermare che i due integrali delle equazioni uddette non ono affatto identici, infatti ottraendo membro a membro i uò crivere iù reciamente: irr attr [.3] attr rev h h vd vd q e quindi attravero la (.3) dalla uddetta ereione i deduce che: vd vd attr rev
34 3 ertanto il lavoro utilizzabile in un moto adiabatico con attrito è emre maggiore di quello corriondente al defluo ioentroico. Tenuto conto della (.6) la (.3) aume la forma: vd vd qattr Eattr [.33] attr rev ereione che riecchia quanto detto in recedenza.
35 3 3. MOTO ADIABATICONEI CONDOTTI CILINDRICI 3.. L ATTRITO NEI FLUIDI COMPRIMIBILI. TEOREMA DI FANNO L analii dimenionale dimotra che nel cao di regimi di moto comletamente viluati il fattore d attrito diende in generale dal numero di Reynold, dal numero di Mach e dall eventuale cabrezza relativa, nel cao di condotti con arete a comortamento non licio; l eerienza erò conferma che er regimi ubonici, o al limite onici, la diendenza del fattore di attrito è tracurabile nei riguardi del numero di Mach di coneguenza er la determinazione del fattore teo oono eere utilizzate con buona aroimazione le tee correlazioni che riguardano il moto dei fluidi incomrimibili. Diveramente accade nel regime ueronico dove il fattore d attrito diende da altri arametri, oltre a quelli ora citati, e ciò trova iegazione nel fatto che in tale regime non i uò avere un moto comletamente viluato in quanto la condizione M uò eere mantenuta er una lunghezza di condotto molto limitata oltre la quale vengono a manifetari i fenomeni d urto, come verrà illutrato oco iù avanti. In tale circotanza lo azio attraverato dal fluido rareenta er intero una regione di ingreo nella quale il fattore d attrito riulta variabile ezione er ezione in quanto diende dal numero di Mach, dal numero di Reynold locale Re( x ), dallo eore iniziale dello trato limite nonché dal grado di turbolenza iniziale; coneguentemente verrebbe anche a cedere l iotei di monodimenionalità del moto icché le equazioni di bilancio recedentemente critte non arebbero iù valide. Il fattore di attrito che viene utilizzato nel defluo ueronico viene definito come un fattore medio aarente che continua a oddifare ancora le equazioni di bilancio nel defluo monodimenionale ma molto difficilmente uò eere determinato con coniderazioni teoriche. Serimentalmente i è vito che i fattori d attrito che i incontrano nel regime ueronico riultano normalmente iù bai di quelli che i manifetano nel moto dei fluidi incomrimibili, in articolare nel cao di condotti a ezione circolare con areti a comortamento licio con riferimento ai cami di variazione: d l 5 d,5 Re 7 4 5, M 3 è tato ricontrato che il fattore di attrito medio è comreo tra i valori:,8, ovvero i ottengono valori di raticamente dimezzati rietto a quelli ottenuti nel moto dei fluidi incomrimibili. Potendo allora erimere gli effetti dell attrito in termini di rorietà medie del fluido nella ezione coniderata e econdo quanto già detto al. ull iotei di monodimenionalità del moto i faccia riferimento all equazione di bilancio di energia meccanica nella forma differenziale la quale tracurando l energia otenziale del camo gravitazionale, in queto cao del tutto ininfluente, e enza cambi di lavoro con l eterno i crive: w d d w dx d che uò eere mea nella forma: dw d dx [3.] w w d tale equazione nel cao di ga erfetto ed in funzione del numero di Mach i uò ancora crivere:
36 33 dw d dx [3.] w M d L equazione differenziale di bilancio di maa er il cao in eame ha ereione: dw d [3.3] w inoltre differenziando l equazione di tato dei ga erfetti riulta: d d dt T [3.4] di coneguenza la [3.3] diviene: d dt dw [3.5] T w Inoltre dall ereione differenziata del numero di Mach: dm dw dt M w T combinata con la [.] i ottiene la variazione relativa della velocità: dw dm [3.6] w M M mentre dalla [3.5] ed ancora attravero la [.]riulta: d dw ( )M w e quindi er la [3.6] i ottiene: d ( )M dm M Sotituendo le [3.6] e [3.7] nella [3.] i crive: M [3.7] ( )M dm dx M M d M M la quale, ommando dentro arentei, aume la forma: M dx d M M 3 dm Si faccia adeo riferimento all equazione: d Td dh che combinata con la [.4] critta in forma differenziale: wdw dh diviene: Td wdw d [3.8]
37 34 Ricavando la variazione relativa di reione dalla (3.) riulta: d wdw w dx d e otituendo nella recedente i ha: ovvero in funzione del numero di Mach: d w dx T d d RM dx d e tenuto conto della [3.8] i erviene all ereione differenziale della variazione di entroia in funzione del olo numero di Mach: R M d M M dm da ea riulta che: M M inoltre, come è emlice verificare, riultando anche: M M i deduce che lo tato di maima entroia i ha in corriondenza del regime onico. Integrando la [3.9] i ottiene: R ln M ln M C ( ) [3.] la quale aieme alla [.8] conente di tracciare nel iano T, le curve del defluo adiabatico, dette linee di Fanno, iù reciamente fiata una temeratura di ritagno T i ottiene un facio di curve ognuna delle quali è valevole er un dato numero di Mach e ciacuna di ee ha un limite, tato di maima entroia, in corriondenza di M ; ricavando dalla [.8] il numero di Mach e otituendo nella [3.] i ottiene l equazione di una curva er quel dato numero di Mach, oia: inoltre eendo: R T T T T ln ln C w c T T [3.] [3.9] [3.] i deduce che le linee a temeratura cotante ono anche linee a velocità cotante coneguentemente gli tati aartenenti al ramo ueriore di ogni curva corriondono a velocità uboniche mentre gli tati corriondenti al ramo inferiore delle curve uddette corriondono a velocità ueroniche, Figura 3. Il vero di evoluzione del defluo è quello indicato dalle frecce in quanto la reenza dell attrito non uò che cauare un aumento di entroia e ertanto e il moto è inizialmente ubonico l aumento di entroia orta ad aumento della velocità, ovvero del numero di Mach, mentre e il moto è inizialmente ueronico i ha una diminuzione di velocità icché in entrambi i cai la velocità del fluido tende al regime onico.
38 35 Da quete coniderazioni i uò adeo enunciare il teorema fondamentale di Fanno, ovvero: nel defluo adiabatico non ioentroico in un condotto cilindrico un moto ubonico non uò mai divenire ueronico ed un moto ueronico, in aenza di onde d urto, non uò mai divenire ubonico, lo tato limite comune è il regime onico. T M M max Figura PARAMETRO LIMITE E GRADIENTE DI PRESSIONE Da quanto finora vito i uò dire che facendo riferimento ad uno tato termodinamico in una certa ezione del condotto in corriondenza della quale il numero di Mach è M eite una lunghezza maima, valutata a artire dalla ezione medeima, alla fine della quale i ha M. Tale lunghezza i uò ottenere integrando la [3.8], oia: che fornice l ereione: lmax ( M ) dx dm d 3 M M M d M lmax M ln M M [3.3] la variabile adimenionale a rimo membro rende il nome di arametro limite di attrito e come i uò oervare ea è funzione del olo numero di Mach; ertanto dato il diametro del condotto ed il numero di Mach in una ezione nota il arametro di attrito conente di determinare la lunghezza l reidua che i uò aegnare al condotto affinché il moto avvenga adiabaticamente enza che i verifichino fenomeni d urto, al limite er l lmax il numero di Mach allo bocco aume valore unitario. Tale lunghezza è molto limitata infatti oervando la (3.3) er una velocità che al limite è infinitamente grande i uò crivere: lmax lim ln d M e quindi er,4 ed un valore medio del fattore di attrito di, la lunghezza in corriondenza della quale i raggiunge il regime onico vale: l 8d max
39 36 La lunghezza tra due ezioni del condotto, Figura 4, in corriondenza delle quali i numeri di Mach ono, riettivamente, M e M i uò ottenere calcolando darima le lunghezze limiti l attravero la [3.3] e oi dall ereione: l max e M max M l l l [3.4] max M max M l M M M l max M l max M Figura 4 vicevera dato il numero di Mach M la [3.4] conente di determinare il numero di Mach incognito allo bocco. Sotituendo la [.] nella [3.5] i ricava la variazione relativa di velocità: dw d w ( )M e quindi tenuto conto che: la (3.) i crive: dalla quale i ricava: w M M [3.5] d w ( )M dx d d ( )M dx M d w [3.6] e ertanto riulta: d M dx d M dx icché i ha una erdita di reione nel regime ubonico. Si oerva inoltre che er M dalla [3.6] i ottiene: d w dx d ovvero il gradiente di reione che i manifeta nei fluidi incomrimibili.
40 STATO TERMODINAMICO DI RIFERIMENTO Anche er il defluo adiabatico nei condotti cilindrici viene coniderato come tato di riferimento quello corriondente alla condizione M, dove i è vito che il fluido raggiunge la maima entroia, ma a differenza dello tato critico ioentroico la condizione uddetta viene raggiunta in modo irreveribile e ertanto delle equazioni critte il recedenza retano valide olo la [.8] e la [.36], ovvero la rima delle [.39], quet ultima viene in tal cao coniderata come quella temeratura caratteritica dello tato critico adiabatico. Se i conidera un roceo adiabatico che arte da uno tato locale (,T,,w) fino a raggiungere lo tato di maima entroia ( c,t c, c,w c ) l equazione di continuità i crive: oia anche: w w w M RT T c M wc RT T c c e quindi er la rima delle [.39] i ottiene: c M M c c / / [3.7] Inoltre tenuto conto dell equazione di tato i uò crivere: c ctc T icché: c Tc c T e tenuto conto della [3.7] e tramite la rima delle [.39] i erviene all ereione: c M M Ancora dall equazione di continuità riulta: e tramite la [3.7] i ha: w c c / w w wc M M / [3.8] [3.9] la quale unitamente alle [3.7], [3.8] e la rima delle [.39] definicono lo tato critico adiabatico ovvero lo tato di maima entroia. Nella Figura 5 è rareentato il roceo i cui etremi ono gli tati ora menzionati, in tal cao in corriondenza dell ioentroica i uò crivere: max c mentre lungo l ioentroica aartenente allo tato locale vale la [.9] e dal raorto di quete reioni di ritagno i ha: M c
41 38 la quale tramite la [3.8] aume la forma: M M ( ) [3.] che fornice il raorto tra la reione di ritagno relativa allo tato locale e quella che i ha nello tato critico adiabatico. T o T T o o c Figura 5 max L aumento di entroia nella uddetta traformazione vale: Tc c c ln T d altra arte lungo l ioentroica locale e quella critica i uò crivere riettivamente: T Too c c To o T e dal raorto di ambo i membri ne riulta: o T c T c o e ertanto l aumento di entroia i uò crivere nella forma: o c ln Rln o o o [3.] ovvero in funzione del raorto tra la reione di ritagno locale e quella aartenente allo tato di maima entroia. Si uò dire che lo tato critico adiabatico è adeo definito in modo comleto in quanto oltre alle equazioni recedenti la [3.] fornice il valore della maima entroia a artire da condizioni locali note FUNZIONAMENTO DEI CONDOTTI MISTI Lo tudio del moto in ugelli e diffuori è tato trattato earatamente da quello nei condotti cilindrici in quanto benché in entrambi i cai il defluo è adiabatico i è vito che olo nel rimo cao è oibile, almeno in rima aroimazione, tracurare gli effetti dell attrito.
42 39 Viene adeo reo in eame lo tudio del moto adiabatico in un condotto cilindrico collegato a monte ad un ugello, queto defluo i uò definire mito ia er geometria che er comortamento fiico del fluido in quanto e nel condotto cilindrico vale il teorema di Fanno nell ugello vale quello di Hugoniot. Queto tudio viene affrontato in maniera ancor iù intetica di quello fatto er gli ugelli ia erché i fenomeni d urto, rinciali reonabili del comortamento del fluido, non vengono qui rei in coniderazione ed anche er gli aetti iù comlei che queto defluo combinato comorta er il quale i rimanda il lettore ai trattati ecifici ull argomento. T o c o a b c d e o c o c c Figura 6 x..4. CONDOTTO ALIMENTATO DA UN CONVERGENTE Nella Figura 6 il condotto è collegato, attravero un ugello convergente, a monte ad un erbatoio con reione e temeratura di ritagno note ed a valle ad un ambiente la cui reione viene fatta decrecere con continuità a artire dal valore della reione di ritagno a monte. Nell ugello il moto è ioentroico mentre nel tratto cilindrico il defluo è adiabatico con attrito. Facendo riferimento al diagramma delle reioni ottotante alla figura i oerva che e la reione nel erbatoio a valle è uguale a quella di ritagno a monte non c è movimento, curva a, mentre er valori via via decrecenti di rietto alla, curve b e c, i realizza il defluo in regime ubonico e nella ezione di ucita i ha M ; ad ogni diminuzione di i verifica un incremento del numero di Mach e quindi un accrecimento della ortata fino a che quando la reione raggiunge il valore critico, curva d, nella ezione di ucita i ha M e la ortata ha valore maimo coì come in corriondenza della ezione di imbocco del tratto cilindrico anche il numero di Mach raggiunge un valore maimo. Per valori di minori della c, curva e, non i manifeta alcuna variazione della ortata che rimane uguale al uo valore maimo corriondente a M anche erché er il teorema di Fanno il numero di Mach in tale ezione non uò uerare il valore unitario.
43 4 Pertanto il defluo all interno del condotto rimane inalterato ma oltre la ezione di ucita il fluido ubice delle onde di eanione er oi raggiungere iù a valle l adeguamento alla reione...5. CONDOTTO ALIMENTATO DA UN CONVERGENTE - DIVERGENTE Il condotto cilindrico viene collegato al erbatoio di monte con un ugello convergente - divergente ed anche qui lo tato di ritagno nel erbatoio è noto coì come uò eere fatta variare la reione dell ambiente rietto alla reione di ritagno del erbatoio; è evidente che in queto cao i deve neceariamente ammettere che nel divergente il moto ia ioentroicamente ueronico altrimenti, er quanto è già noto, i ricadrebbe nel cao recedente. Per tudiare l influenza della reione ul defluo di oono ditinguere tre cai a econda che la lunghezza reale del condotto è minore, uguale o maggiore di quella maima comatibile con lo tato fiico iniziale fiato nella ezione di ingreo del tratto cilindrico, come è rareentato nella Figura 7, nella quale la ezione intermedia rareenta la l max calcolata in corriondenza del numero di Mach nella ezione iniziale del condotto cilindrico. in queto rimo cao la ezione di bocco è la allora er c il moto è - l l max M interamente ueronico nel condotto e olo nella ezione di ucita i ha M, curva e, mentre e c i ha ancora M ma il fluido ubice delle onde di eanione e olo iù a valle i ha l adeguamento alla reione, curva g; e c i ha M ma un onda d urto normale i viene a formare nel condotto, curva d, in diendenza del valore di e tale onda i ota vero monte all aumentare di. T o b a c o ioen. c o adiab. c m d e g h f n Figura 7 - l l max M in queto econdo cao la ezione di bocco è la in corriondenza della quale, calcolata la reione con le equazioni di Fanno, i ha che c er cui il moto nel x
44 4 condotto è ueronico enza onde d urto ovvero e c i ha la curva m mentre e c i hanno onde di eanione, curva n, e quindi l adeguamento alla reione iù a valle, er una articolare reione i viene a formare un onda d urto nella ezione di bocco, curva c. in quet ultimo cao la ezione di bocco è la e il fluido ubice emre - l l max M un onda d urto all interno del condotto e iù reciamente e c i ha M e quindi la ezione del condotto nella quale i forma l onda d urto diende dalla, curva a ; er c, curva f, i ha M e tale valore vale anche er c anche e il fluido ubice onde oblique di eanione, curva h, e olo iù a valle i ha l adeguamento alla reione. Si oerva che man mano che la lunghezza del condotto cilindrico viene incrementata a artire da l l onda d urto normale i ota vero monte fino a formari nella ezione di coneguenza max M il moto in tutto il condotto è interamente ubonico ed in corriondenza della ezione finale i raggiunge il regime onico.
45 4 4. MOTO ISOTERMO NEI CONDOTTI CILINDRICI 4.. PERDITE DI PRESSIONE E PORTATA DI MASSA Si è detto inizialmente che nel cao di comrimibilità la velocità del fluido anche er condotto a ezione cotante varia er effetto dei cambiamenti di denità e ertanto non i annulla la variazione di energia cinetica. Tuttavia e il fluido viaggia di regime laminare tazionario le bae velocità fanno i che le variazioni uddette i oono ritenere raticamente tracurabili ai fini del bilancio di energia meccanica. Si uò ervenire ad un ereione del gradiente di reione in tale regime artendo dal gradiente di reione er un fluido incomrimibile er il quale, come è noto, nel cao di un condotto cilindrico a ezione circolare vale la relazione: 3 w [4.] l d che mea in funzione della ortata di maa diviene: 8 m [4.] 4 l d Queta equazione er un fluido comrimibile deve eere neceariamente critta er un tronco di condotto di lunghezza elementare dx, oia: d 8 m 4 dx d che nel cao del ga erfetto i crive: d 8 RT m 4 dx d icché integrando u tutto il tronco di lunghezza l i ha: ovvero anche: 8 m l 4 RT d 8 m l RT [4.3] 4 d d altra arte e la temeratura del ga è cotante nelle due ezioni etreme i uò crivere: RT RT quindi dalla emiomma riulta: RT mrt e otituendo nella [4.3] i ottiene: 8 m 4 l d [4.4] m relazione analoga alla [4.] ertanto il gradiente di reione di un ga erfetto in regime laminare tazionario i uò ottenere dal corriondente gradiente di reione di un fluido incomrimibile adottando er la denità il valore medio delle denità nelle ezioni etreme del condotto. In regime turbolento le variazioni di velocità coneguenti alle diminuzioni di reione ono ovente iuttoto rilevanti er cui nell equazione di bilancio di energia devono eere comutate le variazioni di energia cinetica anche e, come i avrà modo di vedere, l aroimazione fatta er il regime laminare uò in qualche cao valere anche in tale regime.
46 43 Se la temeratura è cotante l equazione [3.3] diviene: d d e dal confronto con la [3.4] riulta: dw d w icché la [3.] aume la forma: d d dx [4.5] w d Se lo tato fiico iniziale del fluido è caratterizzato dai valori,,w l equazione di bilancio di maa è data da: w w e quindi crivendo: w w w w w e tenuto conto dell equazione di tato riulta anche: w w RT w ertanto l equazione [4.5] i crive: d d dx [4.6] RT w d Se i ammette che f Re ed eendo in tale defluo cot. riulta che: wd Re co t. di coneguenza è anche cot. e quindi integrando la [4.6] i ottiene: che uò eere critta nella forma: l RT w ln d RT l w ln d Si oerva che il logaritmo del raorto delle reioni etreme è amiamente tracurabile quando il condotto non ia troo breve; ad eemio er,3 e e, che in ratica è un raorto etremamente elevato, in un condotto lungo circa diametri i avrebbe: l 3 ln ln,69 d ovvero er le condizioni uddette, abbatanza vantaggioe, il termine logaritmico è circa 45 volte iù iccolo del recedente e quindi raticamente tracurabile; queto ignifica che la variazione di energia cinetica dovuta alle variazioni di denità riulta tracurabile rietto a quella diiata er effetto dell attrito icché la [4.8] diviene: [4.7] [4.8]
47 44 RT l w d che tramite l equazione di tato uò eere anche critta: w l d ereione che fornice il gradiente di reione er il defluo iotermo il quale uò eere determinato come e il fluido foe incomrimibile artendo dai valori iniziali di denità e velocità correggendo oi con il fattore in arentei che a ua volta, eendo, è emre maggiore dell unità. Si uò quindi affermare che: l T cot l cot oia la reitenza effettivamente incontrata dalla corrente fluida è maggiore di quella che i avrebbe e il fluido foe incomrimibile ed avente una denità è ari a quella del ga in corriondenza della ezione iniziale del condotto; d altra arte e i ena che nel moto turbolento la reitenza che incontra il fluido è roorzionale al rodotto w e tenuto conto che w cot. tale reitenza crece al crecere di w oia al diminuire della denità, ciò che ubice il fluido durante il defluo. Si faccia riferimento all equazione [4.7] la quale tramite l equazione di tato del ga uò eere critta: ovvero anche: m l RT ln A d [4.9] m l RT ln A d i uò dunque ricavare la ortata di maa ecifica: m A RT l ln d [4.] ovvero la determinazione della ortata di maa note che iano le reioni nelle ezioni etreme, o quantomeno il valore del loro raorto, in un condotto di dato diametro; nei cai in cui i uò tracurare il termine logaritmico, come vito in recedenza, i ottiene l ereione emlificata: m d A RT l [4.] dalla quale o anche dalla [4.], emre che iano note le reioni uddette, i uò determinare quale diametro deve avere il condotto che deve convogliare una data ortata di maa m.
48 PARAMETRO LIMITE. STATO CRITICO Il gradiente di reione uò eere anche critto in funzione del numero di Mach e i conidera che l equazione [4.5] uò eere mea nella forma: w d dx d w e tenuto conto della [3.5] la recedente diviene: d w dx M d dalla quale i oerva che in corriondenza del valore: M [4.3] [4.] i ha che d facendo cadere in difetto la [4.]; la [4.3] rareenta lo tato critico iotermo in corriondenza del quale il regime iotermo uò eere mantenuto olo teoricamente ma in ratica tale regime arebbe imoibile da realizzare. Si ha allora un effettiva erdita di reione olo er valori di Mach inferiori al valore critico, ovvero riulta: d M dx [4.4] mentre er Mach ueriori al valore critico i ha l inverione del gradiente di reione, oia: d M dx [4.5] Si criva l equazione [4.7] artendo da condizioni iniziali note e facendo riferimento ad una ezione generica del condotto di acia x, er cui: x w ln d ovvero anche: w x ln d quindi ordinando e crivendo la uddetta relazione in funzione del numero di Mach i uò crivere: x ln [4.6] d M La (4.6) è rareentata nel diagramma di Figura 8 dalle linee a tratto continuo ognuna delle quali è determinata er un dato numero di Mach iniziale e fornicono l andamento della reione ( x ) lungo il condotto; le linee a tratto e unto fornicono l andamento della reione er fluido incomrimibile, in tal cao infatti i avrebbe: ovvero in funzione del numero di Mach: x w d
49 46 x d M [4.7] che rareenta l equazione delle oraindicate rette ottenute al variare di M.,8,6,4, x d Figura 8 Come i uò oervare il diagramma mette in evidenza ciò che del reto è già tato dimotrato ovvero che la reione diminuice iù raidamente er il fluidi comrimibili e gli cotamenti ono tanto maggiori quanto maggiore è il numero di Mach iniziale. Fiata la ortata m e la reione iniziale retano anche determinati il valore di M ovvero la curva caratteritica della corrente fluida; noti allora la lunghezza e il diametro del condotto i uò leggere ulla curva uddetta il valore del raorto e quindi, noto il fattore d attrito, ricavare la differenza di reione necearia affinché il condotto oa convogliare la ortata aegnata. Si uò altreì oervare che tutte le curve del uddetto diagramma reentano un unto a tangente verticale il quale rareenta il unto rareentativo dello tato critico, ciò ignifica che e la x lunghezza del condotto è tale che il termine uera l acia in quel unto è imoibile che il d condotto oa convogliare la ortata aegnata qualunque ia il raorto delle reioni nelle ezioni etreme; uò al maimo eere convogliata quella ortata cui corrionde un numero di Mach iniziale l tale che la curva rareentativa abbia tangente verticale rorio nel unto di acia. Scrivendo la d [4.5] in funzione del numero di Mach i ha: d d dx M d quindi ordinando: d dx d M [4.8] e tenuto conto che, er quanto vito in recedenza er la velocità, i uò anche crivere:
50 47 d dm [4.9] M la recedente aume la forma: dm dx d M M e quindi integrando i ha: dalla quale i ottiene: [4.] l max / / / 3 dx M dm M M M dm dm d M M M d lmax M ln ( M ) [4.] M dove il termine a rimo membro rareenta il arametro limite di attrito er il defluo iotermo e la l max rareenta la maima lunghezza di condotto lungo il quale il moto, a artire da una ezione di aegnato numero di Mach, i mantenga iotermo enza che i verifichino fenomeni di dicontinuità nella ezione coniderata. l M M M l max M l max M Figura 9 La Figura 9 è analoga alla fig. 3., fatta eccezione er il numero di Mach critico, e dalla quale è oibile dunque determinare la lunghezza di condotto necearia affinché il moto ai dalla ezione con M alla ezione con M mantenendo il regime iotermo e enza che i verifichino fenomeni d urto; vale ancora l equazione [3.4] dove erò le maime lunghezze relative ai corriondenti numeri di Mach vengono determinate tramite la [4.]. Si uò adeo determinare il raorto di reione corriondente allo tato critico integrando la [4.9], oia: / d dm M dalla quale i ottiene: M M [4.] ertanto la [4.6] in corriondenza dello tato critico diviene: lmax ln( M ) [4.3] d M
51 48 dalla quale riolvendo er tentativi i ottiene il valore del numero di Mach iniziale che darebbe luogo alla maima ortata di fluido che il condotto uò convogliare otituendo tale valore nell ereione: m Aw AM max che uò eere critta in funzione della temeratura: m AM R T max [4.4] tale valore, a differenza della ortata maima che i realizza nel defluo ioentroico, ha olo un ignificato teorico ma non ha alcuna alicazione ratica in quanto, come verrà reciato qui di eguito, lo tato critico iotermo non uò eere realizzato raticamente CONDIZIONE DI ISOTERMICITÀ Si faccia riferimento alla [.8] la quale differenziata diviene: dt T( )MdM ovvero in termini di variazione relativa i crive: dt dm T M M e quindi er la [4.] i erviene all ereione: dt ( )M T KM M dx d la quale aieme alla [4.8] nonché alle già note relazioni: d d dm dw M w [4.5] conente di tabilire il vero di variazione, lungo il defluo iotermo, delle grandezze dinamiche e termiche che lo caratterizzano, riulta infatti: d d d d M M [4.6] dw dw dt dt ertanto la [4.3] rareenta il limite a cui tende il numero di Mach ia artendo da condizioni uboniche che ueroniche, ecludendo in queto econdo cao fenomeni d urto. Inoltre differenziando la [.4] i uò crivere: w dq d h dh c dt e ertanto, tenendo reenti le condizioni [4.3], i avrebbe: M dq
52 49 ciò ignifica che l attrito rovoca una diminuzione di temeratura di coneguenza affinché il moto i mantenga iotermo è necearia una omminitrazione di calore dall ambiente al fluido e finché i verifica tale condizione l aorto di calore comena effettivamente il raffreddamento del fluido mantenendone cotante la temeratura. Mentre e i ha: M dq in tal cao occorrerebbe ottrarre calore al fluido er mantenere il moto iotermo in quanto l attrito caua un aumento della temeratura; in ratica erò queta ituazione non è realizzabile in quanto è tecnicamente imoibile effettuare uno cambio termico convettivo talmente inteno che oa comenare l effetto dell attrito. Infine: M dq in tale circotanza l aorto o la ottrazione di calore non influenza la temeratura la quale in queta circotanza limite rimarrebbe cotante, anche queta ituazione è olo teorica ma di imoibile realizzazione ratica. Si conclude che il defluo iotermo di un ga lungo un condotto cilindrico uò eere realizzato olo er numeri di Mach ufficientemente lontani dal valore critico e lungo condotti con areti molto tramittenti erché olo a tale condizione l azione dell attrito riulta concomitante ad uno cambio termico con l eterno di entità tale da mantenere cotante la temeratura er l intera durata del defluo, ertanto lo tato critico ora definito nonché il valore della ortata corriondente determinato con la [4.5] hanno olo un ignificato teorico.
53 5 5. MOTO CON SCAMBIO TERMICO NEI CONDOTTI CILINDRICI 5.. DEFLUSSO DI RAYLEIGH Si tratta di un moto a regime tazionario, internamente reveribile lungo un condotto cilindrico che i realizza mediante cambio di calore e enza cambi meccanici; oltre ai fenomeni diiativi, con riferimento rinciale ovviamente all attrito, viene anche tracurata la variazione di energia otenziale del fluido. Per lo tudio di queto tio di defluo oltre alle equazioni di bilancio di maa ed energia recedentemente utilizzate è neceario fare riferimento all equazione di bilancio di quantità di moto che nel cao in eame deve eere critta nella forma: w co t [5.] Viene qui reo in eame olo il cao iù emlice oia che la omminitrazione di energia termica venga effettuata dall eterno, come è illutrato nella fig.5., ecludendo il cao in cui vi iano orgenti termiche all interno del condotto dovuti a fenomeni di combutione. q w M T q w M T figura 5. Alicando l equazione (5.) alle ezioni etreme del tronco di condotto i uò crivere: w w ed eendo: l eguaglianza recedente diviene: ovvero anche: w M M M M [5.] M ereione che collega le reioni locali nelle ezioni di ingreo e di ucita ai corriondenti numeri di Mach. Le reioni di ritagno, a monte della omminitrazione di calore, e, a valle, vanno ricavate uonendo che il fluido nell arretari, in corriondenza delle ezioni medeime, non abbia modo di cambiare calore ed il roceo ia reveribile; ertanto l equazione (.9) deve eere alicata ia nella ezione iniziale che in quella finale, i deve dunque crivere:
54 5 inoltre dividendo membro a membro: M M e tenuto conto della (5.) riulta: M M M M M M la quale fornice il raorto tra le reioni di ritagno e, raorto che è divero dall unità e varia al variare dei numeri di Mach locali; è evidente, er quanto i è detto in recedenza, che tale raorto diviene unitario e la corrente fluida non cambia calore con l eterno. Pertanto le grandezze di ritagno che nel moto ioentroico cotituicono un tato termodinamico fio nel defluo di Rayleigh ee variano al variare dello tato termodinamico locale. Nel defluo ioentroico di Hugoniot coì come in quello adiabatico di Fanno lo tato di riferimento è quello che corrionde al regime onico, anche in queto cao torna oortuno cegliere come riferimento la condizione M che viene raggiunta reveribilmente ma con aumento di entroia, come i otrà vedere oco iù avanti oervando la linea di Rayleigh. Coniderando uno tato locale generico la (5.) diviene: [5.5] M che fornice il raorto tra la reione in una ezione qualiai del condotto e la reione che i ha in quella ezione dove riulta M. Se è la reione di ritagno corriondente alla e è quella corriondente ad uno tato di ritagno in una ezione generica la (5.4) aume la forma: M M oia il raorto tra la reione di ritagno locale e quella di riferimento corriondente. Per quanto riguarda la temeratura di ritagno vale ancora l equazione (.8) in quanto è da uorre che nell arreto il fluido ubica una traformazione adiabatica ea erò varia ezione er ezione, econdo l equazione (.7), e ertanto i deve crivere: T M T e quindi facendo il raorto dei membri: T M T [5.3] [5.4] [5.6]
55 5 M T T T T M [5.7] Dall equazione di tato alicata alle ezioni e i uò crivere l eguaglianza: T T dalla quale i ricava il raorto tra le temerature: T T inoltre dall equazione di bilancio di maa, in funzione del numero di Mach, deve eere: w M RT M T w M M RT T otituendo tale raorto nella recedente riulta: T M T M e tenendo conto della (5.) i uò ancora crivere: T M M T M M ertanto la (5.7) aume la forma: M T M M T M M M / [5.9] [5.8] [5.] i ottiene dunque il raorto tra le reioni di ritagno relative agli tati locali delle ezioni e in funzione dei numeri di Mach corriondenti. Se adeo i conidera una generica ezione del condotto il raorto tra la temeratura locale e quella di riferimento corriondente riulta dalla (5.9): M T T M [5.] mentre il raorto tra la temeratura di ritagno locale e quella di riferimento corriondente i ottiene dall equazione (5.): M M T [5.] T M In maniera analoga i uò determinare il raorto tra le denità locali, infatti facendo riferimento alla (5.8) i uò crivere: M T M T /
56 53 e quindi er la (5.9) riulta: M M M M [5.3] allora crivendo la (.33) in corriondenza degli tati e i ha: M ovvero facendo il raorto dei membri: M M M e quindi er la (5.3) i ottiene il raorto tra le denità locali di ritagno in funzione dei oli numeri di Mach corriondenti: M M M M M M [5.4] inoltre coniderando uno tato locale e quello di riferimento i uò crivere, tramite la (5.3) il raorto: M M [5.5] mentre il raorto tra le corriondenti grandezze di ritagno i ottiene dalla (5.4), ovvero: M M M [5.6] Anche la variazione di entroia tra gli tati e uò eere erea in funzione dei numeri di Mach corriondenti, infatti eendo: tramite le (5.) e (5.9) i ottiene: T c ln T c ln M M M KM [5.7] Coniderando uno tato locale generico di entroia e lo tato di riferimento la cui entroia è la uddetta ereione diviene:
57 54 c ln M M dalla quale è immediato verificare che: M M M M [5.8] e ertanto anche nel defluo di Rayleigh lo tato di maima entroia i ha in corriondenza del regime onico. Portando in un diagramma (,M ) la (5.8) i ottiene la linea di Rayleigh illutrata nella figura ottotante. M figura SOMMINISTRAZIONE MASSIMA DI CALORE I raorti tra le varie grandezze in funzione del numero di Mach forniti dalle recedenti ereioni conentono di oter caire come deve avvenire lo cambio termico affinché oa eere realizzato il defluo di Rayleigh. Facendo riferimento alla (5.) i oerva che er un dato valore di T un incremento oitivo del raorto fornito da tale ereione comorta un aumento della temeratura T cui corrionde una omminitrazione di calore, a norma della (.7), mentre un incremento negativo di tale raorto caua una diminuzione di T con coneguente ottrazione di calore. Inoltre dalla 5.), come è immediato verificare, i uò crivere: T M T M T M M T max ertanto la temeratura di ritagno reenta un maimo in corriondenza di M, ovvero nel unto di maima entroia, e oiché la omminitrazione di calore tende a far crecere la T, e quindi
58 55 anche il raorto T / T, il fluido in moto ricevendo calore tende a ortari al regime onico di coneguenza in regime ubonico il numero di Mach crece coì come in regime ueronico eo decrece ed entrambi hanno come limite M ; i deduce ertanto che non è oibile aare dal regime ubonico a quello ueronico, e vicevera, omminitrando emre calore; in corriondenza della ezione in cui i raggiunge il valore M occorre iniziare a ottrarre calore altrimenti i verifica la formazione di onde d urto. In intei e il fluido i trova in regime ubonico omminitrando calore il fluido accelera e tende al regime onico che uò venire uerato olo effettuando una ottrazione di calore a valle della ezione M in tal cao il fluido incrementa la ua velocità, mentre una ottrazione di calore comorta una diminuzione della velocità. Se il fluido i trova in regime ueronico una omminitrazione di calore rovoca una diminuzione della velocità fino al regime onico mentre una ottrazione di calore comorta un aumento della velocità. Da quanto detto i deduce che il calore che i uò omminitrare al fluido ha un limite che diende dalle condizioni in cui viene effettuato il moto. Se in corriondenza di una ezione le condizioni ono date da T ed M la quantità di calore necearia er ortare il fluido fino alla condizione M è data da: max q c T T [5.9] e tale quantità rareenta il maimo calore omminitrabile in quanto, come i è vito, T è il maimo di T. Per otere erimere tale calore in funzione del numero di Mach i coniderino due ezioni generiche e del condotto er cui la quantità di calore da omminitrare al fluido er ortarlo dallo uno tato all altro arebbe data dalla (.7) che in queto cao conviene crivere nella forma: ovvero anche: T q ct T T T q ct T T ereione che, er le (5.) e (.8), diviene: M M M q ct M M M M ertanto e lo tato corrionde al regime onico in corriondenza di uno tato locale generico i uò crivere: M q max ct M M M quindi viluando ed ordinando i ottiene: dalla quale i oerva che: q ct M max M M q max [5.]
59 56 è evidente che queta è una ituazione limite, ea erò erve ad indicare che quando i arte da bai valori del numero di Mach er incrementare la velocità del fluido i devono omminitrare quantità di calore molto elevate. Torna iù conveniente diegnare la linea di Rayleigh nel iano termodinamico (T, ) le cui equazioni arametriche ono date dalle (5.9) e (5.7) critte in corriondenza di una tato iniziale noto, caratterizzato dai valori (T,,M ), e da uno tato locale generico (T,,M ): M M T T M M c ln M M M M attravero le quali ad ogni valore del numero di Mach M corrionde una coia di valori di (T, ) ottenendo coì la curva illutrata nella figura ottotante; i oerva dal diagramma che la maima temeratura locale i raggiunge in condizioni di moto ubonico, d altra arte facendo riferimento alla (5.) e i one: T M M q q M max figura 5.3 T M ne riulta l equazione: che fornice la oluzione: M 3 M 4M M M 3 [5.] ertanto la temeratura locale maima arebbe: T max T [5.] 4
60 57 Si oerva che e nella linea di Rayleigh il fluido evolve in modo internamente reveribile i uò allora crivere l eguaglianza di Clauiu: dq Td inoltre l equazione di bilancio di energia orge: w dq d c dt c dt e dal confronto con la recedente riulta: Td c dt tale relazione conferma quanto detto in recedenza oia che il unto di maima entroia lungo la linea di Rayleigh è anche il unto di maima temeratura di ritagno, nella fig. 5.4 ono rareentati, dalle linee tratteggiate, gli tati di ritagno della linea di Rayleigh. T M (,T ) M M M figura VELOCITÀ DI RIFERIMENTO E VELOCITÀ MASSIMA Per un defluo reveribile che avviene con cambio di calore l equazione di bilancio di energia er un ga erfetto i crive: w c T T q avendo fatto riferimento ad uno tato iniziale dove il fluido ha velocità nulla e temeratura T, tale ereione, er quanto è già tato fatto in recedenza, i uò crivere nella forma: w c c q max [5.3] dalla quale i oerva che anche e il defluo avviene con cambio termico la velocità locale del ga diminuice all aumentare della corriondente velocità del uono, e vicevera, er cui in un dato unto le due velocità aumono ugual valore w fornito dalla uddetta ereione: c w q max [5.4]
61 58 ertanto la velocità di riferimento nel defluo di Rayleigh è emre maggiore di quella che i realizza nel moto ioentroico e tale aumento è funzione della quantità di calore cambiata, in aenza di cambio di calore la (5.4) i identifica con la (.35). La velocità di riferimento uò eere erea in funzione del numero di Mach locale, infatti dall equazione di bilancio di maa critta nella (5.8) e tenuto conto della (5.3) riulta: w M M w M M [5.5] che fornice il raorto delle velocità locali. Allora coniderando uno tato locale generico caratterizzato dai valori w,m e quello di riferimento w, M i uò crivere: w M w M [5.6] ed è facile verificare che alla uddetta ereione i uò ervenire anche attravero la (5.4), con rocedimento meno immediato del recedente EVOLUZIONE DEL DEFLUSSO SULLA LINEA DI RAYLEIGH Per un fluido che i muove lungo la curva di Rayleigh il roblema fondamentale di imortanza ratica è quello della determinazione dello tato termodinamico finale (,T,w,M ) allorquando, come i oerva dalla fig. 5., a artire da uno tato termodinamico iniziale noto (,T,w,M ) ad eo viene omminitrata la quantità di calore q. Lo tato termodinamico iniziale determina nel iano (T, ) una articolare linea di Rayleigh ed inoltre calcolata la temeratura di ritagno iniziale T, tramite la (.8), reta anche determinata la temeratura di ritagno nello tato di riferimento T, attravero la (5.), nonché la temeratura di ritagno finalet, mediante la (.7); tra quete temerature i uò allora verificare che T T oure T T. T T T figura 5.5 Nel cao in cui T T e inizialmente M lo tato finale i trova ancora nel ramo ueriore della linea di Rayleigh, fig.5.5, il defluo è dunque caratterizzato dal tratto ed è
62 59 univocamente determinato dalle relazioni ora critte; e inizialmente è M i oono verificare due ituazioni: - il fluido i muove lungo il tratto ' della linea di Rayleigh, fig.5.6, queta è una oluzione accettabile e ertanto lo tato finale ' è ancora univocamente determinato; - il fluido artendo dallo tato iniziale in corriondenza di un generico tato a ul tratto ueronico della linea di Rayleigh ubice un onda d urto aando allo tato b del ramo ubonico della tea linea di Rayleigh, accade in queto cao che Ta Tb, er oi roeguire ubonicamente fino allo tato finale ", queta è una oluzione da cartare. T T T ' " ' " T a T b T a b '' b ' a figura 5.6 Nel cao limite in cui T T il fluido evolverebbe fino allo tato M ia che viaggia di regime ubonico che ueronico. Nel cao in cui T T il defluo non è realizzabile in quanto la quantità di calore q omminitrata al fluido arebbe maggiore della maima quantità di calore che il fluido uò cambiare lungo la linea di Rayleigh: q c T T max ovvero non verrebbe riettata la condizione rinciale T T T.
63 6 6. CIRCOLAZIONE DEI FLUIDI BIFASE Un fluido i dice bifae quando è cotituito da due fai fiiche ditinti una liquida ed una gaoa. Una micela di acqua ed aria, ad eemio, cotituice una micela bifae, come ure una micela di acqua e vaore d acqua in equilibrio con ea. L interee cientifico e tecnico er quete micele è grandiimo er le notevoli alicazioni che i oono avere. Si eni, ad eemio, agli imianti nucleari, agli imianti olari 3, agli imianti termotecnici civili ed indutriali (i eni alle caldaie e ai generatori di vaore). Il moto delle micele bifae one diveri roblemi di calcolo fluidodinamico er le divere azioni inerziali che eercitano la fae liquida e la fae gaoa. In generale uno tudio analitico comleto richiede l alicazione delle equazioni di Navier Stoe e dell energia (vedi Convezione termica) ia er la fae liquida che er quella gaoa. Inoltre, a caua dei diveri regimi di moto che i oono intaurare nel moto bifae (vedi doo), i ha la doia neceità di crivere ed integrare le uddette equazioni di equilibrio ia nel dominio dello azio (cioè in zone omogenee) che del temo (condizioni temo varianti). Se il moto dei fluidi bifae è aociato anche ad uno cambio energetico (ad eemio in un tubo bollitore di una caldaia o di un imianto nucleare) allora i hanno, contemoraneamente ai fenomeni fluidodinamici, fenomeni di cambiamento di fae (ebollizione e/o condenazione) che comlicano non oco le equazioni di bilancio. Coì, ad eemio, erdite di reione nell ebollizione ottoraffreddata ono iù elevate di quelle in ebollizione ordinaria e ur tuttavia l incremento non è ecceivo. Le erdite di reione bifae ono emre maggiori di quelle monofai e ertanto occorre emre timarle correttamente er evitare roblemi di ottodimenionamento delle ome di circolazione. L equazione dell energia già vita all inizio del coro otto forma di equazione di Bernoulli generalizzata uò eere critta in forma differenziale nella forma: wdw dl w dl d gdz m v d v v Ricordando l equazione di continuità m ws l equazione di Bernoulli generalizzata i uò ancora crivere nella forma: m m dl d dv dz vdl m A) S d S v ove i ha il eguente imbolimo: eo ecifico del fluido, g/m³; denità del fluido, g/m³; v volume ecifico del fluido, m³/g; w velocità del fluido, m/; L m lavoro motore ul fluido, J/g; fattore d attrito del condotto; d diametro (o diametro equivalente) del condotto, m; l lunghezza del condotto, m; reione nel fluido, Pa; m ortata di maa del fluido, g/. g accelerazione di gravità, m²/. Nei reattori ad acqua bollente i ha una circolazione di acqua con iccole ercentuali di vaore in equilibrio termico. Queto fluido aolve ia alle funzioni di refrigerazione che di moderazione neutronica. 3 Le centrali eliotermiche di otenza utilizzano ia micele acqua-vaore (centrali tio Francia) che di metalli liquidi (Sodio fuo o leghe NaK o imilari). Anche i collettori a vetro uano una micela bifaica cotituita da freon liquido e aeriforme.
64 6 Si oervi che qualora ci riferice alla velocità media del fluido nella ezione di aaggio del condotto occorre tenere conto, nelle recedenti relazioni, di un fattore ari a. er moto turbolento e.8 er moto laminare, cioè occorre crivere w al oto della ola velocità. A queta equazione i aocia l equazione dell energia er itemi aerti tazionari: w q l gz h ove i è indicato con: h l entalia del fluido, J/g; q il calore fornito all unità di maa di fluido, J/g; l=l m +l r il lavoro totale fornito all unità di maa di fluido, J/g. Data l arbitrarietà nella celta delle ezioni di integrazione i fa in modo da non avere, all interno del condotto in eame, alcun organo motore e ertanto oiamo annullare il lavoro motore reente nelle recedenti equazioni. Integrando l equazione di Bernoulli generalizzata fra due ezioni e rive di organi motori i ottiene la eguente ereione: m dz m v v vdl S v S d Sli B) Gravimetriche Queta equazione dice chiaramente che la differenza di reione fra la ezione iniziale e finale nel condotto eaminato è omma dei tre termini a econdo membro che erimono, nell ordine: le erdite di reione er effetto della variazione di energia cinetica (erdite di li); er erdite er alleggerimento termico dovute all azione della gravità; le erdite di attrito totali dovute alla vicoità del fluido. Nel cao di moto bifae le erdite di li debbono tenere conto anche delle divere velocità delle due fai e quindi dell attrito virtuale che i viene a determinare nel moto relativo (corrimento o li) della fae iù veloce rietto a quella iù lenta. Queto termine reenta notevoli difficoltà di calcolo anche in coniderazione del tio di moto che i intaura nel condotto. Le erdite gravimetriche ono certamente le iù emlici da valutare, come i vedrà nel roieguo. Le erdite di attrito ono nuovamente comlee da determinare rorio er l eterogeneità del fluido bifae e del tio di moto nel condotto. 6.. TIPI DI MOTO BIFASE Per condotti verticali i è avuto modo di eaminare i regimi di fluo che i intaurano durante l ebollizione dinamica in un tubo bollitore, come illutrato dalla Figura 3. I regimi oono eere: Moto a bolle: il vaore i muove otto forma di bolle are in una matrice di liquido; Moto a tai: il vaore è reente in quantità elevate e tali da creare, er coalecenza fra bolle vicine, dei veri e rori tai interni al condotto; Moto anulare: il liquido i muove in aderenza alle areti e il vaore nel cuore interno della ezione del condotto; Moto a nebbia: il liquido è quai del tutto evaorato ed occua tutto il volume dionibile mentre il liquido, in quantità reiduali, i muove otto forma di minute goccioline are nella matrice di vaore. Ciacuna di quete tiologie di fluo richiede un tio di analii articolare er la neceità, come ora accennato, di dovere integrare le equazioni di Navier Stoe e dell energia in zone di azio eo determinate caualmente e quindi enza alcuna oibilità ratica di reviione analitica. Attrito
65 6 MOTO A NEBBIA MOTO ANULARE MOTO A TAPPI MOTO A BOLLE LIQUIDO CONVEZIONE MONOFASE Figura 3: Regimi di moto in condotto verticale durante l ebollizione Del reto anche l itaurari del regime di moto non è facile da revedere anche e eitono alcune mae erimentali che delimitano, certamente non in modo recio, i cami di eitenza dei vari regimi di fluo. MOTO A BOLLE MOTO A TAPPI MOTO ANULARE MOTO STRATIFICATO Figura 4: Regimi di moto in condotto orizzontale durante l ebollizione Oltre ai regimi viti in recedenza i ha il moto tratificato nel quale la fae liquida i mantiene, er gravità, in bao e la frazione aeriforme nella arte ueriore otto forma di bolle. L intaurari di un regime di moto iuttoto che un altro diende fortemente dai raorti delle ortate della fae liquida e della fae aeriforme. I rofili di velocità nel moto bifae non hanno una definizione ben recia, come del reto i uò intuire, e eo i ricorre a rareentazioni fittizie di tio olinomiali determinate con eerienze mirate er articolari regimi di moto. In Figura 4 i ha un eemio di regimi di fluo er l ebollizione in condotti orizzontali.
66 CALCOLO DELLE PERDITE DI PRESSIONE IN REGIME BIFASE In calcolo delle erdite di reione nel moto bifae è tato oggetto di tudi da diveri decenni. Inizialmente in mancanza di erimentazioni ratiche i è cercato di roorre metodi analitici baati u iotei di moto emlificati e in articolare immaginando che il fluido comleivo bifae foe determinato dalle caratteritiche medie di un fluido omogeneo oortunamente definito. Negli anni ettanta i ono avute le rime erimentazioni di Martinelli e Nelon che hanno ortato alla definizione di metodi emiemirici ritenuti iù affidabili di quelli olamente teorici. Negli anni novanta le eerienze di Thom hanno fornito una metodologia emiemirica comleta oggi ritenuta fondamentale er il calcolo delle erdite di reione in regimi bifai...6. METODO DI HANFORD E uno dei rimi metodi di calcolo analitico delle erdite di reione e i bae u alcune iotei emlificative che qui riortiamo: Si uone il condotto orizzontale e quindi i tracurano le erdite gravitazionali; Il fluido i uone omogeneo avente volume ecifico dato dalla relazione: v v v m l v l con v l volume ecifico del liquido, v v volume ecifico del vaore ed x titolo della micela. Inoltre il unto indica l ingreo del condotto e l ucita. La velocità media del fluido è data dalla relazione invera di Leonardo: w m. Si definice, inoltre, la fluidità (invero della vicoità newtoniana) data dalla S relazione: x x ove, er micele ature, i ha, come i ricorda dalla Termodinamica: v v xv v con la olita convenzione ui edici. La fluidità media del fluido omogeneo è data, analogamente a quanto vito er volume ecifico medio, dalla relazione: m l eendo e l ingreo e l ucita del condotto coniderato. Nel cao di un tubo bollitore o in ogni cao con cambi termici con l eterno l iotei di un fluido omogeneo er lunghi condotti aare oco realitica e in ogni cao fortemente diendente, er via dei volumi ecifici e delle vicoità, dalle reioni locali nelle ezioni di condotto. Pertanto i uò uddividere il condotti in tratti di iccola lunghezza all interno dei quali le iotei di omogeneità aaiono maggiormente valide. Per ogni condotto i uò crivere, con l iotei dz=, l equazione di Bernoulli: m m v v v l S S d ( i) ( i) ( i) ( ) ( ) ( ) ( ) i i i i m ove con l aice (i) i intende il generico tratto del condotto. In ratica artendo dal rimo tratto, nel quale è nota la reione v (), i determina la reione () () () di ucita che è oi la reione di ingreo del econdo tratto, cioè i ha e coì via er gli altri tronchi fino ad arrivare alla d ucita dell ultimo tronco che coincide con la reione finale all ucita del condotto. In definitiva la omma delle equazioni arziali dei ingoli tratti orta all equazione totale: m m v v v l ( i) ( i) ( i) ( i) ( i) m S S d
67 64 Il coefficiente di attrito uò eere calcolato con la claica relazione di Weibach valida er tubi lici: -. x=.84 Re er cui er ogni ingolo tratto i uò crivere l equazione di bilancio 4 : d v v.84 v l S S.8.. ( i) ( i) m ( i) ( i) m () i ( i) ( i) m Per calcolare il volume ecifico medio, v m, occorre conocere come varia il titolo in funzione della lunghezza e della reione arziale del tratto coniderato. L equazione dell energia er il ingolo tratto (emre uoto orizzontale) diviene: q ( i) ( i) e w h L entalia della micela bifae in una generica ezione (i) è dato da: h h xr l ove r è il calore latente di vaorizzazione alla reione arziale nel tratto. Fra le ezioni e di ciacun tratto i ha: h r x r x, l ove r ed r ono i calori latenti di vaorizzazione alle reioni e ed è: h h h l l l la variazione delle entalie ecifiche del liquido alle reioni uddette. Combinando le recedenti equazioni i ha, er la velocità media, l ereione: m m w v vl xvv vl S S Pertanto i ha: w m v x v v v x v v l v l l v l S ove v l e v v ono note una volta conociute le reioni e. Si oervi che i volumi ecifici del liquido, non aena il titolo x uera qualche centeimo, divengono tracurabili di fronte ai volumi ecifici del vaore, er cui la recedente diviene: w m x v v x v v S Con gli vilui ora eoti i uò alicare il metodo di Hanford er aroimazioni ucceive. Nota la reione iniziale del rima tratto i tima la reione di ucita dello teo tratto e i calcola la x dello teo tratto (eventualmente riolvendo l equazione di grado ora indicata). A queto coo, tracurando il termine cinetico (di olito iccolo rietto ai termini termici) i uò crivere: () () () () () () q h r x r x Il calore fornito e () q e uò eere calcolato dalla relazione: 4 Si ricordi che è Re wd wd dm S e quindi è..84re...84 d m S.
68 65 con b erimetro del condotto. nota e quindi: Si calcola oi: q () e () l m () x i ricava qbdz v v x v v () () () () () l v l v v () () () m () v dalla relazione: v () () () m () Ora i ricava il valore della reione di ucita che di olito differice da quella inizialmente timata. Se la differenza è minore dell errore maimo tollerabile allora i rocede con il tratto ucceivo reiterando le oerazioni aena decritte. () Nel cao di differenza maggiore dell errore ammiibile allora i aume la aena calcolata e i riarte er una nuova iterazione fino a quando la differenza fra il valore di calcolo attuale e quello del ciclo recedente è minore dell errore ammiibile. La caduta di reione totale è quindi data da: Oervazioni ul metodo di Hanford. in ( i) ( i), i L iotei di modello omogeneo, alla bae del metodo di Hanford, reuone che la fae aeriforme ia in ercentuale iccoliima (o che i abbia moto a nebbia) o che la reione media ia elevata e vicina alla reione critica del fluido. Si ricordi, infatti, che alla reione critica non i ha differenza fra la fae liquida e quella aeriforme. In quete condizioni la reciione del metodo è dell ordine del 3% che, in mancanza di altri dati erimentali, è da coniderari buona er le alicazioni imiantitiche. Nelle ituazioni divere da quelle ora indicate il metodo di Hanford commette errori non tracurabili. E va utilizzato con molta cautela...7. CONDOTTI VERTICALI - CALCOLO DELLE PERDITE GRAVIMETRICHE Nel cao di condotti verticali occorre valutare anche il termine gravimetrico (rima del tutto tracurato), cioè il termine: dz grav. v Vediamo adeo una emlice metodologia er effettuare queto calcolo. Si uonga di avere un fluo termico uniforme lungo la lunghezza del condotto e che il alto di reione ia iccolo 5. Allora i uò crivere: dqe rdx ovvero: 5 Il alto di reione è ari alla caduta di reione totale e ertanto queto deve eere comunque limitato nelle alicazioni imiantitiche onde evitare ecceive otenze di omaggio.
69 66 qb dqe dz rdx m con z lunghezza del condotto a artire dall ingreo, b il erimetro e q il fluo termico ecifico (J/m²). Queta relazione ci dice che la variazione del titolo è roorzionale alla lunghezza rogreiva, er cui, uonendo che ia x =, i ha: x v vl xvv vl vl z z vv vl l Sotituendo nell ereione di grav i ha (er i=z z ) : dz z z v x v v. ln v v l grav v x v v v v l l Queta erdita va ommata alle erdite er li e er attrito...8. METODO DI MARTINELLI E NELSON Negli anni ettanta, data la comleità analitica del roblema, i effettuarono numeroe eerienze er determinare le cadute di reione in micele bifaiche di acqua ed aria. Inizialmente Lochart e Martinelli definirono un moltilicatore, X tt, definito come radice quadrata del raorto fra la caduta di reione nella fae liquida e la caduta di reione nella fae aeriforme ed è dato a ua volta dalla relazione: X tt.9.5. l x v l v x l v con x titolo del vaore e con il olito ignificato er gli altri imboli. In Figura 5 i ha l andamento delle curve erimentali che fornicono il moltilicatore di Martinelli, Xtt, al variare della reione e del titolo della micela. Si oervi, erò, che il titolo della micela non è cotante lungo il condotto er cui arebbe neceario conocere la legge di variazione di x e rocedere a ucceive integrazioni. Succeivamente ono tate elaborate altre curve erimentali alla bae del metodo di calcolo emiemirico detto di Martinelli e Nelon. Se i uone, almeno inizialmente, che il titolo vari linearmente fra ingreo e ucita (con x= in ingreo del condotto) e che vi ia omminitrazione uniforme di calore allora Martinelli e Nelon definicono il raorto: Fa M ove i ha il eguente imbolimo: Fa caduta di reione er attrito er moto bifae, Pa; Fla caduta di reione er attrito er ortata totale enata di olo liquido, Pa. In definitiva M (emre >) è il raorto fra le cadute di reione er attrito nelle reali condizioni di moto bifae rietto a quelle che i avrebbero, emre er attrito, e la ortata totale foe di olo liquido. Quete ultime ono calcolabili facilmente con i metodi della Fluidodinamica monofae viti nei recedenti caitoli e ertanto e i conoce M di oono calcolare le erdite di attrito bifae mediante la relazione: M Fla Fa Fla Martinelli e Nelon hanno determinato l andamento erimentale di M artendo dalle curve di Lochart Martinelli, come rareentato nell abaco di Figura 6. L abaco fornice M al variare della reione nel condotto er aegnato titolo, x, in ucita.
70 67 Si oervi come ia emre M> (quindi le erdite bifae ono emre maggiori di quelle monofae) e come le curve tendano a congiungeri er la reione critica dell acqua ( bar) laddove non i ha iù alcuna differenza fra la fae liquida e il vaore. Se il titolo in ingreo è x, allora i uò rocedere in queto modo, vedi Figura 7: i calcola la M corriondente alla caduta di reione fittizia di un condotto avente titolo in ingreo nullo e in ucita ari ad x ; Si calcola M er un condotto fittizio nelle condizioni di titolo in ingreo e in ucita x ; Si calcola il fattore M er condotto con titolo in ingreo x e in ucita x dalla differenza: M M M ertanto le erdite di reione ono date da: M M Fa Fla Ricordando quanto detto er le cadute totali di reione: tot Sli Gravimetrico Attrito il metodo di Martinelli e Nelon conente di calcolare le cadute di reione er attrito 5 Xtt 7 bar bat 5 35 bar 7 bar 5 bar x Figura 5: Diagramma del moltilicatore X tt di Martinelli
71 68 M % 8 Totolo ucita 6 Bar. Figura 6: Abaco di Martinelli e Nelon er M M M x= R x=x R x=x L L Figura 7: Condizioni iniziali con titolo non nullo Il termine relativo alle cadute di reione er li uò eere calcolato, emre erimentalmente, onendo: m m li v v R S S con R (ove è, er quanto detto in recedenza, R v v) coefficiente dato dall abaco di Figura 8.
72 69 R % 8% 6% 4%, % %, %, Bar Figura 8: Abaco di Martinelli e Nelon er R Nel cao in cui le condizioni iniziali del titolo iano x allora, in analogia a quanto detto er il calcolo di M e con riferimento alla Figura 7, i rocede coì: Si calcola R er il tratto fittizio con titolo variabile da a x ; Si calcola R er il condotto fittizio con titolo variabile da a x ; Si calcola il valore reale: R=R R. Se nel condotto i hanno anche erdite concentrate allora quete debbono eere valutate er la ola fae liquida er una ortata di liquido equivalente a quella totale. Le erdite di attrito Fla ono date da: Fla Fla ditribuite Fla concentrate e le erdite bifae totali corriondenti i calcolano moltilicando le recedenti er il coefficiente R calcolato come ora ecificato. Oervazioni ul Metodo di Martinelli e Nelon Queto metodo ha come iotei di bae l eitenza di due fai ditinte e quindi è in netta contraoizione con il modello omogeneo di Hanford. Il modello di riferimento è, quindi, quello del moto anulare o del moto tratificato o anche del moto a nebbia. I riultati ottenuti con queto metodo vanno bene fino a titoli elevati in ucita (anche x =). Eo è tutt oggi quello iù utilizzato er ortate ecifiche ( ms) elevate.
73 7 I riultati erimentali, ottenuta da Mucettola del CISE 6, motrano una oravvalutazione di circa il % delle erdite di reione. Ciò è ritenuto dai rogettiti una garanzia di maggior icurezza ia er le inevitabili incertezze rogettuali che er tenere conto dell invecchiamento del condotto e quindi dell aumento delle erdite localizzate 7. Il metodo di Martinelli e Nelon non fornice metodi di calcolo del termine gravimetrico e quindi occorre effettuare earatamente queto calcolo, ad eemio come illutrato in recedenza (..7)...9. METODO DI THOM Le iotei di bae ono quindi analoghe a quelle di Martinelli e Nelon e ertanto i ha un modello a fai earate. Le iotei di bae ono quindi analoghe a quelle di Martinelli e Nelon e ertanto i ha un modello a fai earate. E il metodo emiemirico iù recente e i baa u una erie di eerienze effettuate negli USA negli anni cinquanta u micele di acqua e vaore con reioni variabili da a bar e titolo in ucita variabile da 3 al %. Il fluo termico è tato mantenuto uniforme (iotei fondamentale) lungo la uerficie laterale del condotto. Il titolo iniziale è emre ari a zero. Il metodo di Thom ermette di calcolare tutti e tre i termini (li, gravimetrico e attrito) er la caduta totale di reione mediante abachi erimentali. Analogamente a quanto vito in recedenza i ha ancora la definizione del fattore M: Fa M anche e le curve ono divere da quelle di Figura 6. Le nuove curve ono riortate in Figura 9. Le curve hanno andamento imile e convergono in corriondenza della reione critica dell acqua. Si oervi ancora che Thom tiene conto dell influenza dello corrimento fra le due fae mentre Martinelli e Nelon non ne tenevano conto. Le erdite di li i definicono mediante la relazione: Fla m li R ' v l S e quindi la formulazione è divera da quella di Martinelli e Nelon anche er la reenza del volume ecifico del liquido, v l. Il coefficiente R è riortato nell abaco di Figura er vari titoli di ucita e er varie reioni di ingreo. Infine le erdite gravimetriche ono calcolate mediante la relazione: vuc. dz grav. L ving. v v Il coefficiente è dato dall abaco di Figura er titoli di ucita e reione di ingreo variabili. La erdita totale di reione nel tubo bollitore con titolo iniziale nullo è data da: m L R ' v M tot l Fla S v Sli Gravimetrico Attrito l Thom etende il uo metodo emiemirico anche al cao in cui non ci ia omminitrazione di calore: in queto cao retano le formulazioni recedenti ma il termine di attrito va calcolato utilizzando l abaco di Figura anziché quello di Figura 9. Gli altri coefficienti retano invariati. l 6 Il CISE (Centro Italiano Studi Elettricità) i è occuato di imianti nucleari roonendo, negli anni eanta, un tio di reattore rova elementi combutibili denominato CIRENE (CIe REattore Nebbia) caratterizzato dal moto a nebbia all interno dei canali di refrigerazione. 7 L invecchiamento del condotto orta al deoito di materiali (incrotazioni) e all incremento delle aerità interne.
74 7 M bar Figura 9: Abaco di Thom er M Per condizioni di ingreo divere dal titolo nullo, come illutrato in Figura 7, i rocede allo teo modo già vito er Martinelli e Nelon utilizzando un condotto fittizio tale che er eo il titolo vari da x= ad x=x. Oervazioni ul metodo di Thom Rietto al metodo di Martinelli e Nelon queto metodo reenta errori minimi rietto ai dati erimentali. E aroimato in ecceo quando le ortate ecifiche ono inferiori a 3 g/(cm².). Il metodo è aroimato in difetto er ortate ecifiche elevate, cioè > 3 g/(cm².). Il metodo di Martinelli e Nelon reenta emre valori timati in ecceo rietto ai dati erimentali e l errore i riduce allorquando il titolo di ucita i avvicina al %.
75 7 R ,7,5,, 5 5 bar Figura : Abaco di Thom er R,7,5,, 5,5 bar 3 5 Figura : Abaco di Thom er
76 73 M 7 Senza Fluo Termico bar Figura : Abaco di Thom er M er condotto enza fluo termico... METODO DI CHENOVETH, MARTIN, LESTER Si tratta ancora di un metodo emiemirico di raida alicazione er la rogettazione di imianti indutriali. La ua validità i ha er diametri dei condotti > (quindi tubi bollitori di caldaie e/o generatori di vaore) con micela bifaica acqua aria o acqua vaore. Analogamente ai due metodi recedenti, i definice il fattore M: Fa M con M dati in Figura 3, ove le curve ono in funzione del raorto fra le cadute di reione er attrito nella ola fae vaore rietto a quelle analoghe della fae liquida: Fva Nel calcolare queto raorto i immagina di calcolare le erdite di reione er attrito rima il condotto con olo vaore di ortata ari a quella totale e oi di olo liquido con analoga ortata totale. In acie i ha la frazione di ezione occuata dal liquido, -, eendo la frazione di vuoto definita dal raorto fra l area occuata dal vaore rietto all area totale della ezione del condotto: Fla Fla
77 74 Queto metodo non è molto indicato er bae reioni. S v S M Fva 5 Fla 5,,,,, - Figura 3: fattore M er C-M-L
78 75 7. STABILITÀ DEI TUBI BOLLITORI Negli imianti indutriali (caldaie, generatori di vaore, reattori chimici,.) rivete grande imortanza la tabilità e la icurezza dei tubi bollitori all interno dei quali i hanno i cambiamenti di tato dell acqua (come di qualunque altra otanza). I fenomeni che oono avvenire all interno dei tubi bollitori ono moltelici in funzione del fluo termico, delle rorietà termofiiche del fluido e della toologia dell imianto. 7.. TUBO BOLLITORE ORIZZONTALE Si uonga inizialmente che il tubo bollitore ia orizzontale e a ezione cotante, che ia nota la reione di bocco,, e che ia uniforme e cotante il fluo termico lungo le areti. Quando non c è ebollizione a velocità elevate il numero di Reynold varia oco con il variare della ortata onderale oiché alle diminuzioni di ortata corrionde, a arità di fluo termico, un incremento di temeratura del fluido econdo la relazione: Q e ct f t m eendo t f la temeratura del fluido e t la temeratura della arete. Pertanto la vicoità diminuice ed eendo: 4 Re m d m K d i uò ritenere che il raorto m i mantenga enibilmente cotante. Vicevera avviene e la ortata onderale crece oiché i avrebbe una.diminuzione del alto termico ed un incremento della vicoità dinamica. La caduta di reione nel condotto, nell iotei di aenza di ebollizione e quindi con fluo monofae, è data dalla olita relazione: Lm d S ove er la relazione di Weibach i ha:.84 Re che varia oco eendo Re enibilmente cotante, come ora illutrato. Ne egue che oiamo crivere, raggruando i termini: K m v. che, in coordinate (, m ), vedi Figura 4, è una retta aante er l origine e coefficiente angolare K.(retta OR). Un diagramma iù recio otrebbe eere tracciato er unti calcolando le erdite di reione effettive. La retta OR rareenta le condizioni di funzionamento fino alla ortata m B in cui inizia l ebollizione ottoraffreddata (vedi caitolo dell Ebollizione). Al di otto di queta ortata i hanno erdite di reione crecenti (i ricordi che le erdite bifae ono emre maggiori di quelle monofai) al diminuire della ortata di maa anche erché, a ari fluo termico, crece il titolo di vaore reente.allo bocco abbiamo: ove x è il titolo finale della micela. Q e rx m
79 76 H' B Vaore urricaldato Liquido + Vaore Liquido K R'' V V H S K' Z R R' N'' N B M' M R D D' D'' m m B m M m R Figura 4: Andamento delle reioni al variare della ortata Si ha, quindi, la curva BH di Figura 4 che i raccorda con continuità con la OR in quanto l ebollizione non i reenta contemoraneamente e nella tea forma in tutte le ezioni del condotto. In corriondenza ad un titolo x=5,3 (a econda dei cai), unto V della figura, i ha il maimo della caduta di reione v v. Se la ortata decrece ulteriormente allora diminuice fino al unto S (dove i ha x=) dove i ha la comara del liquido allo bocco.una ulteriore diminuzione della ortata comorta il urricaldamento del vaore (i è quindi in regime nuovamente monofae ma di vaore e non iù di liquido) con andamento lineare con una nuova K. In realtà giunti nel unto Z i ha la bruciatura (burn out) del tubo bollitore. Si oervi che ci i uò ingere fino al unto Z olo e il fluo termico ecifico (cioè er unità di uerficie) è bao. Con i valori correnti dei flui termici i ha la bruciatura molto rima di arrivare ad S, iù reciamente er x=.7.8. Se il fluo termico è articolarmente elevato i uò avere la bruciatura del tubo bollitore già durante l ebollizione ottoraffreddata.... PUNTO DI LAVORO DEL TUBO BOLLITORE Suoniamo di avere la reione iniziale = R, come indicato in Figura 4, ed introduciamo all ingreo del condotto una reitenza localizzata (ad eemio un ugello) tale che i abbia una caduta di reione data da:
80 77 r w m v r r r ' m v S con r funzione della reitenza adottata. In figura i ha la rareentazione della caduta di reione con la retta R D formante con la R R (orizzontale) un angolo tale che ia tag()=r. Il ignificato fiico di quete rette aare evidente e i conidera che er ogni valore della ortata di maa m i hanno egmenti intercetti fra ee che rareentano le cadute di reione r nella reitenza localizzata. I unti M ed N rareentano unti di funzionamento in reenza dell ugello quando all imbocco è alicata una reione =R, coì come i unti R, R rareentano unti oibili di funzionamento in aenza dell ugello. In corriondenza dei redetti unti, infatti, la omma della caduta di reione nell ugello r e nel tubo bollitore eguaglia la caduta di reione totale R. I unti come R ed M ono unti di funzionamento tabile: infatti e er ragioni accidentali la ortata aumenta o diminuice i ha, riettivamente, un difetto o un ecceo di reione motrice che tende a riritinare le condizioni rimitive. Non i uò dire lo teo di R ed N : infatti un aumento accidentale di ortata rovoca un alto reentino in R o in M (riettivamente) mentre una diminuzione di ortata tende ad ealtari ortando il condotto alla bruciatura. Se i ceglie come reione di imbocco K i uò ottenere il funzionamento nel unto R con l introduzione di una reitenza tale che ia: K R r ' tag ' m Per queto valore tracciamo la retta K R tale che ia: R R" K tag ' r ' m R m R Queta retta incontra la curva delle reioni, oltre che in R, anche in K e K. Di queti unti olo R e K ono relativi ad un funzionamento tabile mentre K è intabile e i alta in R o in K. Quindi con la celta della reione R er la reione di imbocco una eventuale intabilità i ferma in K e ertanto, e la bruciatura avviene oltre queto unto, i uò evitare il danno al tubo bollitore. Quando il funzionamento nel unto R è ottenuto con la reione R i è garantiti contro eventuali bruciature er otruzioni accidentali aventi: RD ' r ' m mentre con la reione K queto valore diviene iù elevato, fino a: R" D" r ' m La reione K reenta anche il vantaggio che, in cao di otruzioni che ortino il funzionamento nella curva VS, i ha ancora un funzionamento tabile e la bruciatura uò eere evitata con maggiore facilità e i dione di un aarecchio di allarme acutico. La celta della reione H ulla tangente da R al unto H, oltre a migliorare le condizioni di icurezza recedentemente citati (con riferimento alle otruzioni accidentali) ermette un ritorno automatico delle condizioni dell arco ZSH al unto R. Queto non è oibile con reioni minore di V ; infatti dalla Figura 4 i oerva che e: < V er il ritorno dell arco SV ed R non bata regolare la reitenza di imbocco ma occorre ridurre anche la otenza termica fornita in modo da avere una diminuzione di max (in corriondenza di V). La celta di una reione di imbocco iù elevata di B conente il funzionamento in tutte le condizioni mediante l introduzione di reitenza variabili (aracineche di regolazione); i oono, infatti, interecare con la retta di carico tutti i unti della curva del tubo bollitore ed avere un funzionamento tabile. R R
81 78 In definitiva, la celta della reione a monte di un tubo bollitore va fatta oculatamente in bae al grado di icurezza che i deidera ottenere. Il raggiungimento di condizioni di otimum comorta la neceità di cegliere reioni iuttoto elevate, introducendo all ingreo del condotto reitenze concentrate (ugelli, aracineche, ). Quete reitenze roteggono il tubo bollitore (che di olito funziona in arallelo ad altri tubi) dato che variazioni accidentali della ortata nominale hanno minore eo. L introduzione di ugelli allo bocco (anziché all imbocco) eercita una rotezione, nel eno che fa crecere la reione a monte. In queto cao l ebollizione inizia a temerature iù elevate e quindi er ortate minori. Tuttavia, e l ebollizione inizia allora le condizioni riultano aggravate. L ugello oto all imbocco è emre attraverato da olo liquido mentre e è oto allo bocco è attraverato da una micela di liquido e vaore e quindi roducendo una reitenza maggiore. La ortata, er coneguenza, diminuice raidamente e la bruciatura del condotto viene facilitata. 7.. TUBO BOLLITORE VERTICALE Lo tudio dei tubi bollitori verticali è iù comleo di quello rima motrato di tubi orizzontali. Per queti condotti i oono avere due cai: Moto del fluido dal bao vero l alto: in queto cao i hanno condizioni di tabilità maggiori rietto ai tubi orizzontali; Moto del fluido dall alto vero il bao: le condizioni di icurezza diminuicono rietto al cao di condotto orizzontale.... CALCOLO DELLA PORTATA DI INIZIO E FINE EBOLLIZIONE Ai fini dell analii della tabilità e icurezza di un tubo bollitore è neceario conocere le ortate di inizio e fine ebollizione. Si abbia, quindi, un condotto ottooto a fluo termico Q e eterno (uoto cotante ed uniforme). Il fluido entra alla temeratura t i con entalia h l e ad una reione che oiamo ritenere cotante. Il calore neceario er avere l ebollizione è ari a: q h h el, l l x ove h l è l entalia del fluido in ebollizione alla reione e q e il fluo ecifico (J/g) da fornire al fluido. Noto il fluo totale eterno Q e e la ortata totale di maa i calcola: Qe qe l, m Si uò anche crivere, er la ortata totale e il fluo termico totale, la relazione globale di bilancio: m Qe i h h l l eendo mi la ortata di maa di inizio ebollizione. Suonendo cotante la reione 8 del condotto, alla fine dell ebollizione l entalia del vaore aturo vale: h h r v l eendo r il calore latente di vaorizzazione alla reione coniderata. Il fluo ecifico vale: q h h h r h l v l l l x 8 Si ricordi che le cadute di reione ono emre mantenute bae er evitare grandi otenze di omaggio er il moto del fluido nel condotto coniderato.
82 79 e deve averi: Q hl r hl m e f ove m f è la ortata ecifica di fine ebollizione. Riulta, ertanto: m f Qe h r h l l Le cadute di reione er ortate di maa inferiori a quella di inizio ebollizione, con le olite relazioni er fluo monofae (Weibach): L w L m d v d S v m i, i calcolano. Per il calcolo di i utilizza la olita correlazione er tubi lici.84 Re. Allorquando ha inizio l ebollizione la caduta di reione va calcolata con uno dei metodi rima eoti er le erdite di reione in moto bifae, ad eemio con il metodo di Thom. Il titolo di vaore in ucita dal tubo bollitore i calcola mediante la già citata equazione dell energia: w qe l,, h gz Ponendo x = e tracurando il contributo dei termini meccanici (cinetico e gravimetrico) i uò crivere: ovvero anche: q r x e, Qe rx m Da queta relazione i calcola il titolo in ucita x al variare di m. Noto x i calcola la caduta totale di reione: m L, Fa li grav M, R v Fla l S v con M, R e calcolati con gli abachi di Thom 9. Va oervato, infine, che la ortata allo bocco non uò variare a iacere dovendo eere emre inferiore alla velocità maima (er tubi a ezione cotante) ari a quella del uono, come i è vito er il moto dei fluidi comrimibili EFFETTI DELLA VARIAZIONE DI DENSITÀ NEL MOTO DEI FLUIDI IN CONDOTTI VERTICALI All interno dei tubi bollitori o dei canali di refrigerazione degli imianti nucleari o di reattori chimici i ha moto di fluido con cambiamento di denità, dovuta alle variazioni di temeratura lungo il condotto, che oono rodurre roblemi di intabilità e non adeguatamente controllati. Ambiamo già trovato l equazione A) che qui i riete ricrivendo diveramente il termine cinetico: l 9 E ovvio che lo teo dicoro vale er l alicazione del metodo di Martinelli e Nelon ove, erò, le erdite gravimetriche debbono eere timate earatamente.
83 8 wdw m dl d dz vdl m v d S v Integrando queta equazione fra le ezioni e (ingreo e ucita) e tracurando il termine dovuto al lavoro oitivo del circolatore i ha: wdw dr dz v v In queta equazione occorre oervare che, er condotti a ezione cotante, la variazione di volume ecifico è di olito iccola e quindi le variazioni di velocità ono arimenti iccole e ertanto il termine cinetico aorta contributi tracurabili. Nel termine gravimetrici il eo ecifico varia con la temeratura econdo la legge: tt con coefficiente di dilatazione cubica (o di eanione iobaro già vito in Termodinamica) e t la temeratura corrente. La tea relazione vale er la variazione della denità con la temeratura. Per aldi termici iccoli i uò ritenere arimenti iccola la variazione di denità e ertanto i uò utilizzare il uo valore medio,, fra le due ezioni coniderate e quindi la caduta totale di reione diviene: R z z t t dz, Semre uonendo iccole variazioni dei arametri termofiici e linearizzando le variazioni con l altezza, oiamo ancora crivere: L m z z Q e z z ove i è tenuto conto che è Q c mt t e. d S cm L ultimo termine (negativo) rareenta l alleggerimento termico (thermal buoyancy) della colonna di fluido dovuto al ricaldamento ubito ed è quello che determina il movimento del fluido nei cai di circolazione naturale. La recedente equazione uò eere coì chematizzata:.8 B m Z Am (movimento vero l'alto) m Z Am B m.8 m (movimento vero il bao) ove A e B ono cotanti di raggruamento oitive. Gli indici e i rifericono emre all imbocco e allo bocco, qualunque ia l orientamento del condotto.. Si è anche uoto, econdo la relazione di Weibach er tubi lici, che ia Km ed inoltre i è uoto K / indiendente dalla ortata e ari al uo valore medio fra le due ezioni coniderate. La circolazione naturale non è quai mai utilizzata direttamente er il moto dei fluidi negli imianti ma rareenta emre un elemento di icurezza da coniderare quando viene meno la otenza motrice della oma. Se il fluido uò ancora circolare eo uò traortare calore e quindi mantenere la temeratura del canale otto controllo. In un imianto nucleare o in un reattore chimico o in un generatore di vaore l arreto del fluido all interno dei canali uò ortare facilmente a coi etremamente ericoloi e ditruttivi.
84 8 In Figura 5 i ha la rareentazione grafica della caduta totale di reione ia er moto vero l alto che er moto vero il bao. In ea ono riortati anche gli andamenti dei ingoli termini, B m,.8 Am, Z er i due cai, econdo le recedenti equazioni. Nella figura la ortata m è ota in relazione con Z er il moto vero l alto e con + Z er il moto vero il bao. Le curve in neretto rareentano le combinazioni dei termini, come dianzi ecificato. Al crecere della otenza ceduta al fluido la curva comleiva i ota vero detra, allontanandoi da quella egnata. Si oervi che le due curve (moto vero l alto e moto vero il bao) i raccordano, er continuità, nel modo egnato a tratto unteggiato in figura. Quando la otenza crece il termine.8 Am varia oco mentre cambia molto B m eendo B Q e. Le curve reali i arretano in corriondenza dei unti X nei quali ha inizio l ebollizione. A ieno carico, cioè er il maimo valore di Q e, l ebollizione inizia, come i intuice,a valori iù alti della ortata eendo l aumento di temeratura dato (er quanto detto in recedenza) dalla relazione: t Q e t cm Pertanto quando ci i trova nelle condizioni di fluido lavorante in caldaia o in un reattore nucleare a otenza ridotta occorre fare in modo che il alto di temeratura dello teo fluido ia il iù oibile cotante e ari al valore di regime recedente. Ciò i ottiene riducendo la ortata m in modo roorzionale al calore Q e. Riducendo la ortata m ci i orta in corriondenza del unto M o del unto N (a econda del vero del fluido) di Figura 5. Il movimento in corriondenza di queti unti è tabile: infatti, e er qualivoglia ragione la ortata m crece o diminuice il unto di lavoro i ota a detra o a initra e i determina un difetto di reione motrice che tende a riritinare le condizioni iniziali. Lo teo uccede a initra del unto B. A detra di B i ha, invece, intabilità e i tende vero la condizione del unto X di inizio ebollizione e quindi vero le condizioni di burn out del condotto. Anche er il tratto MB le condizioni oerative non ono buone erché un aumento accidentale della reitenza uò rovocare, con relativa facilità, un alto nel tratto BX della curva. Tutte le circotanze ora indicate debbono eere tenute in conto quando i rogetta un tubo bollitore o un qualunque itema nel quale il fluido lavorante funga da refrigerante er il itema. In definitiva, in bae a quanto detto, il moto vero l alto riulta emre tabile. Tuttavia eo i referice il moto vero il bao er avere di migliori condizioni oerative ai fini della rotezione in cao di incidenti...3. PROGETTO DEI CONDOTTI Si tenga emre reente che l inizio dell ebollizione orta emre ad avere maggiori erdite di reione e quindi aumenti conitenti della reitenza al movimento che facilitano le condizioni di burn out del condotto e ertanto occorre intervenire oortunamente er evitare che quete condizioni i raggiungano. Quando i tubi bollitori ono oti in arallelo (nei generatori termici e nei reattori nucleari i utilizza eo queta configurazione) allora le condizioni oerative divengono iù critiche oiché l aumento della reitenza in un condotto orta ad avere una nuova riditribuzione della ortata negli altri condotti e quindi i ha una variazione rietto alle condizioni nominali di lavoro. Se i oerva la relazione recedentemente ottenuta: L m z z Q e z z d S cm Negli imianti nucleari, ad eemio, il moto vero il bao conente di contenere nella zona inferiore dell imianto il fluido caldo e radioattivo.
85 8 Figura 5: Caduta totale di reione i uò dire che il itema rima dell ebollizione riulta tanto iù tabile quanto iù il termine z z Q relativo alla variazione della denità, e, riulta iccolo rietto a quello delle erdite er cm L m attrito,. d S Cadute di reione molto maggiori delle variazioni di denità Se quet ultimo è relativamente grande allora la rogettazione di condotti in arallelo uò eere effettuata con i metodi viti in recedenza er i condotti in erie e in arallelo.
86 83 Cadute di reione iccole rietto alle variazioni di denità Se il termine di variazione della denità revale u quelle delle erdite di attrito allora i oono avere condizioni di intabilità e i rocede iterativamente nella rogettazione. In ratica i celgono le reioni di imbocco,, e di bocco,, ed i diametri dei condotti. Si calcolano le ortate mi dei ingoli condotti utilizzando la relazione recedente e quindi i calcola la ortata totale m mi. Se la ortata totale m è inferiore a quella deiderata i modificano alcuni N arametri di rogetto e i riete il calcolo fino al raggiungimento delle condizioni finali volute. Si oervi che è emre neceario verificare, oltre alle condizioni di moto, anche quelle di congruenza relative alla tramiione del calore e cioè che la uerficie totale dei condotti ia tale da aicurare lo maltimento del calore Q e e cioè che ia: Cao di circolazione naturale Q K S t e i N i i i Seo i deidera avere una circolazione del fluido di tio naturale allora la driving force è rorio dovuta alla variazione di denità che è in diretta roorzione al calore ricevuto. Pertanto la velocità di regime nei condotti crece e crece la otenza termica ceduta e ciò rovoca una orta di uniformazione delle velocità nei condotti che riduce le tenioni termiche fra le varie zone dell imianto. La circolazione naturale avviene uualmente con bae erdite di reione e ciò orta ad avere diametri di condotti ueriori ai corriondenti a circolazione forzata, come già vito in recedenza. In alcune zone degli imianti nucleari, ad eemio negli chermi radioattivi, i referice avere moto vero l alto a baa velocità e con iccole cadute di reione. Si oervi che le condizioni di circolazione naturale ono emre da rendere in coniderazione er le condizioni di emergenza. Una fermata delle ome di circolazione, infatti, non uò e non deve comortare il blocco del fluido all interno dei tubi bollitori erché ciò rodurrebbe certamente un incidente: il calore fornito non arebbe iù traortato via e quindi i hanno coi o altri diatri. E quanto avvenuto, ad eemio, nel reattore di Chernobil dove la fermata (fore volontaria) delle ome di circolazione ha ortato alla tagnazione del fluido refrigerante con coneguente urricaldamento del nocciolo del reattore nucleare che è fuo.
87 84 INDICE GENERALE. FLUIDI COMPRIMIBILI - Defluo monodimenionale..... Comrimibilità ed eanione..... Velocità del uono e numero di Mach Stati termodinamici articolari Fattore di comrimibilità.... Moto adiabatico nei condotti a ezione variabile Equation Section Moto ioentroico: Velocità e ortata ecifica Teorema di Hugoniot Condizione di funzionamento di un ugello Ugello convergente Ugello convergente - divergente Oervazioni Moto adiabatico con attrito Moto adiabaticonei condotti cilindrici L attrito nei fluidi comrimibili. Teorema di Fanno Parametro limite e gradiente di reione Stato termodinamico di riferimento Funzionamento dei condotti miti Condotto alimentato da un convergente Condotto alimentato da un convergente - divergente Moto iotermo nei condotti cilindrici Perdite di reione e ortata di maa Parametro limite. Stato critico Condizione di iotermicità Moto con cambio termico nei condotti cilindrici Equation Section 5 Defluo di Rayleigh Somminitrazione maima di calore Velocità di riferimento e velocità maima Evoluzione del defluo ulla linea di Rayleigh Circolazione dei fluidi bifae Tii di moto bifae Calcolo delle erdite di reione in regime bifae Metodo di Hanford Oervazioni ul metodo di Hanford Condotti verticali - calcolo delle erdite gravimetriche Metodo di Martinelli e Nelon Oervazioni ul Metodo di Martinelli e Nelon Metodo di Thom... 7 Oervazioni ul metodo di Thom Metodo di Chenoveth, Martin, Leter Stabilità dei tubi bollitori Tubo bollitore orizzontale Punto di lavoro del tubo bollitore Tubo bollitore verticale Calcolo della ortata di inizio e fine ebollizione Effetti della variazione di denità nel moto dei fluidi in condotti verticali Progetto dei condotti... 8
88 85 Cadute di reione molto maggiori delle variazioni di denità... 8 Cadute di reione iccole rietto alle variazioni di denità Cao di circolazione naturale... 83
89 86 INDICE DELLE FIGURE Figura 6 Figura Figura 3: Regimi di moto in condotto verticale durante l ebollizione 6 Figura 4: Regimi di moto in condotto orizzontale durante l ebollizione 6 Figura 5: Diagramma del moltilicatore X tt di Martinelli 67 Figura 6: Abaco di Martinelli e Nelon er M 68 Figura 7: Condizioni iniziali con titolo non nullo 68 Figura 8: Abaco di Martinelli e Nelon er R 69 Figura 9: Abaco di Thom er M 7 Figura : Abaco di Thom er R 7 Figura : Abaco di Thom er 7 Figura : Abaco di Thom er M er condotto enza fluo termico 73 Figura 3: fattore M er C-M-L 74 Figura 4: Andamento delle reioni al variare della ortata 76 Figura 5: Caduta totale di reione 8 INDICE DELLE TABELLE Non è tata trovata alcuna voce dell'indice delle figure.
Turbina a gas - struttura
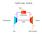 urbina a ga - truttura Fuel Combutore Comreore Ae urbina Aria Ga di carico urbina a ga Il ciclo termodinamico che decrive il funzionamento della turbina è il ciclo Joule Le traformazioni che avvengono
urbina a ga - truttura Fuel Combutore Comreore Ae urbina Aria Ga di carico urbina a ga Il ciclo termodinamico che decrive il funzionamento della turbina è il ciclo Joule Le traformazioni che avvengono
2. METODO DEGLI SPOSTAMENTI O EQUAZIONE DELLA LINEA ELASTICA, PER LA SOLUZIONE DI TRAVI IPERSTATICHE
 METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
0.005m. Termodinamica e trasmissione del calore 3/ed Yunus A. Çengel Copyright 2009 The McGraw-Hill Companies srl RISOLUZIONI CAP.
 Termodinamica e tramiione del calore 3/ed Yunu A. Çengel 1-1 oyright 009 The McGraw-Hill omanie rl RISOUZIONI AP. 1 1.1 e uerfici interna ed eterna di una arete di mattoni ono mantenute a temeratura cotante.
Termodinamica e tramiione del calore 3/ed Yunu A. Çengel 1-1 oyright 009 The McGraw-Hill omanie rl RISOUZIONI AP. 1 1.1 e uerfici interna ed eterna di una arete di mattoni ono mantenute a temeratura cotante.
TERMOFLUIDODINAMICA FLUIDI COMPRIMIBILI ED INCOMPREMIBILI FLUIDI BIFASE PROF. ING. GIULIANO CAMMARATA LUIGI CAMMARATA
 TERMOFLUIDODINAMICA FLUIDI COMPRIMIBILI ED INCOMPREMIBILI FLUIDI BIFASE LUIGI CAMMARATA 06 TERMO-FLUIDODINAMICA i FILE: TERMOFLUIDODINAMICA.doc AUTORI: PC E LUIGI CAMMARATA DATA: AGOSTO 06 www.gcammarata.net
TERMOFLUIDODINAMICA FLUIDI COMPRIMIBILI ED INCOMPREMIBILI FLUIDI BIFASE LUIGI CAMMARATA 06 TERMO-FLUIDODINAMICA i FILE: TERMOFLUIDODINAMICA.doc AUTORI: PC E LUIGI CAMMARATA DATA: AGOSTO 06 www.gcammarata.net
Esercizi svolti di geometria delle aree Alibrandi U., Fuschi P., Pisano A., Sofi A. ESERCIZIO n.7
 ESERCZO n.7 Data la ezione cava riportata in Figura, determinare: a) gli ai principali centrali di inerzia; b) l ellie principale centrale di inerzia; c) il nocciolo centrale di inerzia. cm cm A#7 . Determinazione
ESERCZO n.7 Data la ezione cava riportata in Figura, determinare: a) gli ai principali centrali di inerzia; b) l ellie principale centrale di inerzia; c) il nocciolo centrale di inerzia. cm cm A#7 . Determinazione
CAPITOLO 7 Un modello di scambio. Parte prima
 CPITOLO 7 Un modello di cambio Parte rima Il modello economico dello cambio: oibilità e deideri di cambio nalii delle oibili allocazioni riultanti dallo cambio 2005 EGE e Mario Gilli D. Kre, Microeconomia
CPITOLO 7 Un modello di cambio Parte rima Il modello economico dello cambio: oibilità e deideri di cambio nalii delle oibili allocazioni riultanti dallo cambio 2005 EGE e Mario Gilli D. Kre, Microeconomia
Sistemi aperti. Stato di flusso di massa
 Sitemi aperti ) Concetti di bae ) Primo principio della termodinamica 3) Secondo principio della termodinamica 4) Stati di equilibrio tabile 5) Diagramma energia-entropia 6) Lavoro, non-lavoro e calore
Sitemi aperti ) Concetti di bae ) Primo principio della termodinamica 3) Secondo principio della termodinamica 4) Stati di equilibrio tabile 5) Diagramma energia-entropia 6) Lavoro, non-lavoro e calore
TESTI E SOLUZIONI DEI PROBLEMI
 Univerità degli Studi di Udine, Coro di Laurea in Ingegneria Meccanica A.A. 217/218, Seione di Giugno/Luglio 218, Secondo Appello Eame di FISICA I, Prova critta del 2 Luglio 218 TESTI E SOLUZIONI DEI PROBLEMI
Univerità degli Studi di Udine, Coro di Laurea in Ingegneria Meccanica A.A. 217/218, Seione di Giugno/Luglio 218, Secondo Appello Eame di FISICA I, Prova critta del 2 Luglio 218 TESTI E SOLUZIONI DEI PROBLEMI
Meccanica Applicata alle Macchine Appello del 12/01/2012
 Meccanica Applicata alle Macchine Appello del 12/01/2012 1. Eeguire l analii tatica del meccanimo in figura 2 (cala 1:1). Si calcoli l azione reitente ul membro 5 quando F m =1N. 2. In figura 1 è rappreentato
Meccanica Applicata alle Macchine Appello del 12/01/2012 1. Eeguire l analii tatica del meccanimo in figura 2 (cala 1:1). Si calcoli l azione reitente ul membro 5 quando F m =1N. 2. In figura 1 è rappreentato
SEGNALI E SISTEMI 31 agosto 2017
 SEGNALI E SISTEMI 31 agoto 2017 Eercizio 1. [3+3+3+4 punti] Si conideri il modello ingreo/ucita LTI e cauale decritto dalla eguente equazione differenziale: dove a è un parametro reale. d 2 v(t) 2 +(1
SEGNALI E SISTEMI 31 agoto 2017 Eercizio 1. [3+3+3+4 punti] Si conideri il modello ingreo/ucita LTI e cauale decritto dalla eguente equazione differenziale: dove a è un parametro reale. d 2 v(t) 2 +(1
6.5. La compressione
 6.5. La comreione rofondimenti 6.5.1. I materiali iotroi Mentre alcuni materiali (come l acciaio) hanno un uguale comortamento a trazione e a comreione (ono cioè «materiali iotroi») altri (come le ghie,
6.5. La comreione rofondimenti 6.5.1. I materiali iotroi Mentre alcuni materiali (come l acciaio) hanno un uguale comortamento a trazione e a comreione (ono cioè «materiali iotroi») altri (come le ghie,
Esercizi di Controlli Automatici - 9 A.A. 2009/2010
 Eercizi di Controlli Automatici - 9 A.A. 2009/200 Eercizio. Dato il eguente chema, in cui gli amplificatori operazionali ono uppoti ideali, i calcoli la funzione di traferimento G() tra v in (t) e v out
Eercizi di Controlli Automatici - 9 A.A. 2009/200 Eercizio. Dato il eguente chema, in cui gli amplificatori operazionali ono uppoti ideali, i calcoli la funzione di traferimento G() tra v in (t) e v out
F = 150 N F 1 =? = 3,1 s. 3,2
 ESERCIZI SVOLTI : Principi di Newton Lavoro Energia Prof.. Marletta ITC Zanon - Udine ESERCIZIO (): Una caa di 30 kg viene tirata con una corda che forma un angolo di 50 col pavimento u una uperficie licia.
ESERCIZI SVOLTI : Principi di Newton Lavoro Energia Prof.. Marletta ITC Zanon - Udine ESERCIZIO (): Una caa di 30 kg viene tirata con una corda che forma un angolo di 50 col pavimento u una uperficie licia.
19.12. Impianti motori con turbine a gas
 19.12. Impianti motori con turbine a ga Approfondimenti 19.12.1. Generalità. Il ciclo di Brayton (o ciclo di oule) Il rendimento (h) di un ciclo termodinamico può eere epreo dalla relazione: h q up q inf
19.12. Impianti motori con turbine a ga Approfondimenti 19.12.1. Generalità. Il ciclo di Brayton (o ciclo di oule) Il rendimento (h) di un ciclo termodinamico può eere epreo dalla relazione: h q up q inf
Traiettoria La traiettoria è la linea che unisce le posizioni successive occupate dal punto materiale in movimento. Sistema di riferimento
 Punto materiale Quando l oggetto in movimento è molto piccolo ripetto alla ditanza che percorre, può eere tudiato come e foe un punto (non ha dimenioni, non ha un orientamento). Traiettoria La traiettoria
Punto materiale Quando l oggetto in movimento è molto piccolo ripetto alla ditanza che percorre, può eere tudiato come e foe un punto (non ha dimenioni, non ha un orientamento). Traiettoria La traiettoria
RACCOLTA DI ESERCIZI TRATTI DA TEMI D ESAME - parte 1^
 A.A. 2005/2006 Sitemi energetici (CINDK) RACCOLA DI ESERCIZI RAI DA EMI D ESAME - parte ^. Acqua viene caldata in una pentola ben chiua pota u un fornello mentre viene frullata con un frullatore. Durante
A.A. 2005/2006 Sitemi energetici (CINDK) RACCOLA DI ESERCIZI RAI DA EMI D ESAME - parte ^. Acqua viene caldata in una pentola ben chiua pota u un fornello mentre viene frullata con un frullatore. Durante
Errori e cifre significative. Incontro iniziale LAB2GO
 Errori e cifre ignificative Incontro iniziale LABGO La ditribuzione gauiana f tinyurl.com/labcalcquiz Propagazione degli errori Miure dirette: la grandezza fiica viene miurata direttamente (ad e. Speore
Errori e cifre ignificative Incontro iniziale LABGO La ditribuzione gauiana f tinyurl.com/labcalcquiz Propagazione degli errori Miure dirette: la grandezza fiica viene miurata direttamente (ad e. Speore
Esempi Calcolo Antitrasformate
 Eempi Calcolo Antitraformate Note per il Coro di FdA - Info April, 05 Il punto focale del coiddetto metodo di Heaviide per l antitraformazione di un egnale regolare a traformata razionale conite nel riconocere
Eempi Calcolo Antitraformate Note per il Coro di FdA - Info April, 05 Il punto focale del coiddetto metodo di Heaviide per l antitraformazione di un egnale regolare a traformata razionale conite nel riconocere
Stabilità e punti di equilibrio
 Capitolo 4 Stabilità e punti di equilibrio 4. Stabilità di un itema epreo da un equazione di tato Si è motrato come un itema poa eere epreo con il itema cotituito dalle equazioni 3.6 e 3.7 ovvero: X()
Capitolo 4 Stabilità e punti di equilibrio 4. Stabilità di un itema epreo da un equazione di tato Si è motrato come un itema poa eere epreo con il itema cotituito dalle equazioni 3.6 e 3.7 ovvero: X()
A.A MATERIALI POLIMERICI B. Capitolo 5 Calore specifico
 A.A. 2005-06 MATERIALI POLIMERICI B Capitolo 5 Calore pecifico A preione cotante il calore pecifico c p (JK -1 kg -1 ) o la capacità termica molare (JK -1 mol -1 ) ((298) = M 0 c p(298) con M 0 peo molecolare
A.A. 2005-06 MATERIALI POLIMERICI B Capitolo 5 Calore pecifico A preione cotante il calore pecifico c p (JK -1 kg -1 ) o la capacità termica molare (JK -1 mol -1 ) ((298) = M 0 c p(298) con M 0 peo molecolare
TERMODINAMICA E TERMOFLUIDODINAMICA. Cap. 6 CICLI TERMODINAMICI DIRETTI ED INVERSI
 ERMODINAMICA E ERMOFLUIDODINAMICA Cap. 6 CICLI ERMODINAMICI DIREI ED INVERSI max min Sorgente termica (Bruciatore) Q H = Q in a 2 Caldaia 2 L - = L in L + = L urbina out Pompa Condenatore = 2 = Q C = Q
ERMODINAMICA E ERMOFLUIDODINAMICA Cap. 6 CICLI ERMODINAMICI DIREI ED INVERSI max min Sorgente termica (Bruciatore) Q H = Q in a 2 Caldaia 2 L - = L in L + = L urbina out Pompa Condenatore = 2 = Q C = Q
Appunti ed esercitazioni di Microonde 2
 Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
Esercitazione di Controlli Automatici 1 n 6
 4 maggio 007 Eercitazione di Controlli Automatici n 6 a.a. 006/07 Si conideri il itema della eercitazione n 5 cotituito da un braccio robotico in rotazione, utilizzato per la movimentazione di oggetti.
4 maggio 007 Eercitazione di Controlli Automatici n 6 a.a. 006/07 Si conideri il itema della eercitazione n 5 cotituito da un braccio robotico in rotazione, utilizzato per la movimentazione di oggetti.
Esame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A
 Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c 2 ; P 1 1( ( + 4 ; P 2 ( ( + 1 (
Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c 2 ; P 1 1( ( + 4 ; P 2 ( ( + 1 (
Calcolo della tensione ammissibile Dovendo essere il grado di sicurezza non inferiore a 3 si ricava che il coefficiente di sicurezza γ è 3 per cui:
 Il recipiente diegnato in figura ha una configurazione cilindrica avente diametro interno D = 000 mm è chiuo con fondi emiferici, eo è itemato u due elle A e B pote ad una ditanza L AB = 7000 mm e fuoriece
Il recipiente diegnato in figura ha una configurazione cilindrica avente diametro interno D = 000 mm è chiuo con fondi emiferici, eo è itemato u due elle A e B pote ad una ditanza L AB = 7000 mm e fuoriece
ESERCIZI DI CONTROLLI AUTOMATICI Prof. Gianluigi Pillonetto 21 NOVEMBRE d 2 (t) r(t) e(t) y(t) C(s)G(s)
 ESERCIZI DI CONTROLLI AUTOMATICI Prof. Gianluigi Pillonetto 2 NOVEMBRE 206 Ex. Si conideri il itema di controllo d (t) d 2 (t) C()G() K Calcolare le funzioni di traferimento che legano le eguenti coppie
ESERCIZI DI CONTROLLI AUTOMATICI Prof. Gianluigi Pillonetto 2 NOVEMBRE 206 Ex. Si conideri il itema di controllo d (t) d 2 (t) C()G() K Calcolare le funzioni di traferimento che legano le eguenti coppie
Esercizio. Il circuito di figura rappresenta un filtro passa-banda. Dopo aver ricavato la funzione di trasferimento, sapendo che
 Eercizio Clae 5ª Elettronici Materia Sitemi Argomento Funzioni di traferimento Il circuito di figura rappreenta un filtro paa-banda. Dopo aver ricavato la funzione di traferimento, apendo che R = 2k Ω
Eercizio Clae 5ª Elettronici Materia Sitemi Argomento Funzioni di traferimento Il circuito di figura rappreenta un filtro paa-banda. Dopo aver ricavato la funzione di traferimento, apendo che R = 2k Ω
CONDIZIONI DI RACCORDO DEI CAMPI ELETTROMAGNETICI ˆ = SULL INTERFACCIA TRA DUE MEZZI OMOGENEI
 CONDIZIONI DI RACCORDO DEI CAMPI ELETTROMAGNETICI SULL INTERFACCIA TRA DUE MEZZI OMOGENEI Conideriamo le equazioni di Maxwell in una regione di pazio riempita da un mezzo omogeneo e iotropo caratterizzato
CONDIZIONI DI RACCORDO DEI CAMPI ELETTROMAGNETICI SULL INTERFACCIA TRA DUE MEZZI OMOGENEI Conideriamo le equazioni di Maxwell in una regione di pazio riempita da un mezzo omogeneo e iotropo caratterizzato
Flessione su 4 punti. Configurazione sperimentale. Schematizzazione di calcolo. Studio delle sollecitazioni semplici. Taglio.
 Fleione u punti Configurazione imentale Scematizzazione di calcolo Taglio omento flettente Studio delle ollecitazioni emplici Tratto ollecitato da fleione pura la ua deformata è un arco di cercio Deformazioni
Fleione u punti Configurazione imentale Scematizzazione di calcolo Taglio omento flettente Studio delle ollecitazioni emplici Tratto ollecitato da fleione pura la ua deformata è un arco di cercio Deformazioni
Liceo Scientifico Cassini Esercizi di fisica, classe 3G, foglio7
 Liceo Scientifico Caini Eercizi di fiica, clae 3G, foglio7 Problema1 In una gara ui 200m un corridore percorre i primi 40m con un accelerazione di 1.5 m ed il reto della gara di moto rettilineo uniforme.
Liceo Scientifico Caini Eercizi di fiica, clae 3G, foglio7 Problema1 In una gara ui 200m un corridore percorre i primi 40m con un accelerazione di 1.5 m ed il reto della gara di moto rettilineo uniforme.
Modello di Greitzer (1976) Simulazione del comportamento dinamico di compressori
 Modello di Greitzer (1976) Simulazione del comortamento dinamico di comressori Iotesi del modello. Si consideri un sistema fisico comosto, nell ordine, da un comressore, un lenum ed una valvola di strozzamento.
Modello di Greitzer (1976) Simulazione del comortamento dinamico di comressori Iotesi del modello. Si consideri un sistema fisico comosto, nell ordine, da un comressore, un lenum ed una valvola di strozzamento.
Con riferimento ad uno schema di trave semplicemente appoggiata di lunghezza L = 6 m il momento flettente massimo in mezzeria è pari a:
 Eempio Verifica dell apertura delle feure Si conidera la ezione rettangolare caratterizzata dalle eguenti proprietà: - bae b = 00 mm, - altezza totale h = 00 mm, - copriferro c =0 mm, - altezza utile d
Eempio Verifica dell apertura delle feure Si conidera la ezione rettangolare caratterizzata dalle eguenti proprietà: - bae b = 00 mm, - altezza totale h = 00 mm, - copriferro c =0 mm, - altezza utile d
FUNZIONI DI TRASFERIMENTO
 FUNZIONI DI TRASFERIMENTO Funzioni Di Traferimento La difficoltà maggiore nel trattare i modelli matematici di itemi dinamici lineari è dovuta al fatto che le equazioni delle leggi fiiche che decrivono
FUNZIONI DI TRASFERIMENTO Funzioni Di Traferimento La difficoltà maggiore nel trattare i modelli matematici di itemi dinamici lineari è dovuta al fatto che le equazioni delle leggi fiiche che decrivono
Fondamenti di Automatica Figura 1: Schema di centrifuga industriale: a) vista in assonometria b) vista frontale.
 Fondamenti di Automatica 6-9-26 Figura : Schema di centrifuga indutriale: a) vita in aonometria b) vita frontale. A In Fig..a è riportato lo chema emplificato di una centrifuga orizzontale indutriale di
Fondamenti di Automatica 6-9-26 Figura : Schema di centrifuga indutriale: a) vita in aonometria b) vita frontale. A In Fig..a è riportato lo chema emplificato di una centrifuga orizzontale indutriale di
Compito di Fondamenti di Automatica settembre 2006
 Compito di Fondamenti di Automatica ettembre 2006 Eercizio 1. Si conideri lo chema di figura (operazionale ideale, eccetto per il guadagno che puó eere definito da una G(), reitenze uguali, condenatori
Compito di Fondamenti di Automatica ettembre 2006 Eercizio 1. Si conideri lo chema di figura (operazionale ideale, eccetto per il guadagno che puó eere definito da una G(), reitenze uguali, condenatori
LAVORO ED ENERGIA. 1J = 1N 1m
 ppunti di fiica LVORO ED ENERGI LVORO Nel linguaggio cientifico il termine lavoro ha un ignificato ben precio e talvolta divero da quello che queto termine aume nel linguaggio quotidiano. In fiica il concetto
ppunti di fiica LVORO ED ENERGI LVORO Nel linguaggio cientifico il termine lavoro ha un ignificato ben precio e talvolta divero da quello che queto termine aume nel linguaggio quotidiano. In fiica il concetto
Esercitazione 16 Novembre 2012 Circuiti dinamici del secondo ordine. t come riportato in figura.
 Eercitazione Noembre ircuiti dinamici del econdo ordine ircuito L- erie Per quanto riguarda queto circuito, l eercizio egue la traccia della oluzione del compito d eame numero, reperibile in rete al olito
Eercitazione Noembre ircuiti dinamici del econdo ordine ircuito L- erie Per quanto riguarda queto circuito, l eercizio egue la traccia della oluzione del compito d eame numero, reperibile in rete al olito
PROBLEMI RISOLTI DI DINAMICA
 PROBLEMI RISOLTI DI DINAMICA 1 Un autoobile di aa 100 Kg auenta in odo unifore la ua velocità di 30 / in 0 a) Quale forza agice durante i 0? b) Quale forza arebbe necearia per ipriere un accelerazione
PROBLEMI RISOLTI DI DINAMICA 1 Un autoobile di aa 100 Kg auenta in odo unifore la ua velocità di 30 / in 0 a) Quale forza agice durante i 0? b) Quale forza arebbe necearia per ipriere un accelerazione
Postulato delle reazioni vincolari
 Potulato delle reazioni vincolari Ad ogni vincolo agente u un punto materiale P può eere otituita una forza, chiamata reazione vincolare, che realizza lo teo effetto dinamico del vincolo. reazione vincolare
Potulato delle reazioni vincolari Ad ogni vincolo agente u un punto materiale P può eere otituita una forza, chiamata reazione vincolare, che realizza lo teo effetto dinamico del vincolo. reazione vincolare
Lezione 25 - Flessione deviata e sforzo normale eccentrico
 Lezione 5 - Fleione deviata e forzo normale eccentrico ü [A.a. 011-01 : ultima reviione 1 gennaio 01] Con lo tudio della fleione fuori del piano i e' eaurito l'eame delle ollecitazioni emplici di De Saint
Lezione 5 - Fleione deviata e forzo normale eccentrico ü [A.a. 011-01 : ultima reviione 1 gennaio 01] Con lo tudio della fleione fuori del piano i e' eaurito l'eame delle ollecitazioni emplici di De Saint
Errori di misura. è ragionevole assumere che una buona stima del valore vero sia la media
 Errori di miura Se lo trumento di miura è abbatanza enibile, la miura rietuta della tea grandezza fiica darà riultati diveri fra loro e fluttuanti in modo caratteritico. E l effetto di errori cauali, o
Errori di miura Se lo trumento di miura è abbatanza enibile, la miura rietuta della tea grandezza fiica darà riultati diveri fra loro e fluttuanti in modo caratteritico. E l effetto di errori cauali, o
