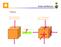
Prova di compressione monoassiale

Transcript

1 Prova di compressione monoassiale σ σ f σ y Y G ε e F OY : comportamento elastico YF : comportamento elastoplastico GB : scarico - ricarico F : rottura σ y : tensione di snervamento σ f : tensione di rottura ε e : deformazione elastica ε p : deformazione plastica O B ε p,g ε

2 In uno stato tensionale piano o tridimensionale, ai concetti di tensione di snervamento e di punto di snervamento devono essere sostituiti quelli di stato tensionale di snervamento e luogo di snervamento Criterio di snervamento: F ( ) σ, ε p = 0 ij ij σ 1 σ 2 σ 3 Incrudimento isotropo Incrudimento cinematico Plasticità perfetta ( ) = 0 F σ ij

3 Deve essere sempre verificata la condizione: F ( p ) σ, ε 0 ij che esprime la condizione che il punto rappresentativo dello stato tensionale può trovarsi solo sulla superficie di snervamento o all interno di essa ij Se df>0, si ha a che fare con un percorso di carico, le deformazioni sono elastoplastiche, la superficie si espande. Se df<0, il percorso è di scarico e le deformazioni sono elastiche. Gli incrementi di deformazione elastica sono funzione solo dei corrispondenti incrementi di tensione, e sono coassiali con essi. Gli incrementi di deformazione plastica sono funzione degli incrementi di tensione, ma sono diretti normalmente a un potenziale plastico In altre parole, gli incrementi di sforzo determinano il valore ma non la direzione degli incrementi di deformazione plastica

4 Per una classe di materiali, detti materiali standard o materiali con legge di flusso associata il potenziale plastico coincide con la funzione di snervamento Questi materiali possono essere definiti stabili secondo Drucker, e quindi: la superficie di snervamento deve essere convessa l incremento di deformazione plastica deve essere normale alla superficie di snervamento e diretto verso l esterno è possibile dimostrare l unicità della soluzione di problemi al contorno valgono i teoremi dell analisi limite

5 Analisi limite consente di calcolare un limite superiore e un limite inferiore del carico di collasso è valida a rigore per un materiale perfettamente plastico con legge di flusso associata può essere applicata a un elemento strutturale, a una struttura, a un continuo studiando diversi sistemi, è spesso possibile restringere l intervallo e talvolta individuare la soluzione esatta

6 Teorema del limite superiore (o teorema del maggiorante, o teorema cinematico) Se esistono un sistema di carichi esterni e un meccanismo di collasso plastico tale che il lavoro dei carichi esterni per un incremento di spostamento sia uguale al lavoro delle forze interne, si verifica il collasso; il sistema di carichi esterni è maggiore o uguale al vero carico di collasso. Il meccanismo di collasso deve essere congruente, ma non necessariamente quello reale; non appaiono le condizioni di equilibrio.

7 Teorema del limite inferiore (o teorema del minorante, o teorema statico) Se esiste un sistema di carichi esterni in equilibrio con una distribuzione di sforzi interni che non ecceda in alcun punto la resistenza del materiale, il collasso non si verifica il sistema di carichi esterni è minore o uguale al vero carico di collasso. Lo stato di sforzo interno non deve essere necessariamente quello che effettivamente si verifica al collasso, ma solo essere equilibrato e compatibile con la resistenza del materiale non appaiono le condizioni di congruenza.

8 F l/2 l Trave costituita da materiale isoresistente con tensione di snervamento pari a σ y Sezione rettangolare b h h M y = 1 6 bh 2 σ y b σ y M f = 1 4 bh 2 σ y

9 F δα δw δα Teorema cinematico 2δα Meccanismo: formazione di tre cerniere plastiche Lavoro delle forze esterne Fδw = Fδαl/2 Lavoro delle forze interne 4M f δα l F α = 2 M F = 8 l 4M f f α bh = 2 l 2 σ y M f = 1 4 bh 2 σ y

10 F δα δw δα Teorema statico 2δα FL/8 FL/8 FL/8 Distribuzione di sforzi interni equilibrata e compatibile se Fl/8 M y Fl 8 = M y = 1 6 bh 2 bh σ y F = 133, l 2 σ y

11 Campo dello sforzo di collasso bh 2 bh 2 1, 33 σ F 2 σ l y l y

12

13

14

15

16

17

18

19 Per applicare l analisi limite a un corpo continuo perfettamente plastico, occorre precisare alcuni caratteri del campo di sforzo e dei meccanismi di collasso Per semplicità ci limiteremo alle condizioni non drenate, e quindi ad un mezzo con ϕ = 0, c = c u

20 Discontinuità delle tensioni Gli stati tensionali, che vengono considerati nel calcolo del limite inferiore, possono presentare discontinuità, a patto che non vengano violate le condizioni di equilibrio σ na = σ nb τ na = τ nb

21 Gli stati tensionali nelle regioni A e B separate dalla discontinuità possono essere caratterizzati dalle quantità p a, r a e p b, r b Traccia del piano sul quale agisce σ 1a Nel passare da A a B attraverso la discontinuità, la tensione principale ruota di un angolo: δ θ = θ b - θ a Angolo in C= 2δθ 360-2θb θa 180-2θb θb Traccia del piano sul quale agisce σ 1b Poli dei due cerchi

22 Se il mezzo è coesivo ed ambedue le regioni A e B sono in stato di rottura, i relativi cerchi di Mohr saranno tangenti all inviluppo di rottura τ = c u AC = cu δ p = 2c u senδθ (p b p a ) = 2c u sen(θ b θ a ) 2θ a 2δθ 2θ b Nel passare da A a B la variazione della tensione normale media è legata alla rotazione della tensione principale massima

23 Ventaglio di discontinuità tensionali θ f = (n-1)δθ Δθ = nδθ θ/n = δθ θ f = Δθ(n-1)/n Δp=n(2c u sen δ θ)= n(2c u sen (θ f / (n-1)) Per n si ha: θf = θ La variazione della direzione delle tensioni principali tra A e B e pari all ampiezza del ventaglio Inoltre si ha: p = 2c u θ

24 Diagrammi degli spostamenti ogni regione del corpo viene indicata con una lettera maiuscola, inclusa la regione che non partecipa al moto che si indica con O Lo spostamento di ogni blocco è rappresentato da un vettore, il cui estremo è indicato con una lettera minuscola il vettore congiungente due punti rappresenta in grandezza e direzione lo spostamento relativo dei due blocchi corrispondenti

25 Ventagli di linee di scorrimento Cinematismo non possibile: violerebbe la continuità del mezzo plastico

26 Ventagli di linee di scorrimento Al tendere di δ θ a 0 si ottiene

27 Spostamento lungo l arco di circonferenza = δw Spostamento fra due settori contigui δw i,j =δwδθ Lavoro in un settore δw = c u R(δwδθ) + c u (Rδθ)δw Lavoro compiuto tra due settori contigui Lavoro compiuto lungo l arco di circonferenza

28 = = f a f u a u w R c w R c W ϑ ϑ ϑ In altri termini, il lavoro compiuto dagli sforzi interni in un ventaglio di discontinuità di apertura θ f per uno spostamento δw a lungo l arco di cerchio è pari al doppio di quello corrispondente ad un settore circolare

29 Carico limite di una fondazione nastriforme su terreno coesivo (argilla satura non drenata; tensioni totali)

30 Limite superiore (teorema cinematico) 1 tentativo δw f = Bδθ/2 δw = Bδθ Lavoro del carico esterno: F u Bδθ/2 Lavoro degli sforzi interni: πbc u Bδθ F u Bδθ/2 = πb 2 c u δθ La forza peso del blocco non compie lavoro perchè lo spostamento del baricentro è orizzontale q lim = F u /B = 2πc u

31 Limite inferiore (teorema statico) Sforzi di taglio nulli su p. verticali Zone I e III: σ z = γz =σ 3 Zone II e IV: σ z =q lim + γz = σ 1 θ = 90 p = 2c u sen θ = 2c u q lim + γz = γz + 4c u p = 2c u q lim = 4c u p = 2c u

32 Limite superiore (teorema cinematico) Tratto L Spostamento Lavoro OA B/ 2 2δw f OB B 2δw f OC B/ 2 2δw f AB B/ 2 2δw f BC B/ 2 2δw f c u Bδw f 2c u Bδw f c u Bδw f c u Bδw f c u Bδw f Lavoro totale = 6c u Bδw f Fδw f = 6c u Bδw f q lim = F/B = 6c u Il lavoro totale della forza peso è nullo

33 Limite inferiore (Teorema statico) Zona I: σ z = γz = σ 3 tensione principale minima Zona III: σ z =q lim + γz = σ 1 tensione principale massima o attraverso le formule generali viste nelle diapositive precedenti oppure per via geometrica con i cerchi di mohr in basso a sinistra θ = 90 ; n = 2 θ f = (n-1)/n θ = 45 δθ = θ/2 = 45 δp = 2c u senδθ = 2 c u p = 2 2 c u p = 2δp = 2 2 c u q lim + γz = 2 2 c u + 2c u + γz q lim = 2(1+ 2)c u

34 Limite superiore (Teorema cinematico) Ventaglio Raggio R = B/ 2 Tratto L Spostamento Lavoro OA B 2 2 δw f B 2 2 δw f c u Bδw f c u Bδw f Ventaglio πc u Bδw f Fδw f = (2 + π)c u Bδw f q lim = F/B =(2 + π)c u

35 Limite inferiore (Teorema statico) Ventaglio Ventaglio Zona I: σ z = γz = σ 3 Zona III: q lim + γz = σ 1 θ f = θ = π/2 p = 2c u θ=πc u dimostrata in precedenza q lim + γz = 2cu + γz + πc u q lim =(2 + π)c u p =2cu θ =πc u

36 Tentativo Limite superiore Limite inferiore 1 2πc u = 6,28 c u 4c u 2 6c u 2(1+ 2)c u = 4,82c u 3 (2+π)c u = 5,14c u (2+π)c u = 5,14c u