Forme alternative delle equazioni
|
|
|
- Giuseppa Maggi
- 5 anni fa
- Visualizzazioni
Transcript
1 Forme alternative delle equazioni In questo capitolo ripresentiamo le diverse forme in cui è comodo porre le equazioni del moto dei fluidi. Particolare attenzione verrà dedicata al caso di fluido non viscoso e non conduttore del calore (equazioni di Eulero, per il rilievo che avrà nel seguito del volume. Indice del capitolo.1 Le diverse formulazioni per le equazioni del moto Le coordinate lagrangiane Le equazioni di Eulero L equazione di continuità XXX L equazione di bilancio della quantità di moto XXX L equazione di bilancio dell energia Casi semplificati Il caso incomprimibile XXX Il caso comprimibile isoentropico La forma di Crocco dell equazione per la quantità di moto Le diverse forme del teorema di Bernoulli Le equazioni di Navier Stokes Il caso incomprimibile La forza di gravità La forma adimensionale delle equazioni Le diverse formulazioni per le equazioni del moto Le equazioni del moto dei fluidi possono essere scritte in diverse formulazioni, più o meno equivalenti e più o meno complesse. Il passaggio dall una all altra forma è comunque un operazione puramente matematica, che non comporta ipotesi
2 4 Capitolo fisiche addizionali. Rispetto alla formulazione integrale, utilizzata come punto di partenza nel Capitolo precedente, l unica richiesta aggiuntiva è la continuità delle funzioni integrande. Esiste anzitutto la forma conservativa, che è quella utilizzata finora, dotata della struttura classica in cui la variazione temporale della quantità conservata viene direttamente legata alla divergenza del suo flusso più un eventuale termine di sorgente. Esiste poi una formulazione, detta non conservativa oppure convettiva, che può essere più semplice e sintetica in alcuni casi e sfrutta l operatore di derivata materiale. Infine, introducendo un opportuno sistema di riferimento in moto localmente con la velocità del fluido (le coordinate lagrangiane, si possono scrivere le equazioni anche nella forma lagrangiana, che verrà descritta nel prossimo Capitolo (limitatamente alle equazioni di bilancio di massa e quantità di moto e che si presenta in generale più complessa delle equivalenti forme euleriane, ma consente talora considerazioni più immediate. Quando infine le relazioni differenziali vengono integrate su un volume V, si ottiene come noto la formulazione integrale, che presenta il fondamentale vantaggio di non richiedere la continuità delle funzioni integrande e che quindi può essere applicata anche in presenza di discontinuità. Vale la pena di notare che studiando la dinamica dei fluidi avremo modo di incontrare casi importanti in cui il campo di moto presenta delle discontinuità..1.1 Le coordinate lagrangiane Le coordinate lagrangiane sono un sistema di riferimento che segue il moto del fluido, e che risulta quindi legato al sistema di riferimento fisso da una relazione che si complica con il trascorrere del tempo. Talvolta è utile scrivere le equazioni del moto dei fluidi rispetto a questo sistema di riferimento, perché in questo modo permettono considerazioni più immediate. Per la definizione delle coordinate lagrangiane, introduciamo a fianco della terna fissa x = (x 1, x, x 3 una ulteriore terna ξ = (ξ 1, ξ, ξ 3 che si muove localmente con la velocità macroscopica del fluido ed è coincidente, al tempo t = 0, con la terna x. La legge di cambiamento di coordinate è data dalla equazione differenziale: x con la condizione iniziale che per t = 0 sia x = ξ. = V(x, t (.1 ξ La derivata materiale nel sistema lagrangiano In un cambio di coordinate spazio-temporali definito da due trasformazioni generiche x = x(ξ, t e t = t(ξ, t, le derivate spaziali e temporali si trasformano nel modo seguente: = x j + ξ i ξ i x j ξ i = x j + x j (.a (.b
3 Forme alternative delle equazioni 5 ξ ξ PSfrag replacements x ξ 3 V ξ 1 x x 1 x 3 Figura.1 La definizione del sistema di coordinate lagrangiane La trasformazione lagrangiana è definita dalla relazione (.1, che per componenti si scrive: x j = V j mentre la coordinata temporale non viene modificata, cioè t = t. La derivata temporale nel sistema ξ diviene quindi = + V j x j e coincide quindi con l operatore di derivata sostanziale o materiale, definito come. Le equazioni di Eulero D Dt = + V (.3 Le equazioni di bilancio per la massa (1.6, la quantità di moto (1.14 e l energia (1.16, ricavate nel caso di equilibrio termodinamico locale ed esclusivamente sulla base di considerazioni di simmetria ed invarianza, prendono il nome di equazioni di Eulero, e valgono per ogni tipo di fluido data la generalità delle ipotesi sulle quali sono fondate. Esse costituiscono un sistema di cinque equazioni differenziali in sei incognite, che diventa un sistema chiuso se si conosce anche l equazione di stato, cioè una relazione funzionale fra le variabili termodinamiche densità, energia interna e pressione. ρ + (ρv = 0 (.4a
4 6 Capitolo [ ρ (ρv (e + V + (ρvv + p I = F (.4b ] [ + ρ (e + V ] V + pv = L (.4c f(ρ, p, e = 0 (.4d..1 L equazione di continuità Forma differenziale conservativa La formulazione conservativa dell equazione di bilancio della massa, come già visto, è: ρ + (ρv = 0 (.5a Forma differenziale convettiva Sviluppando il termine (ρv si giunge alla formulazione non conservativa (detta anche convettiva: ρ + V ρ + ρ V = 0 (.5b Essa può ancora essere riscritta utilizzando l operatore di derivata sostanziale: Dρ Dt + ρ V = 0 (.5c Forma integrale Integrando l equazione (.5a su un volume V delimitato da un contorno V, e sfruttando il teorema della divergenza, si ottiene la formulazione integrale: ρ dv + V V n ρv ds = 0 (.5d.. XXX L equazione di bilancio della quantità di moto La formulazione conservativa di tale equa- Forma differenziale conservativa zione, come già visto, è: (ρv + (ρvv + p I = F (.6a
5 Forme alternative delle equazioni 7 Si giunge alla formulazione convettiva tra- Forma differenziale convettiva sformando (ρvv come: (ρvv = (ρv V + ρ (V V e sfruttando la relazione (che sconta anche l equazione di continuità: (ρv = ρ V + ρv = ρv (ρvv Scrivendo infine per semplicità (p I = p, risulta: ρ V + ρ (V V + p = F (.6b Utilizzando l operatore di derivata sostanziale, si ha anche: COMMENTO ρ DV Dt + p = F (.6c Forma integrale Integrando l equazione (.6a su un volume V, delimitato da un contorno V, e sfruttando il teorema della divergenza, si ottiene la forma integrale: ρv dv + V V n (ρvv + p I ds = V F dv (.6d..3 XXX L equazione di bilancio dell energia Forma differenziale conservativa La formulazione conservativa dell equazione di bilancio per l energia, come già visto, è: [ ρ (e + V ] [ + ρ (e + V ] V + pv = L (.7a Si giunge alla formulazione convettiva ri- Forma differenziale convettiva scrivendo l equazione come: ρ (e + V + ρ (e + V (ρv (e + V + + ρv (e + V + (pv = L
6 8 Capitolo Il primo ed il terzo addendo sono uguali ed opposti, a seguito dell equazione di continuità; l equazione si semplifica quindi come: ρ (e + V + ρv (e + V + (pv = L Si ottiene una forma ancora più semplice sottraendo alla relazione precedente l equazione di bilancio della quantità di moto in forma convettiva (.6b moltiplicata scalarmente per V, cioè: ρ ( ( V V + ρv + V p = V F Il risultato è una equazione evolutiva per la sola energia interna e: ρ e + ρv e + Vp = L V F (.7b Utilizzando il simbolo di derivata sostanziale, si arriva alla forma più compatta: ρ De Dt + Vp = L V F (.7c Forma convettiva per l entropia L equazione dell energia può essere ulteriormente semplificata se la scriviamo in termini della variabile termodinamica entropia s invece che per l energia e. Supponendo nulla per semplicità la forza di volume e quindi il suo lavoro per unità di tempo, la (.7c diviene: ρ De Dt + Vp = 0 La divergenza del vettore velocità può essere ricavata dall equazione di continuità in forma convettiva (.5c; dividendo inoltre per la densità si ottiene: È noto dalla Termodinamica che De Dt p Dρ ρ Dt = 0 T ds = de + pdv in cui v è il volume specifico, ovvero l inverso della densità, mentre s è l entropia per unità di massa. Passando dal volume specifico alla densità si ha anche che: T ds = de p dρ ρ L equazione dell energia diviene quindi, passando dai differenziali alle derivate sostanziali: Ds Dt = 0 (.7d COMMENTO
7 Forme alternative delle equazioni 9 Forma integrale Integrando l equazione (.7a su un volume V, delimitato da un contorno V, e sfruttando il teorema della divergenza, si ottiene la forma integrale: ρ (e + V V dv + V n [ ρ (e + V ] V + pv ds = V L dv (.7e.3 Casi semplificati Spesso sono possibili ipotesi semplificative ulteriori rispetto a quella di fluido non viscoso. Nel seguito si descrivono le equazioni nei due casi importanti di fluido incomprimibile oppure comprimibile ma in moto isoentropico..3.1 Il caso incomprimibile Se nel moto del fluido si possono trascurare gli effetti della sua comprimibilità, si assume che dρ/dp = 0. L equazione di stato, che rappresenta un legame fra le variabili termodinamiche di stato, si riduce in questo caso alla semplice asserzione che la densità rimane costante: ρ = cost. L equazione dell energia si disaccoppia dal sistema delle equazioni di Eulero, e le altre equazioni dinamiche costituiscono un sottosistema indipendente, che può essere risolto separatamente. Tenendo quindi conto della condizione di incomprimibilità, le equazioni (.4a e (.4b possono riscriversi come: V = 0 in cui f = F/ρ è una forza per unità di massa. V + (V V + 1 ρ p = f (.8.3. XXX Il caso comprimibile isoentropico Se l entropia è costante, come conseguenza dell equazione dell energia nella forma (.7d, l equazione di stato nella forma ρ = ρ(p, s si limita ad affermare che la densità è funzione solo della pressione. Si può allora definire un potenziale termodinamico P secondo la relazione: P (p = p p 0 1 ρ(p dp (.9 In questo modo la funzione P coincide con la pressione divisa per la densità nel caso incomprimibile, mentre nel caso isoentropico si identifica con l entalpia.
8 30 Capitolo Grazie alla definizione (.9 di P, l equazione per la quantità di moto per un fluido comprimibile in moto isoentropico (e in generale per tutti i casi in cui l equazione di stato contempli la dipendenza da una sola delle variabili termodinamiche si può scrivere in maniera identica a quella del sistema (.8, cioè a quella per fluido incomprimibile, pur di sostituire il termine di pressione 1/ρ p con P. Il sistema delle equazioni diviene allora: COMMENTO ρ + (ρv = 0 V + (V V + P = f. ( La forma di Crocco dell equazione per la quantità di moto Nei due casi particolari di fluido incomprimibile oppure comprimibile ma in moto isoentropico, l equazione di bilancio per la quantità di moto può essere scritta in una forma particolare che verrà utilizzata nel seguito, e che prende il nome di forma di Crocco. Ricordando l identità vettoriale (B.4 per il doppio prodotto vettoriale, e la particolare espressione (B.9 che essa assume quando il secondo operatore è, si ha che: V ( V = ( V V (V V (.11 L equazione di bilancio per la quantità di moto del sistema (.10 può perciò essere posta anche nella forma: V + ( V V V ( V + P = f Osservando ora che la quantità ( V V rappresenta il gradiente di uno scalare, cioè ( V /, e riunendo tutti i termini sotto l operatore di gradiente, si ha: ( V V + + P + ( V V = f Si introduce ora il vettore vorticità, che è una grandezza derivata definita come rotore del campo di velocità: ω = V L equazione di bilancio della quantità di moto si può scrivere allora, facendo comparire anche la vorticità, nella seguente forma di Crocco: ( V V + + P + ω V = f (.1
9 Forme alternative delle equazioni 31.4 Le diverse forme del teorema di Bernoulli Il fine principale dell Aerodinamica consiste nel calcolo delle forze e dei momenti che agiscono su un corpo solido in moto relativo rispetto ad una corrente fluida. Già si è visto nel paragrafo 1.6 che tale calcolo si riconduce, nel caso non viscoso, al calcolo dell integrale degli sforzi normali sul contorno del corpo. L equazione di bilancio della quantità di moto, nella forma di Crocco (.1 in cui supponiamo f = 0, consente sotto opportune ipotesi di mettere in evidenza il legame fra gli sforzi normali (che nel caso non viscoso coincidono con la pressione e la soluzione del campo cinetico. Questo legame si può considerare un integrale primo del moto. Il caso stazionario Si faccia l ipotesi di moto stazionario. Il primo addendo della (.1 è allora nullo. Moltiplicando scalarmente gli altri due termini per V, si nota che il prodotto V (ω V è identicamente nullo. L equazione si riduce quindi alla forma: ( V V + P = 0 (.13 che esprime la costanza del binomio P + V / lungo ogni linea di corrente. Questa relazione costituisce il classico teorema di Bernoulli, e può essere considerata come un integrale primo delle equazioni del moto. Una volta calcolata la velocità, essa consente immediatamente di risalire alla pressione, e quindi alla forza aerodinamica. Si noti in particolare che, se le linee di corrente provengono dall infinito a monte, dove la soluzione è nota dalle condizioni all infinito, allora il binomio V /+P oltre che costante è da ritenersi noto. Inoltre se le condizioni all infinito sono di moto uniforme, la costante è la medesima in tutto il campo di moto. Con identico procedimento, moltiplicando scalarmente la (.1 per ω invece che per V, si ottiene: ( V ω + P = 0 da cui si deduce che il binomio V / + P è costante anche su linee parallele ad ω, cioè su linee vorticose. Il caso stazionario e irrotazionale Se oltre all ipotesi di stazionarietà si formula anche quella di irrotazionalità ed è V = ϕ, l equazione di bilancio della quantità di moto si riduce a ( ϕ ϕ + P = 0 e quindi il binomio V / + P è costante ovunque nel campo di moto.
10 3 Capitolo Il caso irrotazionale Anche nel caso instazionario, quando il moto è irrotazionale la velocità si può esprimere come gradiente di un potenziale ϕ. L equazione (.1 diviene: ( ϕ ϕ ϕ + + P = 0 Invertendo l ordine di derivazione fra derivate spaziali e temporali, si arriva a scrivere il teorema di Bernoulli nella sua più generale forma instazionaria, nota anche come equazione della pressione. In tutto lo spazio risulta: ϕ + ϕ ϕ + P = cost = f(t (.14 Questa espressione, in cui f è una grandezza a gradiente nullo e quindi può essere solo una funzione del tempo, costituisce, una volta esplicitata rispetto a P, lo strumento più generale per ricavare (nel caso incomprimibile la pressione una volta che sia nota la velocità..5 Le equazioni di Navier Stokes Le equazioni di bilancio per la massa, quantità di moto ed energia ricavate sotto l ipotesi di quasi-equilibrio termodinamico prendono il nome di equazioni di Navier Stokes, e valgono per ogni tipo di fluido data la generalità delle ipotesi sulle quali sono fondate. Esse costituiscono un sistema chiuso di equazioni differenziali, se si conosce anche l equazione di stato, cioè una relazione funzionale fra le variabili termodinamiche densità, energia interna e pressione. ρ + (ρv = 0 (.15a (ρv ( + ρvv + p I + J d Q = F (.15b [ ρ (e + V ] [ + ρ (e + V ] V + pv + J d Q V + Jd E = L (.15c in cui i flussi dissipativi J d Q di quantità di moto e Jd E di energia sono espressi rispettivamente dalle relazioni (1.18 e ( Il caso incomprimibile Nel caso incomprimibile in cui l equazione di stato si riduce a ρ = cost, le equazioni di Navier Stokes assumono una forma più semplice. Come nel caso non viscoso, l equazione dell energia si disaccoppia dal resto del sistema, mentre l equazione di continuità si traduce nella condizione cinematica: V = 0
11 Forme alternative delle equazioni 33 Facendo l ulteriore ipotesi di considerare un fluido a proprietà costanti, l equazione di bilancio (.15b per la quantità di moto diviene: ρ V (VV + ρ + pρ I = F + µ [ V (s] Grazie all ipotesi di incomprimibilità si ottiene che (VV è pari a (V V. Inoltre risulta: ( V (s = ( V = V Dividendo per la densità, si giunge così alla formulazione delle equazioni di Navier Stokes per fluido incomprimibile e a proprietà costanti: V = 0 V + (V V + 1 ρ p = µ ρ V + f.6 La forza di gravità Nel caso incomprimibile, in cui si tratta la densità come una costante, spesso la forza F che compare nel bilancio (.6a e (.15b della quantità di moto viene omessa. La forza di gravità F g è in realtà sempre presente, ma è possibile non scriverla nelle equazioni, grazie al principio di Archimede. Quando il fluido è in quiete, l equazione per la quantità di moto è semplicemente p = F g = ρ g e se la densità è costante l integrale di questa semplice equazione differenziale, perso un asse z nella direzioen opposta a quella individuata dall accelerazione di gravità, è p = ρgz + p, in cui p sta ad indicare un termine costante. Quando il fluido è in moto, si può usare la definizione: p = p + ρgz così che p = p + ρ g. Se, dunque, l equazione viene scritta in modo formalmente identico ma utilizzando la variabile p invece che la p, il termine di gravità scompare dall equazione. Il contributo additivo della forza di gravità (essenzialmente una forza di galleggiamento, per il principio di Archimede spesso è trascurabile o comunque recuperabile a posteriori. L unico caso importante in cui la gravità va esplicitamente tenuta in conto è costituito dai fenomeni di convezione, in cui le variazioni di densità dovute alla temperatura giocano un ruolo essenziale.
12 34 Capitolo.7 La forma adimensionale delle equazioni Le equazioni di Navier Stokes possono essere scritte in forma adimensionale, allo scopo di diminuire il numero di parametri da cui dipende la soluzione. Indichiamo con un asterisco le variabili dimensionali, e consideriamo l equazione di bilancio per la quantità di moto, scritta per semplicità nella forma incomprimibile a proprietà costanti e senza il termine di forza per unità di massa: V + (V V + 1 ρ p = µ ρ V Notiamo anzitutto che il secondo coefficiente di viscosità λ non compare nelle equazioni che regolano il moto di un fluido incomprimibile. Anche nel caso comprimibile però è sufficiente ragionare in termini di un solo coefficiente di viscosità: infatti l ordine di grandezza dei due coefficienti di viscosità è lo stesso. Si introducono ora alcune grandezze di riferimento rispetto a cui rendere adimensionali le variabili: una densità ρ 0, una velocità U 0 ed una lunghezza L 0. Le variabili dimensionali soono legate a quelle adimensionali dalle seguenti relazioni: ρ = ρ 0 ρ; V = U 0 V; x = L 0 x Un tempo adimensionale si può inoltre costruire mediante la t = U 0 /L 0 t, mentre la pressione può essere scritta come p = ρ 0 U 0 p. L equazione si può così riscrivere introducendo le grandezze di riferimento: U 0 L 0 V + U 0 L 0 (V V + ρ 0U 0 ρ 0 L 0 p = µ U 0 ρ 0 L 0 µ V Dividendo ora entrambi i membri dell equazione per U 0 /L 0, a secondo membro resta in evidenza il gruppo µ 0 /ρ 0 U 0 L 0. Definendo numero di Reynolds la quantità adimensionale: Re = ρ 0U 0 L 0 µ l equazione in forma adimensionale diviene: V + (V V + p = 1 Re V Ricordiamo ancora una volta che la trscurabilità o meno dei termini viscosi non può essere dedotta dal semplice fatto che il numero adimensionale Re assuma valori elevati. Nell equazione precedente Re moltiplica le derivate di grado massimo, e la semplice cancellazione dei termini viscosi che contengono le derivate seconde conduce ad un equazione differenziale di natura diversa da quella viscosa.
Flussi comprimibili. 9.1 Comprimibilità di un fluido. Indice del capitolo
 9 Flussi comprimibili XXX RISCRIVERE Quando gli effetti della comprimibilità del fluido non sono trascurabili, le equazioni del moto si traducono ancora, quando la vorticità è nulla, in un equazione per
9 Flussi comprimibili XXX RISCRIVERE Quando gli effetti della comprimibilità del fluido non sono trascurabili, le equazioni del moto si traducono ancora, quando la vorticità è nulla, in un equazione per
Fluidodinamica, Martedì 5 luglio
 Fluidodinamica, Martedì 5 luglio 0.1 Parte di Fluidodinamica I Domanda 1 L equazione di continuità è l espressione matematica della legge di conservazione della massa. Illustrare la sua forma matematica
Fluidodinamica, Martedì 5 luglio 0.1 Parte di Fluidodinamica I Domanda 1 L equazione di continuità è l espressione matematica della legge di conservazione della massa. Illustrare la sua forma matematica
Fenomeni di rotazione
 Fenomeni di rotazione Si e visto che nel caso di un fluido, data la proprietà di deformarsi quando sottoposti a sforzi di taglio, gli angoli di rotazione di un elemento di fluido rispetto ad sistema di
Fenomeni di rotazione Si e visto che nel caso di un fluido, data la proprietà di deformarsi quando sottoposti a sforzi di taglio, gli angoli di rotazione di un elemento di fluido rispetto ad sistema di
Meccanica dei Fluidi
 Meccanica dei Fluidi Jan Pralits Department of Civil, Chemical and Environmental Engineering University of Genoa, Italy jan.pralits@unige.it 2014 Fondamenti dei meccanica dei continui (80939/6CFU) Ing.
Meccanica dei Fluidi Jan Pralits Department of Civil, Chemical and Environmental Engineering University of Genoa, Italy jan.pralits@unige.it 2014 Fondamenti dei meccanica dei continui (80939/6CFU) Ing.
τ ij = pδ ij (30.1.1)
 30. Fluidi I fluidi presentano una varia fenomenologia con moti regolari e moti turbolenti. Le equazioni del moto sono non lineari e, per un gas rarefatto, possono essere derivate da un modello microscopico
30. Fluidi I fluidi presentano una varia fenomenologia con moti regolari e moti turbolenti. Le equazioni del moto sono non lineari e, per un gas rarefatto, possono essere derivate da un modello microscopico
UNIVERSITA DEGLI STUDI DI PAVIA REGISTRO. DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2016/17
 REGISTRO DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2016/17 Cognome e Nome: BISI FULVIO Qualifica: PROFESSORE ASSOCIATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento (6 CFU su un totale di 6+3
REGISTRO DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2016/17 Cognome e Nome: BISI FULVIO Qualifica: PROFESSORE ASSOCIATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento (6 CFU su un totale di 6+3
Equazione dell'energia. Fenomeni di Trasporto
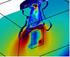 Equazione dell'energia Fenomeni di Trasporto 1 Trasporto convettivo di energia La portata volumetrica che attraversa l elemento di superficie ds perpendicolare all asse x è La portata di energia che attraversa
Equazione dell'energia Fenomeni di Trasporto 1 Trasporto convettivo di energia La portata volumetrica che attraversa l elemento di superficie ds perpendicolare all asse x è La portata di energia che attraversa
Pillole di Fluidodinamica e breve introduzione alla CFD
 Pillole di Fluidodinamica e breve introduzione alla CFD ConoscereLinux - Modena Linux User Group Dr. D. Angeli diego.angeli@unimore.it Sommario 1 Introduzione 2 Equazioni di conservazione 3 CFD e griglie
Pillole di Fluidodinamica e breve introduzione alla CFD ConoscereLinux - Modena Linux User Group Dr. D. Angeli diego.angeli@unimore.it Sommario 1 Introduzione 2 Equazioni di conservazione 3 CFD e griglie
Derivata materiale (Lagrangiana) e locale (Euleriana)
 ispense di Meccanica dei Fluidi 0 0 det 0 = [ (0 ) + ( ( ) ) + (0 0 ) ] = 0. Pertanto, v e µ sono indipendenti tra loro e costituiscono una nuova base. Con essi è possibile descrivere altre grandezze,
ispense di Meccanica dei Fluidi 0 0 det 0 = [ (0 ) + ( ( ) ) + (0 0 ) ] = 0. Pertanto, v e µ sono indipendenti tra loro e costituiscono una nuova base. Con essi è possibile descrivere altre grandezze,
Teoria dei mezzi continui
 Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
SOLUZIONE DELL EQUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME
 SOLUZIONE DELL EUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME Luca Ghezzi May 2 Abstract L equazione del calore di Fourier è risolta analiticamente nel caso di un mezzo
SOLUZIONE DELL EUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME Luca Ghezzi May 2 Abstract L equazione del calore di Fourier è risolta analiticamente nel caso di un mezzo
Lezioni del Corso PROPULSIONE SPAZIALE aa Marcello Onofri VARIABILI TERMODINAMICHE ED EQUAZIONI DI CONSERVAZIONE
 Lezioni del Corso PROPULSIONE SPAZIALE aa 2018-19 Lez. 05 Marcello Onofri VARIABILI TERMODINAMICHE ED EQUAZIONI DI CONSERVAZIONE NOTA: Le variabili termodinamiche d interesse propulsivo da Liepmann H.W.-Roshko
Lezioni del Corso PROPULSIONE SPAZIALE aa 2018-19 Lez. 05 Marcello Onofri VARIABILI TERMODINAMICHE ED EQUAZIONI DI CONSERVAZIONE NOTA: Le variabili termodinamiche d interesse propulsivo da Liepmann H.W.-Roshko
CAPITOLO 3 LA LEGGE DI GAUSS
 CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
UNIVERSITA DEGLI STUDI DI PAVIA REGISTRO. DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2014/15
 REGISTRO DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2014/15 Cognome e Nome BISI FULVIO Qualifica RICERCATORE CONFERMATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento di FENOMENI DI DIFFUSIONE
REGISTRO DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2014/15 Cognome e Nome BISI FULVIO Qualifica RICERCATORE CONFERMATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento di FENOMENI DI DIFFUSIONE
Cinematica. Velocità. Riferimento Euleriano e Lagrangiano. Accelerazione. Elementi caratteristici del moto. Tipi di movimento
 Cinematica Velocità Riferimento Euleriano e Lagrangiano Accelerazione Elementi caratteristici del moto Tipi di movimento Testo di riferimento Citrini-Noseda par. 3.1 par. 3.2 par 3.3 fino a linee di fumo
Cinematica Velocità Riferimento Euleriano e Lagrangiano Accelerazione Elementi caratteristici del moto Tipi di movimento Testo di riferimento Citrini-Noseda par. 3.1 par. 3.2 par 3.3 fino a linee di fumo
6.1 Valori tipici delle grandezze in uno strato limite
 F. Auteri e L. Quartapelle: Fluidodinamica. Capitolo 6 pagina 236 colore nero Ottobre 17, 2006 236 CAPITOLO 6 Equazioni dello strato limite stazionario 2D 6.1 Valori tipici delle grandezze in uno strato
F. Auteri e L. Quartapelle: Fluidodinamica. Capitolo 6 pagina 236 colore nero Ottobre 17, 2006 236 CAPITOLO 6 Equazioni dello strato limite stazionario 2D 6.1 Valori tipici delle grandezze in uno strato
Strato limite compressibile
 Capitolo 9 Strato limite compressibile Dopo aver derivato le equazioni di Navier-Stokes nel Cap. 1 e con l eccezione di quanto visto nel 5.9, si è sempre considerato il caso di un fluido ideale, governato
Capitolo 9 Strato limite compressibile Dopo aver derivato le equazioni di Navier-Stokes nel Cap. 1 e con l eccezione di quanto visto nel 5.9, si è sempre considerato il caso di un fluido ideale, governato
SISTEMI APERTI CON PICCOLO SCAMBIO DI CALORE
 CAPITOLO DODICESIMO SISTEMI APERTI CON PICCOLO SCAMBIO DI CALORE Sistemi aperti con piccolo scambio di calore In alcune applicazioni il fluido che viene trattato da una macchina ovvero viene trasportato
CAPITOLO DODICESIMO SISTEMI APERTI CON PICCOLO SCAMBIO DI CALORE Sistemi aperti con piccolo scambio di calore In alcune applicazioni il fluido che viene trattato da una macchina ovvero viene trasportato
Vd Vd Vd Re = Per definire il REGIME di moto si individua il: Numero indice di Reynolds (adimensionale)
 CINEMATICA Esperienza di Osborne Reynolds (1842-1912) Per basse velocità: moto per filetti viscoso laminare Al crescere velocità: moto di transizione V d V d Per elevate velocità: moto turbolento V d CINEMATICA
CINEMATICA Esperienza di Osborne Reynolds (1842-1912) Per basse velocità: moto per filetti viscoso laminare Al crescere velocità: moto di transizione V d V d Per elevate velocità: moto turbolento V d CINEMATICA
DINAMICA. Forze di massa + Forze di superficie = Forze di inerzia. Forze di massa = ρ fdxdydz. Forze di inerzia = ρ. Adxdydz
 DINMIC Equilibrio idrodinamico Legge di Newton: i F i = m Forze agenti: Forze di massa + Forze di superficie = Forze di inerzia Forze di massa = ρ fdxdydz f = ccelerazione del campo, ovvero forza per unità
DINMIC Equilibrio idrodinamico Legge di Newton: i F i = m Forze agenti: Forze di massa + Forze di superficie = Forze di inerzia Forze di massa = ρ fdxdydz f = ccelerazione del campo, ovvero forza per unità
4. Esercitazione 4: Dimensionamento del primo stadio di un compressore assiale
 4. Esercitazione 4: Dimensionamento del primo stadio di un compressore assiale Lo scopo della presente esercitazione è il dimensionamento del primo stadio di un compressore assiale. Con riferimento alla
4. Esercitazione 4: Dimensionamento del primo stadio di un compressore assiale Lo scopo della presente esercitazione è il dimensionamento del primo stadio di un compressore assiale. Con riferimento alla
Funzioni vettoriali di variabile scalare
 Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Cap. 2. Le equazioni della fluidodinamica
 Cap. 2. Le equazioni della fluidodinamica La formula del trasporto di Reynolds consente di portare la derivata temporale sotto il segno d integrale. Consideriamo una generica quantità f(x, t) contenuta
Cap. 2. Le equazioni della fluidodinamica La formula del trasporto di Reynolds consente di portare la derivata temporale sotto il segno d integrale. Consideriamo una generica quantità f(x, t) contenuta
Corso di MECCANICA DEL VOLO Modulo Prestazioni. Lezione n.2. Prof. D. P. Coiro
 Corso di MECCANICA DEL VOLO Modulo Prestazioni Lezione n.2 Prof. D. P. Coiro coiro@unina.it www.dias.unina.it/adag/ Corso di Meccanica del Volo - Mod. Prestazioni - Prof. D. Corio - Intro Il Velivolo 1
Corso di MECCANICA DEL VOLO Modulo Prestazioni Lezione n.2 Prof. D. P. Coiro coiro@unina.it www.dias.unina.it/adag/ Corso di Meccanica del Volo - Mod. Prestazioni - Prof. D. Corio - Intro Il Velivolo 1
STATICA DEI FLUIDI. Proprietà dei fluidi
 STATICA DEI FLUIDI La statica dei fluidi è interessata allo studio dei fluidi a riposo, per cui in tale ambito si suppone implicitamente che la condizione di quiete iniziale sia sempre soddisfatta. Proprietà
STATICA DEI FLUIDI La statica dei fluidi è interessata allo studio dei fluidi a riposo, per cui in tale ambito si suppone implicitamente che la condizione di quiete iniziale sia sempre soddisfatta. Proprietà
Lezione 5: Richiami di termomeccanica dei mezzi continui
 Lezione 5: Richiami di termomeccanica dei mezzi continui Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di Perugia Dottorato Internazionale Congiunto Firenze Braunschweig Firenze,
Lezione 5: Richiami di termomeccanica dei mezzi continui Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di Perugia Dottorato Internazionale Congiunto Firenze Braunschweig Firenze,
Dinamica del fluidi. A.Stefanel Fisica Cs AGR-SAN Dinamica dei fluidi. A. Stefanel - Fluidodinamica 1
 Dinamica del fluidi A.Stefanel Fisica Cs AGR-SAN Dinamica dei fluidi A. Stefanel - Fluidodinamica 1 Per descrivere il moto di un fluido ci sono due formalismi equivalenti: Lagrange: si descrive il moto
Dinamica del fluidi A.Stefanel Fisica Cs AGR-SAN Dinamica dei fluidi A. Stefanel - Fluidodinamica 1 Per descrivere il moto di un fluido ci sono due formalismi equivalenti: Lagrange: si descrive il moto
Fluidodinamica Computazionale.
 Fluidodinamica Computazionale carmelo.demaria@centropiaggio.unipi.it Fluidodinamica Computazionale (CFD) CFD è l analisi dei sistemi che involvono movimento di fluidi, scambio di calore ed i fenomeni a
Fluidodinamica Computazionale carmelo.demaria@centropiaggio.unipi.it Fluidodinamica Computazionale (CFD) CFD è l analisi dei sistemi che involvono movimento di fluidi, scambio di calore ed i fenomeni a
Correnti incomprimibili non viscose irrotazionali
 F. Auteri e L. Quartapelle: Fluidodinamica. Capitolo 4 pagina 99 colore nero Novembre 1, 006 99 CAPITOLO 4 Correnti incomprimibili non viscose irrotazionali Introduzione In questo capitolo studieremo un
F. Auteri e L. Quartapelle: Fluidodinamica. Capitolo 4 pagina 99 colore nero Novembre 1, 006 99 CAPITOLO 4 Correnti incomprimibili non viscose irrotazionali Introduzione In questo capitolo studieremo un
UNIVERSITA DEGLI STUDI DI PAVIA REGISTRO. DELLE LEZIONI-ESERCITAZIONI- SEMINARI Anno accademico 2013/14
 REGISTRO DELLE LEZIONI-ESERCITAZIONI- SEMINARI Anno accademico 2013/14 Cognome e Nome BISI FULVIO Qualifica RICERCATORE CONFERMATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento di FENOMENI DI DIFFUSIONE
REGISTRO DELLE LEZIONI-ESERCITAZIONI- SEMINARI Anno accademico 2013/14 Cognome e Nome BISI FULVIO Qualifica RICERCATORE CONFERMATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento di FENOMENI DI DIFFUSIONE
Una formulazione equivalente è Il moto di un singolo punto materiale isolato è rettilineo uniforme (o è fermo):
 I PRINCIPI DELLA MECCANICA In queste note i principi della dinamica vengono formulati utilizzando soltanto le definizioni di accelerazione e velocità istantanee della Cinematica. Le lettere in grassetto
I PRINCIPI DELLA MECCANICA In queste note i principi della dinamica vengono formulati utilizzando soltanto le definizioni di accelerazione e velocità istantanee della Cinematica. Le lettere in grassetto
Capitolo 5. Primo principio della Termodinamica nei sistemi aperti
 Capitolo 5. Primo principio della Termodinamica nei sistemi aperti 5.1. I sistemi aperti I sistemi aperti sono quei sistemi termodinamici nei quali, oltre allo scambio di lavoro e calore è possibile lo
Capitolo 5. Primo principio della Termodinamica nei sistemi aperti 5.1. I sistemi aperti I sistemi aperti sono quei sistemi termodinamici nei quali, oltre allo scambio di lavoro e calore è possibile lo
Soluzione Compito di Fisica Generale I Ing. Elettronica e delle Telecomunicazioni 12/01/2018
 Soluzione Compito di isica Generale I Ing. Elettronica e delle Telecomunicazioni 12/01/2018 Esercizio 1 1) Scriviamo le equazioni del moto della sfera sul piano inclinato. Le forze agenti sono il peso
Soluzione Compito di isica Generale I Ing. Elettronica e delle Telecomunicazioni 12/01/2018 Esercizio 1 1) Scriviamo le equazioni del moto della sfera sul piano inclinato. Le forze agenti sono il peso
UNIVERSITA DEGLI STUDI DI PAVIA REGISTRO. DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2015/16
 REGISTRO DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2015/16 Cognome e Nome: BISI FULVIO Qualifica: PROFESSORE ASSOCIATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento (6 CFU su un totale di 6+3
REGISTRO DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2015/16 Cognome e Nome: BISI FULVIO Qualifica: PROFESSORE ASSOCIATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento (6 CFU su un totale di 6+3
Dalla meccanica del continuo alle Equazioni di Lagrange g per i solidi elastici. Dinamica delle Strutture Aerospaziali
 Dalla meccanica del continuo alle Equazioni di Lagrange g per i solidi elastici Franco Mastroddi http://www.diaa.uniroma1.it/docenti/f.mastroddi dal Dinamica delle Strutture Aerospaziali Anno Accademico
Dalla meccanica del continuo alle Equazioni di Lagrange g per i solidi elastici Franco Mastroddi http://www.diaa.uniroma1.it/docenti/f.mastroddi dal Dinamica delle Strutture Aerospaziali Anno Accademico
1. I fluidi e le loro caratteristiche. 2. La pressione in un fluido.
 UNITÀ 8 LA MECCANICA DEI FLUIDI 1. I fluidi e le loro caratteristiche. 2. La pressione in un fluido. 3. La pressione atmosferica. 4. La legge di Stevino. 5. La legge di Pascal. 6. La forza di Archimede.
UNITÀ 8 LA MECCANICA DEI FLUIDI 1. I fluidi e le loro caratteristiche. 2. La pressione in un fluido. 3. La pressione atmosferica. 4. La legge di Stevino. 5. La legge di Pascal. 6. La forza di Archimede.
Possiamo scrivere le tre precedenti espressioni in un'unica equazione matriciale:
 A1. Considerazioni sul cambio di un sistema di riferimento cartesiano ortogonale Sia xyz un sistema di riferimento cartesiano ortogonale di origine O e di riferimento cartesiano pure di origine O. un secondo
A1. Considerazioni sul cambio di un sistema di riferimento cartesiano ortogonale Sia xyz un sistema di riferimento cartesiano ortogonale di origine O e di riferimento cartesiano pure di origine O. un secondo
Numero progressivo: 6 Turno: 1 Fila: 1 Posto: 1 Matricola: Cognome e nome: (dati nascosti per tutela privacy)
 Numero progressivo: 6 Turno: 1 Fila: 1 Posto: 1 Matricola: 0000695216 Cognome e nome: (dati nascosti per tutela privacy) 1. Di quanto ruota in un giorno sidereo il piano di oscillazione del pendolo di
Numero progressivo: 6 Turno: 1 Fila: 1 Posto: 1 Matricola: 0000695216 Cognome e nome: (dati nascosti per tutela privacy) 1. Di quanto ruota in un giorno sidereo il piano di oscillazione del pendolo di
, mentre alla fine, quando i due cilindri ruotano solidalmente, L = ( I I ) ω. . Per la conservazione, abbiamo
 A) Meccanica Un cilindro di altezza h, raggio r e massa m, ruota attorno al proprio asse (disposto verticalmente) con velocita` angolare ω i. l cilindro viene appoggiato delicatamente su un secondo cilindro
A) Meccanica Un cilindro di altezza h, raggio r e massa m, ruota attorno al proprio asse (disposto verticalmente) con velocita` angolare ω i. l cilindro viene appoggiato delicatamente su un secondo cilindro
Convezione in campo diffusivo. Analogia
 Luca Cirelli matr. 219492 Diego Grazioli matr. 210816 Convezione in campo diffusivo INDICE DELLA LEZIONE DEL 16/03/2010 ARGOMENTO: CONVEZIONE IN CAMPO DIFFUSIVO Analogia Scambio Termico e Diffusione...
Luca Cirelli matr. 219492 Diego Grazioli matr. 210816 Convezione in campo diffusivo INDICE DELLA LEZIONE DEL 16/03/2010 ARGOMENTO: CONVEZIONE IN CAMPO DIFFUSIVO Analogia Scambio Termico e Diffusione...
Meccanica dei Fluidi
 POLITECNICO DI MILANO Meccanica dei Fluidi 5. Fluidi Ideali A cura di: Diego Berzi v1.2 Indice 1 Teorema di Bernoulli 3 2 Estensione alle correnti 7 2 1 Teorema di Bernoulli Abbiamo visto Cap. 4, Par.
POLITECNICO DI MILANO Meccanica dei Fluidi 5. Fluidi Ideali A cura di: Diego Berzi v1.2 Indice 1 Teorema di Bernoulli 3 2 Estensione alle correnti 7 2 1 Teorema di Bernoulli Abbiamo visto Cap. 4, Par.
Compito del 14 giugno 2004
 Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
Dinamica dei Fliudi Lezione 09 a.a
 Dinamica dei Fliudi Lezione 09 aa 2009-2010 Simone Zuccher 24 Maggio 2010 Nota Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore (zuccher@sciunivrit) 1 DNS:
Dinamica dei Fliudi Lezione 09 aa 2009-2010 Simone Zuccher 24 Maggio 2010 Nota Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore (zuccher@sciunivrit) 1 DNS:
CAMPI VETTORIALI (Note)
 CAMPI VETTORIALI (Note) Sia v(x,y,z) il vettore che definisce la grandezza fisica del campo: il problema che ci si pone è di caratterizzare il campo vettoriale sia in termini locali, cioè validi punto
CAMPI VETTORIALI (Note) Sia v(x,y,z) il vettore che definisce la grandezza fisica del campo: il problema che ci si pone è di caratterizzare il campo vettoriale sia in termini locali, cioè validi punto
le variazioni del campo si propagano nello spazio con velocità finita
 Campi elettromagnetici e circuiti II, a.a. 2013-14, Marco Bressan LEGGI FONDAMENTALI Lo studio dell interazione elettromagnetica è basato sul concetto di campo elettromagnetico le variazioni del campo
Campi elettromagnetici e circuiti II, a.a. 2013-14, Marco Bressan LEGGI FONDAMENTALI Lo studio dell interazione elettromagnetica è basato sul concetto di campo elettromagnetico le variazioni del campo
Moto irrotazionale ed equazione di Laplace
 4 Moto irrotazionale ed equazione di Laplace L analisi della dinamica della vorticità ha permesso di stabilire che il moto di un fluido non viscoso, incomprimibile oppure comprimibile isoentropico, sotto
4 Moto irrotazionale ed equazione di Laplace L analisi della dinamica della vorticità ha permesso di stabilire che il moto di un fluido non viscoso, incomprimibile oppure comprimibile isoentropico, sotto
Flussi bidimensionali stazionari con piccole perturbazioni
 Capitolo 2 Flussi bidimensionali stazionari con piccole perturbazioni 2.1 Equazione del potenziale Nell ipotesi di fluido ideale ed in assenza di onde d urto, le equazioni di conservazione (1.31), (1.32)
Capitolo 2 Flussi bidimensionali stazionari con piccole perturbazioni 2.1 Equazione del potenziale Nell ipotesi di fluido ideale ed in assenza di onde d urto, le equazioni di conservazione (1.31), (1.32)
Statica ed equilibrio dei corpi
 Statica ed equilibrio dei corpi Avendo stabilito le leggi che regolano il moto dei corpi è possibile dedurre le leggi che regolano il loro equilibrio in condizioni statiche, cioè in assenza di movimento.
Statica ed equilibrio dei corpi Avendo stabilito le leggi che regolano il moto dei corpi è possibile dedurre le leggi che regolano il loro equilibrio in condizioni statiche, cioè in assenza di movimento.
Modellistica di sistemi a fluido
 I fluidi vengono suddivisi in liquidi e gas. Liquidi: sono sempre delimitati da una superficie ben definita, possiedono un volume proprio ma non una forma propria. Gas: sono costituiti da molecole in moto
I fluidi vengono suddivisi in liquidi e gas. Liquidi: sono sempre delimitati da una superficie ben definita, possiedono un volume proprio ma non una forma propria. Gas: sono costituiti da molecole in moto
Operatori vettoriali su R ³
 Operatori vettoriali su R ³ Sui campi scalari e vettoriali tridimensionali è possibile definire degli operatori vettoriali che giocano un ruolo importantissimo anche per le applicazioni nel campo fisico
Operatori vettoriali su R ³ Sui campi scalari e vettoriali tridimensionali è possibile definire degli operatori vettoriali che giocano un ruolo importantissimo anche per le applicazioni nel campo fisico
Capitolo 4: CAMBIAMENTO DI SISTEMA DI UNITÀ
 Capitolo 4: CAMBIAMENTO DI SISTEMA DI UNITÀ 4.1 Grandezze fondamentali e derivate Come abbiamo già osservato la scelta di un Sistema di unità di misura è largamente arbitraria e dettata in gran parte da
Capitolo 4: CAMBIAMENTO DI SISTEMA DI UNITÀ 4.1 Grandezze fondamentali e derivate Come abbiamo già osservato la scelta di un Sistema di unità di misura è largamente arbitraria e dettata in gran parte da
Termodinamica di non-equilibrio
 Termodinamica di non-equilibrio Obiettivo: Una sintesi sui metodi e strumenti utilizzati per descrivere i sistemi macroscopici in condizione di non-equilibrio e la loro dinamica (rilassamento all equilibrio).
Termodinamica di non-equilibrio Obiettivo: Una sintesi sui metodi e strumenti utilizzati per descrivere i sistemi macroscopici in condizione di non-equilibrio e la loro dinamica (rilassamento all equilibrio).
Fluidodinamica, martedì 19 luglio 2011
 Fluidodinamica, martedì 19 luglio 211.1 Parte di Fluidodinamica I Domanda 1 Considerare un fluido sottoposto all azione di un campo di forze esterne conservative, in condizioni statiche e la cui densità
Fluidodinamica, martedì 19 luglio 211.1 Parte di Fluidodinamica I Domanda 1 Considerare un fluido sottoposto all azione di un campo di forze esterne conservative, in condizioni statiche e la cui densità
UNIVERSITA DEGLI STUDI DI PAVIA REGISTRO. DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2017/18
 REGISTRO DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2017/18 Cognome e Nome: BISI FULVIO Qualifica: PROFESSORE ASSOCIATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento (6 CFU su un totale di 6+3
REGISTRO DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2017/18 Cognome e Nome: BISI FULVIO Qualifica: PROFESSORE ASSOCIATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento (6 CFU su un totale di 6+3
Elettronica II Grandezze elettriche microscopiche (parte 1) p. 2
 Elettronica II Grandezze elettriche microscopiche (parte 1) Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it http://www.dti.unimi.it/
Elettronica II Grandezze elettriche microscopiche (parte 1) Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it http://www.dti.unimi.it/
Appunti sull analisi dimensionale per la modellazione del moto uniforme dei fluidi nei condotti circolari. 15 ottobre 2012
 Appunti sull analisi dimensionale per la modellazione del moto uniforme dei fluidi nei condotti circolari 5 ottobre 202 Analisi dimensionale e teorema Π Si consideri la relazione g 0 = f (g, g 2, g 3,...,
Appunti sull analisi dimensionale per la modellazione del moto uniforme dei fluidi nei condotti circolari 5 ottobre 202 Analisi dimensionale e teorema Π Si consideri la relazione g 0 = f (g, g 2, g 3,...,
MECCANICA DEI FLUIDI
 MECCANICA DEI FLUIDI Un fluido è un corpo che non ha una forma propria. La sua forma dipende da altri corpi che lo contengono (per esempio un recipiente, una condotta, ). Un fluido è composto da molte
MECCANICA DEI FLUIDI Un fluido è un corpo che non ha una forma propria. La sua forma dipende da altri corpi che lo contengono (per esempio un recipiente, una condotta, ). Un fluido è composto da molte
6.3 Corrente esterna uniforme: profilo di Blasius
 F. Auteri e L. Quartapelle: Fluidodinamica. Capitolo 6 pagina 247 colore nero Ottobre 17, 26 PARAGRAFO 6.3: Corrente esterna uniforme: profilo di Blasius 247 ν 3 ψ 3 + ψ(x, ) =, ( ) ψ 2 ψ x 2 ψ(x, ) ψ(,
F. Auteri e L. Quartapelle: Fluidodinamica. Capitolo 6 pagina 247 colore nero Ottobre 17, 26 PARAGRAFO 6.3: Corrente esterna uniforme: profilo di Blasius 247 ν 3 ψ 3 + ψ(x, ) =, ( ) ψ 2 ψ x 2 ψ(x, ) ψ(,
Re. Soluzioni esterne e
 Capitolo 7 Re. Soluzioni esterne e vorticità 7.1 Flussi irrotazionali Come si è già visto nel capitolo precedente per Re si ha un problema di perturbazione singolare e la soluzione esterna si ottiene ponendo
Capitolo 7 Re. Soluzioni esterne e vorticità 7.1 Flussi irrotazionali Come si è già visto nel capitolo precedente per Re si ha un problema di perturbazione singolare e la soluzione esterna si ottiene ponendo
Flussi Di Fanno. 1 Definizione del flusso di Fanno
 Flussi Di Fanno 1 Definizione del flusso di Fanno Si consideri un flusso adiabatico all interno di un condotto a sezione costante, in presenza di attrito e senza scambio di lavoro con l esterno. Tale regime
Flussi Di Fanno 1 Definizione del flusso di Fanno Si consideri un flusso adiabatico all interno di un condotto a sezione costante, in presenza di attrito e senza scambio di lavoro con l esterno. Tale regime
Particella in un campo elettromagnetico
 Particella in un campo elettromagnetico Vogliamo descrivere dal punto di vista quantistico una particella carica posta in un campo elettromagnetico. Momento di una particella Dal punto di vista classico
Particella in un campo elettromagnetico Vogliamo descrivere dal punto di vista quantistico una particella carica posta in un campo elettromagnetico. Momento di una particella Dal punto di vista classico
Lezioni L3.a. 5. Teorema dei Campi Conservativi; 7. Teorema di Stokes; 9. Rot E=0. FISICA GENERALE II, Cassino A.A
 Lezioni L3.a 1. Flusso attraverso una superficie;. Scalari, Pseudoscalari, Vettori e Pseudovettori; 3. Campi Scalari e Campi Vettoriali ed operatori; 4. Gradiente, Divergenza, Rotore, Laplaciano; 5. Teorema
Lezioni L3.a 1. Flusso attraverso una superficie;. Scalari, Pseudoscalari, Vettori e Pseudovettori; 3. Campi Scalari e Campi Vettoriali ed operatori; 4. Gradiente, Divergenza, Rotore, Laplaciano; 5. Teorema
Meccanica dei Fluidi
 POLITECNICO DI MILANO Meccanica dei Fluidi 4. Dinamica dei Fluidi A cura di: Diego Berzi v1.2 Indice 1 Bilancio di massa 3 1.1 Forma indefinita......................... 3 1.2 Forma globale...........................
POLITECNICO DI MILANO Meccanica dei Fluidi 4. Dinamica dei Fluidi A cura di: Diego Berzi v1.2 Indice 1 Bilancio di massa 3 1.1 Forma indefinita......................... 3 1.2 Forma globale...........................
Meccanica del punto materiale
 Meccanica del punto materiale Princìpi della dinamica. Forze. Momento angolare. Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro
Meccanica del punto materiale Princìpi della dinamica. Forze. Momento angolare. Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro
CAPITOLO III. La cinematica del moto dei fluidi
 Cap.III La cinematica 37 CAPITOLO III La cinematica del moto dei fluidi 1. - Impostazione del problema. Nel descrivere il moto dei fluidi possiamo seguire due schemi, due grandi vie. La prima consiste
Cap.III La cinematica 37 CAPITOLO III La cinematica del moto dei fluidi 1. - Impostazione del problema. Nel descrivere il moto dei fluidi possiamo seguire due schemi, due grandi vie. La prima consiste
Convezione Conduzione Irraggiamento
 Sommario 1 Dai sistemi discreti ai sistemi continui: equilibrio locale Deviazioni dalle condizioni di equilibrio locale Irreversibilità Equazioni integrali di bilancio 2 In questa lezione... Fenomeno della
Sommario 1 Dai sistemi discreti ai sistemi continui: equilibrio locale Deviazioni dalle condizioni di equilibrio locale Irreversibilità Equazioni integrali di bilancio 2 In questa lezione... Fenomeno della
Equazioni di Maxwell. I campi elettrici e magnetici (nel vuoto) sono descritti dalle equazioni di Maxwell (in unità MKSA)
 Equazioni di Maxwell I campi elettrici e magnetici (nel vuoto) sono descritti dalle equazioni di Maxwell (in unità MKSA) E = ϱ ɛ 0 (1) E = B (2) B = 0 (3) E B = µ 0 j + µ 0 ɛ 0 (4) La forza che agisce
Equazioni di Maxwell I campi elettrici e magnetici (nel vuoto) sono descritti dalle equazioni di Maxwell (in unità MKSA) E = ϱ ɛ 0 (1) E = B (2) B = 0 (3) E B = µ 0 j + µ 0 ɛ 0 (4) La forza che agisce
OSCILLATORE ARMONICO SEMPLICE
 OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
Il TEOREMA DI TRASPORTO DI REYNOLDS
 CAPITOLO 4. Il TEOREMA DI TRASPORTO DI REYNOLDS 4.1 Il Teorema di Trasporto di Reynolds Le leggi di conservazione della Massa, della Quantità di Moto (Momentum) e dell Energia costituiscono le relazioni
CAPITOLO 4. Il TEOREMA DI TRASPORTO DI REYNOLDS 4.1 Il Teorema di Trasporto di Reynolds Le leggi di conservazione della Massa, della Quantità di Moto (Momentum) e dell Energia costituiscono le relazioni
CONDENSATI DI BOSE-EINSTEIN E SUPERFLUIDI
 CONDENSATI DI BOSE-EINSTEIN E SUPERFLUIDI Consideriamo un fluido in una scatola. Questo è un insieme di tanti piccoli costituenti che supponiamo per semplicità essere identici. Dalla meccanica quantistica
CONDENSATI DI BOSE-EINSTEIN E SUPERFLUIDI Consideriamo un fluido in una scatola. Questo è un insieme di tanti piccoli costituenti che supponiamo per semplicità essere identici. Dalla meccanica quantistica
EQUAZIONE DELLA CONTINUITA = Bilancio di massa nel tempo dt. Massa accumulatasi nel sistema. Massa uscente dal sistema. Massa entrante nel sistema
 SISTEMI APERTI Ipotesi: EQUILIBRIO LOCALE in ogni punto del sistema aperto le proprietà termostatice assumono il valore ce avrebbero se nell intorno di quel punto il sistema fosse uniforme Ipotesi: MOTO
SISTEMI APERTI Ipotesi: EQUILIBRIO LOCALE in ogni punto del sistema aperto le proprietà termostatice assumono il valore ce avrebbero se nell intorno di quel punto il sistema fosse uniforme Ipotesi: MOTO
INDICE 1 INTRODUZIONE E CONCETTI DI BASE 1 2 PROPRIETÀ DEI FLUIDI 31
 INDICE PRESENTAZIONE DELLA TERZA EDIZIONE ITALIANA RINGRAZIAMENTI DELL EDITORE PREFAZIONE ALL EDIZIONE AMERICANA GUIDA ALLA LETTURA XIII XV XVII XXII 1 INTRODUZIONE E CONCETTI DI BASE 1 1.1 Introduzione
INDICE PRESENTAZIONE DELLA TERZA EDIZIONE ITALIANA RINGRAZIAMENTI DELL EDITORE PREFAZIONE ALL EDIZIONE AMERICANA GUIDA ALLA LETTURA XIII XV XVII XXII 1 INTRODUZIONE E CONCETTI DI BASE 1 1.1 Introduzione
Domande frequenti durante esame orale
 Domande frequenti durante esame orale Meccanica dei Continui - Meccanica Razionale Marco Modugno Dipartimento di Matematica Applicata, Università di Firenze Via S. Marta 3, 50139 Firenze email: marco.modugno@unifi.it
Domande frequenti durante esame orale Meccanica dei Continui - Meccanica Razionale Marco Modugno Dipartimento di Matematica Applicata, Università di Firenze Via S. Marta 3, 50139 Firenze email: marco.modugno@unifi.it
Le leggi del moto dei fluidi
 1 Le leggi del moto dei fluidi Le equazioni che descrivono il moto dei fluidi vengono ricavate prendendo le mosse da considerazioni di equilibrio meccanico a livello microscopico. Si giunge cosí alle equazioni
1 Le leggi del moto dei fluidi Le equazioni che descrivono il moto dei fluidi vengono ricavate prendendo le mosse da considerazioni di equilibrio meccanico a livello microscopico. Si giunge cosí alle equazioni
SISTEMA SEMPLICE SISTEMA CHIUSO
 SISTEMA SEMPLICE Il sistema semplice è costituito da una sostanza pura il cui stato intensivo sia individuato da due proprietà interne intensive indipendenti. Il sistema semplice comprimibile o sistema
SISTEMA SEMPLICE Il sistema semplice è costituito da una sostanza pura il cui stato intensivo sia individuato da due proprietà interne intensive indipendenti. Il sistema semplice comprimibile o sistema
Fluidodinamica, venerdì 9 settembre 2011
 Fluidodinamica, venerdì 9 settembre 011 Parte di Fluidodinamica I Domanda 1 Le equazioni che governano le correnti incomprimibili devono essere completate con condizioni supplementari per potere determinare
Fluidodinamica, venerdì 9 settembre 011 Parte di Fluidodinamica I Domanda 1 Le equazioni che governano le correnti incomprimibili devono essere completate con condizioni supplementari per potere determinare
Esercizio (tratto dal problema 7.36 del Mazzoldi 2)
 Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
Esercizi su similitudine ed analisi dimensionale
 Esercizi su similitudine ed analisi dimensionale versione 0.3 1 Esercizio Il comportamento aerodinamico di una nuova vettura è caratterizzato dalla relazione fra due parametri adimensionali Π 1 = F Π 2
Esercizi su similitudine ed analisi dimensionale versione 0.3 1 Esercizio Il comportamento aerodinamico di una nuova vettura è caratterizzato dalla relazione fra due parametri adimensionali Π 1 = F Π 2
Prova scritta di Fisica Generale I Corso di studio in Astronomia 16 luglio 2013
 Prova scritta di Fisica Generale I Corso di studio in Astronomia 16 luglio 013 Problema 1 Un cubo di legno di densità ρ = 800 kg/m 3 e lato a = 50 cm è inizialmente in quiete, appoggiato su un piano orizzontale.
Prova scritta di Fisica Generale I Corso di studio in Astronomia 16 luglio 013 Problema 1 Un cubo di legno di densità ρ = 800 kg/m 3 e lato a = 50 cm è inizialmente in quiete, appoggiato su un piano orizzontale.
L equazione di Schrödinger
 1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
Laboratorio di Simulazione Atomistica e Fluidodinamica. Equazione di Stokes e soluzione numerica col metodo degli elementi di contorno
 Laboratorio di Simulazione Atomistica e Fluidodinamica Equazione di Stokes e soluzione numerica col metodo degli elementi di contorno Equazione di Stokes Struttura della lezione: Equazione di Navier Stokes
Laboratorio di Simulazione Atomistica e Fluidodinamica Equazione di Stokes e soluzione numerica col metodo degli elementi di contorno Equazione di Stokes Struttura della lezione: Equazione di Navier Stokes
Elettromagnetismo. Prof. Francesco Ragusa Università degli Studi di Milano. Lezione n
 Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 6 18.10.2017 Divergenza e teorema della divergenza Forma differenziale della Legge di Gauss Energia del campo elettrostatico
Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 6 18.10.2017 Divergenza e teorema della divergenza Forma differenziale della Legge di Gauss Energia del campo elettrostatico
Dinamica del punto materiale
 Dinamica del punto materiale Formule fondamentali L. P. 5 Aprile 2010 N.B.: Le relazioni riportate sono valide in un sistema di riferimento inerziale. Princìpi della dinamica Secondo principio della dinamica
Dinamica del punto materiale Formule fondamentali L. P. 5 Aprile 2010 N.B.: Le relazioni riportate sono valide in un sistema di riferimento inerziale. Princìpi della dinamica Secondo principio della dinamica
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari. (c) e5 e 4 e (2x 3y) dx + (1 + x)dx +
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) agli esercizi del 5.XI.7. Gli integrali richiesti valgono: (a) + ( e ) (b) (c) e5 e e + (d)
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) agli esercizi del 5.XI.7. Gli integrali richiesti valgono: (a) + ( e ) (b) (c) e5 e e + (d)
, con x =, y. 3. Si disegni il grafico delle curve di livello sul piano delle fasi (x, ẋ) al variare di E e si discuta la natura qualitativa del moto.
 7 o tutorato - MA - Prova Pre-Esonero - 8/4/5 Esercizio Una massa puntiforme m è vincolata a muoversi nel piano verticale xy (con x l asse orizzontale e y l asse verticale orientato verso l alto), su una
7 o tutorato - MA - Prova Pre-Esonero - 8/4/5 Esercizio Una massa puntiforme m è vincolata a muoversi nel piano verticale xy (con x l asse orizzontale e y l asse verticale orientato verso l alto), su una
R è definita infine dall insieme delle curve percorse da ogni singolo punto della corda.
 1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
Meccanica. 11. Terzo Principio della Dinamica. Domenico Galli. Dipartimento di Fisica e Astronomia
 Meccanica 11. Terzo Principio della Dinamica http://campus.cib.unibo.it/2430/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. Terzo Principio della Dinamica 2. Centro di
Meccanica 11. Terzo Principio della Dinamica http://campus.cib.unibo.it/2430/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. Terzo Principio della Dinamica 2. Centro di
RICHIAMI DI ELETTROMAGNETISMO
 RICHIAMI DI ELETTROMAGNETISMO Equazioni di Maxwell I fenomeni elettrici e magnetici a livello del mondo macroscopico sono descritti da due campi vettoriali, in generale dipendenti dal tempo, E(x, t), H(x,
RICHIAMI DI ELETTROMAGNETISMO Equazioni di Maxwell I fenomeni elettrici e magnetici a livello del mondo macroscopico sono descritti da due campi vettoriali, in generale dipendenti dal tempo, E(x, t), H(x,
Funzioni di più variabili a valori vettoriali n t m
 Funzioni di più variabili a valori vettoriali n t m Definizione f(x 1, x 2,...x n )=[f 1 (x 1, x 2,...x n ), f 2 (x 1, x 2,...x n ),...f m (x 1, x 2,...x n )] Funzione definita n d m Dove: n = dominio
Funzioni di più variabili a valori vettoriali n t m Definizione f(x 1, x 2,...x n )=[f 1 (x 1, x 2,...x n ), f 2 (x 1, x 2,...x n ),...f m (x 1, x 2,...x n )] Funzione definita n d m Dove: n = dominio
Corso di introduzione all Astrofisica
 Corso di introduzione all Astrofisica I modulo Prof. Giuseppe Bertin Anno accademico 9 Indice Il teorema del viriale. Problema....................................... Equazioni del moto e energia per sistemi
Corso di introduzione all Astrofisica I modulo Prof. Giuseppe Bertin Anno accademico 9 Indice Il teorema del viriale. Problema....................................... Equazioni del moto e energia per sistemi
Lecce- XI scuola estiva di fisica Mirella Rafanelli. I sistemi estesi. La dinamica oltre il punto..
 Lecce- XI scuola estiva di fisica - 2018 Mirella Rafanelli I sistemi estesi La dinamica oltre il punto.. Lecce- XI scuola estiva di fisica - 2018 Mirella Rafanelli Nota bene: quanto segue serve come strumento
Lecce- XI scuola estiva di fisica - 2018 Mirella Rafanelli I sistemi estesi La dinamica oltre il punto.. Lecce- XI scuola estiva di fisica - 2018 Mirella Rafanelli Nota bene: quanto segue serve come strumento
Indice 3. Note di utilizzo 9. Ringraziamenti 10. Introduzione 11
 Indice Indice 3 Note di utilizzo 9 Ringraziamenti 10 Introduzione 11 Capitolo 1 Grandezze fisiche e schematizzazione dei sistemi materiali 13 1.1 Grandezze fisiche ed operazione di misura 13 1.2 Riferimento
Indice Indice 3 Note di utilizzo 9 Ringraziamenti 10 Introduzione 11 Capitolo 1 Grandezze fisiche e schematizzazione dei sistemi materiali 13 1.1 Grandezze fisiche ed operazione di misura 13 1.2 Riferimento
FM210 / MA - Terzo scritto ( ), con l > 0. Il vincolo può supporsi ideale. Oltre alle forze di reazione vincolare, il punto è soggetto a
 FM10 / MA - Terzo scritto (9-9-017) Esercizio 1. Un punto materiale P di massa m è vincolato a muoversi senza attrito sulla superficie di equazione z = l log x +y, con l > 0. Il vincolo può l supporsi
FM10 / MA - Terzo scritto (9-9-017) Esercizio 1. Un punto materiale P di massa m è vincolato a muoversi senza attrito sulla superficie di equazione z = l log x +y, con l > 0. Il vincolo può l supporsi
RISOLUZIONE DI PROBLEMI DI FISICA
 RISOUZIONE DI PROBEMI DI FISICA Problema 1 Una massa puntiforme m = 2 kg è soggetta ad una forza centrale con associata energia potenziale radiale U( r) 6 A =, dove A = 2 J m 6. Il momento angolare della
RISOUZIONE DI PROBEMI DI FISICA Problema 1 Una massa puntiforme m = 2 kg è soggetta ad una forza centrale con associata energia potenziale radiale U( r) 6 A =, dove A = 2 J m 6. Il momento angolare della
Applicazioni. Ogni corpo immerso in un fluido riceve da questo una spinta dal basso verso l'alto pari al peso del volume di fluido spostato
 Applicazioni Legge di Archimede. Ogni corpo immerso in un fluido riceve da questo una spinta dal basso verso l'alto pari al peso del volume di fluido spostato Prima del posizionamento del corpo: volume
Applicazioni Legge di Archimede. Ogni corpo immerso in un fluido riceve da questo una spinta dal basso verso l'alto pari al peso del volume di fluido spostato Prima del posizionamento del corpo: volume
fe s dvol M Fissata una simmetria v in V possiamo allora definire un applicazione lineare
 Dalle simmetrie dell azione alle correnti conservate. Iniziamo come al solito con un modello finito-dimensionale. Sia pertanto una varietà differenziabile compatta dotata di una forma di volume dvol e
Dalle simmetrie dell azione alle correnti conservate. Iniziamo come al solito con un modello finito-dimensionale. Sia pertanto una varietà differenziabile compatta dotata di una forma di volume dvol e
Forze di contatto. Forze. Sistemi in moto relativo. Forze apparenti
 di contatto Le forze di contatto o reazioni vincolari sono forze efficaci che descrivono l interazione tra corpi estesi (dotati di una superficie!) con un modello fenomenologico. La validità della descrizione
di contatto Le forze di contatto o reazioni vincolari sono forze efficaci che descrivono l interazione tra corpi estesi (dotati di una superficie!) con un modello fenomenologico. La validità della descrizione
Soluzione prova scritta Fisica Generale I Ing. Elettronica e Telecomunicazioni 01/02/2019
 Soluzione prova scritta Fisica Generale I Ing. Elettronica e Telecomunicazioni 01/0/019 Esercizio 1 1) Sull uomo agiscono la forza di gravità, la reazione della scala e le sue forze muscolari, mentre sulla
Soluzione prova scritta Fisica Generale I Ing. Elettronica e Telecomunicazioni 01/0/019 Esercizio 1 1) Sull uomo agiscono la forza di gravità, la reazione della scala e le sue forze muscolari, mentre sulla
Equazioni della dinamica dei fluidi
 F. Auteri e L. Quartapelle: Fluidodinamica. Capitolo 2 pagina 25 colore nero Gennaio 6, 2005 25 CAPITOLO 2 Equazioni della dinamica dei fluidi Introduzione In questo capitolo presenteremo il problema del
F. Auteri e L. Quartapelle: Fluidodinamica. Capitolo 2 pagina 25 colore nero Gennaio 6, 2005 25 CAPITOLO 2 Equazioni della dinamica dei fluidi Introduzione In questo capitolo presenteremo il problema del
