Sistemi continui oscillanti unidimensionali (corde vibranti)
|
|
|
- Gustavo Bellucci
- 4 anni fa
- Visualizzazioni
Transcript
1 Edoardo Milotti 4/10/2005 Sistemi continui oscillanti unidimensionali (corde vibranti Consideriamo due oscillatori armonici accoppiati linearmente. Fisicamente ciò si può realizzare, ad esempio, con due masse e tre molle che possono oscillare longitudinalmente, come nella figura qui sotto In questo caso le masse possono oscillare solo in direzione dell asse z, e assumiamo fin d ora che le due masse m siano uguali, e che anche le costanti elastiche k delle tre molle siano le stesse. All equilibrio le tre molle hanno la stessa lunghezza a. Ora introduciamo due coordinate spaziali, x 1 = z 1 z 1 e x 2 = z 2 z 2 che indicano lo spostamento delle due masse dalle posizioni di equilibrio z 1 e z 2, allora la condizione di equilibrio è k(z 1 z 0 + k(z 2 z 1 = 0 k(z 2 z 1 + k(z 3 z 2 = 0 (1 mentre le equazioni del moto per le due masse sono: m z 1 = k(z 1 z 0 + k(z 2 z 1 m z 2 = k(z 2 z 1 + k(z 3 z 2 (2 Sottraendo le equazioni (1 dalle (2 si ottiene m x 1 = kx 1 + k(x 2 x 1 m x 2 = k(x 2 x 1 kx 2 (3 Le stesse equazioni differenziali si possono ottenere anche considerando il circuito mostrato nella figura seguente:
2 Se assumiamo che le tre capacità valgano C e che le due induttanze valgano L, allora le equazioni di Kirchhoff sono: Q Q 1 C + Q C + L di 1 dt = 0 C Q 2 C L di 2 dt I 1 = I + I 2 = 0 (4 e dunque, eliminando I e derivando, si ottiene: L d 2 I 1 dt 2 = I 1 C + 1 C (I 2 I 1 L di 2 dt = 1 C (I 2 I 1 I 2 C (5 e questo sistema differenziale è identico al sistema (3, quando si fa la sostituzione k 1/C m L Come si fa di solito, assumiamo che le soluzioni siano del tipo x k = A k e iωt, allora sostituendo nella (3 otteniamo ω 2 A 1 = ω 2 0 A 1 + ω 2 0 (A 2 A 1 ω 2 A 2 = ω 2 0 (A 2 A 1 ω 2 0 A 2 (6 (con k = mω 0 2. Questo è un sistema di due equazioni lineari, che si può scrivere in forma matriciale ω ω 0 2 ω 0 2 ω 0 ω ω 0 A 1 A 2 = 0 0 (7 Il sistema ha una soluzione non banale (vale a dire non identicamente nulla solo se il determinante della matrice è uguale a 0, cioè solo se
3 ( ω 2 + 2ω = ω 0 4 (8 Dall equazione (8 si trova facilmente che ci sono 4 soluzioni: ω = ±ω 0 e ω = ± 3ω 0. A si ricordi che gli esponenziali immaginari sono combinazioni lineari di senie coseni: con una trasformazione lineare è possibile allora cambiare base e passare alle nuove funzioni di base: cos(ω 0 t, sin(ω 0 t, cos( 3ω 0 t, sin( 3ω 0 t. (9 Si noti che per scrivere questo insieme di soluzione di base reali è necessario di disporre di esponenziali immaginari con frequenza negative (più avanti nel discuteremo in dettaglio cosa questo significhi fisicamente. Prendiamo ora la soluzione con frequenza ω 0, allora la prima equazione del sistema (6 diventa ω 0 2 A 1 = ω 0 2 A 1 + ω 0 2 (A 2 A 1 (10 perciò A 1 = A 2, cioè le due masse oscillano in fase (modo simmetrico. Se prendiamo l altra soluzione con frequenza 3ω 0, allora la prima equazione del sistema (6 diventa 3ω 0 2 A 1 = ω 0 2 A 1 + ω 0 2 (A 2 A 1 (11 perciò A 1 = -A 2, cioè le due masse oscillano sfasate di 180 (modo antisimmetrico. La figura seguente mostra in fasi successive un periodo completo dei due modi di oscillazione, a sinistra c è quello simmetrico, a destra quello antisimmetrico:
4 Ogni altro possibile modo di oscillazione è una combinazione lineare del modo simmetrico e del modo antisimmetrico (questo si vede facilmente notando che 1. le soluzioni relative ai modi normali sono ortogonali tra loro; 2. il sistema è fatto di 2 equazioni di secondo ordine e quindi possono esserci solo 4 soluzioni linearmente indipendenti. Questi due modi di oscillazione che costituiscono una base per lo spazio lineare delle soluzioni, e sono un caso particolare di modi normali. Adesso analizziamo il comportamento di una corda elastica uniforme di lunghezza L e massa M le cui estremità sono fissate, come in figura, e supponiamo di poter scomporre la corda come se fosse fatta da N piccole masse m e da N+1 molle ideali e senza massa con costante elastica k. In questo caso sappiamo che se trattiamo solo le oscillazioni longitudinali ci sono N equazioni differenziali lineari di secondo ordine a coefficienti costanti per ciascuna massa e quindi l intero sistema può venire descritto da 2N equazioni differenziali lineari di primo ordine a coefficienti costanti. Questo significa che lo spazio vettoriale delle soluzioni ha 2N funzioni di base, e sappiamo che possiamo prendere delle funzioni esponenziali come funzioni di base. Sappiamo anche che - visto che non ci sono termini dissipativi, vale a dire termini che includono attrito - le soluzioni devono essere oscillanti e non smorzate e quindi devono essere dei seni e dei coseni. Questo significa che per ogni esponente presente nello spettro degli autovalori c è anche l esponente con segno cambiato - in altri termini ci sono sia frequenze positive sia frequenze negative, e le 2N soluzioni danno solo N frequenze diverse. Trattiamo ora questo sistema come quello che abbiamo analizzato quello con due sole masse: le equazioni differenziali che descrivono le oscillazioni longitudinali sono (utilizzando gli spostamenti x dalle posizioni di equilibrio:
5 x 1 m (x x + T 1 0 m (x x 2 1 x 2 m (x x + T 2 1 m (x x 3 2 x k m (x k + T m (x k +1 x k x N 1 m (x x + T N 1 N 2 m (x x N N 1 x N m (x x + T N N 1 m (x x N +1 N (12 e come si vede l equazione generica nel sistema (12 è x k m (x k + T m (x k +1 x k = = T ( m x k 1 2x k + x k +1 (13 L dove T è la tensione della corda, la distanza (all equilibrio tra due masse è =, ciascuna massa N + 1 vale m = M N, T è la tensione per unità di lunghezza, e sono state introdotte due masse fittizie in posizione 0 e N+1 con la condizione x 0 (t = x N +1 (t = 0. Così come abbiamo trattato le oscillazioni longitudinali possiamo trattare anche le oscillazioni trasversali della corda. In questo caso ci sono però alcune complicazioni aggiuntive che meritano un attenta considerazione: mentre le oscillazioni longitudinali sono unidimensionali, quelle trasversali sono bidimensionali. In particolare, c è disaccoppiamento tra i due gradi di libertà solo se le forze di richiamo sono lineari, e inoltre la bidimensionalità comporta la presenza di stati di polarizzazione diversi. si ottengono equazioni lineari solo se per piccole oscillazioni rispetto allo stato di equilibrio. Siano ora x e y le due coordinate trasversali, e z - come al solito - la coordinata longitudinale, come in figura
6 allora - discretizzando come prima - troviamo che le equazioni del moto per la massa generica k-esima sono m x k = F k,x m y k = F k,y (14 dove F k,x e F k,y sono le componenti x e y della forza di richiamo. D altra parte noi supponiamo che la forza di richiamo sia una forza di tipo elastico, e quindi proporzionale all allungamento della corda, che è dato approssimativamente da 2 + (x k 2 + (y k y k 1 2 (si spieghi come esercizio perché questa è solo un approssimazione. Quindi, se T è la tensione della corda, la componente F k,x vale F k,x (x k 2 + (x k 2 + (y k y k 1 2 F k (x k 2 + (x k 2 + (y k y k 1 2 = (x x k k 1 T 2 + (x k 2 + (y k y k 1 2 T (15 (e analoga per la componente F k,y, allora, in prima approssimazione, le due equazioni differenziali sono indipendenti una dall altra, e quindi il movimento in x è indipendente dal movimento in y. In altre parole, possiamo analizzare indipendentemente il movimento nelle due direzioni, e il moto complessivo è dato dalla sovrapposizione dei moti che avvengono nelle due direzioni. Possiamo allora ignorare una delle due coordinate - ad esempio y - e analizzare solo il moto in x, sapendo che la stessa analisi si ripete per la coordinata y. Per trovare le equazioni del moto nel piano xz cosideriamo allora la figura seguente, in cui sono mostrate tre delle masserelle in cui abbiamo suddiviso la corda
7 La parte in basso mostra come si dispongono le tensioni: la forza risultante dalla somma delle tensioni è data da F k,x (x k T (x k x k +1 = T (x k 1 2x k + x k +1 (16 e quindi si ottiene (ponendo mω 0 2 = T analogamente a quanto fatto sopra x k = ω 0 2 (x k 1 2x k + x k +1 (17 che è formalmente uguale alla (13, e le oscillazioni trasversali si trattano matematicamente come quelle longitudinali. Assumendo che il sistema abbia dimensioni finite, che sia costituito da N sezioni (più due sezioni fittizie che servono ad esprimere le condizioni al contorno e che le condizioni al contorno siano x 0 (t = 0 x N +1 (t = 0 (18 Cerchiamo soluzioni del tipo x n (t = u n e iωt, e sostituendo nella (17 si trova ω 2 u n = ω 0 2 ( (19 x n 1 2x n + x n+1
8 Per soddisfare le condizioni al contorno il vettore u si deve annullare ai bordi, e poiché l equazione per u è un equazione lineare alle differenze finite, tentiamo con una soluzione di prova di tipo sinusoidale che si annulla ai bordi: u n = Asin(kn, dove k = πm e m è un numero intero; tutto funziona se ω e k N + 1 soddisfano la relazione che si ottiene sostituendo u n = Asin(kn dentro l equazione (19 ω 2 sin(kn = ω 0 2 sin k(n 1 ( ( 2sin(kn + sin( k(n + 1 ( = 2ω 0 2 sin(kn cos k 1 (20 Dall equazione (20 vediamo che sia ω, sia k sono funzioni di m (e questa dipendenza la indichiamo con l aggiunta di un indice e sono legate tra loro dalla relazione ω 2 m = 2ω 2 0 ( 1 cos k m (21 Si noti che u n = Asin(k m n è una funzione periodica di m, con periodo N+1, e che si trovano quindi N vettori U non nulli con componenti U n m = Asin(k m n. Le soluzioni dell equazione differenziale originale sono allora u n (t = Asin(k m ne iω mt (22 con k m = πm N + 1, ω 2 m = 2ω 2 0 ( 1 cos k m e 0 m N. Poiché compaiono sia soluzioni con frequenze spaziali negative sia soluzioni con frequenze spaziali positive, è facile riarrangiarle in modo da ottenere nuove soluzioni di base, questa volta puramente reali: u + n (t = Asin(k m ncos(ω m t u n (t = Asin(k m nsin(ω m t (23 La figura che segue mostra la forma della corda ad un certo istante di tempo per soluzioni del tipo (23. Queste soluzioni di base (che permettono di ottenere ogni altra soluzione per mezzo di combinazioni lineari sono dette modi normali.
9 Le condizioni al contorno impongono che gli estremi della corda restino fissi, e inoltre i modi normali hanno anche altri punti fissi detti nodi dell oscillazione (questo concetto si generalizza per oscillazioni in più dimensioni: in due dimensioni ci sono linee nodali, mentre in tre dimensioni ci sono delle superfici nodali. Si noti che m dà il numero di semiperiodi spaziali contenuti tra gli estremi della corda o della linea di trasmissione. A parte il fatto che l ampiezza cambia nel tempo, per i modi normali la forma geometrica della corda resta fissa nel tempo: i modi normali sono un esempio di onda stazionaria. La formula (21 che lega tra loro ω e k è detta relazione di dispersione, e la figura seguente mostra un grafico della relazione di dispersione per N=100: (sull asse orizzontale c è m che è proporzionale a k mentre sull asse verticale c è il rapporto ω m ω 0. Si noti che k ha il significato di "frequenza spaziale", e quindi la relazione di dispersione è una relazione che lega la frequenza temporale a quella spaziale. Nel caso in cui N e m resti finito, allora si può espandere in serie il coseno nella relazione di dispersione, e si ottiene: ω 2 m = 2ω 2 0 ( 1 cos k m ω k m (24 La frequenza spaziale k m ha le dimensioni sbagliate, è un numero puro, e per passare al limite continuo prendendo le unità giuste, introduciamo la frequenza spaziale (il numero d onda per mezzo del limite k m k ; prendiamo anche il limite ω m ω. Infine notiamo che la relazione (24 si può scrivere nella forma ω m 2 ( 2 k m = ω 0 2 (25 e che la costante moltiplicativa c = ω 0 ha le dimensioni di una velocità al quadrato, così che la (25 diventa ω 2 = c 2 k 2 (26 e quindi ω = c k (27
10 La frequenza angolare temporale ω è correlata al periodo temporale T e alla frequenza temporale ν dalla formula ω = 2π = 2πν, e similmente la frequenza angolare spaziale k è correlata al periodo spaziale λ T dalla formula k = 2π, perciò la (27 si può scrivere anche nella forma λ λν = c (28 Inoltre è importante notare che k m n = k m n kz, e quindi le soluzioni (23 diventano x + (t = Asin(kzcos(ωt x (t = Asin(kzsin(ωt (29
Applicazioni delle leggi della meccanica: moto armnico
 Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Cap Moti oscillatori
 N.Giglietto A.A. 005/06- Cap 16.1- Moti oscillatori - 1 Cap 16.1- Moti oscillatori Alcuni tipi di forze o alcune situazioni danno luogo a dei moti di tipo oscillante ovvero a dei moti che si ripetono regolarmente.
N.Giglietto A.A. 005/06- Cap 16.1- Moti oscillatori - 1 Cap 16.1- Moti oscillatori Alcuni tipi di forze o alcune situazioni danno luogo a dei moti di tipo oscillante ovvero a dei moti che si ripetono regolarmente.
R è definita infine dall insieme delle curve percorse da ogni singolo punto della corda.
 1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
Capitolo 12. Moto oscillatorio
 Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Fisica I, a.a Secondo compitino
 Fisica I, a.a. 014 015 Secondo compitino 7 Maggio 015, Ore 11:30 Aula delle lezioni Anna M. Nobili 1 Oscillatore armonico con due masse nel piano Considerate un sistema isolato composto da due corpi di
Fisica I, a.a. 014 015 Secondo compitino 7 Maggio 015, Ore 11:30 Aula delle lezioni Anna M. Nobili 1 Oscillatore armonico con due masse nel piano Considerate un sistema isolato composto da due corpi di
Oscillazioni libere e risonanza di un circuito RLC-serie (Trattazione analitica del circuito RLC-serie)
 III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
Ricordiamo ora che a è legata ad x (derivata seconda) ed otteniamo
 Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
OSCILLATORE ARMONICO SEMPLICE
 OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
Dinamica dei Sistemi Aerospaziali Esercitazione 17
 Dinamica dei Sistemi Aerospaziali Esercitazione 7 9 dicembre 0 M, ft G k, r k, r b z l l y Figura : Sistema a gradi di libertà. Il sistema meccanico rappresentato in Figura è composto da una trave di massa
Dinamica dei Sistemi Aerospaziali Esercitazione 7 9 dicembre 0 M, ft G k, r k, r b z l l y Figura : Sistema a gradi di libertà. Il sistema meccanico rappresentato in Figura è composto da una trave di massa
Moti oscillatori. Parte I Oscillatore armonico
 1 10.1-10.2 OSCILLATORE ARMONICO Parte I Moti oscillatori 1 10.1-10.2 Oscillatore armonico Abbiamo visto che una situazione che si riconduce a soddisfare l equazione differenziale d 2 x(t) dt 2 +ω 2 x(t)
1 10.1-10.2 OSCILLATORE ARMONICO Parte I Moti oscillatori 1 10.1-10.2 Oscillatore armonico Abbiamo visto che una situazione che si riconduce a soddisfare l equazione differenziale d 2 x(t) dt 2 +ω 2 x(t)
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
7. Forze elastiche. Nella figura 1 il periodo è T = 2s e corrisponde ad un moto unidimensionale limitato tra i valori x = 0 ed x = 1.
 1 Moti periodici 7. Forze elastiche Un caso particolare di moto accelerato è un moto periodico. In figura 1 è riportato un esempio di moto periodico unidimensionale. Un moto periodico si ripete identicamente
1 Moti periodici 7. Forze elastiche Un caso particolare di moto accelerato è un moto periodico. In figura 1 è riportato un esempio di moto periodico unidimensionale. Un moto periodico si ripete identicamente
Approfondimenti. Rinaldo Rui. ultima revisione: 31 maggio 2019
 Approfondimenti Rinaldo Rui ultima revisione: 31 maggio 019 5 Oscillazioni e Onde 5. Lezione #1 5..1 Equazione Differenziale delle Onde In tutti i casi analizzati precedentemente si osserva che le onde
Approfondimenti Rinaldo Rui ultima revisione: 31 maggio 019 5 Oscillazioni e Onde 5. Lezione #1 5..1 Equazione Differenziale delle Onde In tutti i casi analizzati precedentemente si osserva che le onde
IL MOTO ARMONICO QUALCHE RIMANDO ALLA FORZA CENTRIPETA E AL MOTO CIRCOLARE
 www.aliceappunti.altervista.org IL MOTO ARMONICO QUALCHE RIMANDO ALLA FORZA CENTRIPETA E AL MOTO CIRCOLARE Nel moto circolare uniforme, il moto è generato da una accelerazione centripeta, diretta verso
www.aliceappunti.altervista.org IL MOTO ARMONICO QUALCHE RIMANDO ALLA FORZA CENTRIPETA E AL MOTO CIRCOLARE Nel moto circolare uniforme, il moto è generato da una accelerazione centripeta, diretta verso
Esame Scritto di Meccanica Quantistica Traccia di soluzione
 Esame Scritto di Meccanica Quantistica Traccia di soluzione 7 Giugno 7. Per esprimere la hamiltoniana data H = P 4m + p m + mω X + x ) in termini di x e x si esegue il cambiamento di coordinate ) X = x
Esame Scritto di Meccanica Quantistica Traccia di soluzione 7 Giugno 7. Per esprimere la hamiltoniana data H = P 4m + p m + mω X + x ) in termini di x e x si esegue il cambiamento di coordinate ) X = x
F = ma = -mω 2 R u r.
 Esercizio a) Sia v F = -ma cp u r = -m u r = -mω R u r. R b) Sia ω = ω u z il vettore velocità angolare del sistema di riferimento O. In questo sistema di riferimento rotante, i vettori velocità v e accelerazione
Esercizio a) Sia v F = -ma cp u r = -m u r = -mω R u r. R b) Sia ω = ω u z il vettore velocità angolare del sistema di riferimento O. In questo sistema di riferimento rotante, i vettori velocità v e accelerazione
Compito di Meccanica Razionale
 Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 30 Gennaio 207 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi in un piano un sistema di riferimento Oxy. In
Compito di Meccanica Razionale Corso di Laurea in Ingegneria Aerospaziale 30 Gennaio 207 (usare fogli diversi per esercizi diversi) Primo Esercizio Si fissi in un piano un sistema di riferimento Oxy. In
Indice slides. 1 Oscillatore semplice 5. 2 Equazione caratteristica 6. 3 Radici complesse 7. 4 Integrale generale 8. 5 Forza Peso 9.
 Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Unità didattica 3. Terza unità didattica (Fisica) 1. Corso integrato di Matematica e Fisica per il Corso di Farmacia
 Unità didattica 3 Elasticità dei materiali Deformazione di un solido..2 Legge di Hooke.. 3 Forza elastica.. 4 Deformazione elastica di una molla... 5 Accumulo di energia attraverso la deformazione elastica..6
Unità didattica 3 Elasticità dei materiali Deformazione di un solido..2 Legge di Hooke.. 3 Forza elastica.. 4 Deformazione elastica di una molla... 5 Accumulo di energia attraverso la deformazione elastica..6
ONDE PROGRESSIVE E REGRESSIVE, ONDE STAZIONARIE
 ONDE PROGRESSIVE E REGRESSIVE, ONDE STAZIONARIE Nel paragrafo 4 del capitolo «e onde elastiche» sono presentate le equazioni e y = acos T t +0l (1) y = acos x+0l. () a prima descrive l oscillazione di
ONDE PROGRESSIVE E REGRESSIVE, ONDE STAZIONARIE Nel paragrafo 4 del capitolo «e onde elastiche» sono presentate le equazioni e y = acos T t +0l (1) y = acos x+0l. () a prima descrive l oscillazione di
Appunti della lezione sulla Equazione Differenziale delle Onde
 Appunti della lezione sulla Equazione Differenziale delle Onde ultima revisione: 21 giugno 2017 In tutti i casi analizzati precedentemente si osserva che le onde obbediscono alla stessa Equazione Differenziale
Appunti della lezione sulla Equazione Differenziale delle Onde ultima revisione: 21 giugno 2017 In tutti i casi analizzati precedentemente si osserva che le onde obbediscono alla stessa Equazione Differenziale
Le onde. F. Soramel Fisica per Medicina 1
 Le onde a) onda sonora: le molecole si addensano e si rarefanno b) onda all interfaccia liquido-aria: le particelle oscillano in alto e in basso c) onda in una corda d) onda in una molla e) onda sismica
Le onde a) onda sonora: le molecole si addensano e si rarefanno b) onda all interfaccia liquido-aria: le particelle oscillano in alto e in basso c) onda in una corda d) onda in una molla e) onda sismica
Lezione XXVIII Sistemi vibranti a 2-n gdl. 6LVWHPLDSLJUDGLGLOLEHUWjQRQVPRU]DWL
![Lezione XXVIII Sistemi vibranti a 2-n gdl. 6LVWHPLDSLJUDGLGLOLEHUWjQRQVPRU]DWL Lezione XXVIII Sistemi vibranti a 2-n gdl. 6LVWHPLDSLJUDGLGLOLEHUWjQRQVPRU]DWL](/thumbs/97/131693920.jpg) 6LVWHLDSLJUDGLGLOLEHUWjQRQVRU]DWL er un sistema non smorzato con gradi di libertà, le equazioni che ne governano il moto possono essere sempre scritte nella forma matriciale dove [ 0 ] e [ ] [ 0 ]{&& [()
6LVWHLDSLJUDGLGLOLEHUWjQRQVRU]DWL er un sistema non smorzato con gradi di libertà, le equazioni che ne governano il moto possono essere sempre scritte nella forma matriciale dove [ 0 ] e [ ] [ 0 ]{&& [()
EFFETTO DEL RESTO DI TAYLOR NELLE PICCOLE OSCILLAZIONI
 EFFETTO DEL RESTO DI TAYLOR NELLE PICCOLE OSCILLAZIONI 1. Piccole oscillazioni Si consideri un sistema meccanico conservativo di energia potenziale U : R n R, M R(t) = U (R(t)), (1.1) R dove M è la matrice
EFFETTO DEL RESTO DI TAYLOR NELLE PICCOLE OSCILLAZIONI 1. Piccole oscillazioni Si consideri un sistema meccanico conservativo di energia potenziale U : R n R, M R(t) = U (R(t)), (1.1) R dove M è la matrice
Costruzioni in zona sismica
 Costruzioni in zona sismica Lezione 8 Sistemi a più gradi di liberà: Oscillazioni libere in assenza di smorzamento N equazioni differenziali omogenee accoppiate tramite la matrice delle masse, la matrice
Costruzioni in zona sismica Lezione 8 Sistemi a più gradi di liberà: Oscillazioni libere in assenza di smorzamento N equazioni differenziali omogenee accoppiate tramite la matrice delle masse, la matrice
Geometria BAER Canale I Esercizi 11
 Geometria BAER Canale I Esercizi 11 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Geometria BAER Canale I Esercizi 11 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Fondamenti di Meccanica Quantistica (Prof. Tarantelli)
 Fondamenti di Meccanica Quantistica (Prof. Tarantelli) 1 MOTO LINEARE E L OSCILLATORE ARMONICO 2 EQUAZIONE DI SCHRODINGER Equazione di Schrödinger: descrive il comportamento di un insieme di particelle:
Fondamenti di Meccanica Quantistica (Prof. Tarantelli) 1 MOTO LINEARE E L OSCILLATORE ARMONICO 2 EQUAZIONE DI SCHRODINGER Equazione di Schrödinger: descrive il comportamento di un insieme di particelle:
Sistemi di equazioni differenziali
 Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Sviluppo in Serie di Fourier
 Capitolo Sviluppo in Serie di Fourier. Proprietà della Serie di Fourier Un segnale reale tempo continuo e periodico di periodo, per il quale sono valide le condizioni di Dirichlet vedi pag. 4 [], può essere
Capitolo Sviluppo in Serie di Fourier. Proprietà della Serie di Fourier Un segnale reale tempo continuo e periodico di periodo, per il quale sono valide le condizioni di Dirichlet vedi pag. 4 [], può essere
Esercizio: pendoli accoppiati. Soluzione
 Esercizio: pendoli accoppiati Si consideri un sistema di due pendoli identici, con punti di sospensione posti alla stessa quota in un piano verticale. I due pendoli sono collegati da una molla di costante
Esercizio: pendoli accoppiati Si consideri un sistema di due pendoli identici, con punti di sospensione posti alla stessa quota in un piano verticale. I due pendoli sono collegati da una molla di costante
Principio di sovrapposizione.
 Principio di sovrapposizione. Il principio di sovrapposizione si applica ogni volta che due (o più) onde viaggiano nello stesso mezzo nello stesso tempo. Le onde si attraversano senza disturbarsi. In ogni
Principio di sovrapposizione. Il principio di sovrapposizione si applica ogni volta che due (o più) onde viaggiano nello stesso mezzo nello stesso tempo. Le onde si attraversano senza disturbarsi. In ogni
Anna M. Nobili: Lezioni Fisica 1 per Chimici a.a
 Anna M. Nobili: Lezioni Fisica 1 per Chimici a.a. 2013-2014 26 Settembre 2013 Grandezze fisiche, dimensioni e unità di misura. Potenze di 10 e loro uso. 3 Ottobre 2013 Grandezze fisiche, dimensioni e
Anna M. Nobili: Lezioni Fisica 1 per Chimici a.a. 2013-2014 26 Settembre 2013 Grandezze fisiche, dimensioni e unità di misura. Potenze di 10 e loro uso. 3 Ottobre 2013 Grandezze fisiche, dimensioni e
Esercitazioni di Meccanica Quantistica I
 Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com
![Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com](/thumbs/67/56787927.jpg) Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
si tratta di una forzante sinusoidale
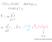 si tratta di una forzante sinusoidale funzione di e quindi di se! è trascurabile AF è massima quando: caratteristiche della forzante: caratteristiche dell oscillatore: qualunque sia t potenza
si tratta di una forzante sinusoidale funzione di e quindi di se! è trascurabile AF è massima quando: caratteristiche della forzante: caratteristiche dell oscillatore: qualunque sia t potenza
Fisica 2C. 3 Novembre Domande
 Fisica 2C 3 Novembre 2006 Domande ˆ i) Si consideri un oscillatore armonico smorzato e forzato da una sollecitazione sinusoidale esterna, la cui equazione é tipicamente s + 2γṡ + ω0s 2 = F cos ωt m 1)
Fisica 2C 3 Novembre 2006 Domande ˆ i) Si consideri un oscillatore armonico smorzato e forzato da una sollecitazione sinusoidale esterna, la cui equazione é tipicamente s + 2γṡ + ω0s 2 = F cos ωt m 1)
Foglio di Esercizi 7 Meccanica Razionale a.a. 2018/19 Canale A-L (P. Buttà)
 Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Prima prova intercorso giovedì 20 aprile 2006
 Prima prova intercorso giovedì 0 aprile 006 aurea in Scienza e Ingegneria dei Materiali anno accademico 005-006 Istituzioni di Fisica della Materia - Prof. orenzo Marrucci Tempo a disposizione: ore e 0
Prima prova intercorso giovedì 0 aprile 006 aurea in Scienza e Ingegneria dei Materiali anno accademico 005-006 Istituzioni di Fisica della Materia - Prof. orenzo Marrucci Tempo a disposizione: ore e 0
FISICA GENERALE I - 10/12 CFU NP II appello di Febbraio A.A Cognome Nome n. matr.
 FISICA GENERAE I - / CFU NP II appello di Febbraio A.A. - 5..4 Cognome Nome n. matr. Corso di Studi Docente Voto 9 crediti crediti crediti Esercizio n. Due masse puntiformi scivolano senza attrito su un
FISICA GENERAE I - / CFU NP II appello di Febbraio A.A. - 5..4 Cognome Nome n. matr. Corso di Studi Docente Voto 9 crediti crediti crediti Esercizio n. Due masse puntiformi scivolano senza attrito su un
DINAMICA DELLE VIBRAZIONI LIBERE DEI SISTEMI A UN GRADO DI LIBERTÁ (SDOF)
 INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF) M. Bozza Copyright AEPRON Tutti i iritti Riservati - www.adepron.it INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF)
INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF) M. Bozza Copyright AEPRON Tutti i iritti Riservati - www.adepron.it INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF)
ONDE. Propagazione di energia senza propagazione di materia. Una perturbazione viene trasmessa ma l acqua non si sposta
 ONDE Propagazione di energia senza propagazione di materia Una perturbazione viene trasmessa ma l acqua non si sposta Le onde meccaniche trasferiscono energia propagando una perturbazione in un mezzo.
ONDE Propagazione di energia senza propagazione di materia Una perturbazione viene trasmessa ma l acqua non si sposta Le onde meccaniche trasferiscono energia propagando una perturbazione in un mezzo.
Corso di Laurea in Fisica Compito di Fisica 3 (Prof. E. Santovetti) 9 febbraio 2018
 Corso di Laurea in Fisica Compito di Fisica 3 (Prof. E. Santovetti) 9 febbraio 8 Problema Si consideri una chitarra classica in cui il diapason (lunghezza totale della corda vibrante) vale l = 65 mm e
Corso di Laurea in Fisica Compito di Fisica 3 (Prof. E. Santovetti) 9 febbraio 8 Problema Si consideri una chitarra classica in cui il diapason (lunghezza totale della corda vibrante) vale l = 65 mm e
P z. OP x, OP y, OP z sono le proiezioni ortogonali di v sugli assi x, y, z, per cui: OP x = ( v i) i. k j. P x. OP z = ( v k) k
 Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
ONDE STAZIONARIE : DESCRIZIONE MATEMATICA
 ONDE STAZIONARIE : DESCRIZIONE MATEMATICA In questi appunti tratterò della descrizione matematica di un onda stazionaria, cioè di come rappresentare un onda stazionaria attraverso un equazione matematica.
ONDE STAZIONARIE : DESCRIZIONE MATEMATICA In questi appunti tratterò della descrizione matematica di un onda stazionaria, cioè di come rappresentare un onda stazionaria attraverso un equazione matematica.
26. Corda elastica SPETTRO DELLA CORDA DISCRETA
 6. Corda elastica I modelli microscopici di un mezzo continuo consistono in sistemi di N particelle, atomi o molecole, che interagiscono tra loro con forze elettromagnetiche. Nei solidi cristallini le
6. Corda elastica I modelli microscopici di un mezzo continuo consistono in sistemi di N particelle, atomi o molecole, che interagiscono tra loro con forze elettromagnetiche. Nei solidi cristallini le
y + P(x) y + Q(x) y = 0 y(x) = c 1y 1(x) + c 2 y 2(x).
 Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
Transitori del secondo ordine
 Università di Ferrara Corso di Teoria dei circuiti Transitori del secondo ordine Si consideri il circuito in figura e si supponga che all istante la corrente della serie e la tensione sul condensatore
Università di Ferrara Corso di Teoria dei circuiti Transitori del secondo ordine Si consideri il circuito in figura e si supponga che all istante la corrente della serie e la tensione sul condensatore
Meccanica Dinamica del punto materiale
 Meccanica 18-19 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente (statico,
Meccanica 18-19 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente (statico,
Analisi del moto dei proietti
 Moto dei proietti E il moto di particelle che vengono lanciate con velocità iniziale v 0 e sono soggette alla sola accelerazione di gravità g supposta costante. La pallina rossa viene lasciata cadere da
Moto dei proietti E il moto di particelle che vengono lanciate con velocità iniziale v 0 e sono soggette alla sola accelerazione di gravità g supposta costante. La pallina rossa viene lasciata cadere da
Sistemi vibranti ad 1 gdl
 Sistemi vibranti ad 1 gdl - vibrazioni forzate - 14 novembre 2 Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ + x = F sin(ωt) (1) dove, con riferimento alla figura
Sistemi vibranti ad 1 gdl - vibrazioni forzate - 14 novembre 2 Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ + x = F sin(ωt) (1) dove, con riferimento alla figura
Coppia di forze ONDE ELASTICHE
 Coppia di forze ONDE ELASTICHE LEZIONE N 26d Corso di fisica II Prof. Giuseppe Ciancio 1 Si definisce onda elastica meccanica, la propagazione di una perturbazione con trasporto di energia ma non di materia,
Coppia di forze ONDE ELASTICHE LEZIONE N 26d Corso di fisica II Prof. Giuseppe Ciancio 1 Si definisce onda elastica meccanica, la propagazione di una perturbazione con trasporto di energia ma non di materia,
Corso di Laurea in LOGOPEDIA FISICA ACUSTICA ONDE (ARMONICHE)
 Corso di Laurea in LOGOPEDIA FISICA ACUSTICA ONDE (ARMONICHE) Fabio Romanelli Department of Mathematics & Geosciences University of Trieste Email: romanel@units.it Le onde ci sono familiari - onde marine,
Corso di Laurea in LOGOPEDIA FISICA ACUSTICA ONDE (ARMONICHE) Fabio Romanelli Department of Mathematics & Geosciences University of Trieste Email: romanel@units.it Le onde ci sono familiari - onde marine,
FM210 - Fisica Matematica 1 Tutorato 11 ( )
 Corso di laurea in atematica - Anno Accademico 3/4 F - Fisica atematica Tutorato (--) Esercizio. Si calcolino i momenti principali di inerzia dei seguenti corpi rigidi rispetto al loro centro di massa:.
Corso di laurea in atematica - Anno Accademico 3/4 F - Fisica atematica Tutorato (--) Esercizio. Si calcolino i momenti principali di inerzia dei seguenti corpi rigidi rispetto al loro centro di massa:.
Appunti sul moto circolare uniforme e sul moto armonico- Fabbri Mariagrazia
 Moto circolare uniforme Il moto circolare uniforme è il moto di un corpo che si muove con velocità di modulo costante lungo una traiettoria circolare di raggio R. Il tempo impiegato dal corpo per compiere
Moto circolare uniforme Il moto circolare uniforme è il moto di un corpo che si muove con velocità di modulo costante lungo una traiettoria circolare di raggio R. Il tempo impiegato dal corpo per compiere
11 Piccole oscillazioni attorno a posizioni stabili
 11 Piccole oscillazioni attorno a posizioni stabili Consideriamo un sistema con l gradi di libertà descrivibile mediante le coordinate lagrangiane (q 1,..., q l ). Supponiamo che i vincoli siano lisci
11 Piccole oscillazioni attorno a posizioni stabili Consideriamo un sistema con l gradi di libertà descrivibile mediante le coordinate lagrangiane (q 1,..., q l ). Supponiamo che i vincoli siano lisci
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale
 Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Corso di Laurea in Ingegneria Meccanica Anno Accademico 2012/2013 Meccanica Razionale
 Ancona, 11 gennaio 2013 Corso di Laurea in Ingegneria Meccanica Anno Accademico 2012/2013 Meccanica Razionale 1. Un punto P di massa m si muove senza attrito su una guida verticale. Una molla di costante
Ancona, 11 gennaio 2013 Corso di Laurea in Ingegneria Meccanica Anno Accademico 2012/2013 Meccanica Razionale 1. Un punto P di massa m si muove senza attrito su una guida verticale. Una molla di costante
Compito di gennaio 2001
 Compito di gennaio 001 Un asta omogenea A di massa m e lunghezza l è libera di ruotare attorno al proprio estremo mantenendosi in un piano verticale All estremità A dell asta è saldato il baricentro di
Compito di gennaio 001 Un asta omogenea A di massa m e lunghezza l è libera di ruotare attorno al proprio estremo mantenendosi in un piano verticale All estremità A dell asta è saldato il baricentro di
Corso:Fisica moderna/calore specifico dei solidi/modello di Debye
 1 / 5 Corso:Fisica moderna/calore specifico dei solidi/modello di Debye Debye riprende l intero modello di Planck per il corpo nero: non solo la quantizzazione dell energia ma anche l idea che vi siano
1 / 5 Corso:Fisica moderna/calore specifico dei solidi/modello di Debye Debye riprende l intero modello di Planck per il corpo nero: non solo la quantizzazione dell energia ma anche l idea che vi siano
Complementi di Analisi per Informatica *** Capitolo 2. Numeri Complessi. e Circuiti Elettrici
 Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici Sergio Benenti Prima versione settembre 2013 Revisione settembre 2017? ndice 21 Circuito elettrico elementare
Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici Sergio Benenti Prima versione settembre 2013 Revisione settembre 2017? ndice 21 Circuito elettrico elementare
CORSO DI COMPLEMENTI DI MECCANICA. Prof. Vincenzo Niola
 CORSO DI COMPLEMENTI DI MECCANICA Prof. Vincenzo Niola SISTEMI A DUE GRADI DI LIBERTÀ Lo studio dei sistemi a più gradi di libertà verrà affrontato facendo riferimento, per semplicità, solo a sistemi conservativi,
CORSO DI COMPLEMENTI DI MECCANICA Prof. Vincenzo Niola SISTEMI A DUE GRADI DI LIBERTÀ Lo studio dei sistemi a più gradi di libertà verrà affrontato facendo riferimento, per semplicità, solo a sistemi conservativi,
Argomenti della Lezione
 ANALISI Argomenti della Lezione 32. Il teorema di unicitá Teorema 32.1. Il problema di Cauchy mx + rx + kx = 0 x(0) = x 0 x (0) = x 1 18 gennaio 2012 ha, per m, r, k tutti e tre non negativi, una e una
ANALISI Argomenti della Lezione 32. Il teorema di unicitá Teorema 32.1. Il problema di Cauchy mx + rx + kx = 0 x(0) = x 0 x (0) = x 1 18 gennaio 2012 ha, per m, r, k tutti e tre non negativi, una e una
Esercizi. Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio
 Esercizi Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio Per ciascun esercizio disegnare su ciascun corpo del sistema il diagramma delle forze, individuando e nominando ciascuna forza.
Esercizi Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio Per ciascun esercizio disegnare su ciascun corpo del sistema il diagramma delle forze, individuando e nominando ciascuna forza.
Esercizi. Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio
 Esercizi Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio Per ciascun esercizio disegnare su ciascun corpo del sistema il diagramma delle forze, individuando e nominando ciascuna forza.
Esercizi Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio Per ciascun esercizio disegnare su ciascun corpo del sistema il diagramma delle forze, individuando e nominando ciascuna forza.
Soluzioni. Foglio 1. Rette e piani. n x + c = 0. (1)
 Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
25 - Funzioni di più Variabili Introduzione
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Corso di Laurea in LOGOPEDIA FISICA ACUSTICA ONDE (ARMONICHE)
 Corso di Laurea in LOGOPEDIA FISICA ACUSTICA ONDE (ARMONICHE) Fabio Romanelli Department of Mathematics & Geosciences University of Trieste Email: romanel@units.it Le onde ci sono familiari - onde marine,
Corso di Laurea in LOGOPEDIA FISICA ACUSTICA ONDE (ARMONICHE) Fabio Romanelli Department of Mathematics & Geosciences University of Trieste Email: romanel@units.it Le onde ci sono familiari - onde marine,
CENTRO DI MASSA. il punto geometrico le cui coordinate, in un dato sistema di riferimento, sono date da:
 CENTRO DI MASSA il punto geometrico le cui coordinate, in un dato sistema di riferimento, sono date da: dove M = m 1 + m 2 +... + m N è la massa totale del sistema e le quantità r i sono i raggi vettori
CENTRO DI MASSA il punto geometrico le cui coordinate, in un dato sistema di riferimento, sono date da: dove M = m 1 + m 2 +... + m N è la massa totale del sistema e le quantità r i sono i raggi vettori
LEZIONE DEL OTTOBRE
 INGEGNERIA GESTIONALE corso di Fisica Generale Prof. E. Puddu LEZIONE DEL 21 22 OTTOBRE 2008 Moti oscillatori 1 Moto armonico Consideriamo una molla di costante elastica k a cui è collegato un corpo di
INGEGNERIA GESTIONALE corso di Fisica Generale Prof. E. Puddu LEZIONE DEL 21 22 OTTOBRE 2008 Moti oscillatori 1 Moto armonico Consideriamo una molla di costante elastica k a cui è collegato un corpo di
8 novembre Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
FISICA APPLICATA 2 FENOMENI ONDULATORI - 1
 FISICA APPLICATA 2 FENOMENI ONDULATORI - 1 DOWNLOAD Il pdf di questa lezione (onde1.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/tsrm/ 08/10/2012 FENOMENI ONDULATORI Una classe di fenomeni
FISICA APPLICATA 2 FENOMENI ONDULATORI - 1 DOWNLOAD Il pdf di questa lezione (onde1.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/tsrm/ 08/10/2012 FENOMENI ONDULATORI Una classe di fenomeni
13. Piccole oscillazioni
 3. Piccole oscillazioni Il moto di un sistema meccanico, soggetto a forze conservative, è approssimabile, nell intorno di un punto di minimo del potenziale, con quello del sistema linearizzato. Questa
3. Piccole oscillazioni Il moto di un sistema meccanico, soggetto a forze conservative, è approssimabile, nell intorno di un punto di minimo del potenziale, con quello del sistema linearizzato. Questa
Compito di Meccanica Razionale M-Z
 Compito di Meccanica Razionale M-Z 11 giugno 213 1. Tre piastre piane omogenee di massa m aventi la forma di triangoli rettangoli con cateti 4l e 3l sono saldate lungo il cateto più lungo come in figura
Compito di Meccanica Razionale M-Z 11 giugno 213 1. Tre piastre piane omogenee di massa m aventi la forma di triangoli rettangoli con cateti 4l e 3l sono saldate lungo il cateto più lungo come in figura
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
e una frequenza = 0 /2 =1/T (misurata in Hertz). Infine è la fase, cioè un numero (radianti) che dipende dalla definizione dell istante t=0.
 8. Oscillazioni Definizione di oscillatore armonico libero Si tratta di un sistema soggetto ad un moto descrivibile secondo una funzione armonica (seno o coseno) del tipo x(t) = Acos( 0 t + ) A è l ampiezza
8. Oscillazioni Definizione di oscillatore armonico libero Si tratta di un sistema soggetto ad un moto descrivibile secondo una funzione armonica (seno o coseno) del tipo x(t) = Acos( 0 t + ) A è l ampiezza
Geometria A. Università degli Studi di Trento Corso di laurea in Matematica A.A. 2017/ Maggio 2018 Prova Intermedia
 Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
rispetto alla configurazione di equilibrio di una o piu grandezze caratteristiche di un sistema fisico
 Fenomeni Ondulatori una perturbazione e la variazione rispetto alla configurazione di equilibrio di una o piu grandezze caratteristiche di un sistema fisico un onda e una perturbazione che si propaga nel
Fenomeni Ondulatori una perturbazione e la variazione rispetto alla configurazione di equilibrio di una o piu grandezze caratteristiche di un sistema fisico un onda e una perturbazione che si propaga nel
Trasmissione e riflessione di onde piane su interfacce dielettriche (incidenza qualsiasi)
 Trasmissione e riflessione di onde piane su interfacce dielettriche (incidenza qualsiasi) Corso di Ottica - Massimo Santarsiero Consideriamo un onda e.m. piana armonica, di pulsazione ω i, che incide con
Trasmissione e riflessione di onde piane su interfacce dielettriche (incidenza qualsiasi) Corso di Ottica - Massimo Santarsiero Consideriamo un onda e.m. piana armonica, di pulsazione ω i, che incide con
(b) 2. Quale delle seguenti affermazioni è corretta? (riscrivere la risposta corretta per esteso e solo sul foglio protocollo
 Esercizio (tratto dal problema 4.6 del Mazzoldi) Sopra un piano orizzontale sono posti due punti materiali di masse m e m 2. Il punto m è attaccato ad una molla di costante elastica k, fissata in x = 0
Esercizio (tratto dal problema 4.6 del Mazzoldi) Sopra un piano orizzontale sono posti due punti materiali di masse m e m 2. Il punto m è attaccato ad una molla di costante elastica k, fissata in x = 0
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
Sistemi vibranti ad 1 gdl
 Università degli Studi di Bergamo Dipartimento di Ingegneria Sistemi vibranti ad 1 gdl - vibrazioni forzate - rev. 1. Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ
Università degli Studi di Bergamo Dipartimento di Ingegneria Sistemi vibranti ad 1 gdl - vibrazioni forzate - rev. 1. Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ
Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema ALFA COGNOME: NOME: MATR.:
 Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema ALFA 1) L applicazione lineare f : R 3 R 2 data da f(x, y, z) = (3x + 2y + z, kx + 2y + kz) è suriettiva A: sempre; B: mai; C: per k 1 D: per k 2;
Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema ALFA 1) L applicazione lineare f : R 3 R 2 data da f(x, y, z) = (3x + 2y + z, kx + 2y + kz) è suriettiva A: sempre; B: mai; C: per k 1 D: per k 2;
8. Energia e lavoro. 2 Teorema dell energia per un moto uniformemente
 1 Definizione di lavoro 8. Energia e lavoro Consideriamo una forza applicata ad un corpo di massa m. Per semplicità ci limitiamo, inizialmente ad una forza costante, come ad esempio la gravità alla superficie
1 Definizione di lavoro 8. Energia e lavoro Consideriamo una forza applicata ad un corpo di massa m. Per semplicità ci limitiamo, inizialmente ad una forza costante, come ad esempio la gravità alla superficie
Vibrazioni Meccaniche
 Vibrazioni Meccaniche A.A. 2-22 Esempi di scrittura dell equazione di moto per sistemi a 2 gdl Turbina Una turbina pone in rotazione un generatore elettrico per mezzo della trasmissione schematizzata in
Vibrazioni Meccaniche A.A. 2-22 Esempi di scrittura dell equazione di moto per sistemi a 2 gdl Turbina Una turbina pone in rotazione un generatore elettrico per mezzo della trasmissione schematizzata in
LEGGI ORARIE DI ALCUNI MOTI PARTICOLARI
 LEGGI RARIE DI ALCUNI MTI PARTICLARI MT RETTILINE UNIFRME (1) v = costante; a = 0 Legge oraria: P(t) v x 0 è la posizione di P all istante t=0 (posizione iniziale) x 0 x(t) P(t=0) v x(t) = v t + x 0 Nel
LEGGI RARIE DI ALCUNI MTI PARTICLARI MT RETTILINE UNIFRME (1) v = costante; a = 0 Legge oraria: P(t) v x 0 è la posizione di P all istante t=0 (posizione iniziale) x 0 x(t) P(t=0) v x(t) = v t + x 0 Nel
Geometria BAER Canale I Esercizi 10
 Geometria BAER Canale I Esercizi 10 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Geometria BAER Canale I Esercizi 10 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
1 Dinamica del punto materiale (Seconda Parte)
 - LEZIONE 5 DEL CORSO DI FISICA PER INFORMATICA - A.A. 2006/2007 Silvio De Siena 1 Dinamica del punto materiale (Seconda Parte) Applicazione della legge di Newton nel caso della forza di richiamo elastica.
- LEZIONE 5 DEL CORSO DI FISICA PER INFORMATICA - A.A. 2006/2007 Silvio De Siena 1 Dinamica del punto materiale (Seconda Parte) Applicazione della legge di Newton nel caso della forza di richiamo elastica.
Esperienza 12: oscillatore. forzato e risonanza. Laboratorio di Fisica 1 A. Baraldi, M. Riccò. Università di Parma. a.a. 2011/2012. Copyright M.
 Esperienza 1: oscillatore Università di Parma forzato e risonanza a.a. 11/1 Laboratorio di Fisica 1 A. Baraldi, M. Riccò Copyright M.Solzi Oscillazioni libere smorzate a.a. 11/1 1: Oscillatore forzato
Esperienza 1: oscillatore Università di Parma forzato e risonanza a.a. 11/1 Laboratorio di Fisica 1 A. Baraldi, M. Riccò Copyright M.Solzi Oscillazioni libere smorzate a.a. 11/1 1: Oscillatore forzato
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier p. 2
 Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it
Formulazione dell equazione del moto. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Formulazione dell equazione del moto Prof. Adolfo Santini - Dinamica delle Strutture 1 Sistema a un grado di libertà In alcuni sistemi strutturali la massa, lo smorzamento e la rigidezza sono concentrati
Formulazione dell equazione del moto Prof. Adolfo Santini - Dinamica delle Strutture 1 Sistema a un grado di libertà In alcuni sistemi strutturali la massa, lo smorzamento e la rigidezza sono concentrati
21 settembre Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Corso di Laurea in Fisica. Geometria. a.a Prof. P. Piazza Soluzione compito a casa del 24/10/09
 Corso di Laurea in Fisica. Geometria. a.a. 29-. Prof. P. Piazza Soluzione compito a casa del 24//9 Soluzione esercizio. Siano A e B due matrici simmetriche e λ un numero reale. Dobbiamo mostrare che anche
Corso di Laurea in Fisica. Geometria. a.a. 29-. Prof. P. Piazza Soluzione compito a casa del 24//9 Soluzione esercizio. Siano A e B due matrici simmetriche e λ un numero reale. Dobbiamo mostrare che anche
Richiami sulle oscillazioni smorzate
 Richiami sulle oscillazioni smorzate Il moto armonico è il moto descritto da un oscillatore armonico, cioè un sistema meccanico che, quando perturbato dalla sua posizione di equilibrio, è soggetto ad una
Richiami sulle oscillazioni smorzate Il moto armonico è il moto descritto da un oscillatore armonico, cioè un sistema meccanico che, quando perturbato dalla sua posizione di equilibrio, è soggetto ad una
MOTO CIRCOLARE VARIO
 MOTO ARMONICO E MOTO VARIO PROF. DANIELE COPPOLA Indice 1 IL MOTO ARMONICO ------------------------------------------------------------------------------------------------------ 3 1.1 LA LEGGE DEL MOTO
MOTO ARMONICO E MOTO VARIO PROF. DANIELE COPPOLA Indice 1 IL MOTO ARMONICO ------------------------------------------------------------------------------------------------------ 3 1.1 LA LEGGE DEL MOTO
Oscillazioni LC Applicando la legge di Faraday: ma Φ B. in direzione I. ovvero. La soluzione di questa equazone e:
 Oscillazioni Applicando la legge di Faraday: E d l d ma Φ B con d l in direzione d E dl ovvero ovvero d + q / n base alla nostra scelta di polarizzazione di pero', si ha' che: dq Segue che: A d d q Allora,
Oscillazioni Applicando la legge di Faraday: E d l d ma Φ B con d l in direzione d E dl ovvero ovvero d + q / n base alla nostra scelta di polarizzazione di pero', si ha' che: dq Segue che: A d d q Allora,
Errata Corrige. Quesiti di Fisica Generale
 1 Errata Corrige a cura di Giovanni Romanelli Quesiti di Fisica Generale per i C.d.S. delle Facoltà di Scienze di Prof. Carla Andreani Dr. Giulia Festa Dr. Andrea Lapi Dr. Roberto Senesi 2 Copyright@2010
1 Errata Corrige a cura di Giovanni Romanelli Quesiti di Fisica Generale per i C.d.S. delle Facoltà di Scienze di Prof. Carla Andreani Dr. Giulia Festa Dr. Andrea Lapi Dr. Roberto Senesi 2 Copyright@2010
Fisica Generale I (primo modulo) A.A , 9 febbraio 2009
 Fisica Generale I (primo modulo) A.A. 2008-09, 9 febbraio 2009 Esercizio 1. Due corpi di massa M 1 = 10kg e M 2 = 5Kg sono collegati da un filo ideale passante per due carrucole prive di massa, come in
Fisica Generale I (primo modulo) A.A. 2008-09, 9 febbraio 2009 Esercizio 1. Due corpi di massa M 1 = 10kg e M 2 = 5Kg sono collegati da un filo ideale passante per due carrucole prive di massa, come in
