e una frequenza = 0 /2 =1/T (misurata in Hertz). Infine è la fase, cioè un numero (radianti) che dipende dalla definizione dell istante t=0.
|
|
|
- Serena Bertolini
- 7 anni fa
- Visualizzazioni
Transcript
1 8. Oscillazioni Definizione di oscillatore armonico libero Si tratta di un sistema soggetto ad un moto descrivibile secondo una funzione armonica (seno o coseno) del tipo x(t) = Acos( 0 t + ) A è l ampiezza del moto (x oscilla fra A e +A). La pulsazione naturale è 0, a cui corrisponde un periodo del moto T = / 0 e una frequenza = 0 / =1/T (misurata in Hertz). Infine è la fase, cioè un numero (radianti) che dipende dalla definizione dell istante t=0. Osserviamo subito che a = d x = A 0 cos( 0 t + ) = 0 x Questa è esattamente l accelerazione a cui è soggetta una massa attaccata ad una molla con costante elastica k, nel piano orizzontale: ma= kx in cui si individua immediatamente la pulsazione naturale (o propria): 0 = k /m. L energia totale per un oscillatore armonico libero è costante: E = 1 mv + 1 kx E = 1 m 0 A sin ( 0 t + ) + 1 ka cos ( 0 t + ) = 1 ka In generale, tutti i sistemi meccanici per i quali l accelerazione risulta del tipo a = 0 x sono oscillatori armonici liberi (non sottoposti ad altre forze).
2 Esempio: calcolare la frequenza di oscillazione di un pendolo costituito da un filo con attaccata una massa m, che descriva oscillazioni con piccoli angoli (pendolo semplice). Scrivendo la legge di Newton nella direzione tangente all arco di traiettoria circolare descritta: Trattandosi di piccole oscillazioni: m dv = mgsin v = d(l) = L d d g L Da cui si deducono la pulsazione e la frequenza: 0 = = g L Essendo l oscillatore armonico necessariamente conservativo, la sua equazione del moto può anche essere ricavata imponendo che l energia meccanica totale sia costante e prendendone la derivata rispetto alla direzione o angolo secondo i quali avviene l oscillazione. Nel caso del pendolo semplice, misurando l energia potenziale della forza peso come U(y) = mgy= mg( L Lcos)= mgl( 1 cos) abbiamo: Imponendo che de/=0: E = 1 mv + mgl( 1 cos) con v = L d m d d + mgld sin = 0
3 da cui nell approssimazione di angoli piccoli si riottiene l equazione di moto del pendolo semplice! Oscillatore forzato A differenza di quello libero, oltre alla forza di richiamo esiste almeno un altra forza agente: ma = kx+ F Se la forza F è costante cambia semplicemente il punto di equilibrio rispetto al quale avvengono le oscillazioni. Se è armonica anch essa, F(t) = F 0 cos( t), determina la frequenza e l ampiezza delle oscillazioni del sistema. Nel caso particolare in cui = 0 = k /m si parla di risonanza. Esempio: una molla con costante elastica k è attaccata ad un soffitto e regge all altra estremità una massa m. Determinare la posizione di equilibrio della massa m. Se da questa posizione m viene tirata verso il basso di una quantità s e poi lasciata libera, determinare l ampiezza e la frequenza delle oscillazioni. La legge di Newton per la massa è: ma= kx+ mg avendo assunto l origine dell asse di riferimento, x=0, coincidente con la posizione di riposo dell estremo inferiore della molla (senza m attaccata). La posizione di equilibrio x e per definizione corrisponde a v=0 e a=0, quindi x e = mg/k. Se ora m viene abbassata di una quantità s e poi rilasciata, ci aspettiamo un moto oscillatorio in su e in giù, simmetrico rispetto alla posizione di equilibrio: x(t) = x e + Acos( 0 t + ) Infatti sostituendo questa legge nell equazione del moto si ottiene: m 0 Acos( 0 t + )= kx e kacos( 0 t + )+ mg
4 che è evidentemente un identità purchè 0 = k /m, che stabilisce la frequenza propria. Per determinare ampiezza e fase imponiamo le condizioni iniziali del moto: x(0) = x e + s v(0) = 0 x e + Acos = x e + s 0 Asin = 0 da cui si ottiene A=s e =0, per cui x(t) = x e + scos( 0 t): le oscillazioni avvengono effettivamente in maniera simmetrica attorno alla posizione di equilibrio. In alternativa, si poteva sfruttare la conservazione dell energia, che stabilisce la corrispondenza tra quota raggiunta e velocità: 1 mv (x) + 1 kx mgx= 1 k x e + s ( ) mg x e + s ( ) Gli estremi di oscillazione si possono ricavare imponendo che v=0, mentre la frequenza di oscillazione si può calcolare prendendo la derivata di quest equazione rispetto a x, come fatto per il pendolo semplice. Oscillatore libero smorzato Consideriamo oltre alla forza elastica anche una forza di attrito viscoso proporzionale e opposta alla velocità: a = k dx x m limitiamoci a considerare uno smorzamento sufficientemente debole da ritenere il moto ancora armonico con la sua frequenza propria ma con un lento smorzamento di ampiezza: x(t) = A(t)cos( 0 t) Si noti che nei casi precedenti l ampiezza era sempre costante nel tempo! Per determinare come varia l ampiezza nel tempo possiamo valutare la potenza media su un periodo di oscillazione ceduta dall oscillatore per effetto dell attrito, assumendo l ampiezza pressochè costante in un singolo periodo di oscillazione: de = f a v = 1 T de = m T t +T t t +T 0 A (t) t [ mv (t)] sin ( 0 t)
5 Poichè la media di sin su un periodo è, e dato che E(t) = 1 ka (t): da ka da = m 0 A = A, da cui A(t) = A(0)e Quindi il moto oscillatorio debolmente smorzato da una forza di attrito viscoso con costante è caratterizzato da un decadimento esponenziale dell ampiezza di oscillazione, lento rispetto al periodo di oscillazione: x(t) = A(0)e t cos( 0 t) t Nel caso di smorzamento forte non è più possibile fare le stesse ipotesi usate in questo calcolo: addirittura lo smorzamento completo (dissipazione dell energia) può avvenire senza che si sia compiuta una singola oscillazione! Oscillatore armonico forzato (caso generale) Consideriamo un termine forzante del tipo F(t) = F 0 cos( t). Consideriamo ancora una forza di attrito proporzionale e opposta alla velocità. L equazione generale del moto per l oscillatore armonico forzato e smorzato è quindi d x dx x = F 0 cos( t) m Trascurando l intervallo di tempo necessario perchè l oscillatore raggiunga una situazione di regime a partire dalle sue condizioni iniziali, possiamo ritenere su basi intuitive che dopo un tempo sufficientemente lungo la forza F detti il ritmo di oscillazione secondo la sua frequenza, per cui x(t) = Acos( t + ) Sia l ampiezza che la fase dipenderanno dalla frequenza forzante.
6 Per determinare A e dobbiamo calcolare le derivate di x(t) e sostituirle nell equazione del moto. Sfruttando le proprietà sin( + ) = sin cos + cos sin cos( + ) = cos cos sin sin Abbiamo infine: [( 0 )cos sin]acos( t) + [( 0 )sin cos]asin( t) = F 0 cos( t) m Affinchè un identità del tipo P sin( t) + Qcos( t) = 0 sia rispettata per ogni istante t occorre che i coefficienti delle funzioni seno e coseno siano nulli, cioè P=Q=0: [( 0 )cos sin]a = F 0 m [( 0 )sin cos]a = 0 Dalla seconda relazione si ottiene la fase (supposta A0): tan() = 0 Elevando a quadrato entrambe le relazioni e sommando membro a membro si ottiene l ampiezza: A() = F 0 /m ( 0 ) + È utile rappresentare graficamente l andamento di ampiezza e fase in funzione della frequenza: per semplicità introduciamo una frequenza e uno smorzamento normalizzati rispetto alla frequenza propria, = / 0 e = / 0. Per capire il significato fisico del notevole aumento di ampiezza per frequenze prossime alla risonanza per piccoli smorzamenti, possiamo calcolare la potenza media trasferita da F alla massa m oscillante durante un periodo di oscillazione: P = F(t) dx = F 0 A cos( t)sin( t + )
7 P = F 0 A cos( t)sin( t)cos + cos ( t)sin) Il primo termine è semplicemente una sinusoide a frequenza doppia, la cui media è zero, mentre la media di cos è ancora : P = F A 0 sin Dalla curva di () si noti che in condizioni di risonanza è ( 0 ) = /, per cui sin( 0 ) = 1 e la potenza trasferita da F alla massa m oscillante è massima. Si noti che in realtà questa conclusione si ottiene in maniera più corretta esaminando direttamente il grafico di P(): il massimo della potenza trasferita coincide infatti con la risonanza indipendentemente dallo smorzamento.
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Applicazioni delle leggi della meccanica: moto armnico
 Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Capitolo 12. Moto oscillatorio
 Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Ricordiamo ora che a è legata ad x (derivata seconda) ed otteniamo
 Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
Appunti sul moto circolare uniforme e sul moto armonico- Fabbri Mariagrazia
 Moto circolare uniforme Il moto circolare uniforme è il moto di un corpo che si muove con velocità di modulo costante lungo una traiettoria circolare di raggio R. Il tempo impiegato dal corpo per compiere
Moto circolare uniforme Il moto circolare uniforme è il moto di un corpo che si muove con velocità di modulo costante lungo una traiettoria circolare di raggio R. Il tempo impiegato dal corpo per compiere
Fisica per scienze ed ingegneria
 Serway, Jewett Fisica per scienze ed ingegneria Capitolo 15 Blocchetto legato ad una molla in moto su un piano orizzontale privo di attrito. Forza elastica di richiamo: F x =-Kx (Legge di Hooke). Per x>0,
Serway, Jewett Fisica per scienze ed ingegneria Capitolo 15 Blocchetto legato ad una molla in moto su un piano orizzontale privo di attrito. Forza elastica di richiamo: F x =-Kx (Legge di Hooke). Per x>0,
L α. α d. 1. calcolare la velocità con cui il corpo raggiunge la sommità del piano [8 punti]
![L α. α d. 1. calcolare la velocità con cui il corpo raggiunge la sommità del piano [8 punti] L α. α d. 1. calcolare la velocità con cui il corpo raggiunge la sommità del piano [8 punti]](/thumbs/103/158585467.jpg) Problema E1 Una molla di costante elastica 500 Nm 1 e di lunghezza a riposo l 0 10 cm si trova in fondo ad un piano lungo L m, con coefficiente di attrito trascurabile e inclinato di un angolo α 30 o rispetto
Problema E1 Una molla di costante elastica 500 Nm 1 e di lunghezza a riposo l 0 10 cm si trova in fondo ad un piano lungo L m, con coefficiente di attrito trascurabile e inclinato di un angolo α 30 o rispetto
Cap Moti oscillatori
 N.Giglietto A.A. 005/06- Cap 16.1- Moti oscillatori - 1 Cap 16.1- Moti oscillatori Alcuni tipi di forze o alcune situazioni danno luogo a dei moti di tipo oscillante ovvero a dei moti che si ripetono regolarmente.
N.Giglietto A.A. 005/06- Cap 16.1- Moti oscillatori - 1 Cap 16.1- Moti oscillatori Alcuni tipi di forze o alcune situazioni danno luogo a dei moti di tipo oscillante ovvero a dei moti che si ripetono regolarmente.
8. Energia e lavoro. 2 Teorema dell energia per un moto uniformemente
 1 Definizione di lavoro 8. Energia e lavoro Consideriamo una forza applicata ad un corpo di massa m. Per semplicità ci limitiamo, inizialmente ad una forza costante, come ad esempio la gravità alla superficie
1 Definizione di lavoro 8. Energia e lavoro Consideriamo una forza applicata ad un corpo di massa m. Per semplicità ci limitiamo, inizialmente ad una forza costante, come ad esempio la gravità alla superficie
Moti oscillatori. Parte I Oscillatore armonico
 1 10.1-10.2 OSCILLATORE ARMONICO Parte I Moti oscillatori 1 10.1-10.2 Oscillatore armonico Abbiamo visto che una situazione che si riconduce a soddisfare l equazione differenziale d 2 x(t) dt 2 +ω 2 x(t)
1 10.1-10.2 OSCILLATORE ARMONICO Parte I Moti oscillatori 1 10.1-10.2 Oscillatore armonico Abbiamo visto che una situazione che si riconduce a soddisfare l equazione differenziale d 2 x(t) dt 2 +ω 2 x(t)
Lez. 9 Moto armonico
 Lez. 9 Moto armonico Prof. 1 Dott., PhD Dipartimento Scienze Fisiche Università di Napoli Federico II Compl. Univ. Monte S.Angelo Via Cintia, I-80126, Napoli mettivier@na.infn.it +39-081-676137 2 1 Un
Lez. 9 Moto armonico Prof. 1 Dott., PhD Dipartimento Scienze Fisiche Università di Napoli Federico II Compl. Univ. Monte S.Angelo Via Cintia, I-80126, Napoli mettivier@na.infn.it +39-081-676137 2 1 Un
Esercitazione 2. Soluzione
 Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
LEZIONE DEL OTTOBRE
 INGEGNERIA GESTIONALE corso di Fisica Generale Prof. E. Puddu LEZIONE DEL 21 22 OTTOBRE 2008 Moti oscillatori 1 Moto armonico Consideriamo una molla di costante elastica k a cui è collegato un corpo di
INGEGNERIA GESTIONALE corso di Fisica Generale Prof. E. Puddu LEZIONE DEL 21 22 OTTOBRE 2008 Moti oscillatori 1 Moto armonico Consideriamo una molla di costante elastica k a cui è collegato un corpo di
Meccanica Dinamica del punto materiale
 Meccanica 13-14 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente y m N mg mg
Meccanica 13-14 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente y m N mg mg
OSCILLATORE ARMONICO SEMPLICE
 OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
Dinamica del punto materiale
 Dinamica del punto materiale Formule fondamentali L. P. 5 Aprile 2010 N.B.: Le relazioni riportate sono valide in un sistema di riferimento inerziale. Princìpi della dinamica Secondo principio della dinamica
Dinamica del punto materiale Formule fondamentali L. P. 5 Aprile 2010 N.B.: Le relazioni riportate sono valide in un sistema di riferimento inerziale. Princìpi della dinamica Secondo principio della dinamica
Nicola GigliettoA.A. 2017/18
 3 ESERCIZIO 1 Esercizio 8.7 8.7 Una massa M=2Kg scivola su una superficie orizzontale liscia con v 1 =4 m/s. Essa va a finire contro una molla comprimendola fino a fermarsi completamente. Dal punto in
3 ESERCIZIO 1 Esercizio 8.7 8.7 Una massa M=2Kg scivola su una superficie orizzontale liscia con v 1 =4 m/s. Essa va a finire contro una molla comprimendola fino a fermarsi completamente. Dal punto in
Esercitazione 2. Soluzione
 Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
mg 2a 1 tan 2 θ = 3 8 m (6)
 Soluzioni Esercizio 1. All equilibrio la forza elastica, la forza peso e la reazione vincolare del piano si bilanciano: F el + P + R n = 0 (1) Se la massa si trova in A, proiettando lungo la direzione
Soluzioni Esercizio 1. All equilibrio la forza elastica, la forza peso e la reazione vincolare del piano si bilanciano: F el + P + R n = 0 (1) Se la massa si trova in A, proiettando lungo la direzione
Esame di Fisica con Laboratorio Corso di Laurea in Scienze dell Architettura Università degli Studi di Udine 29 gennaio 2010 Mario Paolo Giordani
 Esame di Fisica con Laboratorio Corso di Laurea in Scienze dell Architettura Università degli Studi di Udine 29 gennaio 2010 Mario Paolo Giordani Soluzioni Teoria Enunciare sinteticamente chiarendo il
Esame di Fisica con Laboratorio Corso di Laurea in Scienze dell Architettura Università degli Studi di Udine 29 gennaio 2010 Mario Paolo Giordani Soluzioni Teoria Enunciare sinteticamente chiarendo il
F = ma = -mω 2 R u r.
 Esercizio a) Sia v F = -ma cp u r = -m u r = -mω R u r. R b) Sia ω = ω u z il vettore velocità angolare del sistema di riferimento O. In questo sistema di riferimento rotante, i vettori velocità v e accelerazione
Esercizio a) Sia v F = -ma cp u r = -m u r = -mω R u r. R b) Sia ω = ω u z il vettore velocità angolare del sistema di riferimento O. In questo sistema di riferimento rotante, i vettori velocità v e accelerazione
Indice slides. 1 Oscillatore semplice 5. 2 Equazione caratteristica 6. 3 Radici complesse 7. 4 Integrale generale 8. 5 Forza Peso 9.
 Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Moto armonico. A.Solano - Fisica - CTF
 Moto armonico Moti periodici Moto armonico semplice: descrizione cinematica e dinamica Energia nel moto armonico semplice Il pendolo Oscillazioni smorzate Oscillazioni forzate e risonanza Moto periodico
Moto armonico Moti periodici Moto armonico semplice: descrizione cinematica e dinamica Energia nel moto armonico semplice Il pendolo Oscillazioni smorzate Oscillazioni forzate e risonanza Moto periodico
In un punto qualsiasi (P) della traiettoria è definita la direzione tangente t e la direzione perpendicolare n. d dt
 Moti piani su traiettorie qualsiasi In un punto qualsiasi (P) della traiettoria è definita la direzione tangente t e la direzione perpendicolare n. n ˆ P ˆ t traiettoria La velocità in ogni punto della
Moti piani su traiettorie qualsiasi In un punto qualsiasi (P) della traiettoria è definita la direzione tangente t e la direzione perpendicolare n. n ˆ P ˆ t traiettoria La velocità in ogni punto della
Prova Scritta di di Meccanica Analitica. 11 febbraio Problema 1
 Prova Scritta di di Meccanica Analitica 11 febbraio 019 Problema 1 Si consideri un punto materiale P di massa m vincolato a muoversi su una retta orizzontale e connesso mediante una molla di costante elastica
Prova Scritta di di Meccanica Analitica 11 febbraio 019 Problema 1 Si consideri un punto materiale P di massa m vincolato a muoversi su una retta orizzontale e connesso mediante una molla di costante elastica
Anna M. Nobili: Lezioni Fisica 1 per Chimici a.a
 Anna M. Nobili: Lezioni Fisica 1 per Chimici a.a. 2013-2014 26 Settembre 2013 Grandezze fisiche, dimensioni e unità di misura. Potenze di 10 e loro uso. 3 Ottobre 2013 Grandezze fisiche, dimensioni e
Anna M. Nobili: Lezioni Fisica 1 per Chimici a.a. 2013-2014 26 Settembre 2013 Grandezze fisiche, dimensioni e unità di misura. Potenze di 10 e loro uso. 3 Ottobre 2013 Grandezze fisiche, dimensioni e
OSCILLAZIONI SMORZATE E FORZATE
 OSCILLAZIONI SMORZATE E FORZATE Questo esperimento permette di studiare le oscillazioni armoniche di un pendolo e le oscillazioni smorzate e smorzate-forzate. Studiando il variare dell ampiezza dell oscillazione
OSCILLAZIONI SMORZATE E FORZATE Questo esperimento permette di studiare le oscillazioni armoniche di un pendolo e le oscillazioni smorzate e smorzate-forzate. Studiando il variare dell ampiezza dell oscillazione
Equazioni Differenziali
 Equazioni Differenziali Carla A. Ferradini December 9, 217 1 Introduzione e notazioni Un equazione differenziale è un equazione che ha come incognita una funzione. In particolare un equazione differenziale
Equazioni Differenziali Carla A. Ferradini December 9, 217 1 Introduzione e notazioni Un equazione differenziale è un equazione che ha come incognita una funzione. In particolare un equazione differenziale
Unità didattica 3. Terza unità didattica (Fisica) 1. Corso integrato di Matematica e Fisica per il Corso di Farmacia
 Unità didattica 3 Elasticità dei materiali Deformazione di un solido..2 Legge di Hooke.. 3 Forza elastica.. 4 Deformazione elastica di una molla... 5 Accumulo di energia attraverso la deformazione elastica..6
Unità didattica 3 Elasticità dei materiali Deformazione di un solido..2 Legge di Hooke.. 3 Forza elastica.. 4 Deformazione elastica di una molla... 5 Accumulo di energia attraverso la deformazione elastica..6
Fisica 2C. 3 Novembre Domande
 Fisica 2C 3 Novembre 2006 Domande ˆ i) Si consideri un oscillatore armonico smorzato e forzato da una sollecitazione sinusoidale esterna, la cui equazione é tipicamente s + 2γṡ + ω0s 2 = F cos ωt m 1)
Fisica 2C 3 Novembre 2006 Domande ˆ i) Si consideri un oscillatore armonico smorzato e forzato da una sollecitazione sinusoidale esterna, la cui equazione é tipicamente s + 2γṡ + ω0s 2 = F cos ωt m 1)
Corso di Laurea in LOGOPEDIA FISICA ACUSTICA MOTO OSCILLATORIO
 Corso di Laurea in LOGOPEDIA FISICA ACUSTICA MOTO OSCILLATORIO Fabio Romanelli Department of Mathematics & Geosciences University of Trieste Email: romanel@units.it Oscillazione Un oscillazione è la variazione,
Corso di Laurea in LOGOPEDIA FISICA ACUSTICA MOTO OSCILLATORIO Fabio Romanelli Department of Mathematics & Geosciences University of Trieste Email: romanel@units.it Oscillazione Un oscillazione è la variazione,
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
θ = arcos[g/(ω 2 L)]
![θ = arcos[g/(ω 2 L)] θ = arcos[g/(ω 2 L)]](/thumbs/104/163630441.jpg) Esercizio 1 a) Si consideri il sistema di riferimento inerziale con asse z parallelo all asse di rotazione della pallina. La pallina è sottoposta all azione della forza peso (parallela a z) e della tensione
Esercizio 1 a) Si consideri il sistema di riferimento inerziale con asse z parallelo all asse di rotazione della pallina. La pallina è sottoposta all azione della forza peso (parallela a z) e della tensione
IV ESERCITAZIONE. Esercizio 1. Soluzione
 Esercizio 1 IV ESERCITAZIONE Un blocco di massa m = 2 kg è posto su un piano orizzontale scabro. Una forza avente direzione orizzontale e modulo costante F = 20 N agisce sul blocco, inizialmente fermo,
Esercizio 1 IV ESERCITAZIONE Un blocco di massa m = 2 kg è posto su un piano orizzontale scabro. Una forza avente direzione orizzontale e modulo costante F = 20 N agisce sul blocco, inizialmente fermo,
Richiami sulle oscillazioni smorzate
 Richiami sulle oscillazioni smorzate Il moto armonico è il moto descritto da un oscillatore armonico, cioè un sistema meccanico che, quando perturbato dalla sua posizione di equilibrio, è soggetto ad una
Richiami sulle oscillazioni smorzate Il moto armonico è il moto descritto da un oscillatore armonico, cioè un sistema meccanico che, quando perturbato dalla sua posizione di equilibrio, è soggetto ad una
Compito 19 Luglio 2016
 Compito 19 Luglio 016 Roberto onciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 015-016 Compito di Fisica Generale I per matematici 19 Luglio 016
Compito 19 Luglio 016 Roberto onciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 015-016 Compito di Fisica Generale I per matematici 19 Luglio 016
(d) mostrare che l energia meccanica si conserva; (e) utilizzando la conservazione dell energia calcolare l altezza massima dal suolo;
 1 Esercizio Un sasso di massa m.5 Kg viene lanciato dalla cima di una torre alta h 2 m con velocità iniziale di modulo v 12 m/s, ad un angolo ϕ 6 o rispetto all orizzontale. La torre si trova in prossimità
1 Esercizio Un sasso di massa m.5 Kg viene lanciato dalla cima di una torre alta h 2 m con velocità iniziale di modulo v 12 m/s, ad un angolo ϕ 6 o rispetto all orizzontale. La torre si trova in prossimità
Esonero 17 Novembre 2017
 Esonero 7 Novembre 207 Roberto Bonciani e Paolo Dore Corso di Fisica Generale Università degli Studi di Roma La Sapienza Anno Accademico 207-208 Esercizio Un punto materiale P di massa m = g è appoggiato
Esonero 7 Novembre 207 Roberto Bonciani e Paolo Dore Corso di Fisica Generale Università degli Studi di Roma La Sapienza Anno Accademico 207-208 Esercizio Un punto materiale P di massa m = g è appoggiato
si tratta di una forzante sinusoidale
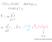 si tratta di una forzante sinusoidale funzione di e quindi di se! è trascurabile AF è massima quando: caratteristiche della forzante: caratteristiche dell oscillatore: qualunque sia t potenza
si tratta di una forzante sinusoidale funzione di e quindi di se! è trascurabile AF è massima quando: caratteristiche della forzante: caratteristiche dell oscillatore: qualunque sia t potenza
Esperienza 12: oscillatore. forzato e risonanza. Laboratorio di Fisica 1 A. Baraldi, M. Riccò. Università di Parma. a.a. 2011/2012. Copyright M.
 Esperienza 1: oscillatore Università di Parma forzato e risonanza a.a. 11/1 Laboratorio di Fisica 1 A. Baraldi, M. Riccò Copyright M.Solzi Oscillazioni libere smorzate a.a. 11/1 1: Oscillatore forzato
Esperienza 1: oscillatore Università di Parma forzato e risonanza a.a. 11/1 Laboratorio di Fisica 1 A. Baraldi, M. Riccò Copyright M.Solzi Oscillazioni libere smorzate a.a. 11/1 1: Oscillatore forzato
Oscillazioni. Capitolo L oscillatore armonico Abbiamo in precedenza (pag. 228) già considerato il caso dell oscillatore armonico, il
 Capitolo 15 Oscillazioni 15.1 L oscillatore armonico Abbiamo in precedenza (pag. 8) già considerato il caso dell oscillatore armonico, il y caso cioè di un corpo che oscilla sotto l azione di una forza
Capitolo 15 Oscillazioni 15.1 L oscillatore armonico Abbiamo in precedenza (pag. 8) già considerato il caso dell oscillatore armonico, il y caso cioè di un corpo che oscilla sotto l azione di una forza
P = mg; F N = mg cosα; F A = µ d F N = µ d mg cosα.
 Esercizio 1 a) Fissiamo un asse di riferimento x parallelo al piano inclinato, diretto verso l alto e con origine nella posizione iniziale del corpo alla base del piano. Sia m la massa del corpo, P la
Esercizio 1 a) Fissiamo un asse di riferimento x parallelo al piano inclinato, diretto verso l alto e con origine nella posizione iniziale del corpo alla base del piano. Sia m la massa del corpo, P la
Compito di Fisica 1 Ingegneria elettrica e gestionale Soluzioni fila B
 Compito di Fisica Ingegneria elettrica e gestionale Soluzioni fila B Massimo Vassalli 9 Gennaio 008 NB: dal momento che i dati numerici degli esercizi non sono comuni a tutti i compiti, i risultati sono
Compito di Fisica Ingegneria elettrica e gestionale Soluzioni fila B Massimo Vassalli 9 Gennaio 008 NB: dal momento che i dati numerici degli esercizi non sono comuni a tutti i compiti, i risultati sono
Compito di Fisica 1 Ingegneria elettrica e gestionale Soluzioni fila B
 Compito di Fisica 1 Ingegneria elettrica e gestionale Soluzioni fila B Massimo Vassalli 26 Marzo 2008 NB: dal momento che i dati numerici degli esercizi non sono comuni a tutti i compiti, i risultati sono
Compito di Fisica 1 Ingegneria elettrica e gestionale Soluzioni fila B Massimo Vassalli 26 Marzo 2008 NB: dal momento che i dati numerici degli esercizi non sono comuni a tutti i compiti, i risultati sono
R è definita infine dall insieme delle curve percorse da ogni singolo punto della corda.
 1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
Poichési conserva l energia meccanica, il lavoro compiuto dal motore è pari alla energia potenziale accumulata all equilibrio:
 Meccanica 24 Aprile 2018 Problema 1 (1 punto) Un blocco di mass M=90 kg è attaccato tramite una molla di costante elastiìca K= 2 10 3 N/m, massa trascurabile e lunghezza a riposo nulla, a una fune inestensibile
Meccanica 24 Aprile 2018 Problema 1 (1 punto) Un blocco di mass M=90 kg è attaccato tramite una molla di costante elastiìca K= 2 10 3 N/m, massa trascurabile e lunghezza a riposo nulla, a una fune inestensibile
Meccanica Dinamica del punto materiale
 Meccanica 18-19 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente (statico,
Meccanica 18-19 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente (statico,
Soluzione prova scritta Fisica Generale I Ing. Elettronica e Telecomunicazioni 01/02/2019
 Soluzione prova scritta Fisica Generale I Ing. Elettronica e Telecomunicazioni 01/0/019 Esercizio 1 1) Sull uomo agiscono la forza di gravità, la reazione della scala e le sue forze muscolari, mentre sulla
Soluzione prova scritta Fisica Generale I Ing. Elettronica e Telecomunicazioni 01/0/019 Esercizio 1 1) Sull uomo agiscono la forza di gravità, la reazione della scala e le sue forze muscolari, mentre sulla
Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com
![Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com](/thumbs/67/56787927.jpg) Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
Attrito statico e attrito dinamico
 Forza di attrito La presenza delle forze di attrito fa parte dell esperienza quotidiana. Se si tenta di far scorrere un corpo su una superficie, si sviluppa una resistenza allo scorrimento detta forza
Forza di attrito La presenza delle forze di attrito fa parte dell esperienza quotidiana. Se si tenta di far scorrere un corpo su una superficie, si sviluppa una resistenza allo scorrimento detta forza
Forze Conservative. In generale il lavoro fatto da una forza (più precisamente, da un campo di forze):
 Forze Conservative In generale il lavoro fatto da una forza (più precisamente, da un campo di forze): L = f i F d r, può dipendere dal percorso seguito dalla particella. Se il lavoro fatto da una forza
Forze Conservative In generale il lavoro fatto da una forza (più precisamente, da un campo di forze): L = f i F d r, può dipendere dal percorso seguito dalla particella. Se il lavoro fatto da una forza
Meccanica Dinamica del punto materiale
 Meccanica 07-08 Dinamica del punto materiale 9 pprossimazioni per piccoli angoli v ± gl sin tan v gl Limite di piccoli angoli: 0 6 cos +... 3 tan + +... 3 3 sin +... Serie di Taylor: pprossimazioni per
Meccanica 07-08 Dinamica del punto materiale 9 pprossimazioni per piccoli angoli v ± gl sin tan v gl Limite di piccoli angoli: 0 6 cos +... 3 tan + +... 3 3 sin +... Serie di Taylor: pprossimazioni per
ESERCIZIO 1 SOLUZIONI
 - ESERCIZIO - Un corpo di massa m = 00 g si trova su un tavolo liscio. Il corpo m è mantenuto inizialmente fermo, appoggiato ad una molla di costante elastica k = 00 N/m, inizialmente compressa. Ad un
- ESERCIZIO - Un corpo di massa m = 00 g si trova su un tavolo liscio. Il corpo m è mantenuto inizialmente fermo, appoggiato ad una molla di costante elastica k = 00 N/m, inizialmente compressa. Ad un
Oscillazioni. Definizione Moto circolare uniforme Moto armonico
 Oscillazioni Definizione Moto circolare unifore Moto aronico Moto aronico e oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Oscillazioni Definizione Moto circolare unifore Moto aronico Moto aronico e oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Errata Corrige. Quesiti di Fisica Generale
 1 Errata Corrige a cura di Giovanni Romanelli Quesiti di Fisica Generale per i C.d.S. delle Facoltà di Scienze di Prof. Carla Andreani Dr. Giulia Festa Dr. Andrea Lapi Dr. Roberto Senesi 2 Copyright@2010
1 Errata Corrige a cura di Giovanni Romanelli Quesiti di Fisica Generale per i C.d.S. delle Facoltà di Scienze di Prof. Carla Andreani Dr. Giulia Festa Dr. Andrea Lapi Dr. Roberto Senesi 2 Copyright@2010
pendolo reversibile TEORIA FISICA
 pendolo reversibile TEORIA FISICA Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile. Si utilizza un pendolo doppio o
pendolo reversibile TEORIA FISICA Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile. Si utilizza un pendolo doppio o
Oscillazioni ed onde meccaniche
 Capitolo Oscillazioni ed onde meccaniche 1. Il moto periodico Quali sono le caratteristiche del moto periodico? Una particella si muove di moto periodico quando continuamente ripassa per le stesse posizioni
Capitolo Oscillazioni ed onde meccaniche 1. Il moto periodico Quali sono le caratteristiche del moto periodico? Una particella si muove di moto periodico quando continuamente ripassa per le stesse posizioni
L Oscillatore Armonico
 L Oscillatore Armonico Descrizione del Fenomeno (max 15) righe Una molla esercita su un corpo una forza di intensità F=-kx, dove x è l allungamento o la compressione della molla e k una costante [N/m]
L Oscillatore Armonico Descrizione del Fenomeno (max 15) righe Una molla esercita su un corpo una forza di intensità F=-kx, dove x è l allungamento o la compressione della molla e k una costante [N/m]
3. Determinare la velocità media nell intervallo [0.5 s; 1.0 s] e confrontarla con la velocità istantanea nel punto medio di tale intervallo;
![3. Determinare la velocità media nell intervallo [0.5 s; 1.0 s] e confrontarla con la velocità istantanea nel punto medio di tale intervallo; 3. Determinare la velocità media nell intervallo [0.5 s; 1.0 s] e confrontarla con la velocità istantanea nel punto medio di tale intervallo;](/thumbs/92/109940598.jpg) Esercizio Una particella si muove lungo una retta seguendo la legge oraria con u 3 m/s e 4 s.. Determinare in quali istanti la particella si trova nell origine;. Disegnare la legge oraria; x(t) u t ( sin
Esercizio Una particella si muove lungo una retta seguendo la legge oraria con u 3 m/s e 4 s.. Determinare in quali istanti la particella si trova nell origine;. Disegnare la legge oraria; x(t) u t ( sin
T= 2π/ ω; ν=1/t = ω/2π Quindi ω = 2π/T = 2πν
 Moti periodici In generale possiamo definire periodici quei fenomeni che si ripetono ad intervalli regolari rispetto ad una variabile indipendente come il tempo, lo spazio o una combinazione di entrambi.
Moti periodici In generale possiamo definire periodici quei fenomeni che si ripetono ad intervalli regolari rispetto ad una variabile indipendente come il tempo, lo spazio o una combinazione di entrambi.
Don Bosco 2014/15, Classe 3B - Primo compito in classe di Fisica
 Don Bosco 014/15, Classe B - Primo compito in classe di Fisica 1. Enuncia il Teorema dell Energia Cinetica. Soluzione. Il lavoro della risultante delle forze agenti su un corpo che si sposta lungo una
Don Bosco 014/15, Classe B - Primo compito in classe di Fisica 1. Enuncia il Teorema dell Energia Cinetica. Soluzione. Il lavoro della risultante delle forze agenti su un corpo che si sposta lungo una
196 L Fs cos cos J 0,98. cos30 135,8 F F// F , N. mv mv
 Problemi sul lavoro Problema Un corpo di massa 50 kg viene trascinato a velocità costante per 0 m lungo un piano orizzontale da una forza inclinata di 45 rispetto all orizzontale, come in figura. Sapendo
Problemi sul lavoro Problema Un corpo di massa 50 kg viene trascinato a velocità costante per 0 m lungo un piano orizzontale da una forza inclinata di 45 rispetto all orizzontale, come in figura. Sapendo
Nome..Cognome.. Classe 4D 18 dicembre VERIFICA DI FISICA: lavoro ed energia
 Nome..Cognome.. Classe 4D 8 dicembre 008 EIFICA DI FISICA: lavoro ed energia Domande ) Forze conservative ed energia potenziale: (punti:.5) a) Dai la definizione di forza conservativa ed indicane le proprietà.
Nome..Cognome.. Classe 4D 8 dicembre 008 EIFICA DI FISICA: lavoro ed energia Domande ) Forze conservative ed energia potenziale: (punti:.5) a) Dai la definizione di forza conservativa ed indicane le proprietà.
Opera rilasciata sotto licenza CC BY-NC-SA 3.0 Italia da Studio Bells (www.studiobells.it)
 Esercizio 001 Si consideri un piano inclinato di un angolo = 30 rispetto all orizzontale e di lunghezza L = 1 m. Sul piano è posta una massa m = 5, 0 kg collegata alla cima del piano tramite una molla
Esercizio 001 Si consideri un piano inclinato di un angolo = 30 rispetto all orizzontale e di lunghezza L = 1 m. Sul piano è posta una massa m = 5, 0 kg collegata alla cima del piano tramite una molla
Lezione XXIV Sistemi vibranti a 1 gdl 67580(17,',0,685$'(//(9,%5$=,21,
 ezione XXIV 658(,,,685$(//(9,%5$,, Tra le applicazioni del nostro oscillatore vi è quella di usarlo come strumento per la misura delle vibrazioni assolute di un corpo Con riferimento alle grandezze indicate
ezione XXIV 658(,,,685$(//(9,%5$,, Tra le applicazioni del nostro oscillatore vi è quella di usarlo come strumento per la misura delle vibrazioni assolute di un corpo Con riferimento alle grandezze indicate
Fisica I, a.a Secondo compitino
 Fisica I, a.a. 014 015 Secondo compitino 7 Maggio 015, Ore 11:30 Aula delle lezioni Anna M. Nobili 1 Oscillatore armonico con due masse nel piano Considerate un sistema isolato composto da due corpi di
Fisica I, a.a. 014 015 Secondo compitino 7 Maggio 015, Ore 11:30 Aula delle lezioni Anna M. Nobili 1 Oscillatore armonico con due masse nel piano Considerate un sistema isolato composto da due corpi di
Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile
 Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile Anno Accademico 2017-2018 A. Ponno (aggiornato al 20 dicembre 2017) 2 Ottobre 2017 2/10/17 Benvenuto, presentazione
Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile Anno Accademico 2017-2018 A. Ponno (aggiornato al 20 dicembre 2017) 2 Ottobre 2017 2/10/17 Benvenuto, presentazione
Meccanica del punto materiale
 Meccanica del punto materiale Princìpi della dinamica. Forze. Momento angolare. Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro
Meccanica del punto materiale Princìpi della dinamica. Forze. Momento angolare. Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro
Attrito statico e attrito dinamico
 Forza di attrito La presenza delle forze di attrito fa parte dell esperienza quotidiana. Se si tenta di far scorrere un corpo su una superficie, si sviluppa una resistenza allo scorrimento detta forza
Forza di attrito La presenza delle forze di attrito fa parte dell esperienza quotidiana. Se si tenta di far scorrere un corpo su una superficie, si sviluppa una resistenza allo scorrimento detta forza
ESERCIZIO SOLUZIONE. 13 Aprile 2011
 ESERCIZIO Un corpo di massa m è lasciato cadere da un altezza h sull estremo libero di una molla di costante elastica in modo da provocarne la compressione. Determinare: ) la velocità del corpo all impatto
ESERCIZIO Un corpo di massa m è lasciato cadere da un altezza h sull estremo libero di una molla di costante elastica in modo da provocarne la compressione. Determinare: ) la velocità del corpo all impatto
Esonero 14 Novembre 2016
 Esonero 14 Novembre 2016 Roberto Bonciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 2016-2017 Esercizio 1 Un corpo di massa m è inizialmente fermo
Esonero 14 Novembre 2016 Roberto Bonciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 2016-2017 Esercizio 1 Un corpo di massa m è inizialmente fermo
DINAMICA DELLE VIBRAZIONI LIBERE DEI SISTEMI A UN GRADO DI LIBERTÁ (SDOF)
 INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF) M. Bozza Copyright AEPRON Tutti i iritti Riservati - www.adepron.it INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF)
INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF) M. Bozza Copyright AEPRON Tutti i iritti Riservati - www.adepron.it INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF)
Oscillatore armonico. LEZ 15 OTTOBRE 2018 e seguenti
 Oscillatore armonico LEZ 15 OTTOBRE 018 e seguenti L OSCILLATORE ARMONICO EQUAZIONE DEI MOTI ARMONICI 3 PERIDODO E FREQUENZA 4 DENTRO LA LEGGE 5 Funzioni seno e coseno Le funzioni seno e coseno sono le
Oscillatore armonico LEZ 15 OTTOBRE 018 e seguenti L OSCILLATORE ARMONICO EQUAZIONE DEI MOTI ARMONICI 3 PERIDODO E FREQUENZA 4 DENTRO LA LEGGE 5 Funzioni seno e coseno Le funzioni seno e coseno sono le
LE FORZE E IL MOTO. Il moto lungo un piano inclinato
 LE FORZE E IL MOTO Il moto lungo un piano inclinato Il moto di caduta lungo un piano inclinato un moto uniformemente accelerato in cui l accelerazione è diretta parallelamente al piano (verso il basso)
LE FORZE E IL MOTO Il moto lungo un piano inclinato Il moto di caduta lungo un piano inclinato un moto uniformemente accelerato in cui l accelerazione è diretta parallelamente al piano (verso il basso)
Teorema dell energia cinetica
 Teorema dell energia cinetica L. P. 23 Marzo 2010 Il teorema dell energia cinetica Il teorema dell energia cinetica è una relazione molto importante in Meccanica. L enunceremo nel caso semplice di un punto
Teorema dell energia cinetica L. P. 23 Marzo 2010 Il teorema dell energia cinetica Il teorema dell energia cinetica è una relazione molto importante in Meccanica. L enunceremo nel caso semplice di un punto
FISICA. La Dinamica: le forze e il moto. Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica
 FISICA La Dinamica: le forze e il moto Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica LA FORZA PESO Come anticipato nella Cinematica, in assenza di attrito con l aria, un oggetto in caduta
FISICA La Dinamica: le forze e il moto Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica LA FORZA PESO Come anticipato nella Cinematica, in assenza di attrito con l aria, un oggetto in caduta
Esercitazione 3. Soluzione. F y dy = 0 al 2 dy = 0.06 J
 Esercitazione 3 Esercizio 1 - Lavoro Una particella è sottoposta ad una forza F = axy û x ax 2 û y, dove û x e û y sono i versori degli assi x e y e a = 6 N/m 2. Si calcoli il lavoro compiuto dalla forza
Esercitazione 3 Esercizio 1 - Lavoro Una particella è sottoposta ad una forza F = axy û x ax 2 û y, dove û x e û y sono i versori degli assi x e y e a = 6 N/m 2. Si calcoli il lavoro compiuto dalla forza
(b) 2. Quale delle seguenti affermazioni è corretta? (riscrivere la risposta corretta per esteso e solo sul foglio protocollo
 Esercizio (tratto dal problema 4.6 del Mazzoldi) Sopra un piano orizzontale sono posti due punti materiali di masse m e m 2. Il punto m è attaccato ad una molla di costante elastica k, fissata in x = 0
Esercizio (tratto dal problema 4.6 del Mazzoldi) Sopra un piano orizzontale sono posti due punti materiali di masse m e m 2. Il punto m è attaccato ad una molla di costante elastica k, fissata in x = 0
Prova del 6 Marzo, Traccia della soluzione. Problema n. 1. BDA = α 2. sin α α = 1 e che analogamente si dimostra l altro limite notevole tan α
 IIASS International Institute for Advanced Scientific Studies Eduardo R. Caianiello Circolo di Matematica e Fisica Dipartimento di Fisica E.R. Caianiello Università di Salerno Premio Eduardo R. Caianiello
IIASS International Institute for Advanced Scientific Studies Eduardo R. Caianiello Circolo di Matematica e Fisica Dipartimento di Fisica E.R. Caianiello Università di Salerno Premio Eduardo R. Caianiello
Prova in itinere di Fisica (I modulo) Scienze e Tecnologie dell Ambiente. Soluzioni
 Prova in itinere di Fisica (I modulo) Scienze e Tecnologie dell Ambiente 30 Novembre 2007 Soluzioni A) a=2at = 24 m/s 2. a m = v(t 1 + t) v(t 1 ) t = 24.6 m/s 2 3) B) s(t 1 ) = s 0 + t1 0 (At 2 + B)dt
Prova in itinere di Fisica (I modulo) Scienze e Tecnologie dell Ambiente 30 Novembre 2007 Soluzioni A) a=2at = 24 m/s 2. a m = v(t 1 + t) v(t 1 ) t = 24.6 m/s 2 3) B) s(t 1 ) = s 0 + t1 0 (At 2 + B)dt
Esercizi aprile Sommario Conservazione dell energia e urti a due corpi.
 Esercizi 2.04.8 3 aprile 208 Sommario Conservazione dell energia e urti a due corpi. Conservazione dell energia. Esercizio Il motore di un ascensore solleva con velocità costante la cabina contenente quattro
Esercizi 2.04.8 3 aprile 208 Sommario Conservazione dell energia e urti a due corpi. Conservazione dell energia. Esercizio Il motore di un ascensore solleva con velocità costante la cabina contenente quattro
Compito di gennaio 2001
 Compito di gennaio 001 Un asta omogenea A di massa m e lunghezza l è libera di ruotare attorno al proprio estremo mantenendosi in un piano verticale All estremità A dell asta è saldato il baricentro di
Compito di gennaio 001 Un asta omogenea A di massa m e lunghezza l è libera di ruotare attorno al proprio estremo mantenendosi in un piano verticale All estremità A dell asta è saldato il baricentro di
Esonero 13 Novembre 2015
 Esonero 13 Novembre 2015 Roberto Bonciani, Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 2015-2016 2 ESONERO 1- FISICA 1 PER MATERMATICA - R. BONCIANI,
Esonero 13 Novembre 2015 Roberto Bonciani, Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 2015-2016 2 ESONERO 1- FISICA 1 PER MATERMATICA - R. BONCIANI,
III ESERCITAZIONE - 21 Ottobre 2013
 III ESERCITAZIONE - 21 Ottobre 2013 I. MOLLA PESANTE Ricavare la soluzione all equazione del moto per una massa m sospesa ad una molla di costante elastica k, libera di oscillare lungo l asse y. Supponiamo
III ESERCITAZIONE - 21 Ottobre 2013 I. MOLLA PESANTE Ricavare la soluzione all equazione del moto per una massa m sospesa ad una molla di costante elastica k, libera di oscillare lungo l asse y. Supponiamo
SOLUZIONI a) Tracciamo il diagramma delle forze in un generico punto sulla traiettoria:
 - ESERCIZIO - Un corpo di massa m è attaccato ad un filo inestensibile di massa trascurabile e lunghezza L. Il corpo percorre una circonferenza sul piano verticale in senso orario, in modo che il filo
- ESERCIZIO - Un corpo di massa m è attaccato ad un filo inestensibile di massa trascurabile e lunghezza L. Il corpo percorre una circonferenza sul piano verticale in senso orario, in modo che il filo
7. Forze elastiche. Nella figura 1 il periodo è T = 2s e corrisponde ad un moto unidimensionale limitato tra i valori x = 0 ed x = 1.
 1 Moti periodici 7. Forze elastiche Un caso particolare di moto accelerato è un moto periodico. In figura 1 è riportato un esempio di moto periodico unidimensionale. Un moto periodico si ripete identicamente
1 Moti periodici 7. Forze elastiche Un caso particolare di moto accelerato è un moto periodico. In figura 1 è riportato un esempio di moto periodico unidimensionale. Un moto periodico si ripete identicamente
POLITECNICO DI MILANO Scuola di Ingegneria Industriale Fondamenti di Fisica Sperimentale, a.a I Appello, 10 luglio 2013
 POLITECNICO DI MILNO Scuola di Ingegneria Industriale Fondamenti di Fisica Sperimentale, a.a. 0-3 I ppello, 0 luglio 03 Giustificare le risposte e scrivere in modo chiaro e leggibile. Sostituire i valori
POLITECNICO DI MILNO Scuola di Ingegneria Industriale Fondamenti di Fisica Sperimentale, a.a. 0-3 I ppello, 0 luglio 03 Giustificare le risposte e scrivere in modo chiaro e leggibile. Sostituire i valori
Esercizi. Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio
 Esercizi Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio Per ciascun esercizio disegnare su ciascun corpo del sistema il diagramma delle forze, individuando e nominando ciascuna forza.
Esercizi Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio Per ciascun esercizio disegnare su ciascun corpo del sistema il diagramma delle forze, individuando e nominando ciascuna forza.
Esercizi. Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio
 Esercizi Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio Per ciascun esercizio disegnare su ciascun corpo del sistema il diagramma delle forze, individuando e nominando ciascuna forza.
Esercizi Diagrammi delle forze (di corpo singolo) per sistemi in equilibrio Per ciascun esercizio disegnare su ciascun corpo del sistema il diagramma delle forze, individuando e nominando ciascuna forza.
Problema 1: SOLUZIONE: 1) La velocità iniziale v 0 si ricava dal principio di conservazione dell energia meccanica; trascurando
 Problema : Un pallina di gomma, di massa m = 0g, è lanciata verticalmente con un cannoncino a molla, la cui costante elastica vale k = 4 N/cm, ed è compressa inizialmente di δ. Dopo il lancio, la pallina
Problema : Un pallina di gomma, di massa m = 0g, è lanciata verticalmente con un cannoncino a molla, la cui costante elastica vale k = 4 N/cm, ed è compressa inizialmente di δ. Dopo il lancio, la pallina
Il Pendolo. Alessio Bianchi 3 maggio 2017
 Il Pendolo Alessio Bianchi 3 maggio 2017 Sommario Verifica dell isocronia di un pendolo con moti di ampiezza A diversi e determinazione delle loro leggi orarie. Verifica grafica della relazione tra x(t)
Il Pendolo Alessio Bianchi 3 maggio 2017 Sommario Verifica dell isocronia di un pendolo con moti di ampiezza A diversi e determinazione delle loro leggi orarie. Verifica grafica della relazione tra x(t)
Fisica Generale I (primo modulo) A.A , 9 febbraio 2009
 Fisica Generale I (primo modulo) A.A. 2008-09, 9 febbraio 2009 Esercizio 1. Due corpi di massa M 1 = 10kg e M 2 = 5Kg sono collegati da un filo ideale passante per due carrucole prive di massa, come in
Fisica Generale I (primo modulo) A.A. 2008-09, 9 febbraio 2009 Esercizio 1. Due corpi di massa M 1 = 10kg e M 2 = 5Kg sono collegati da un filo ideale passante per due carrucole prive di massa, come in
Oscillazioni libere e risonanza di un circuito RLC-serie (Trattazione analitica del circuito RLC-serie)
 III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
ESERCIZIO SOLUZIONE T U E 1. iniziale. finale 0. 2 mv2 o 1. 2 mv kx2 1. o 2 kx2 o
 ESERCIZIO Sia dato un corpo di massa m = 0 kg e velocità v o = 0 m/s che impatta sull estremo libero di una molla di costante elastica k = 000 N/m in modo da provocarne la compressione. Si consideri dapprima
ESERCIZIO Sia dato un corpo di massa m = 0 kg e velocità v o = 0 m/s che impatta sull estremo libero di una molla di costante elastica k = 000 N/m in modo da provocarne la compressione. Si consideri dapprima
esperienze in laboratorio
 esperienze in laboratorio 1 piano inclinato misura del coefficiente di attrito statico 2 molle e bilance 3 pendolo semplice 1 misura del coefficiente d attrito statico Un corpo poggiato su un piano inclinato
esperienze in laboratorio 1 piano inclinato misura del coefficiente di attrito statico 2 molle e bilance 3 pendolo semplice 1 misura del coefficiente d attrito statico Un corpo poggiato su un piano inclinato
Esercitazioni di Fisica 1
 Esercitazioni di Fisica 1 Ultima versione: 6 novembre 2013 Paracadutista (attrito viscoso). Filo con massa che pende da un tavolo. 1 Studio del moto di un paracadutista Vogliamo studiare il moto di un
Esercitazioni di Fisica 1 Ultima versione: 6 novembre 2013 Paracadutista (attrito viscoso). Filo con massa che pende da un tavolo. 1 Studio del moto di un paracadutista Vogliamo studiare il moto di un
Elementi di dinamica delle strutture,
 INTRODUZIONE Una struttura o qualunque sistema meccanico è caratterizzato dinamicamente quando è nota la posizione nello spazio di tutte le masse che lo compongono in ogni istante del suo moto. Un sistema
INTRODUZIONE Una struttura o qualunque sistema meccanico è caratterizzato dinamicamente quando è nota la posizione nello spazio di tutte le masse che lo compongono in ogni istante del suo moto. Un sistema
Soluzione degli esercizi dello scritto di Meccanica del 08/07/2019
 Soluzione degli esercizi dello scritto di Meccanica del 08/07/2019 Esercizio 1 Un asta rigida di lunghezza L = 0.8 m e massa M è vincolata nell estremo A ad un perno liscio ed è appesa all altro estremo
Soluzione degli esercizi dello scritto di Meccanica del 08/07/2019 Esercizio 1 Un asta rigida di lunghezza L = 0.8 m e massa M è vincolata nell estremo A ad un perno liscio ed è appesa all altro estremo
