Elementi di dinamica delle strutture,
|
|
|
- Francesco Bossi
- 4 anni fa
- Visualizzazioni
Transcript
1 INTRODUZIONE Una struttura o qualunque sistema meccanico è caratterizzato dinamicamente quando è nota la posizione nello spazio di tutte le masse che lo compongono in ogni istante del suo moto. Un sistema reale è caratterizzato da massa distribuita in ogni suo volume; possiede quindi infinite masse elementari per cui andrebbero determinate in ogni istante infinte posizioni. E possibile di solito schematizzare un sistema con un numero infinito di gradi di libertà con un sistema avente un numero finito di masse concentrate in punti specifici, sì da ricondursi ad uno schema di calcolo con masse concentrate che fornisca risultati sufficientemente accurati con un onere di calcolo ragionevole. Si consideri un serbatoio d acqua (figura 1) in cui la maggior parte della massa è concentrata nella sommità; per tale sistema l approssimazione di trascurare la massa m distribuita lungo lo stelo rispetto alla massa del serbatoio porta ad una semplificazione ragionevole del problema. E possibile quindi ricondursi ad uno schema chiamato oscillatore ad un grado di libertà poiché consente di descrivere il moto del sistema mediante le sole oscillazioni orizzontali della massa. m m h igura 1. Sistema ad un grado di libertà. Lo stelo, è idealmente supposto privo di massa, conservando, però, tutte le caratteristiche deformative elastiche del sistema originario. Risulta subito chiaro come un tale sistema sia certamente più agevole da trattare rispetto uno schema in cui la massa è supposta distribuita. In generale, risulta ovvio come la schematizzazione debba rispecchiare il più possibile la distribuzione delle masse reali: una ciminiera in mattoni, ad esempio (figura ), ha una massa distribuita in maniera abbastanza uniforme lungo il suo asse, per cui un modello elementare simile al precedente non fornisce risultati sufficientemente accurati. Uno schema che utilizza diverse masse concentrate distribuite in varie posizioni lungo l asse è uno schema certamente più aderente alla realtà; l onere di calcolo però cresce in ragione del numero delle masse utilizzate e quindi dei gradi di libertà del sistema, fornendo risultati tanto più accurati quanto più masse si utilizzano. -1-
2 h/n m n m n-1 m n- h m m 1 m 0 igura. Struttura con infiniti gradi di libertà, schematizzabile solo utilizzando un numero discreto di masse. L OSCILLATORE SEPLICE Si introduce lo studio di un sistema elementare, l oscillatore ad un grado di libertà, che permette la corretta schematizzazione di alcune strutture semplici ma, soprattutto, consente l introduzione di concetti fondamentali della dinamica delle strutture. Tale modello, sotto opportune ipotesi, è utilizzato anche per lo studio di schemi strutturali complessi. La sua rappresentazione meccanica (figura 3) è fornita da: elemento massa responsabile delle forze dinamiche inerziali; elemento molla K ovvero la forza di reazione elastica della struttura; la coordinata spaziale funzione che descrive la posizione della massa in ogni istante. K posizione a riposo: =0 igura 3. Oscillatore semplice. Durante il moto, alla massa sono applicate due forze: una elastica, proporzionale allo spostamento, ed una inerziale, proporzionale all accelerazione del sistema; si utilizzi la seconda legge di Newton per scrivere l equilibrio dinamico del sistema ext = x. --
3 Siccome l unica forza esterna agente sulla massa del sistema è la forza di reazione elastica, l equazione del moto oscillatorio assume la seguente espressione () x() t K x t =, ovvero x() t + K x() t = 0, [1] equazione differenziale del secondo ordine ordinaria, lineare, omogenea a coefficienti costanti ed. Le oscillazioni di tale sistema sono dette libere non smorzate, poiché non è presente alcuna forza esterna e non sono considerati fenomeni dissipativi, in realtà sempre presenti nelle strutture e nei sistemi reali; l oscillatore semplice in tal modo è un sistema che conserva l energia totale. inerzia.. =- = K el igura 4. Equilibrio della massa. Definendo la pulsazione naturale del sistema K ω =, [] l equazione del moto libero non smorzato [1] assume la forma () ω () x t + x t = 0, [3] il cui integrale generale può essere scritto tramite le espressioni, tra loro equivalenti: iωt iωt () 1 x t = A e + A e, [4.a] () ( ω ) ( ω ) x t = B sen t + B cos t, [4.b] 1 () ( ω ϕ ) x t = A sen t +. [4.c] Le coppie di costanti ( A,A 1 ), ( B,B 1 ) e ( ) A,ϕ si ricavano imponendo le condizioni iniziali del moto espresse in termini di velocità e di spostamento iniziali; le costanti A e ϕ definiscono l ampiezza massima dell oscillazione ampiezza A e gli istanti per cui il sistema passa per la posizione di riposo fase ϕ, (figura 5). Il caso in cui si abbiano condizioni iniziali in cui è assegnata la velocità iniziale al sistema mentre lo spostamento iniziale è nullo -3-
4 x () t + ω x() t = 0 x( 0) = 0, [5.a] x( 0) = x to rappresenta il moto di una massa soggetta ad un impulso iniziale I = x to ; assegnando, invece, uno spostamento iniziale al sistema con velocità iniziale nulla x () t + ω x() t = 0 x( 0) = xto, [5.b]. x( 0) = 0 Si descrive il moto oscillatorio di una massa spostata dalla sua posizione di riposo ed abbandonata con velocità nulla. Si ottiene la risoluzione del caso più generale in cui entrambe le condizioni iniziale sono non omogenee, ( ) to, ( ) to x 0 = x x 0 = x, utilizzando l integrale generale dell equazione [3] nella forma [4.c] x() t = A sen( ωt + ϕ) = = A sen ωt cos ϕ + A cos ωt sen ϕ,. ( ) ( ) ( ) ( ) ( ) = ω ( ω ) ( ϕ) ω ( ω ) ( ϕ) x t A cos t cos A sen t sen imponendo le condizioni iniziali si ottiene il seguente sistema x 0 = x to = A sen ϕ ( ) ( ) ( ) = to = ω ( ϕ ) x 0 x A cos da cui derivano le espressioni generali dell ampiezza e della fase del moto per l oscillatore semplice (x to) to A = x + e [6.a] ω tg ( ϕ) xto = ω.. [6.b] x to Le oscillazioni libere sono oscillazioni armoniche (dipendenti da una funzione trigonometrica) con una pulsazione naturale ω, da cui si può definire il periodo proprio del sistema π T0 = [7] ω e la frequenza del moto dell oscillatore f, come inverso del periodo. -4-
5 f = 1 1 K T = ω π = π [8] 0 L oscillatore semplice, essendo un sistema ideale privo di qualunque fenomeno dissipativi, conserva l energia totale acquisita all inizio del moto; l energia totale è data dalla somma dell energia cinetica E CIN, espressa dalla seguente formula 1 1 ECIN = x t A cos t = + e dell energia potenziale U così definita () ω ( ω ϕ), [9] 1 1 U = K x() t KA sen( ωt ϕ) = +, [10] quindi 1 1 ETOT = ECIN U = ω A cos( ωt ϕ) KA sen( ωt ϕ) = 1 KA cos t sen t 1 KA cos t. ( ω ϕ) ( ω ϕ) = = = = A -A T 0 k=0 k=1 k= t = - +k igura 5. Legge oraria della massa dell oscillatore semplice non smorzato. Esempio: L oscillatore semplice può essere efficacemente utilizzato per l analisi di strutture anche complesse in cui la massa può essere concentrata in un unico elemento strutturale, come nel caso dei telai shear-type (figura 6). La massa è concentrata essenzialmente nel traverso, supposto, inoltre, indeformabile, mentre la flessibilità della struttura, K, è concentrata negli elementi verticali di altezza H. t -5-
6 EJ Ø EJ EJ H L igura 6. Telaio tipo shear-type. La rigidezza elastica K del sistema shear-type può essere valutata applicando a livello della massa una forza statica di modulo 1 in direzione delle oscillazioni del sistema (figura 7) e calcolandone lo spostamento δ, che vale 3 H δ = ; 4 EJ 1 EJ per cui la rigidezza totale della struttura è pari a K = = 4. δ H 3 = 1 HEB80 igura 7. Calcolo della rigidezza K della struttura e sezione trasversale delle colonne. Si supponga che le colonne siano realizzate con un profilo in acciaio HEB80 le cui caratteristiche geometriche sono: Area A HEB80 =13140 mm ; omento di inerzia J HEB80 = mm 4 ; altezza H=000 mm. Il modulo elastico dell acciaio è E=10000 N/mm, e si considera la massa complessiva del traverso pari a =1000 kg. Dai dati precedenti si ricava che la rigidezza della struttura è pari a N K = 4 = mm. -6-
7 Dall equazione [8] si ricava che il periodo proprio della struttura è pari 1000 T0 = π = 0.018s L OSCILLATORE SEPLICE ORZATO Si consideri l oscillatore semplice soggetto ad una forza di intensità variabile (t) (figura 8); l equazione del moto diviene in questo caso non omogenea x() t + K x() t = (t) ; [11] dividendo ogni termini per la massa del sistema l equazione [11] assume la forma () ω () x t + x t = (t). [1] 1 Si supponga che la forzante abbia un andamento armonico, ovvero sia una funzione periodica data dall espressione ( ω ) (t ) = sen t, [13] l equazione [13] si modifica nella forma: () ω () ( ω ) x t + x t = sen t. [14] La soluzione dell equazione [14] è data dalla somma dell integrale generale dell equazione omogenea, equazioni [4.a], [4.b] o [4.c], per il moto non forzato ed un integrale particolare, dipendente dal tipo di forzante considerata, del tipo 1 ( ω ) x (t) = A sen t, [15] dove la costante A è determinata sostituendo l equazione [15] nell equazione [14] ( ) ( ) ( ) A ω sen ω t + A ω sen ω t = sen ω t A = = ( ω ω ) ω K 1 [16] con cui si completa l integrale particolare, equazione [15] 1 x 1(t) = sen t ω K 1 ( ω ), che sommato alle soluzioni dell equazione omogenea, [4.b] e [4.c], fornisce la soluzione complessiva del moto dell oscillatore semplice forzato nelle seguenti espressioni equivalenti: -7-
8 1 x t B1 sen t B cos t sen t ω K 1 () = ( ω ) + ( ω ) + ( ω ) 1 x t A sen t sen t ω K 1 () = ( ω + ϕ) + ( ω ), e [17.a] [17.b] nelle quali i termini dipendenti solo da ω rappresentano il contributo delle oscillazioni libere al moto complessivo del sistema, mentre i termini dipendenti anche da ω rappresentano il contributo delle oscillazioni forzate, con una frequenza dipendente A,ϕ si ricavano dall azione perturbante (t). Le coppie di costanti ( ) 1 B,B e ( ) imponendo le condizioni iniziali del moto espresse in termini di velocità e spostamento iniziali. Si pongano come condizioni iniziali spostamento e velocità iniziali nulli, dall equazione [17.a] x ( 0) = B = 0 e [18.a] x ( 0) = ω B1 + = 0 ω K 1 [18.b] per cui l integrale generale [17.a] diviene 1 ω x () t = sen( ω t) sen( ω t) ω K ω. 1 [19] Nel caso in cui la perturbazione della forzante ω è in prossimità della pulsazione ω ω, ovvero prossimo alla condizione di risonanza fondamentale del sistema ( ) ( ω ω ) =, l equazione [19] diviene indeterminata. Si trasformino i termini trigonometrici nel seguente modo ω sen ( ω t ) sen ( ω t ) sen ( ω t ) sen ( ω t ) = ω + ω ω ω = cos t sen t così che l equazione [19] assumi l espressione 1 1 La DIOSTRAZIONE della trasformazione tra le funzioni trigonometriche è riportata alla fine del presente paragrafo. -8-
9 ω + ω ω ω x () t = cos t sen t. ω K 1 diviene Trovandosi in condizioni prossime alla risonanza ( ω ω ) ω ω x () t = cos( ω ) sen t, ω K 1 [0] l equazione [0] espressione che risulta indeterminata quando ω ω, poiché sia il denominatore sia il numeratore tendono simultaneamente a zero. Per tentare di esaminare il comportamento dell oscillatore semplice in questa condizione si applica all espressione precedente il teorema di De L Hospital, derivando sia il numeratore sia il denominatore rispetto a ω. Al tendere di ω ω si ottiene x () t = ( t) cos( t) K ω ω, [1] equazione del moto che rappresenta delle oscillazioni con ampiezza crescente all aumentare del tempo t, crescita che avviene linearmente ed illimitatamente (figura 8), e che è solitamente chiamata battimento. t DIOSTRAZIONE igura 8. enomeno del battimento per un oscillatore semplice. Si dimostra la trasformazione delle funzioni trigonometriche utilizzata per ottenere l equazione [0]; siano α e β tali che α + β = ω t ; α β = ω t sommando e sottraendo ambo i membri delle equazioni precedenti si ottiene -9-
10 ω t+ ω t α =. ω t ω t β = Dalle formule relative al seno della somma si possono scrivere le equazioni sen ( α + β) = sen ( α) cos( β) + cos( α) sen ( β) sen α β = sen α cos β cos α sen β ( ) ( ) ( ) ( ) ( ) che forniscono, sottraendo la seconda alla prima, la relazione sen ( α + β) sen ( α β) = cos( α) sen ( β) + cos( α) sen ( β) = = cos α senβ ( ) ( ) da cui, sostituendo ad α e β le loro espressioni in funzione di ω ed ω si ha la trasformazione utilizzata a pag. 8 ω + ω ω ω sen ( ω t ) sen ( ω t ) = cos t sen t. L OSCILLATORE SEPLICE SORZATO Il moto di un qualsiasi sistema reale, soggetto ad oscillazioni libere, non continua indefinitamente, ma dopo un periodo più o meno lungo si estingue a causa dei fenomeni di attrito che smorzano le ampiezze delle oscillazioni sino all arresto. Tale smorzamento è stato rappresentato in dinamica con modelli più o meno complessi; tra essi un modello di comportamento, a tutt oggi, molto diffuso nella modellazione delle strutture in campo dinamico è il modello ad attrito viscoso. L attrito viscoso, introdotto da Kelvin, assegna alle forze dissipative (o d attrito) presenti una dipendenza dalla velocità istantanea del sistema, secondo la seguente relazione = C x t. V () La presenza di uno smorzamento di tipo viscoso nell oscillatore semplice si può rappresentare con un organo viscoso lineare caratterizzato da una costante C (figura 9). K C igura 9. Oscillatore semplice smorzato. LE OSCILLAZIONI LIBERE CON SORZAENTO L equazione del moto per l oscillatore semplice smorzato è ricavata eseguendo l equilibrio nella direzione del moto di tutte le forze agenti sulla massa (figura 10) -10-
11 () () () x t + C x t + K x t = 0 [] dove C è il coefficiente di attrito viscoso che caratterizza la resistenza viscosa ad una velocità x () t pari ad 1. Dividendo l equazioni [3] per la massa si ottiene l equazione analoga all equazione [3] per l oscillatore smorzato () ξ ω () ω () x t + x t + x t = 0 [3] in cui ξ ω = C. [4] el = K inerzia.. =- V = C igura 10. Diagramma di corpo libero della massa. Il coefficiente x è una costante dimensionale chiamata fattore di smorzamento dell oscillatore semplice; esso dipende solo dai parametri meccanici dell oscillatore tramite la seguente formula C C ξ = = ω K. [5] L equazione differenziale [3] è del secondo ordine, lineare, omogenea ed a coefficienti costanti, la cui equazione caratteristica λ + ξ ω λ + ω = 0 [6] possiede le seguenti due radici ( ) ( ) λ1 = ξ + ξ 1 ω [7.a] λ = ξ ξ 1 ω [7.b] distinte solo se ξ 1, e, a seconda che il fattore di smorzamento sia maggiore o minore dell unità, reali oppure complesse, che portano a soluzioni dell equazione nettamente distinte. IL CASO SOVRASORZATO - ξ >1 Le soluzioni dell equazione caratteristica [6] sono reali e distinte, per cui il moto del sistema diviene aperiodico ed è espresso dal seguente integrale generale dell equazione [3] -11-
12 λ1 t λ () x t A e A e t = 1 +. [8] Si consideri il caso in cui le condizioni iniziali del moto siano caratterizzate da spostamento iniziale non nullo e velocità nulla, x ( 0) = xt0 e x ( 0) = 0 ; sostituendole all interno dell equazione [8] si ottiene il seguente sistema xt0 = A1 + A 0 = λ1 A1 + λ A da cui si ottengono le costanti cercate ( ξ ξ ) xt0 A1 = + 1 ξ 1 e ( ξ ξ ) xt0 A = + 1 ξ 1 [9.a]. [9.b] L espressione completa dell equazione [8] diviene così ξωt xt0 () ( ξ ξ ) ( ξ ξ ) ξ ω ξ 1 t 1 ω t x t = e + 1 e e ξ 1 ; [30] il moto che descrive è aperiodico decrescente: il sistema inizialmente perturbato, dopo aver variato il suo stato ritorno in condizione di riposo; l equazione [30] è tale per cui il sistema tenderà asintoticamente allo stato di quiete, raggiungendolo idealmente solo quando t, tanto più rapidamente quanto più ξ è prossimo all unità; se ν fosse pari ad infinito allora la massa non si muoverebbe dalla posizione iniziale x t0 (figura 11). x t0 igura 11. Andamento della soluzione dell equazione [30] al variare del fattore di smorzamento. t IL CASO DELLO SORZAENTO CRITICO - ξ =1 Il presente caso, in cui ξ =1, la costante dello smorzamento viscoso attuale * vale C = K che è detto smorzamento critico. In questa condizione per l equazione [6] si hanno due soluzioni reali e coincidenti λ1 = λ = ω per cui l integrale generale dell equazione [3] è dato nella seguente forma λ1 t λ t () 1 x t = A e + A t e, [31] nella quale, imponendo le seguenti condizioni iniziali, x ( 0) = xt0 e ( ) ottengono le costanti A 1 e A x 0 = 0, si -1-
13 A1 = xt0 A = ω xt0 con cui l equazione [31] diviene ω t () ( ω ) x t = x e 1+ t. [3] t0 Il moto del sistema è aperiodico decrescente, tendendo asintoticamente alla posizione di riposo, come mostrato in figura 1. t igura 1. Andamento del moto dell oscillatore con smorzamento critico. oto aperiodico. -13-
Lezione 8: Sistemi ad un grado di libertà: l oscillatore elementare (8)
 Lezione 8: Sistemi ad un grado di libertà: l oscillatore elementare (8) Federico Cluni 3 marzo 205 Fattore di amplificazione in termini di velocità e accelerazione Nel caso l oscillatore elementare sia
Lezione 8: Sistemi ad un grado di libertà: l oscillatore elementare (8) Federico Cluni 3 marzo 205 Fattore di amplificazione in termini di velocità e accelerazione Nel caso l oscillatore elementare sia
OSCILLATORE ARMONICO SEMPLICE
 OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
Lezione 7: Sistemi ad un grado di libertà: l oscillatore elementare (7)
 Lezione 7: Sistemi ad un grado di libertà: l oscillatore elementare (7) Federico Cluni 19 marzo 015 1 Pseudo accelerazione La risposta di un oscillatore elementare con massa m, fattore di smorzamento ν,
Lezione 7: Sistemi ad un grado di libertà: l oscillatore elementare (7) Federico Cluni 19 marzo 015 1 Pseudo accelerazione La risposta di un oscillatore elementare con massa m, fattore di smorzamento ν,
Esercitazione 2. Soluzione
 Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
Lezione XXVI Sistemi vibranti a 1 gdl 9,%5$=,21,75$16,725,(
 ezione XXVI 9,%5$=,,75$6,75,( Quando un sistema dinamico viene sollecitato da una eccitazione non periodica applicata improvvisamente, come nel caso di un impulso, le risposte a tali eccitazioni sono dette
ezione XXVI 9,%5$=,,75$6,75,( Quando un sistema dinamico viene sollecitato da una eccitazione non periodica applicata improvvisamente, come nel caso di un impulso, le risposte a tali eccitazioni sono dette
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Lezione 23: Sistemi a più gradi di libertà: sistemi continui (3)
 Lezione 3: Sistemi a più gradi di libertà: sistemi continui 3) Federico Cluni maggio 5 Oscillazioni forzate Si è visto che, nel caso di oscillazioni libere, il moto della trave è dato dalla funzione vx,
Lezione 3: Sistemi a più gradi di libertà: sistemi continui 3) Federico Cluni maggio 5 Oscillazioni forzate Si è visto che, nel caso di oscillazioni libere, il moto della trave è dato dalla funzione vx,
Sistemi vibranti ad 1 gdl
 Sistemi vibranti ad 1 gdl - vibrazioni forzate - 14 novembre 2 Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ + x = F sin(ωt) (1) dove, con riferimento alla figura
Sistemi vibranti ad 1 gdl - vibrazioni forzate - 14 novembre 2 Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ + x = F sin(ωt) (1) dove, con riferimento alla figura
Esercitazione 2. Soluzione
 Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
Formulazione delle equazioni del moto per un sistema lineare a tre gradi di libertà. Proprietà delle matrici di rigidezza e di flessibilità
 Formulazione delle equazioni del moto per un sistema lineare a tre gradi di libertà Proprietà delle matrici di rigidezza e di flessibilità Prof. Adolfo Santini - Dinamica delle Strutture Introduzione In
Formulazione delle equazioni del moto per un sistema lineare a tre gradi di libertà Proprietà delle matrici di rigidezza e di flessibilità Prof. Adolfo Santini - Dinamica delle Strutture Introduzione In
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Sistemi vibranti ad 1 gdl
 Università degli Studi di Bergamo Dipartimento di Ingegneria Sistemi vibranti ad 1 gdl - vibrazioni forzate - rev. 1. Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ
Università degli Studi di Bergamo Dipartimento di Ingegneria Sistemi vibranti ad 1 gdl - vibrazioni forzate - rev. 1. Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ
Applicazioni delle leggi della meccanica: moto armnico
 Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile
 Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile Anno Accademico 2017-2018 A. Ponno (aggiornato al 20 dicembre 2017) 2 Ottobre 2017 2/10/17 Benvenuto, presentazione
Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile Anno Accademico 2017-2018 A. Ponno (aggiornato al 20 dicembre 2017) 2 Ottobre 2017 2/10/17 Benvenuto, presentazione
DINAMICA DELLE VIBRAZIONI LIBERE DEI SISTEMI A UN GRADO DI LIBERTÁ (SDOF)
 INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF) M. Bozza Copyright AEPRON Tutti i iritti Riservati - www.adepron.it INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF)
INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF) M. Bozza Copyright AEPRON Tutti i iritti Riservati - www.adepron.it INAMICA ELLE VIBRAZIONI LIBERE EI SISTEMI A UN GRAO I LIBERTÁ (SOF)
Fisica 2C. 3 Novembre Domande
 Fisica 2C 3 Novembre 2006 Domande ˆ i) Si consideri un oscillatore armonico smorzato e forzato da una sollecitazione sinusoidale esterna, la cui equazione é tipicamente s + 2γṡ + ω0s 2 = F cos ωt m 1)
Fisica 2C 3 Novembre 2006 Domande ˆ i) Si consideri un oscillatore armonico smorzato e forzato da una sollecitazione sinusoidale esterna, la cui equazione é tipicamente s + 2γṡ + ω0s 2 = F cos ωt m 1)
Capitolo 12. Moto oscillatorio
 Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
EFFETTI DELLA DEFORMABILITÀ DINAMICA (MECCANICA DELLE VIBRAZIONI) In realtà essi sono approssimati, pertanto i nostri schemi sono approssimati.
 EFFETTI DELLA DEFORMABILITÀ DINAMICA (MECCANICA DELLE VIBRAZIONI Per le macchine viste finora, è quasi sempre possibile effettuare uno studio considerandole a un solo grado di libertà, dove ogni elemento
EFFETTI DELLA DEFORMABILITÀ DINAMICA (MECCANICA DELLE VIBRAZIONI Per le macchine viste finora, è quasi sempre possibile effettuare uno studio considerandole a un solo grado di libertà, dove ogni elemento
Indice slides. 1 Oscillatore semplice 5. 2 Equazione caratteristica 6. 3 Radici complesse 7. 4 Integrale generale 8. 5 Forza Peso 9.
 Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Lezione 19: Sistemi a più gradi di libertà: sistemi discreti (10)
 Lezione 9: Sistemi a più gradi di libertà: sistemi discreti () Federico Cluni 3 aprile 25 Coefficenti di massa partecipante Si abbia un sistema discreto a più gradi di libertà descritto dalle seguenti:
Lezione 9: Sistemi a più gradi di libertà: sistemi discreti () Federico Cluni 3 aprile 25 Coefficenti di massa partecipante Si abbia un sistema discreto a più gradi di libertà descritto dalle seguenti:
Formulazione dell equazione del moto. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Formulazione dell equazione del moto Prof. Adolfo Santini - Dinamica delle Strutture 1 Sistema a un grado di libertà In alcuni sistemi strutturali la massa, lo smorzamento e la rigidezza sono concentrati
Formulazione dell equazione del moto Prof. Adolfo Santini - Dinamica delle Strutture 1 Sistema a un grado di libertà In alcuni sistemi strutturali la massa, lo smorzamento e la rigidezza sono concentrati
e una frequenza = 0 /2 =1/T (misurata in Hertz). Infine è la fase, cioè un numero (radianti) che dipende dalla definizione dell istante t=0.
 8. Oscillazioni Definizione di oscillatore armonico libero Si tratta di un sistema soggetto ad un moto descrivibile secondo una funzione armonica (seno o coseno) del tipo x(t) = Acos( 0 t + ) A è l ampiezza
8. Oscillazioni Definizione di oscillatore armonico libero Si tratta di un sistema soggetto ad un moto descrivibile secondo una funzione armonica (seno o coseno) del tipo x(t) = Acos( 0 t + ) A è l ampiezza
F = ma = -mω 2 R u r.
 Esercizio a) Sia v F = -ma cp u r = -m u r = -mω R u r. R b) Sia ω = ω u z il vettore velocità angolare del sistema di riferimento O. In questo sistema di riferimento rotante, i vettori velocità v e accelerazione
Esercizio a) Sia v F = -ma cp u r = -m u r = -mω R u r. R b) Sia ω = ω u z il vettore velocità angolare del sistema di riferimento O. In questo sistema di riferimento rotante, i vettori velocità v e accelerazione
Impostazione e controllo del progetto di edifici antisismici in cemento armato secondo le indicazioni delle Norme Tecniche per le Costruzioni 2008
 Corso di aggiornamento Impostazione e controllo del progetto di edifici antisismici in cemento armato secondo le indicazioni delle Norme Tecniche per le Costruzioni 2008 Aula Oliveri, Facoltà di Ingegneria
Corso di aggiornamento Impostazione e controllo del progetto di edifici antisismici in cemento armato secondo le indicazioni delle Norme Tecniche per le Costruzioni 2008 Aula Oliveri, Facoltà di Ingegneria
Calcolo della risposta di un sistema lineare viscoso a più gradi di libertà con il metodo dell Analisi Modale
 Calcolo della risposta di un sistema lineare viscoso a più gradi di libertà con il metodo dell Analisi Modale Lezione 1/ Prof. Adolfo Santini - Dinamica delle Strutture 1 Disaccoppiamento delle equazioni
Calcolo della risposta di un sistema lineare viscoso a più gradi di libertà con il metodo dell Analisi Modale Lezione 1/ Prof. Adolfo Santini - Dinamica delle Strutture 1 Disaccoppiamento delle equazioni
ESERCIZIO 1 (Punti 9)
 UNIVERSITA DI PISA - ANNO ACCADEMICO 7-8 CORSO DI LAUREA IN ING. ELETTRICA (N.O.) CORSO DI PRINCIPI DI MECCANICA E COSTRUZIONI MECCANICHE ESERCIZIO 1 (Punti 9) VERIFICA INTERMEDIA DEL 1-5-1 Data la struttura
UNIVERSITA DI PISA - ANNO ACCADEMICO 7-8 CORSO DI LAUREA IN ING. ELETTRICA (N.O.) CORSO DI PRINCIPI DI MECCANICA E COSTRUZIONI MECCANICHE ESERCIZIO 1 (Punti 9) VERIFICA INTERMEDIA DEL 1-5-1 Data la struttura
Dinamica delle Strutture
 Corso di Laurea magistrale in Ingegneria Civile e per l Ambiente e il Territorio Dinamica delle Strutture Prof. Adolfo SANTINI Ing. Francesco NUCERA Prof. Adolfo Santini - Dinamica delle Strutture 1 Dinamica
Corso di Laurea magistrale in Ingegneria Civile e per l Ambiente e il Territorio Dinamica delle Strutture Prof. Adolfo SANTINI Ing. Francesco NUCERA Prof. Adolfo Santini - Dinamica delle Strutture 1 Dinamica
Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com
![Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com](/thumbs/67/56787927.jpg) Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
Oscillatore semplice: risposta ad eccitazioni arbitrarie. In molte applicazioni pratiche l eccitazione dinamica non è né armonica nè periodica.
 Oscillatore semplice: risposta ad eccitazioni arbitrarie In molte applicazioni pratiche l eccitazione dinamica non è né armonica nè periodica. È necessario dunque sviluppare una procedura generale per
Oscillatore semplice: risposta ad eccitazioni arbitrarie In molte applicazioni pratiche l eccitazione dinamica non è né armonica nè periodica. È necessario dunque sviluppare una procedura generale per
OSCILLAZIONI SMORZATE E FORZATE
 OSCILLAZIONI SMORZATE E FORZATE Questo esperimento permette di studiare le oscillazioni armoniche di un pendolo e le oscillazioni smorzate e smorzate-forzate. Studiando il variare dell ampiezza dell oscillazione
OSCILLAZIONI SMORZATE E FORZATE Questo esperimento permette di studiare le oscillazioni armoniche di un pendolo e le oscillazioni smorzate e smorzate-forzate. Studiando il variare dell ampiezza dell oscillazione
DINAMICA DI SISTEMI AEROSPAZIALI
 DINAMICA DI SISTEMI AEROSPAZIALI Tema d esame 11-07 - 2014 g A l h M, J O d B M B, J B moto definita ai punti precedenti. C m Esercizio 1. Il sistema in figura, posto nel piano verticale, è costituito
DINAMICA DI SISTEMI AEROSPAZIALI Tema d esame 11-07 - 2014 g A l h M, J O d B M B, J B moto definita ai punti precedenti. C m Esercizio 1. Il sistema in figura, posto nel piano verticale, è costituito
Costruzioni in zona sismica
 Costruzioni in zona sismica Lezione 7 Sistemi a più gradi di libertà Il problema dinamico viene formulato con riferimento a strutture con un numero finito di gradi di libertà. Consideriamo le masse concentrate
Costruzioni in zona sismica Lezione 7 Sistemi a più gradi di libertà Il problema dinamico viene formulato con riferimento a strutture con un numero finito di gradi di libertà. Consideriamo le masse concentrate
Anna M. Nobili: Lezioni Fisica 1 per Chimici a.a
 Anna M. Nobili: Lezioni Fisica 1 per Chimici a.a. 2013-2014 26 Settembre 2013 Grandezze fisiche, dimensioni e unità di misura. Potenze di 10 e loro uso. 3 Ottobre 2013 Grandezze fisiche, dimensioni e
Anna M. Nobili: Lezioni Fisica 1 per Chimici a.a. 2013-2014 26 Settembre 2013 Grandezze fisiche, dimensioni e unità di misura. Potenze di 10 e loro uso. 3 Ottobre 2013 Grandezze fisiche, dimensioni e
Esperienza 12: oscillatore. forzato e risonanza. Laboratorio di Fisica 1 A. Baraldi, M. Riccò. Università di Parma. a.a. 2011/2012. Copyright M.
 Esperienza 1: oscillatore Università di Parma forzato e risonanza a.a. 11/1 Laboratorio di Fisica 1 A. Baraldi, M. Riccò Copyright M.Solzi Oscillazioni libere smorzate a.a. 11/1 1: Oscillatore forzato
Esperienza 1: oscillatore Università di Parma forzato e risonanza a.a. 11/1 Laboratorio di Fisica 1 A. Baraldi, M. Riccò Copyright M.Solzi Oscillazioni libere smorzate a.a. 11/1 1: Oscillatore forzato
Risposta temporale: esempi
 ...4 Risposta temporale: esempi Esempio. Calcolare la risposta al gradino unitario del seguente sistema: x(t) = u(t) s + 5 (s + )(s + ) y(t) Il calcolo della trasformata del segnale di uscita è immediato:
...4 Risposta temporale: esempi Esempio. Calcolare la risposta al gradino unitario del seguente sistema: x(t) = u(t) s + 5 (s + )(s + ) y(t) Il calcolo della trasformata del segnale di uscita è immediato:
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
Lezione XXIV Sistemi vibranti a 1 gdl 67580(17,',0,685$'(//(9,%5$=,21,
 ezione XXIV 658(,,,685$(//(9,%5$,, Tra le applicazioni del nostro oscillatore vi è quella di usarlo come strumento per la misura delle vibrazioni assolute di un corpo Con riferimento alle grandezze indicate
ezione XXIV 658(,,,685$(//(9,%5$,, Tra le applicazioni del nostro oscillatore vi è quella di usarlo come strumento per la misura delle vibrazioni assolute di un corpo Con riferimento alle grandezze indicate
Vibrazioni Meccaniche
 Vibrazioni Meccaniche A.A. 2-22 Esempi di scrittura dell equazione di moto per sistemi a 2 gdl Turbina Una turbina pone in rotazione un generatore elettrico per mezzo della trasmissione schematizzata in
Vibrazioni Meccaniche A.A. 2-22 Esempi di scrittura dell equazione di moto per sistemi a 2 gdl Turbina Una turbina pone in rotazione un generatore elettrico per mezzo della trasmissione schematizzata in
ESERCIZIO 1 (Punti 9)
 UNIVERSITA DI PISA - ANNO ACCADEMICO 007-8 CORSO DI LAUREA IN ING. ELETTRICA (N.O.) CORSO DI MECCANICA E TECNICA DELLE COSTRUZIONI MECCANICHE VERIFICA INTERMEDIA DEL 15-06-009 ESERCIZIO 1 (Punti 9) Data
UNIVERSITA DI PISA - ANNO ACCADEMICO 007-8 CORSO DI LAUREA IN ING. ELETTRICA (N.O.) CORSO DI MECCANICA E TECNICA DELLE COSTRUZIONI MECCANICHE VERIFICA INTERMEDIA DEL 15-06-009 ESERCIZIO 1 (Punti 9) Data
CORSO DI COMPLEMENTI DI MECCANICA. Prof. Vincenzo Niola
 CORSO DI COMPLEMENTI DI MECCANICA Prof. Vincenzo Niola SISTEMI A DUE GRADI DI LIBERTÀ Lo studio dei sistemi a più gradi di libertà verrà affrontato facendo riferimento, per semplicità, solo a sistemi conservativi,
CORSO DI COMPLEMENTI DI MECCANICA Prof. Vincenzo Niola SISTEMI A DUE GRADI DI LIBERTÀ Lo studio dei sistemi a più gradi di libertà verrà affrontato facendo riferimento, per semplicità, solo a sistemi conservativi,
Moto armonico. A.Solano - Fisica - CTF
 Moto armonico Moti periodici Moto armonico semplice: descrizione cinematica e dinamica Energia nel moto armonico semplice Il pendolo Oscillazioni smorzate Oscillazioni forzate e risonanza Moto periodico
Moto armonico Moti periodici Moto armonico semplice: descrizione cinematica e dinamica Energia nel moto armonico semplice Il pendolo Oscillazioni smorzate Oscillazioni forzate e risonanza Moto periodico
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA
 DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
Analisi sismica di un sistema lineare viscoso a più gradi di libertà con il metodo dello Spettro di Risposta
 Analisi sismica di un sistema lineare viscoso a più gradi di libertà con il metodo dello Spettro di Risposta Prof. Adolfo Santini - Dinamica delle Strutture 1 Analisi sismica con lo spettro di risposta
Analisi sismica di un sistema lineare viscoso a più gradi di libertà con il metodo dello Spettro di Risposta Prof. Adolfo Santini - Dinamica delle Strutture 1 Analisi sismica con lo spettro di risposta
Compito del 14 giugno 2004
 Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
Esercizio: pendoli accoppiati. Soluzione
 Esercizio: pendoli accoppiati Si consideri un sistema di due pendoli identici, con punti di sospensione posti alla stessa quota in un piano verticale. I due pendoli sono collegati da una molla di costante
Esercizio: pendoli accoppiati Si consideri un sistema di due pendoli identici, con punti di sospensione posti alla stessa quota in un piano verticale. I due pendoli sono collegati da una molla di costante
Foglio di Esercizi 7 Meccanica Razionale a.a. 2018/19 Canale A-L (P. Buttà)
 Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Corso di Costruzioni in Zona Sismica
 Corso di Costruzioni in Zona Sismica Università degli Studi di Cassino e del Lazio Meridionale Ernesto Grande e.grande@unicas.it +39.0776.299.3478 Earthquake Engineering Lecture 5 Sistema a un GdL: vibrazioni
Corso di Costruzioni in Zona Sismica Università degli Studi di Cassino e del Lazio Meridionale Ernesto Grande e.grande@unicas.it +39.0776.299.3478 Earthquake Engineering Lecture 5 Sistema a un GdL: vibrazioni
1 - Matrice delle masse e delle rigidezze
 Cilc per tutti gli appunti (AUOMAZIONE RAAMENI ERMICI ACCIAIO SCIENZA delle COSRUZIONI ) e-mail per suggerimenti SEMPLICE ESEMPIO NUMERICO DEL MEODO DI ANALISI DINAMICA Si vuole qui chiarire con un semplice
Cilc per tutti gli appunti (AUOMAZIONE RAAMENI ERMICI ACCIAIO SCIENZA delle COSRUZIONI ) e-mail per suggerimenti SEMPLICE ESEMPIO NUMERICO DEL MEODO DI ANALISI DINAMICA Si vuole qui chiarire con un semplice
Moti oscillatori. Parte I Oscillatore armonico
 1 10.1-10.2 OSCILLATORE ARMONICO Parte I Moti oscillatori 1 10.1-10.2 Oscillatore armonico Abbiamo visto che una situazione che si riconduce a soddisfare l equazione differenziale d 2 x(t) dt 2 +ω 2 x(t)
1 10.1-10.2 OSCILLATORE ARMONICO Parte I Moti oscillatori 1 10.1-10.2 Oscillatore armonico Abbiamo visto che una situazione che si riconduce a soddisfare l equazione differenziale d 2 x(t) dt 2 +ω 2 x(t)
Richiami sulle oscillazioni smorzate
 Richiami sulle oscillazioni smorzate Il moto armonico è il moto descritto da un oscillatore armonico, cioè un sistema meccanico che, quando perturbato dalla sua posizione di equilibrio, è soggetto ad una
Richiami sulle oscillazioni smorzate Il moto armonico è il moto descritto da un oscillatore armonico, cioè un sistema meccanico che, quando perturbato dalla sua posizione di equilibrio, è soggetto ad una
POLITECNICO DI MILANO Scuola di Ingegneria Industriale Fondamenti di Fisica Sperimentale, a.a I Appello, 10 luglio 2013
 POLITECNICO DI MILNO Scuola di Ingegneria Industriale Fondamenti di Fisica Sperimentale, a.a. 0-3 I ppello, 0 luglio 03 Giustificare le risposte e scrivere in modo chiaro e leggibile. Sostituire i valori
POLITECNICO DI MILNO Scuola di Ingegneria Industriale Fondamenti di Fisica Sperimentale, a.a. 0-3 I ppello, 0 luglio 03 Giustificare le risposte e scrivere in modo chiaro e leggibile. Sostituire i valori
mg 2a 1 tan 2 θ = 3 8 m (6)
 Soluzioni Esercizio 1. All equilibrio la forza elastica, la forza peso e la reazione vincolare del piano si bilanciano: F el + P + R n = 0 (1) Se la massa si trova in A, proiettando lungo la direzione
Soluzioni Esercizio 1. All equilibrio la forza elastica, la forza peso e la reazione vincolare del piano si bilanciano: F el + P + R n = 0 (1) Se la massa si trova in A, proiettando lungo la direzione
Teoria dei Sistemi Dinamici
 Teoria dei Sistemi Dinamici 01GTG - 0GTG Soluzione dell Esame del 03/11/009 1 Esercizio 1 Sistema meccanico 1.1 Testo Si consideri il sistema meccanico planare schematizzato nella Fig. 1, descritto come
Teoria dei Sistemi Dinamici 01GTG - 0GTG Soluzione dell Esame del 03/11/009 1 Esercizio 1 Sistema meccanico 1.1 Testo Si consideri il sistema meccanico planare schematizzato nella Fig. 1, descritto come
Foglio di Esercizi 5 Meccanica Razionale a.a. 2017/18 Canale A-L (P. Buttà)
 Foglio di Esercizi 5 Meccanica Razionale a.a. 017/18 Canale A-L (P. Buttà) Esercizio 1. Su un piano orizzontale sono poste due guide immateriali circolari di centri fissi O 1 e O e uguale raggio r; sia
Foglio di Esercizi 5 Meccanica Razionale a.a. 017/18 Canale A-L (P. Buttà) Esercizio 1. Su un piano orizzontale sono poste due guide immateriali circolari di centri fissi O 1 e O e uguale raggio r; sia
Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile
 Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile Anno Accademico 2016-2017 A. Ponno (aggiornato al 11 gennaio 2017) 2 Ottobre 2016 3/10/16 Benvenuto, presentazione
Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile Anno Accademico 2016-2017 A. Ponno (aggiornato al 11 gennaio 2017) 2 Ottobre 2016 3/10/16 Benvenuto, presentazione
Fisica per scienze ed ingegneria
 Serway, Jewett Fisica per scienze ed ingegneria Capitolo 15 Blocchetto legato ad una molla in moto su un piano orizzontale privo di attrito. Forza elastica di richiamo: F x =-Kx (Legge di Hooke). Per x>0,
Serway, Jewett Fisica per scienze ed ingegneria Capitolo 15 Blocchetto legato ad una molla in moto su un piano orizzontale privo di attrito. Forza elastica di richiamo: F x =-Kx (Legge di Hooke). Per x>0,
Prova TIPO D per: ESERCIZIO 1.
 Prova TIPO D per: Esame di FONDAMENTI DI AUTOMATICA (9 crediti): 6 dei 10 esercizi numerici (nell effettiva prova d esame verranno selezionati a priori dal docente) domande a risposta multipla (v. ultime
Prova TIPO D per: Esame di FONDAMENTI DI AUTOMATICA (9 crediti): 6 dei 10 esercizi numerici (nell effettiva prova d esame verranno selezionati a priori dal docente) domande a risposta multipla (v. ultime
Dinamica del punto materiale
 Dinamica del punto materiale Formule fondamentali L. P. 5 Aprile 2010 N.B.: Le relazioni riportate sono valide in un sistema di riferimento inerziale. Princìpi della dinamica Secondo principio della dinamica
Dinamica del punto materiale Formule fondamentali L. P. 5 Aprile 2010 N.B.: Le relazioni riportate sono valide in un sistema di riferimento inerziale. Princìpi della dinamica Secondo principio della dinamica
Cap Moti oscillatori
 N.Giglietto A.A. 005/06- Cap 16.1- Moti oscillatori - 1 Cap 16.1- Moti oscillatori Alcuni tipi di forze o alcune situazioni danno luogo a dei moti di tipo oscillante ovvero a dei moti che si ripetono regolarmente.
N.Giglietto A.A. 005/06- Cap 16.1- Moti oscillatori - 1 Cap 16.1- Moti oscillatori Alcuni tipi di forze o alcune situazioni danno luogo a dei moti di tipo oscillante ovvero a dei moti che si ripetono regolarmente.
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Dinamica dei sistemi materiali Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Dinamica dei sistemi materiali Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
MOMENTI DI INERZIA PER CORPI CONTINUI
 MOMENTI D INERZIA E PENDOLO COMPOSTO PROF. FRANCESCO DE PALMA Indice 1 INTRODUZIONE -------------------------------------------------------------------------------------------------------------- 3 2 MOMENTI
MOMENTI D INERZIA E PENDOLO COMPOSTO PROF. FRANCESCO DE PALMA Indice 1 INTRODUZIONE -------------------------------------------------------------------------------------------------------------- 3 2 MOMENTI
Valutazione della capacità dissipativa di un sistema strutturale
 Tecniche innovative per l identificazione delle caratteristiche dinamiche delle strutture e del danno Valutazione della capacità dissipativa di un sistema strutturale Prof. Ing. Felice Carlo PONZO - Ing.
Tecniche innovative per l identificazione delle caratteristiche dinamiche delle strutture e del danno Valutazione della capacità dissipativa di un sistema strutturale Prof. Ing. Felice Carlo PONZO - Ing.
Soluzione Compito di Fisica Generale I Ing. Elettronica e delle Telecomunicazioni 09/06/2017
 Soluzione Compito di Fisica Generale I Ing. Elettronica e delle Telecomunicazioni 09/06/017 Esercizio 1 1) Durante il salto dell uomo non sono presenti forze esterne impulsive, per cui la quantità di moto
Soluzione Compito di Fisica Generale I Ing. Elettronica e delle Telecomunicazioni 09/06/017 Esercizio 1 1) Durante il salto dell uomo non sono presenti forze esterne impulsive, per cui la quantità di moto
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale
 Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Ricordiamo ora che a è legata ad x (derivata seconda) ed otteniamo
 Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
Indice 3. Note di utilizzo 9. Ringraziamenti 10. Introduzione 11
 Indice Indice 3 Note di utilizzo 9 Ringraziamenti 10 Introduzione 11 Capitolo 1 Grandezze fisiche e schematizzazione dei sistemi materiali 13 1.1 Grandezze fisiche ed operazione di misura 13 1.2 Riferimento
Indice Indice 3 Note di utilizzo 9 Ringraziamenti 10 Introduzione 11 Capitolo 1 Grandezze fisiche e schematizzazione dei sistemi materiali 13 1.1 Grandezze fisiche ed operazione di misura 13 1.2 Riferimento
Scomposizione in fratti semplici
 0.0.. Scomposizione in fratti semplici La determinazione dell evoluzione libera e dell evoluzione forzata di un sistema lineare stazionario richiedono l antitrasformazione di una funzione razionale fratta
0.0.. Scomposizione in fratti semplici La determinazione dell evoluzione libera e dell evoluzione forzata di un sistema lineare stazionario richiedono l antitrasformazione di una funzione razionale fratta
Fondamenti di Meccanica Esame del
 Politecnico di Milano Fondamenti di Meccanica Esame del 0.02.2009. In un piano verticale un asta omogenea AB, di lunghezza l e massa m, ha l estremo A vincolato a scorrere senza attrito su una guida verticale.
Politecnico di Milano Fondamenti di Meccanica Esame del 0.02.2009. In un piano verticale un asta omogenea AB, di lunghezza l e massa m, ha l estremo A vincolato a scorrere senza attrito su una guida verticale.
PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 2003/ luglio Soluzione
 PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 23/24 2 luglio 24 Esercizio In riferimento allo schema a blocchi in figura. s r y 2 s y K s2 Domanda.. Determinare una realizzazione in equazioni di stato
PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 23/24 2 luglio 24 Esercizio In riferimento allo schema a blocchi in figura. s r y 2 s y K s2 Domanda.. Determinare una realizzazione in equazioni di stato
Soluzione degli esercizi dello scritto di Meccanica del 08/07/2019
 Soluzione degli esercizi dello scritto di Meccanica del 08/07/2019 Esercizio 1 Un asta rigida di lunghezza L = 0.8 m e massa M è vincolata nell estremo A ad un perno liscio ed è appesa all altro estremo
Soluzione degli esercizi dello scritto di Meccanica del 08/07/2019 Esercizio 1 Un asta rigida di lunghezza L = 0.8 m e massa M è vincolata nell estremo A ad un perno liscio ed è appesa all altro estremo
Dinamica del punto ESERCIZI. Dott.ssa Elisabetta Bissaldi
 Dinamica del punto ESERCIZI Dott.ssa Elisabetta Bissaldi Elisabetta Bissaldi (Politecnico di Bari) A.A. 2018-2019 2 Si consideri un corpo di massa m posto alla base di un piano inclinato di un angolo θ,
Dinamica del punto ESERCIZI Dott.ssa Elisabetta Bissaldi Elisabetta Bissaldi (Politecnico di Bari) A.A. 2018-2019 2 Si consideri un corpo di massa m posto alla base di un piano inclinato di un angolo θ,
Costruzioni in zona sismica
 Costruzioni in zona sismica Lezione 8 Sistemi a più gradi di liberà: Oscillazioni libere in assenza di smorzamento N equazioni differenziali omogenee accoppiate tramite la matrice delle masse, la matrice
Costruzioni in zona sismica Lezione 8 Sistemi a più gradi di liberà: Oscillazioni libere in assenza di smorzamento N equazioni differenziali omogenee accoppiate tramite la matrice delle masse, la matrice
Soluzione prova scritta Fisica Generale I Ing. Elettronica e TLC 14 Settembre 2018
 Soluzione prova scritta Fisica Generale I Ing. Elettronica e LC 14 Settembre 2018 Esercizio 1 1) Per il sistema M + m, includendo la descrizione dell interazione gravitazionale come energia potenziale,
Soluzione prova scritta Fisica Generale I Ing. Elettronica e LC 14 Settembre 2018 Esercizio 1 1) Per il sistema M + m, includendo la descrizione dell interazione gravitazionale come energia potenziale,
Coppia di forze ONDE ELASTICHE
 Coppia di forze ONDE ELASTICHE LEZIONE N 26d Corso di fisica II Prof. Giuseppe Ciancio 1 Si definisce onda elastica meccanica, la propagazione di una perturbazione con trasporto di energia ma non di materia,
Coppia di forze ONDE ELASTICHE LEZIONE N 26d Corso di fisica II Prof. Giuseppe Ciancio 1 Si definisce onda elastica meccanica, la propagazione di una perturbazione con trasporto di energia ma non di materia,
θ = arcos[g/(ω 2 L)]
![θ = arcos[g/(ω 2 L)] θ = arcos[g/(ω 2 L)]](/thumbs/104/163630441.jpg) Esercizio 1 a) Si consideri il sistema di riferimento inerziale con asse z parallelo all asse di rotazione della pallina. La pallina è sottoposta all azione della forza peso (parallela a z) e della tensione
Esercizio 1 a) Si consideri il sistema di riferimento inerziale con asse z parallelo all asse di rotazione della pallina. La pallina è sottoposta all azione della forza peso (parallela a z) e della tensione
ANTITRAFORMATE DI LAPLACE MODI DI UN SISTEMA
 CONTROLLI AUTOMATICI Ingegneria della Gestione Industriale e della Integrazione di Impresa http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm La determinazione dell'evoluzione
CONTROLLI AUTOMATICI Ingegneria della Gestione Industriale e della Integrazione di Impresa http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm La determinazione dell'evoluzione
Compito 19 Luglio 2016
 Compito 19 Luglio 016 Roberto onciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 015-016 Compito di Fisica Generale I per matematici 19 Luglio 016
Compito 19 Luglio 016 Roberto onciani e Paolo Dore Corso di Fisica Generale 1 Università degli Studi di Roma La Sapienza Anno Accademico 015-016 Compito di Fisica Generale I per matematici 19 Luglio 016
Numero progressivo: 6 Turno: 1 Fila: 1 Posto: 1 Matricola: Cognome e nome: (dati nascosti per tutela privacy)
 Numero progressivo: 6 Turno: 1 Fila: 1 Posto: 1 Matricola: 0000695216 Cognome e nome: (dati nascosti per tutela privacy) 1. Di quanto ruota in un giorno sidereo il piano di oscillazione del pendolo di
Numero progressivo: 6 Turno: 1 Fila: 1 Posto: 1 Matricola: 0000695216 Cognome e nome: (dati nascosti per tutela privacy) 1. Di quanto ruota in un giorno sidereo il piano di oscillazione del pendolo di
Risposta del rotore allo squilibrio ROTORE DI JEFFCOTT
 Risposta del rotore allo squilibrio ROTORE DI JEFFCOTT 1. Il Rotore è squilibrato à risposta del rotore allo squilibrio 2. Il modello: rotore, cuscinetti e fondamenta 3. Il problema delle vibrazioni 4.
Risposta del rotore allo squilibrio ROTORE DI JEFFCOTT 1. Il Rotore è squilibrato à risposta del rotore allo squilibrio 2. Il modello: rotore, cuscinetti e fondamenta 3. Il problema delle vibrazioni 4.
si tratta di una forzante sinusoidale
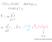 si tratta di una forzante sinusoidale funzione di e quindi di se! è trascurabile AF è massima quando: caratteristiche della forzante: caratteristiche dell oscillatore: qualunque sia t potenza
si tratta di una forzante sinusoidale funzione di e quindi di se! è trascurabile AF è massima quando: caratteristiche della forzante: caratteristiche dell oscillatore: qualunque sia t potenza
Esercizio 1. F a = µ d F n. Nella geometria dell esercizio: F n = mg senα F a = µ d mg cosα.
 Esercizio 1 a forza attrito raente F a è sempre opposta alla velocità Detta la componente F n ella reazione vincolare el piano parallela al piano stesso, vale la seguente relazione: F a = µ F n. Nella
Esercizio 1 a forza attrito raente F a è sempre opposta alla velocità Detta la componente F n ella reazione vincolare el piano parallela al piano stesso, vale la seguente relazione: F a = µ F n. Nella
PIANO di LAVORO A. S. 2013/ 2014
 Nome docente Vessecchia Laura Materia insegnata Fisica Classe Prima E ITIS Previsione numero ore di insegnamento ore complessive di insegnamento 3 ore settimanali di cui in compresenza 1 ora di cui di
Nome docente Vessecchia Laura Materia insegnata Fisica Classe Prima E ITIS Previsione numero ore di insegnamento ore complessive di insegnamento 3 ore settimanali di cui in compresenza 1 ora di cui di
Esame 12/02/2004 Soluzione
 Teoria dei Sistemi Dinamici 1GTG/2GTG Esame 12/2/24 Prego segnalare errori o inesattezze a basilio.bona@polito.it 1 Sistemi di riferimento, rototraslazioni (6 punti) Esercizio 1.1 Costruire la matrice
Teoria dei Sistemi Dinamici 1GTG/2GTG Esame 12/2/24 Prego segnalare errori o inesattezze a basilio.bona@polito.it 1 Sistemi di riferimento, rototraslazioni (6 punti) Esercizio 1.1 Costruire la matrice
Meccanica Dinamica del punto materiale
 Meccanica 18-19 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente (statico,
Meccanica 18-19 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente (statico,
p V Velocita di propagazione del suono ρ = densita del mezzo k = modulo di compressione
 1 Onde longitudinali o acustiche del tutto in generale si definisce onda acustica qualsiasi onda longitudinale dovuta alla perturbazione longitudinale di un qualsiasi mezzo meccanico nello specifico e
1 Onde longitudinali o acustiche del tutto in generale si definisce onda acustica qualsiasi onda longitudinale dovuta alla perturbazione longitudinale di un qualsiasi mezzo meccanico nello specifico e
Fisica Generale I (primo modulo) A.A , 9 febbraio 2009
 Fisica Generale I (primo modulo) A.A. 2008-09, 9 febbraio 2009 Esercizio 1. Due corpi di massa M 1 = 10kg e M 2 = 5Kg sono collegati da un filo ideale passante per due carrucole prive di massa, come in
Fisica Generale I (primo modulo) A.A. 2008-09, 9 febbraio 2009 Esercizio 1. Due corpi di massa M 1 = 10kg e M 2 = 5Kg sono collegati da un filo ideale passante per due carrucole prive di massa, come in
Oscillazioni smorzate, forzate RISONANZA
 Oscillazioni smorzate, forzate RISONANZA 1 Consideriamo un punto materiale P di massa m vincolato ad una guida rettilinea liscia e fissa e soggetto alle seguenti forze: Una forza elastica, esercitata da
Oscillazioni smorzate, forzate RISONANZA 1 Consideriamo un punto materiale P di massa m vincolato ad una guida rettilinea liscia e fissa e soggetto alle seguenti forze: Una forza elastica, esercitata da
Oscillazioni. Definizione Moto circolare uniforme Moto armonico
 Oscillazioni Definizione Moto circolare unifore Moto aronico Moto aronico e oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Oscillazioni Definizione Moto circolare unifore Moto aronico Moto aronico e oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Nome..Cognome.. Classe 4D 18 dicembre VERIFICA DI FISICA: lavoro ed energia
 Nome..Cognome.. Classe 4D 8 dicembre 008 EIFICA DI FISICA: lavoro ed energia Domande ) Forze conservative ed energia potenziale: (punti:.5) a) Dai la definizione di forza conservativa ed indicane le proprietà.
Nome..Cognome.. Classe 4D 8 dicembre 008 EIFICA DI FISICA: lavoro ed energia Domande ) Forze conservative ed energia potenziale: (punti:.5) a) Dai la definizione di forza conservativa ed indicane le proprietà.
Oscillazioni LC Applicando la legge di Faraday: ma Φ B. in direzione I. ovvero. La soluzione di questa equazone e:
 Oscillazioni Applicando la legge di Faraday: E d l d ma Φ B con d l in direzione d E dl ovvero ovvero d + q / n base alla nostra scelta di polarizzazione di pero', si ha' che: dq Segue che: A d d q Allora,
Oscillazioni Applicando la legge di Faraday: E d l d ma Φ B con d l in direzione d E dl ovvero ovvero d + q / n base alla nostra scelta di polarizzazione di pero', si ha' che: dq Segue che: A d d q Allora,
ANTITRASFORMATA DI LAPLACE MODI DI UN SISTEMA
 CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm ANTITRASFORMATA DI LAPLACE MODI DI UN SISTEMA Ing. Federica Grossi Tel.
CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm ANTITRASFORMATA DI LAPLACE MODI DI UN SISTEMA Ing. Federica Grossi Tel.
Stabilità e risposte di sistemi elementari
 Parte 4 Aggiornamento: Settembre 2010 Parte 4, 1 Stabilità e risposte di sistemi elementari Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL: www-lar.deis.unibo.it/~lmarconi
Parte 4 Aggiornamento: Settembre 2010 Parte 4, 1 Stabilità e risposte di sistemi elementari Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL: www-lar.deis.unibo.it/~lmarconi
L α. α d. 1. calcolare la velocità con cui il corpo raggiunge la sommità del piano [8 punti]
![L α. α d. 1. calcolare la velocità con cui il corpo raggiunge la sommità del piano [8 punti] L α. α d. 1. calcolare la velocità con cui il corpo raggiunge la sommità del piano [8 punti]](/thumbs/103/158585467.jpg) Problema E1 Una molla di costante elastica 500 Nm 1 e di lunghezza a riposo l 0 10 cm si trova in fondo ad un piano lungo L m, con coefficiente di attrito trascurabile e inclinato di un angolo α 30 o rispetto
Problema E1 Una molla di costante elastica 500 Nm 1 e di lunghezza a riposo l 0 10 cm si trova in fondo ad un piano lungo L m, con coefficiente di attrito trascurabile e inclinato di un angolo α 30 o rispetto
Meccanica Dinamica del punto materiale
 Meccanica 07-08 Dinamica del punto materiale 9 pprossimazioni per piccoli angoli v ± gl sin tan v gl Limite di piccoli angoli: 0 6 cos +... 3 tan + +... 3 3 sin +... Serie di Taylor: pprossimazioni per
Meccanica 07-08 Dinamica del punto materiale 9 pprossimazioni per piccoli angoli v ± gl sin tan v gl Limite di piccoli angoli: 0 6 cos +... 3 tan + +... 3 3 sin +... Serie di Taylor: pprossimazioni per
VELOCITA' CRITICHE FLESSIONALI
 VELOCITA' CRITICHE FLESSIONALI Si consideri un albero privo di massa recante in posizione intermedia un corpo puntiforme di massa "M". Se la massa viene spostata dalla sua posizione di equilibrio in direzione
VELOCITA' CRITICHE FLESSIONALI Si consideri un albero privo di massa recante in posizione intermedia un corpo puntiforme di massa "M". Se la massa viene spostata dalla sua posizione di equilibrio in direzione
PROVA PARZIALE DEL 27 GENNAIO 2016
 PROVA PARZIALE DEL 27 GENNAIO 2016 February 2, 2016 Si prega di commentare e spiegare bene i vari passaggi, non di riportare solo la formula finale. PROBLEMA 1) Due blocchi, collegati da uno spago privo
PROVA PARZIALE DEL 27 GENNAIO 2016 February 2, 2016 Si prega di commentare e spiegare bene i vari passaggi, non di riportare solo la formula finale. PROBLEMA 1) Due blocchi, collegati da uno spago privo
ANTITRAFORMATE DI LAPLACE MODI DI UN SISTEMA
 CONTROLLI AUTOMATICI Ingegneria Meccatronica http://www.automazione.ingre.unimore.it/pages/corsi/automazione%20industriale.htm ANTITRAFORMATE DI LAPLACE MODI DI UN SISTEMA Ing. Luigi Biagiotti Tel. 051
CONTROLLI AUTOMATICI Ingegneria Meccatronica http://www.automazione.ingre.unimore.it/pages/corsi/automazione%20industriale.htm ANTITRAFORMATE DI LAPLACE MODI DI UN SISTEMA Ing. Luigi Biagiotti Tel. 051
UNIVERSITA DI PISA - ANNO ACCADEMICO CORSO DI LAUREA IN ING. ELETTRICA (N.O.) CORSO DI MECCANICA E TECNICA DELLE COSTRUZIONI MECCANICHE
 UNIVERSITA DI PISA - ANNO ACCADEMICO 007-8 CORSO DI LAUREA IN ING. ELETTRICA (N.O.) CORSO DI MECCANICA E TECNICA DELLE COSTRUZIONI MECCANICHE VERIFICA INTERMEDIA DEL 15-06-009 t1ta0t0nt0ts1e1esercizio
UNIVERSITA DI PISA - ANNO ACCADEMICO 007-8 CORSO DI LAUREA IN ING. ELETTRICA (N.O.) CORSO DI MECCANICA E TECNICA DELLE COSTRUZIONI MECCANICHE VERIFICA INTERMEDIA DEL 15-06-009 t1ta0t0nt0ts1e1esercizio
Sistemi non lineari e Funzione Descrittiva
 Sistemi non lineari e Funzione Descrittiva (Complementi di Controlli Automatici: prof. Giuseppe Fusco) Si consideri il sistema a retroazione rappresentato in Figura 1. In un punto generico della catena
Sistemi non lineari e Funzione Descrittiva (Complementi di Controlli Automatici: prof. Giuseppe Fusco) Si consideri il sistema a retroazione rappresentato in Figura 1. In un punto generico della catena
