APPLICAZIONI DI CP CLP(FD) PROPAGAZIONE DI VINCOLI VINCOLI INTERAZIONE TRA VINCOLI INTERAZIONE TRA VINCOLI
|
|
|
- Giulietta Papi
- 7 anni fa
- Visualizzazioni
Transcript
1 APPLICAZIONI DI CP Outline: Riassunto concetti principali su Constraint Programming Modello propagazione search Applicazioni Scheduling Routing Riconoscimento oggetti Linee di Ricerca aperte a Bologna Allocazione e scheduling per MPSoCs Dynamic Voltage scaling CLP(FD) CLP(FD): Constraint Logic Programming su domini finiti particolarmente adatta a modellare e risolvere problemi a vincoli Modello del problema Le VARIABILI rappresentano le entita del problema Definite su DOMINI FINITI di oggetti arbitrari (normalmente interi) Legate da VINCOLI (relazioni( tra variabili) matematici simbolici Nei problemi di ottimizzazione si ha una FUNZIONE OBIETTIVO Risoluzione Algoritmi di propagazione (incompleti) incapsulati nei vincoli Strategie di ricerca 2 VINCOLI Vincoli matematici: : =, >, <,,, Propagazione: : arc-consistency Vincoli Simbolici [Beldiceanu, Contejean, Math.Comp.Mod. 94] Incapsulano un metodo di propagazione globale ed efficiente Formulazioni piu concise alldifferent([x,...x m ]) tutte le variabili devono avere valori differenti element(n,[x,...x m ],Value) l ennesimo elemento della lista deve avere valore uguale a Value cumulative([s,...s m ], [D,...D n ], [R,...R n ], L) usato per vincoli di capacita vincoli disgiuntivi Vincoli matematici: Esempio X::[..0], Y::[5..5], X>Y Arc-consistency: per ogni valore v della variabile X, se non esiste un valore per Y compatibile con v, allora v viene cancellato dal dominio di X e viceversa X::[6..0], Y::[5..9] dopo la propagazione Esempio 2 X::[..0], Y::[5..5], X=Y X::[5..0], Y::[5..0] dopo la propagazione Esempio 3 X::[..0], Y::[5..5], XY Nessuna propagazione 3 4 INTERAZIONE TRA VINCOLI In generale ogni variabile e coinvolta in molti vincoli. Di conseguenza, ogni cambiamento nel dominio della variabile come risultato di una propagazione puo causare la rimozione di altri valori dai domini delle altre variabili. Prospettiva ad agenti: durante il loro tempo di vita, i vincoli alternano il loro stato da sospesi e attivi (attivati da eventi) INTERAZIONE TRA VINCOLI X = Y + X::[..5], Y::[..5], Z::[..5] Y = Z + X = Z - Esempio: X = Y + X::[..5], Y::[..5], Z::[..5] Y = Z + X = Z - Prima propagazione di X = Y + porta a X::[2..5] Y::[..4] Z::[..5] X = Y + sospeso 5 6
2 INTERAZIONE TRA VINCOLI Seconda propagazione di Y = Z + porta a INTERAZIONE TRA VINCOLI Terza propagazione di Z = X - porta a X::[2..5] Y::[2..4] Z::[..3] Y = Z + suspeso X::[] Y::[2..4] Z::[..3] FAIL Il dominio di Y e cambiato X = Y + viene attivato X::[3..5] Y::[2..4] Z::[..3] X = Y + sospeso L ordine nel quali i vincoli sono considerati (sospesi/risvegliati)) non influenza il risultato MA puo influenzare le prestazioni computazionali 7 8 Vincoli Simbolici: esempio X::[,2,3],X2::[,2,3],X3::[,2,3],X4::[,2,3,4], alldifferent([x,x2,x3,x4]) Vincoli Simbolici: vincoli disgiuntivi Supponiamo di avere due lezioni che devono essere tenute dallo stesso dovente. Abbiamo gli istanti di inizio delle lezioni: LStart e L2Start e la loro durata Duration e Duration2. X X2 2 Insieme di variabili di cardinalita 3 che hanno medesimo dominio i cardinalita 3 Le due lezioni non possono sovrapporsi: LStart + Duration L2Start OR L2Start + Duration2 LStart X3 X4 3 4 X4::[,2,3,4] Due problemi INDEPENDENTI uno per ogni parte della disgiunzione. 9 0 Vincoli Simbolici: vincoli disgiuntivi Due problemi INDEPENDENTI, uno per ogni parte della disgiunzione: una scelta non ha effetto sull altra Trashing Numero esponenziale di problemi: N disgiunzioni Fonte primaria di di complessita in 2 N Problemi in problemi reali Vincoli Simbolici: cumulative([s,...s m ], [D,...D n ], [R,...R n ], L) S,...S m sono istanti di inizio di attivita (variabili con dominio) D,...D n sono durate (variabili con dominio) R,...R n sono richieste di risorse (variabili con dominio) L limite di capacita delle risorse (fisso o variabile nel tempo) Soluzioni proposte: disgiunzione costruttiva operatore di cardinalita meta-constraint cumulative Il vincolo cumulative assicura che max{ j S j is j +D j R i } L 2
3 Vincoli Simbolici: cumulative([,2,4],[4,2,3],[,2,2],3) resources L Vincoli Simbolici: un esempio di propagazione usato nei vincoli sulle risorse e quello basato sulle parti obbligatorie S min 8 S max time Obligatory part 3 4 Vincoli Simbolici: un altra propagazione usata nel vincolo di capacita e quella basata sul edge finding [Baptiste, Le Pape, Nuijten, IJCAI95] Consideriamo una risorsa unaria e tre attivita S S2 4 S Vincoli Simbolici: S S2 S Possiamo dedurre che minimo istante di inizio per S e 8. Considerazione basata sul fatto che S deve essere eseguito dopo S2 e S3. Ragionamento globale: supponiamo che S2 o S3 siano eseguiti dopo S. Allora l istante di fine di S2 e S3 e almeno 3 (elemento non contenuto nel dominio di S2 e S3). 6 RICERCA Vincoli Simbolici: Teorema: [Carlier, Pinson, Man.Sci.95] Sia o un attivita e S un insieme di attivita che utilizzano la stessa risorsa unaria (o non contenuta in S). Il minimo istante di inizio e e, la somma delle durate e D e il massimo istante di terminazione e C. Se e(s+{o}) + D(S+{o}) > C(S) Allora non e possibile che o preceda alcuna operazione in S. Questo implica che il minimo istante iniziale per o puo essere fissato a max {e(s ) + D(S )}. (S S) La propagazione non e e in generale completa. Dopo la propagazione: Trovo una soluzione stop Fallimento backtracking I domini contengono alcuni valori SEARCH Ricerca: : idea Divide il problema in sotto-problemi (BRANCHING) and risolve ciascuno di essi indipendentemente I sottoproblemi devono essere una partizione del problema originale Scopo: mantenere lo spazio di ricerca il piu piccolo possibile per convenzione, i rami di sinistra vengono esplorati per primi. 7 8
4 Esempio INTERAZIONE TRA VINCOLI Seconda propagazione di Y = Z + porta a X::[..5], X = Y + Y::[..5], Y = Z + Z::[..5] X::[2..5] Y::[2..4] Z::[..3] Y = Z + sospeso Prima propagazione di X = Y + porta a Il dominio di Y e cambiato X = Y + viene attivato X::[2..5] Y::[..4] Z::[..5] X = Y + sospeso X::[3..5] Y::[2..4] Z::[..3] X = Y + sospeso 9 NON ABBIAMO UNA SOLUZIONE E SIAMO A UN PUNTO FERMO 20 INTERAZIONE TRA VINCOLI RICERCA Istanzio X a 3 (ho choice points): si sveglia X = Y+ che istanzia Y a 2 P X::[3] Y::[2] Z::[..3] X = Y + RISOLTO P P2 P3 P4..Pn Strategia di Branching GUESS Il dominio di Y e cambiato Y = Z + viene attivato X::[3] Y::[2] Z::[] IN BACKTRACKING ALTRE SOLUZIONI Y = Z + RISOLTO 2 Strategie di Branching definiscono il modo di partizionare il problema P in sottoproblemi piu facili P, P2,, Pn. Per ogni sotto problema si applica di nuovo la propagazione. Possono essere rimossi nuovi rami grazie alle nuove informazioni derivate dal branching 22 RICERCA In Programmazione logica a vincoli la tecnica piu popolare di branching e e detta labelling LABELLING: Seleziona una VARIABILE Seleziona un VALORE nel suo dominio Assegna il VALORE alla VARIABILE EURISTICHE L ordine in cui le variabili e i valori vengono scelti (la search strategy) non influenza la completezza dell algoritmo ma ne influenza penantemente l efficienza. STRATEGIE DI RICERCA: CRITERI GENERALI Scelta della Variabile: : prima istanzio le variabili piu difficili FIRST FAIL: seleziono prima la variabile con dominio piu piccolo MOST CONSTRAINING PRINCIPLE: seleziono prima la variabile coinvolta nel maggior numero di vincoli APPROCCI IBRIDI: combinazioni dei due Scelta del valore: valori piu promettenti prima LEAST CONSTRAINING PRINCIPLE. Sono poi state definite numerose strategie dipendenti dal problema. Attivita di ricerca volta a trovare buone strategie
5 COME SCEGLIERE UNA STRATEGIA Non esistono regole definite per scegliere la migliore strategia di ricerca. Dipende dal problema che dobbiamo risolvere e tipicamente la scelta viene effettuata dopo prove computazionali con diverse strategie CRITERIO: una strategia e piu efficiente se rimuove prima rami dello spazio delle soluzioni. APPLICAZIONI Ci concentriamo su Programmazione a vincoli su domini finiti Applicazioni: Scheduling - Timetabling - Allocazione di risorse Routing Packing - Cutting ottimizzazione PARAMETRI da considerare tempo computazione numero di fallimenti. Riconoscimento di oggetti ammissibilità SCHEDULING - TIMETABLING - ALLOCAZIONE DI RISORSE Tre applicazioni con vincoli e caratteristiche comuni: ci concentriamo sullo scheduling. Lo scheduling è forse l applicazione che ha avuto risultati migliori usando la Programmazione a vincoli flessibilità generalità codifica facile Problema NP-complete studiato nelle comunità di Ricerca Operativa e di Intelligenza Artificiale 27 SCHEDULING: definizione del problema Lo Scheduling riguarda l assegnamento di risorse limitate (macchine, denaro, personale) alle attività (fasi di progetto, servizi, lezioni) sull asse temporale Vincoli restrizioni temporali ordine tra attività due dates - release dates capacità delle risorse tipi diversi di risorse risorse consumabili e rinnovabili Criterio di ottimizzazione makespan (lunghezza dello schedule) bilanciamento delle risorse ritardo sui tempi di consegna costo dell assegnamento delle risorse 28 SCHEDULING: Attività Variabili decisioni : Istante iniziale delle attività Istante finale delle attività (oppure durata se variabile) Risorse Attività alternative (routing alternativi) Tipi di attività interval activity: non può essere interrotta breakable activity: può essere interrotta da breaks preemptable activity: può essere interrotta da altre attività SCHEDULING: Risorse 3. State Tipi di risorse:. Unarie 2. Discrete 3. Con stato 4. Energia 5. Stock Off White Red Black. Capacity Man-hrs Capacity Time Time Time 29 Time 30
6 SCHEDULING: Esempio semplice SCHEDULING: Esempio semplice 6 attività: ogni attività descritta da un predicato task(name,duration,listofprecedingtasks,machine). task(j,3,[],m). task(j2,8,[],m). task(j3,8,[j4,j5],m). task(j4,6,[],m2). task(j5,3,[j],m2). task(j6,4,[j],m2). Le macchine m e m2 sono unarie (capacità ). schedule(data, End, TaksList):- maketaskvariables(data,end, (Data,End,TaskList), precedence(data, TaskList), machines(data, TaskList), minimize(labeltasks(tasklist),end). maketaskvariables([],_,[]). maketaskvariables([task(n,d,_,_) T],End,[ ([task(n,d,_,_) T],End,[Start Var]):- Start::[0..End-D], maketaskvariables(t,end,var). precedence([task(n,_, ([task(n,_,prec,_) T], [Start Var]):- select_preceding_tasks(prec,t,var,,t,var,precvars,precdurations), impose_constraints(start, (Start,PrecVars,PrecDurations), precedence(t,var). Richiesto End: massimo tempo di fine schedule. 3 impose_constraints(_,[],[]). impose_constraints(start,[ (Start,[Var Other],[Dur OtherDur]):- Var + Dur <= Start impose_constraints(start, (Start,Other,OtherDur). 32 SCHEDULING: Esempio semplice SCHEDULING: Soluzione ottima machines(data, TaskList):- tasks_sharing_resource(data,tasklist,sameresource,durations), impose_cumulative(sameresource,durations,use). m impose_cumulative([],[],_). impose_cumulative([listsameres LSR],[ ],[Dur D],[Use U]):- cumulative(listsameres,dur,use,), impose_cumulative(lsr,d,u). labeltasks([]). labeltasks([ ([Task Other]):- indomain(task), labeltasks(other). Si specializza in m2 j j2 j3 3 9 Time cumulative([start,start2,start3],[3,8,8],[,,],) j4 j5 j6 cumulative([start4,start5,start6],[6,3,4],[,,],) 6 9 Time SCHEDULING: Ottimalità minimize: predicato per trovare la soluzione ottima (Branch & Bound) Consideriamo la minimizzazione del makespan: uso una euristica che selezione sempre l attività che può essere assegnata per prima. Come punto di scelta,, la postpone. labeltasks([]). labeltasks(tasklist):- find_min_start(tasklist,first,minstart,others), label_earliest(tasklist,first,minstart,others,postponed). label_earliest(tasklist,first,min,others):- % schedule the task First = Min, labeltasks(others). label_earliest(tasklist,first,min,others):- % delay the task First Min, labeltasks(tasklist). TIMETABLING: definizione del problema Timetabling riguarda la definizione di orari Vincoli restrizioni temporali ordine tra attività due dates - release dates capacità delle risorse risorse discrete Criterio di ottimizzazione costi/preferenze bilanciamento risorse 35 36
7 TIMETABLING: esempio semplice Slot di 4 ore - Corsi che durano da a 4 ore Due corsi non possono sovrapporsi Un corso deve essere contenuto in un singolo slot Preferenze su assegnamento Corso-Slot Massimizzare la somma delle preferenze TIMETABLING: codice con vincoli ridondanti timetable(data,tasks,maxtime,costs):- define_variable_start(tasks,maxtime), define_variable_singlehours(data,singlehours), define_variable_courses3_4hours(data, Courses34Hours), impose_cumulative(tasks), alldifferent(singlehours), alldifferent(courses34hours), Vincoli ridondanti minimize(labeling(tasks),cost). Variabili ridondanti istanti iniziali singole ore corsi che durano 3 o 4 ore Legate tra loro: scambiano i risultati di propagazione TIMETABLING: 0ttimalità e ricerca Strategie di ricerca: quando si considerano problemi di ottimizzazione, possiamo sfruttare informazioni sui costi per definire una buona strategia di ricerca. Esempio: Scegli la variabile che massimizza il regret Regret: differenza tra la primo e il secondo miglior costo per ogni variabile. Combinazione tra regret e first fail Scegli il valore associato al minimo costo Esempio: euristica basata sulla soluzione di un rilassamento Scegli la var che massimizza il regret Come valore scegli la soluzione ottima del rilassamento ROUTING: definizione del problema Il Routing riguarda il problema di trovare un insieme di percorsi coperti da un insieme di veicoli che partono e terminano allo stesso deposito. Vincoli restrizioni temporali: finestre temporali durata massima di un viaggio capacità del veicolo domanda dei clienti Criteri di ottimizzazione numero di veicoli costo di viaggio tempo di viaggio ROUTING: definizione del problema TSP: definizione del problema Il routing è stato risolto con tecniche di ricerca operativa con tecniche di Branch & Bound Programmazione dinamica Ricerca Locale Branch & Cut Column generation TSP è il problema di cercare un cammino Hamiltoniano a costo minimo. Il routing è stato risolto con Programmazione a vincoli Branch & Bound Ricerca Locale Non sono ammessi sottocicli TSPTW: Le finestre temporali sono associate ad ogni nodo E permesso l arrivo prima del tempo, ma non dopo. Componente di base: Travelling Salesman Problem (TSP) e varianti con finestre temporali. 4 Anche trovare un circuito Hamiltoniano (senza minimizzare il costo) ) è NP-completo 42
8 TSP: modello CP TSP: codice Variabili Next associate a ogni nodo.. Il dominio di ogni variabile Next contiene i possibili nodi da visitare dopo Next N nodi N + variabili Next i (il deposito viene duplicato) Per ogni i: Next i i nocycle([next 0, Next ]) n alldifferent([next 0, Next ]) n Costo c ij se Next = j i In alcuni modelli si possono usare variabili ridondanti Prev che indicano il predecessore del nodo. tsp(data, (Data,Next,Costs):- remove_arcs_to_self(next), nocycle(next), alldifferent(next), create_objective(next,costs,z), minimize(labelling(next),z). nocycle: vincolo simbolico che assicura che non ci siano sottocicli in soluzione. create_objective: crea variabili Costs,, e impone un vincolo element tra le variabili Next e Costs. Inoltre, crea una variabile Z che rappresenta la funzione obiettivo come somma di costi TSP: risultati Pura implementazione CP: risultati lontani dagli approcci di Ricerca Operativa. Integrazione di tecniche di Ricerca Operativa in CP: risultati migliori ricerca locale soluzioni ottime di rilassamenti rilassamenti Lagrangiani Problema dell Assegnamento Minimum Spanning Arborescence strategie di ricerca basate su informazioni provenienti dai rilassamenti eliminazione di sottocicli VINCOLI GLOBALI DI OTTIMIZZAZIONE GLOBAL CONSTRAINT OPTIMIZATION COMPONENT LB, x* and grad(x,v) domain reduction variable instantiation COST-BASED FILTERING ALGORITHM FILTERING ALGORITHM Aggiunta di finestre temporali in Ricerca Operativa richiede la riscrittura di molte parti di codice.. In CP è immediata VINCOLI GLOBALI DI OTTIMIZZAZIONE Propagazione basata su Lower Bound: dal LB verso la funzione obiettivoz::[zmin..zmax]: LB < Zmax cost-based filtering: Dalla funzione gradiende verso le variabili decisionali: Per ogni Xi::[v,v2,,vm] e vj esiste una funzione gradiente grad(xi,vj) che misura il costo addizionale se Xi = vj VINCOLI GLOBALI DI OTTIMIZZAZIONE L esempio piu semplice di funzione gradiente è rappresentato dai costi ridotti calcolati dal rilassamento lineare o in alcuni bound combinatori. Esempio: path constraint Se LB + grad(xi,vj) Zmax allora Xi vj classico variable fixing di ricerca operativa
9 PATH CONSTRAINT Dato un grafo diretto G=(V,A) with V = n, associamo ad ogni nodi i una variabile X i il cui dominio contiene i possibili next nel cammino, il path constraint X 0 ::D 0,X ::D,...,X k ::D k path([x 0,X,,X k ]) È vero se e solo sel assegnamento di valori alle variabili X 0,X,,X k definisce un cammino semplice che coinvolge tutti i nodi 0,,k. Duplicando il primo nodo vincolo equivalente al nocycle In generale il vincolo path e un multi-path path([x 0,X,,X k ], NumberOfPaths) 49 MAPPING CP-Model: X i ::[i, i 2,.,i m ] i=0..n path([x 0,X,...,X n ]) C i ::[c i,c i2,,c im ] i=0..n C 0 + +C n = Z minimize(z) X i = i j path ([X 0, X,.., X n ]) C i =c ij Mapping relaxed in ILP-Model min z = c ij x ij iv jv x ij = jv (A) iv x ij = iv (B) jv x ij SV S is jv\s x ij integer x ij = (A) + (B) c ij in z 50 PATH CONSTRAINT RISULTATI SU TSPs Il modello ILP precedente può fornire un bound usando il simplesso oppure algoritmi ad-hoc. Ad esempio con l Hungarian algorithm otteniamo un bound Z AP, una soluzione intera x*, e i costi ridotti. Inoltre, tale algoritmo è incrementale: (O(n 3 ) la prima soluzione, O(n 2 ) ogni ri-computazione). Questo bound puo essere molto scarso (soprattutto per TSP simmetrici). Lo si puo migliorare con la generazione di cutting planes. I piu semplici cutting planes sono I Subtour Elimination Constraints (SECs) la cui separazione è polinomiale. 5 Sebbene CP non sia competitiva con OR branch and cut (risolvono problemi fino a 4K nodi), l aggiunta di vincoli di ottimizzazione permette di risolvere queste istanze in tempi ragionevoli. CP senza vincoli di ottimizzazione non risolve alcuna di queste istanze in un giorno. Le istanze random sono piu semplici. Instance TSP and ATSP instances pure AP AP + cuts Opt Time Fails Opt Time Fails Gr Fri Bays Dantzig > RY48P 4854* > K 52 RISULTATI SU TSPTW Non appena vengono aggiunti al modello time windows o vincoli di precedenza le cose cambiano Il TSPTW ha due componenti principali : una componente di routing che considera l ottimizzazione, ossia cerchiamo il cammino di costo minimo; una componente di scheduling che considera l ammissibilità ossia cerchiamo un cammino che soddisfi i vincoli imposti le visite nelle città sono viste come attività che possono essere svolte all interno di finestre temporali. Tutte le attività sono svolte su una risorsa unaria in modo da non avere sovrapposizioni di visite. 53 RISULTATI SU TSPTW Con i vincoli di ottimizzazione: TSPTW simmetrici: migliorato lo stato dell arte [Pesant et al. 998] Usare cutting planes nel rilassamento dell assegnamento è molto efficace. TSPTW asimmetrici risultati competitivi con metodi branch-and-cut (stato dell arte) Ascheuer, et al. 200 chiusi 4 problemi Usare cutting planes nel rilassamento dell assegnamento è inutile. 54
10 CUTTING & PACKING: definizione Il Packing è il problema di piazzare un numero di pacchi (di dimensioni diverse) in uno o più contenitori in modo tale che non si sovrappongano e minimizzando lo spazio sprecato 2-D PACKING: modello CP Per ogni pezzo da piazzare abbiamo una coppia di variabili che rappresentano le coordinate del punto in basso a sinistra Il Cutting è il problema di tagliare un pezzo in modo di ottenere un dato numero di pezzi di dimensione fissa, minimizzando gli sprechi h (X,Y) d Pezzi: X::[0..D-d] Y::[0..H-h] Molte varianti: strip packing guillottine cuts rotazioni permesse o meno dimensione - 2 dimensioni - 3 dimensioni - 4 dimensioni H D masterpiece o bin D PACKING: modello CP Vincoli: di non sovrapposizione: date due pezzi le cui coordinate sono (X, Y) and (X2, Y2) ) e dimensioni D, H e D2, H2 rispettivamente X+D X2 OR Y+H Y2 OR X2+D2 X OR Y2+H2 Y Forma di disgiunzione pesante: : non c e propagazione anche dopo aver piazzato un pezzo Formulazione con vincoli simbolici: cumulative(xcoordinates,xdimension,ydimension,h) cumulative(ycoordinates,ydimension,xdimension,d) Esiste il vincolo diffn: alldifferent su piu dimensioni PACKING: codice packing(data, (Data,Xcoords,Ycoords,D,H):- create_variables(data, (Data,Xcoords,Ycoords,D,H), state_disjunctive(data, (Data,Xcoords,Ycoords), state_cumulatives(data, (Data,Xcoords,Ycoords,D,H), create_objective(xcoords,ycoords,d,h,z), minimize(label_squares(xcoords,ycoords),z). create_objective: crea una variabile rappresentante lo spazio perso (o il numero di bin se sono più di uno) label_squares seleziona i pezzi più grandi per primi e assegna le coordinate per minimizzare lo spazio perso RICONOSCIMENTO DI OGGETTI: definizione RICONOSCIMENTO DI OGGETTI Problema di riconoscere un oggetto in una scena OGGETTI 3-D S Come descrivere il modello Come fare il mapping MODELLO: Constraint graph Nodi: parti dell oggetto Archi (vincoli): relazioni tra le parti RICONOSCIMENTO: soddisfacimento di vincoli Due viste e i corrispondenti modelli S2 S7 S2 S2 S3 S4 S5 S6 S S3 S4 S5 S6 Is_L S8 Is_L S Is_Rect N S3 P P S4 Is_Rect Is_Rect S6 S5 Is_Rect S8 S7 S8 S7 59 Is_Rect Is_Rect 60
11 RICONOSCIMENTO DI OGGETTI Per riconoscere un oggetto,, un sistema di visione di basso livello deve estrarre dall immagine alcune caratteristiche visuali (superfici, segmenti) SEMPLICE ESEMPIO Rettangolo Quattro lati (variabili) paralleli due a due che si toccano formando un angolo di Possono essere applicate tecniche di soddisfacimento di vincoli per riconoscere un oggetto in una scena X3 X touch X2 L oggetto viene riconosciuto se le caratteristiche estratte soddisfano i vincoli contenuti nel modello I vincoli permettono di ridurre lo spazio di ricerca da esplorare X4 X X2 touch X4 touch touch X ESEMPIO (2) (0,0) (256,256) Rettangolo: modello CP Caratteristiche: segmenti Risolutore di vincoli Sistema di visione touch(x,x2), touch(x2,x3), touch(x3,x4), touch(x,x4), perpend(x,x2), perpend(x2,x3), perpend(x3,x4), perpend(x,x4), same_len(x2,x4), same_len(x,x3), parallel(x2,x4), parallel(x,x3) Modello CP: VINCOLI USER DEFINED Modello CP recognize([x,x2,x3,x4]):- X,X2,X3,X4::[s,s2,,sn], touch(x,x2), touch(x2,x3), touch(x3,x4), touch(x,x4), perpend(x,x2), perpend(x2,x3), perpend(x3,x4), perpend(x,x4), same_len(x2,x4), same_len(x,x3), parallel(x2,x4), parallel(x,x3), labeling([x,x2,x3,x4]). Dare la semantica dichiarativa e operazionale del vincolo: i segmenti sono descritti come fatti: segment(name,x,y,x2,y2) In tutti i linguaggi CP ci sono strumenti che permettono di definire nuovi vincoli. Esempio nella libreria CLP(FD) di ECL i PS e Modello CP: VINCOLI USER DEFINED touch(x,x2) :- dvar_domain(x,d), dvar_domain(x2,d2), arc_cons_(d,d2,dnew), % user defined propagation (dom_compare(>,d,dnew) -> dvar_update(x,dnew); true), arc_cons_2(dnew,d2,d2new), % user defined propagation (dom_compare(>,d2,d2new) -> dvar_update(x2,d2new); true), (var(x),var(x2) -> (make_suspension(touch(x,x2),3,susp), insert_suspension((x,x2), Susp, any of fd, fd)) ; true), wake. Dopo la propagazione,, se il vincolo non è risolto, viene sospeso e svegliato se si verifica un evento su una delle variabili coinvolte (X,X2). 65 Modello CP: SIMMETRIE Simmetrie: esistono quando abbiamo soluzioni equivalenti. Esempi: permulazioni, rotazioni ecc. Prendiamo quattro segmenti che formano un rettangolo s3 Soluzione: X = s s4 s2 X2 = s2 X3 = s3 X4 = s4 Tre soluzioni identiche: X = s2 X = s3 X2 = s3 X2 = s4 X3 = s4 X3 = s X4 = s X4 = s2 X = s3 X = s4 X2 = s4 X2 = s X3 = s X3 = s2 X4 = s2 X4 = s3 s 66
12 Modello CP: SIMMETRIE Problema: si perde tempo per esplorare stati equivalenti che non aggiungono alcuna informazione. Metodi per rimuovere le simmetrie: aggiungere vincoli al modello (esempio ordinamenti tra variabili) aggiungere vincoli dinamicamente nel corso della ricerca modificare la strategia di ricerca per rimuovere le simmetrie. Argomento su cui vi è una ricerca molto attiva ESEMPIO SEMPLICE Pigeonhole problem: : Abbiamo n- gabbie in cui devono essere collocati n piccioni uno per gabbia. Problema chiaramente insolubile ma abbiamo simmetrie di permutazione N piccioni Size Tree Con simmetrie Tempo (s) Size Tree NO simmetrie Tempo (s) COME RIMUOVERE LE SIMMETRIE Abbiamo n variabili P, P n che rappresentano i piccioni e un dominio contenente le gabbie da a n- Usiamo tutti vincoli di diverso binari (per vedere l impatto delle simmetrie) Simmetrie di permutazione n variabili n! stati simmetrici Si può imporre P < P 2, P 2 < P 3.P n- < P n e si rimuovono tutte le simmetrie Game Game 2 Game 3 Game 4 SPORT SCHEDULING Dobbiamo allocare delle partite in diverse settimane Ci sono n squadre (nell esempio esempio da 0 a 7). Tutte le squadre devono giocare contro tutte le altre, quindi in totale ho n*(n-)/2 partite. Devo allocare una partita per ogni cella in modo che in ogni settimana una squadra giochi una sola volta. Week 0 vs 2 vs 3 4 vs 5 6 vs 7 Week 2 0 vs 2 vs 7 3 vs 5 4 vs 6 Week 3 4 vs 7 0 vs 3 vs 6 2 vs 5 Week 4 3 vs 6 5 vs 7 0 vs 4 vs 2 Week 5 3 vs 7 vs 4 2 vs 6 0 vs 5 Week 6 vs 5 0 vs 6 2 vs 7 3 vs 4 Week 7 2 vs 4 5 vs 6 0 vs 7 vs SPORT SCHEDULING: simmetrie SPORT SCHEDULING: simmetrie Le settimane sono simmetriche I Game sono simmetrici Le settimane sono simmetriche I Game sono simmetrici Game Game 2 Game 3 Game 4 Week 0 vs 2 vs 3 4 vs 5 6 vs 7 Week 2 0 vs 2 vs 7 3 vs 5 4 vs 6 Week 3 4 vs 7 0 vs 3 vs 6 2 vs 5 Week 4 3 vs 6 5 vs 7 0 vs 4 vs 2 Week 5 3 vs 7 vs 4 2 vs 6 0 vs 5 Week 6 vs 5 0 vs 6 2 vs 7 3 vs 4 Week 7 2 vs 4 5 vs 6 0 vs 7 vs 3 Game Game 2 Game 3 Game 4 Week 0 vs 2 vs 3 4 vs 5 6 vs 7 Week 2 0 vs 2 vs 7 3 vs 5 4 vs 6 Week 3 4 vs 7 0 vs 3 vs 6 2 vs 5 Week 4 3 vs 6 5 vs 7 0 vs 4 vs 2 Week 5 3 vs 7 vs 4 2 vs 6 0 vs 5 Week 6 vs 5 0 vs 6 2 vs 7 3 vs 4 Week 7 2 vs 4 5 vs 6 0 vs 7 vs
13 SPORT SCHEDULING: simmetrie SPORT SCHEDULING: simmetrie Cambiando l ordine di due settimane trovo una soluzione equivalente Cambiando l ordine di due settimane trovo una soluzione equivalente Game Game 2 Game 3 Game 4 Week 0 vs 2 vs 3 4 vs 5 6 vs 7 Week 2 0 vs 2 vs 7 3 vs 5 4 vs 6 Week 3 4 vs 7 0 vs 3 vs 6 2 vs 5 Week 4 3 vs 6 5 vs 7 0 vs 4 vs 2 Week 5 3 vs 7 vs 4 2 vs 6 0 vs 5 Week 6 vs 5 0 vs 6 2 vs 7 3 vs 4 Week 7 2 vs 4 5 vs 6 0 vs 7 vs 3 Period Period 2 Period 3 Period 4 Week 0 vs 2 vs 3 4 vs 5 6 vs 7 Week 2 3 vs 7 vs 4 2 vs 6 0 vs 5 Week 3 4 vs 7 0 vs 3 vs 6 2 vs 5 Week 4 3 vs 6 5 vs 7 0 vs 4 vs 2 Week 5 0 vs 2 vs 7 3 vs 5 4 vs 6 Week 6 vs 5 0 vs 6 2 vs 7 3 vs 4 Week 7 2 vs 4 5 vs 6 0 vs 7 vs PERCHE PREOCCUPARSENE COME ELIMINARLE: VINCOLI AGGIUNTIVI NEL MODELLO Per una matrice nxm che ha simmetrie di riga e di colonna ci sono n!*m! simmetrie (super-esponenziale) Per ogni soluzione (totale o parziale) ce ne sono n!*m! simmetriche,, ma anche per ogni fallimento Eliminare tutte le simmetrie non e e facile Ci si accontenta spesso di eliminarne alcune, in modo da ottenere un albero ridotto. Solo simmetrie di riga, posso eliminarle con un ordinamento totale sulle righe: Forzare le righe ad essere lessicograficamente ordinate rompe tutte le simmetrie di riga lexicographic ordering A B C D E F [A B C] lex [D E F] lex [G H I] [G H I] lex [D E F] lex [A B C] G H I anti-lexicographic ordering SIMMETRIE DI RIGA E COLONNA Riusciamo a eliminare le simmetrie di riga e colonna singolarmente,, ma se compaiono insieme, imporre gli ordinamenti su righe e colonne non elimina tutte le simmetrie. Good News Una simmetria definisce una classe di equivalenza Due assegnamenti sono equivalenti se una simmetria mappa un assegnamento in un altro. Ogni simmetria ha ALMENO UN elemento in cui SIA le righe SIA le colonne sono ordinate in senso lessicografico Puo non esistere un elemento con le righe ordinate in senso lessicografico e le colonne in senso antilessicografico Per eliminare le simmetrie di riga e colonna possiamo ordinare lessicograficamente righe e colonne (double- lex) 77 78
14 Bad news VANTAGGI CP Una simmetria puo avere piu di un elemento con righe e colonne ordinate lessicograficamente Double-lex lex non elimina tutte le simmetrie Modellazione di problemi semplice Regole di propagazione combinate attraverso vincoli swap the columns swap row and row Flessibilità nel trattamento di varianti di problemi: semplice introduzione di nuovi vincoli interazione trasparente con nuovi vincoli Controllo semplice della ricerca LIMITAZIONI Lato ottimizzazione non molto efficace Problemi sovravincolati: non c e modo di rilassare i vincoli vincoli e preferenze Cambiamenti dinamici: cancellazione/aggiunta di variabili cancellazione/aggiunta di valori nel dominio cancellazione/aggiunta di vincoli 8 CP ESTENSIONI PER L OTTIMIZZAZIONEL TESI DISPONIBILI Integrazione di tecniche di Ricerca Operativa in CP: Solver MP: 2LP [McAloon, Tretkoof PPCP94], OPL [Van Hentenryck, 99], Planner [ILOG Planner Manual] Integrazione di CPLEX e XPRESS (simplesso) in solver FD Integrazione di algoritmi specifici per: calcolare bound costi ridotti Miglioramenti di [Rodosek, Wallace, Hajian [Caseau, Laburthe ICLP97 and CP97], [Focacci, Lodi, Milano ICLP99 and CP99], di branch and bound Hajian Annals OR 97], [Caseau, Laburthe ICLP94 and JICSLP96], [Beringer, DeBacker, LP Formal Method and Pract. Appl. 95] Integrazione di tecniche di local search [DeBacker, Furnon,Shaw CPAIOR99], [Caseau, Laburthe CPAIOR99], [Gendreau, Pesant, Rousseau, Transp. Sci. 98] Integrazione di branch and cut in logica [Bockmayr ICLP95], [Kasper PhD, 99] 82 ALTRE ESTENSIONI Estensioni per problemi sovravincolati [A. Borning OOPSLA87], [A. Borning et al. ICLP89], [M.Jamper PhD, 96] Estensioni per cambiamenti dinamici [R.Dechter, A.Dechter, AAAI88], [Verfaillie, Schiex AAAI94], [Bessiere, AAAI9], [Lamma et al. IJCAI99] Estensioni per problemi multi-criteria TESI DISPONIBILI PER SAPERNE DI PIU.. Conferenze: International Conference on Principles and Practice of Constraint Programming CP International Conference on Practical Applications of Constraint Technology PACT (PACLP) Logic programming (ILPS - ICLP - JICSLP) AI (ECAI - AAAI - IJCAI) OR (INFORMS - IFORS) Conferenza (CP-AI-OR) Libro: : K. Marriott and P. Stuckey Programming with constraints: An Introduction MIT Press 83 84
15 PER SAPERNE DI PIU.. Riviste: Constraint - An International Journal Riviste di AI - LP - OR Applicazioni industriali: COSYTEC, ILOG, ECRC, SIEMENS, BULL News group: comp.constraints Mailing list: CPWORLD@gmu.edu Archivi: 85
SCHEDULING - TIMETABLING - ALLOCAZIONE DI RISORSE APPLICAZIONI. SCHEDULING: Attività. SCHEDULING: definizione del problema
 APPLICAZIONI Ci concentriamo su Programmazione a vincoli su domini finiti SCHEDULING - TIMETABLING - ALLOCAZIONE DI RISORSE Tre applicazioni con vincoli e caratteristiche comuni: ci concentriamo sullo
APPLICAZIONI Ci concentriamo su Programmazione a vincoli su domini finiti SCHEDULING - TIMETABLING - ALLOCAZIONE DI RISORSE Tre applicazioni con vincoli e caratteristiche comuni: ci concentriamo sullo
Ci concentriamo su Programmazione a vincoli su domini finiti
 APPLICAZIONI Ci concentriamo su Programmazione a vincoli su domini finiti Applicazioni: Scheduling - Timetabling - Allocazione di risorse Routing Packing - Cutting ottimizzazione Grafica - Visione Le aste
APPLICAZIONI Ci concentriamo su Programmazione a vincoli su domini finiti Applicazioni: Scheduling - Timetabling - Allocazione di risorse Routing Packing - Cutting ottimizzazione Grafica - Visione Le aste
APPLICAZIONI SCHEDULING - TIMETABLING - ALLOCAZIONE DI RISORSE. Applicazioni: Routing Packing - Cutting. Grafica - Visione Le aste elettroniche
 APPLICAZIONI Ci concentriamo su Programmazione a vincoli su domini finiti Applicazioni: Scheduling - Timetabling - Allocazione di risorse Routing Packing - Cutting ottimizzazione Grafica - Visione Le aste
APPLICAZIONI Ci concentriamo su Programmazione a vincoli su domini finiti Applicazioni: Scheduling - Timetabling - Allocazione di risorse Routing Packing - Cutting ottimizzazione Grafica - Visione Le aste
APPLICAZIONI SCHEDULING - TIMETABLING - ALLOCAZIONE DI RISORSE. Routing Packing - Cutting. Grafica - Visione Le aste elettroniche.
 APPLICAZIONI Ci concentriamo su Programmazione a vincoli su domini finiti Applicazioni: Scheduling - Timetabling - Allocazione di risorse Routing Packing - Cutting ottimizzazione Grafica - Visione Le aste
APPLICAZIONI Ci concentriamo su Programmazione a vincoli su domini finiti Applicazioni: Scheduling - Timetabling - Allocazione di risorse Routing Packing - Cutting ottimizzazione Grafica - Visione Le aste
APPLICAZIONI DI CP. Outline: Riassunto concetti principali su Constraint Programming. Applicazioni. Modello propagazione search
 APPLICAZIONI DI CP Outline: Riassunto concetti principali su Constraint Programming Modello propagazione search Applicazioni Scheduling Routing Riconoscimento oggetti Linee di Ricerca aperte a Bologna
APPLICAZIONI DI CP Outline: Riassunto concetti principali su Constraint Programming Modello propagazione search Applicazioni Scheduling Routing Riconoscimento oggetti Linee di Ricerca aperte a Bologna
Constraint Satisfaction Problems
 Constraint Satisfaction Problems Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 19/03/2018 Constraint Satisfaction problem Fino ad ora ogni stato è stato modellizzato come una
Constraint Satisfaction Problems Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 19/03/2018 Constraint Satisfaction problem Fino ad ora ogni stato è stato modellizzato come una
PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems),, X ik. ) che specificano quali valori delle variabili sono compatibili tra loro,
 PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems) Dato un insieme finito di variabili X, X,, X n D, D,, D n i cui valori appartengono a domini e un insieme di vincoli c(x i, X i,, X ik ) che specificano
PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems) Dato un insieme finito di variabili X, X,, X n D, D,, D n i cui valori appartengono a domini e un insieme di vincoli c(x i, X i,, X ik ) che specificano
PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems) trovare una assegnazione di valori alle variabili che soddisfa i vincoli.
 PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems) Dato un insieme finito di variabili X, X,, X n i cui valori appartengono a domini D, D,, D n e un insieme di vincoli c(x i, X i,, X ik ) che specificano
PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems) Dato un insieme finito di variabili X, X,, X n i cui valori appartengono a domini D, D,, D n e un insieme di vincoli c(x i, X i,, X ik ) che specificano
3.4 Metodo di Branch and Bound
 3.4 Metodo di Branch and Bound Consideriamo un generico problema di Ottimizzazione Discreta dove X è la regione ammissibile. (P ) z = max{c(x) : x X} Metodologia generale di enumerazione implicita (Land
3.4 Metodo di Branch and Bound Consideriamo un generico problema di Ottimizzazione Discreta dove X è la regione ammissibile. (P ) z = max{c(x) : x X} Metodologia generale di enumerazione implicita (Land
Algoritmi esatti. La teoria ci dice che per problemi difficili (come il
 p. 1/4 Algoritmi esatti La teoria ci dice che per problemi difficili (come il KNAPSACK o, ancora di più, il TSP ) i tempi di risoluzione delle istanze, calcolati tramite analisi worst-case, tendono a crescere
p. 1/4 Algoritmi esatti La teoria ci dice che per problemi difficili (come il KNAPSACK o, ancora di più, il TSP ) i tempi di risoluzione delle istanze, calcolati tramite analisi worst-case, tendono a crescere
Problemi di Ottimizzazione
 Problemi di Ottimizzazione Obiettivo: misura della qualità di una soluzione. Vincoli: condizioni che devono essere soddisfatte per ottenere una soluzione ammissibile. Problema di Ottimizzazione: determina
Problemi di Ottimizzazione Obiettivo: misura della qualità di una soluzione. Vincoli: condizioni che devono essere soddisfatte per ottenere una soluzione ammissibile. Problema di Ottimizzazione: determina
PROGRAMMAZIONE LOGICA A VINCOLI PROGRAMMAZIONE LOGICA A VINCOLI
 PROGRAMMAZIONE LOGICA A VINCOLI AI CONSTRAINT SOLVING OPERATIONS RESEARCH CONSTRAINT PROGRAMMING LOGIC PROGRAMMING SOFTWARE ENGINEERING 1 PROGRAMMAZIONE LOGICA A VINCOLI Problemi di soddisfacimento di
PROGRAMMAZIONE LOGICA A VINCOLI AI CONSTRAINT SOLVING OPERATIONS RESEARCH CONSTRAINT PROGRAMMING LOGIC PROGRAMMING SOFTWARE ENGINEERING 1 PROGRAMMAZIONE LOGICA A VINCOLI Problemi di soddisfacimento di
Introduzione al Column Generation Caso di Studio: il Bin Packing Problem
 Introduzione al Column Generation Caso di Studio: il Bin Packing Problem November 15, 2014 1 / 26 Introduzione Il column generation è una metodologia che può essere usata per risolvere problemi di ottimizzazione
Introduzione al Column Generation Caso di Studio: il Bin Packing Problem November 15, 2014 1 / 26 Introduzione Il column generation è una metodologia che può essere usata per risolvere problemi di ottimizzazione
3.2 Rilassamenti lineari/combinatori e bounds
 3.2 Rilassamenti lineari/combinatori e bounds Consideriamo un problema di Ottimizzazione Discreta min{f(x) : x X} e sia z il valore di una soluzione ottima x X. Metodi di risoluzione spesso generano una
3.2 Rilassamenti lineari/combinatori e bounds Consideriamo un problema di Ottimizzazione Discreta min{f(x) : x X} e sia z il valore di una soluzione ottima x X. Metodi di risoluzione spesso generano una
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
Algoritmo di Branch & Bound
 Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Algoritmo di Branch & Bound Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria
Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Algoritmo di Branch & Bound Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria
Algoritmi Euristici. Molti problemi reali richiedono soluzioni algoritmiche
 9 Algoritmi Euristici introduzione Vittorio Maniezzo Università di Bologna 1 Molti problemi reali richiedono soluzioni algoritmiche I camion devono essere instradati VRP, NP-hard I depositi o i punti di
9 Algoritmi Euristici introduzione Vittorio Maniezzo Università di Bologna 1 Molti problemi reali richiedono soluzioni algoritmiche I camion devono essere instradati VRP, NP-hard I depositi o i punti di
PROGRAMMAZIONE LOGICA A VINCOLI
 PROGRAMMAZIONE LOGICA A VINCOLI Michela Milano DEIS - Università di Bologna mmilano@deis deis.unibo.itit http:// ://www-lia.deis.unibo.it/staff/michelamilano/ PROGRAMMAZIONE LOGICA A VINCOLI AI CONSTRAINT
PROGRAMMAZIONE LOGICA A VINCOLI Michela Milano DEIS - Università di Bologna mmilano@deis deis.unibo.itit http:// ://www-lia.deis.unibo.it/staff/michelamilano/ PROGRAMMAZIONE LOGICA A VINCOLI AI CONSTRAINT
Problemi di localizzazione di servizi (Facility Location Problems)
 9. Problemi di Localizzazione di Servizi 1 Problemi di localizzazione di servizi (Facility Location Problems) Dato un insieme di clienti richiedenti una data domanda di merce e dato un insieme di possibili
9. Problemi di Localizzazione di Servizi 1 Problemi di localizzazione di servizi (Facility Location Problems) Dato un insieme di clienti richiedenti una data domanda di merce e dato un insieme di possibili
PROGRAMMAZIONE LOGICA A VINCOLI PROGRAMMAZIONE LOGICA A VINCOLI PROGRAMMAZIONE LOGICA A VINCOLI. Michela Milano PROBLEMI DI SODDISFACIMENTO DI VINCOLI
 PROGRAMMAZIONE LOGICA A VINCOLI PROGRAMMAZIONE LOGICA A VINCOLI AI CONSTRAINT SOLVING OPERATIONS RESEARCH Michela Milano DEIS - Università di Bologna mmilano@deis deis.unibo.itit http:// ://www-lia.deis.unibo.it
PROGRAMMAZIONE LOGICA A VINCOLI PROGRAMMAZIONE LOGICA A VINCOLI AI CONSTRAINT SOLVING OPERATIONS RESEARCH Michela Milano DEIS - Università di Bologna mmilano@deis deis.unibo.itit http:// ://www-lia.deis.unibo.it
Ricerca Operativa A.A. 2007/ Esercitazione di laboratorio: Branch and Bound.
 Ricerca Operativa A.A. 2007/2008 17. Esercitazione di laboratorio: Branch and Bound. Luigi De Giovanni - Ricerca Operativa - 17. Esercitazione di laboratorio: Branch and Bound 17.1 . Luigi De Giovanni
Ricerca Operativa A.A. 2007/2008 17. Esercitazione di laboratorio: Branch and Bound. Luigi De Giovanni - Ricerca Operativa - 17. Esercitazione di laboratorio: Branch and Bound 17.1 . Luigi De Giovanni
Algoritmo dibranch & Bound
 Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Algoritmo dibranch & Bound Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria
Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Algoritmo dibranch & Bound Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria
Teoria della Complessità Concetti fondamentali
 Teoria della Complessità Concetti fondamentali L oggetto della teoria della complessità è stabilire se un problema sia facile o difficile La difficoltà di un problema è una caratteristica generale e non
Teoria della Complessità Concetti fondamentali L oggetto della teoria della complessità è stabilire se un problema sia facile o difficile La difficoltà di un problema è una caratteristica generale e non
PROBLEMI DI SODDISFACIMENTO DI VINCOLI PROGRAMMAZIONE LOGICA A VINCOLI CONSTRAINT GRAPHS. ESEMPIO: Map Coloring
 PROGRAMMAZIONE LOGICA A VINCOLI Problemi di soddisfacimento di vincoli: concetti generali Programmazione Logica vantaggi limiti Programmazione Logica a Vincoli dominio e interpretazione controllo modello
PROGRAMMAZIONE LOGICA A VINCOLI Problemi di soddisfacimento di vincoli: concetti generali Programmazione Logica vantaggi limiti Programmazione Logica a Vincoli dominio e interpretazione controllo modello
PROGRAMMAZIONE LOGICA A VINCOLI PROGRAMMAZIONE LOGICA A VINCOLI
 PROGRAMMAZIONE LOGICA A VINCOLI AI CONSTRAINT SOLVING OPERATIONS RESEARCH CONSTRAINT PROGRAMMING LOGIC PROGRAMMING SOFTWARE ENGINEERING 1 PROGRAMMAZIONE LOGICA A VINCOLI Problemi di soddisfacimento di
PROGRAMMAZIONE LOGICA A VINCOLI AI CONSTRAINT SOLVING OPERATIONS RESEARCH CONSTRAINT PROGRAMMING LOGIC PROGRAMMING SOFTWARE ENGINEERING 1 PROGRAMMAZIONE LOGICA A VINCOLI Problemi di soddisfacimento di
Soluzione dei problemi di Programmazione Lineare Intera
 Fondamenti di Ricerca Operativa T-A a.a. 2014-2015 Soluzione dei problemi di Programmazione Lineare Intera Andrea Lodi, Enrico Malaguti, Daniele Vigo rev. 1.1.a ottobre 2014 Fondamenti di Ricerca Operativa
Fondamenti di Ricerca Operativa T-A a.a. 2014-2015 Soluzione dei problemi di Programmazione Lineare Intera Andrea Lodi, Enrico Malaguti, Daniele Vigo rev. 1.1.a ottobre 2014 Fondamenti di Ricerca Operativa
5.1 Metodo Branch and Bound
 5. Metodo Branch and Bound Si consideri il problema min{ c(x) : x X } Idea: Ricondurre la risoluzione di un problema difficile a quella di sottoproblemi più semplici effettuando una partizione (ricorsiva)
5. Metodo Branch and Bound Si consideri il problema min{ c(x) : x X } Idea: Ricondurre la risoluzione di un problema difficile a quella di sottoproblemi più semplici effettuando una partizione (ricorsiva)
ASSEGNAMENTO DELLE OPERAZIONI DI TAGLIO NELLA PRODUZIONE DI CAPI DI ABBIGLIAMENTO
 ASSEGNAMENTO DELLE OPERAZIONI DI TAGLIO NELLA PRODUZIONE DI CAPI DI ABBIGLIAMENTO Lo scenario produttivo Una nota azienda produce capi di abbigliamento per l alta moda Ogni capo è costituito da vari pezzi
ASSEGNAMENTO DELLE OPERAZIONI DI TAGLIO NELLA PRODUZIONE DI CAPI DI ABBIGLIAMENTO Lo scenario produttivo Una nota azienda produce capi di abbigliamento per l alta moda Ogni capo è costituito da vari pezzi
Soluzione dei problemi di Programmazione Lineare Intera
 Fondamenti di Ricerca Operativa T-A a.a. 2015-2016 Soluzione dei problemi di Programmazione Lineare Intera Andrea Lodi, Enrico Malaguti, Paolo Tubertini, Daniele Vigo rev. 2. ottobre 2016 Fondamenti di
Fondamenti di Ricerca Operativa T-A a.a. 2015-2016 Soluzione dei problemi di Programmazione Lineare Intera Andrea Lodi, Enrico Malaguti, Paolo Tubertini, Daniele Vigo rev. 2. ottobre 2016 Fondamenti di
Prima prova Intermedia di Ricerca Operativa 2 COMPITO A Esercizio 1 (7 punti): LIFO
 Prima prova Intermedia di Ricerca Operativa 2 COMPITO A 13 novembre 2015 Nome e Cognome Matricola: Esercizio 1 (7 punti): Si consideri il seguente problema di programmazione lineare intera. max 32x 1 +
Prima prova Intermedia di Ricerca Operativa 2 COMPITO A 13 novembre 2015 Nome e Cognome Matricola: Esercizio 1 (7 punti): Si consideri il seguente problema di programmazione lineare intera. max 32x 1 +
Possibile applicazione
 p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
Macchine parallele M 1 M 2 M 3 J 1 J 2 LAVORI J 3 J 4
 Macchine parallele M 1 J 1 J 2 LAVORI M 2 J 3 J 4 M 3 Macchine parallele Scheduling su macchine parallele scorrelate R C max Descrizione del problema n lavori devono essere processati da m macchine diverse
Macchine parallele M 1 J 1 J 2 LAVORI M 2 J 3 J 4 M 3 Macchine parallele Scheduling su macchine parallele scorrelate R C max Descrizione del problema n lavori devono essere processati da m macchine diverse
max z = c T x s.t. Ax b
 3 PROGRAMMAZIONE LINEARE A NUMERI INTERI 51 3 Programmazione lineare a numeri interi 3.1 Problemi lineari interi Dato il problema lineare ordinario (PLO): aggiungendo la condizione di integrità: max z
3 PROGRAMMAZIONE LINEARE A NUMERI INTERI 51 3 Programmazione lineare a numeri interi 3.1 Problemi lineari interi Dato il problema lineare ordinario (PLO): aggiungendo la condizione di integrità: max z
Problemi, istanze, soluzioni
 lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
METODI DELLA RICERCA OPERATIVA
 Università degli Studi di Cagliari FACOLTA' DI INGEGNERIA CORSO DI METODI DELLA RICERCA OPERATIVA Dott.ing. Massimo Di Francesco (mdifrance@unica.it) i i Dott.ing. Maria Ilaria Lunesu (ilaria.lunesu@unica.it)
Università degli Studi di Cagliari FACOLTA' DI INGEGNERIA CORSO DI METODI DELLA RICERCA OPERATIVA Dott.ing. Massimo Di Francesco (mdifrance@unica.it) i i Dott.ing. Maria Ilaria Lunesu (ilaria.lunesu@unica.it)
Struttura del Corso. Durata
 Manuel Iori Dipartimento di Scienze e Metodi dell Ingegneria (DISMI) Università degli studi di Modena e Reggio Emilia Via Amendola 2, Pad. Buccola, 42122 Reggio Emilia web: www.or.unimore.it/iori/iori.htm
Manuel Iori Dipartimento di Scienze e Metodi dell Ingegneria (DISMI) Università degli studi di Modena e Reggio Emilia Via Amendola 2, Pad. Buccola, 42122 Reggio Emilia web: www.or.unimore.it/iori/iori.htm
Metodi e Modelli per l Ottimizzazione Combinatoria Cover inequalities
 Metodi e Modelli per l Ottimizzazione Combinatoria Cover inequalities L. De Giovanni M. Di Summa In questa lezione introdurremo una classe di disuguaglianze, dette cover inequalities, che permettono di
Metodi e Modelli per l Ottimizzazione Combinatoria Cover inequalities L. De Giovanni M. Di Summa In questa lezione introdurremo una classe di disuguaglianze, dette cover inequalities, che permettono di
Il problema del commesso viaggiatore e problemi di vehicle routing
 Il problema del commesso viaggiatore e problemi di vehicle routing Laura Galli Dipartimento di Informatica Largo B. Pontecorvo 3, 56127 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 2 Dicembre
Il problema del commesso viaggiatore e problemi di vehicle routing Laura Galli Dipartimento di Informatica Largo B. Pontecorvo 3, 56127 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 2 Dicembre
Algoritmo Branch and Cut (B&C)
 Programmazione Lineare Intera: III Algoritmo Branch and Cut Daniele Vigo DEIS Università di Bologna dvigo@deisuniboit rev.0 aprile 2005 Algoritmo Branch and Cut (B&C) Sviluppato negli anni 90, nasce come
Programmazione Lineare Intera: III Algoritmo Branch and Cut Daniele Vigo DEIS Università di Bologna dvigo@deisuniboit rev.0 aprile 2005 Algoritmo Branch and Cut (B&C) Sviluppato negli anni 90, nasce come
Lezioni di Ricerca Operativa
 Lezioni di Ricerca Operativa Estratto per la parte di programmazione lineare e ottimizzazione sui grafi Corso di Metodi di Ottimizzazione per l'ingegneria della Sicurezza Laurea Magistrale in Ingegneria
Lezioni di Ricerca Operativa Estratto per la parte di programmazione lineare e ottimizzazione sui grafi Corso di Metodi di Ottimizzazione per l'ingegneria della Sicurezza Laurea Magistrale in Ingegneria
Parte V: Rilassamento Lagrangiano
 Parte V: Rilassamento Lagrangiano Tecnica Lagrangiana Consideriamo il seguente problema di Programmazione Lineare Intera: P 1 min c T x L I Ax > b Cx > d x > 0, intera in cui A = matrice m x n C = matrice
Parte V: Rilassamento Lagrangiano Tecnica Lagrangiana Consideriamo il seguente problema di Programmazione Lineare Intera: P 1 min c T x L I Ax > b Cx > d x > 0, intera in cui A = matrice m x n C = matrice
Massimo flusso e matching
 Capitolo Massimo flusso e matching. Problema del massimo matching. Nel problema del massimo matching è dato un grafo non orientato G(V, A); un matching in G è un insieme di archi M A tale che nessuna coppia
Capitolo Massimo flusso e matching. Problema del massimo matching. Nel problema del massimo matching è dato un grafo non orientato G(V, A); un matching in G è un insieme di archi M A tale che nessuna coppia
ALGORITMI DI OTTIMIZZAZIONE M Esercizi Parte I
 ALGORITMI DI OTTIMIZZAZIONE M Esercizi Parte I Esercizio 1 Dati n oggetti ed un contenitore, ad ogni oggetto j (j = 1,, n) sono associati un peso p j ed un costo c j (con p j e c j interi positivi). Si
ALGORITMI DI OTTIMIZZAZIONE M Esercizi Parte I Esercizio 1 Dati n oggetti ed un contenitore, ad ogni oggetto j (j = 1,, n) sono associati un peso p j ed un costo c j (con p j e c j interi positivi). Si
Capitolo 3: Ottimizzazione Discreta. E. Amaldi DEI, Politecnico di Milano
 Capitolo 3: Ottimizzazione Discreta E. Amaldi DEI, Politecnico di Milano 3.1 Modelli di PLI e PLMI Moltissimi problemi decisionali complessi possono essere formulati come problemi di Programmazione Lineare
Capitolo 3: Ottimizzazione Discreta E. Amaldi DEI, Politecnico di Milano 3.1 Modelli di PLI e PLMI Moltissimi problemi decisionali complessi possono essere formulati come problemi di Programmazione Lineare
Problemi dello zaino e di bin packing
 Problemi dello zaino e di bin packing Laura Galli Dipartimento di Informatica Largo B. Pontecorvo 3, 56127 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 2 Dicembre 2014 Ricerca Operativa 2 Laurea
Problemi dello zaino e di bin packing Laura Galli Dipartimento di Informatica Largo B. Pontecorvo 3, 56127 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 2 Dicembre 2014 Ricerca Operativa 2 Laurea
Tecniche di Decomposizione per Programmazione Lineare Intera (Mista)
 Tecniche di Decomposizione per Programmazione Lineare Intera (Mista) Domenico Salvagnin 2011-06-12 1 Introduzione Dato un problema di programmazione lineare intera (mista), non è sempre possibile (o conveniente)
Tecniche di Decomposizione per Programmazione Lineare Intera (Mista) Domenico Salvagnin 2011-06-12 1 Introduzione Dato un problema di programmazione lineare intera (mista), non è sempre possibile (o conveniente)
Il Branch & Bound. Definizione 1. Sia S R n. La famiglia S = {S 1, S 2,..., S k S} tale che S 1 S 2 S k = S viene detta suddivisione di S.
 Il Branch & Bound Il metodo Branch & Bound è una tecnica che permette di risolvere all ottimo un generico problema di Programmazione Lineare Intera. Tale metodo si basa su due concetti cardine: quello
Il Branch & Bound Il metodo Branch & Bound è una tecnica che permette di risolvere all ottimo un generico problema di Programmazione Lineare Intera. Tale metodo si basa su due concetti cardine: quello
Parte III: Algoritmo di Branch-and-Bound
 Parte III: Algoritmo di Branch-and-Bound Divide et Impera Sia z * max {c T x : x S} (1) un problema di ottimizzazione combinatoria difficile da risolvere. Domanda: E possibile decomporre il problema (1)
Parte III: Algoritmo di Branch-and-Bound Divide et Impera Sia z * max {c T x : x S} (1) un problema di ottimizzazione combinatoria difficile da risolvere. Domanda: E possibile decomporre il problema (1)
Appunti di Ricerca Operativa
 Appunti di Ricerca Operativa 2012/2013 Prefazione La Ricerca Operativa è un campo in continua evoluzione, il cui impatto sulle realtà aziendali ed organizzative è in costante crescita. L insegnamento di
Appunti di Ricerca Operativa 2012/2013 Prefazione La Ricerca Operativa è un campo in continua evoluzione, il cui impatto sulle realtà aziendali ed organizzative è in costante crescita. L insegnamento di
Branch and Bound. Branch and Bound p. 1/3
 Branch and Bound Branch and Bound p. 1/3 Branch-and-bound Un esempio di problema di PLI: P 0 : max x 1 + 3x 2 (u 1 ) x 1 1 2 (u 2 ) 5x 1 + 3x 2 5 (u 3 ) x 1 + 7 5 x 2 13 2 x 1,x 2 0 x 1,x 2 I Branch and
Branch and Bound Branch and Bound p. 1/3 Branch-and-bound Un esempio di problema di PLI: P 0 : max x 1 + 3x 2 (u 1 ) x 1 1 2 (u 2 ) 5x 1 + 3x 2 5 (u 3 ) x 1 + 7 5 x 2 13 2 x 1,x 2 0 x 1,x 2 I Branch and
Excel: una piattaforma facile per l ottimizzazione. Excel ha un toolbox di ottimizzazione: Risolutore
 Excel: una piattaforma facile per l ottimizzazione Excel ha un toolbox di ottimizzazione: Risolutore Il problema di produzione con Excel Consideriamo il foglio Excel Variabili di decisione reali c8,d8
Excel: una piattaforma facile per l ottimizzazione Excel ha un toolbox di ottimizzazione: Risolutore Il problema di produzione con Excel Consideriamo il foglio Excel Variabili di decisione reali c8,d8
Programmazione a numeri interi: il metodo del Branch and Bound
 Programmazione a numeri interi: il metodo del Branch and Bound L. De Giovanni G. Zambelli Un problema di programmazione lineare intera è una problema della forma z I = maxc T x Ax b x 0 x i Z, i I. (1)
Programmazione a numeri interi: il metodo del Branch and Bound L. De Giovanni G. Zambelli Un problema di programmazione lineare intera è una problema della forma z I = maxc T x Ax b x 0 x i Z, i I. (1)
Il metodo dei Piani di Taglio (Cutting Planes Method)
 Il metodo dei Piani di Taglio (Cutting Planes Method) E un metodo di soluzione dei problemi (IP) di tipo generale. L idea di base: Se la soluzione di (RL) non è intera allora la soluzione ottima intera
Il metodo dei Piani di Taglio (Cutting Planes Method) E un metodo di soluzione dei problemi (IP) di tipo generale. L idea di base: Se la soluzione di (RL) non è intera allora la soluzione ottima intera
Problemi di Localizzazione Impianti
 Sapienza Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Problemi di Localizzazione Impianti Renato Bruni bruni@dis.uniroma1.it Il materiale presentato è derivato
Sapienza Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Problemi di Localizzazione Impianti Renato Bruni bruni@dis.uniroma1.it Il materiale presentato è derivato
Teoria della Complessità Computazionale
 Teoria della Complessità Computazionale Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it Rev. 1.3, 11/00 rev. 1.3 - Novembre 2000 Teoria della Complessità Studia la difficoltà dei problemi
Teoria della Complessità Computazionale Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it Rev. 1.3, 11/00 rev. 1.3 - Novembre 2000 Teoria della Complessità Studia la difficoltà dei problemi
Tecniche euristiche Ricerca Locale
 Tecniche euristiche Ricerca Locale PRTLC - Ricerca Locale Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali Come ricavare una stima dell ottimo: rilassamenti Rilassamento
Tecniche euristiche Ricerca Locale PRTLC - Ricerca Locale Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali Come ricavare una stima dell ottimo: rilassamenti Rilassamento
1) Disegnare la rete di progetto con le attività sugli archi, e la rete di progetto con le attività sui nodi.
 Un progetto di ricerca e sviluppo di una società si compone di 12 (principali) attività con precedenze, durate normali b ij (in giorni), costi diretti c ij (in dollari) delle attività alla loro durata
Un progetto di ricerca e sviluppo di una società si compone di 12 (principali) attività con precedenze, durate normali b ij (in giorni), costi diretti c ij (in dollari) delle attività alla loro durata
vincolo: una relazione tra variabili che definisce un sottoinsieme del prodotto cartesiano dei domini D 1 xd 2 x...xd n
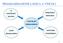 PROGRAMMAZIONE LOGICA A VINCOLI AI CONSTRAINT SOLVING OPERATIONS RESEARCH CONSTRAINT PROGRAMMING LOGIC PROGRAMMING SOFTWARE ENGINEERING 1 PROGRAMMAZIONE LOGICA A VINCOLI Problemi di soddisfacimento di
PROGRAMMAZIONE LOGICA A VINCOLI AI CONSTRAINT SOLVING OPERATIONS RESEARCH CONSTRAINT PROGRAMMING LOGIC PROGRAMMING SOFTWARE ENGINEERING 1 PROGRAMMAZIONE LOGICA A VINCOLI Problemi di soddisfacimento di
Metodo di Quine- McCluskey
 Metodo di Quine- McCluskey Maurizio Palesi Maurizio Palesi 1 Definizioni Date due funzioni f(x 1,x 2,,x n ) e g(x 1,x 2,,x n ) si dice che f copre g (oppure g implica f) e si scrive f g se f(x 1,x 2,,x
Metodo di Quine- McCluskey Maurizio Palesi Maurizio Palesi 1 Definizioni Date due funzioni f(x 1,x 2,,x n ) e g(x 1,x 2,,x n ) si dice che f copre g (oppure g implica f) e si scrive f g se f(x 1,x 2,,x
Tecniche euristiche greedy
 Tecniche euristiche greedy PRTLC - Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali
Tecniche euristiche greedy PRTLC - Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali
1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44;
 1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44; c 24 = 15; c 25 = 12; c 34 = 32; c 35 = 55; c 45 = 24 Si calcoli l ottimo duale (formulazione
1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44; c 24 = 15; c 25 = 12; c 34 = 32; c 35 = 55; c 45 = 24 Si calcoli l ottimo duale (formulazione
Week #9 Assessment. Practice makes perfect... November 23, 2016
 Week #9 Assessment Practice makes perfect... November 23, 2016 Esercizio 1 Un azienda di trasporto deve caricare m camion {1,..., m} in modo da servire giornalmente un dato insieme di clienti. Nei camion
Week #9 Assessment Practice makes perfect... November 23, 2016 Esercizio 1 Un azienda di trasporto deve caricare m camion {1,..., m} in modo da servire giornalmente un dato insieme di clienti. Nei camion
Il problema dello zaino: dalla gita in montagna ai trasporti internazionali. Luca Bertazzi
 Il problema dello zaino: dalla gita in montagna ai trasporti internazionali Luca Bertazzi 0 Ricerca Operativa (Operations Research) The Science of Better Modelli e algoritmi per la soluzione di problemi
Il problema dello zaino: dalla gita in montagna ai trasporti internazionali Luca Bertazzi 0 Ricerca Operativa (Operations Research) The Science of Better Modelli e algoritmi per la soluzione di problemi
Algoritmi Euristici. Corso di Laurea in Informatica e Corso di Laurea in Matematica. Roberto Cordone DI - Università degli Studi di Milano
 Algoritmi Euristici Corso di Laurea in Informatica e Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 14.30-16.30 in Aula Omega Venerdì 14.30-16.30 in
Algoritmi Euristici Corso di Laurea in Informatica e Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 14.30-16.30 in Aula Omega Venerdì 14.30-16.30 in
Sistemi con vincoli. Docente: Francesca Rossi.
 E-mail: frossi@math.unipd.it Scopo del corso Dare le nozioni di base della programmazione con vincoli Come rappresentare un problema reale con un insieme di vincoli Tecniche principali per risolverlo Approccio
E-mail: frossi@math.unipd.it Scopo del corso Dare le nozioni di base della programmazione con vincoli Come rappresentare un problema reale con un insieme di vincoli Tecniche principali per risolverlo Approccio
RICERCA OPERATIVA (a.a. 2015/16) Nome: Cognome: Matricola:
 o Appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si consideri il seguente problema di PL: max x + x x x x x x + x x Si applichi l algoritmo del Simplesso Duale, per via algebrica, a
o Appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si consideri il seguente problema di PL: max x + x x x x x x + x x Si applichi l algoritmo del Simplesso Duale, per via algebrica, a
ESERCIZIO 1: Punto 1
 ESERCIZIO : Punto La seguente matrice è una matrice delle distanze di un istanza del problema del Commesso Viaggiatore. - - - - - - - Calcolare.Il valore del rilassamento che si ottiene determinando l
ESERCIZIO : Punto La seguente matrice è una matrice delle distanze di un istanza del problema del Commesso Viaggiatore. - - - - - - - Calcolare.Il valore del rilassamento che si ottiene determinando l
Metodi di Ottimizzazione per la Logistica e la Produzione
 Metodi di Ottimizzazione per la Logistica e la Produzione Laboratorio Manuel Iori Dipartimento di Scienze e Metodi dell Ingegneria Università di Modena e Reggio Emilia MOLP Parte I 1 / 41 Contenuto della
Metodi di Ottimizzazione per la Logistica e la Produzione Laboratorio Manuel Iori Dipartimento di Scienze e Metodi dell Ingegneria Università di Modena e Reggio Emilia MOLP Parte I 1 / 41 Contenuto della
Programmazione Lineare Intera: Piani di Taglio
 Programmazione Lineare Intera: Piani di Taglio Andrea Scozzari a.a. 2014-2015 April 22, 2015 Andrea Scozzari (a.a. 2014-2015) Programmazione Lineare Intera: Piani di Taglio April 22, 2015 1 / 23 Programmazione
Programmazione Lineare Intera: Piani di Taglio Andrea Scozzari a.a. 2014-2015 April 22, 2015 Andrea Scozzari (a.a. 2014-2015) Programmazione Lineare Intera: Piani di Taglio April 22, 2015 1 / 23 Programmazione
Indice. 1 Introduzione... 1
 Indice 1 Introduzione............................................... 1 2 Esempi di modelli......................................... 7 2.1 Problema della dieta.................................... 7 2.2
Indice 1 Introduzione............................................... 1 2 Esempi di modelli......................................... 7 2.1 Problema della dieta.................................... 7 2.2
Una breve introduzione all implementazione in C di algoritmi su grafo
 Una breve introduzione all implementazione in C di algoritmi su grafo A cura di Gianmaria Leo Introduzione La lezione è un introduzione a concetti e strumenti che permettono l implementazione di algoritmi
Una breve introduzione all implementazione in C di algoritmi su grafo A cura di Gianmaria Leo Introduzione La lezione è un introduzione a concetti e strumenti che permettono l implementazione di algoritmi
RICERCA OPERATIVA. Tema d esame del 04/12/2008 (Simulazione 1)
 RICERCA OPERATIVA Tema d esame del 04/12/2008 (Simulazione 1) COGNOME: NOME: MATRICOLA: 1. Un azienda meccanica deve pianificare il lavoro delle sue tre macchine per un dato giorno. I lotti che è possibile
RICERCA OPERATIVA Tema d esame del 04/12/2008 (Simulazione 1) COGNOME: NOME: MATRICOLA: 1. Un azienda meccanica deve pianificare il lavoro delle sue tre macchine per un dato giorno. I lotti che è possibile
Branch-and-bound per TSP
 p. 1/6 Branch-and-bound per TSP Anche qui, rispetto allo schema generale visto in precedenza dobbiamo specificare: p. 1/6 Branch-and-bound per TSP Anche qui, rispetto allo schema generale visto in precedenza
p. 1/6 Branch-and-bound per TSP Anche qui, rispetto allo schema generale visto in precedenza dobbiamo specificare: p. 1/6 Branch-and-bound per TSP Anche qui, rispetto allo schema generale visto in precedenza
Un approccio esatto per il job shop
 Un approccio esatto per il ob shop Riferimenti lezione: rucker, P., Jurisch,. & Sievers,. (994) branch and bound algorithm for the ob scheduling shop problem, Discrete pplied Mathematics, Vol. 49, No.
Un approccio esatto per il ob shop Riferimenti lezione: rucker, P., Jurisch,. & Sievers,. (994) branch and bound algorithm for the ob scheduling shop problem, Discrete pplied Mathematics, Vol. 49, No.
AMPL Problemi su Reti
 Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
Macchine parallele M 1 M 2 M 3 J 1 J 2 LAVORI J 3 J 4
 Macchine parallele M 1 J 1 J 2 LAVORI M 2 J 3 J 4 M 3 Macchine parallele Scheduling su macchine parallele scorrelate R C max Descrizione del problema n lavori devono essere processati da m macchine diverse
Macchine parallele M 1 J 1 J 2 LAVORI M 2 J 3 J 4 M 3 Macchine parallele Scheduling su macchine parallele scorrelate R C max Descrizione del problema n lavori devono essere processati da m macchine diverse
Gestione della produzione e della supply chain Logistica distributiva
 Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Convergenza dell algoritmo Se non
Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Convergenza dell algoritmo Se non
Ricerca Operativa 2. Ricerca Operativa 2 p. 1/6
 Ricerca Operativa 2 Ricerca Operativa 2 p. 1/6 Introduzione In questo corso ci occuperemo di problemi di ottimizzazione. Ricerca Operativa 2 p. 2/6 Introduzione In questo corso ci occuperemo di problemi
Ricerca Operativa 2 Ricerca Operativa 2 p. 1/6 Introduzione In questo corso ci occuperemo di problemi di ottimizzazione. Ricerca Operativa 2 p. 2/6 Introduzione In questo corso ci occuperemo di problemi
Rilassamento Lagrangiano
 RILASSAMENTO LAGRANGIANO 1 Rilassamento Lagrangiano Tecnica più usata e conosciuta in ottimizzazione combinatoria per il calcolo di lower/upper bounds (Held and Karp (1970)). Si consideri il seguente problema
RILASSAMENTO LAGRANGIANO 1 Rilassamento Lagrangiano Tecnica più usata e conosciuta in ottimizzazione combinatoria per il calcolo di lower/upper bounds (Held and Karp (1970)). Si consideri il seguente problema
Corso di Perfezionamento
 Programmazione Dinamica 1 1 Dipartimento di Matematica e Informatica Università di Camerino 15 febbraio 2009 Tecniche di Programmazione Tecniche di progettazione di algoritmi: 1 Divide et Impera 2 Programmazione
Programmazione Dinamica 1 1 Dipartimento di Matematica e Informatica Università di Camerino 15 febbraio 2009 Tecniche di Programmazione Tecniche di progettazione di algoritmi: 1 Divide et Impera 2 Programmazione
Algoritmi greedy. Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione
 Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione Gli algoritmi greedy sono algoritmi basati sull idea
Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione Gli algoritmi greedy sono algoritmi basati sull idea
Introduzione ai grafi. Introduzione ai grafi p. 1/2
 Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G è costituito da una coppia di insiemi (V,A) dove V è detto insieme dei nodi e A è detto insieme di archi ed è un sottinsieme di tutte
Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G è costituito da una coppia di insiemi (V,A) dove V è detto insieme dei nodi e A è detto insieme di archi ed è un sottinsieme di tutte
3.3 Problemi di PLI facili
 3.3 Problemi di PLI facili Consideriamo un generico problema di PLI espresso in forma standard min{c t x : Ax = b, x Z n +} (1) dove A Z m n con n m, e b Z m. Supponiamo che A sia di rango pieno. Sia P
3.3 Problemi di PLI facili Consideriamo un generico problema di PLI espresso in forma standard min{c t x : Ax = b, x Z n +} (1) dove A Z m n con n m, e b Z m. Supponiamo che A sia di rango pieno. Sia P
5.3 Metodo dei piani di taglio
 5.3 Metodo dei piani di taglio (PLI) min s.v. c T x Ax b x interi X Ipotesi: a ij, c j e b i interi Osservazione: La regione ammissibile di un PLI può essere descritta mediante dei vincoli più o meno stringenti
5.3 Metodo dei piani di taglio (PLI) min s.v. c T x Ax b x interi X Ipotesi: a ij, c j e b i interi Osservazione: La regione ammissibile di un PLI può essere descritta mediante dei vincoli più o meno stringenti
Quinto appello 27/6/ = 4. B b B = 2 b N = 4
 Quinto appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si risolva il problema di PL dato applicando l algoritmo del Simplesso Duale, per via algebrica, a partire dalla base B {, }. Per
Quinto appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si risolva il problema di PL dato applicando l algoritmo del Simplesso Duale, per via algebrica, a partire dalla base B {, }. Per
Ricerca Operativa A.A. 2017/2018
 Ricerca Operativa A.A. 2017/2018 Esercizi su modelli di programmazione lineare intera - Soluzioni Nota Vengono fornite delle possibili soluzioni. Potrebbero esserci soluzioni alternative altrettanto valide.
Ricerca Operativa A.A. 2017/2018 Esercizi su modelli di programmazione lineare intera - Soluzioni Nota Vengono fornite delle possibili soluzioni. Potrebbero esserci soluzioni alternative altrettanto valide.
Allineamento multiplo di sequenze
 Allineamento multiplo di sequenze Bioinformatica a.a. 2008/2009 Letterio Galletta Università di Pisa 22 Maggio 2009 Letterio Galletta (Università di Pisa) Allineamento multiplo di sequenze 22 Maggio 2009
Allineamento multiplo di sequenze Bioinformatica a.a. 2008/2009 Letterio Galletta Università di Pisa 22 Maggio 2009 Letterio Galletta (Università di Pisa) Allineamento multiplo di sequenze 22 Maggio 2009
Capitolo 9: Trattabilitá e intrattabilitá dei problemi
 Capitolo 9: Trattabilitá e intrattabilitá dei problemi 1 La classe P : é considerata tradizionalmente come una caratterizzazione formale dei problemi trattabili. n = 2 n = 5 n = 10 n = 100 n = 1000 n 2
Capitolo 9: Trattabilitá e intrattabilitá dei problemi 1 La classe P : é considerata tradizionalmente come una caratterizzazione formale dei problemi trattabili. n = 2 n = 5 n = 10 n = 100 n = 1000 n 2
Complementi ed Esercizi di Informatica Teorica II
 Complementi ed Esercizi di Informatica Teorica II Vincenzo Bonifaci 21 maggio 2008 4 Problemi di ottimizzazione: il Bin Packing Il problema bin packing è il seguente: dato un insieme di n oggetti di dimensioni
Complementi ed Esercizi di Informatica Teorica II Vincenzo Bonifaci 21 maggio 2008 4 Problemi di ottimizzazione: il Bin Packing Il problema bin packing è il seguente: dato un insieme di n oggetti di dimensioni
COMPITO DI RICERCA OPERATIVA. max 5 2x 1 + 3x 2 x 3 = 2 + x 1 5x 2 x 4 = 5 + x 2. x 5 = 1 + x 1 x 2
 COMPITO DI RICERCA OPERATIVA ESERCIZIO. ( punti) La riformulazione di un problema di PL rispetto alla base B = {x, x, x } è la seguente: max 2x + x 2 x = 2 + x x 2 x = + x 2 x = 2 + x + x 2 x, x 2, x,
COMPITO DI RICERCA OPERATIVA ESERCIZIO. ( punti) La riformulazione di un problema di PL rispetto alla base B = {x, x, x } è la seguente: max 2x + x 2 x = 2 + x x 2 x = + x 2 x = 2 + x + x 2 x, x 2, x,
ALGORITMI DI OTTIMIZZAZIONE M
 ALGORITMI DI OTTIMIZZAZIONE M Paolo Toth (paolo.toth@unibo.it) 051 2093028 Orario di ricevimento: Martedì, 11-13, DEI (II Piano) Alberto Santini (a.santini@unibo.it) Orario di ricevimento: su appuntamento,
ALGORITMI DI OTTIMIZZAZIONE M Paolo Toth (paolo.toth@unibo.it) 051 2093028 Orario di ricevimento: Martedì, 11-13, DEI (II Piano) Alberto Santini (a.santini@unibo.it) Orario di ricevimento: su appuntamento,
Gestione della produzione e della supply chain Logistica distributiva. Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena
 Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Un algoritmo per il flusso a costo minimo: il simplesso
Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Un algoritmo per il flusso a costo minimo: il simplesso
Stime dell ottimo - Rilassamenti. PRTLC - Rilassamenti
 Stime dell ottimo - Rilassamenti PRTLC - Rilassamenti Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali Come ricavare una stima dell ottimo: rilassamenti Rilassamento
Stime dell ottimo - Rilassamenti PRTLC - Rilassamenti Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali Come ricavare una stima dell ottimo: rilassamenti Rilassamento
Metodi e Modelli per l Ottimizzazione Combinatoria Metodi esatti per il problema del commesso viaggiatore
 Metodi e Modelli per l Ottimizzazione Combinatoria Metodi esatti per il problema del commesso viaggiatore L. De Giovanni G. Zambelli Il problema del commesso viaggiatore (Travelling Salesman Problem -
Metodi e Modelli per l Ottimizzazione Combinatoria Metodi esatti per il problema del commesso viaggiatore L. De Giovanni G. Zambelli Il problema del commesso viaggiatore (Travelling Salesman Problem -
Ottimizzazione Combinatoria e Reti (a.a. 2007/08)
 o Appello 6/07/008 Ottimizzazione Combinatoria e Reti (a.a. 007/08) Nome Cognome: Matricola: ) Dopo avere finalmente superato l esame di Ricerca Operativa, Tommaso è pronto per partire in vacanza. Tommaso
o Appello 6/07/008 Ottimizzazione Combinatoria e Reti (a.a. 007/08) Nome Cognome: Matricola: ) Dopo avere finalmente superato l esame di Ricerca Operativa, Tommaso è pronto per partire in vacanza. Tommaso
Constraint Programming
 4 Constraint Programming introduzione Vittorio Maniezzo Università di Bologna 1 Ringraziamenti Questi lucidi derivano anche da adattamenti personali di materiale prodotto (fornitomi o reso scaricabile)
4 Constraint Programming introduzione Vittorio Maniezzo Università di Bologna 1 Ringraziamenti Questi lucidi derivano anche da adattamenti personali di materiale prodotto (fornitomi o reso scaricabile)
Metodi e Modelli per l Ottimizzazione Combinatoria Metodi esatti per il problema del commesso viaggiatore
 Metodi e Modelli per l Ottimizzazione Combinatoria Metodi esatti per il problema del commesso viaggiatore L. De Giovanni M. Di Summa Il problema del commesso viaggiatore (Travelling Salesman Problem -
Metodi e Modelli per l Ottimizzazione Combinatoria Metodi esatti per il problema del commesso viaggiatore L. De Giovanni M. Di Summa Il problema del commesso viaggiatore (Travelling Salesman Problem -
