Programmazione dinamica
|
|
|
- Abele Ruggiero
- 6 anni fa
- Visualizzazioni
Transcript
1 p. 1/1 Programmazione dinamica La programmazione dinamica è un altro approccio che consente di risolvere problemi in modo esatto. Considereremo solo problemi di massimo ma piccole modifiche consentono di applicare tale approccio anche a problemi di minimo. La programmazione dinamica è applicabile a problemi con determinate proprietà che andremo ora ad elencare.
2 p. 2/1 Proprietà Il problema può essere suddiviso in n blocchi. In ogni blocco k, k = 1,...,n ci si trova in uno degli stati s k appartenenti all insieme di stati Stati k. L insieme Stati 1 del blocco 1 è costituito da un singolo stato s 1. In ogni blocco k si deve prendere una decisione d k appartenente ad un insieme di possibili decisioni D k. L insieme di possibili decisioni può dipendere dallo stato s k, ovvero D k = D k (s k ).
3 p. 3/1 Continua Se al blocco k si prende la decisione d k e ci si trova nello stato s k, il blocco k fornisce un contributo alla funzione obiettivo f del problema pari a u(d k,s k ). La funzione obiettivo f sarà pari alla somma dei contributi degli n blocchi (esistono anche varianti in cui i contributi non si sommano ma si moltiplicano tra loro ma qui ne omettiamo la trattazione). Se al blocco k ci si trova nello stato s k e si prende la decisione d k, al blocco k + 1 ci troveremo nello stato s k+1 = t(d k,s k ). La funzione t viene detta funzione di transizione
4 p. 4/1 Il principio di ottimalità Ma la proprietà essenziale è quella che viene chiamata principio di ottimalità: se al blocco k mi trovo nello stato s k, la sequenza di decisioni ottime da prendere nei blocchi k,k + 1,...,n è totalmente indipendente da come sono giunto allo stato s k, ovvero dalle decisioni ai blocchi 1,...,k 1 che mi hanno fatto arrivare allo stato s k.
5 p. 5/1 Nel problema dello zaino blocchi oggetti al blocco k lo stato s k rappresenta la capacità residua dello zaino una volta prese le decisioni relative agli oggetti 1, 2,...,k 1. Quindi gli insiemi di stati possibili in ogni blocco sono: Stati k = {0, 1,...,b} per k = 2,...,n, Stati 1 = {b} D k (s k ) = { {NO} {NO, SI} se s k < p k se s k p k
6 p. 6/1 Continua contributo del blocco k: u(d k,s k ) = { 0 se d k =NO se d k =SI v k (NB: in questo caso il contributo non dipende dallo stato s k ) funzione di transizione: { t(d k,s k ) = s k s k p k se d k =NO se d k =SI
7 p. 7/1 Continua Il principio di ottimalità è soddisfatto: se ho capacità residua dello zaino s k, le decisioni ottime per i blocchi k,k + 1,...,n si ottengono risolvendo un problema dello zaino con i soli oggetti da k fino a n e con capacità dello zaino s k e non dipendono da come sono arrivato ad avere capacità residua s k nello zaino.
8 p. 8/1 Funzione f k La funzione f k (s k) restituisce il valore ottimo delle somme dei contributi dei blocchi k,k + 1,...,n quando si parte dallo stato s k al blocco k. Tipicamente è semplice calcolare f n(s n ) per ogni s n Stati n, cioè il valore ottimo del solo contributo del blocco n quando ci si trova nello stato s n. f n(s n ) = max u(d n,s n ) d n D n (s n ) La corrispondente decisione ottima verrà indicata con d n(s n ). A questo punto posso procedere a ritroso per calcolare f n 1 (s n 1) per ogni s n 1 Stati n 1.
9 p. 9/1 Continua Dato uno stato s n 1 in Stati n 1, considero una generica decisione d n 1 D n 1 (s n 1 ). Il contributo di tale decisione al blocco n 1 è pari a u(d n 1,s n 1 ). Inoltre, mi sposto nello stato s n = t(d n 1,s n 1 ) al blocco n. Da qui sfrutto il principio di ottimalità in base a cui non importa come sono arrivato nello stato t(d n 1,s n 1 ) e posso quindi procedere in modo ottimo da esso con un contributo pari a f n(t(d n 1,s n 1 )).
10 p. 10/1 Riassumendo se mi trovo nello stato s n 1 e prendo la decisione d n 1 il contributo ottimo complessivo dei blocchi n 1 e n sarà dato da u(d n 1,s n 1 ) + f n(t(d n 1,s n 1 )). Tra tutte le possibili decisioni d n 1 la migliore sarà quella che rende massimo il contributo complessivo. Tale decisione viene indicata con d n 1 (s n 1) e si avrà f n 1 (s n 1) = u(d n 1 (s n 1),s n 1 ) + f n (t(d n 1 (s n 1),s n 1 )) = = max d n 1 D n 1 (s n 1 ) [u(d n 1,s n 1 ) + f n(t(d n 1,s n 1 ))].
11 p. 11/1 Continua Una volta calcolati i valori f n 1 (s n 1) per tutti gli stati s n 1 Stati n 1, possiamo continuare a procedere a ritroso. Per il blocco k se mi trovo nello stato s k e considero una generica decisione d k D k (s k ), il contributo di tale decisione al blocco k è pari a u(d k,s k ). Inoltre, mi sposto nello stato s k+1 = t(d k,s k ) al blocco k + 1. Da qui sfrutto il principio di ottimalità in base a cui non importa come sono arrivato nello stato t(d k,s k ) e posso quindi procedere in modo ottimo da esso con un contributo pari a f k+1 (t(d k,s k )).
12 p. 12/1 Quindi se mi trovo nello stato s k e prendo la decisione d k il contributo ottimo complessivo dei blocchi k,k + 1,...,n sarà dato da u(d k,s k ) + f k+1 (t(d k,s k )). da cui, prendendo la decisione che massimizza tale valore, avremo: f k (s k) = max [u(d k,s k ) + fk+1 (t(d k,s k ))], d k D k (s k ) con la corrispondente decisione ottima d k (s k). NB: si noti che poiché si procede a ritroso, i valori f k+1 sono già stati calcolati.
13 p. 13/1 Valore ottimo Arrivati al blocco 1 si ha che Stati 1 è formato da un unico stato s 1 e il valore f 1 (s 1) coincide con il valore ottimo del problema.
14 p. 14/1 Soluzione ottima Per ricostruire la soluzione ottima possiamo partire dal blocco 1: al blocco 1 la decisione ottima è d 1 (s 1) e con tale decisione ci spostiamo allo stato s 2 = t(d 1 (s 1),s 1 ) del blocco 2; al blocco 2 la decisione ottima sarà d 2 (s 2 ). Con tale decisione ci spostiamo allo stato s 3 = t(d 2 (s 2 ),s 2 ) del blocco 3; al blocco 3 la decisione ottima sarà d 3 (s 3 ); si procede in questo modo fino ad arrivare al blocco n.
15 p. 15/1 Algoritmo- valore ottimo Passo 1 Per ogni s n Stati n si calcoli f n(s n ) e la corrispondente decisione ottima d n(s n ). Si ponga k = n 1. Passo 2 Per ogni s k Stati k si calcoli f k (s k) = max [u(d k,s k ) + fk+1 (t(d k,s k ))] d k D k (s k ) e la corrispondente decisione ottima d k (s k). Passo 3 Se k = 1 si ha che f 1 (s 1) è il valore ottimo del problema. Altrimenti si ponga k = k 1 e si ritorni al Passo 2.
16 p. 16/1 Algoritmo - soluzione ottima Passo 1 Si ponga s 1 = s 1 e k = 1. Passo 2 Per il blocco k la decisione ottima è d k (s k ). Si ponga s k+1 = t(d k (s k ),s k ). Passo 3 Se k = n, stop: la soluzione ottima è stata ricostruita ed è rappresentata dalle decisioni d 1(s 1),...,d n(s n). Altrimenti si ponga k = k + 1 e si ritorni al Passo 2.
17 p. 17/1 Complessità Nel problema dello zaino ad ogni blocco dobbiamo calcolare per ognuno dei b + 1 possibili stati, il massimo tra i valori delle decisioni possibili (che sono al più due, ovvero NO o SI). Quindi abbiamo in ogni blocco un numero O(b) di operazioni. Per gli n blocchi il numero totale di operazioni è O(nb). Questa è una complessità esponenziale. Perché? Il valore b è esponenziale rispetto alla sua codifica in codice binario che richiede log 2 (b + 1) bit.
Algoritmi esatti. La teoria ci dice che per problemi difficili (come il
 p. 1/4 Algoritmi esatti La teoria ci dice che per problemi difficili (come il KNAPSACK o, ancora di più, il TSP ) i tempi di risoluzione delle istanze, calcolati tramite analisi worst-case, tendono a crescere
p. 1/4 Algoritmi esatti La teoria ci dice che per problemi difficili (come il KNAPSACK o, ancora di più, il TSP ) i tempi di risoluzione delle istanze, calcolati tramite analisi worst-case, tendono a crescere
Algoritmi greedy. Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione
 Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione Gli algoritmi greedy sono algoritmi basati sull idea
Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione Gli algoritmi greedy sono algoritmi basati sull idea
Algoritmi greedy. Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione
 Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione Gli algoritmi greedy sono algoritmi basati sull idea
Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione Gli algoritmi greedy sono algoritmi basati sull idea
Ricerca Operativa 2. Ricerca Operativa 2 p. 1/6
 Ricerca Operativa 2 Ricerca Operativa 2 p. 1/6 Introduzione In questo corso ci occuperemo di problemi di ottimizzazione. Ricerca Operativa 2 p. 2/6 Introduzione In questo corso ci occuperemo di problemi
Ricerca Operativa 2 Ricerca Operativa 2 p. 1/6 Introduzione In questo corso ci occuperemo di problemi di ottimizzazione. Ricerca Operativa 2 p. 2/6 Introduzione In questo corso ci occuperemo di problemi
METODI DELLA RICERCA OPERATIVA
 Università degli Studi di Cagliari FACOLTA' DI INGEGNERIA CORSO DI METODI DELLA RICERCA OPERATIVA Dott.ing. Massimo Di Francesco (mdifrance@unica.it) i i Dott.ing. Maria Ilaria Lunesu (ilaria.lunesu@unica.it)
Università degli Studi di Cagliari FACOLTA' DI INGEGNERIA CORSO DI METODI DELLA RICERCA OPERATIVA Dott.ing. Massimo Di Francesco (mdifrance@unica.it) i i Dott.ing. Maria Ilaria Lunesu (ilaria.lunesu@unica.it)
PROGRAMMAZIONE DINAMICA
 PROGRAMMAZIONE DINAMICA 6.1 PROGRAMMAZIONE DINAMICA Sebbene elementi del metodo fossero già presenti in tecniche di ottimizzazione note in precedenza, si deve a Bellman lo studio sistematico (iniziato
PROGRAMMAZIONE DINAMICA 6.1 PROGRAMMAZIONE DINAMICA Sebbene elementi del metodo fossero già presenti in tecniche di ottimizzazione note in precedenza, si deve a Bellman lo studio sistematico (iniziato
Programmazione Lineare Intera. Programmazione Lineare Intera p. 1/4
 Programmazione Lineare Intera Programmazione Lineare Intera p. 1/4 Programmazione Lineare Intera Problema di PLI in forma standard: max cx Ax = b x 0, x I n I insieme degli interi. Regione ammissibile:
Programmazione Lineare Intera Programmazione Lineare Intera p. 1/4 Programmazione Lineare Intera Problema di PLI in forma standard: max cx Ax = b x 0, x I n I insieme degli interi. Regione ammissibile:
Algoritmi e Strutture Dati (Mod. B) Algoritmi Greedy (parte I)
 Algoritmi e Strutture Dati (Mod. B) Algoritmi Greedy (parte I) Algoritmi greedy Gli algoritmi per problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione
Algoritmi e Strutture Dati (Mod. B) Algoritmi Greedy (parte I) Algoritmi greedy Gli algoritmi per problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione
Metodi e Modelli per l Ottimizzazione Combinatoria Cover inequalities
 Metodi e Modelli per l Ottimizzazione Combinatoria Cover inequalities L. De Giovanni M. Di Summa In questa lezione introdurremo una classe di disuguaglianze, dette cover inequalities, che permettono di
Metodi e Modelli per l Ottimizzazione Combinatoria Cover inequalities L. De Giovanni M. Di Summa In questa lezione introdurremo una classe di disuguaglianze, dette cover inequalities, che permettono di
Programmazione Dinamica (PD)
 Programmazione Dinamica (PD) Altra tecnica per risolvere problemi di ottimizzazione, piu generale degli algoritmi greedy La programmazione dinamica risolve un problema di ottimizzazione componendo le soluzioni
Programmazione Dinamica (PD) Altra tecnica per risolvere problemi di ottimizzazione, piu generale degli algoritmi greedy La programmazione dinamica risolve un problema di ottimizzazione componendo le soluzioni
Architettura degli Elaboratori
 Architettura degli Elaboratori Rappresentazione dell Informazione Barbara Masucci Cosa studiamo oggi Ø Un moderno elaboratore è un sistema elettronico digitale programmabile Ø Il suo comportamento è flessibile
Architettura degli Elaboratori Rappresentazione dell Informazione Barbara Masucci Cosa studiamo oggi Ø Un moderno elaboratore è un sistema elettronico digitale programmabile Ø Il suo comportamento è flessibile
Ad ogni problema computazionale possiamo associare una misura della sua complessità.
 Problema computazionale: Descrizione dell input, Compito da svolgere. Esempio: SOMMA: INPUT: 2 numeri x e y, COMPITO: stampare x+y. Ad ogni problema computazionale possiamo associare una misura della sua
Problema computazionale: Descrizione dell input, Compito da svolgere. Esempio: SOMMA: INPUT: 2 numeri x e y, COMPITO: stampare x+y. Ad ogni problema computazionale possiamo associare una misura della sua
La Rappresentazione dell Informazione
 La Rappresentazione dell Informazione Maurizio Palesi Sommario In questo documento sarà trattato il modo in cui, in un calcolatore, vengono rappresentati i vari generi di informazione (testi, numeri interi,
La Rappresentazione dell Informazione Maurizio Palesi Sommario In questo documento sarà trattato il modo in cui, in un calcolatore, vengono rappresentati i vari generi di informazione (testi, numeri interi,
Appunti lezione Capitolo 13 Programmazione dinamica
 Appunti lezione Capitolo 13 Programmazione dinamica Alberto Montresor 12 Novembre, 2015 1 Domanda: Fattore di crescita dei numeri catalani Vogliamo dimostrare che cresce almeno come 2 n. La nostra ipotesi
Appunti lezione Capitolo 13 Programmazione dinamica Alberto Montresor 12 Novembre, 2015 1 Domanda: Fattore di crescita dei numeri catalani Vogliamo dimostrare che cresce almeno come 2 n. La nostra ipotesi
Parte III: Algoritmo di Branch-and-Bound
 Parte III: Algoritmo di Branch-and-Bound Divide et Impera Sia z * max {c T x : x S} (1) un problema di ottimizzazione combinatoria difficile da risolvere. Domanda: E possibile decomporre il problema (1)
Parte III: Algoritmo di Branch-and-Bound Divide et Impera Sia z * max {c T x : x S} (1) un problema di ottimizzazione combinatoria difficile da risolvere. Domanda: E possibile decomporre il problema (1)
1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44;
 1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44; c 24 = 15; c 25 = 12; c 34 = 32; c 35 = 55; c 45 = 24 Si calcoli l ottimo duale (formulazione
1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44; c 24 = 15; c 25 = 12; c 34 = 32; c 35 = 55; c 45 = 24 Si calcoli l ottimo duale (formulazione
Introduzione al Column Generation Caso di Studio: il Bin Packing Problem
 Introduzione al Column Generation Caso di Studio: il Bin Packing Problem November 15, 2014 1 / 26 Introduzione Il column generation è una metodologia che può essere usata per risolvere problemi di ottimizzazione
Introduzione al Column Generation Caso di Studio: il Bin Packing Problem November 15, 2014 1 / 26 Introduzione Il column generation è una metodologia che può essere usata per risolvere problemi di ottimizzazione
Parte IV: Rafforzamento di formulazioni e algoritmo dei piani di taglio
 Parte IV: Rafforzamento di formulazioni e algoritmo dei piani di taglio Nozioni di geometria Definizione: Un vettore y R n è combinazione conica dei vettori { 1,, k } se esistono k coefficienti reali λ
Parte IV: Rafforzamento di formulazioni e algoritmo dei piani di taglio Nozioni di geometria Definizione: Un vettore y R n è combinazione conica dei vettori { 1,, k } se esistono k coefficienti reali λ
Problemi e algoritmi. Il che cosa e il come. F. Damiani - Alg. & Lab. 04/05 (da U. de' Liguoro - Alg. & Spe. 03/04)
 Problemi e algoritmi Il che cosa e il come Il che cosa ed il come Problema: descrive che cosa si deve calcolare Specifica (di un algoritmo): descrive che cosa calcola un algoritmo Algoritmo: descrive come
Problemi e algoritmi Il che cosa e il come Il che cosa ed il come Problema: descrive che cosa si deve calcolare Specifica (di un algoritmo): descrive che cosa calcola un algoritmo Algoritmo: descrive come
Programmazione dinamica
 Programmazione dinamica Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Violetta Lonati Programmazione
Programmazione dinamica Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Violetta Lonati Programmazione
Problemi e algoritmi. Il che cosa ed il come. Il che cosa ed il come. Il che cosa e il come
 Problemi e algoritmi Il che cosa e il come Problema: descrive che cosa si deve calcolare Specifica (di un algoritmo): descrive che cosa calcola un algoritmo Algoritmo: descrive come effettuare un calcolo
Problemi e algoritmi Il che cosa e il come Problema: descrive che cosa si deve calcolare Specifica (di un algoritmo): descrive che cosa calcola un algoritmo Algoritmo: descrive come effettuare un calcolo
Parte III: Algoritmo di Branch-and-Bound
 Parte III: Algoritmo di Branch-and-Bound Sia Divide et Impera z* = max {c T x : x S} (1) un problema di ottimizzazione combinatoria difficile da risolvere. Domanda: E possibile decomporre il problema (1)
Parte III: Algoritmo di Branch-and-Bound Sia Divide et Impera z* = max {c T x : x S} (1) un problema di ottimizzazione combinatoria difficile da risolvere. Domanda: E possibile decomporre il problema (1)
Figura 1: 1) Si scriva la formulazione del problema come problema di PLI (con un numero minimo di vincoli) e la matrice dei vincoli.
 ESERCIZIO 1 Sia dato il grafo orientato in Figura 1. Si consideri il problema di flusso a 1 2 4 Figura 1: costo minimo su tale grafo con b 1 = 4 b 2 = 2 b = b 4 = e c 12 = 2 c 1 = 4 c 14 = 1 c 2 = 1 c
ESERCIZIO 1 Sia dato il grafo orientato in Figura 1. Si consideri il problema di flusso a 1 2 4 Figura 1: costo minimo su tale grafo con b 1 = 4 b 2 = 2 b = b 4 = e c 12 = 2 c 1 = 4 c 14 = 1 c 2 = 1 c
Branch and Bound. Branch and Bound p. 1/3
 Branch and Bound Branch and Bound p. 1/3 Branch-and-bound Un esempio di problema di PLI: P 0 : max x 1 + 3x 2 (u 1 ) x 1 1 2 (u 2 ) 5x 1 + 3x 2 5 (u 3 ) x 1 + 7 5 x 2 13 2 x 1,x 2 0 x 1,x 2 I Branch and
Branch and Bound Branch and Bound p. 1/3 Branch-and-bound Un esempio di problema di PLI: P 0 : max x 1 + 3x 2 (u 1 ) x 1 1 2 (u 2 ) 5x 1 + 3x 2 5 (u 3 ) x 1 + 7 5 x 2 13 2 x 1,x 2 0 x 1,x 2 I Branch and
ISTITUZIONI DI ALGEBRA SUPERIORE ESAME
 ISTITUZIONI DI ALGEBRA SUPERIORE ESAME CLAUDIA MALVENUTO 2 GENNAIO 2016 Istruzioni. Completare subito la parte inferiore di questa pagina con il proprio nome, cognome e firma. Scrivere solamente su questi
ISTITUZIONI DI ALGEBRA SUPERIORE ESAME CLAUDIA MALVENUTO 2 GENNAIO 2016 Istruzioni. Completare subito la parte inferiore di questa pagina con il proprio nome, cognome e firma. Scrivere solamente su questi
Corso di Perfezionamento
 Zaino frazionario e Algoritmi golosi 1 1 Dipartimento di Matematica e Informatica Università di Camerino 17 febbraio 2009 0-1 Un ladro entra in un magazzino e trova n oggetti L i-esimo oggetto vale v i
Zaino frazionario e Algoritmi golosi 1 1 Dipartimento di Matematica e Informatica Università di Camerino 17 febbraio 2009 0-1 Un ladro entra in un magazzino e trova n oggetti L i-esimo oggetto vale v i
Ricerca Operativa 2. Ricerca Operativa 2 p. 1/6
 Ricerca Operativa 2 Ricerca Operativa 2 p. 1/6 Introduzione In questo corso ci occuperemo di problemi di ottimizzazione. Tali problemi sono tipicamente raggruppati in classi ognuna delle quali è formata
Ricerca Operativa 2 Ricerca Operativa 2 p. 1/6 Introduzione In questo corso ci occuperemo di problemi di ottimizzazione. Tali problemi sono tipicamente raggruppati in classi ognuna delle quali è formata
Il problema dello zaino
 Il problema dello zaino (knapsack problem) Damiano Macedonio mace@unive.it Copyright 2010 2012 Moreno Marzolla, Università di Bologna (http://www.moreno.marzolla.name/teaching/asd2011b/) This work is licensed
Il problema dello zaino (knapsack problem) Damiano Macedonio mace@unive.it Copyright 2010 2012 Moreno Marzolla, Università di Bologna (http://www.moreno.marzolla.name/teaching/asd2011b/) This work is licensed
idea della crittografia a chiave pubblica
 idea della crittografia a chiave pubblica sviluppare un crittosistema in cui data la funzione di cifratura e k sia computazionalmente difficile determinare d k Bob rende pubblica la sua funzione di cifratura
idea della crittografia a chiave pubblica sviluppare un crittosistema in cui data la funzione di cifratura e k sia computazionalmente difficile determinare d k Bob rende pubblica la sua funzione di cifratura
Economia Aziendale Sistemi di Elaborazione delle Informazioni Università degli Studi di Enna Kore Mario Collotta
 Economia Aziendale Sistemi di Elaborazione delle Informazioni Università degli Studi di Enna Kore Mario Collotta mario.collotta@unikore.it 1 In questa lezione Algoritmi e diagrammi di flusso Consultazione
Economia Aziendale Sistemi di Elaborazione delle Informazioni Università degli Studi di Enna Kore Mario Collotta mario.collotta@unikore.it 1 In questa lezione Algoritmi e diagrammi di flusso Consultazione
L uomo come esecutore di algoritmi
 L uomo come esecutore di algoritmi l L algoritmo è l insieme di azioni elementari che consentono di risolvere un problema trasformando i dati iniziali del problema stesso nel risultato. l Un algoritmo
L uomo come esecutore di algoritmi l L algoritmo è l insieme di azioni elementari che consentono di risolvere un problema trasformando i dati iniziali del problema stesso nel risultato. l Un algoritmo
2.3.3 Cammini ottimi nei grafi senza circuiti
 .. Cammini ottimi nei grafi senza circuiti Sia un grafo G = (N, A) orientato senza circuiti e una funzione di costo che assegna un valore c ij R ad ogni arco (i, j) A circuito Proprietà I nodi di un grafo
.. Cammini ottimi nei grafi senza circuiti Sia un grafo G = (N, A) orientato senza circuiti e una funzione di costo che assegna un valore c ij R ad ogni arco (i, j) A circuito Proprietà I nodi di un grafo
La codifica digitale
 La codifica digitale Codifica digitale Il computer e il sistema binario Il computer elabora esclusivamente numeri. Ogni immagine, ogni suono, ogni informazione per essere compresa e rielaborata dal calcolatore
La codifica digitale Codifica digitale Il computer e il sistema binario Il computer elabora esclusivamente numeri. Ogni immagine, ogni suono, ogni informazione per essere compresa e rielaborata dal calcolatore
1 Programmazione Lineare Intera
 1 Programmazione Lineare Intera Fino ad ora abbiamo affrontato problemi in cui le variabili potevano assumere valori reali. Ora invece ci concentreremo su problemi in cui le variabili possono assumere
1 Programmazione Lineare Intera Fino ad ora abbiamo affrontato problemi in cui le variabili potevano assumere valori reali. Ora invece ci concentreremo su problemi in cui le variabili possono assumere
Fondamenti di Informatica. Ipotesi fondamentale. Irrisolubilità. Prof. V.L. Plantamura Informatica e Comunicazione Digitale a.a.
 Fondamenti di Informatica Prof. V.L. Plantamura Informatica e Comunicazione Digitale a.a. 2006-2007 Ipotesi fondamentale Tesi di Church Qualunque algoritmo può essere espresso sotto forma di matrice funzionale
Fondamenti di Informatica Prof. V.L. Plantamura Informatica e Comunicazione Digitale a.a. 2006-2007 Ipotesi fondamentale Tesi di Church Qualunque algoritmo può essere espresso sotto forma di matrice funzionale
4.4 Programmazione quadratica
 4.4 Programmazione quadratica Minimizzare una funzione quadratica soggetta a vincoli lineari: min 1 2 xt Qx + c t x s.v. a t i x b i i D (P) a t i x = b i i U x R n dove Q matrice n n, D e U sono gli insiemi
4.4 Programmazione quadratica Minimizzare una funzione quadratica soggetta a vincoli lineari: min 1 2 xt Qx + c t x s.v. a t i x b i i D (P) a t i x = b i i U x R n dove Q matrice n n, D e U sono gli insiemi
3.3 FORMULAZIONE DEL MODELLO E CONDIZIONI DI
 3.3 FORMULAZIONE DEL MODELLO E CONDIZIONI DI ESISTENZA DI UN PUNTO DI OTTIMO VINCOLATO Il problema di ottimizzazione vincolata introdotto nel paragrafo precedente può essere formulato nel modo seguente:
3.3 FORMULAZIONE DEL MODELLO E CONDIZIONI DI ESISTENZA DI UN PUNTO DI OTTIMO VINCOLATO Il problema di ottimizzazione vincolata introdotto nel paragrafo precedente può essere formulato nel modo seguente:
Corso di Perfezionamento
 Programmazione Dinamica 1 1 Dipartimento di Matematica e Informatica Università di Camerino 15 febbraio 2009 Tecniche di Programmazione Tecniche di progettazione di algoritmi: 1 Divide et Impera 2 Programmazione
Programmazione Dinamica 1 1 Dipartimento di Matematica e Informatica Università di Camerino 15 febbraio 2009 Tecniche di Programmazione Tecniche di progettazione di algoritmi: 1 Divide et Impera 2 Programmazione
Possibile applicazione
 p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
LA RICORSIONE LA RICORSIONE LA RICORSIONE: ESEMPIO LA RICORSIONE: ESEMPIO LA RICORSIONE: ESEMPIO LA RICORSIONE: ESEMPIO
 LA RICORSIONE Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa La ricorsione consiste nella possibilità di definire una funzione in termini
LA RICORSIONE Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa La ricorsione consiste nella possibilità di definire una funzione in termini
Algoritmi greedy. Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione
 Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione sono algoritmi basati sull idea di fare sempre scelte
Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione sono algoritmi basati sull idea di fare sempre scelte
ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09)
 ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09) DISPENSA N. 4 1. Ricerca Binaria Ricorsiva L algoritmo Ricerca Binaria risolve il problema della ricerca di una chiave in un vettore. È un esempio
ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09) DISPENSA N. 4 1. Ricerca Binaria Ricorsiva L algoritmo Ricerca Binaria risolve il problema della ricerca di una chiave in un vettore. È un esempio
Sommario della lezione:
 Sommario della lezione: Metodologie per il progetto di algoritmi: La Tecnica Divide et Impera Esempi di applicazione a: Ricerca del massimo e minimo di una sequenza di numeri Calcolo di potenze di numeri
Sommario della lezione: Metodologie per il progetto di algoritmi: La Tecnica Divide et Impera Esempi di applicazione a: Ricerca del massimo e minimo di una sequenza di numeri Calcolo di potenze di numeri
Laboratorio di Algoritmi
 Laboratorio di Algoritmi Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 8.30-10.30 in aula 3 Mercoledì 10.30-13.30 in aula 2 Giovedì 15.30-18.30 in
Laboratorio di Algoritmi Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 8.30-10.30 in aula 3 Mercoledì 10.30-13.30 in aula 2 Giovedì 15.30-18.30 in
Esame di Ricerca Operativa - 21 gennaio 2009 Facoltà di Architettura - Udine - CORREZIONE -
 Esame di Ricerca Operativa - 2 gennaio 29 Facoltà di Architettura - Udine - CORREZIONE - Problema ( punti): Un azienda chimica produce quattro tipi di colla, A, B, C, D, utilizzando materie prime P, P
Esame di Ricerca Operativa - 2 gennaio 29 Facoltà di Architettura - Udine - CORREZIONE - Problema ( punti): Un azienda chimica produce quattro tipi di colla, A, B, C, D, utilizzando materie prime P, P
Branch-and-bound per KNAPSACK
 p. 1/1 Branch-and-bound per KNAPSACK Rispetto allo schema generale visto in precedenza dobbiamo specificare: come si calcola un upper bound su un sottinsieme; p. 1/1 Branch-and-bound per KNAPSACK Rispetto
p. 1/1 Branch-and-bound per KNAPSACK Rispetto allo schema generale visto in precedenza dobbiamo specificare: come si calcola un upper bound su un sottinsieme; p. 1/1 Branch-and-bound per KNAPSACK Rispetto
Branch-and-bound per KNAPSACK
 p. 1/1 Branch-and-bound per KNAPSACK Rispetto allo schema generale visto in precedenza dobbiamo specificare: come si calcola un upper bound su un sottinsieme; come si effettua il branching; come si individuano
p. 1/1 Branch-and-bound per KNAPSACK Rispetto allo schema generale visto in precedenza dobbiamo specificare: come si calcola un upper bound su un sottinsieme; come si effettua il branching; come si individuano
5 PROGRAMMAZIONE LINEARE INTERA (PLI) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 5 PROGRAMMAZIONE LINEARE INTERA (PLI) E. Amaldi Fondamenti di R.O. Politecnico di Milano Programma lineare intero: (PLI) min c T x Ax b x 0 intero Ipotesi: A, b interi La condizione di interezza non è
5 PROGRAMMAZIONE LINEARE INTERA (PLI) E. Amaldi Fondamenti di R.O. Politecnico di Milano Programma lineare intero: (PLI) min c T x Ax b x 0 intero Ipotesi: A, b interi La condizione di interezza non è
Operativamente, risolvere un problema con un approccio ricorsivo comporta
 LA RICORSIONE Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa La ricorsione consiste nella possibilità di definire una funzione in termini
LA RICORSIONE Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa La ricorsione consiste nella possibilità di definire una funzione in termini
Capitolo 9: Trattabilitá e intrattabilitá dei problemi
 Capitolo 9: Trattabilitá e intrattabilitá dei problemi 1 La classe P : é considerata tradizionalmente come una caratterizzazione formale dei problemi trattabili. n = 2 n = 5 n = 10 n = 100 n = 1000 n 2
Capitolo 9: Trattabilitá e intrattabilitá dei problemi 1 La classe P : é considerata tradizionalmente come una caratterizzazione formale dei problemi trattabili. n = 2 n = 5 n = 10 n = 100 n = 1000 n 2
Interpolazione e integrazione numerica
 Interpolazione e integrazione numerica Carlo Mancini 16 dicembre 2015 Interpolazione con i polinomi di Lagrange Integrazione numerica Interpolazione con i polinomi di Lagrange - Introduzione Immaginiamo
Interpolazione e integrazione numerica Carlo Mancini 16 dicembre 2015 Interpolazione con i polinomi di Lagrange Integrazione numerica Interpolazione con i polinomi di Lagrange - Introduzione Immaginiamo
Conversione binario-ottale/esadecimale. Conversione binario-ottale/esadecimale. Rappresentazione di Numeri Interi Positivi (numeri naturali)
 Conversione binario-ottale/esadecimale Conversione binario-ottale/esadecimale Nella rappresentazione ottale (B=8) si usano gli 8 simboli,, 2, 3, 4, 5, 6, 7 In quella esadecimale (B=6) i 6 simboli,, 2,
Conversione binario-ottale/esadecimale Conversione binario-ottale/esadecimale Nella rappresentazione ottale (B=8) si usano gli 8 simboli,, 2, 3, 4, 5, 6, 7 In quella esadecimale (B=6) i 6 simboli,, 2,
LA RICORSIONE! Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa
 LA RICORSIONE! Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa La ricorsione consiste nella possibilità di definire una funzione in termini
LA RICORSIONE! Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa La ricorsione consiste nella possibilità di definire una funzione in termini
SIMULAZIONE DELLA PROVA INTERMEDIA DEL CORSO DI CALCOLATORI ELETTRONICI
 SIMULAZIONE DELLA PROVA INTERMEDIA DEL CORSO DI CALCOLATORI ELETTRONICI ESERCIZIO 1 (10 Punti) Si implementi una rete sequenziale la cui uscita valga Z=1 solo quando viene riconosciuta la sequenza in ingresso
SIMULAZIONE DELLA PROVA INTERMEDIA DEL CORSO DI CALCOLATORI ELETTRONICI ESERCIZIO 1 (10 Punti) Si implementi una rete sequenziale la cui uscita valga Z=1 solo quando viene riconosciuta la sequenza in ingresso
Funzioni implicite - Esercizi svolti
 Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Programma del corso. Rappresentazione delle Informazioni. Introduzione agli algoritmi. Architettura del calcolatore
 Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori (Reti Locali, Internet) Elementi di Programmazione Rappresentazione
Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori (Reti Locali, Internet) Elementi di Programmazione Rappresentazione
Prof. Pagani Corrado ALGORITMI E COMPLESSITÀ COMPUTAZIONALE
 Prof. Pagani Corrado ALGORITMI E COMPLESSITÀ COMPUTAZIONALE COMPLESSITÀ DEGLI ALGORITMI L oggetto della teoria della complessità è stabilire se un problema sia facile o difficile In base a quali parametri
Prof. Pagani Corrado ALGORITMI E COMPLESSITÀ COMPUTAZIONALE COMPLESSITÀ DEGLI ALGORITMI L oggetto della teoria della complessità è stabilire se un problema sia facile o difficile In base a quali parametri
Esercizi 3, 1. Prof. Thomas Parisini. Esercizi 3, 3 Regola:
 Esercizi 3, 1 Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Stabilità per sistemi a tempo continuo
Esercizi 3, 1 Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Stabilità per sistemi a tempo continuo
Stabilità per sistemi a tempo continuo
 Esercizi 3, 1 Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Calcolo di Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo
Esercizi 3, 1 Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Calcolo di Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo
Per regnare occorre tenere divisi i nemici e trarne vantaggio. fai ad ogni passo la scelta più conveniente
 Progetto di algoritmi sequenziali (un solo esecutore ) Divide et Impera Per regnare occorre tenere divisi i nemici e trarne vantaggio Greedy fai ad ogni passo la scelta più conveniente Buoni risultati
Progetto di algoritmi sequenziali (un solo esecutore ) Divide et Impera Per regnare occorre tenere divisi i nemici e trarne vantaggio Greedy fai ad ogni passo la scelta più conveniente Buoni risultati
Ricerca di Massimo e Minimo di un Array
 Universitá degli Studi di Salerno Corso di Introduzione agli Algoritmi e Strutture Dati Prof. Ugo Vaccaro Anno Acc. 2014/15 p. 1/18 Ricerca di Massimo e Minimo di un Array Problema. Trova l elemento di
Universitá degli Studi di Salerno Corso di Introduzione agli Algoritmi e Strutture Dati Prof. Ugo Vaccaro Anno Acc. 2014/15 p. 1/18 Ricerca di Massimo e Minimo di un Array Problema. Trova l elemento di
0.1 Complemento diretto
 1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
sono le risorse di calcolo necessarie per la sua l esecuzione di un metodo sono tipicamente:
 Complessità dei metodi e degli algoritmi Carla Binucci e Walter Didimo Efficienza di un metodo Un metodo è tanto più efficiente quanto minori sono le risorse di calcolo necessarie per la sua esecuzione
Complessità dei metodi e degli algoritmi Carla Binucci e Walter Didimo Efficienza di un metodo Un metodo è tanto più efficiente quanto minori sono le risorse di calcolo necessarie per la sua esecuzione
Dualitá. Dualitá p. 1/4
 Dualitá Dualitá p. 1/4 Dualitá p. 2/4 Dualitá Problema di PL in forma standard max cx Ax = b x 0 Chiamato problema primale. A questo associato un altro problema di PL, detto problema duale: min ub ua c
Dualitá Dualitá p. 1/4 Dualitá p. 2/4 Dualitá Problema di PL in forma standard max cx Ax = b x 0 Chiamato problema primale. A questo associato un altro problema di PL, detto problema duale: min ub ua c
Informazione binaria: - rappresentazione dei numeri naturali e interi relativi -
 Informazione binaria: - rappresentazione dei numeri naturali e interi relativi - Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Tipologie
Informazione binaria: - rappresentazione dei numeri naturali e interi relativi - Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Tipologie
Def. La lunghezza media L(C) di un codice C per una v.c. Obiettivo: Codice ottimo rispetto alla lunghezza media. Lunghezza media di un codice
 Lunghezza media di un codice Def. La lunghezza media L(C) di un codice C per una v.c. X con d.d.p. P(x) è data da L(C) = x X p (x) l (x) = E[l(X)] Obiettivo: Codice ottimo rispetto alla lunghezza media
Lunghezza media di un codice Def. La lunghezza media L(C) di un codice C per una v.c. X con d.d.p. P(x) è data da L(C) = x X p (x) l (x) = E[l(X)] Obiettivo: Codice ottimo rispetto alla lunghezza media
Lunghezza media. Teorema Codice D-ario prefisso per v.c. X soddisfa. L H D (X). Uguaglianza vale sse D l i. = p i. . p.1/27
 Lunghezza media Teorema Codice D-ario prefisso per v.c. X soddisfa L H D (X). Uguaglianza vale sse D l i = p i.. p.1/27 Lunghezza media Teorema Codice D-ario prefisso per v.c. X soddisfa L H D (X). Uguaglianza
Lunghezza media Teorema Codice D-ario prefisso per v.c. X soddisfa L H D (X). Uguaglianza vale sse D l i = p i.. p.1/27 Lunghezza media Teorema Codice D-ario prefisso per v.c. X soddisfa L H D (X). Uguaglianza
PROVA SCRITTA DEL CORSO DI. Corso di Laurea in Ingegneria Biomedica, Ingegneria Elettrica ed Elettronica 17 Luglio 2014
 PROVA SCRITTA DEL CORSO DI Corso di Laurea in Ingegneria Biomedica, Ingegneria Elettrica ed Elettronica 7 Luglio 204 NOME: COGNOME: MATRICOLA: ESERCIZIO (8 punti) ) ( punti) Progettare un MUX 4-, utilizzando
PROVA SCRITTA DEL CORSO DI Corso di Laurea in Ingegneria Biomedica, Ingegneria Elettrica ed Elettronica 7 Luglio 204 NOME: COGNOME: MATRICOLA: ESERCIZIO (8 punti) ) ( punti) Progettare un MUX 4-, utilizzando
3.4 Metodo di Branch and Bound
 3.4 Metodo di Branch and Bound Consideriamo un generico problema di Ottimizzazione Discreta dove X è la regione ammissibile. (P ) z = max{c(x) : x X} Metodologia generale di enumerazione implicita (Land
3.4 Metodo di Branch and Bound Consideriamo un generico problema di Ottimizzazione Discreta dove X è la regione ammissibile. (P ) z = max{c(x) : x X} Metodologia generale di enumerazione implicita (Land
Università di Roma Tor Vergata Corso di Teoria dei Fenomeni Aleatori, AA 2012/13. Catene di Markov
 Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Frequenza dei guasti: N GUASTI 0 T N T 0 T! Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Campionando
Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Frequenza dei guasti: N GUASTI 0 T N T 0 T! Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Campionando
Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa
 LA RICORSIONE Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa La ricorsione consiste nella possibilità di definire una funzione in termini
LA RICORSIONE Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa La ricorsione consiste nella possibilità di definire una funzione in termini
$GGL]LRQDWRULPHWRGR &DUU\/RRNDKHDG
![$GGL]LRQDWRULPHWRGR &DUU\/RRNDKHDG $GGL]LRQDWRULPHWRGR &DUU\/RRNDKHDG](/thumbs/70/62471332.jpg) $GGL]LRQDWRULPHWRGR &DUU\/RRNDKHDG Salvatore Orlando & Marta Simeoni Arch. Elab. - S. Orlando 1 $GGL]LRQDWRUL Il circuito combinatorio che implementa l addizionatore a n bit è costruito collegando in sequenza
$GGL]LRQDWRULPHWRGR &DUU\/RRNDKHDG Salvatore Orlando & Marta Simeoni Arch. Elab. - S. Orlando 1 $GGL]LRQDWRUL Il circuito combinatorio che implementa l addizionatore a n bit è costruito collegando in sequenza
Codifica di Huffman e Lempel-Ziv-Welch
 e Lempel-Ziv-Welch 1 A L B E R T O B E L U S S I A N N O A C C A D E M I C O 2 0 1 0 / 2 0 1 1 Tipi di compressione Senza perdita (lossless): permettono di ricostruire perfettamente la rappresentazione
e Lempel-Ziv-Welch 1 A L B E R T O B E L U S S I A N N O A C C A D E M I C O 2 0 1 0 / 2 0 1 1 Tipi di compressione Senza perdita (lossless): permettono di ricostruire perfettamente la rappresentazione
Rappresentazione di numeri interi e frazionari. 28 settembre 2015 (ore 9-11)
 Rappresentazione di numeri interi e frazionari 28 settembre 2015 (ore 9-11) Punto della situazione Vogliamo «dialogare» col computer: impariamo le rappresentazioni in binario Abbiamo visto la rappresentazioni
Rappresentazione di numeri interi e frazionari 28 settembre 2015 (ore 9-11) Punto della situazione Vogliamo «dialogare» col computer: impariamo le rappresentazioni in binario Abbiamo visto la rappresentazioni
Codifica di Huffman e Lempel-Ziv-Welch A L B E R T O B E L U S S I A N N O A C C A D E M I C O /
 Codifica di Huffman e Lempel-Ziv-Welch 1 A L B E R T O B E L U S S I A N N O A C C A D E M I C O 2 0 1 0 / 2 0 1 1 Tipi di compressione Senza perdita (lossless): permettono di ricostruire perfettamente
Codifica di Huffman e Lempel-Ziv-Welch 1 A L B E R T O B E L U S S I A N N O A C C A D E M I C O 2 0 1 0 / 2 0 1 1 Tipi di compressione Senza perdita (lossless): permettono di ricostruire perfettamente
1) Probabilità di errore di trasmissione. 2) Capacità di canale. 3) Esempi di calcolo della capacità. 4) Disuguaglianza di Fano
 Argomenti della Lezione 1) Probabilità di errore di trasmissione ) Capacità di canale 3) Esempi di calcolo della capacità 4) Disuguaglianza di Fano 5) Teorema inverso della codifica di canale 1 Probabilità
Argomenti della Lezione 1) Probabilità di errore di trasmissione ) Capacità di canale 3) Esempi di calcolo della capacità 4) Disuguaglianza di Fano 5) Teorema inverso della codifica di canale 1 Probabilità
Note per la Lezione 6 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 6 Ugo Vaccaro Ancora sulla tecnica Programmazione Dinamica Nella lezione scorsa abbiamo appreso che la tecnica Divide-et-Impera,
Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 6 Ugo Vaccaro Ancora sulla tecnica Programmazione Dinamica Nella lezione scorsa abbiamo appreso che la tecnica Divide-et-Impera,
Appunti sui Codici di Reed Muller. Giovanni Barbarino
 Appunti sui Codici di Reed Muller Giovanni Barbarino Capitolo 1 Codici di Reed-Muller I codici di Reed-Muller sono codici lineari su F q legati alle valutazioni dei polinomi sullo spazio affine. Per semplicità
Appunti sui Codici di Reed Muller Giovanni Barbarino Capitolo 1 Codici di Reed-Muller I codici di Reed-Muller sono codici lineari su F q legati alle valutazioni dei polinomi sullo spazio affine. Per semplicità
LA RICORSIONE. Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa
 LA RICORSIONE Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa La ricorsione consiste nella possibilità di definire una funzione in termini
LA RICORSIONE Una funzione matematica è definita ricorsivamente quando nella sua definizione compare un riferimento a se stessa La ricorsione consiste nella possibilità di definire una funzione in termini
Diverse politiche. La ricorsione PROGRAMMAZIONE TOP-DOWN ESEMPIO. Bottom-Up. Di solito è meglio alternare le due tecniche
 La ricorsione Top-Down Diverse politiche Si parte dal problema generale Poi si sce nei particolari (moduli, funzioni, ecc ) Bottom-Up Si creano prima i moduli e le funzioni base Poi si assemblano nel programma
La ricorsione Top-Down Diverse politiche Si parte dal problema generale Poi si sce nei particolari (moduli, funzioni, ecc ) Bottom-Up Si creano prima i moduli e le funzioni base Poi si assemblano nel programma
Fasi di creazione di un programma
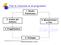 Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
come segue: data una collezione C di elementi e una un elemento che verifica la proprietà P
 Problemi di Ricerca Carla Binucci e Walter Didimo Il problema della Ricerca In generale, il Problema della Ricerca è definito come segue: data una collezione C di elementi e una proprietà P, determinare
Problemi di Ricerca Carla Binucci e Walter Didimo Il problema della Ricerca In generale, il Problema della Ricerca è definito come segue: data una collezione C di elementi e una proprietà P, determinare
5.5 Programmazione quadratica (PQ)
 5.5 Programmazione quadratica (PQ Minimizzare una funzione quadratica soggetta a vincoli lineari: 1 min x t Qx + c t x 2 s.v. a t i x b i i D (P a t i x = b i i U x R n dove Q matrice n n, D e U sono gli
5.5 Programmazione quadratica (PQ Minimizzare una funzione quadratica soggetta a vincoli lineari: 1 min x t Qx + c t x 2 s.v. a t i x b i i D (P a t i x = b i i U x R n dove Q matrice n n, D e U sono gli
Algoritmi e Strutture Dati
 Algoritmi Golosi (Greedy) Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino un algoritmo goloso correttezza Problema della selezione di attività
Algoritmi Golosi (Greedy) Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino un algoritmo goloso correttezza Problema della selezione di attività
Un po di Matematica. Il volo dei numeri di Mario Merz, un'installazione luminosa sulla Mole Antonelliana, rappresenta la successione di Fibonacci
 Un po di Matematica Il volo dei numeri di Mario Merz, un'installazione luminosa sulla Mole Antonelliana, rappresenta la successione di Fibonacci La successione di Fibonacci è una sequenza di numeri naturali
Un po di Matematica Il volo dei numeri di Mario Merz, un'installazione luminosa sulla Mole Antonelliana, rappresenta la successione di Fibonacci La successione di Fibonacci è una sequenza di numeri naturali
Algoritmi golosi. Tecniche di soluzione dei problemi viste finora: Metodo iterativo Divide et impera Programmazione dinamica.
 Algoritmi golosi Tecniche di soluzione dei problemi viste finora: Metodo iterativo Divide et impera Programmazione dinamica Nuova tecnica: Algoritmi golosi Metodo iterativo Soluzione del problema di dimensione
Algoritmi golosi Tecniche di soluzione dei problemi viste finora: Metodo iterativo Divide et impera Programmazione dinamica Nuova tecnica: Algoritmi golosi Metodo iterativo Soluzione del problema di dimensione
MODULO 07. La soluzione dei problemi mediante gli algoritmi
 MODULO 07 La soluzione dei problemi mediante gli algoritmi MODULO 07 Unità didattica 02 Impariamo a fare i diagrammi a blocchi In questa lezione impareremo: come descrivere l algoritmo risolutivo utilizzando
MODULO 07 La soluzione dei problemi mediante gli algoritmi MODULO 07 Unità didattica 02 Impariamo a fare i diagrammi a blocchi In questa lezione impareremo: come descrivere l algoritmo risolutivo utilizzando
AXO Architettura dei Calcolatori e Sistemi Operativi. aritmetica binaria intera
 AXO Architettura dei Calcolatori e Sistemi Operativi aritmetica binaria intera Aritmetica binaria intera Aritmetica binaria: conversioni di base di numero: base 2 base 8 base 10 base 16 Rappresentazione
AXO Architettura dei Calcolatori e Sistemi Operativi aritmetica binaria intera Aritmetica binaria intera Aritmetica binaria: conversioni di base di numero: base 2 base 8 base 10 base 16 Rappresentazione
Codifica binaria: - numeri naturali -
 Codifica binaria: - numeri naturali - Ingegneria Meccanica e dei Materiali Università degli Studi di Brescia Prof. Massimiliano Giacomin Tipologie di codici Per la rappresentazione di: caratteri alfabetici
Codifica binaria: - numeri naturali - Ingegneria Meccanica e dei Materiali Università degli Studi di Brescia Prof. Massimiliano Giacomin Tipologie di codici Per la rappresentazione di: caratteri alfabetici
Notazione posizionale. Codifica binaria. Rappresentazioni medianti basi diverse. Multipli del byte
 Codifica binaria Rappresentazione di numeri Notazione di tipo posizionale (come la notazione decimale). Ogni numero è rappresentato da una sequenza di simboli Il valore del numero dipende non solo dalla
Codifica binaria Rappresentazione di numeri Notazione di tipo posizionale (come la notazione decimale). Ogni numero è rappresentato da una sequenza di simboli Il valore del numero dipende non solo dalla
Allenamento alle Olimpiadi di Informatica
 Giornata di allenamento alle Olimpiadi di Informatica Allenamento alle Olimpiadi di Informatica Obiettivi di questa sessione Illustrare alcuni siti per lo sviluppo di competenze informatiche, anche in
Giornata di allenamento alle Olimpiadi di Informatica Allenamento alle Olimpiadi di Informatica Obiettivi di questa sessione Illustrare alcuni siti per lo sviluppo di competenze informatiche, anche in
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta. Metodi per il calcolo del rango di una matrice
 Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Cosa è l Informatica?
 Cosa è l Informatica? Scienza degli elaboratori elettronici (Computer Science) Scienza dell informazione Scienza della rappresentazione, memorizzazione, elaborazione e trasmissione dell informazione Elaboratore
Cosa è l Informatica? Scienza degli elaboratori elettronici (Computer Science) Scienza dell informazione Scienza della rappresentazione, memorizzazione, elaborazione e trasmissione dell informazione Elaboratore
Informatica. Mario Pavone - Dept. Mathematics & Computer Science - University of Catania. Trasferimento. Ambiente esterno.
 Trasferimento Ambiente esterno Controllo Informatica Mario Pavone - Dept. Mathematics & Computer Science - University of Catania mpavone@dmi.unict.it Cos è l Informatica La scienza della rappresentazione
Trasferimento Ambiente esterno Controllo Informatica Mario Pavone - Dept. Mathematics & Computer Science - University of Catania mpavone@dmi.unict.it Cos è l Informatica La scienza della rappresentazione
Ricerca Operativa. G. Liuzzi. Lunedí 20 Aprile 2015
 1 Lunedí 20 Aprile 2015 1 Istituto di Analisi dei Sistemi ed Informatica IASI - CNR Rilassamento di un problema Rilassare un problema di Programmazione Matematica vuol dire trascurare alcuni (tutti i)
1 Lunedí 20 Aprile 2015 1 Istituto di Analisi dei Sistemi ed Informatica IASI - CNR Rilassamento di un problema Rilassare un problema di Programmazione Matematica vuol dire trascurare alcuni (tutti i)
Laboratorio di Algoritmi e Strutture Dati
 Laboratorio di Algoritmi e Strutture Dati Docente: Camillo Fiorentini 8 gennaio 8 Il problema è simile all esercizio 5.6 del libro di testo di algoritmi (Introduzione agli algoritmi e strutture dati, T.
Laboratorio di Algoritmi e Strutture Dati Docente: Camillo Fiorentini 8 gennaio 8 Il problema è simile all esercizio 5.6 del libro di testo di algoritmi (Introduzione agli algoritmi e strutture dati, T.
Strategie risolutive e algoritmi per problemi di partizionamento ottimo di grafi
 Strategie risolutive e algoritmi per problemi di partizionamento ottimo di grafi Natascia Piroso 12 luglio 2007 Natascia Piroso Partizionamento ottimo di grafi 12 luglio 2007 1 / 17 Definizione Dato un
Strategie risolutive e algoritmi per problemi di partizionamento ottimo di grafi Natascia Piroso 12 luglio 2007 Natascia Piroso Partizionamento ottimo di grafi 12 luglio 2007 1 / 17 Definizione Dato un
Fondamenti di Informatica
 Fondamenti di Informatica AlgoBuild: Strutture iterative e selettive Prof. Christian Esposito Corso di Laurea in Ingegneria Meccanica e Gestionale (Classe I) A.A. 2016/17 AlgoBuild: Strutture iterative
Fondamenti di Informatica AlgoBuild: Strutture iterative e selettive Prof. Christian Esposito Corso di Laurea in Ingegneria Meccanica e Gestionale (Classe I) A.A. 2016/17 AlgoBuild: Strutture iterative
