APPLICAZIONI di MATEMATICA
|
|
|
- Giuseppina Forti
- 5 anni fa
- Visualizzazioni
Transcript
1 APPLICAZIONI di MATEMATICA 1 Serie di poteze e trasformata Zeta 1.1 Serie di Poteze (Richiami) Premettiamo alcui richiami sulle serie di poteze. Sia {a } ua successioe di costati reali o complesse; si chiama allora serie di poteze ua serie del tipo a 0 + a 1 s + a 2 s a s + = a s (1) dove s idica u umero complesso. Ogi serie di poteze del tipo (1) coverge per s = 0. Ioltre se essa coverge per u valore s = s 0 0, allora essa coverge assolutamete per qualsiasi valore della variabile s di modulo miore di s 0. Se ivece per s = s 0 la serie (1) o coverge, allora (1) o coverge per qualsiasi valore della variabile s di modulo maggiore di s 0. I altri termii se (1) coverge per s = s 0, allora (1) coverge assolutamete i tutti i puti iteri alla circofereza di cetro l origie e raggio s 0 ; se ivece (1) o coverge per s = s 0, allora (1) o coverge i tutti i puti esteri a tale circofereza. Vi soo serie di poteze che covergoo solo per s = 0; tale è, ad esempio, la serie 1 + 1!s + 2!s 2 + 3!s 3 + +!s + ; altre serie ivece covergoo per ogi valore della variabile s, come, ad esempio, la serie espoeziale =0 1 + s 1! + s2 2! + s3 3! + + s! +. 1
2 Vi soo ifie delle serie che, per alcui valori di s, di modulo positivo, covergoo e per altri valori di s o covergoo. U esempio i tal seso è dato dalla serie geometrica 1 + s + s 2 + s s + (2) che coverge per valori di s di modulo miore di 1 e o coverge per valori di s di modulo maggiore di 1. Cosideriamo ora ua serie di poteze della forma (1) che, per qualche s 1 0 sia covergete e per altri valori s 2 sia o covergete. A tale serie è possibile associare u umero reale positivo ρ che coicide co l estremo superiore dei moduli dei valori di s per i quali (1) coverge. Pertato (1) coverge assolutamete per ogi s tale che s < ρ; (1) o coverge per ogi s tale che s > ρ. Tale valore ρ prede il ome di raggio di covergeza e la circofereza di cetro l origie e raggio ρ si chiama circofereza di covergeza e il suo itero cerchio di covergeza. Se la serie cosiderata coverge soltato per s = 0, diremo che il suo raggio di covergeza è ullo e porremo, per covezioe, ρ = 0. Aalogamete, se la serie coverge per ogi valore di s, diremo che il suo raggio di covergeza è ifiito e porremo ρ =. I quest ultimo caso il cerchio di covergeza coiciderà co l itero piao complesso. Vediamo ora come può essere determiato il raggio di covergeza. A tal fie ricordiamo la defiizioe di limite superiore di ua successioe. Data ua successioe {g } di umeri reali o egativi, limitata superiormete 1, si chiama limite superiore di {g }, e si idica co lim sup g, il limite dove lim sup g = lim M (3) def M = sup {g, g +1, g +2,...}. Se ivece la successioe {g } è illimitata (superiormete), si poe lim sup g =. 1 Ricordiamo che ua successioe {g } è limitata superiormete se esiste ua costate k tale che g < k, = 0, 1, 2,.... 2
3 Il massimo limite può essere, alterativamete, calcolato el modo seguete. Sia {g } limitata superiormete; essedo a termii o egativi, tale successioe è limitata e quidi ammette sottosuccessioi covergeti. Si cosiderio allora tutte le possibili sottosuccessioi estraibili da {g } e covergeti e sia I l isieme formato da tutti i limiti di tali sottosuccessioi. Allora è possibile dimostrare che lim sup g = max I. Se poi la successioe {g } è covergete, ovviamete si ha lim sup g = lim g. Ad esempio, per la successioe {g } data da { 1 + e pari g = 3 + e dispari si ha lim sup g = 3. Ivece per la successioe {g } data da { 1 + e pari g = 3 + e dispari si ha Ifie per la successioe {g } data da lim sup g =. g = 1 + e si ha lim sup g = lim g = 1. Ciò premesso si ha il seguete Teorema (di Cauchy-Hadamard) Data la serie (1), sia ρ il suo raggio di covergeza. Allora 1 = lim sup a. (4) ρ 3
4 Ad esempio per la serie (2) si ha subito ρ = 1. Per la serie dove a = a s (5) =0 { e e pari dispari si ha facilmete ρ = 1/e. Il raggio di covergeza può essere, talvolta, determiato i forma più agevole, mediate la seguete Proposizioe 1. Sia ρ il raggio di covergeza di (1). Se il limite a +1 lim a (6) esiste fiito, allora Ad esempio per la serie 1 ρ = lim a +1 a. (7) si ha 1 + s + s s s 2 + (8) lim a +1 a = lim 2 ( + 1) 2 = 1 e quidi ρ = 1. La Proposizioe 1 ivece o è applicabile alla serie (5) i quato { a +1 e 2+1 se è pari = a e 2 1 se è dispari e quidi il limite (6) o esiste. Per quato cocere poi il comportameto della serie (1) sulla circofereza di covergeza, possoo presetarsi varie possibilità. La serie data può 4
5 o covergere i essu puto s tale che s = ρ: è questo, ad esempio, il caso della serie (2) per la quale si ha, come si è visto, ρ = 1 e s = 1 (2) o coverge. Ifatti sulla circofereza di covergeza si ha lim s = 1, metre la covergeza di (2) implicherebbe lim s = 0. Altre serie, ivece, covergoo sull itera circofereza di covergeza, come, ad esempio, la serie (8) per la quale si ha, come si è visto, ρ = 1, ed ioltre s = 1 (8) coverge. Altre serie ifie covergoo i alcui puti della circofereza di covergeza e o i altri, come, ad esempio, la serie s s2 2 + s3 s ( 1) (9) per la quale da (7) si ha subito ρ = 1 ed ioltre s = 1 (9) coverge s = 1 (9) o coverge. Come si è visto, la serie (1) coverge assolutamete all itero del cerchio di covergeza. Ricordiamo ioltre che (1) è uiformemete covergete i ogi isieme chiuso coteuto propriamete el cerchio di covergeza. Più i geerale è possibile dimostrare (Teorema di Abel) che se (1) coverge i u puto P apparteete alla circofereza di covergeza, allora (1) coverge uiformemete i ogi settore circolare chiuso Ω di vertice P e coteuto el cerchio di covergeza (vedi Figura 1). 5
6 Ω P Figura 1. Il cerchio di covergeza e il settore circolare Ω Ricordiamo ifie che ogi serie di poteze è derivabile termie a termie all itero del cerchio di covergeza, ossia la serie (1) e la serie a s 1 =1 hao lo stesso raggio di covergeza e ( ) d a s = ds =0 a s 1. =1 1.2 Defiizioe di Trasformata Zeta Poiamo le segueti defiizioi: DEF. Sia {f } ua successioe di umeri, reali o complessi; si chiama raggio di covergeza di {f }, e si idica co R f, il limite superiore 2 lim sup f = R f. (10) 2 Come al solito, co il simbolo f si itede il valore assoluto oppure il modulo a secoda che f sia u umero reale o complesso. 6
7 Come richiamato el precedete paragrafo, R f è fiito se e solo se la successioe { f } è limitata. DEF. Sia {f } ua successioe di umeri reali o complessi aveti raggio di covergeza R f fiito. Si chiama trasformata Zeta di {f } la fuzioe complessa F data da F (z) = f z (11) =0 dove z è u umero complesso tale che z > R f. La defiizioe ora data è be posta, el seso che la serie (11) è covergete i ua opportua regioe del piao complesso. Ifatti vale la seguete Proposizioe 2. Sia {f } ua successioe di umeri reali o complessi avete raggio di covergeza R f fiito. Allora la serie (11) coverge per ogi umero complesso z estero alla circofereza di cetro l origie e raggio R f. Effettuado ifatti i (11) il cambiameto di variabile s = 1/z si ottiee la serie di poteze f s (12) =0 la quale, per i risultati richiamati el precedete paragrafo, coverge per ogi umero complesso s itero alla circofereza di covergeza. Quest ultima ha raggio ρ dato da ρ = 1/R f e pertato (12) coverge per ogi umero complesso s tale che s < 1 R f. Teedo coto che z = 1/s segue che (11) coverge se z > R f. La trasformata Zeta è quidi ua fuzioe (complessa di variabile complessa) defiita i ogi puto estero ad ua opportua circofereza il cui raggio è dato da (10) (vedi Figura 2). 7
8 Im z R f Re z Figura 2. Il piao z e il domiio della trasformata Zeta Essa pertato è defiita i u itoro di ifiito. Scrivedo (11) per esteso si ottiee: 1 F (z) = f 0 + f 1 z + f 1 2 z + + f 1 2 z + (13) e tale serie coverge se z > R f, R f <. Allora la trasformata Zeta o è altro che uo sviluppo i serie di Lauret all ifiito, sviluppo privo di parte pricipale i quato i (13) o compaioo poteze di z ad espoete positivo 3. Da ciò discede subito ua prima proprietà per la trasformata Zeta. Vale ifatti la seguete Proposizioe 3. Sia {f } ua successioe avete raggio di covergeza R f fiito. Allora la sua trasformata Zeta è aalitica per ogi z C, tale che z > R f. Il raggio di covergeza è il miimo tra i raggi delle circofereze tali che la trasformata Zeta è aalitica al suo estero. Vale ifatti: 3 Per tale motivo sarebbe stato più appropriato utilizzare per F il termie Trasformata di Lauret. Si è affermato ivece, i particolare i molti testi tecici, il termie, ache qui usato, Trasformata Zeta. Esso trae la sua origie dal ome impiegato per idicare la variabile da cui dipede F. Tale scelta è suggerita poi dall opportuità di distiguere tale trasformata dalla trasformata di Laplace per la quale viee usata, i particolare elle applicazioi di atura elettroica, la lettera s. 8
9 Teorema (Abel) Sia F (z) la trasformata Zeta di {f }, e sia R f > 0 il suo raggio di covergeza. Allora F ha almeo ua sigolarità sulla circofereza z = R. Il teorema di Abel permette quidi di determiare agevolmete il raggio di covergeza di ua successioe {f } che sia z-trasformabile, ota la sua trasformata F (z). È ifatti sufficiete determiare le sigolarità di F : il raggio di covergeza è il massimo tra i moduli delle sigolarità di F. Per quato riguarda poi l esisteza della trasformata, le successioi z- trasformabili soo quelle per le quali il raggio di covergeza è fiito, ossia quelle la cui crescita è, al massimo, di tipo espoeziale. Vale ifatti la seguete Proposizioe 4. Sia {f } ua successioe di umeri reali o complessi. Tale successioe è z-trasformabile se e solo se esiste ua costate positiva M tale che f M, = 0, 1, 2,... (14) Ioltre la trasformata Zeta è defiita per ogi umero complesso z tale che z > R f dove R f è dato da (10) oppure da f +1 R f = lim f se quest ultimo limite esiste. Ad esempio la successioe {f } data da è z-trasformabile i quato Ioltre, poiché lim f +1 f f = 1! f 1. = lim = 0 tale trasformata è defiita sull itero piao complesso, eccetto l origie. Ivece la successioe {g } data da g = 9
10 o ammette trasformata Zeta, i quato lim sup g = lim =. Come si è visto, il raggio di covergeza è legato alla crescita della successioe {f }. Ad esempio le successioi {a }, {b }, {c }, {d } date, rispettivamete, da soo tutte z-trasformabili, e si ha a = e = 0, 1, 2,... b = = 0, 1, 2,... c = 2 = 0, 1, 2,... d = 4 = 0, 1, 2,... R a = lim sup R b = lim sup R c = lim sup R d = lim sup a = e 1 b = 1 c = 1 d = 4. Vale ifie il seguete Teorema di caratterizzazioe. Teorema 1. Sia F ua fuzioe complessa di variabile complessa. Allora le segueti quattro affermazioi soo equivaleti: 1. F è ua trasformata Zeta; 2. z = è u puto di regolarità o ua sigolarità elimiabile per F ; 3. F è sviluppabile i serie di Lauret all ifiito e lo sviluppo è privo di parte pricipale; 4. F è aalitica per z grade e lim z F (z) existe fiito. Esercizio. Quale delle segueti fuzioi è ua trasformata Zeta? F 1 (z) = si z; F 2 (z) = si(1/z); F 3 (z) = 1/ si z; G 1 (z) = z2 + 1 z ; G 2(z) = z4 + 1 z Risposta: lo soo F 2 e G 1, o lo soo le altre [F 1 ha ua sig. esseziale all ifiito, F 3 ha i s = ua sig. o isolata e G 2 u polo semplice]. 10
11 1.3 Atitrasformata Zeta I questo paragrafo esamieremo il problema dell atitrasformata Zeta, per quato cocere sia l esisteza che il calcolo. Il problema dell uicità è immediatamete risolto. Se ifatti F è ua trasformata Zeta, allora F è sviluppabile i serie di Lauret all ifiito. Poiché lo sviluppo i serie di Lauret è uico, ecessariamete o può esistere più di ua successioe {f } tale che F (z) = Z{f }. Per quato cocere l esisteza, il Teorema visto el precedete paragrafo forisce codizioi ecessarie e sufficieti affiché ua data fuzioe F complessa di variabile complessa sia ua trasformata Zeta. Vediamo ora alcui esempi. Esempio 1. Le fuzioi F 1, F 2, date da F 1 (z) = zez z F 2 (z) = z + 16 o soo trasformate Zeta. Ifatti le sigolarità di F 1 soo z = ±4j e z =. La sigolarità z = è esseziale e quidi la codizioe 2. del Teorema 1 o è verificata. Per quato cocere la fuzioe F 2, essa è defiita i tutto il piao complesso e si ha lim z F 2(z) = 0. Tale fuzioe tuttavia o è aalitica i essu puto del piao complesso 4 e quidi o è sviluppabile i serie di Lauret, é al fiito, é all ifiito. Esempio 2. La fuzioe F data da F (z) = ze1/z z Idicado ifatti co u e v la parte reale e immagiaria di F 2, si ha (z = x + jy) u(x, y) = 1, v(x, y) = 0 x2 + y ed è immediato cotrollare che le formule di Cauchy-Riema o soo soddisfatte. 11
12 è ua trasformata Zeta. Ifatti le sigolarità di F soo collocate ei puti z = 0, z = ±2j. Pertato F è aalitica per z > 2. Ioltre lim F (z) = 0 z e quidi, per il Teorema 1, F è ua trasformata Zeta, e R f = 2. Esempio 3. La fuzioe F 1 data da F 1 (z) = z2 + 6 z è ua trasformata Zeta, metre o lo è la fuzioe F 2 data da F 2 (z) = z3 + 6 z Etrambe queste fuzioi hao due sigolarità al fiito, ei puti z = ±3j. Etrambe pertato soo aalitiche per z > 3. Soo quidi etrambe sviluppabili i serie di Lauret all ifiito. Tuttavia metre lo sviluppo di F 1 è privo di parte pricipale, i quato lim F 1(z) = 1, z lo sviluppo di F 2 ha ua parte pricipale o ulla poiché lim F 2(z) =. z Alla stessa coclusioe si perviee osservado che z = è, per F 1, u puto di regolarità e per F 2 u polo (semplice). Osservazioe Se F (z) è ua fuzioe razioale, ovvero F (z) = N(z)/D(z), N, D poliomi, allora vale la semplice caratterizzazioe: F è ua trasformata Zeta SSE gr(n) gr(d). 12
13 1.4 Calcolo dell Atitrasformata Ricordiamo prelimiarmete che lo sviluppo i serie di Lauret all ifiito di ua geerica fuzioe complessa di variabile complessa g assume la forma dove s è sufficietemete grade e g(s) = + c s + c +1 s + + c 1 1 s + c 0 + c 1 s + + c s + (15) c = 1 2πj Γ g(s) ds (16) s+1 co Γ curva chiusa, semplice, regolare, percorsa i seso positivo (atiorario), coteete al proprio itero tutte le sigolarità di g. Ciò premesso, sia F ua trasformata Zeta. Allora esiste ua successioe {f } tale che per z grade 1 F (z) = f 0 + f 1 z + f 1 2 z +. (17) 2 Cofrotado le formule (15) e (17) si ha allora f = c, = 0, 1, 2,... Pertato, teedo coto di (16), si ha f = 1 F (z) 1 dz = 2πj z +1 2πj Γ Γ F (z)z 1 dz. Tale espressioe cosete di determiare, ota la trasformata F, la successioe {f }. Essa prede ome di formula dell atitrasformata Zeta e scriveremo Z 1 {F (z)} = f = 1 F (z)z 1 dz (18) 2πj dove, ricordiamolo, Γ rappreseta ua curva chiusa, semplice, regolare, percorsa i seso positivo (atiorario) e coteete, al proprio itero, tutte le sigolarità di F. Pertato il calcolo dell atitrasformata è ricodotto al calcolo, per ogi 0, dell itegrale che figura a secodo membro di (18). Normalmete tale 13 Γ
14 itegrale sarà calcolato utilizzado la teoria dei Residui abbiado, i talui casi, quest ultima co la proprietà della covoluzioe discreta, che vedremo i seguito. Completiamo questo paragrafo illustrado altre teciche che cosetoo, co u procedimeto di ricorreza, la determiazioe della successioe {f }. Da (17) si ha subito Teorema (del valore iiziale). Sia {f } ua successioe z-trasformabile. Allora, posto Z{f } = F (z), si ha Ioltre, sempre da (17) si ha e quidi f 0 = lim z F (z) 1 [F (z) f 0 ]z = f 1 + f 2 z + f 1 3 z + 2 f 1 = lim z [F (z) f 0 ]z. Procededo i maiera simile si ha poi f 2 = lim z [F (z) f 0 f 1 1 z ]z2 e così via. Tale procedimeto cosete quidi di determiare, uo dopo l altro, tutti i valori del campioameto {f }. U altra possibilità, per quato riguarda il calcolo dell atitrasformata, è poi la seguete. Effettuiamo i (17) il cambio di variabile z = 1/u: si ottiee allora per u piccolo ( ) 1 F = f 0 + f 1 u + f 2 u 2 +. u Essedo quest ultima ua serie di Taylor di cetro u = 0 si ha allora f = 1 d! du G(u) dove G(u) = F (1/u). u=0 14
15 Esempio 4. Calcolare l atitrasformata Zeta della fuzioe F data da F (z) = 1 z 2 4. La fuzioe F è ua trasformata Zeta i quato è aalitica per z > 2 e lim z F (z) = 0. Dalla formula (18) si ha allora f = 1 2πj C z 1 dz (19) z 2 4 dove C è ua circofereza, percorsa i seso positivo, di cetro l origie e raggio R > 2. Le sigolarità della fuzioe itegrada soo z = ±2 ed ioltre z = 0 quado = 0. D altra parte il coefficiete f 0 può essere calcolato tramite il teorema del valore iiziale, otteedo f 0 = 0. Per 1, applicado i (19) il Teorema dei Residui, si ha [ ] [ ] z 1 z 1 f = Res z 2 4, 2 + Res z 2 4, 2. Essedo z = ±2 poli semplici, si ha allora f = z 1 2z + z 1 z=2 2z = 2 3 ( 2) 3 = 2 3 (1 + ( 1) ). z= 2 I coclusioe: 0 = 0 f = 2 2 = 2k, k N 0 = 2k + 1, k N. Esempio 5. Calcolare l atitrasformata Zeta della fuzioe F data da F (z) = z z Per il Teorema 1, F è ua trasformata Zeta. Applicado la formula (18) si ha f = 1 z 2πj z dz C 15
16 dove C è ua circofereza, percorsa i seso positivo, di cetro l origie e raggio R > 2. Le sigolarità della fuzioe itegrada soo z = ±2j e soo due poli semplici. Applicado allora il Teorema dei Residui si ha f = z 2z + z z=2j 2z = (2j) 1 z= 2j 2 Poiché j = e jπ/2, co facili calcoli si ottiee [ π ] f = 2 1 cos 2 ( 1) = + ( 2j) 1. 2 { ( 1) k 2 2k = 2k + 1, k N {0} 0 = 2k, k N {0}. Osservazioe. Sia F (z) ua trasformata Zeta. Se z = è ua zero di ordie N 1 per F, allora detta {f } l atitrasformata Zeta di F, risulta: f 0 = f 1 =... = f N 1 = 0, f N 0. Ifatti: F (z) = f N /z N + f N+1 /z N , co f N Prime proprietà I questo paragrafo presetiamo alcue proprietà della trasformata Zeta. Le dimostrazioi di queste proprietà soo alla fie del paragrafo. Proposizioe 5 (Liearità). Siao {f }, {g } due successioi z-trasformabili e siao c 1, c 2 due costati complesse. Allora la successioe {h } data da h = c 1 f + c 2 g, = 0, 1, 2,... è z-trasformabile e Z{h } = c 1 Z{f } + c 2 Z{g }. (20) Si osservi che l ipotesi le successioi {f }, {g } soo z-trasformabili o può, i geerale, essere sostituita da la successioe {h } è z-trasformabile. Ad esempio sia c 1 = c 2 = 1 e { f 0 = g 0 = 0 f = g =, = 1, 2, 3,... Allora h = f + g = 0; quidi {h } è z-trasformabile. Tuttavia le successioi {f } e {g } o ammettoo trasformata Zeta e quidi (20) o vale. 16
17 Proposizioe 6 (Proprietà dello smorzameto). Sia {f } ua successioe z-trasformabile e sia F (z) = Z{f }. Fissato u umero ω, reale o complesso, la successioe {g } data da è z-trasformabile e si ha g = f e ω R g = R f e Re ω (21) Z{g } = F (e ω z) (22) Proposizioe 7 (Proprietà della moltiplicazioe per ). Sia {f } ua successioe z-trasformabile e sia F (z) = Z{f }. Allora la successioe {g } data da g = f è z-trasformabile e si ha R g = R f (23) Z{g } = z d F (z). (24) dz Dimostrazioe Proposizioe 5. Essedo {f } e {g } due successioi z-trasformabili, esistoo due costati positive M f e M g, tali che f M f, g M g, = 0, 1, 2,... Posto M = max(m f, M g ) si ha allora e quidi {h } è z-trasformabile. geerale delle serie 5. h ( c 1 + c 2 )M L idetità (20) segue da ua proprietà Dimostrazioe Proposizioe 6. Per la Proposizioe 4, esiste ua costate positiva M tale che f M ; 5 Ricordiamo che se le due serie umeriche a, =0 =0 b 17
18 allora g = f e Re ω ( Me Re ω) e quidi, {g } è z-trasformabile. Ioltre da (25) si ha (25) g = e Re ω f e quidi (21) è verificata. Poedo si ha poi Z{g } = = s = e ω z f e ω z = =0 ( f e ω z ) =0 f s = F (s) =0 e quidi ache (22) è verificata. Dimostrazioe Proposizioe 7. Avedosi lim sup g = lim sup ( ) f = lim sup f e segue che {g } è z-trasformabile e che (23) è verificata. Essedo poi la trasformata Zeta ua serie di poteze, è lecito derivare termie a termie; si ha pertato d dz F (z) = f z 1 da cui, moltiplicado ambo i membri per z, si ottiee subito (23). =1 soo assolutamete covergeti, allora lo è ache la serie e si ha (a + b ) =0 ( ) ( ) (a + b ) = a + b. =0 =0 =0 18
19 2 Campioameti Elemetari Utilizzado la defiizioe e le proprietà viste el Paragrafo precedete calcoliamo la trasformata Zeta di alcue successioi otteute campioado fuzioi elemetari. 2.1 Campioameto costate Sia Allora R f = 1 e per z > 1 si ha f = 1, = 0, 1, 2,... F (z) = Z{1} = =0 z }{{} ( ) = z = z z 1 i quato ( ) è ua serie geometrica di ragioe 1/z. 2.2 Campioameto lieare Sia f =, = 0, 1, 2,... Allora f = 1 e utilizzado la proprietà della moltiplicazioe per (Proposizioe 7), si ottiee per z > 1 Z{} = z d dz z z 1 = 2.3 Campioameto poliomiale Sia z (z 1) 2. f = 2, = 0, 1, 2,... Procededo come el caso precedete, si ottiee per z > 1 Z{ 2 } = z d dz z (z 1) = z2 + z 2 (z 1). 3 19
20 Aalogamete si ha per z > 1 e così via. Z{ 3 } = z d dz z 2 + z (z 1) = z3 + 4z 2 + z 3 (z 1) Campioameto espoeziale Sia f = e T, = 0, 1, 2,... dove T è u fissato umero reale o complesso. Allora f = e T = e Re T. Pertato R f = e Re T. Per z > e Re T, dalla proprietà dello smorzameto (Proposizioe 6) si ottiee Z{e T } = Z{e T 1} = e T z e T z 1 = 2.5 Campioameti trigoometrici Sia f = si(ω), = 0, 1, 2,... z z e T. dove ω è u umero reale fissato. Utilizzado le formule di Eulero e la proprietà dello smorzameto, si ottiee facilmete per z > 1 Similmete si ha Z{si(ω)} = Z{cos(ω)} = z si ω z 2 2z cos ω + 1. z(z cos ω) z 2 2z cos ω + 1. Esempio 6. Calcolare la trasformata Zeta della successioe {f } data da f = e 3 si, = 0, 1, 2,... 20
21 Poiché per z > 1 z si 1 Z{si } = z 2 2z cos per la proprietà dello smorzameto, la successioe {e 3 si } ha raggio di covergeza e 3 e si ha Z{e 3 si } = e 3 z si 1 e 6 z 2 2e 3 z cos Dal Teorema della moltiplicazioe per si ha ifie Z{f } = z d dz e 3 z si 1 e 6 z 2 2e 3 z cos La Proprietà della Traslazioe Poiamo la seguete Def. Sia p u itero positivo fissato. Data la successioe {f } =: f 0, f 1, f 2,..., f,... si chiama successioe traslata i avati di p-passi, o semplicemete successioe traslata, la successioe 0, 0,..., 0, f }{{} 0, f 1, f 2,... p volte I altre parole la successioe traslata i avati di p-passi è la successioe otteuta da {f } iseredo ei primi p posti il valore zero. Tale successioe sarà idicata co il simbolo {f p }. Così, ad esempio, f 3 =: 0, 0, 0, f 0, f 1,... Il motivo del ome è evidete. Se {f } rappreseta ifatti il campioameto di ua fuzioe f, ulla per t < 0, egli istati t = T, allora {f p } è il campioameto della fuzioe traslata f(t pt ) egli stessi istati. Si ha pertato { 0 se < p f p = (26) f p se p. Ciò posto, vale la seguete 21
22 Proposizioe 8 (Proprietà della traslazioe). Sia {f } ua successioe z-trasformabile. Allora ache la successioe traslata {f p } è z-trasformabile, ha lo stesso raggio di covergeza ed ioltre Z{f p } = z p Z{f }. Ifatti, dalla defiizioe di limite superiore, segue subito che {f } e {f p } hao stesso raggio di covergeza. Ioltre, teedo coto di (26), si ha Z{f p } = f p z = =p f i z i p = z p i=0 i=0 f i z i. Esempio 7. Calcolare la trasformata Zeta della successioe {f } data da { e 4 4 f = 0 = 0, 1, 2, 3. Si ha evidetemete dove {g } è la successioe data da f = g 4, = 0, 1, 2,... g = e 16+4, = 0, 1, 2,... Pertato e quidi Z{g } = Z{f } = e16 z z e 4 e 16 z 3 (z e 4 ). 2.7 La Covoluzioe Discreta Poiamo la seguete Def. Siao {f } e {g } due successioi. Si chiama covoluzioe discreta tra le due successioi {f } e {g }, la successioe {h } data da h = f k g k, = 0, 1, 2,... (27) 22
23 La covoluzioe discreta sarà idicata co il simbolo {f g }. Il motivo del ome è, ache i questo caso, evidete. Siao ifatti f, g due fuzioi ulle per t < 0 e sufficietemete regolari; siao poi {f } e {g } i campioameti di tali fuzioi egli istati t = T. Ricordiamo che il prodotto di covoluzioe f g è la fuzioe data da (f g)(t) = t 0 f(τ)g(t τ) dτ. (28) Poiché la sommatoria i (27) è la forma discretizzata dell itegrale che compare i (28), è aturale idicare (27) co l espressioe covoluzioe discreta. Valgoo le proprietà: {f g } = {g f } {f (g 1 + g 2 )} = {f g 1 + f g 2 }. Il seguete risultato illustra ua importate proprietà della covoluzioe discreta. Teorema Siao {f }, {g } due successioi z-trasformabili. Allora ache la covoluzioe discreta {h } = {f g } è z-trasformabile e il suo raggio di covergeza R h verifica la disuguagliaza R h max(r f, R g ) (29) dove R f e R g idicao, rispettivamete, i raggi di covergeza di {f } e {g }. Ioltre si ha Z{h } = Z{f }Z{g }. (30) Esempio 8. Calcolare la trasformata Zeta della successioe {h } data da Evidetemete si ha dove { Allora h = f = g = 1 h = f g Z{h } = Z{}Z{1} = 23 = 0, 1, 2,... z 2 (z 1) 3.
24 Osserviamo che la disuguagliaza (29) può valere ache i seso stretto. Ad esempio svolgere il seguete esercizio. Esercizio. Si cosiderio le due successioi {f }, {g } date rispettivamete da { 1 se = 0 f = 1 e se 1 { 1 se = 0 g = e 1 (e 1) se 1. Dopo avere determiato il raggio di covergeza delle rispettive trasformate Zeta, si scriva esplicitamete la loro covoluzioe discreta h = f g e si provi che, i questo caso, vale R h < max(r f, R g ). Il Teorema della covoluzioe discreta ha alcue semplici ma importati cosegueze. Corollario 1. Se F (z) è la trasformata Zeta di {f }, allora { } Z f k = z z 1 F (z). Corollario 2. Se F (z), G(z) soo le trasformate Zeta di {f } e {g }, rispettivamete, allora l atitrasformata Zeta di F (z)h (z) è la covoluzioe discreta {f g }. Ua applicazioe importate del Corollario 2 è il calcolo dell atitrasformata Zeta el caso o razioale. Esempio 9. Calcolare l atitrasformata Zeta della fuzioe H data da H(z) = 1 z 2 4 e1/z. La fuzioe H è ua trasformata Zeta i quato è aalitica per z > 2 e lim z H(z) = 0. Da (17) si ha allora h 0 = lim z H(z) = 0. 24
25 Per quato riguarda i restati coefficieti h si ha, da (18), h = 1 z 2πj CR 1 z 2 4 e1/z dz (31) dove C R è ua circofereza di cetro l origie, percorsa i seso positivo e di raggio R > 2. Applicado il Teorema dei Residui a (31) si ottiee ( 1) [ ] [ ] z 1 z 1 h = Res z 2 4 e1/z, 0 +Res z }{{} 2 4 e1/z, 2 ( ) [ ] z 1 + Res z 2 4 e1/z, 2. Il calcolo del primo residuo ( ) preseta otevoli difficoltà i quato z = 0 è ua sigolarità esseziale. Il calcolo dell atitrasformata di H può essere affrotato i altro modo osservado che H è il prodotto di due fuzioi F e G, date rispettivamete da F (z) = 1 z 2 4 G(z) = e 1/z. Per il Teorema 1 sia F che G soo, a loro volta, due trasformate Zeta. Posto allora Z 1 {F (z)} = f, Z 1 {G(z)} = g, avedosi H(z) = F (z)g(z) dalla proprietà della covoluzioe discreta si ha h = f g = f k g k. Il problema è pertato ricodotto al calcolo delle atitrasformate di F e di G. L atitrasformata della fuzioe razioale F è stata calcolata ell Esempio 4. Per quato riguarda poi G, è sufficiete ricordare la defiizioe di espoeziale i campo complesso e 1/z = z ! z (z 0). 2! z 25
26 Pertato g = 1!. Esempio 10. Calcolare l atitrasformata Zeta della fuzioe H data da H(z) = z si 1 3z z La fuzioe H è ua trasformata Zeta i quato è aalitica per z > 2 e lim z H(z) = 0. Essedo H o razioale, procediamo come ell esempio precedete. La fuzioe H è ifatti il prodotto delle due fuzioi F e G date da F (z) = z z G(z) = si 1 3z, la prima delle quali è razioale. Etrambe tali fuzioi soo, per il Teorema 1, trasformate Zeta. L atitrasformata {f } della fuzioe F è stata calcolata ell Esempio 5. Per quato riguarda G si ha (z 0) Pertato, posto si ha si 1 3z = z ! 3 3 z ! 3 5 z +. 5 g = Z 1 {G(z)} g = 0 se è pari g 2+1 = ( 1) 1 1 (2 + 1)! L atitrasformata cercata {h } si ottiee allora effettuado la covoluzioe discreta tra le due successioi {f } e {g }. 2.8 Il Teorema del Valore Fiale Aalogamete al Teorema del Valore Iiziale, già visto, che dà ua relazioe tra il comportameto della trasformata Zeta all ifiito e il termie iiziale 26
27 f 0 del campioameto, i alcui casi sussiste ache ua relazioe tra il comportameto all ifiito del campioameto e il valore della trasformata i u puto. Vale ifatti il seguete risultato. Teorema (del valore fiale). Sia {f } ua successioe covergete e- spoezialmete 6. Allora {f } ammette trasformata Zeta e, posto Z{f } = F (z), si ha lim f = lim(z 1)F (z) (32) z 1 dove il limite a secodo membro è iteso el seso che il umero complesso z tede a 1 restado all estero del cerchio di cetro l origie e raggio uitario. Si osservi che la successioe {f } ammette trasformata Zeta i quato, essedo covergete, è limitata e duque R f 1. Pertato il domiio della trasformata o cotiee al proprio itero il puto z = 1 (el caso i cui R f < 1) o ha il puto z = 1 come puto di accumulazioe. I etrambi i casi quidi è lecito calcolare il limite a secodo membro di (32). I particolare, se lim f = l 0, allora (32) diviee lim(z 1)F (z) = l 0. z 1 Teedo coto allora della defiizioe di Residuo, e segue che F ha ecessariamete u polo semplice i z = 1. Notare Bee. Il Teorema del valore fiale richiede, implicitamete, che il raggio di covergeza R f di {f } sia miore o uguale ad 1. Pertato se R f > 1, allora tale Teorema o può essere applicato. Questo è il caso, ad esempio, della fuzioe F (z) = 2(z + 3) 2z 2 13z + 6. Tale fuzioe è ua trasformata Zeta. Essedo z = 1/2 e z = 6 due poli semplici, F è aalitica per z > 6. Allora R f = 6 e il Teorema del valore fiale o può essere applicato. 6 Ricordiamo che ua successioe {f } coverge espoezialmete a l se {f } coverge ad l ed ioltre esistoo due costati positive k, γ tali che per ogi sufficietemete grade si abbia f l ke γ 27
28 2.9 Applicazioi della Trasformata Zeta - Equazioi alle differeze - Teorema del campioameto Il recete sviluppo della tecologia el settore degli elaboratori digitali ha favorito l impiego di modelli discreti ello studio di umerosi problemi fisici, ossia di modelli ei quali le gradezze coivolte soo ote o per ogi valore delle variabili, ma soltato per u isieme discreto di tali valori 7. Spesso tali modelli hao, come legge di equilibrio, equazioi, o sistemi di equazioi, alle differeze. Oltre ai metodi classici impiegati per la loro risoluzioe (metodo matriciale, metodo di ricorreza, ecc.), i molti casi u approccio particolarmete efficace è dato dal metodo della trasformata Zeta. Il vataggio di tale algoritmo cosiste el fatto che esso ricoduce la risolubilità delle equazioi cosiderate a quella di opportue equazioi algebriche. I questo seso quidi svolge ua fuzioe molto simile a quella svolta dalla trasformata di Laplace el caso di sistemi tempo-cotiui, ossia di sistemi modellati da equazioi o sistemi di equazioi differeziali. Si cosideri, ad esempio, la rete RL i Figura 3 e siao rispettivamete R, L i valori della resisteza e dell iduttaza. Sia poi v la f.e.m. applicata e i la correte che percorre il circuito. La legge di equilibrio del circuito aalogico è data dall equazioe differeziale lieare L d i(t) + Ri = v(t). (33) dt L + v i R Figura 3. Circuito RL-serie 7 Nell ambito dell elettroica le gradezze defiite per ogi valore della variabile temporale t soo chiamate aalogiche: le gradezze defiite ivece solo per valori discreti di t soo dette digitali. 28
29 Sia T u itervallo di tempo sufficietemete piccolo; approssimado la derivata di/dt ell istate t = T co il rapporto icremetale all idietro ( ) di i( T ) i( T T ), dt T da (33) si ottiee ossia i(t ) T L i(t ) i(t 1 ) T L L + R T i(t 1) + Ri(t ) v(t ) Posto i = i(t ), v = v(t ), (34) assume la forma i L L + R T i 1 T L + R T v(t ). (34) T L + R T v che è u equazioe alle differeze del primo ordie. Assegata la sequeza di igresso {v }, è possibile risolvere tale equazioe (i.e. determiare la sequeza di uscita {i }) utilizzado varie teciche, tra cui il metodo della trasformata Zeta. Osservado che l equazioe (34) è del tipo: i Ai 1 = Bv, co A, B costati ote e {v } successioe assegata, possiamo applicare la trasformata Zeta ad etrambi i membri, assumedo che {i } e {v } siao z-trasformabili. Posto I(z) = Z{i } e V (z) = Z{v } risulta da cui I(z) A I(z) = BV (z), z I(z) = BzV (z) z A, e atitrasformado si determia la sequeza i uscita {i }. La trasformata Zeta trova u largo impiego o solo ella simulazioe di reti elettriche tramite modelli digitali, ma ache i umerosi altri problemi. Fra essi, di particolare importaza soo quelli coessi co la trasmissioe e 29
30 l elaborazioe di segali digitali. Ricordiamo i proposito che, data ua fuzioe φ (reale o complessa) di variabile reale, si chiama fuzioe campioata o campioameto (di φ), la successioe {φ } = {φ(t )} otteuta campioado la fuzioe φ i ua successioe di istati equispaziati t = T. L ampiezza di tali itervalli prede il ome di itervallo di campioameto. Le fuzioi campioate soo ampiamete utilizzate elle telecomuicazioi per i vataggi che il loro utilizzo comporta e, i questo ambito, la trasformata Zeta si rivela u valido strumeto matematico. Ua proprietà di fodametale importaza delle fuzioi campioate è descritta dal seguete teorema. Teorema (del campioameto). Sia f ua fuzioe trasformabile secodo Fourier e sia F la sua trasformata. Siao ioltre f e F sviluppabili i serie di Fourier i [ L, L], per ogi L > 0. Suppoiamo ifie che F sia a supporto compatto, ossia che esista ua costate B > 0 tale che F (ω) = 0 se ω > 2πB. Sotto queste ipotesi, vale la seguete formula [ π ] f(t) = T + si f(t ) T (t T ) π t T = (35) dove T = 1/(2B). L importaza di tale risultato è evidete. Ifatti da (35) e segue che la fuzioe f è ota o appea siao oti i valori f(t ) che tale fuzioe assume egli istati T. I altre parole, è possibile stabilire ua corrispodeza biuivoca tra le fuzioi verificati le ipotesi del Teorema e u loro campioameto, effettuato i istati di tempo equispaziati. Nell ambito delle telecomuicazioi, tale corrispodeza biuivoca è di otevole importaza, i quato cosete la trasmissioe di segali i forma campioata, seza perdita di iformazioi e la formula (35) permette di ricostruire il segale da u suo campioameto. A ciò si aggiuga il fatto che la trasmissioe di 30
31 segali i forma campioata è molto più agevole di quella di segali aalogici. Nel Teorema precedete l ipotesi cruciale è la seguete F (ω) = 0 per ω 2πB. I altre parole la corrispodeza biuivoca tra segali e loro campioameti ecessita della codizioe che f deve avere spettro ullo al di fuori della bada di pulsazioi [ 2πB, 2πB]. La trasformata Zeta viee utilizzata ache i altre applicazioi, di atura igegeristica e o. Esempi i tal seso si trovao ello studio di processi di cotrollo, ell impiego di filtri digitali, ella teoria delle atee, ell aalisi di reti a scala, i svariati problemi di ottimizzazioe, i questioi di ecoomia, ecc. La trasformata Zeta iterviee ioltre ache ella risolubilità di alcue classi di equazioi differeziali alle differeze, che modellao problemi fisici i cui soo preseti elemeti co memoria. Per tutte queste applicazioi, riviamo ai corsi relativi Esempi ed esercizi Esempio 11. Calcolare la trasformata Zeta della successioe {f } data da { e se = 0, 2, 4,... f = (36) 0 se = 1, 3, 5,... Calcoliamo il raggio di covergeza R f. Avedosi { e 1 > 0, pari f = 0 dispari da (10) si ha R f = e 1. Applicado la defiizioe e osservado che tutti i termii di posto dispari soo ulli, si ha Z{f } = = f z = =0 f 2k z 2k 2ke 2k z 2k. 31
32 Poedo w = z 2 si ottiee Z{f } = 2 ke 2k w k. Ci siamo perciò ricodotti al calcolo della trasformata Zeta della successioe {ke 2k }. Avedosi, per w > 1, w Z{k} = (w 1) 2 applicado la proprietà dello smorzameto si ha da cui ifie Z{ke 2k } = we 2, se w > (e 2 e 2 w 1) 2 z 2 e 2 Z{f } = 2 (37) (e 2 z 2 1) 2 co z > e 1, i accordo co il valore di R f otteuto prima. La trasformata Zeta della successioe (36) può essere calcolata ache co altre teciche. Ad esempio cosiderado la successioe ausiliaria {h } data da { 1 pari h = 0 dispari. Itrodotta tale successioe, si ha f = e h, = 0, 1, 2,... e quidi il problema è, i defiitiva, ricodotto al calcolo della trasformata di {h }. Si ha Z{h } = h z = z z + 4 =0 1 z2 = = se z > 1. 1 z 2 z 2 1 Applicado le proprietà dello smorzameto e della moltiplicazioe per (l ordie è idifferete) si ha ifie ( z > e 1 ) da cui la (37). Z{f } = Z{e h } = z d dz 32 (ze) 2 z 2 e 2 1
33 Esempio 12. Calcolare la trasformata Zeta della successioe {f } data da se è pari, 8 f = 0 se è dispari e se = 8. Per quato riguarda il raggio di covergeza, si ha facilmete R f = 1. Per quato riguarda il calcolo di Z{f }, la successioe {f } può essere pesata come somma di due successioi {g } e {h } date rispettivamete da { se è pari g = 0 se è dispari { 8 + e se = 8 h = 0 altrimeti. Ifatti si ha f = g + h, = 0, 1, 2,... Il calcolo della trasformata è quidi ricodotto al calcolo delle due trasformate Z{g }, Z{h }. Dalla defiizioe si ha subito Ioltre Z{g } = Z{h } = 8 + e z 8. g z = =0 2kz 2k = 2 kz 2k. Poedo allora w = z 2 e applicado la proprietà della moltiplicazioe per, si ha Z{g } = 2 k = 2w (w 1) 2. kw k = 2w d dw w w 1 Pertato Z{f } = 2z 2 (z 2 1) e. 2 z 8 33
34 Si osservi che il cambiameto di variabile w = z 2 è suggerito dal successivo impiego della proprietà della moltiplicazioe per. Si faccia attezioe ifatti che 2 kz 2k o è uguale a 2z d dz z 2k. Esempio 13. Calcolare la trasformata Zeta della successioe {f } data da e se = 0, 4, 8, 12,... f = se = 1, 3, 5, 7,... 0 altrimeti. Per quato riguarda il raggio di covergeza, avedosi e se = 4, 8, 12,... f = se = 1, 3, 5,... 0 altrimeti da (10) si ha subito R f = e. Ioltre pertato Z{f } = f z = f 4k z 4k + (2k + 1)z 2k 1 =0 Z{f } = e 4k z 4k + 2z 1 kz 2k + z 1 z 2k. Poedo w = z 4 ella prima sommatoria e v = z 2 ella secoda e ella terza si ha Z{f } = e 4k w k + 2z 1 kv k + z 1 ossia Z{f } = w w e + v 4 2z 1 (v 1) + v 2 z 1 v 1 34 v k
35 da cui Z{f } = z4 z 4 e + z3 + z 4 (z 2 1). 2 Esercizi. Calcolare la trasformata Zeta dei segueti campioameti, determiado ache il raggio di covergeza. f = e γ, γ C : F (z) = ze γ (z e γ ) 2 f = ( 1) e 6 : F (z) = ze6 (ze 6 + 1) 2 f = e 7 si(4) : F (z) = ze7 si 4(z 2 e 14 ) (z 2 2ze 7 cos 4 + e 14 ) 2 f = ( 1) e 2 si(3) { 4 se è pari 8z 2 f = : F (z) = 0 se è dispari (z 2 1) ; { 2 0 se è pari e 3 f = e 3 : F (z) = se è dispari z(1 e 6 z 2 ) ; { 2 se è pari f = 3 se è dispari e 3 se = 0, 5, 10, 15, 20,... 2 se = 1, 6, 11, 16, 21,... f = se = 2, 7, 12, 17, 22,... 0 altrimeti π se = 3k, k N f = se = 3k + 1, k N. 2 se = 3k + 2, k N 35
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
2.5 Convergenza assoluta e non
 .5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
.5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
LA TRASFORMATA Z. Nel caso di segnali (sistemi) tempo-continui: La trasformata di Laplace generalizza quella di Fourier
 LA TRASFORMATA Z Nel caso di segali (sistemi) tempo-cotiui: La trasformata di Laplace geeralizza quella di Fourier per s= jω ( ω) ( ) + ( ) ( ) st X s = x t e dt + = jωt co ω = 2π f X xte dt Nel caso di
LA TRASFORMATA Z Nel caso di segali (sistemi) tempo-cotiui: La trasformata di Laplace geeralizza quella di Fourier per s= jω ( ω) ( ) + ( ) ( ) st X s = x t e dt + = jωt co ω = 2π f X xte dt Nel caso di
Esponenziale complesso
 Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Siamo interessati a studiare la convergenza della serie e porremo come al solito:
 SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER
 TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
06 LE SUCCESSIONI DI NUMERI REALI
 06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
Metodi Matematici per l Ingegneria
 Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SUCCESSIONI SERIE NUMERICHE pag. 1
 SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
METODI MATEMATICI DELLA FISICA A.A. 2005/2006 Prof. C. Presilla. Prova di recupero 11 settembre 2006
 METODI MATEMATII DELLA FISIA A.A. 2005/2006 Prof.. Presilla Prova di recupero settembre 2006 ogome Nome i sostituzioe delle prove i itiere (segare) 2 pealità esercizio voto 2 3 4 5 6 Esercizio Determiare
METODI MATEMATII DELLA FISIA A.A. 2005/2006 Prof.. Presilla Prova di recupero settembre 2006 ogome Nome i sostituzioe delle prove i itiere (segare) 2 pealità esercizio voto 2 3 4 5 6 Esercizio Determiare
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
Esercitazione n 3. 1 Successioni di funzioni. Esercizio 1: Studiare la convergenza in (0, 1) della successione {f n } dove f n (x) =
 Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Analisi Matematica II
 Corso di Laurea i Matematica Aalisi Matematica II Esercizi sulla covergeza uiforme e sulle serie di fuzioi/poteze Versioe del 28//206 Esercizi tratti dal Giusti Esercizio Giusti 3. e 3.3) Calcolare il
Corso di Laurea i Matematica Aalisi Matematica II Esercizi sulla covergeza uiforme e sulle serie di fuzioi/poteze Versioe del 28//206 Esercizi tratti dal Giusti Esercizio Giusti 3. e 3.3) Calcolare il
Elementi della teoria delle serie numeriche
 Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Def. R si dice raggio di convergenza; nel caso i) R = 0, nel caso ii)
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Analisi e Geometria 1
 Aalisi e Geometria Politecico di Milao Igegeria Preparazioe al primo compito i itiere. Risolvere el campo complesso l equazioe z z = 4z.. Sia f la fuzioe a valori complessi defiita da f(z = per ogi z D,
Aalisi e Geometria Politecico di Milao Igegeria Preparazioe al primo compito i itiere. Risolvere el campo complesso l equazioe z z = 4z.. Sia f la fuzioe a valori complessi defiita da f(z = per ogi z D,
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica I del c.1.
 Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
Analisi Matematica A e B Soluzioni prova scritta n. 4
 Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Insiemi numerici. Sono noti l insieme dei numeri naturali: N = {1, 2, 3, }, l insieme dei numeri interi relativi:
 Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
SERIE DI POTENZE. n=0 a n z n.
 SERIE DI POTENZE 1. Covergeza putuale Data ua successioe di coefficieti (a ) N, a C, e dato u cetro w 0, la relativa serie di poteze è la serie di fuzioi a (z w 0 ) a 0 + a 1 (z w 0 ) + + a (z w 0 ) +.
SERIE DI POTENZE 1. Covergeza putuale Data ua successioe di coefficieti (a ) N, a C, e dato u cetro w 0, la relativa serie di poteze è la serie di fuzioi a (z w 0 ) a 0 + a 1 (z w 0 ) + + a (z w 0 ) +.
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Risoluzione del compito n. 3 (Febbraio 2018/2)
 Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
4 - Le serie. a k = a k. S = k=1
 4 - Le serie E veiamo ad uo degli argometi più ostici (ma ache più iteressati) dell aalisi: le serie. Ricordiamo brevemete cos è ua serie e cosa vuol dire covergeza per ua serie. Defiizioe 1. Data ua successioe
4 - Le serie E veiamo ad uo degli argometi più ostici (ma ache più iteressati) dell aalisi: le serie. Ricordiamo brevemete cos è ua serie e cosa vuol dire covergeza per ua serie. Defiizioe 1. Data ua successioe
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
APPLICAZIONI di MATEMATICA A.A
 APPLICAZIONI di MATEMATICA A.A. 2011-2012 Tracce delle lezioi del 20 e 22 settembre 2011 September 26, 2011 1 Richiami sui umeri complessi 1.1 Forma algebrica. U umero complesso z i forma algebrica è u
APPLICAZIONI di MATEMATICA A.A. 2011-2012 Tracce delle lezioi del 20 e 22 settembre 2011 September 26, 2011 1 Richiami sui umeri complessi 1.1 Forma algebrica. U umero complesso z i forma algebrica è u
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 1
 Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
n 1 = n b) {( 1) n } = c) {n!} In questo caso la successione è definita per ricorrenza: a 0 = 1, a n = n a n 1 per ogni n 1.
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 0: Riferimeti: R.Adams, Calcolo Differeziale - Si cosiglia vivamete di fare gli esercizi del testo. Successioi umeriche:
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 0: Riferimeti: R.Adams, Calcolo Differeziale - Si cosiglia vivamete di fare gli esercizi del testo. Successioi umeriche:
1. Converge. La serie è a segno alterno. Non possiamo usare il criterio di assoluta convergenza, perché
 Soluzioi.. Coverge. La serie è a sego altero. No possiamo usare il criterio di assoluta covergeza, perché log log a = > + e il fatto che la serie i valore assoluto diverge o permette di trarre coclusioi
Soluzioi.. Coverge. La serie è a sego altero. No possiamo usare il criterio di assoluta covergeza, perché log log a = > + e il fatto che la serie i valore assoluto diverge o permette di trarre coclusioi
Equazioni differenziali
 Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
(x log x) n2. (14) n + log n
 Facoltà di Scieze Matematiche Fisiche e Naturali- Aalisi Matematica A (c.l.t. i Fisica) Prova parziale del 8 Novembre 20 Svolgere gli esercizi segueti. Studiare il domiio ed il comportameto della serie
Facoltà di Scieze Matematiche Fisiche e Naturali- Aalisi Matematica A (c.l.t. i Fisica) Prova parziale del 8 Novembre 20 Svolgere gli esercizi segueti. Studiare il domiio ed il comportameto della serie
CAP. V Limiti di funzioni reali
 CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
Lezioni di Matematica 1 - I modulo
 Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
SUCCESSIONI e LIMITI DI SUCCESSIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Successioni cap3b.pdf 1
 SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
Corso Propedeutico di Matematica
 POLINOMI RICHIAMI DI TEORIA Defiizioe: u poliomio ( o fuzioe poliomiale) ella variabile x di grado a coefficieti reali ha la forma A = a0 + a1x + + a 1 x, dove a 0, a 1,..., a soo umeri reali assegati
POLINOMI RICHIAMI DI TEORIA Defiizioe: u poliomio ( o fuzioe poliomiale) ella variabile x di grado a coefficieti reali ha la forma A = a0 + a1x + + a 1 x, dove a 0, a 1,..., a soo umeri reali assegati
0.1 Esercitazioni V, del 18/11/2008
 1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
Università di Trieste Facoltà d Ingegneria. Esercizi sulle serie numeriche e sulle successioni e serie di funzioni Dott.
 e Uiversità di Trieste Facoltà d Igegeria. Esercizi sulle serie umeriche e sulle successioi e serie di fuzioi Dott. Fraco Obersel Esercizio Rispodere alle segueti questioi: a) Siao a 0 + a + a +... b 0
e Uiversità di Trieste Facoltà d Igegeria. Esercizi sulle serie umeriche e sulle successioi e serie di fuzioi Dott. Fraco Obersel Esercizio Rispodere alle segueti questioi: a) Siao a 0 + a + a +... b 0
Calcolo I - Corso di Laurea in Fisica - 31 Gennaio 2018 Soluzioni Scritto
 Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
n=0 a n(z z 0 ) n converge} è chiamato insieme di convergenza della serie; si ha sempre z 0 I e quindi I non è mai vuoto. Nasce quindi una funzione
 Serie di poteze I queste ote esporremo la teoria elemetare delle serie di poteze. No useremo le ozioi di covergeza uiforme e totale, ma dimostreremo ugualmete i modo rigoroso i teoremi di derivazioe ed
Serie di poteze I queste ote esporremo la teoria elemetare delle serie di poteze. No useremo le ozioi di covergeza uiforme e totale, ma dimostreremo ugualmete i modo rigoroso i teoremi di derivazioe ed
Precorso di Matematica, aa , (IV)
 Precorso di Matematica, aa 01-01, (IV) Poteze, Espoeziali e Logaritmi 1. Nel campo R dei umeri reali, il umero 1 e caratterizzato dalla proprieta che 1a = a, per ogi a R; per ogi umero a 0, l equazioe
Precorso di Matematica, aa 01-01, (IV) Poteze, Espoeziali e Logaritmi 1. Nel campo R dei umeri reali, il umero 1 e caratterizzato dalla proprieta che 1a = a, per ogi a R; per ogi umero a 0, l equazioe
Soluzioni. 2 2n+1 3 2n. n=1. 3 2n 9. n=1. Il numero 2 può essere raccolto fuori dal segno di sommatoria: = 2. n=1 = = 8 5.
 60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
SOLUZIONI COMPITO del 04/02/2016 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A
 SOLUZIONI COMPITO del 0/0/06 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A Esercizio Osserviamo, iazitutto, che la serie proposta è ua serie a termii o egativi. Applicado il criterio della radice, dopo
SOLUZIONI COMPITO del 0/0/06 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A Esercizio Osserviamo, iazitutto, che la serie proposta è ua serie a termii o egativi. Applicado il criterio della radice, dopo
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22/11/2013. = a 24 24! log(1 + x) = ( 1) = (24!) 1 24 = 23!. e x2 dx. x 2n
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
( 4) ( ) ( ) ( ) ( ) LE DERIVATE ( ) ( ) (3) D ( x ) = 1 derivata di un monomio con a 0 1. GENERALITÀ
 LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
( 1) k+1 x k + R N+1 (x), k. 1 + x 10 2, 5 R N+1 ( 1 3 ) ) )
 Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
Esercizi sui numeri complessi per il dodicesimo foglio di esercizi
 Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
16 - Serie Numeriche
 Uiversità degli Studi di Palermo Facoltà di Ecoomia CdS Statistica per l Aalisi dei Dati Apputi del corso di Matematica 6 - Serie Numeriche Ao Accademico 03/04 M. Tummiello, V. Lacagia, A. Cosiglio, S.
Uiversità degli Studi di Palermo Facoltà di Ecoomia CdS Statistica per l Aalisi dei Dati Apputi del corso di Matematica 6 - Serie Numeriche Ao Accademico 03/04 M. Tummiello, V. Lacagia, A. Cosiglio, S.
Successioni di funzioni
 Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
PROVA SCRITTA DI ANALISI MATEMATICA 2 Corso di laurea in Matematica 6 Settembre Risoluzione a cura di N. Fusco & G. Floridia
 PROVA SCRIA DI ANALISI MAMAICA Corso di laurea i Matematica 6 Settembre 6 Risoluzioe a cura di N. Fusco & G. Floridia ) Discutere la covergeza putuale e uiforme della serie π arctg )). ) Svolgimeto ):
PROVA SCRIA DI ANALISI MAMAICA Corso di laurea i Matematica 6 Settembre 6 Risoluzioe a cura di N. Fusco & G. Floridia ) Discutere la covergeza putuale e uiforme della serie π arctg )). ) Svolgimeto ):
Proposizione 1. Due sfere di R m hanno intersezione non vuota se e solo se la somma dei loro raggi e maggiore della distanza fra i loro centri.
 Laboratorio di Matematica, A.A. 009-010; I modulo; Lezioi II e III - schema. Limiti e isiemi aperti; SB, Cap. 1 Successioi di vettori; SB, Par. 1.1, pp. 3-6 Itori sferici aperti. Nell aalisi i ua variabile
Laboratorio di Matematica, A.A. 009-010; I modulo; Lezioi II e III - schema. Limiti e isiemi aperti; SB, Cap. 1 Successioi di vettori; SB, Par. 1.1, pp. 3-6 Itori sferici aperti. Nell aalisi i ua variabile
Capitolo 5. Successioni numeriche
 Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Esercitazione n 4. 1 Serie di Taylor. Esercizio 1: Verificare che la funzione. f(x) = 0 se x = 0
 Esercitazioe 4 1 Serie di Taylor Esercizio 1: Verificare che la fuzioe f(x) { e 1/x se x 0 0 se x 0 pur essedo C o è sviluppabile i serie di Taylor i x 0. Sol.: Determiiamo le derivate di f: 0 f (0) lim
Esercitazioe 4 1 Serie di Taylor Esercizio 1: Verificare che la fuzioe f(x) { e 1/x se x 0 0 se x 0 pur essedo C o è sviluppabile i serie di Taylor i x 0. Sol.: Determiiamo le derivate di f: 0 f (0) lim
Università degli Studi di Palermo Facoltà di Economia. Dip. di Scienze Statistiche e Matematiche Silvio Vianelli
 Uiversità degli Studi di Palermo Facoltà di Ecoomia Dip. di Scieze Statistiche e Matematiche Silvio Viaelli Apputi del corso di Matematica Geerale Le Serie Ao Accademico 2009/200 V. Lacagia - S. Piraio
Uiversità degli Studi di Palermo Facoltà di Ecoomia Dip. di Scieze Statistiche e Matematiche Silvio Viaelli Apputi del corso di Matematica Geerale Le Serie Ao Accademico 2009/200 V. Lacagia - S. Piraio
2.4 Criteri di convergenza per le serie
 2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Serie numeriche. Paola Rubbioni. 1 Denizione, serie notevoli e primi risultati. i=0 a i, e si indica con il simbolo +1X.
 Serie umeriche Paola Rubbioi Deizioe, serie otevoli e primi risultati Deizioe.. Data ua successioe di umeri reali (a ) 2N, si dice serie umerica la successioe delle somme parziali (S ) 2N, ove S = a +
Serie umeriche Paola Rubbioi Deizioe, serie otevoli e primi risultati Deizioe.. Data ua successioe di umeri reali (a ) 2N, si dice serie umerica la successioe delle somme parziali (S ) 2N, ove S = a +
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
(a 0, a 1, a 2,..., a n,...) (0, a 0 ), (1, a 1 ), (2, a 2 ),... (1, 3, 5, 7,...) Lezione del 26 settembre. 1. Successioni.
 Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Esercizi svolti su successioni e serie di funzioni
 Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Corso di Analisi Matematica 1 - professore Alberto Valli
 Uiversità di Treto - Corso di Laurea i Igegeria Civile e Igegeria per l Ambiete e il Territorio - 07/8 Corso di Aalisi Matematica - professore Alberto Valli 8 foglio di esercizi - 5 ovembre 07 Taylor,
Uiversità di Treto - Corso di Laurea i Igegeria Civile e Igegeria per l Ambiete e il Territorio - 07/8 Corso di Aalisi Matematica - professore Alberto Valli 8 foglio di esercizi - 5 ovembre 07 Taylor,
ESAME DI MATEMATICA I Modulo di Analisi Matematica Corso 3 Anno Accademico 2008/2009 Docente: R. Argiolas
 ESAME DI MATEMATICA I Modulo di Aalisi Matematica Corso Ao Accademico 8/9 Docete: R Argiolas Cogome Matricola Febbraio 9 ore 9 Aula C Nome Corso voto Esercizio Assegata la fuzioe f ( arcta a Si determii
ESAME DI MATEMATICA I Modulo di Aalisi Matematica Corso Ao Accademico 8/9 Docete: R Argiolas Cogome Matricola Febbraio 9 ore 9 Aula C Nome Corso voto Esercizio Assegata la fuzioe f ( arcta a Si determii
1 Esponenziale e logaritmo.
 Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
PROVE SCRITTE DI ANALISI MATEMATICA II(N.O.), ANNO 2004/05
 PROVE SRITTE DI ANALISI MATEMATIA II(N.O.), ANNO 4/5 Prova scritta del 3/3/5 Esercizio Deotato co A il umero delle lettere del ome, si studi, al variare di α >, l itegrabilita della fuzioe g(x, y) = (x
PROVE SRITTE DI ANALISI MATEMATIA II(N.O.), ANNO 4/5 Prova scritta del 3/3/5 Esercizio Deotato co A il umero delle lettere del ome, si studi, al variare di α >, l itegrabilita della fuzioe g(x, y) = (x
ANALISI MATEMATICA L-B, SERIE. n k=1. n=1
 ANALISI MATEMATICA L-B, 2005-06. SERIE. Serie umeriche reali Defiizioe Cosideriamo ua successioe a,, di umeri reali. Che seso dare alla somma di tutti gli a? Si defiisce ua uova successioe S, ella maiera
ANALISI MATEMATICA L-B, 2005-06. SERIE. Serie umeriche reali Defiizioe Cosideriamo ua successioe a,, di umeri reali. Che seso dare alla somma di tutti gli a? Si defiisce ua uova successioe S, ella maiera
Il caso di coefficienti decrescenti e infinitesimi
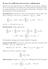 Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Precorso di Matematica. Parte IV : Funzioni e luoghi geometrici
 Facoltà di Igegeria Precorso di Matematica 1. Equazioi e disequazioi Parte IV : Fuzioi e luoghi geometrici Richiamiamo brevemete la ozioe di fuzioe, che sarà utilizzato i quest ultima parte del precorso.
Facoltà di Igegeria Precorso di Matematica 1. Equazioi e disequazioi Parte IV : Fuzioi e luoghi geometrici Richiamiamo brevemete la ozioe di fuzioe, che sarà utilizzato i quest ultima parte del precorso.
Circuiti a tempo discreto Raffaele Parisi
 Uiversità di Roma La Sapieza Laurea specialistica i Igegeria Elettroica Circuiti a tempo discreto Raffaele Parisi : Esempi di Sequeze e di Circuiti TD Sequeze otevoli, periodicità delle sequeze, esempi
Uiversità di Roma La Sapieza Laurea specialistica i Igegeria Elettroica Circuiti a tempo discreto Raffaele Parisi : Esempi di Sequeze e di Circuiti TD Sequeze otevoli, periodicità delle sequeze, esempi
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Trasmissione del calore con applicazioni numeriche: informatica applicata
 Corsi di Laurea i Igegeria Meccaica Trasmissioe del calore co applicazioi umerice: iformatica applicata a.a. 5/6 Teoria Parte IV Ig. Nicola Forgioe Dipartimeto di Igegeria Civile e Idustriale E-mail: icola.forgioe@ig.uipi.it;
Corsi di Laurea i Igegeria Meccaica Trasmissioe del calore co applicazioi umerice: iformatica applicata a.a. 5/6 Teoria Parte IV Ig. Nicola Forgioe Dipartimeto di Igegeria Civile e Idustriale E-mail: icola.forgioe@ig.uipi.it;
Programma (orientativo) secondo semestre 32 ore - 16 lezioni
 Programma (orietativo) secodo semestre 32 ore - 6 lezioi 3 lezioi: successioi e serie 4 lezioi: itegrali 2-3 lezioi: equazioi differeziali 4 lezioi: sistemi di equazioi e calcolo vettoriale e matriciale
Programma (orietativo) secodo semestre 32 ore - 6 lezioi 3 lezioi: successioi e serie 4 lezioi: itegrali 2-3 lezioi: equazioi differeziali 4 lezioi: sistemi di equazioi e calcolo vettoriale e matriciale
Esercitazioni di Geometria II
 Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
1 + 1 ) n ] n. < e nα 1 n
![1 + 1 ) n ] n. < e nα 1 n 1 + 1 ) n ] n. < e nα 1 n](/thumbs/66/54700563.jpg) Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
Corso di laurea in Matematica Corso di Analisi Matematica 1-2 AA Dott.ssa Sandra Lucente Successioni numeriche
 Corso di laurea i Matematica Corso di Aalisi Matematica -2 AA. 0809.. Cooscere. Dott.ssa Sadra Lucete. Successioi umeriche Defiizioe di successioe, isieme degli elemeti della successioe, successioe defiita
Corso di laurea i Matematica Corso di Aalisi Matematica -2 AA. 0809.. Cooscere. Dott.ssa Sadra Lucete. Successioi umeriche Defiizioe di successioe, isieme degli elemeti della successioe, successioe defiita
2,3, (allineamenti decimali con segno, quindi chiaramente numeri reali); 4 ( = 1,33)
 Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
SECONDO ESONERO DI AM1 10/01/ Soluzioni
 Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
La comparsa dei numeri complessi è legata, da un punto di vista storico, alla risoluzione delle equazioni di secondo grado.
 Capitolo 3 3.1 Defiizioi e proprietà La comparsa dei umeri complessi è legata, da u puto di vista storico, alla risoluzioe delle equazioi di secodo grado. L equazioe ammette le soluzioi x 2 + 2px + q =
Capitolo 3 3.1 Defiizioi e proprietà La comparsa dei umeri complessi è legata, da u puto di vista storico, alla risoluzioe delle equazioi di secodo grado. L equazioe ammette le soluzioi x 2 + 2px + q =
Trasmissione del calore con applicazioni numeriche: informatica applicata
 Corsi di Laurea i Igegeria Meccaica Trasmissioe del calore co applicazioi umeriche: iformatica applicata a.a. 17/18 Teoria Parte I Prof. Nicola Forgioe Dipartimeto di Igegeria Civile e Idustriale E-mail:
Corsi di Laurea i Igegeria Meccaica Trasmissioe del calore co applicazioi umeriche: iformatica applicata a.a. 17/18 Teoria Parte I Prof. Nicola Forgioe Dipartimeto di Igegeria Civile e Idustriale E-mail:
Un risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazione ad un risultato di esistenza per le equazioni differenziali ordinarie.
 U risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazioe ad u risultato di esisteza per le equazioi differeziali ordiarie. Voglio comiciare questo secodo icotro co u risultato di compattezza
U risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazioe ad u risultato di esisteza per le equazioi differeziali ordiarie. Voglio comiciare questo secodo icotro co u risultato di compattezza
Prova scritta di Analisi Matematica I 15/09/2010
 Prova scritta di Aalisi Matematica I VO 5/09/00 ) Data la fuzioe f ( ) + a) disegare il grafico illustrado i passaggi fodametali b) Euciare e dimostrare il Teorema di Rolle e se possibile applicarlo a
Prova scritta di Aalisi Matematica I VO 5/09/00 ) Data la fuzioe f ( ) + a) disegare il grafico illustrado i passaggi fodametali b) Euciare e dimostrare il Teorema di Rolle e se possibile applicarlo a
1. Serie Numeriche. 1.1 Serie Numeriche nel campo reale. Definizione 1.1 Data una successione {a n } R costruiamo un altra successione {s n } ponendo
 . Serie Numeriche. Serie Numeriche el campo reale Defiizioe. Data ua successioe {a } R costruiamo u altra successioe {s } poedo s j a j. La coppia ordiata {a }, {s }) si dice serie umerica di termie geerale
. Serie Numeriche. Serie Numeriche el campo reale Defiizioe. Data ua successioe {a } R costruiamo u altra successioe {s } poedo s j a j. La coppia ordiata {a }, {s }) si dice serie umerica di termie geerale
Serie numeriche. Esercizi
 Serie umeriche. Esercizi Mauro Saita, aprile 204. Idice Serie umeriche.. Serie a termii defiitivamete positivi..............................2 Serie a termii di sego altero.................................
Serie umeriche. Esercizi Mauro Saita, aprile 204. Idice Serie umeriche.. Serie a termii defiitivamete positivi..............................2 Serie a termii di sego altero.................................
Compito di Matematica II - 12 Settembre 2017
 Compito di Matematica II - Settembre 7 Corso di Laurea i Ottica e Optometria - A.A. 6/7 Soluzioi degli esercizi. Esercizio. a) Il domiio C è il cerchio di raggio uitario. La fuzioe fx y) = x + y è defiita
Compito di Matematica II - Settembre 7 Corso di Laurea i Ottica e Optometria - A.A. 6/7 Soluzioi degli esercizi. Esercizio. a) Il domiio C è il cerchio di raggio uitario. La fuzioe fx y) = x + y è defiita
1.10 La funzione esponenziale
 6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
AM110 - ESERCITAZIONI V - VI. Esercizio svolto 1. Dimostrare che ogni insieme finito ha un massimo ed un minimo.
 AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
Algoritmi e Strutture Dati (Elementi)
 Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Politecnico di Milano Ingegneria Industriale Analisi 2/II
 Politecico di Milao Igegeria Idustriale Aalisi /II Test di autovalutazioe. Sia S = ( artg +. (a Stabilire se la serie data coverge assolutamete. (b Stabilire se la serie data coverge.. Sia L lo spazio
Politecico di Milao Igegeria Idustriale Aalisi /II Test di autovalutazioe. Sia S = ( artg +. (a Stabilire se la serie data coverge assolutamete. (b Stabilire se la serie data coverge.. Sia L lo spazio
Serie di Fourier / Esercizi svolti
 Serie di Fourier / Esercizi svolti ESERCIZIO. da Si cosideri la fuzioe f : R R, periodica di periodo e data ell itervallo (, ] se
Serie di Fourier / Esercizi svolti ESERCIZIO. da Si cosideri la fuzioe f : R R, periodica di periodo e data ell itervallo (, ] se
