- B.1 - MANUALE DI OTTICA. per la classe seconda (professionale) a cura dei docenti dell'iis G.Galilei - Milano
|
|
|
- Paola Serafini
- 8 anni fa
- Visualizzazioni
Transcript
1 - B.1 - MANUALE DI OTTICA per la classe seconda (professionale) a cura dei docenti dell'iis G.Galilei - Milano Agosto 2010
2 - B.2 -
3 - B.3-1. Diottri sferici e specchi sferici La curvatura di una superficie Una superficie piana può essere descritta come una superficie tale che le normali a tutti i suoi punti sono parallele tra loro. Una superficie sferica è una superficie tale che tutte le normali passano per uno stesso punto. La superficie di una palla da tennis, di una bolla di sapone o della Terra sono esempi di superfici sferiche. Una persona che sta in piedi sulla superficie della Terra rappresenta la normale alla superficie in quel punto. Se si tracciasse una retta dalla testa di questa persona attraverso i suoi piedi e la si prolungasse all ingiù, essa intersecherebbe, nel centro della Terra, le rette tracciate attraverso altre persone che stanno in piedi in altri punti della superficie terrestre. In ottica sono molto comuni superfici quasi perfettamente sferiche perché due superfici strofinate tra loro in generale tendono ad adattarsi l una all altra formando due superfici sferiche, una convessa come una palla e l altra concava come una coppa che si adatta alla palla. Questa è infatti la configurazione che permette loro di muoversi più facilmente strisciando l una sull altra più facilmente; le nostre ossa hanno questa forma nelle articolazioni, dove è necessario un movimento. Una sezione di una qualsiasi superficie sferica è una circonferenza, o parte di una circonferenza, come è mostrato nella figura 1. Ogni circonferenza ha un centro di curvatura C e un raggio di curvatura r, definito come la distanza tra la superficie e il centro di curvatura. Su ciascuna superficie sono mostrate due normali separate dalla stessa distanza misurata sulla superficie. La distanza tra le normali è la stessa nei tre casi, ma l angolo tra le normali è molto diverso. Figura 1. Curvatura e raggi di curvatura. Chiamiamo curvatura della superficie l angolo di cui ruota la superficie lungo un arco di lunghezza unitaria. In ciascuno dei casi mostrati nella figura 1, un oggetto che si muove lungo la circonferenza da P 1
4 - B.4 a P2 parte nella direzione P1D e arriva nella direzione DP2 dopo aver ruotato di un angolo α. Poiché ogni direzione sulla superficie è perpendicolare alla normale in quel punto, l angolo di rotazione α è uguale all angolo tra le normali. Se l angolo è misurato in radianti il suo valore è dato da α (in radianti) p r dove p è la lunghezza dell arco e r il raggio della circonferenza. La curvatura ρ è il valore di α quando p è uno, ossia ρ α 1 p r (1) Quindi la curvatura di una superficie è uguale al reciproco del suo raggio e l unità di misura della curvatura è il reciproco del metro (m-1). Per ottenere valori corretti di ρ attraverso la formula (1) il raggio r deve essere espresso in metri. Una superficie piana può essere considerata come una superficie sferica di curvatura nulla. Diottri sferici e specchi sferici Si dice diottro sferico l'insieme di due mezzi trasparenti diversi separati da una superficie sferica. Un diottro sferico è caratterizzato dalla posizione del suo centro di curvatura C, dal suo raggio r o dalla sua curvatura ρ 1/r, e dagli indici di rifrazione n e n' dei due mezzi trasparenti. Quando un raggio di luce incide sulla superficie di un diottro sferico, è rifratto secondo la legge della rifrazione: n sen i n' sen i' (2) dove i indica l'angolo di incidenza e i' l'angolo di rifrazione, n è l'indice di rifrazione del mezzo da cui proviene il raggio di luce e n' l'indice di rifrazione del mezzo in cui viene rifratto il raggio di luce. La normale alla superfici del diottro nel punto di incidenza è la retta che congiunge il punto di incidenza con il centro di curvatura del diottro. Quindi un raggio di luce diretto verso il centro di curvatura C del diottro passa attraverso la superficie sferica senza essere deviato. Nella figura 2 sono rappresentati i percorsi di diversi raggi, provenienti da un oggetto puntiforme posto a una certa distanza sull asse XX, che incidono sulla superficie di un diottro sferico che separa aria da vetro con indice di rifrazione uguale a 1,5. Si vede che tutti questi raggi sono rifratti verso l asse ma i raggi più periferici o marginali non sono deviati verso lo stesso punto su cui convergono i raggi più vicini all asse. Un diottro sferico quindi non forma, in generale, un immagine puntiforme dell'oggetto puntiforme. La figura 3 rappresenta invece i percorsi di raggi di luce provenienti da un oggetto puntiforme, che incidono sulla superficie di uno specchio
5 - B.5 sferico. Anche in questo caso la superficie sferica è definita dalla posizione del suo centro di curvatura C e dal raggio r o dalla curvatura ρ 1/r. Il percorso dei raggi di luce è calcolato in questo caso utilizzando la legge della riflessione. Anche in questo caso la normale alla superficie dello specchio nel punto di incidenza è la retta che congiunge il punto di incidenza con il centro della superficie sferica. Quindi un raggio di luce che passa per il centro di curvatura C dello specchio viene riflesso indietro lungo lo stesso percorso e ripassa per C. Come nel caso del diottro sferico, anche nel caso dello specchio sferico i raggi periferici non sono deviati verso lo stesso punto su cui convergono i raggi più vicini all'asse. In generale, quindi, uno specchio sferico non forma un'immagine puntiforme di un oggetto puntiforme. Figura 2. Rifrazione su un diottro sferico di raggi di luce provenienti da una sorgente puntiforme. Figura 3. Riflessione su uno specchio sferico di raggi di luce provenienti da una sorgente puntiforme.
6 - B.6 L imperfezione di queste immagini fu scoperta prima per gli specchi sferici. Poiché si sapeva che gli specchi piani producono immagini perfette, Roger Bacon ( ) chiamò questo difetto aberrazione sferica. Oggi sappiamo che anche altre aberrazioni sono presenti nelle immagini prodotte dalle lenti e dagli specchi; verranno discusse più avanti. Il modo più semplice per ottenere, mediante un diottro sferico o uno specchio sferico, immagini che non siano affette da aberrazione sferica è restringere l'apertura della superficie sferica in modo che formino l'immagine solo i raggi di luce che passano vicino al centro di curvatura della superficie e per i quali gli angoli di incidenza, di rifrazione e di riflessione sono molto piccoli. Si utilizza cioè l'approssimazione dell'ottica di Gauss, che come si è già visto consiste nell'approssimare i valori delle funzioni goniometriche degli angoli con i valori degli angoli stessi espressi in radianti, ossia nel porre sen α α ; tg α α e cos α 1 (3) In pratica questa approssimazione può essere utilizzata quando gli angoli hanno valori inferiori a 5. Vedremo che, utilizzando questa approssimazione, un diottro sferico o uno specchio sferico producono un'immagine puntiforme di un oggetto puntiforme. La superficie mostrata nella figura 2, che ha il centro di curvatura all interno del materiale, è una superficie convessa. La superficie mostrata nella figura 3, che ha invece il centro di curvatura nel mezzo da cui proviene la luce, è una superficie concava.
7 - B.7-2. La convenzione dei segni Per calcolare la posizione degli oggetti e delle immagini è necessario adottare delle regole uniformi per misurare le distanze e gli angoli. È importante distinguere tra oggetti e immagini che stanno davanti al diottro o allo specchio da quelli che stanno dietro. Per questo si usano segni negativi e positivi. La convenzione che utilizzeremo fa riferimento alla figura 4 nella quale una superficie sferica rifrangente, S, riceve luce da un oggetto O. Assumeremo sempre che la luce proviene da sinistra. Nell approssimazione dell'ottica di Gauss l immagine è formata in un punto I posto sulla retta che passa per l'oggetto O e per il centro di curvatura C della superficie. Questa retta è detta asse ottico. L asse ottico è una normale alla superficie e il punto in cui interseca la superficie è detto polo o vertice A della superficie. Se si ha una sola superficie sferica si può tracciare un asse per ogni oggetto puntiforme. Quando sono utilizzate due superfici sferiche, come nel caso delle lenti, l asse ottico è la retta che congiunge i due centri di curvatura. Nella maggior parte dei sistemi ottici le superfici hanno un asse comune e il sistema è centrato e simmetrico rispetto a questo asse. Figura 4. Convenzione dei segni. Le definizioni che seguono si applicano a superfici singole e sistemi simmetrici. Distanze lungo l'asse ottico Tutte le distanze sono misurate dalla lente o dallo specchio. Quelle nella stessa direzione della luce incidente hanno valori positivi. Quelle in direzione contraria rispetto alla luce incidente hanno valori negativi. Nella figura 4 la distanza dalla superficie S al punto O è contraria alla direzione della luce incidente e perciò ha un valore negativo. Il raggio di curvatura della superficie, misurato da S a C, ha un valore positivo.
8 - B.8 Distanze perpendicolari all asse ottico Tutte le distanze sono misurate dall asse ottico. Sopra l'asse ottico si hanno valori positivi e sotto l'asse ottico valori negativi. Nella figura 4 il raggio di luce raggiunge la superficie S sopra l asse ottico a un altezza che ha un valore positivo. Angoli Angoli misurati in senso antiorario hanno valori positivi; angoli misurati in senso orario hanno valori negativi: Pendenza dei raggi La pendenza dei raggi è definita come l angolo acuto che va dalla direzione dell asse ottico alla direzione del raggio. Nella figura 4 la pendenza del raggio incidente che parte da O ha un valore positivo, mentre la pendenza del raggio rifratto che giunge in I ha un valore negativo. Angoli di incidenza, riflessione e rifrazione Gli angoli di incidenza, di rifrazione e di riflessione sono misurati dalla normale alla superficie al raggio. Nella figura 4 sia l angolo di incidenza sia l'angolo di rifrazione hanno un valore positivo. Le punte di freccia o le doppie punte di freccia disegnate su un segmento che indica una distanza o su un arco che indica un angolo mostrano il verso nel quale è fatta la misura.
9 - B.9-3. L'equazione sferico gaussiana del diottro La figura 5 mostra un diottro sferico simile a quello della figura 4, ma il raggio incidente è ora diretto verso un punto P dell asse ottico che si trova oltre la superficie sferica. In questa figura quindi tutte le distanze hanno valori positivi, e ciò rende più facile ricavare la relazione tra la distanza s dell'oggetto P dal vertice V del diottro e la distanza s' dell'immagine P' dal vertice V del diottro. Supponiamo che valgano le approssimazioni dell'ottica di Gauss, anche se per rendere più chiara la figura l altezza h e tutti gli angoli sono stati resi molto più grandi di quanto corrisponde ai limiti dell'approssimazione. Figura 5. Rifrazione su una superficie sferica. Usando la legge della rifrazione nella figura 5 abbiamo n sen i n sen i (2) dove i indica l'angolo di incidenza e i' l'angolo di rifrazione, n è l'indice di rifrazione del mezzo da cui proviene il raggio di luce e n' l'indice di rifrazione del mezzo in cui viene rifratto il raggio di luce. Nell'approssimazione dell'ottica di Gauss nella quale possiamo considerare il seno di un angolo uguale al suo valore in radianti, l'equazione (2) si può scrivere ni n i (4) Dalla figura si vede che tg ω h NP (si noti che l angolo ω nella figura è diretto in senso orario e quindi è negativo) che approssimiamo nell'ottica di Gauss con ω h VP (5)
10 - B.10 dato che, poiché h è molto minore di NP e della distanza VP s dell'oggetto P dal vertice V del diottro, si può porre nell'ottica di Gauss NP VP s. Allo stesso modo si ha ω ' h VP' (6) h VC (7) e α Dei triangoli INC e INP si ricava i [90 ( ω)] [90 ( α)] ω α e dai triangoli INC e INP i [90 ( ω )] [90 ( α)] ω α Dalla legge della rifrazione approssimata per l'ottica di Gauss (formula 4) abbiamo allora n(ω α) n (ω α) che dà n ω nω + (n n)α Sostituendo le espressioni (5), (6) e (7) per ω, ω e α e dividendo per h si ottiene n' n n' n + VP' VP VC Poiché abbiamo posto VP s, VP s e VC r, si ha n' n n' n + s' s r (8) Questa è l'equazione gaussiana del diottro sferico, ossia l'espressione che, se valgono le approssimazioni dell'ottica di Gauss (ossia se tutti gli angoli sono piccoli, in pratica minori di 5 ) permette di calcolare la distanza s' dell'immagine P' se sono noti gli indici di rifrazione n e n' dei due mezzi di cui è costituito il diottro, il suo raggio di curvatura r e la distanza s dell'oggetto P dal vertice del diottro. E' conveniente definire due nuove grandezze che rendono l'equazione (8) ancora più semplice. Il rapporto n/s tra l'indice di rifrazione n del mezzo in cui si propaga un raggio di luce e la distanza s del punto da cui il raggio di luce proviene si chiama vergenza e si indica con la lettera greca σ (sigma). Nel nostro caso
11 - B.11 si ha rispettivamente per la luce incidente e per la luce rifratta σ n s e σ n s (9) Un fascio di raggio ha vergenza positiva quando converge verso l'asse ottico, vergenza negativa quando diverge dall'asse ottico, vergenza nulla quando i raggi sono tutti parallelo tra loro. Per la luce che si propaga nel vuoto (o in aria) si ha n 1 e la vergenza coincide con la curvatura ρ del fronte d'onda. L'unità di misura della vergenza è la diottria (simbolo D) che è l'inverso del metro (m-1). Raggi di luce che si propagano nel vuoto e convergono verso un punto posto a 1 m di distanza hanno una vergenza di 1 D. L'equazione (8) mostra che il passaggio della luce attraverso il diottro sferico modifica la vergenza della quantità ϕ n ' n r (10) Questa quantità viene chiamata potere diottrico del diottro e si misura anch'essa in diottrie. L'equazione (8) si può scrivere allora semplicemente come σ' σ + ϕ (11) che esprime il fatto che il diottro modifica la vergenza della luce di una quantità pari al suo potere diottrico: dopo il passaggio attraverso il diottro la vergenza σ' della luce rifratta risulta pari alla vergenza σ della luce incidente più il potere diottrico ϕ del diottro. Il potere diottrico è positivo se il diottro tende a far convergere la luce incidente. La superficie sferica convessa (r > 0) di un mezzo che ha indice di rifrazione maggiore di quello del mezzo circostante (n' > n) ha potere diottrico positivo. Il potere diottrico è invece negativo se il diottro tende a far divergere la luce incidente. La superficie sferica concava (r < 0) di un mezzo che ha indice di rifrazione maggiore di quello del mezzo circostante (n' > n) ha potere diottrico negativo. Una superficie piana ha potere diottrico nullo. La formula (10) può essere scritta infatti come ϕ n' n ( n' n ) ρ r (12) dove ρ 1/r è la curvatura della superficie, che è nulla per una superficie piana. Una superficie piana quindi non modifica la vergenza della luce che incide su di essa. Ponendo ϕ 0 si ottiene immediatamente dall'equazione (11) l'equazione gaussiana del diottro piano:
12 - B.12 - σ' σ (13) e quindi n' n s' s (14) La presenza della superficie del diottro ha, in generale, l'effetto di deviare il raggio di luce incidente. Sempre facendo riferimento alla figura 5, l'inclinazione del raggio incidente IP è data dall'angolo ω mentre l'inclinazione del raggio rifratto IP' è data dall'angolo ω'. Si definisce ingrandimento angolare Iω il rapporto tra le ampiezze di questi due angoli: Iω ω ω (15) Dalle formule (5) e (6) che esprimono le ampiezze degli angoli ω e ω' nell'ottica di Gauss si ricava immediatamente che l'ingrandimento angolare prodotto dal diottro è uguale al rapporto tra la distanza s dell'oggetto e la distanza s' dell'immagine: Iω ω s ω s (16) Per concludere conviene notare una convenzione che abbiamo utilizzato in questo paragrafo e che continueremo a utilizzare nel seguito: i punti sono indicati nel grafici da lettere latine maiuscole (V, P, ecc.); le distanze sono indicate da lettere latine minuscole (s, r, ecc.); i reciproci delle distanze, come la vergenza o la curvatura, sono indicate dalle corrispondenti lettere greche (σ, ρ, ecc.); tutto ciò che si riferisce all'oggetto e al mezzo da cui proviene la luce è indicato senza apice (P, s, n, i, ecc.), le corrispondenti quantità che si riferiscono all'immagine sono indicate con apice (P', s', n', i', ecc.).
13 - B I fuochi del diottro sferico Dall equazione (8) deriva che dato un diottro sferico a ogni punto oggetto P corrisponde un solo punto immagine P. La distanza s' di P dal vertice del diottro può essere calcolata usando questa equazione e inserendo i valori n e n' degli indici di rifrazione, la distanza s dell oggetto e il raggio di curvatura r. Nel caso rappresentato nella figura 5 si ha un oggetto P virtuale (il raggio incidente converge verso P ma non vi passa) e un'immagine P' reale (il raggio rifratto passa realmente per P'). Poiché il percorso della luce è reversibile, le posizioni dell oggetto e dell immagine sono intercambiabili. Quindi nella figura 5 si può anche immaginare la luce come proveniente da P e diretta da destra verso sinistra. Una volta passata attraverso la superficie sferica la luce apparirà come se provenisse da P. Si avrebbe allora un oggetto P' reale e un'immagine P virtuale. Coppie di punti costituiti da un oggetto puntiforme e la sua immagine, che possono essere scambiati l'uno con l'altra come P e P, sono detti punti coniugati. Due di queste coppie di punti coniugati sono di particolare importanza. Quando l oggetto è a una distanza infinita dalla superficie del diottro il fronte d onda incidente è piano e i raggi incidenti sono paralleli. La vergenza di questo fascio di raggi è nulla. La luce rifratta da un diottro con potere positivo convergerà formando un immagine reale nel punto F nella figura 6. Nel caso di un diottro con potere negativo la luce rifratta apparirà come se provenisse da un immagine virtuale posta nel punto F nella figura 7. In entrambi i casi questa immagine, coniugata di un oggetto infinitamente distante, è chiamata il fuoco immagine F del diottro e la sua distanza dal diottro è detta focale immagine f. Poiché in queste condizioni si ha σ 0 e s f, abbiamo, per le equazioni (9) e (11), Figura 6. Diottro positivo (n > n): fuochi.
14 - B.14 - Figura 7. Diottro negativo (n > n): fuochi. n' ϕ f' σ ' e quindi la focale immagine del diottro è data da f ' n' ϕ (17) La focale immagine f di un diottro con potere positivo ha quindi un valore positivo, mentre la focale immagine di un diottro con potere negativo ha un valore negativo. Quando invece l immagine è a una distanza infinita dalla superficie del diottro, il fronte d'onda rifratto è piano e i raggi rifratti sono paralleli. La vergenza di questo fascio è nulla. Il punto in cui deve essere collocato l oggetto è detto fuoco oggetto F. La figura 6 mostra la situazione che si ha con un diottro positivo: l oggetto reale deve essere posto davanti alla superficie. Nel caso di un diottro negativa si deve avere un oggetto virtuale, come mostrato nella figura 7. In entrambi i casi la distanza del fuoco oggetto dal diottro è detta focale oggetto f. Poiché in queste condizioni σ 0 e s f, abbiamo, per le equazioni (9) e (11), σ n ϕ f e quindi la focale oggetto del diottro è data da f n ϕ (18)
15 - B.15 La focale oggetto f di un diottro con potere positivo ha quindi un valore negativo, mentre la focale oggetto di un diottro con potere negativo ha un valore positivo. I piani perpendicolari all asse ottico che passano per i fuochi sono detti piani focali. Entrambi i fuochi di un diottro positivo sono quindi reali, mentre con un diottro negativo entrambi i fuochi sono virtuali. Con entrambi i tipi di diottri le due focali hanno valori di segno opposto; il segno della focale immagine è quello del potere del diottro. Si hanno alcune relazioni interessanti tra le focali f e f' di un diottro, i suoi indici di rifrazione n e n' e il suo raggio di curvatura r. Si ha infatti f n ϕ n f ϕ n n (19) Il rapporto tra le due focali del diottro è quindi uguale al rapporto tra i due indici di rifrazione, cambiato di segno. Utilizzando le focali del diottro si può poi porre modificare l'equazione gaussiana del diottro (8), che riscriviamo così n' n +ϕ s' s (20) in una forma differente. Poiché infatti dalle formule (17) e (18) si ha n' ϕf' e n ϕf', si ha ϕf ϕ f +ϕ s' s e quindi f f + 1 s' s (21) L'ultima relazione interessante si ha considerando che f + f n n n n n n r ϕ ϕ ϕ ( n n ) r (22) La somma algebrica della focale immagine e della focale oggetto è quindi uguale al raggio di curvatura del diottro. Ogni raggio incidente parallelo all asse ottico che si rifrange su un diottro sferico, passerà per il fuoco immagine o divergerà da esso; e ogni raggio incidente che passa per il fuoco oggetto o si propaga verso di esso si propagherà in direzione parallela all asse ottico dopo la rifrazione. Queste proprietà dei fuochi del diottro verranno sfruttate per le costruzioni grafiche che verranno presentate nel prossimo paragrafo.
16 - B.16 -
17 - B L'immagine prodotta da un diottro sferico costruzioni grafiche La maggior parte degli oggetti osservati con gli strumenti ottici non consistono di un singolo punto, ma sono estesi. Per questi oggetti solo un punto può trovarsi sull asse ottico. E' quindi necessario considerare punti fuori-asse. L espressione usata comunemente nella progettazione ottica per indicare questi punti è punti di campo, perché sono oggetti puntiformi posti nel campo di vista della lente o dello strumento. Nella figura 8 il diottro DVE riceve luce da tutti i punti dell oggetto PQ. Il punto P è sull asse del diottro. Un raggio che provenendo da P viaggia lungo questo asse incide normalmente sulla superficie in V e passa attraverso C e P senza essere deviato. Anche dal punto di campo Q parte un raggio che incide normalmente sulla superficie. Anch esso non è deviato e passa per il centro di curvatura C. Nel caso di superficie rifrangenti singole chiamiamo questo raggio il raggio principale dal punto di campo Q, mentre C, il punto dell asse ottico per il quale non vi è deviazione, è chiamato punto nodale. Figura 8. Formazione dell immagine di un punto di campo. Consideriamo la formazione dell'immagine dell'oggetto PQ nel caso generale. L immagine di P deve trovarsi in un punto P' dell asse ottico. Le distanze di P e P' dal centro C del diottro sono pari alle lunghezze dei segmenti CP e CP' e possono essere calcolate utilizzando l'equazione gaussiana del diottro sferico. Anche il raggio principale del punto di campo Q, che passa per Q e per C, può essere considerato un asse del diottro. Se Pp è un arco della circonferenza tracciata con C come centro, l immagine di p è p sull arco P p tracciato con C come centro, perché p dista da C quanto P e quindi p' deve distare da C quanto P'. Il punto di campo Q dista però da C più di p, e quindi, per l'equazione gaussiana del diottro sferico, la sua immagine Q' dovrà distare da C meno di p'. L immagine P'Q' dell'oggetto PQ è perciò un arco più curvo dell'arco di circonferenza P p. Questo effetto di curvatura dell immagine prodotta da un diottro sferico è un'altra aberrazione delle immagini formate da un sistema ottico, chiamata curvatura di campo, che si aggiunge nel caso di oggetti estesi all'aberrazione sferica che abbiamo già discusso.
18 - B.18 Quando PQ è piccolo possiamo utilizzare le approssimazioni dell'ottica di Gauss, perché possiamo ricavare le posizioni delle immagini dei suoi punti utilizzando solo raggi molto vicini all'asse ottico che formano angoli piccoli con la superficie del diottro. In questa approssimazione la curvatura degli archi di circonferenza Pp e P'p' non è apprezzabile e possiamo quindi considerare che se l'oggetto PQ è un segmento rettilineo perpendicolare all'asse ottico anche la sua immagine P'Q' è un segmento rettilineo perpendicolare all asse ottico. Si dice che oggetto e immagine sono in piani coniugati e sono disegnati come nella figura 9. Figura 9. Costruzione grafica dell'immagine di un oggetto esteso prodotta da un diottro sferico. Il modo più semplice per ricavare le dimensioni dell'immagine P Q consiste nel ricorrere a una costruzione grafica. Si sfruttano le proprietà di tre raggi: il raggio principale che parte da Q e passa per C non è deviato dal diottro; il raggio QD' parallelo all asse ottico si comporta come un raggio proveniente da un oggetto distante posto sull asse ottico ed è quindi rifratto verso il fuoco immagine F del diottro; il raggio QF che parte da Q e passa per il fuoco oggetto F del diottro (e potrebbe quindi essere partito da F) è rifratto dal diottro in direzione parallela all'asse ottico. Per costruire graficamente l'immagine P'Q', dati gli indici di rifrazione n e n' e il raggio di curvatura r del diottro, si procede quindi in questo modo: 1) Si tracciano l'asse ottico e la superficie del diottro, rappresentata dalla retta D'E' perpendicolare all'asse ottico (nell'approssimazione dell'ottica di Gauss si trascura, come abbiamo visto, la curvatura delle superfici). 2) Si calcolano con le formule (12), (17) e (18) il potere del
19 - B.19 diottro, la focale oggetto f e la focale immagine f' e si indicano sull'asse ottico le posizioni C del centro del diottro, F del fuoco oggetto e F' del fuoco immagine. 3) Si traccia il raggio principale QCQ' che passa per il centro del diottro senza essere deviato. 4) Si traccia il raggio QD' parallelo all'asse ottico e poi, a partire dal punto D' in cui questo raggio interseca la superficie del diottro, si traccia il raggio rifratto D'F'Q' che passa per il fuoco immagine F'. 5) L'intersezione dei due raggi QCQ' e D'F'Q' individua la posizione dell'estremo Q' dell'immagine. 6) Come verifica, si traccia il raggio QFE' che passa per il fuoco oggetto F e interseca la superficie del diottro in E', e a partire da E' si traccia il raggio rifratto parallelo all'asse ottico. Se la costruzione è stata realizzata correttamente questo terzo raggio deve intersecare i primi due nel loro punto di intersezione Q'. 7) Si traccia infine il segmento P'Q' perpendicolare all'asse ottico che è l'immagine dell'oggetto PQ. Una variante di questo metodo di costruzione può essere utilizzata per ricavare la direzione di un qualunque raggio rifratto da un diottro sferico, se sono noti gli indici di rifrazione n e n' e il raggio di curvatura r del diottro e la direzione del raggio incidente. Facendo riferimento alla figura 10, i passi da eseguire sono i seguenti: 1) Si tracciano l'asse ottico e la superficie del diottro, rappresentata dalla retta D'E' perpendicolare all'asse ottico (nell'approssimazione dell'ottica di Gauss si trascura, come abbiamo visto, la curvatura delle superfici), e il raggio incidente QH. 2) Si calcolano con le formule (12), (17) e (18) il potere del diottro, la focale oggetto f e la focale immagine f' e si indicano sull'asse ottico le posizione C del centro del diottro, F del fuoco oggetto e F' del fuoco immagine. 3) Si traccia un raggio ausiliario KC parallelo a QH e passante per il centro C del diottro. 4) A partire dal fuoco immagine F' si traccia un segmento perpendicolare all'asse ottico e si individua la sua intersezione Q' con il raggio ausiliario KC. 5) Si congiunge il punto di incidenza H del raggio incidente con il punto Q'. Questo è il raggio rifratto dal diottro. 6) Come verifica si traccia un secondo raggio ausiliario FJ
20 - B.20 parallelo a QH e passante per il fuoco oggetto F, e a partire dal punto J in cui questo raggio interseca il diottro si traccia un raggi parallelo all'asse ottico. Se la costruzione è stata realizzata correttamente questo terzo raggio deve intersecare il raggio rifratto HQ' e il raggio ausiliario KC nel loro punto di intersezione Q'. Figura 10. Costruzione del raggio rifratto da un diottro sferico. Questa costruzione si basa sul fatto che un fascio di raggi paralleli QH, KC e FJ che incidono sul diottro vengono fatti convergere in un unico punto Q' posto nel piano focale immagine del diottro. Come nel caso della costruzione precedente, il raggio KC passante per il centro del diottro non viene deviato, mentre il raggio FJ passante per il fuoco oggetto del diottro viene deviato in direzione parallela all'asse ottico.
21 - B L'ingrandimento dell'immagine prodotta da un diottro sferico Ci proponiamo ora di ricavare una formula che permetta di calcolare l'altezza h' dell'immagine P'Q' prodotta dal diottro sferico. Faremo ora riferimento alla figura 11, che riproduce la figura 9 con l'indicazione di tutte le grandezze che utilizzeremo in questo paragrafo. Figura 11. Ingrandimento lineare dell'immagine di un oggetto esteso prodotta da un diottro sferico. Il rapporto tra l'altezza h' dell immagine e l'altezza h dell oggetto è detto ingrandimento lineare I dell immagine: I h h (23) Poiché il raggio principale QCQ non è deviato, i triangoli rettangoli PCQ e P'CQ' sono simili ed è quindi possibile mettere in relazione l altezza dell oggetto h con l altezza dell immagine h e ottenere una formula che permette di calcolare l'ingrandimento lineare dell'immagine in funzione delle posizioni s e s' dell'oggetto e dell'immagine e del raggio di curvatura r del diottro: I h' CP' s ' r h CP s r (24) Notiamo che l ingrandimento lineare è positivo quando l immagine è dritta, ed è negativo quando l immagine è capovolta. Le immagini sono dritte quando si trovano dalla stessa parte del diottro in cui si trova l oggetto e capovolte quando si trovano dall altra parte. Altre formule, che permettono di calcolare l'ingrandimento lineare dell'immagine in funzione delle posizioni s e s' dell'oggetto e dell'immagine e delle focali del diottro si ricavano considerando i due triangoli rettangoli simili D'F'V e Q'F'P':
22 - B.22 I h' P' F' s ' f ' h VF' f' (25) e i due triangoli rettangoli simili QPF e E'VF: I h' VE' f h VF s f (26) Se poi consideriamo il raggio QVQ che passa per il vertice della superficie ed è rifratto in accordo con la legge della rifrazione, che nell'ottica di Gauss si esprime mediante la relazione ni n i (4) ossia n i n i Ricordando la definizione della vergenza ( σ n/s) e che nell'ottica di Gauss il valore della tangente di un angolo si identifica con l'ampiezza dell'angolo espressa in radianti, si ottiene una formula che permette di calcolare l'ingrandimento dell'immagine in funzione della vergenza dei raggio incidente e dei raggi rifratti: I h s ' tg i ' s ' i ' s ' n σ h s tg i si sn' σ ' Un'altra formula importante si ottiene considerando l ingrandimento lineare può essere espresso anche come I (27) che P' Q' x ' VD' f' e I VE' f PQ x Si ha quindi x' f f' x e xx ff (28) dove x e x sono rispettivamente le distanze dell oggetto e dell immagine dal fuoco oggetto e dal fuoco immagine. L'espressione (28) è nota come formula di Newton ed è molto utile per trovare la posizione dell'oggetto o dell'immagine quando sono molto vicini ai rispettivi fuochi, ma non coincidono con essi.
23 - B.23 - Figura 12. Ingrandimento assiale. A partire dalla formula di Newton è immediato ricavare un'espressione per l'ingrandimento assiale dell'immagine. Consideriamo la figura 12 nella quale l'oggetto è esteso lungo l'asse ottico con estremi dati dai segmenti P1Q1 e P2Q2 ed ha quindi lunghezza P1P2 x2 x1. L'immagine di questo oggetto si estende nello spazio compreso tra i segmenti P'1Q'1 e P'2Q'2 ed ha una lunghezza P' 1P'2 x'2 x'1. Si definisce ingrandimento assiale dell'immagine il rapporto Ia x x 2 x1 x x 2 x1 (29) tra la lunghezza dell'immagine misurata lungo l'asse ottico e la lunghezza dell'oggetto misurata anch'essa lungo l'asse ottico. Dalla formula di Newton (28) e dalla formula (19) che dà la relazione tra f e f' si ha x ff n f 2 x n x e quindi l'ingrandimento assiale risulta dato da n f 2 n f 2 n x 2f 2 x1f 2 n x n x 2 x1 n x1 x x1 2 Ia 2 x 2 x1 x 2 x1 x 2 x1 n f 2 n f f n I1I 2 n x 2 x1 n s 2 f s1 f n (30) L'ingrandimento assiale è quindi pari al prodotto dell'ingrandimento laterale dei due estremi dell'immagine, moltiplicato per il rapporto tra i due indici di rifrazione del diottro. Un ultima relazione riguarda le altezze dell oggetto e dell immagine. Dall equazione (27) si ricava h' ns ' h n' s
24 - B.24 che dà n h s nhs Le inclinazioni u e u' del raggio incidente QD' e del raggio rifratto D'Q' rispetto al raggio non deviato QCQ' passante per il centro del diottro sono date, nell'approssimazione dell'ottica di Gauss in cui questi angoli sono piccoli, da u V' D' s ottico, e u' V' D' s' Abbiamo allora n h u nhu e, per ogni altra superficie in un sistema H nh u n h u n h u ecc. (31) Ogni termine ha fattori che si riferiscono solo a una superficie e quindi H è invariante attraverso tutto il sistema. Ciò è molto utile per l analisi delle aberrazioni. La quantità H è detta invariante di Lagrange.
25 - B Gli specchi sferici Sappiamo che anche gli specchi sferici, come i diottri sferici, producono in generale immagini affette da aberrazione sferica. Solo se l'oggetto puntiforme si trova nel centro di curvatura dello specchio i raggi di luce vengono riflessi dallo specchio esattamente nella stessa direzione da cui provengono e si forma un'immagine puntiforme esente da aberrazione coincidente con l'oggetto. Anche nel caso degli specchi sferici, come per i diottri sferici, l'aberrazione sferica può essere ridotta riducendo l'apertura dello specchio. Si possono allora studiare le immagini prodotte dagli specchi sferici nell'approssimazione dell'ottica di Gauss, come si è fatto per i diottri sferici. Si può confrontare la legge della rifrazione n sen i n' sen i' (2) che nell'ottica di Gauss assume la forma ni n'i' (4) con la legge della riflessione che, tenendo conto delle convenzioni sui segni degli angoli (si veda la figura 13), si scrive i i' (5) (avendo indicato con lo stesso simbolo i' l'angolo di rifrazione nel caso della rifrazione e l'angolo di riflessione nel caso della riflessione.) i' riflesso i n n' P i'rifratto Figura 13. Segni degli angoli di riflessione e rifrazione. Dal confronto tra la formula (4) e la formula (5) si vede che, nell'ottica di Gauss, la riflessione si può trattare come una rifrazione tra un mezzo con indice di rifrazione n 1 e un mezzo con indice di rifrazione n' -1. Tutto quanto abbiamo ricavato nei paragrafi precedenti riguardo ai diottri sferici si può applicare quindi agli specchi sferici ponendo per il
26 - B.26 secondo mezzo un indice di rifrazione negativo n' -1. Vediamo comunque le varie formule una per una. L'equazione gaussiana dello specchio sferico si ricava dall'equazione gaussiana del diottro sferico (8) ponendo n 1 e n' -1 e assume la forma s' s r (32) Questa è l'equazione gaussiana dello specchio sferico, ossia l'espressione che, se valgono le approssimazioni dell'ottica di Gauss (ossia se tutti gli angoli sono piccoli, in pratica minori di 5 ) permette di calcolare la distanza s' dell'immagine P' se sono noti il raggio di curvatura r dello specchio e la distanza s dell'oggetto P dal vertice dello specchio. La vergenza del fascio di luce incidente e del fascio di luce riflessa sono ora date da σ 1 s e σ 1 s (33) Nella riflessione sullo specchio sferico la vergenza dei raggi di luce viene modificata della quantità ϕ 2 r (33) che costituisce il potere diottrico dello specchio. Anche nel caso degli specchi l'equazione gaussiana può essere scritta nella forma σ' σ + ϕ (11) Il potere diottrico è positivo se lo specchio tende a far convergere la luce incidente. Uno specchio sferico concavo (r < 0) ha potere diottrico positivo: si ha uno specchio convergente. Il potere diottrico è invece negativo se lo specchio tende a far divergere la luce incidente. Uno specchio sferico convesso (r > 0) ha potere diottrico negativo: si ha uno specchio divergente. Uno specchio piano ha potere diottrico nullo. La formula (33) può essere scritta infatti come ϕ 2ρ (34) dove ρ 1/r è la curvatura della superficie dello specchio, che è nulla per una superficie piana. Quando l oggetto è a una distanza infinita dalla superficie dello specchio il fronte d onda incidente è piano e i raggi incidenti sono paralleli. La vergenza di questo fascio di raggi è nulla. La luce riflessa da uno specchio convergente convergerà formando un immagine reale nel punto F nella figura 14. Nel caso di uno specchio divergente la luce riflessa apparirà
27 - B.27 come se provenisse da un immagine virtuale posta nel punto F nella figura 15. In entrambi i casi questa immagine, coniugata di un oggetto infinitamente distante, è chiamata il fuoco immagine F dello specchio e la sua distanza dallo specchio è detta focale immagine f. Figura 14. Fuochi di uno specchio convergente. Figura 15. Fuochi di uno specchio divergente. Poiché in queste condizioni si ha σ 0 e s f, abbiamo, per le equazioni (32) e (11), σ ' 1 ϕ f' e quindi la focale immagine dello specchio è data da f ' 1 ϕ (35)
28 - B.28 Quando invece l immagine è a una distanza infinita dalla superficie dello specchio, il fronte d'onda riflesso è piano e i raggi riflessi sono paralleli. La vergenza di questo fascio è nulla. Il punto in cui deve essere collocato l oggetto è detto fuoco oggetto F. La figura 14 mostra la situazione che si ha con uno specchio convergente: l oggetto reale deve essere posto davanti alla superficie dello specchio. Nel caso di uno specchio divergente si deve avere un oggetto virtuale, come mostrato nella figura 15. In entrambi i casi la distanza del fuoco oggetto dallo specchio è detta focale oggetto f. Poiché in queste condizioni σ 0 e s f, abbiamo, per le equazioni (32) e (11), σ 1 ϕ f e quindi la focale oggetto dello specchio è data da f 1 ϕ (36) Si vede dalle formule (34), (35) e (36) che il fuoco oggetto e il fuoco immagine di uno specchio sferico coincidono, e si trovano a una distanza dal vertice dello specchio pari alla metà del raggio di curvatura r dello specchio. Consideriamo uno specchio convergente. Quando l'oggetto è a distanza infinita dallo specchio, l'immagine si trova nel fuoco immagine F'. Se l oggetto si avvicina allo specchio, l immagine si allontana. L oggetto e l immagine quindi si avvicinano l uno all altra finché si raggiunge un punto in cui coincidono. Questo punto è il centro di curvatura dello specchio. Quando l oggetto, continuando ad avvicinarsi allo specchio, raggiunge il fuoco oggetto F, l immagine è all infinito e la luce riflessa è parallela all asse. Se l oggetto viene avvicinato ancora allo specchio, la luce riflessa diverge da un immagine virtuale posta dietro lo specchio a una distanza dallo specchio maggiore di quella a cui si trova l oggetto davanti ad esso. Quando l oggetto raggiunge la superficie dello specchio l oggetto e l immagine coincidono di nuovo. Con uno specchio divergente la luce è sempre resa più divergente e quindi si forma sempre un immagine virtuale di un oggetto reale (si veda la figura 15). L'immagine di un oggetto esteso prodotta da uno specchio sferico può essere costruita graficamente con lo stesso metodo utilizzato nel caso del diottro sferico. Consideriamo un oggetto PQ posto davanti a uno specchio concavo ED come nella figura 16. Il modo più semplice per ricavare le dimensioni dell'immagine P Q consiste nel ricorrere a una costruzione grafica. Anche in questo caso si sfruttano le proprietà di tre raggi: il raggio principale che parte da Q e passa per C viene riflesso dallo
29 - B.29 specchio su se stesso; il raggio QD' parallelo all asse ottico si comporta come un raggio proveniente da un oggetto distante posto sull asse ottico ed è quindi riflesso verso il fuoco immagine F dello specchio; il raggio QV che parte da Q e si riflette nel vertice V dello specchio è riflesso con un angolo uguale all'angolo di incidenza e di segno opposto. Figura 16. Costruzione grafica dell'immagine di un oggetto esteso prodotta da uno specchio sferico concavo. Per costruire graficamente l'immagine P'Q', dato il raggio di curvatura r dello specchio, si procede quindi in questo modo: 1) Si tracciano l'asse ottico e la superficie dello specchio, rappresentata dalla retta D'E' perpendicolare all'asse ottico (nell'approssimazione dell'ottica di Gauss si trascura, come abbiamo visto, la curvatura delle superfici).
30 - B.30 2) Si calcolano la focale dello specchio, pari alla metà del raggio di curvatura r dello specchio, e si indicano sull'asse ottico le posizione C del centro del diottro e F' del fuoco. 3) Si traccia il raggio principale QCQ' che passa per il centro dello specchio e viene riflesso su se stesso. 4) Si traccia il raggio QD' parallelo all'asse ottico e poi, a partire dal punto D' in cui questo raggio interseca la superficie dello specchio, si traccia il raggio riflesso D'F'Q' che passa per il fuoco immagine F'. 5) L'intersezione dei due raggi QCQ' e D'F'Q' individua la posizione dell'estremo Q' dell'immagine. 6) Come verifica, si traccia il raggio QV che passa per il vertice dello specchio, e a partire da V si traccia il raggio riflesso con un angolo di riflessione uguale all'angolo di incidenza. Se la costruzione è stata realizzata correttamente questo terzo raggio deve intersecare i primi due nel loro punto di intersezione Q'. 7) Si traccia infine il segmento P'Q' perpendicolare all'asse ottico che è l'immagine dell'oggetto PQ. Nella figura 16 questo metodo è stato utilizzato con uno specchio concavo per costruire in (a) l'immagine reale di un oggetto posto a una distanza s dallo specchio maggiore della focale f, e in (b) per costruire l'immagine virtuale di un oggetto posto a una distanza s dallo specchio minore della focale f. Nella figura 17 invece il metodo è utilizzato per costruire l'immagine virtuale prodotta da uno specchio convesso. Figura 17. Costruzione grafica dell'immagine di un oggetto esteso prodotta da uno specchio sferico convesso. Per calcolare l'ingrandimento dell'immagine prodotta da uno specchio sferico si possono usare le stesse formule (24)-(30) ricavate nel caso del diottro sferico.
31 - B Le lenti sottili Una lente è formata da due diottri. Una lente sferica è formata da due diottri sferici. Le due superfici di una lente sferica hanno ciascuna un centro di curvatura. Indichiamo come superficie anteriore la superficie che rifrange la luce incidente, e come superficie posteriore la superficie su cui avviene la seconda rifrazione. La figura 18.a mostra due superfici sferiche che formano una lente. La superficie anteriore ha il suo centro in C1 e il centro della superficie posteriore è in C2. La retta passante per C1 e C2 è chiamata asse ottico della lente. Non ci sono altri assi. Non è necessario che i raggi delle due sfere siano uguali e da parti opposte della lente. Se una delle due superfici è piana, può essere pensata come una superficie sferica di raggio infinito. L asse ottico è allora la retta che passa per il centro di curvatura dell altra superficie perpendicolarmente alla superficie piana, come mostrato nella figura 18.b. Figura 18. Lenti: vertici e assi ottici. I punti V1 e V2 nei quali l asse ottico interseca le due superfici sono chiamati rispettivamente vertice anteriore e vertice posteriore della lente. La distanza V1V2 è detta spessore della lente. Se lo spessore della lente è così piccolo da poter essere trascurato rispetto alle altre lunghezze considerate (per esempio i raggi di curvatura delle due superfici), la lente si dice sottile e il punto in cui in pratica coincidono i vertici delle due superfici si dice centro ottico O della lente. Le lenti sono normalmente tagliate in modo che viste lungo l asse ottico hanno una forma circolare con centro nel loro centro ottico. Se non è così, si dice che sono decentrate.
32 - B.32 Ogni superficie di una lente sottile ha un potere diottrico. Vedremo più avanti che il potere totale ϕ di una lente dipende dal potere ϕ1 e ϕ2 delle due superfici, dal suo spessore e e dall'indice di rifrazione n del materiale di cui è composta la lente. Si ha infatti ϕ ϕ1 + ϕ2 (e/n)ϕ1ϕ2 (37) Nel caso di una lente sottile per la quale il termine (e/n)ϕ1ϕ2 può essere trascurato il potere totale è dato semplicemente da ϕ ϕ1 + ϕ2 (38) Possono quindi essere usate differenti combinazioni di ϕ1 e ϕ2 per dare lo stesso valore di ϕ. Per esempio, un potere totale di +6 D può essere ottenuto da combinazioni di +3 e +3 D, +4 e +2 D, +6 e 0 D, +10 e 4 D, ecc. Ciò permette di avere differenti forme per lenti di ogni dato potere. Nella figura 19 sono mostrate quattro lenti che hanno lo stesso potere totale (positivo). Queste quattro le lenti, se sono fatte di materiale con indice di rifrazione maggiore di quello del mezzo circostante, tendono a rendere più convergente ogni fronte d onda incidente. Possono quindi essere chiamate lenti convesse, convergenti o positive. La lente A ha superfici di uguale potere positivo (lente equi-convessa). La lente B ha superfici di potere positivo ma differente (lente biconvessa). La lente C ha una superficie di potere nullo (lente piano-convessa), mentre la lente D ha una superficie negativa (menisco convesso). Figura 19. Lenti positive, convesse e convergenti, di uguale potere. Le lenti con potere totale negativo tendono a far divergere la luce e sono dette lenti concave, divergenti o negative. Possono anch esse avere varie forme. Un potere totale di 8 D, per esempio, può essere ottenuto dalla combinazione di 4 e 4 D, di 6 e 2 D, di 8 e 0 D, di 12 e +4 D. Le lenti mostrate nella figura 20 hanno lo stesso potere totale negativo ottenuto con diverse combinazioni di poteri delle due superfici: La lente A ha superfici di uguale potere negativo (lente equi-concava). La lente B ha superfici di potere negativo ma differente (lente biconcava). La lente C ha una superficie di potere nullo (lente piano-concava), mentre la lente D ha una superficie positiva (menisco concavo).
33 - B.33 - Figura 20. Lenti negative, concave e divergenti, di uguale potere.
34 - B Il potere di una lente sottile Come i diottri sferici e gli specchi sferici, anche le lenti cambiano la vergenza della luce proveniente da un oggetto posto davanti ad esse e ne formano un immagine (reale o virtuale). Questo cambiamento di vergenza è dovuto al potere diottrico della lente. Ci proponiamo ora di dimostrare la formula (38) che fornisce il potere diottrico di una lente sottile. Come le immagini prodotte dai diottri sferici e dagli specchi sferici, anche le immagini prodotte dalle lenti sono in generale affette da aberrazione sferica, dovuta ad entrambe le superfici della lente. Vedremo più avanti che l'aberrazione sferica complessiva della lente dipende dalla curvatura di entrambe le superfici: lenti che hanno lo stesso potere diottrico totale ma differente forma possono risentire in misura diversa dell'aberrazione sferica. Come nel caso del diottro sferico o dello specchio sferico, anche nel caso della lente l'aberrazione sferica può essere praticamente eliminata restringere l'apertura della lente in modo che formino l'immagine solo i raggi di luce che passano vicino ai vertici delle due superfici e per i quali quindi gli angoli di incidenza e di rifrazione sono molto piccoli. Utilizziamo cioè anche in questo caso l'approssimazione dell'ottica di Gauss. Consideriamo in successione l'effetto dei due diottri di cui è composta la lente, facendo riferimento alla figura 21. I raggi di curvatura e le distanze dell oggetto e dell immagine sono tutti misurati da O, il centro ottico della lente. Supponiamo che la lente sia sottile e che quindi si possa trascurare il suo spessore e. Figura 21. Rifrazione con una lente sottile. Nella figura 21 la luce incidente è diretta verso il punto P dell'asse ottico, che è l'oggetto (virtuale). Il punto b indica la posizione dell'immagine che si avrebbe se non ci fosse la seconda superficie. Applicando l'equazione gaussiana del diottro sferico alla prima superficie si ha n'1 n1 n'1 n1 + s '1 s1 r1 (39) dove r1 è il raggio di curvatura della prima superficie, s1 la distanza
35 - B.35 dell oggetto P e s 1 la distanza dell immagine intermedia b, n1 l indice di rifrazione del mezzo posto davanti alla lente e n'1 l indice di rifrazione della lente. L immagine intermedia b può essere considerata come l'oggetto (virtuale) per la rifrazione sulla seconda superficie. Applicando l'equazione gaussiana del diottro sferico alla seconda superficie si ha: n' 2 n 2 n' 2 n2 + s'2 s2 r2 (40) dove r2 è il raggio di curvatura della seconda superficie, s2 la distanza dell oggetto b e s 2 la distanza dell immagine finale P', n2 l indice di rifrazione della lente e n 2 l indice di rifrazione del mezzo posto dietro la lente. Poiché la lente è sottile e si assume che lo spessore e sia nullo, anche lo spessore e nel punto in cui il raggio passa attraverso la lente può essere supposto nullo. La distanza s2 di b dalla seconda superficie è perciò uguale alla sua distanza s 1 dalla prima superficie: s2 s 1. L indice di rifrazione ovviamente lo stesso in tutto lo spessore della lente, e perciò n 1 è uguale a n2. Si ha quindi: n2 n'1 s 2 s '1 e l'equazione (39) può essere inserita nell'equazione (40) ottenendo n' 2 n1 n'1 n1 n' 2 n2 + + s ' 2 s1 r1 r2 ossia n' 2 n1 n'1 n1 n' 2 n2 + + s ' 2 s1 r1 r2 (41) L'equazione (41) è l'equazione gaussiana della lente sottile. I termini all'interno della parentesi sono i poteri ϕ1 e ϕ2 dei due diottri, che si sommano per dare il potere diottrico ϕ della lente. L'equazione (41) si può scrivere infatti come: n' 2 n1 n + ϕ1+ ϕ2 1 + ϕ s ' 2 s1 s1 (42) Se la lente è posta in aria n1 e n 2 sono entrambi uguali a uno. Per semplicità l indice di rifrazione della lente può essere indicato con n e quindi n 1 n2 n. Abbiamo ora, dall equazione (41), 1 1 n 1 1 n + + s ' 2 s1 r1 r2 Se la distanza dell oggetto P è ora chiamata semplicemente s e la
36 - B.36 distanza dell immagine finale P' è chiamata s, abbiamo 1 1 n 1 1 n + + s' s r1 r2 e quindi ( n 1) s' s r1 r2 (43) Il potere diottrico ϕ della lente sottile in aria risulta perciò dato da 1 1 ( n 1)( ρ 1 ρ 2 ) ϕ ( n 1) r1 r2 (44) dove ρ1 e ρ2 sono le curvature della superficie anteriore e della superficie posteriore. Se poi consideriamo che la vergenza del raggio incidente è data da σ 1/s e la vergenza del raggio rifratto da σ' 1/s', l'equazione (43) può essere scritta nella forma σ σ + ϕ (45) che mostra in maniera immediata che l'effetto della lente è di modificare la vergenza σ della luce incidente di una quantità ϕ uguale al potere diottrico della lente.
Lenti sottili/1. Menisco convergente. Menisco divergente. Piano convessa. Piano concava. Biconcava. Biconvessa. G. Costabile
 Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Lenti sottili: Definizione
 Lenti sottili: Definizione La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Lenti sottili: Definizione La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Ottica geometrica. L ottica geometrica tratta i. propagazione in linea retta e dei. rifrazione della luce.
 Ottica geometrica L ottica geometrica tratta i fenomeni che si possono descrivere per mezzo della propagazione in linea retta e dei fenomeni di riflessione e la rifrazione della luce. L ottica geometrica
Ottica geometrica L ottica geometrica tratta i fenomeni che si possono descrivere per mezzo della propagazione in linea retta e dei fenomeni di riflessione e la rifrazione della luce. L ottica geometrica
Radiazione elettromagnetica
 Radiazione elettromagnetica Un onda e.m. e un onda trasversa cioe si propaga in direzione ortogonale alle perturbazioni ( campo elettrico e magnetico) che l hanno generata. Nel vuoto la velocita di propagazione
Radiazione elettromagnetica Un onda e.m. e un onda trasversa cioe si propaga in direzione ortogonale alle perturbazioni ( campo elettrico e magnetico) che l hanno generata. Nel vuoto la velocita di propagazione
PROGRAMMA OPERATIVO NAZIONALE
 PROGRAMMA OPERATIVO NAZIONALE Fondo Sociale Europeo "Competenze per lo Sviluppo" Obiettivo C-Azione C1: Dall esperienza alla legge: la Fisica in Laboratorio Ottica geometrica Sommario 1) Cos è la luce
PROGRAMMA OPERATIVO NAZIONALE Fondo Sociale Europeo "Competenze per lo Sviluppo" Obiettivo C-Azione C1: Dall esperienza alla legge: la Fisica in Laboratorio Ottica geometrica Sommario 1) Cos è la luce
Fisica II - CdL Chimica. Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici
 Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
OTTICA TORNA ALL'INDICE
 OTTICA TORNA ALL'INDICE La luce è energia che si propaga in linea retta da un corpo, sorgente, in tutto lo spazio ad esso circostante. Le direzioni di propagazione sono dei raggi che partono dal corpo
OTTICA TORNA ALL'INDICE La luce è energia che si propaga in linea retta da un corpo, sorgente, in tutto lo spazio ad esso circostante. Le direzioni di propagazione sono dei raggi che partono dal corpo
Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale...
 IMMAGINI Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale... 9 Immagini - 1/11 Ottica geometrica È la branca dell ottica che
IMMAGINI Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale... 9 Immagini - 1/11 Ottica geometrica È la branca dell ottica che
Laboratorio per il corso Scienza dei Materiali II
 UNIVERSITÀ DI CAMERINO Corso di Laurea Triennale in Fisica Indirizzo Tecnologie per l Innovazione Laboratorio per il corso Scienza dei Materiali II a.a. 2009-2010 Docente: E-mail: Euro Sampaolesi eurosampaoesi@alice.it
UNIVERSITÀ DI CAMERINO Corso di Laurea Triennale in Fisica Indirizzo Tecnologie per l Innovazione Laboratorio per il corso Scienza dei Materiali II a.a. 2009-2010 Docente: E-mail: Euro Sampaolesi eurosampaoesi@alice.it
1.Visione_01 Ottica geometrica. Prof. Carlo Capelli Fisiologia Corso di Laurea in Scienze delle Attività Motorie e Sportive Università di Verona
 1.Visione_01 Ottica geometrica Prof. Carlo Capelli Fisiologia Corso di Laurea in Scienze delle Attività Motorie e Sportive Università di Verona Obiettivi Principi di refrazione delle lenti, indice di refrazione
1.Visione_01 Ottica geometrica Prof. Carlo Capelli Fisiologia Corso di Laurea in Scienze delle Attività Motorie e Sportive Università di Verona Obiettivi Principi di refrazione delle lenti, indice di refrazione
28/05/2009. La luce e le sue illusioni ottiche
 La luce e le sue illusioni ottiche Cosa si intende per raggio luminoso? Immagina di osservare ad una distanza abbastanza elevata una sorgente di luce... il fronte d onda potrà esser approssimato ad un
La luce e le sue illusioni ottiche Cosa si intende per raggio luminoso? Immagina di osservare ad una distanza abbastanza elevata una sorgente di luce... il fronte d onda potrà esser approssimato ad un
Lo spessimetro ( a cura di Elena Pizzinini)
 Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Università degli studi di Messina facoltà di Scienze mm ff nn. Progetto Lauree Scientifiche (FISICA) Prisma ottico
 Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
MANUALE DI OTTICA. per il secondo biennio dell'indirizzo di ottica (professionale) (Ottica geometrica) a cura dei docenti dell'iis G.
 - C. - MANUALE DI OTTICA per il secondo biennio dell'indirizzo di ottica (professionale) (Ottica geometrica) a cura dei docenti dell'iis G.Galilei - Milano Luglio 0 - C. - INTRODUZIONE Lo studio dell'ottica
- C. - MANUALE DI OTTICA per il secondo biennio dell'indirizzo di ottica (professionale) (Ottica geometrica) a cura dei docenti dell'iis G.Galilei - Milano Luglio 0 - C. - INTRODUZIONE Lo studio dell'ottica
Inserimento di distanze e di angoli nella carta di Gauss
 Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Definizione di lente. Tipi di lenti
 LENTI Sommario Definizione di lente... 2 Tipi di lenti... 2 Punti e piani principali... 5 Punti e piani nodali... 10 Terminologia... 12 Focale, distanze coniugate ed ingrandimento... 19 Immagine generata
LENTI Sommario Definizione di lente... 2 Tipi di lenti... 2 Punti e piani principali... 5 Punti e piani nodali... 10 Terminologia... 12 Focale, distanze coniugate ed ingrandimento... 19 Immagine generata
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Prof. Silvio Reato Valcavasia Ricerche. Il piano cartesiano
 Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
PERCORSO DIDATTICO DI OTTICA GEOMETRICA
 PERCORSO DIDATTICO DI OTTICA GEOMETRICA Tipo di scuola e classe: Liceo Scientifico, classe II Nodi concettuali: riflessione della luce; rifrazione della luce, riflessione totale, rifrazione attraverso
PERCORSO DIDATTICO DI OTTICA GEOMETRICA Tipo di scuola e classe: Liceo Scientifico, classe II Nodi concettuali: riflessione della luce; rifrazione della luce, riflessione totale, rifrazione attraverso
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
 Esperimento 1: Dispersione della luce Materiali e strumenti: Occhiali speciali, luce Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
Esperimento 1: Dispersione della luce Materiali e strumenti: Occhiali speciali, luce Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
1 Introduzione 1. Ottica Geometrica
 1 Introduzione 1 1 Introduzione Ottica Geometrica 1.1 Estratto Lo scopo di questa esperienza è quello di apprendere come la luce interagisce con elementi ottici quali le lenti, e come, in sequito alla
1 Introduzione 1 1 Introduzione Ottica Geometrica 1.1 Estratto Lo scopo di questa esperienza è quello di apprendere come la luce interagisce con elementi ottici quali le lenti, e come, in sequito alla
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Laboratorio di Ottica, Spettroscopia, Astrofisica
 Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Energia potenziale elettrica e potenziale. In queste pagine R indicherà una regione in cui è presente un campo elettrostatico.
 Energia potenziale elettrica e potenziale 0. Premessa In queste pagine R indicherà una regione in cui è presente un campo elettrostatico. 1. La forza elettrostatica è conservativa Una o più cariche ferme
Energia potenziale elettrica e potenziale 0. Premessa In queste pagine R indicherà una regione in cui è presente un campo elettrostatico. 1. La forza elettrostatica è conservativa Una o più cariche ferme
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Parte Seconda. Geometria
 Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : = y
 Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Specchio parabolico: MIRASCOPE. a cura di Pietro Pozzoli
 Specchio parabolico: MIRASCOPE Proprietà coinvolte: Rifrazione dei raggi partenti dal fuoco lungo rette parallele all asse Focalizzazione dei raggi paralleli all asse sul fuoco PUNTO DI VISTA FISICO: Quali
Specchio parabolico: MIRASCOPE Proprietà coinvolte: Rifrazione dei raggi partenti dal fuoco lungo rette parallele all asse Focalizzazione dei raggi paralleli all asse sul fuoco PUNTO DI VISTA FISICO: Quali
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
OTTICA. Ottica geometrica. Riflessione e rifrazione
 Ottica geometrica OTTICA Sappiamo che la luce è un onda elettromagnetica. Essa perciò può non propagarsi in linea retta, analogamente alle altre onde (p. es. quelle sonore). Però, come avviene per tutte
Ottica geometrica OTTICA Sappiamo che la luce è un onda elettromagnetica. Essa perciò può non propagarsi in linea retta, analogamente alle altre onde (p. es. quelle sonore). Però, come avviene per tutte
Il riduttore di focale utilizzato è il riduttore-correttore Celestron f/ 6.3.
 LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi: 1) f(x,y) = y2 x 2 + y 2.
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
LIVELLO STUDENT S1. S2. S3. S4. S5. S6.
 LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
Costruirsi un cannocchiale galileiano
 Costruirsi un cannocchiale galileiano I. INFORMAZIONI PRELIMINARI - IL PRINCIPIO OTTICO Un cannocchiale galileiano impiega due sole lenti. La lente obbiettiva è convergente (piano-convessa), la lente oculare
Costruirsi un cannocchiale galileiano I. INFORMAZIONI PRELIMINARI - IL PRINCIPIO OTTICO Un cannocchiale galileiano impiega due sole lenti. La lente obbiettiva è convergente (piano-convessa), la lente oculare
FUNZIONE. Si scrive: A B f: A B x y=f(x) (si legge: f funzione da A in B) x f y= f(x)
 1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Basi di ottica. n 1. a b. n 2. figura 1 - riflessione. figura 2 - rifrazione. tabella 1. rifrazione n. vuoto 1
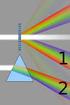 Basi di ottica L'ottica geometrica: riflessione e rifrazione Il comportamento dei raggi di luce viene descritto dalla cosiddetta ottica geometrica. L'ottica geometrica è solo una approssimazione del comportamento
Basi di ottica L'ottica geometrica: riflessione e rifrazione Il comportamento dei raggi di luce viene descritto dalla cosiddetta ottica geometrica. L'ottica geometrica è solo una approssimazione del comportamento
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
IGiochidiArchimede-SoluzioniBiennio 22 novembre 2006
 PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
La misura degli angoli
 La misura degli angoli In questa dispensa introduciamo la misura degli angoli, sia in gradi che in radianti, e le formule di conversione. Per quanto riguarda l introduzione del radiante, per facilitarne
La misura degli angoli In questa dispensa introduciamo la misura degli angoli, sia in gradi che in radianti, e le formule di conversione. Per quanto riguarda l introduzione del radiante, per facilitarne
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Laboratorio di Ottica, Spettroscopia, Astrofisica
 Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Fisica II - CdL Chimica. La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche
 La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
CONI, CILINDRI, SUPERFICI DI ROTAZIONE
 CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
Ottica fisiologica (2): sistemi ottici
 Ottica fisiologica (2): sistemi ottici Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/pmp_2014.html
Ottica fisiologica (2): sistemi ottici Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/pmp_2014.html
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
APPUNTI DI MATEMATICA GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1)
 GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
Corso di Laurea in Scienze della Formazione Primaria Università di Genova MATEMATICA Il
 Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
- Formazione delle immagini per riflessione: specchio sferico
 Ottica geometrica: - condizione di validità: o occorre conrontare la lunghezza d onda λ della luce e le dimensioni degli oggetti su cui la luce incide. Se λ è MINORE, valgono le leggi dell ottica geometrica.
Ottica geometrica: - condizione di validità: o occorre conrontare la lunghezza d onda λ della luce e le dimensioni degli oggetti su cui la luce incide. Se λ è MINORE, valgono le leggi dell ottica geometrica.
SPC e distribuzione normale con Access
 SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Corso di Laurea in Ottica e Optometria Laboratorio di Ottica Geometrica
 Corso di Laurea in Ottica e Optometria Laboratorio di Ottica Geometrica Richiami teorici Equazione della lente sottile in approssimazione parassiale: p + q = () f dove: p = distanza oggetto-lente q = distanza
Corso di Laurea in Ottica e Optometria Laboratorio di Ottica Geometrica Richiami teorici Equazione della lente sottile in approssimazione parassiale: p + q = () f dove: p = distanza oggetto-lente q = distanza
4. Proiezioni del piano e dello spazio
 4. Proiezioni del piano e dello spazio La visualizzazione di oggetti tridimensionali richiede di ottenere una vista piana dell'oggetto. Questo avviene mediante una sequenza di operazioni. Innanzitutto,
4. Proiezioni del piano e dello spazio La visualizzazione di oggetti tridimensionali richiede di ottenere una vista piana dell'oggetto. Questo avviene mediante una sequenza di operazioni. Innanzitutto,
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
Analisi Matematica di circuiti elettrici
 Analisi Matematica di circuiti elettrici Eserciziario A cura del Prof. Marco Chirizzi 2011/2012 Cap.5 Numeri complessi 5.1 Definizione di numero complesso Si definisce numero complesso un numero scritto
Analisi Matematica di circuiti elettrici Eserciziario A cura del Prof. Marco Chirizzi 2011/2012 Cap.5 Numeri complessi 5.1 Definizione di numero complesso Si definisce numero complesso un numero scritto
IL MICROSCOPIO OTTICO. DOWNLOAD Il pdf di questa lezione (microscopio2.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/fistrum/ 09/03/2011
 IL MICROSCOPIO OTTICO DOWNLOAD Il pdf di questa lezione (microscopio2.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/fistrum/ 09/03/2011 Lo scopo di questi appunti è la descrizione dei principi
IL MICROSCOPIO OTTICO DOWNLOAD Il pdf di questa lezione (microscopio2.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/fistrum/ 09/03/2011 Lo scopo di questi appunti è la descrizione dei principi
L elemento fondamentale è l obiettivo, ovvero la lente o lo specchio che forniscono l immagine dell oggetto.
 Il telescopio, è lo strumento ottico impiegato in astronomia, per osservare e studiare gli oggetti celesti. È generalmente separato in due componenti principali: una parte ottica (costituita dal tubo delle
Il telescopio, è lo strumento ottico impiegato in astronomia, per osservare e studiare gli oggetti celesti. È generalmente separato in due componenti principali: una parte ottica (costituita dal tubo delle
Esercizi svolti sui numeri complessi
 Francesco Daddi - ottobre 009 Esercizio 1 Risolvere l equazione z 1 + i = 1. Soluzione. Moltiplichiamo entrambi i membri per 1 + i in definitiva la soluzione è z 1 + i 1 + i = 1 1 + i z = 1 1 i. : z =
Francesco Daddi - ottobre 009 Esercizio 1 Risolvere l equazione z 1 + i = 1. Soluzione. Moltiplichiamo entrambi i membri per 1 + i in definitiva la soluzione è z 1 + i 1 + i = 1 1 + i z = 1 1 i. : z =
3.1 CAPITOLO 3 FORMAZIONE DELLE IMMAGINI
 3.1 CAPITOLO 3 FORMAZIONE DELLE IMMAGINI Il processo di formazione di una immagine da parte di un sistema ottico è facilmente descrivibile in termini di raggi. In figura la scatola rappresenta un generico
3.1 CAPITOLO 3 FORMAZIONE DELLE IMMAGINI Il processo di formazione di una immagine da parte di un sistema ottico è facilmente descrivibile in termini di raggi. In figura la scatola rappresenta un generico
4 La Polarizzazione della Luce
 4 La Polarizzazione della Luce Per comprendere il fenomeno della polarizzazione è necessario tenere conto del fatto che il campo elettromagnetico, la cui variazione nel tempo e nello spazio provoca le
4 La Polarizzazione della Luce Per comprendere il fenomeno della polarizzazione è necessario tenere conto del fatto che il campo elettromagnetico, la cui variazione nel tempo e nello spazio provoca le
Esercizi di Macroeconomia per il corso di Economia Politica
 Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
1 Definizione: lunghezza di una curva.
 Abstract Qui viene affrontato lo studio delle curve nel piano e nello spazio, con particolare interesse verso due invarianti: la curvatura e la torsione Il primo ci dice quanto la curva si allontana dall
Abstract Qui viene affrontato lo studio delle curve nel piano e nello spazio, con particolare interesse verso due invarianti: la curvatura e la torsione Il primo ci dice quanto la curva si allontana dall
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma.
 3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2004
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
PRINCIPIO ESPLICATIVO DEL FUNZIONAMENTO DEI CILINDRI CROCIATI Prof. Luciano Pietropaolo
 PRINCIPIO ESPLICATIVO DEL FUNZIONAMENTO DEI CILINDRI CROCIATI Prof. Luciano Pietropaolo Viene esposto il principio su cui si basa il funzionamento dei cilindri crociati, per l analisi dell astigmatismo
PRINCIPIO ESPLICATIVO DEL FUNZIONAMENTO DEI CILINDRI CROCIATI Prof. Luciano Pietropaolo Viene esposto il principio su cui si basa il funzionamento dei cilindri crociati, per l analisi dell astigmatismo
Formule trigonometriche
 Formule trigonometriche C. Enrico F. Bonaldi 1 Formule trigonometriche In trigonometria esistono delle formule fondamentali che permettono di calcolare le funzioni goniometriche della somma di due angoli
Formule trigonometriche C. Enrico F. Bonaldi 1 Formule trigonometriche In trigonometria esistono delle formule fondamentali che permettono di calcolare le funzioni goniometriche della somma di due angoli
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
CURVE DI LIVELLO. Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello.
 CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Teoria delle code. Sistemi stazionari: M/M/1 M/M/1/K M/M/S
 Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
SEZIONI. Introduzione
 SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
