Matematica generale CTF
|
|
|
- Nicoletta Bossi
- 9 anni fa
- Просмотров:
Транскрипт
1 Successioni numeriche 19 agosto 2015
2 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni
3 Definizione di successione Monotonìa e limitatezza Successioni numeriche Le successioni sono delle funzioni a valori reali (il codominio é l insieme dei numeri reali, R) il cui dominio é l insieme dei numeri naturali, N. Ogni successione associa quindi uno o piú numeri naturali ad un valore reale.
4 Definizione di successione Monotonìa e limitatezza Successioni numeriche Le successioni sono delle funzioni a valori reali (il codominio é l insieme dei numeri reali, R) il cui dominio é l insieme dei numeri naturali, N. Ogni successione associa quindi uno o piú numeri naturali ad un valore reale. Solitamente queste funzioni si descrivono con la seguente notazione: (a n ) n N in cui il pedice n si riferisce al numero naturale a cui a n è associato. (a n ) n N : N R n a n
5 Definizione di successione Monotonìa e limitatezza Successioni numeriche Rappresentazione analitica Quando è possibile determinare l espressione che permette di determinare l n-esimo termine della successione. In questo caso ogni termine è determinato dal valore della funzione f nell n-esimo punto; possiamo scrivere a n = f (n).
6 Definizione di successione Monotonìa e limitatezza Successioni numeriche Rappresentazione analitica Quando è possibile determinare l espressione che permette di determinare l n-esimo termine della successione. In questo caso ogni termine è determinato dal valore della funzione f nell n-esimo punto; possiamo scrivere a n = f (n). Ad esempio a n = 1 n 2 + 1
7 Definizione di successione Monotonìa e limitatezza Successioni numeriche Elencazione Vengono rappresentati solo le immagini della successione in sequenza (solitamente i termini sono distanziati tra loro senza alcuna punteggiatura): a 0 a 1 a 3 a 4...
8 Definizione di successione Monotonìa e limitatezza Successioni numeriche Elencazione Vengono rappresentati solo le immagini della successione in sequenza (solitamente i termini sono distanziati tra loro senza alcuna punteggiatura): a 0 a 1 a 3 a 4... { Ad esempio a n = 1, 1 5, 1 10, 1 17, 1 } 26
9 Definizione di successione Monotonìa e limitatezza Successioni numeriche Per ricorrenza Una successione si può definire per ricorrenza se, una volta imposte condizioni iniziali, ogni termine si può calcolare come funzione di uno o alcuni suoi termini precedenti. Ad esempio, si può definire una successione imponendo la condizione iniziale sul primo termine ed esprimendo la funzione che permette di trovare il{ valore dell n + 1 termine sapendo il valore dell n termine. a0 = 1; (a n ) n N = a n+1 = f (a n ).
10 Definizione di successione Monotonìa e limitatezza Successioni numeriche Per ricorrenza Una successione si può definire per ricorrenza se, una volta imposte condizioni iniziali, ogni termine si può calcolare come funzione di uno o alcuni suoi termini precedenti. Ad esempio, si può definire una successione imponendo la condizione iniziale sul primo termine ed esprimendo la funzione che permette di trovare il valore dell n + 1 termine sapendo il valore dell n termine. (a n ) n N = { a0 = 1; a n+1 = f (a n ). Ad esempio la successione di Fibonacci è una successione di numeri interi positivi in cui ciascun termine, a partire dal terzo, si ottiene come somma dei due termini precedenti: a 1 = 1 a 2 = 1 a n = a n 1 + a n 2
11 Definizione di successione Monotonìa e limitatezza Successioni numeriche Per ricorrenza Un altro esempio è l algoritmo di Erone: questo metodo è un procedimento di calcolo che permette di calcolare la radice quadrata di un numero utilizzando solo le operazioni fondamentali dell aritmetica. Esso si basa su considerazioni geometriche e su il metodo delle approssimazioni successive e proprio per questo, ogni termine lo riusciamo ad esprimere solo conoscendone il precedente ed ancora nessuno ha scoperto l espressione del termine n-esimo mediante rappresentazione analitica. La sua rappresentazione per ricorrenza è la seguente (nella quale il numero di cui cerchiamo la radice quadrata lo mettiamo al posto del parametro k): { a1 = 2 a n = 1 2 ( a n 1 + ) k a n 1
12 Definizione di successione Monotonìa e limitatezza Successioni monotòne Una successione si definisce: crescente se a n+1 a n n N decrescente se a n+1 a n n N strettamente crescente se a n+1 > a n n N strettamente decrescente se a n+1 < a n n N
13 Definizione di successione Monotonìa e limitatezza Successioni limitate Il grafico di una successione è rappresentato da un insieme discreto di punti. Come abbiamo visto per le altre funzioni, anche le successioni possono essere: limitate inferiormente se limitate superiormente se inf a n = m > sup a n = M < + limitate se sono limitate sia inferiormente che superiormente.
14 Successioni convergenti La cosa più interessante per una successione è stabilire cosa succede quando n diventa molto grande, diciamo per n che tende all infinito. Questo è il primo concetto di limite per successione. Distinguiamo questi casi:
15 Successioni convergenti La cosa più interessante per una successione è stabilire cosa succede quando n diventa molto grande, diciamo per n che tende all infinito. Questo è il primo concetto di limite per successione. Distinguiamo questi casi: Una successione a n si dice convergente se per n si avvicina sempre di più ad un valore l R. Si scrive: che, in termini formali, significa: lim a n = l n ε > 0 n N : n > n, a n l < ε.
16 Successioni convergenti La cosa più interessante per una successione è stabilire cosa succede quando n diventa molto grande, diciamo per n che tende all infinito. Questo è il primo concetto di limite per successione. Distinguiamo questi casi: Una successione a n si dice convergente se per n si avvicina sempre di più ad un valore l R. Si scrive: che, in termini formali, significa: lim a n = l n ε > 0 n N : n > n, a n l < ε. Se una successione è convergente allora, comunque io scelga un intorno di l sull asse delle ordinate, da un certo valore n in poi la successione a n rimane sempre limitata a quell intorno.
17 Successioni divergenti La stessa cosa si può definire per una successione divergente positivamente o negativamente:
18 Successioni divergenti La stessa cosa si può definire per una successione divergente positivamente o negativamente: Una successione a n si dice divergente positivamente se per n la successione va a + ; cioè essa non è limitata superiormente. Analogamente si può definire una successione divergente negativamente. lim a n = + n che, in termini formali, significa: M > 0 n N : n > n, a n > M
19 Successioni divergenti La stessa cosa si può definire per una successione divergente positivamente o negativamente: Una successione a n si dice divergente positivamente se per n la successione va a + ; cioè essa non è limitata superiormente. Analogamente si può definire una successione divergente negativamente. lim a n = + n che, in termini formali, significa: M > 0 n N : n > n, a n > M Se una successione è divergente positivamente allora, comunque io scelga un un numero M R sull asse delle ordinate grande a piacere, da un certo valore (n) in poi la successione a n sarà sempre più grande di M per ogni n n.
20 Successioni irregolari Una successione nè convergente nè divergente si dice irregolare.
21 Successioni irregolari Una successione nè convergente nè divergente si dice irregolare. Ad esempio la successione a n = 1 n è convergente al valore 0, la successione a n = n è divergente a + e la successione a n = ( 1) n è oscillante tra 1 e 1 e quindi è irregolare.
22 Permanenza del segno Sia a n una successione convergente a un limite l > 0 allora n : n > n, a n > 0
23 Permanenza del segno Sia a n una successione convergente a un limite l > 0 allora n : n > n, a n > 0 Il teorema della permanenza del segno ci dice che se una successione converge a un valore positivo l allora, da un certo valore in poi, n, la successione sarà sempre positiva. Analogamente, se l < 0, da un certo punto in poi la successione sarà sempre negativa.
24 Permanenza del segno Sia a n una successione convergente a un limite l > 0 allora n : n > n, a n > 0 Il teorema della permanenza del segno ci dice che se una successione converge a un valore positivo l allora, da un certo valore in poi, n, la successione sarà sempre positiva. Analogamente, se l < 0, da un certo punto in poi la successione sarà sempre negativa. Sia a n : N R una successione numerica. Se a n è monotona crescente e superiormente limitata è sempre convergente. Se a n è monotona crescente e illimitata è sempre divergente a +. Se a n è monotona decrescente e inferiormente limitata è sempre convergente. Se a n è monotona decrescente e illimitata è sempre divergente a +.
25 Limite dell algoritmo di Erone Per dimostrare che una successione ammette limite occorre dimostrare che è monotona e limitata; questo non ci permette di stabilire il valore del limite ma solo la sua esistenza. Consideriamo ad esempio l algoritmo di Erone e utilizziamolo per il calcolo ricorsivo di 2. Ricordiamo l algoritmo di Erone
26 Limite dell algoritmo di Erone Per dimostrare che una successione ammette limite occorre dimostrare che è monotona e limitata; questo non ci permette di stabilire il valore del limite ma solo la sua esistenza. Consideriamo ad esempio l algoritmo di Erone e utilizziamolo per il calcolo ricorsivo di 2. Ricordiamo l algoritmo di Erone a 1 = 2 a n = 1 2 ( a n ) a n 1
27 Limite dell algoritmo di Erone Per dimostrare che una successione ammette limite occorre dimostrare che è monotona e limitata; questo non ci permette di stabilire il valore del limite ma solo la sua esistenza. Consideriamo ad esempio l algoritmo di Erone e utilizziamolo per il calcolo ricorsivo di 2. Ricordiamo l algoritmo di Erone a 1 = 2 a n = 1 2 ( a n ) a n 1 Se il limite esistesse, quale sarebbe il suo valore? Se a n l ovviamente anche a n+1 l per n ; quindi facendo il limite ad ambo i membri della formula ricorsiva otteniamo la seguente equazione in l: l = 1 ( l + 2 ) l = 2 2 l
28 Limite dell algoritmo di Erone Rimane però ancora da dimostrare che il limite esiste. Proviamo la sua esistenza dimostrando che la successione è monotòna e limitata. Per prima cosa dimostriamo (con il principio di induzione) che è limitata dal basso, in particolare che a 2 n > 2: a 1 = 2 a 2 1 = 4
29 Limite dell algoritmo di Erone Rimane però ancora da dimostrare che il limite esiste. Proviamo la sua esistenza dimostrando che la successione è monotòna e limitata. Per prima cosa dimostriamo (con il principio di induzione) che è limitata dal basso, in particolare che a 2 n > 2: a 1 = 2 a 2 1 = 4 Ora occorre provare che a 2 n+1 2 > 0 sfruttando l ipotesi induttiva (a2 n > 2): a 2 n+1 2 = ( )) 1 2 (a n + 2an 2 = = (a2 n 2) 2 2 4an 2 > 0 non può essere nullo perché per ipotesi induttiva a 2 n > 2. La successione è quindi limitata dal basso.
30 Limite dell algoritmo di Erone Ora vediamo che la successione è monotòna decrescente, cioè n N, a n+1 < a n : a n a n+1 = a n 1 ) (a n + 2an = > 0 2 La successione è limitata dal basso e monotòna. Quindi il limite esiste e necessariamente è 2.
31 Per dimostrare che una successione è convergente può essere utile sapere che tale successione è sempre compresa tra due successioni convergenti allo stesso limite. Siano a n e b n due successioni tali che lim a n = lim b n = l, allora se n n c n è una terza successione tale che a n < c n < b n per ogni n N, lim c n = l n
32 Per dimostrare che una successione è convergente può essere utile sapere che tale successione è sempre compresa tra due successioni convergenti allo stesso limite. Siano a n e b n due successioni tali che lim a n = lim b n = l, allora se n n c n è una terza successione tale che a n < c n < b n per ogni n N, lim c n = l n Un ragionamento analogo può essere fatto per le successioni divergenti: se a n è una successione divergente a + e c n è una successione tale che c n > a n per ogni n N, allora lim n c n = +
33 La progressione aritmetica è una successione definita per ricorrenza che è possibile definirla anche come una funzione di n N. E definita in modo tale che la differenza tra due termini successivi sia costante;
34 La progressione aritmetica è una successione definita per ricorrenza che è possibile definirla anche come una funzione di n N. E definita in modo tale che la differenza tra due termini successivi sia costante; se a R è il valore iniziale della progressione e d R è quella che si chiama ragione della progressione aritmetica, essa si definisce nel modo seguente: { a1 = a a n = a n 1 + d
35 La progressione aritmetica è una successione definita per ricorrenza che è possibile definirla anche come una funzione di n N. E definita in modo tale che la differenza tra due termini successivi sia costante; se a R è il valore iniziale della progressione e d R è quella che si chiama ragione della progressione aritmetica, essa si definisce nel modo seguente: { a1 = a Possiede una forma analitica: a n = a n 1 + d a 1 = a a 2 = a + d a 3 = (a + d) + d = a + 2d a 4 =(a + 2d) + d = a + 3d a n = a + (n 1)d
36 E chiaramente una successione divergente ma è interessante vedere quanto n vale a n, ovvero la somma dei primi n elementi della successione: k=1 n n n n a n = (a + (n 1)d) = a + d (n 1) k=1 k=1 k=1 k=1
37 E chiaramente una successione divergente ma è interessante vedere quanto n vale a n, ovvero la somma dei primi n elementi della successione: k=1 n a n = k=1 n (a + (n 1)d) = k=1 n a + d k=1 n (n 1) k=1 sfruttando la formula della somma dei primi n numeri naturali, n a + d k=1 n (n 1) = na + d k=1 n(n 1) 2 ( = n a + d n 1 ) = 2 ( ) 2a + (n 1)d n = n 2 2 (a + a + nd) = n 2 (a 1 + a n )
38 Abbiamo così ottenuto: n a n = n 2 (a 1 + a n ) k=1
39 Somma dei dispari Con tale formula possiamo mostrare che la somma dei primi numeri dispari è sempre un quadrato. Infatti, ponendo a = 1 e d = 2 come parametri della progressione aritmetica, otteniamo la sequenza a 1 = 1, a 2 = 3, a 3 = 5, a 4 = 7,... cioè la sequenza di tutti i numeri dispari. Calcoliamo la somma dei primi n termini della progressione (utilizzando la formula vista sopra): n k=1 a k = n 2 (a 1 + a n ) = n (1 + (1 + 2(n 1))) = n2 2
40 Progressione geometrica è una successione definita per ricorrenza in modo tale che il rapporto tra due termini successivi sia costante. Se a R è il valore iniziale della progressione e q R è quella che si chiama ragione della progressione geometrica, essa si definisce nel modo seguente: { a0 = a a n = q a n 1
41 Progressione geometrica è una successione definita per ricorrenza in modo tale che il rapporto tra due termini successivi sia costante. Se a R è il valore iniziale della progressione e q R è quella che si chiama ragione della progressione geometrica, essa si definisce nel modo seguente: { a0 = a a n = q a n 1 Se elenchiamo i primi elementi della progressione ci accorgiamo che essa possiede una forma analitica: a 0 = a a 1 = a q 1 a 2 = (a q) q = a q 2 a 3 = a q 3 a n = a q n
42 Progressione geometrica A differenza delle progressioni aritmetiche, tali successioni non sono sempre divergenti; infatti, indipendentemente dal valore iniziale a, il carattere della progressione dipende strettamente dalla ragione q, si possono presentare diversi casi:
43 Progressione geometrica A differenza delle progressioni aritmetiche, tali successioni non sono sempre divergenti; infatti, indipendentemente dal valore iniziale a, il carattere della progressione dipende strettamente dalla ragione q, si possono presentare diversi casi: se q < 1, allora lim n a n = 0
44 Progressione geometrica A differenza delle progressioni aritmetiche, tali successioni non sono sempre divergenti; infatti, indipendentemente dal valore iniziale a, il carattere della progressione dipende strettamente dalla ragione q, si possono presentare diversi casi: se q < 1, allora lim n a n = 0 se q = 1, allora lim n a n = 1
45 Progressione geometrica A differenza delle progressioni aritmetiche, tali successioni non sono sempre divergenti; infatti, indipendentemente dal valore iniziale a, il carattere della progressione dipende strettamente dalla ragione q, si possono presentare diversi casi: se q < 1, allora lim n a n = 0 se q = 1, allora lim n a n = 1 se q > 1, allora lim n a n = +
46 Progressione geometrica A differenza delle progressioni aritmetiche, tali successioni non sono sempre divergenti; infatti, indipendentemente dal valore iniziale a, il carattere della progressione dipende strettamente dalla ragione q, si possono presentare diversi casi: se q < 1, allora lim n a n = 0 se q = 1, allora lim n a n = 1 se q > 1, allora lim n a n = + se q = 1, la successione oscilla sempre tra 1 e 1.
47 Progressione geometrica A differenza delle progressioni aritmetiche, tali successioni non sono sempre divergenti; infatti, indipendentemente dal valore iniziale a, il carattere della progressione dipende strettamente dalla ragione q, si possono presentare diversi casi: se q < 1, allora lim n a n = 0 se q = 1, allora lim n a n = 1 se q > 1, allora lim n a n = + se q = 1, la successione oscilla sempre tra 1 e 1. se q < 1, la successione oscilla in modo illimitato tra e +.
48 Progressione geometrica A differenza delle progressioni aritmetiche, tali successioni non sono sempre divergenti; infatti, indipendentemente dal valore iniziale a, il carattere della progressione dipende strettamente dalla ragione q, si possono presentare diversi casi: se q < 1, allora lim n a n = 0 se q = 1, allora lim n a n = 1 se q > 1, allora lim n a n = + se q = 1, la successione oscilla sempre tra 1 e 1. se q < 1, la successione oscilla in modo illimitato tra e +.
49 Progressione geometrica Somma dei primi termini E interessante vedere che la somma dei primi n termini della progressione geometrica (poniamo a = 1 per semplicità) vale esattamente: n k=0 q k = 1 qn+1 1 q
50 Progressione geometrica Somma dei primi termini E interessante vedere che la somma dei primi n termini della progressione geometrica (poniamo a = 1 per semplicità) vale esattamente: n k=0 q k = 1 qn+1 1 q Tale formula ci sarà utile quando dovremo stabilire il carattere della cosiddetta serie geometrica. Dimostriamola per induzione:
51 Progressione geometrica Somma dei primi termini Dimostrazione Per n = 0 è facilmente verificata: q 0 = 1 q1 1 q, abbiamo 1 ad entrambi i membri. Supponiamo ora che l ipotesi induttiva sia vera e dimostriamo che n+1 q k = 1 qn+2 1 q k=0
52 Progressione geometrica Somma dei primi termini Dimostrazione Per n = 0 è facilmente verificata: q 0 = 1 q1 1 q, abbiamo 1 ad entrambi i membri. Supponiamo ora che l ipotesi induttiva sia vera e dimostriamo che Partendo dal primo membro n+1 q k = 1 qn+2 1 q k=0 n+1 q k = k=0 n q k + q n+1 k=0
53 Progressione geometrica Somma dei primi termini Dimostrazione per ipotesi induttiva n k=0 q k + q n+1 = 1 qn+1 1 q + q n+1 = 1 qn+2 1 q che è uguale al secondo membro e quindi l affermazione è provata.
54 Siano a n e b n due successioni convergenti, in particolare lim n a n = a R e lim n b n = b R. Valgono le seguenti proprietà (che si possono dedurre facilmente a partire dalla definizione di limite):
55 Siano a n e b n due successioni convergenti, in particolare lim n a n = a R e lim n b n = b R. Valgono le seguenti proprietà (che si possono dedurre facilmente a partire dalla definizione di limite): lim (a n + b n ) = lim (a n) + lim (b n) = a + b n n n
56 Siano a n e b n due successioni convergenti, in particolare lim n a n = a R e lim n b n = b R. Valgono le seguenti proprietà (che si possono dedurre facilmente a partire dalla definizione di limite): lim (a n + b n ) = lim (a n) + lim (b n) = a + b n n n lim (a n b n ) = lim (a n) lim (b n) = a b n n n
57 Siano a n e b n due successioni convergenti, in particolare lim n a n = a R e lim n b n = b R. Valgono le seguenti proprietà (che si possono dedurre facilmente a partire dalla definizione di limite): lim (a n + b n ) = lim (a n) + lim (b n) = a + b n n n lim (a n b n ) = lim (a n) lim (b n) = a b n n n a n se b n 0 per ogni n N, lim = lim n a n = a n b n lim n b n b
58 Siano a n e b n due successioni convergenti, in particolare lim n a n = a R e lim n b n = b R. Valgono le seguenti proprietà (che si possono dedurre facilmente a partire dalla definizione di limite): lim (a n + b n ) = lim (a n) + lim (b n) = a + b n n n lim (a n b n ) = lim (a n) lim (b n) = a b n n n se b n 0 per ogni n N, lim n se c R, lim n c a n = c lim n a n = c a a n b n = lim n a n lim n b n = a b
59 Siano a n e b n due successioni convergenti, in particolare lim n a n = a R e lim n b n = b R. Valgono le seguenti proprietà (che si possono dedurre facilmente a partire dalla definizione di limite): lim (a n + b n ) = lim (a n) + lim (b n) = a + b n n n lim (a n b n ) = lim (a n) lim (b n) = a b n n n a n se b n 0 per ogni n N, lim = lim n a n = a n b n lim n b n b se c R, lim c a n = c lim a n = c a n n se c R, lim n (a n) c = ( lim n a n ) c = a c
60 Siano a n e b n due successioni convergenti, in particolare lim n a n = a R e lim n b n = b R. Valgono le seguenti proprietà (che si possono dedurre facilmente a partire dalla definizione di limite): lim (a n + b n ) = lim (a n) + lim (b n) = a + b n n n lim (a n b n ) = lim (a n) lim (b n) = a b n n n a n se b n 0 per ogni n N, lim = lim n a n = a n b n lim n b n b se c R, lim c a n = c lim a n = c a n n se c R, lim n (a n) c = ( lim n a n ) c = a c Questi calcoli non si possono generalizzare alle successioni divergenti.
61 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Forme indeterminate Il calcolo del limite di una successione può avvenire facilmente attraverso passaggi algebrici che semplificano le forme indeterminate. Le forme indeterminate che si possono verificare nel passaggio al limite sono le seguenti:
62 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Forme indeterminate Il calcolo del limite di una successione può avvenire facilmente attraverso passaggi algebrici che semplificano le forme indeterminate. Le forme indeterminate che si possono verificare nel passaggio al limite sono le seguenti: Tali forme sono indeterminate quando si pensa ad esse come comportamento di una successione cioè quando sono ottenute come limite della successione: la progressione geometrica a n = 1 n è una successione costante sempre uguale a 1, non è una forma indeterminata. Lo sarebbe stata se al posto( di 1 avessimo avuto una successione che tende a 1, come ad esempio ) n n che vedremo nella prossima sezione.
63 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Successioni infinitesime Se si riesce a dimostrare che una successione ammette limite o è divergente, è interessante capire come essa si comporta asintoticamente confrontandola con alcune successioni più elementari come ad esempio la successione costituita dalle potenze di n. Questo si può fare sia per le successioni divergenti, sia per le successioni convergenti. Tra quelle convergenti assumono particolare rilevanza quelle che convergono a 0:
64 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Successioni infinitesime Se si riesce a dimostrare che una successione ammette limite o è divergente, è interessante capire come essa si comporta asintoticamente confrontandola con alcune successioni più elementari come ad esempio la successione costituita dalle potenze di n. Questo si può fare sia per le successioni divergenti, sia per le successioni convergenti. Tra quelle convergenti assumono particolare rilevanza quelle che convergono a 0: Una successione a n si dice infinitesima se lim n a n = 0
65 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Successioni infinitesime Se si riesce a dimostrare che una successione ammette limite o è divergente, è interessante capire come essa si comporta asintoticamente confrontandola con alcune successioni più elementari come ad esempio la successione costituita dalle potenze di n. Questo si può fare sia per le successioni divergenti, sia per le successioni convergenti. Tra quelle convergenti assumono particolare rilevanza quelle che convergono a 0: Una successione a n si dice infinitesima se lim a n = 0 n Esempi: lim n 1 n = 0, quindi a n = 1 n è una successione infinitesima. è una successione infinitesima. Dato α > 0 a n = 1 n α
66 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Comportamento asintotico Il comportamento asintotico di una successione è il comportamento della successione stessa per valori di n molto grande, ad esempio:
67 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Comportamento asintotico Il comportamento asintotico di una successione è il comportamento della successione stessa per valori di n molto grande, ad esempio: 4n 1. La successione a n = 4 + n + 1 2n per n molto grande, cioè si n 1 comporta come un polinomio di primo grado con coefficiente 2 che è divergente e quindi anche a n è divergente.
68 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Comportamento asintotico Il comportamento asintotico di una successione è il comportamento della successione stessa per valori di n molto grande, ad esempio: 4n 1. La successione a n = 4 + n + 1 2n per n molto grande, cioè si n 1 comporta come un polinomio di primo grado con coefficiente 2 che è divergente e quindi anche a n è divergente. n La successione a n = 1 per n molto grande, cioè si n n comporta come una potenza di n di grado 1 2 che è infinitesima e quindi convergente a 0.
69 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Criterio del rapporto per le successioni Se una successione a n è a termini positivi, allora valgono le seguenti affermazioni sul rapporto tra termine a n e il suo successivo:
70 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Criterio del rapporto per le successioni Se una successione a n è a termini positivi, allora valgono le seguenti affermazioni sul rapporto tra termine a n e il suo successivo: a n+1 se lim = l < 1 allora la successione è infinitesima. n a n
71 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Criterio del rapporto per le successioni Se una successione a n è a termini positivi, allora valgono le seguenti affermazioni sul rapporto tra termine a n e il suo successivo: se lim n se lim n a n+1 a n a n+1 a n = l < 1 allora la successione è infinitesima. = l > 1 allora la successione è divergente.
72 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Criterio del rapporto per le successioni Se una successione a n è a termini positivi, allora valgono le seguenti affermazioni sul rapporto tra termine a n e il suo successivo: se lim n se lim n a n+1 a n a n+1 a n = l < 1 allora la successione è infinitesima. = l > 1 allora la successione è divergente. Nel caso il limite sia esattamente 1 non si può stabilire il carattere della successione.
73 Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Criterio del rapporto per le successioni Se una successione a n è a termini positivi, allora valgono le seguenti affermazioni sul rapporto tra termine a n e il suo successivo: se lim n se lim n a n+1 a n a n+1 a n = l < 1 allora la successione è infinitesima. = l > 1 allora la successione è divergente. Nel caso il limite sia esattamente 1 non si può stabilire il carattere della successione. Tale teorema ci permette di stabilire che a n = nα con c > 1 è infinitesima cn cioè una successione esponenziale va più velocemente all infinito di qualsiasi polinomio. Lo stesso si può fare per la successione a n = cn n!
74 Una successione che gioca un ruolo di notevole importanza in matematica è la seguente: ( a n = ) n n
75 Una successione che gioca un ruolo di notevole importanza in matematica è la seguente: ( a n = ) n n Esistono varie dimostrazioni che provano l esistenza del limite di questa successione, una di queste dimostrazioni prova che a n è limitata superiormente dal valore 3 e che è monotona crescente. Tale dimostrazione si può fare per induzione utilizzando la disuguaglianza di Bernoulli e la disuguaglianza tra media geometrica e media aritmetica.
76 Il fatto di sapere che il limite di questa successione esista non ci permette di trovarlo facilmente. L estremo superiore di tale successione infatti non è 3 ma il numero di Nepero e = 2, che viene definito proprio mediante: ( lim ) n := e n n
77 Il limite sopra citato è un limite notevole e si può scrivere in forma più generale nel modo seguente: data una successione a n tale che lim a n = + n allora vale ( lim ) an := e n a n
78 Consideriamo ad esempio la successione b n = quella iniziale nel modo seguente: b n = ( n ) n = [ ( n 2 ( n ) n si può ricondurre a ) n ] 2 2 e 2 per n Utilizzando il limite notevole e il criterio del rapporto per le successioni, si può provare anche che la successione a n = nn n! è divergente e che quindi nn va all infinito molto più velocemente di n!.
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
Limiti e continuità delle funzioni reali a variabile reale
 Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Serie numeriche e serie di potenze
 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Appunti di matematica generale CTF. Alessandro Gambini Federica Ferretti
 Appunti di matematica generale CTF Alessandro Gambini Federica Ferretti 2 dicembre 2015 Indice 1 Concetti di base e insiemi numerici 1 1.1 Insiemi, relazioni e funzioni..................... 1 Simbologia..............................
Appunti di matematica generale CTF Alessandro Gambini Federica Ferretti 2 dicembre 2015 Indice 1 Concetti di base e insiemi numerici 1 1.1 Insiemi, relazioni e funzioni..................... 1 Simbologia..............................
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
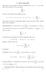 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Appunti di Analisi Matematica 1. Docente: Klaus Engel. Università degli Studi dell Aquila Facoltà di Ingegneria A.A. 2011/12
 Appunti di Analisi Matematica Docente: Klaus Engel Università degli Studi dell Aquila Facoltà di Ingegneria A.A. / http://univaq.it/~engel ( = %7E) (Versione del 4 dicembre ) Note scritte in collaborazione
Appunti di Analisi Matematica Docente: Klaus Engel Università degli Studi dell Aquila Facoltà di Ingegneria A.A. / http://univaq.it/~engel ( = %7E) (Versione del 4 dicembre ) Note scritte in collaborazione
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Anno 3. Funzioni: dominio, codominio e campo di esistenza
 Anno 3 Funzioni: dominio, codominio e campo di esistenza 1 Introduzione In questa lezione parleremo delle funzioni. Ne daremo una definizione e impareremo a studiarne il dominio in relazione alle diverse
Anno 3 Funzioni: dominio, codominio e campo di esistenza 1 Introduzione In questa lezione parleremo delle funzioni. Ne daremo una definizione e impareremo a studiarne il dominio in relazione alle diverse
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
7 - Esercitazione sulle derivate
 7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
I appello - 26 Gennaio 2007
 Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Funzione reale di variabile reale
 Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Equazioni alle differenze finite (cenni).
 AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
11) convenzioni sulla rappresentazione grafica delle soluzioni
 2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
l insieme Y è detto codominio (è l insieme di tutti i valori che la funzione può assumere)
 Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Docente: Anna Valeria Germinario. Università di Bari. A.V.Germinario (Università di Bari) Analisi Matematica ITPS 1 / 22
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
Teoria delle code. Sistemi stazionari: M/M/1 M/M/1/K M/M/S
 Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
LE FUNZIONI E LE LORO PROPRIETÀ
 LE FUNZIONI E LE LORO PROPRIETÀ LE FUNZIONI REALI DI VARIABILE REALE COSA SONO LE FUNZIONI Dati due sottoinsiemi A e B non vuoti di R, una FUNZIONE da A a B è una relazione che associa ad ogni numero reale
LE FUNZIONI E LE LORO PROPRIETÀ LE FUNZIONI REALI DI VARIABILE REALE COSA SONO LE FUNZIONI Dati due sottoinsiemi A e B non vuoti di R, una FUNZIONE da A a B è una relazione che associa ad ogni numero reale
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Funzioni funzione dominio codominio legge argomento variabile indipendente variabile dipendente
 Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
Esercizi di Analisi Matematica I
 Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
ESERCITAZIONI DI ANALISI 1 FOGLIO 1 FOGLIO 2 FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI. Marco Pezzulla
 ESERCITAZIONI DI ANALISI FOGLIO FOGLIO FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI Marco Pezzulla gennaio 05 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) arccos x x + π/3.
ESERCITAZIONI DI ANALISI FOGLIO FOGLIO FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI Marco Pezzulla gennaio 05 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) arccos x x + π/3.
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
1 Alcuni criteri di convergenza per serie a termini non negativi
 Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
la funzione è definita la funzione non è definita Si osservi, infatti, che la radice di un numero negativo non esiste nel campo dei numeri reali.
 1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B. Evento prodotto: Evento in cui si verifica sia A che B ; p(a&b) = p(a) x p(b/a)
 Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
SOLUZIONI D = (-1,+ ).
 SOLUZIONI. Data la funzione f() ( ) ln( ) a) trova il dominio di f b) indica quali sono gli intervalli in cui f() risulta positiva e quelli in cui risulta negativa c) determina le eventuali intersezioni
SOLUZIONI. Data la funzione f() ( ) ln( ) a) trova il dominio di f b) indica quali sono gli intervalli in cui f() risulta positiva e quelli in cui risulta negativa c) determina le eventuali intersezioni
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Applicazioni del calcolo differenziale allo studio delle funzioni
 Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Le equazioni. Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete.
 Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
G3. Asintoti e continuità
 G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
LEZIONE 7. Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2. 2, x3 +2x +3.
 7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
Le funzioni elementari. La struttura di R. Sottrazione e divisione
 Le funzioni elementari La struttura di R La struttura di R è definita dalle operazioni Addizione e moltiplicazione. Proprietà: Commutativa Associativa Distributiva dell addizione rispetto alla moltiplicazione
Le funzioni elementari La struttura di R La struttura di R è definita dalle operazioni Addizione e moltiplicazione. Proprietà: Commutativa Associativa Distributiva dell addizione rispetto alla moltiplicazione
Laboratorio teorico-pratico per la preparazione alle gare di matematica
 Laboratorio teorico-pratico per la preparazione alle gare di matematica Ercole Suppa Liceo Scientifico A. Einstein, Teramo e-mail: [email protected] Teramo, 3 dicembre 2014 USR Abruzzo - PLS 2014-2015,
Laboratorio teorico-pratico per la preparazione alle gare di matematica Ercole Suppa Liceo Scientifico A. Einstein, Teramo e-mail: [email protected] Teramo, 3 dicembre 2014 USR Abruzzo - PLS 2014-2015,
Premessa. Esercitazione. Calcolo del reddito nel Conto del reddito. Calcolo del reddito nel Conto del capitale e nel Conto del reddito
 Sul calcolo del reddito di fine periodo: riflessioni di base 1 INDICE: Premessa Esercitazione Calcolo del reddito nel Conto del capitale Calcolo del reddito nel Conto del reddito Calcolo del reddito nel
Sul calcolo del reddito di fine periodo: riflessioni di base 1 INDICE: Premessa Esercitazione Calcolo del reddito nel Conto del capitale Calcolo del reddito nel Conto del reddito Calcolo del reddito nel
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : = y
 Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Elementi di topologia della retta
 Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
FUNZIONE. Si scrive: A B f: A B x y=f(x) (si legge: f funzione da A in B) x f y= f(x)
 1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Matematica generale CTF
 Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
SUCCESSIONI E SERIE NUMERICHE
 Prof Lonzi Marco Dispense per il Corso di ANALISI MATEMATICA SUCCESSIONI E SERIE NUMERICHE AA 2015/16 1 SUCCESSIONI Dicesi Successione a valori reali ogni funzione 0À Ä, avente cioè per dominio l'insieme
Prof Lonzi Marco Dispense per il Corso di ANALISI MATEMATICA SUCCESSIONI E SERIE NUMERICHE AA 2015/16 1 SUCCESSIONI Dicesi Successione a valori reali ogni funzione 0À Ä, avente cioè per dominio l'insieme
Siano f e g due funzioni, allora x D f D g, cioè appartenente all intersezione dei loro domini, possiamo definire
 Operazioni tra funzioni Siano f e g due funzioni, allora D f D g, cioè appartenente all intersezione dei loro domini, possiamo definire f() ± g(), f() g(), f () g() se g() 0 Es. f() = 4, g() = 3 + D f
Operazioni tra funzioni Siano f e g due funzioni, allora D f D g, cioè appartenente all intersezione dei loro domini, possiamo definire f() ± g(), f() g(), f () g() se g() 0 Es. f() = 4, g() = 3 + D f
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Successioni di funzioni reali
 E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
SOMMARIO. 13.1 I radicali pag. 3. 13.2 I radicali aritmetici pag. 5. 13.3 Moltiplicazione e divisione fra radicali aritmetici pag.
 SOMMARIO CAPITOLO : I RADICALI. I radicali pag.. I radicali aritmetici pag.. Moltiplicazione e divisione fra radicali aritmetici pag.. Potenza di un radicale aritmetico pag.. Trasporto di un fattore esterno
SOMMARIO CAPITOLO : I RADICALI. I radicali pag.. I radicali aritmetici pag.. Moltiplicazione e divisione fra radicali aritmetici pag.. Potenza di un radicale aritmetico pag.. Trasporto di un fattore esterno
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
1 Principali funzioni e loro domini
 Principali funzioni e loro domini Tipo di funzione Rappresentazione Dominio Polinomio intero p() = a n + + a n R p() Polinomio fratto q() 6= q() 2n Radici pari p f() f() 2n+ Radici dispari p f() R Moduli
Principali funzioni e loro domini Tipo di funzione Rappresentazione Dominio Polinomio intero p() = a n + + a n R p() Polinomio fratto q() 6= q() 2n Radici pari p f() f() 2n+ Radici dispari p f() R Moduli
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
21. Studio del grafico di una funzione: esercizi
 1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI
 119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
Derivate Limiti e funzioni continue
 Derivate Limiti e funzioni continue Se il valore di una funzione f() si avvicina al valore l quando si avvicina ad 0 diciamo che f() ha come ite l per tendente ad 0. Noi per rappresentare questo fatto
Derivate Limiti e funzioni continue Se il valore di una funzione f() si avvicina al valore l quando si avvicina ad 0 diciamo che f() ha come ite l per tendente ad 0. Noi per rappresentare questo fatto
Marco Tolotti - Corso di Esercitazioni di Matematica 12 Cfu - A.A. 2010/2011 1
 Marco Tolotti - Corso di Esercitazioni di Matematica 1 Cfu - A.A. 010/011 1 Esercitazione 1: 4/09/010 1. Determinare il dominio delle seguenti funzioni: log a) f() = 5 ( 1). b) g() = log 3 (3 6) log 13.
Marco Tolotti - Corso di Esercitazioni di Matematica 1 Cfu - A.A. 010/011 1 Esercitazione 1: 4/09/010 1. Determinare il dominio delle seguenti funzioni: log a) f() = 5 ( 1). b) g() = log 3 (3 6) log 13.
0 < a < 1 a > 1. In entrambi i casi la funzione y = log a (x) si può studiare per punti e constatare che essa presenta i seguenti andamenti y
 INTRODUZIONE Osserviamo, in primo luogo, che le funzioni logaritmiche sono della forma y = log a () con a costante positiva diversa da (il caso a = è banale per cui non sarà oggetto del nostro studio).
INTRODUZIONE Osserviamo, in primo luogo, che le funzioni logaritmiche sono della forma y = log a () con a costante positiva diversa da (il caso a = è banale per cui non sarà oggetto del nostro studio).
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
Il principio di induzione e i numeri naturali.
 Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
